Analysis of the Variability in the Number of Viable Bacteria after Mild Heat Treatment of Food

Abstract

Variability in the numbers of bacteria remaining in saline solution and whole milk following mild heat treatment has been studied with Listeria innocua, Enterococcus faecalis, Salmonella enterica serovar Enteritidis, and Pseudomonas fluorescens. As expected, the most heat-resistant bacterium was E. faecalis, while P. fluorescens was the least heat resistant, and all bacteria showed greater thermal resistance in whole milk than in saline solution. Despite the differences in the inactivation kinetics of these bacteria in different media, the variability in the final number of bacteria was affected neither by the species nor by the heating substrate, but it did depend on the intensity of the heat treatment. The more severe the heat treatment was, the lower the average number of surviving bacteria but the greater the variability. Our results indicated that the inactivation times for the cells within a population are not identically distributed random variables and that, therefore, the population includes subpopulations of cells with different distributions for the heat resistance parameters. A linear relationship between the variability of the log of the final bacterial concentration and the logarithmic reduction in the size of the bacterial population was found.

The safety and quality of many foods, such as minimally processed foods and some ready-to-eat products, are affected by a combination of multiple sublethal stresses due to processing and storage conditions (17, 32). The use of mild preservative processes instead of harsher ones affects the microbiological risk. It is therefore important to identify potential hazards and to perform accurate quantitative microbial risk assessments including probabilistic modeling approaches (17).

It is unlikely that food products are contaminated by one unique bacterial strain or species. In fact, even cells from a pure culture derived from one cell are not necessarily identical (25). Nauta (16) differentiated between uncertainty, which is due to the lack of perfect knowledge about a parameter and which is reducible by further measurements, and variability, which reflects the true variability of a population and is therefore irreducible. He showed the importance of both parameters in quantitative microbial risk assessment models. The estimation of variability usually refers to the variation in the responses of the individual cells within the population, which may be homogeneous or heterogeneous. In a homogeneous population, the heat resistance parameters of the individual cells are identically distributed random variables. Heterogeneous populations include subpopulations of cells with different distributions for the heat resistance parameters. The heterogeneity of the individual cells or spores within a population is the most accepted explanation for the tails of inactivation curves (1, 30) and unexpected increases in the variability of the number of survivors after heat treatments (7, 8, 30).

The microbial concentration in a food product at a given time is affected by the initial inoculum, the length of the lag phase, and the maximum specific growth rate. The distributions of these variables are required to estimate the distribution of the log of the bacterial concentration at a given time during exponential growth (2). Typically for these estimates, the growth rate is assumed to be constant during the exponential growth phase in a nonfluctuating environment. Under this assumption, variations in the growth rate are assumed to be caused by lack of control over the environmental conditions. Recently, distributions of the length of the lag phase among the surviving cells after different stresses have been measured (6, 9, 14, 18). Usually, the distribution of the initial number of cells in a food product is assumed to be independent of previous processing and storage conditions. However, this may be not the case following stress conditions such as heat treatments. The distribution of the initial number of bacteria may depend on the severity of the previous stress. The purpose of the present work was to analyze the distributions of the concentrations of surviving cells after different heat treatments. To do this, heat treatments of various intensities were applied to the gram-positive bacteria Enterococcus faecalis and Listeria innocua, as well as to the gram-negative bacteria Salmonella enterica serovar Enteritidis and Pseudomonas fluorescens.

MATERIALS AND METHODS

Strains and preparation of inocula.

P. fluorescens (CECT 378), S. enterica serovar Enteritidis (CECT 4300; ATCC 13076), L. innocua (CECT 910; NCTC 11288; ATCC 33090), and E. faecalis (LM24) were maintained at −20°C. Strains were subcultured twice successively in sterilized tryptic soy broth (Pronadisa, Spain) and incubated at 37°C for 24 h, with the exception of P. fluorescens, which was incubated at 25°C for 36 h. Cells were harvested by centrifugation at 15,000 × g and 4°C in a Sorvall RC5B refrigerated centrifuge. The final pellets were resuspended in sterile saline solution (0.75% NaCl).

Inactivation experiments.

Prior to the quantification of the variability in heat resistance, inactivation curves were determined by using temperature-controlled water baths (Bunsen S.A.) set at the target temperatures (Table 1). Temperature was monitored using a thermocouple (Testo 720). Duplicate tubes each containing 9.9 ml of sterile saline solution (0.75% NaCl) or sterile whole milk (Asturiana, Asturias, Spain) were immersed in the water baths and allowed to reach the target inactivation temperature before being inoculated with 100 μl of the bacterial suspensions. At each sampling time, aliquots of 100 μl were removed and immediately mixed with 900 μl of cold sterile saline solution in a tube immersed in an ice water bath. Surviving bacteria were counted on tryptic soy agar (Pronadisa, Spain). Plates were incubated at 37°C for 48 h in the cases of L. innocua, E. faecalis, and S. Enteritidis and at 25°C for 72 h in the case of P. fluorescens. The D value (time at constant temperature for a 1-log reduction of the population) and z value (change of temperature necessary to alter the D value by 1 log) were estimated from the inactivation curves for each bacterium in saline solution and whole milk. By using the D and z values, the times required to obtain 1 to 5 logarithmic reductions in the populations of each bacterium in milk and saline solution at the selected temperatures were estimated. Details of the heat treatments are given in Table 2.

TABLE 1.

D and z values^a

Bacterium	Heating medium	Temp (°C)	D value (min)	SE	z value (°C)	SE
E. faecalis	Saline solution	56	22.03	0.28	6.75	0.005
	Saline solution	59	7.81	0.18
	Saline solution	61	4.00	0.38
	Whole milk	57	61.73	0.08	6.85	0.037
	Whole milk	59	34.84	0.11
	Whole milk	61	18.48	0.17
	Whole milk	64	5.91	0.16
L. innocua	Saline solution	50	45.66	0.11	5.16	0.055
	Saline solution	54	6.61	0.2
	Saline solution	57	2.03	0.37
	Whole milk	50	68.03	0.25	5.72	0.002
	Whole milk	54	13.7	0.11
	Whole milk	57	4.07	0.13
P. fluorescens	Saline solution	45	54.9	0.21	4.19	0.011
	Saline solution	47	18.2	0.15
	Saline solution	49	6.1	0.45
	Whole milk	48	13	0.14	4.74	0.014
	Whole milk	49	7.98	0.34
	Whole milk	51	2.89	0.21
	Whole milk	53	1.16	0.53
S. Enteritidis	Saline solution	50	14.1	0.14	5.74	0.092
	Saline solution	54	3.71	0.25
	Saline solution	59	0.39	0.19
	Whole milk	48	34.6	0.15	6.53	0.027
	Whole milk	56	2.2	0.38
	Whole milk	60	0.49	0.45

^aCalculated from experimental data for E. faecalis, L. innocua, P. fluorescens, and S. Enteritidis in saline solution (NaCl, 0.75%) and whole milk.

TABLE 2.

Concentrations of surviving bacteria after several heat treatments in saline solution (NaCl, 0.75%) and whole milk

Bacterium	Heating medium	Temp (°C)	Length of treatment (min)	No. of samples	Mean concn (log10 CFU/ml) of surviving bacteria	SD	Minimum concn (log10 CFU/ml)	Maximum concn (log10 CFU/ml)
E. faecalis	Saline solution	57	0.0	17	6.20	0.08	6.03	6.29
	Saline solution	57	28.0	70	4.13	0.14	4.02	4.90
	Saline solution	57	42.0	66	3.68	0.24	2.91	3.96
	Saline solution	57	56.0	71	2.55	0.29	2.03	3.00
	Whole milk	61	0.0	10	7.17	0.05	7.14	7.23
	Whole milk	61	28.0	74	5.12	0.08	4.98	5.24
	Whole milk	61	42.0	74	4.35	0.21	4.03	4.71
	Whole milk	61	56.0	75	3.81	0.31	3.26	4.09
L. innocua	Saline solution	54	0.0	15	7.90	0.14	7.63	8.21
	Saline solution	54	13.0	99	5.92	0.23	5.27	6.44
	Saline solution	54	19.5	77	4.95	0.32	4.34	5.86
	Saline solution	54	26.0	96	4.06	0.39	3.03	4.88
	Whole milk	54	0.0	10	7.95	0.03	7.91	7.98
	Whole milk	54	28.0	78	5.82	0.13	5.48	6.00
	Whole milk	54	42.0	77	4.77	0.23	3.89	4.99
	Whole milk	54	56.0	75	3.98	0.41	3.39	4.91
P. fluorescens	Saline solution	48	0.0	10	5.69	0.09	5.57	5.84
	Saline solution	48	2.0	71	4.23	0.19	4.03	4.71
	Saline solution	48	4.0	69	3.50	0.29	3.03	3.93
	Saline solution	48	6.0	70	2.42	0.32	2.03	2.97
	Whole milk	48	0.0	16	6.08	0.10	5.96	6.22
	Whole milk	48	3.0	64	5.12	0.08	5.00	5.28
	Whole milk	48	6.0	60	3.72	0.37	3.07	4.37
	Whole milk	48	9.0	59	3.03	0.41	2.21	3.93
S. Enteritidis	Saline solution	53	0.0	10	8.64	0.06	8.56	8.72
	Saline solution	53	5.3	76	5.24	0.11	5.00	5.46
	Saline solution	53	7.0	74	4.33	0.30	3.00	4.99
	Saline solution	53	8.8	74	3.68	0.30	3.08	4.06
	Whole milk	53	0.0	9	7.13	0.07	7.05	7.25
	Whole milk	53	6.6	76	4.48	0.09	4.00	4.56
	Whole milk	53	8.8	74	3.40	0.30	2.84	3.97
	Whole milk	53	12.0	74	2.49	0.31	1.84	2.97

To quantify the variability in the number of survivors after each heat treatment, tubes (between 60 and 100 for each treatment) containing 9.9 ml of sterile saline solution (0.75% NaCl) or sterile whole milk were immersed in water baths and inoculated as described above. When the heat treatment was complete, an aliquot of 100 μl from every tube was removed and mixed with 900 μl of cold sterile saline solution as described above. To minimize error due to the high number of samples processed, the order of the tubes was the same for inoculation and for sampling and the time spent for inoculation was kept as close as possible to the time spent for sampling.

One hundred microliters of each cooled sample, which was further diluted if needed, was plated onto tryptic soy agar (Pronadisa, Spain) by using a spiral platter system (Eddy Jet; IUL Instruments, Barcelona, Spain). Plates were read with an image analyzer (Countermath Flash; IUL Instruments, Barcelona, Spain) after incubation at 37°C for 24 h in the cases of L. innocua, E. faecalis, and S. Enteritidis or at 25°C for 48 h in the case of P. fluorescens. Several (10 to 20) samples from every batch were untreated controls.

Stochastic model for a theoretical population in which the inactivation times for individual cells are independent and identically distributed.

We estimated the distribution of the final numbers of bacteria after heating for a theoretical population in which the inactivation times for individual cells are independent of one another and identically distributed. For the sake of simplicity, we referred to this population as a homogeneous population. The bacterial concentrations were calculated, and the logarithms of the concentrations were estimated, since log units are the most commonly used units in microbiology.

Let the number of surviving bacteria (X) at time t be modeled as a Poisson process.

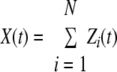(1)

where N is the initial number of bacteria and is a random variable distributed according to Poisson distribution with parameter λ. This assumption is derived from the experimental design and agrees with the initial number of bacteria.

Let us define Z_i(t) as follows:

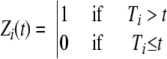(2)

where T_i represents independent and identically distributed random variables expressing the inactivation times for individual cells of the population. For our purpose, it is not necessary to assume any specific distribution for T.

Therefore, the expected value (E) for the number of surviving bacteria at a given time (t) is as follows:

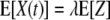(3)

The variance (V) is as follows:

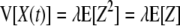(4)

As a result, the values of X(t), the numbers of surviving bacteria at times t, have a Poisson distribution with parameter λ·P(T_i > t), where P(T_i > t) is the probability that the inactivation time of the ith cell is greater than t (10). This is a standard Poisson process in which the variance is equal to the mean. The required transformation to stabilize the variance of X is the square root transformation; however, for the reason mentioned above, we used the logarithmic transformation.

As pointed out by Ratkowsky (21), the expected value and variance for the transformation of a random variable can be approximated using the one-term Taylor series expansion, as follows.

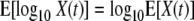(5)

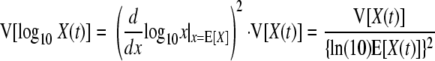(6)

Therefore, for a homogenous population, the relationship between the variability and the expected value of the logarithm of the bacterial concentration after heating at a constant temperature for a certain time, t, can be estimated as follows:

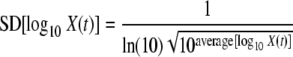(7)

where SD is the standard deviation.

The results obtained for the theoretical homogeneous population were compared with those obtained for the experimentally measured bacterial concentrations after several heat treatments.

Statistical tests.

The variances in the distributions of the concentrations of surviving bacteria were compared using a Bartlett test (31). Data analysis and statistical tests were carried out using the Microsoft Excel add-in Varifit (2).

RESULTS

D and z values were experimentally obtained (Table 1) and used to design the heat treatments in order to obtain several inactivation intensities (Table 2).

Bacteria were more resistant in whole milk than in saline solution. Gram-positive bacteria showed greater D values than gram-negative bacteria. The most heat-resistant species was E. faecalis, while P. fluorescens was the least heat resistant.

The mean and standard error of the final numbers of bacteria were estimated from results for ca. 60 to 100 samples after treatments at different temperatures and for different times (Table 2). The unheated control always showed the smallest standard deviation. The more severe heat treatments gave lower numbers of survivors but greater variability in the final numbers of bacteria. After similar inactivation treatments in saline solution and milk, all strains showed similar degrees of variability in the final concentrations of viable bacteria (Table 2).

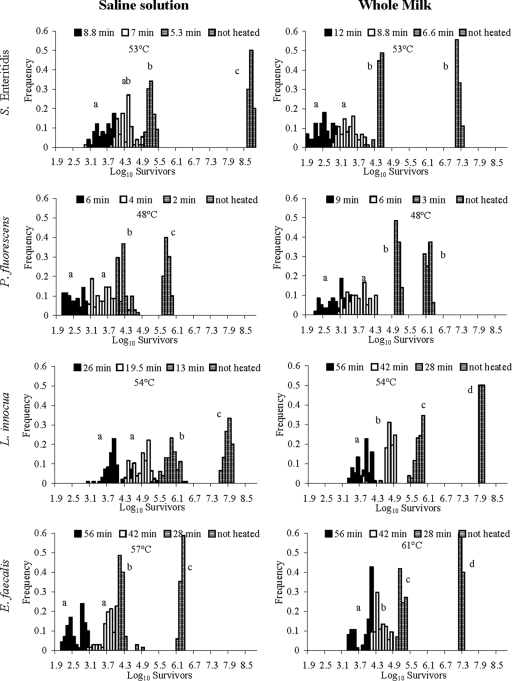
A Bartlett test showed that the variability in the number of bacteria was significantly smaller for the control than for any of the heated samples (Fig. 1). In most of the cases, the variances in the final bacterial concentrations were significantly different for the different heat treatments (Fig. 1). In general, the distributions of the logarithms of the final bacterial concentrations did not show tails and the shapes were nearly symmetric (Fig. 1). In contrast, the distributions of E. faecalis concentrations were bimodal for the most severe heat treatments in both milk and buffer, which may be explained by different thermal-resistance patterns for cells aggregated in chains.

FIG. 1.

Distributions of the logarithm values for the surviving bacterial concentrations in saline solution and whole milk after several heat treatments. Variances labeled with the same letter are not significantly different.

Our results indicate that the distribution of the number of survivors depends on the severity of the treatment. This leads to the idea that the inactivation times for the cells within a population are not identically distributed and that applying heat treatments of different severities allows the survival of different subpopulations. To test this idea, we compared our experimental results with the results for a theoretical population in which the inactivation times for individual cells are independent of one another and identically distributed. As described in Materials and Methods, we referred to this population as a homogeneous population.

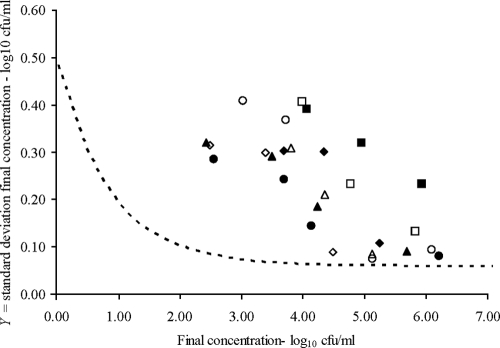
According to the model for the theoretical homogenous population, there is no relation between the variability of the log of the final number of bacteria and the intensity of the heat treatment, as long as the log of the final concentration is greater than 1 (Fig. 2). However, we did not observe this result in our experiments; on the contrary, we observed that the variability of the logarithm of the bacterial concentration after the heat treatment was larger than predicted when a homogeneous population was assumed. Moreover, the observed variability increased as the number of survivors decreased (Fig. 2). Therefore, the inactivation times for the cells within the population were not independent and/or not identically distributed. With our experimental design using saline solution or milk, cell independence can be assumed. Thus, we concluded that the inactivation times for the cells within the population were not identically distributed.

FIG. 2.

Relationship between the logarithm of the final bacterial concentration and its standard deviation after several heat treatments. Results are shown for E. faecalis (circles), L. innocua (squares), P. fluorescens (triangles), and S. Enteritidis (diamonds) in saline solution (filled symbols) and whole milk (empty symbols). The dashed line shows the relationship expected by assuming that the inactivation times of the cells within a population are identically distributed and independent of one another.

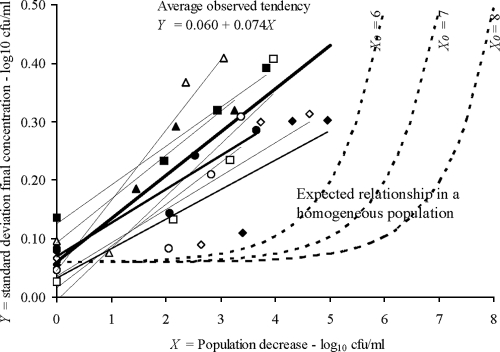
The variability of the final bacterial concentration was expressed as a function of the reduction of the population independently of the initial population (Fig. 3). Here again, the observed variability was larger than the predictions that assumed a homogeneous population, and it increased with the severity of the treatment. The greater the reduction in the population, the greater was the variability of the final concentration. An explicit linear relationship between the variability of the final bacterial concentration and the reduction of the logarithm of the population was estimated from the experimental data (Fig. 3). This relationship was as follows:

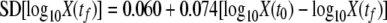(8)

where SD is the standard deviation of the logarithm values for the final concentrations of bacteria [log₁₀X(t_f)], t_f is the final time point, X(t₀) denotes the initial bacterial concentration, and t₀ is time zero.

FIG. 3.

Relationship between the standard deviation of the log of the final bacterial concentration and the decrease in the log of the bacterial concentration after several heat treatments. The symbols are the same as those used in Fig. 2. The continuous lines show the relationships found in our experiments, while the dashed lines show the expected relationships for the log₁₀ of the initial bacterial concentrations (X₀) used in our experiments when the inactivation times for the cells within a population are assumed to be identically distributed and independent of one another.

DISCUSSION

The variability between individual members of a bacterial population can render preservation treatments ineffective, and this variability is not captured in models that assume homogeneous bacterial behavior. Our results showed that the inactivation times for the cells within a population are not identically distributed and that for this reason, as the severity of the heat treatment increases, the variability in inactivation effects increases.

In our work, the microbial inactivation parameters commonly used in food technology, D and z values, were comparable to those obtained by other authors under similar conditions (4, 5, 11, 12, 15, 23) Variability in D values has been analyzed extensively by van Asselt and Zwietering (28), who compared 4,066 D values for pathogens and observed that most factors reported to affect the D value have an influence that is less than the variability of all published D values.

Despite the differences in the inactivation kinetics for the different bacteria and heat treatments, the variability in the final number of bacteria was not affected by the species, medium, or heating temperature, but it depended on the severity of the heat treatment (Fig. 1). Assuming that the inactivation times for the cells within the population are independent and identically distributed, the final number of survivors after a heat treatment has a Poisson distribution. As explained by Ratkowsky (21), the required transformation to stabilize the variance in the number of survivors is the square root transformation, so that the variability and expected value of the square root of the number of survivors are independent of each other. However, given the widespread use in microbiology of logarithmic transformation for bacterial counts, we approximated the relationship between the variance and the expected value of the logarithm of the number of survivors. The variance of the logarithm of the number of survivors is nearly constant if this value is between 1 and 8. If the log number of survivors is smaller than 1, the variance increases abruptly (Fig. 2). Therefore, the relationship in equation 8 is valid only if the final logarithm of the concentration is greater than 1. If it is smaller, the extrapolation may be highly erroneous since the logarithmic function does not stabilize its variance. Regarding other extrapolations, it is worth noting that in this work all inocula were prepared with bacterial cells grown under optimum conditions; other inoculum preparations may change the heat resistance of the cells and therefore the distribution of the final numbers of bacteria.

According to standard models, which assume a homogenous population, the variability of the log of the final number of bacteria is not related to the intensity of the treatment, as long as the log of the final concentration is greater than 1 as explained above. However, we observed that the variability of the log of the number of survivors increased as the severity of the treatment increased and concluded that the inactivation times for the cells within the population were not identically distributed. Heterogeneity, regarding growth parameters, of populations derived from a single cell has already been reported and attributed to differences in the age of the cell structures (25). In the previous work, Stewart et al. (25) observed that after symmetric division, daughter cells inherit a pole or cellular extreme from the original cell and form a new pole. After several divisions, cells with old original poles grow more slowly than those cells with newly formed components. Regarding inactivation parameters, it has been reported that the resistance of the surviving bacteria and spores increases during the inactivation treatment (1, 24), which explains further the heterogeneity of the cells within a population as the result of dynamic survival strategies.

Our finding that the variability of the surviving cells increases with the severity of the heat treatment is consistent with the results of previous studies. A similar increase in variability in L. monocytogenes viability was observed as more intense heating treatments were applied after milk pasteurization (20). Tay et al. (27) observed that the variability in the number of survivors among 10 Listeria strains (9 L. monocytogenes strains and 1 L. innocua strain) was greater after a higher-pressure (500-MPa) treatment than after a lower-pressure (400-MPa) one. In addition, other studies of the effects of heat treatments and other stresses on the variability of cell responses have focused on the lag time. Regarding the coefficient of variation of the lag time, some authors have reported that it is not affected by the intensity of the heat treatment (14) while others have found a general increase after heat treatments and other stresses (6, 11). Therefore, the heterogeneity of the surviving population may also be reflected by greater variability in the repair time needed for the survivors to start dividing.

Zwietering (32) discussed the complexity of assessing safety and microbial quality in minimally processed foods; this complexity is due to wide biological variability (e.g., in the raw material and contaminating organisms involved) and uncertainty about which factors influence product safety or quality. The relationship expressed in equation 8 decreases this uncertainty by quantifying the variability of the inactivation times for the cells within a population. Our results show that this relationship applies to both gram-positive and gram-negative bacteria heated in milk or saline solution at temperatures ranging between 48 and 57°C.

The variability is a fundamental property of microbial populations; its quantitative representation has an important role in many practical applications such as risk assessment (3, 29). Stochastic models for the growth of populations have been developed based on the experimentally measured distributions for the lag times of single cells and spores (13, 14, 18, 19, 26). In those models, the distribution of the initial number of cells was assumed to be independent of the heat treatment or previous stress. Based on the findings of the present study, we can now complete those modeling approaches and risk assessments by including the dependence of the variability in survival rates on the stress applied to the population.