Simulation of Top7-CFr: A transient helix extension guides folding

Abstract

Protein structures often feature β-sheets in which adjacent β-strands have large sequence separation. How the folding process orchestrates the formation and correct arrangement of these strands is not comprehensively understood. Particularly challenging are proteins in which β-strands at the N and C termini are neighbors in a β-sheet. The N-terminal β-strand is synthesized early on, but it can not bind to the C terminus before the chain is fully synthesized. During this time, there is a danger that the β-strand at the N terminus interacts with nearby molecules, leading to potentially harmful aggregates of incompletely folded proteins. Simulations of the C-terminal fragment of Top7 show that this risk of misfolding and aggregation can be avoided by a “caching” mechanism that relies on the “chameleon” behavior of certain segments.

Structure and function of proteins are determined by their amino acid sequence. How proteins find their functional native form is a long-standing question (1–3). Protein synthesis is directional from the N to the C terminus. In proteins with end-toend β-sheets, there is a danger that the N-terminal strand binds to nearby molecules or other parts of the chain, as the strand cannot bind to the C-terminal strand until the molecule is fully synthesized. Misfolding and aggregation may be the consequence. In our simulations, the N terminus of fragment Glu-2–Leu-50 of the 59- residue CFr (Protein Data Bank ID code 2GJH) (4) avoids the risk of misfolding by growing first into a non-native extension of an existing α-helix. Only after the other structural elements have formed and correctly assembled, does the N terminus unfold and attach to the C-terminal β-sheet as its last closing strand.We speculate that such a temporary caching of β-strands is a common mechanism that eases folding and hinders aggregation.

The C-terminal fragment (CFr) (5) of the designed protein Top7 (6) forms a stable homodimer, whose secondary structure remains nearly unchanged up to 98°C and high concentrations of denaturant (4). It is a model for small fast-folding proteins with complex topology and diverse secondary structure elements (see Fig. 1). Such proteins often have long-distance (in sequence) contacts between β-strands. Unlike helix contacts, these depend on the conformation of a large segment between the strands. It is unlikely that these contacts form before the intermediate segment has folded, as this would lead to a large entropic cost, or even interfere with the folding of the connecting segment. For slowfolding proteins, one can conjecture a “backtracking” mechanism (7) where folding succeeds only after breaking of prematurely formed β-contacts. In this study, we explore in silico the behavior of fast-folding proteins, as computational approaches (8,9) can resolve details of folding that are beyond the reach of experiments.

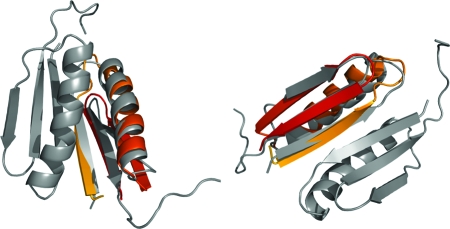
Fig. 1.

Two views of the free-energy minimum structure (in color) superimposed on the experimentally determined structure (gray) for the CFr dimer. The backbone rmsd is 1.7 Å.

Results and Discussion

We find that the CFr monomer folds to a native-like conformation (cf. Fig. 1) with a backbone root mean square deviation (rmsd) of only 1.7 Å. This structure contains all the backbone hydrogen bonds of the experimental native state and represents the global energy minimum in our force field. The free-energy landscape for this protein at 300 K (cf. Fig. 2), shows that the lowest energy structure belongs to a minimum of free energy with rmsd ≈2 Å, implying a unique conformational state. In contrast the low free energy basin around 10 Å contains a large number of dissimilar structures. Competing overlapping low-lying minima with ≈10 kcal/mol higher energies are similar to the native state and contribute to the region in the free-energy landscape in the rmsd range 2.5–5 Å in Fig. 2. These structures have a deformed end of the helix or an off-register attachment of the N-terminal strand with the rest of the β-sheet.

Fig. 2.

Free-energy landscape of CFr monomer at 300 K based on our simulations. The minimum energy state also represents the global free-energy minimum in this case. The free energy was calculated from the observed probabilities of states parametrised by backbone rmsd (Δ_b) and total energy (E) as, $F=-k_{B}T\log \left(\frac{dP}{dEd{\Delta }_b}\right)$). The contour lines are separated by 1k_BT.

Fifteen independent folding events were observed. These events show a systematic pattern for the formation of various native contacts. Snapshots from one trajectory are shown in Fig. 3. Values of different energy terms and other quantities for these snapshots, as well as two animations of the trajectory are given in supporting information (SI) Text and SI Movies 1 and 2. As in the experimental structure, our lowest energy configurations have long-distance β-contacts between strands formed by residues Glu- 2 to Ile-8 and Val-44 to Leu-50. These contacts form late in the folding process. For much of the trajectory, the turn region (Thr- 9–Thr-12) and part of the strand (Glu-2–Ile-8) are incorporated into the neighboring helix, residues Lys-13 through Gly-31 (picture 2 in Fig. 3). This helix forms early and frequently unfolds and refolds. The formation and proper arrangement of the β-hairpin (Tyr-32 through Leu-50) (pictures 3 and 4 in Fig. 3), stabilizes both the helix and the hairpin through hydrophobic contacts. This stabilization does not extend to the non-native appendage formed by residues Glu-2–Thr-12. Unfolding from the helix (picture 5 in Fig. 3), residues 2–8 then attach to the hairpin as the third strand of a β-sheet and complete the native structure (picture 6 in Fig. 3).

Fig. 3.

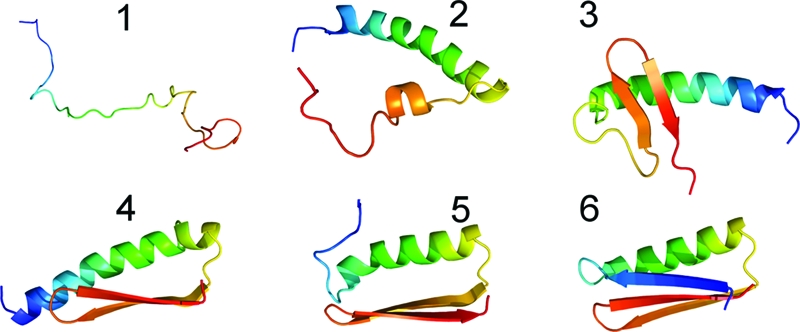
Representative snapshots (1–6) along the folding pathway observed in our simulations. Starting from random initial states (1), the molecule first forms a helix (2) that is often longer than in the native state. The C-terminal hairpin is formed next (3), often away from the helix, before rearranging in a native-like position relative to the helix (4). The helix partially unfolds (5), and the released residues join with the hairpin to complete the native structure (6).

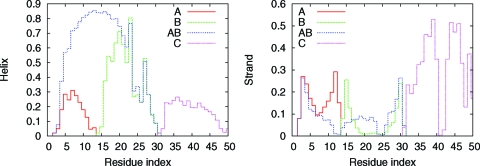
To elucidate our observed caching mechanism in CFr further, we have performed simulations of several isolated segments: (A) Glu-2–Lys-13, (B) Lys-14–Gly-31, (C) Gly-31–Leu-50, and (AB) Glu-2–Gly-31. We find that even in isolation, segments B (helix of CFr) and C (hairpin) have the same folded structure as they have as parts of CFr. The free-energy landscapes of these segments at 300 K (Fig. 4) show dominant minima at small rmsd values compared to the corresponding parts of CFr. This finding indicates that local interactions within these regions predispose them to adopt native-like structures. Segment A remains largely a random coil at all temperatures. The combined segment AB, however, has a tendency to be entirely helical (cf. Fig. 4). In the absence of the β-hairpin C, the residues of segment A extend the helix of segment B. The observed secondary structure propensities, displayed in Fig. 5 as a function of residue index, illustrates this further. The maximum helix propensity of any residue in segment A in isolation is ≈30%, observed near the center of the segment, and only at the lowest temperature. Segment B (Lys-14–Gly-31) maintains a strong helix propensity even as an isolated segment. The helix probability is ≈80% in the center. As the backbone hydrogen bonds break more easily at the ends of a helix than at the center, a reduced helix propensity is observed at both ends of the segment. The helix-forming tendency of A increases dramatically when connected to segment B. In the resulting chain, AB, the helix extends and swallows residues Glu-2–Lys-13. Hence, the template of the helix provided by residues Lys-14–Gly-31 induces a helical state in residues Glu-2–Lys-13, which in isolation shows no clear preference to form secondary structure. Finally for segment C, the free-energy minimum at low heavyatom rmsd (Fig. 4) and the observed strong β–turn–β propensity (Fig. 5) indicate that the C-terminal residues Gly-31–Leu-50 form a β-hairpin even in the absence of the rest of the CFr molecule.

Fig. 4.

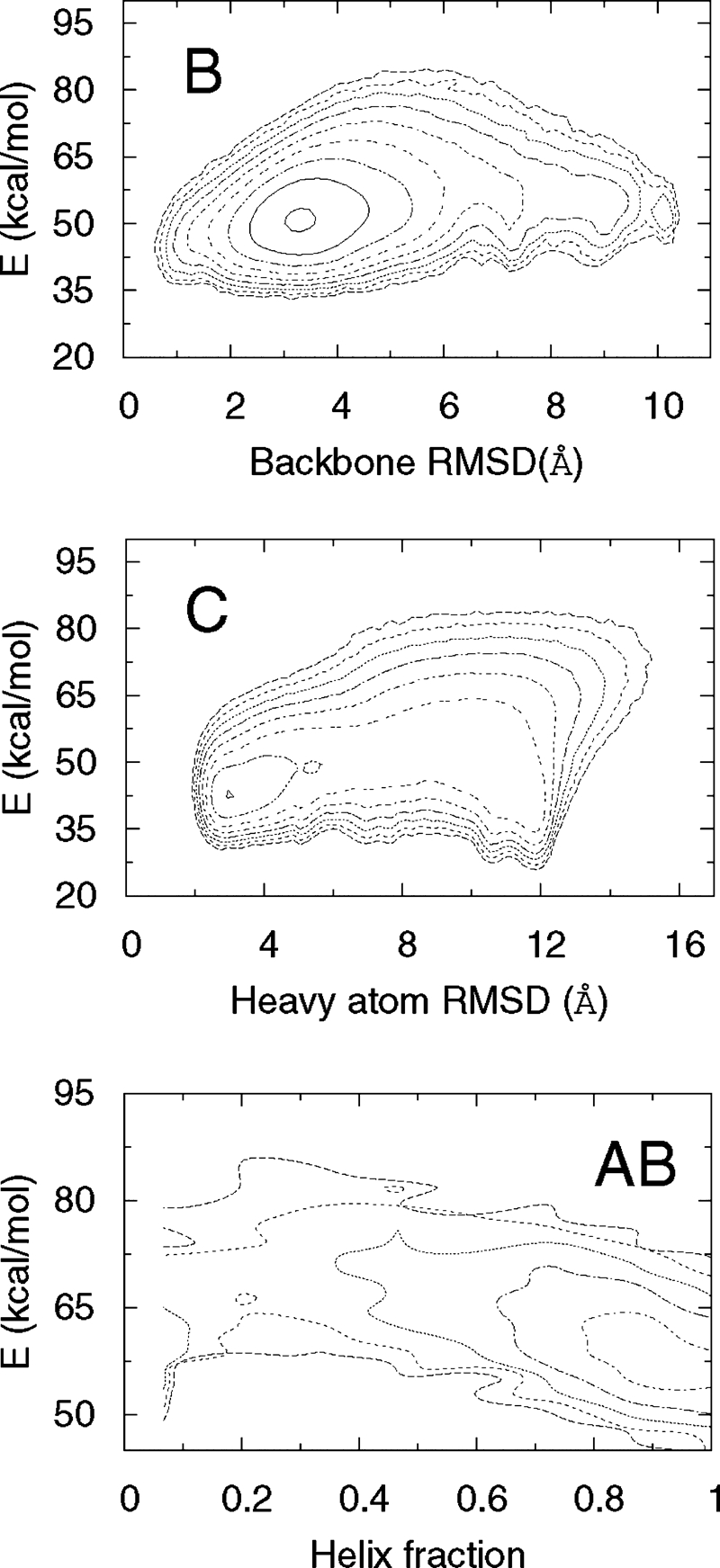
Free-energy landscapes of segments B, C, and AB at 300 K. For C, it is necessary to distinguish between two possible topologies of the β-hairpin, which may have similar values for the backbone rmsd. We therefore use the rmsd over all nonhydrogen atoms as one coordinate for the free-energy map. For AB, because the observed structure involves a significant nonnative component, we use the α-helix content and energy as the two coordinates. Note that for the β-hairpin, the observed global free-energy minimum does not coincide with the global minimum of energy. The contour lines are separated by 1 kbT.

Fig. 5.

Probability of individual residues to be in helix (Left) and strand (Right) states at 274 K. The different curves show the propensities observed in the simulations of four excised segments named A, B, AB, and C, as defined in the text.

The above analysis explains the observed folding (see Fig. 3). In CFr, residues Gly-31–Leu-50 and Glu-2–Gly-31 can fold independently into a hairpin and a helix, respectively. The hairpin sometimes forms away from the helix, and at other times in hydrophobic contact with the helix. In either case, the final result is a state with helix and hairpin in contact. At this point, two secondary structure templates are available to residues Glu-2–Lys-13: the helix formed by residues Lys-14–Gly-31 and the hairpin formed by residues Gly-31–Leu-50. Forming a β-strand is advantageous in terms of hydrophobic contacts with both the hairpin and the helix. Therefore, it is energetically favorable that the long helix partially unfolds and the N-terminal residues join the C-terminal hairpin in a three-stranded β-sheet, completing the native fold. As in the “diffusion collision mechanism” (10), the secondary structure elements form independently and then fuse into the tertiary arrangement. However, in the last part of the pathway certain residues switch from an ordered non-native secondary structure element to the native state with a different secondary structure, like a chameleon changing color in new surroundings.

Replica exchange Monte Carlo simulations, the technique used here, reveal the equilibrium thermodynamic properties of the system, but are not, in general, applicable for the study of kinetic properties. Our results suggest a probable pathway rather than rigorously demonstrating a temporal succession. However, the order of events described above is consistent with the free-energy landscapes of the isolated segments B, AB, and C, as described above, and with the plot of the secondary structure content as a function of the number of native contacts (Fig. 6). As native contacts form, the helix fraction fluctuates about a high value, until the point indicated by an arrow in the plot. At that point, the helix fraction drops rapidly and the strand content rises without much change in the number of native contacts. This indicates the conversion of a nonnative helix into a strand. Afterwards, the secondary structure content changes very slowly with the native contacts, indicating the stabilization of the structure, without formation or dissolution of secondary structure elements.

Fig. 6.

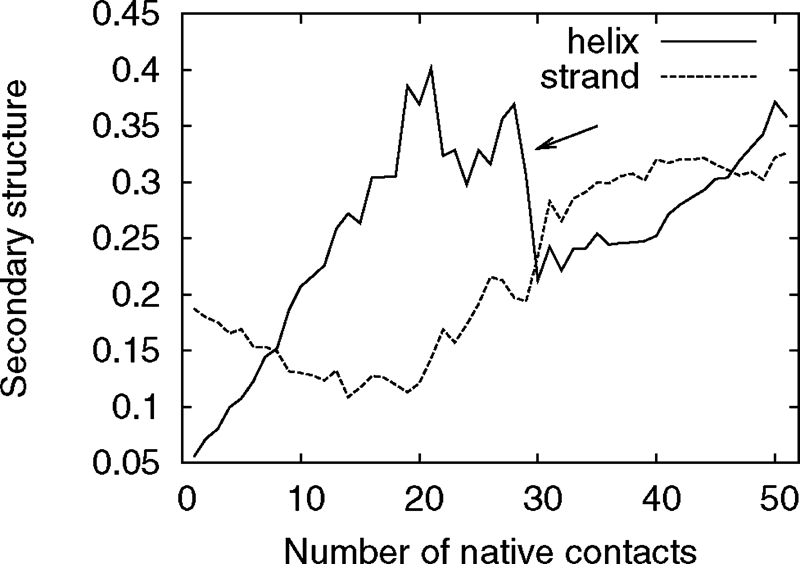
Average deviation of the secondary structure content versus the number of native contacts. There is a sharp decrease in helix fraction (indicated by the arrow) without much change in the nativeness, before the structure stabilizes without further dramatic changes in secondary structure, which indicates the dissolution of non-native helical structures. This statistics for this plot is limited to the observed folding events.

Small peptide segments can adopt a helical or a β-strand secondary structure depending on the solvent or their tertiary structure environment (11,12). Folding pathways involving transitional nonnative helices have been previously reported in the literature in experimental (13–15) as well as computational studies using simplified approaches (16,17). Our results are obtained using first-principle all-atom Monte Carlo simulations. Unlike in the previous computational and experimental studies, the nonnative helix is induced by the presence of a strong helix-former adjacent in sequence. The segment A folds into a helix solely when it finds itself in the neighborhood of a well formed helix B and is not able to interact with a pre-formed β-sheet C. Hence, the temporary caching of this native β-strand as a nonnative helix requires the presence of a strong helix forming region adjacent in sequence.

The CFr-motif occurs, for example, in several superfamilies of the large ferredoxin fold class (SCOP d.58). We postulate that folding through a nonnative intermediate state by the caching mechanism is common in proteins with long-distance β-contacts. Although the idea of nonnative contacts as a way to facilitate folding has been discussed by Plotkin and collaborators (18,19) the folding mechanism in CFr involves also a change of secondary structure. The caching of an N-terminal strand in a helix prevents premature formation of its contacts with other parts of the molecule that have strong β-strand propensities, and also with similar parts in other molecules. Thus, it acts both as a facilitator of folding and an inhibitor of aggregation. This requires that one of the strands exhibits a chameleon behavior (20), i.e., either extends an adjacent helix or forms a β-strand when provided with a template for a β-sheet. We speculate that an analysis of proteins with longdistance β-contacts would reveal such ambiguous propensities. Mutation experiments increasing the sheet propensity of the N terminus of CFr could demonstrate the role of “chameleonicity” for the folding process and therefore validate our hypothesis.

Note that this caching mechanism may lead to quite a different effect for the Top7 molecule, of which CFr is a fragment. The N-terminal strand of CFr lies in the middle of the chain in Top7. Caching it inside a helix likely promotes metastable nonnative β–contacts between the two terminal hairpins, slowing down the folding. This may be one of the reasons for the slow and multiphase folding of Top7 observed in recent experiments (5). Our hypothesis could be tested through mutation experiments focusing on residues in Top7 that correspond to the N terminus of the CFr sequence.

Physics-based all-atom protein simulations are limited to small molecules. For this reason, simple Gō-models (21) are often used to examine the folding dynamics. In Gō-models, the energy function is biased towards forming native contacts and against forming non-native contacts which often leads to smooth, funnel-like energy landscapes. A tacit assumption is that the native contacts can form in an arbitrary order. This assumption is not valid for proteins such as CFr where nonnative interactions facilitate rather than obstruct folding. If the native contacts between the N- and Cterminal strands are formed before the helix, folding to the native state would be sterically impossible. In our model, the occurrence of an intermediate nonnative secondary structure enforces a specific order in the formation of native contacts. Gō-models will need to include such an ordering to have a smooth folding landscape in these cases.

As a monomer, CFr leaves a β-strand with several strongly hydrophobic residues exposed. This suggests an immediate dimerization explaining why only dimers of CFr are observed in experiments. We have tested this conjecture in simulations of two folded monomers that started with random initial positions and orientations. Dimerization occurs quickly though we observe several different binding modes. The energy difference between a state with two isolated monomers and a typical dimer is of the order of 30 kcal/mol, whereas the energy difference between alternative binding modes is within 5 kcal/mol. This energetic degeneracy might be a consequence of our simple force field, which ignores many higher-order effects.

Conclusion

Increased computational power, sophisticated sampling techniques, and improved force fields finally allow a detailed analysis of the folding and interactions of small proteins. Our simulations of CFr reveal a nontrivial folding mechanism that involves caching of its N-terminal β-strand as a nonnative extension of a native α-helix. When the rest of the protein is folded, the N-terminal residues change into a β-strand and join the native β-sheet. We postulate that caching, relying on the chameleon behavior of certain segments, is a common mechanism in the folding of many proteins. It suggests a general function of “chameleonicity” as a means of facilitating folding and inhibiting aggregation of incompletely folded proteins. In this picture, the sequences of naturally occurring proteins are not only selected for their final fold but also to ease folding (5). Hence, in the de novo design of proteins, a sequence should be optimized for both the final fold and a particular folding mechanism.

Methods

This study is based on Monte Carlo simulations with the implicit solvent, all-atom Lund force field (22,23) using the program package ProFASi (Protein Folding and Aggregation Simulator) (24). The force field consists of four terms

where E_exv is a purely repulsive term accounting for excluded volume, E_loc is a local electrostatic term along the backbone, E_hb represents the energy of hydrogen bonds, and Ehp represents hydrophobicity. The force field does not use any information about the native structure. For a detailed description of the energy terms, see ref. 22. Replica exchange (25) is used to enhance sampling of low-energy protein configurations (26). We use 32 replicas with temperatures distributed between 274 and 500 K for the monomer and dimer simulations. The replicas are initialized with random conformations of the molecule and different random number seeds. The Monte Carlo move set for exploring protein conformation space consists of updates of individual degrees of freedom and a semi-local move of the protein backbone (27). The production runs consisted of 1.4 × 1010 elementary Monte Carlo updates per replica for the monomer, and took about 40 days on 32 processors of a Cray-XD1. The dimer simulations with 2 × 109 elementary Monte Carlo updates per replica took ≈12 days.

To determine the propensities of the segments A, B, C, and AB, we used runs with ≈109 elementary Monte Carlo updates. Eight temperatures are used for segments A and B, and 16 temperatures are used for C and AB. The temperatures are distributed as geometric series in the range 274– 374 K. A residue is considered to be in a helix state if its Ramachandran angles satisfy (−90° < φ < −30° and −77° < ψ < −17°) and a strand state if (−150° < φ < −90° and 90° < ψ < 150°). We regard two residues to be in contact if their Cα atoms are within 6 Å from each other.