Abstract
We still know very little about how proteins achieve their native three-dimensional structure in vitro and in the cell. Folding studies as proteins emerge from the mega Dalton-sized ribosome pose special challenges due to the large size and complicated nature of the ribosome-nascent chain complex. This work introduces a combination of three-component analysis of fluorescence depolarization decays (including the presence of two local motions) and in-cone analysis of diffusive local dynamics to investigate the spatial constraints experienced by a protein emerging from the ribosomal tunnel. We focus on E. coli ribosomes and an all-α-helical nascent globin in the presence and absence of the cotranslationally active chaperones DnaK and trigger factor. The data provide insights on the dynamic nature and structural plasticity of ribosome-nascent chain complexes. We find that the sub-ns motions of the N-terminal fluorophore, reporting on the globin dynamics in the vicinity of the N terminus, are highly constrained both inside and outside the ribosomal tunnel, resulting in high-order parameters (>0.85) and small cone semiangles (<30°). The shorter globin chains buried inside the tunnel are less spatially constrained than those of a reference sequence from a natively unfolded protein, suggesting either that the two nascent chain sequences have a different secondary structure and therefore sample different regions of the tunnel or that the tunnel undergoes local structural adjustments to accommodate the globin sequence. Longer globins emerging out of the ribosomal tunnel are also found to have highly spatially constrained slow (ns) motions. There are no observable spectroscopic changes in the absence of bound chaperones.
Keywords: protein folding, ribosome, globin, nascent chain, dynamics, frequency domain fluorometry, cone angle analysis
Introduction
The ability to fold into a native three-dimensional structure is a fundamental property of most proteins in aqueous medium. A general understanding of the principles underlying protein folding has wide-ranging implications for both basic science and life-related phenomena. Yet, despite significant progress in understanding how proteins attain their native state in vitro,1 we still know very little about the effect of the cellular environment on folding. Given that the efficiency of folding bears a direct influence on cell function, the fundamental knowledge gained from in vitro studies is bound to acquire its highest impact when parameters relevant to the cellular environment are taken into account.
The ribosome and molecular chaperones are the two most important players influencing the earliest stages of protein folding in the cell.2 During protein biosynthesis, they pose physical biases to the conformational sampling of nascent chains and serve as potential interaction partners.
This study addresses the general role of the ribosome and other relevant structures as physical biases to the motions experienced by a nascent globin inside and outside the ribosomal tunnel. The crystal structure of the ribosome,3–5 cryo-electron microscopy investigations on ribosome dynamics,6,7 and prior key biochemical and biophysical studies on the ribosomal exit tunnel (see later) provide important reference background knowledge for this work.
The ribosomal exit tunnel (length 100 Å, average width 20 Å) is particularly important as it may influence folding through its natural ability to sequester the C-terminal portion of the nascent chain, its protein/RNA-rich internal surface,8 its cavities,9 and its electrostatic potential.10,11 Both experimental observations and simulations revealed that the tunnel is sufficiently spacious to allow the formation of secondary structure.8,12 Cross-linking experiments suggest that nascent chains up to 33 residues may be highly flexible despite the fairly narrow static dimensions of the tunnel.13 Antibody binding to N-terminal labels14 and Förster resonance energy transfer (FRET)12 showed that the secondary structure of nascent polypeptides inside the ribosomal tunnel is sequence-dependent and different proteins bury variable fractions of their sequence in the tunnel. Specific amino acid combinations (e.g., the SecM sequence) interact with portions of the tunnel (e.g., the L22 protein) so strongly that nascent protein stalling is generated.15,16 The influence of individual amino acid side chains has also been highlighted in a recent computational work.17 Outside the ribosomal tunnel, individual nascent chain structure18 and dynamics,19 or lack thereof, have also been reported.
Cotranslationally active chaperones bound to the ribosomal surface such as E. coli trigger factor (TF) may affect the conformational freedom of nascent proteins due to TF's proximity to the tunnel exit,20,21 and its ability to interact with nascent chains22,23 and protect them from proteolytic cleavage.24,25
DnaK, another cotranslationally active chaperone, affects the conformation of small peptide substrates.26,27 Model studies on the effect of the nonribosome-associated chaperone DnaK on the conformation of much larger substrates (that would otherwise aggregate) showed that interaction of DnaK's substrate binding domain with protein substrates renders them highly conformationally disordered,28 with residual native and nonnative secondary structure.16,29 Interaction of DnaK with polypeptide and protein substrates, including nascent chains, is tightly regulated by the allosteric binding of nucleotides (ATP, ADP) and cochaperones (DnaJ, GrpE).30 This mechanism provides a convenient tool to modulate the extent of nascent chain binding to DnaK.
In summary, previous investigations showed that the ribosomal exit tunnel, ribosome surface, and molecular chaperones have an effect on the conformation of nascent polypeptides. To gain additional insights into the origin of this effect, we focus here on the degree of spatial confinement imposed by the above parameters on the local ns and sub-ns motions of nascent chains. We study the behavior of the globular protein apomyoglobin (apoMb) and take advantage of a model-free equation relating observable fluorescence anisotropy time-dependent decays to the order parameters for spatially confined anisotropic motions, in the case of two local motions. The order parameters (S) derived from the above relation are utilized in the context of a specific in-cone model for conformationally confined local diffusion, to determine cone semiangles (θo). S and θo provide an effective physical view of the spatial biases experienced by ribosome-bound nascent polypeptides.
Results and Discussion
Anisotropy decay of macromolecules experiencing two local motions: dependence on order parameters and core semiangles
The theory underlying the fluorescence anisotropy decay of complex systems characterized by a slow global macromolecular motion and a faster spatially restricted local motion was described by Lipari and Szabo.31 Their approach was originally introduced to interpret the experimental depolarization of fluorescently labeled lipids in biological membranes, a highly confined environment. The Lipari-Szabo analysis is powerful in that it does not depend on the specific model chosen to represent the motions of the probe, that is, it is “model-free.” However, it relies on a few key assumptions on the nature of the system (see Fig. 1). Namely: (a) The fluorophore needs to have axial symmetry. (b) Either the fluorescence absorption or emission dipole of the fluorophore has to be colinear with the fluorophore symmetry axis 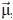 , although the dipoles do not need to be colinear with each other. (c) In a Cartesian macromolecular frame where the z axis is normal to the macromolecular surface [Fig. 1(A,B)], the local (fast, F) motions are completely random in the x–y plane, therefore independent of the azimuthal angle φ. (d) Local and global motions are independent. (e) The rotational correlation times for the global and local motions differ by at least one order of magnitude. For such a system, which experiences one slow global motion and one fast local motion, the fluorescence anisotropy decay can be expressed as31
, although the dipoles do not need to be colinear with each other. (c) In a Cartesian macromolecular frame where the z axis is normal to the macromolecular surface [Fig. 1(A,B)], the local (fast, F) motions are completely random in the x–y plane, therefore independent of the azimuthal angle φ. (d) Local and global motions are independent. (e) The rotational correlation times for the global and local motions differ by at least one order of magnitude. For such a system, which experiences one slow global motion and one fast local motion, the fluorescence anisotropy decay can be expressed as31
| (1) |
where r(t) and r(0) are the anisotropy at times t and 0, respectively, and r(t)/r(0) is equivalent to the autocorrelation function C(t) for the equilibrium orientational distribution of the probe. P2 denotes the second Legendre polynomial for the fast (subscript F) local motion, <…> denotes the equilibrium spatial average over the polar and azimuthal angles of 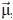 , θ, and φ. The μ(0) and μ(t) symbols denote the unit vectors specifying the orientation of the fast-tumbling unit in a frame rotating with the macromolecule, where the term macromolecule denotes the species with rotational correlation time τc,S experiencing the slow (subscript S) global motion. The latter expression is equivalent to
, θ, and φ. The μ(0) and μ(t) symbols denote the unit vectors specifying the orientation of the fast-tumbling unit in a frame rotating with the macromolecule, where the term macromolecule denotes the species with rotational correlation time τc,S experiencing the slow (subscript S) global motion. The latter expression is equivalent to
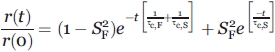 |
(2) |
where 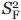 is the order parameter square for the fast motion, and τc,F and τc,S are the rotational correlation times of the fast and slow motions, respectively. By definition, the global motion is characterized by spatially unrestricted dynamics with an order parameter SS = 0.
is the order parameter square for the fast motion, and τc,F and τc,S are the rotational correlation times of the fast and slow motions, respectively. By definition, the global motion is characterized by spatially unrestricted dynamics with an order parameter SS = 0.
Figure 1.
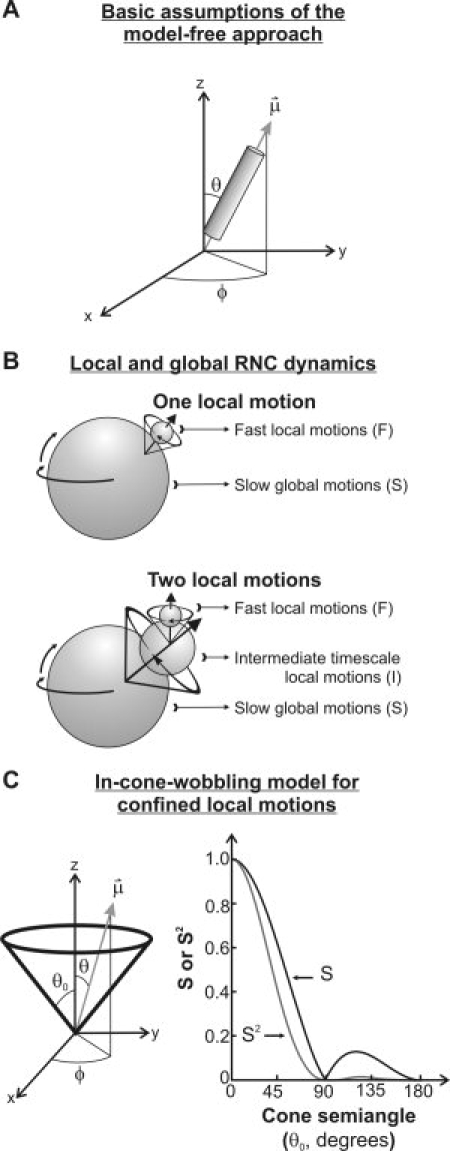
A: General features of the Lipari-Szabo model-free approach describing local motions of an axially symmetric probe (cylinder) by fluorescence depolarization techniques. B: Cartoon representations of the global and spatially confined local dynamics of a macromolecule in the presence of either one or two local motions. Both the fast (F) and intermediate (I) timescale local motions can be analyzed according to the in-cone-wobbling model, assuming all motions to be independent. The global macromolecular slow motions are denoted by the symbol S (not to be confused with the order parameter). C: General features of the in-cone wobbling model describing diffusive local dynamics. The vector (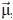 ), defining the fluorophore's symmetry axis, is colinear with either the emission or excitation dipoles of the fluorophore and is allowed stochastic wobbling motions (described by the angle θ) within a static cone defined by the cone semiangle θo, in a reference frame attached to the macromolecule with the z axis representing the normal to the macromolecular surface. The motions are randomly distributed in the XY plane and therefore independent of the azimuthal angle φ. The plot on the right illustrates the dependence of the order parameter S and its square S2 on the cone semiangle θo.
), defining the fluorophore's symmetry axis, is colinear with either the emission or excitation dipoles of the fluorophore and is allowed stochastic wobbling motions (described by the angle θ) within a static cone defined by the cone semiangle θo, in a reference frame attached to the macromolecule with the z axis representing the normal to the macromolecular surface. The motions are randomly distributed in the XY plane and therefore independent of the azimuthal angle φ. The plot on the right illustrates the dependence of the order parameter S and its square S2 on the cone semiangle θo.
In the case of two independent local motions and one global motion, in a system obeying assumptions (a)–(e), where (d) and (e) apply to all three pertinent motions and rotational correlation times (Fig. 1B), the fluorescence anisotropy decay can be expressed as
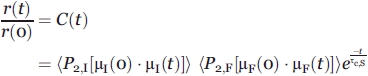 |
(3) |
where the various P2's denote the second Legendre polynomials for the respective fast (F) or intermediate (subscript I) timescale motions in a frame rotating with the macromolecule.
If τc,S ≫ τc,I ≫ τc,F, where τc,I is the rotational correlation times of the intermediate timescale motions, relation (3) can be expressed as32
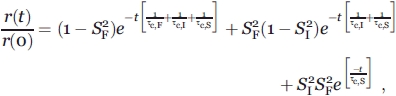 |
(4) |
which is equivalent to
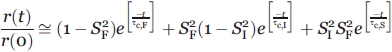 |
(5) |
where 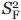 and
and 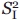 are the squared order parameters of the fast motion and the intermediate timescale motion, respectively. Relations (3) and (5) are to be regarded as model-free, that is, valid regardless of the type of motions (i.e., segmental, diffusive, two-state) experienced by the probe.
are the squared order parameters of the fast motion and the intermediate timescale motion, respectively. Relations (3) and (5) are to be regarded as model-free, that is, valid regardless of the type of motions (i.e., segmental, diffusive, two-state) experienced by the probe.
When a specific model for the probe's local dynamics is applicable, additional motion-specific parameters can be derived. A particularly simple and elegant model proposed by Kinosita et al.33 assumes random diffusional spatially confined local motions across a cone [Fig. 1(C)], and a square potential such that the normalized equilibrium distribution peq(θ) of the angle θ, describing the instantaneous position of the symmetry axis of the probe  follows the relation
follows the relation
| (6) |
| (7) |
For the above model, Kinosita et al. showed that
| (8) |
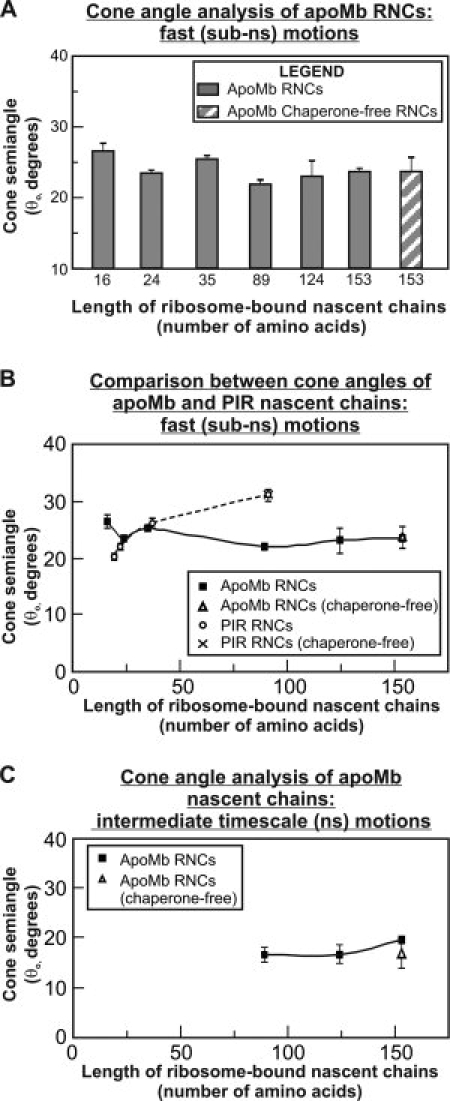
where θo is the limiting cone semiangle of the square potential model. Cone semiangles θo can be determined from relation (8), knowing 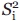 for each of the local motions of interest.
for each of the local motions of interest.
Spatial confinement of nascent apoMb sub-ns local motions
Fluorescence anisotropy is inherently able to detect the local dynamics occurring on a timescale comparable with that of the fluorescence lifetime of the probe. The nascent chains studied here were labeled with BODIPY at their N terminus. The fluorophore has the ability to directly sense its own local dynamics and that of its covalently linked proximal N-terminal residues. In addition, it may also sense the timescale and amplitude of additional local motions occurring in more distal portions of the chain. Data fitting reveals the number of local motions and the apparent rotational correlation time for each motion, providing an estimate of the size of the relevant tumbling unit. Some representative fluorescence depolarization raw data are shown in Figure 2.
Figure 2.
Fluorescence depolarization raw data, multicomponent fits, and curve fitting residuals for ribosome-bound and ribosome-released apoMb153.
A previous study on apoMb ribosome-nascent chain complexes (RNCs) focused on the timescale of the motions19 and showed that the local apoMb RNCs dynamics spans about two orders of magnitude (from sub-ns to ns), as briefly summarized in Table I.
Table I.
Range of Apparent Rotational Correlation Times (τc) Corresponding to Different General Classes of RNC Motionsa
| Dynamic regime | τc |
|---|---|
| Slow (S) motions | ≥0.5 μs |
| Intermediate timescale (I) motions | 1–50 ns |
| Fast (F) motions | 0.1–0.8 ns |
The categories defined in this table reflect previously reported findings (Ellis et al.19).
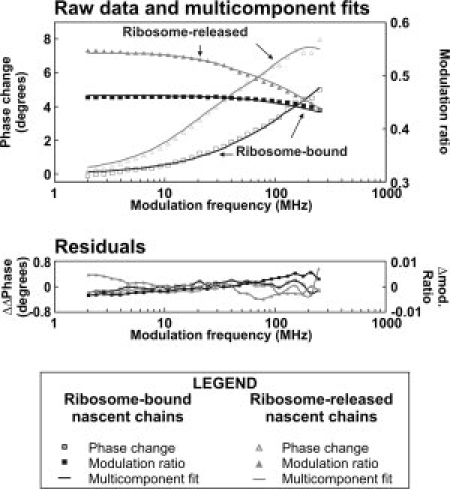
The present work, in contrast, focuses on the spatial confinement and the amplitude of RNC's local motions. The degree of confinement for the local dynamics is quantitatively assessed here by determining order parameters and cone semiangles corresponding to each of the detected motions. We apply the in-cone wobbling model detailed in the previous section, which assumes that nascent chains undergo segmental diffusive random motions across a cone. Cone semiangles for the sub-ns motions of all the apoMb RNCs analyzed here are shown in Figure 3(A). Order parameters are in Table II. The following analysis focuses primarily on the discussion of cone semiangles, given that they provide a more intuitive physical view of the spatial constraints experienced by nascent chains, in relation to the surrounding space.
Figure 3.
A: Cone semiangles for the sub-ns motions of apoMb RNCs sensed by a BODIPY fluorophore covalently linked to the nascent chain N terminus. Data are shown for nascent chains of increasing length, up to the full-length 153-residue protein. RNCs were generated either from a wild type (gray bars) or a Δtig (dashed bars) cell strain. The resuspended RNCs generated from the Δtig strain were treated with the GrpE cochaperone and an excess of ATP to remove any DnaK chaperone bound to the nascent chains. The conditions are denoted as chaperone-free, in that the nascent chain contains no bound chaperone. Error bars comprise ± one standard error. B: Amplitude of the fast (sub-ns) motions experienced by the apoMb and reference PIR nascent polypeptides of increasing length under different conditions. Data were collected for samples prepared from either wild type (○, ▪) or Δtig trigger factor-depleted (×, ▵) cell strains. C: Cone semiangles for the intermediate timescale (ns) motions of apoMb RNCs. These motions are present only for the longest apoMb nascent chains. The 153-residue full-length protein is analyzed in the presence of ribosomes generated either from a wild type (squares) or TF-depleted Δtig (triangles) cell strain. In the latter case, nascent chains were also treated with GrpE and an excess of ATP (chaperone-free conditions).
Table II.
Order Parameters Describing the Spatial Confinement and Dynamic Disorder Associated with the apoMb RNC Local Motions
| Timescales of motion |
||||||||
|---|---|---|---|---|---|---|---|---|
| Fast (sub-ns) |
Intermediate (ns) |
|||||||
| Polypeptide chain | SFa,b |
 a a
|
τc,F (ns)a | SIa,b |
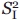 a a
|
τc,I (ns)a | r(0) | Reduced χ2 of fitsc |
| ApoMb16d,e | 0.90 ± 0.06 | 0.8 ± 0.1 | 0.3 ± 0.1 | 0.37 | 1.86 | |||
| ApoMb24d | 0.88 ± 0.01 | 0.78 ± 0.01 | 0.14 ± 0.02 | 0.37 | 0.44 | |||
| ApoMb35d,e | 0.86 ± 0.01 | 0.74 ± 0.01 | 0.4 ± 0.1 | 0.37 | 1.90 | |||
| ApoMb89d,e | 0.93 ± 0.04 | 0.87 ± 0.08 | 0.4 ± 0.1 | 0.96 ± 0.03 | 0.92 ± 0.05 | 5 ± 1 | 0.37 | 0.43 |
| ApoMb124d,e | 0.92 ± 0.05 | 0.85 ± 0.09 | 0.3 ± 0.1 | 0.96 ± 0.03 | 0.92 ± 0.05 | 7 ± 1 | 0.37 | 0.41 |
| ApoMb153d,e | 0.88 ± 0.01 | 0.77 ± 0.03 | 0.3 ± 0.1 | 0.91 ± 0.01 | 0.84 ± 0.01 | 5 ± 1 | 0.37 | 0.26 |
| Chaperone-free apoMb153 RNCsf,e,g | 0.88 ± 0.02 | 0.77 ± 0.02 | 0.1 ± 0.01 | 0.93 ± 0.02 | 0.87 ± 0.03 | 2.2 ± 0.2 | 0.37 | 0.40 |
| Ribosome-released apoMb153d,e,h | 0.82 ± 0.01 | 0.67 ± 0.01 | 0.8 ± 0.1 | 0 | 0 | 41 ± 2 | 0.29 ± 0.02 | 0.74 |
| PIR19d | 0.91 ± 0.01 | 0.83 ± 0.01 | 0.15 ± 0.02 | 0.37 | 0.73 | |||
| PIR22d | 0.89 ± 0.01 | 0.80 ± 0.01 | 0.14 ± 0.03 | 0.37 | 0.46 | |||
| PIR37d | 0.85 ± 0.01 | 0.73 ± 0.01 | 0.12 ± 0.02 | 0.37 | 3.6 | |||
| PIR90d,e | 0.79 ± 0.01 | 0.63 ± 0.02 | 0.29 ± 0.03 | 0.37 | 4.4 | |||
| Chaperone-free PIR90 RNCsf,g | 0.79 ± 0.01 | 0.63 ± 0.03 | 0.14 ± 0.01 | 0.37 | 2.8 | |||
| Ribosome-released PIR90d,h | 0.40 ± 0.02 | 0.17 ± 0.02 | 0.40 ± 0.03 | 0 | 0 | 13 ± 2 | 0.23 ± 0.01 | 0.77 |
Uncertainties are expressed as ± one standard error (2–7 repeats). In case the standard error was smaller than the propagated fitting error of the fluorescence fractions for any of the experimental repeats, the propagated error is reported.
The order parameter is calculated as the square root of the order parameter squared.
Defined as in Jameson and Hazlett.34
RNCs generated in wild-type cell-free strain.
The rotational correlation times and pre-exponential factors for these chain lengths are reproduced from (Ellis et al.19).
These RNCs are generated in Δtig cell-free strains.
Chaperone-free is intended to mean “devoid of any RNC-bound chaperones.”
For these species, the intermediate timescale (I) dynamics denotes global motions.
The sub-ns dynamics is primarily due to motions of the N-terminal BODIPY fluorophore and the immediately adjacent covalently bound amino acids, given that the apparent rotational correlation time τc for these motions (Table I) is comparable with, or slightly larger than the one of the free fluorophore measured in the resuspended ribosome medium (0.12 ± 0.04 ns). Therefore, we interpret the sub-ns motions as indicative of the dynamics of the N-terminal portion of the nascent chain (one to two amino acids, given the experimental apparent rotational correlation time), as sensed by its covalently linked fluorophore. In addition, the fact that the timescale for these motions is consistently and reproducibly within the sub-ns regime also demonstrates unequivocally that the sub-ns local dynamics pertains to a relative small tumbling unit. Therefore, this motion reports on the behavior of the nascent chain N terminus, and it does not reflect the dynamics of a protein-associated nor a ribosome-associated fluorophore. This is true for all nascent chains, regardless of whether their N terminus is inside or outside the ribosomal tunnel.
The most salient features of the order parameter (Table II) and cone angle analysis (see Fig. 3) data, reporting on the spatial confinement of the nascent chain dynamics, are discussed below.
First, the cone semiangles for all of the apoMb fast motions are extremely small at all chain lengths, ranging between about 20 and 30°. Note that the maximum possible cone semiangle, for completely isotropic motions, is 180°. Quite surprisingly, the cone semiangle of nascent apoMb remains small as the nascent protein chain extends from inside to outside the ribosomal tunnel. Given that the apparent τC for the sub-ns motion does not change, the small cone semiangles observed for the longest nascent chains emerging out of the tunnel are not due to the formation of additional interactions involving the N-terminal fluorophore and distal portions of the RNC. On the other hand, we propose that the cone semiangle is small because the nascent chain N terminus senses the presence of surrounding physical biases both inside and outside the ribosomal tunnel. Specifically, the physical structures surrounding the fluorophore and the nascent chain's N terminus, including the ribosomal tunnel, the ribosomal surface and the nascent protein itself induce some spatial confinement limiting the amplitude of the fluorophore/N-terminus motions.
Second, upon apoMb chain elongation from 16 to 24 to 35 amino acids, a local minimum in cone semiangle is found for the 24-residue nascent chain. This result is statistically significant according to the two-tailed Student's t-test (assuming equal population variances). This test shows that (a) the cone semiangle of nascent apoMb16 is significantly larger that of apoMb24, with P < 0.10, and (b) the cone angle of nascent apoMb24 is smaller than the one for apoMb35, with P < 0.05, where P denotes the probability that the data for the two chain lengths are the same. Although the above changes are small in magnitude, the smaller relative cone angle for the 24-residue nascent chain suggests that the N-terminus of apoMb24 samples a significantly more confined region than the apoMb16 and apoMb35 nascent chains. Such a difference is indicative of structural changes by the nascent chain and (or) the ribosomal tunnel environment as the nascent chain gets longer, while still buried within the ribosomal tunnel. In this context, the sub-ns motions of the fluorophore serve as a direct sensor of the ribosomal tunnel and geometrical constraints imposed by the ribosome inner surface. This concept is supported by the fact that the most inner half of the ribosomal tunnel, close to the peptidyl-transferase center (PTC) has a relatively large three-dimensional cleft whereas it gets narrower toward the end of the tunnel. Therefore, as the nascent chain gets longer, its structure and (or) local environment change. The relative increase in cone semiangle as the chain elongates from apoMb24 to apoMb35 is subtle but reproducible. A full interpretation of this widening in cone semiangle relies on the knowledge of the precise secondary structure of the nascent chain, which is still unknown to date. Therefore one can only state, at this juncture, that cone angle analysis of sub-ns local motions of nascent polypeptides is extremely sensitive to changes in the local environment of the short nascent chains extending from apoMb24 to apoMb35.
Third, a comparison with the cone semiangles of the short (16–35 residues) nascent chains of apoMb and the natively unfolded reference sequence known as phosphorylation insulin receptor interaction regions (PIR) leads to very interesting observations [Fig. 3(B)]. Unexpectedly, the cone semiangle for the sub-ns PIR19 local motions is even smaller than that of apoMb16, suggesting either that the two short nascent chains (apoMb and PIR) have a different secondary structure and therefore sample different region of the tunnel, or that the tunnel undergoes local structural adjustments to accommodate the different sequences. Either hypothesis is plausible given that the precise structure of the nascent chain is not known at this time. Examples of the expected range of progression of apoMb16 and PIR19 inside the ribosomal tunnel are provided in Figure 4. The image shows that both sequences are entirely buried in the tunnel, regardless of the specific secondary structure assumed by the nascent chain (helical and fully extended limiting conformations are shown).
Figure 4.
Physical representations of the ribosomal exit tunnel and the shortest apoMb and PIR nascent chains examined in this work. All the ribosomal tunnel images were generated by rolling ball simulations starting from the Haloarcula marismortui structure, as detailed in Ref. 8. A: Space-filling side view of the ribosomal exit tunnel. The peptidyl transferase center (PTC) is in the back of the image. Lines 1–5 show the vertical tunnel slices used in panels D–G. These specific planes were selected because they yield representative views of the tunnel dimensions useful to evaluate the progression of the nascent chain inside the tunnel. B: Space-filling side-view of the ribosomal exit tunnel. C: Space-filling and chemical formula of the BODIPY-labeled nascent chain N terminus. D, F: Pictorial representations of the shortest apoMb and PIR nascent chains examined here, modeled as fully extended chains. The cones shown in the image have dimensions matching the experimental cone semiangles and consistent with the experimentally determined rotational correlation times. Different views showing distinct tunnel slices are displayed. E, G: Pictorial representations of the shortest apoMb and PIR nascent chains as in panels D and F, except that the nascent chains were modeled as α-helices rather than extended chains.
Fourth, the difference in cone semiangle between apoMb and PIR are most pronounced for longer nascent chains. ApoMb89 and PIR90 have a very similar chain length and therefore offer an interesting comparison. In contrast to the case of apoMb16 and PIR19, the cone semiangle of ApoMb89 is significantly smaller (by about 10°) than that of PIR90. Both sequences are sufficiently long to be outside of the ribosomal exit tunnel, regardless of their specific secondary structure. The observed differences may either be due to physical biases imposed by chaperones or to intrinsic differences in the nascent chain structure. Nascent PIR90 RNCs are virtually chaperone-free, unlike apoMb89 RNCs, which carry some TF chaperone (and DnaK) at equilibrium.19
Fifth, the behavior of full-length nascent apoMb, apoMb153 is of interest. The cone angle of this nascent full-length protein, believed to be mostly outside the ribosomal tunnel, is most informative when compared with the chaperone-free conditions. As shown in Figure 3(A), no changes are observed, showing that the confinement of the sub-ns dynamics of the protein's N terminus does not depend on the presence of cotranslationally active chaperones. This result is intriguing because previous reports highlighted the protective role of the TF on nascent chains, emphasizing that TF serves as a cradle to nascent proteins. Our results are not in contrast with the literature. However, they further refine our physical view of cotranslational folding by suggesting that the cradle effect of TF (and the structural biases imposed by DnaK, as both chaperones are present for the full-length chain) does not affect the motions of the nascent chain N terminus. A careful examination of the crystal structure of the ribosomal large subunit in complex with TF21 is consistent with our results in that TF resembles more a protein-size arch than a three-dimensional cavity. The apoMb nascent chain N terminus could then well be in the portion of the native chain not interacting with TF.
Spatial confinement of nascent apoMb local ns motions
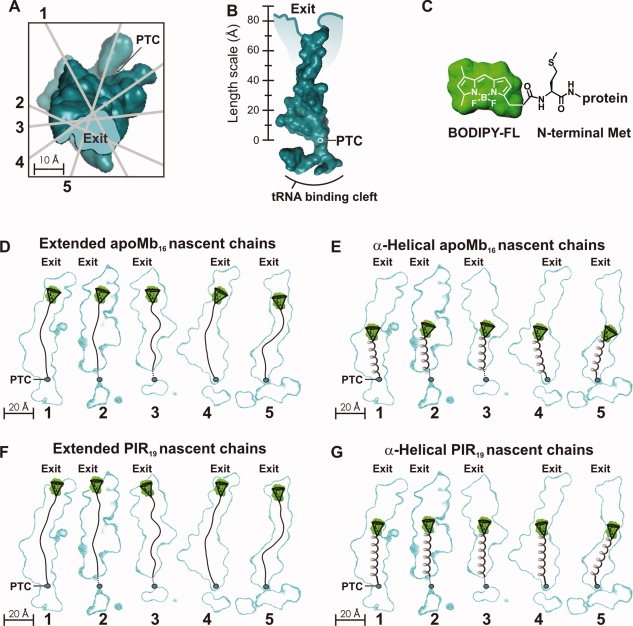
Intermediate timescale (ns) motions are only found in longer apoMb nascent chains. These motions have been proposed to be the signature for an independent nascent chain structural ensemble.19 The observed extent of spatial confinement is severe and it does not depend on chain length nor on the presence/absence of cotranslational chaperones [Fig. 3(C)]. Therefore, the local structures formed by long apoMb nascent chains emerging from the ribosome experience a narrow-angle spatial wobbling.
Variations in the degree of confinement of apoMb nascent chain motions upon release from the ribosome
On nascent chain release from the ribosome, both the spatial confinement and rotational correlation time of the nascent protein change significantly. The raw fluorescence depolarization data for ribosome-bound and ribosome-released apoMb153 are shown in Figure 2. The release of apoMb153 induces a transition from three-component to two-component dynamics, evidenced by the disappearance of the nondecaying fraction of anisotropy due the very slow ribosome motions (in the presence of the faster spatially confined local motions). The spectroscopic signature for this transition can be most clearly appreciated as the pronounced variations in the modulation ratio profile (from flat to curved) of the raw data, on ribosome release of the apoMb153 nascent chain (see Fig. 2).
Upon release from the ribosome, the cone semiangle of apoMb153 increases only slightly, by about 8° [Fig. 5(A)], for the sub-ns motions, consistent with the relief of some residual structural biases present when the nascent protein is ribosome-bound. The increase in the apparent rotational correlation time for these fast motions, already discussed elsewhere,19 points to the presence of local structural rearrangements of the protein's N terminus upon release from the ribosome. Interestingly, the fact that the cone semiangle for the fast sub-ns motions remains fairly small for the fully ribosome-released protein indicates that the apoMb structure surrounding the N terminus poses larger physical biases than the ribosomal surface. As shown in Figure 5, this result is in contrast with the behavior of the natively unfolded PIR chain, whose cone semiangle for the sub-ns motions increases significantly, upon release from the ribosome (see Supporting Information for PIR raw data and curve fits).
Figure 5.
Variations in (A) cone semiangle θo and (B) apparent rotational correlation time before and after the release of full-length apoMb153 and PIR from the ribosome. Error bars denote ± one standard error.
The above data are of straightforward interpretation if one considers that a free fluorophore control (mentioned earlier) exhibits primarily sub-ns motions, thereby excluding the possibility that the RNC-linked fluorophore “sticks” to the ribosome. On the other hand, it is worth mentioning that we cannot technically exclude that the observed cone semiangles may, in part, be rendered narrower than their actual value as a result of some (directly undetectable) fluorophore population interacting persistently with a large structure tumbling on a slow, irresolvable timescale. This scenario appears unlikely given that neither the free fluorophore control nor the ribosome-released fluorescently labeled protein display such long-timescale motions.
As shown by the cone semiangle for the slower ns motions reaching its maximal value (θo = 180°) and by the considerable increase in the apparent rotational correlation time of apoMb153's ns motions upon release from the ribosome [Fig. 5(B)], the bias imposed by the presence of the ribosome disappears and the apparent size of the protein increases greatly [Fig. 5(B)].
The above results offer a low resolution biophysical view of the initial and final stages of protein birth, taking place as the full-length nascent protein is released in solution and reaches its native state.
Equilibrium population analysis of RNCs
The fluorescence depolarization analysis of apoMb RNCs presented here and elsewhere19 assumes that the fluorescence data arise from a unique species undergoing local and global motions. A more accurate analysis of the data, however, should take into account the fact that there may be more than one type of RNC population, in solution.
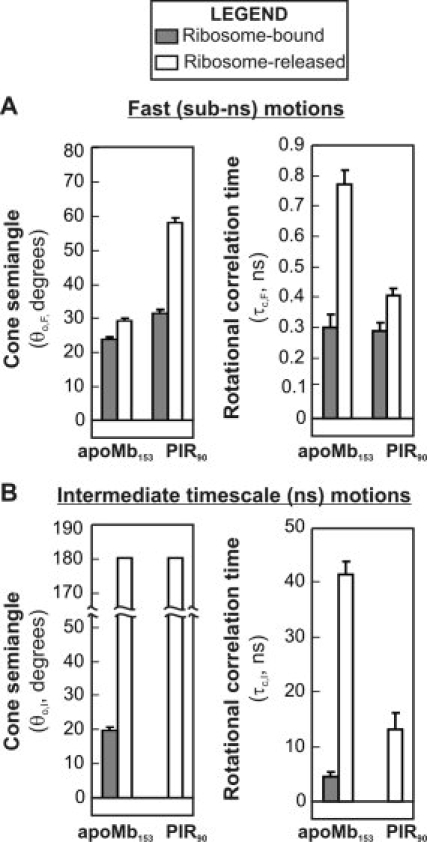
TF undergoes binding/unbinding with both the ribosome and the nascent chain. Assuming that these binding events occur independently of each other, one can postulate the presence of four possible states (1–4 in mutual exchange, as shown in Figure 6(A). We make the reasonable assumption that the system is at equilibrium, under our experimental conditions.
Figure 6.
A: Cartoon representation of the proposed equilibria among different types of apoMb153 RNC populations. TF denotes the trigger factor chaperone. Four species, labeled as 1–4, are postulated to exist. B: Graphical representation of the calculated percent populations of species 1–4 as a function of the binding affinity of TF for ribosome-bound nascent chains, expressed as the KD TF-RNC dissociation constant. This plot assumes that the binding affinity between TF and the ribosome is constant (according to published values38,40) and it does not depend on the affinity between nascent chains and TF. C: Results for low and high values of KD TF-RNC are reported. Supporting information includes the derivation of equations necessary for the plots in Figure 6 (panels B and C).
Although a direct experimental assessment of the equilibrium populations of species 1–4 and the corresponding equilibrium dissociation constants is technically complex and has not been performed yet, it is nonetheless possible to estimate such values from published data addressing (a) the interaction of TF with empty ribosomes (characterized by a dissociation constant denoted as KD,TF-Ribosome35–37) and (b) the overall equilibrium interaction of TF with a number of different RNCs, characterized by an observed dissociation constant denoted as KD,TF-RNC. The latter parameter has been studied quite extensively for a variety of different soluble and membrane proteins (ca. 7)23,38, and it incorporates both the contributions due to interactions between TF and ribosome and the contributions due to interactions between the nascent chain and TF. Thus, the following range of biologically relevant KD,TF-Ribosome and KD,TF-RNC values, related to the relevant thermodynamic steps of Figure 6(A), can be defined
| (9) |
| (10) |
We regard the above numerical values as representative estimates of feasible ranges. Our own experimental measurements of total RNC concentrations, based on fluorescence and radioactive assays, lead to
| (11) |
From the following straightforward definitions of equilibrium
| (12) |
the binding constant illustrating the equilibria between species 2 and 4 and species 1 and 3 can be estimated from the values of KD TF-Ribosome and KD TF-RNC. Simple algebraic manipulations of Eqs. (9)–(12) lead to expressions for the concentrations [1], [2], [3], and [4] as a function of the pertinent equilibrium constants (Supporting Information).
A general view of the dependence of the equilibrium concentration of species 1–4 can be obtained by plotting [1]–[4] as a function of KD,TF-RNC, as shown in Figure 6(B). Such assessment is useful because it shows that species 4 is considerably more populated than the other species, under low affinity conditions. Under high affinity conditions, species 1 and 3, which involve direct interactions between TF and the nascent chain, dominate in solution. Although, in the absence of equilibrium binding data for apoMb, it is not possible to evaluate which specific TF-nascent chain affinity regime applies to our case, some useful assessments can be made. Most notably, species 2, which involves the nascent chain achieving an independent local structure under conditions where TF is bound to the ribosome, is predicted to be poorly populated under all feasible experimental conditions.
The spectroscopic data analysis below, which takes individual RNC populations into account, yields further useful information. In the analysis of the fluorescence depolarization data, we assume that states 1 and 3 contribute only to the fast and slow local motions, whereas states 2 and 4 contribute to all detectable motions, that is, intermediate, fast and slow. For practical purposes, we collect the predictions for states 1 and 3, which do not contribute to the observed intermediate timescale motions (denoted as NC, i.e., noncontributing, in the analysis below) and the predictions for states 2 and 4, which contribute to the intermediate timescale motions (denoted as C).
We assume that (1) the correlation times corresponding to the same types of motions are the same for all populated species, and (2) the S2 for the fast RNC motions are equal in the wild-type and chaperone-free states of apoMb153 (and also equal to the S2 for ribosome-released wild-type apoMb153). The above assumptions are necessary so that the pertinent algebraic expressions can be solved. Assumption 2 is reasonable because the fluorescent probe does not show intrinsic binding to chaperones or the ribosome (e.g., ribosome-released PIR90 shows no affinity for the ribosome), and apoMb's N terminus is predicted to have no affinity for TF.39 In addition, the experimentally observed order parameters for the fast motions of apoMb153 under wild-type and chaperone-free conditions were experimentally shown to be identical.
We have that
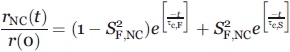 |
(13) |
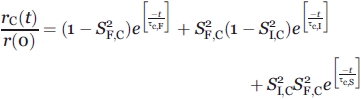 |
(14) |
where 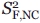 and
and 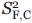 are the squared order parameters for the fast motion of the noncontributing and contributing species, respectively, and
are the squared order parameters for the fast motion of the noncontributing and contributing species, respectively, and 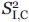 is the squared order parameter for the intermediate timescale motions of the contributing species. The populations and associated order parameters in Eqs. (13) and (14) can be related to the spectroscopically observed fractional intensities according to
is the squared order parameter for the intermediate timescale motions of the contributing species. The populations and associated order parameters in Eqs. (13) and (14) can be related to the spectroscopically observed fractional intensities according to
| (15) |
| (16) |
| (17) |
where fS,obs, fI,obs, and fF,obs are the experimentally determined fractional fluorescence anisotropy decay intensities for wild-type apoMb153. In addition, pNC and pC are the normalized populations for the noncontributing (NC) species and contributing (C) species, respectively. The above set of equations can be solved, given that, as assumed above, 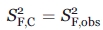 .
.
After the order parameters for all motions are defined, the numerical values can be converted into cone semiangles via Eq. (8).
The predicted results of the above analysis are plotted in Figure 6(C), for both RNC-TF high affinity and low affinity cases. Comparisons with the experimentally determined (non population-resolved) data for wild-type apoMb153 RNCs are also provided. The results are very informative. The predicted cone angles for the fast motions do not depend on the population-discriminated analysis, in any of the nascent chain-TF affinity regimes. This result provides confidence in the validity of the experimental cone angle and order parameter results reported in the previous sections for the fast sub-ns motions. The experimental cone semiangle results for the intermediate timescale (ns) motions of the nascent chain, on the other hand, depend quite significantly on the nascent chain-TF affinity regime (note that only 2 and 4 contribute to intermediate timescale motions). Specifically, under low affinity conditions, the experimentally determined cone angles are similar to those pertaining to species 2 and 4 and primarily reflect the data for the most highly populated species 4. However, if apoMb153 nascent chains have high affinity for TF, the actual cone semiangle for species 2 and 4, dominated by the contribution of species 4, is more than 20° larger than the experimentally observed value.
The population-discriminated analysis presented here is useful to fully understand the effect of TF on nascent chains. In the TF-RNC low affinity regime, 4 is the dominant species in solution both in the absence and presence of TF. Under these conditions, the lack of spectroscopic changes observed upon removal of bound chaperones [see chaperone-free data for apoMb153 in Fig. 3(A,C)] is a mere reflection of the fact that none of the detectable species bears significant RNC-bound TF even before removal of the bound chaperones. In contrast, in the high affinity regime 1, 3, and 4 are comparably populated in the presence of TF [Fig. 6(B)]. However, upon removal of bound TF, the 1 and 3 populations are no longer present and must turn into a TF-free species of type 4. The 2 population is predicted to be small at all times. The only way to reconcile an increase in a 4-type population with the negligible observed spectroscopic changes upon removal of TF is to postulate that the 4-type species experiences even more confined ns motions in the absence of TF.
In summary, if the RNC-TF high affinity regime applies, the lack of spectroscopically observable changes under TF-free conditions suggests that species 4 has narrower-amplitude ns dynamics when TF is not present. Additional studies targeting the measurement of TF-nascent chain dissociation constants and structural investigations in the absence of TF are necessary to shed further light on this issue.
Conclusions
In conclusion, we have shown that dynamic fluorescence depolarization in combination with cone angle analysis in the presence of two local diffusive motions is a powerful tool for the analysis of the confinement of the motions experienced by ribosome-bound nascent chains. The sub-ns and ns motions of nascent apoMb are highly confined and generally only weakly chain-length-dependent, in contrast with the PIR nascent chains, which experience larger variations in cone semiangle with chain length. Small but reproducible changes in cone semiangle for short apoMb nascent chains of different length buried inside the tunnel demonstrate that this analysis is highly sensitive to the progression of the nascent chain within the ribosomal tunnel. Finally, ApoMb experiences dramatic changes in rotational correlation times for both its fast and intermediate timescale local motions upon release from the ribosome, consistent with the presence of large structural changes as release takes place. The variation in θo from about 27° to 180° for the ns motions explicitly shows that the dynamic bias imposed by the ribosome on nascent chains disappears completely, upon release in solution.
Methods
Sample preparation and biochemical characterization
Ribosome-nascent chain complexes (RNCs) were generated, purified, and analyzed from E. coli cell-free systems as described.19 RNCs were labeled with BODIPY-FL (Invitrogen, denoted as BODIPY) by the addition of BODIPY-labeled Met-tRNAfMet, prepared as described,41,42 to produce N-terminally fluorescently labeled nascent polypeptides and proteins. Stalled ribosomes bearing nascent chains of different length were generated in E. coli cell-free systems as described.19 Briefly, 38-nucleotide-long antisense deoxyoligonucleotides (see Supporting Information for DNA sequences) were designed to generate DNA/mRNA hybrids directing sequence-specific mRNA cleavage catalyzed by RNase H. This enzyme is endogenously present in E. coli cell-free systems. Translation of the truncated mRNA resulted in homogeneous samples of ribosome-bound nascent chains of designed chain lengths. The final deoxyoligonucleotide concentration in each cell-free reaction was 0.15 μg/μL. The experimental samples were purified by ultracentrifugation over sucrose cushions to isolate ribosomal complexes and associated chaperones.19
Generation of chaperone-free RNCs
ApoMb and PIR RNCs lacking any bound DnaK and TF chaperones were generated from TF-depleted cell strains (Δtig). Resuspended RNCs were prepared as described earlier. GrpE (2 μM) was added to the medium and the solution was incubated at room temperature for 20 min, followed by incubation (10 min) with additional ATP (30 μM) and KCl (500 μM). The resulting RNCs are denoted here as chaperone-free, as the addition of GrpE and ATP dramatically decreases the substrate affinity for DnaK.30 DnaK release was confirmed by a second ultracentrifugation followed by Western blotting.19 Briefly, RNCs were subject to SDS-PAGE (8% tris-glycine polyacrylamide gel) and transferred to polyvinylidene fluoride (PVDF) membranes. The membranes were then incubated with mouse monoclonal anti-DnaK (Stressgen) antibodies, followed by treatment with goat anti-mouse alkaline phosphatase conjugates (Novagen) for 1 h each. DnaK chaperone concentration was quantified via Lumi-Phos® substrate (Pierce) and compared with calibration standards of known DnaK concentration run in parallel.
Generation of ribosome-released apoMb and PIR
BODIPY-labeled ribosome-released full-length apoMb and PIR were generated from wild-type RNCs on addition of 1.5M NH2OH in the presence of 0.4 μM GrpE, 0.4 μM DnaJ, 30 μM ATP, and 500 μM KCl.
Dynamic fluorescence depolarization data collection and processing
Anisotropy decay data were collected by frequency-domain fluorometry with a Chronos spectrofluorimeter (ISS Inc., Urbana Champaign, IL) equipped with calcite prism polarizers and a laser diode (λex = 473 nm, λem > 510 nm with a 51294 filter, Newport Corp.-Oriel). Lifetime measurements were performed on all samples with vertically polarized excitation and 54.7° polarized emission. All frequency-domain fluorescence data were analyzed with the GLOBALS software43 and decisions regarding 2- vs 3-component fits were carried out as described.19 GLOBALS curve fitting of fluorescence depolarization data yielded rotational correlation times and fractional intensities. The fractional intensities for each of the motions identified by the dynamic fluorescence depolarization experiments correspond to the entire preexponential factors of relations 2, 4, and 5. Such preexponential factors were converted to order parameters by solving the preexponential factor expressions for the pertinent S2. In-cone analysis of the local diffusive motions was carried out with a square potential model33 by determining cone semiangles from Eq. (8).
Error analysis of fluorescence depolarization data
For each of the individual repeats (2–7), the fractional intensities of the fluorescence depolarization decays were converted into S2, S [defined as (S2)1/2] and θo by applying the pertinent equations. The results for each of these parameters were then averaged over all the repeats. Errors on the averages were carried out by two procedures (Methods I and II). According to Method I, the standard error on the mean was computed from the individual S2, S, and θo values used to determine the averages. According to Method II, the curve fitting errors for the fluorescence fractional intensities were used to derive uncertainties in S2, S, and θ0 by error propagation. Such uncertainties were then averaged. For each of the reported parameters (S, S2, and θo), errors were determined by both Methods I and II. The largest of the two values is reported here.
Population analysis of different classes of RNCs
Algebraic and numerical solutions to the equations employed for the population analysis described in the Results and Discussion were obtained with the Maple software package (version 8, Waterloo Maple Inc., 2002).
Acknowledgments
The authors thank A. Szabo, T. Hazlett, E. Gratton, B. Barbieri, and A. Palmer for valuable discussions. They are grateful to P.B. Moore and N.R. Voss for providing coordinates of images of the ribosomal exit tunnel.
Glossary
Abbreviations
- TF
trigger factor
- apoMb
apomyoglobin
- RNC
ribosome-nascent chain complex
- FRET
Förster resonance energy transfer
- PIR
phosphorylated insulin receptor interaction region
- PVDF
polyvinylidene fluoride.
References
- 1.Englander SW, Mayne L, Krishna MMG. Protein folding and misfolding: mechanism and principles. Q Rev Biophys. 2007;40:287–326. doi: 10.1017/S0033583508004654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hartl FU, Hayer-Hartl M. Molecular chaperones in the cytosol: from nascent chain to folded protein. Science. 2002;295:1852–1858. doi: 10.1126/science.1068408. [DOI] [PubMed] [Google Scholar]
- 3.Harms J, Schluenzen F, Zarivach R, Bashan A, Gat S, Agmon I, Bartels H, Franceschi F, Yonath A. High resolution structure of the large ribosomal subunit from a mesophilic eubacterium. Cell (Cambridge, MA) 2001;107:679–688. doi: 10.1016/s0092-8674(01)00546-3. [DOI] [PubMed] [Google Scholar]
- 4.Nissen P, Hansen J, Ban N, Moore PB, Steitz TA. The structural basis of ribosome activity in peptide bond synthesis. Science. 2000;289:920–930. doi: 10.1126/science.289.5481.920. [DOI] [PubMed] [Google Scholar]
- 5.Schuwirth BS, Borovinskaya MA, Hau CW, Zhang W, Vila-Sanjurjo A, Holton JM, and Cate JHD. Structures of the bacterial ribosome at 3.5 .ANG. resolution. Science. 2005;310:827–834. doi: 10.1126/science.1117230. [DOI] [PubMed] [Google Scholar]
- 6.Agrawal RK, Lata RK, Frank J. Conformational variability in Escherichia coli 70S ribosome as revealed by 3D cryo-electron microscopy. Int J Biochem Cell Biol. 1999;31:243–254. doi: 10.1016/s1357-2725(98)00149-6. [DOI] [PubMed] [Google Scholar]
- 7.Tama F, Valle M, Frank J, Brooks CL. Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc Natl Acad Sci USA. 2003;100:9319–9323. doi: 10.1073/pnas.1632476100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Voss NR, Gerstein M, Steitz TA, Moore PB. The geometry of the ribosomal polypeptide exit tunnel. J Mol Biol. 2006;360:893–906. doi: 10.1016/j.jmb.2006.05.023. [DOI] [PubMed] [Google Scholar]
- 9.Amit M, Berisio R, Baram D, Harms J, Bashan A, Yonath A. A crevice adjoining the ribosome tunnel: hints for cotranslational folding. FEBS Lett. 2005;579:3207–3213. doi: 10.1016/j.febslet.2005.03.023. [DOI] [PubMed] [Google Scholar]
- 10.Lu JL, Deutsch C. Folding zones inside the ribosomal exit tunnel. Nature Struct Mol Biol. 2005;12:1123–1129. doi: 10.1038/nsmb1021. [DOI] [PubMed] [Google Scholar]
- 11.Lu JL, Deutsch C. Electrostatics in the ribosomal tunnel modulate Chain elongation rates. J Mol Biol. 2008;384:73–86. doi: 10.1016/j.jmb.2008.08.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Woolhead CA, McCormick PJ, Johnson AE. Nascent membrane and secretory proteins differ in FRET-detected folding far inside the ribosome and in their exposure to ribosomal proteins. Cell. 2004;116:725–736. doi: 10.1016/s0092-8674(04)00169-2. [DOI] [PubMed] [Google Scholar]
- 13.Choi KM, Atkins JF, Gesteland RF, Brimacombe R. Flexibility of the nascent polypeptide chain within the ribosome—contacts from the peptide N-terminus to a specific region of the 30S subunit. Eur J Biochem. 1998;255:409–413. doi: 10.1046/j.1432-1327.1998.2550409.x. [DOI] [PubMed] [Google Scholar]
- 14.Tsalkova T, Odom OW, Kramer G, Hardesty B. Different conformations of nascent peptides on ribosomes. J Mol Biol. 1998;278:713–723. doi: 10.1006/jmbi.1998.1721. [DOI] [PubMed] [Google Scholar]
- 15.Nakatogawa H, Ito K. The ribosomal exit tunnel functions as a discriminating gate. Cell. 2002;108:629–636. doi: 10.1016/s0092-8674(02)00649-9. [DOI] [PubMed] [Google Scholar]
- 16.Woolhead CA, Johnson AE, Bernstein HD. Translation arrest requires two-way communication between a nascent polypeptide and the ribosome. Mol Cell. 2006;22:587–598. doi: 10.1016/j.molcel.2006.05.021. [DOI] [PubMed] [Google Scholar]
- 17.Petrone PM, Snow CD, Lucent D, Pande VS. Side-chain recognition and gating in the ribosome exit tunnel. Proc Natl Acad Sci USA. 2008;105:16549–16554. doi: 10.1073/pnas.0801795105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hsu S-TD, Fucini P, Cabrita LD, Launay H, Dobson CM, Christodoulou J. Structure and dynamics of a ribosome-bound nascent chain by NMR spectroscopy. Proc Natl Acad Sci USA. 2007;104:16516–16521. doi: 10.1073/pnas.0704664104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ellis JP, Bakke CK, Kirchdoerfer RN, Jungbauer LM, Cavagnero S. Chain dynamics of nascent polypeptides emerging from the ribosome. ACS Chem Biol. 2008;3:555–566. doi: 10.1021/cb800059u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baram D, Pyetan E, Sittner A, Auerbach-Nevo T, Bashan A, Yonath A. Structure of trigger factor binding domain in biologically homologous complex with eubacterial ribosome reveals its chaperone action. Proc Natl Acad Sci USA. 2005;102:12017–12022. doi: 10.1073/pnas.0505581102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ferbitz L, Maier T, Patzelt H, Bukau B, Deuerling E, Ban N. Trigger factor in complex with the ribosome forms a molecular cradle for nascent proteins. Nature. 2004;431:590–596. doi: 10.1038/nature02899. [DOI] [PubMed] [Google Scholar]
- 22.Merz F, Boehringer D, Schaffitzel C, Preissler S, Hoffmann A, Maier T, Rutkowska A, Lozza J, Ban N, Bukau B, Deuerling E. Molecular mechanism and structure of trigger factor bound to the translating ribosome. EMBO J. 2008;27:1622–1632. doi: 10.1038/emboj.2008.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rutkowska A, Mayer MP, Hoffmann A, Merz F, Zachmann-Brand B, Schaffitzel C, Ban N, Deuerling E, Bukau B. Dynamics of trigger factor interaction with translating ribosomes. J Biol Chem. 2008;283:4124–4132. doi: 10.1074/jbc.M708294200. [DOI] [PubMed] [Google Scholar]
- 24.Hoffmann A, Merz F, Rutkowska A, Zachmann-Brand B, Deuerling E, Bukau B. Trigger factor forms a protective shield for nascent polypeptides at the ribosome. J Biol Chem. 2006;281:6539–6545. doi: 10.1074/jbc.M512345200. [DOI] [PubMed] [Google Scholar]
- 25.Tomic S, Johnson AE, Hartl FU, Etchells SA. Exploring the capacity of trigger factor to function as a shield for ribosome bound polypeptide chains. FEBS Lett. 2006;580:72–76. doi: 10.1016/j.febslet.2005.11.050. [DOI] [PubMed] [Google Scholar]
- 26.Chen ZJ, Kurt N, Rajagopalan S, Cavagnero S. Secondary structure mapping of DnaK-bound protein fragments: chain helicity and local helix unwinding at the binding site. Biochemistry. 2006;45:12325–12333. doi: 10.1021/bi0612263. [DOI] [PubMed] [Google Scholar]
- 27.Landry SJ, Jordan R, McMacken R, Gierasch LM. Different conformations for the same polypeptide bound to chaperones DnaK and GroEL. Nature. 1992;355:455–457. doi: 10.1038/355455a0. [DOI] [PubMed] [Google Scholar]
- 28.Kurt N, Rajagopalan S, Cavagnero S. Effect of Hsp70 chaperone on the folding and misfolding of polypeptides modeling an elongating protein chain. J Mol Biol. 2006;355:809–820. doi: 10.1016/j.jmb.2005.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kurt N, Cavagnero S. Nonnative helical motif in a chaperone-bound protein fragment. Biophys J. 2008;94:L48–L50. doi: 10.1529/biophysj.107.127647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mayer M, Bukau B. Hsp70 chaperones: cellular functions and molecular mechanism. Cell Mol Life Sci. 2005;62:670–684. doi: 10.1007/s00018-004-4464-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lipari G, Szabo A. Effect of librational motion on fluorescence depolarization and nuclear magnetic resonance relaxation in macromolecules and membranes. Biophys J. 1980;30:489–506. doi: 10.1016/S0006-3495(80)85109-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Szabo A. Theory of fluorescence depolarization in macromolecules and membranes. Biophys J. 1984;45:A327–A327. [Google Scholar]
- 33.Kinosita K, Jr., Ikegami A, Kawato S. On the wobbling-in-cone analysis of fluorescence anisotropy decay. Biophys J. 1982;37:461–464. doi: 10.1016/S0006-3495(82)84692-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jameson D, Harlett T. Time-resolved fluorescence in biology and biochemistry. In: Dewey GT, editor. Biophysical and biochemical aspects of fluorescence spectroscopy. New York: Plenum; 1991. pp. 105–133. [Google Scholar]
- 35.Maier R, Eckert B, Scholz C, Lilie H, Schmid FX. Interaction of trigger factor with the ribosome. J Mol Biol. 2003;326:585–592. doi: 10.1016/s0022-2836(02)01427-4. [DOI] [PubMed] [Google Scholar]
- 36.Patzelt H, Kramer G, Rauch T, Schonfeld HJ, Bukau B, Deuerling E. Three-state equilibrium of Escherichia coli trigger factor. Biol Chem. 2002;383:1611–1619. doi: 10.1515/BC.2002.182. [DOI] [PubMed] [Google Scholar]
- 37.Raine A, Ivanova N, Wikberg JES, Ehrenberg M. Simultaneous binding of trigger factor and signal recognition particle to the E. coli ribosome. Biochimie. 2004;86:495–500. doi: 10.1016/j.biochi.2004.05.004. [DOI] [PubMed] [Google Scholar]
- 38.Raine A, Lovmar M, Wikberg J, Ehrenberg M. Trigger factor binding to ribosomes with nascent peptide chains of varying lengths and sequences. J Biol Chem. 2006;281:28033–28038. doi: 10.1074/jbc.M605753200. [DOI] [PubMed] [Google Scholar]
- 39.Patzelt H, Rudiger S, Brehmer D, Kramer G, Vorderwulbecke S, Schaffitzel E, Waitz A, Hesterkamp T, Dong L, Schneider-Mergener J, et al. Binding specificity of Escherichia coli trigger factor. Proc Natl Acad Sci USA. 2001;98:14244–14249. doi: 10.1073/pnas.261432298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Maier R, Scholz C, Schmid FX. Dynamic association of trigger factor with protein substrates. J Mol Biol. 2001;314:1181–1190. doi: 10.1006/jmbi.2000.5192. [DOI] [PubMed] [Google Scholar]
- 41.Gite S, Mamaev S, Olejnik J, Rothschild K. Ultrasensitive fluorescence-based detection of nascent proteins in gels. Anal Biochem. 2000;279:218–225. doi: 10.1006/abio.1999.4472. [DOI] [PubMed] [Google Scholar]
- 42.Hardesty B, Kramer G, Ramachandiran V. Cotranslational incorporation of chemically modified initiator tRNA. Recent Res Dev Anal Biochem. 2001;1:39–48. [Google Scholar]
- 43.Beechem JM. Fluorescence spectroscopy data analysis environment a second generation global analysis program. In: Lakowicz J, Gratton E, editors. Time-resolved laser spectroscopy in biochemistry. Bellingham: SPIE; 1988. pp. 70–81. [Google Scholar]


