Abstract
In this work, an investigation of efficiency enhancing methods and cross-section data in the BEAMnrc Monte Carlo (MC) code system is presented. Additionally, BEAMnrc was compared with VMC++, another special-purpose MC code system that has recently been enhanced for the simulation of the entire treatment head. BEAMnrc and VMC++ were used to simulate a 6 MV photon beam from a Siemens Primus linear accelerator (linac) and phase space (PHSP) files were generated at 100 cm source-to-surface distance for the 10×10 and 40×40 cm2 field sizes. The BEAMnrc parameters∕techniques under investigation were grouped by (i) photon and bremsstrahlung cross sections, (ii) approximate efficiency improving techniques (AEITs), (iii) variance reduction techniques (VRTs), and (iv) a VRT (bremsstrahlung photon splitting) in combination with an AEIT (charged particle range rejection). The BEAMnrc PHSP file obtained without the efficiency enhancing techniques under study or, when not possible, with their default values (e.g., EXACT algorithm for the boundary crossing algorithm) and with the default cross-section data (PEGS4 and Bethe–Heitler) was used as the “base line” for accuracy verification of the PHSP files generated from the different groups described previously. Subsequently, a selection of the PHSP files was used as input for DOSXYZnrc-based water phantom dose calculations, which were verified against measurements. The performance of the different VRTs and AEITs available in BEAMnrc and of VMC++ was specified by the relative efficiency, i.e., by the efficiency of the MC simulation relative to that of the BEAMnrc base-line calculation. The highest relative efficiencies were ∼935 (∼111 min on a single 2.6 GHz processor) and ∼200 (∼45 min on a single processor) for the 10×10 field size with 50 million histories and 40×40 cm2 field size with 100 million histories, respectively, using the VRT directional bremsstrahlung splitting (DBS) with no electron splitting. When DBS was used with electron splitting and combined with augmented charged particle range rejection, a technique recently introduced in BEAMnrc, relative efficiencies were ∼420 (∼253 min on a single processor) and ∼175 (∼58 min on a single processor) for the 10×10 and 40×40 cm2 field sizes, respectively. Calculations of the Siemens Primus treatment head with VMC++ produced relative efficiencies of ∼1400 (∼6 min on a single processor) and ∼60 (∼4 min on a single processor) for the 10×10 and 40×40 cm2 field sizes, respectively. BEAMnrc PHSP calculations with DBS alone or DBS in combination with charged particle range rejection were more efficient than the other efficiency enhancing techniques used. Using VMC++, accurate simulations of the entire linac treatment head were performed within minutes on a single processor. Noteworthy differences (±1%–3%) in the mean energy, planar fluence, and angular and spectral distributions were observed with the NIST bremsstrahlung cross sections compared with those of Bethe–Heitler (BEAMnrc default bremsstrahlung cross section). However, MC calculated dose distributions in water phantoms (using combinations of VRTs∕AEITs and cross-section data) agreed within 2% of measurements. Furthermore, MC calculated dose distributions in a simulated water∕air∕water phantom, using NIST cross sections, were within 2% agreement with the BEAMnrc Bethe–Heitler default case.
Keywords: Monte Carlo, efficiency, variance reduction techniques, cross sections
INTRODUCTION
Monte Carlo (MC) simulation techniques are presently considered to be the most reliable method for radiation therapy treatment planning.1, 2 A number of general-purpose Monte Carlo code systems, namely, EGSnrc,3MCNP,4PENELOPE,5 and GEANT4,6 are often used to study several dosimetry-based challenges posed in radiation therapy. A common example is the simulation of coupled electron-photon transport in the linear accelerator (linac) treatment head to generate phase space (PHSP) files with information on the beam’s energy and spatial and angular distributions, which can then be used to create photon and electron beam models for treatment planning.
However, long simulation times involved when using the general-purpose Monte Carlo code systems have led to the development of special-purpose MC programs such as PEREGRINE,7 voxel Monte Carlo series of codes (VMC∕XVMC∕VMC++),8, 9, 10, 11 macro Monte Carlo (MMC),12MCDOSE∕MCSIM,13, 14 dose planning method (DPM),15, 16, 17 and BEAMnrc,18 an EGSnrc Monte Carlo user code that, with large efficiency improvements, is fast enough for radiotherapy planning simulations.19, 20 These special-purpose MC code systems use sophisticated efficiency improvement tools, such as variance reduction techniques (VRTs) to drastically reduce the central processing unit (CPU) time for a given uncertainty level of a quantity of interest (e.g., dose, fluence). Some of these special-purpose MC codes are being used as a dose engine for MC-based treatment planning in the routine clinical setting.7, 21, 22, 23
Approximate efficiency improving techniques (AEITs) and VRTs can significantly increase the efficiency of a Monte Carlo calculation. VRTs do not change the physics and therefore do not bias the results. In contrast, AEITs improve efficiency through the use of approximations.24 Examples of VRTs are bremsstrahlung photon splitting, Russian Roulette, and photon interaction forcing; examples of AEITs are charged particle range rejection (RR), use of electron and photon transport cutoff energies, and the condensed history technique25 for charged particle transport. The use of sophisticated variance reduction and approximate efficiency improving techniques, combined with parallel processing in computer clusters and the continuing increase in computing power, will help make MC-based treatment planning a mainstay option in radiation oncology departments.1, 2, 26, 27
Here, we investigate the efficiency enhancing methods and cross-section data available in the BEAMnrc MC code system and their effect on the accuracy of calculated fluence and dose distributions. In addition, BEAMnrc calculations are compared with another special-purpose MC code system, VMC++. BEAMnrc provides the user with a variety of options for variance reduction and approximate efficiency improving techniques, making it fast enough for the simulation of linac treatment heads, while VMC++ has recently been enhanced for the simulation of the entire treatment head.28BEAMnrc efficiency improvement studies on specific techniques such as the charged particle range rejection,29, 30 bremsstrahlung photon splitting,19, 31 and a new implementation of the condensed history technique32 have been presented during release of the code, however, no systematic study on the improvement in efficiency when using these techniques, separately or combined with each other, has, recently, been presented. Three main areas were considered.
-
(1)
An investigation of the influence of different photon and bremsstrahlung cross-section data available in BEAMnrc on the accuracy of calculated fluence and dose distributions. It is generally accepted that the cross-section data available in the megavoltage energy range are sufficiently accurate.1, 33 Recently, measurements of bremsstrahlung in the radiotherapy energy range from thick targets have been used to benchmark fluence calculated using different cross-section data,34 however, there has yet to be a study comparing the dose distributions for megavoltage photon beams using different cross-section data.
-
(2)
A systematic study of the influence of efficiency enhancing methods available in BEAMnrc on the accuracy of calculated fluence and dose distributions. The following efficiency enhancing methods were considered: charged particle range rejection, boundary crossing algorithm (BCA), bremsstrahlung photon splitting, Russian Roulette, and photon interaction forcing.
-
(3)
An evaluation of the accuracy and efficiency of theVMC++ MC code system for photon beam accelerator modeling. VMC++ is a well known special-purpose MC code system for accurate electron and photon dose calculations.8, 9, 10, 11, 35 Recently, a comparison study of simulated linac heads between VMC++ and BEAMnrc MC code systems for 6 and 18 MV photon beams from Varian-like machines has been reported.28 In our study, VMC++ was compared with BEAMnrc for a 6 MV photon beam from a Siemens Primus linac.
Finally, DOSXYZnrc,36 an EGSnrc MC user code, was used to calculate dose distributions in a water phantom, which were compared with measured data, and in a simulated water∕air∕water phantom using a selection of PHSP files generated with BEAMnrc and VMC++ as input sources. This was performed to validate the accuracy of the fluence calculated with the various VRTs, AEITs, and cross-section data.
MATERIALS AND METHODS
The 2007 release version of BEAMnrc and the VMC++ MC code systems were used to simulate a 6 MV photon beam from a Siemens Primus linac. A research version of VMC++, distributed by the National Research Council of Canada in executable form, was used in this work. The two MC code systems were used to generate PHSP files at 100 cm source-to-surface distance (SSD) for the 10×10 and 40×40 cm2 field sizes, defined by the collimating jaws. The initial number of histories was set to obtain approximately the same number of particles in the PHSP files, i.e., 50 and 100 million for the 10×10 and 40×40 cm2 field sizes, respectively.
The current version of BEAMnrc allows the user to choose three photon cross sections: PEGS4 (default), XCOM, EPDL; two bremsstrahlung cross sections: Bethe–Heitler (default), NIST; two boundary crossing algorithms: EXACT (default) and PRESTA-I; three photon splitting techniques: uniform bremsstrahlung splitting (UBS), selective bremsstrahlung splitting (SBS), and directional bremsstrahlung splitting (DBS).18 All of these options were considered in addition to charged particle range rejection and photon interaction forcing, alone or in combination with the photon splitting technique. The electron and photon cutoff energies were set to 0.7 and 0.01 MeV total energy (which includes the electron rest mass energy for the charged particle), respectively. Table 1 shows how the BEAMnrc parameters∕techniques investigated were grouped, in a total of 21 different configurations. The parameter values chosen for the different techniques are recommendations from previous published works19, 30 or are considered to be reasonable estimates, based on information from the BEAMnrc developers. In each BEAMnrc simulation performed, only one of the parameters∕techniques was changed while the others were maintained at their default values, unless stated otherwise.
Table 1.
The BEAMnrc parameters∕techniques investigated were organized in four groups: (1) photon and bremsstrahlung cross sections, (2) approximate efficiency improving techniques (AEITs), (3) variance reduction techniques (VRTs), and (4) a VRT in combination with an AEIT. The default values of some parameters are in bold type while the default for others (not bolded) are without the specific VRT or AEIT. UBS stands for uniform bremsstrahlung splitting, SBS for selective bremsstrahlung splitting, DBS for directional bremsstrahlung splitting, NBRSPL for bremsstrahlung splitting number N for number of forced photon interactions, and ARR for augmented range rejection.
| Group | Parameters∕techniques | Parameters∕techniques values | |
|---|---|---|---|
| Cross sections | Photon | PEGS4, XCOM, EPDL | |
| Bremsstrahlung | BH, NIST | ||
| AEITs | Charged particle range rejection (RR)a | ESAVE=2 MeV, except, target=0.7 MeV | |
| Boundary crossing algorithm (BCA) | EXACT, PRESTA-I | ||
| VRTs | Bremsstrahlung photon splittingb | UBS | NBRSPL=250, Russian Roulette OFF |
| NBRSPL=750, Russian Roulette ON | |||
| SBS | NBRSPL=1000, Russian Roulette OFF | ||
| NBRSPL=2500, Russian Roulette ON | |||
| DBS | NBRSPL=1000, with electron splitting | ||
| NBRSPL=2500, no electron splitting | |||
| Bremsstrahlung photon splitting+ photon interaction forcing (PF) | N=5 no bremsstrahlung splitting | ||
| N=5 UBS (NBRSPL=250, Russian Roulette (OFF) | |||
| N=5 SBS (NBRSPL1000, Russian Roulette OFF) | |||
| N=5 DBS (NBRSPL=1000, with electron splitting) | |||
| VRT+AEIT | Bremsstrahlung photon splitting+ charged particle range rejection | UBS (NBRSPL=250, Russian Roulette OFF) RR (ESAVE=2 MeV, except target=0.7 MeV) | |
| SBS (NBRSPL=1000, Russian Roulette OFF) RR (ESAVE=2 MeV, except target=0.7 MeV) | |||
| DBS (NBRSPL=1000, with electron splitting) RR (ESAVE=2 MeV, except target=0.7 MeV) | |||
| DBS (NBRSPL=1000, with electron splitting) ARR (ESAVE=2 MeV, except target=0.7 MeV) | |||
In total, 42 PHSP files were generated at 100 cm SSD, for the two field sizes simulated with BEAMnrc and VMC++. The mean energy, planar fluence, and spectral and angular distributions were extracted from the PHSP files, using a radius consisting of 75% of the field size (half-width of the field size plus an additional margin that includes the penumbral region), i.e., 7.5 and 30 cm for the 10×10 and 40×40 cm2 field sizes, respectively. BEAMDP (Ref. 37) was used to obtain their average values and uncertainties in bins of equal width or area within a circular region of interest centered at the z-axis. The mean energy and planar fluence were extracted from the PHSP in circular ring bins of equal area, the spectral distribution in energy bins of equal bin width, and the angular distribution in angular bins of equal bin width. The PHSP file from the simulation with BEAMnrc default parameters∕techniques was taken as the “base line” and the remaining phase space files were compared to it for accuracy verification. The physical quantities mentioned above were used to calculate the Monte Carlo simulation efficiencies for the PHSP files generated with the different classes of efficiency enhancing methods in BEAMnrc and with VMC++. A selection of the PHSP files generated withBEAMnrc and VMC++ was subsequently used to validate the MC calculated central and off-axis dose profiles with measurements for the two field sizes at 100 cm SSD, using DOSXYZnrc. The measurements were performed in a Scanditronix–Wellhofer water phantom scanning system (IBA Dosimetry, Schwarzenbruck, Germany) with a Wellhofer IC-10 cylindrical ionization chamber (active volume=0.125 cm3; active diameter=6 mm). Additionally, MC dose calculations were performed in a simulated water∕air∕water phantom. The electron and photon cutoff energies were set to 0.521 and 0.01 MeV, total energy (which includes the electron rest mass energy for the charged particle), respectively. In DOSXYZnrc and for the calculations in the water phantom, the “HOWFARLESS” option was used. It has been reported that this option increases the efficiency of homogeneous phantom calculations,38 however, no photon splitting or charged particle range rejection were employed.36 The homogeneous water phantom dimensions were 30×30×30 and 60×60×30 cm3 for the 10×10 and 40×40 cm2 field sizes, respectively, using cubic voxels, 0.5 cm on a side. An additional phantom with a 5 cm air gap embedded in water was also simulated for dose computations. All MC simulations were performed on a 2.6 GHz Opteron cluster, using ten CPUs per simulation.
In the following sections, brief descriptions of theBEAMnrc and VMC++ parameters and values used in this study are presented. In addition, the methods for performing the efficiency and statistical uncertainty calculations are described.
Photon and bremsstrahlung cross sections
The current version of BEAMnrc allows the user to choose three different photon cross sections: “Storm-Israel (PEGS4),” which is the standard PEGS4 cross sections and the default photon cross section;39 “EPDL,” which uses the cross sections from the evaluated photon data library (EPDL) from Lawrence Livermore National Laboratory;40 and “XCOM,” which uses the XCOM photon cross sections from Berger and Hubbell.41
The default differential cross section for the bremsstrahlung interactions is Bethe–Heitler (BH).42 The user has also the choice of using the differential cross sections from NIST.43, 44, 45 In the megavoltage energy range, the BH cross section is obtained from the first Born approximation with an empirical correction factor,42 while the NIST cross section uses partial wave analysis calculations for electron energies below 2 MeV.45 Above 50 MeV, the NIST differential cross section is evaluated by using a combination of the screened BH differential cross section with various forms of the Coulomb correction.46 Between 2 and 50 MeV, the NIST cross section uses cubic spline interpolations of the cross sections from the lower and higher energies.
Phase space files were generated for the three different photon cross sections, maintaining all other parameters shown in Table 1 with their default values, i.e., BH bremsstrahlung differential cross section was used with no VRTs, no charged particle range rejection, and the EXACT option for the boundary crossing algorithm. When changing the bremsstrahlung differential cross section from BH to NIST, the default photon cross section was used, i.e., PEGS4.
Approximate efficiency improving techniques
Charged particle range rejection
In charged particle RR, the particle’s history is terminated whenever its residual range is so low that it cannot escape from the current region or reach the region of interest. In BEAMnrc, the particle’s history is terminated only if its energy is below a predefined energy threshold (ESAVE), minimizing the possibility of not creating bremsstrahlung photons that could escape the region. In our study, ESAVE was set to 2 MeV in all component modules with the exception of the target where the electron cutoff energy value was used, as recommended in Sheikh–Bagheri et al.30 When using DBS with electron splitting (more on this technique below) together with the option of charged particle range rejection, the augmented range rejection (ARR) scheme can also be used. This is a technique, recently introduced in BEAMnrc,18 that is more efficient than the standard range rejection scheme just described. Augmented range rejection is identical to the standard RR with the exception that all “nonfat” charged particles (i.e., particles with a weight equal to the inverse of the bremsstrahlung splitting number, NBRSPL) that cannot escape a region and with energy above ESAVE are subjected to Russian Roulette. Augmented range rejection accounts correctly for bremsstrahlung production, since charged particles surviving Russian Roulette and with their weight increased by a factor of NBRSPL still have a chance to undergo bremsstrahlung events.18 If ESAVE is set to be greater than the electron cutoff energy, augmented range rejection is a mixture between VRT and AEIT because charged particles with energies above ESAVE are subject to Russian Roulette, which is a VRT, and charged particles with energies below ESAVE are range rejected.
Charged particle range rejection was used independently and in conjunction with the three different options for bremsstrahlung photon splitting (see Table 1).
Boundary crossing algorithm
The boundary crossing algorithm together with the electron transport algorithm constitutes the condensed history technique used by a particular MC code system.24 InBEAMnrc, the user has the choice of two different BCA: PRESTA-I and EXACT, where the latter is the default option.47 We investigated the differences between the PRESTA-I and EXACT BCA implementations in the calculated fluence.
Variance reduction techniques
Bremsstrahlung photon splitting, Russian Roulette, and electron splitting
The three options for bremsstrahlung photon splitting were used in this study, i.e., uniform bremsstrahlung splitting, selective bremsstrahlung splitting, and directional bremsstrahlung splitting. Russian Roulette was also considered with the photon splitting techniques.18
When using UBS, each bremsstrahlung event produces a predefined number of bremsstrahlung photons, each having a weight equal to the inverse of the splitting number (NBRSPL) times the weight of the electron that underwent the bremsstrahlung event. With SBS, the value of NBRSPL is changed in order to maximize the splitting of photons aimed into the field and to minimize unnecessary splitting of photons aimed away from the field.18 Two values are considered for the number of splitting photons, NBRSPL and the background splitting number which is defined as one-tenth of the maximum. The SBS routine also requires information on the SSD and on a field size defined at SSD, in order to calculate the relevant angle for photon splitting.18 The BEAMnrc user’s manual recommends that the field size should be defined by the larger side of the treatment field plus 10 cm at 100 cm SSD, however, in this study we added 20 cm based on the study by Kawrakow et al.19 Finally, when DBS is used, NBRSPL is defined together with the field radius, which must include, as a minimum, the entire treatment field. The option for electron splitting, in DBS, improves precision of the electron fluence calculation in the PHSP file.19
Table 2 summarizes the relevant parameters used, where the values chosen follow the recommendations of Kawrakow et al.19 If the user is not interested in improving the electron fluence at the bottom of the accelerator, UBS and SBS are used with Russian Roulette, DBS is used with no electron splitting, and NBRSPL is changed accordingly to higher values (see Table 2).
Table 2.
Bremsstrahlung splitting techniques and the values used for the relevant parameters.
| NBRSPL | BackgroundNBRSPL | Effective field size (SBS) or splitting field radius (DBS) (cm) | Russian Roulette | Electron splitting | ||
|---|---|---|---|---|---|---|
| 10×10 cm2 | 40×40 cm2 | |||||
| UBS | 250 | ⋯ | ⋯ | ⋯ | Off | ⋯ |
| 750 | ⋯ | ⋯ | ⋯ | On | ⋯ | |
| SBS | 1000 | 100 | 30 | 60 | Off | ⋯ |
| 2500 | 250 | 30 | 60 | On | ⋯ | |
| DBS | 1000 | ⋯ | 10 | 30 | On | On |
| 2500 | ⋯ | 10 | 30 | On | Off | |
Bremsstrahlung photon splitting was used independently and in conjunction with photon interaction forcing or charged particle range rejection (see Table 1). When photon splitting was used together with the other techniques, only the cases with improved photon and electron fluence were considered, i.e., UBS and SBS were used with no Russian Roulette and DBS with electron splitting. Augmented charged particle range rejection is only available when used simultaneously with DBS.18
Photon interaction forcing
With photon interaction forcing, the user can force photons to interact up to a user-defined number of times, N, in specified component modules within a simulation. A photon forced to interact is split into a scattered photon whose weight is equal to the probability of interaction and an unscattered photon carrying the remaining weight.18 The unscattered photon proceeds as if no interaction has taken place and is not forced to interact within the specified forcing zone. Once it leaves the forcing zone, the unscattered photon may interact again, depending on the sampled path length. On the other hand, the scattered photon can be forced to interact again in the forcing zone, depending on how many forced interactions are still available. The photon forcing parameters can also be passed onto secondary photons and this feature is particularly useful to improve calculation efficiency for bremsstrahlung photon interactions, especially when combined with bremsstrahlung photon splitting.18 In this study, when photon forcing was used, photons were forced to interact five times and all component modules were considered to undergo photon forcing.
VMC++
When compared with general-purpose MC code systems, VMC++ shows a significant decrease in CPU time to achieve comparable statistical precision and accuracy not only in the calculation of dose distributions but also in the generation of phase space files at the bottom of the linac. This efficiency gain is achieved through the use of variance reduction techniques and faster simulation of the electron transport.10, 11, 28VMC++ uses four main VRTs to improve its efficiency, namely, directional radiative splitting, which is an extension of the DBS technique found in BEAMnrc, rotational splitting, bremsstrahlung cross section enhancement, and electron importance. More details on how these VRTs work within the VMC++ code system can be found in Hasenbalg et al.28 At run time, the executable VMC++ file dynamically loads into memory a shared library containing detailed information about the geometry of the linac treatment head, while the MC transport and variance reduction parameters are controlled by the user in a separate input file. The full treatment head simulation is performed and a PHSP file is generated at 100 cm SSD, with the same properties of a BEAMnrc phase space file. Table 3 shows the values employed in theVMC++ calculations for the relevant MC transport and variance reduction parameters.
Table 3.
MC transport and variance reduction parameters used in the VMC++ calculations.
| Monte Carlo transport parameters | |
|---|---|
| Maximum electron step, smax (cm) | 10 |
| Maximum electron loss per step (MeV) | 0.25 |
| Bremsstrahlung production threshold, ap (MeV) | 0.05 |
| Delta particle production threshold, ae (MeV) | 0.25 |
| Variance reduction parameters | |
| Radiative splitting number | 4096 |
| Electron splitting number | 64 |
| Rotational parameter δ (cm) | 1.5 |
| Cross section enhancement for bremsstrahlung α (MeV−4) | 0.0035 |
| Electron importances, EI | 2nn=0,1,…,9 |
Efficiency calculations
The performance of the various VRTs∕AEITs combinations in BEAMnrc and of VMC++ was specified by the efficiency ε given by
| (1) |
where s is an estimate of the uncertainty on the quantity of interest and t is the CPU time required to obtain this uncertainty.
It is important to correctly define a measure of the overall uncertainty on the quantity of interest in order to accurately evaluate the efficiency of a particular MC simulation algorithm. Rogers and Mohan48 suggested an “average” uncertainty as a measure of the overall uncertainty of a MC dose patient calculation, obtained as
| (2) |
where Di is the dose in the i-voxel and ΔDi is the corresponding statistical uncertainty. Only the voxels with a dose greater than 50% of the maximum dose are accounted for in the calculation of this average quantity. To better evaluate to what extent the statistical fluctuations affect the efficiency of MC simulations, different levels of “overall” uncertainty were considered in this study,
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where is the uncertainty of the quantity of interest and its average in a given bin. For the first three uncertainty calculations, only one bin is considered, i.e., the central bin (c) and the bins with the maximum (M) and the minimum (m) values in the plot. The fourth uncertainty calculation considers only the bins with values greater than 50% of the maximum value (50%) and, finally, the fifth uncertainty calculation uses all bins (a) in the plot.
RESULTS AND DISCUSSION
CPU time
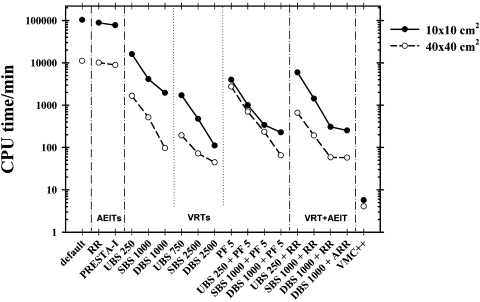
Figure 1 shows the CPU time spent generating PHSP files at 100 cm SSD for the 10×10 and 40×40 cm2 field sizes, using the different efficiency improvement methods available in BEAMnrc and for VMC++. The CPU times were scaled to a single 2.6 GHz Opteron processor.
Figure 1.
CPU time (log scale) spent generating phase space files at 100 cm SSD for the 10×10 and 40×40 cm2 field sizes, using VMC++ and the different AEITs and VRTs available in BEAMnrc (see Table 1). CPU time is scaled to that of a single 2.6 GHz Opteron processor. The label “default” refers to BEAMnrc simulation using default parameters∕techniques.
BEAMnrc simulation using only the default parameters∕techniques took approximately 72 and 7.7 days to generate PHSP files at 100 cm SSD for the 10×10 and 40×40 cm2 field sizes, respectively. The PHSP generated for the smaller field size has, approximately, eight times higher fluence per unit area than the 40×40 cm2 field size because its cross-sectional area is 16 times smaller and it has approximately half the number of particles, thus taking about eight times longer to generate the PHSP file. The PHSP files generated with VMC++ took approximately 6 and 4 min for the 10×10 and 40×40 cm2 field sizes, respectively, representing a CPU saving time of approximately 18 000 and 2700 when compared with BEAMnrc default case. This considerable speed gain owes to the sophisticated variance reduction techniques available in VMC++.
For both field sizes, changing the boundary crossing algorithm from EXACT to PRESTA-I or employing charged particle range rejection produced only a small decrease in the CPU time, i.e., the PHSP files were generated approximately 1.2 times faster than using EXACT for the BCA or no RR techniques (BEAMnrc default). When using only bremsstrahlung photon splitting, the greatest CPU time saving is when DBS is used with and without electron splitting, for both field sizes, i.e., (a) DBS with NBRSPL=1000 and with electron splitting (∼53 and ∼115 times faster for the small and large field sizes, respectively), generating PHSP files with improved photon and electron fluence; (b) DBS with NBRSPL=2500 and with no electron splitting (∼930 and ∼250 times faster for the small and large field sizes, respectively), representing the case where the user is not interested in improving the electron fluence in the PHSP file. If one excludes the group where improved electron fluence in the PHSP file is not relevant, the following techniques generated the PHSP files with the greatest CPU saving time: (a) DBS with NBRSPL=1000 combined with photon interaction forcing, for the small field size (∼455 times faster); (b) DBS with NBRSPL=1000 combined with augmented charged particle range rejection, for the large field size (∼194 times faster). However, as demonstrated in Sec. 3C, PHSP files generated the fastest do not necessarily have the highest efficiency.
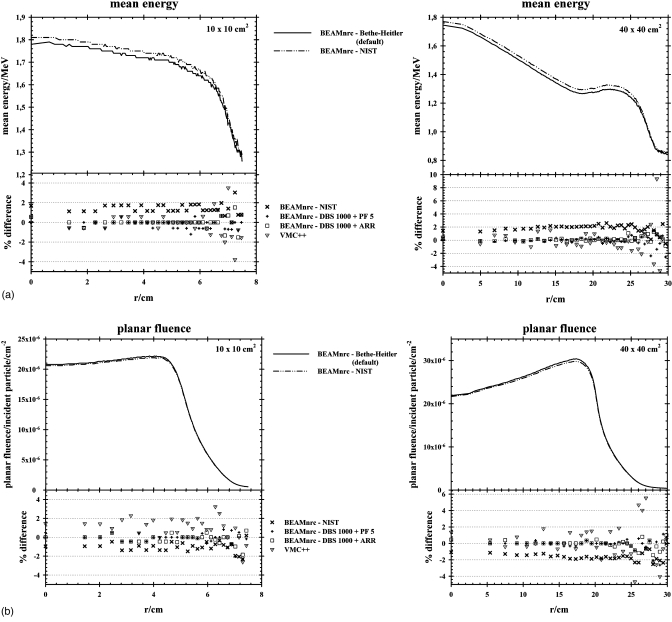
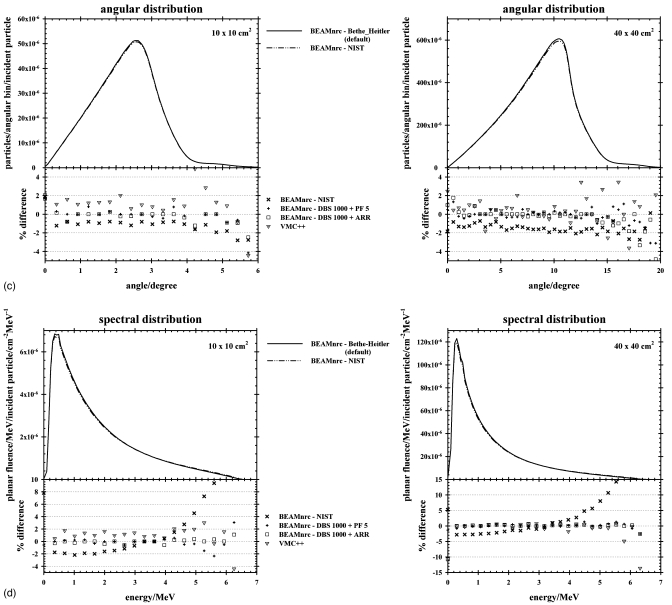
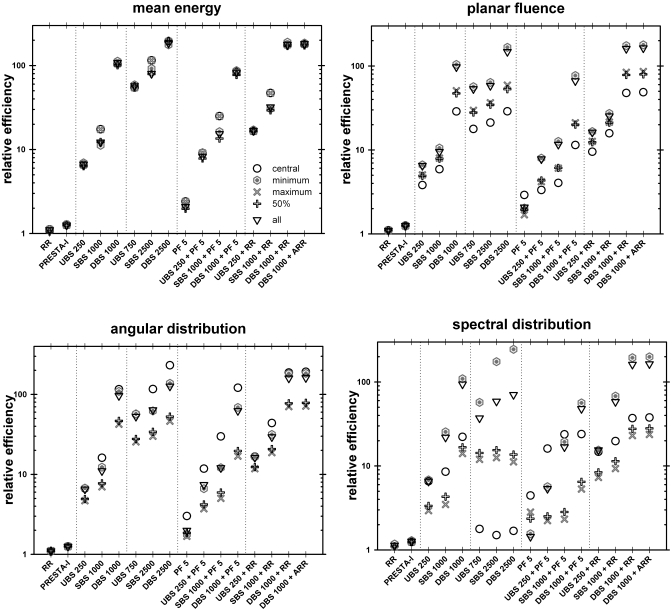
Phase space analysis
Figure 2 shows the mean energy, planar fluence, and angular and spectral distributions for the BEAMnrc PHSP files generated at 100 cm SSD with BH (default) and NIST bremsstrahlung cross sections. The percentage difference between BEAMnrc with default parameters∕techniques andVMC++ and a selection of other BEAMnrc PHSP files is also shown. Similarly to the cases of DBS combined with augmented charged particle range rejection and with photon forcing, the remaining data matched within 1% with the BEAMnrc default case and are not plotted here.
Figure 2.
(a) Mean energy, (b) planar fluence, and (c) angular and (d) spectral distributions for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections and for the 10×10 and 40×40 cm2 field sizes. The percentage difference between BEAMnrc with the default parameters∕techniques and NIST, DBS combined with photon forcing (DBS 1000+PF 5), DBS combined with augmented charged particle range rejection (DBS 1000+ARR), and VMC++ is also shown.
For both field sizes, the quantities extracted from the PHSP file generated with BEAMnrc using NIST differential bremsstrahlung cross section showed differences of ±1%–3%, on average, when compared with those ofBEAMnrc generated with BH (default). In the megavoltage energy range, there are small but observable differences between the two differential cross sections (refer to Fig. 7 of the EGSnrc manual3) and it has been previously reported that differences in bremsstrahlung data resulted in differences in absolute photon output in linac modeling studies.33 Faddegon et al.34 used published experimental benchmarks to evaluate the accuracy of thick-target bremsstrahlung photons calculated with several MC code systems, namely, EGSnrc, GEANT4, and PENELOPE. They concluded that MC simulation is capable of calculating the fluence differential in energy to 10% in intermediate energy. EGSnrc and PENELOPE were found to be the most accurate amongst the codes tested.34EGSnrc calculations with the NIST bremstrahlung cross-section option were “preferred” over those with the BH option. The VMC++ results show considerable fluctuations in the percentage difference because of higher statistical uncertainty on the data, especially at larger distances from the irradiated field.
Performance of the efficiency enhancing techniques in BEAMnrc and of VMC++
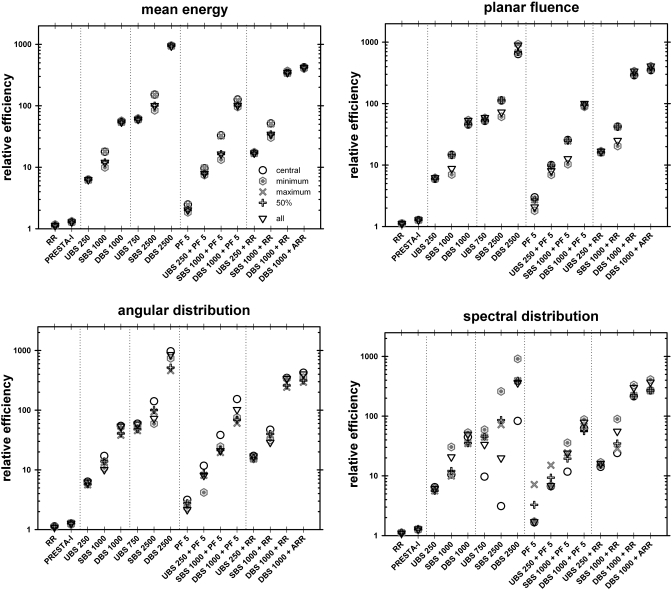
The efficiency of the MC simulations using the different efficiency enhancing techniques available in BEAMnrc relative to the efficiency obtained for the BEAMnrc default case are shown in Figs. 34 for the 10×10 and 40×40 cm2 field sizes, respectively.
Figure 3.
Efficiencies for 10×10 cm2 field size, relative to the efficiency obtained for the BEAMnrc default case. The uncertainty was calculated in five different ways, i.e., using only the central bin, the bins with the minimum and maximum values, the bins with values greater than 50% of the maximum value, and, finally, considering all bins.
Figure 4.
Efficiencies for the 40×40 cm2 field size, relative to the efficiency obtained for the BEAMnrc default case. The uncertainty was calculated in five different ways, i.e., using only the central bin, the bins with the minimum and maximum values, the bins with values greater than 50% of the maximum value, and, finally, considering all bins.
For the 10×10 cm2 field size and for the case of improved photon and electron fluence at 100 cm SSD, the PHSP file generated the fastest with BEAMnrc was the combination of DBS with photon interaction forcing, taking approximately 3.8 h (see Fig. 1). However, the highest relative efficiencies were obtained for the combination of DBS with augmented charged particle range rejection (DBS 1000+ARR) and for DBS with no electron splitting (DBS 2500) for the mean energy, planar fluence, and angular distribution, regardless of the measure used to estimate the uncertainty (see Fig. 3). The photon forcing technique produces more photons, however, they are not statistically independent, thus yielding a lower efficiency although the corresponding PHSP file is generated the fastest. Figure 4 shows, for the 40×40 cm2 field size, that as the quantity of interest is changed from planar fluence to spectral distribution, other efficiency enhancing techniques yield higher relative efficiencies for certain estimates of the uncertainty, which was not observed for the smaller field size, with exception for the spectral distribution. For a particular efficiency enhancing technique used in BEAMnrc, the difference between the relative efficiencies obtained using the various estimates of the uncertainty increases as one changes from planar fluence to spectral distribution; this situation is clearly more evident for the larger field size (see Figs. 34). The variance for the 40×40 cm2 field size is larger than that for the 10×10 because the fluence per unit area (for the 40×40) is about eight times lower than for the 10×10 cm2 field size. The main reason for the variation in the relative efficiencies between 10×10 and 40×40 is the inherently different approaches used with the various VRTs in increasing importance within different regions of the phase space.24 For the 10×10 cm2 field size, the fraction of “useful” phase space, from a spatial point of view, is much less than that of the 40×40 cm2 field size. For instance, in the DBS case, the variance within the field for the 10×10 cm2 field size will be lower than that for the 40×40 cm2 field size due to the increased fluence per unit area, but it will increase quickly outside the field, and for all regions outside the useful 10×10 phase space. For the 40×40 cm2 field size, the variance will also be low in the field and will increase outside the field, but the region of useful phase space will be much greater than that for the 10×10. Since the efficiencies are calculated over the entire phase space distribution (spatially), the relative efficiencies between the 10×10 and 40×40 cm2 field sizes will clearly be much different.
VMC++ CPU time and relative efficiencies for the 10×10 and 40×40 cm2 field sizes are shown in Table 4, where for the same quantity of interest, noticeable discrepancies between the different ways used to report the uncertainty estimate are observed. As with the different efficiency enhancing techniques used in BEAMnrc, a similar field size trend is seen with VMC++, i.e., relative efficiencies are clearly lower for the larger field size (see Figs. 34 and Table 4). The efficiency enhancing techniques used inVMC++, which maximizes the tracking of the particles aimed into the field of interest and minimizes unnecessary splitting of photons aimed away from the field, give lower statistical fluctuations in the center part of the field than on the field edges. This effect increases with field size, and depending on the uncertainty measure used, can result in increased uncertainties with VMC++ for larger field sizes. For instance, there are results for the 40×40 cm2 field size where BEAMnrc using DBS combined with augmented charged particle range rejection gives higher relative efficiencies than VMC++. However, to put this in context, for an equal number of particles generated in the phase space file, VMC++ is approximately 15 times faster than BEAMnrc case. Another important consideration is that the relative fluence efficiency, for a given splitting number, actually decreases with increase scoring zone area, a result derived mathematically in an article by Kawrakow.49 It is shown that for a given, fixed scoring zone of side of 1 cm or less, the efficiency of DBS highest (relative to UBS) and drops quickly approaching that of UBS when the scoring zone side increases beyond 4 cm.49 A limitation of our work is that, in using BEAMDP, nonuniform scoring zone areas (i.e., concentric circles of increasing area) were used to reconstruct the fluence distributions. Therefore, the actual relative efficiencies possible with DBS were underestimated. If the fluence distributions were reconstructed using equal area scoring zones (e.g., 1×1 cm2) the relative efficiencies observed with VMC++ and BEAMnrc (using DBS) would have been much higher.
Table 4.
VMC++ CPU time and relative efficiencies for the 10×10 and 40×40 cm2 field sizes. Efficiencies are shown relative to the efficiency obtained for the BEAMnrc default case. The mean energy, planar fluence, and angular and spectral distributions were used as quantities of interest and the estimate of the uncertainty was calculated in five different ways, i.e., using only the central bin (c), using the bins with the minimum (m), and maximum (M) values, using the bins with values greater than 50% of the maximum value, and, finally, considering all bins.
| 10×10 cm2 | 40×40 cm2 | ||
|---|---|---|---|
| CPU time (min) | 5.7 | 4.1 | |
| Mean energy efficiencies | c | 17 836.6 | 525.6 |
| m | 1 055.3 | 71.0 | |
| M | 7 759.6 | 525.6 | |
| 50% | 1 397.6 | 62.2 | |
| All | 1 397.6 | 60.8 | |
| Planar fluence efficiencies | c | 9 873.3 | 237.7 |
| m | 840.2 | 44.4 | |
| M | 1 101.3 | 36.3 | |
| 50% | 1 322.5 | 47.0 | |
| All | 1 183.3 | 48.0 | |
| Angular distribution efficiencies | c | 17 058.7 | 2096.9 |
| m | 14 816.7 | 182.9 | |
| M | 939.9 | 33.8 | |
| 50% | 1 226.4 | 42.7 | |
| All | 12 520.0 | 54.8 | |
| Spectral distribution efficiencies | c | 293.4 | 16.1 |
| m | 1 576.5 | 63.4 | |
| M | 1 104.8 | 30.4 | |
| 50% | 1 147.1 | 34.2 | |
| All | 905.6 | 55.9 | |
The results presented emphasize the importance of using a proper measure of the uncertainty on the quantity of interest in the calculation of the efficiency of a MC simulation. Estimates of the uncertainty using a significant number of bins (e.g., all bins or bins with 50% of the maximum value) within the field under analysis must be considered, in order to wash out the statistical fluctuations from the individual bins. In addition, the relative efficiencies are dependent on the quantity of interest chosen, although one can claim from this study that BEAMnrc MC calculations with the directional bremsstrahlung splitting technique yields the highest efficiency for all quantities of interest analyzed.
Dose distributions
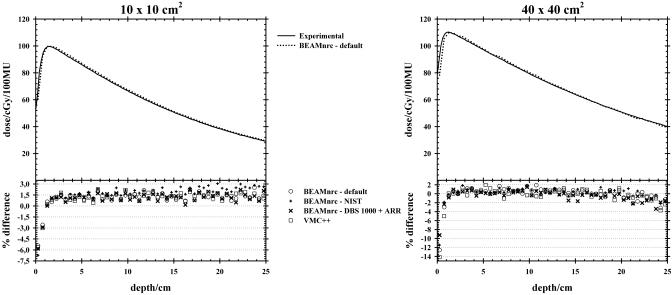
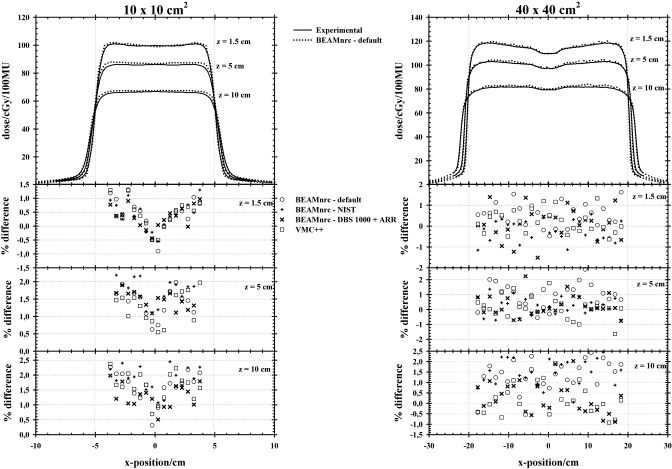
Figures 56 show the measured and MC calculated (BEAMnrc default parameters∕techniques) central and off-axis dose profiles, in a water phantom for the 10×10 and 40×40 cm2 field sizes. The percentage difference between measured and a selection of MC calculated central and off-axis dose profiles is also shown. For both field sizes, the results were normalized to the linac calibration point in cGy per 100 MU, i.e., at the depth of maximum dose on the central axis for the 10×10 cm2 field size and at 100 cm SSD.
Figure 5.
Measured and calculated (BEAMnrc default parameters∕techniques) central-axis dose profiles in a water phantom for the 10×10 and 40×40 cm2 field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference between measured and a selection of MC calculated central-axis dose profiles is also shown.
Figure 6.
Measured and MC calculated (BEAMnrc default parameters∕techniques) off-axis dose profiles in a water phantom for the 10×10 and 40×40 cm2 field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference, in the central region of the field and at different depths, between measured and a selection of MC calculated off-axis dose profiles is also shown.
The percentage difference between MC calculations and measured data on the central axis was, on average, within 1%, although greater differences were observed in the buildup region. For off-axis dose profiles, the agreement between MC calculations and measurement, at different depths, was within 2% in the central region of the field. Good overall agreement in the dose distribution was also obtained for the NIST case (see Figs. 56), although differences of ±1%–3% in the physical quantities extracted from the NIST and BH bremsstrahlung cross-section PHSP files were observed (see Sec. 3B).
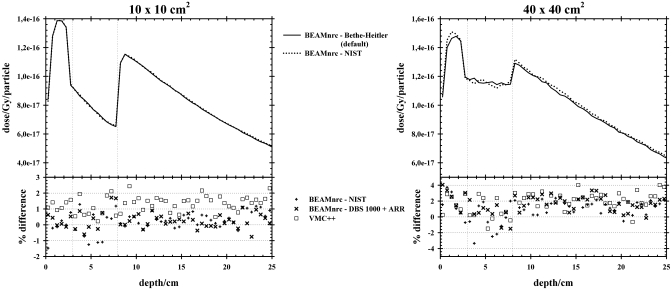
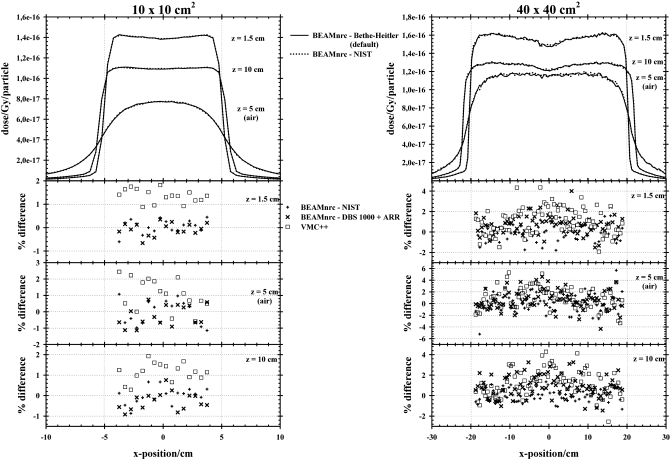
Figures 78 show the central and off-axis dose profiles for BEAMnrc calculations with BH (default) and NIST bremsstrahlung cross sections in a water phantom with a 5 cm air gap. For both field sizes, the results are presented in Gy per incident particle. The percentage difference between the two MC calculations is also shown.
Figure 7.
Central-axis dose profiles for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections in a water phantom with a 5 cm air gap and for the 10×10 and 40×40 cm2 field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference between the two MC calculated data is also shown.
Figure 8.
Off-axis dose profiles for BEAMnrc with BH (default) and with NIST bremsstrahlung cross sections in a water phantom with a 5 cm air gap and for the 10×10 and 40×40 cm2 field sizes. The calculations were performed with an average fractional uncertainty in the dose [for voxels with dose values greater than 50% of the maximum dose (Ref. 36)] of less than 0.01 (1%). The percentage difference, in the central region of the field and at different depths, between the two MC calculated data is also shown.
For both the 10×10 and 40×40 cm2 fields, the agreement between BH and NIST-based calculations was, on average, within 2%, as noted in the central axis depth and profile doses, including the air gap region for the 10×10 cm2 field size. Larger differences (up to a maximum of 4%) were noted for the 40×40 cm2 field size in the buildup and air-gap regions due to statistical fluctuations resulting primarily from the latent variance in the PHSP file for this large field size. These results are highly suggestive that the differences found in the phase space analysis between calculations using the BH and NIST cross sections are insignificant when the end point under consideration is dose computed within the phantom, even under extreme conditions, as illustrated with the simulated water∕air∕water phantom.
CONCLUSIONS
An investigation of the efficiency enhancing methods and cross-section data available in the BEAMnrc MC code system and comparisons with the VMC++ MC code system were performed. BEAMnrc is a well-established code system, which has been used for many years as a major tool for simulation of linear accelerator treatment heads, and is often considered a “benchmarking code” in this area of research.29 Both BEAMnrc and VMC++ are well-established programs for radiotherapy planning simulations although BEAMnrc was developed specially for the generation of PHSP files whileVMC++ was built initially for fast dose calculations in the patient and has recently been extended to allow the calculation of PHSP files. The two MC programs generate accurate PHSP files of the linear accelerator for subsequent planning or dosimetric verification purposes in a relatively short amount of time when the appropriate efficiency enhancing tools are used. The efficiency of BEAMnrc PHSP simulations is significantly improved, with directional bremsstrahlung splitting combined with augmented charged particle range rejection, for the two field sizes studied. VMC++ can also be used to perform accurate simulations of the entire linac treatment head within minutes on a single processor, which represents an invaluable resource for MC calculations for planning purposes. Although significant differences in the mean energy, planar fluence, and angular and spectral distributions were observed when comparing the NIST and BH bremsstrahlung cross-section PHSP files, they were not reflected in the calculated dose distribution in a water phantom with and without an air gap.
There is another viewpoint concerning PHSP simulations of the linac treatment head, which should be considered. If one uses VRTs (e.g., bremsstrahlung splitting) then the uncertainty in the patient dose distribution increases versus the no-VRT case for the same number of particles in the PHSP file. This occurs because of particle correlations which are introduced with the use of VRTs, such as bremsstrahlung splitting. Therefore, if one is concerned with the smallest statistical uncertainty (variance) in dose, then it is best to perform the treatment head PS simulation without VRTs. The tradeoff is that the no-VRT simulation is much slower, although if this simulation is being performed just once for subsequent use then it is a reasonable approach. On the other hand, if one is interested in the most efficient PS simulation (note that efficiency is the inverse product of variance and time), then it is necessary to use VRTs. The major advantage of using aggressive VRTs is the significant improvement in calculation time without a compromise in the accuracy of the patient dose computation. This is essential if one is considering real-time MC simulation of the treatment head and patient.
ACKNOWLEDGMENTS
This work was supported in part by Grant Nos. R01CA106770 and R01CA104777 from the NIH∕NCI and Grant No. 03-028-01-CCE from the American Cancer Society.
References
- Chetty I. J., Curran B., Cygler J. E., DeMarco J. J., Ezzell G., Faddegon B. A., Kawrakow I., Keall P. J., Liu H., Ma C.-M., Rogers D. W. O., Seuntjens J., Sheikh-Bagheri D., and Siebers J. V., “The AAPM Task Group Report No. 105: Issues associated with clinical implementation of Monte Carlo-based external beam treatment planning,” Med. Phys. 34(12), 4818–4853 (2007). 10.1118/1.2795842 [DOI] [PubMed] [Google Scholar]
- Reynaert N., van der Marck S. C., Schaart D. R., Van der Zee W., Van Vliet-Vroegindeweij C., Tomsej M., Jansen J., Heijmen B., Coghe M., and De Wagter C., “Monte Carlo treatment planning for photon and electron beams,” Radiat. Phys. Chem. 76(4), 643–686 (2007). 10.1016/j.radphyschem.2006.05.015 [DOI] [Google Scholar]
- Kawrakow I. and Rogers D. W. O., “The EGSnrc code system: Monte Carlo simulation of electron and photon transport,” National Research Council of Canada Technical Report No. PIRS-701, 2003.
- Brown F. B., “MCNP—A general Monte Carlo N-particle transport code, version 5,” Los Alamos National Laboratory Report No. LA-UR-03, 2003.
- Salvat F., Fernández-Varea J. M., and Sempau J., “PENELOPE-2006: A code system for Monte Carlo simulation of electron and photon transport,” Proceedings of a Workshop∕Training Course, OECD (2006).
- Agostinelli S. et al. , “GEANT4—a simulation toolkit,” Nucl. Instrum. Methods Phys. Res. A 506(3), 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- Hartmann Siantar C. L. et al. , “Description and dosimetric verification of the PEREGRINE Monte Carlo dose calculation system for photon beams incident on a water phantom,” Med. Phys. 28(7), 1322–1337 (2001). 10.1118/1.1381551 [DOI] [PubMed] [Google Scholar]
- Kawrakow I., Fippel M., and Friedrich K., “3D electron dose calculation using a voxel-based Monte Carlo algorithm (VMC),” Med. Phys. 23(4), 445–457 (1996). 10.1118/1.597673 [DOI] [PubMed] [Google Scholar]
- Fippel M., “Fast Monte Carlo dose calculation for photon beams on the VMC electron algorithm,” Med. Phys. 26(8), 1466–1475 (1999). 10.1118/1.598676 [DOI] [PubMed] [Google Scholar]
- Kawrakow I. and Fippel M., “Investigation of variance reduction techniques for Monte Carlo photon dose calculation using XVMC,” Phys. Med. Biol. 45(8), 2163–2183 (2000). 10.1088/0031-9155/45/8/308 [DOI] [PubMed] [Google Scholar]
- Kawrakow I., “VMC++, electron and photon Monte Carlo calculations optimized for radiation treatment planning,” in Advanced Monte Carlo for radiation physics, particle transport simulation and applications: Proceedings of the Lisbon Monte Carlo 2000 Meeting, edited by Kling A., Barao F., Nakagawa M., Távora L., and Vaz P. (Springer, Berlin, 2001), pp. 229–236.
- Neuenschwander H. and Born J. E., “A macro Monte Carlo method for electron beam dose calculations,” Phys. Med. Biol. 37(1), 107–125 (1992). 10.1088/0031-9155/37/1/007 [DOI] [Google Scholar]
- Ma C.-M., Li J. S., Pawlicki T., Jiang S. B., and Deng J., “MCDOSE—A Monte Carlo dose calculation tool for radiation therapy treatment planning,” in Proceedings of the 13th ICCR, edited by Bortfeld T. and Schlegel W. (Springer-Verlag, Heidelberg, 2000), pp. 411–413.
- Ma C.-M., Li J., Pawlicki T., Jiang S., Deng J., Chen L., Wang L., Price R., McNeely S., Ding M., Fourkal E., and Qin L., “MCSIM: A Monte Carlo dose verification tool for radiation therapy treatment planning and beam delivery (Abstract),” Med. Phys. 29(6), 1316 (2002). 10.1118/1.1521121 [DOI] [Google Scholar]
- Sempau J., Wilderman S. J., and Bielajew A. F., “DPM, a fast, accurate Monte Carlo optimized for photon and electron radiotherapy treatment planning dose calculations,” Phys. Med. Biol. 45(8), 2263–2291 (2000). 10.1088/0031-9155/45/8/315 [DOI] [PubMed] [Google Scholar]
- Chetty I. J., Tyagi N., Rosu M., Charland P. M., McShan D. L., Ten Haken R. K., Fraass B. A., and Bielajew A. F., “Clinical implementation, validation and use of the DPM Monte Carlo code for radiotherapy treatment planning,” Nuclear Mathematical and Computational Sciences: A Century in Review, a Century Anew, Gatlinburg, TN (American Nuclear Society, LaGrange Park, Vol. 119 (on CD Rom) 1–17 (2003). [Google Scholar]
- Fragoso M., Pillai S., Solberg T. D., and Chetty I. J., “Experimental verification and clinical implementation of a commercial Monte Carlo electron beam dose calculation algorithm,” Med. Phys. 35(3), 1028–1038 (2008). 10.1118/1.2839098 [DOI] [PubMed] [Google Scholar]
- Rogers D. W. O., Walters B., and Kawrakow I., “BEAMnrc users manual,” National Research Council of Canada Technical Report No. 509 (A), 2006.
- Kawrakow I., Rogers D. W. O., and Walters B. R. B., “Large efficiency improvements in BEAMnrc using directional splitting,” Med. Phys. 31(10), 2883–2898 (2004). 10.1118/1.1788912 [DOI] [PubMed] [Google Scholar]
- Kawrakow I. and Walters B. R. B., “Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc,” Med. Phys. 33(8), 3046–3056 (2006). 10.1118/1.2219778 [DOI] [PubMed] [Google Scholar]
- Cygler J. E., Daskalov G. M., Chan G. H., and Ding G. X., “Evaluation of the first commercial Monte Carlo dose calculation engine for electron beam treatment planning,” Med. Phys. 31(1), 142–153 (2004). 10.1118/1.1633105 [DOI] [PubMed] [Google Scholar]
- Ding G. X., Duggan D. M., Coffey C. W., Shokrani P., and Cygler J. E., “First macro Monte Carlo based commercial dose calculation module for electron beam treatment planning—new issues for clinical consideration,” Phys. Med. Biol. 51(11), 2781–2799 (2006). 10.1088/0031-9155/51/11/007 [DOI] [PubMed] [Google Scholar]
- Popple R. A., Weinberg R., Antolak J. A., Ye S.-J., Pareek P. N., Duan J., Shen S., and Brezovich I. A., “Comprehensive evaluation of a commercial macro Monte Carlo electron dose calculation implementation using a standard verification data set,” Med. Phys. 33(6), 1540–1551 (2006). 10.1118/1.2198328 [DOI] [PubMed] [Google Scholar]
- Sheikh-Bagheri D., Kawrakow I., Walters B., and Rogers D. W. O., in Integration of New Technologies into the Clinic: Monte Carlo and Image-Guided Radiation Therapy, edited by Curran B. H., Balter J. M., and Chetty I. J. (Medical Physics, Windsor, 2006), pp. 71–91. [Google Scholar]
- Berger M. J., in Methods of Computational Physics, edited by Alder B., Fernbach S., and Rotenberg M. (Academic, New York, 1963), Vol. I, pp. 135–215. [Google Scholar]
- Ma C.-M. and Jiang S. B., “Monte Carlo modelling of electron beams from medical accelerators,” Phys. Med. Biol. 44(12), R157–R189 (1999). 10.1088/0031-9155/44/12/201 [DOI] [PubMed] [Google Scholar]
- Verhaegen F. and Seuntjens J., “Monte Carlo modelling of external radiotherapy photon beams,” Phys. Med. Biol. 48(21), R107–R164 (2003). 10.1088/0031-9155/48/21/R01 [DOI] [PubMed] [Google Scholar]
- Hasenbalg F., Fix M. K., Born E. J., Mini R., and Kawrakow I., “VMC++ versus BEAMnrc: A comparison of simulated linear accelerator heads for photon beams,” Med. Phys. 35(4), 1521–1531 (2008). 10.1118/1.2885372 [DOI] [PubMed] [Google Scholar]
- Rogers D. W. O., Faddegon B. A., Ding G. X., Ma C.-M., Wei J., and Mackie T. R., “BEAM: A Monte Carlo code to simulate radiotherapy treatment units,” Med. Phys. 22(5), 503–524 (1995). 10.1118/1.597552 [DOI] [PubMed] [Google Scholar]
- Sheikh-Bagheri D., Rogers D. W. O., Ross C. K., and Seuntjens J. P., “Comparison of measured and Monte Carlo calculated dose distributions from the NRC linac,” Med. Phys. 27(10), 2256–2266 (2000). 10.1118/1.1290714 [DOI] [PubMed] [Google Scholar]
- Sheikh-Bagheri D., “Monte Carlo study of photon beams from medical linear accelerators: optimization, benchmark and spectra,” Ph.D. thesis, Carleton University, 1999. [Google Scholar]
- Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 27(3), 485–498 (2000). 10.1118/1.598917 [DOI] [PubMed] [Google Scholar]
- Fraass B. A., Smathers J., and Deye J., “Summary and recommendations of a National Cancer Institute workshop on issues limiting the clinical use of Monte Carlo dose calculation algorithms for megavoltage external beam radiation therapy,” Med. Phys. 30(12), 3206–3216 (2003). 10.1118/1.1626990 [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Asai M., Perl J., Ross C., Sempau J., Tinslay J., and Salvat F., “Benchmarking of Monte Carlo simulation of bremsstrahlung from thick targets at radiotherapy energies,” Med. Phys. 35(10), 4308–4317 (2008). 10.1118/1.2975150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner J., Siebers J., and Kawrakow I., “Dose calculation validation of VMC++ for photon beams,” Med. Phys. 34(5), 1809–1818 (2007). 10.1118/1.2714473 [DOI] [PubMed] [Google Scholar]
- Walters B., Kawrakow I., and Rogers D. W. O., “DOSXYZnrc users manual,” National Research Council of Canada, Technical Report No. PIRS-794, 2006.
- Ma C.-M. and Rogers D. W. O., “BEAMDP as a general-purpose utility,” National Research Council of Canada Technical Report No. PIRS-509 (E), 2004.
- Walters B. R. B. and Kawrakow I., “A “HOWFARLESS” option to increase efficiency of homogeneous phantom calculations with DOSXYZnrc,” Med. Phys. 34(10), 3794–3807 (2007). 10.1118/1.2776258 [DOI] [PubMed] [Google Scholar]
- Storm E. and Israel H. I., “Photon cross-sections from 1 keV to 100 MeV for elements Z=1 to Z=100,” At. Data Nucl. Data Tables 7(6), 565–681 (1970). 10.1016/S0092-640X(70)80017-1 [DOI] [Google Scholar]
- Cullen D. E., Perkins S. T., and Rathkopf J. A., “The 1989 Livermore evaluated photon data library (EPDL),” Lawrence Livermore National Laboratory Report No. UCRL-ID-103424, 1990.
- Berger M. J. and Hubbell J. H., “XCOM: photon cross-sections on a personal computer,” NIST Report No. NBSIR87-3597, 1987.
- Koch H. W. and Motz J. W., “Bremsstrahlung cross-section formulas and related data,” Rev. Mod. Phys. 31(4), 920–955 (1959). 10.1103/RevModPhys.31.920 [DOI] [Google Scholar]
- Seltzer S. M. and Berger M. J., “Bremsstrahlung spectra from electron interactions with screened atomic nuclei and orbital electrons,” Nucl. Instrum. Methods Phys. Res. A 12(1), 95–134 (1985). 10.1016/0168-583X(85)90707-4 [DOI] [Google Scholar]
- Seltzer S. M. and Berger M. J., “Bremsstrahlung energy spectra from electrons with kinetic energy from 1 keV to 10 GeV incident on screened nuclei and orbital electrons of neutral atoms with Z=1–100,” At. Data Nucl. Data Tables 35(3), 345–418 (1986). 10.1016/0092-640X(86)90014-8 [DOI] [Google Scholar]
- Pratt R. H., Tseng H. K., Lee C. M., Kissel L., MacCallum C., and Riley M., “Bremsstrahlung energy spectra from electrons of kinetic energy 1 keV⩽T1⩽2000 keV incident on neutral atoms 2⩽Z⩽92,” At. Data Nucl. Data Tables 20(2), 175–209 (1977); 10.1016/0092-640X(77)90045-6 [DOI] [Google Scholar]; Pratt R. H., Tseng H. K., Lee C. M., Kissel L., MacCallum C., and Riley M., At. Data Nucl. Data Tables 26(5), 477–481E (1981). 10.1016/0092-640X(81)90015-2 [DOI] [Google Scholar]
- Salvat F., Fernández-Varea J. M., Sempau J., and Llovet X., “Monte Carlo simulation of bremsstrahlung emission by electrons,” Radiat. Phys. Chem. 75(10), 1201–1219 (2006). 10.1016/j.radphyschem.2005.05.008 [DOI] [Google Scholar]
- Walters B. and Kawrakow I., “Technical note: overprediction of dose with default PRESTA-I boundary crossing in DOSXYZnrc and BEAMnrc,” Med. Phys. 34(2), 647–650 (2007). 10.1118/1.2402342 [DOI] [PubMed] [Google Scholar]
- Rogers D. W. O. and Mohan R., “Questions for comparison of clinical Monte Carlo codes,” in Proceedings of the 13th ICCR, edited by Bortfeld T. and Schlegel W. (Springer-Verlag, Heidelberg, 2000), pp. 120–122.
- Kawrakow I., “On the efficiency of photon beam treatment head simulations,” Med. Phys. 32(7), 2320–2326 (2005). 10.1118/1.1943808 [DOI] [PubMed] [Google Scholar]