Effects of source-to-listener distance and masking on perception of cochlear implant processed speech in reverberant rooms

Abstract

Two experiments examined the effects of source-to-listener distance (SLD) on sentence recognition in simulations of cochlear implant usage in noisy, reverberant rooms. Experiment 1 tested sentence recognition for three locations in the reverberant field of a small classroom (volume=79.2 m³). Subjects listened to sentences mixed with speech-spectrum noise that were processed with simulated reverberation followed by either vocoding (6, 12, or 24 spectral channels) or no further processing. Results indicated that changes in SLD within a small room produced only minor changes in recognition performance, a finding likely related to the listener remaining in the reverberant field. Experiment 2 tested sentence recognition for a simulated six-channel implant in a larger classroom (volume=175.9 m³) with varying levels of reverberation that could place the three listening locations in either the direct or reverberant field of the room. Results indicated that reducing SLD did improve performance, particularly when direct sound dominated the signal, but did not completely eliminate the effects of reverberation. Scores for both experiments were predicted accurately from speech transmission index values that modeled the effects of SLD, reverberation, and noise in terms of their effects on modulations of the speech envelope. Such models may prove to be a useful predictive tool for evaluating the quality of listening environments for cochlear implant users.

INTRODUCTION

The intelligibility of speech in rooms is affected by reverberation. Reverberant sound energy typically creates a temporal “smearing” of speech that imposes overlap masking on contiguous phonemes, lengthens the durations of words, and fills quiet and∕or low-intensity speech segments with unwanted sound (Bolt and MacDonald, 1949; Houtgast and Steeneken, 1985; Nabelek et al., 1989; Dreschler and Leeuw, 1990; Helfer, 1994; Culling et al., 2003). As a result, intelligibility decreases in conjunction with the reductions in speech envelope modulation depth imposed by temporal smearing (Houtgast and Steeneken, 1985). Competing speech and other ambient noises, being similarly affected, interact with the distorted speech to reduce intelligibility more than either noise or reverberation would alone (Duquesnoy and Plomp, 1980; Nabelek and Robinson, 1982; Crandell and Smaldino, 2000). These reductions are particularly severe for listeners with impaired hearing, who typically require less noise and reverberation to achieve the same intelligibility as listeners with normal hearing (Finitzo-Hieber and Tillman, 1978; Duquesnoy and Plomp, 1980; Helfer and Wilber, 1990).

The temporal effects of reverberation on speech may pose a particular challenge for cochlear implant (CI) users, who receive their auditory cues from temporal envelope modulations in a limited number of spectral channels. Temporal envelope modulations suffice to provide intelligible speech for as few as four spectral channels under ideal conditions (Shannon et al., 1995; Dorman et al., 1997). However, when the channels’ envelope modulations are low-pass filtered with cutoff frequencies in the 8–16 Hz range, intelligibility decreases (Fu and Shannon, 2000; Xu and Zheng, 2007). Reverberation, which can act as a low-pass filter for envelope modulations in this frequency range (Houtgast and Steeneken, 1985), has similarly been shown to degrade intelligibility for listening through actual or simulated implants in rooms that listeners with normal hearing would find acceptable (Iglehart, 2004; Poissant et al., 2006).

Studies of intelligibility for implant users in reverberant spaces have typically focused on the use of frequency modulation (FM) or sound field devices to improve intelligibility (Crandell et al., 1998; Iglehart, 2004; Anderson et al., 2005), with mixed results. Few studies have focused on the specific effects of reverberation and noise on implant processed speech. Poissant et al. (2006) used simulations of both reverberation (Allen and Berkley, 1979; Peterson, 1986) and implant processing (Qin and Oxenham, 2003) to investigate the effects of reverberation on the intelligibility of implant processed sentence key words in a small classroom. Results showed that speech recognition scores decreased in conjunction with decreases in the number of spectral channels and∕or the room’s uniform absorption coefficient (α). For example, intelligibility scores for a six-channel implant simulation in quiet decreased from 87% correct to 22% correct when the reverberation time (RT₆₀) was increased from 0 to 520 ms, a RT₆₀ value considered acceptable by ANSI classroom standards (ANSI, 2002). These intelligibility decreases were subsequently worsened by mixing the target speech with either speech-spectrum noise or two-talker babble, both of which further reduced intelligibility for speech in quiet with RT₆₀=266 ms by nearly 40% when added at a +8 dB signal-to-noise ratio (SNR). No significant interaction between levels of SNR and levels of RT₆₀ or masker type were observed, a finding that contrasted markedly with previous data showing more severe effects for noise and reverberation combined than for the combination of their individual effects (Nabelek and Mason, 1981; Loven and Collins, 1988; Helfer and Wilber, 1990; Payton et al., 1994) or more efficient masking for competing speech than for speech-spectrum noise in both simulated and actual implant systems (Qin and Oxenham, 2003; Stickney et al., 2004). Statistically significant positive correlations between intelligibility scores and computed speech transmission index (STI) values (Houtgast and Steeneken, 1985) for each noise type indicated a strong relationship between intelligibility and the envelope modulations of the vocoded reverberated speech. The STI data of Poissant et al. (2006) used a modified computation intended for use with nonlinear signal processors such as those common to CIs (Goldsworthy and Greenberg, 2004).

The listening difficulties observed by Poissant et al. (2006) are not unexpected, given the placement of the listener in the room’s reverberant field. However, the degree of difficulty observed was remarkable considering the small size of the room (volume=79.2 m³) and short source-to-listener distance (SLD) of 4 m, and was far greater than the difficulties normally associated with the magnitude of STI values computed in that study. Under the study’s conditions, most of the sound energy reaching the listener consisted of “early” reflections arriving 50–80 ms after the direct sound. The auditory system usually integrates early reflections together with the direct sound to increase both the perceived loudness and the intelligibility of speech (Lochner and Burger, 1964; Latham, 1979; Bradley, 1986a, 1986b). Such increases can be particularly important in noisy conditions (Bradley et al., 2003). Studies exploring the relationship between RT₆₀ and intelligibility in both quiet and noisy classrooms (Bistafa and Bradley, 2000; Yang and Hodgson, 2006) indicate that the RT₆₀ value giving the best intelligibility in noise increases as room volume and noise-to-signal ratio increase. These increases in RT₆₀ were associated with better intelligibility for hearing impaired subjects when sources of noise (e.g., neighboring students) were closer to the listener than sources of speech (e.g., instructors and∕or audio equipment). There, early reflections comprised a greater proportion of speech energy than of noise energy, compensating in part for the proximity of the noise and enhancing the intelligibility of the speech.

At present, it is not known how well implant users can integrate early reflections with direct sound as described above. The results of Poissant et al. (2006) suggest that signals comprised largely of early reflections may be less intelligible for implant users than signals comprised largely of direct arrivals. This hypothesis, if true, has important implications for implant users since recommendations for improving classroom acoustics often include increasing the level of early reflections (Siebein et al., 2000; Bradley et al., 2003). One simple way to evaluate this hypothesis is to compare intelligibility scores for speech received at small SLDs (having strong contributions from direct sound) with those for speech received at large SLDs (having strong contributions from reflected sound). Listeners with normal temporal integration abilities would be expected to recognize speech at the front and rear of the room with equal facility [assuming equal sound pressure levels (SPLs)]; listeners showing deficits in integration ability would be expected to show significant differences between the two locations. This approach is followed in the present work.

Another remarkable aspect of the Poissant et al. (2006) study was the strong correlation observed between computed STI values and measured intelligibility scores. Although the standard STI computation is widely used in assessment of listening rooms and sound reinforcement systems, it is not recommended for use in assessing vocoder systems or predicting intelligibility for hearing impaired listeners (IEC, 2002). Goldsworthy and Greenberg (2004) noted that nonlinear operations commonly found in speech processing systems (e.g., power spectrum subtraction) produce artifacts that distort the association between STI values and intelligibility scores. They subsequently proposed several modifications to the STI that appeared to eliminate these distortions. While they noted that the STI would be a good candidate measure for predicting intelligibility for CI users, they did not present STI data for either simulated or actual CI processed speech. The data of Poissant et al. (2006) for simulated CI speech with 6-channel and 12-channel vocoders supported their assumptions while drawing attention to effects of subject proficiency. Specifically, the relationship between STI values and intelligibility scores was shown to depend on the number of vocoder channels, with individual STI values mapping to higher scores for the 12-channel vocoder than for the 6-channel vocoder. This finding reflects a fundamental difference between the STI, which does not account for subject proficiency, and measures like the Articulation Index (ANSI, 1969) and Speech Intelligibility Index (ANSI, 1997) that can model subject proficiency (reflected through hearing thresholds) for intelligibility prediction with individual subjects. The influence of proficiency on STI-based predictions has been addressed in work with subjects with sensorineural hearing losses (HLs) (Dreschler and Leeuw, 1990; Duquesnoy and Plomp, 1980), but not in work with implant users. The present work directly examines the relationship between proficiency, STI, and intelligibility for implant simulations, where proficiency is modeled as the number of vocoder channels available to the listener.

The purpose of the present study was to investigate the effects of SLD on the intelligibility of CI processed speech and on the STI as a predictor of CI speech intelligibility in both quiet and noisy reverberant rooms. Two experiments were conducted. Experiment 1 investigated the effects of SLD and number of available spectral channels on intelligibility in quiet and in noise for implant processed speech in the small classroom evaluated by Poissant et al. (2006) to determine whether reducing SLD would lead to better performance. The results of Experiment 1 provide a measure of the listener’s ability to take advantage of early reflections in that small room. Experiment 2 investigated the individual and combined effects of reverberation, SLD, and noise on processed speech intelligibility in a second, slightly larger classroom. Reverberation in this room was determined by specifying various values of α; this, in combination with the larger room volume, makes it possible to evaluate listener performance at SLDs that are both less than and greater than the room’s critical distance (i.e., the SLD at which direct and reverberant sound energies are equal).

The STI analysis in the present work uses the traditional STI approach (Houtgast and Steeneken, 1985), which differs from the newer envelope-regression based STI approach of Goldsworthy and Greenberg (2004) chosen by Poissant et al. (2006) for its ability to accommodate nonlinearly processed signals. The Goldsworthy∕Greenberg (2004) approach produces STI values that correlate well with traditional STI values for unvocoded speech in noisy and∕or reverberant conditions. For vocoded speech, Poissant et al. (2006) found that the Goldsworthy∕Greenberg (2004) approach produced STI values that were compressed nonlinearly into a narrower range than traditionally produced values. The upper bound of this range was dependent (in an undetermined manner) on the number of vocoder channels used. These unexamined phenomena are a reflection of the vocoder’s effects on the speech signal, and are worthy of study in a separate investigation that focuses on the mathematics of vocoder processing and STI computation. To expedite the present work, we chose to use the traditional STI approach, which, in addition to being widely studied, is currently the only STI version that has been shown to correlate consistently with measures of early reflection benefit (Bradley et al., 1999, 2003).

EXPERIMENT 1: EFFECTS OF DISTANCE AND NUMBER OF SPECTRAL CHANNELS ON INTELLIGIBILITY OF PROCESSED SENTENCES

Methods

Subjects

Twelve adult listeners (ten females and two males) participated in experiment 1. The subjects’ ages ranged from 19 to 31 years (mean age=23.8 years). All subjects were native speakers of American English who had passed a screening for normal hearing (thresholds ≤20 dB HL). None of the subjects had participated in previous simulation experiments. The subjects were compensated for their participation with partial course credit.

Materials

Stimuli for experiment 1 were the same as those used by Poissant et al. (2006), and are described briefly here. The stimuli consisted of 360 sentences (Helfer and Freyman, 2004), each containing three key words in common use (Francis and Kucera, 1982). The sentences were assigned to 1 of 24 topics (e.g., food, clothing, and politics) used to help listeners direct their attention to the target speaker when sentences were heard in the presence of competing speakers. The sentences were uttered by a female speaker with an American English dialect and digitally recorded in a sound-treated booth (IAC 1604) with 16-bit resolution at a 22 050 Hz sampling rate.

Signal processing

The signal processing utilized in this investigation was used previously in Poissant et al., 2006 and consists of (optional) noise addition followed in sequence by reverberation simulation and (optional) CI simulation. These processes are described below.

Noise addition. The sentence recordings described above were input to subsequent simulators either as recorded in quiet or with speech-spectrum noise added at SNRs of +8 or +18 dB, with one exception: SNRs for “unprocessed” conditions (described below) included −8 and +8 dB. The +8 and +18 dB SNRs were chosen to facilitate direct comparisons of the present results with data from previous studies using the same stimuli and simulators (Poissant et al., 2006; Whitmal et al., 2007); the −8 dB SNR replicated a condition used in previous studies with the topic sentence recordings (Helfer and Freyman, 2004, 2005). Maskers for each sentence were derived from scaled segments of the speech-spectrum noise as in Poissant et al., 2006.

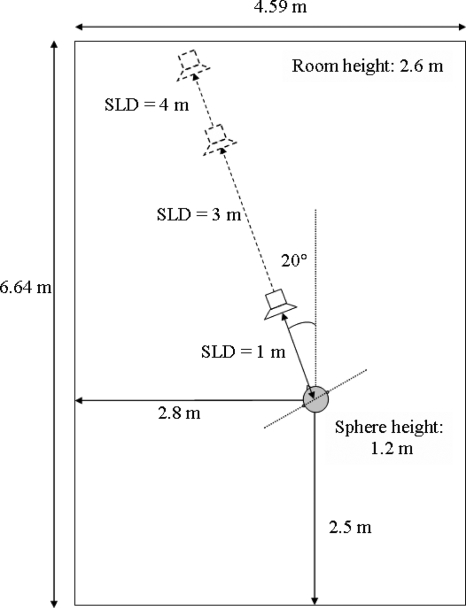
Reverberation simulation. The reverberation simulation utilized an image-source software model (Allen and Berkley, 1979; Peterson, 1986) of a small rectangular classroom with uniform, frequency-independent absorption on all surfaces. The dimensions for the ideal classroom were taken from a real rectangular classroom at the University of Massachusetts Amherst. Figure 1 provides details of the dimensions of the room, the orientation of a simulated listener’s head (modeled as a sphere), and the relative positions of the listener’s head and the target source. The source (modeled by the software as omnidirectional) was placed at each of three locations located 1, 3, or 4 m from the listener at a 0° azimuth. Since most real-world sources exhibit some directionality that can improve intelligibility by boosting direct-to-reverberant energy ratio, the model used here represents a worst-case scenario. α was set to 0.25, a previously explored value (Poissant et al., 2006) expected to provide challenging listening conditions. The theoretical critical distance (Kuttruff, 1979) for this room configuration is

$$d_c=\frac{1}{4}\sqrt{\frac{S\alpha }{\pi }}=0.774\text{m},$$ (1)

with S being the total surface area of the room’s walls, floor, and ceiling. All listening positions would therefore be expected to be in the reverberant field. Accordingly, direct-to-reverberant energy ratios of −2.9, −12.4, and −14.5 dB were measured at SLDs of 1, 3, and 4 m, respectively.

Figure 1.

Schematic for the reverberation simulation of experiment 1, illustrating the dimensions of the room, the orientation of the sphere modeling the listener’s head, and the relative positions of the sphere and the target source within the room (adapted from Poissant et al., 2006).

The room models were used to generate impulse responses for each SLD condition. Each impulse response was convolved with the sentence recordings to produce reverberant speech. For sentences in noise, the sequence of noise addition and convolution had the effect of placing the speech and noise in the same source location. RT₆₀ values derived from reversed-time integrations of the three squared impulse responses (Schroeder, 1965) in the 1000 Hz octave-band over the −5 to −30 dB decay range were approximately 520 ms, well within the recommended range for classrooms of this size (ANSI, 2002). It should be noted that the RT₆₀ value for this room is larger than the RT₆₀ of 425 ms reported by Poissant et al. (2006) for the same room. There, RT₆₀ was predicted from Sabine’s (1922) theoretical formula as

$${\text{RT}}_{60}=\frac{0.161V}{S\alpha },$$ (2)

where V was the room volume in m³. The discrepancy between predicted and measured RT₆₀ values is consistent with the recent work of Lehmann and Johansson (2008), who showed that the Sabine (1922) formula tends to underpredict RT₆₀ values in image-source room simulations. RT₆₀ values used in the remainder of the paper will therefore refer only to times derived from impulse responses using Schroeder’s (1965) method.

The effect of reverberation on presentation level was assessed by comparing the A-weighted rms level of a 15-s recording of anechoic speech (i.e., measured after setting α=1 within the simulation) with the A-weighted level of the same speech measured at each of the three listener positions. For anechoic speech of 65 dBA at 1 m, measured speech levels at the 1, 3, and 4 m positions were 67.7, 64.8, and 63.5 dBA, respectively. These small differences in level as a function of SLD are consistent with theoretical predictions for a classroom of this size (Barron and Lee, 1988; Sato and Bradley, 2008). All speech signals were subsequently presented to the subjects at 65 dBA, with the level held constant to differentiate the effects of reflection patterns at each position from any effects of level difference.

Implant processing simulation. Reverberated sentences were either processed by one of three tone-excited channel vocoder systems (i.e., systems with 6, 12, and 24 channels) implemented in MATLAB (Mathworks, Natick, MA), or subjected to no further processing or reduction in bandwidth (subsequently referred to as unprocessed). The implementations of the vocoder systems followed those of Qin and Oxenham (2003). For each vocoder, the input speech was filtered into contiguous frequency bands in the 80–6000 Hz range, each with equal width on an equivalent-rectangular-bandwidth scale (Glasberg and Moore, 1990). Center frequencies and bandwidths for each of the processors are provided in Table 1. The envelope of each band was extracted via half-wave rectification and low-pass filtering and used to modulate a pure tone located at the band’s center frequency. The bandwidth of the low-pass filter was the smaller of 300 Hz or half the analysis bandwidth. The tones for all bands were then scaled and added electronically to produce a simulated implant processed signal with a rms level of 65 dBA.

Table 1.

Center frequencies and bandwidths, expressed in hertz, for each of three experimental vocoder systems.

Channels	Parameters	Band values
6	CF	180	446	885	1609	2803	4773
	BW	201	331	546	901	1487	2453
12	CF	124	224	353	519	731	1005	1355	1806	2385	3128	4084	5310
	BW	88	113	145	186	239	307	395	507	651	836	1074	1379
24
Bands 1–12	CF	101	145	194	251	315	387	469	562	668	787	923	1077
	BW	41	47	53	60	68	77	87	99	112	127	144	163
Bands 13–24	CF	1251	1448	1671	1925	2212	2538	2906	3324	3798	4335	4944	5634
	BW	185	210	238	269	305	346	392	444	503	571	647	733

CF=center frequency of channel and BW=bandwidth of channel.

Procedure

Subjects listened to the 360 sentences while seated in a double-walled sound-treated booth (IAC 1604) during one 90-min listening session. Subjects were given breaks in the middle of each session. Each combination of the 3 noise conditions, 4 processing conditions, and 3 SLDs was used to process 1 of 36 ten-sentence lists. The presentation order of conditions for the subjects was determined by a 36×12 Latin rectangle, with the ordering of sentences for each list randomized. The presentation level for the sentences (65 dBA) was calibrated daily using repeated loops of the speech-spectrum noise described above.

Custom MATLAB software (executed on a laptop computer inside the test booth) was used to present the sentences to the subject and to score the number of key words correctly recognized by her or him. The laptop screen prompted the subject with the word “Ready?” and the sentence topic exactly 2 s before the sentence was presented. The sentence was then retrieved from the remote computer’s hard disk, converted to an analog signal by the computer’s sound card (SigmaTel High Definition Audio Codec) using 16-bit resolution at a 22 050 Hz sampling rate, and input to a headphone amplifier (Behringer Pro-XL HA4700) driving a pair of Sennheiser HD580 circumaural headphones. The subject then typed the sentence as heard into a text window and submitted it to the software. Subjects were instructed to type any portion of the sentence that was intelligible, or “I don’t know” if the sentence was completely unintelligible. The subjects’ typed responses were later proofread by the authors, with obvious spelling mistakes and homophone substitutions corrected prior to scoring.

Practice materials were limited to ten sentences per vocoder, presented without feedback at the beginning of the experiment. The ten sentences were processed with the 3 m SLD simulation, with five presented in quiet and five presented in speech-spectrum noise at +8 dB SNR. The sentences used for practice were not used in the main experiment.

Computation of STI values

The STI is a frequency-weighted average of seven octave-band apparent signal-to-noise ratios (aSNRs), given as

$$\text{STI}=\frac{{\sum }_{i=1}^7{w}_i\left({\text{aSNR}}_i\right)+15}{30},$$ (3)

where w_i was an empirically derived weight for band i (Houtgast and Steeneken 1985). aSNR values can range from −15 (representing poor intelligibility) to +15 dB (representing excellent intelligibility); consequently, STI values range from 0 (poor intelligibility) to 1 (excellent intelligibility). aSNR values are calculated from modulation transfer functions (MTFs) that quantify changes in modulation depth

$${\text{aSNR}}_i=10{\text{log}}_{10}\left[\frac{{\text{MTF}}_i}{1-{\text{MTF}}_i}\right],$$ (4)

where i=1,2,…,7 denotes the octave band and MTF_i denotes measurable reductions in modulation depth for band i, measured in and averaged over 14 one-third-octave spaced modulation frequencies between 0.63 and 12.5 Hz. For the case of speech-in-noise in an ideal room with a diffuse reverberant field, the theoretical modulation depth reduction m_i(f) in band i at modulation frequency f is

$$m_i\left(f\right)=\frac{1}{\sqrt{1+{\left(2\pi f{\text{RT}}_{60}∕13.8\right)}^2}}\left[\frac{1}{1+{10}^{-{\text{SNR}}_i∕10}}\right],$$ (5)

where SNR_i was the SNR in decibels for band i (Houtgast et al., 1980). Equation 5 illustrates two factors affecting envelope modulations: low-pass filtering attributable to reverberation, and frequency-independent attenuation attributable to additive noise. In practice, MTF values are derived from responses to input probe signals consisting of amplitude modulated noise or speech (Steeneken and Houtgast, 1982; Payton and Braida, 1999).

In the present work, STI values for all conditions of reverberation and noise were measured in MATLAB on a Pentium 4 personal computer, using the approach of Houtgast and Steeneken (1973). Briefly, MTFs were computed from probe signals consisting of speech-spectrum noise with 100% sinusoidal intensity modulation at each of the 14 modulation frequencies mentioned above. The probe signals were convolved with the room impulse responses and filtered (using eighth-order Butterworth filters) into one of the seven octave bands. Intensity envelopes for the band-limited signals were then computed by squaring and low-pass filtering the signals with a 300 Hz fourth-order Butterworth low-pass filter. The modulation depths of the intensity envelopes for each frequency were then measured and averaged across frequency to produce a modulation index.

Results

Intelligibility scores

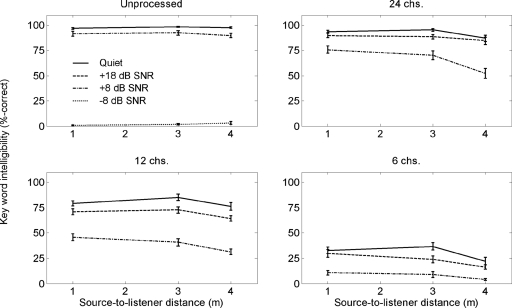
Intelligibility scores for experiment 1 were derived from the percentage of correctly repeated key words per condition. Mean intelligibility scores for each channel configuration are shown in Fig. 2. As expected, the best performance was observed for unprocessed speech in quiet, with average scores ranging between 92.8% and 94.2% correct. Average scores in quiet for the 24-channel vocoder at SLDs of 1 and 3 m were within the same range as the unprocessed scores: average scores for the 12- and 6-channel vocoders were considerably lower (76.5% and 32.3% correct, respectively). This relationship between available channels and intelligibility scores is similar to that observed by Poissant et al. (2006). The best performance in quiet for each vocoder was observed at the 3 m SLD. Scores in quiet at the 1 m SLD were slightly lower than 3 m SLD scores, with average differences of 0.8%, 6.1%, and 5.0% observed for 24-, 12-, and 6-channel vocoders, respectively. Scores in quiet for each vocoder at the 4 m SLD were (on average) 7.8% below corresponding scores at the 1 m SLD.

Figure 2.

Speech recognition performance for unprocessed∕natural speech and 24-, 12-, and 6-channel vocoded speech in quiet and in noise as a function of SLD in the experiment 1 room simulation. Error bars represent ±1 standard error.

Performance in all listening conditions decreased considerably in the presence of noise. Adding noise at a +18 dB SNR reduced average scores for 24-, 12-, and 6-channel vocoders by 3.1%, 7.4%, and 9.3%, respectively. In each case, the largest reductions were observed for scores at the 3 m SLD, which subsequently became less than or equal to scores at 1 m. Adding noise at a +8 dB SNR reduced average scores overall by 22.8%, 35.1%, and 22.6%, respectively. Effects of decreasing SLD were most evident at the +8 dB SNR. Scores decreased by between 14% and 20% for 24- and 12-channel vocoders when SLD was increased from 3 to 4 m, while a smaller decrease of 6% (presumably denoting a floor effect) was observed for the 6-channel vocoder. In contrast, unprocessed scores in noise at +8 dB SNR dropped (on average) only 4.5% below corresponding scores in quiet, and showed little variation with respect to SLD. Scores for unprocessed speech at −8 dB SNR (a challenging SNR) were less than 3% correct for all SLDs.

Subject scores were converted to rationalized arcsine units (Studebaker, 1985) and input to a repeated-measures analysis of variance of intelligibility scores. Within-subject factors for the analysis of variance included the number of channels (F[3,306]=1188.91, p<0.0001), SLD (F[2,306]=30.67, p<0.0001), and SNR (F[3,306]=687.11, p<0.0001), all of which were statistically significant. All first-order interactions between main factors were significant. Post hoc tests using the Tukey honestly significant difference criterion (α=0.05) indicated that (a) scores at 4 m were significantly lower than scores at 1 or 3 m, (b) scores at 1 and 3 m were not significantly different from each other, (c) scores for 6-, 12-, and 24-channel processors were all significantly different from each other, and (d) scores for each SNR were all significantly different from each other.

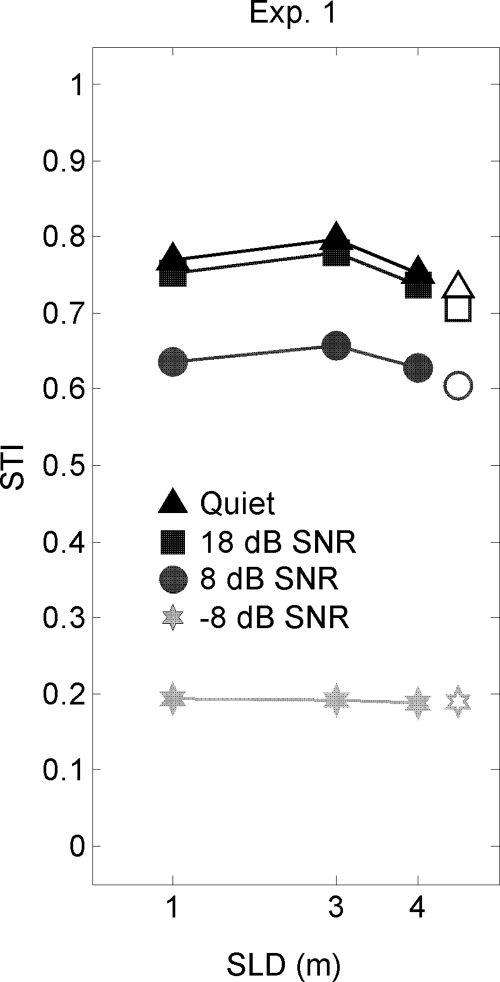
STI values

STI values for the listening conditions of experiment 1 are shown in Fig. 3. Measured values are represented by filled symbols; theoretical values in the reverberant field [computed according to Eq. 5] are represented by unfilled symbols. The measured and theoretical values are in good agreement at a SLD of 4 m. Overall, STI values in Fig. 3 range between 0.63 and 0.8 as the SNR ranges from +8 dB to +∞ (i.e., quiet), a range denoting “good” to “excellent” signal quality for listeners with normal hearing (Houtgast et al., 1980). An example of this signal quality is illustrated by Payton and Braida (1999), who showed that the 0.63–0.8 STI range corresponded to an (approximate) intelligibility range of 88% correct to 96% correct1 for key words in unprocessed nonsense sentences in reverberation and∕or noise. Similarly, the present study’s average intelligibility scores for unprocessed speech remained above 90% correct for SNR≥+8 dB. For vocoded speech, the same increases in SNR and STI are associated with substantial increases in intelligibility (on average, 24%), with the rate of increase rising sharply as the number of channels increases. The largest increase (54%) is observed for the 12-channel vocoder, a configuration for which neither floor nor ceiling effects were observed.

Figure 3.

STIs for the listening conditions of experiment 1 in quiet and in speech-spectrum noise as a function of SLD. Unfilled symbols depict predictions of STI values for reverberant-field listener locations as modeled by Eq. 5.

In contrast, SLD has much less influence on STI and intelligibility than SNR. Increases in SLD from 1 to 4 m were associated with decreases of only 0.04 in average STI and 7.4% in the average intelligibility score. The relatively minor effects of SLD on STI are expected, and may be attributed in part to the small size of the room and to placement of the three listening positions in the room’s reverberant field. A small increase of 0.026 in average STI is also observed as SLD increases from 1 to 3 m: This increase is associated with increased intelligibility scores at 3 m in quiet and at +18 dB SNR.

The coincidence of higher intelligibility scores and higher STI values at the 3 m SLD warranted further investigation. Toward this end, the impulse response filters for each listener position were partitioned into three smaller filters: one producing direct sound arrivals (time span: 0–3 ms), one producing early reflections (time span: 3–50 ms), and one producing later reflections (time span: 50–500 ms). The filters were each convolved with a 15-s recording of speech and A-weighted rms output levels were recorded for each filter’s output. The A-weighted levels of the direct, early, and late portions of the received signal are shown below in Table 2. At the 1 m SLD, direct and early arrivals are nearly equal in level, and are each at least 4 dB higher than late arrivals, which may be likened to additive noise in this situation (Lochner and Burger, 1964). At the 3 m SLD, early reflections increase in level while late reflections decrease slightly; providing an 8.6 dB early-to-late reflection ratio. The rms direct arrival level is approximately 3 dB below the late reflection “noise floor,” with some direct arrivals likely audible. The combination of strong early reflections and potentially audible direct arrivals is associated with a small increase in performance for implant simulations. At the 4 m SLD, the early-to-late ratio decreases to 5.7 dB, while the direct level drops more than 6 dB below the late reflection level. The combination of these two decreases is associated with a decrease in performance for implant simulations. In contrast, performance for unprocessed speech is not affected by SLD or the changes in early-to-late reflection ratio that are associated with SLD. These findings suggest that simulated implant users may have some limited ability to utilize early reflections, albeit only in the presence of detectable direct arrivals. This dependence on direct arrivals will be explored further in experiment 2.

Table 2.

A-weighted SPLs for direct, early, and late arrivals in experiment 1 listening conditions.

SLD (m)	Direct	Early	Late
1	60.5	62.4	56.1
3	52.3	64.2	55.6
4	51.3	63.6	57.9

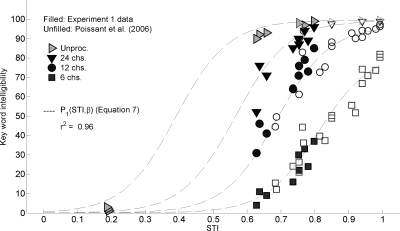
Relationship between STI values and intelligibility scores

The similarities between trends in STI and intelligibility data suggest a strong association between STI and intelligibility scores. This association is depicted in Fig. 4, which plots the intelligibility scores for each channel configuration as a function of STI. The data obtained by Poissant et al. (2006) for these listening conditions are plotted for reference. To better explore this association, percent-correct intelligibility curves for each channel configuration were initially fit by sigmoid functions of the form

$$P_0\left(\text{STI}\right)=\frac{100}{1+{10}^{-\left[C_1\left(\text{STI}-C_2\right)+C_3\right]}},$$ (6)

where C₁, C₂, and C₃ were fitting constants corresponding to the slope, x-value, and y-value of a reference point on the curve. (C₃=0 for reference points at the 50%-correct level.) These initial attempts revealed logarithmic relationships between both C₁ and C₂ and the channel bandwidth as measured in units of “Cams” (i.e., equivalent-rectangular bandwidth; Glasberg and Moore, 1990). This observation led to the use of a sigmoid function model with logarithmically varying fitting coefficients

$$P_1\left(\text{STI},\beta \right)=\frac{P_{\text{max}}\left(\right)}{1+{10}^{-\left[\left(5.59-0.04\text{\hspace{0.17em}ln}\beta \right)\left(\left(\text{STI}-0.43-0.18\text{\hspace{0.17em}ln}\beta \right)-0.58\right)\right]}},$$ (7)

where β represented the channel bandwidth in Cams (i.e., 27.92 Cams divided by the number of channels), P_max(β) was the maximum intelligibility score measured for a vocoder with channel bandwidth of β, and the number of available channels for unprocessed speech was assumed to equal 64 (Shannon et al., 2004). P_max(β) data from both studies were described well by the equation

$$P_{\text{max}}\left(\beta \right)=99.2+1.179\beta -0.977{\beta }^2.$$ (8)

The good agreement between the data and Eq. 7 suggests that preserving the fidelity of envelope modulations (and thus maximizing STI) will result in the best possible intelligibility.

Figure 4.

Speech recognition performance for 6-, 12-, and 24-channel vocoded speech and unprocessed∕natural speech in the simulated room of experiment 1 and Poissant et al. (2006) as a function of STI. Data from experiment 1 are represented by filled symbols: data from Poissant et al. (2006) are represented by unfilled symbols. The dashed line depicts predicted recognition performance as modeled by Eq. 7.

EXPERIMENT 2: EFFECTS OF DISTANCE AND ROOM ABSORPTION ON INTELLIGIBILITY OF PROCESSED SENTENCES

The results of experiment 1 indicate that simulated implant users seated near the front of a small classroom will have speech recognition scores that are slightly (but not significantly) higher than scores for users in the reverberant field of the classroom. The differences between positions are smallest for listeners in quiet with 12 or more spectral channels, and substantially larger for listeners with fewer channels available and∕or noise present. Listeners with normal hearing exhibited no difficulties in any position, presumably because they were able to make better use of early reflections than the simulated implant users. This finding suggests that simulated implant performance will be greatest only when both direct arrivals and early reflections are much higher in level than the reverberant field. The purpose of experiment 2 was to test this hypothesis with simulated implant users in a larger classroom containing listener positions with both positive and negative direct-to-reverberant energy ratios.

Methods

Subjects

Nine adult listeners (eight females and one male) participated in experiment 2. The subjects’ ages ranged from 22 to 38 years (mean age=26.4 years). All of the subjects were native speakers of American English with normal hearing (thresholds ≤20 dB HL). None of the subjects had participated in previous CI simulation experiments. All subjects were paid for their participation.

Materials and processing

Processing for experiment 2 was similar to that of experiment 1, with noteworthy changes in noise, reverberation, and vocoder conditions.

Noise processing. The 360-sentence recordings of experiment 1 were input to the simulators either as recorded in quiet or with either the speech-spectrum noise of experiment 1 or two-talker babble added at a SNR of 18 dB. The two-talker babble was the same as that used in Poissant et al., 2006, derived from digital recordings of two college-aged female students speaking different sets of syntactically correct nonsense sentences. Pauses between sentences were removed to produce two recordings of continuous speech, which were then matched in rms level and combined to produce two-talker babble.

Reverberation simulation. The reverberation simulator of experiment 1 was used to model an idealized rectangular classroom (6.7×10.1×2.6 m³) with each of the four values of α (1.0, 0.7, 0.4, and 0.25) used in Poissant et al., 2006. The dimensions for the ideal classroom were taken from a real rectangular classroom at the University of Massachusetts Amherst. The details of the room simulation are identical to those of Fig. 1 with several notable exceptions: the larger room width and length, the distance between the listener position and most distant wall (increased proportionally to 2.8 m), and selected SLDs of 1, 4, or 7 m. The 1000 Hz octave-band RT₆₀ values for the three positions (measured as in experiment 1) were approximately 680 ms for α=0.25, 380 ms for α=0.4, and 170 ms for α=0.7. Theoretical critical distances and measured direct-to-reverberant energy ratios for each position in the three reverberant rooms are shown in Table 3. The chosen combinations of SLDs and α values place the 1 m SLD position near the theoretical critical distance for α=0.25, and within the critical distance for α=0.4 and 0.7. The 4 and 7 m positions remain in the reverberant field for α<1.

Table 3.

Direct-to-reverberant energy ratios (in decibels) for experiment 2 listening conditions in reverberant rooms.

SLD (m)	α
	0.25	0.40	0.70
1	−0.62	2.31	7.55
4	−11.93	−8.57	−2.04
7	−15.49	−11.95	−4.68
dc (m)	1.05	1.33	1.75

As in experiment 1, all speech signals were presented to the subjects at 65 dBA. Unnormalized speech levels at each position for a 65 dBA direct field at 1 m are shown in Table 4. Level differences were, as in experiment 1, consistent with theoretical predictions (Barron and Lee, 1988; Sato and Bradley, 2008). It should be noted that without SPL normalization listeners in rooms with α=0.7 or α=1.0 could receive speech at levels near 50 dB SPL, a level that has been shown to impair intelligibility for implant users (Skinner et al., 1997; Firszt et al., 2007). Since large interstimulus presentation level differences could confound effects of early reflections, we chose to present all signals at the same level as in experiment 1. Actual implant users would have similar capabilities to compensate for these differences by manually adjusting microphone sensitivity (Donaldson and Allen, 2003; James et al., 2003) and∕or using adaptive dynamic range optimization or other automatic gain control algorithms to amplify soft speech (James et al., 2002; Dawson et al., 2004).

Table 4.

A-weighted SPLs for experiment 2 listening conditions when the direct field SPL at 1 m equals 65 dBA.

SLD (m)	α
	0.25	0.40	0.70	1.00
1	68.5	67.2	66.0	65.0
4	64.9	62.0	57.2	53.0
7	63.7	60.0	53.7	48.1

Implant simulation. The reverberated sentences were processed by only the six-channel vocoder of experiment 1, which, in previous work (Whitmal et al., 2007), was determined to correspond to the effective number of channels many CI listeners can access (Dorman and Loizou, 1998), and represents a configuration for which simulation results are similar to results from CI systems (Dorman et al., 1998; Friesen et al., 2001).

Procedure

Testing procedures for experiment 2 were similar to those of experiment 1, with one notable change: combinations of the three noise conditions (quiet, speech-spectrum noise at +18 dB SNR, and two-talker babble at +18 dB SNR), four absorption coefficients, and three SLDs were used to process each of the 36-sentence lists. Practice materials consisted of 40 sentences, divided into 8 groups of 5 and presented without feedback at the beginning of the experiment. Each group of practice sentences was processed by a unique combination of two SLDs (1 and 7 m), two absorption coefficients (α=1.0 and 0.4), and two noise conditions (quiet and speech-spectrum noise at +18 dB SNR). The practice sentences were not used in the main experiment.

Computation of STI values

STI computations for experiment 2 followed the procedures used for experiment 1.

Results

Intelligibility scores

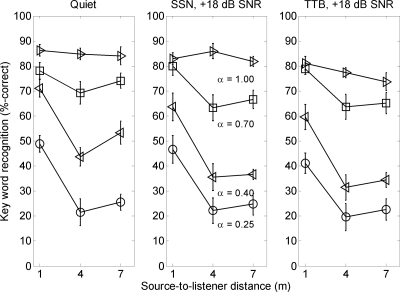
Intelligibility scores for experiment 2 were derived from the percentage of correctly repeated key words per condition. Mean intelligibility scores for listening in quiet and in the two noise conditions are shown in Fig. 5. Scores in quiet were strongly dependent on α, with the average score at 1 m decreasing from 82.3% correct to 48.9% correct as α decreased from 1.00 to 0.25. Intelligibility scores in quiet also decreased as the SLD increased from 1 to 4 m, with average decreases of 8.9%, 27.4%, and 27.4% observed for α=0.7, 0.4, and 0.25, respectively. In general, average scores at 7 m were approximately equal to average scores at 4 m. For α=0.4 in quiet, average scores at 7 m (53.33% correct) were higher than scores at 4 m (43.70% correct), an advantage that, while unexpected, is not statistically significant.

Figure 5.

Speech recognition performance for six-channel vocoded speech in quiet (left panel), speech-spectrum noise (center panel), and two-talker babble (right panel) as a function of SLD and room absorption coefficient in the experiment 2 room simulation. Error bars represent ±1 standard error.

Average scores in noise were lower than average scores in quiet, with the degree of difference determined by values of α. For α=1.0, average scores for the speech-spectrum noise condition were approximately equal to scores in quiet, and 6.33% higher than scores for the two-talker babble condition. For α<1.0, average speech-spectrum noise scores were approximately equal to average two-talker babble scores. The advantage observed for speech-spectrum noise in anechoic conditions and the equivalence of speech-spectrum noise and two-talker babble in reverberant conditions are both consistent with results from previous work (Poissant et al., 2006; Whitmal et al., 2007). As α decreased, the differences between scores in quiet and corresponding scores in noise also decreased, such that scores in quiet and in noise were approximately equal when α=0.25.

Subject scores were converted to rationalized arcsine units (Studebaker, 1985) and input to a repeated-measures analysis of variance of intelligibility scores. All within-subject factors for the analysis of variance were statistically significant; these included α (F[3,236]=460.24, p<0.0001), SLD (F[2,236]=89.49, p<0.0001), and noise condition (F[2,236]=16.65, p<0.0001). The first-order interaction between α and SLD (F[6,236]=11.98, p<0.0001) was significant, reflecting the tendency of intelligibility in the reverberant field to worsen as α increased. The first-order interaction between α and noise condition (F[6,236]=2.24, p=0.04) was also significant, reflecting the tendency for speech-spectrum noise scores to match scores in quiet for α=1.0 and match two-talker babble scores for α<1.0. Post hoc tests using the Tukey honestly significant difference criterion at the 0.05 level indicated that (a) scores at 1 m were significantly higher than scores at 4 or 7 m, (b) scores at 4 and 7 m were not significantly different from each other, (c) scores for each α value were all significantly different from each other, and (d) scores for each noise condition were all significantly different from each other.

To further explore the significance of adding reverberation, four post hoc analyses of variance of scores obtained for individual values of α were conducted. These analyses indicated that (a) for α=1.0, scores for quiet and speech-spectrum noise were significantly greater than scores for two-talker babble; (b) for α<1.0, there were no significant differences between speech-spectrum noise and two-talker babble; (c) for α=0.25 and 0.7, scores in quiet were not significantly different from scores in speech-spectrum noise or two-talker babble; and (d) for α=1.0, SLD was not a significant factor.

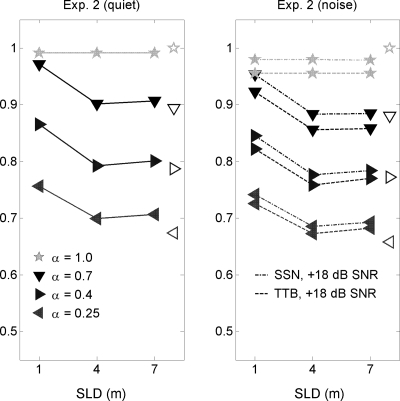
STI values

STI values for the listening conditions of experiment 2 are shown in Fig. 6. As with experiment 1, measured and theoretical values are represented by filled and unfilled symbols, respectively. Two other similarities between these data and those of experiment 1 are evident. First, the measured and theoretical STI values of Fig. 6 are also in good agreement for positions in the reverberant field (SLD≥4 m). Second, the range of experiment 2 STI values (0.63–0.99) also reflects good signal quality, and increases in STI over this range (whether produced by changes in SNR or α) are likewise associated with increases in intelligibility. Unlike experiment 1, however, the larger room volume and variable range of α values used in experiment 2 enabled changes in SLD to have a greater effect on STI (and envelope modulations) than changes in SNR. When SLD was increased from 1 to 4 m, the average STI decreased by 0.068 for α=0.4 or 0.7, with intelligibility decreases of 27.4% and 8.9%; for α=0.25, average STI decreased by 0.055 and intelligibility decreased by 27.4%. These changes in STI (and intelligibility) are consistent with trends observed in an idealized model of direct field contributions to the STI (Houtgast et al., 1980). Adding speech-spectrum noise to the speech decreased average STI values by less than 0.020 and intelligibility scores by 4.2%; adding two-talker babble to the speech decreased average STI values by between 0.036 and 0.048 and intelligibility scores by 7.4%. The larger STI decrease associated with adding two-talker babble is presumably caused by the envelope modulations of the babble, which act to reduce the average modulation depth attributable to the target speech.

Figure 6.

(a) STIs for the listening conditions of experiment 2 in quiet as a function of SLD and room absorption. (b) STIs for the listening conditions of experiment 2 in speech-spectrum noise (dashed∕dotted line) and in two-talker babble (dashed line) as a function of SLD and room absorption. Unfilled symbols depict predictions of STI values for reverberant-field listener locations as modeled by Eq. 5.

The impulse response filters for each listener position were partitioned into three smaller filters as in experiment 1. A-weighted levels of the direct, early, and late portions of the received signal for each combination of SLD and α are shown in Table 5. For α=0.25, direct field intensity drops below both early and late reflection intensities as SLD increases; intelligibility is best at the 1 m SLD, where the direct field is stronger than both the early and late reflections. Similar patterns are apparent for α=0.40 and α=0.70, albeit with both higher intelligibility and higher direct-to-reverberant energy ratios observed at all SLDs.

Table 5.

A-weighted SPLs for direct, early, and late arrivals in experiment 2 reverberant listening conditions.

SLD (m)	Direct	Early	Late
α=0.25
1	61.4	60.8	56.2
4	52.7	63.2	58.3
7	49.6	63.4	58.9
α=0.4
1	62.5	60.0	50.8
4	55.4	63.5	55.9
7	53.0	64.0	55.9
α=0.7
1	63.7	56.4	36.8
4	60.3	62.1	44.8
7	59.7	63.6	44.8

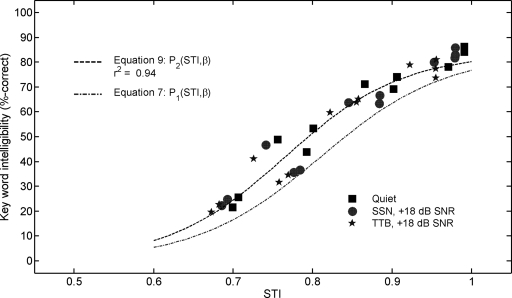
Relationship between STI values and intelligibility scores

The relationship between STI and intelligibility data for experiment 2 is depicted in Fig. 7, along with a best-fit modified sigmoid curve (dashed line)

$$P_2\left(\text{STI},\beta \right)=\frac{P_{\text{max}}\left(\beta \right)}{1+{10}^{-\left[\left(3.08+1.82\text{\hspace{0.17em}ln}\beta \right)\left(\left(\text{STI}+0.005-0.50\text{\hspace{0.17em}ln}\beta \right)+0.02\right)\right]}}.$$ (9)

The good agreement between the data and Eq. 9 suggests that the effect of increasing SLD is, like noise and reverberation, manifested as distortions in envelope modulation that reduce intelligibility. Figure 7 also displays the best-fit line for experiment 1 data (dotted-dashed line), which falls (on average) 7.9% below the line for experiment 2. This large difference may be attributable in part to differences in experimental conditions and subject acclimatization. Although the subjects for each experiment listened to the same sentences, experiment 1 subjects were confronted with more adverse conditions (SNR=−8 and +8 dB) than experiment 2 subjects. Moreover, experiment 1 subjects listened to four different vocoders while experiment 2 subjects listened to only one. Reducing the time that experiment 1 subjects listened to the six-channel vocoder under favorable conditions may have prevented them from acclimating to the vocoder as well as the experiment 2 subjects did.

Figure 7.

Speech recognition performance for six-channel vocoded speech in the simulated room of experiment 2. The dashed line depicts predicted recognition performance as modeled by Eq. 9; the dotted-dashed line depicts predicted recognition performance as modeled by Eq. 7 for experiment 1 data.

DISCUSSION

Effects of SLD on intelligibility

For speech processed in a way that makes it vulnerable to the effects of reverberation (i.e., when it is vocoded with a restricted number of spectral channels), we found that SLD can matter a great deal to speech understanding in a large room. The degree to which benefits of reductions in SLD will be realized will depend on the size of the room and the levels of reverberation and ambient noise, as well as whether or not the separation between source and listener is within (or close to) the critical distance of the room. In experiment 1, subjects demonstrated a modest benefit from reducing SLD in each vocoder configuration in at least some conditions (e.g., those that did not produce ceiling or floor effects). This finding is likely a result of the fact that the signal reaching them was comprised largely of early reflections, rather than direct sound. Experiment 2, conducted within a larger simulated room, produced results that demonstrated a much more promising effect of decreasing SLD on understanding of CI processed speech in reverberant spaces. Again, changes in distance that kept the listener rather deep in the reverberant field (i.e., from 7 to 4 m) had no positive impact on performance. However, once the listener’s position crossed from the reverberant to the direct field (or even close to the direct field), very large improvements were realized. In quiet, the extent of SLD-produced improvements was commensurate with the differences in direct-to-reverberant energy ratio for the 1 and 4 m SLDs. This is evident in Fig. 5, which indicates large improvements in intelligibility for α≤0.40 when SLD was reduced from 4 to 1 m, a smaller improvement for α=0.70, and no significant (or expected) improvement for α=1.0. In all cases, the improved scores were significantly lower than scores observed at 1 m for α=1.0 (see Fig. 7), indicating that the effects of reverberation could not be completely eliminated. These findings underscore our inability to fully compensate for the detrimental effects of reverberation simply by reducing the SLD.

STI-based predictions of intelligibility

The STI has been shown to be an accurate and reliable predictor of speech intelligibility in reverberation and noise for normal-hearing listeners. For this reason, the STI and variants such as the rapid STI (Steeneken and Houtgast, 1982) or the STIPA metric for public address systems (Steeneken et al., 2001; Bjør, 2004) have been widely used in the assessment of classrooms and sound reinforcement systems. In particular, several investigators (Bradley, 1986b; Bradley et al., 1999; Siebein et al., 2000; Crandell et al., 2004) have advocated using STI values (computed from actual room impulse response measurements) to evaluate the suitability of classrooms and identify problems for remediation. Other investigators have used the STI to guide the design of simulated classrooms that optimize speech intelligibility (Bistafa and Bradley, 2000, 2001; Yang and Hodgson, 2006).

The present results suggest that the STI can also be used to accurately predict intelligibility in simulations of CI processing. The uses of the STI in room design and assessment described above may therefore also be applicable to CI simulations. Moreover, the good agreement observed between predicted STI values [computed via Eq. 5] and measured STI values further suggests that the quality of seating in the reverberant field in a room can be estimated simply for simulated CI users if the volume, reverberation time, and SNR are known. Seating in the direct field poses a greater challenge for such simple estimates, since closed-form equations modeling room acoustics for the STI (e.g., Houtgast et al., 1980) are unable to accurately model effects of early reflections.

Comparisons with previous vocoder experiments

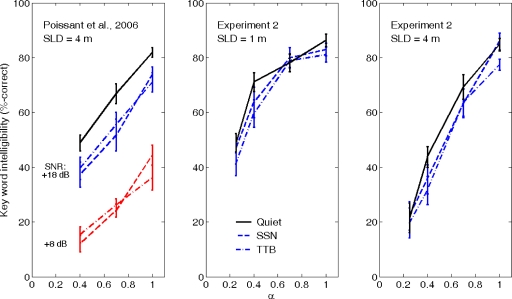
One goal of the present study was to extend the results of Poissant et al. (2006) concerning reverberation and noise effects on vocoded speech intelligibility. This previous study included two experiments that used the room model of the present experiment 1 with a SLD of 4 m and various values of α. Mean scores in quiet for the present experiment 1 and for the first experiment of Poissant et al. (2006) at 4 m with α=0.25 were nearly identical. The second experiment of Poissant et al. (2006) examined performance in quiet and noise as a function of α for 6-channel and 12-channel vocoders. Their data (shown in the left panel of Fig. 8) indicated that (a) intelligibility increased in a near-linear fashion as α increased from 0.4 to 1.0, (b) the effects of speech-spectrum noise and two-talker babble on intelligibility were not significantly different, and (c) scores for all conditions increased at the approximate rate of 5% per 0.1 increase in α without any significant interaction between the number of channels, noise level, and α. As a result, the effects of reverberation and noise on intelligibility appeared to be additive, a result that differed markedly from those of previous studies showing interactions between noise and reverberation for unprocessed speech (Nabelek and Mason, 1981; Loven and Collins, 1988; Helfer and Wilber, 1990; Payton et al., 1994).

Figure 8.

Speech recognition performance for six-channel vocoded speech in experiment 2 of Poissant et al. (2006), experiment 2 of the present work at a 1 m SLD (center panel), and a 7 m SLD (right panel) as a function of room absorption coefficient. Error bars represent ±1 standard error.

In the present experiment 2, performance was evaluated in a larger room for a six-channel vocoder at three different SLDs. Intelligibility scores for the six-channel vocoder are plotted in Fig. 8 as functions of α and SNR for SLD=1 m (center panel) and SLD=4 m (right panel); the patterns of results for 7 m mirrored that of the 4 m data and therefore the 7 m data are not presented. Scores in quiet are similar in value to those measured in experiment 2 of Poissant et al. (2006), as are scores in noise at α=0.4 and 1.0. Moreover, the curves for scores in quiet and at +18 dB SNR are nearly parallel, which, aside from ceiling and floor effects, reflects the same limited interaction observed by Poissant et al. (2006).

Implications for listeners with CIs

The present study used channel vocoders to model speech perception of CI users in reverberant environments. Numerous studies (e.g., Dorman and Loizou, 1998; Friesen et al., 2001) have shown that experiments with channel vocoders can approximate best-case performance for implant users. To the extent that vocoded speech resembles implant processed speech, the present results suggest that intelligibility for implant users can improve when SLD is reduced. While modest improvement may occur as SLD decreases within the reverberant field, striking and important improvements are seen when distance decreases enough to place the listener within, or even close to, the direct field. These effects seem to be well captured by the STI (as shown in a comparison between Figs. 57), which may prove to be a helpful predictive tool. In everyday listening environments, this means that room size will be a key factor in determining potential benefit from preferential seating. For example, in the smaller classroom modeled in experiment 1, the listener remained in the reverberant field even when seated 1 m from the sound source. It is unlikely that CI users will easily be able to position themselves closer than 1 m to most talkers. In the larger modeled room of experiment 2, listeners seated at a 1 m SLD were within (or very close to) the direct field, whereas listeners seated at a 2 m SLD would have been within the reverberant field. As a result, merely reducing the SLD from 2 to 1 m would be expected to be associated with large improvements in performance.

It is also important to note that the intelligibility gained by reducing the SLD in rooms with low-to-moderate levels of absorption did not fully compensate for the intelligibility lost to reverberation (see Fig. 7). These findings highlight the very important negative impact of reverberation and suggest that one of the first steps in improving speech understanding for a CI user in a real-world environment (e.g., a classroom or a conference room) should be to reduce the level of reverberation to the greatest extent possible. However, as there are limits to our ability to ensure appropriate levels of reverberation in all environments in which a CI user may converse, we must remain ever cognizant of making recommendations for preferential seating as we have demonstrated that reliance on decreasing SLD will prove beneficial in improving speech understanding, particularly if the listener is able to move within the critical distance of the room. Another very important and perhaps fail-safe strategy for improving intelligibility of CI users in real-world environments is the use of an FM system or similar remote assistive listening device to replace the reverberated signal reaching the listener with a clean near-field signal. It is also important to remember that only the smearing aspect of reverberation was simulated in the present investigation; the rms levels across conditions were equated. This was done in order to allow for an investigation of the specific impact of temporal smearing on intelligibility in listeners who essentially have access to only envelope cues. At the same time, however, it means that the present data are not influenced by any increase in level that would typically accompany reverberation as well as any increases in intensity that occurs when SLD decreases. Such increases could potentially improve performance for some CI users.

The present study considered only speech and noise arriving coincidentally from the same source. In typical settings it is likely that speech and noise would be spatially distinct, allowing individuals with normal hearing to make use of binaural processes to separate the target from the masker. While a changing trend toward bilateral implantation is observable, the majority of CI users have received just one implant. As unilateral listeners, their best hope of benefit from spatially separated signal and noise sources is a head shadow effect when the noise is located on the side of their head opposite from their implant. Further, for those users who are bilaterally implanted, uncoordinated input to the two clinical speech processors could impose limitations on the use of cues that would result in the ability to suppress noise in favor of speech (i.e., the “binaural squelch” effect) and other expected speech-in-noise improvements afforded to listeners with binaural hearing (MacKeith and Coles, 1971). Finally, it is also possible that CI users might benefit from spatial differences in early reflection patterns, which have been shown to increase the effective signal level and improve intelligibility in some situations (Barron and Lee, 1988; Yang and Hodgson, 2006; Sato and Bradley, 2008). This possibility will be explored in future investigations.

SUMMARY AND CONCLUSIONS

Speech intelligibility for listeners using CIs can be compromised by the temporal smearing effects of reverberation and additive noise. For vocoder simulations in normally hearing listeners, the effects of both factors can be reduced substantially by moving the listener as close as possible to the speech source provided that the reduction in distance places the listener in or very near the direct field. The present study investigated the potential benefits of this strategy for CI users in two simulated classrooms. Results of the study suggest that CI users should receive some benefit by moving closer to the speech source in large rooms with low-to-moderate absorption. Limited benefits are expected in small rooms where all listener positions are in the reverberant field.