Matching the waveform and the temporal window in the creation of experimental signals

Abstract

When a periodic waveform with a discrete-harmonic spectrum is temporally windowed to make a signal, its spectrum becomes a continuous function of frequency. However, there are discrete-frequency representations for windowed signals such as the Fourier series representation of a periodically extended signal. This article introduces the concept of matching between the temporal window and the periodic waveform. Matching leads to a discrete-frequency representation in which the Fourier transform of the windowed signal preserves the amplitudes and phases of the waveform on the set of original waveform frequencies. Generating signals with matched window and waveform leads to important control of experiments.

INTRODUCTION

Auditory scientists generate experimental stimuli, signals, or noise, for presentation to humans and other animals. Often those stimuli are specified in terms of their spectral properties. Psychoacoustician A might specify a broadband complex tone having harmonics with equal amplitudes and Schroeder phases. Physiologist B might specify a narrow-band noise with Rayleigh-distributed amplitudes and alternating phases. Hearing scientist C might specify a five-component signal with constant phases. In all these cases, the experimenter expects that the specified spectral properties will be preserved, at least to a good approximation, in the stimulus presented to the listener.

Spectral properties

When a stimulus is initially defined in terms of exact discrete spectral properties, it can be represented as a sum of cosines with component amplitudes C_n,

$$x\left(t\right)=\sum _{n=0}^N{C}_n\cos ({\omega }_{n}t+{\varphi }_n),$$ (1)

where component angular frequencies ω_n and phases ϕ_n are arbitrary. In what follows, this wave will be called the “unlimited-duration waveform” or the “waveform.” Because its duration is unlimited, it has a bandlimited Fourier transform given by

$$X\left(\omega \right)={\int }_{-\infty }^{\infty }dt{e}^{-i\omega t}x\left(t\right)$$ (2)

or

$$X\left(\omega \right)=\pi \sum _{n=-N}^N{X}_n\delta (\omega -{\omega }_n),$$ (3)

where X_n=C_n exp(iϕ_n), ω_−n=−ω_n, C_−n=C_n, and ϕ_−n=−ϕ_n. With these conditions, X_−n is equal to the complex conjugate, $X_n^{*}$, and x(t) is a real function (see, for instance, Hartmann, 1998).

Finite-duration signals

The infinitely sharp spectrum of Eq. 3 applies only to an unlimited-duration waveform. In practice, a signal is presented to a listener with a finite total duration, T_D. The finite-duration signal is created by multiplying waveform x(t) by a temporal window function, w(t), to create the final signal y(t),

$$y\left(t\right)=w\left(t\right)x\left(t\right).$$ (4)

The finite duration leads to the well-known “spectral splatter” wherein the power spectrum acquires power outside the frequency band of the original waveform. The spectrum becomes a continuum with all frequencies, inside and outside the waveform band, represented more or less.

We consider the case in which signal y(t) can be represented on the finite interval by a Fourier series,

$$y^{\prime }\left(t\right)=\sum _{n=1}^{N^{\prime }}{C}_n^{\prime }\cos (2\pi nt∕T_D+{\varphi }_n^{\prime })(0<t\le T_D),$$ (5)

where the designation y^′(t) distinguishes the finite-duration signal from y(t), which is defined for all time. The fundamental angular frequency of the series is 2π∕T_D, a function of the window duration. All the other frequencies in the series are harmonics, n(2π∕T_D). The finite-duration signal can be periodically extended forward and backward in time to fill the entire time axis, creating the periodically-extended signal,

$$\underset{̱}{y}\left(t\right)=\sum _{n=1}^{N^{\prime }}{C}_n^{\prime }\cos (2\pi nt∕T_D+{\varphi }_n^{\prime })(-\infty <t<\infty ).$$ (6)

At this point in the development, we introduce the concept of matching the temporal window and the waveform. In the simplest case, the temporal window that defines the finite interval in Eq. 5 is rectangular. If the original unlimited-duration waveform x(t) contains power only on a set of harmonic frequencies {ω_n=nω_o} where the fundamental angular frequency ω_o happens to be related to the duration T_D by ω_o=2π∕T_D, then the terms in the Fourier series y^′(t) are the same as the terms in the sum for the waveform x(t). Specifically, $C_n^{\prime }=C_n$, ${\varphi }_n^{\prime }={\varphi }_n$, and N=N^′. The window and the waveform are matched. Because the duration T_D is equal to the period of the waveform, x(t), the periodically-extended signal $\underset{̱}{y}\left(t\right)$ is the same as x(t).

Equation 5, in terms of the duration T_D, is not the only possible Fourier series. It is possible to represent y on the finite interval T_D in terms of any long time, T_L,

$$y_L\left(t\right)=\sum _{n=1}^{N^{\prime }}{C}_{L,n}\cos (2\pi nt∕T_L+{\varphi }_{L,n}),$$ (7)

so long as T_L>T_D. However, to do that, the amplitudes and phases, C_L,n and ϕ_L,n, must be chosen to force y_L(t) to be zero within the part of the T_L interval that is not included in the T_D interval. The frequencies, amplitudes, and phases in this representation do not agree with those in the original periodic waveform, x(t).

Temporal windows

The section above, unifying the waveform, the Fourier series, and the periodically-extended signal when the waveform and window are matched assumes a rectangular temporal window. Although the rectangular window leads to simple mathematics, it is not often used in practice. A rectangular window produces discontinuities in the signal and∕or its derivatives at the onset and offset; these cause audible clicks that may be distracting to human or animal listeners. The clicks by themselves may be spurious stimuli, detracting from the intended purpose of the band-limited amplitude and phase cues of the desired stimulus. In order to reduce onset and offset clicks, it is usual to apply a temporal window which turns the stimulus on and off more gradually.

When a window other than a rectangular window is applied to the waveform, interesting possibilities arise. It is possible to retain the periodically-extended signal, which includes information about the temporal window. Alternatively, and this is the point of the present article, it is possible to maintain the matching concept so that the Fourier transform of the windowed signal preserves the spectral amplitudes and phases of the waveform on the set of waveform frequencies. If the window and waveform are not matched, the spectrum is not preserved on any set of frequencies. Then the spectrum of the signal presented to the listener becomes out of control, more or less depending on details. It seems likely that experimenters often use temporal windows and waveforms that are not matched because the matching conditions are not immediately obvious, as described below.

SPECTRAL CONSEQUENCES OF TEMPORAL WINDOWING

The spectral consequences of temporal windowing appear in the Fourier transform of y(t), namely, Y(ω). Because y(t)=w(t)x(t) is a product, Y(ω) is given by the convolution

$$Y\left(\omega \right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }d{\omega }^{\prime }W(\omega -{\omega }^{\prime })X\left({\omega }^{\prime }\right).$$ (8)

Because X(ω) is a sum of delta functions from Eq. 3, the integral is easy to do, and

$$Y\left(\omega \right)=\frac{1}{2}\sum _n{X}_{n}W(\omega -{\omega }_n).$$ (9)

According to Eq. 9 the spectrum of the final windowed signal can be found from the spectrum of the infinite-duration waveform if we know the Fourier transform of the temporal window, W(ω).

Rectangular window

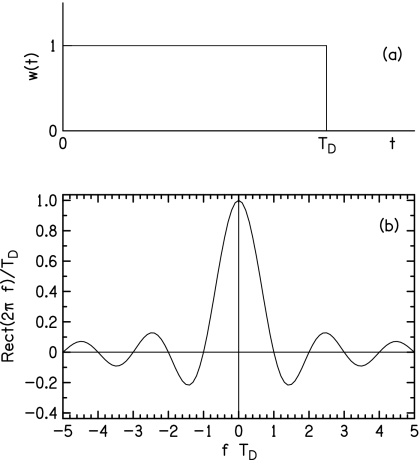
The rectangular window extends from t=0 to t=T_D, as shown in Fig. 1a. The Fourier transform is W_Rect, given by

$$W_{\mathrm{Rect}}\left(\omega \right)=\mathrm{Rect}\left(\omega \right)e^{-i\omega T_D∕2},$$ (10)

where “Rect(ω)” is

$$\mathrm{Rect}\left(\omega \right)=\frac{2\sin (\omega T_D∕2)}{\omega }.$$ (11)

This Fourier transform is the product of two factors. Function Rect is the Fourier transform of the rectangular window translated backward in time by half its duration so that it is symmetrical about the origin. Because of this symmetry, Rect is entirely real. The other factor is a phase factor, exp(−iωT_D∕2), and its role is to translate the rectangle forward again, back to where it belongs.

Figure 1.

Rectangular temporal window. (a) The window as a function of time. (b) The Fourier transform of the rectangular window apart from the phase factor. The Fourier transform is zero for integer values of fT_D.

Function Rect(2πf)∕T_D is plotted in Fig. 1b. Rect(2πf)∕T_D is a sinc function. The figure shows that the sinc function is zero for integer values of fT_D. The duration of time that appears in the argument of the sinc function (T_D for the rectangular window) will be called the “significant duration, T_S.”

Knowing the Fourier transform of the window, we now know the Fourier transform Y,

$$Y\left(\omega \right)=\frac{T_D}{2}\sum _n{X}_n\frac{\sin [(\omega -{\omega }_n)T_D∕2]}{(\omega -{\omega }_n)T_D∕2}\exp [-i(\omega -{\omega }_n)T_D∕2].$$ (12)

Transform Y(ω) includes all the details of the temporally windowed signal y(t). If the waveform and the rectangular window are matched, as described in Sec. 1, then waveform frequencies ω_n are given by ω_n=nω_o, where ω_oT_D=2π. When Y(ω) is evaluated at those frequency values, we find a revealing equation,

$$Y\left(m{\omega }_o\right)=\frac{T_D}{2}\sum _n{X}_n\frac{\sin \pi (m-n)}{\pi (m-n)}\exp [-i\pi (m-n)].$$ (13)

The sinc function in the sum is zero for all values of n except when n=m. When n=m then the sinc function equals 1. Thus the sinc function has become a Kronecker delta function, and Eq. 13 simplifies to

$$Y\left(m{\omega }_o\right)=\frac{T_D}{2}{X}_m.$$ (14)

Because Eq. 14 holds for both positive and negative values of m, both the amplitude and the phase of the original, unlimited-duration signal are correctly represented in the Fourier transform Y(ω) when evaluated at the special frequencies ω=mω_o. In this sense, the spectrum is preserved. The values of the Fourier transform at these special frequencies Y(mω_o) are related to the Fourier series coefficients in Eq. 5 by a constant factor,

$$Y\left(m{\omega }_o\right)=\frac{T_D}{2}{C}_m^{\prime }\exp \left(i{\varphi }_m^{\prime }\right).$$ (15)

The development of this last equation gives insight as to why the spectrum is preserved on the set of frequencies {ω_m=mω_o}. The reason is that the unlimited-duration waveform is matched to the rectangular window because its fundamental frequency ω_o is equal to 2π∕T_D causing the sinc function to be a Kronecker delta function. Matching has effectively made the window disappear for these special frequencies. For the rectangular window, the total duration T_D is also the significant duration. As an example, if we would like to use a 100-ms, rectangularly-windowed signal, we would choose the frequencies to be integer multiples of 10 Hz, i.e., ω₀=2π⋅10, to obtain a complete set of expansion functions. In Secs. 2B, 2C, it will be shown that the same principle can be used to match the waveform (characterized by a fundamental ω_o) and the time window (characterized by a significant duration, T_S) for other forms of time window. An interesting alternative window is the raised cosine.

Raised-cosine window

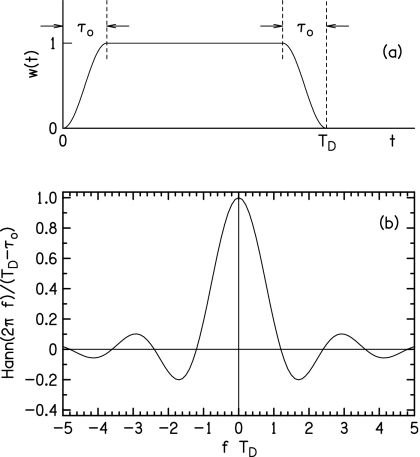
The raised-cosine window (derived from the Hanning or Hann window) is shown in Fig. 2a. It has a onset edge given by [1−cos(πt∕τ_o)]∕2, where τ_o is the edge duration. The overall duration is T_D, and the offset edge is the reverse of the onset edge making the window symmetrical.

Figure 2.

Raised-cosine temporal window for τ_o=T_D∕6. (a) The window as a function of time. The full-on duration is T_D−2τ_o. (b) The Fourier transform of the raised-cosine window apart from the phase factor. The Fourier transform is zero when fT_D is somewhat larger than integer values.

As for the rectangular window, the Fourier transform of the raised-cosine window can be written in terms of a real function multiplied by a time-delay phase factor. A half dozen pages of algebra suffice to show that the Fourier transform is

$$W_{\text{Hann}}\left(\omega \right)=\text{Hann}\left(\omega \right)e^{-i\omega T_D∕2},$$ (16)

where Hann is the transform of the symmetrical window, again involving the sinc function,

$$\text{Hann}\left(\omega \right)=\frac{2\cos (\omega {\tau }_o∕2)}{1-{(\omega {\tau }_o∕\pi )}^2}\cdot \frac{\sin [\omega (T_D-{\tau }_o)∕2]}{\omega }.$$ (17)

Function Hann(2πf)∕(T_D−τ_o) is plotted in Fig. 2b.

For windows other than rectangular, such as the raised-cosine window, the significant duration is not equal to the total duration T_D. For the raised-cosine window, Eq. 17 shows that the significant duration is T_S=T_D−τ_o. Therefore, the fundamental angular frequency of the unlimited-duration waveform needs to be ω_o=2π∕(T_D−τ_o) in order for the window and the waveform to be matched. That result was not immediately obvious.

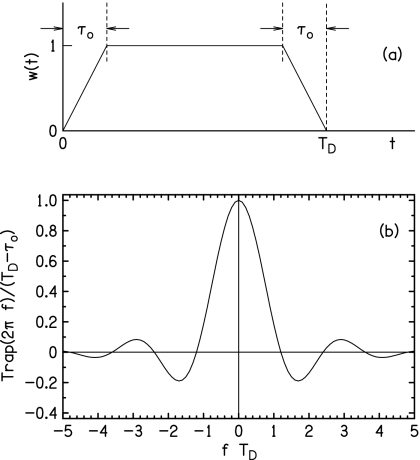
Trapezoid window

The trapezoid window is shown in Fig. 3a. It has straight-line onset and offset edges, both with duration τ_o. The Fourier transform of the trapezoid (less than half a dozen pages of algebra) is given by Eq. 18 and is shown in Fig. 3b.

$$W_{\mathrm{Trap}}\left(\omega \right)=\mathrm{Trap}\left(\omega \right)e^{-i\omega T_D∕2},$$ (18)

where “Trap” is the transform of the symmetrical trapezoid window,

$$\mathrm{Trap}\left(\omega \right)=\frac{4\sin (\omega {\tau }_o∕2)}{\omega {\tau }_o}\cdot \frac{\sin [\omega (T_D-{\tau }_o)∕2]}{\omega }.$$ (19)

It is evident that the significant duration for the trapezoid window is again T_S=T_D−τ_o.

Figure 3.

Trapezoid temporal window for τ_o=T_D∕6. (a) The window as a function of time. The full-on duration is T_D−2τ_o. (b) The Fourier transform of the trapezoid window apart from the phase factor. The Fourier transform is zero when fT_D is somewhat larger than integer values.

The different temporal windows described above lead to different amounts of spectral splatter. A good predictor for splatter is the high-frequency asymptotic behavior of the Fourier transforms. As shown in Eqs. 11, 19, 17, respectively, the rectangular window spectrum decreases as ω⁻¹, the trapezoid window spectrum decreases as ω⁻², and the raised-cosine window spectrum decreases as ω⁻³. These asymptotic behaviors cannot be seen well on the spectral plots in Figs. 123 because the horizontal axis does not extend to high frequencies.

MATCHING AND MISMATCHING

Alternative representations

Sections 1, 2 can be interpreted as follows: When a signal is created by windowing an unlimited-duration waveform, the spectrum becomes a continuous function of frequency. However, there are several possible discrete-frequency representations of this spectrum. One representation begins with a long analysis interval, T_L, longer, perhaps much longer, than T_D. This long time interval is padded with zeros outside the signal interval. The spectrum will consist of lines at frequencies n∕T_L. It will include the window information and will also force the signal to be zero outside the signal interval. This representation contains the most information, and it incorporates the fact that the signal does not live forever. However, it does not resemble the spectrum of the waveform. In this representation, much of the spectral power for major components of the waveform can reside in frequencies very different from the frequencies in the waveform.

A second representation periodically extends the signal as windowed. If the window has overall duration T_D, the Fourier transform of the periodically-extended signal exists only on harmonics of a fundamental frequency 2π∕T_D. This Fourier transform includes information about the window shape as an integral part of the signal. To the extent that window W(ω) decreases with increasing ω, this Fourier representation is band limited. However, the spectrum of the periodically-extended signal does not agree with the spectrum of the original unlimited-duration waveform because the window is not matched to the waveform. Also, because the periodically-extended signal is an artifice, which enables the discrete-frequency representation but does not force the waveform to zero outside the signal interval, this Fourier representation is incomplete.

A third representation of the signal is the matching approach suggested in this article. The Fourier transform of the window indicates the significant duration T_S. If the unlimited-duration waveform consists of harmonics of fundamental frequency ω_o=2π∕T_S, then the waveform is matched to the window. Then the spectrum of the signal evaluated on these harmonics is the same as the spectrum of the unlimited-duration waveform. Matching the window and the waveform causes the window to disappear in this representation, and the spectrum is said to be under control. As an example of this control, the spectrum of a filtered windowed waveform becomes the same as for a windowed filtered waveform, as shown in the Appendix. The order of windowing and filtering operations does not matter if window and waveform are matched.

The rectangular window is a special case. When a rectangularly-windowed signal is periodically extended, it becomes equivalent to the waveform that matches the window. For the rectangular window, one can have both a continuous periodic extension and waveform matching. However, the continuous spectrum may not be sufficiently band limited to avoid distracting transients.

An example with three steps

Spectral effects of temporal windows that are matched or mismatched to the waveform can be illustrated by a simple example with five spectral components. We suppose that the unlimited-duration waveform is a narrow noise band, 40 Hz wide centered at 500 Hz, with amplitudes and phases (expressed in degrees) chosen haphazardly:

$$x\left(t\right)=0.3\cos (360\cdot 480t-45)+1.0\cos (360\cdot 490t-5)+0.2\cos (360\cdot 500t+17)+0.5\cos (360\cdot 510t+143)+0.8\cos (360\cdot 520t-17).$$ (20)

The spectrum of the unlimited-duration waveform is shown in Table 1, row (a).

Table 1.

Spectra for matched and mismatched windowed signals are given in the form level (dB) ∣ phase (degrees). (a) Spectrum of the standard unlimited-duration signal from Eq. 20. The experimenter wants to preserve this spectrum. The amplitudes from the second line are converted to levels in decibels for better comparison with other parts of the table. Step 1: Row (a) is also the spectrum of the rectangularly-windowed signal. Step 2: Row (b) is the spectrum of the windowed signal with mismatched window and waveform. Step 3: Row (c) is the spectrum of the windowed signal with matched window and waveform. Row (d) is the spectrum of the windowed signal with the 500-Hz component shifted by 180° using mismatched window and waveform. The levels are computed with respect to the largest component in row (b) to make the binaural comparison correct. Row (e) is the spectrum of the windowed signal with the 500-Hz component shifted by 180° using a matched window and waveform.

Frequency (Hz)	480	490	500	510	520
Amplitude	0.3	1.0	0.2	0.5	0.8
(a) Standard:	−10.5 ∣ −45	0.0 ∣ −5	−14.0 ∣ 17	−6.0 ∣ 143	−1.9 ∣ −17
(b) Mismatched:	−12.2 ∣ −73	0.0 ∣ −5	−20.7 ∣ 70	−2.3 ∣ 151	−2.1 ∣ −20
(c) Matched:	−10.5 ∣ −45	0.0 ∣ −5	−14.0 ∣ 17	−6.0 ∣ 143	−1.9 ∣ −17
(d) 180 - Mismatched:	−12.1 ∣ −63	+0.4 ∣ −4	−8.3 ∣ −174	−2.7 ∣ 148	−2.1 ∣ −18
(e) 180 - Matched:	−10.5 ∣ −45	0.0 ∣ −5	−14.0 ∣ −163	−6.0 ∣ 143	−1.9 ∣ −17

The fundamental frequency of the unlimited-duration waveform in Eq. 20 is 10 Hz because we want to make a noise that is approximately 100 ms long. In a first step, we use a rectangular window with a duration T_D=100 ms. Because the window and the waveform are matched, the spectrum of the 100-ms noise preserves the amplitudes and phases of the unlimited-duration waveform. The Fourier series spectrum, equivalent to the spectrum of the periodically-extended signal, is equal to the spectrum of the unlimited-duration waveform and is again given by Table 1, row (a).

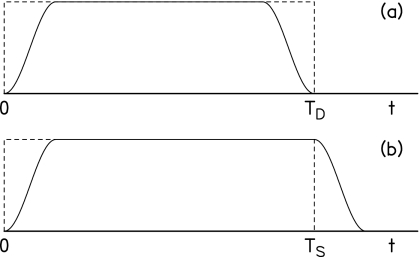
In a second step, we apply a 10-ms raised-cosine edge to the beginning and end of the 100-ms noise, as shown in Fig. 4a. The total duration remains T_D=100 ms, the full-on duration becomes 80 ms, and the significant duration in Eq. 17 becomes T_D−τ_o=90 ms. This value of significant duration would match a waveform having a fundamental frequency of 1000∕90 Hz, but it does not match our chosen fundamental frequency of 10 Hz. The Fourier series spectrum for harmonics of 10 Hz is shown in Table 1, row (b). It does not look good. Both the amplitude spectrum and the phase spectrum are distorted because these spectra are trying to capture some elements of the window. In addition, there is spectral splatter for harmonics of 10 Hz outside the original 40-Hz band not shown in the table. Further, the spectrum Y(ω) looks no better on a different set of frequencies because the waveform, with its fundamental of 10 Hz, is fundamentally incompatible with this raised-cosine window. By mismatching window and waveform, we have lost precise control of the final spectrum.

Figure 4.

Mismatched and matched windows. (a) The rectangular window (dashed) matches a waveform with fundamental frequency 1∕T_D. The raised-cosine window does not match. (b) Both the rectangular window and the raised-cosine window match a waveform with fundamental frequency 1∕T_S, where T_S is the significant duration.

In a third step, we retain the 10-ms raised-cosine edge at the beginning and end, but we let the total duration be T_D=110 ms, as shown in Fig. 4b. Then the significant duration is 100 ms, and that matches a fundamental frequency of 10 Hz. The amplitude and phase spectra, computed at multiples of 10 Hz, are shown in Table 1, row (c). Table 1, row (c) is identical to Table 1, row (a), and there is no spectral splatter for harmonics of 10 Hz outside the original 40-Hz band. What we have given up in exchange for a controlled spectrum is the periodically-extended signal. The 10-Hz fundamental frequency is incompatible with periodic extension of the 110-ms signal.

Binaural consequences

Because research in binaural hearing requires signals with precise interaural amplitude and phase properties, it is interesting to investigate the binaural consequences of windowing waveforms. In this investigation, we imagine that we intend to synthesize signals for the left and right ears where the interaural differences are specified in the spectra of the unlimited-duration waveforms. We would like to know about the effects on these interaural differences if we apply a temporal window to the waveforms. The following facts apply.

 • If the period of the waveforms is equal to the significant duration of the temporal window, or an integral submultiple of it, then the amplitudes and phases on waveform frequencies in both the left and right channels are unchanged by windowing. Consequently, the interaural properties, interaural phase difference (IPD), and interaural level difference (ILD), after the window is applied, are the same as the interaural properties of the waveforms on those frequencies. Life is good binaurally.

 • If the only interaural differences are an IPD (Δϕ) and an ILD (g) applied identically to all components in the spectrum of the unlimited-duration signal, then the interaural spectral properties of the signal after the window is applied are the same as for the unlimited-duration signal whatever the temporal window. It takes only a few lines of mathematics to prove this fact, starting with Eq. 8. If the waveform in the left ear is x_L(t), then the windowed-signal spectrum in the left ear is

$$Y_L\left(\omega \right)=\frac{1}{2\pi }\int d{\omega }^{\prime }W(\omega -{\omega }^{\prime })X_L\left({\omega }^{\prime }\right),$$ (21)

and the windowed-signal spectrum in the right ear is

$$Y_R\left(\omega \right)=\frac{1}{2\pi }\int d{\omega }^{\prime }W(\omega -{\omega }^{\prime })\left[g\left({\omega }^{\prime }\right)e^{i\Delta \varphi \left({\omega }^{\prime }\right)}\right]X_L\left({\omega }^{\prime }\right),$$ (22)

where g is the gain leading to the ILD and Δϕ is the interaural phase shift.

By hypothesis, the gain and interaural phase shift are independent of frequency ω^′, and they can be extracted from the integral. Consequently,

$$Y_R\left(\omega \right)=\left(g{e}^{i\Delta \varphi }\right)Y_L\left(\omega \right),$$ (23)

which says that the signals after windowing have the same interaural relationships as the unlimited-duration waveforms. This binaural invariance always holds good, whether or not the waveform and window are matched. Again, life is good binaurally.

 • If the ILD or the IPD is not the same for all frequencies, then a mismatch between the waveform and the window leads to a distorted interaural spectrum. The effects may or may not be important. For instance, if an interaural time difference (ITD) is applied, the IPD is different for different frequencies, but it may not be very different, especially for a narrow-band noise. Given an applied ITD in the range of a typical experiment (<1 ms) and a critical-band noise, the spectral distortion may not be severe. It depends partly on the number of components in the waveform and partly on luck.

By contrast, a dramatic phase change can lead to dramatic distortion. For instance, one might try to create an NoSπ stimulus by synthesizing two channels that are identical except that the phase of one component is reversed by 180°. Then a mismatch between waveform and window [Fig. 4a] leads to serious distortion, where the interaural amplitudes and phases of the windowed signal do not resemble the desired stimulus.

For example, beginning with the five-component waveform of Eq. 20, and reversing the phase of the center component (500 Hz) leads to the interaural differences shown in Table 1, row (d). The IPDs for the five components are expected to be 0°, 0°, 180°, 0°, and 0°. The actual IPDs for the mismatched condition can be obtained by subtracting Table 1, row (b) from Table 1, row (d). They are 10°, 1°, 116°, −3°, and 2°. The expected phase shift of 180° has been turned into 116°. Further, reversing the phase of the central component has changed the amplitudes of the components. The level of the central component has changed by more than 12 dB. That was not at all intended.

By contrast, if the matched window shown in Fig. 4b is used then reversing the phase of the central component leads to the spectrum shown in Table 1, row (e). Comparison with Table 1, row (c) shows that the only interaural difference is the 180° phase shift of the central component as expected. To create a controllable stimulus like this, it is essential that the waveform and window be matched.

Size of the distortion

The discrepancies between the spectrum of the mismatched windowed signal and the spectrum of the unlimited-duration waveform on the set of waveform frequencies were examined for the particular waveform given in Eq. 20. That waveform had a relatively small amplitude for the central component, and it is partly for this reason that the desired IPD of 180° was so badly violated in the windowed binaural signal. It became 116°. That kind of result is expected. When the waveform and window are not matched, the amplitude of any particular component in the windowed signal becomes a linear combination of the amplitudes of all the other components, more or less, depending on all the phases. A component of the original unlimited-duration signal that is small is particularly vulnerable to distortion by other components with larger amplitudes. Although the distortion seen for this particular waveform is large, it is not atypical for this case of mismatched waveform and window. Other choices of original amplitudes and phases lead to distortions that are as large or larger.

In the example above, the waveform and window are only somewhat mismatched. Because the window has a total duration T_D=100 ms and a raised-cosine edge of τ_o=10 ms, the edges of the window account for only 20% of the total window. The window is not greatly different from a rectangular window, which would preserve the spectrum.

If the calculations leading to Table 1 are repeated except that the edge duration is increased to τ_o=20 ms, then the spectral distortion is correspondingly more dramatic. For instance, in the windowed binaural signal the IPD of the central component becomes −43° degrees instead of 180°. Generally, as the edge duration becomes a greater fraction of the total duration, the effect of mismatch becomes larger.

Because the distortion of the spectrum for a given component in a mismatched case is a linear combination of amplitudes for all the other components, one expects the distortion to be larger when there are more components. Thus, the distortion observed in the above example with only five components may underestimate the typical distortion. However, the form of W(ω) shows that the coefficients in the linear combination decrease as the component contributing to distortion is farther away from the particular component of interest. For the raised-cosine window, it decreases as the cube of the distance in frequency, which is better than the trapezoid window.

PRACTICAL CONSIDERATIONS

Tones

Section 3 above, including the five-component example, dealt with a dense spectrum, where the spacing between adjacent components in the signal was as small as was allowed by the window, namely, 2π∕T_S. It is, of course, possible to use only a subset of the allowed set of frequencies to create a tone. A complex tone with fundamental angular frequency M(2π∕T_S), second harmonic 2M(2π∕T_S), and so on with integer M is also matched to the window with significant duration T_S.

Discrete Fourier transform

Thus far, the matching principle has been developed in terms of signals that are continuous functions of time. The principle also applies to discrete time (sampled) signals as well and to the discrete Fourier transform (DFT). As noted in the Introduction, an experimenter normally creates a signal beginning with an intended spectrum. In a digital implementation, the experimenter chooses a sample rate and a signal duration so that the intended spectrum can be represented as a spectral array (Proakis and Manolakis, 1992). Applying an inverse DFT, or inverse fast Fourier transform, produces a function of time, which is then given a temporal window to make the signal. This approach to signal generation does not match the waveform and the window.

In order to match the waveform and the window, the spectral array should be represented assuming that the signal duration will be the significant duration T_S, not the signal duration T_D. As a result, the inverse DFT will lead to a function that has duration T_S. That duration is not long enough because the duration of the intended signal, T_D, is always longer than T_S. For instance, for the raised-cosine window, the duration is T_D=T_S+τ_o. However, by its nature, the inverse DFT produces a function of time that is periodically extended. Consequently, it is only necessary to repeat a portion of that function in order to produce a function with duration T_D. That function can then be multiplied by the temporal window, and the final signal will correspond to a matched waveform and window.

DISCUSSION

Experimenters initially specify their signals in terms of a desired spectrum. Precise spectral requirements in terms of discrete frequencies imply a waveform of unlimited duration. For instance, an experimenter might specify a 500-Hz sine tone or a noise with a rectangular bandwidth of 40 Hz. These are statements about infinitely long waveforms, but a signal as actually used in real life has a finite duration, imposed by a temporal window. Making the duration finite inevitably has spectral consequences. The windowed signal, as presented to a listener, does not have the spectrum as specified.

Summary of matching. This article has considered temporal windowing procedures that are spectrum preserving and windowing procedures that are not spectrum preserving. The spectrum to be preserved (or not) is that of a periodic waveform, where the spectrum exists only on a set of harmonically related frequencies {f_n=nf_o}. The rectangular window with duration T_D preserves the spectrum if f_oT_D=1. On the set of harmonic frequencies {nf_o}, the rectangularly-windowed signal has no power outside the band of desired spectral components; i.e., there is no spectral splatter on harmonics. Further, within the band of desired components the spectrum of the windowed signal has exactly the amplitudes and phases of a periodically-extended signal. The rectangular window is conceptually simple because the matched unlimited-duration waveform is the same as the periodically-extended signal.

The purpose of this article was to point out that spectral preservation arises from properties of the Fourier transform of the temporal window. It was shown that if the window and waveform are matched, then the spectrum is preserved. The rectangular window with duration T_D is matched to the waveform made from spectral components with frequencies that are harmonics of 1∕T_D. If some other form of temporal window, having overall duration of T_D, is used, then the window is not matched by a waveform made from harmonics of 1∕T_D. Instead, the match between window and waveform must be made in view of the significant duration T_S that appears in the Fourier transform of the window. For example, the raised-cosine window shown in Fig. 2 having a total duration of T_D and a Hanning edge with duration τ_o at each end is matched by a waveform with period T_S=T_D−τ_o. A waveform that is matched to a window that is not rectangular is not equal to the periodically-extended signal with period T_D. Given that the periodically-extended signal is only a fiction, extrapolated from the Fourier series, giving it up entails little cost.

Value of matching. Because matching the waveform and the window only preserves the spectrum on a specific set of frequencies, one may well ask whether there is a value to matching. One value is that the frequencies of this set are the most important frequencies in the windowed signal. They are almost certain to be the frequencies with the largest amplitudes and the most power. Also, they are the frequencies that are initially specified by the experimenter.

However, sometimes experimenters make no attempt to match. For instance, an experimenter may compute a noise waveform using a band of spectral components spaced by only 1 Hz, give it a duration (e.g., 100 ms) using a nonrectangular window of some form, and present it to a listener. If the window is smooth, the spectral splatter outside the band may be held to some designated limits. Although the phases and amplitudes within the band of the windowed noise are not preserved, nor are they equal to those of the periodically-extended waveform with a period of 1 s, that may not be of much concern to the experimenter. It may be that one set of amplitudes and phases is as good as any other.

Creating waveforms in this way, with no regard for matching, leads to the widest possible variety of signals in the experiment. However, the spectrum is not well controlled. Generating noise stimuli in this way is like using a thermal noise generator and bandpass filter for the waveform and an analog multiplier for the window. Stimuli like these would not be appropriate for reproducible noise experiments where the stimulus spectrum needs to be known exactly. An alternative procedure for reproducible noise is to begin with a desired spectrum, create a windowed stimulus violating all the matching rules, and then test the windowed stimuli for approximate agreement with the desired spectral properties. That approach has been taken by a number of experimenters, e.g., Goupell and Hartmann, 2007. It is normally necessary to reject a large number of candidate stimuli.

Generalization. The mathematical development in this article considered three temporal windows, rectangular, raised cosine, and trapezoidal. Conditions for matching to a waveform were found for all three of those windows. Is it possible to generalize this development? Can one say that for every form of temporal window there is some way to obtain a matching condition? Apparently not. The matching conditions for the three windows depended on Fourier transforms that contained a sinc-function factor. On a set of matching harmonics, the sinc function became a Kronecker delta. Other windows do not have a sinc-function factor, a Gaussian window, for example. The matching conditions as derived in this article would not work for such a window.

Signal detection theory. In the theory of signal detection, the number of degrees of freedom in a signal is given by 2W_bT_D, where W_b is the bandwidth (Green and Swets, 1966). This result implicitly assumes a rectangular temporal window. That can be seen as follows: For a rectangular window, the frequency spacing in the spectrum of the periodically-extended signal is 1∕T_D. The number of independent spectral components is then simply the bandwidth divided by the frequency spacing. The factor of 2 arises because specifying each component requires two variables, an amplitude and a phase. According to the theory of this article, if the window is not rectangular, the number of degrees of freedom is smaller. For instance, for a raised-cosine window, the number of degrees of freedom is 2W_b(T_D−τ_o).

The ongoing signal. This article has been concerned with the Fourier transform of a windowed signal. The signal originates in a waveform of unlimited duration, but in the end, the window, of whatever form, is considered to be an integral part of the signal being Fourier transformed. That point of view is not necessarily perceptually relevant. It may be that the listener’s decisions are affected only by the ongoing portion of the signal. For instance, if the listener’s task is to evaluate the pitch of a one-second periodic complex tone, it is unlikely to matter whether the stimulus is turned on with one kind of temporal window or another. Then the most relevant spectral representation would be the spectrum of the unlimited-duration waveform. Spectral distortions caused by a mismatched raised-cosine window would be unimportant because that window plays a role that is merely cosmetic. Its smooth edges eliminate unaesthetic clicks.

Relevance of the spectrum. For some stimuli, particularly those that are very short, the temporal window contributes importantly to the power spectrum of the signal presented to a listener. Sometimes considering the entire power spectrum leads to a insights into perception (e.g., Green, 1968; Hartmann and Sartor, 1991). However, the power spectrum may not always provide the most relevant physiological or psychological representation of the stimulus. That is particularly true for the simple spectrum obtained by matching the waveform and window as described in this article. What is one to make of the fact that on one set of frequencies there is spectral splatter but on another set of frequencies there is none? Alternatives to the spectral representation are available, e.g., the wavelet or Wigner distribution, but they have had negligible impact on auditory science compared to the Fourier spectral representation, which maps to place in the auditory system.

Another alternative to a spectral representation is to build a mathematical model of the system of interest—anything from outer ear to cortex—and to use the time-dependent windowed signal y(t) as the input to the model. Whether the essential stimulus attributes lie in the onset, offset, window, or ongoing signal then becomes a characteristic of the model. The spectrum itself plays no role.

Final word. When it is important to control the spectrum of a windowed stimulus, there is a value to matching the waveform and the window. To match the window and waveform it is necessary to know the Fourier transform of the windowing function. Control may be particularly important in some binaural experiments where differences in the signals to the two ears become important.

APPENDIX: FILTERED FUNCTIONS

If waveform and window are matched, the spectrum of a windowed filtered signal is the same as the spectrum of a filtered windowed signal, where the spectrum is defined on the discrete set of frequencies that are harmonics in the waveform. The order of operations does not matter. This appendix proves that fact. It begins with the windowed filtered signal.

If the waveform x(t) is filtered with transfer function H(ω), the Fourier transform of the filtered waveform is H(ω)X(ω). If the filtered waveform is then windowed with temporal window w(t), the Fourier transform is given by the convolution from Eq. 8,

$$Y_1\left(\omega \right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }d{\omega }^{\prime }W(\omega -{\omega }^{\prime })H\left({\omega }^{\prime }\right)X\left({\omega }^{\prime }\right).$$ (A1)

Because Eq. 3 expresses X(ω) as a sum of delta functions, the integral is easy to do, and

$$Y_1\left(\omega \right)=\frac{1}{2}\sum _{n=-\infty }^{\infty }W(\omega -{\omega }_n)H\left({\omega }_n\right)X_n.$$ (A2)

If x(t) is periodic with fundamental frequency ω_o, and if Y₁ is evaluated on harmonics of ω_o, then

$$Y_1\left(m{\omega }_o\right)=\frac{1}{2}\sum _{n=-\infty }^{\infty }W\left[(m-n){\omega }_o\right]H\left(n{\omega }_o\right)X_n.$$ (A3)

Reversing the order of the operations above produces a filtered windowed signal. Beginning with Eq. 8 for the windowed waveform and then filtering with transfer function H leads to the Fourier transformed signal

$$Y_2\left(\omega \right)=\frac{1}{2\pi }H\left(\omega \right){\int }_{-\infty }^{\infty }d{\omega }^{\prime }W(\omega -{\omega }^{\prime })X\left({\omega }^{\prime }\right).$$ (A4)

Using Eq. 3 to write X(ω^′) in terms of discrete harmonic frequencies and again evaluating at those frequencies lead to

$$Y_2\left(m{\omega }_o\right)=\frac{1}{2}H\left(m{\omega }_o\right)\sum _{n=-\infty }^{\infty }W\left[(m-n){\omega }_o\right]X_n.$$ (A5)

According to the development in this appendix, ω_o is the fundamental frequency of the waveform. If the window is matched to the waveform, then W[(m−n)ω_o]=W_oδ_m,n, where W_o is a constant. Then Eq. A3 for Y₁ and Eq. A5 for Y₂ are the same, and

$$Y_2\left(m{\omega }_o\right)=Y_1\left(m{\omega }_o\right)=\frac{1}{2}H\left(m{\omega }_o\right)W_o{X}_m.$$ (A6)

The filtered windowed signal is equal to the windowed filtered signal. If the waveform and the window are not matched, W[(m−n)ω_o] is not diagonal on m and n and the filtered windowed signal is different from the windowed filtered signal.