Abstract
Shock waves in liquids are known to cause spherical gas bubbles to rapidly collapse and form strong re-entrant jets in the direction of the propagating shock. The interaction of these jets with an adjacent viscous liquid is investigated using finite-volume simulation methods. This configuration serves as a model for tissue injury during shock-wave lithotripsy, a medical procedure to remove kidney stones. In this case, the viscous fluid provides a crude model for the tissue. It is found that for viscosities comparable to what might be expected in tissue, the jet that forms upon collapse of a small bubble fails to penetrate deeply into the viscous fluid “tissue.” A simple model reproduces the penetration distance versus viscosity observed in the simulations and leads to a phenomenological model for the spreading of injury with multiple shocks. For a reasonable selection of a single efficiency parameter, this model is able to reproduce in vivo observations of an apparent 1000-shock threshold before wide-spread tissue injury occurs in targeted kidneys and the approximate extent of this injury after a typical clinical dose of 2000 shock waves.
INTRODUCTION
We consider a small gas-filled bubble being compressed rapidly by a shock wave (see Fig. 1) and its subsequent jetting toward a viscous material. This configuration is motivated by medical procedures such as shock-wave lithotripsy, during which shock waves are directed toward kidney stones in the hope of fracturing them into “passable” pieces. At clinical shock-wave doses, there appears to be significant collateral injury to the kidney,1, 2 which is implicated in certain short- and long-term complications.3 The action of cavitation bubbles is implicated in this injury.4, 5
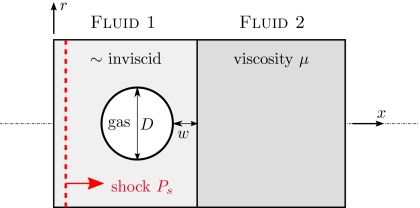
Figure 1.
Configuration schematic (see text).
Bubble expansion, caused by the negative-pressure phase of the lithotripter wave,6 has been suggested as a potential mechanism of the injury,7 but the bubble collapse is also potentially damaging. It is known that a bubble can collapse asymmetrically leading to the formation of a so-called re-entrant jet,8, 9 which starts from where the shock first encounters the bubble and is able to penetrate the bubble’s far side with sufficient velocity to damage nearby material. This is one of the mechanisms thought to cause cavitational damage in engineered systems in cases where the flow’s dynamic pressure causes the cavitation and subsequent collapse.8 The shock sensitivity of explosives also appears to depend on this jetting mechanism. In this case, the formation of local hot spots in the material by the dissipation associated with this jetting seems to increase the overall explosive sensitivity of energetic materials to shock-like mechanical impacts.10, 11
In tissues, this jetting has been hypothesized to be the mechanism of mechanical injury during lithotripsy (e.g., see the recent discussion of Klaseboer et al.12), and it is potentially the mechanism by which bubbles subjected to bursts of high-intensity focused ultrasound (HIFU) can erode tissue (e.g., Ref. 13). HIFU is also well known to cause thermal injury to tissue, but our concern is with mechanical effects at energy deposition rates that preclude significant heating. Thermal injury is not expected in lithotripsy.14
Simulations of collapsing bubbles typically neglect viscosity,12, 15, 16, 17, 18, 19, 20, 21 which is indeed justified based on the Reynolds numbers of the jets expected under typical conditions,20 though for very small bubbles viscous effects have been identified for non-shock-induced (so-called Rayleigh) collapse near a wall.22 The re-entrant jets for lithotripter shocks appear to have speeds of around 1000 m∕s,12 so for a 1 mm diameter bubble in water the jet Reynolds number is about 106. Even if we assume that the re-entrant jet diameter is only 1% of the bubble diameter, this Reynolds number is still 104. However, the significantly smaller bubbles that might form in microvessels in the kidney (say, 20 μm diameter) and the significantly higher viscosities of tissue (at least hundreds of times that of water) can lead to re-entrant jets with Reynolds numbers of around unity. This suggests that tissue viscosity might play a significant role in suppressing the jetting and any injury it might cause. Recent experiments involving laser-induced bubble growth and collapse in viscous fluids suggest that higher viscosity fluids both suppress the strength of the jetting and slow the time scale of the collapse.23
Viscosity has also recently been proposed to be important for the confinement of bubble expansion when subjected to model lithotripter shock profiles.24 Assuming spherical symmetry, we recently generalized the well-known Rayleigh–Plesset bubble dynamics model to account for confinement by an elastic membrane and an extensive Voigt visco-elastic material.24 Results suggest that even the highest estimates of tissue elasticity fail to suppress bubble growth significantly, but because of the small scales and nature of the expansion, even moderate estimates of tissue viscosity were able to play a substantive role is suppressing bubble expansion.
Though kidney injury directly motivates this study, it should also be clear that connection of the present study to tissue and its injury is loose since we neglect its elastic character altogether and study the collapsing bubble’s interaction with a viscous fluid. Our Newtonian viscosity can, of course, provide only an approximate model for tissue viscosity under small deformations and only the crudest possible model for the dissipation associated with the mechanical disruption of tissue. That understood, this type of interaction does not appear to have been studied and a linear viscosity model is clearly a reasonable start for investigating phenomenology. Extending the type of simulations employed herein to tissue-like visco-elasto-plastic models would be a non-trivial task. Furthermore, any such attempts to refine the tissue model would remain only phenomenological because of the lack of detailed constitutive models for the mechanics of tissue injury.
Section 2 introduces the physical model for studying jetting penetration of the viscous “tissue.” The numerical scheme is summarized in Sec. 3, and simulation results along with a simple model reproducing the jet penetration depth are presented in Sec. 4. In Sec. 5, this simple model is incorporated into a phenomenological model for the spreading of tissue injury with the thousands of shocks of a typical treatment. There it is shown to be successful at reproducing some in vivo observations of kidney injury during lithotripsy.
THE MODEL CONFIGURATION
We are interested primarily in the effect of a pre-existing bubble as it collapses on an adjacent viscous fluid, particularly the penetration depth of the jet, which motivates the configuration shown in Fig. 1. The shock propagates perpendicular to the viscous fluid. The only length scales are the bubble diameter D and its distance w from fluid 2 which has viscosity μ. Both the viscous and nearly inviscid (μ1) liquids have a density ρ that is 1000 times that of the gas in the bubble. This density ratio is so large that the density of the gas is expected to have negligible influence on the subsequent jetting dynamics. Simulations confirm that doubling it does not change any of the results we discuss. There are thus only two parameters we consider: s=w∕D and , the second of which is the Reynolds number based on shock pressure jump Ps and density ρ, which is commonly used in studies of shock-induced pore collapse (e.g., Ref. 25). For the nearly inviscid fluid, we take , so we do not expect significant viscous effects in the collapse itself. Five Reynolds numbers are simulated (Re=0.4, 4, 13.3, 40, and 400), which we anticipate should show highly dissipative to relatively inviscid behavior. We also consider s=0, 0.25, and 0.5, and shall see in Sec. 4 that the bubble collapse and peak jet velocity is insensitive to s for this range.
The non-dimensional parameters s and Re guide our investigation of the relative effects of bubble proximity and viscosity, but our simulations are also motivated by the specific bubble-in-tissue application. The parameters considered correspond approximately to a 20 μm diameter air bubble in water at atmospheric pressure being compressed by a Ps=40 MPa shock, as might be delivered by a typical lithotripter.26 The liquid densities are both 1000 kg∕m3. The lowest tissue viscosity we consider is μ=0.01 Pa s, which corresponds roughly to tissue viscosity deduced via the small fast deformations of dissipating ultrasonic shear waves.27, 28, 29 Our results (Sec. 4) show that indeed there is little viscous dissipation in this case. The highest viscosity we consider is μ=10 Pa s, which corresponds to more standard, high amplitude but slower rate, deformations.30 This range of viscosities is discussed in more detail elsewhere.24 Because of the current activity in this specific area, we choose to present mostly dimensional results for this particular system.
It is known that the shock might couple with on-going oscillations of the bubble, affecting both collapse time and apparent jet strength,31 which has been studied in some detail via boundary integral simulation methods.12 However, to simplify our investigation we consider the bubble to be of fixed volume before the interaction with the shock. We anticipate that the jet formation will occur almost independently of its subsequent interaction with the viscous half-space, which is indeed confirmed in Sec. 4. So, assuming the oscillations are relatively weak, the current jet penetration results should apply to a transient or oscillating bubble so long as the jet strength is properly accounted for.
The equations governing the system are
| (1) |
| (2) |
| (3) |
where ρ is the density, p is the pressure, u is the velocity, E is the total energy (kinetic plus internal), and τ are the Newtonian-fluid viscous stresses. These equations are written compactly here in three-dimensions, but the simulation model is constrained to be axisymmetric. The liquid thermodynamics are modeled via a stiffened equation of state,
| (4) |
where e is the mass-specific internal energy. The model parameters in Eq. 4 are selected to be p∞=3×108 Pa and γ=7, which provides an approximate model for water.32 The bubble contents are modeled by the ideal gas equation of state: Eq. 4 with p∞=0 and γ=1.4.
Here we consider only the collapse and jetting process for a pre-existing spherical bubble. In lithotripsy, these are expected to be due to gas being pulled out of solution by the negative portion of the lithotripter wave, which follows the shock.4, 6 The numbers of such bubbles are also expected to increase with subsequent shocks and the intensity of shock-induced collapse has motivated a close examination of their potential role in stone breaking.19 The jetting in this case also seems to be somewhat stronger than in corresponding Rayleigh collapse.20 While dissolution and diffusion are expected to be important for the formation of the gas bubbles, the collapse and jetting are expected to occur too quickly for any significant phase change or thermal transfer between the bubble and the surrounding fluid to affect the subsequent jet formation. Inclusion of such factors is important for calculating peak temperatures for asymmetric collapses,33 and presumably for behavior of the collapsed bubble upon re-expansion, but the jet formation is expected to be governed by mass and momentum conservation considerations that are independent of the microscopic details of the final collapsed condition. Simulation models that do not attempt to resolve the heat transfer, diffusion, and high-temperature effects in the equation of state behavior have indeed shown collapse dynamics that seem to match corresponding experimental data (e.g., Ref. 16). We follow this approach and neglect these factors, though our simulation does include liquid compressibility and viscosity, which are also often omitted from simulations. We also neglect surface tension. Weber numbers We=ρU2D∕σ based on bubble diameter, peak calculated jet velocities (see Sec. 4), and the surface tension of blood [σ=0.06 N∕m (Ref. 34)] are around 5×105 and would be roughly the same for water. Thus, inertia is clearly expected to dominate surface tension for jet formation, justifying its neglect here.
For the small bubbles of interest, we shall see that the entire collapse and jetting penetration of the viscous fluid takes place in ≲0.25 μs, with conclusions about suppressed penetration available after around 0.05 μs. For these times, a lithotripter shock can be assumed to have a sharp rise and then constant pressure. In water, where the pressure profiles are typically measured, the shock-wave pressure has an unresolvably fast rise time [theoretically around 0.15 ns (Ref. 35)] before it drops approximately linearly over about 1 μs.26 So by the time there would any significant decrease in the wave pressure, the bubble in our simulations will have collapsed to such a small size that its dynamics will not affect the subsequent jetting.
NUMERICAL SOLVER
The basic simulation approach is similar to that of Johnsen and Colonius,18 who also considered bubble collapse by lithotripter shocks, though our objectives and the details of our algorithm are different. Our finite-volume solver for Eqs. 1, 2, 3, 4 uses a TVD reconstruction with a minmod limiter36 and a HLLC (Ref. 37) approximate Riemann solver. These are standard techniques for single-phase gas dynamics calculations involving shocks. To track the three fluids in our system (the gas, fluid 1, and fluid 2), we also transport two phase variables, which are used to demark the different regions that the different fluids occupy: ϕg=1 in the bubble and is 0 elsewhere, and ϕs=1 in fluid 2 and is zero elsewhere. A wide class of level-set or phase-field schemes models the interfaces, which in reality are molecularly thin, with a mesh-resolved though narrow continuous variation of ϕ between its extreme values on either side. With such a “smeared” interface model, the transport of the different ϕ’s is governed by
| (5) |
| (6) |
Numerical diffusion in general will further smear these interfaces in time, which greatly degrades the quality of long-time solutions. However, we have designed special terms based on initialization of the phase field using a tanh profile diffused over a few grid cells and keeping this profile fixed as it advects during the simulation.38, 39 When coupled into the overall numerical scheme, this preserves the sharpness of the ϕ representation of the material boundaries. These and all the details of the inviscid portion of the scheme are presented in full elsewhere.40 Viscous terms appearing in Eqs. 2, 3 are discretized using a standard second-order finite-volume scheme in a way that keeps the overall method conservative. A four-stage third-order accurate semi-implicit Runge–Kutta method41 is used to treat viscous terms implicitly and effectively avoids the strong stability restriction encountered by explicit time integration methods for the higher viscosities. The resulting coupled system of linear equations for momentum in the x and r directions is solved using the BICGSTAB (Ref. 42) algorithm.
Solutions with finite-volume solvers are not potentially as fast as with boundary-element methods,16 but the inclusion of viscosity seems to preclude boundary-only discretizations since Green’s functions are only available in the inviscid and strictly viscous limits. Boundary integrals would also be inconsistent with our current simulations in which we wish to track the fluid jet even after the bubble has collapsed to very small (negligible in our model) size. Perhaps not essential, but potentially important, a finite-volume solver also allows explicit two-way coupling of the shock propagation and the bubble response. The simulations presented herein required 1–3 processor-days to complete, which is still very fast given the availability of parallel systems. The longest of times were required for the most viscous cases because of longer convergence times for the implicit time advancement.
The axisymmetric computational domain extends 100 μm in x and out to 50 μm in r and was discretized by 800×400 mesh points in these two directions, respectively. For all the penetration distances calculated, less than a 10% change was observed for a 400×200 mesh calculation. The fluid 1∕fluid 2 boundary was at x=45 μm and the shock was initialized using the shock-jump conditions for Eq. 4 at x=10 μm. Simulations were run with time step Δt adjusted to fix the CFL number: Δt(c+∣u∣)max∕Δx=0.3, where Δx is the mesh spacing.
RESULTS
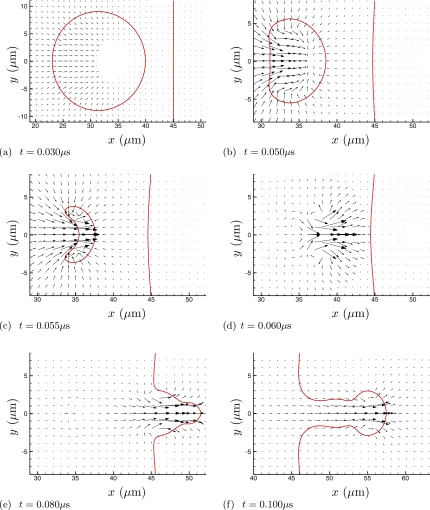
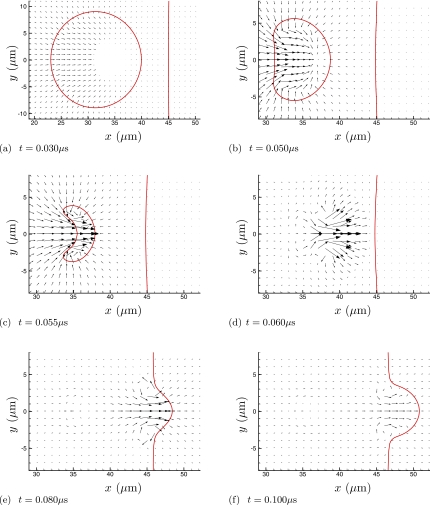
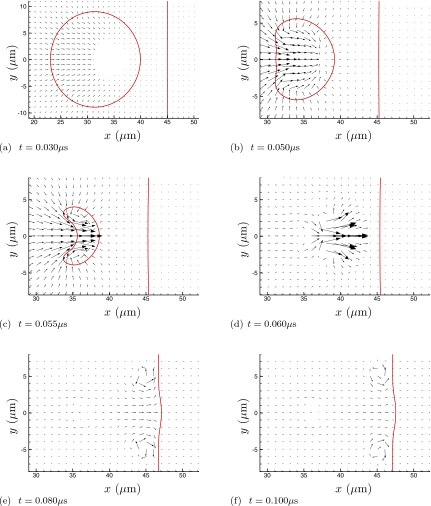
Figures 234 visualize the collapse and re-entrant jetting. For the higher viscosity cases (Fig. 3 and especially Fig. 4), the penetration of the jet into fluid 2 appears to be suppressed. But it is also clear from frame (c) of all three figures that the initial asymmetric collapse and jet formation is insensitive to the viscosity of fluid 2. Quantitative comparisons of velocities confirm this. Peak x-direction velocities through the entire collapse and jet formation are nearly the same for all cases, as can be seen in Table 1, though the viscous resistance of fluid 2 does increase jet velocities a bit. (The peak jet velocity of 1.2 km∕s is similar to that found for similar shocks by others.19, 43) The influence of the viscous fluid 2 is strongest when the bubble is directly in contact with fluid 2 (the w=0 case) up through μ=1 Pa s, though this trend reverses for the highest viscosity. Except perhaps for the w=0 case, we can conclude that the collapse and initial jet formation are insensitive to the viscosity of fluid 2. A more significant increase in jetting velocity is seen for the case of a bubble adjacent a solid wall,19, 43 which is presumably mostly due to the reflection of the shock. Our results, in which there is no acoustic impedance mismatch, suggest that there might also be a relatively small hydrodynamic influence from the wall. In all cases, the bubble collapses as it should to a size that is too small to be resolved by the numerical scheme, but because of this small size and mass it will also not affect the subsequent jetting dynamics.
Figure 2.
Velocity vectors at times during the collapse and jetting for the μ=0.1 Pa s case with w=D∕4=5 μm. Note that the scale is different in (a) to show the full bubble at the beginning of its collapse. The lines show the ρ=0.5ρliquid and ϕf=0.5 isopleths. The vector associated with only every eighth mesh point in each coordinate direction is plotted. For reference, in (a), the shock front is just leaving the region shown.
Figure 3.
Same as Fig. 2 for the μ=1 Pa s case.
Figure 4.
Same as Fig. 2 for the μ=10 Pa s case.
Table 1.
Peak jet velocities in km∕s for all cases.
| μ (Pa s) | w=0 | w=D∕4 | w=D∕2 |
|---|---|---|---|
| 0.01 | 1.27 | 1.28 | 1.29 |
| 0.10 | 1.37 | 1.30 | 1.29 |
| 1.30 | 1.46 | 1.31 | 1.30 |
| 1.00 | 1.60 | 1.30 | 1.29 |
| 10.0 | 1.39 | 1.44 | 1.34 |
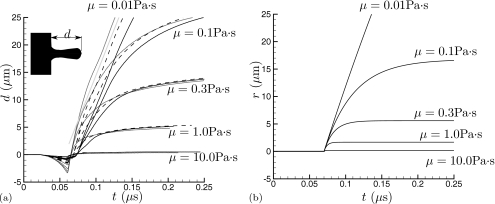
Our principal interest is the distance d(t) to which the jet penetrates the viscous material, because this is presumably related to disruption of tissue and the spreading of injury. To account for the small uniform advection due to the post-shock velocity, d(t) is taken to be the x distance between the fluid 1∕fluid 2 interface at the r=50 μm, where the post-shock x velocity is steady and uniform, and the interface location at r=0. This penetration depth is plotted in Fig. 5a. In all cases, our metric shows that the interface-bubble separation first decreases, an effect which is particularly pronounced for the w=0 cases. It is pulled this way by the initial collapse, which is relatively symmetric at first, and because the bubble shields the interface at r=0 from the shock’s acceleration, which has been noted previously in the context of interaction with kidney stones.19 This can be seen in the (b) frames of Figs. 234. After the initial attraction of the interface toward the collapsing bubble, Fig. 5a shows that increasing viscosity substantially slows the jet and suppresses its penetration into fluid 2. The minor changes in peak jet velocity seen in Table 1 do not lead to significant differences in penetration depth, nor do the different distances between the bubble and the wall. The penetration increases linearly in time for the lowest viscosity cases, which shows that it is indeed nearly inviscid as anticipated based on the Reynolds number estimates in Sec. 2.
Figure 5.
Penetration distance d into the viscous region. (a) Simulation results for different initial bubble offsets distances: (⋯⋯⋅⋅) w=0; (----) w=D∕4=5 μm; and (——) w=D∕2=10 μm. The different sets of curves are for different viscosities as labeled. The straight gray line is for reference. (b) The penetration model 7 with to=0.7 μs to facilitate comparison.
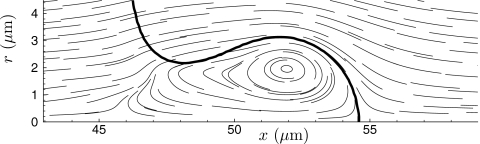
For the cases with substantial penetration, visualizations such as in Fig. 6 show that the leading portion of the jet has a vortex-ring character. Recognizing that it is roughly spherical and that the jet’s fluid is inviscid, we can estimate the drag on the penetrating fluid by the value for an inviscid fluid sphere in a viscous fluid flowing without significant inertia: 4πVμa, where a is its radius and V is its speed. We rely on the geometric insensitivity of flow in the Stokes limit in making this estimate. The penetration depth history for t≥t0 can then be estimated via a solution of the equation of motion as
| (7) |
where Vo is the initial velocity. This velocity is estimated by identifying the speed of a moving frame of reference that has a stagnation point on the r=0 interface between fluid 1 and fluid 2 at the beginning of penetration. For the μ=0.3 Pa s, w=D∕4 case, this velocity is Vo=410 m∕s. Given the similarity of the collapses (Figs. 234) and of the peak velocities (Table 1), we take this Vo for all cases. The sphere radius is taken to be 3.5 μm, based on visualizations. This is, of course, an approximation since it is not exactly the same for all the test cases and can also vary in time for a single case. We also neglect the fact that the vortex-ring “sphere” has a trailing tail of low viscosity fluid and that a significant portion of its trajectory for the higher viscosity cases involves its entry into the viscous fluid, where it should have less drag. Both of these factors would tend to cause Eq. 7 to underpredict penetration depth. We also do not expect perfect numerical agreement since Reynolds numbers are only around unity, and so not in the strictly viscous limit where the 4πVoμa applies exactly. Despite all these approximations, the predictions from Eq. 7 are remarkably good, as seen in Fig. 5b. They are within a factor of 2 with those from the simulations in Fig. 5a, which is as good a comparison as can be expected given the crudeness of this model. Given the translational velocity and diameters of a jet formed by a collapsed bubble, it seems that this model can provide an estimate of penetration depth, trajectory, and perhaps most useful whether or not significant penetration can be expected. It predicts the behavior of both the most viscous and most inviscid cases almost perfectly, though the latter is merely a consequence of the Stokes drag also being near zero for this low value of μ. We could not expect to predict the eventually slowing of this vortex-ring jet given that the drag is not expected to be Stokesian in this case.
Figure 6.
Streamlines of penetrating jet in frame of reference translating to the right at for the μ=0.3 Pa s case. The thick line is the ϕs=0.5 isopleth.
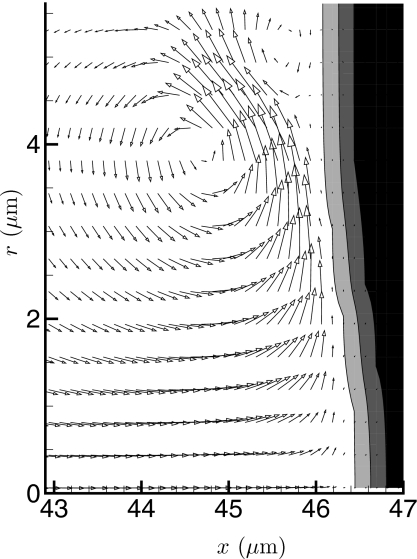
When the viscosity is high, the jet obviously does not penetrate the viscous fluid substantially. However, it does cause apparently large shear stresses on it. These simulations were not designed to resolve the thin boundary layers in fluid 1, so we are unable to calculate this stress precisely. The several-mesh-point thickness of the material interfaces in our numerical solution also makes this more challenging. It seems that over an order of magnitude more mesh points in the wall normal direction would be needed to resolve the boundary layers. However, we can estimate the wall rate of strain, which can be seen to be high in Fig. 7. The peak y velocity adjacent fluid 2 is vmax=866 m∕s. Assuming a linearly decreasing velocity between this peak and the ϕs=0.5 contour with μ1=0.001 Pa s gives a shear stress estimate τw=2.3 MPa. This high level is transient but well over what is needed to cause large deformations and potential injury to cells, which typically have an ∼1 kPa Young modulus (e.g., Ref. 44). This “scrubbing” action of the jet when penetration is resisted might explain the apparent damage of the endothelium observed in blood vessels containing cavitation nuclei and subjected to HIFU.45 The velocity in fluid 2 in this case remains low. Any elasticity would, of course, further resist deformation.
Figure 7.
Velocity vectors showing the high strain rate parallel to the viscous region for the highest viscosity case (μ=10 Pa s) at simulation time t=0.83 μs. Only every third vector is shown in the y direction. The gray levels show the finite thickness phase-field model of the interface between the two fluids. The contour levels are ϕ=0.01,0.5,0.99.
A MODEL FOR INJURY SPREAD
Injury background
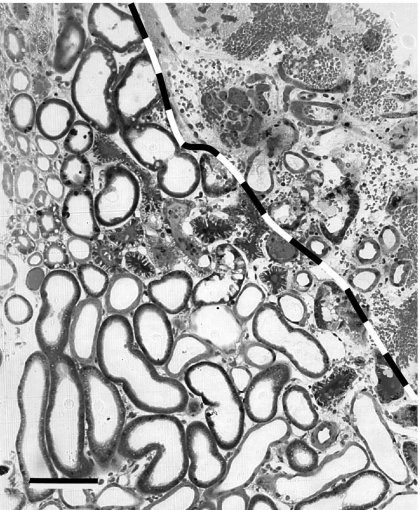
Images of the microstructure of injured kidneys, such as that reproduced in Fig. 8, suggest that injury spreads in sharp fronts behind which the tissue appears utterly disrupted.46 The tissue in this image was fixed by vascular perfusion immediately following the delivery of 1000 shock waves. This rapid fixing and relatively short treatment time was done so that the primary mechanical shock-wave injury could be distinguished from any subsequent injury due to hypoxia or other mechanisms. The Donier HM-3 used in this study is expected to have a peak shock pressure of about 40 MPa,26 which matches our shock model. The area of complete disruption in Fig. 8 is bounded approximately with the line added to the image. The tubules on the other side of this line and a few isolated in the disrupted region appear intact, but when examined in greater detail the cells there show blebbing and enlarged electron-clear vacuoles suggestive of localized ischemic injury.46 The cells and tubules near this borderline also seem to show more injury on sides adjacent to the disrupted area,46 which is consistent with the apparent spreading character of the injury. Within about three tubules from the disrupted region, the tissue appears completely normal.
Figure 8.
Image of renal injury similar to that of Shao et al. (Ref. 46) with line added demarking the apparently sharp boundary between regions of utterly disrupted (top, right) and intact tubules. The intact tubules immediately adjacent the line drawn show signs of ischemic injury, but within 3 or so tubules distances, they appear completely normal (bottom, left). The scale bar is approximately 50 μm wide.
Our principal concern is the primary mechanical disruption and its spread. We assume that jet penetration causes the disruption and that the mechanical effect of this disruption is to significantly reduce the dissipative resistance of the tissue. Simplistically, the viscosity of any material depends on how it irreversibly transports momentum when transversely sheared. When disrupted at a microscopic level, as we see in Fig. 8, this should be strongly suppressed. In our model this is represented by a drop in viscosity down to a level that offers little resistance to bubble-collapse induced jetting, such as that of fluid 1. For the 20 μm diameter bubbles of the simulations, this would need to be ≲0.1 Pa s, which is over a factor of 20 higher than the viscosity of whole blood. For larger bubbles, the viscosity of the damaged tissue would need to be proportionally less. Bleeding into this lesion will also reduce the local viscosity toward that of blood, which is not expected to significantly suppress bubble jetting. The numerous small specks in the obviously injured region in Fig. 8 are red blood cells.
From Fig. 8, it appears that the spreading occurs along a front that roughly tracks the tissue microstructure. However, to attempt to relate the general features of the spreading to our jetting model, we assume that the region of injury is spherical with radius R(t). This R(t), of course, should only be regarded as the scale of the injured zone. Many factors are expected to affect its actual shape, including the local microstructure of the kidney and the direction of the shock waves; spherical injury per se is not expected and not observed. Indeed, if shock-induced collapse is the root mechanism, we might expect spreading to predominantly occur in the direction of shocks, perhaps leading to roughly a cone shape lesion. Unfortunately, lesion shapes have not yet be quantified sufficiently to make any such assessment of lesion geometry, though this would be interesting and potentially important. The jetting instability of collapsing bubbles is also potentially important, and by its nature might be expected to be more isotropic in its action, perhaps leading to lesions that are roughly spherical. Johnsen and Colonius20 showed that jet velocities formed by such Rayleigh collapses are not too different from shock-induced collapse, and so should also be governed approximately by Eq. 8. It would be overly ambitious given current understanding to propose a model for the detailed structure of injury. What we hope to see with our single-length-scale model is that Eq. 7 leads to a spreading that is consistent with the observations in lithotripsy. It should take around 1000 shocks before widespread injury is observed,2, 46 yet upon reaching a typical clinical dose of 2000 shocks the injury should have an ∼1 cm scale,46, 47 whatever its actual shape. Lesion geometric effects will be grouped into an undetermined efficiency parameter g.
The model
The apparent success of Eq. 7 for penetration depth plus some additional assumptions yields a crude but interesting and potentially relevant description of injury spread through a tissue whose resistance to injury is primarily dissipative. From Eq. 7 we take the depth of injury of a single jet to be
| (8) |
where f is the diameter of the penetration relative to the bubble diameter. This expression follows from Eq. 7 with t→∞ and a=fD∕2. Based on our simulations, f≈0.35. This jet may be shock induced, as in the simulations in this paper, but it also might occur as a bubble is first expanded by the negative-pressure portion of a lithotripter wave and then collapses. We recognize that this penetration distance is approximately independent of bubble stand-off distance [e.g., Fig. 5a].
We assume that injury starts in a small region of radius R(t)=Ro and that there are few such regions in the kidney. Adding cavitation nuclei to the systemic circulation is seen to significantly increase injury all over the kidney,48 which suggests that its initiation under normal conditions is indeed a rare event. The nature of this initial injury under normal circumstances remains unclear, but it has been speculated about for some time. It has been suggested that it might start in some small, slow-flowing vessel in which cavitation nuclei can grow because they are not advected away between shock waves. The expansion of these might initiate injury.4, 7 It might also start at a site of shock-shear induced bleeding.4, 46, 49, 50 A shear-formed lesion with pooled blood would presumably be more receptive to cavitation injury. Here, we simply assume that this initial region has a radius Ro≈5 μm, corresponding to a small blood vessel.
The size of the injured region R(t) is assumed to restrict the maximum size of a bubble that may exist there, thus permitting larger bubbles to exist as injury spreads. For large injury zones, however, we assume that finite surface tension or other factors such as the debris left behind by the tissue disruption take over to limit the maximum size of the bubble to some Dm. Pictures of bubbles in water at the target focal point of a lithotripter suggest an upper limit on bubble size of 0.5–1 mm.4, 51 Respecting these two limiting behaviors, we choose to model the bubble diameter by the continuous function
| (9) |
and take Dm=0.5 mm. An implicit assumption is that after the compression phase of the lithotripter wave passes there is an expansion, which causes the bubbles to re-grow. This is potentially destructive, but based on resistance to expansion estimates,24 we assume that this action does not extend R(t) when the bubbles are still small. It is also presumed that the violent action of the collapsing and re-expanding bubbles spread bubbles and effectively spawn new nuclei throughout the region of injury. It should be clear that D and Dm in Eq. 9 refer to their size when the next shock comes. Here the bubble is thought to be primarily composed of gas which has come out of solution.6 At atmospheric pressure, the lifetimes of these bubbles for typical lithotripter shocks is thought to be around 60 s.4
Assuming that the volume of the injury increases by the volume of the jet penetration and using Eq. 8, the predicted growth rate of the region of injury is thus
| (10) |
We take Vo=410 m∕s based on the jet penetration data from Sec. 4 and the shock-wave delivery rate Sr=1∕s. The viscosity associated with the disruption of tissue at this scale is quite uncertain; following on the discussion in Sec. 2 we take it to be μ=1 Pa s. Finally, the parameter g is included in Eq. 10 as a model of damage efficiency. It accounts for the finite diameter of the jet in eroding the tissue, anisotropy of the spreading of a non-spherical lesion, and any other factors (e.g., out of phase bubbles with the shock) that mediate the spreading rate. It has long been known with regard to the cavitation damage of surfaces in high-speed liquid flows that only a small fraction (e.g., g≈10−4) of collapsing bubbles manage to actually damage the surface.8 Anisotropy of spreading, such as spreading predominantly in the shock direction, will reduce g accordingly. Without the possibility of firmer estimates, we can consider g, or perhaps g∕μ together, as a single adjustable parameter to see if we can match any of the phenomenology observed in actual tests with kidney tissue, with the expectation that g will be well less than unity though well more than the ≈10−4 value for flow driven cavitation because the bubbles are confined by the tissue.
To craft Eq. 10, we assume that the injured region expands spherically due to shock induced jetting. In Sec. 5A, we recognized that R(t) can only in truth be considered a scale of the region of injury. We should also recognize that shock-induced jetting is not the only potential for spreading injury as the bubbles become larger. Bubble expansion is potentially injurious for larger bubbles and so is the jetting associated with any Rayleigh (non-shock-induced) collapse of expanded bubbles. The basic model we construct here can include the details of the micromechanisms of injury as they are better understood; for now, the principal objective with this model is to show that its basic precepts lead to an apparent injury threshold and injury extent comparable to observation.
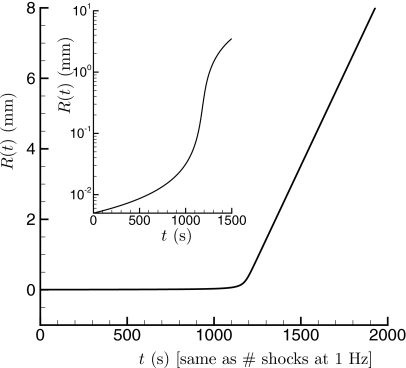
An R(t) solution for g=0.01 is shown in Fig. 9. The most interesting aspect of this solution is the clear threshold behavior: R(t) remains small for t≲1000 s, which corresponds well with observations from pig kidneys.2 This switch-over point is particularly sensitive to g. After that point, there is a change to rapidly increasing injury. For these model parameters, R(t) reaches nearly 1 cm, which is indeed comparable with the lesion size observed in kidney tissue.46, 47 The long-time spreading rate and therefore the lesion size is sensitive to Dm, but it is noteworthy that with a reasonable estimate of Dm from in vito lithotriptor bubbles sized, a single g seems to capture both the threshold and extent of injury.
Figure 9.
Model for injury size: a solution of Eq. 10 for parameters discussed in the text.
While this crude model does indeed predict behavior that is consistent with observations concerning the threshold behavior and lesion sizes observed, it does not explain the apparent increase of injury with increasing shock-wave delivery rate.52, 53 This rate dependence might be associated with the formation of the initial injury. Increased time between shocks to advect cavitation nuclei in the blood stream away from the focal region or the need for an initial insult via a non-cavitational mechanism might both introduce a rate dependence by delaying the onset of the above spreading mechanism.50 The bubble diameter D, modeled as time independent in Eq. 9, also has the potential to introduce a rate dependence. It is expected that with sufficient time the bubbles will effectively vanish, though this is expected to be slow at typical conditions.4 Thus, the expected shock-rate dependence of D or Dm might also introduce rate dependence into the model. Such a dependence could be included by modeling bubble diffusion,4, 6 but the model is probably in need of further testing before building upon it would be fruitful. Tests with erodible materials with known material properties and observable bubble dynamics would be invaluable for assessing this in greater detail.
SUMMARY
In summary, we have shown that viscous resistance of the kind expected in tissue can significantly suppress penetration of bubble-collapse induced jetting. A simple model, which matches these data, was built into a phenomenological model for spreading injury via this mechanism. With one adjustable parameter (g), which we can only anticipate to be well less than unity, this model reproduces the apparent ∼1000-shock threshold behavior seen in shock-wave injury of kidneys. For reasonable estimates of the maximum in vivo bubble size, the extent of predicted contiguous injury is comparable to that observed.
ACKNOWLEDGMENTS
Portions of this work were supported by NIH Grant No. PO1-DK043881 and the U.S. Department of Energy through the University of California under Subcontract No. B523819.
References
- Evan A. P. and McAteer J. A., “Q-effects of shock-wave lithotripsy,” in Kidney Stones: Medical and Surgical Management, edited by Coe F. L., Favus M. J., Pak C. Y. C., Parks J. H., and Preminger G. M. (Lippincott-Raven, Philadelphia, 1996), pp. 549–570. [Google Scholar]
- Evan A. P., Willis L. R., Lingeman J. E., and McAteer J. A., “Renal trauma and the risk of long-term complications in shock wave lithotripsy,” Nephron 78, 1–8 (1998). 10.1159/000044874 [DOI] [PubMed] [Google Scholar]
- Evan A. P. and Willis L. R., “Extracorporeal shock wave lithotripsy: Complications,” in Smith’s Textbook on Endourology, edited by Smith A. D., Badlani G. H., Bagley D. H., Clayman R. V., Docimo S. G., Jordan G. H., Kavoussi L. R., Lee B. R., Lingeman J. E., Preminger G. M., and Segura J. W. (BC Decker, Inc., Hamilton, Ontario, 2007), pp. 353–365. [Google Scholar]
- Bailey M. R., Crum L. A., Evan A. P., McAteer J. A., J. C.WilliamsJr., Sapozhnikov O. A., Cleveland R. O., and Colonius T., “Cavitation in shock wave lithotripsy,” in The Fifth International Symposium on Cavitation, Osaka, Japan (2003), No. Cav03-OS-2-1-006.
- Bailey M. R., Pishchalnikov Y. A., Sapozhnikov O. A., Cleveland R. O., McAteer J. A., Miller N. A., Pishchalnikova I. V., Connors B. A., Crum L. A., and Evan A. P., “Cavitation detection during shock-wave lithotripsy,” Ultrasound Med. Biol. 31, 1245–1256 (2005). 10.1016/j.ultrasmedbio.2005.02.017 [DOI] [PubMed] [Google Scholar]
- Church C. C., “A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter,” J. Acoust. Soc. Am. 86, 215–227 (1989). 10.1121/1.398328 [DOI] [PubMed] [Google Scholar]
- Zhong P., Cioanta I., Zhu S., Cocks F. H., and Preminger G. M., “Effects of tissue contraint on shock wave-induced bubble expansion in vivo,” J. Acoust. Soc. Am. 104, 3126–3129 (1998). 10.1121/1.423905 [DOI] [PubMed] [Google Scholar]
- Benjamin T. B. and Ellis A. T., “The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries,” Philos. Trans. R. Soc. London, Ser. A 260, 221–240 (1966). 10.1098/rsta.1966.0046 [DOI] [Google Scholar]
- Naude C. F. and Ellis A. T., “On the mechanisms of cavitation damage by nonhemispherical cavities collapsing in contact with a solid boundary,” ASME J. Basic Eng. 83, 648–656 (1961). [Google Scholar]
- Bourne N. K. and Field J. E., “Shock-induced collapse and luminescence by cavities,” Philos. Trans. R. Soc. London, Ser. A 357, 295–311 (1999). 10.1098/rsta.1999.0328 [DOI] [Google Scholar]
- Kedrinskii V. K., “The role of cavitation effects in the mechanisms of destruction and explosive processes,” Shock Waves 7, 63–76 (1997). 10.1007/s001930050064 [DOI] [Google Scholar]
- Klaseboer E., Fong S. W., Turangan C. K., Khoo B. C., Szeri A. J., Calvisi M. L., Sankin G. N., and Zhong P., “Interaction of lithotripter shockwaves with single inertial cavitation bubbles,” J. Fluid Mech. 593, 33–56 (2007). 10.1017/S002211200700852X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z., Fowlkes J. B., and Cain C. A., “A new strategy to enhance cavitational tissue erosion using a high-intensity, initiating sequence,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 53, 1412–1424 (2006). 10.1109/TUFFC.2006.1665098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturtevant B., “Shock wave physics of lithotriptors,” in Smith’s Textbook of Endourology, edited by Smith A. D. (Quality Medical, St. Louis, MO, 1996), Vol. 1, pp. 529–552. [Google Scholar]
- Klaseboer E. and Khoo B. C., “An oscillating bubble near an elastic material,” J. Appl. Physiol. 96, 5808–5818 (2004). 10.1063/1.1803925 [DOI] [Google Scholar]
- Pearson A., Blake J. R., and Otto S. R., “Jets in bubbles,” J. Eng. Math. 48, 391–412 (2004). 10.1023/B:engi.0000018172.53498.a2 [DOI] [Google Scholar]
- Lee M., Klaseboer E., and Khoo B. C., “On the boundary integral method for the rebounding bubble,” J. Fluid Mech. 570, 407–429 (2007). 10.1017/S0022112006003296 [DOI] [Google Scholar]
- Johnsen E. and Colonius T., “Implementation of WENO schemes in compressible multicomponent flow problems,” J. Comput. Phys. 219, 715–732 (2006). 10.1016/j.jcp.2006.04.018 [DOI] [Google Scholar]
- Johnsen E. and Colonius T., “Shock-induced collapse of a gas bubble in shockwave lithotripsy,” J. Acoust. Soc. Am. 124, 2011–2020 (2008). 10.1121/1.2973229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnsen E. and Colonius T., “Numerical simulations of non-spherical bubble collapse,” J. Fluid Mech. 629, 231–262 (2009). 10.1017/S0022112009006351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Z. and Gracewski S. M., “The behaviour of a gas cavity impacted by a weak or strong shock wave,” J. Fluid Mech. 309, 183–209 (1996). 10.1017/S0022112096001607 [DOI] [Google Scholar]
- Popinet S. and Zaleski S., “Bubble collapse near a solid boundary: a numerical study of the influence of viscosity,” J. Fluid Mech. 464, 137–163 (2002). 10.1017/S002211200200856X [DOI] [Google Scholar]
- Liu X., He J., Lu J., and Ni X., “Effect of liquid viscosity on a liquid jet produced by the collapse of a laser-induced bubble near a rigid boundary,” Jpn. J. Appl. Phys. 48, 016504 (2009). 10.1143/JJAP.48.016504 [DOI] [Google Scholar]
- Freund J. B., “Suppression of shocked-bubble expansion due to tissue confinement with application to shock-wave lithotripsy,” J. Acoust. Soc. Am. 123, 2867–2874 (2008). 10.1121/1.2902171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran L. and Udaykumar H. S., “Simulation of void collapse in an energetic material, Part 1: Inert case,” J. Propul. Power 22, 947–958 (2006). 10.2514/1.13146 [DOI] [Google Scholar]
- Cleveland R. O., Bailey M. R., Fineberg N., Hartenbaum B., Lokhandwalla M., McAteer G. A., and Sturtevant B., “Design and characterization of a research electrohydraulic lithotripter patterned after the Dornier HM3,” Rev. Sci. Instrum. 71, 2514–2525 (2000). 10.1063/1.1150643 [DOI] [Google Scholar]
- Girnyk S., Barannik A., Barannik E., Tovstiak V., Marusenko A., and Volokhov V., “The estimation of elasticity and viscosity of soft tissues in vitro using the data of remote acoustic palpation,” Ultrasound Med. Biol. 32, 211–219 (2006). 10.1016/j.ultrasmedbio.2005.11.015 [DOI] [PubMed] [Google Scholar]
- Madsen E. L., Sathoff H. J., and Zagzebski J. A., “Ultrasonic shear wave properties of soft tissues and tissue like materials,” J. Acoust. Soc. Am. 74, 1346–1355 (1983). 10.1121/1.390158 [DOI] [PubMed] [Google Scholar]
- Frizzell L. A., Carstensen E. L., and Dyro J. F., “Shear properties of mammalian tissues at low megahertz frequencies,” J. Acoust. Soc. Am. 60, 1409–1411 (1977). 10.1121/1.381236 [DOI] [PubMed] [Google Scholar]
- Nasseri S., Bilston L. E., and Phan-Thien N., “Viscoelastic properties of pig kidney in shear, experimental results and modelling,” Rheol. Acta 41, 180–192 (2002). 10.1007/s003970200017 [DOI] [Google Scholar]
- Sankin G. N., Simmons W. N., Zhu S. L., and Zhong P., “Shock wave interaction with laser-generated single bubbles,” Phys. Rev. Lett. 95, 034501 (2005). 10.1103/PhysRevLett.95.034501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courant R. and Friedrichs K. O., Supersonic Flow and Shock Waves (Wiley-Interscience, New York, 1948). [Google Scholar]
- Szeri A. J., Storey B. D., Pearson A., and Blake J. R., “Heat and mass transfer during the violent collapse of nonspherical bubble,” Phys. Fluids 15, 2576–2586 (2003). 10.1063/1.1595647 [DOI] [Google Scholar]
- Rosina J., Kvasnak E., Suta D., Kolarova H., Malek J., and Krajci L., “Temperature dependence of blood surface tension,” Physiol. Res. 56, S93–S98 (2007). [DOI] [PubMed] [Google Scholar]
- Averkioua M. A. and Cleveland R. O., “Modeling of an electrohydraulic lithotripter with the kzk equation,” J. Acoust. Soc. Am. 106, 102–112 (1999). 10.1121/1.427039 [DOI] [PubMed] [Google Scholar]
- LeVeque R. J., Finite Volume Methods for Hyperbolic Problems (Cambridge University Press, Cambridge, 2002). [Google Scholar]
- Toro E. F., Spruce M., and Speares W., “Restoration of the contact surface in the HLL-Riemann solver,” Shock Waves 4, 25–34 (1994). 10.1007/BF01414629 [DOI] [Google Scholar]
- Olsson E., Kreiss G., and Zahedi S., “A conservative level set method for two phase flow II,” J. Comput. Phys. 225, 785–807 (2007). 10.1016/j.jcp.2006.12.027 [DOI] [Google Scholar]
- Sun Y. and Beckermann C., “Sharp interface tracking using the phase-field equation,” J. Comput. Phys. 220, 626–653 (2007). 10.1016/j.jcp.2006.05.025 [DOI] [Google Scholar]
- Shukla R. K., Pantano C., and Freund J. B., “An interface capturing method for simulation of multiphase compressible flows,” J. Comput. Phys. submitted (2009).
- Kennedy C. A. and Carpenter M. H., “Additive Runge-Kutta schemes for convection-diffusion-reaction equations,” Appl. Numer. Math. 44, 139–181 (2003). 10.1016/S0168-9274(02)00138-1 [DOI] [Google Scholar]
- van der Vorst H. A., “Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems,” SIAM (Soc. Ind. Appl. Math.) J. Sci. Stat. Comput. 13, 631–644 (1992). [Google Scholar]
- Turangan C. K., Jamaluddin A. R., Ball G. J., and Leighton T. G., “Free-Lagrange simulations of the expansion and jetting collapse of air bubbles in water,” J. Fluid Mech. 598, 1–25 (2008). 10.1017/S0022112007009317 [DOI] [Google Scholar]
- Karcher H., Lammerding J., Huang H., Lee R. T., Kamm R. D., and Kaazempur-Mofrad M., “A three-dimensional viscoelastic model for cell deformation with experimental verification,” Biophys. J. 85, 3336–3349 (2003). 10.1016/S0006-3495(03)74753-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang J. H., Tu J., Brayman A. A., Matula T. J., and Crum L. A., “Correlation between inertial cavitation dose and endothelial cell damage in vivo,” Ultrasound Med. Biol. 32, 1611–1619 (2006). 10.1016/j.ultrasmedbio.2006.07.016 [DOI] [PubMed] [Google Scholar]
- Shao Y., Connors B. A., Evan A. P., Willis L. R., Lifshitz D. A., and Lingeman J. E., “Morphological changes induced in the pig kidney by extracorporeal shock wave lithotripsy,” Anat. Rec. 275A, 979–989 (2003). 10.1002/ar.a.10115 [DOI] [PubMed] [Google Scholar]
- Blomgren P. M., Connors B. A., Lingeman J. E., Willis L. R., and Evan A. P., “Quantitation of shock wave lithotripsy-induced lesion in small and large pig kidneys,” Anat. Rec. 249, 341–348 (1997). [DOI] [PubMed] [Google Scholar]
- Matlaga B. R., McAteer J. A., Conors B. A., Handa R. K., Evan A. P., Williams J. C., Lingeman J. E., and Willis L. R., “Potential for cavitation-mediated tissue damage in shockwave lithotripsy,” J. Endourol 22, 121–126 (2008). 10.1089/end.2007.9852 [DOI] [PubMed] [Google Scholar]
- Lokhandwalla M. and Sturtevant B., “Mechanical haemolysis in shock wave lithotripsy (SWL): I. Analysis of cell deformation due to SWL flow-fields,” Phys. Med. Biol. 46, 413–437 (2001). 10.1088/0031-9155/46/2/310 [DOI] [PubMed] [Google Scholar]
- Freund J. B., Colonius T., and Evan A. P., “A cumulative shear mechanism for tissue damage initiation in shock-wave lithotripsy,” Ultrasound Med. Biol. 33, 1495–1503 (2007). 10.1016/j.ultrasmedbio.2007.03.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pishchalnikov Y. A., McAteer J. A., and Williams J. C., “Effect of firing rate on the performance of shock wave lithotriptors,” BJU Int. 102, 1681–1686 (2008). 10.1111/j.1464-410X.2008.07896.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAteer J. A., Evan A. P., J. C.Williams, Jr., and Lingeman J. E., “Treatment protocols to reduce renal injury during shock wave lithotripsy,” Curr. Opin. Neurol. 19, 192–195 (2009). 10.1097/MOU.0b013e32831e16e3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evan A., McAteer J. A., Connors B. A., Blomgren P. M., and Lingeman J. E., “Renal injury during shock wave lithotripsy is significantly reduced by slowing the rate of shock wave delivery,” BJU Int. 100, 624–628 (2007). 10.1111/j.1464-410X.2007.07007.x [DOI] [PubMed] [Google Scholar]