Substituent Effects in Cation/π Interactions and Electrostatic Potentials above the Center of Substituted Benzenes Are Due Primarily to through-Space Effects of the Substituents

Abstract

Substituent effects in cation/π interactions have been examined using the M05-2X DFT functional and CCSD(T) paired with triple-ζ quality basis sets. In contrast to popular, intuitive models, trends in substituent effects are accounted for primarily by direct, through-space interactions with the substituents. While there is some scatter in the data, which is attributed to π-polarization, the trend in substituents effects in cation/π interactions is captured by an additive model in which the substituent is isolated from the aryl ring. Similarly, changes in the electrostatic potential at a point above the center of substituted benzenes arise largely from through-space effects of the substituents. π-polarization is not the dominant underlying cause.

Cation/π interactions are ubiquitous in molecular biology, drug design, and host-guest chemistry.^1,2 These strong non-covalent interactions, which often involve an alkali metal or tetraalkylammonium cation interacting with the face of an aromatic ring, were thrust into the limelight by Dougherty and co-workers. ^1,3–6 Substituent effects in cation/π interactions have been exploited to characterize binding sites of nicotinic acetylcholine receptors and have provided insight into these systems in the absence of detailed structural information.⁵

While numerous factors contribute to binding,⁷ substituent effects in cation/π interactions are usually explained using simple electrostatic models.¹ Mecozzi, West, and Dougherty⁶ demonstrated that the electrostatic potential (ESP) evaluated at a single point above the center of a substituted aryl ring predicts the strength of the cation/π interaction; more negative ESPs indicate stronger interactions. In this context, Dougherty et al.^1,6 stressed the importance of inductive effects over π-resonance, based on correlations with σ_m rather than σ_p. However, Hunter and co-workers and others⁸ have attributed substituent effects to the polarization of the aryl π-system. Below, we show that π-polarization models of the cation/π interaction are flawed; substituent effects arise primarily from direct, through-space interactions with the substituents.

Interaction energies [E_int(C₆H₅X), kcal mol⁻¹] for Na⁺ above the center of 25 substituted benzenes were computed using M05-2X/6-311+G(2df,2p).⁹ The equilibrium distance (R_e) of Na⁺ above the ring centroid was found by scanning normal to the benzene plane at 0.05 Å intervals with the substituted benzene fixed at the M05-2X/6-31+G(d) optimized geometry. The mean R_e value for the 25 systems studied is 2.37 Å. CCSD(T) energies were evaluated for five substituents (H, CN, F, CH₃, and NH₂) at M05-2X geometries using the cc-pCVTZ basis set for Na and aug-cc-pVTZ otherwise. These correlated computations, denoted CCSD(T)/AVTZ henceforth, employed the standard frozen-core approximation for all atoms except Na, for which only the 1s orbital was frozen. M05-2X slightly overestimates the C₆H₅X^⋯Na⁺ binding energy relative to CCSD(T). However, this overbinding is systematic and there is a very strong linear correlation (r = 0.9999, see SI Figure S1) between the M05-2X and CCSD(T) data. M05-2X computations were executed with NWChem^10,11 using a DFT quadrature grid with 70 radial and 590 angular points while Molpro¹² was used for CCSD(T). Final M05-2X and CCSD(T) energies were counterpoise corrected.

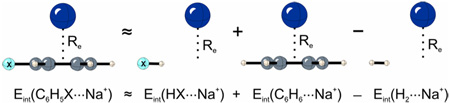
To understand the role of the aryl π-system, a ‘truncated’ model was constructed by replacing the phenyl ring in the equilibrium C₆H₅X^⋯Na⁺ geometry with a hydrogen atom. This hydrogen was placed along the C–X bond, and the H–X distance was optimized with all other internal coordinates fixed. A similar model has been used to study substituent effects in the benzene dimer.¹³

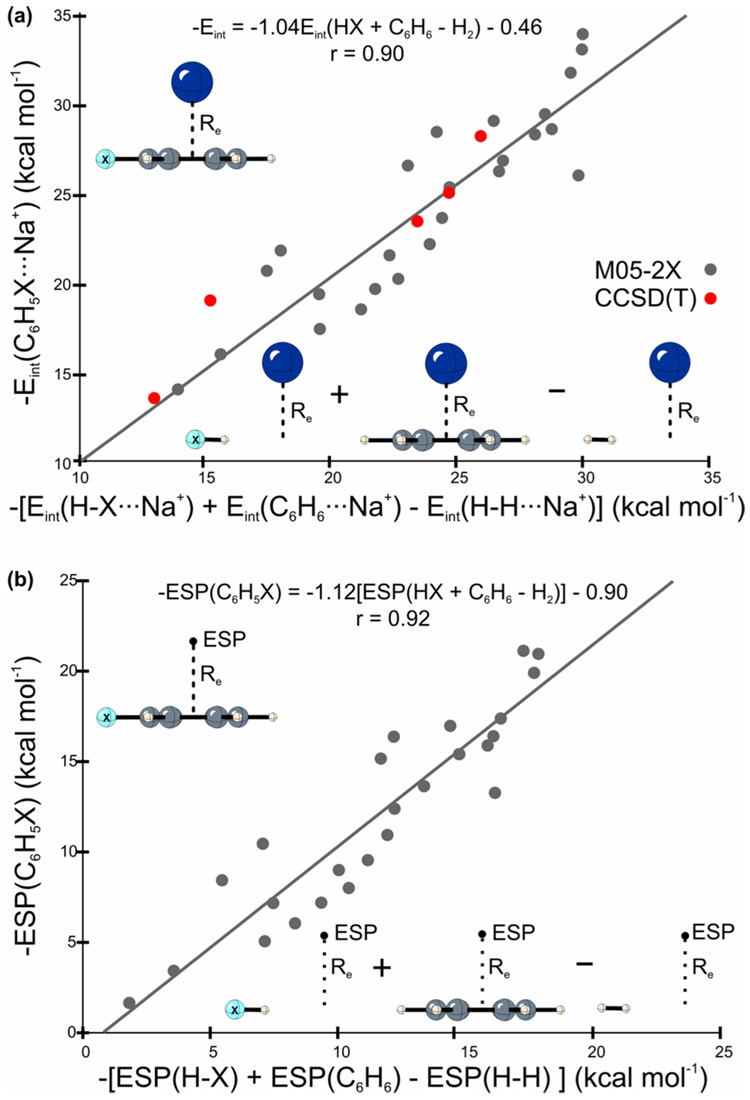
In Figure 1(a), E_int(C₆H₅X) is plotted against the sum of interaction energies for the truncated model system and benzene. To approximately account for the ‘extra’ two hydrogens, the interaction energy of H₂ with Na⁺ at the R_e distance for the corresponding C₆H₅X^⋯Na complex was subtracted from this sum to yield an additive approximation to the cation/π binding energy [E_int(HX) + E_int(C₆H₆) – E_int(HH)]. In this additive model there can clearly be no polarization of the benzene π-system, and any effect of the substituent must involve through-space interactions with the substituents. There is a good correlation (r = 0.90) between the interaction energies for C₆H₅X^⋯Na⁺ and this additive model, with unit slope. There are clear outliers (see Table 1); for several systems there are significant (> 3 kcal mol⁻¹) deviations between our additive model and results for the intact substituted rings. These deviations occur for strong π-electron acceptors, for which the additive model overestimates E_int, or strong π-donors, for which E_int is underestimated. In these limiting cases, donation or withdrawal from the π-system presumably plays a role. Indeed, the differences between interaction energies for the substituted aromatic ring and our additive model correlate with the resonance parameter R (r = 0.88, see SI Figure S2), supporting the involvement of π-resonance in the observed deviations. However, the overall trend in substituent effects in cation/π interactions does not depend on the π-system of the phenyl ring, but is accounted for by through-space interactions of the substituents. Frontera et al.¹⁴ recently reported through-space substituent effects in complexes of paracyclophanes with Na⁺ and Li⁺ in which the substituents were on the non-complexed phenyl ring.

Figure 1.

(a) M05-2X/6-311+G(2df,2p) (gray) and CCSD(T)/AVTZ (red) interaction energies of Na⁺ with C₆H₅X versus a simple additive model (kcal mol⁻¹). Least squares fit applied only to the M05-2X data; (b) M05-2X/6-311+G(2df,2p) ESPs evaluated at a single point above the center of the ring of substituted benzenes versus the ESP at that point from a simple additive model (kcal mol⁻¹). All quantities evaluated at the equilibrium C₆H₅X^⋯Na⁺ geometries.

Table 1.

M05-2X/6-311+G(2df,2p) interaction energies for Na⁺ with C₆H₅X [E_int(C₆H₅X)] and the additive model [E_int(HX + C₆H₆ – H₂)], and ESPs for C₆H₅X and (HX + C₆H₆ – H₂), all in kcal mol⁻¹. All quantities evaluated at the corresponding equilibrium C₆H₅X^⋯Na⁺ distance. CCSD(T)/AVTZ interaction energies are in parentheses.

X	Eint(C6H5X)	Eint(HX + C6H6 – H2)a	ESP(C6H5X)	ESP(HX + C6H6 – H2)b
N(CH3)2	33.9	30.0	21.1	17.3
NHCH3	33.1	30.0	21.0	17.9
NH2	31.8 (28.2)	29.5 (26.0)	19.9	17.7
CH2OH	29.5	28.5	17.4	16.4
NHOH	29.1	26.5	17.0	14.4
SCH3	28.6	28.8	15.4	14.8
OCH3	28.5	24.2	16.4	12.2
CH3	28.3 (25.0)	28.1 (24.7)	16.4	16.1
H	26.9 (23.5)	26.9 (23.5)	15.9	15.9
OH	26.6	23.1	15.2	11.7
SH	26.3	26.7	13.6	13.4
SiH3	26.0	29.9	13.3	16.2
CCH	25.4	24.7	12.4	12.2
CO2CH3	23.6	24.4	10.9	12.0
COCH3	22.2	23.9	9.5	11.2
F	21.8 (19.0)	18.0 (15.3)	10.4	7.1
COOH	21.5	22.3	9.0	10.1
OCF3	20.7	17.5	8.4	5.5
BF2	20.2	22.7	8.0	10.4
CHO	19.7	21.8	7.2	9.4
CF3	19.4	19.5	7.2	7.5
SiF3	18.5	21.2	6.0	8.3
NO	17.4	19.6	5.0	7.1
CN	16.0 (13.5)	15.6 (13.1)	3.4	3.6
NO2	14.0	13.9	1.6	1.8

^aE_int(HX + C₆H₆ – H₂) = E_int(HX) + E_int(C₆H₆) – E_int(HH)

^bESP(HX + C₆H₆ – H₂) = ESP(HX) + ESP(C₆H₆) – ESP(HH).

To further explain this non-intuitive behavior, changes in the ESP above the center of substituted benzenes were examined (see Table 1). ESPs evaluated at the position of Na in the C₆H₅X^⋯Na⁺ complexes are plotted against an additive model of ESPs in Figure 1(b). The additive ESP comprises the ESP above the hydrogen capped substituent (positioned exactly as in the C₆H₅X^⋯Na⁺ dimer) plus the ESP above benzene minus the ESP due to H₂, all evaluated at the position of sodium in C₆H₅X^⋯Na⁺.

There is a strong correlation between these two sets of ESPs (r = 0.92), indicating that π-polarization has no appreciable net effect on the ESPs above the center of substituted benzenes. Instead, changes in ESPs arise from through-space substituent effects. Such long-range effects are readily explained by the 1/r dependence of the ESP on surrounding charges. Apparently, the aryl π-system provides a relatively constant backdrop on top of which the through-space electrostatic effects of the substituents are superimposed. As with the cation/π interactions, there are some deviations between our additive model and the explicitly computed ESPs. These deviations again correlate with the resonance parameter R (r = 0.92; see SI Figure S3), indicating some involvement of π-polarization.

The electrostatic nature of substituent effects in cation/π interactions has long been established.^1,3,6 While the present results support Dougherty’s electrostatic model, the common assumption that these electrostatic effects are a result of π-polarization is incorrect. Substituent effects in cation/π interactions, and the related changes in the ESP above the center of substituted benzenes, do not arise mainly from polarization of the benzene π-system. Instead, these effects can be accounted for primarily by through-space effects of the substituents. In general, π-polarization appears to play only a minor role. The present findings challenge deep-rooted intuitions concerning the polarization of the aryl π-system in substituted benzenes and have broad implications due to the use of substituted aromatic amino acid analogs in the characterization of cation binding sites⁵ and the employment of ESPs of substituted aromatic rings in pharmacophor modeling. Implications of the present findings for substituent effects in general non-covalent interactions with aromatic rings will be discussed in forthcoming publications.

Supplementary Material

1_si_001. Supporting Information Available.

Full citation for refs ¹⁰ and ¹²; plot comparing CCSD(T) and M05-2X results; plots of differences between additive models and E_int(C₆H₅X^⋯Na⁺) and ESP(C₆H₅X) versus R; Cartesian coordinates and electronic energies.