Abstract
The time evolution of zero-quantum-coherences (ZQCs) is insensitive to magnetic field inhomogeneity. Using a 2D indirect ZQC detection method it is shown that high-resolution 1H NMR spectra can be obtained from rat brain in vivo at 11.74 T that are immune to magnetic field inhomogeneity. Simulations based on the density matrix formalism, as well as in vitro measurements are used to demonstrate the features of 2D ZQC NMR spectra. Unique spectral information which is normally not directly available from regular 1H NMR spectra can be extracted and used for compound identification or improved prior knowledge during spectral fitting.
Keywords: zero-quantum-coherences, indirect detection, rat brain
INTRODUCTION
Proton NMR spectroscopy is a powerful, non-invasive technique to characterize the metabolic status of tissue. In the brain, 1H NMR spectroscopy has been applied to a wide range of neurological and psychiatric disorders where it has been successful in localizing the foci of epileptic seizures (1), categorizing tumors (2) and studying the relation between energy metabolism and neurotransmission (3). Furthermore, it shows great potential as a diagnostic tool in the early stages of Alzheimer’s disease (4,5).
However, in vivo NMR spectroscopy is challenging due to magnetic field inhomogeneity induced by differences in magnetic susceptibility between tissues and air (6). This results in broader spectral lines and hence a lower spectral resolution. Since the susceptibility-induced inhomogeneity scales linearly with the magnetic field strength it can greatly diminish the spectral resolution advantage of high-field NMR.
The most commonly employed method to mitigate the effects of magnetic field inhomogeneity is to counteract the inhomogeneity with active shimming (7,8). While this can be an extremely efficient technique for high-resolution liquid-state NMR, the large magnet bore size for humans and animals pose severe limitations on the efficiency of active shimming in vivo. Though recent developments in the areas of localized shimming (9), dynamic shimming (10) and passive shimming (11) will lead to a greatly improved magnetic field homogeneity over larger areas, significant residual magnetic field inhomogeneity is currently the rule for most in vivo NMR studies. Furthermore, none of the proposed techniques can counteract dynamic microscopic susceptibility gradients that lead to a shortening of the apparent T2 relaxation time (12) and hence an increase in spectral line width at higher magnetic fields.
It is well-known that the evolution of zero-quantum-coherences (ZQCs) is insensitive to magnetic field inhomogeneity (13). A limited number of reports have used this fact to obtain 1H NMR spectra derived from ZQCs for the assignment of resonances in high-resolution NMR (14,15). Within the in vivo NMR community, ZQCs have mainly been used as a means of achieving spectral editing (16–18). Ryner et al. (19) have demonstrated the utility of ZQCs to obtain high-quality 2D NMR spectra on phantoms in a clinical MRI environment. Here we show that ZQCs can be used to obtain high-resolution 1H NMR spectra from rat brain in vivo that are immune to magnetic field inhomogeneity. Furthermore, unique spectral information which is normally not directly available from regular 1H NMR spectra can be extracted and used for compound identification or improved prior knowledge during spectral fitting.
METHODS
General
All experiments were performed on a 11.74 T Magnex magnet equipped with 9 cm diameter gradients (395 mT/m in 180 μs, Magnex Scientific, Oxford, UK) interfaced to a Bruker Avance console and operated from a Linux computer running Paravision 3.0.1. RF transmission and signal reception was performed with a 14 mm diameter single-turn surface coil tuned to the proton frequency (499.814 MHz).
In vitro experiments and simulations
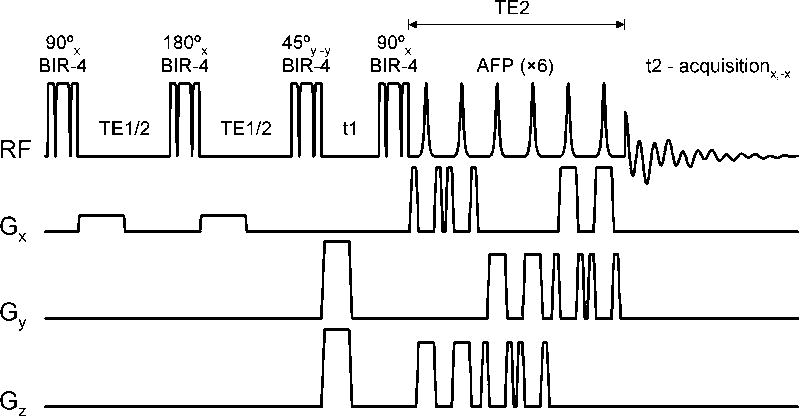
All in vitro experiments were performed on a 18 mm diameter glass sphere filled with 100 mM aspartic acid (Sigma-Aldrich, St. Louis, MO) in water (pH = 7.1) at ambient temperature (circa 16 °C). Fig. 1 shows the NMR pulse sequence used in all in vitro and in vivo experiments, as well as all simulations. The preparation module (90°(x) – TE1/2 – 180° – TE1/2 – 45°(y)) was preferred over the conventional module (90°(x) – TE1/2 – 180° – TE1/2 – 90°(x)) because it offers a means to eliminate all resonances from uncoupled spin-systems. The conventional preparation module brings all uncoupled spin-systems to the longitudinal axis where they can not be differentiated from ZQCs. As a result, uncoupled spin-systems will appear on the (0, ω2) midline. Since the uncoupled spin-systems do not decay during t1 due to T2 relaxation (but actually increase due to T1 relaxation recovery), Gibbs ringing from the uncoupled resonances will interfere with smaller signals from coupled spin-systems resonating off the midline at (ω1 = ωZQC, ω2). The preparation module shown in Fig. 1 allows suppression of uncoupled spin-systems due to the phase relation between the excitation and mixing pulses. Coherences from uncoupled spin-systems remain in the transverse plane following the mixing pulse and are subsequently dephased by the magnetic field crusher gradient. In practice, the phase of the mixing pulse was fine-tuned (with a 1° resolution) on the water resonance to provide optimal suppression of uncoupled spins. The magnetic field crusher gradient was implemented as a 2.0 ms 200 mT/m gradient along two orthogonal axes. The efficiency of the preparation module (90°(x) – TE1/2 – 180° – TE1/2 – 45°(y)) to generate and (indirectly) detect ZQCs is 25% for a weakly-coupled two-spin-system (TE1 = 1/2J). The 45° nutation angle leads to a 50% signal loss, whereas the destruction of all double-quantum-coherences during t1 constitutes an additional 50% signal loss. Larger spin-systems or spin-systems with a range of scalar coupling values will have a decreased ZQC detection efficiency.
Figure 1.
NMR pulse sequence for the generation of 2D NMR spectra through indirect detection of intra-molecular zero-quantum-coherences from 3D spatially localized volumes. t1 and t2 correspond to the indirect and direct detection periods, whereas TE1 and TE2 are optimized to provide the highest signal recovery for a given scalar-coupled spin-system. The phase of the 45° mixing pulse is cycled (+y, −y) in concert with the receiver phase (+x, −x) in order to eliminate unwanted signals created by T1 recovery during the t1 period.
Following the 90°(x) read pulse, single-scan spatial localization is achieved with three pairs of adiabatic full passage (AFP) pulses (20). In order to eliminate signal (especially water signal) generated by T1 relaxation recovery during the t1 period the 45° mixing pulse, as well as the receiver phase, was phase cycled through +y, −y. While the receiver gain setting is limited by the recovered water signal during the longest t1 delay, the dynamic range of the receiver was sufficiently large not to cause a degradation in signal-to-noise ratio. In order to avoid signal loss and artifacts due to incorrect nutation angles, all pulses were executed as B1-insensitive adiabatic RF pulses. In particular, all non-selective pulses were executed as BIR-4 pulses (21), with a pulselength = 1.0 ms and a bandwidth × pulse length product R of 150. The selective pulses were executed as 1.0 ms hyperbolic secant AFP pulses with R = 20 (22).
Simulations were performed in Matlab 7.0.4 (The Mathworks, Natick, MA) using home-written software based on the density matrix formalism. The effects of shaped RF pulses and magnetic field gradients as used in spatial localization and water suppression were quantitatively included in the simulations. The effects of relaxation were not included and effective T2 relaxation during the t1 and t2 periods were approximated by multiplying the simulated data with a decreasing exponential function, corresponding to a 3 Hz line width.
The AMX spin-system of aspartate was used in the simulations and is characterized by δH2 = 3.8914 ppm, δH3 = 2.8011 ppm, δH3′ = 2.6533 ppm and 3JH2H3 = 3.647 Hz, 3JH2H3′ = 9.107 Hz, 2JH3H3′ = −17.427 Hz as determined by Govindaraju et al. (23). While strong coupling effects (24) were quantitatively simulated, aspartate essentially acts as a weakly-coupled spin-system at 500 MHz.
In vivo experiments
Three male Sprague-Dawley rats (214 ± 21 g, mean ± SD) were prepared in accordance to the guidelines established by the Yale Animal Care and Use Committee. The animals were tracheotomized and ventilated with a mixture of 70 % nitrous oxide and 28.5 % oxygen under 1.5 % halothane anesthesia. A femoral artery was cannulated for monitoring of blood gases (pO2, pCO2), pH and blood pressure. Physiological variables were maintained within normal limits by small adjustments in ventilation (pCO2 = 33–45 mm Hg; pO2 > 120 mm Hg; pH = 7.20–7.38; blood pressure = 90–110 mm Hg). After all surgery was completed, anesthesia was maintained by 0.3 – 0.8 % halothane in combination with 70 % nitrous oxide. During NMR experiments animals were restrained in a head holder, while additional immobilization was obtained with d-tubocurarine chloride (0.5 mg/kg/40 mins, i.p.). The core temperature was measured with a rectal thermosensor and was maintained at 37 ± 1 °C by means of a heated water pad.
The magnetic field homogeneity was adjusted over a 5 × 5 × 5 mm cubic volume using the FASTMAP method (8), typically resulting in 18 Hz water line widths in vivo. Signal was acquired with the sequence shown in Fig. 1 from a 6 × 5 × 6 mm (= 180 μL) volume placed centrally in the rat brain, encompassing cerebral cortex, corpus callosum, hippocampus and sub-cortical structures. Signal acquisition was performed with TR/TE1/TE2 = 1,500/50/50 ms over a 6,000 Hz spectral width in the direct dimension (1,024 data points) with 256 t1 increments of 0.667 ms, leading to a 1,500 Hz spectral width in the indirect dimension (8 averages per t1 increment). 2D NMR spectra were zero-filled to 2,048 × 2,048 and processed in absolute value with 1 Hz line-broadening in the direct F2 dimension. Water suppression was achieved with SWAMP (25), an adiabatic analog of conventional CHESS water suppression.
RESULTS
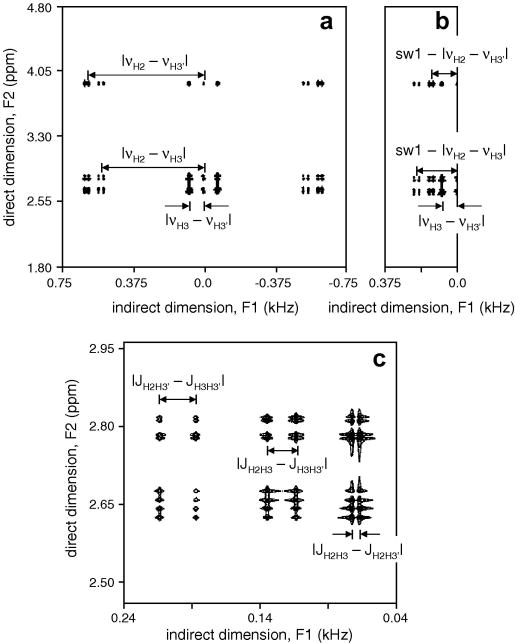
Fig. 2A shows the simulation results for aspartate with TE1/TE2 = 35/25 ms and an effective line width of 1.0 Hz in both dimensions. It follows that while the resonances in the direct (F2) dimension appear at their respective Larmor frequencies, the resonances in the indirect (F1) dimension appear at positions given by the frequency difference of the spins involved in the zero-quantum transition, as described previously (13–15). Since in vivo NMR is always limited by time constraints, an effective way to increase the temporal resolution is to decrease the spectral width SW1 in the indirect dimension, by taking fewer, but larger time increments. Fig. 2B shows the simulation for a spectral width of 750 Hz, half of that in Fig. 2A. Resonances with frequencies above SW1/2 will experience aliasing and will resonate at apparent lower frequencies (e.g. |νH2 − νH3| will appear at SW1 – |νH2 − νH3|). However, when the sample contains known compounds, the reduced spectral width can be chosen such that spectral overlap due to aliasing does not occur. Fig. 2C shows an expansion of the H3/H3′ region extracted from Fig. 2B. Within the multiplets, the resonances along the indirect F1 dimension are split by the passive coupling constant, which represents the absolute difference between scalar coupling constants not actively involved in the zero-quantum transition (26).
Figure 2.
Simulated 2D ZQC NMR spectra of aspartate. (A) Spectrum acquired with 1,500 Hz spectral bandwidth in the indirect dimension, created by 0.667 ms t1 increments. The spectrum is symmetrical around F1 = 0 with all resonances appearing at the frequency difference of the scalar-coupled spins. (B) Increasing the t1 increments to 1.33 ms reduces the spectral bandwidth to 750 Hz thereby leading to aliasing of resonances. (C) Zoomed region extracted from the spectrum shown in (B). Resonances within a multiplet are split by the scalar coupling difference with passive spins. See text for details.
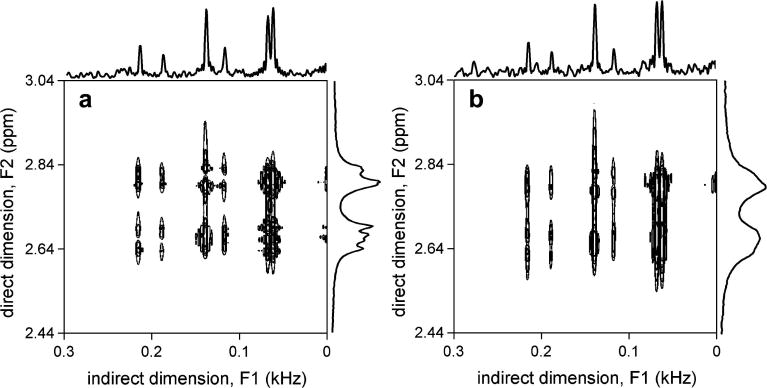
Fig. 3 shows an experimental in vitro verification of the appearance of 2D ZQC spectra, as well as their immunity to magnetic field inhomogeneity. Fig. 3A shows a 2D ZQC spectrum under conditions of good magnetic field homogeneity (FWHM of water resonance = 7 Hz). The spectrum appears similar to those in Fig. 2, with three pairs of doublets with high spectral resolution along the F1 dimension (FWHM = 4.2 ± 0.2 Hz as measured over 6 resonances). Despite the reasonable magnetic field homogeneity, the direct F2 dimension is significantly broadened relative to the indirect F1 dimension making determination of scalar coupling constants or frequencies difficult. Fig. 3B shows the 2D ZQC NMR spectrum in the presence of lower magnetic field homogeneity (FWHM of water resonance = 20 Hz). While the spectral resolution in the indirect F1 dimension remains virtually unchanged (FWHM = 4.1 ± 0.2 Hz as measured over 6 resonances), the spectral lines in the direct F2 dimension are significantly broadened. This confirms the theoretical prediction that the evolution of ZQCs is independent of magnetic field homogeneity. The apparently lower signal-to-noise ratio along the trace from the F1 dimension has two origins. Firstly, in order to achieve the highest possible spectral resolution in the F1 dimension, no apodization was applied, whereas the F2 dimension was line-broadened by 1 Hz. Secondly, the residual scan-to-scan water signal changed in amplitude and phase, leading to a variable baseline in the F2 dimension which appears as noise in the F1 dimension, similar to t1 noise in other multidimensional NMR experiments. Removing the water signal in each FID prior to 2D FFT, for example by HLSVD (27), will decrease the apparent noise significantly.
Figure 3.
In vitro 2D ZQC NMR spectra of aspartate in the presence of relatively (A) high and (B) low magnetic field homogeneity. The frequency width at half maximum (FWHM) of the water resonance is 7 and 20 Hz in (A) and (B), respectively. While the spectral resolution along the direct F2 dimension significantly decreases in (B), the spectral resolution along the indirect F1 dimension is virtually independent of the magnetic field homogeneity. The spectral region shown is zoomed and centered on the ZQC cross peaks of the aspartate H3-H3′ resonances.
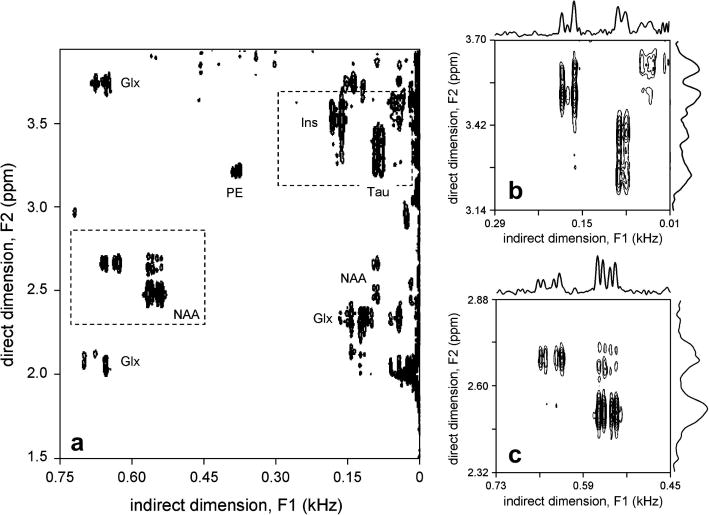
Fig. 4 shows typical 2D ZQC spectra acquired from rat brain in vivo. In less than one hour, most of the dominant scalar-coupled resonances can be readily detected as off-center peaks. Especially, NAA, glutamate and glutamine (Glx), taurine and myo-inositol are directly visible. At the lowest contour level, an off-center peak of phosphoryl ethanol amine (PE) is also visible at (3.22 ppm, 0.38 kHz). The coupling partner at (3.98 ppm, 0.38 kHz) is observable, but falls outside the displayed spectral ranges. Figs. 4B and C show 2D ZQC spectra zoomed around the Tau/Ins and NAA regions, respectively. The advantages of indirect ZQC detection can be clearly seen from the projections along the F1 and F2 dimensions. While the magnetic field homogeneity across the localized volume was reasonable (FWHM for water = 19 Hz), the resonances along the direct F2 dimension are relatively broad, offering no possibility of differentiating partially overlapping resonances or accurately measuring chemical shift or scalar coupling constants of individual resonances. The spectral resolution along the indirect F1 dimension is not sensitive to magnetic field inhomogeneity, leading to an average line width of 5.2 ± 0.4 Hz, as measured over 10 (absolute-valued) resonances.
Figure 4.
In vivo 2D ZQC NMR spectra acquired of rat brain. (A) Total 2D ZQC NMR spectrum, showing residual signal from uncoupled spins at F1 = 0, as well as significant ZQC cross peaks for NAA, Glx, Ins, Tau and PE. (B, C) 2D ZQC NMR spectrum from the (B) Ins/Tau and (C) NAA spectral regions as shown in (A). Note that the spectral ranges in (B) and (C) are 280 Hz in both dimensions, thereby directly revealing the increased spectral resolution in the indirect F1 dimension.
Similar results were obtained post-mortem (data not shown). While the line width of the lactate doublet at 1.31 ppm along the F2 dimension measured 42.6 ± 3.4 Hz, the lactate line width along the indirect F1 dimension measured 5.3 ± 0.3 Hz and could be clearly detected as an expected triplet resonance.
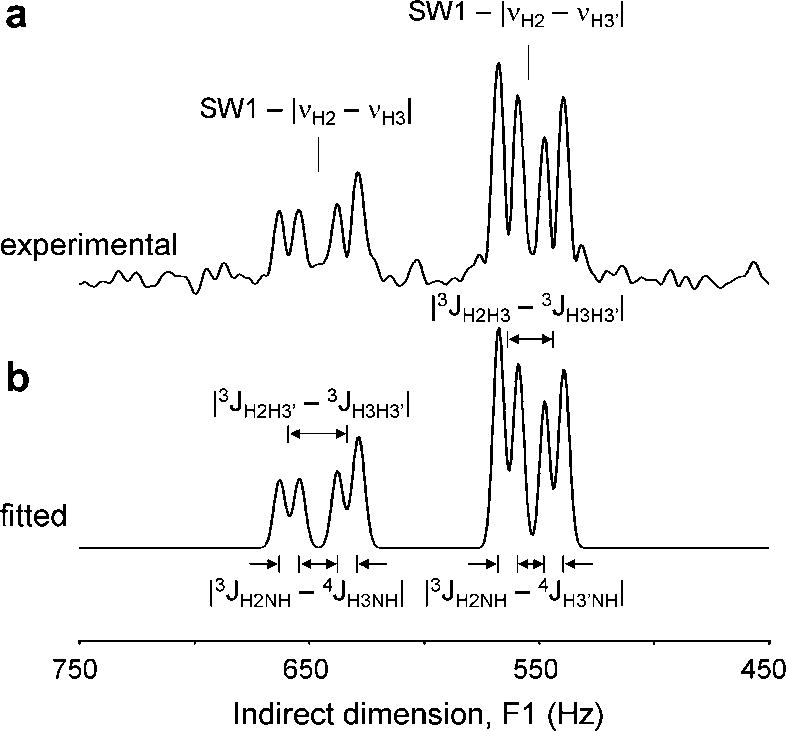
The indirect F1 dimension readily allows measurement of chemical shift differences as well as scalar coupling differences. Fig. 5 shows the determination of quantitative frequency differences on the NAA-H3/H3′ multiplet. The center frequencies of the cross peaks along the indirect F1 dimension were determined as |νH2 − νH3| = 854.1 ± 0.2 Hz and |νH2 − νH3′| = 946.6 ± 0.2 Hz, respectively (mean SD, N = 3). This is in excellent agreement with reported in vitro values for NAA (23), δH2 = 4.3817 ppm, δH3 = 2.6727 ppm and δH3′ = 2.4863 ppm, which would give |νH2 − νH3| = 854.2 Hz and |νH2 − νH3′| = 947.3 Hz at 11.74 T (499.814 MHz). Note that this information is not obtainable along the direct F2 dimension since the NAA H2 resonance is typically obliterated by the water suppression and the NAA H3 and H3′ resonances are significantly broader. The splitting of the multiplets along the indirect F1 dimension is caused by the absolute difference in scalar coupling to passive spins. For example the H2H3 multiplet splitting occurs due to coupling with the H3′-spin (|3JH2H3′ − 3JH3H3′| = 25.4 ± 0.1 Hz), as well as to the NH amide proton (|3JH2NH − 4JH3NH| = 8.6 ± 0.7 Hz), while the H2H3′ multiplet is split by the H3-spin (|3JH2H3 − 3JH3H3′| = 19.7 ± 0.2 Hz) and the NH amide proton (|3JH2NH − 4JH3′NH| = 8.5 ± 0.8 Hz). Using literature values (23) for the scalar coupling constants, 3JH2H3 = 3.9 Hz, 3JH2H3′ = 9.8 Hz, 2JH3H3′ = −15.6 Hz and 3JH2NH = 7.9 Hz gives excellent agreement for |3JH2H3′ − 3JH3H3′| = 25.4 Hz, |3JH2H3 − 3JH3H3′| = 19.5 Hz and |3JH2NH − 4JH3NH| = |3JH2NH − 4JH3′NH| = 7.9, whereby 4JH3NH = 4JH3′NH = 0.0 Hz. The value for 3JH2NH as reported by Govindaraju et al. (23) is incorrect and was experimentally measured on a 10 mM NAA sample (pH = 7.1, 310 K) at 500 MHz. Note that the high spectral resolution information on chemical shifts and scalar couplings would be impossible to obtain directly from the direct F2 dimension due to the significantly broader line widths.
Figure 5.
(A) Absolute-valued projection onto the indirect F1 axis of the NAA spectral region of the 2D ZQC NMR spectrum shown in Fig. 4C. (B) Result of spectral fitting using eight Gaussian lines. The fitted spectrum reveals two absolute frequency differences and four absolute scalar coupling differences, as indicated. See text for details.
DISCUSSION
Here we have presented the indirect detection of ZQCs to obtain high-resolution 1H NMR spectra of rat brain in vivo. Projections along the indirect dimension showed greatly improved spectral resolution when compared to the commonly observed direct dimension. Furthermore, the spectral resolution was independent of the macroscopic magnetic field homogeneity and was highly reproducible across different animals.
The frequency and scalar coupling differences found in vivo were in excellent agreement with published values determined in vitro. However, changes in molecular environment, cation binding, temperature, ionic strength and pH can lead to differences between the determined in vitro values and the in vivo situation. The outlined method offers a powerful technique to obtain this information at high resolution in vivo. This is especially prudent for spectral quantification methods, like LCmodel (28), where exact knowledge of scalar coupling constants and chemical shifts is essential for optimal performance.
Even though the spectral resolution in the indirect dimension is greatly increased when compared to the direct dimension, it is not necessarily optimal for a number of reasons. Firstly, the spectra were presented in absolute value mode. A phase-sensitive display would allow a higher spectral resolution, but only when the dispersive component is minimized by optimizing the preparation time TE1. Secondly, the (phase-sensitive) line-width in the indirect dimension is proportional to the ZQC transverse relaxation rate R2,ZQC. Since two spins contribute to the relaxation process, R2,ZQC is in general faster than the relaxation rate of the corresponding single-quantum-coherences, leading to broader spectral lines. Finally, since the 2D resonances appear at chemical shift differences, rather than absolute chemical shifts, the effective spectral dispersion range has decreased. However, despite these considerations the results in Figs. 4 and 5 clearly demonstrate that 2D ZQC NMR greatly increases the effective spectral resolution, giving rise to new information not available along the direct dimension.
It is well-known that 1D and 2D NMR experiments can in principle achieve identical sensitivities (29). However, several experimental considerations will decrease the sensitivity of the outlined 2D ZQC method. Firstly, T2 relaxation during t1 diminishes the signal intensity. Secondly, t1-noise is not negligible and as a result increases the apparent noise level. Thirdly, the intensity of a 1D spectral line is distributed across multiple lines in 2D, as shown for aspartate in Fig. 2. Finally, the efficiency of generating and detecting ZQCs is 25% at best. Using sub-optimal delays with multi-spin-systems further decreases the detection efficiency. Taking all these factors together can lead to a 5 to 10-fold reduction in signal intensity as compared to a conventional 1D NMR spectrum. It is therefore not recommended to use 2D ZQC NMR as a standard method to obtain metabolic information in vivo. The outlined sensitivity analysis of course ignores the fact that 2D methods generally have increased and unique information content. It is these unique spectral features of 2D ZQC NMR that can be utilized in particular applications for which it is not possible to obtain relevant spectral information by conventional 1D techniques. These applications can include the acquisition of proton spectra from areas with poor magnetic field homogeneity, like the frontal cortex, olfactory bulb, but also organs like liver, kidney and prostate. Furthermore, 2D ZQC NMR can aid in applications that are characterized by severe spectral overlap, such as the separation of lactate and lipids in tumors and muscle. 2D ZQC NMR also has significant potential for ex vivo measurements, like those on brain slices or perfused organs. As these measurements are typically performed at high magnetic fields with optimized RF coils, sensitivity is less of a restriction. Furthermore, for measurements of stable metabolite levels, the low temporal resolution of 2D ZQC NMR is not a limitation.
Absolute quantification of metabolites from 2D NMR spectra is typically more complicated than their 1D NMR equivalents. The additional complications originate from the fact that magnetic field inhomogeneity and intrinsic T2 relaxation can lead to partial cancellation of anti-phase cross peaks in 2D NMR spectra. However, through the use of careful quality control protocols including shimming and line width measurements, it is possible to achieve reproducible quantification of cross peaks (30,31). The quantification of 2D ZQC NMR spectra does not require additional considerations.
It is important to differentiate between the detection of intra-molecular ZQCs as described here and the detection of inter-molecular ZQCs (32–34), which was applied to the in vivo detection of metabolites by Faber et al. (35). While both techniques achieve an increased spectral resolution along the indirect dimension, the principles and applications of the two techniques widely differ. The detection of intra-molecular ZQCs as described here is strictly limited to scalar-coupled spin-systems. The detection of inter-molecular ZQCs relies on long range dipolar field interactions between solvent (i.e. water) and metabolites, and thus allows the detection of scalar-coupled, as well as non-coupled spins. Furthermore, while the method described here completely refocuses magnetic field inhomogeneity, the improvement in spectral resolution during the detection of intermolecular ZQCs relies on the refocusing of magnetic field inhomogeneity over distances larger than the dipolar correlation distance. Depending on the specific magnetic field gradients in the sample, this can lead to some residual line broadening (35).
In summary, it has been demonstrated that the indirect detection of intra-molecular ZQCs can generate high-resolution NMR spectra of the rat brain in vivo. Despite the lower sensitivity, 2D ZQC NMR allows the collection of unique spectral information in vivo that is not accessible by conventional 1D NMR techniques.
Acknowledgments
This research was supported by NIH grant R21 CA118503 (R.A.G). The authors thank Bei Wang for expert animal preparation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Hetherington HP, Kuzniecky RI, Pan JW, Mason GF, Morawetz R, Harris C, Faught E, Vaughan T, Pohost GM. Proton nuclear magnetic resonance spectroscopic imaging of human temporal lobe epilepsy at 4.1 T. Ann Neurol. 1995;38:396–404. doi: 10.1002/ana.410380309. [DOI] [PubMed] [Google Scholar]
- 2.Preul MC, Caramanos Z, Collins DL, Villemure JG, Leblanc R, Olivier A, Pokrupa R, Arnold DL. Accurate, noninvasive diagnosis of human brain tumors by using proton magnetic resonance spectroscopy. Nat Med. 1996;2:323–325. doi: 10.1038/nm0396-323. [DOI] [PubMed] [Google Scholar]
- 3.de Graaf RA, Mason GF, Patel AB, Rothman DL, Behar KL. Regional glucose metabolism and glutamatergic neurotransmission in rat brain in vivo. Proc Natl Acad Sci USA. 2004;101:12700–12705. doi: 10.1073/pnas.0405065101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shonk TK, Moats RA, Gifford P, Michaelis T, Mandigo JC, Izumi J, Ross BD. Probable Alzheimer disease: diagnosis with proton MR spectroscopy. Radiology. 1995;195:65–72. doi: 10.1148/radiology.195.1.7892497. [DOI] [PubMed] [Google Scholar]
- 5.Kantarci K, Jack CR, Jr, Xu YC, Campeau NG, O’Brien PC, Smith GE, Ivnik RJ, Boeve BF, Kokmen E, Tangalos EG, Petersen RC. Regional metabolic patterns in mild cognitive impairment and Alzheimer’s disease: A 1H MRS study. Neurology. 2000;55:210–217. doi: 10.1212/wnl.55.2.210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23:815–850. doi: 10.1118/1.597854. [DOI] [PubMed] [Google Scholar]
- 7.Romeo F, Hoult DI. Magnet field profiling: analysis and correcting coil design. Magn Reson Med. 1984;1:44–65. doi: 10.1002/mrm.1910010107. [DOI] [PubMed] [Google Scholar]
- 8.Gruetter R. Automatic, localized in vivo adjustment of all first- and second-order shim coils. Magn Reson Med. 1993;29:804–811. doi: 10.1002/mrm.1910290613. [DOI] [PubMed] [Google Scholar]
- 9.Koch KM, Sacolick LI, Nixon TW, McIntyre S, Rothman DL, de Graaf RA. Dynamically shimmed multivoxel 1H magnetic resonance spectroscopy and multislice magnetic resonance spectroscopic imaging of the human brain. Magn Reson Med. 2007;57:587–591. doi: 10.1002/mrm.21141. [DOI] [PubMed] [Google Scholar]
- 10.Koch KM, McIntyre S, Nixon TW, Rothman DL, de Graaf RA. Dynamic shim updating on the human brain. J Magn Reson. 2006;180:286–296. doi: 10.1016/j.jmr.2006.03.007. [DOI] [PubMed] [Google Scholar]
- 11.Koch KM, Brown PB, Rothman DL, de Graaf RA. Sample-specific diamagnetic and paramagnetic passive shimming. J Magn Reson. 2006;182:66–74. doi: 10.1016/j.jmr.2006.06.013. [DOI] [PubMed] [Google Scholar]
- 12.de Graaf RA, Brown PB, McIntyre S, Nixon TW, Behar KL, Rothman DL. High magnetic field water and metabolite proton T1 and T2 relaxation in rat brain in vivo. Magn Reson Med. 2006;9:386–394. doi: 10.1002/mrm.20946. [DOI] [PubMed] [Google Scholar]
- 13.Aue WP, Bartholdi E, Ernst RR. Two-dimensional spectroscopy. Application to nuclear magnetic resonance. J Chem Phys. 1976;64:2229–2246. [Google Scholar]
- 14.Pouzard G, Sukumar S, Hall LD. High resolution, zero quantum transition (two-dimensional) nuclear magnetic resonance spectroscopy: spectral analysis. J Amer Chem Soc. 1981;103:4209–4215. [Google Scholar]
- 15.Muller L. Mapping of spin-spin coupling via zero-quantum coherence. J Magn Reson. 1984;59:326–331. [Google Scholar]
- 16.Sotak CH, Freeman D. A method for volume-localized lactate editing using zero-quantum coherence created in a stimulated-echo pulse sequence. J Magn Reson. 1988;77:382–388. doi: 10.1002/mrm.1910070315. [DOI] [PubMed] [Google Scholar]
- 17.Doddrell DM, Brereton IM, Moxon LN, Galloway GJ. The unequivocal determination of lactic acid using a one-dimensional zero-quantum coherence-transfer technique. Magn Reson Med. 1989;9:132–138. doi: 10.1002/mrm.1910090116. [DOI] [PubMed] [Google Scholar]
- 18.van Dijk JE, Bosman DK, Chamuleau RAFM, Bovee WMMJ. A localized in vivo detection method for lactate using zero quantum coherence techniques. Magn Reson Med. 1991;22:493–498. doi: 10.1002/mrm.1910220256. [DOI] [PubMed] [Google Scholar]
- 19.Ryner LN, Sorenson JA, Thomas MA. 3D localized 2D NMR spectroscopy on an MRI scanner. J Magn Reson B. 1995;107:126–137. doi: 10.1006/jmrb.1995.1068. [DOI] [PubMed] [Google Scholar]
- 20.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 21.Garwood M, Ke Y. Symmetric pulses to induce arbitrary flip angles with compensation for RF inhomogeneity and resonance offsets. J Magn Reson. 1991;94:511–525. [Google Scholar]
- 22.Silver MS, Joseph RI, Hoult DI. Highly selective π/2 and π pulse generation. J Magn Reson. 1984;59:347–351. [Google Scholar]
- 23.Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR Biomed. 2000;13:129–153. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 24.Chandrakumar N, Chandrasekaran F. Strongly coupled zero-quantum spectra. J Magn Reson. 1992;96:657–662. [Google Scholar]
- 25.de Graaf RA, Nicolay K. Adiabatic water suppression using frequency selective excitation. Magn Reson Med. 1998;40:690–696. doi: 10.1002/mrm.1910400508. [DOI] [PubMed] [Google Scholar]
- 26.Sorensen OW, Eich GW, Levitt MH, Bodenhausen G, Ernst RR. Product operator formalism for the description of NMR pulse experiments. Prog NMR Spectroscopy. 1983;16:163–192. [Google Scholar]
- 27.van den Boogaart A, van Ormondt D, Pijnappel WWF, de Beer R, Ala-Korpela M. In: Mathematics and signal processing III. McWhirter JG, editor. Clarendon Press; Oxford: 1994. [Google Scholar]
- 28.Provencher SW. Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med. 1993;30:672–679. doi: 10.1002/mrm.1910300604. [DOI] [PubMed] [Google Scholar]
- 29.Ernst RR, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Clarendon Press; Oxford: 1987. [Google Scholar]
- 30.Thomas MA, Yue K, Binesh N, Davanzo P, Kumar A, Siegel B, Frye M, Curran J, Lufkin R, Martin P, Guze B. Localized two-dimensional shift correlated MR spectroscopy of human brain. Magn Reson Med. 2001;46:58–67. doi: 10.1002/mrm.1160. [DOI] [PubMed] [Google Scholar]
- 31.Schulte RF, Boesiger P. ProFit: two-dimensional prior-knowledge fitting of J-resolved spectra. NMR Biomed. 2006;19:255–263. doi: 10.1002/nbm.1026. [DOI] [PubMed] [Google Scholar]
- 32.Deville G, Bernier M, Delrieux JM. NMR multiple spin echoes in solid 3He. Phys Rev B. 1979;19:5666–5688. [Google Scholar]
- 33.Bowtell R, Bowley RM, Glover P. Multiple spin echoes in liquids in a high magnetic field. Phys Rev B. 1990;88:643–651. [Google Scholar]
- 34.He Q, Richter W, Vathyam S, Warren WS. Intermolecular multiple-quantum coherences and cross correlations in solution nuclear magnetic resonance. J Chem Phys. 1993;98:6779–6800. [Google Scholar]
- 35.Faber C, Pracht E, Haase A. Resolution enhancement in in vivo NMR spectroscopy: detection of intermolecular zero-quantum coherences. J Magn Reson. 2003;161:265–274. doi: 10.1016/s1090-7807(03)00006-5. [DOI] [PubMed] [Google Scholar]