Abstract
Motivation: The comprehensive information of small molecules and their biological activities in PubChem brings great opportunities for academic researchers. However, mining high-throughput screening (HTS) assay data remains a great challenge given the very large data volume and the highly imbalanced nature with only small number of active compounds compared to inactive compounds. Therefore, there is currently a need for better strategies to work with HTS assay data. Moreover, as luciferase-based HTS technology is frequently exploited in the assays deposited in PubChem, constructing a computational model to distinguish and filter out potential interference compounds for these assays is another motivation.
Results: We used the granular support vector machines (SVMs) repetitive under sampling method (GSVM-RU) to construct an SVM from luciferase inhibition bioassay data that the imbalance ratio of active/inactive is high (1/377). The best model recognized the active and inactive compounds at the accuracies of 86.60% and 88.89 with a total accuracy of 87.74%, by cross-validation test and blind test. These results demonstrate the robustness of the model in handling the intrinsic imbalance problem in HTS data and it can be used as a virtual screening tool to identify potential interference compounds in luciferase-based HTS experiments. Additionally, this method has also proved computationally efficient by greatly reducing the computational cost and can be easily adopted in the analysis of HTS data for other biological systems.
Availability: Data are publicly available in PubChem with AIDs of 773, 1006 and 1379.
Contact: ywang@ncbi.nlm.nih.gov; bryant@ncbi.nlm.nih.gov
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
PubChem is a public repository for small molecules and their biological properties. It was created as a component of the Molecular Libraries Roadmap (Zerhouni, 2003) initiated by the National Institutes of Health (NIH), which aims to discover chemical probes through high-throughput screening (HTS) of small molecules to support chemical biology research (Zerhouni, 2003, 2006). Currently, PubChem contains nearly 40 million unique chemical structure and >50 million biological test results for >600 protein targets. Analyzing the tremendous amount of biological activity data in PubChem (Wang et al., 2009) (http://pubchem.ncbi.nlm.nih.gov) remains a great challenge for chemical biology and cheminformatics researchers.
Until recently, HTS data was largely owned by pharmaceutical industries with only limited access to the public research community. The comprehensive information of small molecules and their biological activities in PubChem brings great opportunities for academic researchers in the chemical biology, medicinal chemistry and cheminformatics fields (Oprea et al., 2007; Ovaa and van Leeuwen, 2008; Rosania et al., 2007; Southan et al., 2007) to access and utilize large scale biological activity data to meet their research goals. Several groups have attempted to develop methods to analyze the data in this database (Guha and Schurer, 2008; Han et al., 2008; Hur and Wild, 2008; Nakai et al., 2009; Xie and Chen, 2008). Xie and Chen (2008) presented a strategy to select a diverse compounds subset from the PubChem database. Cao et al. (2008) developed a novel maximum common substructure-based algorithm to predict drug-like compounds from PubChem bioassay data. Rohrer and Baumann (2009) used a refined nearest neighbor analysis method to design benchmark datasets for virtual screening based on information in the PubChem database.
However, working with the bioassay data in PubChem was impeded by the imbalanced nature of HTS data. The data imbalance problem exists in a broad range of experimental data, but only recently has it attracted close attention from researchers (Barandela et al., 2003; Weiss, 2004). Data imbalance occurs when one of the classes in a dataset is represented by a very small number of samples compared to the other classes, which is usually of great interest (Barandela et al., 2003; Weiss, 2004). This issue might skew the prediction accuracy of classification models (Guha and Schurer, 2008; Hsieh et al., 2008), resulting in a weakened performance of machine learning algorithms (Kang and Cho, 2006). In HTS experiments, usually tens of thousands of compounds are screened, but only a small fraction of tested compounds turns out to be active, while the rest are inactive. Thus, HTS data is typically imbalanced in general with a small ratio of active compounds to inactive ones. Although many researchers (Guha and Schurer, 2008; Han et al., 2008; Weis et al., 2008) have noticed this problem when using the data in PubChem, to the best of our knowledge, there has been no method reported to tackle this problem effectively. Han et al. (2008) suggested that the data imbalance issue hindered the bioactivity classification accuracy. Guha et al. developed a random forest ensemble model designed to alleviate the imbalance of the dataset in cell toxicity prediction (Guha and Schurer, 2008). Weis et al. (2008) suggested the assay data be carefully selected from PubChem to attempt to avoid using the imbalanced data in their study.
Recently Tang et al. (2009) conducted an exhaustive comparative study of the currently reported state-of-the-art methods and proposed the granular sampling strategy to rebalance the originally imbalanced data. In this study, we adopted this method to HTS data analysis and investigate the strategies to mine the highly imbalanced luciferase inhibition bioassay data in PubChem (PubChem AID of 773, 1006 and 1379). HTS experiments often employ luciferase reporter genes and measure luminescence readouts (Fan and Wood, 2007). The intrinsic luciferase inhibition property of small molecules has been identified as one of the major screening artifacts (Auld et al., 2009; Fan and Wood, 2007; Inglese et al., 2007) for hits identification in such HTS experiments. Therefore, we also wanted to develop a virtual screening method to classify luciferase inhibitors, and to filter out potential interference molecules in luciferase-based HTS assays by taking the advantage of large scale luciferase inhibition profiling screening results recently available in the PubChem BioAssay database.
In addition to the data imbalance problem, HTS datasets can be large, containing test results for hundreds of thousands of chemical samples. It is a time-consuming process to build and optimize statistical models using such HTS data. Therefore, any improvement to computational efficiency could allow more data to be analyzed in less time. Moreover, HTS data are also noisy in general (Diller and Hobbs, 2004; Weis et al., 2008), and one needs to be cautious when utilizing and analyzing the data. Strategies to address these issues are also explored in this study.
2 METHODS
2.1 PubChem fingerprint
PubChem fingerprints were used to characterize chemical compounds in this study. PubChem 2D chemical structure fingerprint is an 881-dimension binary (0/1) vector. Each bit represents a Boolean determination of the absence or presence of a specific element, a type of ring system, atom pairing, or atom environment (nearest neighbors), etc. A detailed description of this fingerprint system is available at ftp://ftp.ncbi.nlm.nih.gov/pubchem/specifications/pubchem_fingerprints.txt
2.2 Dataset
Three bioassay data entries in PubChem (PubChem BioAssay accession: AID: 773, AID: 1006 and AID: 1379) for screening luciferase inhibitors were used to construct the training dataset. The HTS experiments were performed by two independent screening laboratories with AID: 1006 and AID: 773 by the Burnham Center for Chemical Genomics, and AID: 1379 by the NIH Chemical Genomics Center (NCGC). The assay of AID: 773 contained 237 active and 33 inactive compounds out of 270 tested ones; the assay of AID: 1006 contained 2976 active and 192 590 inactive compounds out of 195 566 tested ones; and the assay of AID: 1379 contained 565 active, 197 543 inactive and 982 inconclusive compounds out of 199 080 tested compounds (Table 1). A majority of the compounds screened by the assay of AID: 773 were also tested by the other two assays with 267 and 270 compounds in common with the assays of AID: 1006 and AID: 1379, respectively. The compounds screened by assays of AID: 1006 and AID: 1379 also had a substantial overlap of 187 138 compounds in common. However, the bioactivity outcomes, i.e. active or inactive, of a single compound, did not completely agree with each other in these three assays, which may be due to experimental noise or artifacts in the HTS assay (Diller and Hobbs, 2004; Weis et al., 2008). Therefore, we treated an active compound as a positive sample if at least two assays considered it ‘active’. Similarly, we treated an inactive compound as a negative sample by the confirmation of at least two assays. Compounds without confirmed bioactivity outcome were excluded in this study. A total of 487 positive and 183 667 negative compounds were included in the final dataset, which was denoted as (487+183 667) in following descriptions. Other datasets, in this study, was similarly denoted with the first number represents the active compounds, with the second number represents the inactive ones.
Table 1.
Three assays of luciferase inhibitors used in this study
| AIDa | Active | Inactive | Inconclusive | Total |
|---|---|---|---|---|
| 773 | 237 | 33 | 0 | 270 |
| 1006 | 2976 | 192 590 | 0 | 195 566 |
| 1379 | 565 | 197 543 | 982 | 199 080 |
aPubChem BioAssay accession.
The final dataset had an imbalance ratio of 1/377 (active/inactive), or <0.3% active samples were contained in this dataset. To keep the data imbalanced, we randomly split the whole dataset (487+183 667) into training data (dataset I) and blind testing data (dataset II) with the ratio of 80/20 that 80% (390+146 934) of the whole dataset (dataset I) was used for constructing model and the other 20% (97+36 733) (dataset II) for blind testing (Table 2).
Table 2.
Datasets used in this study
| Number | Type | Active compounds | Inactive Compounds | Imbalance ratioa |
|---|---|---|---|---|
| I | Training | 390 | 146 934 | 1:377 |
| II | Blind testing | 97 | 36 733 | 1:379 |
aImbalance ratio denotes the ratio of active compounds to inactive ones in the dataset.
2.3 Modeling with support vector machine
We used support vector (SV) machine (SVM), Libsvm (Chang and Lin, 2001), for this study. According to the statistical learning theory (Corinna and Vapnik, 1995), an optimal hyperplane is drawn by the SVM model to separate active and inactive samples with a maximum distance between the two classes. However, in an imbalanced situation that the majority class exceeds the minority class by a significant amount, the model likely pushes the ideal hyperplane towards the minority class (Tang and Zhang, 2006; Wu and Chang, 2005), resulting in classifying most observations into the class in which the majority samples belong.
To avoid this distortion, we explored two methodologies in this study: one was to rebalance the dataset with GSVM-RU method (Tang et al., 2009); the other was to evaluate the model performance with vigorous evaluation metrics independent of data distribution (Kubat and Matwin, 1997).
2.4 GSVM-RU undersampling method
The GSVM-RU method (Tang and Zhang, 2006; Tang et al., 2009) was used to sample the majority class in order to rebalance the dataset. As only SVs are important for SVM model classification (Corinna and Vapnik, 1995) that removing non-SV samples does not substantially affect the model performance. This method provides a mean to extract important samples from the dataset and to eliminate the unimportant ones. Based on this theory, GSVM-RU extracted the samples from the majority class according to their contributions to the classification in sampling process.
The GSVM-RU method treated all positive samples as important due to their rarity. However, for the negative samples, only SVs were considered important. Because of the large amount of negative samples, it was hard to extract all informative ones by using a single SVM, regardless of parameter tuning. Despite this, a fraction of informative samples can still be identified and extracted. These informative inactive samples (SVs) were removed from the original dataset to form a smaller dataset. A new SVM was then modeled with the reduced dataset to identify another part of the informative negative samples. This process was repeated as needed. Finally, the negative samples extracted from the previous sampling runs were discarded, and only the newly extracted inactive samples were retained and aggregated together with the positive samples to produce the training set, on which the final SVM model is built. Upon the completion of sampling, a final SVM was built and optimized with linear and radius-based function (RBF) kernels. The flow chart of this strategy is shown in Figure S3 in the Supplementary Material.
2.5 Model evaluation
The 5-fold cross-validation method was used to evaluate the performance of the SVM model. The whole dataset (dataset I) was randomly split into five folds, with four folds used for training and the other fold for testing. This process was repeated in turn and the final average performance was calculated. In addition to evaluate the generalization of the final SVM model, a blind test was carried out with dataset II, which was not involved in training process.
To consider the imbalance issue in this study, the receiver operating characteristic (ROC) curve and geometric mean (G-mean) value were used, which were suggested as good indicators dealing with such problems for their independence from the sample distribution between classes (Barandela et al., 2003; Kubat and Matwin, 1997). In addition, the common metrics of sensitivity, specificity and overall accuracy (Li et al., 2007; Li and Lai, 2007) were also calculated:
| (1) |
| (2) |
| (3) |
where, TP, FP, TN and FN denote true positive, false positive, true negative and false negative, respectively. G-mean that tries to maximize the accuracy on each of the two classes while keeping them balanced is calculated as following:
| (4) |
3 RESULTS
3.1 Sampling the majority (inactive) data of dataset I
The training set (dataset I) contained 390 active compounds and 146 934 inactive compounds, with <0.3% of the data active and ∼99.7% inactive resulting in a ratio of active to inactive of 1/377. Due to the rarity of active data, we assumed all 390 active compounds positive in the training set. For the majority class (inactive), the data was sampled through multiple rounds of sampling as described in Section 2. The significant compounds after sampling were identified to construct the negative data in the final training set. Based on the positive and the sampled negative data, the SVM model with linear and RBF kernels were built and optimized.
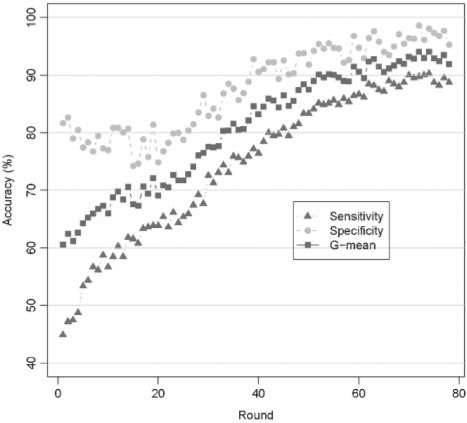
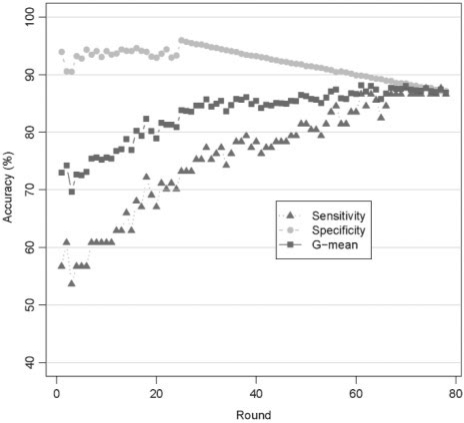
We used the GSVM-RU method to sample the inactive compounds based on their significance to the classification. The compounds identified in the previous round of sampling were excluded in the subsequent round. Considering the efficiency, we used the linear kernel of Libsvm with default parameters and 5-fold cross-validation in this process. Meanwhile, sensitivity, specificity and G-mean value were calculated to evaluate the performance of each model (Fig. 1).
Fig. 1.
The 5-fold cross-validation results of the training dataset in sampling process. The squares in the solid line (blue) represent the G-mean values. The filled circles in the dashed line (green) and the triangles in the dotted line (red) represent specificity and sensitivity, respectively.
The G-mean value increased from around 60% to over 90% in the sampling process (Fig. 1). Similarly, the sensitivity and specificity improved gradually as well, with the specificity consistently 5–10% higher than the corresponding sensitivity of each model. These data indicate that the SVM model performance improved continuously during the sampling process with the discrimination of inactive compounds slightly better than that of active ones. Moreover, the steady increasing of the model performance confirmed that the negative samples close to positive samples were being extracted step by step.
In addition, we observed a variation of the performance of the SVM model at the beginning of the sampling process. It is because that there are many inactive compounds close to the active ones, which are hard to be extracted for a single SVM model. However, as the sampling process is continued, it became relatively stable and the results converged starting from sampling round 67. At this point, the sample process was considered complete. The 358 sampled inactive compounds obtained in the sampling process were used together with the 390 active ones to produce the final training set, which was used to build and optimize a SVM model with linear and RBF kernels.
3.2 Optimizing the SVM model
We used two kernels of linear and non-linear functions, i.e. RBF kernel, to train the SVM model. For linear kernel, we tuned the single parameter of cost C to optimize the SVM model; while for RBF kernel, we optimized both cost C and gamma using the grid tool in Libsvm. The 5-fold cross-validation results of the linear model and the non-linear model are shown in Table 3. The sensitivities of these two models were similar (88.46%); however, the specificity of the RBF SVM was slightly higher than that of the linear model, and it outperformed the linear model by two percent with the highest G-mean of 91.66%. For both the linear and the RBF SVMs, the specificity exceeded the sensitivity, which may be due to the plenty sampling of inactive sample space.
Table 3.
The 5-fold cross-validation results of linear kernel SVM and RBF kernel SVM
| Kernel type | Sensitivity (%) | Specificity (%) | Accuracy (%) | G-mean (%) |
|---|---|---|---|---|
| Linear | 88.46 | 91.34 | 89.84 | 89.89 |
| RBF | 88.46 | 94.97 | 91.58 | 91.66 |
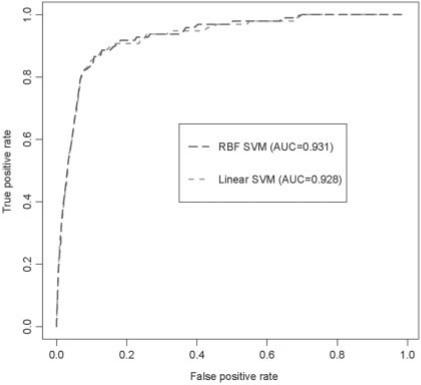
Similar results were observed in the ROC curves in Figure 2. The dotted and dashed lines of the curve represent the performance of the linear SVM and RBF SVM, respectively. The AUC is proportional to the model performance. The AUC of the RBF SVM (0.931) was slightly greater than that of the linear one (0.928). These data suggest that both models performed well in the 5-fold cross-validation tests with the RBF kernel slightly outperforming the linear kernel model.
Fig. 2.
The ROC curves of the SVM with linear and RBF kernels. The dashed line (blue) and dotted line (red) represent RBF SVM model and linear SVM, respectively. AUC (the area under the curve) is proportional to the model performance.
In summary, both G-mean values and ROC curves show the good performance of the SVM models in the 5-fold cross-validation, with the RBF SVM model consistently producing slightly better results.
3.3 Evaluating models with blind test
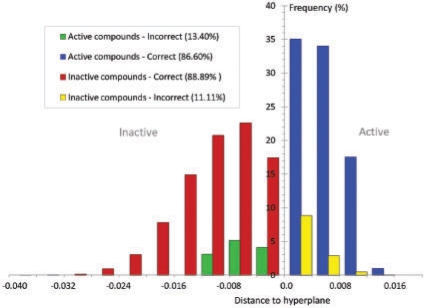
For a statistical model, it may perform perfectly in training, but poorly in testing due to over-fitting, resulting in a bad generalization. Here, the generalization of the SVM model was evaluated with a blind test where the testing dataset (dataset II) was excluded from the training process in advance. This dataset contained 97 active and 36 733 inactive compounds (Table 4). Both the linear and the RBF SVMs successfully recognized 84 out of 97 active compounds, with an equal accuracy of 86.60%. The performances for recognizing inactive compounds were similar for both the linear SVM (88.36%) and the RBF SVM (88.89%). The RBF SVM identified 32 651 from 36 733 inactive compounds, exceeding the linear SVM by ∼200 hits. The G-mean value shows a similar trend with the accuracies of the linear SVM model and RBF SVM model as 87.48% and 87.74%, respectively. These data indicate the RBF SVM performs slightly better than the linear SVM. These blind testing results are very close to those of the 5-fold cross-validation testing, suggesting that both the linear and non-linear SVM have good generalizations. We observed a clear separation of active and inactive compounds by the optimized SVM model as shown in Figure 3.
Table 4.
Blind testing resultsa
| Kernel type | Active accuracy (%) | Inactive accuracy (%) | G-mean (%) |
|---|---|---|---|
| Linear | 86.60 (84/97) | 88.36 (32 457/36 733) | 87.48 |
| RBF | 86.60 (84/97) | 88.89 (32 651/36 733) | 87.74 |
aThe numbers in parentheses show how many samples are correctly recognized out of the total testing ones.
Fig. 3.
Distribution of the prediction results of testing samples. The blue and red bars represent the correctly classified active compounds and inactive compounds, respectively. While the yellow and green bars denote the misclassified active samples and inactive samples instead, respectively.
3.4 Fingerprint features
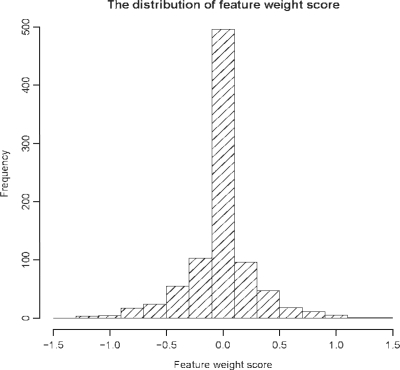
We used PubChem fingerprint to characterize each of the compounds in this study. A PubChem fingerprint contains 881 binary bits that indicate the presence or absence of a certain group of chemical features in a compound. We calculated the weight of each feature using the linear SVM to examine their contributions to the classification. We found that the contribution to the classification varied among the observed chemical features. A positive score signifies that the feature is important to positive samples, while a negative score signifies the feature is important to the negative samples. In general, the absolute value of a feature score is proportional to its contribution to the SVM classification. About half of the features have a score between −0.1 and 0.1, indicating these features are less important to the classification (Fig. 4). The top 30 fingerprint features with higher weight score for active compounds are listed in Table S1 in the Supplementary Material. We noticed that some of the high-score features recognized in this study are indeed important structure features observed in the active compounds. For example, the feature of C(∼ N)(∼ N) (no. 6 in Table S1 in the Supplementary Material), is part of the scaffold of benzimidazole analogs, one luciferase inhibitor cluster; the features of C:S:C-C and S-C:C-N (no. 24, 30 in Table S1 in the Supplementary Material) are part of the scaffold of 2-Phenylbenzothiazole analogs (Auld et al., 2008; 2009). Thus, this work may provide useful insights into the structure components critical for luciferase inhibition activity.
Fig. 4.
The distribution of PubChem fingerprint score of the compounds according to the contribution to the classification.
4 DISCUSSION
One of the main difficulties of working with HTS data arises from the fact that HTS data is highly imbalanced with only a handful of hits identified often out of a huge amount of tested compounds (Fig. S1 in the Supplementary Material). Most of the HTS assays in PubChem screened a large library of chemical compounds, where only a small fraction of the tested compounds were considered as hits and reported ‘active’ in PubChem. A distribution of the imbalance ratios of 258 distinct HTS assays in PubChem deposited by the NIH Chemical Genomics Center (NCGC) is shown in Figure S1 in the Supplementary Material, from which we observed almost ratios are under 1/10. Here, we investigated an approach for building an SVM model on the highly imbalanced dataset of the luciferase inhibition HTS assay in PubChem (PubChem AID: 773, 1006 and 1379). The best SVM model successfully distinguished the active compounds at an accuracy of 86.60% and the inactive compounds at an accuracy of 88.89%, with a total accuracy of 87.74% by critical evaluation test.
Ideally, the standard SVM draws an optimal hyperplane to separate positive data from negative data with maximum distance. However, the SVM model that is constructed from an imbalanced dataset tends to draw the hyperplane away from the ideal place and towards the minority side. Thus, the model is likely to classify most objects into the majority class, leading to great disparity between specificity and sensitivity, regardless of the parameter optimization. As a result, the predictability of such a model can be substantially poor.
The GSVM-RU method, which is based on the statistical learning theory (Corinna and Vapnik, 1995), to under sample the majority class and minimize the information loss of the majority class, achieved good performances on imbalanced HTS data. To look into the progress of the sampling process, we not only built the final well-optimized RBF SVM model based on the converged sampling results at sampling round 67, but also built a SVM model on the sampled compounds at the end of each round of sampling process. For each round of the sampling, we tested the performance of the constructed SVM model with the blind test dataset, which contained 97 active compounds and 36 733 inactive compounds that all were excluded from the sampling process (Fig. 5). The initial model was able to recognize the inactive compounds very well at the accuracy of >90%, while it could only correctly classify the active compounds at accuracy of 60% or even less at the beginning. As the sampling process proceeded, however, the ability of the SVM model to recognize the active compounds increased dramatically from <60% to >85% after certain steps. These observations agreed well with the results in sampling process. Meanwhile, the discrimination of inactive compounds only decreased ∼5%. These results indicate that the hyperplane of the SVM model moved gradually from the minority class side towards to the majority class side (negative samples), in other words, it was pulled back to the ideal place. The entire recognition ability (G-mean value) of the SVM model increased from ∼70 % to >87.74%.
Fig. 5.
Blind test results of each model over the sampling process. The squares in the solid line (blue) represent the G-mean values. The circles in the dashed line (green) and the triangles in the dotted line (red) represent specificity and sensitivity, respectively.
Another concern is the evaluation metrics selection when evaluating statistical models built on HTS data. Some of the commonly used metrics, such as overall accuracy [equation (3)], can lead to poor predictability when they are used for evaluating models built on imbalanced datasets as the evaluation metrics are dependent on the data distribution. Indeed, using inappropriate metrics is another reason for prediction distortion when optimizing model on imbalanced data. For instance, for a dataset with the positive/negative sample ratio of 1/9, although all samples are predicted to be negative, the overall accuracy is still 90%. For this reason that we used G-mean value and ROC curve, which are independent of the data distribution, to evaluate the performance of the SVM.
Furthermore, the size of HTS data, which usually contains hundreds of thousands of compounds, presents another challenge. Training and optimizing a statistical model on such a large dataset can be extremely time-consuming. The undersampling method in this study was computationally efficient, and it successfully downsized the dataset from more than one hundred thousand compounds to several hundreds of compounds, thus greatly reduced the computational cost in the optimized process and significantly increasing the efficiency of the SVM model. In other words, the GSVM-RU method provides a strategy for data sampling or data cleaning of a big dataset.
In addition, due to experimental conditions or the complexity of the biological system, there may be a certain amount of false positives and false negative data in HTS assays. We found that assay bioactivity results for certain compounds conflicted with each other even when they were provided by the same laboratory. For this reason, we carefully prepared the dataset in our study and used only compounds with bioactivity outcome, i.e. active versus inactive, which were confirmed by at least two assays.
Chemical space coverage is indeed an important issue in cheminformatics research. The chemical space coverage was estimated based on 2D chemical structure similarity using Tanimoto score of 0.90 as the threshold. Of the active compounds, 88.30% in the dataset are similar to the active compounds used in the model building, while ∼1.4% of the inactive compounds in the entire dataset are similar to one or more of the inactive compounds selected by the sampling procedure. The high coverage of active compounds indicates a strong structure–active relationship (SAR) among this group of compounds. Unlike the traditional clustering methods, such as k-mean, which finds the most featured representatives of a class, the strategy of the GSVM-RU method used in this study is to find the samples close to the border between two classes, which are used to draw the separating hyperplane. It means the other samples far away from hyperplane are discarded when a model is built. The entire training dataset was used in the searching of the optimized hyperplane. The final coverage (1.4%) for the ‘inactive’ compounds was calculated using the samples close to the separating hyperplane which were derived at the end of the sampling process. The confidence of the prediction of a compound is proportional to the distance to the hyperplane. The distribution of the blind test samples are shown in Figure 3, from which we observed that compounds that were not correctly predicted are basically close to the hyperplane. In addition, we also investigated the chemical property space coverage and plotted the distribution of rule of five properties (molecular weight, XlogP, hydrogen donor, hydrogen acceptor) for this dataset as shown in Figure S2 in the Supplementary Material, which is coincident with the distribution of the bioactive molecules observed in another work (Frimurer et al., 2000).
We used PubChem 2D fingerprints to characterize chemical compounds. A PubChem fingerprint indicates the presence/absence of a certain chemical feature in a studied compound. As the 881 features did not make equal contribution to the classification, we further carried out a feature selection to reduce potential data noise, though no significant improvement of the model performance has been achieved on this regard. We used the default PubChem fingerprint as the chemical structure descriptor in this study for it is readily available for public usage. We anticipate that a combination with some other molecular descriptors might further improve the classification performance and help to identify the relationship between a molecular structure and its biological activity. We plan to evaluate this factor in the future study by combining other molecular descriptors, including 3D molecular descriptors. Bioluminescent assays are a popular technology used in HTS experiments (Fan and Wood, 2007). Luciferase inhibition is one of the main sources of interference in such assays, which causes artifacts, and complicates the interpretation of the experimental data and the identification of HTS hits (Auld et al., 2008, 2009). Development of a computational tool which could facilitate the selection of chemical compounds for HTS screening and assist the interpretation of the resulting bioassay data was another motivation of this study. Several large-scale HTS experimental results of luciferase inhibitor screening have recently been deposited in the PubChem BioAssay database. The satisfactory performances in both cross-validation and blind test process have demonstrated the good generalization of the SVM model developed in this study, and suggests its potential application in virtual screening for compounds with luciferase inhibition or other types of biological activity. It needs to be pointed out that the development of the model is a learning process. Thus, the potential of the developed model is intrinsically limited to the known active compounds and the properties used for training. With the growth of the additional chemical classes of compounds to be screened, a more robust model may be developed with the availability of biologically interesting small molecules from a diverse compound library.
5 CONCLUSION
In this study, we used the GSVM-RU method to construct a SVM model on the extremely imbalanced HTS data [the imbalance ratio of 1:377 (active/inactive)] obtained from several luciferase inhibitor assays in PubChem. The best model recognized the active and inactive compounds at the accuracies of 86.60 and 88.89%, respectively, with an accuracy of 87.74% in critical evaluation. These results demonstrate the robustness of the model in handling the intrinsic imbalance problem in HTS data and indicate that the model can be used as a virtual screening tool to identify potential interference compounds in luciferase-based HTS experiments. Additionally, this method has also proved computationally efficient by greatly reducing the computational cost and can be easily adopted in the analysis and interpretation of HTS data for other biological systems.
ACKNOWLEDGEMENTS
We thank the National Institutes of Health Fellows Editorial Board.
Funding: Intramural Research Program of the National Institutes of Health, National Library of Medicine.
Conflict of Interest: none declared.
REFERENCES
- Auld DS, et al. Characterization of chemical libraries for luciferase inhibitory activity. J. Med. Chem. 2008;51:2372–2386. doi: 10.1021/jm701302v. [DOI] [PubMed] [Google Scholar]
- Auld DS, et al. A basis for reduced chemical library inhibition of firefly luciferase obtained from directed evolution. J. Med. Chem. 2009;52:1450–1458. doi: 10.1021/jm8014525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barandela R, et al. Strategies for learning in class imbalance problems. Pattern Recogn. 2003;36:849–851. [Google Scholar]
- Cao Y, et al. A maximum common substructure-based algorithm for searching and predicting drug-like compounds. Bioinformatics. 2008;24:i366–i374. doi: 10.1093/bioinformatics/btn186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Lin C-J. LIBSVM : a library for support vector machines. 2001 Available at http://www.csie.ntu.edu.tw/∼cjlin/libsvm. [Google Scholar]
- Corinna C, Vapnik V. Support vector network. Mach. Lear. 1995;20:273–297. [Google Scholar]
- Diller DJ, Hobbs DW. Deriving knowledge through data mining high-throughput screening data. J. Med. Chem. 2004;47:6373–6383. doi: 10.1021/jm049902r. [DOI] [PubMed] [Google Scholar]
- Fan F, Wood KV. Bioluminescent assays for high-throughput screening. Assay Drug Dev. Technol. 2007;5:127–136. doi: 10.1089/adt.2006.053. [DOI] [PubMed] [Google Scholar]
- Frimurer TM, et al. Improving the odds in discriminating “drug-like” from “non drug-like” compounds. J. Chem. Inf. Comput. Sci. 2000;40:1315–1324. doi: 10.1021/ci0003810. [DOI] [PubMed] [Google Scholar]
- Guha R, Schurer SC. Utilizing high throughput screening data for predictive toxicology models: protocols and application to MLSCN assays. J. Comput. Aided Mol. Des. 2008;22:367–384. doi: 10.1007/s10822-008-9192-9. [DOI] [PubMed] [Google Scholar]
- Han L, et al. Developing and validating predictive decision tree models from mining chemical structural fingerprints and high-throughput screening data in PubChem. BMC Bioinformatics. 2008;9:401–408. doi: 10.1186/1471-2105-9-401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh JH, et al. Differentiation of AmpC beta-lactamase binders vs. decoys using classification kNN QSAR modeling and application of the QSAR classifier to virtual screening. J. Comput. Aided Mol. Des. 2008;22:593–609. doi: 10.1007/s10822-008-9199-2. [DOI] [PubMed] [Google Scholar]
- Hur J, Wild DJ. PubChemSR: a search and retrieval tool for PubChem. Chem. Cent. J. 2008;2:11–17. doi: 10.1186/1752-153X-2-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inglese J, et al. High-throughput screening assays for the identification of chemical probes. Nat. Chem. Biol. 2007;3:466–479. doi: 10.1038/nchembio.2007.17. [DOI] [PubMed] [Google Scholar]
- Kang P, Cho S. Neural Information Processing. Heidelberg: Springer Berlin; 2006. EUS SVMs: ensemble of under-sampled SVMs for data imbalance problems; pp. 837–846. [Google Scholar]
- Kubat M, Matwin S. Proceedings of the 14th International Conference on Machine Learning. Morgan Kaufmann; 1997. Addressing the curse of imbalanced training sets: one-sided selection; pp. 179–186. [Google Scholar]
- Li Q, Lai L. Prediction of potential drug targets based on simple sequence properties. BMC Bioinformatics. 2007;8:353–363. doi: 10.1186/1471-2105-8-353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q, et al. A large descriptor set and a probabilistic kernel-based classifier significantly improve druglikeness classification. J. Chem. Inf. Model. 2007;47:1776–1786. doi: 10.1021/ci700107y. [DOI] [PubMed] [Google Scholar]
- Nakai R, et al. Ranking the selectivity of PubChem screening hits by activity-based protein profiling: MMP13 as a case study. Bioorg. Med. Chem. 2009;17:1101–1108. doi: 10.1016/j.bmc.2008.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oprea TI, et al. Systems chemical biology. Nat. Chem. Biol. 2007;3:447–450. doi: 10.1038/nchembio0807-447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ovaa H, van Leeuwen F. Chemical biology approaches to probe the proteome. Chembiochem. 2008;9:2913–2919. doi: 10.1002/cbic.200800454. [DOI] [PubMed] [Google Scholar]
- Rohrer SG, Baumann K. Maximum unbiased validation (MUV) data sets for virtual screening based on PubChem bioactivity data. J. Chem. Inf. Model. 2009;49:169–184. doi: 10.1021/ci8002649. [DOI] [PubMed] [Google Scholar]
- Rosania GR, et al. A cheminformatic toolkit for mining biomedical knowledge. Pharm Res. 2007;24:1791–1802. doi: 10.1007/s11095-007-9285-5. [DOI] [PubMed] [Google Scholar]
- Southan C, et al. Complementarity between public and commercial databases: new opportunities in medicinal chemistry informatics. Curr. Top Med. Chem. 2007;7:1502–1508. doi: 10.2174/156802607782194761. [DOI] [PubMed] [Google Scholar]
- Tang Y, Zhang Y-Q. Proceedings of 2006 IEEE International Conference on Granular Computing (IEEE-GrC2006) Atlanta: 2006. Granular SVM with repetitive undersampling for highly imbalanced protein homology prediction; pp. 457–460. [Google Scholar]
- Tang Y, et al. SVMs modeling for highly imbalanced classification. IEEE Trans. Syst., Man, Cybern. - Part B Cybern. 2009;39:281–288. doi: 10.1109/TSMCB.2008.2002909. [DOI] [PubMed] [Google Scholar]
- Wang Y, et al. PubChem: a public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009;37:W623–W633. doi: 10.1093/nar/gkp456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weis DC, et al. Data mining PubChem using a support vector machine with the Signature molecular descriptor: classification of factor XIa inhibitors. J. Mol. Graph. Model. 2008;27:466–475. doi: 10.1016/j.jmgm.2008.08.004. [DOI] [PubMed] [Google Scholar]
- Weiss GM. Mining with rarity: a unifying framework. SIGKDD Explor. Newsl. 2004;6:7–19. [Google Scholar]
- Wu G, Chang EY. KBA: kernel boundary alignment considering imbalanced data distribution. IEEE Trans. Knowl. Data Eng. 2005;17:786–795. [Google Scholar]
- Xie XQ, Chen JZ. Data mining a small molecule drug screening representative subset from NIH PubChem. J. Chem. Inf. Model. 2008;48:465–475. doi: 10.1021/ci700193u. [DOI] [PubMed] [Google Scholar]
- Zerhouni E. Medicine. The NIH Roadmap. Science. 2003;302:63–72. doi: 10.1126/science.1091867. [DOI] [PubMed] [Google Scholar]
- Zerhouni EA. Clinical research at a crossroads: the NIH roadmap. J. Investig. Med. 2006;54:171–173. doi: 10.2310/6650.2006.X0016. [DOI] [PubMed] [Google Scholar]