Strategies for nanoplasmonic core-satellite biomolecular sensors: Theory-based Design

Abstract

We present a systematic theoretical study of core-satellite gold nanoparticle assemblies using the Generalized Multiparticle Mie formalism. We consider the importance of satellite number, satellite radius, the core radius, and the satellite distance, and we present approaches to optimize spectral shift due to satellite attachment or release. This provides clear strategies for improving the sensitivity and signal-to-noise ratio for molecular detection, enabling simple colorimetric assays. We quantify the performance of these strategies by introducing a figure of merit. In addition, we provide an improved understanding of the nanoplasmonic interactions that govern the optical response of core-satellite nanoassemblies.

Coupled noble metal nanoclusters have localized surface plasmon resonances (LSPR) in the visible spectrum that are highly dependent upon the overall construct geometry, interparticle distance, and the dielectric permittivity of the surrounding medium. Variations of nanoassemblies have included lattice networks,^{1, 2} dimer and trimer configurations,^{3, 4} and core-satellite constructs.^{4, 5, 6, 7} These nanoassemblies have enabled investigations of plasmon coupling^{8, 9} and plasmon-based detection of biological and chemical analytes.^{10, 11, 12}

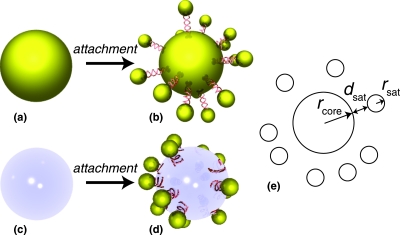
While core-satellite nanoassemblies are a promising platform for plasmon-based detection, basic questions remain on how to maximize their sensitivity. For example, will many small satellite nanoparticles produce a larger shift-upon-attachment (or release) than a few large ones? What is the importance of the core particle size? What is the optimal core-satellite linker distance? These questions are critical for the next generation of sensors, since optimization of core-satellite scattering spectra will maximize the signal-to-noise ratio during spectroscopic sensing, enabling simple colorimetric assays and improving sensitivity. In addition, the core-satellite system serves as a platform to understand the fundamentals of plasmon coupling in nanoassemblies. We illustrate the core-satellite nanoassembly in Fig. 1.

Figure 1.

The core-satellite nanoassembly; (a) gold core nanoparticle with (b) gold satellites attached via a molecular linker to form a core-satellite nanoassembly; (c) and (d) alternatively, gold satellites may attach to a glass core nanoparticle; (e) a schematic of the core-satellite system with the key geometric parameters labeled.

While theoretical results for cluster assemblies have been reported,^{8, 13, 14} this letter represents the first systematic study of the core-satellite nanoplasmonic system. The exact solution of electromagnetic scattering by a single sphere was solved by Gustav Mie over 100 years ago,^{15, 16} but only recently has this technique been extended to the case of multiple spheres at arbitrary distances, with the Generalized Multiparticle Mie (GMM) solution.^{17, 18, 19, 20, 21} Using this exact solution, we compute the scattering cross section of core-satellite nanoparticle assemblies. We assume both the core and satellites are made of gold, with complex permittivity ϵ given by an analytical model²² of the experimental data²³ for bulk gold, and with relative permeability μ=1. The surrounding medium is assumed to be free-space with ϵ=μ=1. For comparison, we also consider glass core nanoparticles, with ϵ=2.25.

To model the stochastic nature of satellite positions around the core, satellites were successively placed around the core at a fixed radius using a random number generator, until the desired number of satellites was reached. For all spectra shown in this letter, ten such random core-satellite assemblies were generated, and the scattering results were averaged to give more physically relevant results, and to avoid trends due to symmetric placement of satellites. Even for nanoassemblies with defined satellite placement,² nanoassemblies are typically at random orientations relative to the polarization of the incident light; hence a stochastic model is relevant to a wide range of physical systems.

Four primary handles exist to potentially vary the optical properties, and most importantly the shift-upon-attachment (or release), of the core-satellite system: the satellite number n_sat, the satellite radius r_sat, the core radius r_core, and the satellite distance d_sat (Fig. 1). Herein we demonstrate the importance of each of these parameters. We focus on shift-upon-attachment, defined as the difference in the LSPR wavelength between the entire core-satellite assembly and that of the single core particle: Δλ=λ_{peak,core+sat}−λ_peak,core. This shift is identical (but opposite in sign) for shift-upon-release of satellites.

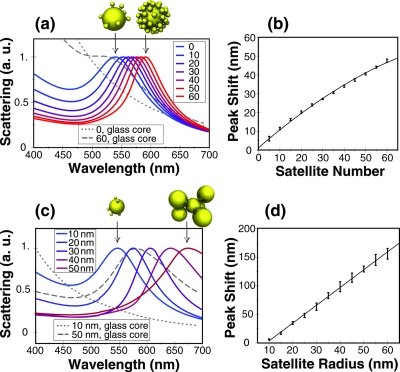
As satellite number increases, a nearly linear redshift occurs in the scattering spectrum, as shown in Figs. 2a, 2b. For the physically relevant parameters chosen (r_core=50 nm, r_sat=10 nm, and d_sat=2 nm), this redshift is roughly 1 nm per satellite; hence a 50 nm redshift is achievable by nearly maximizing coverage of satellites, and these peak shifts are similar to that seen in comparable experimental systems.⁸ The redshift upon satellite attachment is caused by the local plasmonic coupling between the core and satellite nanoparticles. In this case, since both the core and satellite sizes are much smaller than the incident wavelength of light, the quasistatic approximation is valid and the interaction can be closely modeled by coupled dipoles. We note that the plasmon bandwidth decreases with increasing satellite number, and this effect is also due to the local plasmonic coupling, while the small particle size prevents damping effects from broadening the plasmon bandwidth. Since a glass core with 60 gold nanoparticle satellites shows only a broad peak near 550 nm [dashed line in Fig. 2a], it is clear that both the plasmon shift and bandwidth narrowing are due primarily to core-satellite interactions and not satellite-satellite interactions.

Figure 2.

Effect of varying satellite number and size; normalized scattering cross section of core-satellite nanoassemblies for (a) increasing satellite number (r_core=50 nm, r_sat=10 nm, and d_sat=2 nm) and (c) increasing satellite radius (r_core=50 nm, n_sat=5 nm, and d_sat=2 nm); the peak shift Δλ for increasing (b) satellite number and (d) satellite radius; solid line shown as a guide, error bars represent standard deviation from ten randomly generated core-satellite assemblies.

Both the peak shift and the plasmon bandwidth are important in the figure of merit (FOM) for detecting plasmonic peak shifts.²⁴ To take into account both of these effects, for core-satellite systems we define FOM=Δλ∕FWHM, where FWHM is the full width at half maximum of the plasmon band. For 60 satellite nanoparticles, the FOM=0.64

While increasing satellite number presents one strategy for maximizing shift-upon-attachment, increasing the satellite size presents another scheme, as shown in Figs. 2c, 2d. In varying the satellite radius from 10 to 50 nm, a 150 nm redshift is seen in the plasmon band. This relationship is also nearly linear, with a 3 nm redshift per 1 nm increase in satellite radius. As the satellite radius increases past 50 nm, the plasmon band broadens significantly. This is mainly due to retardation effects as the nanoassembly size becomes significant compared to the wavelength of light. Radiation damping, which depends on particle volume, has been shown to be largely responsible for redshifts in both near- and far-fields scattered from nanoparticles as they increase in size.²⁵ Therefore, compared to the “many small satellite” approach, the “few large satellites” approach takes advantage of the increases in redshift due to the nanoassembly size becoming large compared to the wavelength of incident light. As Fig. 2 shows, the latter approach can generate much larger peak shifts. Hence, increasing satellite size presents a method of creating larger shift-upon-attachment versus using many smaller satellites. We believe this approach has been greatly under-utilized in the literature—the FOM for five 60 nm satellites reaches FOM=1.52, over twice that of the “many small satellite” approach.

We note that the spectra of nanoassemblies with few satellites show wider variation due to the stochastic nature of satellite placement. For example, with only a handful of satellites, there is a greater chance they may be placed out of the plane of the incident electric field and only weakly couple to the core nanoparticle. In contrast, for large satellite numbers, the variation between assemblies is reduced, as shown in the standard deviation in peak shift in Fig. 2b versus Fig. 2d. The physical importance of this phenomenon may also depend on the mechanism of satellite attachment. We also note that again both the plasmon shift and bandwidth properties are due primarily to core-satellite interactions, since a broad peak near 575 nm is observed for r_sat=50 nm gold satellites and a glass core [dashed line in Fig. 2c].

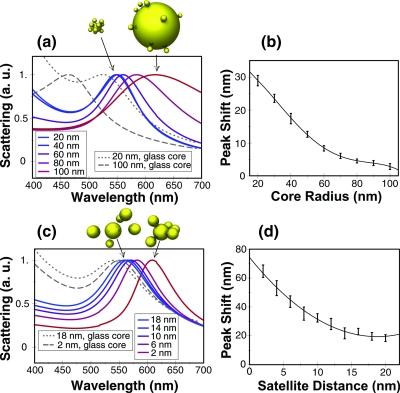
Next, we consider the effect of the core size in Fig. 3a. Again, retardation effects occur as the core radius increases, broadening the spectral peak, and the peak shift decreases with increasing core size. This result is consistent with that shown for increasing satellite size—if we consider the ratio of the satellite size to the core size, in both Figs. 2c, 2d and Figs. 3a, 3b, an increasing ratio causes an increased peak difference upon attachment. The relationship between peak shift and core sphere size is approximately linear in the quasistatic regime (core radius <50 nm), while the relationship becomes nonlinear for larger core sizes as damping effects become significant and the peak shift becomes small [Fig. 3b]. In contrast, without the core-satellite coupling, the plasmon peak is blueshifted for a glass core [Fig. 3a], and for large glass cores a broad peak emerges near 450 nm due to the glass. These results might lead one to conclude that minimizing the core size is a desirable route to increasing peak shift. While this is correct, it is limited by the following practical concerns: nanoparticle absorption scales with the particle volume, while scattering scales with the volume squared. Thus, smaller particles become difficult to observe and the absorption signal will become large compared to the scattered signal. In addition, the reduced surface area for smaller particles limits the number of satellites that can be attached. Thus, for scattering detection schemes, a minimum core radius of r_core≈25 nm is desirable.

Figure 3.

Effect of varying core size and satellite distance; normalized scattering cross section of core-satellite systems for (a) increasing core radius (r_sat=10 nm, n_sat=10, and d_sat=2 nm) and (c) increasing satellite distance (r_core=50 nm, r_sat=30 nm, and n_sat=5 nm); the peak shift Δλ for increasing (b) core radius and (d) satellite distance; solid line shown as a guide, error bars represent standard deviation from ten randomly generated core-satellite assemblies.

Finally, we consider the importance of the distance between the core and satellite particles, typically determined experimentally by a chemical linker, such as an oligonucleotide. As shown in Figs. 3c, 3d, decreases in core-satellite distance cause an increase in the redshift in a nonlinear fashion. To take advantage of this nonlinearity, particularly close core-satellite distances (<5 nm) are desirable. This nonlinearity is due to the rapidly decaying near field, determined by distance⁻³ in the quasistatic approximation, and typical decay lengths are tens of nanometers. This gap-dependent redshift behavior has been observed and predicted in many different systems, for example molecular rulers⁹ and particle dimer systems.²⁶ With a glass core, only a minimal redshift occurs when the satellite distance decreases; hence core-satellite interactions again dominate the satellite distance dependence. We note that the assumptions of classical electromagnetics are no longer physically valid when the gap size is less than ≈2 nm; hence this was the smallest gap distance used in this study.

We believe the strategies described here are achievable with current fabrication techniques. Core-satellite architectures of noble metal and silica nanoparticles have been demonstrated primarily using directional conjugation methods, specifically, by combining complementary motifs that tether nanoparticles to a linking agent, such as a modified oligonucleotide functionalized with a high affinity biomolecule. Directional assembly commonly exploits binding motifs such as mercaptan∕metal,^{2, 6, 7, 9, 27} biotin∕streptavidin,^{9, 27} antibody∕antigen,²⁸ digoxingenin∕antidigoxigenin,⁹ and cyclic disulfide phosphoramidite moiety∕Ag²⁹ bonds. The directional hybridization of half complementary, modified oligonucleotides further extends directional arrangement of nanoassembled constructs.^{7, 27} Additionally, two-dimensional analogs of the three-dimensional core-satellite structures could conceivably be fabricated using top-down methods such as photo, nanoimprint, electron beam, focused ion beam, or soft lithographies.

To conclude, we have demonstrated simple strategies for improving shift-upon-attachment or shift-upon-release for core-satellite systems. While increasing satellite number produces a near linear redshift reaching ≈50 nm, a larger shift (≈150 nm) can be achieved by increasing satellite size in the same system. Core size should be minimized, constrained by the minimum size required for detection of the core scattering signal. Linker distances should be minimized to improve core-satellite coupling, which scales nonlinearly with distance. By taking these simple strategies into account, more sensitive and higher shift-upon-attachment core-satellite nanoplasmonic sensors are achievable.