Effect of pressure on electrospray characteristics

Abstract

An experimental study of pulsating electrosprays operated at subambient pressure is reported. The pressure domain that affords stable electrospray operation appears to be limited by the vapor pressure of the liquid. The voltage driving the electrospray is shown to have a logarithmic dependence on pressure. The observed scaling amends the relationship currently used to calculate the electric field at the tip of the meniscus of an electrified liquid.

Zeleny¹ conducted the first rigorous studies of what he described as discharges from liquid points, phenomena known today as electrosprays. In his experiments, a minimal pressure difference delivered electrified liquid at the tip of a glass capillary for spraying against a planar counterelectrode. In a similar geometry, Eyring et al.² studied the electric field E when applying a voltage V between a hyperbolic metal electrode polished to a radius of curvature r and a metallic disk situated at a distance d. In a simplified form, the electric field was expressed as a function of a constant c:³

$$E=\frac{cV}{r\text{\hspace{0.17em}ln}\left(4d∕r\right)}.$$ (1)

This relationship is currently in use to estimate the electric field at the tip of a rounded liquid meniscus. A semispherical liquid drop is in equilibrium if the pressure drop across the liquid interface (p−p₀) is balanced by its surface tension (γ):p−p₀=γ∕r, where r is the radius of curvature of the meniscus. Under the influence of E, r changes to compensate for the pressure produced by electrical forces p_E=ε₀E²∕2, where ε₀ is vacuum permittivity. Once the electric field surpasses a threshold at a critical voltage, a singularity is induced, which reshapes the meniscus into a cone and triggers the ejection of charged liquid from its apex.^{4, 5, 6} The cone-jet electrospray regime⁷ is established if the charge is generated electrochemically at the same rate as it is ejected; however, when operated close to the threshold electric field, supply disruptions lead to discontinuous regimes that have been described as burst,⁸ pulsating,⁹ or astable.¹⁰

One of the most important applications of electrosprays is in mass spectrometry (MS) ionization sources.¹¹ The small charged droplets experience cycles of solvent evaporation followed by charge reduction through Rayleigh fission events or field evaporation.^{12, 13, 14, 15} The charged aerosol produced by electrosprays at atmospheric pressure must be transferred into a very low pressure environment for the MS analyses. This is generally accomplished by several stages of differential pumping. Ion funnels¹⁶ can be employed to improve the ion transfer efficiency through intermediate chambers in the 1–30 torr range, while traditional radio frequency (rf) ion guides are broadly used in lower pressure regimes. A typical electrospray ionization (ESI)-MS interface employs a heated capillary inlet enabling sampling of the electrospray while providing supplemental thermal energy to aid desolvation of the charged droplets. Most of the charged aerosol is “lost” to the front or inside the heated capillary of such interfaces,¹⁷ constraining sensitivity and detection limits. To eliminate the losses associated with such inlets, we have been exploring ESI at subambient pressures.¹⁸

Early low pressure electrospray studies focused on providing thrust for microsatellites.^{19, 20, 21}Later, liquid metal ion sources²² and electrosprays of glycerol solutions²³ were employed with limited success as vacuum ion sources for MS. The low vapor pressure, which makes glycerol an ideal candidate for vacuum electrospray, impedes efficient ion production from its droplets. Although droplets of volatile solvents move faster through the cycles of solvent evaporation and Rayleigh fission to finally liberate gas-phase ions, the pressure domain ensuring reliable electrospray operation is expected to be limited by the liquid vapor pressure.

A stable electrospray is desired for ion production at reduced pressures, but effective desolvation is also required. At atmospheric pressure droplet thermalization by collisions with ambient gas molecules limits cooling due to solvent evaporation. At lower pressures droplets can cool more significantly and even freeze, slowing desolvation and inhibiting ion formation. The optimum conditions for MS studies is likely a compromise between those facilitating efficient desolvation and ion production (high pressures) and those eliminating the losses associated with the transmission through the atmospheric pressure interface (low pressures). An effective compromise requires a better understanding of electrosprays using MS-compatible liquids operated at reduced pressures. Of particular interest is electrospraying at pressures allowing effective ion funnel operation.

Solvents typical for reversed-phase liquid chromatography-MS analyses (0.07% trifluoroacetic acid and 0.13% acetic acid in a 70:30 water:acetonitrile solution with the conductivity, κ=0.235 S∕m) were electrosprayed inside a rough pumped chamber equipped with choke and leak valves, which ensured coarse and fine pressure tuning, respectively. The values corresponding to water:acetonitrile binary mixtures were used for relative permittivity²⁴ ε=65.68, density²⁵ ρ=893 kg∕m³, surface tension²⁶ γ=0.0529 N∕m. Electrospray emitters²⁷ with 10 μm inner diameters were mounted on a translation stage against a planar metal counterelectrode. The voltage was applied to the metal union holding the emitter, and electrospray currents were measured by monitoring the voltage across a 10 MΩ resistor connecting the counterelectrode to electrical ground. Although electrosprays were reproducibly produced at atmospheric pressure with flow rates as low as 20 nL∕min,²⁸ the low-flow electrosprays proved increasingly erratic with decreasing pressure. To ensure improved reproducibility and greater confidence in the experimental data, the present studies were performed at flow rates between 100 and 300 nL∕min. Because the flow rates are outside the cone-jet stability island,²⁹ the electrospray was operated in the pulsating regime; under these conditions, the electrospray current increased linearly with the applied voltage.

We note that Eq. 1 was derived for solid electrodes and may need to be amended for application to liquid interfaces. Indeed, there is no consensus over the value of the constant c.^{30, 31} Additionally, Eq. 1 does not reflect the potential effect of pressure, which is expected to influence other operating parameters. The meaning of the parameter r is also vague due to the dynamic nature of the liquid interface,³² whose radius of curvature goes through a wide range of values during each pulsation cycle. In a first approximation, we can consider that the relevant value of r is of the same order of magnitude as the relaxation length³³r^*=(Qεε₀∕κ)^1∕3, which is ∼0.16 μm at a flow rate of Q=100 nL∕min. For decreasing meniscus radii, the hydrodynamic relaxation time τ_H=r³∕Q becomes much faster than the charge relaxation time τ_C=εε₀∕κ, leading to singularity development. During each pulsation cycle, the singularity is a temporal barrier marking the transition from a regime dominated by conductive charge transport to a regime dominated by convective charge transport. The electric field E^* established at the onset of the singularity is expected to define the charge distribution along the liquid meniscus and the current delivered by the electrospray. In each set of experiments, the voltage was continuously adjusted to maintain a preselected electrospray current. It was explicitly assumed that—for constant liquid flow rate—the delivery of a constant electrospray current was the result of constant E^*.

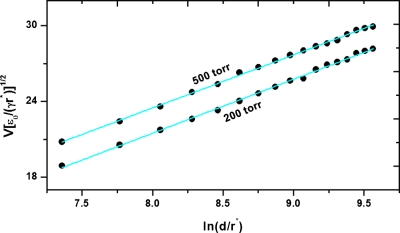
Figure 1 shows data obtained at p₁=200 and p₂=500 torr for an electrospray generating 75 nA at 100 nL∕min. The applied voltage and the emitter to counterelectrode distance follow the trend V∼ln d implied by formula 1 for constant electric field. At each distance, the voltage difference required to maintain the same spray current at the two pressures was ΔV=60±5 V. Assuming that the drop in pressure is balanced by a corresponding decrease in electrical pressure, the equation p₂−p₁=Δp_E can be solved to estimate r=0.66 μm, a value larger but of the same magnitude as r^*. The description based on a liquid interface in equilibrium suggests a linear dependence between the applied voltage and the square root of the pressure inside the vacuum chamber $V\sim p_0^{1∕2}$. However, the assumption of equilibrium is simplistic; the forces acting on the pulsating meniscus induce large accelerations during the pulsation cycle.

Figure 1.

Voltage required to maintain an electrospray current of 75 nA at 100 nL∕min as a function of distance between emitter and counterelectrode. Distance and voltage values normalized with critical radius r^* and critical voltage [γr^*∕ε₀]^1∕2, respectively.

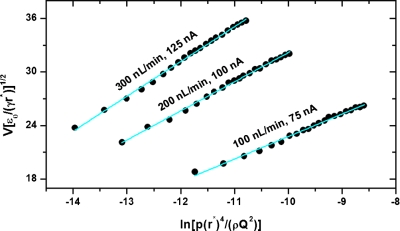
Figure 2 shows the dependence of the pressure on the applied voltage required to maintain spray currents of 75, 100, and 125 nA at flow rates of 100, 200, and 300 nL∕min, respectively. Similar data were obtained at 200 nL∕min with the electrospray current maintained at 75, 100, and 125 nA (data not shown). At 200 nL∕min, the electrospray generating 100 nA operates close to the middle of the voltage domain providing linear dependence between current and applied voltage. The linearity between the electrospray current and the applied voltage was tested throughout the entire pressure domain studied. The slope of the spray voltage-current characteristic curves increased from 0.19 nA∕V at pressures greater than 400 torr to 0.25 nA∕V at 30 torr (data not shown).

Figure 2.

Effect of pressure on the applied voltage at several liquid flow rates. Pressure values normalized with critical dynamic pressure ρQ²∕(r^*)⁴.

Sudden termination of the spray at pressures exceeding 50 torr was rare; however, maintaining long-term electrospray operation at lower pressures proved increasingly challenging. We conducted experiments at pressures as low as 30 torr where the electrospray failure rate increased significantly. The vapor pressure of the liquid appears to set this physical limitation; the liquid starts boiling when the pressure inside the chamber reaches its vapor pressure, making electrospray operation problematic. The vapor pressure p_v∼45 torr at 25 °C can be estimated for the water:acetonitrile binary mixture based on the vapor pressures of the pure liquids.³⁴ Liquid at room temperature is continuously supplied to the emitter tip; however, the temperature at the liquid interface is expected to be lower due to the heat exchange accompanying solvent evaporation. The dynamic nature of the meniscus and unknown gas flow patterns make it difficult to estimate the interface temperature based on mass and heat transfer equations. An upper limit of 18 °C was calculated based on the p_v=f(T) dependence when the liquid vapor pressure was estimated at 30 torr. Neglecting the heat exchange with the gas, energy conservation considerations imply that the percentage of liquid evaporation is Δm∕m=cΔT∕ΔH, where the symbols stand for the change in liquid mass due to evaporation (Δm), total liquid mass (m), specific heat (c), the temperature change (ΔT), and the evaporation enthalpy (ΔH). By using the specific heat (91.46 J∕mol K) and the evaporation enthalpy (33.25 kJ∕mol) of acetonitrile (which is more volatile than water), we estimate an evaporation rate of less than 2% for a 7 °C temperature drop.

The data in Fig. 2 suggests a linear dependence (R²>0.99) between the logarithm of the pressure inside the vacuum chamber and the voltage required to maintain a given spray current. Assuming that the current emitted by the electrospray is a good indicator of the electric field established at the liquid meniscus, the scaling law E∼V∕ln(p₀) emerges, which amends formula 1 when used to calculate the electric field at the tip of a rounded liquid meniscus. The underlying physics behind this scaling law is not clear yet, but we shall further discuss several factors (e.g., solvent evaporation, surface tension, surface fluctuations) that may affect the dynamics of the electrified liquid meniscus as the pressure in the vacuum chamber approaches the liquid vapor pressure.

Liquid evaporation is driven by solvent molecules that have sufficient translational energy to overcome their noncovalent interactions in the condensed phase. Many molecules lose their energy due to gas-phase collisions and return into the liquid phase, establishing equilibria between the gaseous and liquid phase species. If the vapor species are continuously removed—as in the case of our experiments—molecules with significant translational energy have statistically more chances to evaporate when the pressure decreases. Increased evaporation rate leads to lower effective electrospray flow rates, which generate smaller currents at the same voltage.²⁹ To provide the same current at lower pressures, the voltage should increase—a trend opposing that observed experimentally. Based on the I∼Q^1∕2 scaling law,³³ the current should decrease by less than 1% for a 2% evaporation rate; to offset this current drop the voltage applied to an electrospray generating 100 nA at 200 nL∕min needs to increase by 4–5 V, depending on the chamber pressure.

The surface tension describes the forces acting on the liquid molecules at the gas-liquid interface. The interaction between the liquid molecules and gas molecules weakens as the gas pressure decreases, leading to increased surface tension.³⁵To counteract the larger surface tension, the voltage should also increase to maintain the same current, another trend opposing experimental observations. However, as the pressure drops, a larger number of liquid molecules possess sufficient translational energy to leave the liquid phase, increasingly undermining the structure of the interface. Increased surface tension and smaller numbers of gas molecules have opposing effects on the amplitude of surface fluctuations. This phenomenon may be the result of increasing surface fluctuations as the pressure approaches the vapor pressure of the liquid.

The validity of the E∼V∕ln(p₀) scaling law is clearly dependent on the validity of the assumption that similar electrospray currents reflect similar electric fields established at the liquid meniscus. While we cannot provide irrefutable evidence in support of this assumption, we point out that the generation of similar electrospray currents likely implies similar charge density along the liquid meniscus, which is strongly related to the electric field. In the context of the previous research that initially revealed formula 1,^{2, 3} the linearity between V and ln d demonstrated by Fig. 1 may also suggest that the electrospray current is a good indicator of the field established at the liquid meniscus.

The E∼V∕ln(p₀) scaling law and the limitations imposed by the solvent vapor pressure will aid the optimization of the next generation of electrospray-based ion sources,¹⁸ which promise to eliminate the losses and biases associated with conventional mass spectrometer interfaces.