Abstract
The majority of intramammary infections with Escherichia coli in dairy cows result in transient infections with duration of about 10 days or less, although more persistent infections (2 months or longer) have been identified. We apply a mathematical model to explore the role of an intracellular mammary epithelial cell reservoir in the dynamics of infection. We included biological knowledge of the bovine immune response and known characteristics of the bacterial population in both transient and persistent infections. The results indicate that varying the survival duration of the intracellular reservoir reproduces the data for both transient and persistent infections. Survival in an intracellular reservoir is the most likely mechanism that ensures persistence of E. coli infections in mammary glands. Knowledge of the pathogenesis of persistent infections is essential to develop preventive and treatment programmes for these important infections in dairy cows.
Keywords: mathematical model, mastitis, Escherichia coli, persistent infection
1. INTRODUCTION
Mastitis is one of the most important production and welfare diseases affecting dairy cows. In recent decades, coliform infections have been identified in an ever increasing proportion of mastitis cases [22]. Among the coliform bacteria Escherichia coli is the dominant pathogenic species in dairy cow mastitis [5, 26]. The typical infection pattern for E. coli intramammary infection includes a clinically severe inflammatory response by the host with outcomes of either elimination of coliforms within 96 h of the initial infection [20, 23] or a deleterious outcome for the host including shock, sepsis and often death [8, 9]. In addition to severe disease several authors have reported persistent and clinically less severe E. coli infection [11, 12, 15].
Persistent E. coli infections are not uncommon in other organs or species. In particular, persistent infections of the human female urinary tract are often observed, and have inspired research into the pathogenesis of persistent E. coli infections [1, 6, 7, 14, 16, 21]. There is still debate about the precise mechanisms involved with persistent urinary tract infections, but it is clear that fimbriae that enable adhesion to bladder epithelial cells [6] and subsequent invasion of bladder epithelial cells, together with prolonged intracellular survival of the bacteria play an important role in persistence of infection [1]. A number of similarities between persistent urinary tract and persistent intramammary E. coli infections have been noted [11].
Recent studies on bovine infection patterns and immune response mechanisms have identified complex patterns of innate and adaptive immune mechanisms [2, 3] after intramammary challenge with E. coli and other mastitis – causing pathogens. Lipopolysacharides (LPS) in the bacterial cell wall are recognized by host cell receptors (such as Toll-like receptor-4) on macrophages that circulate in milk. The recognition of LPS by the host cell receptors leads to a cascade of events and eventually to an increased production of pro-inflammatory cytokines [2, 3]. These cytokines have, amongst other characteristics, a chemotactic effect on polymorphonuclear cells (PMN) in the bloodstream, which are, consequently, attracted into the mammary gland towards the site of infection where they attempt to phagocytise and kill the bacterial invaders [9, 23]. The outcome of the bacterial invasion into the mammary gland is eventually determined by the host response and the ability of the bacterial pathogen to circumvent or evade this host response [9, 20]. One of the mechanisms that bacterial pathogens employ to persist in the host is the creation of an intracellular niche [6], the importance of this in E. coli mastitis has not yet been established.
Mathematical modelling may be valuable in providing insight into the mechanisms of persistent infections, both at the population level [28] and the individual animal level [10, 17]. The model described by Detilleux et al. [10] models transient infections and includes the compartments: milk, blood leukocytes and bacteria in milk. This simple model was fitted to transient infection data, but it does not adequately describe the complex pathogenesis of bacterial infections that is essential to reproduce the dynamics of both transient and persistent intramammary infections.
In this study, we aim to improve understanding of the pathogenesis of transient and persistent intramammary E. coli infections. In particular, we are interested in understanding the processes that underlie the divergence in E. coli infection outcome (elimination or persistence): why do a majority of intramammary E. coli infections results in transient infections and how do other E. coli intramammary infections result in persistent infections?
2. MATERIALS AND METHODS
2.1. The model
We model the interaction between the bovine immune system and numbers of E. coli in milk and in intracellular reservoirs in a quarter (1 of the 4 compartments of the bovine mammary gland). We assume that the total number of colony forming units (cfu) of E. coli in milk (E) grows exponentially, but the bacteria are phagocytised and killed by macrophages and PMN [18]. Bacteria can move between milk and an intracellular mammary epithelial cell reservoir (I) [11]. From numerous challenge infections it is known that production of pro-inflammatory cytokines (C +) is stimulated by contact between bacteria and immune cells, either macrophages (M) or PMN (P) [4]. The production of pro-inflammatory cytokines is inhibited by the presence of anti-inflammatory or inhibitory cytokines (C −), which increase at a rate dependent on the concentration of pro-inflammatory cytokines, thus there is a negative feedback loop [2–4]. The macrophages present in the milk are assumed to remain at a constant concentration, whereas the concentration of PMN increases at a rate dependent on the concentration of pro-inflammatory cytokines present in the milk [23].
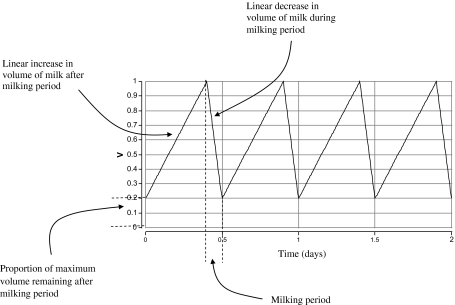
An additional process that determines the bacterial dynamics is the twice daily process of milking which rapidly depletes the volume of milk in the mammary gland, and so changes the population size of the bacterial cells. We assume a time dependent function, V, that defines the linearly changing volume of milk in the quarter (Fig. 1).
Figure 1.
Annotated functional form (not to scale during milking periods) of the milk volume before, during and after milking.
This simplified description of inflammatory dynamics leads to the following series of differential equations for the concentrations of cytokines (C + and C −), and the numbers of PMN (P) and E. coli cfu (E) in milk (which decreases due to milking, see Appendix for derivation) and intracellular E. coli (I):
| (1) |
In all equations, t represents time in days. The initial values of these variables were set to 0, except for E, which had a low initial infection level of 1 cfu/mL (or 250 cfu in total immediately after milking) representing initial invasion. The baseline level for M was set at 5 000 and P was set at 25% of 50 000 (see below). The parameters are defined in Table I and discussed in more detail below.
Table I.
Model parameter definitions, initial values and model estimates.
| Symbol | Definition | Initial value | Estimated value | Units |
|---|---|---|---|---|
| Parameters with the same value for all cows | ||||
| gcp | Baseline growth rate of pro-inflammatory cytokines in absence of anti-inflammatory cytokines. Stimulated by contact between E. coli and macrophages | Unknown | 0.0024 | day−1 |
| icp | Inhibitory effect of anti-inflammatory cytokines on growth of pro-inflammatory cytokines | Unknown | 0.035 | none |
| gca | Rate of growth of anti-inflammatory cytokines (dependent on concentration of pro-inflammatory cytokines) | Unknown | 9.8e-5 | |
| ge | Growth rate of E. coli in milk | 25.8–46.1 | 34 | day−1 |
| dp | Rate of loss of PMN from milk | 0.1–1.8 | 0.10 | day−1 |
| dc | Rate of loss of cytokines | 0.7–17 | 10 | day−1 |
| M | Baseline number of macrophages in milk | 5 000 (fixed) | Cells/mL | |
| Vmax | Maximum volume of milk in a quarter | 2.5 (fixed) | Litre | |
| Dmilk | Duration of milking | 5/(60 × 24) (fixed) | Day | |
| pmilk | Proportion of milk remaining after milking | 0.1 (fixed) | None | |
| k | Killing rate by macrophages (M and P) | 3.6e-6–4.8e-6 | 1.0e-5 | Cell/day |
| σE | Mean standard deviation of the model fit from the data for log E. coli concentration | Unknown | 0.54 | log cells/mL |
| σS | Mean standard deviation of the model fit from the data for log somatic cell concentration | Unknown | 0.75 | log cells/mL |
| Parameters that have a different value for each type of infection (transient, persistent) | ||||
| a | Rate of movement of E. coli from milk to intra-cellular reservoirs | Unknown | 0.51 (transient) 5.1 (persistent) | day−1 |
| b | Rate of movement of E. coli from intra-cellular reservoirs to milk | Unknown | 0.55 (transient) 7.5e-3 (persistent) | day−1 |
| Parameters that have a different value for each individual cow | ||||
| di | Death rate of E. coli in intra-cellular reservoirs | ~ 1 (transient) ~ 0.1 (persistent) | 2.1, 0.9, 1.4, 1.2, 1.4, 1.8, 1.9 (transient)0.1 (persistent) | day−1 |
| gp | Rate of influx of PMN into the milk in presence of pro-inflammatory cytokines | Unknown | 0.02, 0.04, 0.02, 0.03, 0.03, 0.50, 2.0, 0.8, 6.0, 2.0, 0.3 | day−1 |
To explore fadeout of the bacterial population, the model equations for the bacterial populations (E and I) were discretised using the Euler approximation with an interval, dt, of 1 s. The equations for the concentrations of immune cells and cytokines remained deterministic and continuous. Thus producing a stochastic version of the bacterial population section of the model as follows:
| (2) |
where Θ[x] is sampled from a Poisson distribution of mean x. The Poisson distribution is a discrete distribution and expresses the probability of a number of events (of the type that occur with a known average rate and independently of the time since the previous event) occurring in a fixed period of time. An event in this case is defined as a change in the population size due to growth, killing or milking. This distribution therefore appears to be the most appropriate for this system.
2.2. Biological data
2.2.1. Differential cell counts in milk
Basic milk somatic cell counts (SCC) at the time of initial infection were estimated using data from healthy non-infected quarters [13]. Differential milk leukocyte counts for healthy cows (n = 21) with low SCC milk (SCC < 200 000 cells/mL, [25]) in early lactation (22 ± 4 d after calving), mid lactation (185 ± 6 d after calving) and late lactation (245 ± 12 d after calving) were used [12]. Approximately 10% of all somatic cells in a healthy quarter are macrophages and 25% PMN. If we assume 50 000 cells/mL in a healthy quarter [24], then cells/mL and approximately 25% would be PMN.
Washout of cells and bacteria due to milking is estimated at about 90% (see also [10]). With a milk yield of 2.5 kg per quarter (i.e. V max = 2 500 mL) and acceptable milk withhold of 0.25 kg at the end of milking, it is reasonable to assume that 90% of cells and bacteria are removed at each milking (i.e. p milk = 0.1).
2.2.2. Killing capacity of PMN
No direct data on bacterial killing were available for bovine intramammary PMN or macrophages. To obtain a quantitative estimate of killing capacity we utilized data from a mouse model of E. coli infection published by Iwahi and Imada [16], in which the susceptibility of E. coli to killing by murine peritoneal exudate PMN was evaluated. A 0.05-mL volume of bacterial suspension (2 × 107 to 8 × 107 cfu/mL) was mixed with 0.25 mL of PMN suspension (6 × 106 to 8 × 106 cells/mL). A killing rate of approximately 1 log per hour was observed, with a decreasing rate of killing over time. This estimate was very similar to an estimate used by Detilleux et al. [10]. This corresponds to an estimate of k between 4.8 × 10−6 and 3.6 × 10−6 cell/day (See Appendix for the derivation of these values).
2.2.3. Growth of E. coli in vitro and in vivo
Data on growth of E. coli both in vitro and in vivo were taken from experiments by Kornalijnslijper et al. [18, 19], in which 200 μL of bacterial suspension (aiming at an inoculum of 100 cfu) was added to 10 mL whole milk. Bacterial counts in whole milk after 6 h of incubation varied up to a 100-fold between individual cows (3.8–6.0 log10 cfu/mL) [18]. This corresponds to a value of g e between 25.8 and 46.1 day−1 (See Appendix for the derivation of these values).
2.2.4. Cytokine dynamics
Data on cytokine dynamics during E. coli infection were taken from Bannerman et al. [2, 4]. In this study, cows were challenged with approximately 72 cfu of E. coli. Sterile milk samples were collected from all quarters at 0, 8, 16, 24, 32, 40 and 48 h after challenge and evaluated for cytokine profiles, cfu and SCC. An ELISA assay was used to measure the concentrations of IL-8 and TNF-α in milk obtained from quarters infused with E. coli, and saline controls. As expected, pro-inflammatory cytokines increased rapidly after intramammary challenge [2–4]. An increase was observed at 8 h after challenge and the concentration peaked at 16 h after challenge. Pro-inflammatory cytokine concentrations then dropped and reached baseline values between 32 and 48 h after challenge. Inhibitory cytokines (IL-10) showed a rapid increase at 16 h post-challenge (at the peak of pro-inflammatory cytokines) and peaked at 24 h post-challenge. Thereafter the concentration dropped and fell back to baseline at 72 h after challenge [2]. No data were available in peer-reviewed publications for cytokine profiles in persistent E. coli infections. However, a similar study using a Klebsiella challenge provides some insight in cytokine dynamics in more persistent gram-negative infections [3]. The model output was considered with reference to this general behavior and timescale. Cytokines have a half-life (T) of between 1 and 24 h [4]. Thus the rate of loss, d c is given by . Then d c is between 0.69 and 17, which are the upper and lower limits used for estimation of this parameter.
2.2.5. Intracellular E. coli
Data on intracellular survival of E. coli were taken from an in vitro study [11] in which E. coli strains from transient and persistent field infections were compared in adhesion and invasion assays. MAC-T cells were infected at a multiplicity of infection of 10 (10 bacteria per epithelial cell) for 1 h. The E. coli strains associated with persistent infections were 10 times more invasive than strains associated with transient infections. This translates to the constraint of the value for the parameter, a, for chronic infections being 10 times its value for acute infections.
Intracellular survival of E. coli strains in MAC-T cells was studied by gentamycin protection assays. MAC-T cells were infected with E. coli strains for 1 h, after which extracellular bacteria were killed by exposure to gentamycin (100 μg/mL), an extracellular antibiotic, for 2 h. MAC-T cells were incubated for a further 2, 24 and 48 h. The number of intracellular bacteria surviving was determined by disrupting the cell wall and plating and counting cfu. Strains of E. coli from transient infections showed a decrease of the number of viable bacteria to approximately 80% of the initial concentration after 48 h. In contrast, the number of cfu for persistent strains had almost doubled during the same time period (180% of baseline). These findings are in concordance with similar observations in mouse urinary tract epithelial cells [1, 21]. We use an initial value of d i = 0.1 day−1 for chronic infections. This is equivalent to intracellular survival for an average of 10 days [21]. To be conservative with regard to the importance of the intracellular reservoir we initially assumed no growth in the intracellular reservoir.
2.2.6. E. coli infection data
E. coli intramammary challenge longitudinal infection data used in this modelling study were gathered from several published [11, 12, 19, 27] and unpublished studies1. We identified a total of 7 transient infections (cow numbers: 218, 4 003, 4 310, 7 036, 9 658, 2 058 and 2 109, all from Kornalijnslijper et al. [18] and VanWerven et al. [27]) and 4 persistent infections (cow numbers: 171 103 (from Dogan et al. [11]), 3a, 3b and 3c (from Döpfer et al. [12]). All data used for simulations are summarized in Tables II and III.
Table II.
Data for seven transient infections. Cows 218, 4 003, 4 310, 7 036, 9 658, 2 058, and 2 109 are from Van Werven et al. [27]. Time is in days, lg(E) is log10 E. coli cfu/mL, lg(S) is log10 SCC/mL.
| Time (days) | Cow number |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 218 |
4 003 |
4 310 |
7 036 |
9 658 |
2 058 |
2 109 |
||||||||
| Lg(E) | Lg(S) | Lg(E) | Lg(S) | Lg(E) | Lg(S) | Lg(E) | Lg(S) | Lg(E) | Lg(S) | Lg(E) | Lg(S) | Lg(E) | Lg(S) | |
| 0 | 0 | 5.0 | 0 | 4.4 | 0 | 4.0 | 0 | 4.0 | 0 | 4.4 | 0 | 4.0 | 0 | 5.4 |
| 1 | 9.0 | 7.0 | 5.9 | 7.0 | 7.7 | 6.9 | 8.7 | 5.6 | 8.6 | 6.7 | 5.3 | 7.0 | 3.7 | 6.3 |
| 2 | 5.2 | 7.0 | 6.5 | 7.0 | 6.2 | 7.0 | 6.4 | 7.0 | 4.9 | 7.0 | 2.4 | 7.0 | 0 | 7.0 |
| 3 | 4.1 | 7.0 | 6.0 | 7.0 | 5.0 | 7.0 | 5.4 | 7.0 | 4.9 | 7.0 | 2.4 | 7.0 | 0 | 6.9 |
| 4 | 3.6 | 7.0 | 5.7 | 5.5 | 5.1 | 6.9 | 5.5 | 6.8 | 4.5 | 6.5 | 2.2 | 6.8 | 0 | 6.4 |
| 5 | 2.9 | 7.0 | 5.0 | 6.8 | 4.5 | 7.0 | 4.5 | 7.0 | 4.2 | 6.8 | 0 | 7.0 | 0 | 6.3 |
| 6 | 3.2 | 7.0 | 4.9 | 6.4 | 3.3 | 7.0 | 3.9 | 7.0 | 3.7 | 6.8 | 0 | 7.1 | 0 | 7.0 |
| 7 | 0 | 7.0 | 4.0 | 6.2 | 3.0 | 7.0 | 2.3 | 7.0 | 3.1 | 7.0 | 0 | 6.6 | 0 | 6.3 |
| 8 | 0 | 7.0 | 3.4 | 7.0 | 2.4 | 7.0 | 2.3 | 7.0 | 3.4 | 7.0 | 0 | 6.4 | 0 | 5.8 |
| 9 | 0 | 7.0 | 3.1 | 7.0 | 2.3 | 7.0 | 1.7 | 7.0 | 2.9 | 7.0 | 0 | 6.2 | 0 | 6.0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||
Table III.
Data for four persistent infections. Cow 171 103 is from Dogan et al. [11] and cows 3a, 3b and 3c are from Dopfer et al. [12]. Time is in days, lg(E) is 10 log E. coli cfu/mL, lg(S) is 10 log SCC/mL.
| Time (days) | Cow number |
|||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 171 103 |
Time (days) | 3a |
Time (days) | 3b |
Time (days) | 3c |
||||||||||||||||||||
| lg(E) | lg(S) | days | lg(E) | lg(S) | lg(E) | lg(S) | days | lg(E) | lg(S) | lg(E) | lg(S) | days | lg(E) | lg(S) | lg(E) | lg(S) | days | lg(E) | lg(S) | |||||||
| 0 | 4.3 | 41 | 3.9 | 7.1 | 0 | 3.5 | 6.7 | 41 | 3.6 | 6.4 | 0 | 2.0 | 6.7 | 41 | 3.6 | 6.9 | 0 | 3.0 | 6.8 | 41 | 2.0 | 5.7 | ||||
| 1 | 5.5 | 42 | 2.0 | 7.1 | 1 | 3.8 | 6.6 | 42 | 3.4 | 6.2 | 1 | 2.8 | 6.6 | 42 | 2.6 | 6.8 | 1 | 2.0 | 6.6 | 42 | 2.0 | 6.5 | ||||
| 2 | 3.5 | 43 | 1.9 | 6.7 | 2 | 4.2 | 6.5 | 43 | 3.8 | 6.1 | 2 | 2.3 | 6.8 | 43 | 3.2 | 6.6 | 2 | 0 | 6.4 | 43 | 0 | 6.1 | ||||
| 3 | 3.0 | 44 | 2.8 | 7.2 | 3 | 3.5 | 6.2 | 44 | 3.1 | 6.9 | 3 | 2.5 | 6.8 | 44 | 3.4 | 6.8 | 3 | 0 | 6.1 | 44 | 2.3 | 5.8 | ||||
| 4 | 3.1 | 45 | 3.2 | 7.0 | 4 | 4.1 | 6.8 | 45 | 3.3 | 7.0 | 4 | 2.5 | 6.6 | 45 | 3.3 | 6.7 | 4 | 0 | 5.6 | 45 | 2.0 | 5.4 | ||||
| 5 | 5.8 | 46 | 3.3 | 7.3 | 5 | 2.9 | 6.8 | 46 | 3.6 | 6.6 | 5 | 3.5 | 6.9 | 46 | 2.4 | 6.8 | 5 | 2.0 | 5.5 | 46 | 2.3 | 5.5 | ||||
| 6 | 4.3 | 47 | 3.7 | 7.1 | 6 | 2.9 | 6.7 | 47 | 3.6 | 6.5 | 6 | 3.3 | 7.0 | 47 | 2.5 | 6.8 | 6 | 2.5 | 5.5 | 47 | 3.1 | 7.0 | ||||
| 7 | 4.7 | 48 | 4.8 | 7.3 | 7 | 2.0 | 6.5 | 48 | 4.5 | 6.5 | 7 | 3.5 | 6.8 | 48 | 2.6 | 6.6 | 7 | 0 | 6.3 | 48 | 2.3 | 6.7 | ||||
| 8 | 3.9 | 49 | 4.3 | 5.2 | 8 | 2.0 | 6.7 | 49 | 3.3 | 6.5 | 8 | 3.2 | 6.8 | 49 | 2.7 | 6.4 | 8 | 2.0 | 6.2 | 49 | 2.3 | 6.6 | ||||
| 9 | 3.9 | 50 | 4.4 | 5.5 | 9 | 2.0 | 6.3 | 50 | 3.3 | 6.3 | 9 | 2.4 | 6.7 | 50 | 6.3 | 9 | 2.0 | 6.4 | 50 | 2.3 | 6.5 | |||||
| 10 | 4.4 | 51 | 4.3 | 7.4 | 10 | 3.1 | 6.7 | 51 | 3.4 | 6.4 | 10 | 2.3 | 6.7 | 51 | 3.4 | 6.4 | 10 | 0 | 6.1 | 51 | 3.3 | 6.2 | ||||
| 11 | 4.5 | 52 | 4.7 | 7.4 | 11 | 2.3 | 6.7 | 52 | 3.3 | 6.4 | 11 | 2.2 | 6.7 | 52 | 3.3 | 6.4 | 11 | 2.0 | 5.8 | 52 | 0 | 6.4 | ||||
| 12 | 4.2 | 53 | 5.2 | 7.4 | 12 | 2.0 | 6.7 | 53 | 4.0 | 6.1 | 12 | 2.2 | 6.5 | 53 | 4.0 | 6.1 | 12 | 2.3 | 6.2 | 53 | 2.0 | 5.9 | ||||
| 13 | 4.7 | 54 | 5.4 | 7.0 | 13 | 3.3 | 6.5 | 54 | 3.8 | 6.1 | 13 | 2.1 | 6.5 | 54 | 3.8 | 6.1 | 13 | 0 | 5.9 | 54 | 0 | 5.7 | ||||
| 14 | 4.0 | 55 | 5.4 | 7.0 | 14 | 3.2 | 6.7 | 55 | 3.3 | 6.9 | 14 | 2.1 | 6.3 | 55 | 3.3 | 6.9 | 14 | 2.3 | 5.7 | 55 | 2.6 | 6.9 | ||||
| 15 | 3.9 | 5.2 | 56 | 5.5 | 7.0 | 15 | 2.8 | 6.7 | 56 | 4.0 | 6.8 | 15 | 2.0 | 6.0 | 56 | 4.0 | 6.8 | 15 | 0 | 6.2 | 56 | 0.0 | 6.6 | |||
| 16 | 4.1 | 7.3 | 57 | 3.2 | 7.2 | 16 | 2.5 | 6.6 | 57 | 3.4 | 6.6 | 16 | 2.0 | 6.1 | 57 | 3.4 | 6.6 | 16 | 2.0 | 5.3 | 57 | 2.3 | 6.3 | |||
| 17 | 3.0 | 7.0 | 58 | 2.3 | 6.6 | 17 | 4.3 | 6.4 | 58 | 3.7 | 6.1 | 17 | 2.5 | 6.7 | 58 | 3.7 | 6.1 | 17 | 0 | 5.4 | 58 | 2.0 | 6.4 | |||
| 18 | 3.0 | 5.9 | 59 | 2.6 | 6.7 | 18 | 2.8 | 6.7 | 59 | 4.0 | 6.2 | 18 | 4.2 | 6.9 | 59 | 4.0 | 6.2 | 18 | 2.3 | 5.8 | 59 | 0 | 6.0 | |||
| 19 | 3.6 | 7.4 | 60 | 2.9 | 6.9 | 19 | 2.0 | 6.7 | 60 | 4.1 | 6.3 | 19 | 4.4 | 6.8 | 60 | 4.1 | 6.3 | 19 | 0 | 6.4 | 60 | 0 | 5.9 | |||
| 20 | 3.7 | 7.4 | 61 | 1.8 | 7.2 | 20 | 2.8 | 6.5 | 61 | 3.5 | 6.5 | 20 | 4.7 | 6.8 | 61 | 3.5 | 6.5 | 20 | 2.0 | 6.1 | 61 | 0 | 5.5 | |||
| 21 | 4.1 | 7.5 | 62 | 3.1 | 7.4 | 21 | 3.2 | 6.7 | 62 | 4.1 | 6.6 | 21 | 3.9 | 7.0 | 62 | 4.1 | 6.6 | 21 | 2.0 | 5.9 | 62 | 2.7 | 5.5 | |||
| 22 | 2.4 | 7.2 | 63 | 3.5 | 7.2 | 22 | 3.6 | 6.5 | 63 | 4.0 | 6.4 | 22 | 3.6 | 7.0 | 63 | 4.0 | 6.4 | 22 | 2.3 | 6.5 | 63 | 2.0 | 6.7 | |||
| 23 | 1.9 | 6.9 | 64 | 2.1 | 7.0 | 23 | 3.5 | 6.3 | 64 | 4.4 | 6.1 | 23 | 4.1 | 6.7 | 64 | 4.4 | 6.1 | 23 | 2.0 | 6.3 | 64 | 2.0 | 6.3 | |||
| 24 | 2.3 | 7.1 | 65 | 2.0 | 6.4 | 24 | 3.4 | 6.8 | 65 | 4.5 | 6.5 | 24 | 4.4 | 7.0 | 65 | 4.5 | 6.5 | 24 | 2.5 | 6.4 | 65 | 2.0 | 6.0 | |||
| 25 | 1.3 | 7.1 | 66 | 3.5 | 7.3 | 25 | 2.6 | 7.0 | 66 | 3.9 | 6.5 | 25 | 3.5 | 6.7 | 66 | 3.9 | 6.5 | 25 | 0 | 6.3 | 66 | 2.5 | 6.5 | |||
| 26 | 2.4 | 6.6 | 67 | 2.6 | 7.2 | 26 | 3.7 | 6.9 | 67 | 3.8 | 6.4 | 26 | 3.7 | 6.9 | 67 | 3.8 | 6.4 | 26 | 0 | 6.0 | 67 | 0 | 5.7 | |||
| 27 | 0.0 | 7.3 | 68 | 2.3 | 6.6 | 27 | 3.4 | 6.4 | 68 | 3.5 | 6.5 | 27 | 4.2 | 7.0 | 68 | 3.5 | 6.5 | 27 | 2.3 | 5.8 | 68 | 6.8 | ||||
| 28 | 0.0 | 6.9 | 69 | 3.1 | 7.2 | 28 | 3.7 | 7.0 | 69 | 3.4 | 6.4 | 28 | 4.2 | 6.8 | 69 | 3.4 | 6.4 | 28 | 2.3 | 5.9 | 69 | 3.4 | 6.6 | |||
| 29 | 2.5 | 7.0 | 70 | 2.4 | 6.7 | 29 | 3.1 | 7.0 | 70 | 3.3 | 6.2 | 29 | 3.1 | 6.8 | 70 | 3.3 | 6.2 | 29 | 2.0 | 5.7 | 70 | 3.7 | 6.1 | |||
| 30 | 2.7 | 6.2 | 71 | 2.4 | 7.1 | 30 | 2.3 | 6.6 | 71 | 3.9 | 6.1 | 30 | 2.0 | 6.7 | 71 | 3.9 | 6.1 | 30 | 2.9 | 5.8 | 71 | 4.0 | 6.2 | |||
| 31 | 2.0 | 4.1 | 72 | 2.5 | 6.9 | 31 | 2.9 | 6.5 | 72 | 4.1 | 5.9 | 31 | 2.5 | 6.7 | 72 | 4.1 | 5.9 | 31 | 2.0 | 6.5 | 72 | 4.1 | 6.3 | |||
| 32 | 2.5 | 7.1 | 73 | 1.3 | 6.6 | 32 | 3.6 | 6.1 | 32 | 2.9 | 6.4 | 32 | 2.0 | 6.1 | 73 | 3.5 | 6.5 | |||||||||
| 33 | 3.3 | 7.4 | 74 | 3.2 | 7.4 | 33 | 3.5 | 6.1 | 33 | 3.3 | 6.7 | 33 | 2.0 | 6.2 | 74 | 4.1 | 6.6 | |||||||||
| 34 | 3.1 | 7.2 | 75 | 2.5 | 7.2 | 34 | 3.4 | 6.7 | 34 | 2.0 | 6.6 | 34 | 2.7 | 6.0 | 75 | 4.0 | 6.4 | |||||||||
| 35 | 2.7 | 4.9 | 35 | 3.9 | 6.5 | 35 | 2.0 | 6.4 | 35 | 2.0 | 6.6 | 76 | 4.4 | 6.1 | ||||||||||||
| 36 | 3.6 | 6.4 | 36 | 3.8 | 6.4 | 36 | 3.2 | 6.6 | 36 | 2.0 | 6.1 | 77 | 4.5 | 6.5 | ||||||||||||
| 37 | 3.4 | 7.0 | 37 | 4.0 | 6.3 | 37 | 3.5 | 6.9 | 37 | 2.3 | 6.6 | 78 | 3.9 | 6.5 | ||||||||||||
| 38 | 3.9 | 7.0 | 38 | 4.0 | 6.6 | 38 | 3.5 | 6.9 | 38 | 2.5 | 6.4 | 79 | 3.8 | 6.4 | ||||||||||||
| 39 | 3.3 | 7.0 | 39 | 3.0 | 6.2 | 39 | 3.3 | 6.8 | 39 | 2.0 | 6.4 | 80 | 3.5 | 6.5 | ||||||||||||
| 40 | 3.5 | 7.1 | 40 | 3.4 | 6.5 | 40 | 3.6 | 6.8 | 40 | 2.0 | 6.1 | 81 | 3.4 | 6.4 | ||||||||||||
2.3. Parameter estimation
The model predictions for the logarithms of the E. coli and somatic cell concentrations generated using (1) were fitted to the data. The parameters were estimated within Berkeley-Madonna [28], by maximising likelihood assuming a normal distribution of error. The initial values for the parameter estimation process are given in Table I. We assume that if the dataset includes a zero value and the model predicts a value less than or equal to zero (that is less than or equal to 1 cell/mL), then this is the best fit for this point due to limits of detection. We also assume that the persistent infections had reached equilibrium when they were sampled.
3. RESULTS
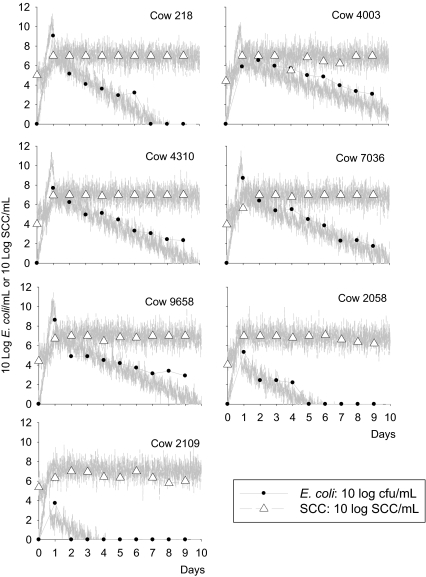
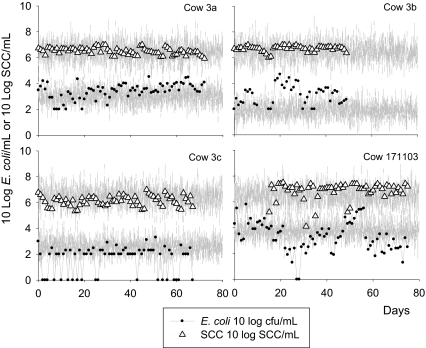
The model reproduced the data with the estimated parameter values as given in Table I. The optimised negative log-likelihood was 650.35. The model also reproduced both transient and persistent infection behaviour (see Figs. 2 and 3).
Figure 2.
Observed (points) and model predicted (lines) bacteria count and SCC data for seven cows with transient infections. Cow numbers are shown on the top-right of each graph. The model prediction is a single realisation of the stochastic version of the model including variation in measurement based on the standard deviations of the model fit to the data (σ E and σ S).
Figure 3.
Observed (points) and model predicted (lines) bacteria count and SCC data for four cows with a persistent infection. The model prediction is a single realisation of the stochastic version of the model including variation in measurement based on the standard deviations of the model fit to the data (σ E and σ S).
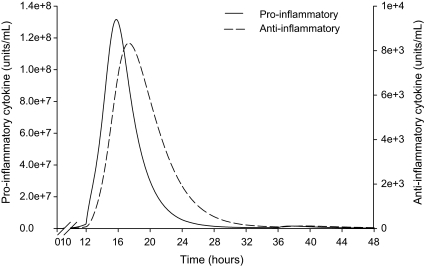
For all cows, the model consistently predicted a 3 h difference between the timing of the peak of pro- and anti-inflammatory cytokine concentrations. The model also predicted that the pro-inflammatory cytokines peak within the range of 13 to 22 h after infection for all cows and that the anti-inflammatory cytokines show a rapid increase that started just before the peak in pro-inflammatory cytokines. Figure 4 shows an example of this predicted behaviour for cow number 218. The sampling frequency of the experiment by Bannerman et al. [4] was every 8 h. Therefore from the data we can conclude that the delay between peaks should be between 4 and 12 h. The model predicts an approximate 3 h difference which is somewhat lower than the range predicted by experimental data. Thus, the model is qualitatively but not quantitatively capturing the cytokine dynamics and a more complex model of the mechanism would be required for a more precise quantitative prediction of this phenomenon.
Figure 4.
Dynamics of the concentrations of pro- and anti-inflammatory cytokines predicted by the model for cow number 218.
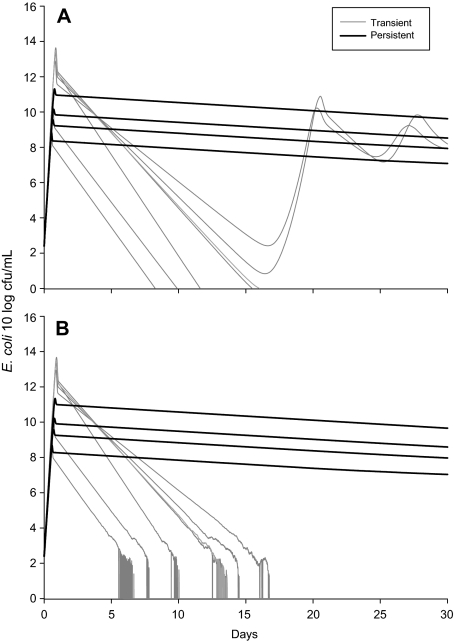
The key result from our model is the transition from transient to steady state dynamics for the two distinct types of infection. The output from the stochastic and deterministic versions of the model in Figure 5 is the model predictions for the total bacterial population in the milk and the intracellular reservoir combined. We use this output to demonstrate the potential for the animal to clear the infection due to very low numbers after the first 5 to 12 days. This would correspond with an observed clearance in 2 to 10 days since only the concentration in the milk was being observed in the experiment and so this value would drop below the detection limit (of about 1 cfu/mL) 2 or 3 days before true clearance by the animal. For transient infections, the number of bacteria drop below 10 cfu (not per mL but in the whole cow), whereas for the persistent infections the number of bacteria never drop below 106.5 cfu in the whole cow: with approximately 2 500 mL of milk in the gland (quarter) this would equate to approximately 4 × 103 cfu/mL for a persistently infected quarter (see Fig. 3).
Figure 5.
Predicted total numbers of E. coli cfu in the mammary gland and the intracellular reservoir combined for seven transient and four persistent infections from the deterministic (A) and stochastic (B) versions of the model.
This value of the nadir in E. coli bacterial numbers was highly sensitive to the assumed duration of survival of bacteria in the intracellular reservoir. This duration of survival has a threshold value for simulations of the stochastic model of about 1 day where below the threshold fadeout was most likely and above the threshold persistence was more likely. For these sets of models we assumed this duration to be approximately 10 days (an alternative estimate of 2 days was also considered with similar results) for persistent infections and estimated (by fitting) the duration to be about 0.8 days for transient infections.
The discretized stochastic model was run 1 000 times and fadeout in the transiently infected cows and no fadeout in the persistently infected cows was predicted for 996 out of 1 000 runs. In four runs one or more of the modelled transient infections did not fadeout. In 1 000 runs the modelled persistent infections did not fadeout. This result confirms the conclusion from the deterministic model that the nadir in E. coli bacterial numbers for transient infections after the initial acute phase will generally result in fadeout of the bacterial population and thus clearance of infection.
4. DISCUSSION
The mathematical model presented reproduces the observed dynamic behaviour of both transient and persistent infections. The predicted time-dependent behaviour of the pro- and anti-inflammatory cytokine concentrations is also consistent with our current biological knowledge.
We show that for parameter values suitable for transient infections, the model predicts that the total number of bacteria in the mammary gland drops to values at which spontaneous clearance of the infection is highly likely due to stochastic effects. The predicted minimum level of bacteria present is sensitive to changes in the duration of survival in the intracellular reservoir. Long durations of survival in the intracellular reservoir correspond with high bacteria counts in the nadir of cfu following the acute phase, indicating a failure to spontaneously clear the infection and thereby leading to a persistent infection. Hence, the key parameters distinguishing transient from persistent infections were the parameters a, b and d i (respectively the rates of movement of bacteria between the milk and the intra-cellular reservoir and the intracellular bacterial death rate). These three parameters were indeed different between transient and persistent infections when estimated from observed data (Tab. I).
Our parameter estimates were very similar to the estimates used by Detilleux et al. [10], although the current model is obviously more complex and needed additional input data. However, estimates of key parameters such as bacterial growth rate (1.40 per hour) and concentration reduction rate due to killing (240 × 10−6 μL/cell per hour) were very similar to previous simulation models [10] where the growth rate estimates ranged from 0.54 to 0.8 per hour and those for the killing rate ranged from 184 × 10−6 to 431 × 10−6 μL/cell per hour. Since both our model and previous models validated their estimates on actual observed data, this is not really surprising.
The purpose of this analysis was to propose the most likely explanation for why some E. coli infections persist in the mammary gland, whilst others do not. We propose that bacterial strains that result in persistent infections are more effective (by an order of magnitude) at surviving in an intra-cellular reservoir in mammary epithelial cells. This is consistent with a related E. coli survival mechanism where intracellular biofilm-like structures, called intracellular bacterial communities, were associated with persistent E. coli infections [7]. Other candidate explanations from the analysis are due to differences at the host response rather than the bacterial strain level [8, 23]. Namely that (a) persistent infections occur when there is a lower or delayed influx of PMN in the presence of pro-inflammatory cytokines [20, 27], or (b) persistent infections result from a short half-life and decreased functionality of PMN such as impaired phagocytosis and/or killing capacity [9, 23]. However, these alternative explanations are unlikely to be a general mechanism responsible for creating the observed patterns. In the case of low or delayed PMN influx, the model predicts unrealistically high numbers of E. coli during the transient infection dynamics. In the case of a short life expectancy of PMN, our model would require an unrealistically short half-life to be able to fit data for cows with a persistent intramammary infection. Also, there is good in vitro experimental evidence to suggest that E. coli strains present in persistent infections have different attributes from those present in transient infections [11], thereby suggesting that the difference in pathogenesis between transient and persistent infections is due to the type of bacteria rather than the type of response mounted by individual cows.
Although macrophages, PMN and lymphocytes will probably undergo some homing towards the supramammary lymphnodes [24], we did not include this behaviour in the model. We also ignored the potential impact of memory dependent immunity, since it is generally assumed that antibody mediated immune response mostly reduces clinical severity and has relatively little impact on the incidence of infection or the distinction between transient and persistent infection [29]. In future generations of our infection model, more components of the immune response may be added and evaluated for their importance. The hypothesis of a longer survival time in an intracellular epithelial reservoir, resulting in persistent rather than transient infections, appeared to be supported by the data and our current knowledge of the biology of these infections.
Acknowledgments
The Wellcome Trust-Mahidol University-Oxford Tropical Medicine Research Programme is funded by the Wellcome Trust of Great Britain. Y.H. Schukken and G.F. Medley acknowledge the support of the BBSRC (BBS/S/04854).
APPENDIX
Derivation of equation for E. coli
The variables are expressed as concentrations apart from bacterial load and PMN which is expressed in absolute numbers. We assume that milking does not alter the concentrations of any of these quantities and thus there is no loss term in the concentration formulae. However, milking will affect numbers of cells in the milk thus the following analysis was performed in order to predict total bacterial load. Let concentration of E. coli be X. Then the differential equation for concentration of E. coli is given by:
Then the total number, E, is given by:
Since the volume, V, also varies in time, the differential of E is derived using the product rule:
Thus combining the two previous equations gives the following formula for the rate of change of E. coli cfu in the milk:
then
where is the rate of change of the volume of milk.
The differential equation for the numbers of PMN in the milk is derived similarly.
Killing rate, k:
Given 0.25 mL of p (6 to 8) × 106 cells/mL PMN added to 0.05 mL of E. coli. solution. Then the number of PMN cells would be 0.25 p × 106 and the volume would be 0.25 + 0.05 = 0.3 mL. Thus the concentration, P, of the resulting solution is . Then, given a killing rate of k cell day−1, the concentration of E. coli over time, y, is given by the following:
Since a reduction of one log per hour is observed: t = 1/24, , In y 0 − ln y = 1 then , so for p = 6, k = 4.8 × 10−6 and for p = 8, k = 3.6 × 10−6.
Growth rate of bacteria in milk, g e:
Let x(t) = x 0 exp(g e t) where x is the concentration of E. coli over time, x 0 is the initial concentration and t is time, then
Then, the upper limit of g e is (6−1)/(0.25 log10 e) or equal to 46.1, and the lower limit of g e is (3.8−1)/(0.25 log10 e) or equal to 25.8.
Footnotes
Döpfer D., Ph.D. Thesis, Utrecht University, 2000.
References
- 1.Anderson G.G., Dodson K.W., Hooton T.M., Hultgren S.J., Intracellular bacterial communities of uropathogenic Escherichia coli in urinary tract pathogenesis, Trends Microbiol. (2004) 12:424–430 [DOI] [PubMed] [Google Scholar]
- 2.Bannerman D.D., Paape M.J., Lee J.W., Zhao X., Hope J.C., Rainard P., Escherichia coli and Staphylococcus aureus elicit differential innate immune responses following intramammary infection, Clin. Diagn. Lab. Immunol. (2004) 11:463–472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bannerman D.D., Paape M.J., Hare W.R., Hope J.C., Characterization of the bovine innate immune response to intramammary infection with Klebsiella pneumoniae, J. Dairy Sci. (2004) 87:2420–2432 [DOI] [PubMed] [Google Scholar]
- 4.Bannerman D.D., Pathogen-dependent induction of cytokines and other soluble inflammatory mediators during intramammary infection of dairy cows, J. Anim. Sci. (2008) 87:10–25 [DOI] [PubMed] [Google Scholar]
- 5.Barkema H.W., Schukken Y.H., Lam T.J.G.M., Beiboer M.L., Wilmink H., Benedictus G., Brand A., Incidence of clinical mastitis in dairy herds grouped in three categories by bulk milk somatic cell counts, J. Dairy Sci. (1998) 81:411–419 [DOI] [PubMed] [Google Scholar]
- 6.Bergsten G., Wullt B., Svanborg C., Escherichia coli, fimbriae, bacterial persistence and host response induction in the human urinary tract, Int. J. Med. Microbiol. (2005) 295:487–502 [DOI] [PubMed] [Google Scholar]
- 7.Berry R.E., Klumpp D.J., Schaeffer A.J., Urothelial cultures support intracellular bacterial community formation by uropathogenic Escherichia coli, Infect. Immun. (2009) 77:2762–2772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Burvenich C., Van Merris V., Mehrzad J., Diez-Fraile A., Duchateau L., Severity of E. coli mastitis is mainly determined by cow factors, Vet. Res. (2003) 34:521–564 [DOI] [PubMed] [Google Scholar]
- 9.Burvenich C., Monfardini E., Mehrzad J., Capuco A.V., Paape M.J., Role of neutrophil polymorphonuclear leukocytes during bovine coliform mastitis: physiology or pathology?, Verh. K. Acad. Geneeskd. Belg. (2004) 66:97–150 [PubMed] [Google Scholar]
- 10.Detilleux J., Vangroenweghe F., Burvenich C., Mathematical model of the acute inflammatory response to Escherichia coli in intramammary challenge, J. Dairy Sci. (2006) 89:3455–3465 [DOI] [PubMed] [Google Scholar]
- 11.Dogan B., Klaessig S., Rishniw M., Almeida R., Oliver S.P., Simpson K.W., Schukken Y.H., Adherent and Invasive Escherichia coli are associated with persistent bovine mastitis, Vet. Microbiol. (2006) 116:270–282 [DOI] [PubMed] [Google Scholar]
- 12.Döpfer D., Barkema H.W., Lam T.J.G.M., Schukken Y.H., Gaastra W., Recurrent clinical mastitis caused by Escherichia coli in dairy cows, J. Dairy Sci. (1999) 82:80–85 [DOI] [PubMed] [Google Scholar]
- 13.Dosogne H., Vangroenweghe F., Mehrzad J., Massart-Leen A.M., Burvenich C., Differential leukocyte count method for bovine low somatic cell count milk, J. Dairy Sci. (2003) 86:828–834 [DOI] [PubMed] [Google Scholar]
- 14.Franco A.V., Recurrent urinary tract infections, Best Pract. Res. Clin. Obstet. Gynaecol. (2005) 19:861–873 [DOI] [PubMed] [Google Scholar]
- 15.Green M.J., Green L.E., Medley G.F., Schukken Y.H., Bradley A.J., Influence of dry period bacterial intramammary infection on clinical mastitis in dairy cows, J. Dairy Sci. (2002) 85:2589–2599 [DOI] [PubMed] [Google Scholar]
- 16.Iwahi T., Imada A., Interaction of Escherichia coli with polymorphonuclear leukocytes in pathogenesis of urinary tract infection in mice, Infect. Immun. (1988) 56:947–953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kirschner D., Marino S., Mycobacterium tuberculosis as viewed through a computer, Trends Microbiol. (2005) 13:206–211 [DOI] [PubMed] [Google Scholar]
- 18.Kornalijnslijper J.E., van Werven T., Daemen A.J., van den Broek J., Niewold T.A., Rutten V.P., Noordhuizen-Stassen E.N., In vitro growth of mastitis-inducing Escherichia coli in milk and milk fractions of dairy cows, Vet. Microbiol. (2003) 91:125–134 [DOI] [PubMed] [Google Scholar]
- 19.Kornalijnslijper J.E., Daemen A.J., van Werven T., Niewold T.A., Rutten V.P., Noordhuizen-Stassen E.N., Bacterial growth during the early phase of infection determines the severity of experimental Escherichia coli mastitis in dairy cows, Vet. Microbiol. (2004) 101:177–186 [DOI] [PubMed] [Google Scholar]
- 20.Lohuis J.A., Schukken Y.H., Henricks P.A., Heyneman R., Burvenich C., Verheijden J.H., et al. , Preinfection functions of blood polymorphonuclear leukocytes and the outcome of experimental Escherichia coli mastitis in the cow, J. Dairy Sci. (1990) 73:342–350 [DOI] [PubMed] [Google Scholar]
- 21.Mulvey M.A., Schilling J.D., Hultgren S.J., Establishment of a persistent Escherichia coli reservoir during the acute phase of a bladder infection, Infect. Immun. (2001) 69:4572–4579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Olde Riekerink R.G., Barkema H.W., Kelton D.F., Scholl D.T., Incidence rate of clinical mastitis on Canadian dairy farms, J. Dairy Sci. (2008) 91:1366–1377 [DOI] [PubMed] [Google Scholar]
- 23.Paape M., Mehrzad J., Zhao X., Detilleux J., Burvenich C., Defense of the bovine mammary gland by polymorphonuclear neutrophil leukocytes, J. Mammary Gland. Biol. Neoplasia (2002) 7:109–121 [DOI] [PubMed] [Google Scholar]
- 24.Saad A.M., Ostensson K., Flow cytofluorometric studies on the alteration of leukocyte populations in blood and milk during endotoxin-induced mastitis in cows, Am. J. Vet. Res. (1990) 51:1603–1607 [PubMed] [Google Scholar]
- 25.Schepers A.J., Lam T.J., Schukken Y.H., Wilmink J.B., Hanekamp W.J., Estimation of variance components for somatic cell counts to determine thresholds for uninfected quarters, J. Dairy Sci. (1997) 80:1833–1840 [DOI] [PubMed] [Google Scholar]
- 26.Schukken Y.H., Grommers F.J., Vandegeer D., Brand A., Incidence of clinical mastitis on farms with low somatic-cell counts in bulk milk, Vet. Rec. (1989) 125:60–63 [DOI] [PubMed] [Google Scholar]
- 27.VanWerven T., NoordhuizenStassen E.N., Daemen A.J., Schukken Y.H., Brand A., Burvenich C., Preinfection in vitro chemotaxis, phagocytosis, oxidative burst, and expression of CD11/CD18 receptors and their predictive capacity on the outcome of mastitis induced in dairy cows with Escherichia coli , J. Dairy Sci. (1997) 80:67–74 [DOI] [PubMed] [Google Scholar]
- 28.Wearing H.J., Rohani P., Keeling M.J., Appropriate models for the management of infectious diseases, PLoS Med. (2005) 2:e174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wilson D.J., Grohn Y.T., Bennett G.J., González R.N., Schukken Y.H., Spatz J., Comparison of J5 vaccinates and controls for incidence, etiologic agent, clinical severity, and survival in the herd following naturally occurring cases of clinical mastitis, J. Dairy Sci. (2007) 90:4282–4288 [DOI] [PubMed] [Google Scholar]