Forward Dynamics Simulations Provide insight into Muscle Mechanical Work during Human Locomotion

Abstract

Complex musculoskeletal models and computer simulations can provide critical insight into muscle mechanical work output during locomotion. Simulations provide both a consistent mechanical solution that can be interrogated at multiple levels (muscle fiber, musculotendon, net joint moment and whole body work) and an ideal framework to identify limitations with different estimates of muscle work and the resulting implications for metabolic cost and efficiency.

INTRODUCTION

Complex musculoskeletal models and computer simulations are becoming an integral part of analyzing human movement over a wide range of topics, from understanding fundamental muscle coordination principles (e.g., (35)) to identifying potential injury mechanisms (e.g., (26)). Muscle-actuated forward dynamics simulations are particularly powerful because they allow for the identification of causal relationships between the neural control inputs, muscle force and power output, and the task performance (see (35) for review). Understanding these relationships without simulation analsyes is challenging because of the highly complex and nonlinear nature of the musculoskeletal system, with its corresponding dynamic coupling that causes muscles to influence the system in counterintuitive ways. Simulations also allow estimation of quantities that are difficult or impossible to measure in vivo such as joint and tissue loading, muscle fiber and/or tendon force and power, and elastic energy storage and return in tendons.

Of particular interest to analyses of human movement is muscle mechanical work, as it is often used to compare estimates of the work required to perform locomotor tasks such as walking and running, understand how energy is generated, absorbed and/or transferred among the body segments, identify impairments associated with neurological deficits, and estimate metabolic cost and efficiency. We have previously used simulation analyses to gain insight into the mechanical work requirements of human locomotion and elucidate limitations associated with experimentally derived measures of muscle work. Our central premise is that external measures of mechanical work cannot accurately quantify work performed by muscles, and as a consequence, may bias estimates of efficiency during locomotion. Accordingly, detailed forward dynamics simulations and metabolic energy cost models derived from experimental data will be critical to understanding the mechanics and energetics of human locomotion.

RELATIONSHIPS BETWEEN INTERNAL, EXTERNAL, JOINT AND MUSCLE WORK

A number of methods have been used over the years to estimate the total muscle mechanical work with internal, external and/or joint work-based quantities. Internal work is defined as the sum of the absolute changes in body segment kinetic and potential energy and is considered to be the work necessary to move the body segments relative to the body’s center-of-mass (e.g., (33)) or with respect to an inertial reference frame (e.g., (34)). External work is defined as the mechanical work done on the body’s center of mass (e.g., computed as the time-integral of the product of the measured ground reaction force and body center-of-mass (COM) velocity during walking or running, (33)) or an external load (e.g., during pedaling, (32)). Joint work, which is generally considered to be a more accurate estimate of musculotendon work than external or internal work, is computed as the time-integral of net joint power calculated using standard inverse dynamics techniques. Although these measures have been used in a wide range of studies to estimate muscle work, simulation studies have been useful in quantifying the acknowledged limitations with these methods (i.e., lack of independence between internal and external work, inability to account for co-contraction and elastic energy storage and return, etc.).

Simulations provide an ideal framework to make this assessment since they provide an example performance in which every source of mechanical work associated with a given locomotor task (e.g., from muscle fibers, tendons and passive structures) and the level of co-contraction can be precisely quantified. We used simulation analyses of pedaling to demonstrate how the work done by individual muscles to accelerate the leg segments ends up as external work at the pedal (13). Muscles accelerate the leg segments early in the downstroke and that energy is recovered later in the downstroke as the legs do mechanical work on the external load, which results in deceleration of the leg segments. As a result, significant energy is transferred from the legs to the crank without negative work being done by the muscles to decelerate the leg segments. Thus, internal work, which attributes all reductions in system energy to muscles, does not provide a valid measure of the energetic cost of moving the legs in pedaling. These results provided theoretical validation for our experimental work that showed large changes in internal work were not associated with similar changes in joint work during pedaling (12). Similarly, we used other pedaling simulations to assess the ability of various measures of mechanical energy expenditure (MEE) to estimate muscle mechanical work (17). Two distinct pedaling simulations were generated at the same pedaling rate and power output, with one being optimized to reduce MEE by minimizing eccentric muscle contractions. Comparison was made between muscle fiber work and MEE, which was quantified by three methods: 1) internal work, 2) net joint work and 3) intercompensated joint work (i.e., negative work from one joint was transferred to the adjacent joint where energy is being generated (positive work) via biarticular muscles). The three MEE measures greatly underestimated the muscle fiber work with errors reaching as high as 40% (17). Errors in the MEE methods were mainly attributed to their inability to account for co-contractions of antagonistic muscle groups. The simulations showed that muscles can absorb considerable power even when the net joint power is positive, which occurred in pedaling primarily due to one muscle generating positive work during activation while the antagonist muscle continues to generate force (and thus negative work) during deactivation.

Recently, we used simulations to investigate the ability of internal, external and joint work to estimate muscle mechanical work in human walking (21). Unlike in pedaling where the pedal reaction force rotates the crank, walking has no associated displacement at the endpoint due to the external reaction force. Thus, external work has been defined as the work done by the ground reaction force on the body’s center of mass. However, similar to pedaling, there are regions of co-contraction that occur during the gait cycle and unlike pedaling, energy is likely dissipated when the feet collide with the ground during walking. Thus it was unclear if internal, external or joint work could provide a more reasonable estimate of musculotendon and/or muscle fiber work during walking than they do during pedaling, or if they would be subject to the same limitations.

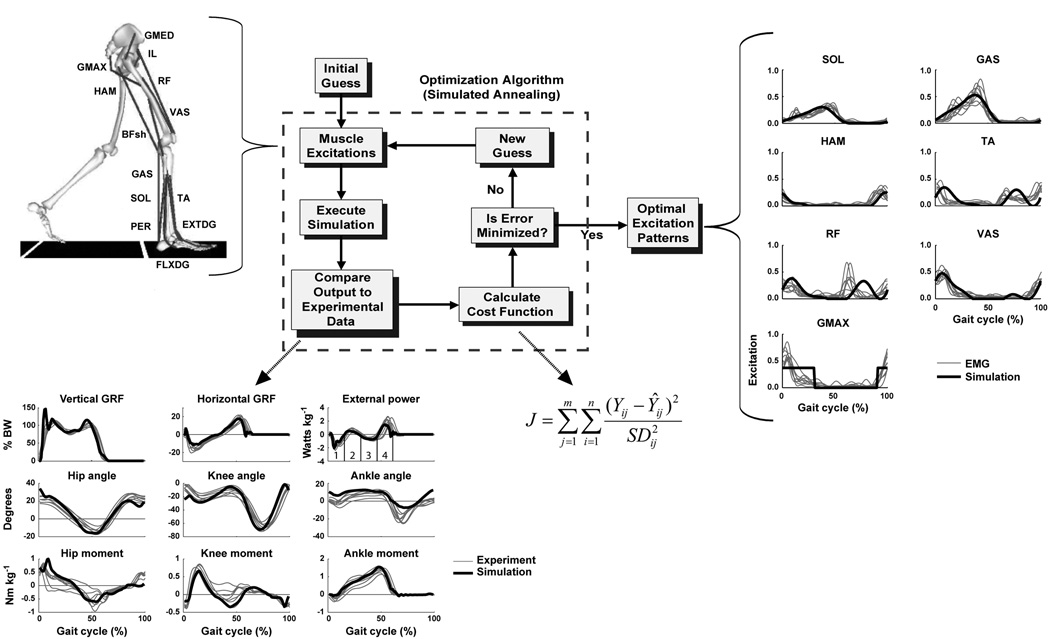
To address these questions regarding the use of internal, external and joint work-based quantities to estimate muscle work, a muscle-actuated forward dynamics walking simulation was generated that emulated subjects walking at 1.5 m/s (Fig. 1). The simulation was generated using SIMM/Dynamics Pipeline (MusculoGraphics, Inc., Santa Rosa, CA, USA) and SD/FAST (PTC, Needham, MA, USA). Dynamic optimization was used to fine-tune the muscle excitation patterns with a cost function that minimized the difference between the simulation and experimental kinematics (i.e., the time history of the trunk trajectory and hip, knee and ankle angles) and ground reaction force (GRF) data such that the simulation emulated well the group averaged subject data. Constraints were placed on the excitation magnitude and timing in the optimization algorithm to ensure the muscles generated force in the appropriate region of the gait cycle. From the simulation, total joint work (i.e., the time-integral of absolute value of joint power over a full gait cycle) was found to underestimate total musculotendon work due primarily to agonist-antagonist co-contractions (21). This occurred despite the inclusion of joint work by passive structures and biarticular muscle work, each of which acted to decrease the underestimation and cannot normally be accounted for in an inverse dynamics based calculation of total joint work. Muscle co-contractions can easily be determined in the model as the difference between total muscle joint work (i.e., the time integral of the muscle joint power at each joint spanned by a muscle, which is equivalent to joint power in the absence of passive joint power) and total musculotendon work (i.e., the time integral of the musculotendon power, which is the product of corresponding musculotendon force and velocity vectors). Co-contraction is inevitable in most human movement tasks due to joint stability needs, movement control complexity, synergistic muscle activity and the influence of activation and deactivation dynamics. Note that in contrast to our findings in total joint work, we did find that when the net passive joint work over the gait cycle is negligible (e.g., during slow walking), net joint work (i.e., the time-integral of net joint power) was comparable to the net musculotendon work (and net muscle fiber work since net tendon work is zero over a complete gait cycle). Thus, during walking conditions when passive joint work is negligible, net joint work provides a reasonable estimate of net muscle work. However, net muscle work is of limited utility since it provides neither insight into total mechanical work nor metabolic cost or efficiency.

Figure 1.

The musculoskeletal model and optimization framework used to generate forward dynamics simulations. The model consisted of a trunk (head, arms, torso and pelvis) and left and right legs (femur, tibia, patella, rear-foot, mid-foot and toes). Only the 13 muscle groups for the right leg are shown, which included GMED (anterior and posterior portion of gluteus medius), IL (iliacus, psoas), RF (rectus femoris), VAS (3-component vastus), TA (tibialis anterior, peroneus tertius), PER (peroneus longus, peroneus brevis), FLXDG (flexor hallucis longus, flexor digitorum longus), EXTDG (extensor hallucis longus, extensor digitorum longus), SOL (soleus, tibialis posterior), GAS (medial and lateral gastrocnemius), BFsh (biceps femoris short head), HAM (medial hamstrings, biceps femoris long head) and GMAX (gluteus maximus, adductor magnus). The Optimization Algorithm fine-tunes the muscle excitation patterns for each muscle group to produce a well-coordinated walking pattern that emulates the human subject data by minimizing cost function J. Y is the experimental data, Ŷ is the corresponding simulation data. The excitation patterns are defined by muscle EMG or a rectangular pattern if no EMG data is available. As seen in the Optimal Excitation Patterns, the resulting excitation patterns agree well with the human subject EMG data. For comparison purposes, the experimental EMG patterns (group mean ± s.d.) were normalized to the peak simulation excitation magnitude. The excitation patterns for the small muscles that primarily control the foot (PER, FLXDG, EXTDG) are omitted in the Optimal Excitation Patterns comparison. The Compare Output to Experimental Data shows how well the simulation emulates the experimental hip, knee and ankle joint angles, vertical and horizontal GRFs, and joint moments over the gait cycle (i.e., from right heel-strike to right heel-strike). [Adapted from Neptune RR, Clark DJ, Kautz SA. Modular control of human walking: a simulation study. Journal of Biomechanics. (2009, in press). Copyright © 2009 Elsevier. Used with permission.]

The simulation analysis also showed that neither total external nor total internal work (nor their sum) provided a reasonable estimate of total musculotendon work, which is consistent with the previous pedaling studies noted above (12, 17). External work in particular is often used to infer muscle work and metabolic cost in walking (e.g., (6)). However, external power is a net measure that cannot partition out the amount of positive and negative muscle work that is performed during a given locomotor task and thus is not well suited for predicting muscle work or metabolic cost. Support for these limitations predicted by simulation analyses were provided in a recent study of amputee walking that showed despite a 26% increase in metabolic cost compared to non-amputees walking at the same speed (1.3 m/s), there was no difference in total absolute external work and there was no correlation between metabolic and total external mechanical power (10). Thus, simulations were useful in showing that joint work is limited in its ability to estimate musculotendon work, and that external and/or internal work do not provide a reasonable estimate of musculotendon work.

MUSCLE WORK REQUIREMENTS DURING WALKING

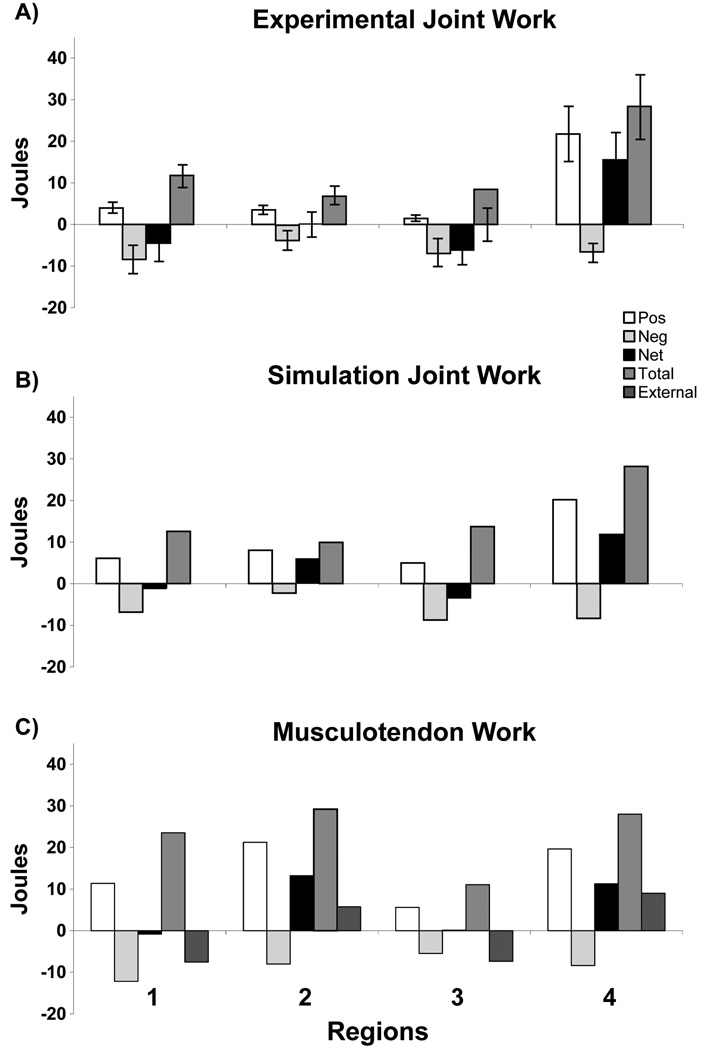
Inverted pendulum models of walking predict that little muscle work is required for the exchange of body potential and kinetic energy in single-limb support. Based in part on external power analyses, previous studies have suggested that the primary mechanical energetic cost of walking is associated with the requirement to redirect the motion of the COM in double support during the step-to-step transition (6, 14), which is most efficiently done by the ankle plantar flexors (14). However, these simple inverted pendulum models without articulated joints do not capture the multi-muscle, multi-segmental properties of walking, co-excitation of muscles to coordinate segmental power flow, or simultaneous production of positive and negative muscle work. We used a muscle-actuated forward dynamics simulation of walking to address two important questions inspired by step-to-step transition theory (18): 1) can the potential and kinetic energy of the body be exchanged with little muscle work; and 2) does the net work output and the mechanical energetic cost for muscles occur primarily in double support. Note that we have generated improved simulations since our original publication that more closely replicates experimental human subject data (Fig. 2) and the conclusions remain robust. Contrary to the predictions of step-to-step transition theory, we found that significant muscle work occurs throughout the gait cycle and particularly in early single-limb support (Fig. 2, Region 2). In this region, co-contraction occurs among the hip and knee flexors and extensors to control hip and knee flexion (e.g., knee flexion peaks near 30 degrees) and provides lower limb stability. Muscle work is then needed to accelerate the hip and knee into extension and the COM vertically, thus raising the COM and providing body support (18). Without this muscle force (work), the joints would collapse rather than extend, and the trunk would not rise. These simulation results are consistent with Sawicki and Ferris (22) who used metabolic measurements and powered ankle exoskeletons to replace ankle plantar flexor power during push-off in double support (Region 4). They found that at the preferred speed/step length combination (1.25 m/s), elastic energy stored in the Achilles’ tendon accounted for 59% of the total ankle musculotendon positive work and that the positive work generated by the ankle muscles in late stance only accounted for 18% of the total net metabolic power. They concluded that the metabolic cost of walking is most likely dominated by positive muscle work at the proximal joints (i.e., hip and knee) that accounts for the remaining 82% of the total net metabolic power. The results of Sawicki and Ferris (22) support the simulation results and further highlight the inherent limitations of studies that rely on external power to infer muscle mechanical work or metabolic cost.

Figure 2.

Comparison between A) experimental joint work, B) simulation joint work and C) corresponding simulation musculotendon work in each region defined by the positive/negative crossing points of the external power trajectory (see external power in Fig. 1). The simulations showed the musculotendon work is significant in Region 2, which is necessary to decelerate hip and knee flexion, provide lower-limb stability and accelerate the body center-of-mass vertically to provide body support.

THE EFFECT OF WALKING SPEED ON MUSCLE MECHANICAL WORK

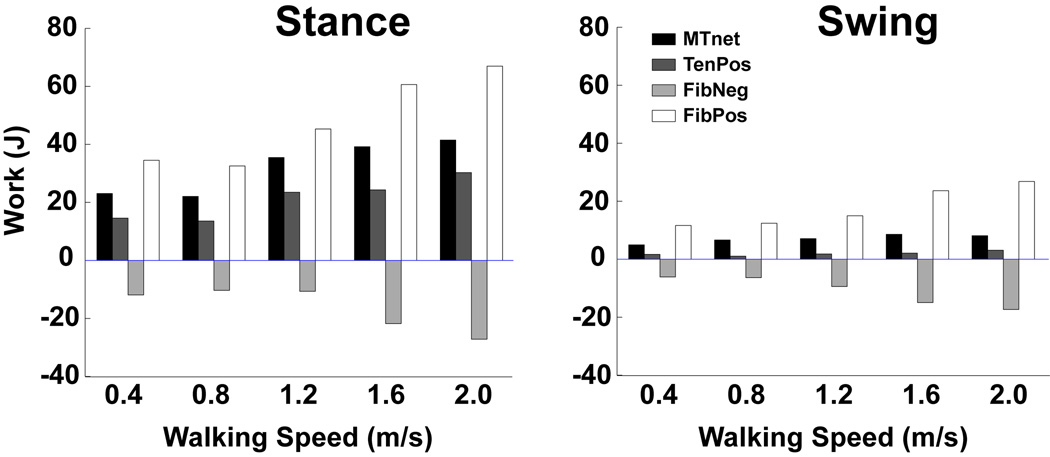
Simulations have also provided novel insight into understanding the relationship between individual muscle function and mechanical work as walking speed increases. During normal walking, we often need to modulate speed over a large range; however there is poor understanding of how the neuromotor patterns adapt to the changing biomechanical demands of increased speed. Thus, we used muscle-actuated forward dynamics simulations to identify functional and energetic adaptations in individual muscles in order to walk at faster steady-state speeds (16). We expected the largest adaptations to occur in stance where muscles provide body support and forward propulsion, while recognizing that increases in the mechanical work of the swing phase muscles would likely be needed to account for the increased importance of accelerating and decelerating the leg as walking speed increased. The simulations showed that the relative contributions of different muscle groups to trunk support, forward propulsion or leg swing (i.e., muscle function) remained invariant, although the magnitude of each contribution systematically increased with speed (16). Trunk support (vertical acceleration) was provided primarily by the hip and knee extensors in early stance and the plantar flexors in late stance, while trunk propulsion (horizontal acceleration) was provided primarily by the soleus and rectus femoris in late stance. The simulations also highlighted the importance of initiating and controlling leg swing as there was a dramatic increase at the higher walking speeds in iliopsoas muscle work to accelerate the leg in pre- and early swing, which coincided with an increase in the biarticular hamstring muscle work to decelerate the leg in late swing. At higher walking speeds, the difference in positive fiber work between the stance and swing phase decreased. As a result, the positive fiber work performed during swing increased from 25% to 29% of the total fiber work (stance + swing) with increasing walking speed (Fig. 3). These results were consistent with the estimate of Doke et al. (5) that moving the legs represents nearly 1/3 of the total energetic cost of walking at 1.3 m/s, and Umberger (27) who used a metabolic cost model with simulation analyses to estimate that 29% of the total metabolic cost of walking occurs during swing. Interestingly, the simulations also showed that walking near self-selected speeds (1.2 m/s) improved the elastic energy storage and recovery in the uniarticular ankle plantar flexor tendons and reduced negative fiber work relative to faster or slower speeds (Fig. 3), which has implications for understanding preferred walking speed selection. Thus, simulation analyses proved useful in gaining insight into the neuromotor mechanisms underlying speed regulation in walking and the results provide a basis for comparison with pathological populations.

Figure 3.

Total muscle fiber and tendon work across increasing walking speeds (net musculotendon work (MTnet), positive tendon work (TenPos, elastic energy recovered from the tendon), negative fiber work (FibNeg) and positive fiber work (FibPos)). The percent difference in muscle work between stance and swing decreases as walking speed increases. Note, the percent of elastic energy recovery in the tendons (Ten Pos/ (FibPos +TenPos)) was maximized at 30% when walking at 1.2 m/s, which is near the preferred walking speed. [Adapted from Neptune RR, Sasaki K, Kautz SA. The effect of walking speed on muscle function and mechanical energetics. Gait Posture. 2008; 28(1): 135–43. Copyright © 2008 Elsevier. Used with permission.]

RELATING MUSCLE MECHANICAL WORK TO METABOLIC COST

An important area for future research will be to better understand the efficiency of musculoskeletal systems during natural movements. Traditionally, mechanical efficiency has been expressed as the ratio of positive work (e.g., joint work, external work or muscle work) to metabolic cost, although some authors have suggested that negative work should also be included in the denominator of the efficiency calculation (efficiency = W⁺ / (E+W^–)·, where W⁺ is the positive work, W^– is the negative work, and E is the metabolic energy expenditure) because negative work has the potential to be returned as positive work later in the gait cycle (19). Using the latter approach, Umberger and Martin (30) examined the influence of walking stride rate on efficiency using joint work. Their results showed that when walking at 1.3 m/s, subjects had an efficiency of 0.38. To compare the results from our walking simulations with the experimentally determined efficiency, we used the same equation and metabolic cost as Umberger and Martin (30) to calculate mechanical efficiency from our simulation joint work (21). The results showed that the simulation had similar efficiency (∼ 0.40) as the experimental subjects. However, using simulations we were also able to examine efficiency at the muscle fiber level (positive fiber work/metabolic cost) and found an efficiency of 0.59. Note, we did not need to include negative fiber work in the denominator as the theoretical upper limit for how much elastic energy could be returned as positive work later in the gait cycle since we could extract the fiber work directly from the simulation. Sawicki and Ferris (22) computed ankle joint musculotendon efficiency across speeds and found values near .61 at the preferred speed/step length combination, which they attributed to elastic energy storage and return in the Achilles’ tendon. These results highlight that net joint work-based measures of mechanical work likely underestimate positive work due to factors such as inevitable co-contraction of antagonist muscles. It should be noted that our estimates for efficiency are high relative to the traditional values of 0.20–0.30 measured in isolated muscles or muscle fibers (e.g., (24)). This discrepancy could be due to a number of factors associated with the model such as unaccounted or underestimated elasticity in the muscle fibers, tendon and other structures, an overestimate of the energy lost at foot–ground contact, an overestimate of the resting baseline metabolic cost used to determine net metabolic cost, unmodeled stretch-induced force enhancement, or the fact that the efficiency measured in isolated muscle fibers is not the same as whole-body efficiency. This later point has been the topic of considerable debate and future work is needed to better understand efficiency in the context of whole-body movements (see target article by van Ingen Schenau et al. (31) and the subsequent responses for a detailed discussion).

METABOLIC COST MODELS

To further understand the relationships between muscle mechanical work and efficiency, detailed models of muscle metabolic cost are needed. There are multiple approaches to modeling the energetics of muscle contractions. Since AF Huxley’s original sliding-filament model, a number of authors have developed mathematical models that examine contraction energetics at the level of individual cross-bridges (for review see (24)). The advantage of this approach is that the parameters in the model have direct links to the underlying biological processes. However, many of the values for these parameters are not well known, especially for humans. Unfortunately, these models do not lend themselves to inclusion in simulation analyses due to their complexity, and they are not easily integrated with the relatively simple and computationally efficient Hill-type muscle models commonly used in forward dynamics simulations. Because of this limitation, a number of phenomenological models (e.g., (2, 28)) have been developed which calculate metabolic cost based on the outputs from Hill-type muscle models.

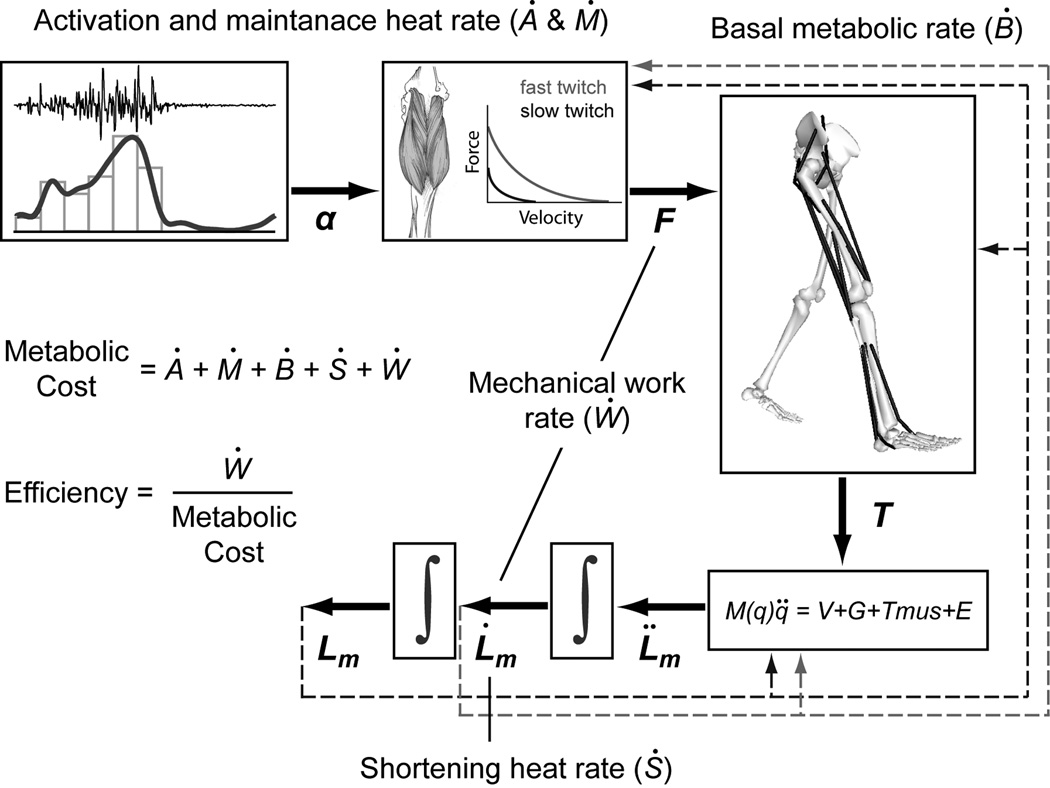
To estimate the total energy used by a muscle during contractions, these models include not only the mechanical power but also the rate that heat is produced (Fig. 4). Parameters common to such models include activation heat rate, maintenance heat rate, shortening heat rate, and mechanical work rate (e.g., (2, 8, 28)), while some also include basal metabolic rate (2) or heat dissipated in elastic structures (8). Obtaining appropriate values for these parameters remains one of the primary challenges for use in simulation analyses of human movement. Few of these parameters can be measured directly in humans and are often estimated from measurements made on isolated muscles (or muscle fibers) from animals such as mice or frogs. Yet, of the studies that have compared simulated results with existing empirical metabolic cost data (2, 27, 28), there has been relatively good agreement at multiple levels of complexity (e.g., isolated muscles, single joint or whole body movements). However, measurements using techniques such as near infrared spectroscopy (NIRS) or magnetic resonance spectroscopy (MRS) will be essential to further refine and validate the models.

Figure 4.

A schematic of a general muscle metabolic cost model implemented in a forward dynamics simulation framework. Activation heat rate (Ȧ) and maintenance heat rate (Ṁ) are commonly grouped together and depend on the muscle activation and the percentage of fiber types for each muscle. Basal heat rate (Ḃ) is based on the basal metabolic rate of muscle and is function of muscle mass. Shortening heat rate (Ṡ) is a function of muscle activation, muscle fiber type and rate of muscle shortening or lengthening. Mechanical work rate (Ẇ) is the product of muscle force and rate of muscle length change. The total metabolic rate for each muscle is the sum of the rates of heat production and mechanical work.

Because humans and other animals generally choose to perform tasks using mechanics that reduce metabolic energy consumption, muscle energetics models have frequently been used in optimization objective functions in simulation studies. Applications have ranged from using metabolic cost models to examine motor unit recruitment patterns (8) and the influence of muscle fiber type composition on metabolic cost in pedaling (29) to evaluate alternative gait strategies (23) and predict overall walking mechanics (1). Studies such as these provide insight into the relationship between metabolic cost and an individual’s morphology or strategies used to perform a given locomotor task.

As the estimates of individual parameters become more accurate, so too will the models and simulations of muscle energetics. Current models remain an excellent tool for examining relative differences between muscles (e.g., proportions of fiber types) or experimental conditions (e.g., differences in speed or load). Future studies may use muscle energetics models to tease out the timing and distribution of energy consumption among muscles or to examine the efficiency of individual muscles during various movement tasks. In addition, such models can be combined with forward dynamics simulations and design optimization to help improve rehabilitation outcomes. For example, orthotic or prosthetic devices can be optimized to minimize metabolic cost during walking or running. Thus, the development of accurate and computationally efficient models has a wide range of promising applications that make this a fruitful area for continued research.

POTENTIAL LIMITATIONS OF SIMULATION ANALYSES

Simulation studies face many challenges, with establishing validity being one of the primary challenges because many of the quantities being investigated cannot be measured – hence the reason for using simulation in the first place. Modeling requires assumptions regarding anatomy, muscle physiology and structural and mechanical properties including the interaction between the model and the ground. However, if quantities such as muscle work are of interest, confidence in the results can be gained when 1) each muscle is excited at the appropriate point in the gait cycle, 2) the overall mechanics of the movement are sufficiently similar to the experimental observations, 3) energy/momentum balances are assured, and 4) the results are insensitive to moderate variations in model parameters. Note that to achieve appropriate timing of muscle excitation, the timing in the optimization can be constrained to closely match measured EMG timing (e.g., Fig. 1). Comparisons with experimental observations (e.g., joint motion, ground reaction forces and inverse dynamics-based quantities) can be used to confirm that the overall mechanics of the movement are sufficiently similar to the experimental observations (Fig. 1), and this is inherent in the process of the optimal tracking we typically use. Further comparisons can be made using experimental techniques such as magnetic resonance imaging (MRI) to confirm and refine the musculoskeletal model geometry, muscle architecture and mechanics, and joint kinematics (for review, see (3)), and high speed ultrasound to verify muscle-tendon interactions and elastic energy storage and return (e.g., (7, 11)). Such techniques will be essential in future studies to validate the model across multiple scales of the musculoskeletal system to aid in model development and validation and ultimately improve the accuracy and utility of modeling and simulation techniques.

However, achieving a close comparison between all experimental and simulation data can be difficult in part because experimental data has its own limitations, which are often not acknowledged or tested for explicitly. For example, there is always some degree of error (both marker registration errors and skin movement artifact errors) associated with the experimental body segment kinematics that a kinematically consistent simulation model will have difficulty tracking (e.g., (4)). Joint moment-based quantities derived from inverse dynamics often have high residuals at the terminal link due to dynamic inconsistency between the GRFs and body segment kinematics (e.g., (20)). This results in experimental mechanical work quantities that are not dynamically consistent, with the errors being difficult to identify because there is not an independent method available to validate joint work quantities since the amount of energy dissipated in the musculoskeletal system (e.g., viscous damping in body tissues) and in the environment (e.g., foot-ground contact) are not known. In addition, the simulation data is generally compared with group average data, which are often heavily smoothed and represent theoretical trajectories that an individual human subject may not be able to produce in a single walking trial. The advantage of forward dynamics simulations is that they are dynamically consistent and satisfy the fundamental laws of physics at each point in the gait cycle while being constrained to be consistent with our current models of the muscle force-length-velocity-activation relationships. Despite these challenges, a number of carefully designed experimental studies have recently confirmed different aspects of the simulation results (9, 15, 25). For example, McGowan et al. (15) designed an experimental study that manipulated body weight and body mass independently to confirm the predictions from computer simulation studies that the uniarticular and biarticular ankle plantar flexors have distinct functional roles in walking (i.e., although both the gastrocnemius and soleus contribute to body support, the soleus is the primary contributor to trunk forward propulsion). Similarly, Hernández et al. (9) used muscle electrical stimulation to confirm the non-intuitive simulation prediction that that the rectus femoris acts to accelerate the hip into extension rather than flexion during the early swing phase of walking. Such studies are critically needed to further validate the use of simulation as a powerful tool to analyze various aspects of human locomotion.

SUMMARY

Muscle mechanical work is an important biomechanical quantity in analyses of human locomotion; however, current experimental methods are limited in their ability to quantify it accurately. Muscle-actuated forward dynamics simulations provide a consistent mechanical solution that can be interrogated at multiple levels (muscle fiber, musculotendon, net joint moment and whole body work) to gain insight into mechanical work requirements of human locomotion and better understand the limitations associated with experimentally derived measures of muscle work. Future work integrating detailed and computationally efficient metabolic cost models with forward dynamics simulations holds great promise to investigate individual muscle and whole body energetics and efficiency across a wide range of locomotor tasks and patient populations.