Modeling the bicoid gradient: Diffusion and reversible nuclear trapping of a stable protein

Abstract

The Bicoid gradient in the Drosophila embryo provided the first example of a morphogen gradient studied at the molecular level. The exponential shape of the Bicoid gradient had always been interpreted within the framework of the localized production, diffusion, and degradation model. We propose an alternative mechanism, which assumes no Bicoid degradation. The medium where the Bicoid gradient is formed and interpreted is very dynamic. Most notably, the number of nuclei changes over three orders of magnitude from fertilization, when Bicoid synthesis is initiated, to nuclear cycle 14 when most of the measurements were taken. We demonstrate that a model based on Bicoid diffusion and nucleocytoplasmic shuttling in the presence of the growing number of nuclei can account for most of the properties of the Bicoid concentration profile. Consistent with experimental observations, the Bicoid gradient in our model is established before nuclei migrate to the periphery of the embryo and remains stable during subsequent nuclear divisions. Published by Elsevier Inc.

Introduction

Studies of the spatial distribution and transcriptional effects of the Bicoid protein in the Drosophila embryo provided the first experimental example of pattern formation by a morphogen gradient (Driever and Nusslein-Volhard, 1988a,b, 1989; Driever et al., 1989; Ephrussi and St Johnston, 2004; Struhl et al., 1989). Bicoid is a homeodomain transcription factor, which is translated from maternally deposited transcript at the anterior of the embryo and forms a gradient that patterns the anterior–posterior (AP) embryonic axis by controlling the expression of multiple zygotic genes. The expression thresholds of Bicoid targets are determined by multiple effects, including the strength and number of the Bicoid binding sites, and combinatorial interactions with other transcription factors (Driever et al., 1989; Lebrecht et al., 2005; Ochoa-Espinosa et al., 2005). Bicoid also acts as a translation repressor and mediates the formation of the posterior-to-anterior gradient of Caudal, a product of uniformly distributed maternal transcript (Zamore and Lehmann, 1996).

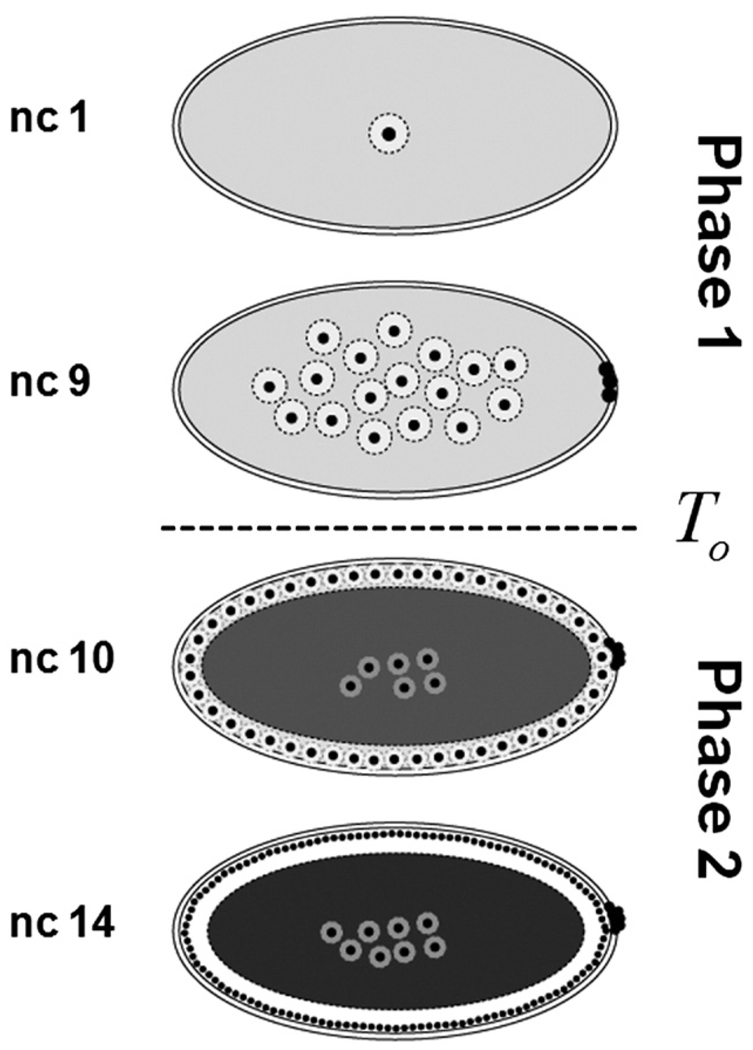
All of the previously published quantitative models of the Bicoid gradient formation neglect the fact that the medium where it is formed and interpreted–the syncytial embryo–is very dynamic (Bergmann et al., 2007; Gregor et al., 2005; Houchmandzadeh et al., 2002; Tostevin et al., 2007). The most pronounced changes are associated with the number and the spatial distribution of nuclei (Foe and Alberts, 1983). The formation of the gradient is believed to start at egg deposition. This is followed by 13 nuclear divisions. During the first 9 nuclear division cycles nuclei are distributed essentially uniformly throughout the embryo. During the last nuclear cycles, however, nuclei are distributed as a monolayer at the plasma membrane (Fig. 1).

Fig. 1.

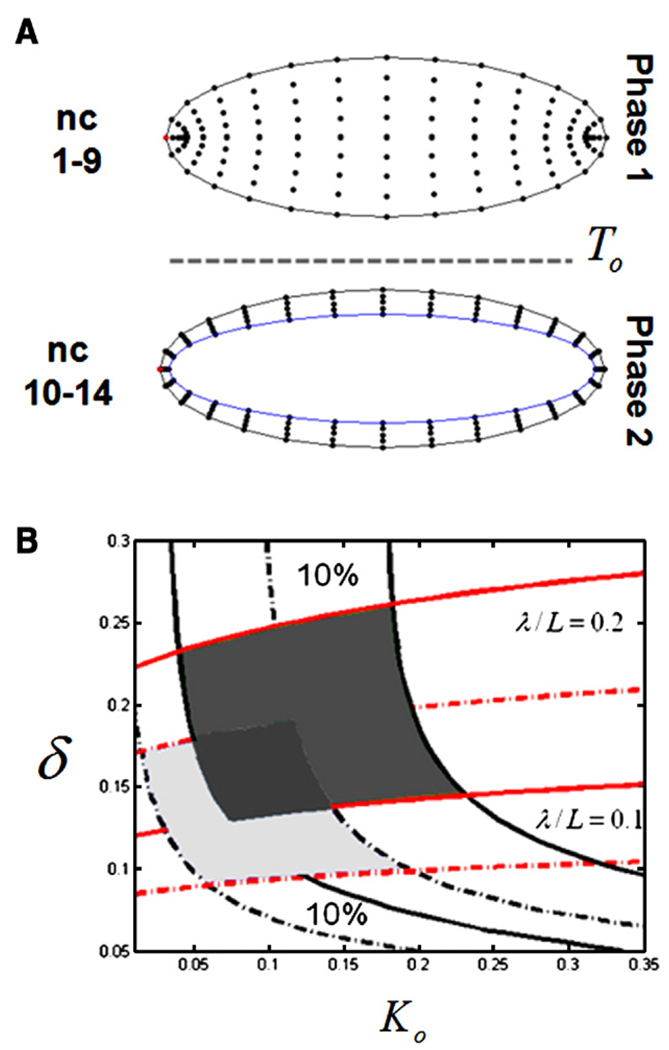
Summary of changes in the number and distribution of nuclei in the syncytial embryo. Following egg deposition, nuclei divide thirteen times in a common cytoplasm. This process stage can be split into two temporal phases. During phase one (nuclear cycles 1 to 9), nuclei are distributed in the bulk of the embryo and surrounded by cytoplasmic islands. At nuclear cycle 10 nuclei move to the outer plasma membrane and a clear rim of cytoplasm appears at the cortex of the embryo. During phase two (nuclear cycles 10 to 14), nuclei are distributed under the plasma membrane. At this stage, yolk occupies the center of the embryo and appears to be impermeable to Bicoid.

The exponential shape of the Bicoid gradient is consistent with and had always been interpreted within the framework of a model in which the gradient is formed by localized production, diffusion, and uniform degradation (Gregor et al., 2005; Houchmandzadeh et al., 2002). Within the framework of this model, degradation ensures the stability of the Bicoid concentration profile, which would otherwise continue to spread throughout the embryo. Measurements of Bicoid diffusivity were reported (Gregor et al., 2005, 2007), but the rate of Bicoid degradation remains uncertain.

Given the uncertainty in the rate of Bicoid degradation, we asked whether a gradient, which appears stable on the timescale of observations, can be established without the degradation at all. Recent live-imaging experiments established that Bicoid undergoes rapid nucleocytoplasmic shuttling (Gregor et al., 2007). Thus, nuclei can be viewed as reversible traps that slow down Bicoid diffusion. Based on this, we hypothesized that the increase in the number of nuclei can counteract its local growth in time and/or diffusive spread. To explore the feasibility of this mechanism, we formulated a model of Bicoid diffusion and reversible trapping by the growing number of nuclei. Analysis of this model revealed that it can capture most of the experimentally observed properties of the Bicoid gradient (Gregor et al., 2005, 2007). Furthermore, we find that, within the framework of this model, nuclei do not contribute significantly to the shape of the Bicoid gradient. Consistent with experimental observations, the Bicoid gradient in our model is established before nuclei migrate to the periphery of the embryo and remains stable during subsequent nuclear divisions.

Results and discussion

Model for Bicoid diffusion and nuclear trapping

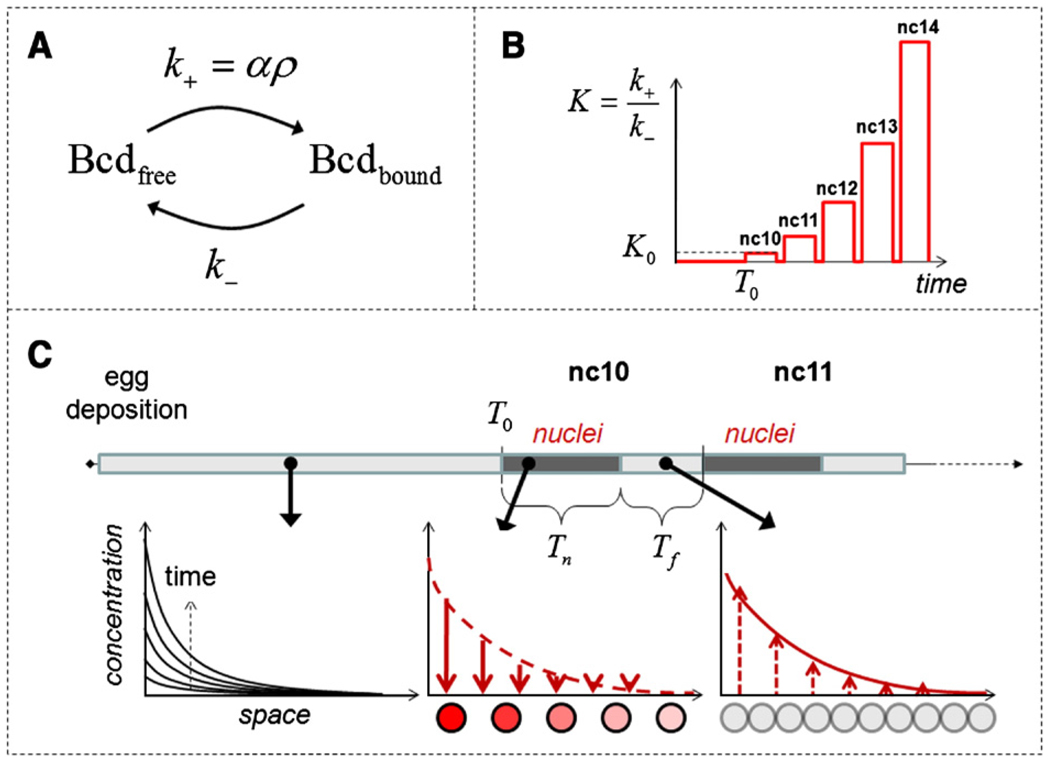
Consider a one-dimensional model of the embryo of length L. Bicoid molecules are produced at a constant rate Q at the anterior end of the embryo (x = 0); the posterior of the embryo (x = L) is impermeable to Bicoid. The embryo is modeled as a homogeneous medium, where nuclei are uniformly distributed with the density ρ (number of nuclei per unit length). Bicoid can exist in two states: free, where it is moving with diffusivity D, and bound, where it is confined to the nucleus and can be considered immobile. The transitions between the free and bound states are modeled by first order processes with the rate constants k₊ and k₋ (Fig. 2A). We assume that the forward nuclear trapping rate constant is proportional to the nuclear density: k₊ = αρ; this is a standard assumption in the theory of diffusion-influenced reactions (Rice, 1985; Torquato, 1991). Based on this, we can write the following set of equations for the concentrations of the free and bound Bicoid molecules, denoted by C_f = C_f (x, t) and C_b = C_b (x, t), respectively:

$$\frac{\partial C_{\mathrm{f}}}{\partial t}=D\frac{{\partial }^2{C}_{\mathrm{f}}}{\partial x^2}-k_{+}{C}_{\mathrm{f}}+k_{-}{C}_{\mathrm{b}}$$ (1)

$$\frac{\partial C_{\mathrm{b}}}{\partial t}=k_{+}{C}_{\mathrm{f}}-k_{-}{C}_{\mathrm{b}}$$ (2)

$$\begin{array}{cc}D\frac{\partial C_{\mathrm{f}}}{\partial x}{|}_{x=0}=-Q,\hfill & D{\frac{\partial C_{\mathrm{f}}}{\partial x}|}_{x=L}=0\hfill \end{array}$$ (3)

Fig. 2.

Model of Bicoid diffusion and reversible trapping by nuclei, see text for details. (A) Bicoid exists in two states: freely diffusing and immobile/nuclear. The transitions between the two states are described by first-order processes. The forward nuclear trapping rate constant is proportional to the nuclear density. (B) The time-dependent nuclear density in the syncytial embryo is translated into the time-dependent equilibrium constant for the nucleocytoplasmic shuttling of Bicoid (see text for details). nc10, nc11, etc. denote the nuclear cycles 10, 11, etc. (C) Schematic representation of the dynamics of the Bicoid gradient. From t = 0 to t = T₀, Bicoid diffusion is essentially unaffected by nuclei. This “free-diffusion” phase (bottom left panel; curves represent diffusive spread of Bicoid from the constant source the boundary) is followed by the phase with much greater value of the nucleocytoplasmic shuttling equilibrium constant. Each of the five nuclear cycles during this phase is in turn composed of two stages, with and without the nuclei. T_n,i and T_f,i denotes the durations of the nuclear and free periods, respectively. The gradient of nuclear Bicoid is formed at the beginning of each nuclear cycle (bottom middle panel). When nuclei dissolve Bicoid is again freely diffusing (bottom right panel).

Recent measurements with the GFP-tagged Bicoid in live embryos have shown that Bicoid rapidly equilibrates between the cytoplasmic and nuclear compartments (Gregor et al., 2007), suggesting that the free and bound populations of Bicoid are in local equilibrium. This leads to C_b/C_f = K, where K ≡ k₊/k₋ = αρ/k₋ is the equilibrium constant for nucleocytoplasmic shuttling at a given nuclear density. Just as the nuclear density, the equilibrium constant is a function of time but does not depend on the spatial coordinate. From this, the local concentrations of free and bound Bicoid molecules can be expressed as functions of the total concentration of Bicoid, C_tot(x, t) ≡ C_b(x, t) + C_f(x, t):

$$\begin{array}{ll}{C}_{\mathrm{f}}(x,t)=\frac{C_{\text{tot}}(x,t)}{1+K},\hfill & C_{\mathrm{b}}(x,t)=\frac{{\mathit{\text{KC}}}_{\text{tot}}(x,t)}{1+K}\hfill \end{array}$$ (4)

Using this after adding Eq. (1) and Eq. (2), we get the following equation for C_tot (x, t):

$$\frac{\partial C_{\text{tot}}}{\partial t}=\frac{D}{1+K}\frac{{\partial }^2{C}_{\text{tot}}}{\partial x^2}$$ (5)

The variables in our model can be related to the intensities in the fluorescent images of Bicoid in embryos in the following way (Gregor et al., 2005, 2007; Houchmandzadeh et al., 2002). The intensity in the epifluorescence images of Bicoid antibody stainings can be considered proportional to the total concentration of Bicoid: C_tot (x, t). On the other hand, the signal intensity in measurements which detect Bicoid level inside a single nucleus can be considered proportional to the ratio of the local concentration of bound Bicoid molecules and the current nuclear density (Gregor et al., 2007):

$$n(x,t)=\frac{C_{\mathrm{b}}(x,t)}{\rho (t)}.$$ (6)

which is the number of Bicoid molecules per nucleus at a given location.

Model for the dynamics of the medium

At a given nuclear density, our model of Bicoid dynamics is identical to other models of diffusion in the presence of immobile reversible traps, used to describe growth factor diffusion in tissues and calcium diffusion in cells (Dowd et al., 1999; Wagner and Keizer, 1994). The key difference is introduced by accounting for the dynamics of nuclear density (Fig. 1). Bicoid translation is believed to start at egg deposition and fertilization. Until the 9th nuclear cycle, the nuclei are distributed in three dimensions (Foe and Alberts, 1983), and most of the volume of the embryo is presumably available for Bicoid diffusion. After the 10th nuclear cycle, the nuclei are distributed in a two-dimensional layer on the surface of the embryo. This leads to a sharp increase in the nuclear density (an order of magnitude, based on simple geometric considerations) and affects the binding/dissociation equilibrium. According to our model, changes in the nuclear density are translated into changes of the equilibrium constant for reversible trapping of Bicoid by nuclei.

To model these dynamics, we split the entire process into two phases (Fig. 1, Fig. 2B, C). The first phase lasts from t = 0 to t = T₀; this corresponds to cycles 1 through 9, when the effect of nuclei on the Bicoid gradient can be neglected. The second phase, representing nuclear cycles 10–14, is composed of five time intervals. At t = T₀, nuclei appear at a starting density ρ₀, which translates into a starting value of the equilibrium constant, K₀, and a new value for the effective diffusivity, D / (1 + K₀). This “nuclear” period, which corresponds to the interphase, lasts T_n,1 units of time, after which the nuclei membranes break down during mitosis, Bicoid molecules captured in the nuclei are released, and diffusion constant returns to its original value.

After this “nuclei-free” period, which lasts T_f,1 time units, nuclei reappear with the doubled density 2ρ₀. This doubles the equilibrium constant and lowers the effective diffusivity to D / (1 + 2K₀). The cycle repeats five times. The durations of the periods with and without the nuclei during each of these cycles are denoted by T_n,i and T_f,i, respectively (i = 1, 2, 3, 4, 5). Thus, the dynamics of the Bicoid profiles is described by Eq. (4) with cycle-dependent diffusivity (Fig. 2C).

Analysis of the model

Consider first the idealized scenario, in which the durations of the nuclear and nuclei-free parts of the nuclear cycles do not vary with time. In this case, the dynamics of Bicoid profile is completely determined by four dimensionless parameters:

$$\begin{array}{cccc}\delta =\sqrt{\frac{{\mathit{\text{DT}}}_0}{L},}\hfill & \beta =\frac{T_{\mathrm{f}}+T_{\mathrm{n}}}{T_0},\hfill & \mathrm{\gamma }=\frac{T_{\mathrm{n}}}{T_{\mathrm{f}}+T_{\mathrm{n}}},\hfill & K_0\hfill \end{array}$$ (7)

The first of these parameters, δ, quantifies the spreading of Bicoid before nuclear arrives at the periphery of the embryo. The second parameter, β, is the ratio of the length of the nuclear cycle to the duration of the first phase. The third parameter, γ, characterizes the ratio of the time intervals with and without nuclei within the nuclear cycle. Finally, K₀ is the starting value of the equilibrium constant for nucleocytoplasmic shuttling.

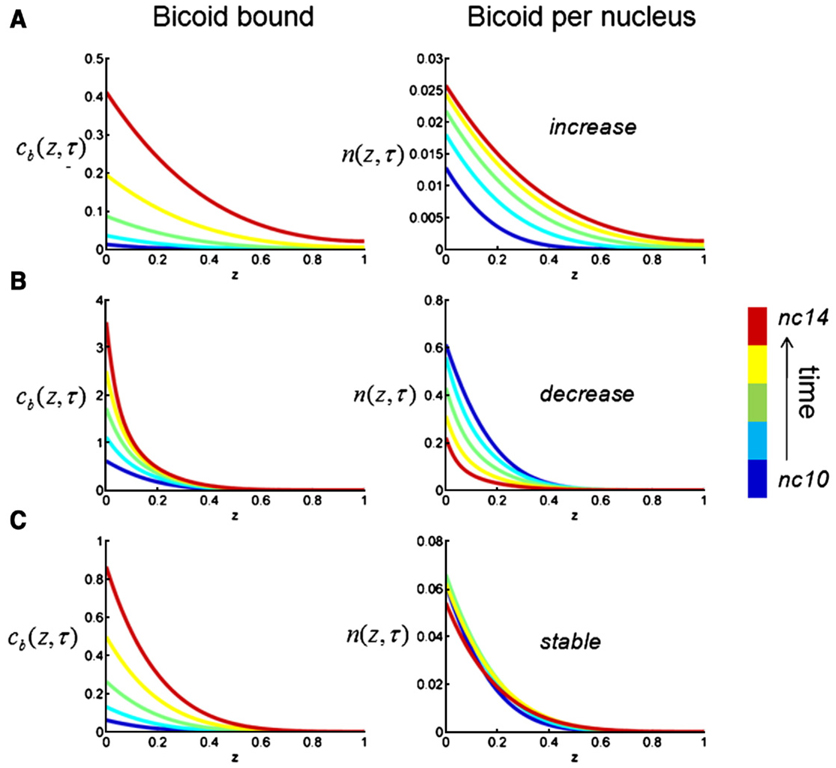
We will first treat β, γ, δ, and K₀ as free parameters and explore the dynamics total and nuclear concentrations of Bicoid that can be predicted by our model. Since there is no Bicoid degradation in our model, the model predicts that the total concentration of Bicoid increases as a function of time throughout the embryo, for all values of model parameters. Since the concentration of the bound Bicoid molecules is an increasing function of the total Bicoid concentration (Eq. (4)), this predicts that the profile of the bound Bicoid molecules, C_b (x, t), should increase throughout the embryo (Fig. 3, left). However, the spatial profile of Bicoid concentration per nucleus, n(x, t), can increase, decrease, or remain almost invariant with time, depending on the model parameters (Fig. 3, right). Only the latter regime is consistent with the recent experimental observations (Gregor et al., 2007). In the rest of the paper, we call this regime “stable”.

Fig. 3.

Computational analysis of the simplified model in which the durations of the nuclear and free portions of the nuclear cycles are constant. The local dimensionless concentration of Bicoid molecules in the bound state, c_b (z), is always increasing (left), however the local concentration of the Bicoid molecules per nucleus (n(z), right) can increase, decrease, and remain quasi-invariant with time. Examples A–C correspond to the following values of model parameters: A − δ = 0.17, K₀ = 0.01, β = 1, γ = 1; B − δ = 0.17, K₀ = 0.9, β = 0.2, γ = 1; C − δ = 0.17, K₀ = 0.05, β = 0.2, γ = 1. The plot shows the results of numerical solution of the dimensionless problem; see Materials and methods for the details of nondimensionalization and numerical methods.

The nature of the stable behavior

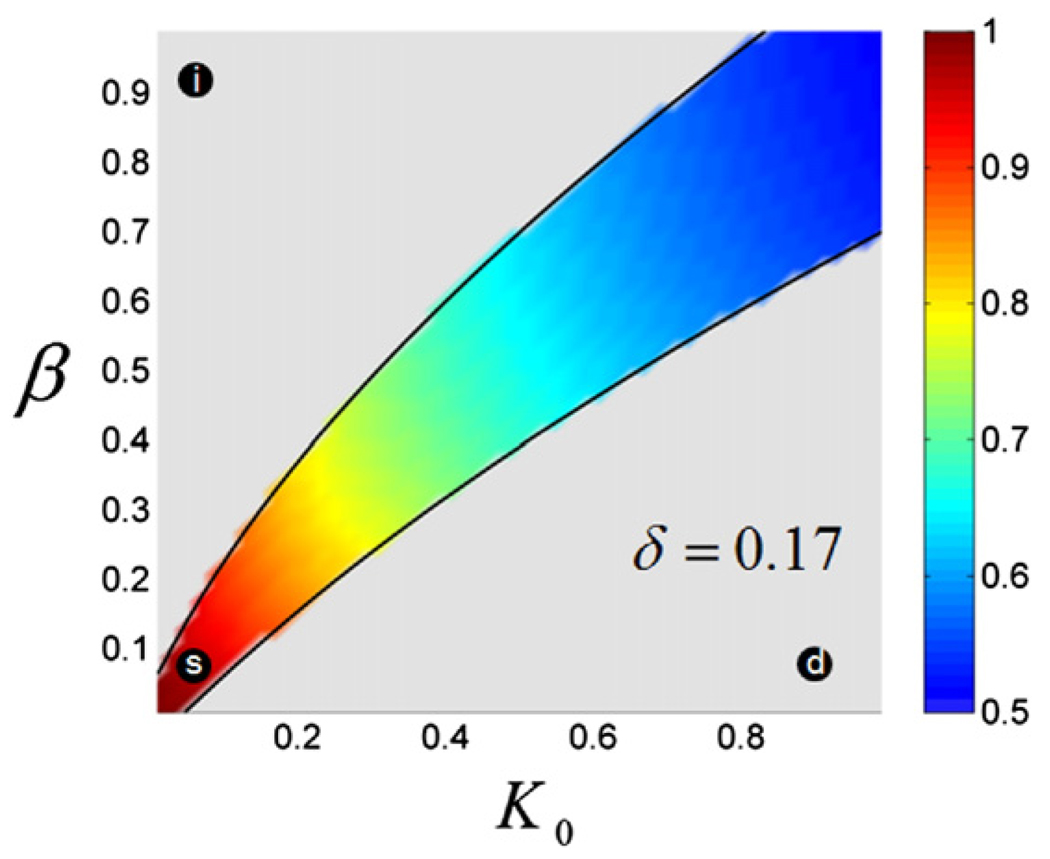
The parameters of our model do not have to be fine-tuned in order to generate the stable profiles of nuclear Bicoid (n(x, t)) in the face of the steady increase of the nuclear density. For example, Fig. 4 shows the two-dimensional projection (on the (β, K₀) plane) of the region of the parameter space that leads to gradients that at are least 10% accurate over the last 5 nuclear cycles. This projection has been calculated for δ = 0.17, which corresponds to the middle of the estimated range of Bicoid diffusivity (Gregor et al., 2005, 2007) and γ = 1, which corresponds to the case when the nuclei reform very quickly after the breakdown of the nuclear envelope (Gregor et al., 2007). We found that the boundaries of this stable region depend smoothly on the remaining parameters (γ and δ). Thus, the existence of the stable dynamics of the profiles of nuclear Bicoid is a robust feature of the model.

Fig. 4.

Stable gradients in the simplified model. The shaded region in the (β, K₀) plane corresponds to nuclear gradients that are at least 10% accurate over the five last nuclear cycles; see Materials and methods for the description of the accuracy criterion. The region has been computed for γ = 1 and δ = 0.17. The gradients above this region are steadily increasing as a function of nuclear density, while those below this region are steadily decreasing. The black circles correspond to the increasing (i), decreasing (d), and stable (s) gradients shown in Fig. 3. The color shading of the region shows the ratio of the widths (second moments) of the gradients, n(z, t), with and without the nuclei; see Materials and methods for details.

As in any diffusion and trapping problem, nuclei, which act as reversible traps in our model, can work both locally and nonlocally (Bressloff and Earnshaw, 2007; Casanova and Struhl, 1993; Chen and Struhl, 1996; Goentoro et al., 2006; Hufnagel et al., 2006; Lander, 2007). In the local regime, the traps affect only the local amounts of bound molecules, whereas in the nonlocal regime the traps can also influence the entire profile of free and bound molecules. The contribution of the non-local effect can be assessed by comparing the spatial spread of the Bicoid profiles in the presence and absence of nuclei. Fig. 4 shows the two-dimensional map of the ratio of the widths of the spatial profiles (within the stable region) of free Bicoid molecules with and without nuclei. For small values of β and K₀, the shapes of the gradients with and without nuclei are essentially identical. In this regime, which corresponds to fast nuclear cycles and small values of the binding equilibrium constant, nuclei just change the local density of the nuclear Bicoid molecules. The nonlocal effect, where nuclei affect the shape of the gradient, becomes important for larger values of β and K₀.

Model-based analysis of experimental observations

To better characterize the regime in which the system operates, we constrained the parameters of our model using three sets of experimental observations, each of which characterizes a different aspect of the formation of the Bicoid gradient. First, we used the measurements of the durations of different phases of the nuclear cycles (Foe and Alberts, 1983). These observations specify T₀, T_n,i, and T_f,i in our model; notice that now the durations of nuclear cycles are not identical, and each of them is characterized by its own pair of β and γ (Fig. 5). The values of remaining parameters δ and K₀ can be constrained by the quantitative measurements of the spatial decay length of the Bicoid gradient at cycle 14 (Gregor et al., 2005) and the information about the temporal accuracy of the nuclear levels of Bicoid during the cell cycles 10 to 14 (Gregor et al., 2007).

Fig. 5.

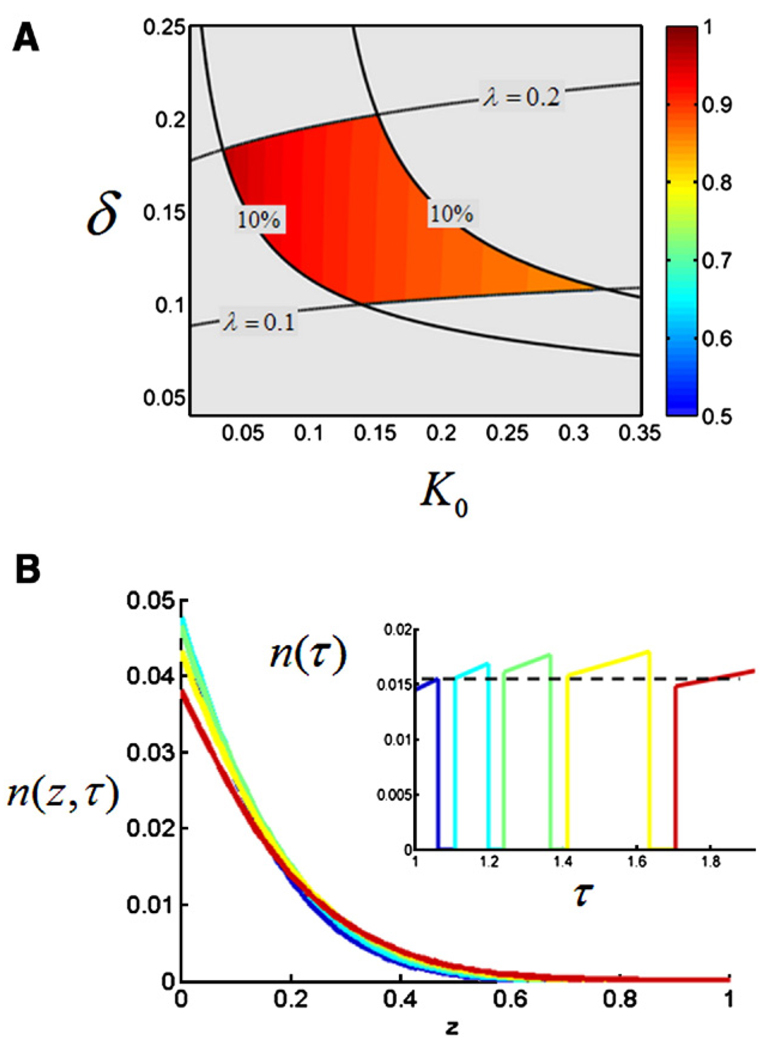
Model-based analysis of quantitative measurements of the Bicoid gradient. (A) Specifying the times of nuclear divisions leaves δ and K₀ as the only free parameters in the model. Their values are constrained to the shaded region by the experimental measurements of the shape and the accuracy of the Bicoid gradients. The shaded region is bounded by four sets of curves. The gradients above the upper curve are too shallow, while the ones below the bottom curve are too sharp. The sharpness of the gradient is determined by fitting it to an exponential profile; λ is the parameter of the fit. The bounds for the allowable range of the values of λ is provided by the experimentally available information about the distribution function of gradient decay lengths (Gregor et al., 2005). At the same time, only the gradients between the vertical lines satisfy the criterion of 10% accuracy over the five last nuclear divisions. (B) Dynamics of the gradient of nuclear Bicoid, n(z, r), computed for δ and K₀ inside the data consistency region. The inset shows the time course of the nuclear levels of Bicoid at z = 0.2, computed for K₀ = 0.15, δ = 0.15.

Specifically, we determined those values of δ and K₀, which predict the gradients that are at least 10% accurate in the anterior region of the embryo over the 5 last nuclear cycles and are consistent with the experimental measurements of the sharpness of the Bicoid gradient at nuclear cycle 14 (Gregor et al., 2005; Gregor et al., 2007). In this way we could constrain the values of δ and K₀ to the region shown in Fig. 5A. Every point within this region predicts stable nuclear gradients that are neither too shallow nor too sharp and are consistent with the dynamics of nuclear densities. With all the parameters of the model constrained in this way, we asked whether the stable gradients are generated due to the local or nonlocal effect of the nuclei. As before, we compared the ratio of the widths of the gradients with and without the nuclei (Fig. 5A). Based on this calculation, we concluded that the effect of nuclei is mainly local. This is not surprising since the average length of the late nuclear cycles corresponds to β ~ 0.1, which corresponds to the local regime in Fig. 4.

Thus, our analysis suggests that nuclei do not play a major role in determining the shape of the gradient and can be viewed as essentially inert sensors of the preestablished concentration field established from t = 0 to t = T₀. This is the main result of our analysis.

Analysis of the three-dimensional model

So far we have analyzed a one-dimensional model. Mean-while, an embryo is a rather complex three-dimensional object and its geometry might affect our conclusions. To quantify this effect we extended our model to a more realistic three-dimensional geometry. Since the early embryo is close to a prolate spheroid, the prolate spheroidal coordinate system is a natural coordinate system to model diffusion inside the embryo (Abramowitz and Stegun, 1964). In the revised model, during the first phase, Bicoid diffuses inside a three-dimensional spheroid with the aspect ratio corresponding to the major axes of the real embryo (Fig. 6A). After T₀, Bicoid diffuses inside a shell between the outer surface of the embryo and the surface of the yolk (Fig. 6B). All processes were the same as in the one-dimensional model, except that nuclei were included from t = 0, so that the diffusion coefficient is rescaled as in Eq. (5) throughout the first phase as well. To compare the resulting profiles with the one-dimensional model, we averaged the solution over the direction normal to the surface of the embryo. For the same value of the parameters, the shape of the profile is only slightly affected by the geometry (data not shown). Overall, our previously obtained conclusions remain valid, but the stability region is slightly shifted (Fig. 6B). Based on this, we conclude that our biophysical model is robust with respect to the approximations of system geometry.

Fig. 6.

Analysis of the three-dimensional model. (A) Finite difference grids used to solve the problem in the prolate spheroidal coordinate system (see text for details). (B) Comparison of the regions of the parameter space consistent with the experimentally derived quantitative properties of the Bicoid gradient: light gray—one-dimensional model, dark gray—three-dimensional model.

Concluding remarks

We have shown that a model with Bicoid diffusion and reversible trapping by nuclei can account for the experimentally observed length scale of the Bicoid gradient and its stability over multiple nuclear divisions. If this model is correct, then the Bicoid protein should be stable on the timescale on which the Bicoid gradient is formed. This prediction can be tested by careful measurements of Bicoid stability. Another prediction is that local defects in nuclear density should generate only local defects in the profile of nuclear Bicoid. This can be tested by imaging the Bicoid gradients in mutants with late defects in nuclear migration.

We have constrained the parameters in our model based on the observations of the Bicoid concentration profile. We can now work backwards and use the estimates of the dimensionless parameters in the model to quantify the rates of microscopic properties of the processes that contribute to the formation of the Bicoid gradient. For example, based on the estimated range for the parameter δ in the model, the size of the embryo (L), and the duration of first period in our model (T₀), we can get an estimate for the free diffusivity of Bicoid: D = δ²L²/T. Using this formula and extreme values for δ in Fig. 6B, we get 0.9 µm²/s<D<3.6 µm²/s. This is close to the range of experimentally reported Bicoid diffusivities, providing an additional consistency check for our assumptions (Gregor et al., 2005, 2007).

Similar to the diffusion and degradation model, our model does not readily account for scaling of the gradient with the size of the embryo (Gregor et al., 2005). A model where Bicoid degradation occurs in the nuclei can account for scaling but is not consistent with the stability of the gradient as a function of time, unless one assumes a very special correlation between nuclear density, nuclear size, and volume of the cortical cytoplasm (Gregor et al., 2007). The validity of this assumption is difficult to test at this time. While the scaling performance of our model can be improved by changing the time at which the nuclei migrate to the periphery, more detailed analysis of the gradient scaling in our model requires additional measurements of nuclear dynamics in insects with embryos of different lengths. We conclude that the model based on diffusion and reversible nuclear trapping presents at this time a viable alternative to the diffusion and degradation model and should be considered in analyzing the properties of the Bicoid gradient (Crauk and Dostatni, 2005; Ephrussi and St Johnston, 2004; Gibson, 2007; Gregor et al., 2005; Houchmandzadeh et al., 2002; Jaeger et al., 2007; Lebrecht et al., 2005; Reinitz, 2007; Tostevin et al., 2007).

The structure of the models that will be eventually used to describe the Bicoid gradient may turn out to be very similar to those used to describe morphogens in cellular tissues, with nuclei being the analogs of cells, and nucleocytoplasmic shuttling being the analog of ligand trafficking (Reeves et al., 2006; Vincent and Dubois, 2002). Thus, studies of the Bicoid gradient might provide insights into the operation of a large number of developmental patterning contexts.

Materials and methods

Nondimensionalization and numerical solution

The model is nondimensionalized using the following set of transformations: z = x / L, τ = t / T₀, and c(z, τ) = DC(x, t) / QL. The dimensionless form of Eq. (5) is given by: $\frac{\partial c_{\text{tot}}}{\partial \tau }=\frac{{\delta }^2}{1+K(\tau )}\frac{{\partial }^2{c}_{\text{tot}}}{\partial z^2}$ , where $\delta =\sqrt{{\mathit{\text{DT}}}_0/L}$ , and the value of K is zero during the nuclei-free periods and equal to 2ⁿK₀ (n = 0, 1, 2, 3, 4) during the nuclear periods of the division cycles. The dimensionless problem is discretized with centered finite differences on a uniform grid with 100 nodes, and the resulting system is solved using the ode15s solver in Matlab. From this solution for c_tot(z, τ), c_b(z, τ) is found as K(τ)c_tot(z, τ) / (1+K(τ)). The profiles of the dimensionless levels of Bicoid per nucleus are given by c_b(z, τ)/2ⁿ, n = 0, 1, 2, 3, 4.

Stability of the gradients

The gradients of the nuclear Bicoid levels were shown to be at least 10% accurate over the last five nuclear cycles between 10% and 50% of the embryo length (Gregor et al., 2007). Based on this, the stability of the gradients predicted by the model was computed as follows. First, we computed the space-dependent relative change (gain) of the gradient between the two successive nuclear cycles: g_{i, i−1} (z) = (n_i(z) − n_i−1(z)) / n_i−1(z), where 0.1 <z<0.5. We have then averaged this function over space and over consecutive cycles. If the absolute value of the result was less than 0.1, the gradient is considered stable.

Computing the width of the gradient

The spatial spread of the Bicoid gradient was computed as the second moment, σ, of the concentration profile of the total Bicoid at the last nuclear cycle: $\sigma ={\displaystyle {\int }_0^1{z}^2{c}_{\text{tot}}(z)\mathrm{d}z/}{\displaystyle {\int }_0^1{c}_{\text{tot}}(z)\mathrm{d}z}$.

Modeling in prolate spheroidal coordinate system

The prolate spheroidal coordinate system was used to model the embryo as an ellipsoid with the major and minor axes equal to 500 µm and 190 µm, respectively. For the second phase, the inner boundary was defined by the smaller ellipsoid, with axes equal to 240 µm and 132 µm.We used a point source at the anterior tip of the embryo and rescaled the problem using the same definition of the dimensionless parameters as in the one-dimensional model. We assumed that, during the nuclear phases, nuclei were uniformly distributed in the space available for Bicoid diffusion. All the timings for each nuclear cycles were taken from experimental data (Foe and Alberts, 1983). A second-order centered finite difference algorithm was used to solve the resulting initial value problem on a uniform 30 × 30 grid.