Abstract
The statistical reliability of diffusion property measurements was evaluated in ten healthy subjects using deterministic fiber tracking to localize tracts affected in motor neuron disease: corticospinal tract (CST), uncinate fasciculus (UNC), and the corpus callosum in its entirety (CC), and its genu (GE), motor (CCM), and splenium (SP) fibers separately. Measurements of fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (λ1), transverse diffusivity (λ⊥), and volume of voxels containing fibers (VV) were obtained within each tract. To assess intra-rater and inter-rater reliability, two raters carried out fiber tracking five times on each scan. Scan-rescan and longitudinal reliability were assessed in a subset of four subjects who had six scans, with two sets of three scans separated by one year. The statistical reliability of repeated measurements was evaluated using intra-class correlation coefficients (ICC) and coefficients of variation (CV). Spatial agreement of tract shape was assessed using the kappa (κ) statistic.
Results
Repeated same-scan fiber tracking evaluations showed good geometric alignment (intra-rater κ > 0.90, inter-rater κ > 0.76) and reliable diffusion property measurements (intra-rater ICC > 0.92, inter-rater ICC > 0.77). FA, MD, and λ⊥ were highly reliable with repeated scans on different days, up to a year apart (ICC > 0.8). VV also exhibited good reliability, but with higher CVs. We were unable to demonstrate reproducibility of λ1. Longitudinal reliability after one year was improved by averaging measurements from multiple scans at each timepoint. Fiber tracking provides a reliable tool for the longitudinal evaluation of white matter diffusion properties.
Keywords: diffusion tensor imaging, tractography, fiber tracking, corticospinal tract, corpus callosum, test-retest reliability
Introduction
Diffusion tensor imaging (DTI) has been widely used to study the integrity of white matter tracts in a variety of neurological diseases since its introduction in 1994 (Basser et al., 1994). Most studies have assessed fractional anisotropy (FA) and mean diffusivity (MD) in regions of interest (ROIs) within white matter tracts that were identified by anatomical landmarks. More recently, deterministic fiber tracking algorithms have been used to reconstruct white matter tracts (Catani et al., 2002; Conturo et al., 1999; Wakana et al., 2004) by mapping tensors with a common direction (Mori et al., 1999) on the assumption that the primary diffusion direction is aligned parallel to fibers within the tracts (Le Bihan et al., 1986; Pierpaoli et al., 1996). For each tract that is localized by fiber tracking algorithms, values of anisotropy, diffusivity, and volume of “fibers” can be calculated over its tracked extent.
Normative data for FA and MD measurements have been established for a number of tracts and anatomical structures (Huisman et al., 2006; Hunsche et al., 2001; Lee et al., 2008). Most studies using DTI in neurological disorders have measured FA and MD. In a number of diseases, such as amyotrophic lateral sclerosis (ALS) (Ciccarelli et al., 2006; Ellis et al., 1999; Iwata et al., 2008; Sach et al., 2004; Sage et al., 2007; Yin et al., 2008), primary lateral sclerosis (PLS) (Ulug et al., 2004), frontotemporal dementia (FTD) (Matsuo et al., 2008), multiple sclerosis (Cassol et al., 2004), and stroke (Gupta et al., 2006; Moller et al., 2007), DTI has demonstrated quantifiable changes in these water diffusion properties compared to healthy controls. The decreases in FA and increases in MD that are measured in these disorders provide evidence for disruption of tissue microstructure, including axons and myelin in various white matter tracts (Basser and Pierpaoli, 1996; Pierpaoli et al., 2001). There are a relatively small number of reports on changes in other quantitative fiber tracking measures in neurological disease (Thomas et al., 2005; Wang et al., 2006; Yin et al., 2008).
In the field of motor neuron disease (MND) research, there is a need for quantitative objective markers to assess corticospinal or upper motor neuron (UMN) dysfunction and disease progression (Dengler et al., 2005; Floyd et al., 2009; Mitsumoto et al., 2007; Wang and Melhem, 2005). DTI may be a promising marker to follow longitudinal changes in white matter tracts in neurodegenerative diseases. Correlations between clinical ratings and imaging findings of FA and MD in the corticospinal tract were seen in ALS using both 2D-ROI and fiber tracking techniques (Ellis et al., 1999; Sage et al., 2007; Schimrigk et al., 2007). Additionally, in ALS, changes in FA are measurable prior to the observation of clinical signs (Sach et al., 2004). DTI has been successful in following longitudinal changes in various white matter tracts with disease progression or therapeutic interventions in multiple sclerosis and stoke (Cassol et al., 2004; Gupta et al., 2006; Liang et al., 2008; Moller et al., 2007; Reich et al., 2006). However, for longitudinal studies to be feasible in motor neuron disorders, it is imperative to establish that DTI measurements can be made reliably on individual subjects.
There are several sources of variability in DTI measures including noise, partial volume effects, and variations in manual ROI placement techniques (Farrell et al., 2007; Ozturk et al., 2008; Schimrigk et al., 2007). In fiber tracking, in particular, sources of variability include localization of white matter tracts by human raters, as well as changes in MRI scanner characteristics and subject alignment from scan to scan (Holodny et al., 2005; Huang et al., 2004; Pierpaoli et al., 2001; Reich et al., 2006; Wakana et al., 2007). Previous studies using 2D-ROI anatomical analysis methods showed high reproducibility of evaluations of FA and MD from same-subject scans performed on separate days (Bonekamp et al., 2007; Pfefferbaum et al., 2003; Schimrigk et al., 2007). Recent studies have indicated that fiber tracking may provide more reproducible fiber tract measures (Partridge et al., 2005). Studies that performed fiber tracking on a single set of data using anatomically-based ROI algorithms showed high reproducibility of repeated measurements of FA and MD both by a single rater and between multiple raters (Huang et al., 2004; Stieltjes et al., 2001; Wakana et al., 2007). To our knowledge, only two previous studies, both using probabilistic tracking methods, investigated the scan-rescan reliability of fiber tracking in various white matter tracts (Ciccarelli et al., 2003; Heiervang et al., 2006). However, the scan-rescan reliability and longitudinal variability of numerous fiber tracking measurements, particularly over longer time frames, is not well established.
The goals of this study were to assess the intra-rater and inter-rater reliability of measurements of FA and MD in several white matter tracts that are affected in MND and related disorders, such as FTD (Geser et al., 2009; Matsuo et al., 2008), using fiber tracking methods to define the tracts of interest. Intra-class correlation coefficients (ICCs) and coefficients of variation (CVs) were calculated to assess statistical reliability of repeated measurements. Spatial agreement of tract shape was evaluated with Cohen’s kappa (κ). Specifically, we evaluated the corticospinal tract (CST), uncinate fasciculus (UNC), and the corpus callosum (CC). Because the CC is made up of fibers arising from several areas that may be differentially affected in MNDs, we assessed the CC in its entirety and separately assessed its genu (GE), motor fibers (CCM), and splenium (SP) of the corpus callosum. We also evaluated the reliability of several diffusion measurements that have received less mention in past publications: axial diffusivity (λ1) and transverse diffusivity (λ⊥), which, when used cautiously, may be useful in classifying white matter degeneration (Pierpaoli et al., 2001; Wheeler-Kingshott and Cercignani, 2009), as well as the volume of voxels containing fibers (VV). Additionally, we quantified the scan-rescan and longitudinal reliability of repeated diffusion property measures for a clinically salient interval of one year.
Materials and methods
Subjects
Ten healthy volunteers (mean age 59.3 years, range 50–72, 5 males and 5 females) underwent DTI MRI scanning. All subjects had normal neurological exams and no history of psychological illness. A subset of four subjects repeated the DTI MRI scan six times, with two sets of three scans separated by approximately one year. All subjects gave written informed consent to participate in the study, which was approved by the Institutional Review Board.
MRI Data Acquisition
All imaging was performed at 3T (Philips Intera and Philips Achieva MRI scanners, Best, The Netherlands) using a receive-only, eight channel SENSE headcoil. All subjects were scanned once on the 3T Philips Intera, and these scans were used to assess intra-rater and inter-rater reliability. For assessment of scan-rescan reliability and longitudinal reliability, MRI scans were performed on four subjects on two different scanners; the first set of three was performed on a 3T Philips Intera and the second set was performed on a 3T Philips Achieva. The same scanning sequence was performed on each scanner. Multi-slice diffusion weighted imaging was acquired using a single-shot spin-echo echo-planar sequence (55 contiguous slices, slice thickness = 2.5mm, matrix = 96×96 reconstructed to 128×128, FOV = 240×240, TE = 86ms). Slices were aligned parallel to the AC-PC line. Diffusion weighting was performed along 32 noncollinear directions with a b-value of 1000sec/mm2 and a single volume was collected with no diffusion gradients applied (b0). The diffusion sequence was repeated 4 times to increase the signal to noise ratio. An axial T2-weighted image with the same slice positions as the DTI scans was also collected for anatomical guidance (55 contiguous slices, slice thickness = 2.5mm, matrix = 128×128, FOV = 240×240, TR/TE = 5400ms/100ms).
Data Processing
Image processing was performed using both FSL (University of Oxford, UK) (Smith et al., 2004) and DtiStudio (Johns Hopkins University, Baltimore, MD, USA) (Jiang et al., 2006). The DTI volumes were corrected for movement and eddy current distortion using FSL’s FLIRT, a linear image registration tool (Jenkinson and Smith, 2001). The registered images were masked to remove skull and non-brain tissue using the FSL Brain Extraction Tool (BET) (Smith, 2002).
The diffusion volumes were then imported into DtiStudio for visual inspection and removal of images with artifacts. To ensure that the same anatomy was analyzed for each subject, slices from the top of the cortex to 3 slices inferior to the most caudal slice containing the middle cerebellar peduncle were included in the tensor analysis. Using DtiStudio, a 3×3 diffusion tensor was calculated for each voxel using multivariate linear fitting. The tensors were diagonalized to obtain the eigenvalues (λ1, λ2, and λ3) and eigenvectors (v1, v2, and v3) for each voxel, from which FA, MD, and color maps were derived (Pajevic and Pierpaoli, 1999; Pierpaoli et al., 1996; Xue et al., 1999). The eigenvector (v1) associated with the largest eigenvalue (λ1) is assumed to represent the local fiber direction (Xue et al., 1999).
Fiber Tracking
Fiber tracking was performed in DtiStudio using the Fiber Assignment by Continuous Tracking (FACT) method (Mori et al., 1999; Xue et al., 1999) on the following tracts: right and left side corticospinal tract, right and left side uncinate fasciculus, entire corpus callosum, genu, motor fibers of the corpus callosum, and splenium. Tracking was initiated at an FA value of 0.2 and was terminated when FA fell below 0.2 or the angle between two adjacent eigenvectors was greater than 40 degrees.
Corticospinal Tract (CST)
The CST was tracked bilaterally using a multiple-ROI approach as outlined by Wakana and colleagues (Wakana et al., 2007). The first “OR” ROI was drawn on an axial slice of the color map to include the entire cerebral peduncle at the level of the decussation of the superior cerebellar peduncle. A second “AND” ROI was then drawn around the primary motor cortex fiber bundle, one slice superior to the bifurcation of the motor and sensory fibers at the level of the central sulcus. “NOT” ROIs were then used to remove any non-CST fibers that crossed the midline into the contralateral hemisphere or projected to the cerebellum.
Uncinate Fasciculus (UNC)
The UNC was tracked bilaterally using a multiple-ROI approach as outlined by Wakana and colleagues (Wakana et al., 2007). The first “OR” ROI was drawn around the entire temporal lobe on the posterior-most coronal slice that contains a separation of the temporal and frontal lobes. A second “AND” ROI was then drawn around the entire frontal lobe on the same coronal slice.
Corpus Callosum – Entire (CC)
The CC was tracked in its entirety using a single “OR” ROI on the mid-sagittal slice as described in Catani and colleagues (Catani et al., 2002).
Genu of the Corpus Callosum (GE)
The genu, as defined by Witelson in 1989 (Witelson, 1989), was tracked using a single “OR” ROI on the mid-sagittal slice that encompasses the entire anterior bend of the corpus callosum, with the posterior boundary of the ROI aligned with the interior bend of the genu. The posterior boundary of the ROI was drawn vertically in order to exclude rostral fibers of the callosum.
Motor Fibers of the Corpus Callosum (CCM)
To localize the motor fibers of the corpus callosum, we isolated CC fibers that connected the right and left side motor cortexes. First, an “OR” ROI was drawn around the entire CC on the mid-sagittal slice. Next, an “AND” ROI was drawn around the entire left side motor cortex, one slice superior to the bifurcation of the motor and sensory fibers at the level of the central sulcus. A second “AND” ROI was drawn around the right side motor cortex in the same manner.
Splenium of the Corpus Callosum (SP)
The splenium is defined anatomically as the posterior bulbous region of the corpus callosum (Witelson, 1989). First, the anterior boundary of the splenium was identified by examining coronal color map slices for a broadening of the CC posterior to the isthmus. The anterior-most coronal slice that did not contain the isthmus was used as a vertical marker in the sagittal plane. Next, a single “OR” ROI was drawn around the posterior of the CC on the mid-sagittal slice, using the coronal slice as the anterior border of the ROI.
Measurements of mean FA, mean MD (trace/3, 10−3 mm2/s), mean λ1 (axial diffusivity, 10−3 mm2/s), mean λ⊥ (transverse diffusivity, the average of λ2 and λ3, the two smallest eigenvalues, 10−3 mm2/s), and volume of voxels containing fibers (VV) were then calculated within each localized tract. VV was calculated by multiplying the total number of voxels that were occupied by the reconstructed fibers by the voxel size (1.875mm*1.875mm*2.5mm).
Study 1: Intra-rater and Inter-rater Reliability
Two raters experienced in fiber tracking independently performed measurements to assess intra-rater reliability. Fiber tracking was repeated by each rater five times on the same scan from each of the ten subjects, with evaluations separated by at least four days. Inter-rater reliability was assessed using the mean of the five measures for each rater.
Study 2: Scan-rescan and Longitudinal Reliability
To assess the scan-to-scan reliability of fiber tracking, a subset of four subjects was scanned six times on two different but similar scanners, and fiber tracking was carried out once on each scan by Rater 1. The six scans were split into two sets of three scans, with each set obtained on separate occasions within a one-month period on the same scanner. The second set of three scans was obtained one year after the first on a different 3T Philips MRI scanner. Within each set, the scan-rescan reliability takes into account the variability introduced by changes in the MRI scanner environment and head alignment within the scanner without changes to MRI scanner hardware and software.
To evaluate longitudinal reliability, measurements from the first set of scans were compared to those from the second set of scans collected one year later. This assessment of longitudinal reliability measures the additional variability contributed by changes to the MRI scanner hardware and software over time. In addition, an important question for the feasibility of using DTI for clinical purposes is whether reliability is significantly improved by performing more than one scan at each timepoint. This question was assessed by calculating reliability statistics using one (Longitudinal-Single Scan), two (Longitudinal-Average of 2), or three (Longitudinal-Average of 3) scans from each set.
Statistical Analysis
Values are expressed as mean ± SD throughout. To quantify reliability, intraclass correlation coefficients (ICCs) were calculated for measures of FA, MD, λ1, λ⊥, and VV within the CST, UNC, CC, GE, CCM, and SP using a two-way random-model analysis of variance with absolute agreement. ICC values greater than 0.80 were defined as excellent agreement and values between 0.60 and 0.79 were defined as substantial agreement (Shrout and Fleiss, 1979). Absolute p values are reported. The coefficient of variation (CV) was also calculated to describe the variability of each measurement. To evaluate differences between right and left side measurements in the CST and UNC, students’ t-tests were performed with a 95% confidence interval. Wilcoxon signed-rank tests were performed on the repeated FA and MD measurements in Study 2 to determine if aging had an effect on the data over a one-year period. Statistics were calculated using SPSS Statistics, Release 17.0.0.
Spatial agreement of tract shape was evaluated with Cohen’s kappa (κ) using a process outlined by Wakana et. al. (Wakana et al., 2007). Results from each of the 5 fiber tracking trials performed by each rater in Study 1 were converted to a binary format in which pixels that contained the tract were set to 1 and all other pixels were set to 0. Two fiber tracking trials were then superimposed, creating four pixel categories: (1) pixels that did not contain the tract in both trials (nn), (2) pixels that contained the tract in only one of the two trials (pn, np), and (3) pixels that contained the tracts in both trials (pp). Expectation values, observed agreement, and expected agreement were calculated from these pixel categories (see Wakana et. al. 2007 for equations). κ was calculated using: κ=(observed agreement-expected agreement)/(100-expected agreement). The κ evaluations were conducted in a pair-wise manner, using all possible combinations of the fiber tracking trials. The pair-wise combination of trials yielded 10 combinations for each intra-rater evaluation and 25 combinations for each inter-rater evaluation. An average κ was calculated for each measurement within each tract. κ values are considered as “substantial” agreement from 0.61 – 0.80 and “almost perfect” agreement from 0.81 – 1.0 (Landis and Koch, 1977).
Results
Study 1: Intra-rater and Inter-rater Reliability
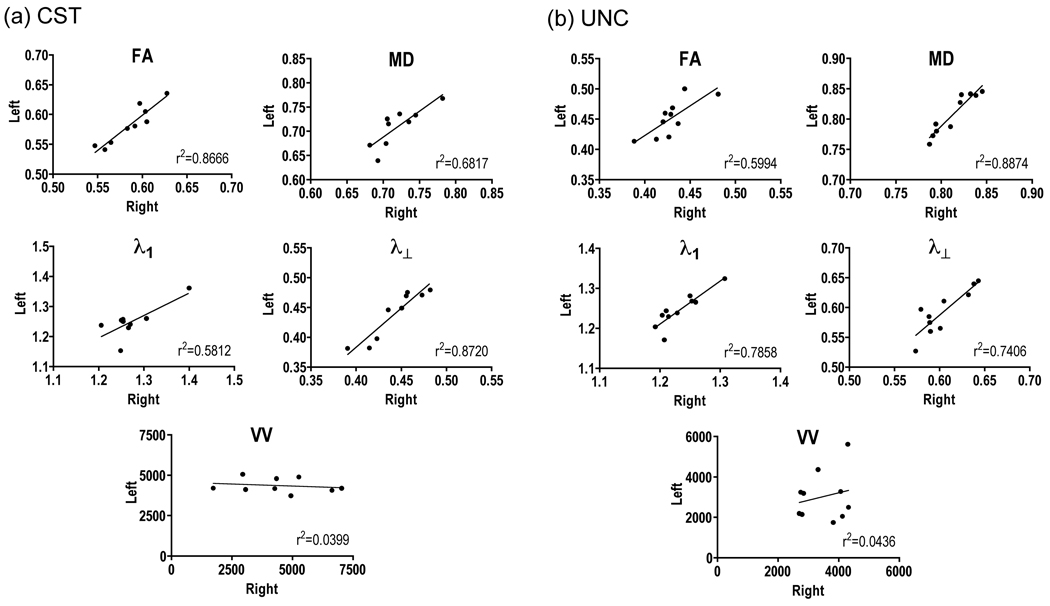
The FA and MD values obtained in the CST were consistent with previous studies using similar tracking techniques (Reich et al., 2006; Yin et al., 2008), although values of axial and transverse diffusivity (λ1, λ⊥) in the CST were slightly lower than previously reported (Reich et al., 2006). Measurements of FA, MD, λ1, λ⊥ and VV in the UNC fall within the range of previously reported values in studies using similar tracking protocols (Hasan et al., 2009; Malykhin et al., 2008; Matsuo et al., 2008; Wakana et al., 2007). FA measurements in the left side UNC were significantly larger than in the right side (t = −3.767, p = 0.004). No other significant differences were found in measurements between the right and left sides in the CST or UNC (Figure 1). Right and left side measurements in the CST and UNC were significantly correlated for FA, MD, λ1, and λ⊥ (r2 > 0.5812. p < 0.017), but not for measurements of VV (r2 < 0.0436, p > 0.5625).
Fig. 1.
Plots of right and left side measurements of FA, MD, λ1, λ⊥, and VV in the (a) corticospinal tract and (b) uncinate fasciculus.
With one exception, the intra-rater and inter-rater reliability (Table 1) of fiber tracking measurements in all evaluated tracts was extremely high, with ICCs > 0.8. The only measurement that did not meet the criterion for excellent reliability was inter-rater VV measurements in the left side CST (ICC = 0.77). Intra-rater and inter-rater measurements in the CC, when assessed in its entirety with a single ROI, were particularly reliable, with ICCs near unity and a small CV for all diffusion parameters measured. Measurements in the CST, UNC, GE, CCM, and SP were also reliable, but were slightly more variable than those of the CC. Nevertheless, the CVs of FA, MD, λ1, and λ⊥ in these tracts were less than 1% for both intra-rater and inter-rater measurements. In contrast, measures of VV, which were particularly affected by individual differences in tract shape among subjects, were more variable, with CVs between 2.1% and 10.2% for intra-rater measurements and 1.9% and 25.3% for inter-rater measurements.
Table 1.
Intra-rater and inter-rater reliability
| Intra-Rater | Inter-Rater | ||||||
|---|---|---|---|---|---|---|---|
| Measurement | Mean ± SD | ICC | p | CV (%) | ICC | p | CV (%) |
| CST (Right Side) | |||||||
| FA | 0.584 ± 0.024 | 0.98 | < 0.001 | 0.4 | 0.99 | < 0.001 | 0.5 |
| MD | 0.718 ± 0.028 | 0.99 | < 0.001 | 0.3 | 1.00 | < 0.001 | 0.1 |
| λ1 | 1.267 ± 0.053 | 0.99 | < 0.001 | 0.3 | 0.99 | < 0.001 | 0.3 |
| λ⊥ | 0.443 ± 0.026 | 0.99 | < 0.001 | 0.3 | 0.81 | < 0.001 | 0.4 |
| VV | 4512 ± 1625 | 0.95 | < 0.001 | 5.4 | 0.95 | < 0.001 | 7.6 |
| CST (Left Side) | |||||||
| FA | 0.583 ± 0.031 | 1.00 | < 0.001 | 0.2 | 0.99 | < 0.001 | 0.6 |
| MD | 0.725 ± 0.158 | 1.00 | < 0.001 | 0.2 | 0.99 | < 0.001 | 0.4 |
| λ1 | 1.250 ± 0.051 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.2 |
| λ⊥ | 0.439 ± 0.039 | 1.00 | < 0.001 | 0.2 | 0.98 | < 0.001 | 0.9 |
| VV | 4362 ± 877 | 0.92 | < 0.001 | 4.8 | 0.77 | 0.014 | 12.6 |
| UNC (Right Side) | |||||||
| FA | 0.429 ± 0.023 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.2 |
| MD | 0.813 ± 0.020 | 1.00 | < 0.001 | 0.1 | 1.00 | < 0.001 | 0.1 |
| λ1 | 1.233 ± 0.033 | 0.99 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.2 |
| λ⊥ | 0.603 ± 0.025 | 0.92 | < 0.001 | 0.4 | 1.00 | < 0.001 | 0.1 |
| VV | 3500 ± 679 | 0.96 | < 0.001 | 3.0 | 0.98 | < 0.001 | 3.0 |
| UNC (Left Side) | |||||||
| FA | 0.452 ± 0.029 | 1.00 | < 0.001 | 0.3 | 1.00 | < 0.001 | 0.1 |
| MD | 0.808 ± 0.032 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.1 |
| λ1 | 1.246 ± 0.042 | 0.93 | < 0.001 | 0.4 | 0.99 | < 0.001 | 0.2 |
| λ⊥ | 0.589 ± 0.035 | 1.00 | < 0.001 | 0.2 | 0.99 | < 0.001 | 0.8 |
| VV | 3033 ± 1166 | 0.96 | < 0.001 | 5.1 | 0.99 | < 0.001 | 1.9 |
| CC (Entire) | |||||||
| FA | 0.574 ± 0.025 | 1.00 | < 0.001 | < 0.05 | 1.00 | < 0.001 | < 0.05 |
| MD | 0.826 ± 0.047 | 1.00 | < 0.001 | < 0.05 | 1.00 | < 0.001 | < 0.05 |
| λ1 | 1.441 ± 0.063 | 1.00 | < 0.001 | < 0.05 | 1.00 | < 0.001 | < 0.05 |
| λ⊥ | 0.518 ± 0.044 | 1.00 | < 0.001 | < 0.05 | 1.00 | < 0.001 | < 0.05 |
| VV | 100440 ± 14585 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.3 |
| GE | |||||||
| FA | 0.510 ± 0.033 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.2 |
| MD | 0.836 ± 0.054 | 0.99 | < 0.001 | 0.3 | 1.00 | < 0.001 | 0.3 |
| λ1 | 1.365 ± 0.116 | 0.99 | < 0.001 | 0.3 | 1.00 | < 0.001 | 0.2 |
| λ⊥ | 0.566 ± 0.059 | 0.99 | < 0.001 | 0.4 | 1.00 | < 0.001 | 0.4 |
| VV | 13563 ± 3500 | 0.94 | < 0.001 | 4.4 | 0.97 | < 0.001 | 4.8 |
| CCM | |||||||
| FA | 0.496 ± 0.168 | 0.99 | < 0.001 | 0.4 | 0.98 | < 0.001 | 0.6 |
| MD | 0.676 ± 0.230 | 0.99 | < 0.001 | 0.4 | 1.00 | < 0.001 | 0.3 |
| λ1 | 1.162 ± 0.394 | 0.95 | < 0.001 | 0.7 | 0.99 | < 0.001 | 0.6 |
| λ⊥ | 0.433 ± 0.150 | 0.99 | < 0.001 | 0.6 | 1.00 | < 0.001 | 0.5 |
| VV | 4415 ± 2883 | 0.97 | < 0.001 | 10.2 | 0.87 | 0.004 | 25.3 |
| SP | |||||||
| FA | 0.610 ± 0.028 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.3 |
| MD | 0.829 ± 0.048 | 0.99 | < 0.001 | 0.4 | 1.00 | < 0.001 | 0.2 |
| λ1 | 1.492 ± 0.062 | 1.00 | < 0.001 | 0.1 | 1.00 | < 0.001 | 0.1 |
| λ⊥ | 0.497 ± 0.047 | 1.00 | < 0.001 | 0.2 | 1.00 | < 0.001 | 0.3 |
| VV | 49940 ± 8767 | 0.98 | < 0.001 | 2.1 | 0.98 | < 0.001 | 3.3 |
Abbreviations: ICC=intraclass correlation coefficient, CV=coefficient of variation, CST=corticospinal tract, UNC=uncinate fasciculus, CC=corpus callosum, GE=genu, CCM=corpus callosum motor fibers, SP=splenium, FA=fractional anisotropy, MD=mean diffusivity, λ1=axial diffusivity, λ⊥=transverse diffusivity, VV=volume of voxels containing fibers. Units: 10−3 mm2/s (MD, λ1, λ⊥), mm3 (VV).
κ values of spatial agreement of tract shape (Table 2) demonstrated “almost perfect” agreement for intra-rater and inter-rater fiber tracking trials in all tracts, except for the inter-rater evaluation of CCM, which demonstrated “substantial” agreement (κ = 0.76).
Table 2.
κ values of intra-rater and inter-rater reliability
| Tract | Intra-Rater | Inter-Rater |
|---|---|---|
| CST (Right Side) | 0.96 | 0.93 |
| CST (Left Side) | 0.96 | 0.88 |
| UNC (Right Side) | 0.98 | 0.97 |
| UNC (Left Side) | 0.97 | 0.96 |
| CC (Entire) | 1.00 | 1.00 |
| GE | 0.98 | 0.96 |
| CCM | 0.90 | 0.76 |
| SP | 0.99 | 0.98 |
Abbreviations listed in table 1.
Study 2: Scan-rescan and Longitudinal Reliability
To assess scan-rescan reliability, measurements were compared within each set of three scans that had been obtained on the same scanner on separate occasions within a one-month span (Table 3, left columns). Measurements of FA, MD, and λ⊥ in all tracts had excellent reliability between scans (ICC > 0.8), and low variability in measurement, with CVs under 2.5 percent. Measures of VV also had good scan-rescan reliability, but these measures had greater variability, with CVs between 4.1% and 21.8%. Measurements of λ1 were not reproducible between scans in the CST. ICC values for λ1 ranged from 0.58 to 0.90 in the remaining tracts. Wilcoxon signed–rank tests discovered no trend in FA or MD measurements in any of the evaluated tracts from one year to the next (Z < 2, p > 0.05).
Table 3.
Scan-rescan and longitudinal reliability
| Scan-Rescan | Longitudinal Single Scan |
Longitudinal Average of 2 |
Longitudinal Average of 3 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measurement | ICC | p | CV(%) | ICC | p | CV(%) | ICC | p | CV(%) | ICC | p | CV(%) |
| CST (Right Side) | ||||||||||||
| FA | 0.93 | < 0.001 | 1.3 | 0.92 | 0.011 | 1.3 | 0.93 | 0.017 | 1.6 | 0.96 | 0.013 | 1.3 |
| MD | 0.83 | < 0.001 | 1.4 | 0.99 | < 0.001 | 0.4 | 0.99 | < 0.001 | 0.6 | 0.98 | 0.004 | 0.7 |
| λ1 | U | 0.684 | 1.3 | 0.05 | 0.472 | 0.7 | U | 0.838 | 0.9 | 0.93 | 0.040 | 0.3 |
| λ⊥ | 0.93 | < 0.001 | 1.9 | 0.97 | 0.002 | 1.3 | 0.97 | < 0.001 | 1.8 | 0.97 | 0.008 | 1.7 |
| VV | 0.86 | < 0.001 | 7.4 | 0.97 | 0.003 | 4.2 | 0.99 | 0.002 | 2.3 | 0.98 | 0.004 | 3.7 |
| CST (Left Side) | ||||||||||||
| FA | 0.96 | < 0.001 | 1.5 | 0.98 | 0.002 | 1.0 | 0.99 | 0.002 | 1.3 | 1.00 | < 0.001 | 0.6 |
| MD | 0.83 | < 0.001 | 1.5 | 0.92 | < 0.001 | 1.4 | 0.95 | < 0.001 | 1.6 | 0.97 | 0.005 | 0.9 |
| λ1 | U | 0.461 | 1.4 | 0.16 | 0.159 | 1.2 | 0.14 | 0.235 | 1.1 | 0.27 | 0.378 | 0.9 |
| λ⊥ | 0.94 | < 0.001 | 2.3 | 0.97 | < 0.001 | 1.8 | 0.98 | < 0.001 | 2.2 | 0.99 | < 0.001 | 1.0 |
| VV | 0.77 | < 0.001 | 8.7 | 0.97 | 0.002 | 3.0 | 0.99 | < 0.001 | 2.6 | 0.99 | 0.002 | 3.3 |
| UNC (Right Side) | ||||||||||||
| FA | 0.89 | < 0.001 | 1.3 | 0.88 | 0.034 | 1.0 | 0.97 | 0.009 | 0.9 | 0.98 | 0.007 | 0.8 |
| MD | 0.91 | < 0.001 | 1.4 | 0.48 | 0.046 | 3.8 | 0.83 | 0.007 | 2.8 | 0.87 | 0.002 | 2.5 |
| λ1 | 0.80 | < 0.001 | 1.5 | 0.22 | 0.148 | 3.6 | 0.64 | 0.019 | 2.9 | 0.73 | 0.003 | 2.5 |
| λ⊥ | 0.94 | < 0.001 | 1.5 | 0.65 | 0.025 | 3.9 | 0.91 | 0.005 | 2.7 | 0.92 | 0.002 | 2.6 |
| VV | 0.68 | < 0.001 | 12.3 | 0.85 | 0.046 | 6.9 | 0.99 | < 0.001 | 3.1 | 0.96 | 0.013 | 6.4 |
| UNC (Left Side) | ||||||||||||
| FA | 0.88 | < 0.001 | 2.0 | 0.84 | 0.023 | 2.8 | 0.92 | 0.003 | 2.6 | 0.96 | 0.002 | 1.6 |
| MD | 0.92 | < 0.001 | 1.2 | 0.97 | 0.005 | 0.8 | 0.99 | 0.003 | 0.8 | 0.99 | 0.004 | 0.8 |
| λ1 | 0.79 | < 0.001 | 1.1 | 0.65 | 0.091 | 1.4 | 0.84 | 0.040 | 1.4 | 0.84 | 0.061 | 1.4 |
| λ⊥ | 0.93 | < 0.001 | 1.9 | 0.97 | 0.003 | 1.4 | 0.98 | < 0.001 | 1.4 | 0.99 | < 0.001 | 0.9 |
| VV | 0.73 | < 0.001 | 21.8 | 0.82 | 0.051 | 9.6 | 0.89 | 0.021 | 12.2 | 0.98 | < 0.001 | 7.1 |
| CC (Entire) | ||||||||||||
| FA | 0.87 | < 0.001 | 1.4 | 0.74 | 0.019 | 2.6 | 0.86 | 0.018 | 2.4 | 0.91 | 0.005 | 1.7 |
| MD | 0.83 | < 0.001 | 1.2 | 0.96 | 0.006 | 0.8 | 0.99 | 0.003 | 0.5 | 0.98 | 0.004 | 0.7 |
| λ1 | 0.61 | 0.004 | 1.3 | 0.21 | 0.296 | 1.6 | 0.84 | 0.025 | 1.1 | 0.83 | 0.049 | 1.0 |
| λ⊥ | 0.87 | < 0.001 | 2.0 | 0.97 | < 0.001 | 1.3 | 0.97 | 0.005 | 1.6 | 0.99 | < 0.001 | 0.9 |
| VV | 0.92 | < 0.001 | 4.1 | 0.94 | 0.004 | 5.2 | 0.98 | < 0.001 | 3.0 | 0.99 | < 0.001 | 2.4 |
| GE | ||||||||||||
| FA | 0.97 | < 0.001 | 1.0 | 0.84 | 0.009 | 2.3 | 0.93 | < 0.001 | 2.4 | 0.94 | < 0.001 | 2.0 |
| MD | 0.91 | < 0.001 | 1.3 | 0.84 | 0.017 | 1.7 | 0.97 | 0.003 | 0.9 | 0.98 | < 0.001 | 1.0 |
| λ1 | 0.80 | < 0.001 | 1.2 | 0.31 | 0.011 | 2.8 | 0.64 | 0.002 | 2.2 | 0.73 | 0.003 | 2.1 |
| λ⊥ | 0.95 | < 0.001 | 1.6 | 0.93 | 0.016 | 1.7 | 0.99 | 0.003 | 1.1 | 1.00 | < 0.001 | 0.6 |
| VV | 0.91 | < 0.001 | 6.9 | 0.92 | < 0.001 | 7.2 | 0.98 | 0.003 | 4.0 | 1.00 | < 0.001 | 2.4 |
| CCM | ||||||||||||
| FA | 0.80 | < 0.001 | 1.4 | 0.83 | 0.039 | 1.3 | 0.90 | 0.042 | 1.2 | 0.95 | 0.023 | 1.0 |
| MD | 0.90 | < 0.001 | 1.9 | 0.84 | 0.006 | 3.3 | 0.95 | < 0.001 | 2.5 | 0.95 | 0.003 | 2.1 |
| λ1 | 0.90 | < 0.001 | 1.9 | 0.87 | 0.006 | 2.4 | 0.93 | 0.006 | 1.8 | 0.97 | < 0.001 | 1.8 |
| λ⊥ | 0.85 | < 0.001 | 2.5 | 0.82 | 0.009 | 4.4 | 0.93 | 0.005 | 3.4 | 0.94 | 0.005 | 2.6 |
| VV | 0.97 | < 0.001 | 18.3 | 0.98 | 0.002 | 12.9 | 0.99 | 0.003 | 21.0 | 0.98 | 0.005 | 16.4 |
| SP | ||||||||||||
| FA | 0.82 | < 0.001 | 1.6 | 0.71 | 0.036 | 2.7 | 0.82 | 0.034 | 2.6 | 0.91 | 0.007 | 1.7 |
| MD | 0.81 | < 0.001 | 1.5 | 0.85 | 0.044 | 1.7 | 0.96 | 0.012 | 1.4 | 0.95 | 0.023 | 1.3 |
| λ1 | 0.58 | 0.006 | 1.5 | U | 0.582 | 2.3 | 0.86 | 0.085 | 1.2 | 0.78 | 0.148 | 1.4 |
| λ⊥ | 0.84 | < 0.001 | 2.5 | 0.92 | 0.004 | 2.2 | 0.94 | 0.010 | 2.5 | 0.97 | 0.006 | 1.8 |
| VV | 0.92 | < 0.001 | 4.6 | 0.94 | 0.010 | 5.3 | 0.99 | 0.002 | 2.9 | 0.99 | 0.002 | 2.3 |
Abbreviations: See table 1, U=unreliable (ICC < 0.01). Units: 10−3 mm2/s (MD, λ1, λ⊥), mm3 (VV).
Longitudinal reliability was evaluated by comparing the measurements from the first set of scans to measurements on the second set of scans that were performed a year later. To assess the utility of doing more than one scan at each timepoint, the ICCs and CVs were calculated separately using just the first scan of each set, using the means of the first two scans in each set, and using the means of all three scans (Table 3, columns Longitudinal-Single Scan, Average of 2, and Average of 3). Using only the first scan in each set of three, the longitudinal reliability of FA, MD, λ⊥, and VV was generally high (ICC > 0.8) with few exceptions. Reliability could not be established for measurements of λ1.
Adding the second and third scan in each set and comparing the means of each set led to progressively better reliability and lower CVs. Using two scans from each set was sufficient to produce ICCs > 0.8 for all measures except λ1, and reliability was similar to or better than the scan-rescan reliability, with the exception of MD in the right side UNC. Using two scans from each set also reduced the CVs to less than 4% for measures of FA, MD, λ1, and λ⊥ in all tracts. Using three scans from each set produced similar or better results than when only two scans were averaged, however, ICC for λ1 was still less than 0.8 in a number of tracts.
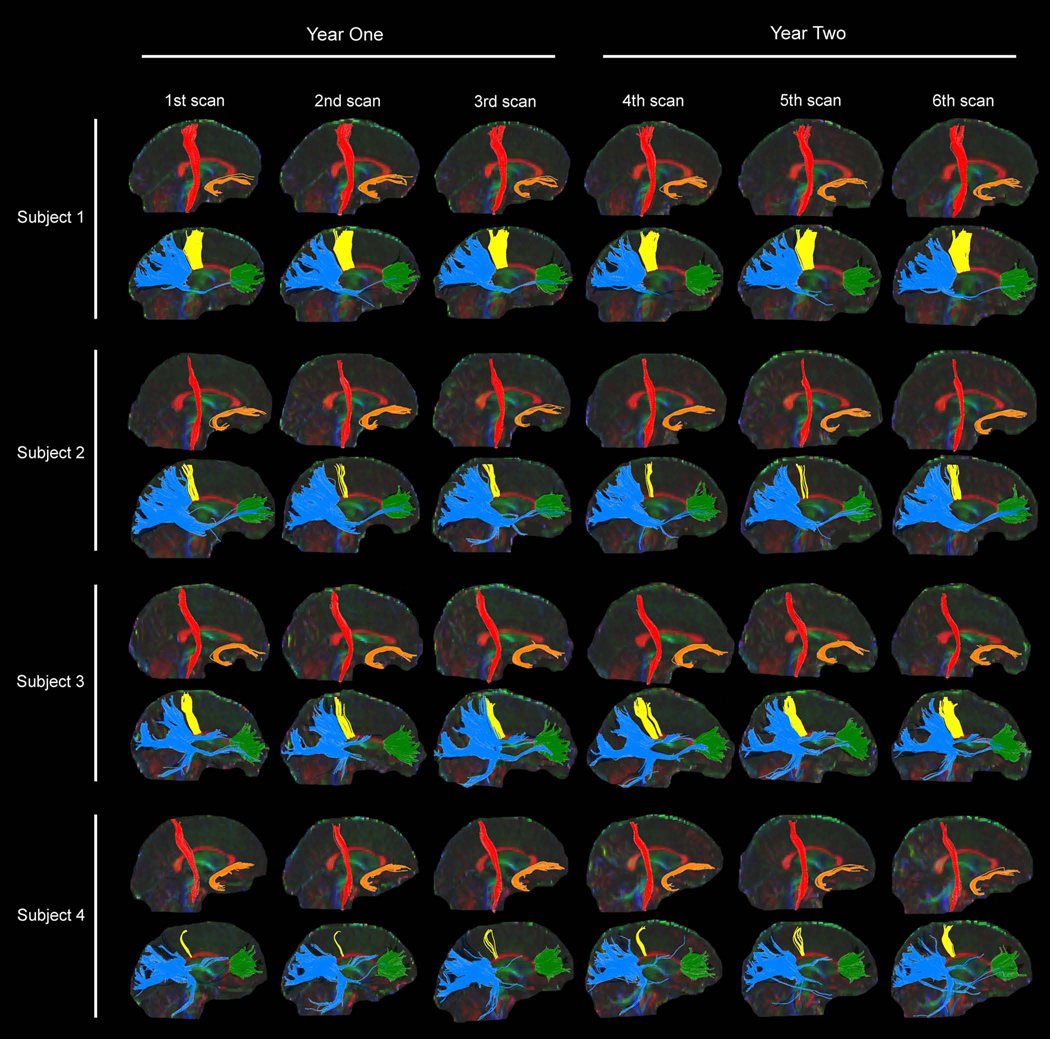
As with the intra-rater and inter-rater results, scan-rescan and longitudinal reliability of VV measurements varied among subjects. Figure 2 illustrates the fiber tracking results from each of the six scans for each subject. Fiber tracking in individual subjects was influenced by the anatomy of their tracts, and in particular, the relationship of the localized tracts to nearby and crossing fibers.
Fig. 2.
Fiber tracking results from each of the four subjects that underwent six repeat MRI scans. Right side corticospinal tract (CST) is red, right side uncinate fasciculus (UNC) is orange, genu (GE) is green, corpus callosum motor fibers (CCM) is yellow, and splenium (SP) is blue.
Discussion
Fiber tracking optimizes the localization of white matter tracts in the brain by minimizing the influence of human inconsistencies in ROI placement (Catani et al., 2002; Partridge et al., 2005; Wakana et al., 2007) and reducing the impact of partial volume effects that may dilute diffusion measurements in a 2D-ROI approach (Partridge et al., 2005; Schimrigk et al., 2007). In contrast to studies that evaluate diffusion properties at discrete levels within the area of a specific 2D-ROI (Bonekamp et al., 2007; Schimrigk et al., 2007), fiber tracking allows for a more simplified whole-tract evaluation of degeneration, a method that has demonstrated group differences and correlations with clinical measures in several diseases (Ciccarelli et al., 2006; Iwata et al., 2008; Matsuo et al., 2008; Moller et al., 2007; Sage et al., 2007; Yin et al., 2008). Diffusion property measurements obtained by fiber tracking have the potential for use as a marker for upper motor neuron involvement in motor neuron disease and for use in the longitudinal evaluation of disease progression or therapeutic intervention, provided that the reliability of such measures can be established.
Our study has shown that fiber tracking produces reliable measurements of diffusion properties in white matter tracts that are affected in motor neuron disease. Intra-rater and inter-rater reliability met the criterion for excellent agreement for repeated measurements of fractional anisotropy (FA) and mean diffusivity (MD) in all studied tracts: the corticospinal tract (CST), uncinate fasciculus (UNC), entire corpus callosum (CC), genu (GE), corpus callosum motor fibers (CCM), and splenium (SP). Measures of FA and MD were also highly reliable with repeated scans on different days, up to a year apart, even obtained with different scanners. In addition to FA and MD, the eigenvalues provide information about the architecture of fibers within a tract, and, when cautiously analyzed, may be useful in identifying different types of degeneration (Pierpaoli et al., 2001; Wheeler-Kingshott and Cercignani, 2009). Measurements of transverse diffusivity (λ⊥), which characterizes diffusivity of water molecules perpendicular to the fibers, also had excellent within-scan and scan-rescan reliability. However, we were unable to demonstrate reproducibility of axial diffusivity (λ1) measurements. The volume of voxels containing fibers (VV), calculated from the number of voxels containing fibers, also exhibited good reliability, although the measurements were more variable. Averaging measures from two scans at each timepoint produced excellent reliability (ICC > 0.8) and reduced variability (CV < 4%) for FA, MD, and λ⊥ in all evaluated tracts. FA and MD measurements in the CST also demonstrated high reliability when using data from only a single scan at each timepoint. We conclude that DTI fiber tracking shows promise as a tool for quantitative serial evaluations of the integrity of white matter tracts.
Fiber tracking of various white matter tracts has been previously reported using both probabilistic and deterministic fiber tracking methods. Probabilistic tracking produces a connectivity map based on the probability of a connection between voxels in various regions of the brain. While this method has its benefits and was shown to be a reliable method for tracking FA and MD in the CST over time (Ciccarelli et al., 2003; Heiervang et al., 2006), it is computationally intensive and less easily applied in a clinical environment. Prior studies using deterministic fiber tracking methods have quantified reliability by evaluating the spatial agreement of repeated fiber tracking trials, as we have done in this study with the κ statistic. Consistent with our findings, they reported high intra-rater and inter-rater κ values in the CST and UNC (Stieltjes et al., 2001; Wakana et al., 2007). While this type of evaluation is a good measure of fiber tracking reliability, it does not provide information on the reliability of diffusion property measurements within the localized tracts.
In our study, diffusion property measurements within the CC, which was tracked in its entirety with a single ROI in the mid-sagittal plane, had near perfect intra-rater and inter-rater reliability. Other tracts localized using a single ROI, such as the GE and SP, also exhibited extremely high reliability for all measures, as indicated by ICC and κ values near unity and low CV. It is possible that this tracking methodology eliminated some of the user error associated with slice and anatomy selection of a multiple-ROI approach, such as that used to track the CST, UNC, and CCM in this study.
From data collection to analysis, there are many sources of variability in DTI. In addition to noise, artifacts, partial-volume effects, propagation errors, and human inconsistencies in ROI placement, another factor affecting the accuracy of fiber tracking is contamination of the tensor calculation by “crossing” and “kissing” fibers within a single voxel (Farrell et al., 2007; Ozturk et al., 2008; Reich et al., 2006; Schimrigk et al., 2007). Since the procedure used here for DTI fiber tracking involves creating a single tensor for each voxel, the primary diffusion direction within the voxel may be shifted when multiple fibers from different tracts lie within a single voxel, causing redirection or truncation of tracked fibers (Holodny et al., 2005). Multiple fibers from the same tracts may also have different primary diffusion directions within the same voxel, particularly at branch points. This variability will be tract specific: a tightly packed fiber bundle without interference from neighboring tracts will be more reliably reproduced over time than one with branch points and intersecting tracts.
Of the tracts evaluated in this study, the CST was most likely to be affected by “crossing” fibers. The CST is a tightly bound fiber bundle for portions of its traverse. However, there are several portions where neighboring fibers may interfere with its course. As it arises in the cortex, CST axons from the hand and face regions originate more laterally than axons from the foot region, where they intersect with axons traveling in the superior longitudinal fasciculus. Truncation of these laterally arising fibers (Holodny et al., 2005) did not contribute to variability in this study, because we were not able to track CST fibers into the hand or face regions of the cortex in any of these subjects. The tracking of CST fibers is also susceptible to redirection by callosal fibers crossing toward the midline. Lastly, incorrect truncation of tracking may occur in the pons as CST fibers intersect with transverse fibers (Holodny et al., 2005; Pierpaoli et al., 2001). The UNC and CCM were most likely to experience interference from “kissing” fibers that run parallel with the longitudinal course of the tracts. The UNC is a U-shaped fiber bundle that connects the frontal and temporal lobes. It travels in close proximity to both the inferior fronto-occipital fasciculus and inferior longitudinal fasciculus (Wakana et al., 2007). Fiber pathways in the CCM run tightly parallel to corticofugal fibers at the level of the internal capsule. The reliability of fiber tracking of the CC overall is not highly affected by interference from neighboring tracts, and may be high due to the comparatively large number of fibers evaluated (approximately 18% of total white matter volume). The CCM fibers, which make up only 4% of the total CC fibers, on average, had high variability of VV measurements, while the GE and SP, which account for approximately 63% of callosal fibers, had relatively low variability of VV measurements. Regions of truncation and misdirection of tracked fibers can be appreciated in the scan-to-scan fiber tracking results (Figure 2). Interestingly, a visual inspection of the tracking results suggests that areas of inaccurate tracking were reproduced consistently from scan to scan. The shape and complexity of these tracts in individual subjects affect the reproducibility of tracking. In light of this variation in reliability, for clinical purposes, it may be useful to establish measures of reliability for specified tracts in an individual patient to determine whether they are a candidate for longitudinal evaluation by DTI.
We developed our fiber tracking methods for the genu and splenium based on a combination of established callosal segmentation methods and classic anatomical definitions (Witelson, 1989). Previous fiber tracking studies have performed callosal segmentation based on the cortical regions in which CC fibers terminate (Abe et al., 2004; Ciccarelli et al., 2003; Dougherty et al., 2007; Heiervang et al., 2006; Hofer and Frahm, 2006; Huang et al., 2005; Park et al., 2008). However, the genu and splenium are not traditionally defined by their projections. Thus, our methodology did not involve secondary ROIs to define regions of termination. Instead, each tract was isolated with a single ROI in the mid-sagittal plane, with the posterior boundary of the GE and anterior boundary of the SP determined by anatomical definition. This methodology proved to be reliable for all measures except λ1. In contrast, the CCM was tracked based on the termination of callosal fibers in the right and left side motor cortexes. Because the splenium projections were not limited to any particular cortical regions, there was occasional overlap between CCM and anterior SP fibers.
We are unable to definitively explain the unreliability of the λ1 measurement. The ICC calculation of this measurement was consistently poor for scan-rescan and single-scan longitudinal reliability (i.e. when not averaging measurements from multiple scans) across a number of the tracts that we evaluated. ICC is a measurement of the relationship between within-subject variance and between-subject variance. When ICC is low, it suggests that there is more variance within-subjects than between-subjects. This could be due either to high variability within subjects, which would indicate low reliability of the measure or an underpowered sample size, or it could be due to very low inter-subject variance of the λ1 measurement across the control population. In each case where λ1 had an ICC value below 0.8, the CV was low: under 1.4% for the CST, 3.6% for the UNC, and 2.8% for the CC (including each segmented portion).
Although previous studies have demonstrated changes in aging in certain white matter tracts (Nusbaum et al., 2001; Yoon et al., 2008), some associated with cognitive function (Abe et al., 2002; Nusbaum et al., 2001; Pfefferbaum et al., 2000; Yoon et al., 2008), there was no clear trend in our study of diffusion measurements in these tracts over time. However, it is likely that a 1-year evaluation period is not long enough to recognize small age-related declines. We also found no differences in right and left side measurements in the CST but significantly larger FA in the left UNC compared to the right, an observation that has been found inconsistently in other studies (Hasan et al., 2009; Kubicki et al., 2002; Malykhin et al., 2008; Rodrigo et al., 2007; Taoka et al., 2006; Wakana et al., 2007).
Recent advances in fiber tracking software and methodology should be considered in a longitudinal study of DTI in neurological disease. Advanced fiber tracking algorithms that calculate multiple fiber directions within a single voxel have been developed to better model regions with crossing fibers (Dell'Acqua et al., 2007; Kreher et al., 2005; Staempfli et al., 2006; Tuch et al., 2003). Not only will this serve to improve tracking reliability by reducing improper fiber truncation and redirection, but it will potentially extend the evaluation of the CST to the hand and face regions of the primary motor cortex. Limb-specific longitudinal observations could be valuable to clinicians in their evaluation of patients with progressive neurodegenerative diseases that progress in an asymmetric fashion, such as ALS. Atlas-based tractography and automated ROI placement programs have also been developed for a number of white matter tracts, including the CST (Hagler et al., 2008; Zhang et al., 2008). Another recently developed analysis tool called Tract-Based Spatial Statistics (TBSS) is an unbiased and automated whole-brain analysis technique that compares diffusion tensor properties between multiple subjects (Smith et al., 2006). Unlike conventional voxel-based morphometry, TBSS does not require perfect brain alignment or smoothing, and instead projects brains onto an “FA skeleton” prior to comparison. Although these programs serve to eliminate human error in ROI placement, they require alignment to standardized space, introducing another potential source of variability, and, in the case of atlas-based tractography programs, do not always correctly isolate the white matter tract of interest (Zhang et al., 2008).
Measurements of water diffusion properties reflect the structure and architecture of axons in white matter tracts. Our study has shown that using fiber tracking to localize white matter tracts affected in motor neuron disease leads to highly reproducible measures of FA, MD and transverse diffusivity. VV may also be useful in restricted tracts where high reliability can be established. Because diffusion properties have been shown to vary along the length of a tract (Reich et al., 2006; Wakana et al., 2007), the fiber tracking approach offers the advantage of assessing these quantities over a defined length, and thus may detect changes that would be missed in measurements taken from individual slices or ROIs. The reproducibility of fiber tracking measurements on repeat scans over one year offers a methodology for detection of longitudinal changes in motor neuron disease.
Acknowledgment
We would like to thank John Ostuni for his invaluable assistance with Linux scripting for FSL image processing. This research was supported by the Intramural Research Program of the NIH, National Institute of Neurological Disorders and Stroke.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abe O, Aoki S, Hayashi N, Yamada H, Kunimatsu A, Mori H, Yoshikawa T, Okubo T, Ohtomo K. Normal aging in the central nervous system: quantitative MR diffusion-tensor analysis. Neurobiol Aging. 2002;23:433–441. doi: 10.1016/s0197-4580(01)00318-9. [DOI] [PubMed] [Google Scholar]
- Abe O, Masutani Y, Aoki S, Yamasue H, Yamada H, Kasai K, Mori H, Hayashi N, Masumoto T, Ohtomo K. Topography of the human corpus callosum using diffusion tensor tractography. J Comput Assist Tomogr. 2004;28:533–539. doi: 10.1097/00004728-200407000-00016. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Bonekamp D, Nagae LM, Degaonkar M, Matson M, Abdalla WM, Barker PB, Mori S, Horska A. Diffusion tensor imaging in children and adolescents: reproducibility, hemispheric, and age-related differences. Neuroimage. 2007;34:733–742. doi: 10.1016/j.neuroimage.2006.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassol E, Ranjeva JP, Ibarrola D, Mekies C, Manelfe C, Clanet M, Berry I. Diffusion tensor imaging in multiple sclerosis: a tool for monitoring changes in normal-appearing white matter. Mult Scler. 2004;10:188–196. doi: 10.1191/1352458504ms997oa. [DOI] [PubMed] [Google Scholar]
- Catani M, Howard RJ, Pajevic S, Jones DK. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage. 2002;17:77–94. doi: 10.1006/nimg.2002.1136. [DOI] [PubMed] [Google Scholar]
- Ciccarelli O, Behrens TE, Altmann DR, Orrell RW, Howard RS, Johansen-Berg H, Miller DH, Matthews PM, Thompson AJ. Probabilistic diffusion tractography: a potential tool to assess the rate of disease progression in amyotrophic lateral sclerosis. Brain. 2006;129:1859–1871. doi: 10.1093/brain/awl100. [DOI] [PubMed] [Google Scholar]
- Ciccarelli O, Parker GJ, Toosy AT, Wheeler-Kingshott CA, Barker GJ, Boulby PA, Miller DH, Thompson AJ. From diffusion tractography to quantitative white matter tract measures: a reproducibility study. Neuroimage. 2003;18:348–359. doi: 10.1016/s1053-8119(02)00042-3. [DOI] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci U S A. 1999;96:10422–10427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell'Acqua F, Rizzo G, Scifo P, Clarke RA, Scotti G, Fazio F. A model-based deconvolution approach to solve fiber crossing in diffusion-weighted MR imaging. IEEE Trans Biomed Eng. 2007;54:462–472. doi: 10.1109/TBME.2006.888830. [DOI] [PubMed] [Google Scholar]
- Dengler R, von Neuhoff N, Bufler J, Krampfl K, Peschel T, Grosskreutz J. Amyotrophic lateral sclerosis: new developments in diagnostic markers. Neurodegener Dis. 2005;2:177–184. doi: 10.1159/000089623. [DOI] [PubMed] [Google Scholar]
- Dougherty RF, Ben-Shachar M, Deutsch GK, Hernandez A, Fox GR, Wandell BA. Temporal-callosal pathway diffusivity predicts phonological skills in children. Proc Natl Acad Sci U S A. 2007;104:8556–8561. doi: 10.1073/pnas.0608961104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis CM, Simmons A, Jones DK, Bland J, Dawson JM, Horsfield MA, Williams SC, Leigh PN. Diffusion tensor MRI assesses corticospinal tract damage in ALS. Neurology. 1999;53:1051–1058. doi: 10.1212/wnl.53.5.1051. [DOI] [PubMed] [Google Scholar]
- Farrell JA, Landman BA, Jones CK, Smith SA, Prince JL, van Zijl PC, Mori S. Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. J Magn Reson Imaging. 2007;26:756–767. doi: 10.1002/jmri.21053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Floyd AG, Yu QP, Piboolnurak P, Tang MX, Fang Y, Smith WA, Yim J, Rowland LP, Mitsumoto H, Pullman SL. Transcranial magnetic stimulation in ALS: utility of central motor conduction tests. Neurology. 2009;72:498–504. doi: 10.1212/01.wnl.0000341933.97883.a4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geser F, Martinez-Lage M, Kwong LK, Lee VM, Trojanowski JQ. Amyotrophic lateral sclerosis, frontotemporal dementia and beyond: the TDP-43 diseases. J Neurol. 2009 doi: 10.1007/s00415-009-5069-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta RK, Saksena S, Hasan KM, Agarwal A, Haris M, Pandey CM, Narayana PA. Focal Wallerian degeneration of the corpus callosum in large middle cerebral artery stroke: serial diffusion tensor imaging. J Magn Reson Imaging. 2006;24:549–555. doi: 10.1002/jmri.20677. [DOI] [PubMed] [Google Scholar]
- Hagler DJ, Jr., Ahmadi ME, Kuperman J, Holland D, McDonald CR, Halgren E, Dale AM. Automated white-matter tractography using a probabilistic diffusion tensor atlas: Application to temporal lobe epilepsy. Hum Brain Mapp. 2008;31:31. doi: 10.1002/hbm.20619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan KM, Iftikhar A, Kamali A, Kramer LA, Ashtari M, Cirino PT, Papanicolaou AC, Fletcher JM, Ewing-Cobbs L. Development and aging of the healthy human brain uncinate fasciculus across the lifespan using diffusion tensor tractography. Brain Res. 2009;1276:67–76. doi: 10.1016/j.brainres.2009.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heiervang E, Behrens TE, Mackay CE, Robson MD, Johansen-Berg H. Between session reproducibility and between subject variability of diffusion MR and tractography measures. Neuroimage. 2006;33:867–877. doi: 10.1016/j.neuroimage.2006.07.037. [DOI] [PubMed] [Google Scholar]
- Hofer S, Frahm J. Topography of the human corpus callosum revisited--comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage. 2006;32:989–994. doi: 10.1016/j.neuroimage.2006.05.044. [DOI] [PubMed] [Google Scholar]
- Holodny AI, Watts R, Korneinko VN, Pronin IN, Zhukovskiy ME, Gor DM, Ulug A. Diffusion tensor tractography of the motor white matter tracts in man:Current controversies and future directions. Ann N Y Acad Sci. 2005;1064:88–97. doi: 10.1196/annals.1340.016. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang J, Jiang H, Wakana S, Poetscher L, Miller MI, van Zijl PC, Hillis AE, Wytik R, Mori S. DTI tractography based parcellation of white matter: application to the mid-sagittal morphology of corpus callosum. Neuroimage. 2005;26:195–205. doi: 10.1016/j.neuroimage.2005.01.019. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang J, van Zijl PC, Mori S. Analysis of noise effects on DTI-based tractography using the brute-force and multi-ROI approach. Magn Reson Med. 2004;52:559–565. doi: 10.1002/mrm.20147. [DOI] [PubMed] [Google Scholar]
- Huisman TA, Loenneker T, Barta G, Bellemann ME, Hennig J, Fischer JE, Il'yasov KA. Quantitative diffusion tensor MR imaging of the brain: field strength related variance of apparent diffusion coefficient (ADC) and fractional anisotropy (FA) scalars. Eur Radiol. 2006;16:1651–1658. doi: 10.1007/s00330-006-0175-8. [DOI] [PubMed] [Google Scholar]
- Hunsche S, Moseley ME, Stoeter P, Hedehus M. Diffusion-tensor MR imaging at 1.5 and 3.0 T: initial observations. Radiology. 2001;221:550–556. doi: 10.1148/radiol.2212001823. [DOI] [PubMed] [Google Scholar]
- Iwata NK, Aoki S, Okabe S, Arai N, Terao Y, Kwak S, Abe O, Kanazawa I, Tsuji S, Ugawa Y. Evaluation of corticospinal tracts in ALS with diffusion tensor MRI and brainstem stimulation. Neurology. 2008;70:528–532. doi: 10.1212/01.wnl.0000299186.72374.19. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jiang H, van Zijl PC, Kim J, Pearlson GD, Mori S. DtiStudio: resource program for diffusion tensor computation and fiber bundle tracking. Comput Methods Programs Biomed. 2006;81:106–116. doi: 10.1016/j.cmpb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Kreher BW, Schneider JF, Mader I, Martin E, Hennig J, Il'yasov KA. Multitensor approach for analysis and tracking of complex fiber configurations. Magn Reson Med. 2005;54:1216–1225. doi: 10.1002/mrm.20670. [DOI] [PubMed] [Google Scholar]
- Kubicki M, Westin CF, Maier SE, Frumin M, Nestor PG, Salisbury DF, Kikinis R, Jolesz FA, McCarley RW, Shenton ME. Uncinate fasciculus findings in schizophrenia: a magnetic resonance diffusion tensor imaging study. Am J Psychiatry. 2002;159:813–820. doi: 10.1176/appi.ajp.159.5.813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–174. [PubMed] [Google Scholar]
- Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161:401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
- Lee CE, Danielian LE, Thomasson D, Baker EH. Normal regional fractional anisotropy and apparent diffusion coefficient of the brain measured on a 3 T MR scanner. Neuroradiology. 2008;13:13. doi: 10.1007/s00234-008-0441-3. [DOI] [PubMed] [Google Scholar]
- Liang Z, Zeng J, Zhang C, Liu S, Ling X, Xu A, Ling L, Wang F, Pei Z. Longitudinal investigations on the anterograde and retrograde degeneration in the pyramidal tract following pontine infarction with diffusion tensor imaging. Cerebrovasc Dis. 2008;25:209–216. doi: 10.1159/000113858. [DOI] [PubMed] [Google Scholar]
- Malykhin N, Concha L, Seres P, Beaulieu C, Coupland NJ. Diffusion tensor imaging tractography and reliability analysis for limbic and paralimbic white matter tracts. Psychiatry Res. 2008;164:132–142. doi: 10.1016/j.pscychresns.2007.11.007. [DOI] [PubMed] [Google Scholar]
- Matsuo K, Mizuno T, Yamada K, Akazawa K, Kasai T, Kondo M, Mori S, Nishimura T, Nakagawa M. Cerebral white matter damage in frontotemporal dementia assessed by diffusion tensor tractography. Neuroradiology. 2008;50:605–611. doi: 10.1007/s00234-008-0379-5. [DOI] [PubMed] [Google Scholar]
- Mitsumoto H, Ulug AM, Pullman SL, Gooch CL, Chan S, Tang MX, Mao X, Hays AP, Floyd AG, Battista V, Montes J, Hayes S, Dashnaw S, Kaufmann P, Gordon PH, Hirsch J, Levin B, Rowland LP, Shungu DC. Quantitative objective markers for upper and lower motor neuron dysfunction in ALS. Neurology. 2007;68:1402–1410. doi: 10.1212/01.wnl.0000260065.57832.87. [DOI] [PubMed] [Google Scholar]
- Moller M, Frandsen J, Andersen G, Gjedde A, Vestergaard-Poulsen P, Ostergaard L. Dynamic changes in corticospinal tracts after stroke detected by fibretracking. J Neurol Neurosurg Psychiatry. 2007;78:587–592. doi: 10.1136/jnnp.2006.100248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Nusbaum AO, Tang CY, Buchsbaum MS, Wei TC, Atlas SW. Regional and global changes in cerebral diffusion with normal aging. AJNR Am J Neuroradiol. 2001;22:136–142. [PMC free article] [PubMed] [Google Scholar]
- Ozturk A, Sasson AD, Farrell JA, Landman BA, da Motta AC, Aralasmak A, Yousem DM. Regional differences in diffusion tensor imaging measurements: assessment of intrarater and interrater variability. AJNR Am J Neuroradiol. 2008;29:1124–1127. doi: 10.3174/ajnr.A0998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn Reson Med. 1999;42:526–540. [PubMed] [Google Scholar]
- Park HJ, Kim JJ, Lee SK, Seok JH, Chun J, Kim DI, Lee JD. Corpus callosal connection mapping using cortical gray matter parcellation and DT-MRI. Hum Brain Mapp. 2008;29:503–516. doi: 10.1002/hbm.20314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partridge SC, Mukherjee P, Berman JI, Henry RG, Miller SP, Lu Y, Glenn OA, Ferriero DM, Barkovich AJ, Vigneron DB. Tractography-based quantitation of diffusion tensor imaging parameters in white matter tracts of preterm newborns. J Magn Reson Imaging. 2005;22:467–474. doi: 10.1002/jmri.20410. [DOI] [PubMed] [Google Scholar]
- Pfefferbaum A, Adalsteinsson E, Sullivan EV. Replicability of diffusion tensor imaging measurements of fractional anisotropy and trace in brain. J Magn Reson Imaging. 2003;18:427–433. doi: 10.1002/jmri.10377. [DOI] [PubMed] [Google Scholar]
- Pfefferbaum A, Sullivan EV, Hedehus M, Lim KO, Adalsteinsson E, Moseley M. Age-related decline in brain white matter anisotropy measured with spatially corrected echo-planar diffusion tensor imaging. Magn Reson Med. 2000;44:259–268. doi: 10.1002/1522-2594(200008)44:2<259::aid-mrm13>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Barnett A, Pajevic S, Chen R, Penix LR, Virta A, Basser P. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage. 2001;13:1174–1185. doi: 10.1006/nimg.2001.0765. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Reich DS, Smith SA, Jones CK, Zackowski KM, van Zijl PC, Calabresi PA, Mori S. Quantitative characterization of the corticospinal tract at 3T. AJNR Am J Neuroradiol. 2006;27:2168–2178. [PMC free article] [PubMed] [Google Scholar]
- Rodrigo S, Oppenheim C, Chassoux F, Golestani N, Cointepas Y, Poupon C, Semah F, Mangin JF, Le Bihan D, Meder JF. Uncinate fasciculus fiber tracking in mesial temporal lobe epilepsy. Initial findings. Eur Radiol. 2007;17:1663–1668. doi: 10.1007/s00330-006-0558-x. [DOI] [PubMed] [Google Scholar]
- Sach M, Winkler G, Glauche V, Liepert J, Heimbach B, Koch MA, Buchel C, Weiller C. Diffusion tensor MRI of early upper motor neuron involvement in amyotrophic lateral sclerosis. Brain. 2004;127:340–350. doi: 10.1093/brain/awh041. [DOI] [PubMed] [Google Scholar]
- Sage CA, Peeters RR, Gorner A, Robberecht W, Sunaert S. Quantitative diffusion tensor imaging in amyotrophic lateral sclerosis. Neuroimage. 2007;34:486–499. doi: 10.1016/j.neuroimage.2006.09.025. [DOI] [PubMed] [Google Scholar]
- Schimrigk SK, Bellenberg B, Schluter M, Stieltjes B, Drescher R, Rexilius J, Lukas C, Hahn HK, Przuntek H, Koster O. Diffusion tensor imaging-based fractional anisotropy quantification in the corticospinal tract of patients with amyotrophic lateral sclerosis using a probabilistic mixture model. AJNR Am J Neuroradiol. 2007;28:724–730. [PMC free article] [PubMed] [Google Scholar]
- Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, Behrens TE. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23 Suppl 1:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Staempfli P, Jaermann T, Crelier GR, Kollias S, Valavanis A, Boesiger P. Resolving fiber crossing using advanced fast marching tractography based on diffusion tensor imaging. Neuroimage. 2006;30:110–120. doi: 10.1016/j.neuroimage.2005.09.027. [DOI] [PubMed] [Google Scholar]
- Stieltjes B, Kaufmann WE, van Zijl PC, Fredericksen K, Pearlson GD, Solaiyappan M, Mori S. Diffusion tensor imaging and axonal tracking in the human brainstem. Neuroimage. 2001;14:723–735. doi: 10.1006/nimg.2001.0861. [DOI] [PubMed] [Google Scholar]
- Taoka T, Iwasaki S, Sakamoto M, Nakagawa H, Fukusumi A, Myochin K, Hirohashi S, Hoshida T, Kichikawa K. Diffusion anisotropy and diffusivity of white matter tracts within the temporal stem in Alzheimer disease: evaluation of the "tract of interest" by diffusion tensor tractography. AJNR Am J Neuroradiol. 2006;27:1040–1045. [PMC free article] [PubMed] [Google Scholar]
- Thomas B, Eyssen M, Peeters R, Molenaers G, Van Hecke P, De Cock P, Sunaert S. Quantitative diffusion tensor imaging in cerebral palsy due to periventricular white matter injury. Brain. 2005;128:2562–2577. doi: 10.1093/brain/awh600. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Wedeen VJ. Diffusion MRI of complex neural architecture. Neuron. 2003;40:885–895. doi: 10.1016/s0896-6273(03)00758-x. [DOI] [PubMed] [Google Scholar]
- Ulug AM, Grunewald T, Lin MT, Kamal AK, Filippi CG, Zimmerman RD, Beal MF. Diffusion tensor imaging in the diagnosis of primary lateral sclerosis. J Magn Reson Imaging. 2004;19:34–39. doi: 10.1002/jmri.10433. [DOI] [PubMed] [Google Scholar]
- Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, Hua K, Zhang J, Jiang H, Dubey P, Blitz A, van Zijl P, Mori S. Reproducibility of quantitative tractography methods applied to cerebral white matter. Neuroimage. 2007;36:630–644. doi: 10.1016/j.neuroimage.2007.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher LM, van Zijl PC, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wang S, Melhem ER. Amyotrophic lateral sclerosis and primary lateral sclerosis: The role of diffusion tensor imaging and other advanced MR-based techniques as objective upper motor neuron markers. Ann N Y Acad Sci. 2005;1064:61–77. doi: 10.1196/annals.1340.013. [DOI] [PubMed] [Google Scholar]
- Wang S, Poptani H, Bilello M, Wu X, Woo JH, Elman LB, McCluskey LF, Krejza J, Melhem ER. Diffusion tensor imaging in amyotrophic lateral sclerosis: volumetric analysis of the corticospinal tract. AJNR Am J Neuroradiol. 2006;27:1234–1238. [PMC free article] [PubMed] [Google Scholar]
- Wheeler-Kingshott CA, Cercignani M. About "axial" and "radial" diffusivities. Magn Reson Med. 2009;61:1255–1260. doi: 10.1002/mrm.21965. [DOI] [PubMed] [Google Scholar]
- Witelson SF. Hand and sex differences in the isthmus and genu of the human corpus callosum. A postmortem morphological study. Brain. 1989;112(Pt 3):799–835. doi: 10.1093/brain/112.3.799. [DOI] [PubMed] [Google Scholar]
- Xue R, van Zijl PC, Crain BJ, Solaiyappan M, Mori S. In vivo three-dimensional reconstruction of rat brain axonal projections by diffusion tensor imaging. Magn Reson Med. 1999;42:1123–1127. doi: 10.1002/(sici)1522-2594(199912)42:6<1123::aid-mrm17>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Yin H, Cheng SH, Zhang J, Ma L, Gao Y, Li D, Lim CC. Corticospinal tract degeneration in amyotrophic lateral sclerosis: a diffusion tensor imaging and fibre tractography study. Ann Acad Med Singapore. 2008;37:411–415. [PubMed] [Google Scholar]
- Yoon B, Shim YS, Lee KS, Shon YM, Yang DW. Region-specific changes of cerebral white matter during normal aging: a diffusion-tensor analysis. Arch Gerontol Geriatr. 2008;47:129–138. doi: 10.1016/j.archger.2007.07.004. [DOI] [PubMed] [Google Scholar]
- Zhang W, Olivi A, Hertig SJ, van Zijl P, Mori S. Automated fiber tracking of human brain white matter using diffusion tensor imaging. Neuroimage. 2008;42:771–777. doi: 10.1016/j.neuroimage.2008.04.241. [DOI] [PMC free article] [PubMed] [Google Scholar]