Statistical Methods for Analysis of High-Throughput RNA Interference Screens

Abstract

RNA interference (RNAi) has become a powerful technique for reverse genetics and drug discovery and, in both of these areas, large-scale high-throughput RNAi screens are commonly performed. The statistical techniques used to analyze these screens are frequently borrowed directly from small-molecule screening; however small-molecule and RNAi data characteristics differ in meaningful ways. We examine the similarities and differences between RNAi and small-molecule screens, highlighting particular characteristics of RNAi screen data that must be addressed during analysis. Additionally, we provide guidance on selection of analysis techniques in the context of a sample workflow.

Introduction

In recent years, large-scale RNAi libraries that are designed to target complete genomes have been produced for multiple organisms. When arrayed in 96- or 384-well microplates, with each well containing reagents that are, in theory, directed against only one gene, genome-scale RNAi screens are possible using high-throughput screening (HTS) technologies that were developed for small-molecule screening¹. Here, we present a sample workflow for analyzing assay-endpoint readouts from high throughput RNAi screening data with guidance on choice and application of relevant statistical methods. Most of the work discussed in this review focuses on RNAi screens using synthetic small interfering RNA (siRNA), but the methods are also applicable to RNAi screens performed in microplates with other silencing reagents, including shRNA (small hairpin RNA), esiRNAs (endoribonuclease-prepared siRNA), and dsRNA (double stranded RNA).

Comparing data characteristics of RNAi and small molecule screens

In spite of their dependence on techniques developed for small molecule screens, many groups have observed anecdotally that there are non-trivial differences between RNAi and small-molecule HTS data. To more fully characterize such possible differences, we have compared existing data sets from more than 19 optimized siRNA screens and more than 13 mammalian cell-based small molecule screens carried out at the ICCB-Longwood Screening Facility at Harvard Medical School (Supplementary Table 1). Lilliefors tests on the distribution of measured values across plates containing different siRNA or small molecule reagents showed that more siRNA screening data were normally distributed. In addition, three simple measures of assay robustness were investigated: signal-to-background ratio (S/B), coefficient of variation, and Z′-factor as a measure of the signal window. The median signal to background ratio, comparing plate mean positive control signal to plate mean negative control, was about 2-fold lower for the siRNA screens compared to the cell-based small molecule screens. The median coefficient of variation for siRNA assays was twice that of the small molecule assays (26.5% vs. 13.4%, respectively). Consistent with the decreased S/B ratio and increased variability of siRNA screens, the Z′-factors from siRNA screens tended to be low (frequently between 0.0 and 0.5). Thus, overall we find that the siRNA screens are less robust by these standard measures than small molecule screens. Several plausible reasons for these differences exist, as outlined below.

Library design

In theory, most siRNA reagents in a genome-scale library should have an expressed cellular target and knockdown of each target may have physiological effects; RNAi reagents thus have a higher intrinsic probability for impacting the overall network biology. In contrast, most compounds in small-molecule screening libraries have no effect on cell pathways because they lack cellular targets and are de facto negative controls.

Transfection

Even under well-controlled conditions, the transfection process, especially transfection efficiency, is a major source of variability for siRNA screens. Transfection also causes cell stress and can affect cell viability, which may have variable and indirect phenotypic effects in cellular assays.

Kinetics and mechanism of RNAi action

While small molecules rarely affect the actual abundance of the target protein itself, RNAi reagents reduce—and in some cases nearly eliminate—the target gene product in the cell². Because of this mechanistic difference, RNAi reagents generally require 48–72 hours for maximal effect, whereas small molecules can directly affect their protein targets within hours. This increased time between cell plating and assay endpoints leads to greater impact of cell culture and environmental variation on phenotypes and more assay variability in RNAi screens. In addition, the “window” of maximal RNAi effect likely varies for each gene, but typically a single endpoint is chosen for a screening assay². Assaying too early for a given gene produces a false negative, while assaying too late may lead to false positives due to downstream effects, thus contributing to weaker, more variable phenotypes in RNAi screens.

Number and quality of controls

RNAi positive controls generally have weaker effects than small molecule positive controls and, due to variations in transfection efficiencies, may exhibit more inter-well variability than small molecule controls. Furthermore, while small-molecule screens utilize vehicle-only wells as negative controls, no such universal negative control exists for siRNA screens since RNAi screens usually involve complex delivery vehicles that alone can have biological effects, and even “non-targeting” siRNA controls may exhibit off-target effects in some cell lines³. Sequence-specific off-target effects of RNAi^4,5,6 due to partial sequence complementarity between siRNA and messenger RNA complicate interpretation of RNAi experiments. The mechanisms by which the off-target effects occur are not yet completely understood and thus they cannot be fully eliminated experimentally.

Since many judgment calls are required in the selection of HTS data analysis strategies, RNAi researchers should be aware of these differences in order to make appropriate analysis choices, as discussed below.

RNAi Screening Analysis Workflow

Data analysis takes much longer than most screening groups have anticipated—sometimes longer than the wet-lab screen itself^7,8. Below, we present a sample workflow for analyzing RNAi HTS data from individual assays with quantitative output. We provide guidance on choice and application of relevant statistical methods (also summarized in Table 1 and in Supplementary Table 2). Researchers should keep in mind that, in most situations, there is no single “correct” analysis method for any data set.

Table 1.

Statistical Analysis Methods for Hit Identification

Strategy	Formulae	Advantages	Disadvantages
Mean + or − k standard deviations	Hit with increased activity = any sample whose value is >= sample mean + k standard deviations; Hit with decreased activity = any sample whose value is <= sample mean − k standard deviations	Easy to calculate Easily linked to hit p-values	Sensitive to outliers Can miss weak positives Requires multiple comparison corrections if using p-values
Median + or − k MAD	Hit with increased activity = any sample whose value is >= sample median + k MADs; Hit with decreased activity = any sample whose value is <= sample median − k MADs	Easy to calculate Can identify weaker hits Not very sensitive to outliers	Not easily linked to hit p-values
Multiple t-tests	Hit = any reagent for which t-test between samples at two conditions < threshold (usually p = 0.05 or p = 0.01)	Simple to calculate Provides hit p-values	Requires triplicates, at minimum Sensitive to outliers Inappropriate if data is not normally distributed Requires multiple comparison corrections of p-values
Quartile-based	Hit with increased activity = any sample whose value is > Q3 + c IQR Hit with decreased activity = any sample whose value is < Q1 − c IQR	Easy to calculate Can identify weaker hits Not sensitive to outliers Good for non-symmetrical data distributions	Limited additional power over median + or − k MAD for approximately normal data Not easily linked to hit p-values Not available in most analysis software
SSMD	Appropriate equations depends on whether goal is control of rates of false negatives, false positives or both	Allows control of both false positive and false negative rate Not dependent upon sample size Linked to rigorous probability interpretation	Not available in most analysis software Not intuitive for many biologists
RSA	Iterative ranking algorithm that cannot be reduced to a single equation	Can identify weaker hits Not sensitive to outliers Provides hit p-values May reduce false-positives due to off-target effects of single reagents	Difficult to calculate May have limited utility for pool-based screens
Rank-product	Iterative ranking algorithm that cannot be reduced to a single equation	Provides hit p-values Can identify weaker hits Not sensitive to outliers	Difficult to calculate Requires many replicates
Bayesian	Appropriate equations depend on whether negative-control or activation-inhibition-negative control model is applied	Provides hit p-values Not sensitive to outliers Allows direct calculation of false discovery rate Includes both experiment-wide and plate-wide information Uses both negative controls and samples	Difficult to calculate Not intuitive for many biologists

MAD, median absolute deviation; IQR, interquartile range; SSMD, Strictly Standardized Mean Difference; RSA, Redundant siRNA Activity

It is worth noting that successful data analysis depends critically on careful experimental design and assay development prior to the primary screen. Plate layout and placement of control reagents is important because RNAi screens are particularly susceptible to edge effects or drifting values across a plate; several suggested layouts have been published^9,10,11. It is advisable to randomize reagent plating location to avoid systematic effects of grouped similar reagents (although not all labs find this technically feasible). Additionally, siRNA screens of whole genomes can be carried out in < 30,000 wells and thus can be performed routinely in duplicate or higher replicate numbers to decrease both false positive and false negative rates¹².

Step 1: Data Triage

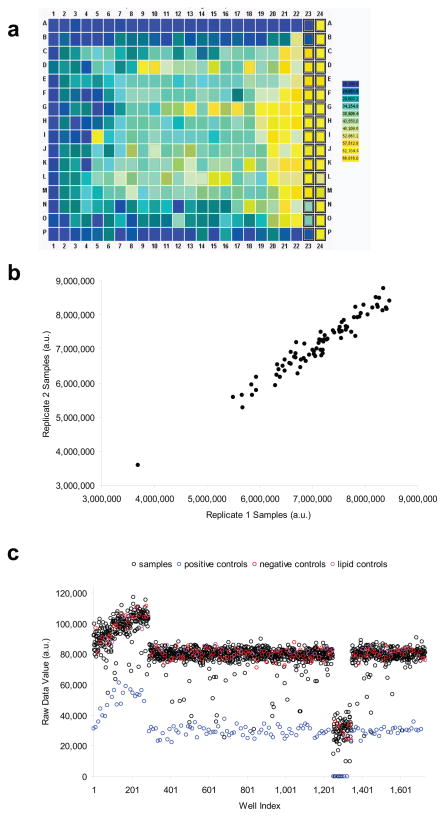
To ensure a successful high-throughput screen, data should be examined while the screen is in progress to allow the identification of potential problems as they occur. Plate visualization is one of the most effective techniques for uncovering undesirable patterns that might indicate technical problems (e.g. extreme edge effects or a clogged plate filler manifold). Library plates that have much higher hit rates than others can also be uncovered by data visualization. Such an observation would suggest that targeting reagents are non-randomly plated in the library and that sample-based normalization strategies are inappropriate (Box 1). Visualization formats developed for small-molecule screens¹³, including heat maps and plate-well scatter plots to display overall screen performance, as well as replicate correlation plots to visualize overall reproducibility (Fig. 1), are equally helpful for RNAi screens. Calculation of various quality metrics (discussed below) on plates as they are screened can also help ensure the production of usable data.

Box 1. Normalization strategies: control-based versus sample-based.

Some normalization techniques compare individual experimental sample values to aggregated values of controls, while others use the samples themselves as de facto negative controls. Some, though not all, techniques can accommodate either approach. The use of samples as de facto negative controls can provide more accurate measurements because there are usually more experimental samples than controls on an assay plate. Additionally, some assays lack good negative controls that work effectively across all plates. In such cases, the best available choice is to use the majority of sample wells as a negative reference. However, this approach is based on the assumption that most samples do not display biological effect in the assay being analyzed, This assumption needs to be explicitly assessed by RNAi screeners for their particular assay, especially when using screening libraries where reagents targeting structurally or functionally related genes are plated together, or when using a very general assay such as cell viability in which many RNAi reagents may actually have a biological effect. Clearly, this assumption will also be violated in the case of confirmatory screens where many primary screening positive reagents are evaluated on the same assay plate. In these cases, screeners should consider including a large number of each type of control²² on each assay plate and utilizing control-based statistics instead.

The use of samples as de facto negative controls is especially problematic for non-robust normalization methods that use statistical measures (such as mean and standard deviation) that are strongly sensitive to outliers in the data. Such methods may be strongly affected in RNAi screens containing either large numbers of hits or very strong hits (which will constitute “outliers” in the sample data).

Figure 1.

Methods for visualizing data outputs of a screen. (a) heat map of raw values from a hypothetical 384-well plate with strong edge effects; (b) replicate correlation plots of raw values from two hypothetical replicates of the same master plate showing good agreement and suggesting overall good reproducibility; and (c) plate-well scatter plot of raw values from a hypothetical screen of eighteen 96-well plates including evidence of drift in the first three plates and a plate with unusually low values near the end of the screen.

Step 2: Normalization

Normalization is a process intended to remove systematic errors from the data and to allow comparison and combination of data from different plates in the screen. Normalization is generally performed per plate, but is occasionally performed per-experiment when there is a known confounding per-plate bias such as a large number of true hits on a particular plate (which may occur when plating of library reagents has been non-random—for example, when screening a transcription factor siRNA library for genes involved in stem cell differentiation).

Many normalization methods have been developed (see Malo et al 2006⁹ for an overview). An important issue in this area is the use of on-plate controls vs. samples for normalizing (Box 1). Most RNAi screeners will find that one of the following methods is suitable to their data and analysis capacities, and will probably receive acceptable results with any reasonable choice. As evidence of this, Wiles et al 2008 investigated the effects of seven normalization techniques (six of which had not previously been applied to RNAi screens) on validation rates of hits selected for secondary screening from a large-scale Drosophila RNAi screen, but concluded that no single method excelled.¹⁴.

Fraction or percent of control

One common approach, often favored by biologists for its easy calculation and interpretability, is division of each sample value by the mean of the control of interest (either negative or positive). This method requires a large number of controls in order to provide adequate estimation of their mean. Additionally, this method is adequate only for tightly distributed and “well-behaved” data as it incorporates no information on the variation of the sample measurements and is sensitive to outliers in the controls.

Fraction or percent of samples

In another common normalization approach, the mean of the samples on the plate may be substituted for the mean of negative controls in the percent of control calculation, which reduces the need for large numbers of controls but may exacerbate the issue of non-robustness (Box 1). A more robust variation on this method that is adequate for many screens is division of each sample value by the median of all samples on the plate, although this method still cannot incorporate information on the degree of variation in the sample data.

z-score and robust z-score

z-score (the number of standard deviations from the mean) is frequently used to normalize data in a way that provides explicit information on the strength of each siRNA relative to the rest of the sample distribution. An advantage of z-score is its incorporation of information on the variation in sample measurements, but this method also depends on the use of samples as de facto negative controls. Because z-score is sensitive to outliers, a variation known as the robust z-score, which substitutes the outlier-insensitive median and median absolute deviation (MAD) for mean and standard deviation in the z-score calculation, is generally considered preferable for RNAi screens.

B score

The above techniques, like most normalization methods, can account for cross-plate systematic effects but not within-plate systematic effects. If data triage has identified the presence of within-plate systematic effects, the B score normalization¹⁵ may be applied to remove row, column, or well-level effects by iterative application of the Tukey median polish algorithm. B score is relatively robust to outliers; however, because its calculation examines the entire plate to identify systematic effects, it essentially uses the samples as negative controls.

The first three approaches can be easily calculated using standard spreadsheet formulae, while the B score cannot since it is based on an iterative algorithm. However, a version of the B score is available in the cellHTS2 package¹⁶ of the open-source Bioconductor bioinformatics software.

Step 3: Calculation of Quality Metrics

Before proceeding to intensive analysis, a screener must ensure that the resulting data meet the minimum standards of quality to permit legitimate conclusions.

Z′- or Z-Factor

By far the most common quality metrics reported for both RNAi screens and small-molecule screens are Z- and Z′-factor¹⁷. Z′-factor is often used during assay optimization because it is based on controls, while Z-factor may be used during screening to assess performance of the screen on actual samples. Note that the Z′- and Z-factor should not be confused with the z-score discussed above.

$$\begin{array}{c}{\text{Z}}^{\prime }-\text{factor}=1-(3{\sigma }_{\text{ct}}+3{\sigma }_{\text{cb}})/\mid {\mu }_{\text{ct}}-{\mu }_{\text{cb}}\mid \\ \text{Z}-\text{factor}=1-(3{\sigma }_{\text{s}}+3{\sigma }_{\text{c}})/\mid {\mu }_{\text{s}}-{\mu }_{\text{c}}\mid \end{array}$$

where μ indicates mean, σ indicates standard deviation, “ct” indicates the top control, “cb” indicates the bottom control, “s” indicates sample value, and “c” indicates negative control. The range of both measures is negative infinity to one, with > 0.5 as a very good assay, > 0 an acceptable assay, and < 0 an unacceptable assay

A potential issue in using the Z′-factor as a measure of assay resolution is that it is possible to generate a high Z′-factor using a very strong positive control which may not realistically represent more moderate screening positives. This issue is of special concern for RNAi screens, where weak effects might be biologically meaningful and in which the signal-to-background ratio can be of lower magnitude than in small-molecule screens (Supplementary Table 1). Thus, researchers are advised whenever possible to use positive controls that are similar in strength to the hits they anticipate finding. It may also be necessary to adjust Z′-factor quality guidelines for RNAi screens; the authors of this manuscript have found that assays with Z′-factors of zero or greater have been successful in identifying validated hits when library plates were screened in duplicate or triplicate.

Strictly Standardized Mean Difference (SSMD)

Researchers desiring a more statistically rigorous means to address the limitations of moderate controls are advised to adopt the Strictly Standardized Mean Difference. SSMD, which was developed for use with RNAi screening, is the ratio between the difference of the means and the standard deviation of the difference between two populations (such as positive and negative controls)¹⁸.

$$\text{SSMD}=({\mu }_1-{\mu }_2)/\surd ({{\sigma }_1}^2+{{\sigma }_2}^2)$$

Acceptable values for SSMD depend on the strength of the positive controls used, but SSMD has been shown to be an accurate, less conservative indicator of quality than Z′- or Z-factor, as demonstrated by examples in which signal-to-noise ratio and Z-factor quality metrics produce misleading results but SSMD correctly passes the data in question¹⁸. Indeed, one of the authors of this review has incorporated the use of SSMD into quality assessment workflows and has found it more informative in the context of RNAi screening than the Z′-factor in some cases. In one case, assaying was performed 20 hours after known maximal response in order to identify long-term repressors; this extended timeline caused increased variability in high controls that decreased the Z′-factor below standard acceptable thresholds for the majority of assay plates. SSMD, on the other hand, accurately captured the clear difference between the high and low populations.

Receiver Operator Characteristic (ROC) Curves

The Receiver Operating Characteristic curve¹⁹ has been used as a quality metric in microarray transcriptomics^20,21, and as it provides a quick and intuitive understanding of dynamic ranges in data given positive and negative controls, we here highlight it for use in RNAi screening. ROC curves plot sensitivity versus 1 - specificity (see Supplementary Table 2 for definitions). The area under the ROC curve can be used as a quality metric, where an area of one represents a perfect predictor while area of 0.5 represents performance as bad as random chance. One advantage of ROC curves is that multiple thresholds for defining positives and the resulting trade-offs between sensitivity and specificity can easily be investigated by plotting multiple ROC curves. This method has been used to compare validation performance of hits generated from differently normalized RNAi data¹⁴.

Step 4: Hit Identification

The identification of “hits” or “screening positives” is the goal of any primary RNAi screen, and yet remains a point of considerable contention in data analysis. Hit identification is, essentially, the process of deciding which sample values differ meaningfully from those of the negative controls. While some screeners select a discrete number of top scoring samples as screening positives (often as determined by follow-up capacity), a wide range of hit identification techniques is available. The selected hit list forms the basis for further validation screens or investigations.

To reduce the risk of false positives, many practitioners recommend screening multiple reagents targeting the same gene of interest and selecting hits based on the combined results⁶; generally, genes are chosen as hits when a majority of tested reagents are screening positives, although the Redundant siRNA Activity technique described below offers a more rigorous approach to combining the results of multiple reagents. False positives may also be limited by combining information from multiple screening outputs²², an approach that has become particularly viable with the advent of high-content screening. While the techniques of multiparametric analysis are complex and beyond the scope of this work, a useful overview is available in Ainscow 2007²³. Such approaches may identify real hits that have high variability in a single read-out metric²².

Below we discuss the features of both small-molecule derived techniques (mean + or − k standard deviations, median + or − k MAD and multiple t-tests) and RNAi techniques (quartile-based selection, SSMD for hit identification, redundant siRNA activity, rank product, and Bayesian models).

Mean + or − k Standard Deviations

This approach, which involves selecting a standard deviation threshold (k) of the normalized data relative to the mean and identifying positives as samples that surpass this threshold, is by far the most frequently used hit identification technique in RNAi screening literature (e.g., Bard et al 2006²⁴, DasGupta et al 2005²⁵). It is often used with z-score normalization, but is sometimes used on data that has been normalized by other approaches (such as the B score). This method is particularly appropriate for normally distributed data because the standard deviations from the mean link to an estimate of the probability that hit values are significantly different than the distribution of values for de facto negative controls. Another advantage is that this method is very easy to calculate and implement; however, it is not robust to outliers. Thus, especially for data in which outliers appear frequently, the application of the commonly used 3 standard deviation cut-off with this approach tends to miss weak hits, while lowering the standard deviation threshold to capture such hits may unacceptably increase the rate of false positives^26,27.

Median + or − k MAD

An improvement on the mean + or − k standard deviations approach is median + or − k median absolute deviation (MAD) (e.g., Muller et al 2005²⁸). This method is robust to outliers and has been shown to identify weak hits in RNAi data more effectively than mean + or k standard deviations while still capturing the strong hits and controlling false positives²⁷; it has also been shown to generate fewer false negatives than mean + or − k standard deviations when applied a non-normal data distribution²⁷, and is also very easy to calculate and implement (although it sacrifices the former method’s easy link to a probability distribution). For these reasons, Chung et al 2008²⁷ recommend it as the first-choice approach for hit selection in RNAi screens.

Multiple t-tests

For certain assays, such as those comparing RNAi treatment in the presence of drug versus RNAi treatment alone, it may be appropriate assess the difference in means between replicates for each condition with multiple t-tests (e.g., Whitehurst et al 2007²⁹). This approach is simple to implement and understand, but it requires three or more replicates of each condition and assumes normality of the replicate data. In addition, it is imperative to apply multiple-comparison corrections to the resulting p-values of each individual test if a high false positive rate cannot be tolerated³⁰, and results of such t-tests are sensitive to outliers³¹.

Quartile-Based Selection

Researchers who determine that their data distribution is not symmetrical may wish to employ the quartile-based hit identification method. This approach sets upper and lower hit selection thresholds based on number of interquartile ranges above or below the first and third quartiles of the data. Like median + or − k MAD, the quartile method has been shown to identify both strong hits and weak ones while controlling false positives²⁶. Although this method is easy to calculate, it has not been generally implemented in the RNAi screening community, perhaps because of its modest improvement over the more common median + or − k MAD approach on approximately normal data. Additionally, in quartile-based selection, as in many other robust methods, the rankings produced are not easily translatable into p-values.

SSMD for Hit Identification

The Strictly Standardized Mean Difference metric discussed earlier can be employed for hit identification by screeners concerned with controlling the rate at which siRNAs that have real large or moderate effects fail to be identified as screening positives as well as the rate at which siRNAs that should be considered negative are identified as screening positives³². Formulae are provided^33,34 for calculating the SSMD limits for hit selection based on the desired false positive level, false negative level, or both; while these require a large number of negative controls (> 50), follow-up work³¹ provided suggested SSMD cut-offs for screens without large numbers of negative samples, such as confirmatory screens.

While the SSMD metric has linear relationship to z-score when only one replicate per siRNA is measured in a screen, these statistically based guidelines may make SSMD more meaningfully interpretable to researchers. Currently SSMD-based hit identification is not calculated by standard analysis packages and is not trivial to implement from scratch.

Redundant siRNA Activity (RSA)

The Redundant siRNA Activity (RSA) analysis method³⁵ is appropriate for researchers seeking to integrate information about multiple RNAi reagents tested for each gene. RSA ranks silencing reagents according to experimental effect and assigns a p-value to all reagents for a single gene based on whether the reagents for that gene are distributed significantly higher in the rankings than would be expected by chance. Because of its use of chance performance as a basis for statistical calculations, RSA is able to provide p-values for gene hits without sacrificing robustness.

Positive reagents identified by this method were found to have higher rates of reconfirmation than those identified with conventional methods, with discrepancies attributable to low reproducibility of orphan individual siRNAs with high activities³⁵. While RSA is not currently included in common analysis software packages, its developers have made available implementations in C# (for Windows), R, and Perl (see http://carrier.gnf.org/publications/RSA/).

Rank-Product

Screeners intending to perform screens in biological replicate and seeking a robust hit identification approach that provides estimated p-values may also wish to consider the Rank-Product method, originally developed for use with microarray data³⁶. The premise of the Rank-Product approach is that a consistent hit should be highly ranked in each independent biological replicate set. The rank-product statistic for each sample across all independent sets estimates this consistency; it can then be translated into a measure of statistical significance by comparing the observed rank product statistic to a rank product statistic obtained from a large number of simulated data sets (providing the statistic expected by chance).

This approach provides p-values for potential hits without requiring the assumption of an underlying probability distribution, but does require significant computation and several replicates per screen to work. While similar to RSA in its comparison of true data rankings to those produced by chance, it does not depend on the use of multiple different RNAi reagents per gene. A Rank-Product implementation suited for use with RNAi screening data has recently been made available as part of the RNAither package³⁷ in the Bioconductor open-source bioinformatics software.

Bayesian Models

Screeners with appropriate computational resources who seek explicit estimated probabilities that a given siRNA has no effect, an inhibition effect, or an activation effect (rather than the single score produced by other methods) may wish to employ a Bayesian approach described recently by Zhang et al 2008³⁸. Bayesian statistics use Bayes’ Theorem to calculate the probability that a particular hypothesis is true given the observed evidence, and offer a means to update these probabilities when additional evidence is collected. Zhang et al identify three hypotheses of interest (an siRNA has no effect, an siRNA has an activation effect, or an siRNA has an inhibition effect) and develop two models to describe the posterior probability that each of these hypotheses are true for a particular sample given the evidence of this sample’s observed value. The first, and simpler, model is based on using only the negative controls to describe the posterior distribution of the true mean value for the sample given the observed data value. The second, more complex model describes a posterior distribution that assumes the availability of data from both positive-inhibition and positive-activation controls as well as negative controls. Both models also provide the means to calculate the false discovery rate associated with any given hit threshold, but are usable only on screens done in singlicate.

A strength of this approach is that it incorporates both plate-wide and experiment-wide information as well as (depending on the model used) information from both negative controls and the assumed de facto negative samples. When several hit identification approaches were compared, Zhang et al found the simpler Bayesian model to perform best, followed by plate-wise median + or − k MAD. Unfortunately, although the published Bayesian models show great promise, they have not yet been incorporated into commonly available analysis software and are not trivial to implement. Until software applications implementing Bayesian modeling are available, the plate-wise median + or −k MAD approach may be the best alternative.

Conclusions and Future Directions

High-throughput RNAi offers a wealth of exciting new data, but also new challenges in the statistical interpretation of this data. When considering appropriate statistical techniques for quality control and hit-selection in HTS, it is important to keep in mind that statistical analysis methods developed in industry for small-molecule screening and therapeutic lead identification are optimized for a very low false positive rate. RNAi screens, however, appear inherently more variable and often produce a broader range of biological hits. Thus, researchers applying small molecule techniques to RNAi data should have a clear understanding of the implicit assumptions and limitations, and possibly apply altered thresholds to account for common RNAi-specific data features. Several methods for RNAi HTS data analysis have been developed specifically with these issues in mind.

The statistical methods outlined here, while certainly not comprehensive, offer effective, practical tools for RNAi HTS analysis. However, further work is needed; many analysis techniques continue to favor conservative limits on false positive rates, which artificially reduce the number of weak and/or variable yet biologically important hits found in screens. In addition, many researchers are investigating the use of microscopy-based high content assays, which may eventually offer even more statistical power by providing multiple readouts and finer characterization of phenotypic results. However, statistical techniques and software for these assays are still in their infancy; no doubt this area will see significant development effort in the coming years.

Finally, it should be emphasized that rigorous secondary screening is necessary to validate primary screen findings⁶. Even the best statistics cannot establish the biological significance of genes identified as primary hits.