Testing signal-detection models of yes/no and two-alternative forced-choice recognition memory

Abstract

The current study compared three models of recognition memory in their ability to generalize across yes/no and two-alternative forced-choice (2AFC) testing. The unequal-variance signal-detection model assumes a continuous memory strength process. The dual-process signal-detection model adds a threshold-like-recollection process to a continuous familiarity process. The mixture signal-detection model assumes a continuous memory strength process, but the old item distribution consists of a mixture of two distributions with different means. Prior efforts comparing the ability of the models to characterize data from both test formats did not consider the role of parameter reliability, which can be critical when comparing models that differ in flexibility. Parametric bootstrap simulations revealed that parameter regressions based on separate fits of each test type only served to identify the least flexible model. However, simultaneous fits of ROC data from both test types with goodness-of-fit adjusted using AIC successfully recovered the true model that generated the data. With AIC and simultaneous fits to real data, the unequal-variance signal-detection model was found to provide the best account across yes/no and 2AFC testing.

Recognition memory refers to the ability to appreciate that a stimulus was previously encountered. In the recognition memory literature, two basic recognition test formats are widely used, namely, yes/no and two-alternative forced-choice (2AFC). In the yes/no format, targets from a list are randomly intermixed with lures, and these items are presented one at a time for a decision (yes or no). In the 2AFC format, pairs of items are presented on the recognition test instead. One item of the pair is a target and the other is a lure, and the participant’s job is to choose the target (e.g., left or right). It has long been known that, all else being equal, performance on the 2AFC test is reliably better than performance on the yes/no test. A viable quantitative model of recognition memory should be able to accurately predict the degree of improvement when the format changes from yes/no to 2AFC, and the current study differentiates between models of recognition memory on this basis.

Differentiating between competing models by evaluating their ability to predict performance is complicated by the fact that models differ in a number of ways. As an analogy, consider high school students who take the Scholastic Aptitude Test (SAT) to obtain admission to undergraduate institutions. The SAT measures critical thinking skills in three areas (mathematics, critical reading, and writing), yet institutions often simply sum the scores across the three areas and compare that value to some criterion of acceptance. If each of these three area tests is valid and captures a different ability, why would institutions sum the scores? The reason is that with a limited number of observations, a complex theory (e.g., that scholastic aptitude is based on separate abilities) can exhibit less predictive reliability than a less complex theory (e.g., that scholastic aptitude reflects a single ability), depending on what the model is asked to predict. Thus, while acknowledging that there is no single cause of a student’s aptitude, institutions nevertheless sum SAT scores because this is the most reliable method for predicting overall undergraduate education performance (i.e., generalizing to college grades in general, rather than grades in specific classes). These considerations suggest that greater predictive reliability does not automatically imply that the simpler model is also the more valid model. Its predictive success can arise either because it is the more valid model or because it is a simpler model that most effectively predicts a summary variable.

Similar issues of model flexibility, parameter reliability, and generalization are important in elucidating the mechanisms that underlie recognition memory. A model that has more parameters may provide a better description of the observed data, yet fail in terms of its ability to generalize. This is alternatively termed flexibility or complexity, and it refers to the ability of a model to flexibly capture many data patterns, resulting in a solution that is assuredly fitting sampling noise, and thus failing to generalize (e.g., Myung, 2000; Pitt & Myung, 2002). However, assessing generalization with models that differ in flexibility is non-trivial, and the exact manner in which one assesses generalization needs to be carefully examined. For example, simply examining parameter regressions across different testing situations is confounded with the issue of parameter reliability. In the present study, we shed light on these matters and perform both behavioral and simulation studies to determine the best method for comparing models of recognition memory in their ability to generalize across two different test formats. We show that past attempts to deal with the relationship between yes/no and 2AFC performance were potentially compromised by a failure to consider the tradeoff between predictive accuracy and model complexity. We highlight a distinction between model recovery, which is the ability to identify which model is most likely the generating model behind the observed data versus parameter recovery, which is the ability to identify the particular parameter values that generated the observed data under the assumption that a certain model is true. Because these are not necessarily related to each other (i.e., there could be a problem with model recovery, but not parameter recovery, or vice versa), a careful consideration of this distinction is needed to choose appropriate analyses. The goal of this study is to examine which model should be preferred (i.e., model recovery, rather than parameter recovery) and to underline that the technique of parameter recovery is inappropriate to compare competing models. Actual model recovery simulation studies are a better test for model selection, and we use the simulation study to examine model recovery, which is an issue of what data patterns can or cannot be fit rather than whether the parameters are sufficiently constrained.

Three Models Based on Signal Detection Theory

Signal detection theory (SDT) has long been a dominant theoretical framework and mathematical tool for understanding how people make decisions on recognition memory tasks (Green & Swets, 1966; Macmillan & Creelman, 2005). The theory provides a precise description and graphic notation for analyzing decision making under uncertainty. The application of SDT offers useful parametric measures such as d' (sensitivity) and β (bias) as well as an ability to predict the shape of a receiver operating characteristic (ROC). An ROC is a plot of the hit rate as a function of the false alarm rate and is typically obtained by use of confidence judgments. A simple version of the SDT, the equal-variance signal-detection (EVSD) model, involves two equal-variance Gaussian distributions (one for targets and the other for lures) and predicts a symmetrical curvilinear ROC. However, a large number of studies in recognition memory have observed asymmetrical ROCs (e.g., Glanzer, Kim, Hilford, & Adams, 1999; Ratcliff, Sheu, & Gronlund, 1992). To account for this asymmetry, three variants of the EVSD model have been advanced: (1) the unequal-variance signal-detection (UVSD) model, (2) the dual-process signal-detection (DPSD) model (Yonelinas, 1994), and (3) the mixture signal-detection (MSD) model (DeCarlo, 2002).¹

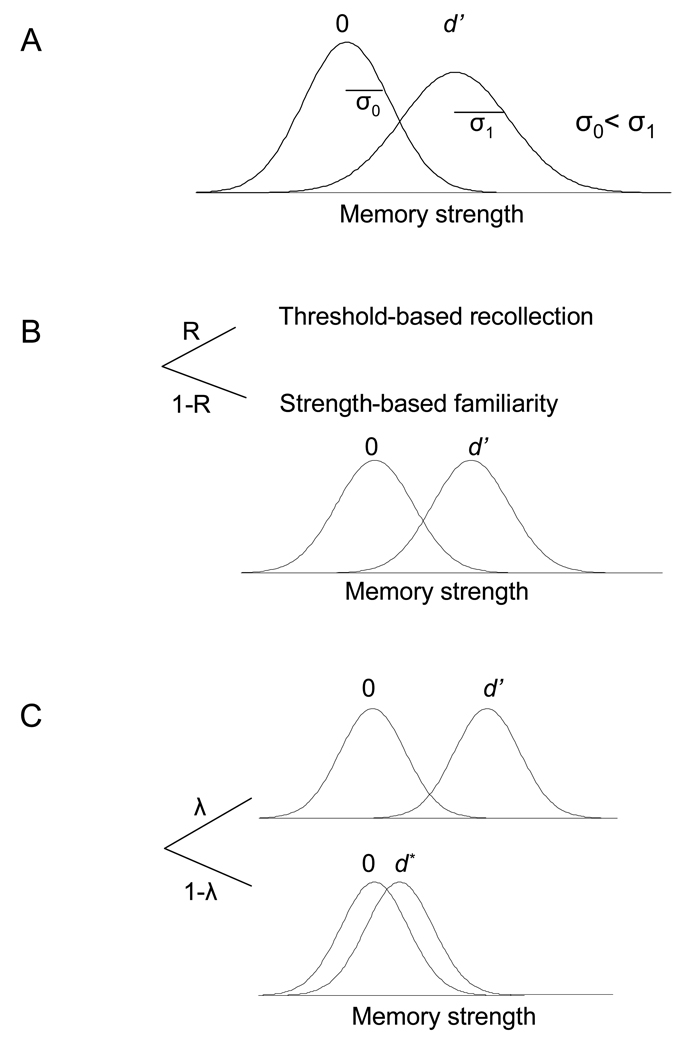
Figure 1 illustrates the three signal-detection models. The UVSD model assumes that recognition decisions result from a strength-based process that is governed by two unequal-variance Gaussian distributions, and it turns out that the standard deviation of the target distribution exceeds that of the lure distribution (Figure 1A). The DPSD model assumes that recognition decisions are based either on a threshold-based, recollection (R) process that only applies to targets or on a strength-based, familiarity process for targets and lures that is characterized by an EVSD model (Figure 1B). The MSD model holds that recognition memory decisions are based on a continuous memory strength variable, but the target distribution consists of a mixture of two equal-variance Gaussian distributions (based on a mixing probability, λ) with different means: the higher mean distribution for attended items and the lower mean (d^*) distribution for partially or not attended items (Figure 1C).

Figure 1.

Three signal-detection models. (A) Unequal-variance signal-detection (UVSD) model; (B) Dual-process signal-detection (DPSD) model; (C) Mixture signal-detection (MSD) model.

Each of the three models contains one or two more parameters than the EVSD model. The UVSD adds one additional parameter (the ratio of the standard deviation of the lure distribution to that of the target distribution: slope or s) as does the DPSD model (the probability of threshold recollection). The MSD model adds two additional parameters to the EVSD model, namely, the mean of the upper target distribution and the probability (λ) that a target item will be drawn from that distribution instead of the lower distribution.

The DPSD and MSD models are both hybrid models that combine continuous, strength-based and discrete, probabilistic processes. Although the two models assume different processes of memory, mathematically, the DPSD model is nested under the MSD model, with the extra parameter of upper mean in the MSD model determining this nesting relationship. In the DPSD model, it is assumed that familiarity does not support higher levels of confidence than recollection. Mathematically, recollection is equivalent to the higher Gaussian distribution in the MSD model having a mean of infinity. In other words, when the upper mean is set to infinity, then the mixing proportion in the MSD model is identical to the probability of recollection in the DPSD model. However, the DPSD model is a subset of the MSD model because the MSD model allows the mean of the higher distribution to take on any positive value including infinity.

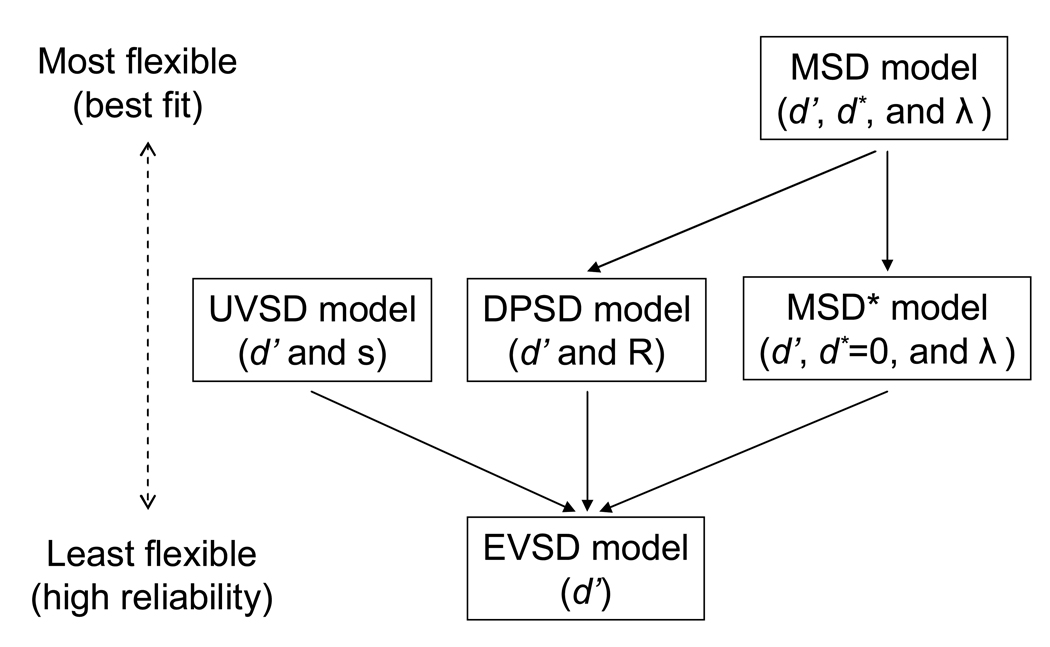
From a statistical viewpoint, Figure 2 represents a nested hierarchy of the models for recognition memory. These hierarchical relationships between the models are indicated by unidirectional solid line arrows connecting the models. The EVSD model is a nested subset of the UVSD (by setting the ratio of standard deviations to 1) or DPSD (by setting the probably of recollection to 0) model, and so the EVSD model is the least flexible model (having only a single parameter).² As indicated above, the DPSD model is nested under the MSD model, and so the MSD model (3 parameters) is more flexible than the DPSD model (2 parameters), which is in turn more flexible than the EVSD model. There is no nested relationship between the UVSD and DPSD models, each of which has 2 parameters. Furthermore, because there is no nesting relationship between the UVSD and MSD models, these models cannot be directly compared in terms of flexibility even though the MSD model contains an additional parameter. Finally, as an attempt to constrain parameters within the MSD model, a subset of the MSD model where d^* is set to zero, the MSD* model is included (i.e., participants pay full attention on some items and do not attend at all on others). Since the MSD* model has 2 free parameters, there is no nested relationship with the UVSD model and with the DPSD model, and the EVSD model is nested under the MSD* model. We consider two kinds of model comparison, one in which the models being compared have different numbers of free parameters (i.e., vertically compared, as shown in Figure 2), and the other in which the models being compared have the same number of free parameters (i.e., horizontally compared, as shown in Figure 2). One goal of the current study is to assess model flexibility for non-nested model comparison through simulation studies.

Figure 2.

Nested hierarchy for the signal-detection models. Unidirectional, solid line arrows between models indicate subset relations between models. The bidirectional, dotted line arrow on the left-hand side represents the degree of the flexibility and reliability.

Testing Models and Yes/No and 2AFC Recognition Memory

In prior research, the ability of these three models to fit yes/no recognition data has been presented as evidence of their validity. For instance, Yonelinas (1994; 1997; 1999; also see a review, Yonelinas & Parks, 2007) argued that the DPSD model fits some data better than the EVSD or UVSD model, whereas others (e.g., Heathcote, 2003; also see a review, Wixed, 2007a) argued that the UVSD model typically provides a superior fit. Providing another example, DeCarlo (2007) demonstrated that the MSD model fits mirror effect (Glanzer & Adams, 1985) recognition results more accurately than the DPSD or UVSD model.

A model’s ability to describe a set of data is often assessed using maximum likelihood estimation and the chi-square goodness-of-fit statistic. For the hierarchical relationships illustrated in Figure 2, standard comparison procedures for nested models (e.g., Batchelder & Riefer, 1990) can be used; this comparison examines the difference in chi-square error between the nested models with one degree of freedom, corresponding to the one extra parameter. This test indicates whether the extra flexibility associated with the extra parameter is justified. Other traditional methods for model comparison should be used when comparing non-nested models that differ in the number of free parameters. These include Akaike’s information criterion (AIC: Akaike, 1973) and the Bayesian information criterion (BIC: Schwarz, 1978). However, these techniques assume that each additional parameter provides the same amount of extra flexibility, which may be incorrect depending on the particular models. Therefore, we performed simulations to determine the appropriate information criterion when comparing the models, which are non-nested and differ in the number of parameters.

Instead of maximum likelihood estimation and goodness-of-fit comparisons, another approach to model testing is generalization across tasks. Several previous studies have used the two different but theoretically related recognition memory tasks – namely, yes/no and 2AFC – to test whether a model provides appropriate estimates across different testing formats (e.g., Green & Moses, 1966; Jesteadt & Bilger, 1974; Kroll, Yonelinas, Dobbins, & Frederick, 2002; Smith & Duncan, 2004; Wickelgren, 1968). Much of the early work focused simply on the relationship between yes/no d' and 2AFC d' (e.g., Green & Moses, 1966; Jesteadt & Bilger, 1974; Wickelgren, 1968). To additionally assess generalization across a range of criteria, two recent studies used the ROC analysis of yes/no and 2AFC tasks to compare competing models of recognition memory (Kroll et al., 2002; Smith & Duncan, 2004). Kroll et al. (2002) found that the DPSD model correctly predicted proportion correct in 2AFC based on fits to yes/no data, but the EVSD model was shown to perform less well. However, Smith and Duncan (2004) pointed out several possible problems with this analysis. First, because many different combinations of parameters for a yes/no model can give rise to the same percent correct value on a 2AFC test, the important question is not whether a model can predict percent correct but whether the model’s parameters are consistent across the two tasks (a more stringent test). Also, in finding fault with the signal-detection model, Kroll et al. (2002) focused mainly on the EVSD model, whereas the UVSD model is the more appropriate competitor.

Smith and Duncan (2004) addressed these concerns by approaching the problem in a different way. Specifically, they compared the UVSD and DPSD models by fitting the two models separately to the yes/no ROC data and to the 2AFC ROC data to provide two estimates of model parameters based on data from the same participants under each test format.³ Each model assumes a particular relationship between parameters estimated from yes/no data versus parameters estimated from 2AFC data, and so the parameters based on yes/no were converted to equivalent parameters if instead memory had been tested with 2AFC. A simple linear regression was then performed for the predicted parameter values estimated from the yes/no data as compared to the observed parameter values estimated from the 2AFC data. This simple linear regression thus produced a percent variance accounted for value that was used to compare the models. Although we adopted the same procedures as Smith and Duncan (2004) used, we note that these procedures could just as easily take parameters from 2AFC data and convert them to equivalent yes/no parameters, thus performing regression with equivalent yes/no parameters. This would presumably produce similar, but not necessarily identical results depending on the error in estimating parameters from yes/no versus the error in estimating parameters from 2AFC. Nevertheless, this highlights the fact that neither direction for the transformation and comparison is more predictive than the other. For this reason, we adopt the more neutral descriptive term, parameter regression in referring to this model generalization procedure.

Next, we consider the theoretical conversion from yes/no parameters to equivalent 2AFC parameters. The SDT model assumes that the relation between yes/no and 2AFC data is as follows:

$$d{\text{'}}_{2AFC}=\frac{2d_{\mathit{\text{Yes}}/\mathit{\text{No}}}}{\sqrt{s^2+1}},$$

where d_Yes/No is the difference between the means measured in units of the target distribution standard deviation, and s is the slope of the ROC based on the yes/no data (d_Yes/No is equal to d'_Yes/No when s = 1). Unlike the decision axis of yes/no which is memory strength (or familiarity), the decision axis of 2AFC is the difference between the memory response to the left choice versus the right choice (rather than comparison to a criterion). Therefore, this model assumes a symmetrical 2AFC ROC even if the yes/no ROC is asymmetrical (i.e., even if s is less than 1). If s is equal to 1 in the yes/no data, then the UVSD model reduces to the EVSD model, and the relation between the two tasks is summarized by the well-known √2 d' conversion (Macmillan & Creelman, 2005). For the DPSD model, its recollection parameter should be the same across test formats (i.e., R_2AFC = R_Yes/No), and the familiarity parameter is converted by the √2 rule d'_2AFC = √2 d'_Yes/No

Using these procedures, Smith and Duncan (2004) found that the d' regression across test formats of the UVSD model accounted for 66% of the variance. In contrast, the DPSD model performed much worse, especially the recollection component; the familiarity parameter d' only accounted for 31% of the variance and the recollection parameter accounted for less than 1% of the variance. Based on these results, Smith and Duncan (2004) rejected the DPSD model in favor of the UVSD model. However, it is important to note that parameter regressions were performed on a single parameter (d') for the UVSD model, whereas 2 different regressions were performed for the DPSD model (d' and R). As explained next, this occurred because the UVSD model is more constrained in fitting 2AFC data, and this greater constraint may have produced more reliable parameter estimates, which serves as confounding factor in using the method of parameter regressions.

More generally, the technique of separately fitting yes/no and 2AFC data and then examining parameter regressions is flawed both because it is a test of parameter recovery rather than model recovery, and because 2AFC ROC data are symmetric and are therefore less able to constrain the parameters. Figure 2 illustrates why parameter regressions across tasks may not be an appropriate method of model comparison. As indicated in the figure, model flexibility and parameter reliability are inversely related such that the fewer parameters involved, the higher is parameter reliability. As such, a model with low flexibility (e.g., the one-parameter EVSD model) may yield highly reliable parameters values, and thus good parameter regressions across tasks (e.g., people with high d' in one task have high d' in the other task), even though the EVSD model is known to produce consistently poor fits to yes/no ROC data (i.e., the EVSD model is rejected based on goodness-of-fit). These considerations may explain why the DPSD model performed so poorly in terms of parameter regressions across test formats. Although the DPSD model and UVSD model have the same number of free parameters when they are fit to a yes/no ROC, the UVSD model effectively has one fewer parameter when the models are fit to 2AFC ROC data. For both of the EVSD and UVSD models, 2AFC ROCs should be symmetric, which means that the UVSD slope parameter will always be 1 (except for random error). Thus, for the UVSD model (as well as the EVSD model), only one parameter (d') is needed to provide a good fit. For the DPSD model, 2AFC ROCs are either symmetric (when R = 0) or very slightly asymmetric with other parameter values (a very subtle difference from the 2AFC ROC symmetry, and perhaps not noticeably so). Thus, the parameters of the DPSD model as applied to 2AFC ROC data are not easily identifiable (i.e., low parameter reliability). As a consequence, it is not surprising that the parameters of the DPSD model yielded a low regression between yes/no and 2AFC tasks; for the DPSD model, 2 parameters from the yes/no fit were regressed onto the 2 parameters from the 2AFC fit. In contrast, for the UVSD model, 2 parameters from the yes/no fit (d' and slope) were used together to produce a single regression for the single parameter from the 2AFC fit (d', with slope assumed to be 1). Given the greater parametric complexity of the DPSD model for 2AFC ROC data, the reliability of its parameter estimates might be worse even if it is the correct model (similar to the SAT example discussed earlier).

In light of these potential drawbacks to the parameter regression analysis, we adopted a different approach to determine which model was best able to account for yes/no and 2AFC performance on a recognition memory task. First, we replicated and re-examined part of the Smith and Duncan (2004) method by presenting subjects with a single list of words and then testing their memory using the two recognition test formats (yes/no for some items, and 2AFC for others). In this way, we held memory constant while changing the decision rule. However, instead of using the parameter regression approach that Smith and Duncan (2004) used for model comparison, we fit each model to the two ROC data sets simultaneously.

Beyond replacing Smith and Duncan’s (2004) method – that is, replacing separate fits and parameter regressions with simultaneous fits – the other change was that we included the MSD model as a third detection model capable of fitting asymmetric yes/no ROCs. We also added the EVSD model to help clarify the issues of model flexibility and parameter reliability; even though the EVSD model is known to produce a bad fit to yes/no ROC data, if our hypotheses regarding complexity and parameter reliability are correct, then the EVSD model should produce the highest parameter regression across test formats, even while producing the worst simultaneous fit to the data of both formats. As indicated earlier, the assumed relationship between d'_Yes/No and d'_2AFC for the EVSD model is the √2 rule (i.e., d'_2AFC = √2 d'_Yes/No). For the MSD model, the parametric relationships between yes/no and 2AFC are as follows; the means of the two target distributions should be related by the √2 rule (i.e., d^*_2AFC = √2 d^*_Yes/No, and d'_2AFC = √2 d'_Yes/No), and the attention parameter should be the same (i.e., λ_2AFC = λ_Yes/No).⁴ In contrast to the greater parameter reliability with the simplicity of the EVSD model, it is expected that the MSD model’s parameters will be even less reliable because d^*, d', and λ are all estimated from the same ROC data. For the MSD model, 2AFC ROCs are either symmetric (when λ = 0, .5, or 1) or very slightly asymmetric (like those for the DPSD model). In other words, 2AFC ROCs do not constrain the parameters of the MSD model, and so the model has two redundant parameters to fit the shape of the 2AFC ROC. Thus, the MSD model is expected to produce the worst parameter regressions even though it can potentially produce the best simultaneous fit to the data of both test formats.

To validate our approach, we additionally quantified model mimicry, which is defined as the ability of a model to account for data generated by a competing model (for the issue of model mimicry, see e.g., Navarro, Pitt, & Myung, 2004; van Zandt & Ratcliff, 1995; Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). Even if a model fits a set of data better than competitor models, this need not indicate that the winning model is closest to the true generative process underlying the data, particularly if the winning model is overly flexible. As such, a choice between models should be based on a measure that takes into account and properly adjusts for the flexibility of the models. The approach we used can be illustrated as follows. Given two models A and B, suppose that model B is found to provide a superior fit. Before concluding that it is the superior model, we generate artificial simulated data sets from both models and then fit both models to the artificial data produced by model B as well as produced by the alternative model. Suppose we find that model B is better able to account for data than model A even when the data were generated by model A. In that case, the observed goodness-of-fit advantage for model B when fitting the real data should be reinterpreted as possibly resulting from model B’s inherent flexibility (not its theoretical validity). We used just this artificial data approach to determine the appropriate criterion (e.g., AIC and BIC) in comparing goodness of for the EVSD, UVSD, DPSD, and MSD models as simultaneously applied to yes/no and 2AFC recognition data. These artificial data simulations also demonstrate that the technique of parameter regressions is flawed (which involves the issue of parameter recovery), and that a simultaneous fitting method is more appropriate for model selection (which validates model recovery).

To perform the simultaneous yes/no and 2AFC fits to real data, we obtained the data from Smith and Duncan’s (2004) Experiment 2. We also conducted the following similar experiment.

Method

Participants

Thirty-four undergraduate students at the University of California, San Diego were recruited and received credit for psychology courses in return for their participation.

Materials

Stimuli for the experimental trials consisted of 490 moderately high-frequency (an average of 80 times per million; norms from Kucera & Francis, 1967), singular noun words from 5 to 8 letters in length. Two hundred and eighty of the 490 words were randomly assigned as study items. Seventy and 140 of the 280 study items were randomly assigned as old for yes/no task and for 2AFC task, respectively. Seventy and 140 of the remaining 210 words were randomly assigned as new for yes/no task and for 2AFC task, respectively. For the practice trials, there were 9 study items (3 and 6 as old for yes/no task and for 2AFC task, respectively) and 9 new items (3 and 6 for yes/no task and for 2AFC task, respectively), which were not included for data analyses.

Procedure

The procedure was identical to that of Smith and Duncan’s (2004) Experiment 2 except as noted. During the study, participants were told that they would be asked to remember a word list. The 280 study items were presented, and each word appeared in the center of the computer screen at a time for 5 s. After the study, test instructions were presented. For the yes/no test trials, participants were told that they would be given a single word and asked to press one of the response keys, ‘certain no’, ‘probably no’, ‘guess no’, ‘guess yes’, ‘probably yes’, and ‘certain yes’ (we put the labels on the keyboard), depending on whether or not they thought the item was the one they studied. For the 2AFC test trials, participants were told that they would be given two words and asked to press one of the response keys, ‘certain left’, ‘probably left’, ‘guess left’, ‘guess right’, ‘probably right’, and ‘certain right’, depending on which left/right choice word they believed to be the studied item. After they understood the instructions, one of the tests was given per trial at the test phase. The participants of Smith and Duncan (2004) were asked to try to use each response key an equal number of times to scale their confidence judgments. By contrast, the participants in this study did not receive such instructions and were allowed to press whatever they wanted; asking participants to spread their responses evenly across the confidence categories might seem contrary to the DPSD model in which recollected items demand high-confidence responses (Parks & Yonelinas, 2007; Wixted, 2007a; 2007b). The assignment of study and test items and the test order for yes/no and 2AFC were randomized anew for each participant.

Results

We fitted the three signal-detection models to both the data of Smith and Duncan’s (2004) Experiment 2 and the data of our experiment, and report here both sets of findings.⁵ The data of one participant from Smith and Duncan’s experiment and one participant from our experiment were excluded because there were too many missing response categories to allow for model fitting.

We first briefly report the overall results of ROC analyses. Then, generalization across the two recognition tasks is evaluated in two different ways, first, by regressing the expected proportion correct in 2AFC based on model fits of the yes/no ROC data, as Kroll et al. (2002) did, and second, by examining parameter regressions, as Smith and Duncan (2004) did. The limitations of these methods are then described. Finally, simultaneous fits across the two tasks are performed to determine the best model, which is a method that we validate through a simulation study.

ROC analyses

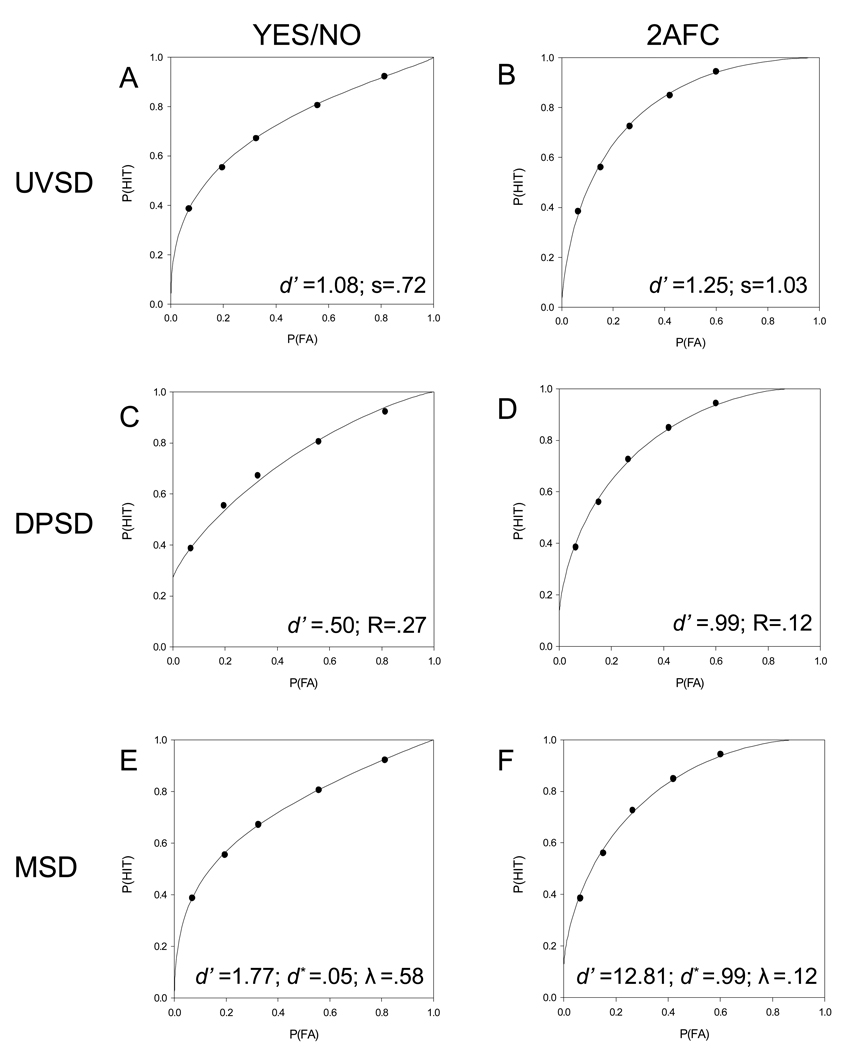
Parameter estimates from both group data and individual data were computed. Figure 3 shows the group ROC fits and parameter estimates for the UVSD, DPSD, and MSD models. For the yes/no test (left-hand side), the group data were well fit by the UVSD and MSD models, χ²(3) = 1.88, p = .60; and χ²(2) = 2.11, p = .35, respectively, whereas the DPSD model showed significant statistical deviation from the data, χ²(3) = 19.82, p < .001. From the individual data analysis, 93.94%, 78.79%, and 89.28% of the data were well fit by the UVSD, DPSD, and MSD models, respectively. For completeness, only 58.62% and 60.61% of the data were well fit by the EVSD model for Smith and Duncan’s experiment and ours, respectively. For the 2AFC test (right-hand side), the group data were well fit by the DPSD and MSD models, χ²(3) = 5.59, p = .13; and χ²(2) = 5.59, p = .06, respectively, and the UVSD model showed marginal deviation, χ²(3) = 7.83, p = .05. From the individual data analysis, 93.94%, 96.43%, and 92.86% of the data were well fit (i.e., observed deviations did not exceed chance) by the UVSD, DPSD, and MSD models, respectively.⁶ Not surprisingly, 93.10% and 93.94% of the data were well fit by the EVSD model for Smith and Duncan’s experiment and ours, respectively. These findings show that the UVSD, DPSD, and MSD models somewhat equally well account for both yes/no and 2AFC ROC data, and that 2AFC ROCs do not constrain the parameters of these models at all (i.e., the extra component of each model is not needed to fit the shape of the 2AFC ROC). These are goodness-of-fit results to each task separately; next we turn to the various techniques for assessing generalization across test format.

Figure 3.

ROC curves for yes/no (left) and 2AFC (right) fits of the UVSD model (top: graphs A and B), DPSD model (middle: graphs C and D), and MSD model (bottom: graphs E and F).

Accuracy regression

Observed proportion correct in 2AFC (M = .73, SD = .13) was regressed onto the expected proportion correct based on the yes/no data as determined by each of the models. All models including the EVSD model produced nearly identical regressions: R²(31) = .69, p < .001, using the data from our experiment; and R²(27) = .69~.70, p < .001, using the data from Smith and Duncan’s (2004) Experiment 2. These findings suggest that regressing expected accuracy onto observed accuracy, as Kroll et al. (2002) did, may not be a useful way to differentiate models.

Parameter regressions

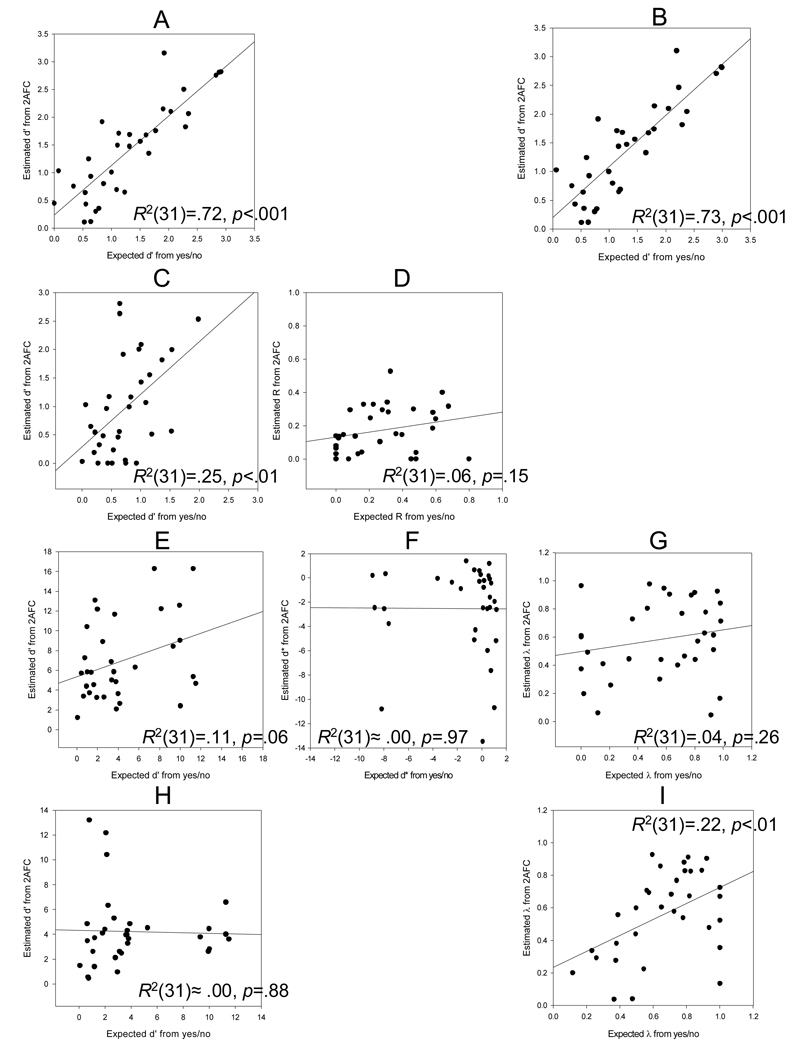
Figure 4 shows the 2AFC parameters expected from yes/no data for each participant plotted against parameters estimated from the 2AFC data. The figure also shows the results of a regression analysis performed on each scatter plot. The regression analysis of d' for each of the UVSD and DPSD models produced a significant linear relationship (Figure 4A and C, respectively), but estimates of R for the DPSD model from yes/no did not match R in 2AFC (Figure 4D). These findings are consistent with those of Smith and Duncan’s (2004) Experiment 2. The regression analyses of d', d^*, and λ for the MSD model did not produce significant linear relationships (Figure 4E, F, and G, respectively). When d^* was set to zero, the analysis of λ for the MSD* model yielded a significantly improved regression line but that of d' did not (Figure 4I and H, respectively). However, the regression analysis of d' for the EVSD model yielded a significant linear relationship (Figure 4B), producing the highest percent variance accounted for, R².

Figure 4.

Scatter plots from the regression analysis. A = d'_2AFC expected from d'_Yes/No in the UVSD model; B = d'_2AFC expected from d'_Yes/No in the EVSD model; C = d'_2AFC expected from d'_Yes/No in the DPSD model; D = R_2AFC expected from R_Yes/No in the DPSD model; E = d'_2AFC expected from d'_Yes/No in the MSD model; F = d^*_2AFC expected from d^*_Yes/No in the MSD model; G = λ_2AFC expected from λ_Yes/No in the MSD model; H = d'_2AFC expected from d'_Yes/No in the MSD^* model; I = λ_2AFC expected from λ_Yes/No in the MSD^* model.

We next conducted the regression analysis using simulated data under the situation that the DPSD model was true to examine whether the DPSD model could produce reasonable parameter regression in the best case scenario where the data was generated by the DPSD model. A failure to find good regression in this case would demonstrate that parameter regression might be misleading due to low parameter reliability. Using parameter values of the DPSD model that resulted from the separate fits to observed 2AFC data and yes/no data for each of our 33 participants, we then generated 33 artificial data sets for equivalent simulated participants, with a set of artificial 2AFC and yes/no data per simulated participant. Finally, we fit both the DPSD and UVSD models to the yes/no and 2AFC simulated data and performed regression analyses on the parameters estimated from each test format (just as we did for the empirical data).

The results from the parameter regression analyses for the DSPD model were somewhat better for the simulated data than they were for the real data, specifically, for d', R²(31) = .49, p < .001; and for R, R²(31) = .17, p < .05. However, the regression analysis for d' in fitting the UVSD model to these artificial data generated from the DPSD model also showed a significant linear relationship, R²(31) = .81, p < .001, and, more importantly, provided a much higher R² than the DPSD model. In other words, the parameter regression for the UVSD model was better than for the DPSD model even though the DPSD model was the true model for these simulated data. We next performed the same analyses for the 29 subjects of Smith and Duncan’s (2004) Experiment 2. As reported by Smith and Duncan (2004), the regression for the DPSD model based on the actual data for the d' and R parameters was R²(27) = .32, p < .05, and R²(27) = .002, p > .05, respectively (p. 621). Using parameter values of the DPSD model, we generated 29 artificial data sets and found modest improvements in the d' and R regression analyses, R²(27) = .43, p < .001, and R²(27) = .43, p < .001, respectively. For d' of the UVSD model, the regression based on true data produced R²(27) = .55, p < .05 (p. 621), whereas our simulated data (as generated by the DPSD model) showed a similarly high value for d', R²(27) = .68, p < .001. Thus, using a parameter regression test, the UVSD model outperformed the DPSD model even when the DPSD model generated the data. These findings suggest that the regression test is not a useful way to differentiate between these models, particularly considering that different numbers of parameters are estimated from the 2AFC data, which is likely to influence parameter reliability. Similar considerations would apply to the MSD model, which is likely to perform even worse in a regression analysis because it has yet another parameter to estimate from the 2AFC ROCs.

Simultaneous fits

The method we used to test the models was to simultaneously fit them to the yes/no and 2AFC data for each subject while requiring that the expected relationship between the parameters holds true. Thus, for example, when the EVSD model was fit to the data from a particular subject, all of the criteria were free to differ with test formats except that d'_2AFC was constrained to equal √2 d'_Yes/No. We performed these simultaneous fits for each model using our data as well as the data from Smith and Duncan’s (2004) Experiment 2. For each fit, the only constraint was that the theoretical relationship between a 2AFC parameter and its yes/no counterpart was enforced.

Before concluding that one of the models is the best based only on goodness-of-fit to empirical data, we generated simulated data on a per participant basis for each model using the model’s parameter estimates obtained from that model's simultaneous fit of the real data (the simulated data per individual had the same number of observations).⁷ That is, we fit each model simultaneously to the yes/no and 2AFC data of each individual, and then we used these best fitting parameters to generate one artificial data set according to each of the 3 models (the UVSD, DPSD, and MSD model). In parametric bootstrap simulations (Efron, 1979; Efron & Tibshirani, 1993), a model with a single set of parameters is used to generate many simulated data sets. Our simulations also produced many simulated data sets, but this was done as a function of individual differences (i.e., one artificial data set per individual based on fits of the models to each individual). In this manner, we generated data for 3 different artificial experiments, with each of these 3 artificial experiments in accord with a particular model (the UVSD, DPSD, or MSD model). Finally, we fit each of these 3 artificial experiments 4 different ways (including the EVSD model), to see if we could recover the true model that generated the data. If a model is best able to simultaneously account for the yes/no and 2AFC data that were in fact generated by that model, then goodness-of-fit for simultaneous fits is appropriate for model selection. Because these models differ in number of parameters, rather than using raw goodness-of-fit, we examined both AIC and BIC values, which correct for the number of parameters. As reported next, AIC produced values that allowed for recovery of the model that generated the data, and so we report the AIC values below⁸; for completeness, the BIC values are available at Appendix A.

Table 1 shows the AIC results of the parametric bootstrap analysis by summing across individuals. For both Smith and Duncan’s (2004) Experiment 2 and our experiment, the models were successfully recovered. That is, each model provided the best fit to its own simulated data. These findings suggest that the simultaneous fitting method using the AIC correction provides a valid method of identifying the true underlying model (unlike the regression analysis discussed earlier). Thus, we turn now to a discussion of the simultaneous fits of the competing models to real data, considering goodness-of-fit according to AIC, which was demonstrated to recover the true model.

Table 1.

Model Recovery: AIC Value and Rank Order of Simultaneous Fit to Simulated Data

		Smith & Duncan’s Experiment 2				Our Experiment
		Fitted model				Fitted model
		UVSD	DPSD	MSD	EVSD	UVSD	DPSD	MSD	EVSD
True model	UVSD	1	3	2	4	1	3	2	4
		20536	20623	20603	20804	25795	25877	25873	25956
	DPSD	2	1	3	4	2	1	3	4
		20889	20859	20896	20994	26085	26051	26109	26160
	MSD	3	2	1	4	2	3	1	4
		20791	20787	20784	20903	25747	25771	25739	25846

Note. The number on the top per cell represents the rank order (i.e., 1 = the best, and 4 = the worst), and the number on the bottom represents the AIC (Akaike information criterion) value; AIC = −2log(L) + 2V where L and V represent the maximum likelihood and number of free parameters that enter into the likelihood calculation, respectively; UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD = mixture signal detection; EVSD = equal-variance signal detection.

As shown in Table 2, for the empirical data from two experiments (i.e., Smith & Duncan’s Experiment 2 and our data), the UVSD model was best able to describe the relationship between yes/no and 2AFC recognition performance, providing the lowest AIC value. For Smith and Duncan’s data, the UVSD model provided the best fit for 65% of the participants. The DPSD model was second best, providing the best fit to 21% of the participants, and the MSD model was third in terms of AIC value (but providing the best fit for 0% of the participants). We also computed Akaike weights (Akaike, 1978; Wagenmakers & Farrell, 2004), which are calculated by using the raw AIC values and can be interpreted as conditional probabilities for each model. From an inspection of the Akaike weights in Table 2, the UVSD model is 1.88 and 3.50 times more likely to be the best model than are the DPSD and MSD models, respectively (i.e., .49/.26 and .49/.14). For our data, the UVSD model provided the best fit for the largest group of participants (40%). The DPSD model was third in terms of AIC value, providing the best fit to 24% of the participants. The MSD model was second in terms of AIC value but provided the best fit for the smallest group of participants (12%). The UVSD model is 1.38 and 1.56 times more likely to be the best model than are the DPSD and MSD models, respectively (i.e., .36/.26 and .36/.23). On the whole, our results support Smith and Duncan’s (2004) conclusion that the UVSD model is best able to account for yes/no and 2AFC recognition performance even though we take issue with the method they used to arrive at that conclusion. Somewhat surprisingly, the MSD model performed poorly, capturing 12% of the participants in our data but none of the participants in Smith and Duncan’s data. However, AIC penalizes the MSD model for including an additional parameter, and so this is not the same as saying that the MSD model fit the data poorly in terms of chi-square goodness-of-fit.

Table 2.

Model Comparison: AIC Value, Rank Order of Simultaneous Fit to Empirical Data, Akaike weight, and Percentage of the Best Simultaneous Fit

	Smith & Duncan’s Experiment 2				Our Experiment
	UVSD	DPSD	MSD	EVSD	UVSD	DPSD	MSD	EVSD
	1	2	3	4	1	3	2	4
AIC	20750	20799	20827	20987	25997	26026	26022	26167
w(AIC)	.49	.26	.14	.11	.36	.26	.23	.15
Best fit	65 %	21 %	0 %	14 %	40 %	24 %	12 %	24 %

Note. The number on the top of the raw of AIC (Akaike information criterion) represents the rank order (i.e., 1 = the best, and 4 = the worst); w(AIC) = the Akaike weight; UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD = mixture signal detection; EVSD = equal-variance signal detection.

Furthermore, we followed the same procedure to compare the models, the UVSD, DPSD, and MSD* models. We generated data for 3 different artificial experiments, with each of these 3 artificial experiments in accord with a particular model, and fit each of these 3 artificial experiments 3 different ways. Because these models have the same number of parameters, we used raw goodness-of-fit. Table 3 shows the goodness-of-fit by summing across individuals. For both Smith and Duncan’s (2004) Experiment 2 and our experiment, the models were successfully recovered, and therefore we report the simultaneous fits of the competing models to real data.

Table 3.

Model Recovery: Chi-square Value and Percentage of the Best Simultaneous Fit to Simulated Data

		Smith & Duncan’s Experiment 2			Our Experiment
		Fitted model			Fitted model
		UVSD	DPSD	MSD*	UVSD	DPSD	MSD*
True model	UVSD	181.96	289.40	224.65	207.17	292.63	258.04
		62 %	21 %	17 %	70 %	15 %	15 %
	DPSD	213.76	182.82	223.81	287.81	262.26	315.80
		21 %	62 %	17 %	27 %	61 %	12 %
	MSD*	237.56	215.05	160.93	307.78	337.48	248.97
		14 %	24 %	62 %	12 %	24 %	64 %

Note. UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD* = mixture signal detection (with d^*=0).

As shown in Table 4, for the empirical data from two experiments, the UVSD model was best able to describe the relationship between yes/no and 2AFC recognition performance, which is consistent with the findings when the full version of the MSD model was compared with the UVSD and DPSD models.⁹ For Smith and Duncan’s data, the UVSD model provided the best fit for 69% of the participants. The DPSD model was second best, providing the best fit to 17% of the participants, and the MSD model was third, providing the best fit for 14% of the participants. For our data, the UVSD model provided the best fit for the largest group of participants (43%). The DPSD model was third in terms of chi-square goodness-of-fit, providing the best fit to 36% of the participants. The MSD model was second in terms of chi-square goodness-of-fit but provided the best fit for the smallest group of participants (21%). These results also show that the UVSD model is best able to account for yes/no and 2AFC recognition performance even when the MSD model is reasonably constrained to have only two free parameters (i.e., the MSD* model), like the UVSD and DPSD models.

Table 4.

Model Comparison: Chi-square Value and Percentage of the Best Simultaneous Fit to Empirical Data

	Smith & Duncan’s Experiment 2			Our Experiment
	UVSD	DPSD	MSD*	UVSD	DPSD	MSD*
Chi-square	196.68	245.24	278.54	277.59	322.54	301.61
	(p = .59)	(p < .05)	(p < .001)	(p < .05)	(p < .001)	(p < .001)
Best fit	69 %	17 %	14 %	43 %	36 %	21 %

Note. UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD^* = mixture signal detection (with d^*=0).

Finally, we consider the 4 possible nested model comparisons according to Figure 2, not only to provide a method based on statistical analyses for quantifying the degree of misfit in light of the number of free parameters, but also to examine whether we find converging evidence in concert with the AIC results. First, the DPSD and MSD models were compared by taking advantage of the fact that the DPSD model is nested under the MSD model.¹⁰ If there is no significant difference in chi-square value between these two models with one degree of freedom for each participant, then the conclusion would be that adding a free parameter to the MSD model cannot be justified and may merely capture random error. Comparing the fit across participants in Smith and Duncan’s (2004) Experiment 2 for the DPSD model revealed no significant improvement in the fit for the MSD model, χ²(29) = 35.09, p = .20. However, there was a significant improvement of the MSD model compared to the DPSD model for the data of our experiment, χ²(33) = 83.90, p < .001. Second, we applied the same analysis to the MSD versus MSD* models. Adding the free parameter, d^* to the full version of the MSD model was justified, χ²(29) = 68.40, p < .001; χ²(33) = 62.98, p < .01, for Smith and Duncan’s data and our data, respectively. Third, we applied the same analysis to the DPSD versus EVSD models. Adding a free parameter to the DPSD model compared to the EVSD model was justified, χ²(29) = 336.40, p < .001; χ²(33) = 274.46, p < .001, for Smith and Duncan’s data and our data, respectively. The last nested model comparison was conducted between the UVSD versus EVSD models. There was also a significant improvement of the UVSD model compared to the EVSD model, χ²(29) = 384.95, p < .001; χ²(33) = 319.41, p < .001, for Smith and Duncan’s data and our data, respectively. These findings provide the same conclusions as found with AIC.

Discussion

The present study used various methods to examine signal-detection models of recognition memory using data that were obtained from two different tasks, yes/no and 2AFC. First, we found that using the parameters estimated from yes/no ROC to make model-specific predictions of proportion correct on the 2AFC task was not an appropriate method of model selection. The EVSD model as well as all three of the considered SDT model variants predicted proportion correct equally well. Second, a theory-driven comparison of parameters using regression analyses based on separate ROC fits of the two tasks merely served to identify the least flexible model (with the best parameter recovery), not the most valid model. In fact, using that method, the EVSD model provided the best account. Moreover, in our simulation studies, this method failed to identify the DPSD model even when the simulated data were generated by that model. These findings confirm that parameter regressions are inadequate as a method for comparing the models in terms of their ability to generalize across test format. By contrast, our simulation studies indicated that simultaneous fits of both tasks successfully recovered the true model (good model recovery). Using that method, we determined that the UVSD model produced the most parsimonious interpretation of performance on the yes/no and 2AFC tasks.

The role of parameter reliability in model selection

The testing of quantitatively instantiated models is one of the most important aspects of scientific inquiry. The goal is to select the most parsimonious model that gives an accurate description of psychological phenomena. Goodness-of-fit measures are extensively used to measure the adequacy of a model to account for the data, and the model that provides the smallest deviation is often preferred. A possible problem with this method of model selection is that flexible models can fit data well even if they are invalid. Taking a different approach, Smith and Duncan (2004) argued that best-fitting parameter estimates may not generalize across tasks if a model fits well only because it is highly flexible. They instead tested the ability of competing models to produce expected parameter estimates across two different tasks that were theoretically related to each other, namely, yes/no and 2AFC recognition, and they found that the UVSD model exhibited the best expected relationship according to linear regression.

However, a model that produces the best expected relationship between its estimated parameters in different situations is not necessarily the most valid model. Instead, such a model may simply be the least flexible model, thus producing the most reliable parameter estimates. In Smith and Duncan’s (2004) regression technique, the EVSD model enjoys an advantage even though it is not likely to be a viable model of recognition memory. In fact, this result is hardly surprising because reliability is maximized when it is measured through the total variability in the instrument. This also explains why all models (including the EVSD model) predicted proportion correct equally well; all models were compared in terms of a single entire measure, proportion correct. Indeed, we found highly reliable parameter values of the UVSD model even when it was fit to data generated by the DPSD model. It should be noted that it is not because the UVSD model is more flexible than the DPSD model (and therefore the UVSD model mimics the DPSD model). It is instead because a single parametric prediction of the UVSD model (namely, d'_2AFC) is derived from both d'_Yes/No and slope, whereas the predicted d'_2AFC and R_2AFC of the DPSD model were each calculated separately from the corresponding yes/no parameters.

Although the use of parameter reliability is not appropriate for model selection, it is true that reliability sets a limit on validity. If a measure is unreliable, it obviously cannot be shown to be valid. Indeed, the regression coefficient indicates the extent of the tradeoff between parameters in a model. In other words, parameters play off against one another for the better fit, which can happen more often to more flexible models. Although the focus of this paper is on model recovery, not on parameter recovery as indicated earlier, the parameter reliability can be examined. Appendix B shows the regressions between the generating and recovered parameter values of the simultaneous fits, which reveals overall good parameter recovery for the simultaneous fitting technique (except for d' of the MSD model of Smith and Duncan’s data).

Model flexibility

Any goodness-of-fit measure reflects the model’s ability to approximate the underlying cognitive process as well as its ability to fit random error. The process of model selection is complicated because in most cases, a model with more free parameters provides better fits but is more flexible and may therefore overfit the data. In the worst-case scenario, a good fit can be accomplished by a model that is extremely good at fitting noise even though it provides a poor approximation of the cognitive process. It is undesirable to refer to the most complex model as the best, and instead it is generally accepted that the best model is the one that provides an adequate account of the data while using a minimum number of parameters (e.g., Myung, 2000; Pitt & Myung, 2002; Wagenmakers & Farrell, 2004).

Because it has an extra parameter, it is clear that the MSD model is more flexible than the DPSD model, and a relevant question is whether such flexibility is warranted. The MSD model is mathematically identical to the DPSD model not only when the MSD model has an extremely high value of d' but also under following situations: (1) when d' of the DPSD model is equal to d' of the MSD model, which is also equal to d^* of the MSD model, and R of the DPSD model is zero; (2) when λ of the MSD model is equal to 1, R is equal to 0, and d' of the DPSD model is equal to d' of the MSD model; and (3) when λ and R are equal to 0, and d' of the DPSD model is equal to d' of the MSD model. Indeed, such cases were found in around 38% of Smith and Duncan’s (2004, Experiment 2) data and 36% of our data. Moreover, the low reliability of each parameter value but still good fits of the MSD model suggest that there are multiple ways in which parameters conspire to capture the same or similar data. For example, because both the DPSD and MSD models contain two types of target (recollected versus familiar targets for the DPSD model, and low versus high attention targets for the MSD model), overall hit rates can remain unchanged in these models while the mixture between the two types of target trades off with the hit rate provided by each type of target. Such tradeoffs, or high interchangeability between parameters, may in fact be psychologically valid and reflect different shapes in the ROCs. However, without clear a priori theoretical grounds, it is difficult to produce an unequivocal conclusion from the results.

There have been a handful of measures in model selection to dispel the problems of model flexibility although there is no clear consensus as to which of these techniques is most accurate. Furthermore, the definition of an accurate method for comparing models depends on the chosen properties that are to be optimized in an application of a model. An early and well-known measure that penalizes flexible models, AIC, addresses the most salient difference among models, namely the number of free parameters. The logic behind AIC is that the better fit obtained with the more parameters should justify the necessity of those parameters in more accurately capturing data. BIC is another popular measure of theoretical approaches. While the aim of AIC is to reduce errors and to modify overestimation, the use of BIC is to interpret data as a Bayesian measure that handles uncertainty based on probability distributions. However, BIC sometimes penalizes a model having additional parameters too much (i.e., a conservative criterion). Beyond this difference, both AIC and BIC ignore the functional form of the models under consideration, and they both penalize models based on the number of free parameters. Yet this is assuredly incorrect, and the ability of a model to fit data is not purely a function of the number of parameters. The ability to fit data also depends on a model’s functional form (e.g., for some models, an extra parameter may allow a higher degree of additional freedom to capture data). To address the functional form of a model, another tool is to investigate model mimicry (e.g., using simulation studies), which can help to identify the relative flexibility of models even if they have the same number of free parameters. Assessing model mimicry can be accomplished by using a parametric bootstrap based on the full sample of the observed data, or perhaps in concert with a nonparametric bootstrap to incorporate sampling error in the data. Furthermore, one could perform a parametric bootstrap without any reference to observed data.¹¹ In the current case, we used a simulation analysis to ask a specific question; For these particular data, which goodness of fit measure (AIC or BIC) penalized for the number of free parameters in such a way as to enable model recovery. However, the conclusion from this simulation study is not expected to generalize to other models or even to other data.

Finally, beyond the issue of goodness of fit, we also took it a step farther. Myung (2000) argued that one way to improve model selection is to assess how well a model’s fit to one data sample generalizes to other samples generated by the same process. In essence, that is the method that we used in this study. That is, simultaneous fits were used to compare models in their ability to generalize across different tasks that are theoretically closely related to each other, and the UVSD model emerged as the most viable model.

The role of recollection and familiarity

In light of much evidence supporting the dual-process theory of recognition, one might wonder how the models under consideration here can be reconciled with recollection and familiarity. This question is especially relevant to the UVSD model in terms of its superior ability to simultaneously account for yes/no and 2AFC recognition performance. The DPSD model is inherently a dual-process model. In the DPSD model, recollection is viewed as a categorical, threshold-based process, and familiarity is viewed as a continuous process (Yonelinas, 1994). Participants are assumed to rely on the recollection process alone whenever possible (and it is assumed to always support high confidence) and to otherwise rely on familiarity (which is associated with varying degrees of confidence). The UVSD model, by contrast, is not as readily reconciled with dual-process theory. However, Wixted (2007a; 2007b) proposed that recognition memory decisions are based on memory strength, where strength is a function of recollection and familiarity combined. The combined model views both recollection and familiarity as continuous processes and suggests that different sources of evidence are summed into an aggregate variable upon which the decision is based. According to this view, the UVSD model is compatible with dual-process theory even though decisions are based on a unidimensional memory strength variable.

The same logic can be applied to the MSD model because the MSD model also assumes dual processes. The two old distributions in the MSD model are based on a unidimensional memory strength variable (or familiarity), and they are mixed together on the basis of attention (DeCarlo, 2002). In similar vein, participants may rely on memory strength where familiarity and attention processes are combined.

Conclusion

Our study investigated how well three different models of recognition memory can account for data from two theoretically related tasks. The results are of both methodological and theoretical interest. At the methodological level, our results suggest that one previously used method based on regression analysis serves only to identify the least flexible model (not the most valid model). By contrast, the simultaneous fitting method is better able to identify the true model while maintaining the principle of parsimony. Our analysis also underscores the importance of investigating model mimicry as a tool of model selection. At the theoretical level, our findings suggest that, among the three models considered here, the UVSD model is best able to describe the relationship between yes/no and 2AFC recognition performance.

Appendix A

The BIC values are reported in Appendix A that we compared the models having different numbers of parameters, the UVSD, DPSD, MSD, and EVSD models. As reported in Table A1, BIC produced values that did not allow for recovery of the model that generated the data. BIC penalizes the model having more parameters too much for including the additional parameters, and sometimes the EVSD model even the best fit the data (it should be noted that this does not mean that BIC is inappropriate in general to compare competitive models). For the empirical data of the two experiments, the UVSD model was best able to describe the relationship between yes/no and 2AFC recognition performance as shown in Table A2. Although this is consistent with the finding of AIC, we do not discuss this BIC result because of its failure of the model recovery.

Table A1.

Model Recovery: BIC Value and Rank Order of Simultaneous Fit to Simulated Data

		Smith & Duncan’s Experiment 2				Our Experiment
		Fitted model				Fitted model
		UVSD	DPSD	MSD	EVSD	UVSD	DPSD	MSD	EVSD
True model	UVSD	1	2	4	3	1	3	4	2
		21689	21776	21861	21851	27107	27189	27305	27149
	DPSD	3	1	4	2	3	2	4	1
		22041	22011	22154	22040	27398	27363	27541	27353
	MSD	2	1	4	3	2	3	4	1
		21943	21939	22042	21950	27060	27083	27171	27039

Note. The number on the top per cell represents the rank order (i.e., 1 = the best, and 4 = the worst), and the number on the bottom represents the BIC (Bayesian information criterion) value; BIC = −2log(L) + Vlog(n) where L, V, and n represent the maximum likelihood, number of free parameters, and number of observations that enter into the likelihood calculation, respectively; UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD = mixture signal detection; EVSD = equal-variance signal detection.

Table A2.

Model Comparison: BIC Value, Rank Order of Simultaneous Fit to Empirical Data Schwarz weight, and Percentage of the Best Simultaneous Fit

	Smith & Duncan’s Experiment 2				Our Experiment
	UVSD	DPSD	MSD	EVSD	UVSD	DPSD	MSD	EVSD
	1	2	4	3	1	2	4	3
BIC	21903	21951	22085	22034	27309	27339	27454	27360
w(BIC)	.45	.22	.02	.31	.35	.24	.05	.36
Best fit	48 %	45 %	0 %	7 %	40 %	36 %	0 %	24 %

Note. The number on the top of the raw of BIC (Bayesian information criterion) represents the rank order (i.e., 1 = the best, and 4 = the worst); w(BIC) = the Schwarz weight; UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD = mixture signal detection; EVSD = equal-variance signal detection.

Appendix B

Model parameter estimates of simultaneous fit are reported in Appendix B. Additionally, the proportion of variability between parameter estimate of empirical data and parameter estimate of simulated data is presented.

Table B.

Mean Parameter Estimate of Simultaneous Fit and Coefficient of Determination (R²) between Parameter Estimate of Empirical Data and Parameter Estimate of Simulated Data

		Smith & Duncan’s Experiment 2			Our Experiment
Model	Parameter	Empirical	Simulated	R2	Empirical	Simulated	R2
UVSD	d'	1.93 (.11)	1.93 (.11)	.94***	1.34 (.15)	1.30 (.14)	.98***
	s	.63 (.03)	.62 (.03)	.45***	.74 (.04)	.75 (.04)	.80***
DPSD	d'	.92 (.10)	.92 (.10)	.76***	.64 (.07)	.68 (.08)	.61***
	R	.39 (.03)	.36 (.04)	.77***	.27 (.04)	.24 (.04)	.80***
MSD	d'	6.61 (.71)	5.11 (.72)	.08NS	6.27 (.85)	5.48 (.82)	.16*
	d*	.54 (.13)	.28 (.17)	.76***	.08 (.14)	−.09 (.16)	.34***
	λ	.51 (.04)	.60 (.05)	.64***	.45 (.05)	.50 (.06)	.61***
MSD*	d'	3.07 (.31)	3.38 (.60)	.57***	3.68 (.52)	3.49 (.52)	.18*
	λ	.76 (.03)	.78 (.03)	.74***	.60 (.05)	.61 (.04)	.51***

Note. Standard errors of the mean are in parentheses; UVSD = unequal-variance signal detection; DPSD = dual-process signal detection; MSD = mixture signal detection; MSD^* = mixture signal detection (with d^*=0).

^***p < .001;

^*p < .05;

^NSp = .14.