Abstract
Interprotein electron transfer plays an important role in biological energy conversion. In this work the electron transfer reaction between cytochrome c2 (cyt) and reaction center (RC) was studied to determine the mechanisms coupling association and electron transfer. Previous studies have shown that mutation of hydrophobic residues in the reaction interface, particularly Tyr L162, change the binding affinity and rates of electron transfer at low ionic strength. In this study the effect of ionic strength on the second order electron transfer rate constant k2, between cyt c2 and native or mutant RCs was examined. Mutations of hydrophobic and hydrogen bonding residues caused k2 to decrease more rapidly with increasing ionic strength. This change is explained with a transition state model by a switch from a diffusion-limited reaction in native RCs, where electron transfer occurs upon each binding event, to a fast exchange reaction in the Tyr L162 mutant, where dissociation occurs before electron transfer and k2 depends upon the equilibrium between bound and free protein complexes. The difference in ionic strength dependence is attributed to a smaller effect of ionic strength on the energy of the transition state compared to the bound state due to larger distances between charged residues in the transition state. This model explains the faster dissociation rate at higher ionic strength that may assist rapid turnover important for biological function. These results provide a quantitative model for coupling protein association with electron transfer and elucidate the role of short-range interactions in determining the rate of electron transfer.
Interprotein electron transfer reactions (1) play important roles in many biological systems necessary for energy conversion such as photosynthesis and respiration. These reactions between electron transfer partners involve the processes of protein association (2-4) and electron transfer (5) which must be optimized to achieve the necessary high turnover rates.. In this paper we examine the interprotein electron transfer reaction between cytochrome c2 and bacterial reaction center (6) in order to understand the molecular basis for the association and electron transfer processes. The effect of mutating hydrophobic residues in the interface region between the two proteins on the ionic strength dependence of the second order electron transfer rate was studied. The results are quantitatively described by a transition state model These studies demonstrate the role of long-range electrostatic and short-range hydrophobic interactions on association and electron transfer.
The interprotein electron transfer reaction between cytochrome c2 and bacterial reaction center plays an important role in photosynthetic electron transfer(7, 8). The reaction center is the membrane bound protein responsible for the initial light-induced electron transfer reaction in photosynthesis. The charge separation results in the oxidation of a primary donor, D, a bacteriochlorophyll dimer, and the reduction of a bound quinone acceptor, Q. Cyclic electron transfer coupled to proton pumping across the photosynthetic membrane is achieved when electrons from the RC are transferred through the cytochrome bc1 complex then carried back to reduce the oxidized D+ by the water soluble electron transfer protein, cytochrome c2.
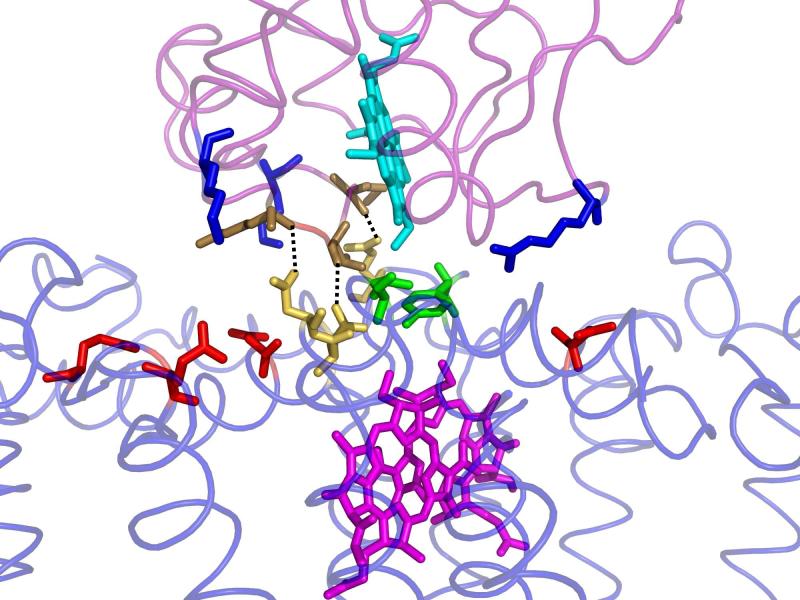
The structure of the complex between cyt c2 and RC from Rb. sphaeroides has been determined by x-ray crystallography (9). Measurement of the electron transfer rate in the co-crystal gave the same value as in solution, ke =1.0×106 s−1, indicating that the cyt:RC complex in the crystal is in the active configuration for electron transfer. In the crystal structure, the cyt c2 is bound on the surface of the RC with the redox active cofactors, heme and BChl2 in close proximity, separated by the key residue Tyr L162 on the RC surface (Figure 1). The interface region between the two proteins can be divided into two domains; a central hydrophobic domain consisting of residues making van der Waals, cation-pi and hydrogen bond contacts surrounded by an electrostatic domain consisting of oppositely charged residues separated by solvent.
Figure 1.
The structure of the cytochrome c2:RC complex. The cofactors heme (Turquoise) on the cyt and bacteriochlorophyll dimer (Purple) on the RC are connected through a tightly packed interface region containing hydrophobic residues Tyr L162 and Leu M191 (Green) and hydrogen bonding residues Asn M187, Asn M188, and Gln L258(Yellow). Outside this tightly packed central region is a region of solvent separated complementary charged residues; negatively charged (Red) residues on the RC and positively charged (Blue) residues on the cyt (Axelrod et. al (9), PDB 1L9B).
The reaction between cyt and RC have been extensively studied (10-12) (for a review see (6)). Since the electron transfer reactions are light induced, pulsed laser measurements can be used to determine the microscopic rate constants. The simplest scheme (12) that can account for the light induced electron transfer reactions for RCs from Rb. sphaeroides is shown below.
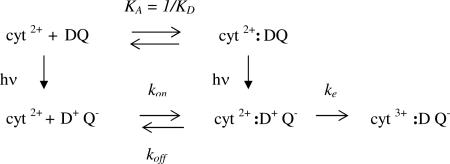 |
(1) |
Prior to illumination, the reduced cyt and RC are in equilibrium between a bound and free state as shown in the top line (association constant KA =1/KD~106 M−1). Light absorption following a short laser pulse leads to electron transfer forming the oxidized donor/ reduced quinone acceptor DQ+hν → D+Q−. In the fraction of RCs having a bound cyt the first order electron transfer reaction occurs in the time scale of microseconds (ke ~ 106 s−1). For the fraction of RCs lacking bound cyt, the reaction occurs via a second order reaction where the second order rate constant k2 ~109 s−1M−1 at low ionic strength. The dissociation rate for the cyt c2 is fast (koff ~ 103 s−1 at low ionic strength) (13, 14) allowing fast turnover for cyclic electron transfer.
The second order rate constant k2, is arguably the most important parameter for the function of the proteins. The value of k2 is governed by the values of the rates of association kon, dissociation koff and electron transfer ke (1).
| (2) |
At low ionic strength ke>>koff for the reaction between cyt c2 and RC, k2 is in the diffusion limited regime where k2 = kon ~109 s−1M−1. In this regime electron transfer is limited by the rate of protein association and independent of the electron transfer rate ke, consistent with the finding that k2 is independent of the driving force for electron transfer (15).
The molecular basis for binding and electron transfer has been studied. The role of charged residues was demonstrated by many studies which showed the decrease in the second order reaction rate with increasing ionic strength (11, 14, 16-22) This has been supported by chemical modification of charged residues (23) and by site directed mutagenesis (12, 24). The role of hydrophobic and hydrogen bonding residues has been demonstrated by site directed mutagenesis (21, 25, 26). Mutations of residues found in the interface between the two proteins in the co-crystal structure change the values of ke, KA, and k2. However, the mutations of charged residues and neutral residues have characteristically different effects. Mutations of charged residues in the solvent separated interface region alter k2 in parallel with changes in the binding affinity KA. However, these mutations have little effect on the value of ke, (12) which indicates that the short range interactions responsible for electron tunneling occur across the hydrophobic short-range interaction domain in the center of the contact interface. The complementary charged residues across the binding interface are solvent separated and do not make strong tunneling contacts. Mutations of hydrophobic residues (21, 25) in the central contact region change both KA and ke indicating that hydrophobic interactions are important both for binding and electron tunneling. The effect of hydrophobic mutations on k2 is complex. For mutations with small effects on KA, k2 is relatively unchanged, indicating that the short range interactions do not greatly affect the association rate kon but exert their effect by changing the dissociation rate koff. However mutations which have larger effects on koff and ke, can bring the second order reaction into the fast exchange regime (ke < koff). For these mutants k2 depends on the equilibrium binding constant KA (Eq. 2) and the value of k2 decreases greatly due to weaker binding.
In this work we study the effect of ionic strength on the second order rate constant k2 for native RCs and three mutant RCs. having neutral changes to hydrophobic residues at the binding interface. The mutated residues shown in Figure 1 include two hydrophobic residues, Tyr L162, and Leu M191 which are in van der Waals contact with the cyt, and three hydrogen bonding residues Asn M187, Asn M188 and Gln L258 which form hydrogen bonds to the cyt c2. The residues were all mutated to Ala. The hydrophobic residues were studied as single mutants (YA L162 and LA M191) while the three hydrogen bonded residues were mutated together to form a triple mutant (called 3xHbond). The RCs were chosen to represent different reaction regimes for the electron transfer reaction based on their electron transfer properties at low ionic strength. The RCs studied were: 1) native RCs which display diffusion limited reaction with ke> koff. 2) YA L162 RCs where mutation increases koff and decreases ke resulting in a fast exchange reaction with ke< koff. 3) LA M191 and 3xHbond RCs which are in the diffusion limited regime at low ionic strength but ke is decreased and koff is increased so that at high ionic strength the reaction is expected to be in the fast exchange regime. The results show that the hydrophobic mutations of neutral residues can have significant effects on the ionic strength dependence of the second order electron transfer rate. The effects of increasing salt concentration are explained by the difference in the ionic strength dependence of the association rate and the equilibrium binding constant. The data are quantitatively fit by a transition state model in which the effects of ionic strength have different effects on the energies of the transition state and bound state. These results show the importance of both electrostatic and hydrophobic interactions to the rate of inter-protein electron transfer.
Materials and Methods
Sample Preparation
The native RCs were isolated from the carotenoidless strain Rb. sphaeroides R-26. Mutant RCs were expressed in Rb. sphaeroides,ΔLM1 and prepared and characterized as previously described (25, 26). RCs were isolated in 15 mM Tris-HCl pH 8, 0.025% lauryl dimethylamine-N-oxide (LDAO), 0.1 mM EDTA following published procedures (27). The final ratio of absorbance, A280/A800, was ≤ 1.5. The RC samples were then dialyzed for two days against buffer (10 mM Hepes pH 7.5, 0.04% dodecyl-β-D-maltoside (Anatrace)). Cyt c2 was isolated and purified as previously reported (28) to an absorbance ratio A280/A420 ≤ 0.3. A mixture of hydroquinone and quinone (~ 50 mM QoH2 and 50 mM Qo) added prior to the measurement to keep the cyt in the reduced state.
Kinetic Measurements
The kinetic measurements were made using a pulsed laser source and monitoring apparatus previously described (26). The transient absorbance measurements were made by monitoring the absorbance change at 865 nm due to the oxidation and re-reduction of the primary donor D. The ionic strength of the solution was changed by addition of KCl. RC samples were dissolved in (10 mM Hepes pH 7.5, 0.04% dodecyl-β-D-maltoside (Anatrace)). The second order rate constant k2 was determined from the initial slope of the plot of the observed rate of the slow phase for electron transfer versus the free cyt in solution. The binding constant KA was determined from a plot of the fraction with fast kinetics (due to bound cyt) as a function of free cyt (26). In earlier studies of the cyt RC reaction additional first order electron transfer components were observed (11, 18, 21) The observation of additional kinetic components is dependent on sample preparation and may be due to aggregation (29). In addition, the value of KD was found to be dependent on RC concentration suggesting an aggregation effect. (26). In order to avoid these problems the concentration of RCs was kept low (≤ 0.5 μM) in order to prevent effects due to aggregation.
Modeling the Electron Transfer Rate Constant
Transition State Model
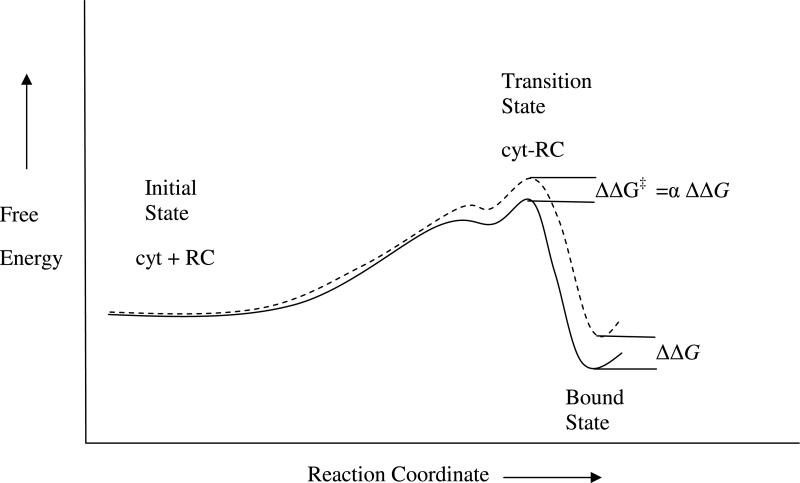
The ionic strength dependence of the electron transfer rate k2 between cyt and RCs is modeled by changes in the association and dissociation rates for formation of the bound state active in electron transfer. The rate constant for protein association, i.e. kon, involves the formation of a transient transition state leading to the bound state (3). The reaction coordinate diagram for association to form the bound state is depicted in Figure 2 (12, 30). The solid line represents the change in free energy in going from the isolated proteins to the bound complex. As the two proteins come together the free energy increases due to loss of translational entropy until long range electrostatic interactions bring the complementary charged surfaces of the cyt and RC to form a loosely bound encounter complex. In the encounter complex the two protein surfaces are brought together by long-range electrostatic interactions between complementary positive and negative charges but short-range contacts important for electron transfer (i.e. the heme edge and Tyr L162) have not been formed. Fluctuations of the orientation two proteins in the encounter complex brings them to the transition state, an ensemble of configurations in which the short range contacts are oriented properly to form close contacts. The transition state is a small subset of configurations in the encounter complex and part of the transition state barrier is due to the translational and conformational entropy. This is emphasized in multidimensional energy landscape pictures of the reaction coordinate for protein association (3).
Figure 2.
Reaction coordinate diagram for association of the active cyt:RC complex for low ionic strength (solid line) and high ionic strength (dashed line). The energies of the separated proteins are set equal at the left. The change due to ionic strength of the rate of association kon is dependent on the change in energy of the transition state ΔΔG‡ while the change in the binding equilibrium constant KA is dependent on the change in energy of the bound state ΔΔG. The parameter α is the ratio of the change in energy of the transition state ΔΔG‡ and bound state ΔΔG due to ionic strength. (Modified from (12))
The structure of the transition state ensemble for the cyt c2-RC complex has been modeled by electrostatic calculations based on mutant data (12, 31). At the transition state the cyt c2 was found to be well separated from the RC. The distance between the heme edge and Tyr L162 in the transition state was estimated to be 8-10 Å farther than in the bound state. Following the formation of the transition state the complex proceeds rapidly to the state active in electron transfer, presumably by forming short range contacts between cyt and RC. The structure of the active bound state is not known conclusively since electron transfer can occur over long distances (5). However it is assumed to be similar to the co-crystal structure where short range contacts between the heme edge and the RC surface are present and electron transfer occurs. The structure of the state active in electron transfer is discussed below.
The dotted line in Figure 2 represents the effect of ionic strength on the free energies of the states along the reaction coordinate. The addition of salt lowers the energy of the system by interactions between ions in solution and charged surface residues. The stabilization is expected to be greater for the separated proteins in the initial state than for the transition state or bound state where access of the ions in solution to charged residues in the binding interface is hindered by interprotein interactions. In this figure the energies of the two systems are adjusted to be equal at the initial state where the proteins are separated. The changes in energy appear as increases in the energy of the transition state ΔΔG‡ and bound state ΔΔG relative to the initial state. If the distance between the cyt and RC are different in the transition state and bound state, as previously proposed (12, 31), then the access to ions and ionic screening should be different as well. This should result in different changes in the transition state energy and binding energy due to ionic strength. In this model the change in the activation energy for the association rate ΔΔEon is the change in energy of the transition state, ΔΔG‡, and is taken to be a fraction α of the free energy change in the bound state.
| (3) |
The value of α determines the relative ionic strength dependence of the binding constant KA and second order rate constant kon. For α=1, KA and kon have the same dependence on ionic strength. For smaller values of α, kon has a weaker dependence on ionic strength than KA. The ionic strength dependence of the dissociation rate koff also depends on α. The transition state model for the dissociation rate assumes a pseudo-equilibrium between the bound state and transition state. Thus, the change in the activation energy for the dissociation rate ΔΔEoff is given by the difference between the changes in energies of the two states.
| (4) |
For α =1 the dissociation rate should not change, for smaller values of α, the change in activation energy for dissociation should be negative and the dissociation rate should increase.
Ionic strength dependence of k2
The ionic strength dependence of the association and dissociation rates may be used to model the second order rate constants. We use a phenomenological expression based on the Debye-Hückel limiting law (32) for the ionic strength dependence of the association and dissociation rate constants. The association and dissociation rate constants at ionic strength I (kon(I) and koff(I)) vary exponentially with the square root of the ionic strength at low ionic strengths.
| (5) |
| (6) |
Where kon(0) and koff(0) are the association and dissociation rate constants at zero ionic strength. This expression is usually used to model the interaction between small ions at low ionic strength <10 mM. However, we find that it accounts for the ionic strength behavior of highly charged proteins over a wider range of ionic strengths. The parameters γ, Ω describe the ionic strength dependence of the activation energies for association, dissociation respectively. They are related to α by
| (7) |
Since these parameters have opposite signs (for α <1) the association and dissociation rate constants change in opposite directions, i.e. kon decreases and koff increases.
The association constant as a function of ionic strength KA(I) is give by
| (8) |
The value of the second order rate constant for different mutant (m) RCs as a function of ionic strength is formulated as
| (9) |
Where kcm is an additional parameter that represents the limiting value of k2 at high ionic strength. The superscript m indicates the values for different native and mutant RCs.
Main Assumptions in the model
The main assumptions in determining the parameters in the model are:
- The electron transfer rate in the bound state does not change with ionic strength either for native or mutant RCs. This is justified by measurements made over a limited range (see below)
(10) The value of α is the same for all RCs. This assumes that the transition state for binding is the same for all mutant RCs. The rationale for this is that the transition state is determined by electrostatic interactions which are not changed in the present mutant RCs.
Results
Electron Transfer Rate Measurements
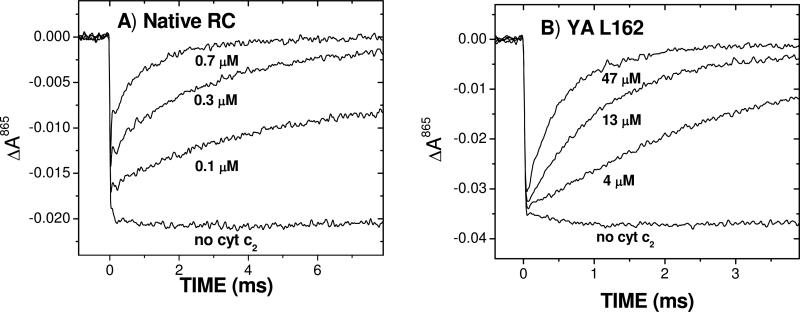
The measurements of the rates of electron transfer were made by monitoring the reduction of the oxidized donor by reduced cyt c2 following a laser flash (Figure 3 and Table 1). The kinetics for native RCs and YA L162 RC show qualitatively different behavior as was reported earlier (12, 25). For native RCs the recovery was biphasic where the amplitudes of the two phases are dependent on the concentration of cyt. The rate of the fast phase was independent of cyt concentration and is due to the first order electron transfer (ke) from bound cyt to RC (Figure 3A). The rate of the slow phase was dependent on the cyt concentration and is due to the second order reaction (k2) from cyt to RC. For the reaction of cyt c2 with the YA L162 RCs the reaction was monophasic at all cyt concentrations (Figure 3B). The rate of the reaction increased with cyt concentration approaching a maximum at high concentrations. For LA M191 and 3xHbond RCs the reaction was biphasic at low ionic strength but became monophasic at high ionic strength. The second order rate constants were obtained from the initial slope in a plot of the observed rate of the slow phase vs cyt concentration.
Figure 3.
Transient absorbance changes due to electron transfer from cyt c2 to RC following a laser flash. A) Native RCs showing biphasic kinetics characteristic of a diffusion limited reaction. The fast absorption change (τ =10−6 s) immediately following the laser flash due to reaction of bound cyt c2 is not resolved in these traces.B) YA L162 RCs showing monophasic kinetics characteristic of a fast exchange reaction. The concentrations of the free cytochrome are as indicated. The concentration of RCs are 0.18 μM (native) and 0.46 μM (YA L162) (10 mM Hepes pH 7.5, 0.04% dodecyl-β-D-maltoside).
Table 1.
Rate and Equilibrium Constants for Native and Mutant RCs(a)
| RC | ke (s−1) | KD (M) | kon (s−1 M−1) | kc (s−1M−1) |
|---|---|---|---|---|
| Native | 1.0×106 | 3.0×10−7 | 3.0×109 | 3.0×106 |
| LA M191 | 1.1×105 | 3.0×10−6 | 1.8×109 | 3.0×106 |
| 3xHbond | 9.0×104 | 4.5×10−6 | 3.4×109 | 1.5×106 |
| YA L162 | 8.3×103 | 3.0×10−5 | >2×108(b) | 1.0×105 |
Values for ke and KD for Native, LA M191 and YA L162 RCs at low ionic strength (5 mM) were from (25); for 3xHbond RCs from (26). Values for kon and kc were used to fit the data in Fig. 4 using Eq. 9. The uncertainty in the fitted values was estimated to be 10% for kon and 30% for kc.
In the fast exchange limit kon is not well determined but must be faster than k2 (observed)
Ionic strength dependence of second order rate constants
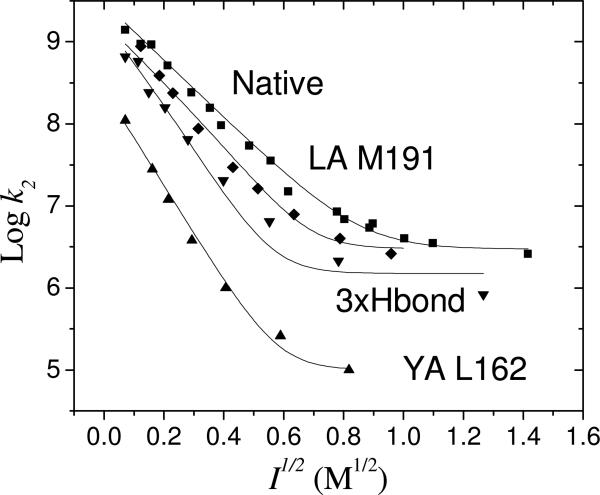
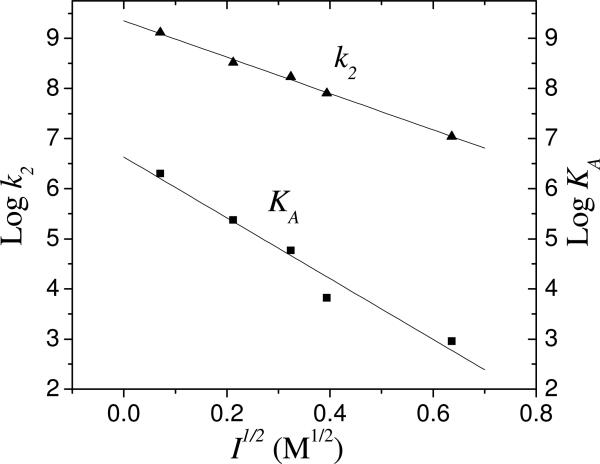
The second order rate constant k2 for electron transfer from cyt c2 to RC was measured as a function of ionic strength for native and mutant RCs. Figure 4 shows a logarithmic plot of the rate constants vs the square root of the ionic strength. The rates are decreased at increasing ionic strength as expected for ionic screening of electrostatic interactions. At low ionic strengths the plots are linear as expected from simple Debye-Huckle considerations. At high ionic strength the rates appear to level off and approach a limiting value. The solid lines are fits to the transition state model.
Figure 4.
Plot of k2 vs I1/2 for native and mutant RCs. Native (■), LA M191 (◇), 3xHbond (▼), YA L162 (▲). The solid lines are fits to Eq. 9.
Native RCs have a high value of the second order rate constant (k2 = 3.0×109 s−1 M−1 extrapolated to zero ionic strength) which decreases with increasing ionic strength. LA M191 and 3xHbond RCs approach close to the same value of k2 at low ionic strength and high ionic strength, however the slope for the mutants are steeper than that of the native. Tyr L162 RCs have a lower value of the second order rate constant at low ionic strength than native RCs (by ~10 fold). In addition the rate decreases more rapidly with increasing ionic strength than that of native RCs. The mutant electron transfer rate is ~100 fold slower than the native rate at close to physiological ionic strength conditions (~0.15 M). Wachveitl et al (21) measured the ionic strength dependence of a series of mutation to Tyr L162. They found decreases in the rate constant k2 for mutation of Tyr 162 to Gly similar to our result for the Tyr L162→Ala mutation. However they found a different ionic strength dependence. The difference may be due to the difference in the mutated residues or differences in the conditions of the experiment.
The experimental values for k2 in figure 4 were fitted using eq. 9 to test the transition state model. Although there are many parameters in the model, they are readily evaluated. The values for ke, and KD were obtained from previous measurements on native and mutant RCs at low ionic strength (Table 1) (17, 26). The kon and kc were obtained as the limiting rates at high and low ionic strength. The values were obtained by fitting are shown in Table 1. The values of γ, Ω and α were constrained to be the same for all RCs. The best values obtained by global fitting were γ=8.07 ± 0.6 M−1/2, Ω = −5.56 ± 0.6 M−1/2, and α=0.59±0.05. A key parameter in the fitting is the value for the ratio of the change in the transition state energy for association relative to the change in the binding energy, α=0.59. This ratio is approximately the ratio of slope of log k2 vs I1/2 for native RCs and YA L162 RCs in Figure 4 which are determined by a kinetic process and a pre-equilibration process. The modeling resulted in a reasonably good fit to the data. Although this simple model does not give an exact fit to the data, it does correctly predict the trend of a faster decrease in k2 with ionic strength associated with the transition from the diffusion limited reaction to the fast exchange limit.
Ionic Strength dependence of KA
The ionic strength dependence of KA was measured for native RCs in order to derive an independent measure of α to compare the value obtained for the mutant YA L162 RCs. The measured values of KA as well as k2 are shown in figure 5 along with the calculated value of koff (Figure 6). The value of α was determined from the ratio of the slope of the plot of logk2 vs I1/2 to the slope of the plot of logKA vs I1/2 for native RCs where it is assumed that kon=k2 in the diffusion limit. The result was a value of α=0.60± 0.05. This is in good agreement with the value for α=0.59±0.5 calculated from fitting the values of k2 vs I1/2 for native and mutant RCs.
Figure 5.
Ionic strength dependence of the binding constant KA (■) and the second order rate constant k2 (▲) for native RCs. The value of kon is equal to that of k2 assuming a diffusion limited reaction. The ratio of the slopes of log kon and log KA vs I1/2 gives a value of α=0.60 ± 0.05 in good agreement with the value of α=0.59 ± 0.05 obtained from the fitting of the ionic strength dependence of k2 in native and YA L162 RCs.
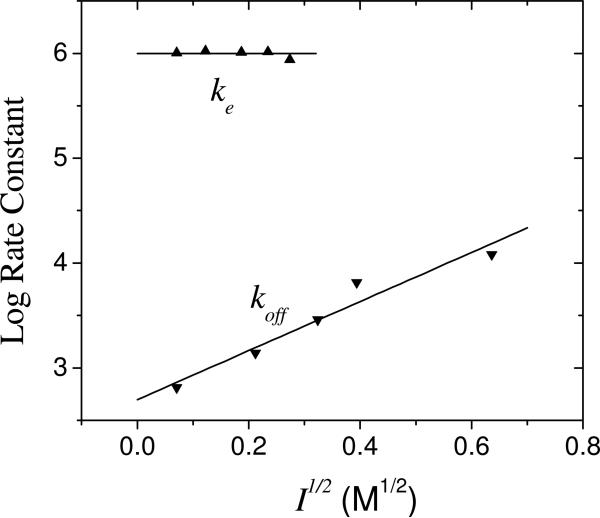
Figure 6.
Ionic strength dependence of koff and ke for native RCs. The value of koff was calculated from Eq.8. The value of koff was always less than the value of ke=106 s−1 justifying the assumption of a diffusion limited rate even at higher ionic strength.
The dissociation rate koff was calculated from the association rate and the equilibrium constant (koff=kon/KA). The value of koff increases with increasing ionic strength (Figure 6). However, even at relatively high ionic strength it was slower than the electron transfer rate in the bound state ke=106 s−1. The value of ke was found to be independent of ionic strength over the limited range of ionic strengths where it could be measured due to weaker binding at high ionic strength.
Discussion
Ionic strength dependence of k2
The ionic strength dependence of k2 (i.e. the initial slope of the plot of log k2 vs I1/2) is different for native and mutant RCs (Figure 4). Although changes have been observed previously for mutations of charged residues (24) it was not clear how to explain the changes due to the neutral mutations considered in this study. The results of the ionic strength dependence of k2 can be explained by changes in dissociation and electron transfer rates that change the reaction from the diffusion limit to the fast exchange limit according to a transition state model.
In native RCs the electron transfer rate in the bound state is faster than dissociation (ke > koff) leading to a second order rate that is diffusion controlled. Although the dissociation rate koff increases with increasing salt concentration, the value of ke is so much greater than koff at low ionic strength (103 fold) that even at high ionic strength ke>koff (See Figure 5) the reaction remains in the diffusion controlled regime. Thus, the ionic strength dependence of k2 should be kinetically controlled and determined by the changes in the rate of association. Consequently, the ionic strength dependence, logk2 vs I1/2 should have a slope proportional to ΔΔG‡ =αΔΔG.
The mutation of the critical Tyr L162 residue resulted in a YA L162 mutant that exhibits a steeper dependence of k2 with ionic strength than native RCs (Figure 4). This mutation reduces the electron transfer rate ke and increases the dissociation rate koff, resulting in a reaction that is in the fast exchange regime (koff>ke). In this limit the cyt comes on and off several times before electron transfer can occur and the rate is proportional to the probability of a cyt being in the binding site. Thus, the rate constant becomes k2 = keKA and the ionic strength dependence should be due to changes in the equilibrium constant KA for binding to the active state. For this case the initial slope in a plot of logk2 vs I1/2 for this mutant should be proportional to the free energy for binding to the active state, ΔΔG. The initial slope of the ionic strength dependence of k2 (Figure 4) for this mutant is very similar to the ionic strength dependence of the equilibrium constant KA for binding of cyt c2 to native RCs (Figure 5) consistent with both effects resulting from changes in the binding energy, ΔΔG. The steeper slope for the YA L162 RCs compared to native RCs indicates a larger change in the binding energy compared to the activation energy (ΔΔG‡ /ΔΔG = α =0.59).
The ionic strength effects on k2 for the LA M191 RC and 3xHbond RCs is intermediate between the native and YA L162 mutant (Figure 4). The mutated residues are close to Tyr L162 on the RC surface and are in contact with the cyt in the co-crystal structure. The mutant RCs have lower binding affinities KA (~10 fold) and slower electron transfer rates ke (~10 fold). However, the changes in koff and ke are not as great as for the YA L162 RC and thus the reaction is diffusion controlled at low ionic strength. However, as the ionic strength increases, the dissociation rate increases until it exceeds the (slower) electron transfer rate. As this happens, the reaction changes from the diffusion limited regime to the fast exchange regime which is more sensitive to the ionic strength. The observed changes in slope are in accord with the transition state model (Fig. 4).
Ionic strength effects on transition state and bound state, α
The value of α is related to the effect of ionic strength on the rates of association and dissociation. For α =1 (i.e. Ω = 0 from Eq. 7) the dissociation rate would not increase with ionic strength and for α=0.5 (Ω = −γ from Eq. 7) the decrease in the association rate would be equal to the increase in the dissociation rate. The ionic strength dependencies of protein association and dissociation reactions in a recent compilation by Zhou (33) show changes in the rate of association due to ionic strength were much larger than changes in the rate of dissociation that indicate values of α in the range α >0.67. The value of α~0.60 found in the present study is low compared to other protein systems. Consequently, for the cyt RC system there is an appreciable increase in the dissociation rate with ionic strength. Gerencser et al (14) have previously observed an increase in dissociation of cytochrome c from the RC with increasing ionic strength and proposed that this increase may be important for the cyt RC system in order that the dissociation is not rate limiting for turnover at high light intensity. Perhaps a lower value of α may be a characteristic of protein association reactions that require a fast dissociation necessary for rapid turnover.
What determines the value of α? The molecular basis for α is due to the structures of the transition state and bound state. For α = 1 the transition state and bound state would be similar. Lower values of α indicate that the transition state and bound state are different. Previous studies on the cyt RC reaction compared the change in k2 and KA due to mutation of charged residues in the cyt-RC interface found the ratio of the change in transition state energy to binding energy to be α(mutations) = 0.40±0.06. (12) This low value was explained by the longer average distance between complementary charges in the transition state leading to lower changes in Coulomb energies which vary as 1/ r (30, 31). In the present study the change in energy is due to ionic strength not mutation of charged residues. Thus, the values of α determined in the two cases do not have to be identical. However, the principle reason for the difference in free energy, i.e. a larger separation between charged residues at the interface, remains the same. The larger separation between charges in the transition state may allow greater access to salt that can reduce the energy of the transition state relative to the bound state. This may explain the relatively low values of α due to ionic strength. The structural basis for the ionic strength dependence of the rates of protein association has been studied by electrostatic calculations of the free energy stabilization at the transition state (34). Calculations on the cyt c2:RC complex should help to identify the origin of the changes in the transition state and bound state energies due to ionic strength.
Model for binding and electron transfer
The structural basis for interprotein electron transfer has been a topic of active research. Hoffman and co-workers have described three regimes for the energy landscape of interprotein electron transfer; simple, gated and dynamic docking (35). The reaction between native RC and cyt c2 is consistent with the simple regime under diffusion-limited conditions where the active state is bound specifically by short range hydrophobic and hydrogen bond contacts. The reaction of the YA L162 mutant RC having altered hydrophobic contacts with cyt c2, is consistent with a dynamic docking mechanism where the bound cyt may be in rapid equilibrium between several states including inactive as well as active states.
The structure of the state active in electron transfer is a critical question. Since electron tunneling can occur over long distances, as two proteins approach each other electron transfer may occur from any number of the ensemble of configurations (36). Two limiting cases have been considered for the cyt RC reaction, a tight binding model and a loose binding model. In the tight-binding model the cyt c2 is in a bound state which is optimized for electron transfer by close van der Waals tunneling contact between the two proteins (37). An alternative loose-binding model involves a distribution of cyt:RC configurations held together by long range electrostatic interactions. In the loose-binding model, van der Waals contact between proteins is not necessary and electron transfer can occur in theory through intervening water (38, 39).
The ionic strength dependence of k2 in the fast exchange limit gives information about the state active in electron transfer and can help distinguish between the tight binding and loose binding models. The ionic strength dependence of a loosely bound cyt i.e. as in an encounter complex bound by long range electrostatic interactions, where the cyt and RC are well separated, would be expected to be weaker than that for the bound state and similar to that of the transition state. Thus, in the fast exchange limit a loose binding model would give an ionic strength dependence similar to that for k2 in native RCs. In contrast, for the tight binding model the active state would have ionic strength dependence similar to that for the binding of cyt to native RC. Thus, the similarity between the ionic strength dependence for k2 in YA L162 RCs (Figure 4) to that for KA for the binding of cyt to native RCs (Fig. 5) indicates that in the YA L162 mutant RC electron transfer occurs from a tightly bound cyt with a configuration similar to that for the active state of the native cyt c2 RC complex in solution. This active state in solution is presumed to have a similar structure to the structure of the co-crystal since the electron transfer rates ke are the same (9). Although the detailed features of the contact interface between cyt and RC in the active complex may be different in mutant and native complexes, overall features should be similar: the two proteins should be in close contact at the tunneling interface region in the active state and the distances between charged residues should be similar to account for the similarity in the ionic strength dependence. In summary, the ionic strength studies support the tight binding model for the reaction between cyt c2 and RC in which the structure of the active state for electron transfer involves close contact between protein residues at the tunneling interface and does not involve long range electron transfer through water.
Functional features of the active site
The results from this study demonstrate the high degree of optimization of the cyt RC reaction. This optimization reflects the importance for rapid turnover needed to provide energy to the organism. For native RCs the reaction is diffusion controlled even at high ionic strength. Even in mutant RCs for which the binding KA and electron transfer rates ke are greatly reduced, the second order rate constant is still fast even at high ionic strength (Figure 4). For native RCs and two mutant RCs the limiting rate is kc ~ 3×106 s−1M−1. This rate is typical for the association of proteins at high ionic strength (40). Mutation of Tyr L162 greatly reduces the second order rate constant. The limiting rate at high ionic strength is much lower than for native RCs. However, even for this case the second order rate constant at physiological ionic strength (~ 0.15 M) is greater than 106 s−1M−1. This rate should be fast enough to support fast electron transfer in the confines of the bacterial membranes where the cyt concentration may be relatively high (41) and reaction rates are increased due to reduction in dimensionality (42). Indeed, the YA L162 mutant is able to grow under normal photosynthetic growth conditions (data not shown). Thus, while short range hydrophobic interactions are important in binding and electron transfer, the cyt RC reaction does not critically rely on the detailed structure of the contact interface. This suggests that only a rough match between the two contact surfaces is necessary as opposed to a detailed lock and key fit.
The robust nature of the cyt RC reaction may be attributed to the design of the protein-protein interface. Desirable features of the binding reaction that allow the system to search quickly through different configurations to attain the active configuration are the same as for protein folding (43). These include the absence of high barriers and the absence of traps (i.e. long lived bound inactive states) as well as a well defined and stable final state. The cyt-RC interface accomplishes this using a small central region with short-ranged binding interactions close to the region of highest electronic interaction surrounded by a region of charged residues. These features are shared by many protein-protein interfaces (44). A notable feature of the cyt - RC interface is the protrusion of the hydrophobic binding surface (Figure 1). The key contact residue Tyr L162 sticks out over BChl2 which allows it to make strong tunneling contact with the heme edge even when the charged residues are far apart. These structural features may be responsible for the relatively low value of α which may contribute to the fast dissociation rate. Based on structures of protein-protein interfaces a suggestion has been made that fast dissociation rate may be associated with poor packing (45). In the case of the cyt:RC complex the loose packing of the region between charged residues may facilitate the faster dissociation under physiological conditions while still retaining the small region of hydrophobic short range contacts important for specific binding and fast electron transfer.
Conclusions
The ionic strength effects on the second order rate constant k2 for electron transfer between cyt c2 and native and mutant RCs can be changed by mutations of neutral hydrophobic and hydrogen bonding residues. The loss of hydrophobic interactions causes k2 to decrease more rapidly with increasing ionic strength. These changes can be explained by changes to the rates of binding and electron transfer due to neutral residues leading to a change from the diffusion limit to the fast exchange limit. The ionic strength effects can be described by a transition state model in which the stronger ionic strength dependence in the fast exchange limit is due to differences in the structure of the active bound state and transition state. The difference between the transition state and bound state structures causes the dissociation rate to increase with increasing ionic strength. This fast dissociation rate is an important feature for protein-protein reactions that require a high turnover. The ionic strength dependence of the YA L162 mutant RC second order reaction with cyt (in the fast exchange limit) is similar to that for the binding of cyt to Native RCs suggesting that the structure of the active state is similar for both cases. This suggests that the structure of the state active in the second order electron transfer reaction is similar to that of the structure of the co-crystal complex with close van der Waals contact between reaction partners.
Acknowledgements
We wish to thank Charlene Chang for assistance in construction of the mutants, Osamu Miyashita, Jose Onuchic and Huan-Xiang Zhou for useful discussions on electron transfer and protein association.
Abbreviations
- cyt c2
cytochrome c2
- RC
reaction center
- Rb
Rhodobacter
- Q0
2,3-dimethoxy-5-methylbenzoquinone
- D
primary electron donor (bacteriochlorophyll dimer)
- D+
photo-oxidized primary electron donor
- ke
first order electron transfer rate
- k2
second order rate constant
- kon
association rate
- koff
dissociation rate
- KA
association constant
- KD
dissociation constant
- Ea
activation energy
- ΔΔG
change in binding free energy
- ΔΔG‡
change in transition state free energy
- α
ratio of change in transition state energy to change in binding energy
Footnotes
This work was supported by NIH grant GM 41637.
References
- 1.Bendall D. In: Protein electron transfer. Bendall D, editor. Bios Scientific Publishers Ltd; Oxford, UK: 1996. pp. 43–68. [Google Scholar]
- 2.Janin J. The kinetics of protein-protein recognition. Proteins: Structure, Function and Genetics. 1997;28:153–161. doi: 10.1002/(sici)1097-0134(199706)28:2<153::aid-prot4>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 3.Schreiber G, Haran G, Zhou H-X. Fundamental aspects of protein-protein association kinetics. Chem. Rev. 2009;109:839–860. doi: 10.1021/cr800373w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Berg OG, von Hippel PH. Diffusion-controlled macromolecular interactions. Ann. Rev. Biophys. Biophys. Chem. 1985;14:131–160. doi: 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 5.Onuchic JN, Beratan DN, Winkler JR, Gray HB. Pathway analysis of protein electron-transfer reactions. Annu. Rev. Biophys. Biomol. Struct. 1992;21:349–77. doi: 10.1146/annurev.bb.21.060192.002025. [DOI] [PubMed] [Google Scholar]
- 6.Tiede D, Dutton P. In: The photosynthetic reaction center. Deisenhofer J, Norris J, editors. Academic Press; San Diego: 1993. pp. 258–288. [Google Scholar]
- 7.Blankenship RE. Molecular mechanisms of photosynthesis. Blackwell Science Inc; London: 2002. [Google Scholar]
- 8.Feher G, Allen JP, Okamura MY, Rees DC. Structure and function of bacterial photosynthetic reaction centers. Nature (London) 1989;339:111–116. [Google Scholar]
- 9.Axelrod HL, Abresch EC, Okamura MY, Yeh AP, Rees DC, Feher G. X-ray structure determination of the cytochrome c2:Reaction center electron transfer complex from Rhodobacter sphaeroides. J.Mol. Biol. 2002;319:501–515. doi: 10.1016/S0022-2836(02)00168-7. [DOI] [PubMed] [Google Scholar]
- 10.Overfield RE, Wraight CA, Devault DC. Microsecond photooxidation kinetics of cytochrome c2 from rhodopseudomonas sphaeroides: In vivo and solution studies. FEBS Lett. 1979;105:137–142. doi: 10.1016/0014-5793(79)80903-5. [DOI] [PubMed] [Google Scholar]
- 11.Moser C, Dutton PL. Cytochrome c and c2 binding dynamics and electron transfer with photosynthetic reaction center protein and other integral membrane redox proteins. Biochemistry. 1988;27:2450–2461. doi: 10.1021/bi00407a031. [DOI] [PubMed] [Google Scholar]
- 12.Tetreault M, Rongey SH, Feher G, Okamura M. Interaction between cytochrome c2 and the photosynthetic reaction center from Rhodobacter sphaeroides: Effects of charge-modifying mutations on binding and electron transfer. Biochemistry. 2001;40:8452–8462. doi: 10.1021/bi010222p. [DOI] [PubMed] [Google Scholar]
- 13.Graige M, Feher G, Okamura M. Conformational gating of the electron transfer reaction QA-.QB --> QAQB-. in bacterial reaction centers of Rhodobacter sphaeroides determined by a driving force assay. Proc. Natl. Acad. Sci. U. S. A. 1998;95:11679–84. doi: 10.1073/pnas.95.20.11679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gerencser L, Laczko G, Maroti P. Unbinding of oxidized cytochrome c from photosynthetic reaction center of Rhodobacter sphaeroides is the bottleneck of fast turnover. Biochemistry. 1999;38:16866–75. doi: 10.1021/bi991563u. [DOI] [PubMed] [Google Scholar]
- 15.Lin X, Williams JC, Allen J, Mathis P. Relationship between rate and free energy difference for electron transfer from cytochrome c2 to the reaction center in Rhodobacter sphaeroides. Biochemistry. 1994;33:13517–23. doi: 10.1021/bi00250a002. [DOI] [PubMed] [Google Scholar]
- 16.Ke B, Chaney TH, Reed DW. The electrostatic interaction between the reaction center bacteriochlorophyll derived from Rsp. sphaeroides and mammalian cytochrome c and its effects on light activated electron transport. Biochim. Biophys. Acta. 1970;216:373–383. doi: 10.1016/0005-2728(70)90229-x. [DOI] [PubMed] [Google Scholar]
- 17.Prince RC, Cogdell RJ, Crofts AR. The photo-oxidation of horse heart cytochrome c and native cytochrome c2 by reaction centres fromRhodopseudomonas spheroides r-26. Biochim. Biophys. Acta. 1974;347:1–13. doi: 10.1016/0005-2728(74)90194-7. [DOI] [PubMed] [Google Scholar]
- 18.Overfield RE, Wraight CA. Oxidation of cytochromes c and c2 by bacterial photosynthetic reaction centers in phospholipid vesicles. 1. Studies with neutral membranes. Biochemistry. 1980;19:3322–3327. doi: 10.1021/bi00555a034. [DOI] [PubMed] [Google Scholar]
- 19.van der Wal H, van Grondelle R, Millett F, Knaff D. Oxidation of cytochrome c2 and of cytochrome c by reaction centers of Rhodospirillum rubrum and Rhodobacter sphaeroides. The effect of ionic strength and of lysine modification on oxidation rates. Biochim. Biophys. Acta. 1987;893:490–498. doi: 10.1016/0005-2728(87)90100-9. [DOI] [PubMed] [Google Scholar]
- 20.Venturoli G, Melandri B, Gabellini N, Oesterhelt D. Kinetics of photosynthetic electron transfer in artificial vesicles reconstituted with purified complexes from Rhodobacter capsulatus. I. The interaction of cytochrome c2 with the reaction center. Eur. J. Biochem. 1990;189:105–12. doi: 10.1111/j.1432-1033.1990.tb15465.x. [DOI] [PubMed] [Google Scholar]
- 21.Wachtveitl J, Farchaus J, Mathis P, Oesterhelt D. Tyrosine 162 of the photosynthetic reaction center l-subunit plays a critical role in the cytochrome c2 mediated rereduction of the photooxidized bacteriochlorophyll dimer in Rhodobacter sphaeroides. 2. Quantitative kinetic analysis. Biochemistry. 1993;32:10894–904. doi: 10.1021/bi00091a045. [DOI] [PubMed] [Google Scholar]
- 22.Witthuhn VC GJ, Hong SJ, Halls S, Rott MA, Wraight CA, Crofts AR, Donohue TJ. Reactions of isocytochrome c(2) in the photosynthetic electron transfer chain of Rhodobacter sphaeroides. Biochemisty. 1997;36:903–911. doi: 10.1021/bi961648k. [DOI] [PubMed] [Google Scholar]
- 23.Long J, Durham B, Okamura M, Millett F. Role of specific lysine residues in binding cytochrome c2 to the Rhodobacter sphaeroides reaction center in optimal orientation for rapid electron transfer. Biochemistry. 1989;28:6970–6974. doi: 10.1021/bi00443a029. [DOI] [PubMed] [Google Scholar]
- 24.Caffrey MS, Bartsch RG, Cusanovich MA. Study of the cytochrome c2-reaction center interaction by site-directed mutagenesis. J. Biol. Chem. 1992;267:6317–6321. [PubMed] [Google Scholar]
- 25.Gong X, Paddock M, Okamura M. Interactions between cytochrome c2 and photosynthetic reaction center from Rhodobacter sphaeroides: Changes in binding affinity and electron transfer rate due to mutation of interfacial hydrophobic residues are strongly correlated. Biochemistry. 2003;42:14492–500. doi: 10.1021/bi035603c. [DOI] [PubMed] [Google Scholar]
- 26.Abresch E, Paddock M, Villalobos M, Chang C, Okamura M. Interaction between cytochrome c2 and the photosynthetic reaction center from Rhodobacter sphaeroides: Role of interprotein hydrogen bonds in binding and electron transfer. Biochemistry. 2008;47:13318–13325. doi: 10.1021/bi801675a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Paddock ML, Adelroth P, Chang C, Abresch EC, Feher G, Okamura MY. Identification of the proton pathway in bacterial reaction centers: Cooperation between Asp-m17 and Asp-l210 facilitates proton transfer to the secondary quinone (QB). Biochemistry. 2001;40:6893–6902. doi: 10.1021/bi010280a. [DOI] [PubMed] [Google Scholar]
- 28.Bartsch R. In: The photosynthetic bacteria. Clayton R, Sistrom W, editors. Plenum Press; New York: 1978. pp. 249–279. [Google Scholar]
- 29.Tiede DM, Littrell K, Marone PA, Zhang R, Thiyagarajan P. Solution structure of a biological bimolecular electron transfer complex: Characterization of the photosynthetic reaction center-cytochrome c2 protein complex by small angle neutron scattering. J. Appl. Cryst. 2000;33:560–564. [Google Scholar]
- 30.Miyashita O, Onuchic J, Okamura M. Transition state and encounter complex for fast association of cytochrome c2 with bacterial reaction center. Pro. Natl. Acad. Sc.i U S A. 2004;101:16174–9. doi: 10.1073/pnas.0405745101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Miyashita O, Onuchic JN, Okamura MY. Continuum electrostatic model for the binding of cytochrome c2 to the photosynthetic reaction center from Rhodobacter sphaeroides. Biochemistry. 2003;42:11651–11660. doi: 10.1021/bi0350250. [DOI] [PubMed] [Google Scholar]
- 32.Atkins PW. Physical chemistry. W. H. Freeman and Company; New York: 1990. [Google Scholar]
- 33.Zhou H-X. Association and dissociation kinetics of colicin e3 and immunity protein 3: Convergence of theory and experiment. Protein Sci. 2003;12:2379–2382. doi: 10.1110/ps.03216203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Alsallaq R, Zhou H-X. Prediction of protein-protein association rates from a transition state theory. Structure. 2007;15:215–224. doi: 10.1016/j.str.2007.01.005. [DOI] [PubMed] [Google Scholar]
- 35.Liang ZX, Kurnikov IV, Nocek JM, Mauk AG, Beratan DN, Hoffman BM. Dynamic docking and electron-transfer between cytochrome b(5) and a suite of myoglobin surface-charge mutants. Introduction of a functional-docking algorithm for protein-protein complexes. J. Am. Chem. Soc. 2004;126:2785–2798. doi: 10.1021/ja038163l. [DOI] [PubMed] [Google Scholar]
- 36.McLendon G. Control of biological electron transport via molecular recognition and binding: The “velcro” model. Structure and Bonding. 1991;75:160–174. [Google Scholar]
- 37.Aquino A, Beroza P, Beretan D, Onuchic J. Docking and electron transfer between cytochrome c2 and the photosynthetic reaction center. Chem. Phys. 1995;197:277–288. [Google Scholar]
- 38.Lin J, Beratan DN. Simulation of electron transfer between cytochrome c2 and the bacterial photosynthetic reaction center: Brownian dynamics analysis of the native proteins and double mutants. J. Chem. Phys. 2005;109:7529–7534. doi: 10.1021/jp045417w. [DOI] [PubMed] [Google Scholar]
- 39.Miyashita O, Okamura MY, Onuchic JN. Interprotein electron transfer from cytochrome c2 to photosynthetic reaction center: Tunneling across an aqueous interface. Proc. Natl. Acad. Sci. U S A. 2005;102:3558–3563. doi: 10.1073/pnas.0409600102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Northrup SH, Erickson HP. Kinetics of protein-protein association explained by Brownian dynamics computer simulation. Proc Natl Acad Sci U S A. 1992;89:3338–3342. doi: 10.1073/pnas.89.8.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Crofts AR, Wraight CA. The electrochemical domain of photosynthesis. Biochim. Biophys. Acta. 1983;726:149–185. [Google Scholar]
- 42.Adam G, Delbruck M. In: Structural chemistry and molecular biology. Rich A, Davidson N, editors. Freeman and Company; San Francisco: 1968. [Google Scholar]
- 43.Onuchic J, Wolynes P. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 44.Bogan A, Thorn K. Anatomy of hot spots in protein interfaces. J. Mol. Biol. 1998;280:1–9. doi: 10.1006/jmbi.1998.1843. [DOI] [PubMed] [Google Scholar]
- 45.Crowley P, Carrondo M. The architecture of the binding site in redox protein complexes: Implications for fast dissociation. Proteins. 2004;55:603–612. doi: 10.1002/prot.20043. [DOI] [PubMed] [Google Scholar]