Prostate Brachytherapy Seed Reconstruction with Gaussian Blurring and Optimal Coverage Cost

Abstract

Intraoperative dosimetry in prostate brachytherapy requires localization of the implanted radioactive seeds. A tomosynthesis-based seed reconstruction method is proposed. A three-dimensional volume is reconstructed from Gaussian-blurred projection images and candidate seed locations are computed from the reconstructed volume. A false positive seed removal process, formulated as an optimal coverage problem, iteratively removes “ghost” seeds that are created by tomosynthesis reconstruction. In an effort to minimize pose errors that are common in conventional C-arms, initial pose parameter estimates are iteratively corrected by using the detected candidate seeds as fiducials, which automatically “focuses” the collected images and improves successive reconstructed volumes. Simulation results imply that the implanted seed locations can be estimated with a detection rate of ≥ 97.9% and ≥ 99.3% from three and four images, respectively, when the C-arm is calibrated and the pose of the C-arm is known. The algorithm was also validated on phantom data sets successfully localizing the implanted seeds from four or five images. In a Phase-1 clinical trial, we were able to localize the implanted seeds from five intraoperative fluoroscopy images with 98.8% (STD=1.6) overall detection rate.

I. INTRODUCTION

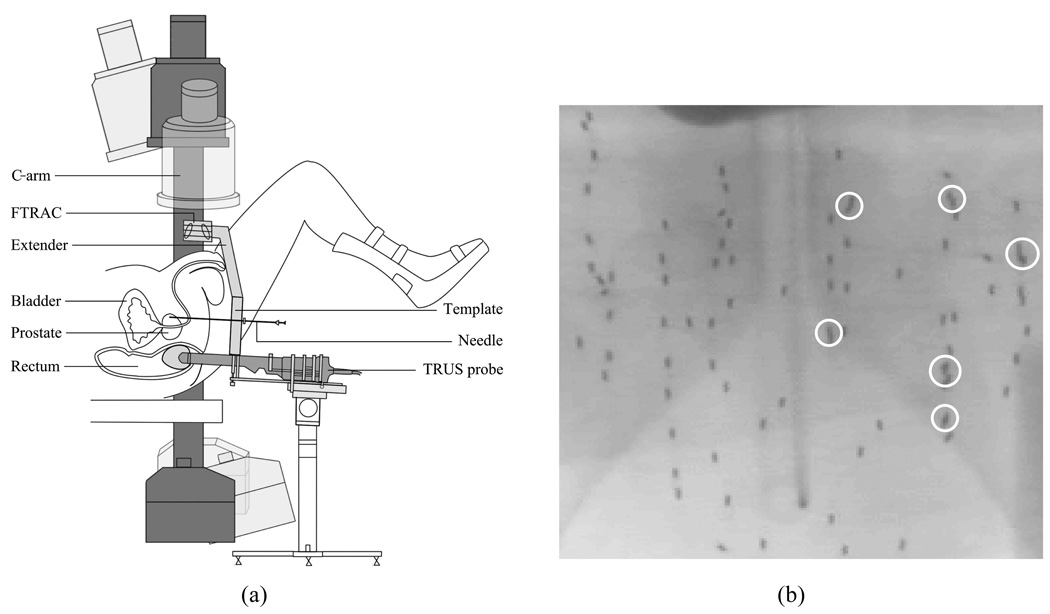
Prostate cancer is one of the most common cancers in North America with 186,320 estimated new cases comprising about 25% of all new cancers found in men and 28,660 estimated deaths in 2008 in the United States alone [1]. On the positive side, prostate cancer can be very effectively treated if detected early; in fact, about 91% of new cases are expected to be diagnosed early enough in order to yield a near 100% 5-year relative survival rate [1]. Brachytherapy is a definitive treatment for low risk prostate cancer; it achieves outcomes that are comparable to radical prostatectomy and external-beam radiation therapy [2]–[4]. Brachytherapy involves permanent implantation of radioactive seeds into the prostate. Its success mainly depends on the ability to deliver a sufficient amount of therapeutic dose to the target gland while sparing adjacent healthy organs and structures, e.g. rectum, urethra, and nerve bundles, from excessive radiation. Typically, an implantation plan is made preoperatively based on an ultrasound volume study with a set of axial image slices of the prostate and idealistic seed implant patterns. Transrectal ultrasound (TRUS) is widely used during the procedure to guide the surgeon to insert the needle and deliver the seeds to the preplanned location in the target gland [5]. However, implanting the seeds at the exact planned locations is difficult because of procedural variations such as patient motion, needle deviation, and soft tissue deformation including edema [5]–[7]. Also, although TRUS images can be readily used to localize the prostate boundary, they do not visualize the locations of the seeds very well. Therefore, systems that use ultrasound and X-ray fluoroscopy have been developed to overcome these limitations as depicted in Fig. 1(a) [8], [9]. These systems can thereby permit both monitoring of the implant process and reconstruction of the implanted seeds for intraoperative treatment optimization purposes. X-ray projection images are usually acquired using conventional mobile C-arms, and the reconstruction problem is to estimate the 3-D locations of the implanted seeds from two or more projection images.

Fig. 1.

(a) A schematic describing prostate brachytherapy procedure. C-arm has limited mobility due to the limited space near the patient. (b) An example anterior-posterior fluoroscope image with 84 implanted ¹⁰³Pd seeds. White circles indicate overlapping seeds and a shadow of pelvis is shown in the background.

In order to successfully reconstruct and localize the implanted seeds using a mobile C-arm, the following problems should be considered. (1) Since most mobile C-arms frequently utilized for surgery in most hospitals do not have encoded joints and may not be isocentric, the pose and the perspective geometry of the C-arm where each projection image is acquired is unknown. The C-arm wheels may also move (usually accidentally) during change of pose between acquiring images. (2) The images taken by the C-arm show nonlinear geometric distortion due to the nature of the X-ray image intensifier (XRII) which is the detector used in most mobile C-arms. (3) The angular separation of the source positions where the projection images are acquired is limited due to the limited space in the operating room near the patient. In a clinical setting, usually the C-arm can have rotational mobility of source angle separation less than 25° around the anterior-posterior (AP) axis (see Fig. 1(a)) [10]. (4) There is inconsistency in the number of actually implanted seeds and the seeds shown in each projection image, and also the number of seeds shown at different projection images may be different due to the overlapping or clustered seeds. (5) The number of projection images acquired during the procedure should be minimized in order to avoid unnecessary radiation and to save processing time.

Reconstruction of the implanted brachytherapy seed locations from a limited number of X-ray images, like that shown in Fig. 1(b), is a well studied problem. In the methods reported in [10]–[22], 2-D coordinates of all the seeds in all the projection images are first identified and then a seed-matching problem between the seeds found in different images is solved. Three-dimensional coordinates of the seeds are calculated using the seed correspondences and the projection geometry of the X-ray system (essentially by triangulation). A significant problem with these approaches arises from the fact that overlapping seeds are common [21], and reliable automatic identification and localization of every seed in every image is difficult. Because of this, manual interaction is almost always needed, and even then some seeds cannot be reliably identified because one seed completely hides another.

There has been some research on solving the 3-D seed reconstruction problem in cases where seeds cannot be reliably identified and localized on the 2-D projection images—this scenario is called the incomplete data problem. Narayanan et al. [23] proposed a pseudo-seed-matching strategy coupled with an epipolar geometry-based reconstruction. This method requires at least one of the three images to be complete (2-D coordinates of all the seeds have to be identified), however, or it may or may not reliably reconstruct the 3-D seed positions of the hidden seeds. Su et al. [24] proposed an adaptive grouping technique which divides the seed images into groups for efficient seed reconstruction and is capable of handling the incomplete data problem. However, it may fail to detect overlapping seeds when the projection with the largest number of seed images among the divided groups is incomplete. Also, incorrect division of triplets, referred to as “overdividing” may cause false positive seeds. Lam et al. [25] proposed a Hough trajectory method which uses the fact that there is a unique trajectory in Hough feature space for each seed coordinate in 3-D. This algorithm requires an impractically large number of projections (> 10) and a large source angle separation, which may not be practical. Murphy and Todor [26] proposed a forward iterative method and reported preliminary simulation results to offer a proof of feasibility. Further demonstrations of this approach on real data, however, have not been presented.

There are also tomosynthesis-based algorithms that are able to automatically solve the incomplete data problem. Messaris et al. [27] used classical tomosynthesis to localize objects such as radioactive seeds and proposed an approach to maximization of localization accuracy and efficiency by correlating tomographic and projectional images. Their method, unfortunately, requires extensive user interaction in all phases of the process which is clinically impractical. Tutar et al. [28] proposed a selective backprojection method which is a modified tomosynthesis technique. Their seed detection and false positive (FP) seed removal process is very sensitive to C-arm pose estimation errors, and it also requires a relatively large number of images (≥ 7) and wide image acquisition angles (≥ 30°) not achievable in most OR settings.

This paper describes an improved tomosynthesis-based seed localization method. Tomosynthesis is a method to reconstruct a 3-D volume from multiple projection images acquired within a limited angle [29], [30]. A decisive advantage of using tomosynthesis-based approach for reconstructing the implanted brachytherapy seeds is that all the seeds (including overlapping ones) can be completely reconstructed without explicit prior identification of the 2-D coordinates of the seeds in the projection images. We compute Gaussian-blurred images that we reconstruct into a 3-D volume. Then, we calculate candidate seed positions from the reconstructed volume. We formulate an FP seed removal process as an optimal coverage problem, and it allows us to remove FP seeds from the candidate seeds and to reduce the number of required images. Also, a C-arm auto-focus process enables us to use images of which corresponding poses are not well estimated.

The remainder of this paper is organized as follows. In Section II, the imaging system including geometric distortion correction, calibration, and tracking of the C-arm is described. In Section III, we describe the key idea of our method using a simple example followed by a detailed description of the proposed method which consists of (1) binary seed-only image computation and seed region labeling, (2) Gaussian blurring, (3) volume reconstruction and candidate seed detection, (4) C-arm auto-focusing, (5) false positive seed removal. Numerical results based on simulations, five phantom data sets, and eighteen clinical data sets are presented in Section IV. Finally, the paper concludes in Section V.

II. APPARATUS

X-ray fluoroscopy images of the implanted seeds are acquired using a mobile C-arm with XRII detector. Most XRII-based C-arm images show a significant amount of nonlinear geometric distortion and nonuniform intensity distortion that vary with pose, time, and location. As we explain later in Section III-B, we pre-process the fluoroscopy images into binary seed-only images, and thus non-uniform intensity distortions do not affect our tomosynthesis reconstruction. However, nonlinear geometric distortion in the image causes errors in the reconstruction by shifting the location of the 2-D projected seeds. Thus prior to reconstruction, geometric distortion correction of the image is necessary. At the same time, calibration and pose tracking are necessary to reconstruct a volume from images taken at arbitrary positions of the C-arm. In the calibration process, we need to determine intrinsic camera parameters of the C-arm (image pixel size and focal spot, i.e. the 3-D location of the X-ray source with respect to each image plane). Since the pixel size of the detector remains the same throughout the life of the C-arm, the C-arm calibration problem reduces to estimation of the focal spot. However, since the location of the focal spot varies as the pose of the C-arm changes, it should be computed from pose to pose at which each image is taken. In order to save time in the operating room, we perform the distortion parameter computation and calibration process only once. We mount a calibration fixture developed earlier by Jain et al. [31] on the intensifier tube, and take a representative image within an expected range of the C-arm movement. Since we acquire images within a small angle variation range, the estimation errors do not critically affect the reconstruction result [32]. The intrinsic camera parameters and the geometric dewarp parameters of the C-arm are estimated based on this image prior to the surgery.

Although the intrinsic camera parameters of the C-arm can be determined before the surgery, the pose parameters (3 parameters for rotation and 3 parameters for translation) of the C-arm must be computed at each image acquisition pose. Although external tracking devices can be used for this purpose, they are very expensive and add to the physical limitations and complexity in the operating room—e.g., line of sight requirements and metal object distortions. Instead, in our experiments, the pose of the C-arm was computed using a fluoroscope tracking radiographic fiducial structure (FTRAC) that provides an estimation accuracy of 0.56 mm in translation and 0.33° in orientation [33]. These accuracies are comparable to those of external tracking devices. In our system, FTRAC is mounted to the seed insertion template with a connector, and its relative position with respect to the template is known. Since the seed insertion template is registered to TRUS in the calibration process of the commercial brachytherapy treatment planning system, the seed positions computed from X-ray fluoroscopy images can be transformed to the TRUS frame by known transformation. Therefore, dose distribution can be computed from the seed positions and overlaid to the prostate volume without requiring an additional registration process between TRUS and fluoroscopy.

III. METHODS

A. Key Idea

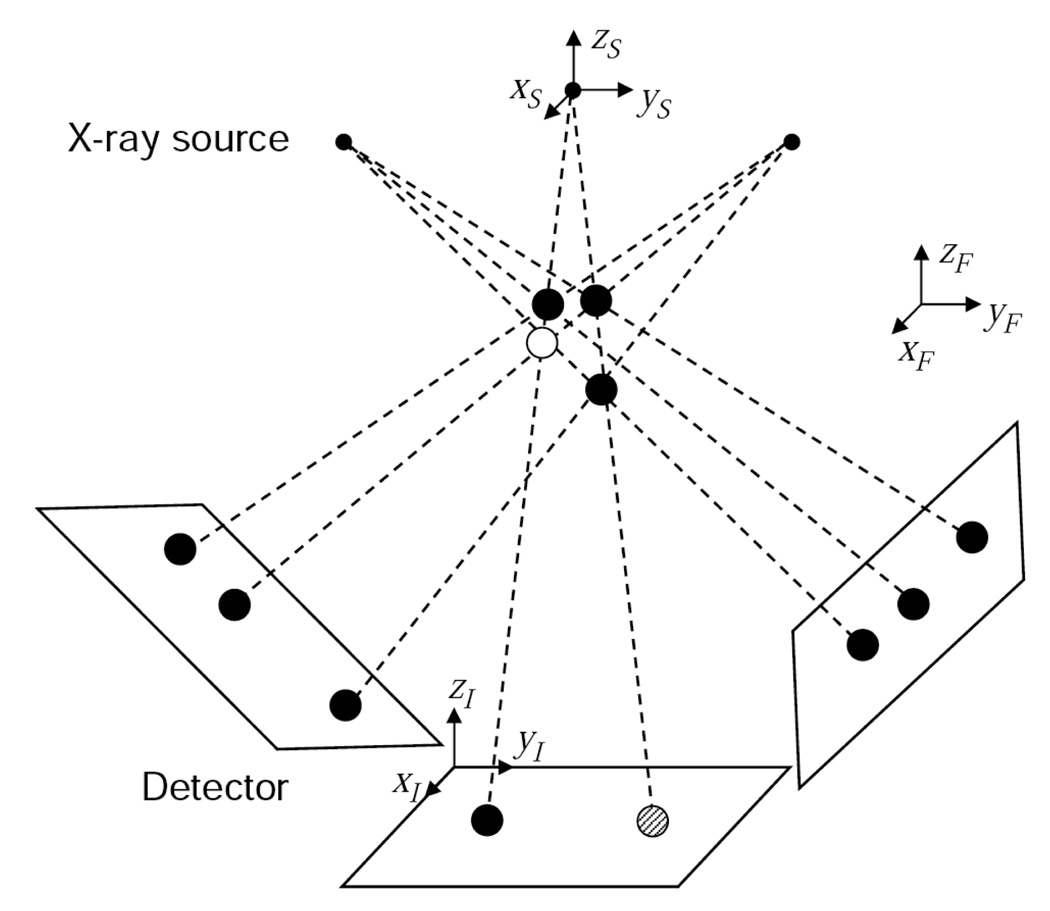
Fig. 2 shows a simple example that can be encountered when reconstructing seeds from a limited number of projection images. Three projection images of three seeds (black circles) are acquired at three different cone beam X-ray source positions. All three seeds are detected in two projections, but only two seeds are visible in the middle image due to the overlapping seeds. Our goal is to find the 3-D locations of the true seeds using these three projection images. What most of the previously proposed algorithms try to do is to (1) identify all three seeds in all projection images and find their 2-D coordinates, (2) find the correspondence of the seeds between projection images, and (3) find the 3-D locations of the seeds by computing symbolic intersections of the backprojection lines of corresponding seeds. When there are overlapping seeds as in this example (shaded circle), establishing the correct correspondence is challenging. When it is wrong, then seeds are positioned in entirely incorrect positions—e.g., at one of the other intersection points of the dotted backprojection lines.

Fig. 2.

Example tomosynthesis geometry with three true seeds (black circles), one false positive seed (white circle). In the middle image, two seeds are overlapped (shaded circle). There are three coordinate systems: global reference coordinates (ℱ), X-ray source coordinates (𝒮), and image coordinates (ℐ).

The tomosynthesis approach backprojects and sums the seed locations on the 2-D X-ray images into 3-D space, which has the effect of growing “bright spots” where the true seeds actually exist. This is done without requiring seed correspondences or trying to identify overlapping seeds. However, as can be seen from the figure, false positive (FP) seeds (white circle) can be introduced in the reconstructed volume because these locations are also consistent with the projected seed locations. To address this situation, our strategy is to treat all initially reconstructed seeds as “candidate seeds” and to try to iteratively remove the FP seeds. In this simple example, four candidate seeds are identified in the initial reconstruction and they appear to be legitimate in every projection image. But, in fact, the FP seed can be identified by successively removing each seed and examining the consistency of the remaining seed constellation relative to the acquired projection images. In particular, it can be seen that if any one of the true seeds is removed, then it is impossible for the three projection images to have been generated by the remaining candidates; if the FP seed is removed, however, the projection images are reproduced perfectly. Following this observation, the condition that each seed in every projection image must be “covered” by at least one of the candidate seeds has become our core principle for FP seed removal. In reality, however, seeds are crowded within a small space and a real seed may occupy the FP seed location, where every seed in every projection image is covered without this true seed, although the probability of such a situation could be small. This necessitates a more sophisticated FP seed elimination process based on our core principle. Starting from this intuition and considering this possible situation, we have developed a theoretical framework for removing FP seeds and localizing the implanted brachytherapy seeds based on tomosynthesis reconstruction. We now describe the algorithm in detail.

B. Binary Seed-only Image Computation and Seed Region Labeling

We assume that the seed regions in each image are extracted and binary seed-only images are computed from geometric distortion-corrected images as Tutar et al. did in [28]. Since there are various seed segmentation algorithms [8], [34]–[37], we do not address segmentation methods in this paper.

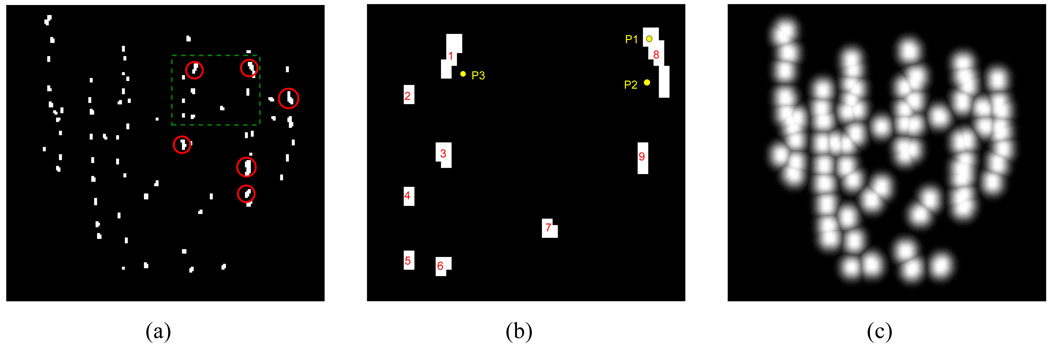
Our method is more robust to additional spurious seeds that can be mistakenly introduced to the binary seed-only images than seed-matching-based methods. In the seed-matching-based approach, 2-D seed coordinates computed from the spurious seeds in the seed-only images will affect the seed-matching process, resulting in erroneous matching. In our method, additional spurious seeds in the 2-D seed-only images will not create false positive seeds in the 3-D reconstruction unless there are supporting seeds that correspond to these seeds on the other images (it is almost impossible that a spurious seed introduced in an image has corresponding seeds in all the other 4–5 images). What is more important is to guarantee that the binary seed-only images include all the seeds because any missing seed in a seed-only image may result in missing a seed in the reconstruction. Considering these possible scenarios and the fact that seed-only images are the basis of our method, it is important to take an effort to ensure that the seed-only images are accurate. On the positive side, brachytherapy seeds look very dark in the fluoroscopy images compared to other structures, so it can be detected with sufficient accuracy by using various available segmentation algorithms. Fig. 3(a) shows an example binary seed-only image.

Fig. 3.

(a) Binary seed-only image of the patient fluoroscopy image shown in Fig. 1(b). Red circles indicate example overlapping seeds which are indicated as white circles in Fig. 1(b). (b) Example seed region labeling of the seeds inside the green-dashed box in (a). (c) Gaussian-blurred image of (a).

Once the binary seed-only images are computed, seed regions are clustered and labeled using connected component labeling [38], [39]. We use these labels during the FP seed removal process that we describe in Section III-F. Since exact identification of the 2-D coordinates of all seeds is not necessary, different labels are assigned to isolated seed regions even though they may correspond to more than one projected seed. An example of a labeled binary seed-only image is shown in Fig. 3(b). In this figure, regions 1 and 8 have at least two seeds, but only one label is assigned to each region.

C. Gaussian Blurring

Since the size of a brachytherapy seed is very small, only a small number of pixels contribute to the image of a seed. As a consequence, even minor calibration and pose estimation errors may result in missing seeds in the tomosynthesis reconstruction. The possible shifts of the projected points caused by calibration and pose estimation errors are more than just 1–2 pixels in general (see Section IV-D). Therefore, it is obvious that there will be missing seeds in the reconstruction if the size of the seed region is small. We may increase the size of the seed region by simple dilation to solve this problem, but then the size of the seed region will be too big, making neighboring seed regions connected to one another, which is equivalent to creating overlapping seeds in the images. Also, by increasing the size of the seed region too much, there will be many merged seeds each of which appear to be one big seed but actually contain multiple seeds in the reconstructed volume.

In order to overcome these limitations, we use Gaussian-blurred images for our reconstruction. From the binary seed-only images, we first compute distance maps using a distance transform. The distance transform assigns the Euclidean distance between each pixel and its nearest seed region to the image [40]. In the distance map, pixels inside a 2-D seed region take a value of zero and the label of the nearest 2-D seed region becomes the label value of the pixel. Fig. 3(b) shows an example of a binary seed-only image with 9 labeled seed regions. In this figure, d(P1) = 0 because P1 is inside seed region 8, and d(P2) and d(P3) are the Euclidean distances from the points P2 and P3 to the nearest boundaries of seed regions 8 and 1, respectively where d(·) is the distance map of the image. Also, the pixels associated with points P1, P2, and P3 have label values of 8, 8, and 1, respectively.

We then blur the binary seed-only images based on the distance maps by unit-height Gaussian function defined as

$$I_g(\mathbf{x})=\text{exp}\left[\frac{-d{(\mathbf{x})}^2}{2{\sigma }^2}\right],$$ (1)

where I_g(·) is the Gaussian-blurred image and σ² controls the width of the blur. The pixel value inside the seed regions is 1 and the pixel value tapers down as the distance between the pixel and the nearest seed region increases. The insight behind this approach is that a pixel closer to a seed region has a higher probability that it belongs to a true seed region. Likewise, a pixel farther from seed regions has a lower probability of belonging to a true seed region. Note that our Gaussian blurring is different from general Gaussian blurring that usually convolves a Gaussian kernel with the image. Since we use a distance map for blurring, the blurred image takes values between 0 and 1, which is not the case in general Gaussian blurring. Also, we cluster the pixels based on the computed labels and blurring is computed within each cluster so that it can be utilized for subsequent FP seed removal described in Section III-F. Fig. 3(c) shows an example of a Gaussian-blurred image.

D. Volume Reconstruction and Candidate Seed Detection

The geometry of a C-arm imaging system, depicted in Fig. 2, has three related coordinate systems: the global reference coordinates ℱ, the source coordinates 𝒮, and the image coordinates ℐ. By using a tracking system, the location and orientation of the source coordinate system can be determined relative to the laboratory frame. Specifically, the tracking system estimates a 3 × 3 rotation matrix ^SR_F and a 3 × 1 translation vector ^St_F that together take a vector in ℱ into one in 𝒮. We note that the C-arm is not necessarily isocentric, so the relationship between the two frames cannot be further constrained. Through prior calibration, the C-arm’s focal length f can be determined and an image origin (o_x, o_y) in ℐ can be specified. Putting all this together, we can specify a 3 × 4 projection matrix ^IF_F that projects a point in homogeneous global reference coordinates ℱ to a point in homogeneous image coordinates ℐ, as follows

$${}^I{\mathbf{F}}_F=\left[\begin{array}{cccc}\hfill -\frac{f}{S_x}\hfill & \hfill 0\hfill & \hfill o_x\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{f}{S_y}\hfill & \hfill o_y\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{cc}{}^S{\mathbf{R}}_F& {}^S{\mathbf{t}}_F\\ 0^T& 1\end{array}\right]$$ (2)

where S_x and S_y are the pixel sampling intervals along the x_I and y_I axes of the image, respectively.

Given a projection matrix for each image, we reconstruct a 3-D volume V (x) using backprojection, which is equivalent to a generalized form of tomosynthesis for arbitrary orientations. Specifically, a voxel value at × is computed by

$$V(\mathbf{x})=\frac{1}{N_p}{\displaystyle \sum _{i=1}^{N_p}{I}_g^i({}^I{\mathbf{F}}_F^i{\mathbf{x}}_h)}$$ (3)

where ${}^I{\mathbf{F}}_F^i$ is a projection matrix corresponding to the ith image, N_p is the number of projection images, x_h is a homogeneous coordinate representation of x, and $I_g^i(·)$ is the ith Gaussian-blurred image computed by (1). Since the reconstructed voxels take values between 0 to 1 (due to the nature of the Gaussian-blurred images), we can extract the candidate seed regions by thresholding. In our simulation, phantom, and clinical studies, the threshold varied within a small range, e.g. 0.9–1.0, thus making the automatic thresholding possible. We then label the extracted seed regions using connected component labeling [38], [39]. We consider each labeled seed region as a candidate seed and compute its centroid. When adjacent seeds are physically touching to each other or are placed very close to each other, these seeds may end up being connected and appear to be one larger seed in the reconstruction due to its blurred nature (note that the 3-D volume is reconstructed from blurred 2-D images) and the C-arm pose estimation errors, a situation that can be detected by the size of each reconstructed seed volume. In such a case, we select a seed with median size among candidate seeds, use it as a template to match filter the connected seed region in order to separate the connected seeds. Then, we compute the centroid of each separated seed.

E. C-arm Auto-focusing Using Detected Candidate Seeds

Gaussian blurring allows the algorithm to avoid missing seeds in the presence of errors in C-arm calibration and pose estimation. In practice, however, it is often necessary to correct the estimated C-arm camera parameters. In our clinical workflow, C-arm calibration is performed prior to the surgery at one representative pose. But, since the intrinsic camera parameters of the C-arm vary with its pose, using one set of fixed intrinsic camera parameters may cause errors in the pose estimation. Also, we use a tracking fiducial (FTRAC) that relies on features pre-segmented in the image for the C-arm pose estimation. Therefore, errors in image distortion correction, calibration, and feature segmentation propagate to tracking results. However, the main advantage of using a tracking fiducial is that a residual error of the C-arm pose estimation can be computed. Specifically, we compare the features projected from the model onto each image using the estimated pose with the features shown in the image. The computed residual error provides quantitative measure of the accuracy of calibration and pose estimation. Thus, if the residual error is relatively large, it is desirable to correct the C-arm camera parameters to improve on the reconstruction. Incorrectly estimated camera parameters can be automatically adjusted by using candidate seeds as fiducials. We call this a “C-arm auto-focus” procedure. We first compute a reconstruction using images whose corresponding residual pose errors are small among the acquired images, and detect candidate seeds. Then, we use the Gaussian-blurred images as cost functions and adjust the camera parameters of the remaining images so that these images are focused to the candidate seeds by solving following optimization problem.

$$\widehat{e}=\text{arg}\underset{e}{\text{min}}\left[-{\displaystyle \sum _{j=1}^{N_c}{I}_g^i\left({}^I{\mathbf{F}}_F^i(e){\mathbf{x}}_j\right)}\right]$$ (4)

where N_c is the number of candidate seeds, x_j is the homogeneous coordinates of the jth candidate seed, ${}^I{\mathbf{F}}_F^i$ is the projection matrix in the ith image computed by (2), $I_g^i(·)$ is the ith Gaussian-blurred image computed by (1), and e = (θ, t, f, o_x, o_y) is a nuisance parameter which includes rotation θ, translation t, focal length f, and the image origin o_x, o_y. Since we already have initial estimates of e and the estimation errors are not huge, we can constrain the range of each parameter. Starting from the initial estimation of the calibration and pose parameters, we solve this constrained optimization problem using sequential quadratic programming (SQP) [41]–[43]. The Hessian of the Lagrangian is updated by the BFGS formula [43]–[48]. The optimization is implemented using the MATLAB 7.1 command ‘fmincon’ [49]. The automatically focused images (note that these images are not used for the initial reconstruction) are incorporated into the initial reconstruction to obtain the final reconstruction.

F. False Positive Seed Removal

Initially detected candidate seeds include a significant amount of FP seeds since only a limited number of projection images are used for 3-D reconstruction. Therefore, an FP seed elimination process is critical for the success of the tomosynthesis-based approach. We formulate this process as an optimal coverage problem. Optimal coverage problems arise in various applications such as wireless sensor networks or so called art gallery problem [50], [51]. The objective in these problems is to select a minimum subset that covers a given set of “client” points from a given set of “server” points. Local cost functions are first defined on all the selected server points, and a global cost function is determined as a summation of the local cost functions. The problem can be solved by optimizing a global cost function. Similarly, the goal of the FP seed removal process is to find N_t true seeds from N_c candidate seeds such that all 2-D seed regions are covered in all projection images. However, since the optimal coverage problem is NP-hard [50], [51] and its computational complexity is $O(C_{N_t}^{N_c})$ , where $C_{N_t}^{N_c}$ means N_c choose N_t, it is practically impossible to find the global optimum for a large number of implanted seeds. Instead of solving the global optimization problem using the global cost, we find an approximate optimal solution by a greedy search using the local cost. We also reduce the size of the problem by using clustered binary seed-only images for regularization. We now describe the FP seed removal process in detail.

Let x_n ∈ ℝ³ be a 3-D coordinate of the nth candidate seed, Pⁱ be a projection operator which projects a 3-D point onto the ith image plane, and ${\mathbf{x}}_n^i=P^i{\mathbf{x}}_n$ be a 2-D coordinate of the projection of x_n in the ith image. For each ${\mathbf{x}}_n^i$ ,let $d^i({\mathbf{x}}_n^i)$ be a Euclidean distance to the nearest seed region from ${\mathbf{x}}_n^i$ which is calculated from the distance map described in Section III-C, and $L^i({\mathbf{x}}_n^i)$ be a label which is assigned to the candidate seed based on the labeling results described in Sections III-B and III-C. Note that $d^i({\mathbf{x}}_n^i)=0$ if ${\mathbf{x}}_n^i$ is inside a seed region. If there are $N_L^i$ seed regions in the ith seed-only image and they are labeled as $1,2,\cdots N_L^i$ , the projections of the N_c candidate seeds on the ith image are clustered into $N_L^i$ sets ${\mathrm{\Omega }}_l^i$ , such that in the ith image, the following holds true:

$$L^i({\mathbf{x}}_1)=L^i({\mathbf{x}}_2),\text{for}\forall {\mathbf{x}}_1,{\mathbf{x}}_2\in {\mathrm{\Omega }}_l^i,l=1,2,\cdots ,N_L^i.$$ (5)

A seed region with label l is covered by $\Vert {\mathrm{\Omega }}_l^i\Vert$ seeds, where $\Vert {\mathrm{\Omega }}_l^i\Vert$ is the cardinality of the set ${\mathrm{\Omega }}_l^i$ and $\Vert {\mathrm{\Omega }}_l^i\Vert$ ≥ 1. Since overlapping seed regions are considered as one seed region in the seed-only image, then $N_L^i\le N_c$ .

The size of our optimization problem can be reduced by clustering seeds in each image. If a seed region in an image is covered only by one seed, then this seed must be classified as true, otherwise this seed region cannot be covered. Let G be a set of such seeds, i.e.,

$$\mathbf{G}={\cup }_{i=1}^{i=N_p}\{\mathbf{x}|L^i(P^i\mathbf{x})=l\text{and}\Vert {\mathrm{\Omega }}_l^i\Vert =1,l=1,2,\cdots ,N_L^i\}$$ (6)

where N_p is the number of projection images. Once G is determined, then the optimization problem is reduced to choose (N_t − ‖G‖) seeds from (N_c − ‖G‖) candidate seeds.

In order to create a proper cost function, we use the following observation: An FP seed is projected either 1) close to some true seeds if the image contributes to create this particular FP seed or 2) far away from the seed regions if the image does not contribute to create that FP seed. In either case, true seeds are not always projected close to other true seeds; they are projected close together when their actual 3-D locations are close or when they are hidden in a 2-D projection. But, importantly, we have never encountered a case where a true seed is hidden in all images. Thus, a cost function for a given seed can be defined as a function of the closest distances between the projections of a seed and the projections of all other true seeds, and the distance between the projection of the seed and the nearest seed region in all images. Based on this idea, we define a local cost function as:

$$C(x_n)=-{\displaystyle \sum _{i=1}^{N_p}\frac{1+D^i({\mathbf{x}}_n)}{1+d^i({\mathbf{x}}_n)},\text{for}\text{all}}{\mathbf{x}}_n\in \mathbf{S}\backslash \mathbf{G}$$ (7)

where S is a set of candidate seeds, dⁱ(x_n) is the distance between the projected point of x_n and the nearest seed region in the ith image, and

$$D^i({\mathbf{x}}_n)=\underset{m\ne n}{{\displaystyle \text{min}}}\Vert P^i{\mathbf{x}}_n-P^i{\mathbf{x}}_m\Vert ,\text{for}{\mathbf{x}}_m\in \mathbf{S}.$$

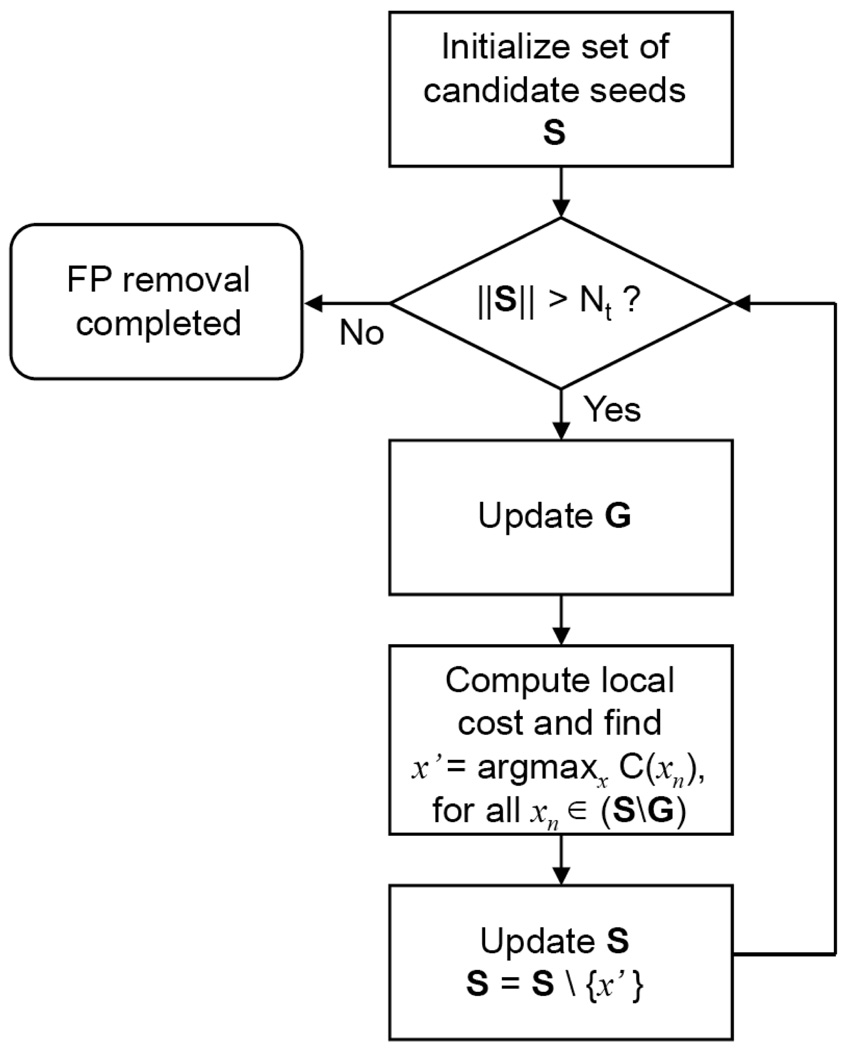
We iteratively remove FP seeds by greedy search. During each iteration, from S we remove one seed with the largest cost computed by (7). We also update G if there are additional seeds that cover some seed regions alone having removed the FP seed. Iteration continues until N_t seeds are left in S. A flowchart explaining the FP seed removal process is shown in Fig. 4.

Fig. 4.

A flowchart explaining the FP seed removal process.

IV. NUMERICAL RESULTS

A. Simulations

We performed simulation studies using synthetic projection images. We considered a nominal 50 cc prostate, with six different seed densities from 1.0 to 2.25 seeds/cc with a step size of 0.25 seeds/cc resulting in N_t = {54, 60, 72, 84, 96, 112} implanted seeds, respectively. Each seed was represented by a cylinder with diameter of 0.8 mm and length of 1.45 mm which are similar to the X-ray visible diameter and length of an ¹⁰³Pd seed. Multiple seeds could be placed next to one another as happens in real implantation, but they could not share the same position due to their physical size. The focal length of the C-arm and the pixel size of the image were 1000 mm and 0.44×0.44 mm², respectively. The voxel size of the reconstruction was 0.5×0.5×0.5 mm³.

Due to the limited mobility of the C-arm in the operating room, we can only rotate the C-arm within a very narrow cone about the AP axis. When the source angle separation between image acquisition poses is small, the uncertainty in depth information is proportionately magnified. As a consequence, the reconstruction may fail to detect true seeds and generate FP seeds at incorrect positions. Therefore, it is necessary to evaluate the accuracy and robustness of our method to small source angle separations. In our clinical setting, the C-arm can have mobility inside a 25° cone centered on the AP axis (see Fig. 1(a)). We consider five different X-ray source angle separations from 5° to 25° with a step size of 5° to test the algorithm for various angle separations.

Ideal simulations

We first evaluate the proposed method on simulation data sets created under the assumption that the C-arm is calibrated and the pose of the C-arm is known without error. For each case (combination of seed density and the source angle separation), we generated ten data sets, and created six projection images in each data set. From six available images in each data set, three and four images were selected to compute the reconstructions. A total of $1000(=C_3^6\text{combinations}\times 10\text{data}\text{sets}\times 5\text{angle}\text{separations})$ simulations were performed using three images and $750(=C_6^4\text{combinations}\times 10\text{data}\text{sets}\times 5\text{angle}\text{separations})$ simulations were performed using four images. Since there was no calibration and pose estimation error, we used small σ, e.g., 1.0 pixel = 0.44 mm. The estimated seed positions were compared to the ground truth. Fig. 5 shows a typical synthetic image and the estimated seed centroids projected onto the image.

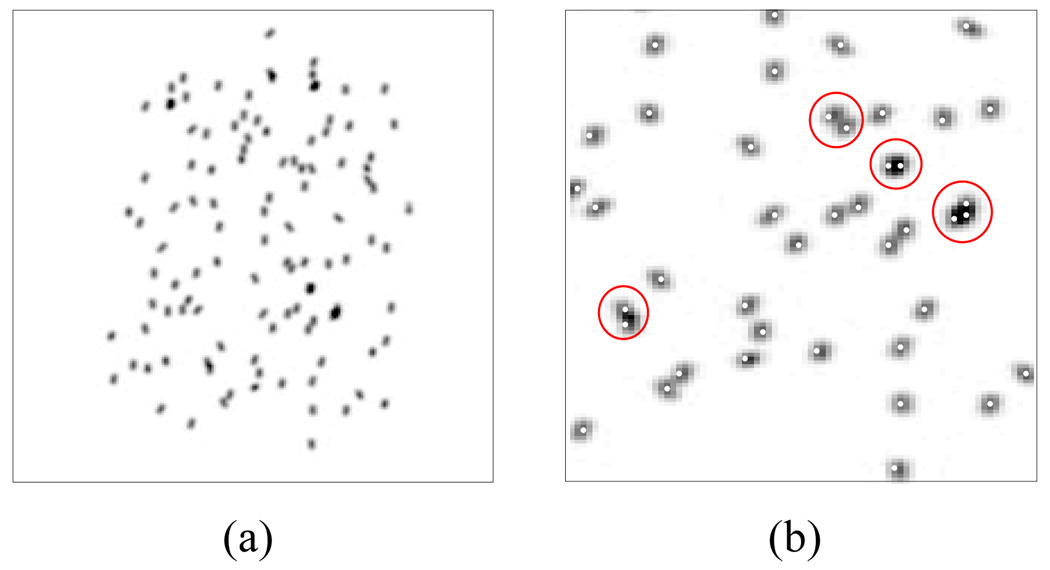
Fig. 5.

(a) Synthetic projection image with 112 seeds. (b) Estimated seed centroids projected onto (a). Red circles indicate example overlapping seeds.

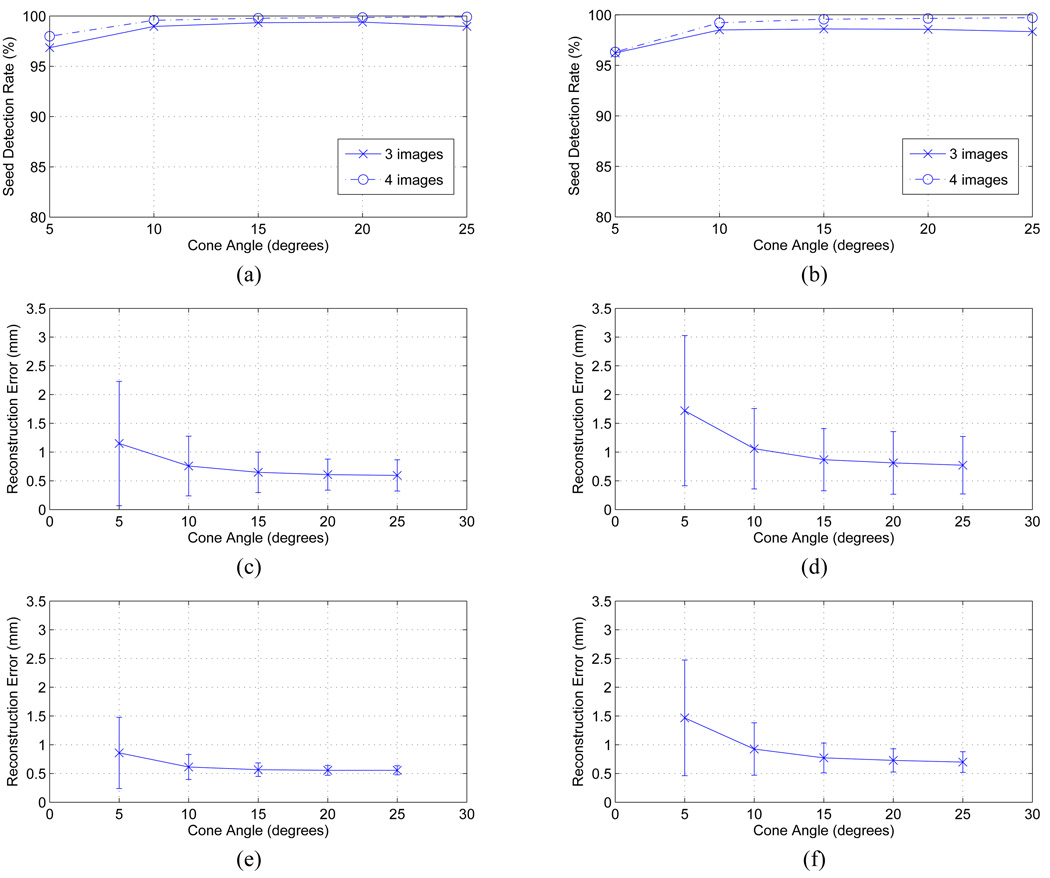
Figs. 6(a), (c), and (e) show the seed detection rate and reconstruction error, respectively, as functions of the source angle separation. The results show that the proposed algorithm can almost perfectly localize the implanted seeds with a detection rate of ≥ 99.0% on average using either 3 or 4 images when the image acquisition angle is ≥ 10°. Even when the image acquisition angle separation is 5°, the algorithm is still able to localize the seeds with a detection rate of > 96.5% and > 97.5% using 3 and 4 images, respectively. It is observed that the larger source angle separation allows the algorithm to recover the seed locations more accurately (smaller mean reconstruction errors). Reconstruction results for each seed density averaged over the source angle separations of 10°–25° are also shown in Table I.

Fig. 6.

Plots showing the relationship between reconstruction quality and source angle separation when (a, c, e) there is no C-arm calibration and pose error and (b, d, f) there are realistic calibration and pose estimation errors. (a, b) Seed detection rate. Three and four images are used. (c, d) Reconstruction errors when three images are used. (e, f) Reconstruction errors when four images are used.

TABLE I.

Simulation results when the C-arm is calibrated and the pose of the C-arm is known without error. The results for each seed density are averaged over the source angle separations varying from 10° to 25° with a step size of 5° (total 800 simulations). The averaged results are rounded up to one digit after the decimal point which would be enough for clinically meaningful data analysis.

Num of seeds	Num of images	Number of seeds		Mean ± STD error (mm)
		candidate	correctly detected
54	3	55.1	53.9 (99.8%)	0.6 ± 0.2
	4	54.0	54.0 (100.0%)	0.6 ± 0.1
60	3	61.6	59.8 (99.7%)	0.6 ± 0.3
	4	60.1	60.0 (100.0%)	0.6 ± 0.1
72	3	74.8	71.8 (99.7%)	0.6 ± 0.3
	4	72.1	72.0 (100.0%)	0.6 ± 0.1
84	3	87.7	83.4 (99.3%)	0.6 ± 0.3
	4	84.0	83.8 (99.8%)	0.6 ± 0.1
96	3	104.9	94.6 (98.5%)	0.7 ± 0.4
	4	96.7	95.7 (99.7%)	0.6 ± 0.1
112	3	124.3	109.6 (97.9%)	0.7 ± 0.5
	4	112.6	111.2 (99.3%)	0.6 ± 0.2

Realistic simulations

We introduced C-arm calibration and pose estimation errors to the same data sets described in the ideal simulations. We added truncated additive white Gaussian noise (AWGN) to the known C-arm pose parameters. Here we considered the pose recovery results of prior phantom experiments using the FTRAC fiducial in [33, Section 7-B]. For rotation, AWGN with mean 0.33° and standard deviation (STD) 0.21° was added to the known rotation at each pose around a random rotation axis. And for translation, AWGN with means (μ_x, μ_y, μ_z) = (0.07, 0.04, 0.55) mm and STD’s (σ_x, σ_y, σ_z) = (0.05, 0.03, 0.32) mm was added to each known translation. Also, we added zero mean AWGN with STD’s 2 mm and 0.44 mm to the known focal length of the C-arm and the image origin, respectively. The added noise was truncated at 3×STD from the mean. We used the same combinations of seed densities and source angle separations as previous simulations. The voxel size of the reconstruction was also the same, but the σ was chosen to be larger than the previous simulations, e.g. σ = 2.0 pixel = 0.88 mm or σ = 3.0 pixel = 1.32 mm, depending on the number of images used and the source angle separation.

Figs. 6(b), (d), and (f) show the seed detection rate and the mean reconstruction errors, respectively, as functions of the angular separation. The results show that the algorithm can successfully localize the seeds even when the image acquisition angle separation is 5°, but the performance is more reliable when the angle separation is ≥ 10°. Also, note that the reconstruction error decreases as the image acquisition angle separation increases. The simulation results averaged over the source angle separations of 10° − 25° are shown in Table II. The results show that the detection rate is ≥ 96.7% and ≥ 98.8% with three and four images, respectively, under the realistic conditions when the angle separation is ≥ 10°.

TABLE II.

Simulation results when random C-arm calibration and pose estimation errors are introduced. The results for each seed density are averaged over the source angle separations varying from 10° to 25° with a step size of 5° (total 800 simulations). The averaged results are rounded up to one digit after the decimal point which would be enough for clinically meaningful data analysis.

Num of seeds	Num of images	Number of seeds		Mean ± STD error (mm)
		candidate	correctly detected
54	3	57.6	53.7 (99.4%)	0.8 ± 0.5
	4	54.3	54.0 (100.0%)	0.8 ± 0.3
60	3	65.4	59.7 (99.5%)	0.8 ± 0.4
	4	60.5	59.9 (99.8%)	0.8 ± 0.2
72	3	80.5	71.3 (99.0%)	0.9 ± 0.6
	4	72.9	71.9 (99.9%)	0.8 ± 0.3
84	3	96.4	82.7 (98.5%)	0.9 ± 0.5
	4	85.5	83.7 (99.6%)	0.8 ± 0.3
96	3	108.3	93.9 (97.8%)	0.9 ± 0.6
	4	100.8	95.3 (99.3%)	0.8 ± 0.3
112	3	128.8	108.3 (96.7%)	0.9 ± 0.7
	4	118.9	110.6 (98.8%)	0.8 ± 0.4

Effects of C-arm auto-focusing

In this simulation experiment, we added noise to each C-arm camera parameter and reconstructed the seeds with and without the auto-focusing. As described in Sec. III-E, we considered rotation (3 parameters), translation (3 parameters) and focal spot (3 parameters, comprising the focal length and the image origin). We generated 150 data sets with 84 implanted seeds in a 50 cc prostate with a seed density of 1.75 seeds/cc. For each data set, four images were synthetically generated in a 20° cone centered on the AP axis. In each data set, we assumed that the calibration and the pose estimation errors of one image (the “bad” image) is relatively large and must be corrected while the remaining images are accurate (the “good” images). In order to create bad images, we separately added rotation, translation, and calibration errors to the known parameters. Rotation errors varied from 0° to 5° in increments of 0.5° and translation errors varied from 0 mm to 10 mm in increments of 1 mm. We incorporated the fact that translation errors in depth are always significantly greater than those parallel to the plane [33]. The error in knowing the focal spot varied from 0 mm to 20 mm with a step size of 2 mm; the fact that focal length errors are always larger than image origin errors was incorporated in error generation.

A total of 1650 (150 data sets × 11 noise levels) simulations for each error type were generated. Given a simulated data set, we first computed a reconstruction using all four images without auto-focus. We then computed a reconstruction using auto-focus assuming the bad image was known to the algorithm. An initial reconstruction based on three good images was first computed and then the bad image was automatically focused using candidate seeds detected from the initial reconstruction. The bad image was then added to the initial reconstruction with corrected camera parameters to compute the final reconstruction.

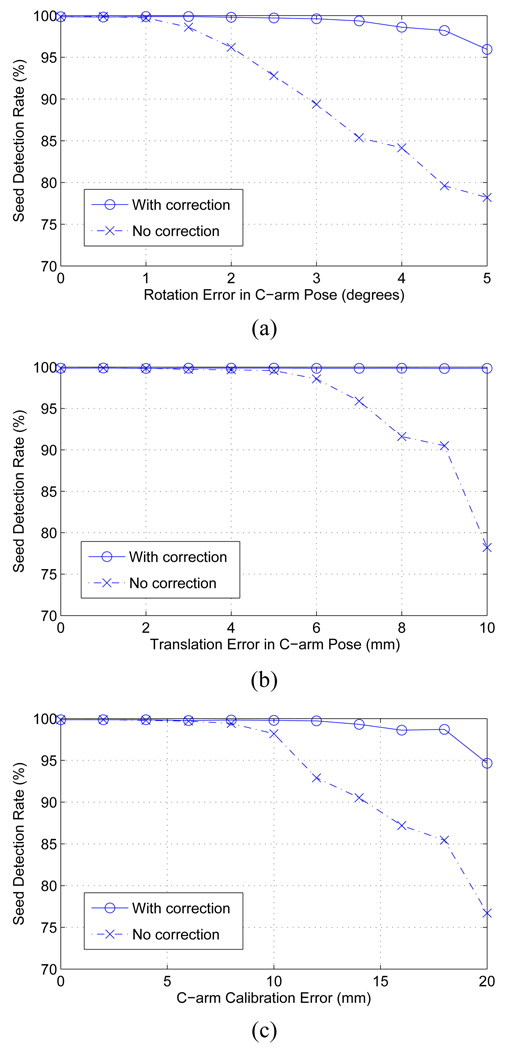
The reconstruction results with and without the auto-focus process are shown in Fig. 7. The results show that our tomosynthesis-based algorithm with Gaussian blurring is robust to calibration and pose estimation errors, and also that the overall reconstruction can be improved by adjusting the erroneous calibration and pose parameters. Previous ideal and realistic simulations imply that three good images are enough to get reasonably good initial reconstruction.

Fig. 7.

Performance of the C-arm auto-focus process for (a) rotation error in the C-arm pose, (b) translation error in the C-arm pose, and (c) focal spot error in the C-arm calibration.

B. Phantom Experiments

We evaluated our method on five phantom data sets. The precisely fabricated phantom consists of twelve 5 mm thick acetol slabs, each having at least a hundred holes with 5 mm spacing where seeds can be positioned (see Fig. 8(a)). The FTRAC was precisely attached to the phantom in a known position so that the seed positions were known, thus establishing a ground truth [10, Section III-C]. Radio-opaque seeds each with a length of 4.9 mm and a diameter of 0.8 mm (similar in size to that of ¹²⁵I seeds) were inserted into the slabs keeping seed density constant at about 1.56 seeds/cc. Five data sets were generated with 42, 57, 72, 87, and 102 inserted seeds. For each data set, we collected six images within a 20° cone around the AP axis using a Philips Integris V3000 fluoroscope. We selected four, five, and six images from the acquired images in each data set, based on residual errors provided by the FTRAC software, and used them for 3-D reconstructions. The voxel size of the 3-D reconstructions was 0.5 × 0.5 × 0.5 mm³, and σ = 3 pixels = 1.32 mm, was used. For images with large pose estimation residual errors, we performed the C-arm auto-focus process to adjust the camera parameters. A typical phantom image with an FTRAC and 102 seeds is shown in Fig. 8(b). Fig. 8(c) shows the estimated seed centroids projected onto one of the projection images (note the significant number of overlapping or clustered seeds in this view). We computed the reconstruction errors by comparing positions of the detected seeds and the ground truth, as shown in Table III. We were able to localize the implanted seeds with a detection rate of ≥ 96.1%, ≥ 98.3% and ≥ 98.6% from four, five, and six projection images, respectively. The mean reconstruction errors were slightly larger than those in the simulations since the radio-opaque size of the implanted seeds is bigger. The results imply that we are able to localize the seeds from four or more images with clinically acceptable seed detection rate.

Fig. 8.

(a) Phantom with FTRAC attached. (b) Phantom image with 102 implanted seeds. (c) Estimated seed centroids projected onto (b).

TABLE III.

Phantom experiment results.

Num of seeds	Num of images	Number of seeds		Mean ± STD error (mm)
		candidate	correctly detected
42	4	43	42 (100%)	1.7 ± 0.6
	5	42	42 (100%)	1.3 ± 0.5
	6	42	42 (100%)	1.1 ± 0.4
57	4	60	56 (98.3%)	0.8 ± 0.7
	5	58	56 (98.3%)	0.8 ± 0.7
	6	57	57 (100%)	0.8 ± 1.0
72	4	77	72 (100%)	1.2 ± 0.9
	5	74	72 (100%)	1.0 ± 0.4
	6	72	72 (100%)	1.0 ± 0.4
87	4	94	84 (96.6%)	0.7 ± 0.7
	5	96	86 (98.6%)	0.7 ± 0.5
	6	91	86 (98.6%)	0.7 ± 0.4
102	4	119	98 (96.1%)	2.0 ± 0.9
	5	107	102 (100%)	1.1 ± 0.5
	6	104	102 (100%)	1.1 ± 0.5

C. Clinical Experiments

The proposed method was validated on clinical data acquired from six patients during actual brachytherapy surgeries. All procedures followed IRB approved protocols and patient consent was obtained. For each patient, we acquired two sets of images during the procedure and one set of images at the end of the procedure so that there are different number of implanted seeds in each set. The C-arm was calibrated prior to each surgery and X-ray images of the implants were taken within a 20° cone centered on the AP axis using an OEC 9800 fluoroscope. We corrected the geometric distortion of each image and computed the corresponding C-arm pose using the FTRAC that was precisely attached to the needle insertion template in a known position. Various numbers of ¹⁰³Pd seeds with a length of 4.5 mm and a diameter of 0.8 mm (radio-opaque size of the x-ray marker is about three times shorter than the size of the outside capsule) were implanted. Based on the residual pose estimation errors computed by the FTRAC software, we selected five images with the smallest errors for reconstruction. The C-arm auto-focus process adjusted the camera parameters of the images with large residual pose errors.

The reconstruction voxel size was 0.5 × 0.5 × 0.5 mm³, and the value of σ was slightly bigger than the value used in the phantom studies, e.g. σ = 5 pixels = 2.2 mm, due to the relatively small radio-opaque size of the ¹⁰³Pd seeds. Fig. 9 shows a typical patient image and reconstruction results. Out-of-focus images such as Fig. 9(b) were automatically focused by the auto-focus process, and overlapping seeds were automatically detected by the algorithm as shown in Fig. 9(c). In Fig. 9(c), one might observe that the estimated seed centroids in the lower right corner seem to show a systematic shift from the shadow of real seeds. When we reproject the reconstructed seed centroids onto the images used for the reconstruction, shifts of the reprojected seeds from the seeds observed in the image look random. A systematic shift happens when the estimated poses of the C-arm in one or more images are incorrect, but it is global rather than local. Although shifts are usually random, this kind of local shift, which looks like systematic, may happen due to incorrect geometric image distortion correction even when all the C-arm poses are good. Since we compute the geometric distortion pattern of the C-arm fluoroscopy image prior to the implantation at one representative pose as described in Section II and use computed dewarp parameters for geometric distortion correction for all images, geometric distortion correction of each image is incorrect even though it is reasonably good and does not critically affect the reconstruction result. In a region where actual geometric distortion is slightly different from the computed distortion pattern, such distortion may not be accurately corrected and reconstructed seeds from that region may show a slight systematic shift when reprojected onto the image.

Fig. 9.

(a) Patient image showing 77 seeds and the FTRAC. (b) Estimated seed centroids projected onto (a) before (red dots) and after the C-arm auto-focus (white dots). (c) Estimated seed centroids projected onto (a). Red circles indicate example overlapping seeds.

Since the exact locations of the seeds were unknown, we visually assessed the correspondences between the projection of the estimated seeds and the actual seeds in the images. For a quantitative measure, we compared the estimated seed locations with those computed by an existing algorithm, MARSHAL [10]. MARSHAL is a correspondence-based algorithm that requires an exact identification of the seeds in all 2-D projection images. The number of visually matched seeds for each case and the differences between two reconstructions were shown in Table IV. The results show that our method can successfully localize the implanted seeds with overall detection rate of 98.8% (STD=1.6) which is clinically adequate. The reconstructed seed locations computed by the proposed algorithm agreed to those computed by MARSHAL with overall mean difference of 0.8 mm.

TABLE IV.

Clinical experiment results. Number of matched seeds are counted by visual assessment and the reconstruction differences are computed by comparing the estimated seed locations computed by the proposed algorithm with those computed by the marshal algorithm.

Patient number	Number of seeds			Mean ± STD difference (mm)
	implanted	candidate	matched
1	22	22	21 (95.5%)	0.6 ± 0.2
	44	46	43 (97.7%)	0.7 ± 0.5
	66	75	66 (100%)	0.7 ± 0.6
2	39	39	39 (100%)	0.6 ± 0.4
	82	84	82 (100%)	0.6 ± 0.6
	84	85	83 (98.8%)	1.0 ± 0.8
3	33	33	33 (100%)	0.4 ± 0.3
	67	67	65 (97.0%)	0.9 ± 0.8
	70	68	68 (97.1%)	1.2 ± 1.4
4	35	35	35 (100%)	0.4 ± 0.3
	68	70	68 (100%)	0.6 ± 0.6
	77	82	76 (98.7%)	1.4 ± 0.8
5	24	24	24 (100%)	0.8 ± 1.2
	48	50	46 (95.8%)	1.1 ± 1.2
	53	56	52 (98.1%)	1.4 ± 1.4
6	33	33	33 (100%)	0.7 ± 0.6
	61	63	61 (100%)	0.6 ± 0.3
	66	70	66 (100%)	0.8 ± 0.6

D. Determination of σ

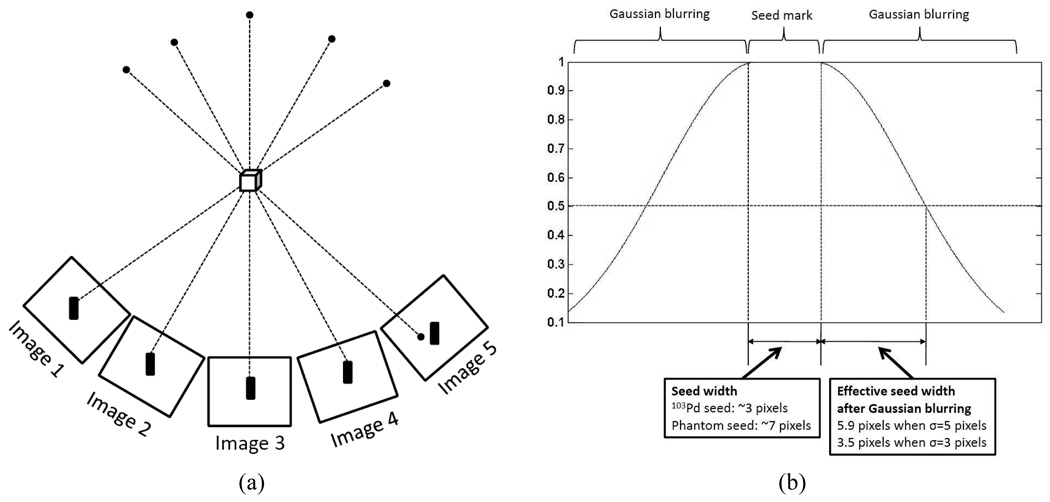
The size of σ determines the width of the blur, therefore should be determined considering the size of the seeds, and the C-arm calibration and pose errors. Since various factors cause shift in the projection, it is hard to analytically determine the value of σ. In order to have information about the possible shift in the projection images due to C-arm calibration and pose estimation errors, we analyzed the phantom data sets. For five phantom data sets each of which has six projection images, we compared the 2-D seed positions obtained from projection images with the projection of the ground truth 3-D seeds, and observed that the projected points are shifted less than about 7 pixels (there will be no shift when the C-arm pose is exactly known).

Let us consider an extreme case as shown in Fig. 10(a) where a voxel is reconstructed from five images and thresholded at 0.9 (note that our threshold varies between 0.9 and 1.0), and also this voxel corresponds to a seed mark in every image except for one. In order for this voxel to be reconstructed as a part of a seed after thresholding, the Gaussian-blurred pixel value in image 5 associated with this voxel has to be over 0.5 (note that V = (1+1+1+1+0.5)/5 = 0.9 by (3)). When σ = 5 pixels, the Gaussian-blurred image has I_g = 0.5 at d = 5.9 pixels (3.5 pixels for σ = 3) from the boundary of the binary seed mark as in Fig. 10(b) (see (1) for the computation of I_g and d). For our phantom and ¹⁰³Pd seeds, the widths (length of the short axis) of the projected seeds are about 7 and 3 pixels, respectively. With σ = 3 and 5, total about (7/2+3.5) = 7 pixels and (3/2+5.9) = 7.4 pixels may contribute to the reconstruction, which cover the expected shift (< 7 pixels) in our system. Too small σ may result in missing seeds in the reconstruction if the C-arm calibration and pose estimation errors are relatively large (even though the error is within allowable range). By increasing the σ, the effective (or relevant) area of each seed mark is increased, which is helpful for detecting seeds under large C-arm calibration and pose errors. However, too big σ will result in too many connected (or merged) seed regions in the reconstructed volume, each of which appears to be one big seed but actually contains multiple seeds.

Fig. 10.

(a) Reconstruction of a voxel from five images. C-arm calibration and pose estimation of image 5 is not accurate. (b) Cross-sectional plot of a Gaussian-blurred seed region.

E. Computation Time

In actual clinical use, the entire seed reconstruction process from image acquisition to seed localization must be completed within a limited time, so computation time must also be minimized. The proposed algorithm was implemented using MATLAB 7.1 [49] and tested on a Pentium4 2.92 GHz PC (current code is not optimized for best performance). On a typical clinical data set of 5 images, computation time of the complete workflow, from binary seed-only image computation to 3-D seed localization, was about 100 seconds. Furthermore, an experienced technician can acquire 5 fluoroscopy images less than a minute and each C-arm pose can be recovered by the FTRAC software within seconds [33]. This implies that seed reconstruction process takes less than 3 minutes, which would be acceptable for intraoperative use. Computation time can be further reduced by using optimized C/C++ implementation.

V. CONCLUSION

We proposed a novel tomosynthesis-based prostate brachytherapy seed reconstruction method. The attractive feature of the proposed method is that it can automatically recover all the seeds, including overlapping or clustered seeds, without involving explicit identification of the 2-D coordinates of the seeds in the fluoroscopy images. Gaussian blurring combined with distance map enables the algorithm to reconstruct seeds under realistic calibration and pose estimation errors of the C-arm. In addition, a C-arm auto-focus process enables the algorithm to utilize out-of-focus images after automatic adjustment of the C-arm camera parameters. A false positive seed removal process based on an optimal coverage cost successfully extract the true seeds from the candidate seeds and allows us to reduce the number of required projection images compared to the other tomosynthesis-based algorithms [27], [28].

Simulation studies show that the proposed algorithm requires only three or four images to detect the implanted seeds with a detection accuracy of ≥ 97.9% when the C-arm is accurately calibrated and the pose of the C-arm is accurately estimated with angle separation ≥ 10°. Simulation results with the calibration and pose estimation errors also show that the implanted seeds can be localized from three and four images with a detection rate of ≥ 96.7% and ≥ 98.8%, respectively, when the angle separation is ≥ 10°. In case the image acquisition angles are very small, it is natural for the algorithm to have difficulty in detecting all true seeds correctly. However, simulations with varying angular separation show that the algorithm is robust to angle separation up to 5° cone angle centered on the AP-axis. The proposed algorithm was also evaluated on various phantom data sets showing that ≥ 96.1%, ≥ 98.3%, and ≥ 98.6% of the implanted seeds can be correctly reconstructed from four, five, and six projection images, respectively.

We also validated the algorithm using eighteen clinical data sets and showed that it can successfully localize the implanted seeds with clinically adequate accuracy and seed detection rate of 98.8% on average. In our clinical trial, three data sets were acquired: two times during the procedure and one after all seeds were inserted. It is anticipated that, in normal clinical practice, either one or two dosimetry reconstructions will be performed. If a single reconstruction is performed, it will be at the end after all seeds are inserted. If two dosimetry assessments are performed, one would most likely occur after placement of approximately half the number planned seeds to be implanted, with the second dosimetry reconstruction performed after all seeds are implanted. The case of a single dosimetry reconstruction will be most likely. In the case of a mid-procedure reconstruction, it might be beneficial to utilize previously identified seed positions as a prior to help reconstructing the remaining seeds. However, if only one reconstruction is performed upon exit, then this prior information may not be available in general. More significantly still, there is often significant edema and seed migration during the procedure, which precludes a reconstruction to serve as a prior for subsequent reconstructions. As Jain et al. reported in [52], seeds may migrate as much as 15 mm between the first and last reconstruction.

One might consider using preoperative or intraoeratively updated implant plan as prior information. The prior information of seed positions can be used for C-arm tracking as well as the seed reconstruction. Murphy and Todor [26] proposed to use such prior information for simultaneously estimating C-arm calibration, C-arm pose, and the seed positions. They were successful in simulations, but this far no follow-up results have been published on actual patient or even phantom data. In all, extensive studies would be necessary to achieve a clinically viable implant reconstruction method that makes use of statistically unreliable prior information.

Our objective in this paper was to use a non-isocentric average common C-arm, the kind of device that the majority of practitioners have in their brachytherapy procedues. There are several brachytherapy implant reconstruction methods that consider only isocentric source-detector geometry, e.g. [19], [23], [28]. (Actually, in these works, the fluoroscopy images were acquired with radiation therapy simulators, which have been rapidly disappearing from the radiation oncology clinic in contemporary practice.) When source-detector motion is confied to isocentric in-planar rotation, the reconstruction problem is much simpler than our problem because pose of the imaging device can be determined by an angle and the reconstruction can be computed by simple isocentric tomosynthesis equations [28]. Therefore, our method can be used with more sophisticated fluoroscopy device such as isocentric flat-panel C-arm by straightforward modification (6 degree of freedom pose parameters are replaced by an angle and modification of the reconstruction algorithm for isocentric tomosynthesis is trivial). We must also note that the main reason why isocentric C-arms are very slow to spread into brachytherapy is that the currently used patient stirrups, OR table, and brachytherapy mount all preclude using the C-arm in cone-beam tomography mode, thus rendering the most expensive features of the C-arm (flat panel, isocentric geometry, and motorized rotation) unusable. In all, we expect that in the foreseeable future, quantitative coupling of conventional TRUS and conventional manual non-isocentric C-arm will function as a very effective guidance and dosimetry tool.

In contrast to seed-matching-based algorithms such as MARSHAL [10] that use triangulation and compute symbolic intersections to reconstruct the seed positions, our tomosynthesis-based algorithm reconstructs the entire volume of interest and therefore requires somewhat longer computation time. Our method is fully automatic, and thus will save time in the operating room by obviating manual intervention typically required in seed segmentation and fixing apparently erroneous seed matches. Also, our current MATLAB prototype has not been optimized for speed and memory efficiency. Tutar et al. [28], for example, demonstrated that a tomosynthesis-based method can be adequately optimized for practical application in surgery, and we note that our algorithm requires even fewer images than Tutar’s.

Intraoperative seed localization is critical because it allows the surgeon to monitor the implant procedure and achieve optimal dose distribution to eradicate cancer and minimize unnecessary toxicity to the adjacent tissues. The proposed seed reconstruction method appears to be sufficiently accurate, robust, and computationally fast for intraoperative dosimetry in prostate brachytherapy procedures.