Genome-wide association scans for secondary traits using case-control samples

Abstract

Genome-wide association studies (GWAS) require considerable investment, so researchers often study multiple traits collected on the same set of subjects to maximize return. However, many GWAS have adopted a case-control design; improperly accounting for case-control ascertainment can lead to biased estimates of association between markers and secondary traits. We show that under the null hypothesis of no marker-secondary trait association, naïve analyses that ignore ascertainment or stratify on case-control status have proper Type I error rates except when both the marker and secondary trait are independently associated with disease risk. Under the alternative hypothesis, these methods are unbiased when the secondary trait is not associated with disease risk. We also show that inverse-probability-of-sampling-weighted (IPW) regression provides unbiased estimates of marker-secondary trait association. We use simulation to quantify the Type I error, power and bias of naïve and IPW methods. IPW regression has appropriate Type I error in all situations we consider, but has lower power than naïve analyses. The bias for naïve analyses is small provided the marker is independent of disease risk. Considering the majority of tested markers in a GWAS are not associated with disease risk, naïve analyses provide valid tests of and nearly unbiased estimates of marker-secondary trait association. Care must be taken when there is evidence that both the secondary trait and tested marker are associated with the primary disease, a situation we illustrate using an analysis of the relationship between a marker in FGFR2 and mammographic density in a breast cancer case-control sample.

Introduction

Genome-wide association studies (GWAS) require massive investments of time and money, so researchers are understandably looking to maximize return by studying multiple traits collected on the same set of subjects. For example, recent GWAS for height [Lettre, et al. 2008; Sanna, et al. 2008; Weedon, et al. 2007] and body mass index [Loos, et al. 2008] were conducted using samples from multiple GWAS which were originally conducted to find markers associated with risk of diabetes, breast and prostate cancers, and other traits. An explicit goal of the NHGRI's dbGAP and PhenX projects is to facilitate the sharing and harmonization of data on multiple traits relevant to human health collected on samples that have already been genotyped as part of a GWAS. Considering the large sample sizes necessary to minimize the chances of both the false positive and false negative results when conducting GWAS [Chanock, et al. 2007; Hunter and Kraft 2007], combining existing GWAS data even when the trait under study was not the primary outcome of all (or perhaps even any) of the component studies is an attractive, quick and inexpensive option.

However, many GWAS to date have adopted a case-control design that implicitly conditions on a primary disease outcome. This non-random ascertainment from the study base can in principle lead to inflated Type I error rate for tests of association between markers and a secondary trait that either ignore ascertainment (i.e. treat the sample as representative of the entire study base) or "adjust for" ascertainment by conditioning on disease status (e.g. restricting analysis to controls or including case-control status as a covariate in a regression model). These commonly-used analysis approaches can also provide biased estimates of the effect of marker genotypes on the secondary trait under the alternative hypothesis where there is a direct effect of the marker on the secondary trait.

Richardson et al. [Richardson, et al. 2007] recently showed that if an exposure (in the GWAS context: marker genotype) and a secondary trait are each independently associated with a disease trait, then estimates of exposure-secondary trait association are typically biased. In response, we argued [Kraft 2007] that for binary genotypes and binary secondary traits this is the only situation where the odds ratio relating the secondary trait to genotype in the ascertained sample differed from the same odds ratio in the general population. In other words, if the marker is not associated with the primary disease or the secondary trait is not associated with the primary disease, the secondary trait-marker genotype odds ratio from the case-control study is not biased. Here we extend this result to general (ordinal, categorical) genotypes and general (ordinal, categorical, continuous) secondary traits. We demonstrate that bias can occur if the secondary trait is a cause of the primary disease. We show that common analytical approaches (including the common practice of restricting to controls) are not always effective at eliminating bias, and may in some circumstances increase the amount of bias observed. We illustrate that the degree of this bias is dependant on the rarity of the primary disease and the strength of the association between the secondary and primary traits as well as the association between the tested marker and the primary trait.

In the setting of most GWAS, where the magnitudes of the marker-phenotype association are often low, common analytical approaches will have appropriate Type I error rates and good power. Moreover, replication in further studies that have not been ascertained on the basis of the primary trait will help reduce the risk of false positives due to ascertainment bias. When the strength of the association between the secondary and primary traits is high, however, and the marker is thought to be associated with the primary trait – see for example the recent series of papers regarding the interrelatedness of 15q24/15q25.1, smoking behavior and lung cancer [Amos, et al. 2008; Chanock and Hunter 2008; Hung, et al. 2008] Thorgeirsson, et al. 2008] – special care will be needed to avoid bias in estimating the effect of the marker on the secondary trait. We address how to handle this type of situation.

Richardson et al. [Richardson, et al. 2007] also proposed using inverse-probability-of-sampling weighted (IPW) regression to estimate genotype-secondary trait association when case and control sampling fractions are available. These sampling fractions will be available for case-control studies nested within a prospective cohort, for example [Langholz, et al. 1999]. We illustrate why this approach provides unbiased estimates of genotype-secondary trait association even when both the genotype and secondary trait are independently associated with primary disease outcome and verify that it does so via simulation. We also investigate the relative power for IPW regression and commonly-used analyses in situations where the latter provide valid (or nearly valid) tests.

The outline of the remainder of this paper is as follows. In the first section, we investigate the circumstances under which commonly-used analyses that either ignore case-control ascertainment or stratify on disease status provide valid tests of the null hypothesis of no direct marker-secondary trait association and the circumstances where they provide unbiased estimates of marker-secondary trait association. We also describe IPW regression and provide some motivation for why it provides valid tests and unbiased estimates. In the second section we quantify Type I error rates, power, and bias for commonly-used analyses and IPW regression via simulation. In the third section we illustrate the various methods by applying them to a study of the association between a SNP in fibroblast growth factor receptor 2 (FGFR2 [MIM 176943]) and mammographic density in a sample of breast cancer cases and controls. Finally, we discuss the implications of our qualitative and quantitative results for the design and analysis of GWAS and candidate gene studies of secondary traits using samples ascertained on the basis of another trait.

Type I error rate and bias: qualitative results

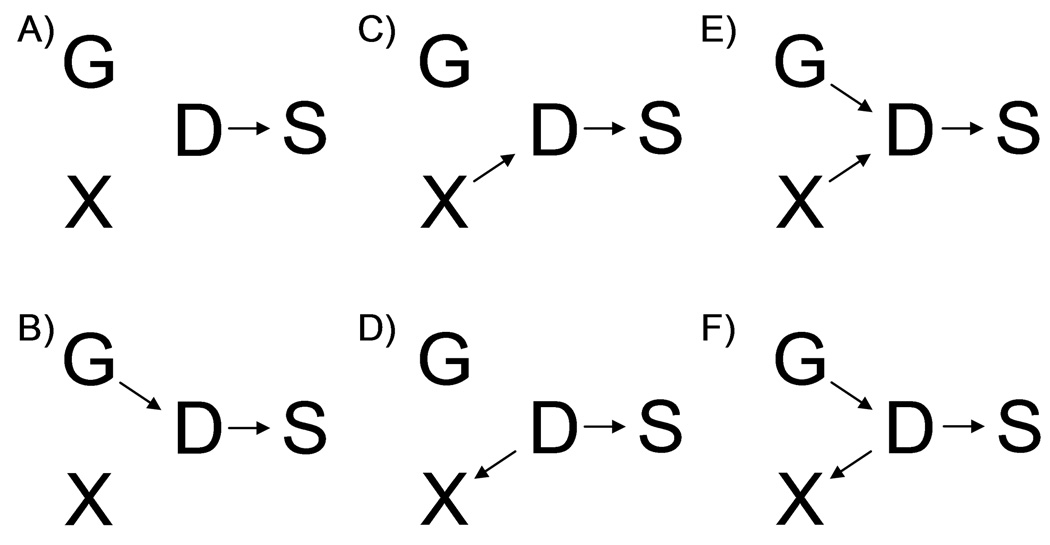
Figure 1 presents directed acyclic graphs (DAGs) for the joint, cross-sectional distribution of marker genotype(s) G, secondary trait X, primary (disease) phenotype D, and ascertainment (sampling) indicator S in the study base (e.g. underlying cohort for a nested case-control study). Here S=1 if a subject was selected to be in the case-control study, and S=0 otherwise. We use these DAGs as convenient representations of the joint G, X, D, and S distribution, based on conditional probabilities and assumptions of conditional independence [Greenland, et al. 1999]. For example, the single arrow from D to S implies that S is independent of G and X, conditional on D. This is a reasonable assumption in many cases, but may not be true. (If participation rates vary by ethnicity, for example, then ascertainment may be associated with both D and G; or the ascertainment scheme may directly depend on both D and X, for example if controls in a prostate cancer study are required to have low PSA levels [Eeles, et al. 2008].) We also assume there are no measured or unmeasured confounders of the G-X relationship. It is possible these exist—again perhaps due to population stratification—but our goal here is to determine when the case-control sampling design per se induces bias in measures of genotype-secondary trait association. Finally, we assume there are no arrows leading from X, D, or S into G, based on the directionality of any causal relationships among G, X, and D (genetic variation causes traits, not vice versa).

Figure 1.

Directed Acyclic Graphs (DAGs) describing the joint probabilities and conditional independence structure for genotype (G), disease status (D), secondary trait (X), and sampling indicator (S) for the six scenarios described in the text.

We can make inferences about the independence or non-independence of G and X conditional on D or S using the topology of these DAGs and the following simple rules [Lauritzen, et al. 1990] Robins, et al. 2001]. We create a "moralized ancestral graph" for X and G and a set of conditioning variables C by first removing any variables (and any corresponding edges) not in AN[{X,G} ∪ C]. Here AN[{X,G} ∪ C] denotes the set of ancestors of variables in {X,G} ∪ C, where a variable is an ancestor of a second variable if there is a directed path from the first to the second. We then connect any two variables that share a common child (i.e. there is an arrow from each into a third variable) with a non-directed edge. (The graph is "moralized" because all parents are "married.") Therefore, in scenario E the moralized ancestral graph for X and G conditional on S would have a line connecting G and X to indicate that they share a common child (D); scenario C, however, would have no such line as G is not a cause of D in scenario C.

It can be shown that G and X are independent conditional on a set of variables C if and only if any path from G to X in the moralized ancestral graph passes through some variable in C [Lauritzen, et al. 1990; Robins, et al. 2001]. In scenarios A, B, C and D in Figure 1, there is no path from G to X in the moralized ancestral graph, so commonly-used analyses that condition on S (by restricting to a case-control sample but otherwise ignoring ascertainment) or condition on D and S (by including case-control status as a covariate in a regression model, or by restricting analysis to cases or controls) provide valid tests of the null hypothesis of G-X independence. In scenario E, G and X are connected by an edge in the moralized ancestral graphs conditional on S or {S,D}, so none of the commonly-used analyses of case-control data provide valid tests of the null hypothesis. In scenario F, the analysis that conditions on S but not D (e.g. regressing X on G in a case-control sample but ignoring ascertainment) does not provide a valid test of the null hypothesis of no direct effect of G on X, while analyses that condition on both S and D (by stratifying on case-control status or restricting to cases or controls) do provide valid tests of this hypothesis.

We note that for prospectively collected X (e.g. for nested case-control studies where information on dietary patterns or anthropometry or plasma biomarkers et cetera are collected at baseline on a cohort of disease-free subjects) scenarios D and F are unlikely (but not impossible: some of the cohort may have had undiagnosed disease at baseline). These two scenarios are more likely when X is collected retrospectively, after a subject's diagnosis (as in a classic case-control study); "reverse causality" is a concern in this context. Subject matter considerations may also rule out some of these scenarios; for example, onset of menarche predates diagnosis with breast cancer by several decades, so scenario F where disease status causes age at menarche in the general population is unrealistic.

These qualitative results on presence or absence of bias under the null can also be derived using the rules of conditional probability—in fact the results on DAGs and conditional independence used in the previous paragraphs are based on these rules [Lauritzen, et al. 1990; Robins, et al. 2001]. In Appendix 1 we use the basic rules of probability to infer the presence or absence of bias under the alternative, when there is a direct effect of genotype on the secondary trait (an arrow from G to X). Conclusions about the presence or absence of bias in Scenarios A-F under the null or alternative summarized in Table I. Neither these calculations nor the DAGs are able to clearly illustrate the potential magnitude of the bias; therefore, we investigate the magnitude of bias via simulation in the next section.

Table I.

Presence or absence of bias in measures of marker-secondary trait association under the null and alternative hypotheses of commonly-used analyses that condition on case-control ascertainment or disease status

		Conditioning event C
		S1	{S,D}2
Scenario A	Null	No Bias	No Bias
	Alternative3	No Bias	No Bias
Scenario B	Null	No Bias	No Bias
	Alternative	No Bias	No Bias
Scenario C	Null	No Bias	No Bias
	Alternative	Bias4	Bias
Scenario D	Null	No Bias	No Bias
	Alternative	Bias	Bias
Scenario E	Null	Bias	Bias
	Alternative	Bias	Bias
Scenario F	Null	Bias	No Bias
	Alternative	Bias	Bias

¹Conditions only on ascertainment, S=1; e.g. analyses that ignore case-control sampling

²Conditions on ascertainment (by restricting to case-control sample) and case-control status D, e.g. analyses restricted to controls (or cases) or stratified by case-control status

³Relationships among G, X and D as in the corresponding null scenario, with the addition of a directed edge from G to X

⁴Measures of the G–X relationship conditional on C may not reflect the G–X relationship in the general population

Finally, the DAGs in Figure 1 also provide some insight into how IPW regression removes any bias induced by sampling conditional on D. If G and X were available on the entire study base, then regressing X on G (and not conditioning on either D or S) provides a valid test of the null hypothesis of G-X independence in scenarios A through E, because the corresponding moralized ancestral graphs do not contain a path from G to X. (Scenario F is a special case where X and G are marginally associated, because G influences X through the intermediate D.) Loosely, IPW approximates the study base by upweighting each sampled subject so that he or she stands in for multiple individuals in the study base. For example, say there are 10,000 individuals in the study base, of whom 500 have the disease. Genotype and secondary trait information are collected on a case-control sample consisting of all 500 cases and 1,000 randomly selected controls. Then in an IPW analysis, each case stands in for his- or herself, while each control represents his- or herself and 8.5 other controls. Thus IPW regression "recreates" the study base and allows for unbiased estimation of the G-X association. A variance correction is needed to account for the fact that subjects in the case-control sample are "stand-ins" for multiple subjects in the study-base; this correction is easily implemented in standard software (Appendix 2). Although our discussion of IPW regression has been rather heuristic, we note that the procedure (and corresponding variance corrections) can be placed on solid theoretical grounds by considering the case-control study as a two-stage design [Reilly and Pepe 1995; Siegmund, et al. 1999] or missing data problem [Robins 1995; Robins, et al. 1995; Wacholder 1996].

Type I error rate and bias: quantitative results (simulation study)

To quantify the power and bias of commonly-used analyses and IPW regression for secondary traits in a case-control sample, we simulated case-control studies drawn from an underlying cohort of size n. Diallelic genotypes G_i for subjects i=1,…,n were sampled assuming the cohort was in Hardy Weinberg Equilibrium with a minor allele frequency of 0.13 (carrier prevalence of 0.25). We focused our simulation study on the prospective scenarios in Figure 1 (A, B, C and E), so we sampled the continuous trait X_i conditional on G_i. X_i was drawn from a normal distribution with mean=β_XG Z(G_i) and standard deviation=1, where Z(G_i) was an additive coding for the genotype (Z(G_i)=number of minor alleles carried by subject i). Disease status D_i was sampled conditional on G_i and X_i as a Bernoulli random variable with logit{P(D_i=1|X_i,G_i)} = β₀+β_DG G_i+ β_DX X_i. Case-control samples were generated by sampling all n₁ cases from the simulated cohort and randomly sampling n₁ controls from the n₀=n-n₁ disease-free subjects.

We simulated 108 scenarios, varying four parameters: disease prevalence κ^∈ {0.001,0.01,0.10,0.20}; the percent of variance in X explained by G = r²_XG^∈{0, 0.005, 0.01}; the increase in log odds of disease per copy of the minor allele = β_DG^∈ {0, log(1.7)/2, log1.7}; and the increase in log odds of disease per unit change in X = β_DX^∈ {0,log(2)/2,log(2)}. The mean change in X per copy of the minor allele (β_XG) and the baseline odds parameter β₀ were chosen to be consistent with r²_XG and κ, respectively. We varied the underlying cohort size n so that on average approximately n₁=1,000 cases and n₀=n₁=1,000 controls were sampled in all scenarios. A total of 5,000 replicate data sets were simulated for each scenario.

We conducted the following seven analyses for each simulated data set:

1. Full cohort analysis: simple linear regression of X on G in the full cohort.

2. "Unadjusted" case-control analysis: simple linear regression of X on G in the case-control sample (ignoring D).

3. "Adjusted" case-control analysis: regress of X on G and an indicator for case-control status D in the case-control sample.

4. Controls only: simple linear regression of X on G among controls.

5. Cases only: simple linear regression of X on G among cases.

6. Joint analysis: regress X on G, an indicator for D, and the product interaction term D×G; test the joint null hypothesis that there is no main effect of G and no D×G interaction (leads to a 2 d.f. test for association between X and G [Kraft, et al. 2007]).

7. IPW regression: regress X on G using weights w₁=1 for cases and w₀=n₀/n₁ for controls and apply appropriate variance correction (Appendix 2).

The bias of each of the seven methods for each condition was obtained by subtracting the expected value β_XG from the mean estimated β_XG. The probability of rejecting the null hypothesis under each of the methods and scenarios was estimated when applying nominal significance thresholds of α=0.05, 0.01, and 0.001.

Type I error and power

Table II and Table III summarize the Type I error rates across 18 of the null scenarios (β_XG=0) we considered. (Results for κ=0.001 and κ=0.20 are not shown but similar to those for κ=0.01 and κ=0.10, respectively). As predicted by the theoretical considerations in the previous section, all of the analysis methods for the case-control data had appropriate Type I error rate as long as either β_DX=0 or β_DG =0, and the IPW regression analysis had appropriate Type I error rates for all of the scenarios considered. For rare disease (κ=0.01; Table II), we did not detect any inflation in Type I error for analyses that condition on case-control status (Analyses 3–6) even when both X and G directly influence disease; for more common disease (κ=0.10; Table III) we did detect an inflation in Type I error rates for these analyses when X and G each directly influence disease. "Unadjusted" tests (Analysis 2) had noticeably inflated Type I error rates whenever β_DX≠0 and β_DG≠0, although the inflation decreases as the disease becomes more common (and the case-control sample becomes more representative of the cohort as a whole).

Table II.

Type I error rates for six analyses of marker-secondary trait association in a case-control sample (and an analysis in the full underlying cohort); rare disease (1% prevalence)

		ORDG=1			ORDG=1.3			ORDG=1.7
		βDX=0	βDX=ln(2)/2	βDX=ln2	βDX=0	βDX=ln(2)/2	βDX=ln2	βDX=0	βDX=ln(2)/2	βDX=ln2
		ORDX=1	ORDX=1.4	ORDX=2	ORDX=1	ORDX=1.4	ORDX=2	ORDX=1	ORDX=1.4	ORDX=2
1. Full cohort	α=0.05	0.049	0.051	0.049	0.051	0.053	0.051	0.049	0.057	0.053
	α=0.01	0.009	0.010	0.008	0.010	0.011	0.013	0.011	0.011	0.013
	α=0.001	0.001	0.001	0.001	0.002	0.001	0.001	0.002	0.001	0.002
2. Unadjusted	α=0.05	0.052	0.053	0.049	0.050	0.078	0.152	0.051	0.172	0.469
	α=0.01	0.010	0.011	0.009	0.011	0.022	0.050	0.011	0.059	0.251
	α=0.001	0.001	0.001	0.001	0.001	0.003	0.010	0.002	0.013	0.081
3. Adjusted	α =0.05	0.052	0.052	0.051	0.050	0.049	0.050	0.049	0.053	0.049
	α=0.01	0.010	0.009	0.008	0.011	0.011	0.009	0.011	0.013	0.010
	α=0.001	0.001	0.001	0.002	0.002	0.001	0.001	0.002	0.001	0.001
4. Controls only	α =0.05	0.050	0.052	0.047	0.048	0.046	0.049	0.053	0.052	0.052
	α=0.01	0.012	0.010	0.010	0.010	0.009	0.007	0.011	0.010	0.011
	α=0.001	0.001	0.001	0.002	0.002	0.001	0.001	0.001	0.001	0.001
5. Cases only	α =0.05	0.056	0.043	0.048	0.046	0.052	0.052	0.051	0.049	0.052
	α=0.01	0.011	0.010	0.010	0.009	0.008	0.013	0.010	0.010	0.009
	α=0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001
6. Joint analysis	α =0.05	0.056	0.049	0.046	0.046	0.048	0.050	0.053	0.054	0.052
	α=0.01	0.010	0.010	0.010	0.012	0.009	0.008	0.011	0.010	0.010
	α=0.001	0.001	0.001	0.002	0.002	0.001	0.001	0.001	0.001	0.000
7. IPW regression	α =0.05	0.058	0.046	0.048	0.049	0.054	0.055	0.054	0.049	0.051
	α=0.01	0.010	0.010	0.011	0.010	0.009	0.014	0.012	0.011	0.010
	α=0.001	0.001	0.002	0.002	0.002	0.001	0.002	0.001	0.001	0.001

Note: Italicized cells represent scenarios that qualitative arguments suggest may be biased.

Table III.

Type I error rates for marker-secondary trait association; common disease (10% prevalence)

		ORDG=1			ORDG=1.3			ORDG=1.7
		βDX=0	βDX=ln(2)/2	βDX=ln2	βDX=0	βDX=ln(2)/2	βDX=ln2	βDX=0	βDX=ln(2)/2	βDX=ln2
		ORDX=1	ORDX=1.4	ORDX=2	ORDX=1	ORDX=1.4	ORDX=2	ORDX=1	ORDX=1.4	ORDX=2
1. Full cohort	α=0.05	0.052	0.051	0.052	0.052	0.045	0.049	0.051	0.051	0.047
	α=0.01	0.010	0.012	0.010	0.010	0.010	0.011	0.009	0.012	0.008
	α=0.001	0.002	0.002	0.001	0.001	0.001	0.001	0.001	0.001	0.002
2. Unadjusted	α=0.05	0.051	0.052	0.047	0.055	0.059	0.077	0.052	0.084	0.148
	α=0.01	0.009	0.008	0.009	0.010	0.012	0.025	0.013	0.021	0.046
	α=0.001	0.001	0.001	0.000	0.001	0.001	0.003	0.001	0.003	0.009
3. Adjusted	α=0.05	0.050	0.050	0.050	0.056	0.056	0.065	0.050	0.081	0.170
	α=0.01	0.010	0.009	0.010	0.010	0.011	0.015	0.012	0.020	0.058
	α=0.001	0.001	0.000	0.001	0.001	0.001	0.003	0.001	0.003	0.009
4. Controls only	α=0.05	0.048	0.055	0.053	0.048	0.051	0.064	0.050	0.071	0.136
	α=0.01	0.011	0.013	0.008	0.011	0.010	0.013	0.009	0.015	0.043
	α=0.001	0.001	0.001	0.001	0.001	0.000	0.002	0.001	0.002	0.007
5. Cases only	α=0.05	0.045	0.050	0.049	0.049	0.051	0.051	0.054	0.062	0.084
	α=0.01	0.008	0.011	0.010	0.011	0.010	0.011	0.011	0.016	0.020
	α=0.001	0.002	0.001	0.001	0.001	0.001	0.001	0.002	0.001	0.003
6. Joint analysis	α=0.05	0.046	0.053	0.041	0.050	0.052	0.051	0.053	0.064	0.116
	α=0.01	0.010	0.010	0.006	0.010	0.008	0.010	0.011	0.014	0.033
	α=0.001	0.001	0.001	0.000	0.001	0.000	0.002	0.001	0.002	0.004
7. IPW regression	α=0.05	0.047	0.051	0.052	0.053	0.052	0.048	0.051	0.051	0.050
	α=0.01	0.009	0.011	0.010	0.012	0.012	0.011	0.012	0.010	0.009
	α=0.001	0.002	0.001	0.001	0.001	0.001	0.002	0.001	0.001	0.002

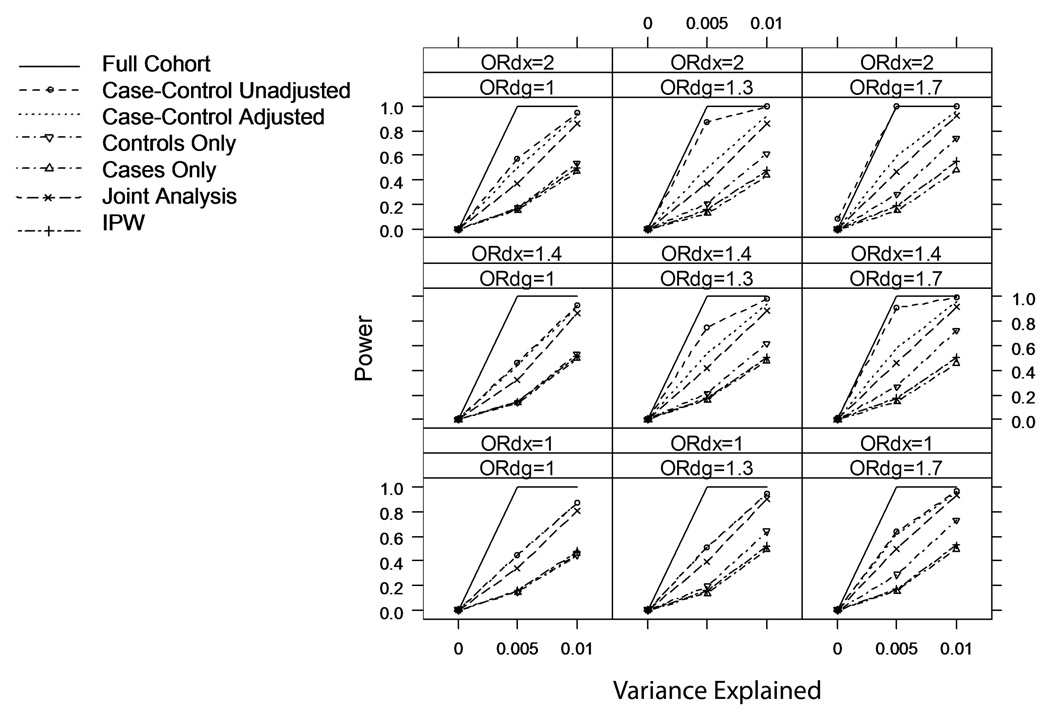
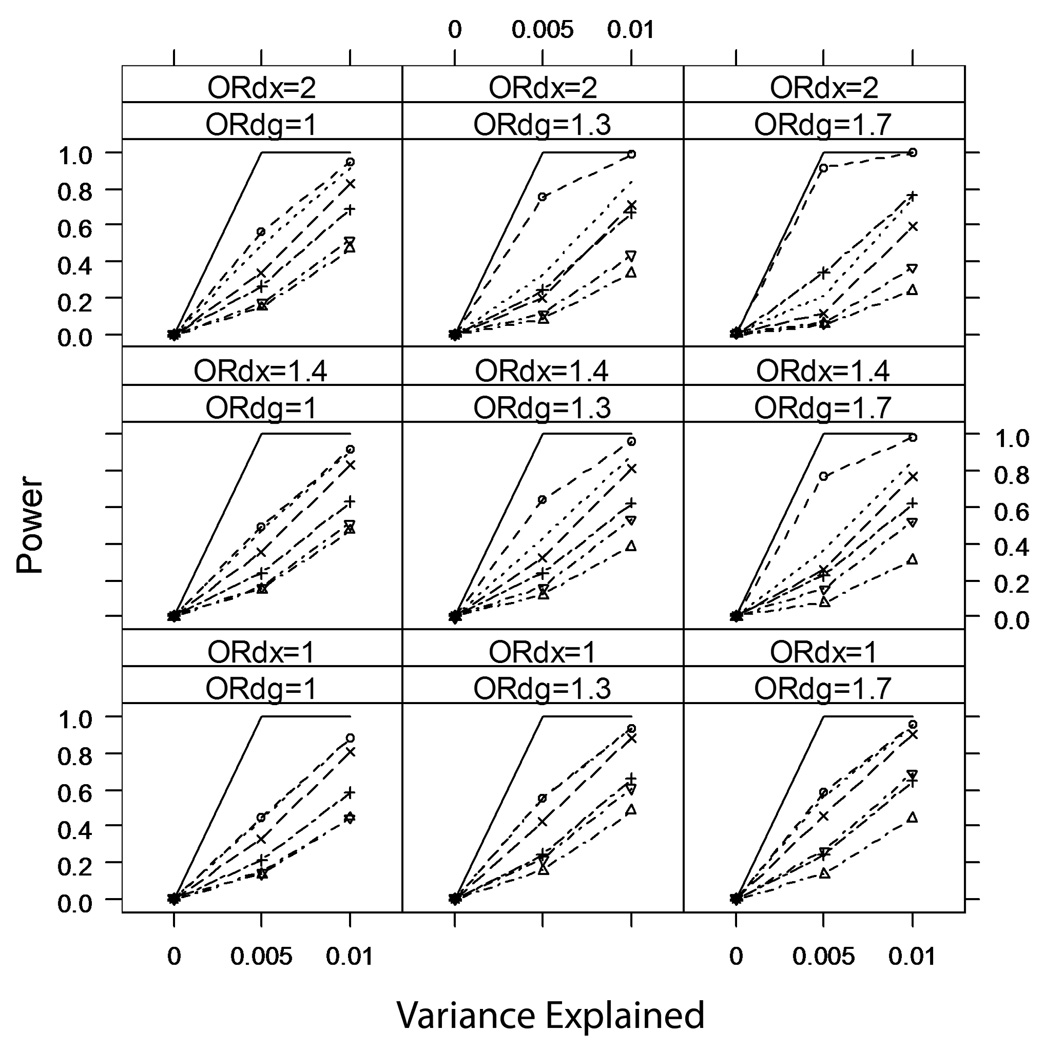
Figure 2 and Figure 3 summarize the power of tests based on these seven analyses over all scenarios with κ=0.01 and κ=0.10. Not surprisingly, analyses restricted to cases or controls generally have less power than any of the analyses that use the entire case-control sample. Due to the relatively large variance in parameters estimates from IPW regression, tests from Analysis 7 generally have the lowest power of the analyses that use the entire case-control sample. For more common disease (κ=0.10 or 0.20 [not shown]), there are scenarios (namely when β_DX≠0 and β_DG≠0) where IPW has greater power than analyses that adjust for case-control status (Analyses 3 and 6), because the adjusted analyses are biased towards the null in these scenarios (Figure 4). However, the IPW regression analysis still has lower power than the unadjusted analysis (Analysis 2) in these scenarios. This is an unfair comparison, as the unadjusted analysis has inflated Type I error rate for tests of β_XG=0 in these scenarios, but we note that the inflation is small (Table II) and the unadjusted analysis provides a valid test of the joint null hypothesis β_XG=0 and β_DG=0.

Figure 2.

Power of six analyses of marker-secondary trait association in a case-control sample (and an analysis in the full underlying cohort); rare disease (prevalence κ=0.01), nominal Type I error rate α=0.001.

Figure 3.

Power of six analyses of marker-secondary trait association in a case-control sample (and an analysis in the full underlying cohort); common disease (prevalence κ=0.10), nominal Type I error rate α=0.001.

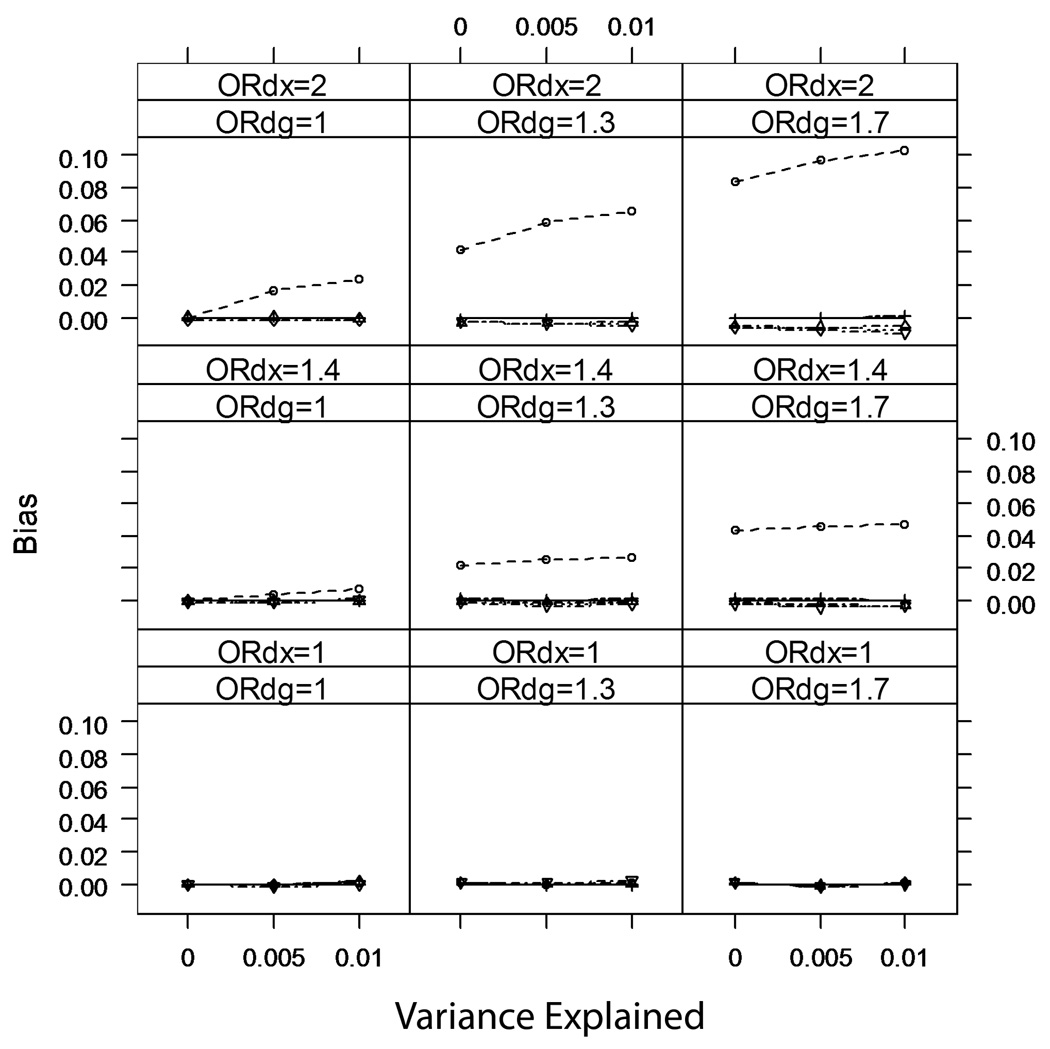
Figure 4.

Average bias of analyses of marker-secondary trait association; rare disease (prevalence κ=0.01).

Among the commonly-used analyses, the unadjusted analysis (Analysis 2) always has greater power than any adjusted analyses (Analyses 3–6), although we caution that for rare disease (κ=0.01) the unadjusted analysis can have a strikingly inflated Type I error rate whenever both β_DX≠0 and β_DG≠0.

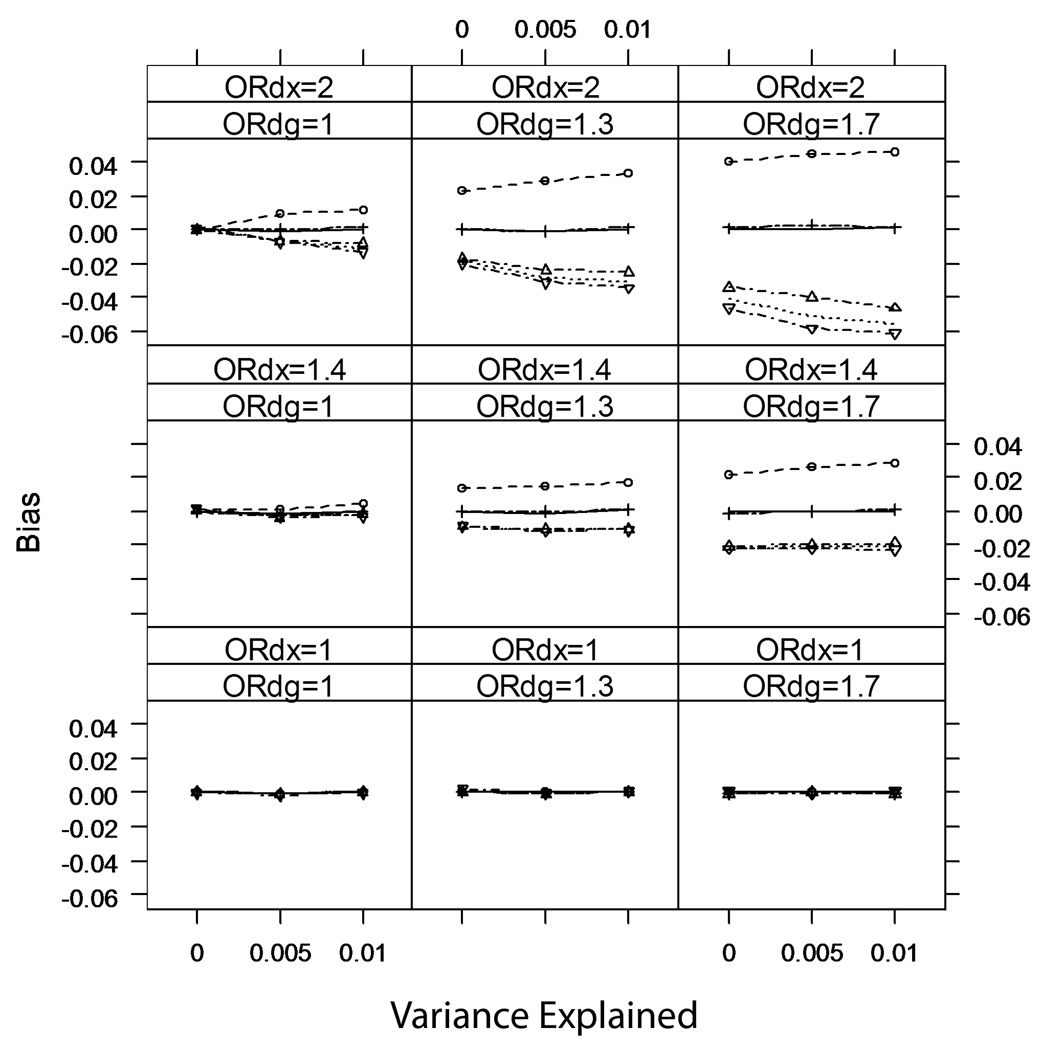
Bias

Figure 4 and Figure 5 show the average bias over the simulated scenarios for rare (κ=0.01) and common (κ=0.10) disease, respectively. As predicted, none of the analyses are biased when β_DX=0. When β_DX≠0, the commonly used analyses can be biased, although for rare disease, methods that condition on case-control status (Analyses 3–6) have no perceptible bias (p>0.05) when β_DG=0. The bias for the unadjusted method is small (magnitude<3.5% of the true β_XG) when β_DX is modest (a 1.3-fold increase in disease odds per standard deviation change in X). When both the secondary trait and the marker are independently associated with disease risk (β_DX≠0 and β_DG≠0), the unadjusted analysis can be quite biased.

Figure 5.

Average bias of analyses of marker-secondary trait association; common disease (prevalence κ=0.10).

For common disease, all methods except IPW regression have detectable bias when both β_DX≠0 and β_DG≠0. The unadjusted analysis overestimates β_XG, while the adjusted analyses underestimate β_XG. In particular, the analysis restricted to controls has the greatest magnitude of bias among the adjusted analyses. This may seem counter-intuitive; but we note that while for rare disease controls are fairly representative of the underlying population (even when β_DX≠0 and β_DG≠0), for common disease controls will not be representative of the underlying population if β_DX≠0 and β_DG≠0.

IPW regression has no detectable bias in any of the situations we simulated.

Example: FGFR2 and mammographic density

To illustrate the application of these methods, we present several tests for association between the FGFR2 SNP rs2981582 and pre-diagnostic mammographic density in a set of 790 breast cancer cases and 1,140 controls from the Nurses' Health Study. This study was approved by the Committee on the Use of Human Subjects in Research at Brigham and Women’s Hospital.

Both FGFR2 rs2981582 and mammographic density are known to be risk factors for breast cancer, and in fact both are significantly associated with risk in this data set [Easton, et al. 2007; Hunter, et al. 2007]. The crude, marginal per-minor-allele odds ratio of breast cancer risk for rs2981582 is 1.32 (CI: 1.16–1.51), and the crude, marginal odds ratio comparing the 80th percentile of mammographic density in controls to the 20th percentile was 2.33 (CI: 1.91–2.86). The association between rs2981582 and breast cancer risk remains significant (p<0.0001) after adjusting for mammographic density, and the per-allele odds ratio changes little (OR: 1.34; CI: 1.17–1.52). Thus, based on our qualitative and quantitative results, this is a situation where the commonly-used methods may provide biased estimates of the association between FGR2 rs2981582 and mammographic density. However, as this sample was nested within a cohort study, we can estimate the case and control sampling fractions and conduct an IPW regression analysis.

The underlying cohort for this nested case-control study consisted of 29,625 women in the Nurses' Health Study who were cancer-free when they gave a blood sample from 1989 to 1990. Of the 934 eligible women in this cohort who developed breast cancer by 1998, 790 had available genotype and mammographic density data. Controls selected for genotyping were matched to individual cases on age and menopausal status at blood draw and were required to be breast-cancer-free up to the case's date of diagnosis; 1,440 genotyped controls had available mammographic density data. The sampling fractions by age, menopausal status at blood draw and case-control status are given in Table IV. Because controls were matched to cases on age and menopausal status, we use these stratified sampling fractions in the IPW regression analysis. (Controls were also matched on post-menopausal hormone use at blood draw and other variables related to plasma biomarker ascertainment--e.g. time of day of blood draw; for simplicity we ignore these factors in this illustration.)

Table IV.

Sampling fractions for the FGFR2-mammographic density association analysis

	Cases in blood cohort		Cases in blood cohort with genotypes and mammographic density		Case sampling fractions		Controls in blood cohort		Controls in blood cohort with genotypes and mammographic density		Control sampling fractions
Age	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
40–44	10	4	8	4	0.80	1.00	577	121	14	1	0.02	0.01
45–49	96	26	83	21	0.86	0.81	3710	1309	117	31	0.03	0.02
50–54	95	80	83	73	0.87	0.91	2840	2954	94	89	0.03	0.03
55–59	26	183	23	157	0.88	0.86	1037	5045	28	227	0.03	0.04
60–64	1	218	1	183	1.00	0.84	396	5445	0	285	-	0.05
65–	0	195	0	154	-	0.79	179	5054	0	254	-	0.05

We regressed square-root transformed mammographic density on rs2981582 under an additive model using six different methods (Analyses 2–7, listed above); the results are summarized in Table V. All of these methods yielded similar effect estimates, suggesting no direct association between rs2981582 and mammographic density. This is consistent with the results from our simulation study, which suggest that for a rare outcome and little or no association between the tested marker and the secondary trait, Analyses 3–7 have no detectable bias, while the bias for unadjusted case-control analysis (Analysis 2) is small, leading to a slight inflation in the Type I error rates. As expected, Analyses 2 and 3 (unadjusted and naively adjusted analyses) had the smallest standard errors, while methods that reduce sample size (case-only and control-only analyses) or adjust for weighting (IPW) yielded much larger standard errors. It is important to note that not applying the proper variance correction (Appendix 2) in the IPW analysis would have falsely deflated our standard error from 0.096 to 0.073.

Table V.

Association between FGFR2 rs2981582 and mammographic density in a Nurses' Health Study breast-cancer case-control sample

Analytic Approach	Mean Difference	Standard Error	P-value
2. Unadjusted analysis	−0.0017	0.0681	0.97
3. Adjusted analysis	−0.0577	0.0672	0.39
4. Controls only	−0.0339	0.0922	0.71
5. Cases only	−0.0864	0.0979	0.37
6. Joint analysis  (controls)	−0.0339	0.0922	0.14
(cases)	−0.0864	0.0979
7. IPW regression	0.0055	0.0960	0.95

Note: Mean difference is the per-minor-allele change in mean square-root transformed mammographic density, estimated using each of the six approaches outlined in the text.

Discussion

We have shown analytically (and verified through simulation) that under the null hypothesis of no direct association between marker genotypes and a secondary trait, several simple, commonly-used analyses of genotype-secondary trait association in case-control samples have appropriate Type I error rates as long as either the marker or the secondary trait is not associated with disease risk in the study base. In particular, the naive analysis that ignores case-control ascertainment and treats the sample as if it were cross-sectional provides a valid test in these situations, as does the analysis that simply includes case-control status as a covariate in a regression of a secondary trait on marker genotype, and the analysis restricted to controls. Moreover, when the secondary trait is independent of disease risk, these simple analyses provide unbiased estimates of measures of marker-secondary trait association.

These results have important implications for genome-wide association scans of secondary traits, both those that have already been conducted—which have typically used one of these simple analyses—and those yet to come. For those secondary traits that are not associated with disease risk, these simple analyses are easily conducted using standard software for genome-wide association analyses (e.g. PLINK [Purcell, et al. 2007]) and provide valid tests and unbiased estimates of the marker-secondary trait association in the study base for all markers, even those associated with disease risk. There is no need to restrict analysis to controls to preserve test validity or remove bias—which is encouraging, as restricting to controls greatly reduces sample size and power.

For those secondary traits that are associated with disease risk—often the case, as researchers are interested in discovering the variants that influence risk factors for disease (e.g. mammographic density or age at menarche for breast cancer)—these standard approaches provide valid tests as long as the tested marker is not independently associated with disease risk (Figure 1, Scenarios A, C and D). Considering that the vast majority of tested markers are in fact not independently associated with disease risk, these simple analyses will provide near-nominal control of the expected number of false positive tests across all tested markers. For example, if 500 out of 500,000 markers are truly associated with disease risk, and we assume a ten-fold increase in the nominal Type I error rate of 0.001 for these 500 markers (larger than any inflation we observed in our simulation studies), then we expect 499,500×0.001 + 500×0.010 = 504.5 significant tests instead of 500. Furthermore, any association seen in the initial scan should be replicated in an appropriate independent sample [Chanock, et al. 2007]—preferably a cross-sectional sample, or perhaps a case-control study for a disease not associated with the secondary trait. Similarly, the fact that these simple analyses provide biased estimates of the marker-secondary trait association in the general population for those few makers that are associated with both disease risk and the secondary trait is not of vital importance in the genome-wide scan context, where the primary goal is to discover loci associated with the secondary trait. Larger, appropriately-designed follow-up studies will be required to characterize the marker-secondary trait association in different populations.

The problem of increased Type I error rate for these simple analyses is arguably even less of an issue for meta-analyses of multiple genome-wide studies, some of which were originally case-control studies for different diseases related to the secondary trait, some of which were case-control studies for disease unrelated to the secondary trait, and some of which were cross-sectional or originally designed to study the secondary trait (i.e. the trait may be secondary for some studies and primary in others). In this situation, the bias under the null hypothesis will be reduced by averaging the biased estimates from some studies with the unbiased estimates from others. (Under the alternative, some of the heterogeneity in measures of marker-secondary trait association may be due to differences in ascertainment across studies.)

Throughout this paper we have assumed that the probability of being sampled depends only upon case-control status. As we mentioned above, this will not be the case in some situations. However, in these situations the corresponding DAG can be drawn and inferences about the presence or absence of bias under the null hypothesis can be made using the rules we have outlined. For example, if controls are sampled conditional on the secondary trait (e.g. a prostate cancer case-control study where controls are required to have low PSA levels), the DAGs in Figure 1 can be modified by adding a directed arrow from X to S.

An earlier letter [Kraft 2007] examining the presence of bias in measures of association between marker genotypes and a secondary trait in case-control studies was restricted to the special case where the marker genotype and secondary trait were binary, and the measure of interest was the genotype-secondary trait odds ratio. The qualitative arguments we have made in this paper (based either on DAG theory or conditional probabilities) make no assumptions about the distributional forms of the marker genotypes G or secondary trait X. In particular, G could represent an additive, dominant, or general coding of a marker genotype, or indeed some coding for a multi-marker genotype, while X could be binary, categorical or continuous; for continuous X we did not assume normality or any other particular form for the distribution.

In contrast to scans testing many markers for association with a secondary trait, the bias induced by the case-control design will be a concern when the goal of the study is characterizing the relationship between a marker and a secondary trait that are both known to influence disease risk. In particular, some loci may have pleiotropic effects and influence disease risk both through their association with the secondary trait and another independent causal mechanism. For example, it is of great current interest to determine whether variants in the 15q25.1 region are associated with lung cancer indirectly, because of their association with smoking behavior, or if they are also associated with lung cancer along a second, distinct causal pathway [Chanock and Hunter 2008]. We have shown that when sampling fractions are known, IPW regression provides unbiased estimators of measures of association between the marker and secondary trait in case-control studies. Further work is necessary to examine the degree of bias induced using incorrect sampling fractions, or developing more efficient, unbiased methods. Of course, when characterization of the secondary marker-trait association is a primary goal, the analytic problem can be avoided at the design phase; convenience samples from an existing GWAS may not be the best choice. The savings in genotyping costs for a small number of markers may be too small to offset concerns regarding analytic validity.

Appendix 1

In general, the probability of X conditional on G and S in scenarios where there is no edge connecting X to D in the Directed Acyclic Graph is:

$$\text{Pr}(\mathrm{X}|\mathrm{G},\mathrm{S})=\frac{{\displaystyle {\sum }_{\mathrm{D}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X},\mathrm{G})\text{Pr}(\mathrm{X}|\mathrm{G})}}{{\displaystyle {\sum }_{\mathrm{D},\mathrm{X}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X},\mathrm{G})\text{Pr}(\mathrm{X}|\mathrm{G})}}$$ [1]

Under the assumption that Pr(D|X,G)=Pr(D|G) (i.e. in scenarios A and B, or when there is a directed arrow from G to X but no edge connecting X and D) expression [1] reduces to Pr(X|G)—so the distribution of X in the case-control sample is identical to that in the underlying study base. Under the assumption that Pr(X|G)=Pr(X) and Pr(D|X,G)=Pr(D|X) (Scenario C), expression [1] simplifies to:

$$\frac{{\displaystyle {\sum }_{\mathrm{D}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X})\text{Pr}(\mathrm{X})}}{{\displaystyle {\sum }_{\mathrm{D},\mathrm{X}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X})\text{Pr}(\mathrm{X})}}$$

Although this is not identical to the distribution of X in the study base, X remains independent of G, so tests of G-X independence should have valid Type I error rates. However, when there is a directed edge from G to X, expression [1] becomes

$$\frac{{\displaystyle {\sum }_{\mathrm{D}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X})\text{Pr}(\mathrm{X}|\mathrm{G})}}{{\displaystyle {\sum }_{\mathrm{D},\mathrm{X}}\text{Pr}(\mathrm{S}|\mathrm{D})\text{Pr}(\mathrm{D}|\mathrm{X})\text{Pr}(\mathrm{X}|\mathrm{G})}}$$ [2]

which does not in general simplify to Pr(X|G). Thus under the alternative the distribution of G and X in the ascertained sample is not identical to the distribution in the study base, and measures of the G-X association in the case-control sample (or restricted to either controls or cases) will in general be biased, i.e. they will not reflect the G-X relationship in the study base. (The odds ratio relating a binary exposure X to a binary genotype G is one exception to this rule [Kraft 2007].) The magnitude of the bias is not clear from expression [2]; we investigate the magnitude of bias via simulation.

Similar calculations lead to conclusions about the presence or absence of bias in Scenarios A-F under the null or alternative summarized in Table I.

Appendix 2

The following SAS and R code perform IPW regression with appropriate variance correction (via the weight statement in PROC GENMOD or weights option in the geeglm() function. Here id is a unique subject identifier; X is a continuous trait; G is some coding for marker genotypes (e.g. count of minor alleles); and weight is the (known) inverse probability of being sampled into the case-control data set.

SAS

proc genmod data=fgfrw;

• class id;

• model X = G;

• weight weight;

• repeated subject=id;

run;

R

library(geepack)

ipw.fit <- geeglm(X∼G,weights=weight,id=id)