Mechanical Forces of Fission Yeast Growth

Abstract

Mechanical properties of fungal cells participate in the control of cell size, morphogenesis and function [1-4]. Tip growth can be understood by a viscoelastic model in which growth is derived by high internal turgor pressure and cell wall elasticity. To understand how these properties regulate growth in the rod-shaped fission yeast Schizosaccaromyces pombe, we measure key parameters by using femtoliter cylindrical PDMS microchambers with varying elasticity as force sensors for single cells. By buckling cells in these chambers, we determine the elastic surface modulus of the cell wall to be 20.2 ± 6.1 N.m^-1. By analyzing the growth as they push against the walls of the chamber, we derive force-velocity relationships and values for internal effective turgor pressure of 0.85 ± 0.15 MPa and a growth stalling force of 11 ± 3 μN. The behavior of cells buckling under the force of their own growth provides an independent test of this model and parameters. Force generation is dependent on turgor pressure and a glycerol synthesis gene gpd1⁺ (glycerol-3-phosphate dehydrogenase), and is independent of actin cables. This study develops a quantitative framework for tip cell growth and characterize mechanisms of force generation that could contribute, for instance, in fungal invasion into host tissues.

Results and Discussion

Viscoplastic model for fission yeast tip growth

A mechanical view of fungal tip can be described in terms of a viscoelastic model, which has been proposed previously to describe mechanisms of cell shape control and growth in large green algae and plant cells [2, 3, 5-8]. In this model, a high turgor pressure produces the work necessary to deform the new cell wall deposited at cell tips. Growth appears effectively as a viscoplastic process: At a critical value of the pressure, P_c, the wall reaches a threshold strain (the plastic yield strain) and is deformed irreversibly. The growth rate of the cell, v₀, is proportional to the strain in the wall in excess of this threshold, so that:

$$v_0\propto \frac{(P-P_c)}{E_{cw}},$$ (Eq. 1)

where E_cw is the Young's elastic modulus of the wall and P, the total turgor pressure (Figure 1A, see Supplementary material). Here, we provide a test of this mechanical view by experimentally measuring the key parameters and assessing the effect of external forces on growth rates.

Figure 1. Microfabricated chambers as single-cell force sensors for studying the mechanical properties of fission yeast cell.

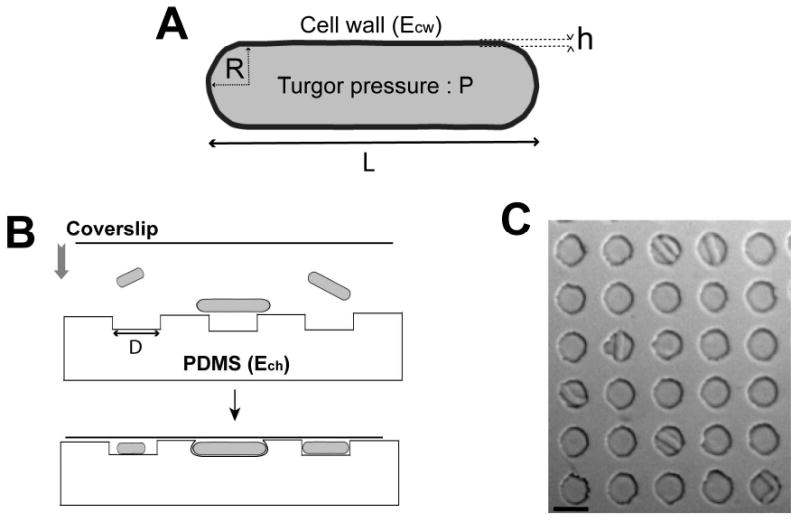
A) Parameters of a fission yeast cell. The cell wall layer has an elastic modulus, E_cw, and a thickness h. The turgor pressure inside the cell is P. The rod-shaped cell has a radius R and a length L. B) Schematic showing how yeast cells are placed into the PDMS chambers. C) Top-view image of several chambers with cells inside. Bar=10μm.

Microfabricated PDMS chambers as force sensors for single cells

We devised microfabricated PDMS chambers as single-cell force sensors for fission yeast cells. Previous approaches to measure those mechanical properties in diverse fungi include assaying the effects of extracellular osmolarity [1, 9, 10], the ability of a cell to penetrate or pierce materials [1, 11], strain gauges and waveguide microscopy, and atomic force microscopy (AFM) [1, 12-16]. On the whole however, definitive quantitative data for these parameters have been lacking, given the significant discrepancies between many of these approaches, as well as caveats and technical complexities associated with each.

PDMS arrays contained about 10000 microfabricated cylindrical chambers, 5μm deep with a diameter D ranging from 10 to 50 μm [17]. We varied the elasticity (Young's modulus, E_ch) of the PDMS, from typically 0.1 to 1.5 MPa by adjusting the ratio of polymer vs. cross-linker (Figure S1). Fission yeast cells were placed between the PDMS array and a glass coverslip and pushed into the chambers by slightly pressing the coverslip (Figure 1B and 1C). We analyzed fission yeast cells of different length between approximately 8 to 25 μm by using a cdc25-22 mutant at 25°C, which grows longer than wildtype cells because of a cell cycle delay in G2 phase. The radius of the cell is largely insensitive to these changes in length and remains around 2μm [18]. As controls, we analyzed cells placed in larger chambers in which the cells did not contact the sides of the chambers (Movie 1). In general, cells that were bent or growing against the edge of the chamber continued in the cell cycle to divide. To test if the stress response pathways are induced in these bent cells, we monitored the stress reporters sty1-GFP and pap1-GFP, which relocalize from the cytoplasm to the nucleus in the presence of osmotic or oxidative stress [19-21]. We noted no marked change in the distribution of these markers when the cells were growing under constraint or even when buckling (Figure S2), indicating that these conditions do not cause high levels of cell stress.

Measuring cell wall elasticity

We first sought to estimate the elasticity of the cell wall. In these experiments, we pushed the cells into chambers smaller than the length of the cells and immediately imaged. In general, in stiff chambers, cells were immediately bent in the chamber, while in softer chambers, the cell deformed the chamber (Figure 2A). As an illustration of the elasticity of the cell wall, in rare cases, cells were observed to pop out of the well and straightened out within seconds, even after being repeatedly pushed back into the well (Movie 2).

Figure 2. Measuring fission yeast cell wall elastic modulus.

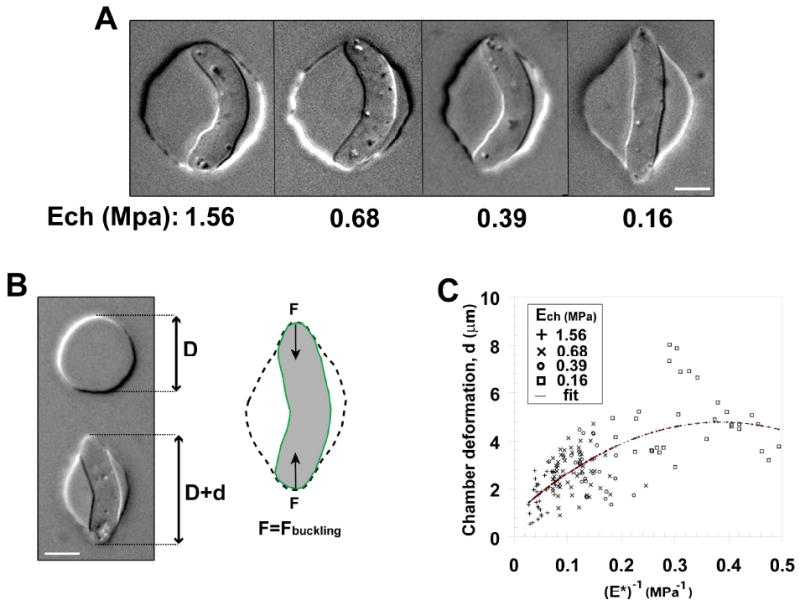
A) Single fission yeast cells with similar cell length were pushed into chambers smaller than the cells. Chambers with decreasing elastic moduli E_ch (from left to right) are shown. Bars = 5μm. B) Illustration of the method used to compute chamber deformation. (Left) The initial chamber diameter, D, is measured on the surrounding chambers (precision better than 5%) and the deformation, d, is measured along the force axis. (Right) The force from the chamber deformation equilibrates the buckling force. Because this buckling force is proportional to the cell wall surface modulus, this method allows for a direct calculation of the cell wall surface modulus at the single cell level. Bar = 5μm. C) Plot of the chamber deformation as a function of the inverse of the scaled chamber elastic modulus (E*, see eq. 4) obtained from 155 single cells. Different symbols correspond to different chamber elastic moduli, as shown in the legend. The fit used is parabolic to account for second order saturations at larger deformation. The imprecision in the measurement is found to be higher than the scattering of the data around the proposed fit. The strain is NM11.

The deformation of the chamber by the cell provided a measurement of the elasticity of the cell wall. For this measurement, we used the buckling transition from a straight shape to a bent shape; this transition is induced by the longitudinal forces exerted by the chamber on the cell. The threshold force for buckling is given by:

$$F_B=\frac{{\pi }^2{R}^{3}h{E}_{cw}}{{L_T}^2},$$ (Eq. 2)

with L_T the distance between cell tips along the force axis, R, the cell's radius and h the cell wall thickness (see supplementary material, [22]). Note that this equation does not include turgor pressure since it is compensated by the tension in the wall. The deformation of the chamber (Figure 2B), d = L_T - D, concomitantly provides a measurement of the force F exerted by the cell on the chamber (see supplementary material):

$$F=\frac{8}{3}{E}_{ch}Rd,$$ (Eq. 3)

The balance of forces F_B=F leads to:

$$d=\left(\frac{3{\pi }^2}{8}\frac{R^2}{{(D+d)}^2{E}_{ch}}\right)E_{cw}h=\frac{E_{cw}h}{E\ast },$$ (Eq. 4)

where we introduced E* as a re-scaled elastic modulus for the chamber. This relation allows for computing the surface modulus of the cell wall, σ_cw = E_cwh (Figure 2B).

We measured the behavior of cells of varying length in chambers of varying diameters and elasticity, allowing us to vary d and E* by an order of magnitude. Figure 2C depicts measurements of 155 cells. Although we obtained a good linear scaling between d and (E*)^-1 at small deformation, at very high deformation saturation was noted; this property may arise from a non-linear elastic response of the material (Figure S1B). We thus used a second order polynomial fit where the linear term corresponds to the surface modulus, and obtained σ_cw=20.2 ± 6.1 N.m^-1. As the thickness of the fission yeast cell wall (h) has been measured by electron microscopy to be around 200 nm [23], our measurements estimate the Young's elastic modulus of the fission yeast cell wall to be : E_cw=101 ± 30 MPa.

This elastic modulus was independent of cell length (correlation coefficient: R²=0.07) and did not vary significantly between interphase and mitotic cells. We note that this measurement corresponds to the elasticity of the side wall in this buckling experiment. However we predict that although the elasticity of the cell tips may be slightly softer than this measured value, to account for localized cell growth, it is likely to be similar, as demonstrated by the near-uniform response of the cell wall to osmotic shock or when pushing against the wall of the chamber (see below).

Force-velocity relationships of cell growth

Next, we sought to measure the force exerted by the growth of single cells, using the chambers of varying stiffness as force sensors. In principle, the maximum force of cell growth can be estimated by measuring the external force required to stall growth, the “stall force.” In these experiments, we introduced into the chambers cells that were initially shorter than the diameter of the chamber. Over time, the cells elongated and when both cell ends contacted the wall of the chamber, the cells pushed against the chamber (Figure 3A and Movie 3). As growth patterns change over the cell cycle, we focused our analysis to only interphase cells growing from both cell tips in a bipolar manner [18]. Depending on the stiffness of the PDMS, the growth of the cells often deformed the chamber from a round into an oval (or a “letter Greek Φ” shape). The force exerted by the chamber increased as the chamber was progressively deformed, much like a spring being stretched. The different rates of growth of the cell and deformation of the chamber provided a measurement of a force-velocity relationship. We established this relation by tracking growth rates prior (free growth= v₀) and after (constrained growth= v) the cell began to deform the chamber at different force (F) (Figure 3B). After the cell began to deform the chamber, we observed a clear decrease in growth rate (Figure 3C). The corresponding force-velocity relationship obtained from tracking 22 individual cells depicted a gradual decrease in growth rates as the external force was increasing (Figure 3C). The external force of the chamber may oppose turgor stress on the cell wall, which leads to an artificial reduction of the effect of turgor and a reduction of the growth rate, so that (see supplementary material):

Figure 3. Force-velocity relations for fission yeast cell growth.

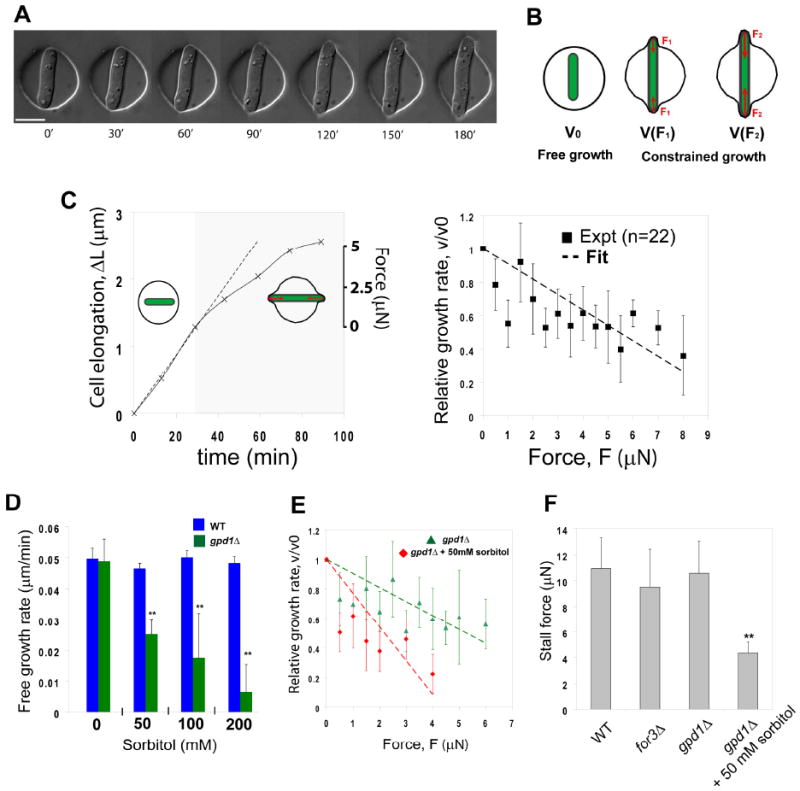
A) Time-lapse sequence of a fission yeast cell growing in and deforming a chamber made of soft PDMS (elastic modulus = 0.16 Mpa). Bar=10μm. B) Schematic illustrating the basis of the experiments: the free growth rate, v₀, is measured before the cell is deforming the chamber. When the cell deforms the chamber, the force from the deformation opposes turgor and may reduce the growth rate, v(F). As the cell deforms more and more the chamber, the force increases (F₂>F₁), which may continue changing the growth rate. C) Cell growth under an external force. (Left part) Examples of growth curves of a single cell growing in a stiff chamber (E_ch=0.65MPa). The dotted lines follow the free growth rate as measured before contact. The gray part highlights the phase of growth under external force. The left axis plots the cell elongation: ΔL=L(t)-L(t=0). The right axis plots the external force of the deformed chamber. (Right part) Force-velocity plot. Each point is averaged on typically 3-4 different experimental sets, and forces are binned to keep a sample size almost constant. The vertical error bars represents the standard deviations. The dotted line plots a linear fit that correspond to eq. 5. D) Free growth rate measured in bipolar wild-type and gpd1Δ cells in the presence of increasing concentrations of sorbitol (0. 0.05, 0.1 and 0.2M). n=10 cells for each condition. E) Force-velocity plot of gpd1Δ cells in the absence and in the presence of 0.05M sorbitol. n=15 cells in both conditions. F) Stalling forces extrapolated from force-velocity curves in the indicated mutants and conditions. The yeast strains are: NM11, NM183 and NM209 (all in a cdc25-22 background and grown at 25C). ** Student T-test, P<0.005.

$$\frac{v(F)}{v_0}=\left(1-\frac{F}{\pi R^2\Delta P}\right)$$ (Eq. 5)

Here ΔP=P-P_c is the effective turgor pressure (Eq. 1). Note that we could not experimentally measure a stall force, because this force is typically higher than the buckling force; the cell usually buckles before stalling, which allows growth to resume (Movie 4;see below). However, by linearly fitting the experimental data, and extrapolating the fit to v(F) = 0, we could derive an estimate of the stalling force of 11 ± 3 μN.

Growth rates and forces depend on internal turgor pressure

We next tested the role of turgor pressure on force production. We predicted that increasing the extracellular osmolarity in the media would cause a relative decrease in internal turgor pressure and thus a decrease in force production. However, wildtype cells have a complex compensatory osmotic stress response: when osmolarity of the external media is increased by additional of sorbitol, wildtype cells initially shrink, but then within 10-30 min recover their initial turgor values [24] (Movie 5). This recovery is dependent on the synthesis of intracellular glycerol, which is catalyzed by the enzyme gpd1p (glycerol-3-phosphate dehydrogenase) [25-27] (Movie 6). The gpd1Δ mutant cell is viable, as gpd1⁺ shares some functional redundancy with a second glycerol-3-phosphate dehydrogenase gene gpd2⁺ (data not shown, [24]), but is sensitive to hyperosmotic medium. Thus, to avoid most of the complex dynamic effects of stress regulation, we examined the effects of altering osmolarity of the media in gpd1Δ mutant cells.

First, we incubated cells in different concentrations of sorbitol and monitored free growth rates in the subsequent 2 hours. We found that gpd1Δ mutants grew significantly slower at 0.05M sorbitol and stopped growing at concentrations exceeding 0.2M. Under the same conditions, wild-type cells did not exhibit any notable change in their growth rate (Figure 3D).

Second, we examined the force-velocity behavior of gpd1Δ mutants growing in chambers. In the absence of sorbitol, gpd1Δ cells did not show significant differences in behavior with wild-type cells (Figure 3E and S3B). In contrast, gpd1Δ cells in 0.05 M sorbitol exhibited a force-velocity curve with a significantly smaller slope; a derived stalling force in this mutant was typically 2-3 times lower than in the absence of sorbitol (Figure 3E and 3F). Thus, in these conditions, gpd1Δ mutant cells, which are defective in turgor pressure regulation, produce less force. These results support a view that internal turgor pressure, regulated by intracellular glycerol concentration, controls cell growth rates and force production.

Growth force is independent of actin cables

As the actin cytoskeleton is critical for force generation in the migration of animal cells [28], we also tested if actin affects force production in S. pombe. In interphase cells, actin is organized in actin cables, which regulate polarized cell growth, and actin patches, involved in endocytosis. Although total inhibition of F-actin by Latrunculin A immediately halts growth, probably through many indirect effects, we probed the role of actin cables by examining for3Δ cells, which lack actin cables, but still exhibit polarized cell growth [29]. Interestingly, for3Δ cells did not show any major difference in our assays, as compared to wild-type cells. Free growth rate and force-velocity behavior were similar, and the stalling force of for3Δ cells was not significantly smaller than that of wild-type cells (Figure 3F and S3B). Thus these findings show that actin cables are not required for force production.

Cells buckle from the force of their own growth

As an independent test of our measurements and model, we investigated the behavior of cells that buckle from the force of their own growth. We grew cells in very stiff chambers (E_ch=1.55 MPa) that are mostly not deformed by the cells. When they elongated to the walls of the chamber, they grew and buckled under their own pushing force (Figure 4A and Movie 7). The buckling event usually happened quite abruptly in a time as short as 5 min (see rate of angle change between the tips in figure 4B). In a subset of cells that buckled and later septated, we could observe that the 2 daughter cells recovered immediately in a straight shape (Movie 8).

Figure 4. Cell buckling under its own pushing force.

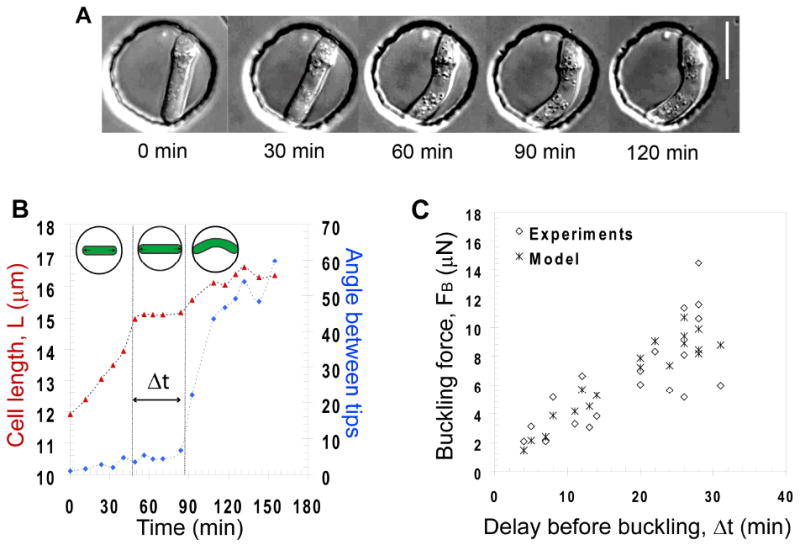
A) Time-lapse sequence of a fission yeast cell growing and buckling under its own pushing force in a rigid chamber. Bar=10μm. B) Example of a growth curve of a cell buckling in a 15μm chamber. The delay, Δt during which the cell length stalls is indicated. The angle between cell tips represented on the left axis in blue is used to detect the onset of buckling. C) Buckling force, F_B plotted as a function of the delay, Δt, along with values predicted from the model. The yeast strains are NM11 and FC1234.

Growth curves revealed that when cells reached the chamber side, their growth slowed down and then stopped for a reproducible time period before buckling occurred (Figure 4B). By analyzing cells of different lengths, we saw that the delay before buckling, Δt, was inversely correlated with cell length (Figure 4B and 4C).

These experiments provided us with an independent way to test our measurements from the previous experiments. On the one hand, knowing the elasticity of the cell wall, the buckling event provides a value of the external force F=F_B (Eq. 2) at the moment of buckling. On the other hand, we could obtain the evolution of the force before buckling from our growth law (supplementary material). Plugging the values obtained from the first sets of experiments (E_cw, ΔP) into a model adapted to these dynamic buckling experiments allowed to compare the experimental data to their theoretical counterparts (Figure 4C and supplementary material). The overall agreement obtained was found to be within the range of error in our measurements. Thus, this analysis, using a different approach, provides an independent confirmation for the values of the mechanical parameters and supports our model for cell growth.

In summary, we have introduced a novel simple approach for studying mechanical aspects of living cells using microchambers. The general experimental and theoretical approaches could be adapted to many walled-cell types. The measurements of the cell wall surface modulus have a resolution on the order of 1 N.m^-1 and should be valid up to 50 N.m^-1. The external forces can be resolved within typically 0.5 μN and may be measured at values reaching 50-70 μN.

The present study supports a view that polarized cell growth in fission yeast is driven by high internal turgor pressure that is partially contained by a stiff but elastic cell wall. The elastic modulus measured of E_cw=101 ± 30 MPa is globally similar to previously reported values of other fungi cell wall: 110 ± 10 MPa for A. nidulans [30] and 112 ± 6 MPa for S. cerevisiae [13] measured by other means. This stiffness is similar to that of rubber. The effective turgor pressure that drives growth is of about 0.85 MPa. This may correspond to a total turgor pressure around 0.95 MPa (see supplementary material). The osmotic potential corresponding to this turgor pressure would be generated by a concentration of about 0.4M glycerol. This globally matches the concentration of external sorbitol at which the cell starts to notably shrink (data not shown). Finally, some mathematical models can estimate the size of walled cells from their mechanical properties [2]. Injecting our measured values in these models return a size that corresponds to fission yeast typical size.

The derived stall force suggest that the growing cell tip is able to resist forces of up to 11 μN, yielding a stalling pressure of about 1 μN.μm^-2. This corresponds to the force experienced by a palm of a hand holding approximately 100-300 kg, illustrating the considerable strength exerted by these microbial cells. As a comparison, the forces generated at the leading edge of migrating animal cells is 100-1000 times less, on the order of 10-100 nN [31].

Mechanical forces are likely to be key factors in fungal pathogenesis [1]. Plant pathogen fungi form appressoria structures, which raise turgor pressure to breach the plant cell wall for host invasion [32]. Candida albicans can pierce through the membranes of macrophages [33, 34]. There has been question whether fungi invade host membranes using mechanical force, as opposed to more chemical mechanisms. The mechanical resistance of cutaneous tissue is typically on the order of 1-10μN.μm^-2 [1]. Our measurements of a similar magnitude suggests that the impressive mechanical growth forces from the fungal tip can be a major factor in driving host invasion.

Material and Methods

Chamber microfabrication

Microchambers were fabricated using standard soft-lithography methods [35]. Chambers are cylindrical, 5μm deep and with diameters varying between 10 and 50μm (10-12-15-20-25-30-35-40-50μm). PDMS of varying elastic moduli were generated by using different ratios of polymer vs crosslinker (see Figure S1) and baking 4h at 65°C. The corresponding values of the elastic moduli were calculated by pulling on a large PDMS rectangle (typically 20 × 50 × 100 mm³) with increasing forces and measuring the deformation in length along the force axis. The value was computed using:

$$\frac{\Delta L}{L}=\frac{F}{E_{ch}s},$$

where s is the cross section area and L the length of the rectangle. The PDMS chambers were activated using a plasma cleaner (Harrick Plasma).

Microscopy and Image Analysis

Microscopy was performed at room temperature (23-27°C) with an inverted microscope provided with a motorized stage (Ludl). For force-velocity relations establishment, each typical experimental set was performed using a motorized stage so that 10 to 15 movies could be performed for each set. Cells growing in a bipolar manner were selected by tracking the growth from each tip relative to a fixed fiduciary mark (a birthscar) on the cell. GFP-tubulin and CHD-GFP confocal stacks were performed on a spinning-disk confocal fluorescent microscope. Images were acquired with OpenLab 4.0.4 (Improvision) and processed and analyzed with Image J and Matlab.

Yeast Strains, Media, and Genetic Methods

Standard methods for S. pombe media and genetic manipulations were used (http://www-rcf.usc.edu/∼forsburg/). Strains used in this study are listed in Table S1. Cells were grown to exponential phase in YE5S liquid media at 25°C before being placed into the chambers. GFP-labeled tubulin was used to monitor the stage of the cell cycle, and the cdc25-22 mutation was used to delay slightly the G2-stage of the cell cycle to produce cells with longer lengths. Chambers were incubated at room temperature of approximately 23-27°C degrees. Hydroxyurea (HU) employed in Figure 4, was used at a final concentration of 25mM from a 60× stock solution in water and was added to the cell 2h before the experiment.