Abstract
Previous studies on high molecular weight DNA found that backbone damage, as monitored by free base release, is relatively independent of the type of base; i.e., the yields of all four bases were nearly equal. This could be due to a lack of influence of any given base over damage to its own deoxyribose or it could be a consequence of averaging out disparities due to each base sampling a wide range of base contexts. This study is aimed at distinguishing between these two possibilities. Transparent films, prepared from palindromic oligodeoxynucleotides of d(CTCTCGAGAG), d(CTCTCGAGAGp), d(pCTCTCGAGAGp), d(GAGAGCTCTC), d(ACGCGCGCGT), d(AACGCGCGCGTT), d(CTCTCTTAATAATTATAATTATTAAGAGAG), and d(CTCTCTTAATATTAAGAGAG), were used for this investigation. The DNA films, hydrated to ~2.5 waters per nucleotide, were irradiated at RT under air using X-rays generated by a tungsten tube, immediately dissolved in nuclease-free water, and stored at 277 K for 24 h, and then unaltered free base release was measured using HPLC. Yields of free base release were based on a target mass consisting of the DNA and one counterion + 2.5 H2O/nucleotide. The yields of each base, G(C), G(G), G(T), and G(A) were determined for each of the above sequences. The observed yields lead to the following conclusions: (i) base release at the oligomer ends is favored over release at internal positions (called the end effect), (ii) phosphorylation of the OH moiety at the oligomer ends quenches the end effect, (iii) the magnitude of the end effect is influenced by the base at the end and the bases proximal to it, and (iv) the release of base is influenced by the base and its context.
Introduction
Radiation damage to the deoxyribose of DNA results in stable end products consisting of strand breaks (sb) and free base release (fbr).1–4 Understanding the reaction mechanisms that lead to these products following the direct interaction of ionizing radiation with DNA is central to determining risk due to radiation exposure at low dose and low dose rate. The mechanism appeared to be straightforward: one-electron oxidation of (ejection of an electron from) the DNA backbone produces a radical cation (also referred to as a hole) that deprotonates to yield a neutral carbon centered deoxyribose radical, and in the presence of water, these neutral radicals react to give sb and fbr. One would expect, therefore, that the strand break site should be independent of the base at that site,5 and the probability of observing release of a free base should be independent of base type. By studying oligodeoxynucleotides of known sequence, we have recently found that this is not the case.6
In a study of a series of oligodeoxynucleotides with the repeating sequences of d(CG)n and d(GC)n, where n was varied from 2 to 10, the yields of free base release, G(fbr), and yields of deoxyribose radicals, GdRib(fr), were measured.7 These palindromic sequences self-associate to form duplex DNA, i.e., (d(CG)n)2. For (d(CG)n)2 at small n, the yield of released Gua, G(G), was more than twice the yield of Cyt, G(C). At large n, G(G) ≈ G(C). In addition, GdRib(fr) < G(fbr); the yield of deoxyribose trapped radicals was not large enough to account for the yield of free base release. A model was proposed to explain these findings.7
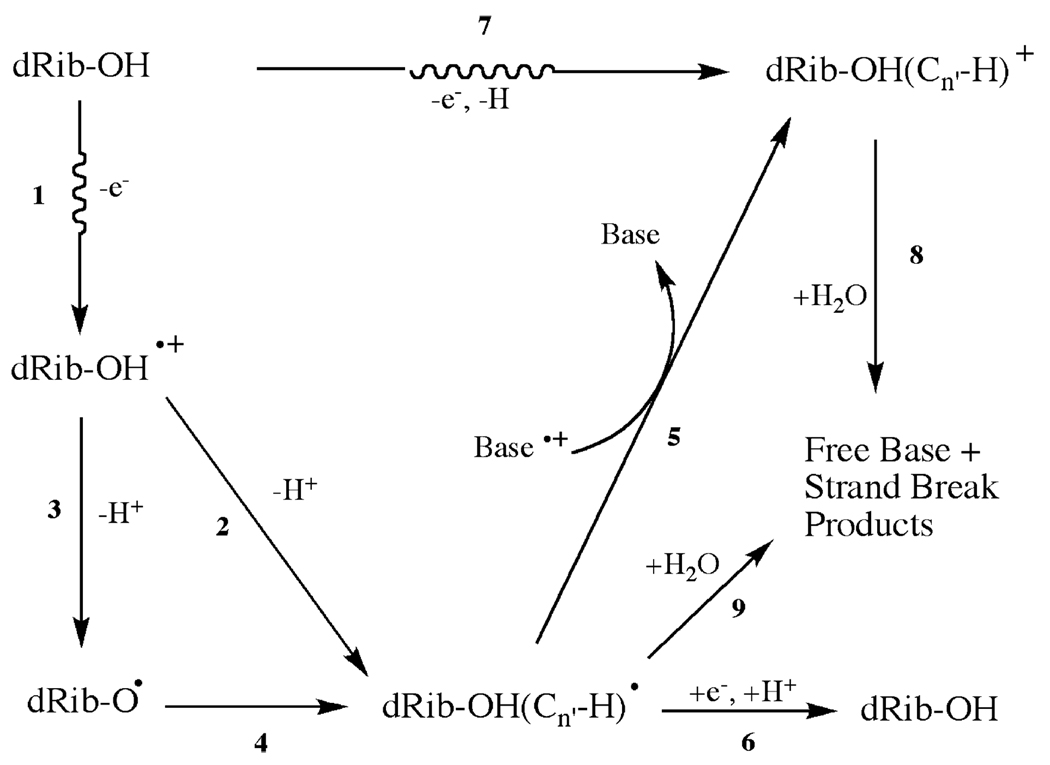
Central to the proposed model are the reaction pathways shown in Scheme 1. In this scheme, oligodeoxynucleotides with strand ends containing either a 3′-OH or 5′-OH are designated dRib-OH. When energy deposition results in a one-electron oxidation (Reaction 1), the radical cation dRib-OH•+ is produced. Upon deprotonation at one of the five carbons, a neutral carbon centered radical dRib-OH(Cn′-H)• is formed (Reaction 2); alternatively, deprotonation at −OH gives an alkoxy radical, dRib-O• (Reaction 3). The highly reactive dRib-O•, via H transfer or H abstraction, creates a second pathway for the formation of dRib-OH(Cn′-H)• (Reaction 4). Reaction 3 must be competitive with hole transfer into the base stack for there to be a preference for deoxyribose radical formation at the terminal positions. If a base radical cation, Base•+, encounters the dRib-OH(Cn′-H)• radical, electron transfer produces the carbocation, dRib-OH(Cn′-H)+ (Reaction 5). If an electron is returned to dRib-OH(Cn′-H)•, possibly mediated by a base radical anion, Base•−, subsequent protonation reverses the damage to parent (Reaction 6). Reaction 7 is a molecular pathway leading to a carbocation. (When energy deposition leads to product in the absence of a trappable radical intermediate, this is called a molecular pathway.) The carbocation formed by Reaction 7 is indistinguishable from the one formed via Reactions 1–5. Reactions 1–7 are solid state reactions, taking place in the DNA films. When the films are dissolved in water, Reactions 8 and 9 lead to free base release and strand break products.
SCHEME 1.
Proposed Model Showing the Alkoxy Radical Pathway, Reactions 3 and 4, a Pathway Available Only at the Strand Endsa
a All pathways leading to free base release are influenced by the transfer of holes and excess electrons through the DNA matrix. But only one pathway, Reaction 5, depends specifically on the one-dimensional diffusion of the hole through the base stack.
Mathematical equations were derived to describe the yield of free base release as a function of CG-oligomer length.7 Two reaction pathways in the model were key. First, strand ends are more labile than internal sites because of chemistry mediated by the OH moiety (Reactions 3 and 4). Second, short-range mobility of holes through the base stack influences the yield of carbocation via Reaction 5 and subsequently the yield of free base. The relative importance of these pathways was investigated here by exploring a wider range of sequences and by varying the composition of the oligomer ends.
Materials and Methods
Palindromic oligodeoxynucleotides of d(CTCTCGAGAG), d(CTCTCGAGAGp),d(pCTCTCGAGAGp),d(GAGAGCTCTC), d(CTCTCTTAATATTAAGAGAG) ≡ 20mer, d(CTCTCTTAATAATTATAATTATTAAGAGAG) ≡ 30mer, d(ACGCGCGCGT), and d(AACGCGCGCGTT), purified by standard desalting, were purchased from Integrated DNA Technologies. All but two of these oligomers have no OH moiety at their termini; these exceptions are labeled showing the phosphate at the 3′ end in one case and at the 5′ and 3′ end in the other case. The oligodeoxynucleotides were used as supplied without any further purification. All eight sequences are palindromic, giving rise to duplex DNA. OmniPur nuclease-free water was from EM Science, Merck. DNA bases used as reference for HPLC experiments were from Sigma. All other chemicals and solvents were Baker Analyzed and were used as received from Mallinckrodt Baker, Inc.
Film Preparation
Transparent films were prepared from 10–12 µL drops of 5–7 mM oligodeoxynucleotides in nuclease-free water deposited on Teflon Petri dishes that had been washed with (i) deionized water and (ii) methanol and (iii) finally rinsed with nuclease-free water. The drops were dehydrated and equilibrated against a relative humidity of 8% maintained by a reservoir of saturated NaOH solution to obtain DNA films.8 To achieve maximum duplex form of the oligodeoxynucleotides, the temperature was initially maintained at 277 K for a minimum of 7 days. During this time, the droplets shrank and became viscous. The samples were then brought to room temperature (RT) to reach the final hydration state, which is assumed to be 2.5 waters per nucleotide based on studies of high molecular weight DNA by Swarts, et al.9 and by others cited in their paper.
The films were weighed to ± 1 µg using a Cahn C-30 Microbalance and harvested after reaching a steady state mass. The concentration of oligodeoxynucleotides was chosen to give a film mass of 200–250 µg. The fraction of film mass attributable to oligodeoxynucleotide was determined from measurements of optical density (OD) at 256 nm by dissolution of the films in nuclease-free water after X-irradiation.
In preparation for X-irradiation and HPLC, the weighed Teflon grown films were placed in plastic vials with a wall thickness of 0.5 mm and sealed under air with screw caps seated against siliconized ‘O’ rings. Prior to loading, the vials were pre-equilibrated to 8% relative humidity for 4–5 days at RT.
Irradiation
X-rays were generated by a Varian/Eimac OEG-76H tungsten tube operated at 70 kV and 20 mA. The X-ray beam was filtered by aluminum foil (40 µm thick) in addition to the wall(s) of the respective sample containers. X-irradiation of the films was at RT with a dose rate of 2.2 kGy/min at the face of the plastic vial. Attenuation by the wall was 52%, resulting in a dose rate of 1.05 kGy/min at the sample. The attenuation was determined by exposing radiochromic films (Far West Technologies) inside and outside the plastic vials, then measuring their OD at 600 nm. The radiochromic films were calibrated using a 60Co γ source with a known dose rate.
Following X-irradiation, the DNA films were immediately dissolved in nuclease-free water at a ratio of 1 µg of film to 1 µL of water and stored at 277 K for 24 h. In preparation for HPLC measurements, aliquots of the DNA solution were combined with a solution containing uracil as an internal standard and sodium acetate as a buffer (pH 6.8). This brought the final concentrations to 80–100 µM oligodeoxynucleotide, 10 µM uracil, and 50 mM sodium acetate.
HPLC
Solutions at pH 6.8 were injected into a Waters Alliance HPLC system equipped with a 2690 solvent delivery system, Waters 996 PDA detector, and an autosampler with temperature controller. The autosampler temperature was maintained at 277 K, minimizing variations due to changes in sample temperature. The unaltered free base was separated on a Phenomenex Columbus C-18 reverse-phase column (4.6 × 250 mm, 5 µ, 110 Å pore size) at 303 K using 40 mM ammonium acetate (pH 6.8) as a mobile phase and by applying a linear gradient 0.9–10% of acetonitrile over 25 min. The unaltered free bases were detected by their absorbance at 254 nm and were quantified by comparison with uracil as the internal standard6 using Millennium Software (Waters Co., Milford, MA).
Calculation of Yields
Yields were based on a target mass consisting of the DNA and one Na+ plus 2.5 H2O per nucleotide. The remainder of the film mass is assumed to be excess salt and, as such, was assumed not to be part of the target mass.
Results
Absolute Yields
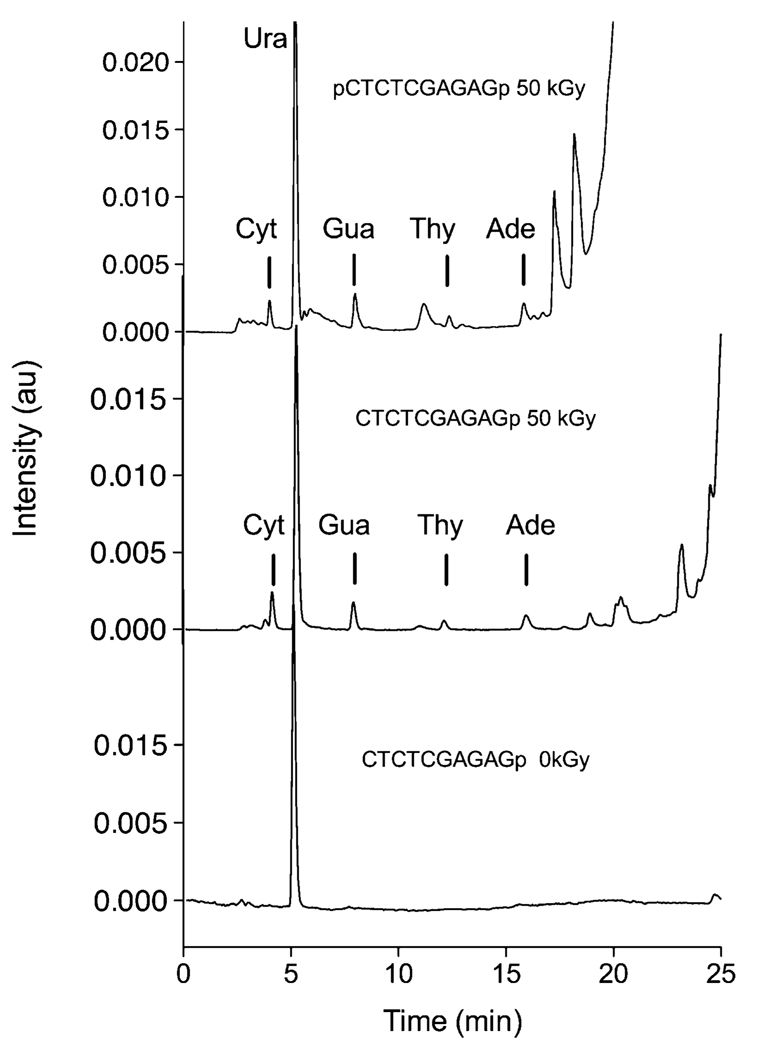
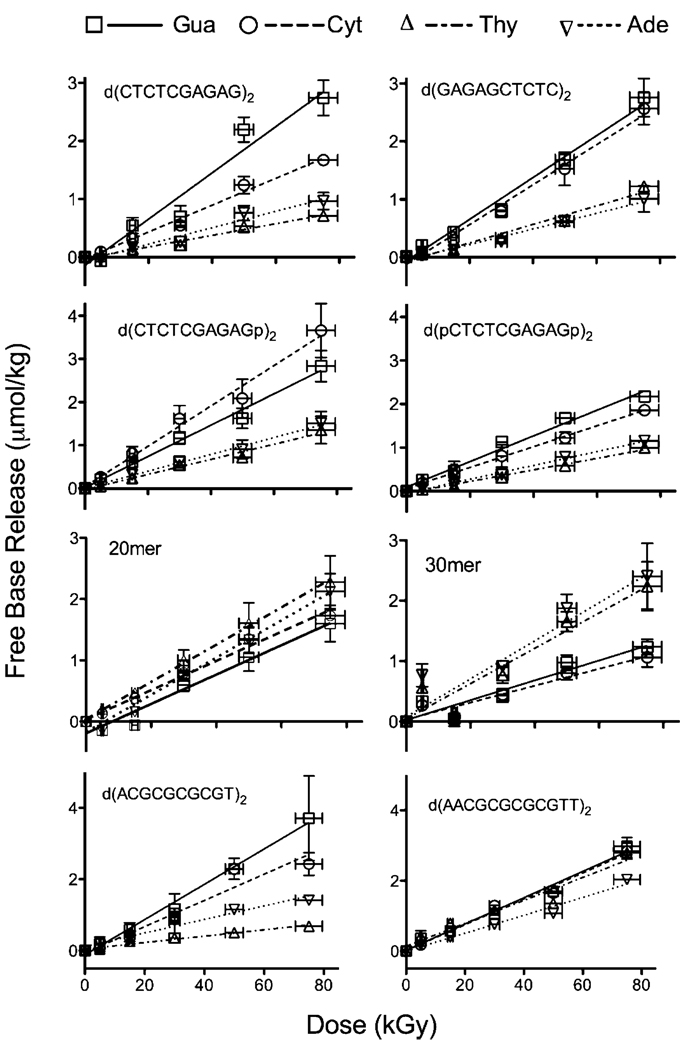
Figure 1 shows HPLC chromatograms for d(CTCTCGAGAGp)2 and d(pCTCTCGAGAGp)2 X-irradiated to a dose of 50 kGy compared with the background of d(CTCTCGAGAGp)2 at zero dose. Figure 2 shows the dose response data for each of the four DNA bases released from each of eight oligomers. The slope of the linear fit to these data determined the chemical yields for Cyt, Gua, Thy, and Ade (referred to as G(C), G(G), G(T), and G(A), respectively). These yields are provided in the first four columns of Table 1. Also given in Table 1 are the total free base release, Gtot(fbr), the ratio for the yield of Gua to Cyt, RG/C, and the ratio for the yield of Ade to Thy, RA/T.
Figure 1.
HPLC chromatogram of oligodeoxynuclotide films X-irradiated at room temperature.
Figure 2.
Dose response curves for the release of cytosine (○), guanine (□), thymine (Δ), and adenine (∇) from oligodeoxynucleotide films X-irradiated at RT. For each base, the data from two separate experiments were fit to a straight line. The slope of each line was used as a measure of the chemical yields given in Table 1. For all of the data sets, the background at zero dose was subtracted; this made it easier to compare the data sets and did not alter the G values or their standard deviations.
TABLE 1.
Radiation Chemical Yields for Oligodeoxynucleotide Films, with DNA Hydration Levels of Г~ 2.5 Waters/Nucleotide, X-Rrradiated at RTa
| oligodeoxynucleotide |
G(base) ≡ yield of base (nm/J) |
Gtot(fbr)d |
||||||
|---|---|---|---|---|---|---|---|---|
| base | C | G | T | A | (nm/J) | RG/C = G(G) ÷ G(C) | RA/T = G(A) ÷ G(T) | |
| 1 | d(CTCTCGAGAG)2 | 23.0 | 39.8 | 10.0 | 14.1 | 86.9 | 1.7 | 1.4 |
| 1.3 | 4.2 | 0.7 | 1.4 | 4.7 | 0.2 | 0.1 | ||
| 2 | 20merb | 23.9 | 24.0 | 30.4 | 30.4 | 108.7 | 1.0 | 1.0 |
| 1.3 | 2.5 | 0.7 | 2.1 | 3.6 | 0.1 | 0.1 | ||
| 3 | 30merc | 14.0 | 16.4 | 29.2 | 31.5 | 91.1 | 1.2 | 1.1 |
| 1.9 | 2.8 | 4.2 | 6.2 | 8.2 | 0.2 | 0.2 | ||
| 4 | d(GAGAGCTCTC)2 | 34.4 | 36.0 | 15.9 | 13.4 | 99.7 | 1.0 | 0.8 |
| 1.9 | 2.2 | 1.4 | 0.7 | 3.3 | 0.1 | 0.1 | ||
| 5 | d(pCTCTCGAGAGp)2 | 23.9 | 29.5 | 13.3 | 15.9 | 82.6 | 1.2 | 1.2 |
| 0.8 | 2.0 | 0.7 | 0.8 | 2.4 | 0.1 | 0.1 | ||
| 6 | d(CTCTCGAGAGp)2 | 46.7 | 36.2 | 17.5 | 19.5 | 119.9 | 0.8 | 1.1 |
| 2.8 | 1.9 | 1.2 | 0.7 | 3.7 | 0.0 | 0.0 | ||
| 7 | d(ACGCGCGCGT)2 | 36.7 | 49.4 | 9.0 | 19.0 | 114.1 | 1.3 | 2.1 |
| 4.7 | 2.1 | 0.9 | 1.9 | 5.6 | 0.1 | 0.2 | ||
| 8 | d(AACGCGCGCGTT)2 | 36.8 | 37.4 | 32.6 | 25.5 | 132.3 | 1.0 | 0.8 |
| 2.2 | 2.4 | 4.1 | 1.9 | 5.6 | 0.1 | 0.1 | ||
Standard deviations (±1 sd) are shown in parentheses. For the yields, sd’s were based on two independent data sets fit simultaneously to a straight line. For the ratios, standard statistical procedures were used: (A ± a)/(B ± b) = (D ± d), where A/B = D, then d = D*[(a/A)2 + (b/B)2]1/2.
20mer = d(CTCTCTTAATATTAAGAGAG)2.
30mer = d(CTCTCTTAATAATTATAATTATTAAGAGAG)2
Gtot(fbr) = G(G) + G(C) + G(A) + G(T).
It was changes in RG/C in our earlier work on d(GC)n that first drew our attention to an end effect; e.g., d(CG)5 and d(CG)10 gave RG/C =1.9 ± 0.1 and 1.1 ± 0.1, respectively.7 Similar changes were observed in the work reported here, as can be seen by comparing RG/C in rows 1 and 2 of Table 1. The decamer, d(CTCTCGAGAG)2, with Cyt at the 5′ end and Gua at the 3′ end, gave RG/C = 1.7 ± 0.2. When the oligomer was lengthened to a 20mer by inserting a 10 bp AT stretch between the CT and GA tracks, RG/C dropped to 1.0 ± 0.1. With regard to RG/C, therefore, there appears to be a similar response to changes in oligomer length. But unlike the d(GC)n series, the oligomers listed in Table 1 differ from one another in their GC/AT ratios. For this reason, we recast the yields in a form that adjusts for differences between oligomers with differing GC: AT ratios.
Yields Adjusted for GC/AT Ratio of Oligomers
Here we define M(base) as the degree to which a base modifies its own release. The calculation of M(base) is shown in Table 2. The mole fraction of each base within an oligomer (F%(base)), which is relevant to the relative efficiency of base release from the oligomer, is expressed as percentages in the first four-column group in Table 2. The next four-column group gives the yield of each base recast as a percentage of total free base release (G%(base)). If the mole percent and yield percent are the same, i.e., F%(base) = G%(base), then the degree of deoxyribose damage modification that can be attributed to that base and its site (averaged over all sites containing that base) is 1.0; i.e., on average, the base and its site exert no net effect on the probability of its deoxyribose being damaged. If M(base) > 1, the base sensitizes its own deoxyribose to damage; if M(base) < 1, the base protects its deoxyribose. Using M values, we are able to compare base release across oligomers of differing GC/AT ratios.
TABLE 2.
Yields Shown in Table 1 Recast to Show the Degree of Modification, M(base), by Each of the Four Basesa,b
| oligomer |
F%(base) = mole fraction of base in oligomer (%) |
G%(base) = G(base) ÷ Gtot(fbr) (%) |
M(base) = G%(base) ÷ F%(base) |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| base | C | G | T | A | C | G | T | A | C | G | T | A |
MG+C = M(G) + M(C) |
MA+T = M(A) + M(T) |
MG/A = M(G) ÷ M(A) |
MC/T) M(C) ÷ M(T) |
|
| 1 | d(CTCTCGAGAG)2 | 30 | 30 | 20 | 20 | 26 | 46 | 12 | 16 | 0.9 | 1.5 | 0.6 | 0.8 | 2.4 | 1.4 | 1.9 | 1.5 |
| 2 | 7 | 1 | 2 | 0.1 | 0.2 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.1 | ||||||
| 2 | 20merc | 15 | 15 | 35 | 35 | 22 | 22 | 28 | 28 | 1.5 | 1.5 | 0.8 | 0.8 | 2.9 | 1.6 | 1.8 | 1.8 |
| 1 | 3 | 2 | 3 | 0.1 | 0.2 | 0.1 | 0.1 | 0.2 | 0.1 | 0.2 | 0.1 | ||||||
| 3 | 30merd | 10 | 10 | 40 | 40 | 15 | 18 | 32 | 35 | 1.5 | 1.8 | 0.8 | 0.9 | 3.3 | 1.7 | 2.1 | 1.9 |
| 3 | 5 | 8 | 10 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 | 0.3 | 0.4 | 0.3 | ||||||
| 4 | d(GAGAGCTCTC)2 | 30 | 30 | 20 | 20 | 35 | 36 | 16 | 13 | 1.2 | 1.2 | 0.8 | 0.7 | 2.4 | 1.5 | 1.8 | 1.4 |
| 2 | 3 | 2 | 1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||||||
| 5 | d(pCTCTCGAGAGp)2 | 30 | 30 | 20 | 20 | 29 | 36 | 16 | 19 | 1.0 | 1.2 | 0.8 | 1.0 | 2.2 | 1.8 | 1.2 | 1.2 |
| 1 | 3 | 1 | 1 | 0.04 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||||||
| 6 | d(CTCTCGAGAGp)2 | 30 | 30 | 20 | 20 | 39 | 30 | 15 | 16 | 1.3 | 1.0 | 0.7 | 0.8 | 2.3 | 1.5 | 1.2 | 1.8 |
| 3 | 2 | 1 | 1 | 0.1 | 0.1 | 0.1 | 0.04 | 0.1 | 0.1 | 0.1 | 0.1 | ||||||
| 7 | d(ACGCGCGCGT)2 | 40 | 40 | 10 | 10 | 32 | 43 | 8 | 17 | 0.8 | 1.1 | 0.8 | 1.7 | 1.9 | 2.5 | 0.7 | 1.0 |
| 4 | 3 | 1 | 2 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.3 | 0.2 | 0.2 | ||||||
| 8 | d(AACGCGCGCGTT)2 | 33 | 33 | 17 | 17 | 28 | 28 | 25 | 19 | 0.8 | 0.8 | 1.5 | 1.2 | 1.7 | 2.6 | 0.7 | 0.6 |
| 2 | 3 | 4 | 2 | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 | 0.3 | 0.1 | 0.2 | ||||||
Standard deviations (±1 sd) are shown in parentheses. For the yields, sd’s were based on two independent data sets fit simultaneously to a straight line. For the ratios, standard statistical procedures were used: (A ± a)/(B ± b) = (D ± d), where A/B = D, then d = D*[(a/A)2 + (b/B)2]1/2.
M(base) equals 1.0 when the yield of a base expressed as a percentage of the total fbr, G%(base), is equal to the mole fraction, F%(base), of that base in the oligomer. When M(base) = 1.0, the base does not, on average, modify its own release. Likewise, when the sum MG+C = M(G) + M(C) = 2.0, the two bases combined do not, on average, modify their own release. M(base) > 1.2 are highlighted in bold, and M(base) < 0.8 are underlined.
20mer = d(CTCTCTTAATATTAAGAGAG)2
30mer = d(CTCTCTTAATAATTATAATTATTAAGAGAG)2
Discussion
End Effect
First we summarize the evidence that, for the shorter oligomers, there is a significant end effect. The M values for the lead oligomer, d(CTCTCGAGAG)2, are given in Row 1 of Table 2. The sum of the M values for each conjugate pair, MG+C = M(G) + M(C) and MA+T = M(A) + M(T), would equal 2.0 if the bases do not modify damage of their deoxyribose. In rows 1–6, where the ends were occupied by G and C, MG+C > 2.0 and MA+T < 2.0. These inequalities were reversed when the ends were occupied by A and T (rows 7 and 8), indicating that being at the end position is more important than which base is at the end. Another indicator is the comparison of the ratios MG/A = M(G)/M(A) and MC/T = M(C)/M(T). When the end positions were occupied by Gua and Cyt, MG/A and MC/T were ≥ 1.2, and when the ends were occupied by Ade and Thy these ratios dropped to ≤ 1.0. These comparisons show that release of either base of a conjugate pair was enhanced when that conjugate pair occupied the end positions.
Evidence that the end effect is in part, or entirely, due to the presence of the terminal OH moiety was obtained by phosphorylation of the ends. Of the five of the oligomers containing Gua at the 3′ end, three of them gave remarkably high M values: the oligomers in rows 1–3 gave M(G) = 1.5–1.8. When the 3′ end was phosphorylated, see rows 5 and 6, M(G) dropped to 1.0–1.2. For Cyt at the 5′ end, there was a similar drop in M(C), from 1.3 to 1.0, when comparing d(CTCTCGAGAGp)2 (row 5) with d(pCTCTCGAGAGp)2 (row 6).
We propose that the mechanism by which the OH moiety sensitizes base release is through the advantageous formation of the alkoxy radical, as shown in reactions 3 and 4 (Scheme 1). It is known from previous studies10,11 that the highly reactive alkoxy radicals are often found trapped in crystals of carbohydrates, including nucleosides and nucleotides, when irradiated at low temperatures. The O–H deprotonation reaction is likely to be faster than C–H deprotonation reaction, favoring primarily formation of alkoxy radicals over carbon-based radicals. Secondary reactions may convert these into carbon-based radicals through intramolecular hydrogen transfer. If so, phosphorylation of the oligomer ends would prevent formation of the alkoxy radical, thereby eliminating this reaction pathway and quenching the end effect.
Influence of the Base on Its Own Release
Gua appears to sensitize its own release, and Thy appears to protect itself from release. For each of the oligomers in rows 1–7, M(G) ≥ 1.0 and M(T) ≤ 0.8. Evidence that these biases were not exclusively due to the end effect comes from the observation that, when both ends of d(CTCTCGAGAG)2 were phosphorylated, M(G) remained high and M(T) remained low, 1.2 ± 0.1 and 0.8 ± 0.1, respectively. This later point presumes the end effect is fully quenched by phosphorylation.
Influence of Base Sequence
As pointed out under End Effect, when Ade and Thy are at the terminal positions, the M values shifted to favor these two bases. MA+T, for d(ACGCGCGCGT)2 and d(AACGCGCGCGTT)2 given in rows 7 and 8 of Table 2, was 2.5 ± 0.3 and 2.6 ± 0.3, respectively. Note that in the decamer M(A) was about twice M(T), whereas in the dodecamer, M(T) was larger than M(A). In fact, for this dodecamer, M(T) was 2 times larger than it was in any of the other seven oligomers. Since Thy is on the same end in both the decamer and dodecamer, this is a sequence effect. In this case, a Thy adjacent to another Thy responds differently than a Thy adjacent to a Gua. The release of Thy was, therefore, sequence dependent.
Another example of sequence dependence can be seen by comparing rows 1–3 with d(GAGAGCTCTC)2 in row 4. Gua at the 3′ end resulted in relatively large values of M(G), 1.5–1.8, but when Gua was moved to the 5′ end, M(G) dropped to 1.2. Conversely, switching Cyt from the 5′ end to the 3′ end increased M(C) from 0.9 to 1.2. Therefore, the magnitude of the end effect was influenced by which base was positioned at which end. Further, in general, the lability of the deoxyribose at the 3′ end appears to be greater than at the 5′ end, which is consistent with our earlier findings on base release7 and strand break products.12
Importance of Hole Transfer
We suggest that hole transfer rates play an important role in determining whether or not the deoxyribose of a particular base within a particular sequence is damaged. Because damage at the ends is greater than internal sites, the effect of hole transfer is more easily observed in short oligomers where the end effect is prominent. (This does not mean that the importance of hole transfer is confined to the end effect.) For example, a good explanation for the 2-fold increase in M(T) in going from d(ACGCGCGCGT)2 to d(AACGCGCGCGTT)2 is that the rate of hole transfer from the terminal Thy is reduced when Thy is two bases removed from Gua instead of adjacent to Gua. A reduction in rate of hole transfer from Thy increases the probability of forward reactions that fix the damage at thymine’s deoxyribose. In addition, because Thy is a good electron trap, the Thy adjacent to the terminal Thy should help protect the terminal deoxyribose from electron return (see Reaction 6 of Scheme 1) and thus prevent a backward reaction.
In contrast to the results reported here, high molecular weight DNA showed only small differences between G values for each of the four bases.9,13 The larger differences reported in Table 1 point to the likelihood that in high molecular weight DNA there exists a larger disparity in G values than what has been observed to date, the reduction in disparity being a consequence of averaging over a wide variety of sequences. This raises the prospect of finding sequences in DNA that are either resistant or sensitive to strand breaks produced by the direct effect.
Conclusions
Phosphorylation of the OH moiety quenches the end effect. This is consistent with our model that proposes an alkoxy radical intermediate to explain enhanced free base release at the oligomer ends.
Base composition at one end of the oligomer influences fbr at the other end when the oligomer length is 10 bp or less.
The magnitude of the end effect is influenced by the base at the end and the bases proximal to it.
The yield of fbr from internal sites is influenced by the base at that site and its context.
Acknowledgment
The authors thank Kermit R. Mercer for is excellent technical support and Dr. Yuriy Razskazovskiy for helpful suggestions. The project described was supported by Award Number R01CA032546 from the National Cancer Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
References and Notes
- 1.Becker D, Sevilla MD, editors. Radiation damage to DNA and related biomolecules. Vol. 16. Cambridge, UK: The Royal Society of Chemistry; 1998. p. 79. [Google Scholar]
- 2.Bernhard WA, Close DM. DNA damage dictates the biological consequence of ionizing radiation: the chemical pathways. In: Mozumder A, Hatano Y, editors. Charged particle and photon interactions with matter. Vol. 471. New York: Marcel Dekker; 2003. [Google Scholar]
- 3.Sevilla MD, Becker D, editors. ESR studies of radiation damage to DNA and related biomolecules. Vol. 19. Cambridge, UK: The Royal Society of Chemistry; 2004. p. 243. [Google Scholar]
- 4.von Sonntag C. Free-radical-induced DNA damage. Germany: Springer-Verlag; 2006. [Google Scholar]
- 5.Razskazovskiy Y, Debije MG, Bernhard WA. Radiat. Res. 2003;159:663. doi: 10.1667/0033-7587(2003)159[0663:sbpixc]2.0.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sharma KK, Purkayastha S, Bernhard WA. Radiat. Res. 2007;167:501. doi: 10.1667/RR0847.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sharma KK, Razskazovskiy Y, Purkayastha S, Bernhard WA. J. Phys. Chem. B. 2009;113:8183. doi: 10.1021/jp900803b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Greenspan L. J. Res. Natl. Bur. Stand. A. 1977;81A:89. [Google Scholar]
- 9.Swarts SG, Sevilla MD, Becker D, Tokar CJ, Wheeler KT. Radiat. Res. 1992;129:333. [PubMed] [Google Scholar]
- 10.Box HC, Budzinski EE, Freund HG. J. Chem. Phys. 1984;81:4898. [Google Scholar]
- 11.Bernhard WA, Close DM, Hüttermann J, Zehner H. J. Chem. Phys. 1977;67:1211. [Google Scholar]
- 12.Razskazovskiy Y, Debije MG, Howerton SB, Williams LD, Bernhard WA. Radiat. Res. 2003;160:334. doi: 10.1667/rr3051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roginskaya M, Bernhard WA, Razskazovskiy Y. Radiat. Res. 2006;166:9. doi: 10.1667/RR3571.1. [DOI] [PMC free article] [PubMed] [Google Scholar]