Agonist and blocking actions of choline and tetramethylammonium on human muscle acetylcholine receptors

Abstract

Choline has been used widely as an agonist for the investigation of gain-of-function mutants of the nicotinic acetylcholine receptor. It is useful because it behaves like a partial agonist. The efficacy of choline is difficult to measure because choline blocks the channel at concentrations about four times lower than those that activate it. We have fitted activation mechanisms to single-channel activity elicited from HEK-expressed human recombinant muscle nicotinic receptors by choline and by tetramethylammonium (TMA). Channel block by the agonist was incorporated into the mechanisms that were fitted, and block was found not to be selective for the open state. The results also suggest that channel block is very fast and that the channel can shut almost as fast as normal when the blocker was bound. Single-channel data are compatible with a mechanism in which choline is actually a full agonist, its maximum response being limited only by channel block. However, they are also compatible with a mechanism incorporating a pre-opening conformation change (‘flip’) in which choline is a genuine partial agonist. The latter explanation is favoured by concentration jump experiments, and by the fact that only this mechanism fits the TMA data. We propose that choline, like TMA, is a partial agonist because it is very ineffective (approximately 600-fold less than acetylcholine) at eliciting the initial, pre-opening conformation change. Once flipping has occurred, all agonists, even choline, open the channel with similar efficiency.

Introduction

Block of nicotinic ion channels is ubiquitous. It has been seen with every agonist that has been tested appropriately. These include acetylcholine, carbachol, suberyldicholine (Sine & Steinbach, 1984; Ogden & Colquhoun, 1985), decamethonium (Adams & Sakmann, 1978; Marshall et al. 1991), tetraethylammonium, tetramethylammonium (TMA; Akk & Steinbach, 2003) and choline (Grosman & Auerbach, 2000; Purohit & Grosman, 2006).

Acetylcholine itself blocks the channel only at concentrations much higher than those needed to activate the channel. In the case of TMA, the margin is narrower, but still sufficient to allow activation to be investigated without too many problems from blockage (Lape et al. 2008). However, the situation is reversed for choline, which activates the channel only at concentrations that are larger than those needed for block (Purohit & Grosman, 2006). This sort of intense channel block makes investigation of mechanisms very difficult; in particular, it can be hard to tell whether agonists such as choline have a limited maximum open probability (P_open) because they are partial agonists (i.e. when bound, they are not good at holding the channel open) or because they are effective blockers (Marshall et al. 1991). This is an important question for choline, which is believed to have low efficacy on muscle nicotinic acetylcholine receptors because of a slow channel opening rate constant (Grosman & Auerbach, 2000). This property makes choline an attractive tool in the characterization of the single-channel kinetics of gain of function mutants, where the channel opening rate constant is increased beyond its wild-type value of about 50 000 s⁻¹ for acetylcholine.

One of our aims in the present work was to investigate the efficacy of choline and to estimate its gating constants by exploiting the increased resolution allowed by time-course fitting idealisation and by the power of our mechanism-fitting analysis, which can resolve opening rates of up to at least 130 000 s⁻¹ (Burzomato et al. 2004; Lape et al. 2008). Examining how choline and TMA block the channel was a necessary step in this analysis, given that our own recent data on the mechanism of partial agonism of TMA (Lape et al. 2008) suggested that block of the nicotinic channel by TMA itself is not a simple open pore block. Earlier studies have also proposed that block by a related quaternary ammonium compound, tetraethylammonium, can be explained only by a more complex mechanism, which allows the channel to close on the blocker (Akk & Steinbach, 2003).

Global fitting of mechanisms to single-channel data has recently identified, for receptors in the nicotinic superfamily, kinetic shut states that may represent activation intermediates between the agonist-bound resting state and the opening of the channel. The intermediate state results from a conformational change that may be concerted (‘flip’ model, Burzomato et al. 2004) or not (individual ‘priming’ of each binding site; Mukhtasimova et al. 2009). It was therefore necessary to test on the TMA and choline data a mechanism that incorporates such a pre-opening conformational change in the activation path.

The present data suggest that the channel of the muscle nicotinic acetylcholine receptor can close while blocked by agonist and that both choline and TMA are partial agonists because of their weakness in triggering the initial conformational change (‘flipping’) rather than because of any deficiency in their ability to open the channel once flipped. An alternative interpretation of the single-channel data suggested that choline might be a full agonist, the maximum response being limited by trapped channel block, but the results of concentration jump experiments are not consistent with this interpretation.

Methods

Cell culture and transfection of cells

Human embryonic kidney (HEK293) cells, obtained from the American Type Culture Collection (ATCC), were maintained in Dulbecco's modified Eagle's medium containing 10% (v/v) fetal bovine serum and 1% (v/v) penicillin–streptomycin solution (10 000 units ml⁻¹ penicillin and 10 mg ml⁻¹ streptomycin; Gibco, UK) at 37°C. Cells plated onto polylysine-coated coverslips in 35 mm culture dishes were transfected by a Ca²⁺-phosphate co-precipitation method (Groot-Kormelink et al. 2002) with pcDNA3.1 plasmids (Invitrogen, The Netherlands) containing inserts encoding the human muscle acetylcholine receptor subunits α1, β1, δ, ɛ (GenBank accession numbers Y00762, X14830, X55019, X66403), enhanced green fluorescent protein (eGFP; Clontech, UK) or no insert (non-coding plasmid). The mixture of DNA used for the cell transfection contained 5% acetylcholine receptor subunit DNA (α1, β1, δ, ɛ ratio 2: 1: 1: 1), 65% eGFP DNA, and 30% non-coding plasmid. Each cell culture dish was transfected with a total amount of 3 μg of DNA.

Single-channel recordings and analysis

All recordings were performed in the cell-attached configuration using choline or TMA as agonists in the pipette, and an extracellular solution containing (mm): 5.4 NaCl, 142 KCl, 1.8 CaCl₂, 1.7 MgCl₂ and 10 Hepes (pH adjusted to 7.4 with KOH; osmolarity 320 mosmol l⁻¹). The pipette solution was made before recording by mixing a stock solution (containing (mm): 5.4 NaCl, 142 KCl, 1.8 CaCl₂, 1.7 MgCl₂, 10 Hepes and 100 TMA or choline (pH adjusted to 7.4 with KOH)) with standard extracellular solution to obtain the required agonist concentration. Chemicals were obtained from Sigma-Aldrich (NaCl, Hepes and KOH) or Fluka (KCl, CaCl₂, MgCl₂, TMA and choline). Choline (initial purity >99%) was further purified by recrystallization from an ethanol solution followed by drying of the crystals in a low-temperature oven.

Patch pipettes were made from thick-walled borosilicate glass (GC150F, Harvard Instruments) and coated near the tip with Sylgard 184 (Dow Corning). Electrode resistance was in the range of 8–15 MΩ after fire-polishing. Single-channel currents were recorded with an Axopatch 200B amplifier (Molecular Devices, CA, USA), filtered at 10 kHz (4-pole low-pass Bessel filter; sampling rate 100 kHz) and stored directly on the computer hard drive.

The high K⁺ ion concentration in the extracellular solution (142 mm) means that the cell resting potential is expected to be near 0 mV. Thus, the transmembrane potential of the patch during cell-attached recording is approximately equal to the absolute value of the holding potential but of opposite sign. We did not correct for junction potential, as with our solutions this is expected to be at most 1 mV (as calculated in Clampex 9, Molecular Devices). All experiments were done at 19–21°C.

For off-line analysis, data were filtered digitally (Gaussian filter) using the program FILTSAMP to achieve a final cut-off frequency of 3–8 kHz and re-sampled at 33–100 kHz. Open times, shut times and amplitudes were idealized by time-course fitting with the SCAN program and dwell-time distributions were fitted with mixtures of exponential densities using the EKDIST program after imposing a resolution of 20–100 μs. For each recording, 10 000–15 000 transitions were fitted. The term ‘apparent open time’ here is used to mean the duration of time for which the channel appears to be continuously open, regardless of transitions, real or artefactual, between different open levels: this is the quantity described in the programs as an ‘open period’. For full descriptions and download of the analysis programs see http://www.ucl.ac.uk/pharmacology/dc.html.

Clusters of activations separated by long sojourns in desensitized states (Sakmann et al. 1980) were detected at concentrations equal to or greater than 10 mm for choline and 1 mm for TMA. Usually it was evident that all openings within a cluster came from the same channel, so they could be used for the calculation of the probability of being open, P_open (i.e. the fraction of time for which the channel is open, estimated as the ratio between the total open time per cluster and the cluster length). The Hill equation was fitted to P_open–concentration data using CVFIT. The Hill equation is different from that predicted by the fitted mechanisms, and is used for empirical description only. Curves of P_open as a function of concentration were calculated in SCALCS, for each reaction scheme, using the fitted rate constants. The calculation of predicted P_open curves in HJCFIT showed that the missed event correction had little effect on the predicted curves.

Since we do not know the number of channels in the patch, it is essential for model fitting to divide the idealised single-channel record into stretches that are likely to be the activity of one individual channel. When openings are sparse (at low agonist concentrations) such stretches are short, each consisting of a single activation (i.e. a burst of openings) of the channel. At higher agonist concentrations, long stretches of data with high P_open can be obtained: these clusters of openings are separated by long desensitised gaps. The high P_open would make it obvious if a second channel opened, so such clusters can be assumed to come from one individual channel. The division of the record into one-channel stretches was achieved by defining a critical shut time, t_crit, on the basis of inspection of the shut time distribution. Sometimes this process can be ambiguous but our conclusions do not depend critically on this choice. The shut time distributions for the model fits are shown only up to t_crit, because shut times longer than this were not used for fitting.

Recordings made at different concentrations of agonist were grouped arbitrarily into sets for simultaneous fitting. Each set included one recording at each of the three concentrations used (0.5, 1 and 20 mm for choline and 0.1, 1 and 10 mm for TMA) and the sets were independent, i.e. each individual patch was included in only one set. The data reported here are the results of fitting three or four such replicate sets. The rate constants in the tables are averages of the values from each replicate set together with their coefficient of variation (also from replicates). Records that showed obvious heterogeneity, as judged mainly by occurrence of clusters of openings with abnormally high P_open, were excluded (about 10% of records).

After the fit, HJCFIT calculates (with full missed event correction) the predicted shape of a range of plots of the data, such as the P_open curve, the distributions of apparent open and closed times and the apparent open–shut correlations, in order to allow a comparison of these predictions with the experimental results and judge how well the fitted mechanism and the rate constant values can describe the data. Correlation plots display the conditional mean apparent open times (predicted and observed) plotted as a function of the adjacent shut times, i.e. the plot shows the mean of the open times found adjacent to shut times in a chosen range (the calculation of the predicted conditional distribution is described in Colquhoun et al. 1996; see also Colquhoun et al. 2003).

The temporal resolution of TMA- or choline-activated single-channel records at negative transmembrane potential rapidly worsened at concentrations higher than 1 mm for both agonists, because the reduction in the apparent channel amplitude (Fig. 1) meant that a progressively larger fraction of short closings was missed. The resolution imposed on records at lower concentrations (1 mm or lower) of choline or TMA was in the range of 17–25 μs, but at concentrations of 10–20 mm a resolution of 50–100 μs was the best that could be achieved.

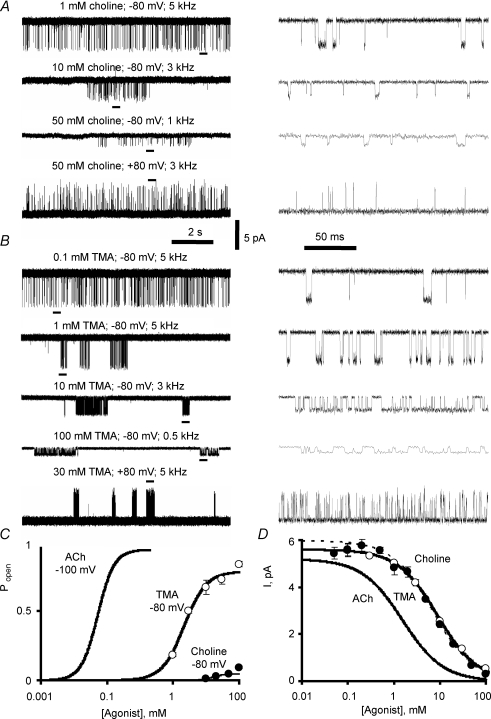
Figure 1. Single-channel activity of adult muscle nicotinic receptors in the presence of increasing concentrations of TMA or choline.

The records in A and B were obtained in the cell-attached configuration at −80 or +80 mV membrane potential and low-pass filtered as indicated. The black bars under the left-hand traces mark the groups of openings shown at an expanded time scale on the right. The plots in C show the relation between cluster P_open and agonist concentration, fitted by a Hill equation (n= 5–141 clusters, from 1 to 3 different patches per concentration, see Table 1 for details). Data for acetylcholine are shown for reference, and are taken from Lape et al. (2008). The Hill equation is not, of course, the correct equation to describe the receptor mechanism, but these fits serve to obtain an estimate of EC₅₀ by interpolation and to give an empirical indication of the steepness of the curve. In the case of choline, the highest point on the P_open curve, at 100 mm choline, was considered to be not very reliable because of the very small apparent amplitude of the channels at this concentration. Therefore the fit shown in Fig. 1C was done by fixing the maximum at 0.05, the value found at 50 mm choline. For choline at −80 mV the fitted values were: P_open(max) = 0.05 (fixed), EC₅₀= 42.7 ± 4.6 mm, n_H= 1.2 ± 0.2; for TMA at −80 mV: P_open(max) = 0.78 ± 0.05, EC₅₀= 2.2 ± 0.5 mm, n_H= 1.3 ± 0.4; for TMA at +80 mV: P_open(max) = 0.16 ± 0.02, EC₅₀= 6.4 ± 1.9 mm, n_H= 1.2 ± 0.4. The panel in D shows the decrease in single-channel current with increasing agonist concentrations also fitted with a Hill equation (in this case with the slope constrained to −1 on the assumption of simple Langmuir binding of the blocker; dashed line, Hill equation fitted to choline experimental points; continuous lines, fits to TMA and acetylcholine experimental points; filled circles, choline; open circles, TMA, n= 2–4 patches). This fit gave an estimate of the equilibrium constant for channel block of 6.9 ± 0.3 mM for choline and 8.9 ± 0.6 mM for TMA (TMA and acetylcholine data from Lape et al., 2008).

Fast concentration jumps and analysis

Concentration jumps were performed on outside-out patches using a theta tube (14-072-01, Hilgenberg, Malsfeld, Germany) with the tip cut to a final diameter of approximately 150 μm and driven by a piezo-stepper (Burleigh Instruments, NY, USA). The agonist, TMA, choline or acetylcholine, was washed in or out through the double-barrelled perfusion system. The exchange time was measured by application of a solution diluted to 30% (70% water), before each experiment (to optimize the position of the electrode) and after rupture of the patch. Only those patches in which the exchange time was faster than 200 μs were included in the analysis. A minimum of five individual responses, separated by at least 20 s, were used to generate an ensemble average (patch response). Only those experiments in which the run-down between the average of the first and last three responses in a series was less than 5% were included in the analysis. Digitised macroscopic currents were fitted with one or two exponential functions (equally weighted least-squares criterion) with the CLAMPFIT program (Molecular Devices).

Results

Before considering mechanisms, the results will be described empirically, in terms of dose–response curves and open and shut time distributions.

Empirical description of muscle acetylcholine receptor single-channel currents activated by choline or TMA

Dose–response curves

Single-channel currents activated by choline (Fig. 1A) or TMA (Fig. 1B) were recorded from HEK293 cells transfected with adult human wild-type nicotinic αβδɛ receptor cDNAs.

At negative transmembrane potential (−80 mV) and low agonist concentrations, activations were sparse, occurring as bursts of one or more openings (Fig. 1A and B top traces). At higher agonist concentrations (10 mm or greater for choline and 1 mm or greater for TMA), very long shut times appeared in the record, giving the channel activity the appearance of being grouped into clusters. During these long silent periods all the receptors in the patch are in long-lived desensitised states (Sakmann et al. 1980) and a cluster arises when one (or more) of the channels exits from desensitisation. The probability of the channel being open, P_open, is the fraction of time for which the channel is open, and is estimated as the ratio between the total open time per cluster and the cluster length. It increased with agonist concentration as bursts of openings became more closely spaced, reaching 84 ± 1% at 100 mm TMA (see Table 1). Similar behaviour was observed when channels were activated by choline, with the difference that it was more difficult to detect clusters unambiguously because they were longer and had a much lower P_open than those observed with TMA, reaching a maximum value of only 9% (±1%, Table 1). When clusters have these properties, it is possible for two clusters to overlap without giving rise to double openings (Colquhoun & Hawkes, 1990).

Table 1.

Cluster characteristics in the single-channel records from human muscle acetylcholine nicotinic receptor activated by choline or TMA

Agonist (mm)	Popen	Length (s)	Length range (s)	Number of clusters (number of patches)
Choline, −80 mV
10	0.0093 ± 0.005	3.45 ± 1	1.4–9.4	9 (1)
20	0.0290 ± 0.003	1.55 ± 0.3	0.19–4.1	17 (1)
50	0.0426 ± 0.004	1.61 ± 0.3	0.11–7.6	38 (3)
100	0.0918 ± 0.01	1.15 ± 0.2	0.38–2.8	11 (2)
TMA, −80 mV
1	0.179 ± 0.008	0.53 ± 0.07	0.06–2.2	57 (2)
3	0.50 ± 0.01	0.22 ± 0.03	0.02–1.0	68 (2)
10	0.66 ± 0.01	0.22 ± 0.02	0.03–1.0	86 (3)
30	0.74 ± 0.02	0.17 ± 0.02	0.04–0.6	36 (2)
100	0.836 ± 0.006	0.38 ± 0.02	0.09–1.9	141 (3)
TMA, +80 mV
1	0.022 ± 0.004	0.7 ± 0.2	0.5–1.3	5 (1)
3	0.042 ± 0.001	0.6 ± 0.1	0.1–1.9	19 (1)
10	0.11 ± 0.01	0.30 ± 0.07	0.02–0.8	13 (1)
30	0.13 ± 0.01	0.34 ± 0.08	0.07–0.9	15 (1)
100	0.16 ± 0.01	0.33 ± 0.06	0.02–1.9	48 (2)

Cluster apparent open probability and cluster length are expressed as mean ±s.d.m.

At positive membrane potential (+80 mV) the single-channel activations also appeared as single openings or bursts of openings but with reversed direction (Fig. 1A and B, bottom traces). Bursts activated by TMA clustered at the same concentrations as at negative transmembrane potentials, but had a much lower P_open, with a maximum value of 16 ± 1% at 100 mm TMA. However, there was apparently no clustering of choline activations even at the highest choline concentrations used (100 mm), maybe because, at positive membrane potential, choline clusters were so long and low in P_open that it was impossible to identify them.

Agonist concentration–response curves, on an absolute scale from 0 to 1, were constructed by plotting the cluster P_open against agonist concentration and fitted with a Hill equation (Fig. 1C).

Channel block by agonist

It is obvious from the records in Fig. 1A and B that at −80 mV the apparent amplitude of single-channel currents decreased with increasing choline or TMA concentration. This phenomenon suggests that choline or TMA, like other agonists (Ogden & Colquhoun, 1985; Colquhoun & Ogden, 1988; Akk & Steinbach, 2003), block the channel pore and that the blockages are too brief to be resolved as closures. Figure 1D (filled circles, choline; open circles, TMA) shows the apparent amplitude as a function of agonist concentration. The points are means from two to four patches. At −80 mV, fits with a Hill–Langmuir equation (n_H constrained to −1; Fig. 1D, lines) estimate the equilibrium constant for channel block as 6.9 ± 0.3 mm for choline and 8.9 ± 0.6 mm for TMA. Apparently choline or TMA block was very much weaker at positive membrane potential since single-channel amplitude remained almost constant with increasing agonist concentration (not shown, for TMA see Lape et al. 2008).

The distribution of apparent open times

After idealisation by time-course fitting (program SCAN; (http://www.ucl.ac.uk/Pharmacology/dc.html), the apparent open and shut time distributions were plotted and fitted with mixtures of exponential probability density functions using the EKDIST program. The term ‘apparent’ is used here to indicate that the true duration of an opening or a shutting may be lengthened by our inability to detect short-lived events.

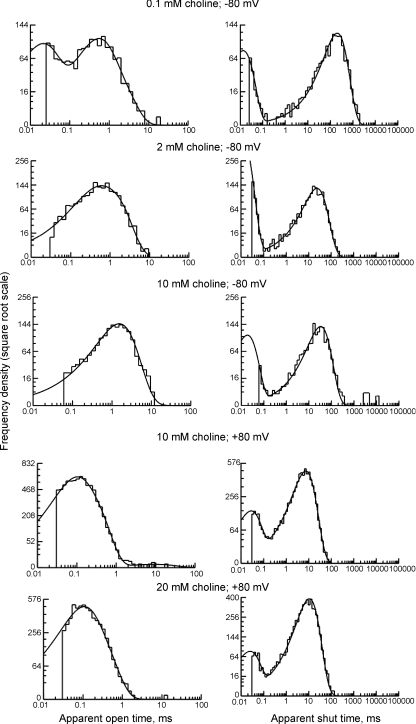
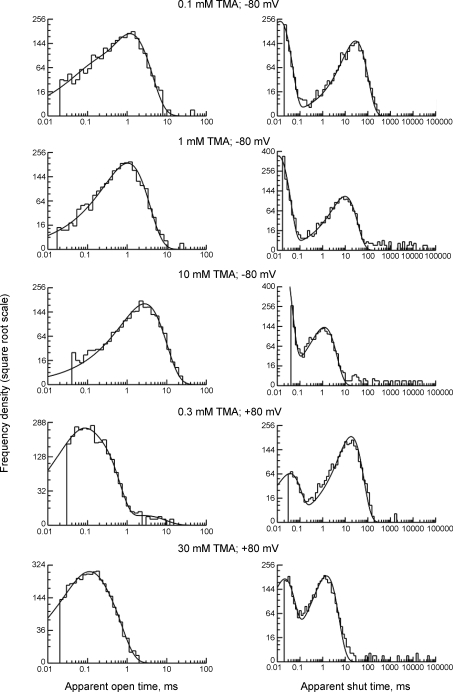
Examples of open time distributions for various choline and TMA concentrations are shown in Figs 2 and 3 (left column). At −80 mV, three exponential components were needed to fit the open time distributions at the lowest choline concentrations (below 0.2 mm). At intermediate choline concentrations (0.2–2 mm) and at the lower TMA concentrations (below 1 mm), the open time distributions had two obvious components. Just one component (the slowest) was sufficient at higher choline or TMA concentrations (see also Table 2 for a summary of time constants and fractional areas). A similar disappearance of the faster components in the open time distributions has been observed for single-channel currents activated by acetylcholine in nicotinic receptor channels (Colquhoun & Sakmann, 1985; Milone et al. 1997; Hatton et al. 2003) and by glycine in both homomeric and heteromeric glycine-activated channels (Beato et al. 2004; Burzomato et al. 2004). In all of these cases the phenomenon has been attributed to the progressive loss, as agonist concentration is increased, of short-lived apparent openings from channels that have not got all of their binding sites occupied by agonist.

Figure 2. Dwell time distributions for channel activity elicited by choline.

Distributions of apparent open times (left column) and apparent shut times (right column) are shown for recordings at −80 mV and (bottom two rows) at +80 mV. Continuous lines show the fit of mixtures of exponential probability density functions (pdfs) to the distributions. Apparent open time distributions were fitted with one (2 and 10 mm at −80 mV), two (20 mm at +80 mV) or three (0.1 mm at −80 mV and 10 mm at +80 mV) component exponential pdfs. Shut time distributions were fitted with two component exponential pdfs. As choline concentration increases, a progressively longer dead time has to be imposed on the data, because of the decrease in the apparent amplitude of the channel currents, see Methods).

Figure 3. Dwell time distributions for channel activity elicited by TMA.

Distributions of apparent open times (left column) and apparent shut times (right column) are shown for recordings at −80 mV and (bottom two rows) at +80 mV. Continuous lines show the fit of mixtures of exponentials. The number of components was one (open time distributions for 1 mm and 10 mm at −80 mV) or two (all other distributions).

Table 2.

Empirical fit of mixtures of exponential probability density functions to the distributions of apparent open times from human muscle acetylcholine nicotinic receptor activated by choline or TMA

Agonist (mm)	V (mV)	τ1 (ms)	Area 1 (%)	τ2 (ms)	Area 2 (%)	τ3 (ms)	Area 3 (%)	n
Choline
0.05	−80	0.029	24	0.207	42	0.94	34	1
0.1	−80	0.031 ± 0.01	31 ± 20	0.464 ± 0.004	52 ± 20	1.44 ± 0.2	17 ± 1	2
0.2	−80	—	—	0.377 ± 0.01	55 ± 9	0.90 ± 0.2	45 ± 8	2
0.5	−80	—	—	0.307 ± 0.03	43 ± 20	0.83 ± 0.01	57 ± 20	2
1	−80	—	—	0.226	50	0.60	50	1
2	−80	—	—	0.280 ± 0.009	33 ± 2	0.90 ± 0.06	67 ± 2	2
5	−80	—	—	—	—	1.08	100	1
10	−80	—	—	—	—	1.30 ± 0.2	100	3
20	−80	—	—	—	—	1.32 ± 0.04	100	2
50	−80	—	—	—	—	2.02 ± 0.05	100	2
5	+80	0.047	29	0.20	71	2.58	0.3	1
10	+80	0.065	43	0.18	57	5.87	0.1	1
20	+80	0.084	59	0.20	41	—	—	1
50	+80	0.067 ± 0.005	64 ± 3	0.32 ± 0.01	36 ± 3	—	—	2
TMA
0.1	−80			0.077 ± 0.03	12 ± 3	0.99 ± 0.1	88 ± 3	3
1	−80			—	—	1.27 ± 0.2	100	2
3	−80			—	—	1.60 ± 0.02	100	2
10	−80			—	—	2.09 ± 0.3	100	3
30	−80			—	—	2.93 ± 0.03	100	2
100	−80			—	—	9.94 ± 1	100	3
0.3	+80			0.052	42	0.18	57	1
1	+80			0.057	53	0.38	48	1
3	+80			0.113	62	0.27	38	1
10	+80			0.140	84	0.36	16	1
30	+80			0.075	46	0.21	54	1
100	+80			0.076 ± 0.02	32 ± 10	0.31 ± 0.01	68 ± 10	2

n, number of patches. Time constants and areas are expressed as mean ±s.d.m.

At +80 mV membrane potential, the distributions of apparent open times for choline or TMA were fitted well by a mixture of two exponential components (Figs 2, 3 and Table 2). A third, slower exponential component (time constant 4.3 ± 1.5 ms; n= 4) was observed at 5–10 mm choline but its fractional area was low (0.4 ± 0.2%; n= 4).

The distribution of apparent shut times with choline or TMA as agonist

Typical apparent shut time distributions are shown in the right columns of Figs 2 (choline) and 3 (TMA). All could be fitted well with a mixture of only two exponential components at both negative and positive potential (see Table 3 for summary). No intermediate shut time (of the sort seen with acetylcholine as agonist, Colquhoun & Sakmann, 1985; Hatton et al. 2003) could be detected. The time constant of the slower component was concentration dependent and was highly variable at the same concentration in different patches, presumably due to the presence of different numbers of channels. The time constant of the fast component did not vary noticeably with the agonist concentration, but was slower at positive (5–50 mm choline: 27 ± 4 μs; n= 5 patches; 1–100 mm TMA: 28 ± 2 μs; n= 7 patches) than at negative (0.05–20 mm choline: 13.0 ± 0.8 μs; n= 17 patches; 0.1–30 mm TMA: 12.8 ± 0.5 μs; n= 13 patches) membrane potentials. The relative area of the faster component (that with the smallest time constant) was greater at the lower choline concentrations (0.1–5 mm) and seemed to decrease at higher concentrations, although this could be a result of the rapid loss of temporal resolution that accompanies greater channel block at agonist concentrations higher than 1 mm. This fast exponential component is similar in time constant to that observed when acetylcholine is the agonist (about 12 μs; Hatton et al. 2003), but has not been previously detected in studies of choline using the segmental K-means (SKM) transition detection method, despite an effective bandwidth of approximately 18 kHz at pre-idealization filtering (Grosman et al. 2000; see Qin et al. 1996 for SKM method). It is clearly of interest to understand whether such short shuttings are blockages (as in the case of suxamethonium; Marshall et al. 1990) or originate from multiple openings of doubly occupied channels before dissociation (nachschlag shuttings, Colquhoun & Sakmann, 1985). At positive membrane potentials there is little channel block so only the latter are seen.

Table 3.

Empirical fit of mixtures of exponential probability density functions to the distributions of apparent shut times from human muscle acetylcholine nicotinic receptors activated by choline or TMA

Agonist (mm)	V (mV)	τ1 (ms)	Area 1 (%)	τ2 (ms)	Area 2 (%)	n
Choline
0.05	−80	0.016	26	1200	74	1
0.1	−80	0.013 ± 0.0005	42 ± 0.4	170 ± 30	58 ± 0.5	2
0.2	−80	0.011 ± 0.0002	49 ± 1	120 ± 70	51 ± 1	2
0.5	−80	0.012 ± 0.0003	50 ± 8	130 ± 80	50 ± 8	2
1	−80	0.012 ± 0.001	63 ± 2	98 ± 60	37 ± 2	2
2	−80	0.010 ± 0.001	73 ± 2	52 ± 30	27 ± 2	2
5	−80	0.011	75	51	25	1
10	−80	0.016 ± 0.002	65 ± 20	52 ± 20	31 ± 10	2
20	−80	0.08	4	50	96	1
50	−80	0.056	43	39	57	1
5	+80	0.018	43	3.1	57	1
10	+80	0.027	24	7.4	76	1
20	+80	0.024	17	11	83	1
50	+80	0.032 ± 0.01	22 ± 9	72 ± 6	70 ± 10	2
TMA
0.1	−80	0.012 ± 0.0004	57 ± 3	59 ± 40	43 ± 3	3
1	−80	0.014 ± 0.003	72 ± 3	8.9 ± 0.9	28 ± 3	2
3	−80	0.011 ± 0.00005	81 ± 1	2.41 ± 0.01	19 ± 1	2
10	−80	0.013 ± 0.0007	83 ± 3	1.4 ± 0.3	17 ± 3	3
30	−80	0.014 ± 0.0008	92 ± 1	1.2 ± 0.2	9 ± 1	2
100	−80			0.98 ± 0.1	100	3
0.3	+80	0.036	24	18	76	1
1	+80	0.030	54	17	46	1
3	+80	0.032	31	5.4	69	1
10	+80	0.024	35	2.1	66	1
30	+80	0.021	47	1.6	53	1
100	+80	0.028 ± 0.002	32 ± 2	1.5 ± 0.2	62 ± 2	2

n, number of patches. Time constants and areas are expressed as mean ±s.d.m.

Apparent bursts and the effect of block

It is seen from the raw data in Fig. 1 that channel activations by low concentrations of agonist appear as single or multiple openings. In order to investigate characteristics of those activations (bursts), the idealised single-channel records produced by SCAN were separated into bursts using a critical shut time, t_crit, between two components in the shut time distribution. This value was defined using the Jackson criterion (Jackson et al. 1983), which minimizes the total number of misclassified intervals.

At negative membrane potentials, with low agonist concentrations (up to 1 mm), the mean apparent burst length was 0.74 ± 0.06 ms and 1.7 ± 0.4 ms for choline and TMA, respectively (n= 7 and 5 patches). Both choline and TMA activations were shorter than those elicited by low concentrations of acetylcholine (3.4 ± 0.3 ms; n= 7 patches; Lape, R., unpublished data; acetylcholine below 1 μm). They were shorter both because on average individual apparent openings were shorter and also because the apparent number of openings per burst was smaller with choline or TMA (1.17 ± 0.04 and 1.5 ± 0.1, n= 7 and 5, respectively) than with acetylcholine (2.23 ± 0.07, n= 7).

Care is needed in the interpretation of bursts of openings, because there are two distinct mechanisms that cause bursting behaviour. In the absence of channel block, openings occur in closely spaced groups as a result of oscillations between the open state and the adjacent shut state (with occasional sojourns in the monoliganded shut state followed by re-opening). This is the explanation of bursting behaviour that was proposed by Colquhoun & Hawkes (1977) and by Colquhoun & Sakmann (1981, 1985).

Blockage of the open channel also causes transient interruptions of the current (Neher & Steinbach, 1978; Ogden & Colquhoun, 1985; Akk & Steinbach, 2003). In the simplest case of selective open channel block, the mean duration of blockages will be 1/k_−B where k_−B is the dissociation rate constant for the blocker leaving the open channel. Some blockers dissociate slowly from the open channel, and produce very long blockages (of the order of 1 s for tubocurarine (Colquhoun et al. 1979). The agonist suberyldicholine produces blockages that are much shorter, being on average about 5 ms long (Ogden & Colquhoun, 1985), but these blockages are still long enough that they can be distinguished clearly from the spontaneous nachschlag gaps. In the case of acetylcholine itself, the blockages are much briefer, and their mean duration, about 20 μs, is similar to that of the nachschlag gaps, so the two types of short shut times are indistinguishable.

When the rates are in the right range, as for suberyldicholine, individual channel activations at low agonist concentrations will be made up of one or more bursts. Each opening in a burst is separated by a nachschlag gap, and each burst within a single activation is separated by blockages. This situation can be described in a very general way by the theory for clusters of bursts developed by Colquhoun & Hawkes (1982) and this was done for the case of channel blockage by Ogden & Colquhoun (1985; Appendix 2).

In the case of very fast channel block (when both blocking and unblocking rates are very fast) blockages are very frequent at high concentrations but each blockage has a very short lifetime. If the blocked state lifetime is much shorter than the resolution, then most, if not all, blockages are missed. In this situation, what appears to be an opening is actually a burst of openings separated by unresolved blockages. In the simplest case in which only the open channel is blocked, each opening would be shortened but the apparent opening, actually a burst of openings, would be lengthened (Neher & Steinbach, 1978; Ogden & Colquhoun, 1985). In the case of a single open state, with shutting rate α₂ in the absence of block, the mean length of this apparent opening, μ_bst, will be

(1)

where we define the normalised blocker concentration, c_B, as the blocker concentration [B] expressed as a multiple of its equilibrium constant, K_B,

(2)

An observed burst will consist of one or more of these lengthened apparent openings separated by spontaneous nachschlag shuttings.

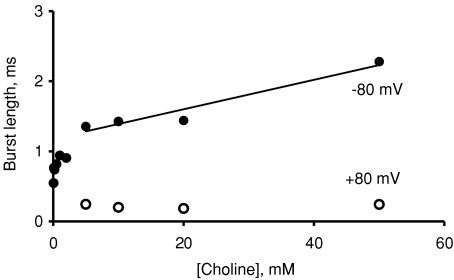
The observed mean burst length is plotted against choline concentration in Fig. 4. The plot shows that the mean burst length increases with increasing concentration, but not linearly as would be predicted by eqn (1) if choline can combine with the channel only when it is open (‘simple block’). This is complicated by the fact that, unlike the work of Neher & Steinbach (1978), our blocker is also an agonist and the nicotinic receptor channel has more than one open state and more than one type of burst. Both monoliganded and diliganded bursts occur, particularly at low agonist concentrations. At agonist concentrations high enough to give predominantly the fully liganded bursts, we could expect eqn (1) to apply if the agonist acts as a pure open channel blocker. This means that burst length should increase linearly with agonist concentration and this seems to occur at choline concentrations greater than 2 mm. However, the slope of the fit for points above 2 mm gives an estimate for K_B of 60 mm, much higher than the more reliable value of 6.9 mm estimated from the reduction in apparent single-channel current amplitude; see Fig. 1D.

Figure 4. Changes in burst length as a function of choline concentration.

The plot shows that the increase in burst length at negative potential is not linear over the whole range of choline concentrations (filled circles). The line is the fit of eqn (1) to the mean burst length at concentrations higher than 2 mm. This yields an estimate of K_B of 60 mm (compare with the 6.9 mm value obtained from the decrease in channel amplitude in Fig. 1D). These data do not support the hypothesis that choline is a pure open channel blocker. Open symbols are data at positive membrane potentials, where there is little channel block.

The discrepancy between these estimates of K_B suggests that choline does not act as simple fast open channel blocker. This is in agreement with the findings of Akk & Steinbach (2003) and suggests that channels blocked by choline can shut (Lingle, 1983; Gurney & Rang, 1984). If the channel can close (and exit the burst states) while it is still blocked, the mean burst length would be shorter than predicted for a selective open channel blocker. In cases like the present one, in which essentially all blockages are too brief to be resolved, non-selective block would lead to similar effects on both the mean length of apparent openings, and on the mean length of an apparent burst (Ogden & Colquhoun, 1985; Appendix 2).

Plots of mean burst length are impossible for TMA because bursts cannot be separated unambiguously at concentrations higher than 1 mm (see shut time distributions in Fig. 3).

Fitting reaction mechanisms

The HJCFIT method (Colquhoun et al. 2003) was used to fit several putative mechanisms directly to idealised single-channel records. Idealised data from several recordings, each made at a different concentration, were fitted simultaneously. Simultaneous fits provide more information than fitting one record at a time, because a single set of rate constants has to describe the observations at all concentrations. This means, in favourable cases, that estimates can be made of all the rate constants, without having to resort to fixing a rate constant, or to constraining rate constants to produce a specified EC₅₀ (Colquhoun et al. 2003). Single-channel records were divided arbitrarily into sets, each set containing recordings made at three different concentrations. Each set gave an estimate of the rate constants in the mechanism, and their means and coefficient of variation of the mean are tabulated in the tables together with the equilibrium constants (calculated from the mean rate constants).

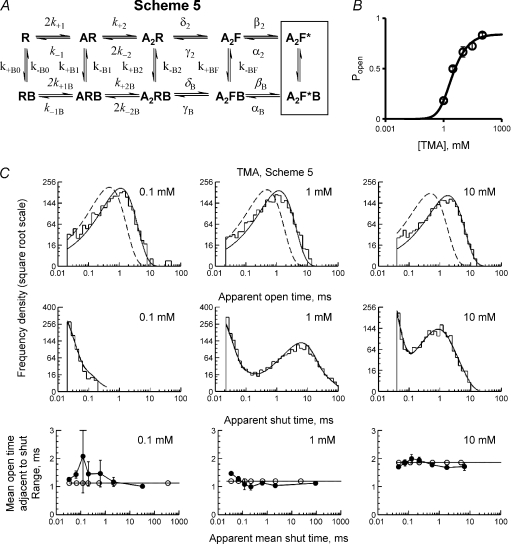
In order to obtain results that have physical meaning it is essential that the mechanism that is fitted is sufficiently close to physical reality. We have already shown (Lape et al. 2008) that the flip mechanism in Fig. 5 (Scheme 1) describes well the behaviour of nicotinic receptors activated by TMA, so it seems obvious that the same mechanism should be used for choline, though the less favourable ratio of blocking concentration to activating concentration makes testing mechanisms harder. In addition we now wish to include blockage in the mechanism explicitly, in order to understand how the agonist blocks the channel. A series of mechanisms, shown in Fig. 5, were tested for their ability to predict the open and shut distributions, correlation plots (see Methods) and concentration–response (P_open) curves. Three of the mechanisms shown in Fig. 5 (Schemes 2, 4 and 5) include block of channels by the agonist.

Figure 5. Mechanisms.

Schemes 1 and 2 show the ‘flip’ scheme (Lape et al. 2008) and the ‘flip’ scheme extended to allow selective block by agonist of the mono- and diliganded open channel. Boxes around the mono- and diliganded open and blocked states show that these are treated as compound states at each level of ligation (see text). Scheme 3 is an activation mechanism for the muscle nicotinic receptor without a pre-opening conformational change (Colquhoun & Sakmann, 1985). This is extended in Scheme 4 to allow fast block of the mono- and diliganded open channel and trapped block of the diliganded channel (A₂RB in Scheme 4). Because of their fast equilibration, non-trapped blocked states are treated as compound states together with their connected open states at each level of ligation (denoted by boxes, see text). Scheme 5 incorporates fast block and trapped block into an activation mechanism with a pre-opening conformational change (Lape et al. 2008). The channel can open when diliganded (monoliganded openings are relatively rare at the agonist concentrations used in our records). Trapped block states (the four states on the left end of the bottom line in the scheme) can be accessed from any level of ligation. A fast-equilibrating blocked state is also included (A₂F*B) and is treated as a compound state together with the open state A₂F* (denoted by a box).

Allowance for fast channel blocking action

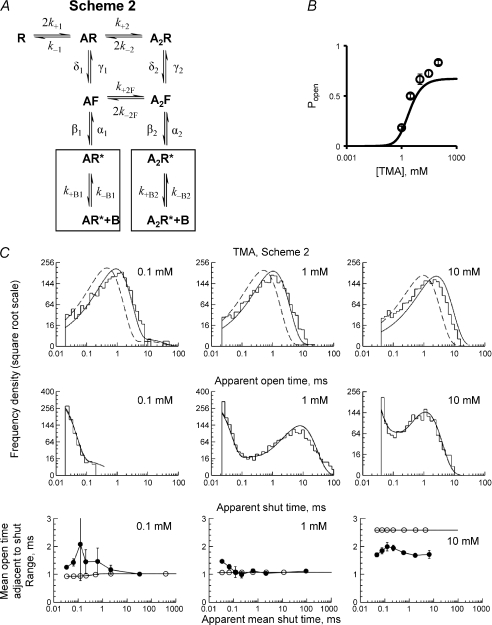
Attempts to fit the flip mechanism with selective open channel block (Scheme 2 in Fig. 5) to either the choline or the TMA data failed when the blocking and unblocking rates were free parameters. Most frequently the fits did not converge, or converged to solutions with physically implausible rate constants. This is hardly surprising since Fig. 4 already suggests that block is not selective for the open state.

There is another, less obvious, technical reason why attempts to fit the rates for very fast block might not work. For example, if we suppose that the association rate constant for TMA block is similar to that measured for acetylcholine (86 × 10⁶m⁻¹ s⁻¹; Lape et al. 2008, supplementary material), and that TMA blocks channels only when they are open, the following predictions can be made. For a concentration of TMA that causes 50% block, an apparent opening would consist of a burst of roughly 280 very brief openings and blockages, each with mean duration about 1.5 μs. Filtering would make this look like a single opening with half the true amplitude. Essentially all the blockages would be too short to be resolved (with a resolution of 30 μs there would be less than a 1 in 10⁶ chance of any blockage being resolved in an apparent opening).

Such very short shuttings and openings create a difficulty in using HJCFIT. This program uses the distributions of observed, or apparent, openings and shuttings with allowance for missed events (HJC distributions), in order to calculate the likelihood of the observed sequence of open and shut times. The definition of an apparent opening that is used in HJCFIT is as follows. An apparent opening starts with an opening that is longer than the resolution and continues until a shutting is encountered that is longer than the resolution (Hawkes et al. 1990, 1992; Colquhoun & Hawkes, 1995a). This means that all shuttings within an apparent opening are shorter than the resolution, but openings, other than the first opening, may be of any length. An analogous definition is used for apparent shut times. The same definition is used by other programs such as QUB (http://www.qub.buffalo.edu), though only HJCFIT uses an exact calculation of the distribution of the apparent opening length. Under most circumstances this definition works well, but it breaks down in the case of very fast channel block. If, as with TMA, we have a mean open time of about 1.5 μs, then an opening longer than the resolution (as required for an apparent opening to start) hardly ever occurs and the missed event correction no longer works.

In view of this difficulty, an alternative approach can be used, based on the principle that two (or more) states that are connected by very fast rates behave as though the states in question are permanently at equilibrium, so they can be treated kinetically as a single (compound) state. An appropriate mechanism for fast open channel block is shown as Scheme 2 in Fig. 5. The effect of irresolvably fast channel block is to create a compound ‘open’ state (shown within the boxes in Fig. 5). Although labelled ‘open’, it is actually blocked for part of the time and the apparent open time in fact is a sequence of short openings interrupted by short blockages. Filtering makes this look like a single opening with reduced amplitude. While in the compound open state, the receptor spends a fraction of the time 1/(1 +c_B) in the open state A₂R* (or AR*), the state from which normal closure is possible, and a fraction of time c_B/(1 +c_B) in the very brief blocked state, A₂R*B (or AR*B). This has the effect of making the channel shutting rate appear to be reduced by a factor of 1/(1 +c_B), so it looks as though it is concentration dependent. The rates of block and unblock do not appear in this, but only the equilibrium constant for block, because of the assumption that the block rate is so fast that the blocking reaction is at equilibrium throughout. Thus, for example, the rate of leaving the diliganded compound open state in Scheme 2 (Fig. 5) is not α₂ but α₂/(1 +c_B). The fitting process estimates the values of the elements of the Q matrix, and the element that refers to closing of the diliganded open channel is set to α₂/(1 +c_B), during each iteration, with the appropriate value of c_B for each data set. After using Q to calculate the likelihood, the element(s) of Q that have been so modified are multiplied by (1 +c_B) to give an estimate of α₂. The value of c_B was calculated using the value K_B estimated from the concentration dependence of the reduction in apparent channel amplitude (see Fig. 1D).

Fit of the flip mechanism with fast-equilibrating, selective open channel block

It turned out that fits of the flip mechanism with the fast block correction (Scheme 2, Fig. 6B and C; see also fit summary in Table 4) were not as good as without it (Lape et al. 2008). Although the predicted distribution of apparent open times at the lower TMA concentration (0.1 and 1 mm) superimposes on the observations quite well, at the higher concentration (10 mm; Fig. 6C, top row) the prediction is poor. The observed predominant mean apparent open time is about 1.5 times shorter than predicted if TMA produced simply selective fast open channel block. Therefore we investigated a possibility that the blocked channel can shut (Lingle, 1983; Gurney & Rang, 1984; Ogden & Colquhoun, 1985, Appendix 2; Purohit & Grosman, 2006).

Figure 6. Fitting the ‘flip’ scheme with selective fast open channel block to channel activity evoked by a range of TMA concentrations at −80 mV.

A, Scheme 2, the ‘flip’ scheme with selective block by agonist. The data points in B show cluster P_open produced by TMA and the continuous line is the predicted concentration–P_open curve obtained from fitting Scheme 2 to the idealised single-channel records. The dwell-time distributions in C (top two rows) show data (histograms) from one of the 3 fitted sets, and the lines represent the shape of these distributions predicted from the HJCFIT fit of Scheme 2 with the resolution of our experimental records (continuous lines) and at infinite resolution (dashed lines). The bottom row in C shows the open–shut time correlations in the records of this set (filled circles with error bars) and the predictions for these correlations calculated from the HJCFIT fits (hollow circles without error bars).

Table 4.

Results of Scheme 2 fit to TMA-activated human muscle acetylcholine nicotinic single-channel data

	TMA, −80 mV
	Rate constant	±CV (%)
α1 (s−1)	809	72
β1 (s−1)	6.96	87
α2 (s−1)	2360	16
β2 (s−1)	55 600	13
γ1 (s−1)	22 600	63
δ1 (s−1)	4970	59
γ2 (s−1)	12 000	33
δ2 (s−1)	1120	19
k+2F (m−1 s−1)	1.07 × 106	35
k−2F (s−1)	6400	41
k+1=k+2 (m−1 s−1)	1.04 × 106	36
k−1=k−2 (s−1)	2690	35
E1=β1/α1	0.021	75
E2=β2/α2	24	8
F1=δ1/γ1	0.23	20
F2=δ2/γ2	0.11	21
KB=k−1B/k+1B=k−2B/k+2B (mm)	10	fixed
KF=k−2F/k+2F (mm)	3.9	42
KD=k−1/k+1=k−2/k+2 (mm)	2.8	30

Scheme 2 has 14 parameters in total but only 11 of them are free to fit (one rate is set by microscopic reversibility and two are constrained by the assumption that the two binding sites are equivalent and independent). Estimates of rate constants are means of fits to three data sets and CV is the coefficient of variation of this mean. The estimates of the equilibrium constants are averages of the values obtained from the ratio of the appropriate rate constants for each separate fit.

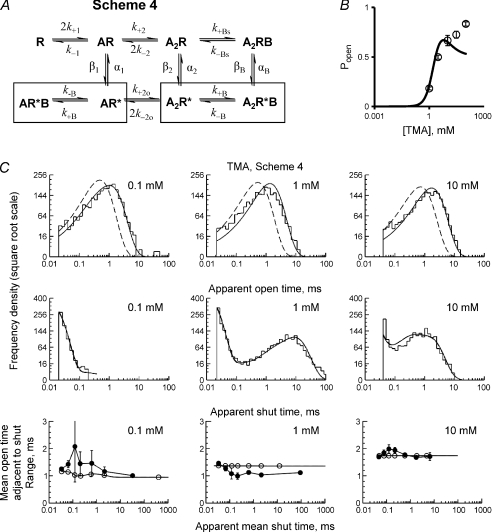
A trapped block mechanism that neglects the flip states

We investigated first the possibility of trapped block in a mechanism without an intermediate flip state. The mechanism in Scheme 3 (Fig. 5; Colquhoun & Sakmann, 1985; Hatton et al. 2003) was in common use before the introduction of intermediate (flip) states, and so seemed to be a good starting point. In Scheme 4 (Figs 5 and 7A) it was extended by adding mono- and diliganded fast-equilibrating block states (AR*B and A₂R*B, both forming compound states with their connected open states, as indicated by the boxes) and a trapped block state (A₂RB) connected to the diliganded blocked and resting states.

Figure 7. Fitting a trapped block mechanism without an intermediate ‘flip’ state to channel activity evoked by a range of TMA concentrations at −80 mV.

A, Scheme 4. The data points in B show cluster P_open produced by TMA. Note that the continuous line is the predicted concentration–P_open curve obtained from fitting Scheme 4 to the idealised single-channel records and that it does not describe well the observations. Panel C compares the prediction of the best HJCFIT fit of Scheme 4 with the actual data from one of the four fitted sets, displayed as dwell-time histograms (top two rows) and open–shut correlation plots (for details see Fig. 6).

Fits of TMA single-channel records to Scheme 4 predicted apparent open and shut time distributions quite well at lower concentrations, but the prediction of the apparent shut time distribution at 10 mm were consistently poor, as shown in Fig. 7C. The prediction of the P_open curve was also bad (Fig. 7B). Furthermore, the variability of the estimates of the rate constants in this mechanism for TMA was very high, especially for association rate constants and monoliganded openings (Table 5). Scheme 4 is inadequate to describe TMA data.

Table 5.

Results of Scheme 4 fitted to TMA- or choline-activated human muscle acetylcholine nicotinic single-channel data

	TMA, −80 mV		Choline, −80 mV
	Rate constant	±CV (%)	Rate constant	±CV (%)
α1 (s−1)	1550	35	7880	8
β1 (s−1)	122	47	3	16
α2 (s−1)	2540	7	4770	22
β2 (s−1)	70 200	6	62 900	39
αB (s−1)	541	18	519	20
βB (s−1)	699	16	17	14
k+Bs (m−1 s−1)	1530	99	225	50
k−Bs (s−1)	0.369	98	0.00648	56
k+2o (m−1 s−1)	4.65 × 108	95	21	13
k−2o (s−1)	76 600	97	0.000292	11
k+1=k+2 (m−1 s−1)	6.24 × 105	12	3.32 × 104	35
k−1=k−2 (s−1)	7310	8	14800	34
E1=β1/α1	0.10	29	0.00044	21
E2=β2/α2	28	5	14	10
EB=βB/αB	1.5	26	0.036	18
KB=k−B/k+B (mm)	10	fixed	10	fixed
KBs=k−Bs/k+Bs (μm)	550	31	27	25
KDo=k−2o/k+2o (μm)	47	35	14	10
KD=k−1/k+1=k−2/k+2 (mm)	12	7	473	13

Scheme 4 has 14 parameters in total but only 10 of them are free to fit (two are calculated from detailed microscopic reversibility and two are constrained as a result of the assumption that the two binding sites are equivalent and independent). Estimates of rate constants are averages of fits to three (choline) or four (TMA) data sets, with the appropriate CV from replicates. The estimates of the equilibrium constants are averages of the values obtained from the ratio of the appropriate rate constants for each separate fit.

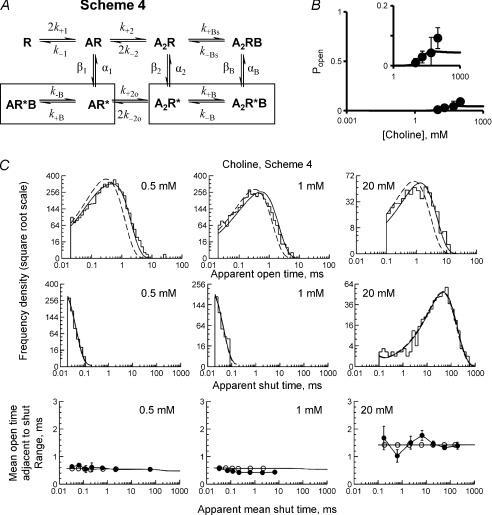
For choline the fits of the same set of single-channel records to the mechanism in Scheme 4 are shown in Fig. 8B and C; estimated rate constants are in Table 5. In contrast with the results with TMA, the fits were good. The predicted P_open curve for choline described accurately the experimental points (Fig. 8B) and the distributions of apparent dwell times were predicted well by the results of the fit (Fig. 8C). The trapped block lifetime (mean life of state A₂RB) in such fits was in the 50–70 ms range and this is similar to the mean for the slow intra-cluster shut time component.

Figure 8. Fitting a trapped block mechanism without an intermediate ‘flip’ state to channel activity evoked by a range of choline concentrations at −80 mV.

A, Scheme 4. The data points in B show cluster P_open produced by choline and the continuous line is the predicted concentration–P_open curve obtained from fitting Scheme 4 to the idealised single-channel records. Panel C compares the prediction of the best HJCFIT fit of Scheme 4 with the actual data from one of the three fitted sets, displayed as dwell-time histograms (top two rows) and open–shut correlation plots (for details see Fig. 6).

It is important to notice that, according to this fit, choline is not a partial agonist at all. The main (diliganded) opening rate constant is estimated to be β₂= 63400 s⁻¹, almost as big as for acetylcholine, and the equilibrium constant for the opening step, E₂= 14, predicts that if block did not occur, the maximum P_open would reach 0.94. The observed P_open is so much smaller (below 0.1) because of the relatively long-lived trapped block, not because of low efficacy. In interpreting these numbers it must be remembered that Scheme 4 (Fig. 8A) does not contain an intermediate flip state, so β₂ and E₂ are the overall values for going from the diliganded resting shut conformation to the open conformation.

The fits obtained with Scheme 4 were good for choline (though not for TMA), but we can obtain just as good a fit with rather different assumptions using Scheme 5 (Figs 5 and 9A). It is possible, in principle, to distinguish between Schemes 4 and 5 by means of jumps in choline concentration (see below, and Fig. 11).

Figure 9. Fitting a trapped block mechanism with an intermediate ‘flip’ state to TMA data at −80 mV.

A, Scheme 5. The data points in B show cluster P_open produced by TMA and the continuous line is the predicted concentration–P_open curve obtained from fitting Scheme 5 to the idealised single-channel records. Panel C compares the prediction of the best HJCFIT fit of Scheme 5 with the actual data, displayed as dwell-time histograms (top two rows) and open–shut correlation plots (for details see Fig. 6).

Figure 11. Macroscopic currents activated by TMA or choline concentration jumps.

A and B, upper traces are open tip responses to 30% diluted control solution (average of 15 sweeps). Bottom traces are typical current responses to concentration steps of 0.1, 1 and 10 mm TMA (A; averages of 6 to 12 sweeps) or 1 and 10 mm choline (B; averages of 5 and 8 sweeps, respectively) at −80 mV. Note the sudden increase in current at the end of 10 mm TMA or choline concentration steps. Panel C shows that a single exponential (continuous line) adequately fits the off-jump of the current response to 10 mm choline (the experimental record, averaged as in panel B, is shown by the dots). D shows for comparison a single-exponential fit (continuous line) to the off-current (dots) calculated from Scheme 4 for a 5 ms 10 mm choline pulse. Note the residual slow component. Panel E shows that the experimental off-current after a 5 ms pulse of choline (response as in C, dots) is in good agreement with the predictions of Scheme 5 (continuous line). The semi-logarithmic display emphasizes that most of the off-current has a fast decay. Note that Scheme 5 predicts that the shape of the off-current is the same after short or long pulses (5 or 50 ms, the latter not shown). Panel F shows a semi-logarithmic plot of the predictions of Scheme 4 for off-jump responses after a 5 or 50 ms 10 mm choline pulse. Both decay biexponentially, and the slow component is much more prominent after long pulses. As shown in E, the off-current after 5 ms pulses did not display any detectable slow component. Experimental responses to 50 ms choline applications are shown in panels G and H. Most patches (7 out of 9) behaved like patch 1 (G), and showed only a fast decay. The two remaining patches had biexponential decay as shown in H (see text).

Trapped block with a flip mechanism

We now think that the best description of nicotinic receptor activation contains an intermediate pre-open shut state (the flipped conformation, Burzomato et al. 2004; Lape et al. 2008; the primed state, Mukhtasimova et al. 2009). Therefore we next tried a mechanism of this sort, but with the addition of block that is not selective for the open state, but can occur from any state, as shown in Scheme 5 (Fig. 9A; Ogden & Colquhoun, 1985). The monoliganded flipped and open states were not included in Scheme 5 because the occupancies of these states were low (less than 1% for all concentrations used, as seen from the fits of TMA records in Lape et al. 2008). In this case, unlike Scheme 4, the blocked state that is connected directly to the open state is assumed to be very short-lived, as indicated by the box in Fig. 9A.

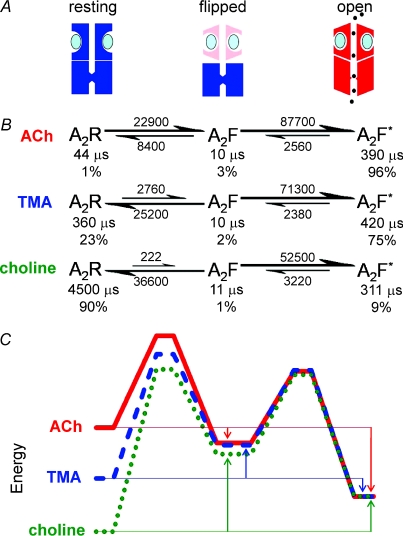
For TMA an example of a fit of Scheme 5 to results is shown in Fig. 9B and C and averaged fit results are summarised in Table 6. In this case, the distribution of apparent open times is predicted accurately at both low and high concentrations of TMA (Fig. 9C; top row). Moreover, shut time distributions and correlation plots are predicted well (Fig. 9C; middle and bottom rows, respectively). The mean value of the rate constant for shutting from the open state was α₂= 2370 s⁻¹, and for shutting from the blocked state was α_B= 1550 s⁻¹ (Table 6), so the channel shows almost the same tendency to shut when it is blocked as when it is not. The mean opening transition rate for the unblocked diliganded channel with TMA was β₂= 71300 s⁻¹, similar to that for acetylcholine (Hatton et al. 2003; Lape et al. 2008) and the mean opening rate constant for the blocked channel, β_B= 49000 s⁻¹, was almost as fast. TMA nevertheless is a partial agonist because it is poor at producing the flipping step, not because it cannot open the channel well once flipped (Lape et al. 2008).

Table 6.

Results of fitting Scheme 5 fit to TMA- or choline-activated single-channel data

	TMA, −80 mV		Choline, −80 mV
	Rate constant	±CV (%)	Rate constant	±CV (%)
α2 (s−1)	2380	12	3220	14
β2 (s−1)	71 300	9	52 500	5
αB (s−1)	1550	19	908	71
βB (s−1)	49 000	9	30 000	46
γ2 (s−1)	25 200	14	36 600	23
δ2 (s−1)	2760	10	222	20
γB (s−1)	13 900	53	104 000	79
δB (s−1)	1530	7	72	36
k−BF (s−1)	9460	6	23 600	33
k+BF (m−1 s−1)	9.14 × 105	16	2.28 × 106	59
k−B2 (s−1)	74	27	70	23
k+B2 (m−1 s−1)	3990	10	18 100	27
k−B1 (s−1)	28	8	1270	86
k+B1 (m−1 s−1)	4940	22	125 000	69
k−B0 (s−1)	32	29	127	45
k+B0 (m−1 s−1)	11 700	11	8510	19
k+1=k+2 (m−1 s−1)	4.17 × 106	4	2.11 × 106	74
k−1=k−2 (s−1)	8230	8	10 300	22
k+1B=k+2B (m−1 s−1)	2.40 × 107	10	6.61 × 106	50
k−1B=k−2B (s−1)	117 000	14	29 800	58
E2=β2/α2	30	4	17	11
EB=βB/αB	35	18	70	79
F2=δ2/γ2	0.11	5	0.0062	4
FB=δB/γB	0.20	28	0.0017	38
KB (mm)	10	fixed	9	fixed
KBF=k−BF/k+BF (mm)	11	18	37	79
KB2=k−B2/k+B2 (mm)	17	24	4.1	24
KB1=k−B1/k+B1 (mm)	6.8	26	7.8	31
KB0=k−B0/k+B0 (mm)	2.9	34	20	62
KD=k−1/k+1=k−2/k+2 (mm)	2.0	12	12	41
KDB=k−1B/k+1B=k−2B/k+2B (mm)	5.2	20	5.9	39
β2 (eff) (s−1)	7040		317
E2 (eff)	2.96		0.098

Scheme 5 has 24 parameters but only 16 of them are free (four calculated from microscopic reversibility and four constrained as a consequence of the assumption that the two binding sites are equivalent and independent). Estimates of rate constants are averages of fits to three (choline) or four (TMA) data sets with their coefficient of variation. The estimates of the equilibrium constants are averages of the values obtained from the ratio of the appropriate rate constants for each separate fit. The last two rows give the values of the effective diliganded opening rate constant, β₂ (eff) and of the effective diliganded gating constant, E₂ (eff). These two values describe the overall transition from resting to open conformation so they are the values that are directly comparable with β₂ and E₂ in mechanisms that do not contain a flip state, as in Scheme 4 and Table 5. Note, K_B for choline fits with Scheme 5 was fixed to 9 mm instead of 10 mm used in all other fits because 1 of 3 sets failed to converge with K_B fixed to 10 mm.

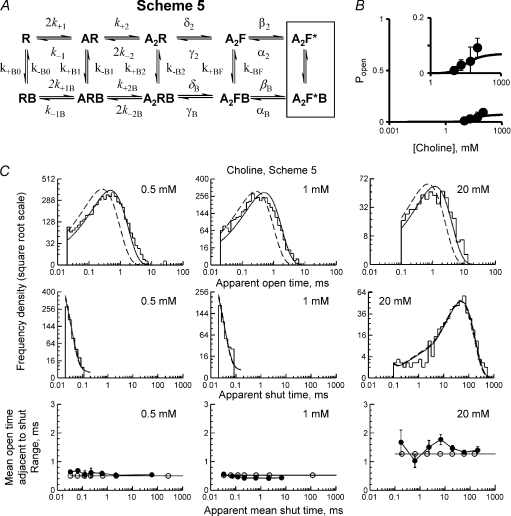
For choline, the fits of the mechanism in Scheme 5 to the single-channel openings are shown in Fig. 10B and C and summarised in Table 6. Again, a flip mechanism which allows the blocked channel to close predicts well the apparent open and shut time distributions and correlation plots. As in the case of TMA, the choline-activated channel can gate with similar efficacy whether or not its channel is blocked. The interpretation of this fit is quite different from that with Scheme 4. In this case, choline is a genuine partial agonist. Although the actual open–shut transition is similar for choline and acetylcholine, as reported for TMA by Lape et al. (2008), the flipping step is even less efficient for choline than for TMA, with an equilibrium constant, F₂, of only 0.0062, rather than 0.1 for TMA (Table 6), and 3.8 for acetylcholine. The effective efficacy for diliganded openings is

(3)

For choline we find E_eff= 0.098 which predicts a maximum P_open=E_eff/(1 +E_eff) = 0.089, consistent with the observed maximum of about 9% (Table 1). In contrast, E_eff for TMA is 2.96 (Table 6) which predicts a maximum P_open of 0.75, as observed (cf. fitted maximum P_open value of 0.78, Fig. 9B). Likewise, the effective opening rate constant, when the flip state is ignored, is

(4)

(Lape et al. 2008). For choline we find β_2eff= 307 s⁻¹, compared with the estimate of the actual opening rate of β₂= 52 500 s⁻¹ (Table 6). So the effective channel opening rate is much slower for choline than for TMA for which we find β_2eff= 7040 s⁻¹ compared with β₂= 71 300 s⁻¹ (Table 6).

Figure 10. Fitting a trapped block mechanism with an intermediate ‘flip’ state to choline data at −80 mV.

A, Scheme 5. The data points in B show cluster P_open produced by choline and the continuous line is the predicted concentration–P_open curve obtained from fitting Scheme 5 to the idealised single-channel records. Panel C compares the prediction of the best HJCFIT fit of Scheme 5 with the actual data, displayed as dwell-time histograms (top two rows) and open–shut correlation plots (for details see Fig. 6).

The shut time distribution at the highest choline concentration consists mostly of shuttings with a mean length of around 50 ms (Fig. 10C, middle row, right). In the case of Scheme 4, these shut times arose in part from the long-lived trapped block state (A₂RB in Scheme 4, Fig. 8), which had a mean lifetime of 50–70 ms (Table 5) but the fit of Scheme 5 (Fig. 10, Table 6) suggests that there are no such long-lived shut states. At 20 mm choline, no individual shut state has a mean lifetime longer than about 90 μs, so it is not obvious why there should be a component of shut times with a mean duration as long as 50 ms. The 50 ms shut time component in this case results from oscillations between the leftmost six shut states in Scheme 5 (i.e. any resting R state in Fig. 10A). This can be shown by inspection of the distributions of the shut times that start in a particular specified shut state. These conditional distributions give the latency until the next opening when you start from the specified shut state. With the fit in Table 6 it is found that starting in any of the leftmost six shut states gives a mean latency of 42–46 ms before the next opening occurs. Once the channel has left the flipped conformation, there will be a shut time with a mean of about this length before the next opening occurs. That is the origin of the 50 ms shut time component. Since all of the individual shut states are short-lived, the length of this latency to the next opening must result from oscillations among the shut states before opening occurs.

After a fit has been achieved, HJCFIT prints these mean ‘latencies to next opening’, as an aid to placing a physical interpretation on the observations. Their calculation follows from results given by Colquhoun & Hawkes (1982, 1995b).

The probability density function for the duration of a shut time is

(5)

where p_F(0) is a row vector that contains the probabilities that a shut time starts in each of the shut states, Q_FF is the submatrix of Q that refers to transitions between shut states, and u_F is a unit column vector. To obtain shut time distributions conditional on which shut state the shut time starts in, we use, in place of the usual equilibrium initial vector, a vector p(0) in which all elements are set to zero apart from the element for the starting state in which we are interested, for which it is set to 1. The mean shut time, from Colquhoun & Hawkes (1982) is p_F(0)(−Q_FF)⁻¹u_F, so the mean shut time conditional on starting in shut state i is just the sum of the ith row of (−Q_FF)⁻¹.

Experimental and calculated concentration jumps with TMA or choline

The fits to single-channel records described so far fail to distinguish between two possibilities for choline. Fits of similar quality can be obtained with Scheme 4 (Fig. 8, Table 5) and with Scheme 5 (Fig. 10, Table 6). It is important to try to distinguish between the two schemes, as they disagree in their estimates of efficacy. The former fits suggest that choline is really a full agonist, and the low observed maximum response is a result of relatively long-lived (60 ms) trapped block of the channel by choline. The latter fit implies that choline is a genuine partial agonist and that all blockages are brief. These two different interpretations of the single-channel data can be distinguished, in principle, by concentration jumps.

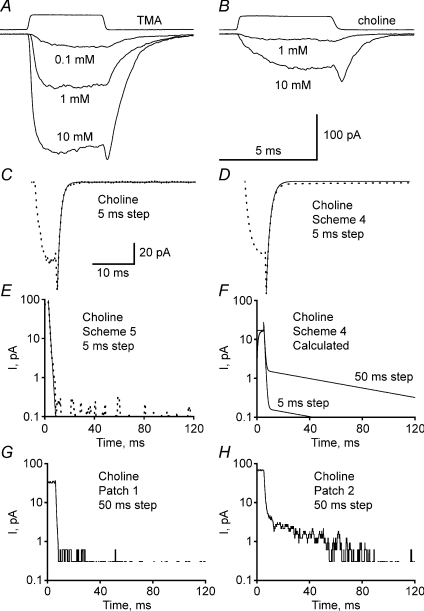
Macroscopic currents activated by TMA or choline were recorded from outside-out patches in response to fast steps in agonist concentration. The upper trace in Fig. 11A is the open tip response to 30% diluted control solution (average of 15 sweeps). The average exchange time of the open tip response was 0.102 ± 0.003 ms during the rising phase (20 to 80%) and 0.132 ± 0.009 ms during the falling phase (80 to 20%; n= 14).

Figure 11A depicts typical current responses to 4 ms concentration steps of 0.1, 1 and 10 mm TMA (averages of 6 to 12 sweeps) at −80 mV transmembrane potential. When activated by 10 mm TMA, currents rose to peak with a time constant, τ_on, of 0.30 ± 0.04 ms (n= 10 patches) and deactivated after the end of the concentration step with a time constant, τ_off, of 0.98 ± 0.07 ms (n= 10 patches; about 4 ms concentration step). Note that at the end of the 10 mm TMA concentration step there is a sudden increase in current. This off-response is commonly seen with fast channel blockers that dissociate from the channel before the channel closes and dissociation from the agonist binding site occurs (Maconochie & Steinbach, 1998; Legendre et al. 2000).

Similar macroscopic currents were evoked by choline concentration steps. Figure 11B shows current responses to 5 ms concentration steps of 1 and 10 mm choline at −80 mV transmembrane potential. No detectable current was evoked by 0.1 mm choline. There was an abrupt current increase at the end of the 10 mm choline concentration pulse, similar to that seen in responses to 10 mm TMA. This is probably due to relief from the fast block (see above), as this increase in current after switching to zero agonist concentration does not occur at a positive membrane potential (+80 mV) where little channel block occurs (Lape et al. 2008). In response to short (4–5 ms) jumps with 10 mm choline, currents rose with a time constant τ_on= 1.0 ± 0.2 ms (n= 4 patches) and fell to baseline after the end of the concentration step with τ_off= 0.76 ± 0.07 ms (n= 4 patches).

The dotted line in Fig. 11C shows the experimental current response to a short (5 ms) pulse of choline (10 mm), and the dotted line in Fig. 11D shows the response that is calculated from the rate constants found by fitting Scheme 4 to single-channel results with choline. The continuous line shows the result of fitting a single-exponential decay to the points on the off-relaxation in both Fig. 11C and D. This fits well the experimental record, but not the prediction of Scheme 4 because this has a slow component of decay with a time constant of about 60 ms: Scheme 5 predicts no such slow tail (see Fig. 11E). This tail originates from re-opening of the channel after entry into the trapped block state (mean lifetime, 50–70 ms). The calculations suggested that the slow component predicted by Scheme 4 carried around half the current, but because it is about 60 times slower than the fast component, it has only about one-sixtieth of the amplitude (at t= 0). That makes it hard to detect. After subtracting the baseline (mean of the last 20 ms of the trace), we re-plotted the observed current (Fig. 11E) on a semi-log scale. No trace of the slow component can be seen in the experimental currents evoked by 5 ms pulses. This is in good agreement with the results of the fit of Scheme 5 to single-channel data. This predicts (continuous line in Fig. 11E) a τ_off for choline macroscopic currents of around 0.9 ± 0.2 ms (n= 3 sets; Table 7), very similar to the experimental value of 0.76 ± 0.07 ms (n= 4 patches) and to the mean burst length measured in single-channel experiments (0.8 ms at −80 mV; 0.05–5 mm choline).

Table 7.

Rise and decay time constants of experimental macroscopic TMA or choline concentration jump current responses and of simulated macroscopic currents

	τon (ms)	τ1off (ms)	τ2off (ms)	A2/A1 (%)	n
Choline, 10 mm
Experiment; 5 ms	(0.8 ± 0.1 (n= 13))	0.76 ± 0.07	—	—	4
Experiment; 50 ms (one component)		1.1 ± 0.2	—	—	7
Experiment; 50 ms (two components)		1.0 ± 0.1	30 ± 20	5.2 ± 0.6	2
Simulation Scheme 4; 5 ms	1.3 ± 0.2	1.0 ± 0.2	60 ± 8	0.9 ± 0.5	3
Simulation Scheme 4; 50 ms	1.3 ± 0.2	1.0 ± 0.2	60 ± 8	10 ± 5	3
Simulation Scheme 5; 5 ms	0.9 ± 0.3	0.9 ± 0.2	—	—	3
TMA, 10 mm
Experiment; 5 ms	0.30 ± 0.04	0.98 ± 0.07	—	—	10
Simulation Scheme 4; 5 ms	0.31 ± 0.04	0.56 ± 0.04	1.8 ± 0.2	40 ± 30	3
Simulation Scheme 5; 5 ms	0.54 ± 0.02	1.8 ± 0.3	—	—	3

Currents were simulated using the rate constants obtained from fits to Scheme 4 or Scheme 5 as responses to 5 or 50 ms 10 mm agonist square pulse. τ_on, on-relaxation time constant (from fits of one exponential for experiments and predictions for simulated traces). τ_off, off-relaxation time constant (from fits of one or two exponentials for experiments and predictions for simulated traces). A2/A1 is ratio of current amplitudes of off-relaxation components. n, patch or set number. Time constants are given as mean ±s.d.m.

On the other hand, Scheme 4 predicts a biexponential decay (dots in Fig. 11D and line in 11F), with a small-amplitude slow component. Judging whether this is present or not requires inspecting the current rather close to the baseline. If there is an additional slow component, and this is due to the accumulation of long-lived shut states, then longer jumps might be expected to make this component more easily detectable and help us distinguish between the schemes. In principle, the relaxation should be described by the sum of five exponential components because Scheme 4 has six kinetically distinguishable states (Colquhoun & Hawkes, 1977), though numerical calculations show that only one or two of these are likely to be measurable: the rest are either too fast, or too small in amplitude to be detectable. Since the agonist concentration is (in principle) always zero during the off-relaxation, the five time constants should always be the same, regardless of the length of the pulse or the concentration during the pulse. They come from the eigenvalues of the Q matrix at zero concentration. However, the relative amplitudes of the five components will depend on the occupancies of each state at t= 0, at the end of the pulse. A longer pulse should allow more receptors to reach the trapped block state in Scheme 4, and hence increase the amplitude of the slow component. This is shown in Fig. 11F, where calculated off-responses to 5 ms and 50 ms choline concentrations steps are shown. As expected, the off-response calculated from Scheme 5 is the same (continuous line in Fig. 11E), whether the pulse is short or long. Additional experiments with longer, 50 ms pulses of choline (10 mm) again produced off-currents with only a single exponential decay with a time constant around 1 ms (as long as the open tip response had a rise time of less than 200 μs and did not show oscillations). This result was seen in 7 out of 9 patches (example patch in Fig. 11G; Table 7), and it again favours Scheme 5. However, in 2 patches out of 9 (example patch 2 in Fig. 11H) there was a small and variable slow component with an amplitude less than 6% of the fast component (at t= 0). Thus, the results from long pulse experiments overall favour Scheme 5, but cannot be regarded as conclusive.

Some of the parameter estimates in our fits to the single-channel data were not well defined, as judged by the large coefficient of variation obtained from replicate sets (see Tables) and from the internal errors calculated from the covariance matrix by HJCFIT (not shown). It is important to know how much the values of these ill-defined rate constants affect the predictions for the time course of the macroscopic response to a pulse of agonist. We tested systematically how sensitive the off-jump predictions are to changing the values of each of the rate constants in the mechanism. In Scheme 4, the off-relaxation was very sensitive only to the values of α₂, β₂, α_B and β_B, all of which are well defined (Table 5). For example, changing α₂ or β₂ by a factor of 10 strongly affected the fast time constant (5- to 10-fold change) of the calculated off-relaxation, while changing β_B by a factor of 10 strongly affected the slow time constant (10- to 40-fold change). Changing any of α₂, β₂, α_B or β_B by the same factor had an effect on relative amplitude of the slow off-relaxation component (2- to 20-fold change). In contrast, changing any of the other rate constants by a factor of 10 had a very small effect (not more than 2% change) on the time constants or the relative amplitudes of the off-relaxation. For Scheme 5, the rate constants are better defined than for Scheme 4 (Table 6) but again it was found that the time constant for the single component off-relaxation depended mainly on the values of α₂, β₂ and γ₂, all of which are well defined (τ changed 2- to 10-fold after changing any of these constants by a factor of 10).

To summarize our results, the single-channel data could only be fitted with a trapped-block with flip mechanism (Scheme 5) for TMA. In the case of choline, we could not distinguish between Scheme 5 and a trapped-block without flip mechanism (Scheme 4) on the basis of the single-channel data. The off-currents recorded after concentration jumps with high concentrations of choline appeared on the whole also to be better predicted by Scheme 5.

Discussion

The main aim of this paper is to discover whether choline is a genuine partial agonist, or whether its small maximum response is a result solely of channel block. In order to do this it is necessary to investigate the nature of the channel block produced by choline.

The results of the maximum likelihood fits of several possible mechanisms to single-channel data at a range of agonist concentrations, and those of the concentration jump experiments, suggest that choline is probably a genuine partial agonist, for the same reason that TMA is partial (Lape et al. 2008), namely because it is weak at triggering the initial conformational change in the receptor activation. The present experiments also showed that choline is not a selective open channel blocker (see discussion in the section below). This probably occurs because the channel can close and return to the resting state while blocked by choline (or indeed TMA, see Lape et al. 2008, supplementary data). In order to account for all the features of the data, the mechanism we propose (Scheme 5 in Fig. 5) incorporates a pre-opening conformational change and both a fast open-channel blocked state and several shut (trapped) blocked states.

Mechanisms of block

The concept of open channel block was first proposed to explain the behaviour of squid axon voltage-gated potassium currents in the presence of intracellular quaternary ammonium compounds (Armstrong, 1966, reviewed in Hille, 2001 and Armstrong, 2007) and was extended to ligand-gated ion channels by Adams (1976, 1977) and by Ruff (1976, 1977) who applied it to the effects of barbiturates and local anaesthetics on muscle nicotinic receptors. The predictions of the simplest sequential mechanism (i.e. the channel can be blocked only when open and can close only when unblocked) were first tested on single-channel data by Neher & Steinbach (1978), who found that it could describe the block of muscle acetylcholine receptors by local anaesthetics (QX222).

It is worth recapitulating here the predictions that can be made for the effects of channel block on single-channel records. If there is a single blocked state that can be entered and left only when the channel is open, then the duration of blockages will be exponentially distributed with mean length 1/k_−B, dependent only on the dissociation rate constant for unblocking. When a channel opens, a blocking molecule may enter and leave the open channel several times (the number of times being a random variable, 0, 1, … times, geometrically distributed). If the channel is blocked at least once, and then re-opens, the result will be a burst of openings, each opening separated by a blockage. As the blocker concentration is increased, blockages become more frequent and the length of this burst will increase, and this increase will be linear when the block is selective for the open state (eqn (1), Neher & Steinbach, 1978; Ogden & Colquhoun, 1985). In this case, the total open time per burst is predicted to be unchanged by the blocker and is 1/α, regardless of blocker concentration. A rigorous treatment of this problem was given by Ogden & Colquhoun, 1985 (Appendix 2).

In practice, the way in which these predictions can be used depends on the ability to detect blockages and bursts. It is useful to distinguish three cases, according to the mean duration of the channel blockages.

Firstly, when blockages are so brief that essentially none of them can be detected, then the burst of openings (separated by unresolved blockages) looks like a single long apparent opening with an amplitude that appears to be reduced by a factor equal to the fraction of time that the apparent opening spends in brief, undetected, blocked state(s). Scheme 5 falls into this category as does the fast block part of Scheme 4.

Secondly, blockages that are long enough that a sufficient number of them can be measured (mean duration roughly 10 μs to tens of milliseconds) result in the appearance of recognisable bursts of openings separated by resolved blockages. This is the most favourable case for analysis. For example, the potent agonist suberyldicholine is also a blocker (Sine & Steinbach, 1984) and produces blockages with mean length of about 5 ms (Ogden & Colquhoun, 1985). The 50–70 ms ‘trapped’ blockages postulated in Scheme 4 (Fig. 5) form part of the burst in a similar way. The lifetime of acetylcholine blockages is about 10–18 μs (Ogden & Colquhoun, 1985; Lape et al. 2008, supplementary information), i.e. in the same range of the nachschlag gap length (Hatton et al. 2003; Lape et al. 2008, supplementary information), sufficiently long that a proportion of them can be detected so they too fall into this category.

The third case occurs when blockages are very long, as inferred for (+)-tubocurarine by Colquhoun et al. (1979). If, as in this case, blockages may last for several seconds, it becomes impossible to detect on a single-channel record whether an individual opening is a re-opening of the channel as it unblocks, or whether it is a separate activation of the channel after a return to the resting state. In such cases, bursts of openings separated by blockages cannot be identified in the experimental record.

It is clear from the reduction in the apparent amplitude of the openings (Fig. 1D) that block by both choline and TMA falls (at least partially) into the first, very fast, category. The observed burst length increases with choline concentration, but this increase is not linear (Fig. 4), which suggests block is not selective for the open state (see also Akk & Steinbach, 2003). In addition to that, the estimate of K_B obtained from fitting eqn (1) to the choline burst length at high concentration is about 8-fold higher than that obtained from the apparent reduction in single-channel current amplitude. Clearly, these observations are not consistent with a selective block of open channels, and unsurprisingly, the scheme that postulates this block mechanism, Scheme 2 (Fig. 5) failed to fit results with either choline or TMA.

It was recognised early that channel block may not be selective for the open state. Even potassium channels in the squid axon can close while blocked by quaternary ammonium compounds (Armstrong, 2007). The possibility that a blocker could bind to both the open and closed states of a ligand-gated channel was first suggested for procaine (Adams, 1977). Interestingly, even block by QX222 could not be accounted for by a single, open-channel blocked state when data at higher QX-222 concentrations were examined with better recording resolution (Neher, 1983). Similarly, results that could not be explained by a selective open channel block mechanism were obtained for neuronal and muscle nicotinic receptors with a variety of compounds that include tetraethylammonium (Adler et al. 1979; Akk & Steinbach, 2003), TMA (Akk & Steinbach, 2003), chlorisondamine (Lingle, 1983), methonium compounds (Gurney & Rang, 1984), isoflurane (Dilger et al. 1992) and acetylcholine itself (Maconochie & Steinbach, 1998). It seems that the channel is more likely to be able to close with the blocker molecule inside it when the molecule is small (Gurney & Rang, 1984). Both of the agonists used in this study, TMA and choline, are relatively small molecules.

Is choline a genuine partial agonist?

We found that, in order to get good fits to our single-channel data, it was necessary to use mechanisms that allow the blocked channel to close and return to the resting state without re-opening. Schemes 4 and 5 both have this property and both give good fits to the single-channel choline data. However, these two schemes differ radically in the way they describe the block and the results of fitting them differ radically in the explanation they provide for the small maximum response seen with choline. Put another way, Schemes 4 and 5 differ in the interpretation they place of the component of shut times seen with choline that has a mean of about 60 ms (Table 3).

Scheme 4 (Fig. 5D) postulates that there is a single long-lived (about 60 ms) trapped-blocked state (A₂RB), as well as the fast-blocked states that are responsible for the decrease in the apparent amplitude of openings at high concentrations. Entry into this trapped block state followed by re-opening contributes to the observed 60 ms shut time (see Results). The existence of both slow and fast blocked states is sufficient to limit the maximum response (P_open) to about 9%, as observed, despite the fact that the fit predicts that choline is actually a full agonist, almost as good at opening channels as acetylcholine itself. This prediction comes, essentially, from the existence of very short shut times, similar to those seen with acetylcholine, and when these are interpreted as brief sojourns in A2R before re-opening, they imply a fast channel opening rate.

An alternative view of the interpretation of short shuttings was provided by the ‘flip model’, first described for glycine receptors (Burzomato et al. 2004) and subsequently found to give a good description of the response of nicotinic receptors to acetylcholine and TMA (Lape et al. 2008), so it was natural to try the same sort of mechanism for choline. Scheme 5 (Fig. 5) differs from Scheme 4 in two important ways. Firstly, it contains a flipped state, a short-lived shut conformation that follows binding but precedes opening. Secondly, it does not postulate the existence of a single long-lived blocked state. Block of the open channel is unresolvably fast (A₂F*B), and accounts for the decrease in apparent channel amplitude with concentration. In addition to that, block can occur for any of the states in the activation mechanism, i.e. for the flipped state and for the resting states at all levels of liganding. The results of fitting Scheme 5 imply that: (a) the 60 ms component of shut times seen with choline (Table 3) is not generated by sojourns in any single state, but rather by oscillations between the six leftmost shut states in Scheme 5, none of which individually has a mean lifetime longer than 90 μs at high concentrations of choline, (b) the opening and shutting rates of the channel are quite similar to those for acetylcholine itself, so generating the observed component of very short shut times (mean 18 μs, Table 3), and (c) choline is nevertheless a weak partial agonist because the equilibrium constant for flipping of the diliganded receptor is very small (F₂= 0.0062, Table 6).

Two arguments favour Scheme 5 rather than Scheme 4. First, Scheme 4 predicts a slow (about 60 ms) component in the off-relaxation (‘deactivation’) following a pulse of agonist. We could detect no such component (see Results), but this cannot be regarded as conclusive because the predicted amplitude of the slow component was small under the conditions where measurements could be made. Second, it was clear that Scheme 4 could not provide a good fit for TMA, and it would be surprising if TMA and choline did not have qualitatively similar modes of action. For these reasons we prefer Scheme 5 as the most likely description of the action of choline. According to this interpretation, choline is a partial agonist in the same sense that TMA is partial (Lape et al. 2008), but choline is much weaker.

Another mechanism that postulates intermediate states on the activation pathway between agonist binding and channel opening has been proposed recently. It has also been applied to single-channel data from muscle nicotinic receptors (Mukhtasimova et al. 2009). They called the intermediate states ‘primed’, rather than ‘flipped’. This model is not used here, largely because it has too many free parameters for all of them to be defined. Its relationship to our approach will be discussed fully in a future publication.

The block by choline and by tetraethylammonium has been recently investigated (Akk & Steinbach, 2003; Purohit & Grosman, 2006). Our findings are in good agreement with both studies, which have analysed agonist-activated single-channel burst lengths and have concluded that the channel can close while blocked and that there is also very fast open channel block, manifest as a reduction in apparent channel amplitude. Akk & Steinbach (2003) have estimated that the closing rate constant of the channel is not affected by the presence of tetraethylammonium trapped in the channel, whereas Purohit & Grosman (2006) have concluded that the choline-blocked channel closes about 10 times more slowly than the unblocked one. Our analysis shows only a small slowing (about 3-fold) of the closing rate when the channel is blocked by choline, and practically no slowing with TMA. The discrepancy with Purohit & Grosman (2006) might stem from the fact that we used maximum likelihood fit of a more detailed mechanism to single-channel records observed at a range of concentrations.

In order to compare the choline results with previous studies that did not include a flip state, we need to look at the effective opening transition rate, β_2eff, for going from the resting conformation to the open state and the corresponding effective equilibrium constant 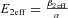. These are calculated as in eqns (3) and (4). For choline we find E_eff= 0.098 which predicts a maximum P_open=E_eff/(1 +E_eff) = 0.089, consistent with the observed maximum of about 9% (Table 1). In contrast, E_eff for TMA is 2.96 (Table 6) which predicts a maximum P_open of 0.75, as observed (cf. fitted maximum P_open of 0.78; Fig. 9B; cf. the values for ACh E_eff= 27.2 and maximum P_open= 0.96, Lape et al. 2008). Likewise, the effective opening rate constant, when the flip state is ignored, is given by eqn (4) (Lape et al. 2008). For choline we find β_2eff= 307 s⁻¹, compared with the estimate of the actual opening rate of β₂= 52 500 s⁻¹ (Table 6). So the effective channel opening rate is much slower for choline than for TMA for which we find β_2eff= 7040 s⁻¹ compared with β₂= 71 300 s⁻¹ (Table 6; compare values for ACh β_2eff= 69 400 s⁻¹ and β₂= 87 700 s⁻¹). The values of E_eff and of β_2eff found here can be compared with values of E and β₂ estimated by others on the basis of mechanisms that do not contain the flip state (and with simpler descriptions of channel block). Our value of β_2eff= 307 s⁻¹ for choline is similar to the overall opening rate constant of 257 s⁻¹ reported by Grosman & Auerbach (2000), though somewhat faster than the values reported by De Rosa et al. (2002) and Bouzat et al. (2002) or by Akk et al. (2005), which are in the range of 50–110 s⁻¹. These papers estimated the efficacy of choline at 0.035 to 0.05, values somewhat smaller than our estimate of E_eff= 0.098.

The present results also confirm our recent findings for channel activation by TMA (Lape et al. 2008), because the values of the gating rate constants that we obtained were not materially changed by introducing a detailed description of the block mechanism (see Table 6).

The energetic view of the proposed mechanism

The transitions between states for the saturated receptor are shown diagrammatically in Fig. 12. The resting (shut) channel changes conformation to reach a partially activated state (flipped), still shut, but with increased affinity for the agonist (ellipses). It is from this flipped state that the channel can open (right). The reaction rates for channel activation by acetylcholine, TMA and choline differ largely in the first step, the flipping. A channel occupied by acetylcholine does not stay long in the resting state, but quickly flips. When TMA, or especially choline are bound, the channel takes a long time to flip, so it spends much more time in the closed resting state. Once the channel has reached the flipped intermediate state, it opens quickly, regardless of which agonist is bound. With acetylcholine almost every time a channel flips it will open (the probability of opening, rather than unflipping, is 91%), but for choline this probability is 59% so with choline the channel must flip an average of 1.4 times before the channel opens.

Figure 12. Activation of the muscle nicotinic receptor by acetylcholine, TMA and choline.

A, diagrammatic representation of the transitions between the three states of the fully saturated receptor, from left to right, resting, flipped and open (blocked states are excluded). B, the rate constants for transitions are marked on the arrows (units are s⁻¹), and the size of the arrow is a rough reflection of the transition rate. The mean lifetime of each state is shown together with the proportion of time (percentage) spent by a bound channel in each of the states at equilibrium (the equilibrium occupancy). Choline and TMA values are those from Scheme 5 which interprets their action as genuine partial agonism, due to reluctance to enter the flip state. Acetylcholine values are from Lape et al. (2008). C, energy diagrams for saturated receptors with three agonists, acetylcholine (continuous line), TMA (dashed line) and choline (dotted line), showing the two steps, from resting to flipped and from flipped to open. The calculations used a frequency factor of 10⁷ s⁻¹ (Andersen, 1999) and the lines are shifted vertically so that they meet at the open state.

The energy diagram in Fig. 12C makes it obvious that the main differences between the agonists are in how easily they can take the first step, from resting to flipped. For the overall transition from the resting conformation to the open state, acetylcholine is strongly downhill (maximum P_open= 0.96), and TMA is slightly downhill, corresponding to the fact that its maximum P_open (0.75) is a bit over 50%. In contrast, choline is strongly uphill, corresponding to the maximum P_open of about 0.09. In contrast, the open–shut transition is essentially identical for acetylcholine and TMA and very similar for choline too. It is in the resting to flipped transition that the explanation for partial agonism lies. It is downhill only for acetylcholine (F₂= 3.8) but uphill for TMA (F₂= 0.11) and strongly uphill for choline (F₂= 0.0062; Lape et al. 2008 and Table 6).

In summary, the balance of evidence favours the view that choline and TMA open the channel as well as acetylcholine itself, but that TMA, and especially choline, are nevertheless genuine partial agonists because they are bad at producing the initial conformation change that must precede opening.

Glossary

Abbreviations

P_open

probability of being open

pdf

probability density function

s.d.m.

standard deviation of the mean

TMA

tetramethylammonium

Author contributions

All of the authors contributed to this study and approved the final manuscript. The experimental work was carried out by R.L. and P.K. at University College London.