Dielectrophoretic Separation of Cancer Cells from Blood

Abstract

Recent measurements have demonstrated that the dielectric properties of cells depend on their type and physiological status. For example, MDA-231 human breast cancer cells were found to have a mean plasma membrane specific capacitance of 26 mF/m², more than double the value (11 mF/m²) observed for resting T-lymphocytes. When an inhomogeneous ac electric field is applied to a particle, a dielectrophoretic (DEP) force arises that depends on the particle dielectric properties. Therefore, cells having different dielectric characteristics will experience differential DEP forces when subjected to such a field. In this article, we demonstrate the use of differential DEP forces for the separation of several different cancerous cell types from blood in a dielectric affinity column. These separations were accomplished using thin, flat chambers having microelectrode arrays on the bottom wall. DEP forces generated by the application of ac fields to the electrodes were used to influence the rate of elution of cells from the chamber by hydrodynamic forces within a parabolic fluid flow profile. Electrorotation measurements were first made on the various cell types found within cell mixtures to be separated, and theoretical modeling was used to derive the cell dielectric parameters. Optimum separation conditions were then predicted from the frequency and suspension conductivity dependencies of cell DEP responses defined by these parameters. Cell separations were then undertaken for various ratios of cancerous to normal cells at different concentrations. Eluted cells were characterized in terms of separation efficiency, cell viability, and separation speed. For example, 100% efficiency was achieved for purging MDA-231 cells from blood at the tumor to normal cell ratio 1:1 × 10⁵ or 1:3 × 10⁵, cell viability was not compromised, and separation rates were at least 10³ cells/s. Theoretical and experimental criteria for the design and operation of such separators are presented.

I. Introduction

The ability to identify, characterize, and purify cell subpopulations is fundamental to numerous biological and medical applications, often forming the starting point for research protocols and the basis for current and emerging clinical protocols. For example, cell separation can make possible life-saving procedures, such as autologous bone marrow transplantation for the remediation of advanced cancers, where the removal of cancer-causing metastatic cells from a patient’s marrow is necessitated [1]. In other applications, such as the study of signaling between blood cells [2], [3], highly purified cell subpopulations permit studies that would otherwise be impossible. Current approaches to cell sorting most frequently exploit differences in cell density [4], specific immunologic targets [5], or receptor–ligand interactions [6] to isolate particular cells. These techniques are often inadequate, and sorting devices capable of identifying and selectively manipulating cells through novel physical properties are, therefore, desirable. To this end, we and others have applied the principles of ac electrokinetics, not only for the dielectric characterization of mammalian cells through the method of electrorotation (ROT) [7]–[10], but also for cell discrimination and sorting [11]–[15]. In these techniques, cells become electrically polarized when they are subjected to an ac electric field. If that field is inhomogeneous, then the cells experience a lateral dielectrophoretic (DEP) force, the frequency response of which is a function of their intrinsic electrical properties [13]. In turn, these properties depend strongly on cell composition and organization, features that reflect cell morphology and phenotype. Cells differing in their electrical polarizabilities can, thus, experience differential forces in the inhomogeneous electric field [16], [17]. It follows that DEP not only offers a way to discriminate between different cell types, but also provides a physical force with which to drive their separation.

Previously, we and our collaborators demonstrated that DEP can be used, on a microscopic scale, to separate bacteria from erythrocytes [18], viable from nonviable yeast cells [19], and erythroleukemia cells from erythrocytes [15]. However, the differences in the electrical polarizabilities of the cell types in those various mixtures were greater than those to be expected in many typical cell sorting applications. Therefore, we refined the DEP methodology and constructed a dielectric affinity column. We showed that such a column could be used to separate and harvest viable HL-60 human leukemia cells and MDA-231 metastatic breast cancer cells from whole human blood [16], [17]. In this paper, we expand on the principles of cell sorting by dielectric affinity and derive expressions that allow optimal cell sorting conditions and efficiencies to be assessed. We extend the principle to other human breast cancer cell lines and conclude that the cell dielectric properties, determined by cell surface morphology, cell size, and other factors, can be exploited for dielectrophoretic separation of different cell types.

II. Methods

A. Cell Preparations

Tumor cell lines MDA-231, MDA-435, and MDA-468 were originally isolated from pleural effusions of human breast cancer patients at the University of Texas M. D. Anderson Cancer Center and started in culture by Cailleau et al. [20]. These lines are of interest because they have different abilities to form tumors and to metastasize in nude mice [21]. Cells were cultured in RPMI 1640 medium, supplemented with 5% fetal bovine serum, 20 mM HEPES, and 1 mM L-glutamine in vented plastic flasks under a 5% CO₂-95% air atmosphere at 37 °C. All cultures were free of, and periodically checked by radionucleic acid hybridization assay (Gen-Probe, Inc.) for, mycoplasma. Tumor cells were harvested from 60% to 80% confluent cultures by brief exposure to 0.25% trypsin-0.02% EDTA solution. Human blood was obtained through the public supply (Gulf Coast Regional Blood Bank). Cells (EDTA anticoagulant) were washed twice in three volumes Ca²⁺/Mg²⁺-free Hanks’ buffered saline solution to remove serum. Cell viabilities were determined prior to use and following DEP sorting by trypan blue dye exclusion.

B. Electrorotation Measurements

The dielectric properties of single, isolated, viable cells were measured using the ROT technique. Cell suspensions were prepared in 8.5% (w/v) sucrose plus 0.3% (w/v) dextrose buffer to provide an isotonic supporting medium of low conductivity. Hemisodium EDTA was used to adjust the suspension to a conductivity of 56 mS/m to maximize the accuracy of derived dielectric parameters [22]. EDTA also chelated divalent cations and helped prevent cell adhesion to the surfaces of the ROT chamber. 100/μL of suspension containing approximately 5 × 10⁴ cells/mL was sealed into the electrode chamber, and cells were allowed to settle onto the glass substrate of a polynomial electrode [10], [15], [23] (about 30 s). A rotating field in the frequency range 100 Hz–140 MHz was then established by applying four sinusoidal waves (1 V rms) in phase quadrature to the electrode array from a signal generator custom-built according to the principles of Hölzel [24]. Electric fields at much higher strengths than used for our ROT measurements [15] have been shown to not seriously affect cell membrane integrity or cell growth [17]. ROT spectra were measured by timing rotation rates of individual cells at four points per decade over the frequency range studied. Cells that were at least four diameters apart were studied, so as to avoid interferences from cell–cell dielectric interactions. Measurements were made on at least 20 cells of each type.

The single-shell dielectric model [8], [15], [25], which has been shown to represent a reasonable approximation for mammalian cells in the frequency range of interest here, was used to analyze the cell dielectric properties, as described previously in [10]. This analysis can provide estimates of the cell membrane specific capacitance C_spec and the cell interior permittivity ε_in and conductivity σ_in. We have shown previously that these analysis procedures provide parameter estimates typically within 10% of the true values at a confidence level of 90% [22]. For the purpose of the present study, we focused on the cell membrane specific capacitance C_spec, the parameter that was found to dominate cell separation behavior in the frequency range investigated. The parameter sensitivity analysis [22] showed that the specific capacitance could most accurately be measured under conditions that minimized the influence of the (small) plasma membrane conductivity. This accounts for our choice of a suspension conductivity of 56 mS/m, which effectively suppressed any significant influence of the membrane conductivity on the ROT responses. Sizes of the cells undergoing ROT study were determined microscopically, either by measurement against a micrometer scale or else by image analysis of cell area.

C. Dielectric Separation Chambers

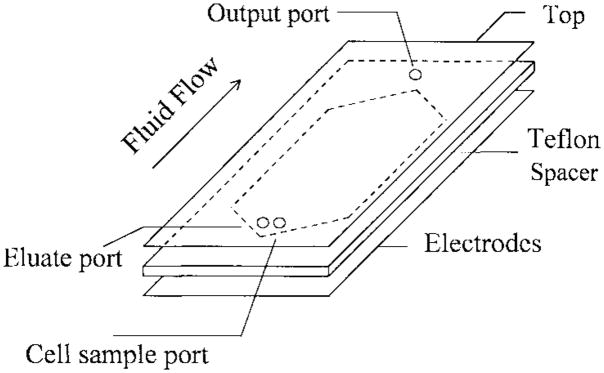
Chambers, as schematically shown in Fig. 1, consisted of two 2-mm thick glass walls of 25-mm × 75-mm dimensions sealed along their long edges with UV-curing epoxy glue. The lower wall was equipped with an interdigitated electrode (see Fig. 2) of 0.2-μm gold fabricated by microphotolithography. Prior to assembly, small holes were drilled in the top chamber wall with a diamond drill, and Teflon tubes (to fit 20-gauge syringe needles) were glued (Impruv, Loctite) in place to form ports for injection and removal of cell suspensions and eluate buffers. Wall spacing was maintained by a Teflon gasket of 100-μm thickness having a slot of 1.5-cm width running along the active length of the separator. The gasket slot was tapered to points at either end, below each chamber port. Fluid injected through the inlet port thus spread out as it traveled along the widening taper, exhibited a constant flow rate over most of the active region of the electrode where the sides of the gasket slot were parallel, and finally narrowed again along the taper to the outlet port.

Fig. 1.

The schematic drawing of a dielectric-affinity separation chamber. In operation, the cell mixture sample is loaded into the chamber through the cell sample port. Then, appropriate electrical signals are applied to the DEP electrode array. Fluid flow is then started by pumping eluate through the eluate inlet port. The eluted cells are collected at the chamber output port at the other end of the chamber.

Fig. 2.

Sequence of cell separation by dielectric affinity chambers. (a) After DEP collection at 500 kHz, all cells were accumulated at electrode edges before the fluid flow was started. (b) The DEP frequency was dropped to 50 kHz and fluid flow started at 10 μL/min. Blood cells were released and carried off by the eluate (these cells appear as streaks between the electrodes), while human breast cancer cells were retained. (c) Cancer cells remained on the electrode tips after blood cells had been swept downstream.

D. Cell Separations

In separation experiments, 10⁵–10⁶ cells were injected to fill 50% of the chamber. Cells were suspended in isotonic 8.5% sucrose plus 0.3% dextrose buffer of conductivity ~10 mS/m. A 500-kHz electrical signal of 2 V rms, provided by a function generator with FM and AM sweeping capabilities (BK Precision Electronics), was applied initially to collect all cells. Fluid flow, provided by two digital syringe pumps (KD Scientific, Boston, MA) connected in push–pull configuration between the chamber inlet and outlet ports, was then started at a rate of between 5–100 μL/min and the field frequency was lowered to that predicted from the ROT analysis as optimal for separation (see later). Cells were collected as they eluted from the chamber. After all cells freed by the reduction of field frequency had been swept out, the field was removed, and the cells that had been retained were released, eluted, and collected separately.

Breast tumor cells were prelabeled to facilitate tracking during separation experiments by incubation for 10 min in 25 μg/mL BCECF-AM (Molecular Probes), a fluoresceine probe that is irreversibly accumulated by cells through the action of nonspecific esterases. BCECF is only accumulated by viable cells and, therefore, simultaneously acted as a viability indicator during cell tracking. This technique was found to allow convenient identification of tumor cells, which appeared under fluorescent microscopy as brilliant spheres against a dark field of unlabeled cells, and even a single tumor cell within a very large unlabeled population (>10⁵ blood cells) could be identified and tracked. This method of tumor cell detection was found to be very effective, allowing every tumor cell in the starting cell mixture to be accounted for following separation. In this way, the efficiencies in the various separation experiments could be accurately assessed. The separation chamber was mounted on a Microphot-SA microscope (magnification X50–X600) equipped with epifluorescence, video-recording capabilities, and a Matrox image analysis system to allow observation of any section of the glass-walled chamber. This permitted manual or automated counting of BCECF-labeled versus unlabeled cells on the electrode and allowed observations of the trajectories, elevations, interactions, and distributions of fluorescently labeled cells during separations.

Known starting ratios of human breast tumor to blood cells, ranging from 1:3 to 1:3 × 10⁵ were mixed and injected into the separators in different experiments. Separation efficiencies were assessed by collecting separated fractions and observing the changes in tumor cell to blood cell ratios.

III. Results and Discussion

A. Cell Separations

A typical sequence of purging MDA-231 cells from blood using a dielectric affinity column is shown in Fig. 2. After positive DEP collection of all the cells at electrode edges with applied signals of 500 kHz at 2 V rms [Fig. 2(a)], the fluid flow was started at a desired rate (5–10 μL/min). Then, the frequency of the applied signals was lowered to an optimal value (80 kHz) for cell separation, as predicted from ROT analysis. Blood cells were carried away with eluate, while the MDA-231 cells were retained by the electrodes [Fig. 1(b)]. After 10–20 min (depending on the fluid flow rate), all blood cells had eluted from the chamber and had been collected, leaving the MDA-231 cells behind [Fig. 1(c)]. The voltage was then turned off to release the tumor cells held by DEP, and these were then eluted and collected separately.

Table I summarizes the separation efficiency for removal of MDA-231 breast cancer cells from blood (similar separation efficiencies were determined for MDA-435 and MDA-468 cells, data not shown here). In these experiments, specific target ratios of MDA-231/blood cells were mixed, and the actual ratios were then determined by counting individual, fluorescently labeled tumor cells in the dielectric affinity column before and after separation. It is apparent from Table I that the cell retention efficiency for breast tumor cells was high. When the ratio of breast cancer cells/blood cells exceeded about 1:1 × 10⁴, it was not feasible to count individual breast cancer cells on the electrode. In this case, we examined the eluted cell fractions in an effort to detect cancer cells that had escaped from the electrode array.

TABLE I.

Counts of MDA-231 Human Breast Cancer Cells in the Dielectric-Affinity Column Before and After Separation^†

Target Ratio	Measured starting Ratio	Tumor cells on electrodes before Separation‡	Tumor cells on electrodes after Separation‡	Efficiency of purging tumor cells
1:3	1:2.9	N/A	N/A	>95%
1:103	1:1.1×103	N/A	N/A	>95%
1:104	1:1.2×104	98	94	96%
1:104	1:1.8×104	56	53	95%
1:105	1:0.9×105	3	3	100%
1:3×105	1:2.8×105	1	1	100%

^†: Applied voltage = 2 V rms at 50 kHz; eluate flow rate = 5 μL/min; suspension conductivity =10 mS/m.

^‡: The in-situ counting of tumor cells in the separation column was made for the tumor to normal cell ratio higher than 1:10⁴. Below that, the counting involved too many cells and purging efficiencies were estimated by counting residual tumor cells that contaminated the “supposed” blood cell fraction.

The viability of the tumor cells was determined following separation by trypan blue exclusion. It was found that the tumor cells, despite being subjected to electrical fields of relatively high strength (>2.5 × 10⁴ V/m), had viabilities exceeding 95%, if they were allowed to recover in culture media at 37 °C for 3 h. Although the cell viability assayed with trypan blue was low if cells were examined immediately following separation in sucrose suspension, our data nevertheless suggest that cells can recover from any detrimental electric-field effects. A systematic investigation of electrical field effect that may influence cell integrity and viability is in progress.

The cell sorting rate in these separation experiments was about 10³/s, similar to that of the conventional fluorescent-activated cell sorters (FACS) [26]. We expect that this DEP sorting rate will be readily increased by two orders of magnitude if the dielectric affinity column is scaled up to a larger size.

B. Separation Mechanics

The DEP cell sorting described here involves the selective removal of cells from their dielectrophoretic potential wells by applied fluid forces. Cells in shallow wells were swept away by fluid flow and harvested, while cells in deeper wells were held in place by the DEP forces until the field was removed. We refer to a sorting chamber designed for this purpose as a dielectric affinity column [16], [17]. In order for cell separation to occur, the DEP force component on the immobilized cell type in the fluid-flow direction must exceed the hydrodynamic Stokes forces, while the hydrodynamic forces must, in turn, be greater than the DEP forces on the cell types to be swept away. We have shown previously that this occurs when

$$r_{1}Re[f_{CM1}]k_{yl}>\alpha \frac{\langle v\rangle }{V^2}>r_{2}Re[f_{CM2}]k_{y2}$$ (1)

where α = 36πcη/wε_s is a hydrodynamic constant for a given chamber geometry and eluate, and r₁ and r₂ are the radii of the respective cell types having Claussius-Mossotti factors f_CM1 and f_CM2. The left- and right-hand terms of this inequality determine the relative DEP forces on the different cell types, while the center term reflects the competition between the mean fluid flow rate 〈v〉 and the applied voltage V. Factors k_y1 and k_y2 are geometrical terms that depend on the electrode design and are calculated from electric field simulations [13], [27], [28]. Since factors k_y1and k_y2 are essentially the same for all the cells in the separation mxiture, the parameter determining whether two cell types can be separated is the product between the cell radius and the real part (Re[f_CM]) of the Clausius-Mossotti factor f_CM. The factors f_CM, reflecting the magnitude and polarity of the induced polarization in the cells by the applied field, are given by

$$f_{CM}=\frac{({\epsilon }_p-{\epsilon }_s)-i({\sigma }_p-{\sigma }_s)/(2\pi f)}{({\epsilon }_p+2{\epsilon }_s)-i({\sigma }_p+2{\sigma }_s)/(2\pi f)}$$ (2)

where ε and σ refer to the dielectric permittivity and conductivity, and the subscripts p and s indicate the cells and their susenpending medium, respectively. Evidently, f_CM depends critically on the suspension medium characteristics (ε_s and σ_s), on the applied frequency (f) and, more importantly from the point of view of cell separation, on the dielectric properties of the cells (ε_p and σ_p, which are, in general, frequency dependent). It follows that the separation of dissimilar cell types can be brought about if it is possible to adjust the suspension conditions, the frequency, and the flow rate and voltage to satisfy (1).

C. Derivation of Re[f_CM]

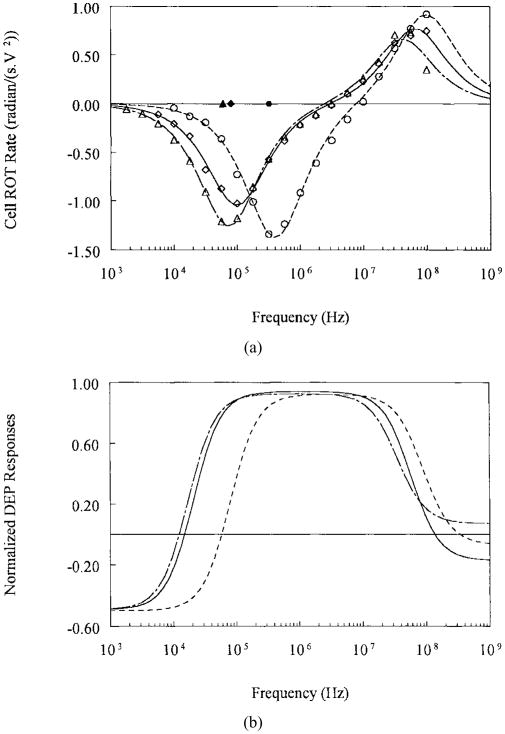
We determined the frequency dependence of the real part of the Clausius–Mossotti factor Re[f_CM] from the cellular dielectric parameters derived by fitting measured ROT spectra of individual cells to the single-shell dielectric model. Typical ROT spectra obtained for T-lymphocytes, MDA-231, and MDA-468 cells are shown in Fig. 3(a). Cells exhibited antifield rotation in the low-frequency range (<1–10 MHz) and cofield rotation for the higher frequencies. It is well established that the antifield and cofield peak frequencies are determined by dielectric characteristics of the plasma membrane and the cell interior, respectively [7], [10]. Because we chose relatively modest suspension conductivities to suppress the influence of membrane conductance on the ROT responses, the membrane capacitance was effectively the only cell dielectric parameter to influence the antifield rotation in the low frequency range. The peak frequencies of T-lymphocytes were more than twice those for the MDA cells, and it follows that there were significant differences between the membrane capacitance of these cell types (Table II). Since our cell separation operated in the frequency range in which cell dielectrophoretic responses were dominated by membrane capacitance, this parameter formed the basis for the cell sorting described here.

Fig. 3.

(a) Typical ROT spectra for the human breast cancer cell lines MDA-231 (◇), MDA-468 (△) and for T-lymphocytes (o) in isotonic sucrose suspension of conductivity 56 mS/m. Continuous curves are the best fits of single-shell dielectric model [8], [15], [25]. (b) DEP responses for the same cell types calculated from the dielectric parameters derived from the ROT spectra for the conditions used in cell separation experiments MDA-231 cells (—), MDA-468 (— –), and for T-lymphocytes (– – –).

TABLE II.

Dielectric and Surface Area Parameters for Several Cell Types From ROT Measurements

Cell Type	r (μm)	Cspec.(mF/m2)	Specific area, φ	fo/σs(MHz.m/S)
RBC	2.8±0.1	9±0.8	1	10.0
T-lymphocyte	3.5±0.2	11±1.1	1.2	6.6
Hepatocyte	10±0.61	80±17	8.9	0.32
DS19	5.9±0.45	17.4±2.0	1.93	2.5
HL-60	5.8±0.42	15±1.9	1.67	2.9
MDA-231	6.2±0.58	25.9±3.7	2.88	1.6
MDA-435	7.7±0.72	13.5±1.9	1.5	2.4
MDA-468	7.2±0.66	27.5±4.2	3.06	1.3

Typical dependencies of Re[f_CM] on the field frequency, calculated from the mean cell dielectric parameters, are shown in Fig. 3b, and the values of the predicted DEP crossover frequencies (the frequencies at which the DEP force changes direction) normalized against suspension conductivity are given in Table II. Re[f_CM] is negative (negative DEP force repelling cells from high field regions) at frequencies below 10 ~ 50 kHz. With increasing frequency, the Re[f_CM] becomes steadily greater until it reaches a maximal positive value at 50 ~ 250 kHz. The breast tumor cells exhibited a negative to positive DEP force transition at frequencies (~10 kHz), significantly lower than T-lymphocytes (~50 kHz) or erythrocytes (~70 kHz, data not shown). Thus, it was possible to operate the separation chambers under applied frequency conditions (50 kHz for the purging MDA231 cells) where the tumor cells were retained by strong positive DEP force (Re[f_CM] = +0.5 for MDA231 cells) at the electrode edges while the fluid drag forces removed the blood cells that experienced negative forces (Re[f_CM] = −0.1).

By using k_y values derived from simulations for the electrode characteristics [19] and Re[f_CM] values determined from ROT measurements, and by applying (1), we were able to achieve selective DEP retention of various human breast cancer cells from blood (see, for example, Table I). Excellent separation and recovery efficiencies were obtained because, in each case, the tumor cells were retained in the chamber indefinitely by the DEP forces, while blood cells were swept out by the force of the fluid.

The separation inequality (1) was derived for the idealized case of two isolated, individual cells. However, in reality, several deviations from this idealized condition occurred in the practical separation chambers used here. First, individual cells within a population of a single type are not identical, but heterogeneous, in their dielectric properties. Indeed, an important and dangerous characteristics of tumor cell populations, from the clinical standpoint, is a large degree of such heterogeneity [29]. For example, the derived membrane capacitance for MDA231 cells was found to range from 19 to 33 mF/m². To achieve efficient separations, it is necessary for all the individual cells in a mixture to satisfy (1). The smallest difference in membrane capacitance between MDA cells and lymphocytes, as determined from electrorotation measurements, was 19 versus 13 mF/m². Fortunately, inequality (1) still held even for this most unfavorable case, accounting for the good separation efficiencies observed for these cell types. Secondly, closely neighboring cells in a cell mixture tend to exhibit dipole-dipole interactions under the influence of the applied field [30]. Such effects, which can lead to attractive forces between cells, are not taken into account in the derivation of the inequality (1). In our previous papers, the technique of “swept frequencies” was employed in order to subject cells to DEP conditions that periodically discouraged and tended to break up close cell associations. We recognize, however, that more efforts need to be given to this problem, in order that DEP separators can be efficient at high cell concentrations.

D. Cell Dielectric Properties

The complex permittivity of a living cell can be approximated, according to the single-shell dielectric model, as

$${\epsilon }_p^{\ast }={\epsilon }_{\text{mem}}^{\ast }\left[\frac{{\left(\frac{r}{r-d}\right)}^3+2\left(\frac{{\epsilon }_{\text{in}}^{\ast }-{\epsilon }_{\text{mem}}^{\ast }}{{\epsilon }_{\text{in}}^{\ast }+2{\epsilon }_{\text{mem}}^{\ast }}\right)}{{\left(\frac{r}{r-d}\right)}^3-\left(\frac{{\epsilon }_{\text{in}}^{\ast }-{\epsilon }_{\text{mem}}^{\ast }}{{\epsilon }_{\text{in}}^{\ast }+2{\epsilon }_{\text{mem}}^{\ast }}\right)}\right]$$ (3)

where ${\epsilon }_{\text{in}}^{\ast }(={\epsilon }_{\text{in}}-i{\sigma }_{\text{in}}/\omega )$ is the effective complex permittivity of the cell interior and ${\epsilon }_{\text{mem}}^{\ast }(={\epsilon }_{\text{mem}}-i{\sigma }_{\text{mem}}/\omega )$ is that of the cell membrane. The plasma membrane of a living cell is many orders of magnitude less conducting than the cell interior (σ_mem ≪ σ_in), thus, at frequencies well below the Maxwell-Wagner relaxation frequency (~ MHz), the factor

$$\left(\frac{{\epsilon }_{\text{in}}^{\ast }-{\epsilon }_{\text{mem}}^{\ast }}{{\epsilon }_{\text{in}}^{\ast }+2{\epsilon }_{\text{mem}}^{\ast }}\right)\approx 1.$$ (4)

Now, if the membrane thickness (d) is very small relative to cell radius (d ≪ r), then the cell complex permittivity simplifies to

$${\epsilon }_p^{\ast }=\frac{r}{d}{\epsilon }_{\text{mem}}^{\ast }=r\left(C_{\text{spec}}-j\frac{G_{\text{spec}}}{2\pi f}\right)$$ (5)

where C_spec and G_spec are the specific membrane capacitance and conductance, respectively. This indicates that in the low frequency range, the complex permittivity of a living cell is simply that of the plasma membrane multiplied by the ratio of cell radius to membrane thickness. In the suspensions of modest conductivities used in our ROT measurements and cell separations, the influence of the membrane conductance was effectively suppressed because σ_s ≪ σ_mem. As a result, the plasma membrane capacitance determined the cell dielectric properties in the frequency range of the cell separations and served as the separation criterion.

Three possible explanations might account for the differences observed in the specific membrane capacitance values for the different cell types (see Table II), namely, differences in the thickness, composition, and folding of the membrane. We demonstrated earlier that differences in membrane composition or thickness between DS19 cells could not account for the relatively large membrane capacitance changes observed before and after induced differentiation [15]. Therefore, we undertook both scanning and transmission electron microscopic studies to investigate the extent of membrane structural changes during DS19 differentiation, and these measurements suggested that the key parameter determining membrane capacitance differences was membrane folding. We verified this by manipulating membrane folding of DS19 cells by altering the suspending medium osmolality, thereby expanding or compressing the cell body and subjecting the membrane to conformational changes [10]. Our findings were in complete agreement with those reported by Arnold and his co-workers [31]. This principle, that complex membrane structures give rise to large membrane specific capacitances, is further confirmed by measurements on other cell types, including hepatocytes (see Table II). In that extreme case, the membrane-specific capacitance exceeds that expected of a smooth, lipid bilayer by a factor of ten. In order to quantify the amount of membrane folding, we defined a membrane-specific area parameter φ to represent the ratio of the actual membrane area that covers a cell to the membrane area that would be required to cover a smooth sphere of the same average diameter. Thus, φ would assume the value 1 for a perfectly smooth cell and higher values for cells exhibiting surface complexity. Such complexity includes any morphological feature that increases cell surface area, including villi, microvilli, blebs still attached to the cell body, folds, ridges, and ruffles. Our SEM studies confirmed that φ changed from 1.5–2.0 to 2.1–2.5 when the DS19 cells were moved from a low osmolality (210 mOs) to a high osmolality (410 mOs) solution and that this change was paralleled by the measured alterations in specific capacitance from 15.8 to 20.5 mF/m² [10]. They also revealed that the surface of hepatocytes were richly covered with microvilli, giving rise to an eightfold to tenfold excess of membrane compared with a smooth sphere. Based upon this concept, and the calculation that a smooth lipid/protein bilayer has a capacitance of ~9 mF/m² [7], [32], values of φ for the various cell types investigated here are given in Table II.

When cells are suspended in a medium of lower conductivity than the cytoplasm (as in our case with DEP and ROT studies in which intact cells having their normal physiological cytoplasmic complement of KCl were supported by a sucrose medium of low conductivity), the Claussius–Mossotti factor can be approximated, using (5), as

$$f_{CM}=\left[\frac{\frac{r}{d}\phi {\epsilon }_{\text{mem}}-i\frac{{\sigma }_s}{2\pi f}}{\frac{r}{d}\phi {\epsilon }_{\text{mem}}+2i\frac{{\sigma }_s}{2\pi f}}\right]$$ (6)

in the frequency range that is dominated by cell membrane effects. Here, ε_mem is the (real) membrane electrical permittivity, σ_s the suspending medium conductivity, and f the applied field frequency.

To further quantify the differences between dielectrophoretic responses of different cell types in terms of membrane folding effects, we examine the DEP crossover frequency f_o at which cells experience zero DEP forces, i.e., when

$$Re(f_{CM})=0.$$ (7)

Based on (6) and (7), the DEP crossover frequency can be then expressed as

$$f_o=\frac{\kappa {\sigma }_s}{r\phi }$$ (8)

where κ = 28.1 Hz · m²/S. Thus, cells having a large radius r and a large membrane folding factor φ exhibit a small DEP crossover frequency f_o and, under the separation conditions used in this work, they would experience large positive DEP forces and become immobilized on electrodes and held against the external hydrodynamic forces. Values of f_o, normalized with respect to the suspension conductivity, for several cell types examined here are given in Table II.

E. Cell Separability

It is of interest to quantify the ease with which different cell types can be separated from one another. This problem can be addressed theoretically by defining a “separability” factor that reflects the expected differences in the DEP forces that will be experienced by the cell types to be separated. For the dielectric affinity method described here, a measure of this difference can be derived from (1) by comparing the extreme left- and right-hand terms and defining a separability factor S as

$$S=r_{1}Re[f_{CM1}]-r_{2}Re[f_{CM2}].$$ (9)

Since the factors Re[f_CM] are frequency-dependent, a differential calculus analysis, based on the f_CM defined in (6), gives the maximum separability as

$$S_{\text{MAX}}=\frac{r_1}{2}\left[\frac{2r_1^2{\phi }_1^2\vartheta -1}{r_1^2{\phi }_1^2\vartheta +1}\right]-\frac{r_2}{2}\left[\frac{2r_2^2{\phi }_2^2\vartheta -1}{r_2^2{\phi }_2^2\vartheta +1}\right]$$ (10)

where

$$\vartheta =\left\{\frac{r_2\sqrt{{\phi }_2}-r_1\sqrt{{\phi }_1}}{r_1{r}_2(r_2{\phi }_2^2\sqrt{{\phi }_1}-r_1{\phi }_1^2\sqrt{{\phi }_2})}\right\}.$$

The corresponding optimum frequency is derived as

$$f_{\text{MAX}}=\frac{{\sigma }_s\sqrt{\vartheta }}{\pi C_o}$$ (11)

where C_o is the specific capacitance of a smooth membrane. Although complicated, the maximum separability parameters depend only on the radii r₁ and r₂ and the membrane specific area terms φ₁ and φ₂ for the two cell types. The optimum frequency is a function of not only the cell radii and specific area factors, but also of the suspension conductivity σ_s. These results are derived under the assumption that: 1) the suspension conductivity is high enough to effectively suppress the influence of membrane conductance on cell electrokinetic responses; 2) the separation operates at frequencies much lower than the Maxwell-Wagner polarization frequency; and 3) the membrane morphology dominates the membrane-specific capacitance. Under these conditions, the separability of two cell types by DEP affinity can be predicted from the knowledge of cell radii and membrane morphology alone.

Table III illustrates the application of this analysis to the cell types investigated here. The largest differences for cell radii and membrane-specific area factors occurred between red blood cells (RBC’s) and MDA-468 cells (Table I), resulting in the largest S_MAX value for these two cell types. On the other hand, RBC’s and T-lymphocytes had the smallest S_MAX values, due to the relatively small difference in their properties, indicating that their separation is correspondingly more difficult. However, in our preliminary experiments, we were able to readily separate RBC’s from T-lymphocytes using the dielectric affinity column, showing that this cell sorting method can discriminate cell types having values as low as 10 and can, therefore, by extension, separate all the cell types shown in Table III. Furthermore, in ROT experiments on MDA-231, we observed membrane-specific capacitance values for cells ranging from 19 to 32 mF/m², corresponding to specific area factors of 2.1 and 3.6, respectively. Since these extremes correspond to an S_MAX value of 18 (in the units of Table III), it should be relatively easy to separate subpopulations of MDA-231 cells according to their dielectric properties using this separation method.

TABLE III.

Separation Factors S_MAX, Calculated Using Equation (10)

Cell Type	RBC	T-lymphocyte	HL60	MDA231
RBC
T-lymphocyte	9.6
HL60	38	29
MDA--231	50	44	21
MDA-435	56	46	17	14
MDA-468	61	55	33	12

Data for the cells are taken from Table II. By selecting a cell type in the top row and determining the number in the column below it corresponding to another cell type in the left column, the relative ease with which the two cell types may be separated can be read off. Parameters are scaled by × 10⁷.

One can further predict the optimum field frequencies for separation using (11) for the cell types shown in Table III for any given conductivity of the suspension medium. This approach was employed in our experiments for removing MDA cells lines from blood and proved to be successful. The ability to identify the optimum separation conditions is significant in achieving the best separation efficiency since the trial-and-error method may not readily yield the best results.

IV. Conclusions

The efficient removal of human breast cancer cells from blood using the dielectric affinity column method was demonstrated for tumor to normal cell ratios as low as 1:3 × 10⁵. The cell separability analysis allowed the quantitative comparison of the relative ease of separation of the cell types studied and the prediction of the optimum cell sorting conditions. Under the operating conditions reported here for the dielectric column, it was concluded that surface morphology coupled with cell size dominates cell dielectrophoretic responses and acts as the sorting criterion.

Because ac electrokinetic devices exploit intrinsic cellular properties as both a characterization and sorting criterion, they offer the advantage that cell modification, such as by stains or antibodies, is unnecessary. This is significant from a research standpoint, where unmodified cells are desirable, and from a clinical standpoint, where specific antibodies or markers might not be available. Furthermore, parameters by which cells are identified in current sorting and characterization technologies, including centrifugal techniques [4], [33], cell electrophoresis [34], hydrophobic affinity [35], rosetting [36], fluorescence-activated sorting [37], affinity column [38], and magnetic-antibody [39] methods, play little or no role in ac electrokinesis. It follows that the approach of dielectric affinity separation might be applied as an adjunct to conventional methods to yield overall improved discrimination, speed, and efficiency for diagnostic and cell-separation applications. As an example, the molecular polymerase chain reaction (PCR) method is proving to be capable of detecting cancer cells at a concentration of about 1 per 10⁵ normal cells [40]. If the cells were presorted by ac electrokinetic means, this sensitivity might be enhanced by many orders of magnitude (possibly to a limit set by how much blood can be sampled from the patient). Finally, the cell sorting rate in our procedure is similar to that of the conventional flow cytometric methods, exceeding 10³ cells/s in our small prototype separator and scaleable to at least 10⁵ cells/s. Therefore, we believe that the techniques shown here may find useful applications in many experimental and clinical areas.