Free Energy Calculations for DNA Near Surfaces Using an Ellipsoidal Geometry

Abstract

The change in some thermodynamic quantities such as Gibbs' free energy, entropy and enthalpy of the binding of two DNA strands (forming a double helix), while one is tethered to a surface and are analytically calculated. These particles are submerged in an electrolytic solution; the ionic strength of the media allows the linearized version of the Poisson-Boltzmann equation (from the theory of the double layer interaction) to properly describe the interactions [13]. There is experimental and computational evidence that an ion penetrable ellipsoid is an adequate model for the single strand and the double helix [22–25]. The analytic solution provides simple calculations useful for DNA chip design. The predicted electrostatic effects suggest the feasibility of electronic control and detection of DNA hybridization in the fast growing area of DNA recognition.

1 Introduction

The thermodynamics of the binding of free DNA species differs with the binding of DNA species immobilized on surfaces because of the interaction with the surface. Polarization fields change the electrostatic contribution to the binding free energy [8–10]. While simulation shows many packing complications near surfaces [11, 12], electrostatics is clearly a dominant driving force in hybridization that is altered by surfaces.

On a DNA chip, or DNA micro array, we have thousands of single strand DNA fragments (probes) immobilized within a square micron on a surface as well as a similar amount of free single strand DNA fragments (target) in solution that will bind to (hybridize) the probes forming a double helix DNA (complex). By this process one may perform a massive parallel DNA sequence analysis. This is of great interest because of applications like genetic screening, drug discovery and design, DNA computing and other related applications [13]. The DNA micro array is a fundamental tool which is transforming genetic science into genetic technology as has been proved by its widespread implementation [13].

In the last few years great effort has been made to analyze this problem by experimental [22,23] and computational [24,25] approaches, but there is not much progress on faster analytical models. Previous work in this laboratory used a spherical representation for the short DNA oligomers such a system (Vainrub and Pettitt) [8–10]. While much information was obtained from such an approach a more realistic model would be desirable. We propose an analytic solution to the electric potential for ellipsoids over a plane using the linearized version of the Poisson-Boltzmann equation, this will allow us to calculate some thermodynamic properties of the system. We model the DNA species (double helix and single strand) as an ellipsoid. The surface effects may be considered for either the case of a dielectric surface where we have a constant charge distribution or a conductor such as a metal where the potential is constant. Note that in the classical method using image charges one will have a sign reversal for the interaction with the images in these two cases. We consider both types of surfaces below.

2 Thermodynamics of binding

The most important thermodynamic features to analyze to have a better picture of the phenomena and improve DNA microarray design are the Gibbs free energy change ΔG, the entropy change ΔS and the enthalpy change ΔH upon hybridization. These quantities determine the melting temperature of the system and ultimately the efficiency of the microarray. Assuming that the process is reversible, the free energy is a state variable, and hence, we make use of the fact that we need not construct a hybridization coordinate but simply require knowledge of the work to bring a single strand versus a double strand to within a certain distance and angle of a surface.

We take a closer look to the process we are analyzing. We have a DNA segment tethered to a plane in a single strand configuration. At the same time we have a finite concentration of DNA segments floating freely in a dielectric liquid, usually salt water and/or formamide. A diffusive search begins for the strands complementary to the one tethered which will hybridize to it. We expect there will be a change in the free energy, the enthalpy and the entropy for the system due to the presence of a surface. Our interest is to understand the influence of the plane or surface to this reaction. In other words, we want to calculate the difference in the binding's free energy when it happens in the bulk liquid electrolyte and when it happens near the surface.

We call G the Gibbs' free energy of formation in the bulk and Gⁱ the Gibbs' free energy of formation when one of the species is tethered to the surface. So we have:

$$G=G_c-G_p-G_t.$$ (2.1)

And similarly:

$$G^i=G_c^i-G_p^i-G_t,$$ (2.2)

where G_c, G_p and G_t are the energies for the complex, the probe and the target while the super index i stands for immobilized, which does not apply to the target because it was not immobilized when it was formed. Now, the difference is:

$$\Delta G=G^i-G=(G_c^i-G_c)-(G_p^i-G_p),$$ (2.3)

where the terms in parenthesis correspond to the interaction of the complex and the probe with the plane; we will rename them V_c and V_p as in the notation previously used by Vainrub and Pettitt [8–10]. So, the equation now reads:

$$\Delta G=V_c-V_p.$$ (2.4)

Once we calculate the Gibb's free energy, getting the entropy is straight forward. We will differentiate the free energy with respect to temperature taking advantage of the fact that there are simple representations of the dielectric response with respect to temperature [8] instead of using the Markus [16] and Overbeek [17] method.

$$\Delta S=-\left(\frac{\partial \Delta G}{\partial T}\right).$$ (2.5)

Finally, we will calculate the enthalpy's change using the definition:

$$\Delta G=\Delta H-T\Delta S.$$ (2.6)

3 Electric double-layer interaction

Since the Poisson-Boltzmann(PB) equation was proposed by Gouy [18] in 1910 and Chapman [19] in 1913, it has been of great use in describing the electrostatic interaction of charges in electrolytic solutions. Because of its importance in different areas, a great effort has been made to find simpler and more accurate solutions for different geometries. An approximation that has proven to work well for low ionic strength, is the Linearized Poisson-Boltzmann (LPB) [12], which has the general form [3]:

$${\nabla }^2\Psi ={\kappa }^2\Psi -\left(\rho /\epsilon {\epsilon }_0\right),$$ (3.1)

where Ψ is the electric potential, ε is the relative dielectric constant, ε₀ is the electrical permittivity of vacuum and κ² is the inverse of the Debye length, defined by:

$$\frac{1}{{\kappa }^2}=\left(\frac{\epsilon {\epsilon }_0{k}_{B}T}{2c_0{e}^2}\right).$$ (3.2)

Here k_B is the Boltzmann constant, T the temperature, c₀ the concentration of the 1-1 type electrolyte and e the charge of the electron. Through out the paper we use $\frac{1}{\kappa }=0.3$ nm which corresponds to a concentration of 1 M NaCl at room temperature. This is a higher concentration than often used with linear PB.

Our particular configuration consists of a DNA species (double helix or single strand) and a plane to which the species will be tethered. It was proposed by Vainrub and Pettitt [8] that an ion penetrable particle is a reasonable model for a short DNA species, regardless of it being a single strand or a double helix. This was based on computer simulations where ions and water have been shown to penetrate quite close to the helix axis [20, 21] and the random nature of conformations for single strands. Since that region is encompassed by our ellipsoids we must allow ions to penetrate in this mean field treatment [8]. Geometrically, this shape is as close as we can get with an orthogonal separable set of coordinates. Physically this model is reasonably accurate as experimentally one find electrolytes inside the DNA as well [22, 23]. From the mathematical point of view, this conditions mean that the field and its first derivative are continuous at the particle-solvent boundary (ξ₀):

$${\Psi }_{{\xi }_{0-}}={\Psi }_{{\xi }_{0+}},{\left(\frac{\partial \Psi }{\partial \xi }\right)}_{{\xi }_{0-}}={\left(\frac{\partial \Psi }{\partial \xi }\right)}_{{\xi }_{0+}}.$$ (3.3)

Now we have a closed solution for the ellipsoid's contribution, plus these conditions are immediately achieved when we superpose more than one field, as far as all of them are continuous and well behaved. An advantage of this condition is that the electric field generated by the species doesn't get altered by its proximity to the plane, and the total field is just the sum of both fields (plane and spheroid).

In Appendix 1 we solve Eq. (3.1) for the homogeneous case (ρ = 0), using prolate ellipsoidal coordinates by first separating the variables and then using a solution as a power series, as was proposed by Aoi [4]. The solution has the general form:

$$\Psi =\sum _{m=0}^{\infty }\sum _{n=m}^{\infty }{A}_{mn}{R}_{mn}(\xi )S_{mn}(\eta ){\Phi }_n(\mathit{\varphi }),$$ (3.4)

where A_mn is a constant to be determined by the specific boundary conditions. The particular solution to Eq. (3.1), subject to conditions (3.3) is explained in detail in Appendix 2.

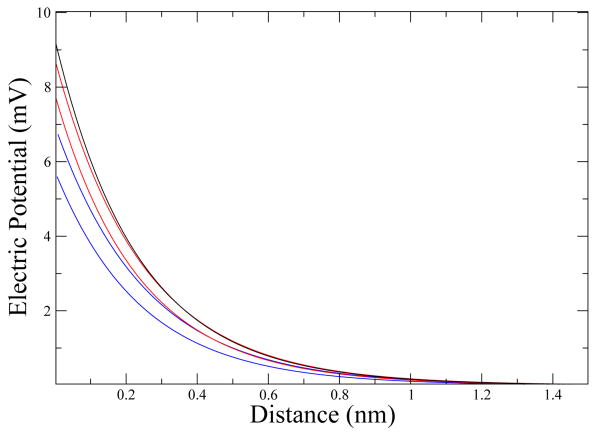
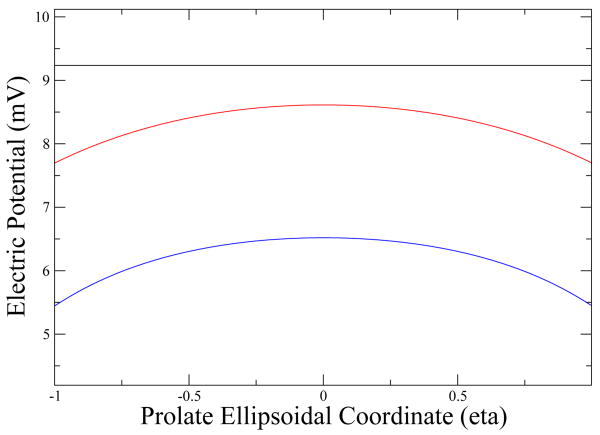
We are interested in understanding the difference between the ellipsoidal approximation and the exact analytic solution for a perfect sphere used previously [8]. We will analyze three different ellipsoids: ellipsoid “a” is practically a sphere, it has a major axis, minor axis ratio of 1 + 1 × 10⁻⁹, ellipsoid “b” has a ratio of 1.2 and ellipsoid “c” a ratio of 1.4. The volume (4.2nm³) is conserved in all three cases. In Fig. 1, we can see the electric potential right outside the ellipsoid for the three cases and for different directions. As a complement to this graph, in Fig. 2 we see how the electric potential varies depending on the configuration of the ellipsoid with the surface.

Figure 1. Electric potential.

Distance zero corresponds to the boundary of the ellipsoid and then it follows a path perpendicular to it. The black line is for ellipsoid a (sphere); the red lines are for ellipsoid b and the blue lines are for ellipsoid c. In ellipsoids b and c we have two lines, the upper one following a path perpendicular to the ellipsoid's axis and the lower one following a path parallel to the ellipsoid's axis.

Figure 2. Electric potential at the ellipsoid's boundary.

We plot the potential at the boundary versus the prolate ellipsoidal coordinate η The black line corresponds to ellipsoid a which does not change because of its symmetry, the red line corresponds to ellipsoid to ellipsoid b and the blue line corresponds to ellipsoid c; as expected, the potential diminishes in all directions as we deviate from a spherical shape.

The solution for the electric potential of ellipsoid a converges exactly using only the first term of the series, giving almost the same answer (average difference smaller than 10⁻⁵mV) that we get with the exact solution using spherical coordinates [5]; The solution to ellipsoid b converges with an average difference of 4.7×10⁻³ using the first three terms of the series while the solution to ellipsoid c converges with an average difference of 3.3×10⁻³ using six terms. For this particular κ, the solution is convergent for a major-minor axis ratio of roughly 1.5; but the range of this theory can be expanded by changing κ via the electrolyte concentration.

If we compare our results with numerical solutions [24] or Monte Carlo simulations [25] we can see promising results qualitatively, especially outside the ellipsoid which is of most interest. Quantitatively with our generic set of models we are at worst a factor of 2.5 off from detailed models. This is attributed to the fact that we are considering the charge distribution which constant inside the ellipsoid, but the charge concentrates near the surface in a helical pattern in a real DNA molecule and since we are holding the volume of the ellipsoid constant the diameter for all but model a) is not representative of the detailed models. This affects the result because the electric potential outside the ellipsoid depends only on the charge distribution at the surface of the ellipsoid. The consideration of a general charge distribution involves a different solution of Eq. (3.1) because it is not a homogeneous equation anymore. This work, utilizing ellipsoids fit to the shape of DNA, is in progress and will be published in the future.

Now that we have the electric potential generated by the ellipsoid, we can calculate the Gibbs' free energy's change ΔG, the enthalpy's change ΔH and the temperature times the change in entropy TΔS.

4 Gibbs' free energy

For the case at hand, we have three dielectric regions: the DNA which we take as an ellipsoid, the saline solution and the surface substrate. The dielectric constant in the solution is taken as 78.17 which corresponds to the solution (almost pure water) at room temperature. This constant is also used for inside the ellipsoid because most of the volume is occupied by the solution.

To completely specify the system, we need to know what kind of plate we have. In DNA microarrays we most often find dielectrics (e.g., glass) and conductors (e.g., gold) used as the substrate for chips (the plane). These two possibilities represent two different physical situations: if it is a dielectric, it will have a constant surface charge density (case 1), positive or negative; but if it is a conductor it will generate a constant electric potential at its surface (case 2). The dielectric constant of the plate is thus specified by the boundary conditions used. We need no specific regions since do not calculate the electric potential inside of the surface.

4.1 Case 1: Plane with constant charge density

To keep the plate at a constant charge density, we use the method of images, with a mirror ellipsoid placed symmetrically at the other side of the plane. This ellipsoid has a charge density equal in magnitude and sign with respect to the original spheroid so that the derivative of the total potential vanishes at the plane.

The total electric potential in the liquid has three sources, hence:

$$\Psi ={\Psi }_e+{\Psi }_i+{\Psi }_p,$$

where the subscripts e, i and p stand for ellipsoid, image and plane. To calculate the Gibbs free energy, we assume that its only source is the electrostatic interaction. We integrate the charge times the field all over the surface of the plane, and the volume of the spheroid:

$$\Delta G={\mathit{\int }}_V\rho \left({\Psi }_i+{\Psi }_p\right)dV+{\mathit{\int }}_S\sigma \left({\Psi }_e+{\Psi }_i\right)dV.$$ (4.1)

Obviously, we do not integrate over the image ellipsoid because it is virtual and its only purpose is to fix the boundary conditions in the region of interest, i.e., provide the polarization field.

Considering our goal, we wish to calculate the difference in ΔG between a double helix and a single strand. Due to the linear dependence of the electric potential with the charge, this is equivalent to calculating the difference in Gibbs' free energy between an ellipsoid with twice the charge (double helix) minus the Gibbs' free energy of the original ellipsoid (single strand) with corrections for the solution strands.

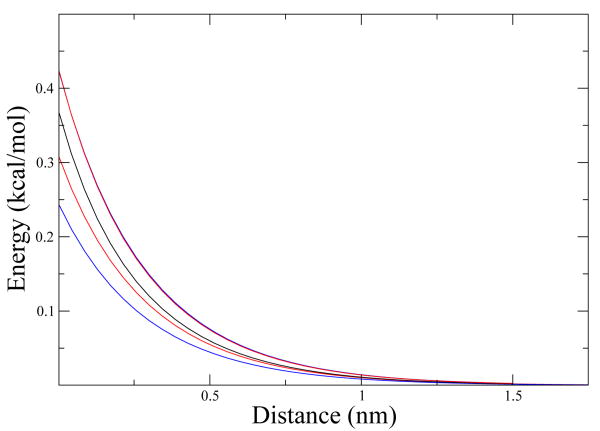
Now, using Eq. (4.1) for the three different ellipsoids at different positions and orientations we generate ΔG in Fig. 3.

Figure 3.

ΔG The black line corresponds to ellipsoid a, the red lines correspond to ellipsoid b and the blue lines to ellipsoid c. Ellipsoids b and c have two lines each, the lines above the black line correspond to the ellipsoid oriented with its axis parallel to the plane and the lines below when oriented perpendicular to the plane. It is worth noting that the two lines above, from ellipsoid b and ellipsoid c, almost match perfectly. The plane was kept with a charge density of .36 electrons/nm².

4.2 Case 2: Plane with constant electric potential

To keep the electric potential constant, we use the same method of images we used in case 1, but the image now has the opposite charge, so that the contribution of both ellipsoids vanishes in the plane. Hence, Eq. (4.1) will change to:

$$\Delta G={\mathit{\int }}_V\rho \left({\Psi }_i+{\Psi }_p\right)dV.$$ (4.2)

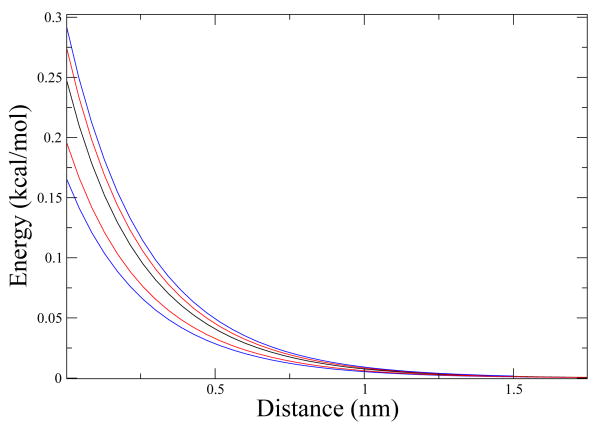
Similarly to Fig. 3, we generate Fig. 4 using Eq. (4.2).

Figure 4.

ΔG We use the same color code as in Fig. 3. The plane was kept at a constant electric potential of 25 mV.

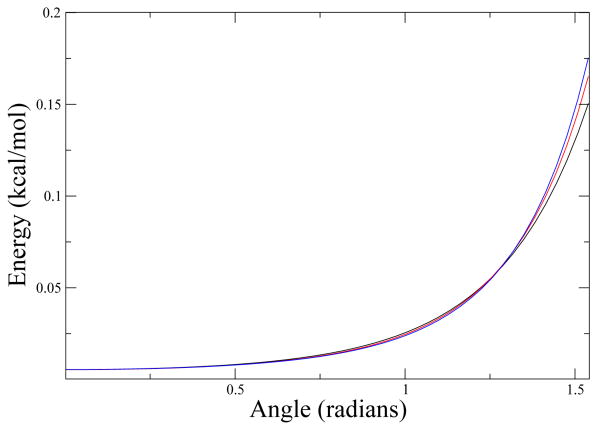
Another interesting variation in ΔG to analyze, is the tilting of an ellipsoid while one of its ends is held fixed. This is similar to the situation of a DNA species tethered to a surface, which is the case in the DNA chip. In Fig. 5 we plot this situation, the ellipsoids are fixed in a position so that when they are parallel to the plane (as close as they get), they are .1 nm away from it.

Figure 5.

ΔG We use the same color code as in Fig. 3. In the x axis we have the angle of inclination of the ellipsoid in radians, zero being when the ellipsoid's axis is perpendicular to the surface and π/2 when parallel.

As we can see in the graph, the difference is only noticeable when the ellipsoid major axis is parallel to the plane. We expect the difference to be more significant when the ellipsoid has a bigger ratio of mayor and minor axis. This will be addressed in future works.

It is also worth noting that as the ellipsoid's axis ratio grows, ΔΔG grows faster at angles closer to π/2 and even slower for smaller angles.

5 Entropy and enthalpy

Now that we have ΔG, we can calculate the entropy by differentiating the Gibbs' free energy.

$$\Delta S=-\frac{\partial \Delta G}{\partial T}.$$ (5.1)

However, we know that ΔG depends on T only through κ and ε, and that κ depends on ε by Eq. (3.2), so we get:

$$-\Delta S={\left(\frac{\partial \Delta G}{\partial \kappa }\right)}_{\epsilon }\left(\frac{\partial \kappa }{\partial T}\right)+\left[{\left(\frac{\partial \Delta G}{\partial \epsilon }\right)}_{\kappa }+{\left(\frac{\partial \Delta G}{\partial \kappa }\right)}_{\epsilon }\left(\frac{\partial \kappa }{\partial \epsilon }\right)\right]\left(\frac{\partial \epsilon }{\partial T}\right)$$

and simply using Eq. (3.2)

$$\begin{array}{cc}\frac{\partial \kappa }{\partial T}=\frac{-\kappa }{2T},& \frac{\partial \kappa }{\partial \epsilon }=\frac{-\kappa }{2\epsilon }.\end{array}$$

The value of ∂ε/∂T depends on the system and will be taken experimentally. For water at room temperature we know that (T/ε) (∂ε/∂T) = -1.35. Now all we have missing is ∂ΔG/∂κ and ∂ΔG/∂ε, which can be calculated numerically.

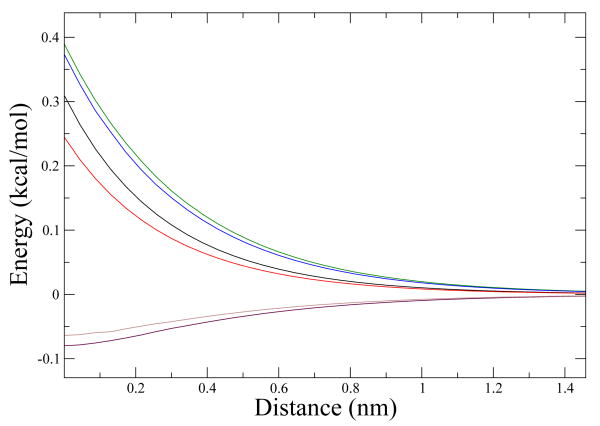
In Fig. 6 we plot these three thermodynamic variables for ellipsoid b and ellipsoid c. As we can see, both of them have the same tendency in the three thermodynamic variables, but they differ quantitatively.

Figure 6.

ΔG, ΔH and -TΔS The black and the red lines are ΔG for ellipsoid b and ellipsoid c, the green and the blue lines are ΔH for ellipsoid b and c and the maroon and gray lines in the bottom are −TΔS.

6 Conclusion

The thermodynamic modeling of DNA near surfaces currently requires approximations to be handled analytically. Here we developed a mathematical and thermodynamical framework to better understand the behavior of charged ellipsoids inside an electrolyte solution near a surface where the interactions are governed by the double-layer theory through the Poisson-Boltzmann equation.

We demonstrated significant differences in the thermodynamic variables as well as in the electrostatic potential between the ellipsoid, and the perfect sphere. We found significant differences when considering an ellipsoidal model for a DNA species over a perfect sphere model used before by in this laboratory [4].

The model of an ion penetrable sphere with the charges at the surface has proven to give qualitatively good results when compared to experiments [4]. Our crude, unfitted model is about a factor of two away from atomic results. This verifies the general approach we have taken. We believe that if we modify the charge distribution and the geometry of the ellipsoid to more accurately reflect the distribution in DNA we will have a more accurate model for wider applications. This work is in progress.

A Appendix 1

We need to solve the linearized Poisson-Boltzmann (LPB) equation which has the general form:

$${\nabla }^2\Psi ={\kappa }^2\Psi -\frac{\rho }{\epsilon {\epsilon }_0}.$$ (A.1)

If ρ is constant, we first solve the homogeneous case (ρ = 0). The explicit form of the LPB equation in ellipsoidal coordinates is:

$$\begin{array}{c}\frac{\partial }{\partial \eta }\left[(1-{\eta }^2)\frac{\partial \Psi }{\partial \eta }\right]+\frac{\partial }{\partial \xi }\left[({\xi }^2-j)\frac{\partial \Psi }{\partial \xi }\right]\\ +\frac{{\xi }^2-j{\eta }^2}{({\xi }^2-j)(1-{\eta }^2)}\frac{{\partial }^2\Psi }{\partial {\mathit{\varphi }}^2}=a^2{\kappa }^2({\xi }^2-j{\eta }^2)\Psi ,\end{array}$$

where j = 1 for prolate ellipsoidal and j = −1 for oblate ellipsoidal. Because of the shape of DNA, we use prolate ellipsoidal coordinates in the rest of the paper, although the transformation from prolate to oblate coordinates can easily be done by letting ξ → ±iξ and a → ∓ia, where a is half the distance between the two foci of the ellipsoid.

Assuming a solution of the form:

$$\Psi =\sum R_{mn}(\xi )S_{mn}(\eta ){\Phi }_m(\mathit{\varphi }),$$ (A.2)

we can separate the three variables into the three equations:

$$\frac{\partial }{\partial \eta }\left[(1-{\eta }^2)\frac{\partial S_{mn}(\eta )}{\partial \eta }\right]+\left({\eta }^2{c}^2-\frac{m^2}{1-{\eta }^2}+{\lambda }_{mn}\right)S_{mn}(\eta )=0,$$ (A.3)

$$\frac{\partial }{\partial \xi }\left[(1-{\xi }^2)\frac{\partial R_{mn}(\xi )}{\partial \xi }\right]+\left({\xi }^2{c}^2-\frac{m^2}{1-{\xi }^2}+{\lambda }_{mn}\right)R_{mn}(\xi )=0,$$ (A.4)

$$\frac{{\partial }^2}{\partial {\mathit{\varphi }}^2}\Phi (\mathit{\varphi })=-m^2\Phi (\mathit{\varphi }),$$ (A.5)

where we have used c² = a²κ². The solution to (A.5) is trivial:

$$\Phi (\mathit{\varphi })=C_{mn}\text{cos}(m\mathit{\varphi })+D_{mn}\text{sin}(m\mathit{\varphi }).$$ (A.6)

Evidently C_mn and D_mn are constants determined by the boundary conditions. The other two equations, (A.3) and (A.4), have the same form but their variables belong to different domains (η ∈ [−1,1], ξ ∈ [1,∞)) and therefore their solutions will be different.

Let us first solve Eq. (A.3). Noting its similarity with the associated Legendre's differential equation (clearly, if c² → 0 the equation would be Legendre's and the solution would simply be the set of its associated polynomials) and knowing that c² is indeed small, we propose a solution of the form:

$$S_{mn}(\eta )=\sum _{s=0}^{\infty }{A}_{mn,s}{P}_{m+s}^m.$$ (A.7)

To find an equation for A_mn,s we substitute (A.7) into Eq. (A.3) and use the Legendre's polynomial recursive relation:

$$P_n^m=\eta \frac{(2n-1)}{(n-m)}{P}_{n-1}^m-\frac{(n+m-1)}{(n-m)}{P}_{n-2}^m$$ (A.8)

to get the equation:

$$[c^2\beta (s)+{\lambda }_{mn}-(m+s)(m+s+1)]A_{mn,s}+c^2\alpha (s)A_{mn,s+2}+c^2\gamma (s)A_{mn,s-2}=0$$ (A.9)

valid for s > 2, and where:

$$\alpha (s)=\frac{(s+2m+2)(s+2m+1)}{(2s+2m+s)(2s+2m+3)},$$ (A.10)

$$\beta (s)=\frac{2s^2+4sm+2s+2m-1}{(2s+2m-1)(2s+2m+3)},$$ (A.11)

$$\gamma (s)=\frac{s(s-1)}{(2s+2m-3)(2s+2m-1)}.$$ (A.12)

As we can see from Eq. (A.9), the recursive relation of A_mn,s only involves terms with s + 2, s and s − 2. Therefore m + s will be even if n is even and odd if n is odd.

We could estimate λ_mn through a heuristic trial and error procedure; but instead we propose an expansion of it as a power series on c²:

$${\lambda }_{mn}=\sum _{r=0}^{\infty }{\Lambda }_{mn,r}{(c^2)}^r,$$ (A.13)

and the same approach is proposed for A_mn,s

$$A_{mn,s}=\sum _{r=0}^{\infty }{a}_{mn,s,r}{(c^2)}^r.$$ (A.14)

To find a recursive relation for Λ_mn and a_mn,s,r we substitute (A.13) and (A.14) into (A.9) and find:

$${\Lambda }_{mn,r}=-\alpha (n-m)a_{mn,n-m+2,r-1}-\beta (n-m)a_{n,n-m,r-1}-\gamma (n-m)a_{mn,n-m-2,r-1}$$

as well as:

$$\begin{array}{l}{a}_{mn,s,r}=\left[\frac{1}{{\Lambda }_0-(m+s)(m+s+1)}\right]\times [\alpha (s)a_{mn,s+2,r-1}\\ +\beta (s)a_{mn,s,r-1}+\gamma (s)a_{mn,s-2,r-1}+\sum _{p=1}^{r-1}{\Lambda }_p{a}_{mn,s,r-p}].\end{array}$$

This expressions are valid for r ≥ 1 and the second one is only valid for s ≠ n − m. If s = n − m then a_mn,s,r = 0. It is worth mentioning that the starting assumption in Eq. (A.7) implies that Λ_mn,0 = n (n + 1) and a_mn,s,0 = 1 when s = n − m.

To solve Eq. (A.3) we can use a similar procedure as we did with (A.7), only using the following integral transform to have it in the appropriate domain [1,4]:

$$R_{mn}(\xi )=\frac{\pi }{2}{\mathit{\int }}_1^{\infty }{c}^m{e}^{-c\xi \eta }{({\xi }^2-1)}^{\frac{m}{2}}{(1-{\eta }^2)}^{\frac{m}{2}}{S}_{mn}(\eta )d\eta$$ (A.15)

from which we get:

$$R_{mn}^{(1)}(c,\xi )=\sum _{s=0,1}^{\infty }{A}_{mn,r,s}{\left(\frac{{\xi }^2-1}{{\xi }^2}\right)}^{\frac{m}{2}}\times \frac{(2m+s)!}{s!}{I}_{m+s}(c\xi ),$$

and similarly

$$R_{mn}^{(2)}(c,\xi )=\sum _{s=0,1}^{\infty }{A}_{mn,r,s}{\left(\frac{{\xi }^2-1}{{\xi }^2}\right)}^{\frac{m}{2}}\times \frac{(2m+s)!}{s!}{K}_{m+s}(c\xi ),$$

where I_m+s (cξ) and K_m+s (cξ) are the modified spherical Bessel functions of the first and second kind respectively.

Now, if cξ is small, we face another problem. $R_{mn}^{(2)}(c,\xi )$ diverges because K_n (cξ) diverges to infinity. Then we use the expression proposed by Aoi [4], where using the orthogonality of the solutions for different m or n, and the known exact solution for the LPB in spherical coordinates (transforming it to prolate ellipsoidal coordinates). We obtain [1,3]

$$\begin{array}{c}{R}_{m(m+2s)}^{(2)}(c,\xi )={({\xi }^2-1)}^{m/2}\sum _{q=0}^{\infty }{\omega }_{2q}\times K_{m+q}\left[\frac{c}{2}(\xi +\sqrt{{\xi }^2-1})\right]\\ \times I_{m+q}\left[\frac{c}{2}(\xi -\sqrt{{\xi }^2-1})\right],\end{array}$$ (A.16)

$$\begin{array}{c}{R}_{m(m+2s+1)}^{(2)}(c,\xi )=\xi {({\xi }^2-1)}^{m/2}\sum _{q=0}^{\infty }{\omega }_{2q+1}\times K_{m+q+1}\left[\frac{c}{2}(\xi +\sqrt{{\xi }^2-1})\right]\\ \times I_{m+q+1}\left[\frac{c}{2}(\xi -\sqrt{{\xi }^2-1})\right],\end{array}$$ (A.17)

where

$$\begin{array}{c}{\omega }_{2q}=(2m+2q+1)\sum _{s=0}^q\sum _{t=s}^q{(-1)}^t{2}^{m+2s+1}\\ \times \frac{(2m+q+t)!(2m+2s)!(2t)!(t+m+s)!}{t!(m+t)!(q-t)!(2s)!(t-s)!(2t+2m+2s+1)!}{A}_{mn,2s},\end{array}$$ (A.18)

$$\begin{array}{c}{\omega }_{2q+1}=(2m+2q+3)\sum _{s=0}^q\sum _{t=s}^q{(-1)}^t{2}^{m+2s+2}\\ \times \frac{(2m+q+t+2)!(2m+2s+1)!(2t+1)!(t+m+s+1)!}{t!(m+t+1)!(q-t)!(2s+1)!(t-s)!(2t+2m+2s+3)!}{A}_{mn,2s+1}.\end{array}$$ (A.19)

Using this functions, R_mn (ξ) has the following form:

$$R_{mn}=A_{mn}^{\prime }{R}_{mn}^{(1)}(\xi )+A_{mn}^{″}{R}_{mn}^{(2)}(\xi ).$$ (A.20)

B Appendix 2

In Appendix 1, we developed an analytic solution to the LPB for the homogeneous case (ρ = 0), but this is not true for inside the ellipsoid. None the less, if the charge distribution inside the spheroid is homogeneous, we just have to add a term to the solution we already have. A more complete general solution for our system is

$$\begin{array}{cc}\Psi =\sum _{mn}{R}_{mn}(\xi )S_{mn}(\eta ){\Phi }_m(\mathit{\varphi }),& \text{for}\xi \ge {\xi }_0,\\ \Psi =\sum _{mn}{R}_{mn}^{\prime }(\xi )S_{mn}(\eta ){\Phi }_m(\mathit{\varphi })+\frac{\rho }{\epsilon {\epsilon }_0{\kappa }^2},& \text{for}\xi <{\xi }_0.\end{array}$$

If the charge distribution is homogeneous, then we have axial symmetry, and the solution will no longer depend on φ, so m = 0. Besides, from basic electrostatics, we know that Ψ has to vanish as ξ → ∞, so $R_{mn}^{(1)}(\xi )$ is unphysical for ξ ≥ ξ₀. On the other hand, Ψ can not diverge at the origin (ξ = 1); it has to be a maximum, hence we get the condition:

$$\frac{\partial \Psi }{\partial \xi }|{|}_{\xi =1}=0.$$

Under these conditions, the solution now has the form:

$$\begin{array}{cc}\Psi =\sum _n{A}_n{R}_n^{(2)}(\xi )S_n(\eta ),& \text{for}\xi \ge {\xi }_0,\\ \Psi =\sum _n{B}_n\left(R_n^{(1)}(\xi )-\frac{R_n^{\prime (1)}(1)}{R_n^{\prime (2)}(1)}{R}_n^{(2)}(\xi )\right)\times S_n(\eta )+\frac{\rho }{\epsilon {\epsilon }_0{\kappa }^2},& \text{for}\xi <{\xi }_{\text{0}},\end{array}$$

for simplicity, we rename:

$$\begin{array}{c}{R}_{n,\mathit{\text{in}}}(\xi )=\left(R_n^{(1)}(\xi )-\frac{R_n^{\prime (1)}(1)}{R_n^{\prime (2)}(1)}{R}_n^{(2)}(\xi )\right),\\ R_{n,\mathit{\text{out}}}(\xi )=R_n^{(2)}(\xi ),\end{array}$$

where A_n and B_n are constants to be determined by the conditions in Eq. (3.3). Taking this into account, making use of the orthogonality of the functions, and the properties of the Legendre's polynomials, we obtain

$$\begin{array}{c}{A}_{2n}=\frac{-D_{2n}}{\mathit{\text{detC}}}{R}_{n,\mathit{\text{in}}}({\xi }_0),\\ B_{2n}=\frac{-D_{2n}}{\mathit{\text{detC}}}{R}_{n,\mathit{\text{out}}}({\xi }_0),\\ D_{2n}=\frac{(\rho /\epsilon {\epsilon }_0{\kappa }^2)A_{2n,0}}{{\sum }_{w=0}^{\infty }\left[{(A_{2n,2w})}^2/(4w+1)\right]},\\ \mathit{\text{detC}}=R_{2n,\mathit{\text{out}}}^{\prime }({\xi }_0)R_{2n,\mathit{\text{in}}}({\xi }_0)-R_{2n,\mathit{\text{out}}}({\xi }_0)R_{2n,\mathit{\text{in}}}^{\prime }({\xi }_0).\end{array}$$

The subindexes have changed to 2n because only the even terms survive in the previous procedure. Thus the solution for an ion penetrable, homogeneously charged spheroid is fully determined.