Abstract
A general framework of image-based geometric processing is presented to bridge the gap between three-dimensional (3D) imaging that provides structural details of a biological system and mathematical simulation where high-quality surface or volumetric meshes are required. A 3D density map is processed in the order of image pre-processing (contrast enhancement and anisotropic filtering), feature extraction (boundary segmentation and skeletonization), and high-quality and realistic surface (triangular) and volumetric (tetrahedral) mesh generation. While the tool-chain described is applicable to general types of 3D imaging data, the performance is demonstrated specifically on membrane-bound organelles in ventricular myocytes that are imaged and reconstructed with electron microscopic (EM) tomography and two-photon microscopy (T-PM). Of particular interest in this study are two types of membrane-bound Ca2+-handling organelles, namely, transverse tubules (T-tubules) and junctional sarcoplasmic reticulum (jSR), both of which play an important role in regulating the excitation-contraction (E-C) coupling through dynamic Ca2+ mobilization in cardiomyocytes.
Keywords: Ventricular myocyte, Electron tomography, Two-photon microscopy, Image analysis, Geometric modeling, Mesh generation
1. Introduction
Confocal laser-scanning microscopy is being widely used to study subcellular structures at the cell-wide scale (Saetersdal et al., 1992; Soeller and Cannell, 1999). However, the limited resolution of light microscopy (LM) often leaves many structural details unclear. By contrast, electron microscopy (EM), together with 3D tomographic reconstruction techniques, can reveal anatomical details of membrane systems at nanometer resolutions. For example, in the study of cardiomyocytes, ryanodine receptors (RyR’s) on sarcoplasmic reticulum (SR) membrane can be visible as individual “foot” structures in two-dimensional (2D) EM (Franzini-Armstrong et al., 1999). However, with EM we can only “see” a small area of the structures of interest. In addition, 3D electron tomographic analysis of cellular structures still remains a demanding task, due to various experimental and computational challenges. While the confocal microscopy and electron microscopy have their own pros and cons, a combination of both techniques would create a better view of cardiomyocytes at both nano- and micro-scales.
Computer-aided mathematical simulation, on the other hand, has become popular in studying biological behaviors for its efficiency in both time and cost and for its ability of investigating some activities beyond the experimental limits (e.g., (Michailova et al., 2002)). Depending on the size and nature of a biological system, stochastic methods based on Monte Carlo simulation and deterministic methods utilizing partial differential equations (PDEs) have been the primary techniques. A particular example that has a strong connection to our current studies is the mathematical simulation of calcium dynamics in cardiomyocytes. Computer models have been introduced to simulate Ca2+ spark generation (Izu et al., 2001; Koh et al., 2006), Ca2+ wave initialization and propagation (Izu et al., 2006, 2001), and Ca2+ buffering and diffusion (Michailova et al., 2002). All these studies, however, were conducted on simplified geometries such as cylindrical or rectangular shapes. As pointed out in (Izu et al., 2006; Koh et al., 2006), a small geometric change, even in the case the change is uniformly applied, can greatly influence the behaviors of Ca2+ spark generation and wave propagation in computer simulation.
Although neither imaging nor simulation will be addressed in detail in the present paper, we predict that building 3D high-fidelity geometric models from imaging data would make mathematical simulation more accurate, which in turn could provide us a better understanding of the biological system being investigated. With the advancement of EM and LM imaging technologies in visualizing subcellular structures and increasing demands on realistic geometric models from solvers to numerically simulate biological systems, we believe that it is now timely and significant to bridge the gap between imaging and simulation such that the structural information can be integrated into mathematical models. Most 3D imaging data are currently given as a uniformly digitized cubic volume, where each grid point has a density (scalar) value. However, many numerical solvers need surface and/or volumetric meshes as inputs to define the domains in which the simulation is conducted. The gap between imaging and simulation, therefore, includes at least two steps: (1) extracting features (boundaries or skeletons) from imaging data, and (2) generating meshes from the features detected. In addition, image pre-processing is usually necessary for better feature extraction, when the original image is noisy or the contrast between features and backgrounds is low.
To this end, we present in this paper a number of image analysis and geometric processing algorithms that perform directly on 3D imaging data to construct high-fidelity geometric models represented by surface and/or volumetric meshes. While most of these algorithms had been detailed individually in our previous work (Bajaj et al., 2003b; Yu and Bajaj, 2004, 2005; Yu et al., 2008), their integration into a single pipeline is not straightforward and has not yet been addressed before. One of the challenges is that the features extracted from images are represented by zigzag boundaries or skeletons consisting of discrete voxels. Generating high-fidelity and smooth meshes from such features needs careful justification, which was not previously discussed (Yu et al., 2008). Our goal here is to describe a general framework of image-based geometric processing that can be applicable to 3D imaging data that range in scales across the molecular, cellular, and organ levels.
To test the procedure and performance of our computational framework, we choose to model membrane-bound organelles that regulate calcium mobilization in ventricular myocytes. Of particular interest in the current study are two types of membrane-bound Ca2+-regulating organelles, namely, transverse tubules (T-tubules) and junctional sarcoplasmic reticulum (jSR). T-tubules, found in adult mammalian ventricular cardiomyocytes and skeletal muscle cells (Brette and Orchard, 2007), are deep invaginations of plasma membranes and play a critical role in rapid propagation of depolarization from surface membranes to interiors of these cells. The Ca2+-signaling process, known as Ca2+-induced Ca2+ release (CICR), is carried out within a number of narrow micro-domains (or dyadic clefts) that span 10~15 nm between the cytoplasmic sides of T-tubular membrane and adjacent jSR membrane in ventricular myocytes (Bers, 2001; Fabiato, 1985; Franzini-Armstrong et al., 1999). At a larger scale, the cell-wide excitation and contraction are governed by the beat-by-beat global Ca2+ change that is known to be the temporal and spatial summation of individual Ca2+-releasing events following the propagation of membrane excitation through the T-tubule network. Given these different scales, both EM and two-photon microscopy (T-PM) images shall be utilized to extract individual dyadic clefts and cell-wide T-tubular systems. Numerical simulation of Ca2+ dynamics that uses the geometric models generated by our approaches will not be discussed in the current paper.
We describe the technical aspects of the pipeline of image-preprocessing (Section 2.2), feature extraction (2.3), and geometric mesh modeling (2.4). In particular, anatomical models of cardiac membrane organelles are generated by applying the aforementioned approaches to both electron microscopy (Section 3.1) and light microscopy (3.2) images. The selection of iso-surfaces is critical in determining the geometry of T-tubules and jSR, and is discussed in detail in Sections 4.1 and 4.2 respectively. Section 4.3 analyzes quantitatively the spatial organization of T-tubules. The software implementation of all the algorithms employed in the current study is briefly described in Section 4.4. While the usefulness of the algorithmic tool-chain has been demonstrated on a variety of biological images in the current study, the challenges of feature extraction and further development of downstream mathematical simulation are discussed in Sections 4.5 and 4.6.
2. Materials and Methods
2.1. Microscopy Imaging and 3D Reconstruction
The enhanced staining strategy of membrane organelles in cardiomyocytes and the reconstruction of 3D density maps will be described in detail elsewhere (Hayashi et al, manuscript in preparation). Briefly, adult mouse hearts were perfusion-fixed through the apex of the left ventricle with a sodium cacodylate buffer containing 3% dextran, 3% dextrose, and 50 mM CaCl2 in the presence of 3% glutaraldehyde. Several 1mm-cubic tissue blocks were obtained and treated with 0.8% potassium ferrocyanide and 2% osmium tetroxide for 2 hours at 4 °C. They were further incubated with 1% uranyl acetate, dehydrated in a graded series of ethanol solutions at room temperature, and embedded in Durcupan ACM (Electron Microscopy Sciences, PA) in a vacuum oven, as described in (Perkins et al., 1997). Sections (thickness: 500 nm) were imaged in a JEOL 4000EX intermediate high voltage EM system operated at 400 kV. The tilt series images recorded with a 4K × 4K charge-coupled device camera (16 bits per pixel) were processed with the IMOD suite (Boulder Laboratory for 3D Electron Microscopy of Cells, University of Colorado, Boulder, CO) to create a 3D tomographic map.
Adult mouse ventricles were perfusion-fixed through the ascending aorta with a sodium cacodylate buffer containing 4% paraformaldehyde and immediately vibratome-sectioned to 40–80 µm thickness. The sections were incubated with 0.01 mg/ml wheat germ hemagultinin (WGA) conjugated with Alexa Fluor 488 at 4 °C and visualized using a two-photon microscope (RTS 2000, objective: 60x oil, NA=1.45, ex 800 nm, em 508–558, 59 nm/pixel). The 3D maps are computed by interpolating a stack of 2D fluorescent images in the order of their depth indices.
2.2. Image Pre-processing
In the current study, we applied a localized contrast enhancement method to both EM and LM images. The method was developed in our earlier studies (Yu and Bajaj, 2004). The basic idea is to design an adaptive one-dimensional transfer function, which maps a narrow intensity range to a broader one for each individual voxel according to the local average and local minimum and maximum in a suitable neighborhood. This method can be thought of as a localized version of the classical contrast manipulation technique (Gonzalez and Woods, 1992; Pratt, 1991), but it also inherits the advantages of both the adaptive histogram equalization (Caselles et al., 1998; Stark, 2000) and the retinex model (Jobson et al., 1997).
We also reduced noise in the current EM and LM data using the bilateral pre-filtering (Elad, 2002; Tomasi and Manduchi, 1998) coupled to an evolution-driven anisotropic geometric diffusion PDE (partial differential equation) (Barash, 2002). The PDE model is:
| (1) |
The efficacy of this method is based on a careful selection of the anisotropic diffusion tensor Dσ based on estimates of the normal and principal curvature directions of the isosurface (level-set) in three dimensions (Bajaj et al., 2003a). The diffusion coefficients along the three independent directions of the feature boundary were determined by the local second order variation of the intensity function at each voxel. In order to estimate continuous first and second order partial derivatives, a tricubic B-spline basis was used to approximate locally the original intensity (Bajaj and Yu, 2005; Jiang et al., 2003).
2.3. Feature Extraction
To extract the geometric features of adjoining T-tubules and jSR, we employed both boundary segmentation and skeletonization that were all performed directly on 3D imaging data except the manual placement of seed points on 2D slices (see below). We first applied multi-seeded image segmentation as described earlier (Bajaj et al., 2003b; Yu and Bajaj, 2005). This approach is an enhanced variant of the well-known fast marching method (Malladi and Sethian, 1998; Sethian, 1996). In this method, a contour is initialized from a pre-chosen seed point, and then keeps growing until a certain stopping condition is reached. Every voxel is assigned with a value called time (denoted by T), which is initially zero for seed points and infinite for all other voxels. Repeatedly, the voxel on the marching contour with minimal time value is deleted from the contour and the time values of its neighbors are updated according to the following equation:
| (2) |
where F(x) is called speed function that is usually determined by the gradients of the input maps (e.g., F(x) = e−α‖∇I(x)‖, where α > 0 and I(x) is the original map). The neighbors, if they are updated for the first time, are then inserted into the contour. In order to segment multiple targets, we chose one or more seeds for each of the objects. Every seed initiated a contour and all contours started to grow simultaneously and independently. Two contours corresponding to the same object were merged into a single one, while two contours belonging to different objects stopped on their common boundaries. Seeds could be defined by the critical points that can be detected automatically using the gradient vector diffusion in (Yu and Bajaj, 2005). For images containing multiple features (e.g., T-tubules and jSR), we classified the seeds into one of those features before they were used for segmentation. To simplify this process, we assigned manually at least one seed for each of the features and the rest of the seeds were then automatically classified (Yu and Bajaj, 2005).
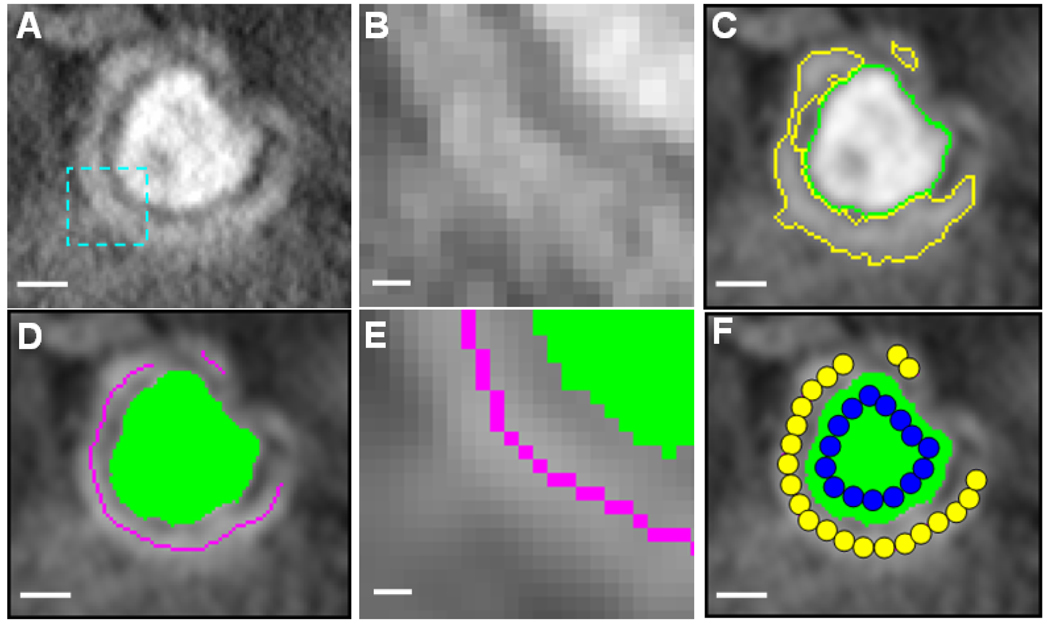
As an example, Fig. 1A shows a cropped cross-section of a 3D electron tomographic map of a ventricular cardiomyocyte (intensity inverted). The image noise can be seen more clearly in a zoomed-in region in Fig. 1B. To segment the boundary of the T-tubule, we first grouped all seeds into two classes, one corresponding to the T-tubule and the other to the rest, based on their intensity values. With a user-defined threshold and the multi-seeded fast marching method, we then extracted the T-tubular structure from the EM map (the most inner curve in green in Fig. 1C). Although the exact boundary of jSR was not well defined in the maps due to the high noise level, the segmented T-tubule provided a good “reference” to distinguish between jSR and background noise. We assumed that all seeds that were outside but within a certain distance (45 nm) to T-tubules be classified as jSR seeds. The rest of the seeds were treated as background noise. Using the multi-seeded method and three classes of seeds obtained, we were able to segment out both T-tubular and jSR structures as illustrated in Fig. 1C.
Figure 1.
Illustrations of image analysis and geometric modeling. (A) A 3.5nm-thick slice of the electron tomogram of a ventricular cardiomyocyte. This small region, showing a single T-tubule (in the middle) surrounded by junctional sarcoplasmic reticulum (jSR), was taken from a large 3D reconstructed EM map. The size of this sub-volume is 101×91×51 voxels (3.5 nm/voxel). Due to the staining methods specifically used in the current study, T-tubular structures in the EM maps are significantly ``darker" than SR and background noise (Note: intensity shown here has been inverted). (B) A close look at the image in the rectangular area indicated in (A). (C) The T-tubule and jSR are segmented using an automatic algorithm. (D) The skeletons of jSR (the curves in magenta) are automatically extracted based on the segmented jSR from (C). (E) A close look at the skeletons and boundaries in the same area indicated in (A). (F) Schematic illustration of the sphere-packing method to create pseudo-molecules of T-tubules and jSR. Scale bars: 50 nm in (A,C,D,F) and 10 nm in (B,E).
As the boundary of jSR was not precisely detected, we decided to adopt a weaker shape descriptor, namely skeleton or median curve (surface) to represent geometric features of jSR. A simple definition of a skeleton can be given by so-called grass fire model – the boundary of an object is set on fire and the skeleton is the loci where the fire fronts meet and quench each other (Blum, 1967). A typical computer implementation of this model is by iterative thinning, a process of repeatedly peeling the voxels lying on the boundaries of an object until the skeletons are reached (Lam et al., 1992). The segmented boundary of jSR (Fig. 1C) provided a good starting point to find the skeletons. Fig. 1D shows a cross-section of the jSR skeletons (the curves in magenta) we extracted using the topology-preserving iterative 3D thinning method as described in (Palagyi et al., 2001). The same skeleton extraction strategy was also applied to the LM images of T-tubules, as will be demonstrated in the Results or Fig. 4B and C. Note that T-tubules in LM data were treated as piece-wise 1D curves instead of 2D surfaces as employed in EM studies.
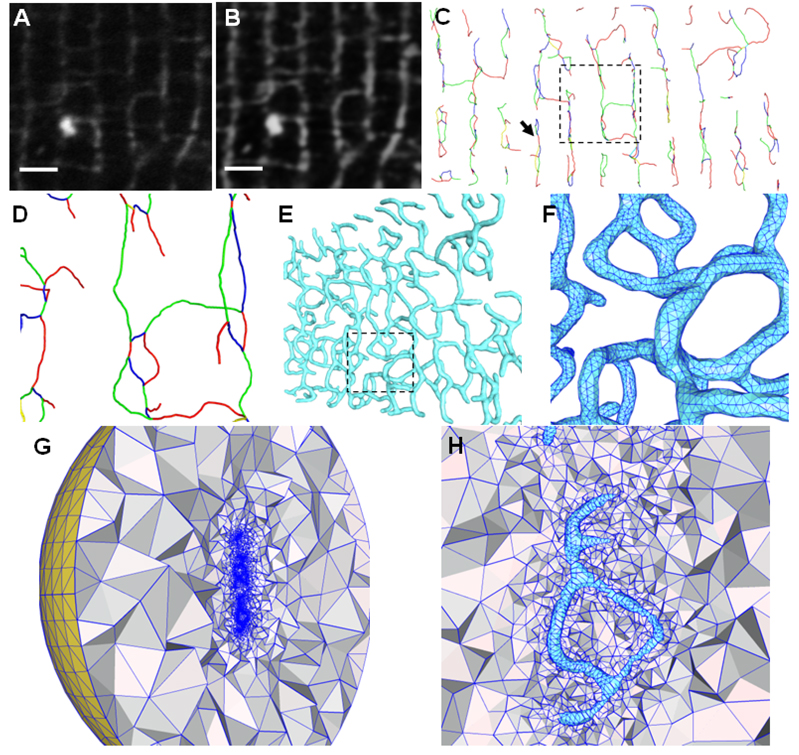
Figure 4.
Illustrations of image pre-processing and geometric modeling of T-tubules from light microscopic images. (A) The original T-PM image (a small portion of the cross-section). (B) The image after contrast enhancement and noise reduction. (C) The skeletons extracted directly from the 3D LM images. All adjacent branches have been colored differently to distinguish between them, although the color scheme used does not convey any biological information. A close view of the rectangular region is shown in (D) with a small amount of rotation to the left to demonstrate the 3D network in the depth direction. (E) The surface triangulation is constructed based on the skeletons using the pseudo-molecule approach. The model is rotated to the left by about 45°. The rectangular region, with triangulation details, is enlarged in (F). (G) and (H) show the tetrahedral mesh bounded by the surface triangulation of (E). A large artificial bounding sphere (yellow in (G)) will serve as the domain boundary to solve simulation problems. Note that the T-tubular structures (in cyan) near the center in (H) are empty and the tetrahedral meshes exist only between T-tubules and the bounding sphere. The region in (H) roughly corresponds to that indicated by the arrow in (C). Scale bars in (A,B): 2 µm.
2.4. Geometric Modeling and Mesh Generation
Both the boundaries of T-tubules and the skeletons of jSR extracted above were represented by a number of voxels (see Fig. 1E for zoomed-in boundaries and skeletons). However, mathematical simulation often requires surface or volumetric meshes. We therefore converted the voxel-based features into realistic 3D geometric models represented by triangular and/or tetrahedral meshes. In our recent studies, we had developed a feature-preserving, adaptive mesh generation and refinement scheme, in which the inputs can be one of three types: a molecule (represented by a list of atoms), a scalar 3D volume, or a user-defined triangular surface mesh (Yu et al., 2008). However, neither the segmented T-tubules nor the skeletonized jSR in the aforementioned EM or LM studies were in any of these three forms. In the following we shall explain how to convert the extracted boundary or skeletal information into pseudo-molecular models and then generate meshes from such models.
The boundary voxels of the segmented T-tubules formed a zigzag surface (Fig. 1E). In order to get a smooth boundary, we placed a sphere with a fixed radius of 3.5 nm (equal to one voxel size) on each voxel about 7.0 nm (or two-voxel size) away from the boundary (as illustrated by blue circles inside the T-tubule in Fig. 1F). All these spheres were treated as atoms, constituting a so-called pseudo-molecular model, which we used as an input in our mesh generation toolchain. In a similar way, we built a pseudo-molecule from the skeletons of jSR by placing a sphere on each of the voxels on the skeletons as illustrated by yellow circles on the jSR in Fig. 1F. Given a molecule, we first generated a 3D density map by treating each atom as a Gaussian-like smoothly decaying scalar function in 𝕽3 (Blinn, 1982; Duncan and Olson, 1993; Grant and Pickup, 1995). The molecular surface was then approximated by appropriate level sets (or isocontours) of the Gaussian function (Zhang et al., 2006) as follows:
| (3) |
where the negative parameter Bi is called blobbyness that controls the spread of electron density of each atom. We usually treat the blobbyness as a constant parameter (denoted by B0) for all atoms. xi and ri are the center and radius of the ith atom. T0 is the iso-value corresponding to the molecular surface. We shall discuss in Section 4 how to choose appropriate iso-values to extract surfaces (membranes) of T-tubules and jSR.
The surface triangulation of 3D density maps was constructed by the marching cube method (Lorensen and Cline, 1987). The quality of the meshes was then improved by moving the vertices while retaining the sharp features and smoothness on the original surfaces as described in (Yu et al., 2008). The surface meshes was also selectively coarsened or refined, meaning that the regions of less interest were sparsely meshed such that the size of the resulting mesh was small enough for numerical solvers to handle big systems. The volumetric (tetrahedral) meshes were constructed from the post-processed surface meshes using the constrained Delaunay triangulation as implemented in Tetgen (Si, 2004; Si and Gartner, 2005). In (Yu et al., 2008), we had shown that meshes generated by this toolchain had much higher quality than those without quality improvement or meshes generated by other tools such as MSMS (Sanner et al., 1996). Similar sphere-packing and mesh generation techniques were also applied to LM images, and T-tubular network structures were modeled with high-quality surface and volumetric meshes.
3. Results
3.1. Modeling T-tubules and jSR from EM Data
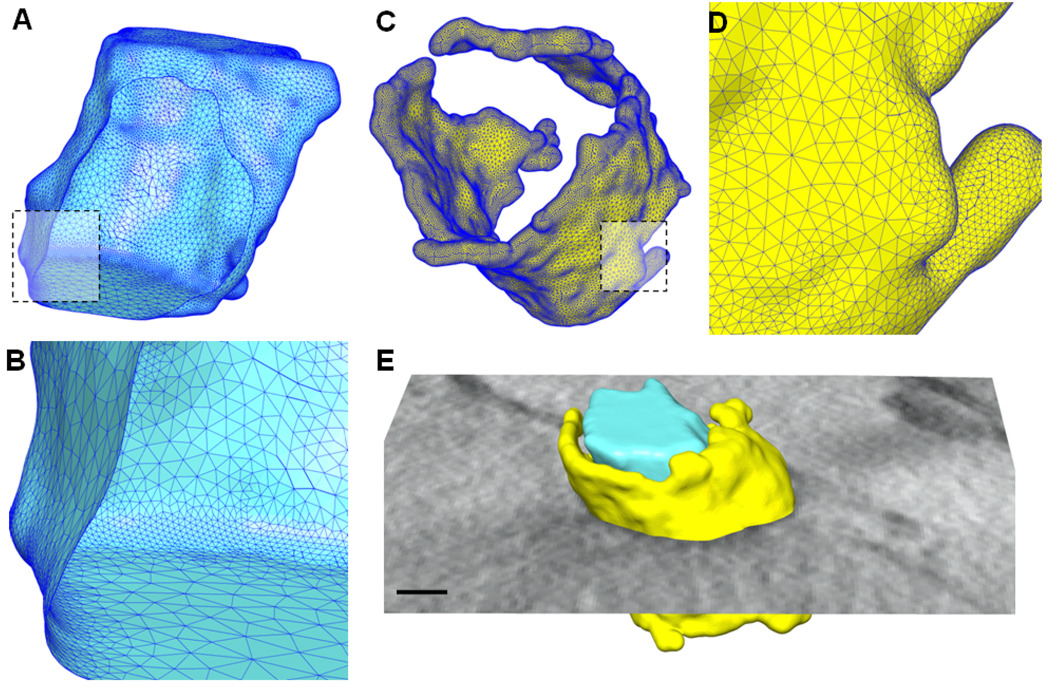
A tomographic EM reconstruction (density map) was obtained from the mouse myocardium, in which the staining contrasts of T-tubules and SR were selectively enhanced. The 3D density map was first pre-processed using the contrast enhancement and noise reduction methods, followed by the extractions of T-tubules and jSR using the segmentation and skeletonization approaches, as described in the Methods. Finally high quality meshes were generated from the extracted boundaries of T-tubules and skeletons of jSR and visualized using the UCSF Chimera tool (Pettersen et al., 2004). Fig. 2A shows the extracted triangular surface mesh of the T-tubule corresponding to the features shown in Fig. 1. The mesh in the front was cut out so that the mesh behind is visible from inside. The mesh near the dashed rectangle in Fig. 2A is enlarged and shown in Fig. 2B, from which we can clearly see the quality of the triangular mesh generated using our meshing toolchain. Fig. 2C shows the mesh of jSR extracted from the EM images using the skeletonization approach. The estimation of the thickness of jSR will be discussed in Section 4.2. From this 3D model of jSR, we can see that jSR covers T-tubules irregularly. A close view of the mesh quality is shown in Fig. 2D. Fig. 2E shows the extracted T-tubule, jSR, together with one cross-section of the original density EM map.
Figure 2.
Feature extraction and mesh generation on the EM data shown in Fig. 1. (A) High-quality triangular surface mesh is generated from the auto-segmented T-tubule. The mesh in the front is cut out so that we can clearly see the interior of the mesh. (B) A close view of the surface mesh in the rectangular area as indicated in (A). (C) The computed surface mesh for jSR based on its skeletons. (D) A close view of the rectangular area in (C). (E) The T-tubule and jSR are put together with a cross section of the original map. Scale bar in (E): 50 nm.
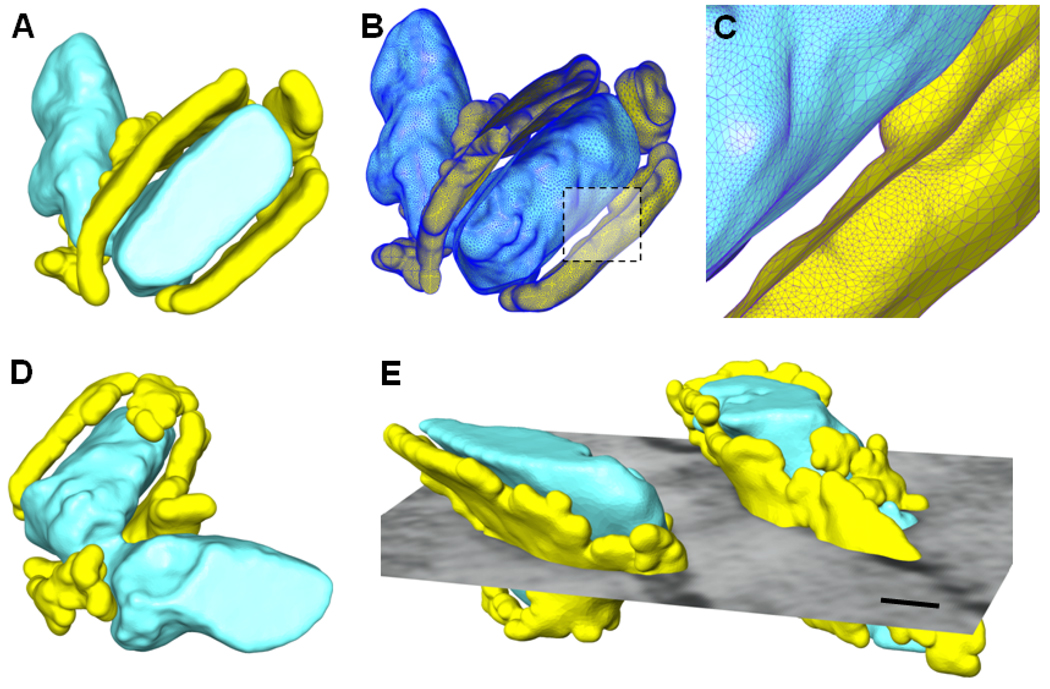
The feature extraction and geometric modeling techniques applied to the current study demonstrate that there are significant variations in the size, shape, and orientation of dyads, the anatomical and functional couplings between T-tubules and jSR, visualized by EM tomography. In the particular model shown in Fig. 3A–D, the T-tubule associated with the dyad is connected to the non-dyadic region of T-tubules with a neck (see Fig. 3A and D for two views). The dyadic and non-dyadic T-tubules shown here have different orientations and shapes, and the neck connecting both T-tubules appears to be significantly thinner than other regions of the T-tubules. A great amount of jSR extends from the dyad to cover partially the neck. The cross-section of T-tubules in this model demonstrates an elliptic shape instead of a circular one as seen in Fig. 2. The triangulated surface mesh with the front portion cut out is shown in Fig. 3B and a closer view of the dyadic cleft (indicated by the dashed rectangle) is given in Fig. 3C. Another example of the feature extraction and mesh generation is shown in Fig. 3E, where two T-tubules are close to each other and surrounded by individual jSR. Again, these two T-tubules demonstrate a notable difference in shape and size. An interesting observation from this example is that T-tubules are not always separated by a regular distance but instead they could get very close yielding an irregular 3D distribution in cardiomyocytes.
Figure 3.
More examples of geometric modeling from EM imaging data. (A) The surfaces rendering of the extracted T-tubules (the thick structures in cyan) surrounded by jSR (the thin structures in yellow). (B) The surface mesh representation with the front part cut out. (C) A close view of the dyadic cleft as indicated by the dashed rectangle in (C). (D) Another view of the same model as shown in (A). (E) Another example of geometric modeling of T-tubules (the thick structures in cyan) and the surrounding jSR (the thin structures in yellow). A cross section of the original image is shown together with the models. Scale bar in (E): 50 nm.
3.2. 3D T-tubular Network from Light Microscopy Images
With a combination of image pre-processing, skeleton extraction, and mesh generation, we have also successfully constructed realistic 3D T-tubular systems from the T-PM images of mouse ventricular myocytes. We tested our algorithms and software tools on a volume of 21.1 µm × 10.7 µm × 2.4 µm, cropped from the T-PM data we collected. This sub-volume was first pre-processed by our 3D contrast enhancement and noise reduction algorithms as discussed in Section 2.2. Fig. 4A and B show an example of T-PM images of T-tubular structures of mouse ventricular myocytes, corresponding respectively to the cross-section of the original image and the image after contrast enhancement and noise reduction. It is obvious that the contrast enhancement, coupled with the image smoothing, significantly improves the image quality, making the subsequent feature extractions (skeletonization, in particular) much easier and more reliable.
Fig. 4C and D show the extracted skeletons of T-tubules using the iterative thinning approach as outlined in Section 2.3. Note that each branch is composed of a number of very short “line segments” with significantly varying lengths. From both pictures, we can see that the skeletons provide us very useful information on the 3D topology of the T-tubular network, although they do not contain any thickness information regarding the T-tubules. However, we can “recover” the thickness of T-tubules and build high-quality geometric surface meshes using the sphere-packing approach. Specifically, we place a number of spheres with a fixed radius along the extracted skeletons of T-tubules, with one sphere centering on each line segment. These spheres are then treated as a pseudo-molecule and fed into our mesh generation toolchain (Yu et al., 2008), to thicken T-tubular skeletons, assuming their diameter is roughly 250 nm, based on the previous experimental observation (Soeller and Cannell, 1999). The “thickened” T-tubules are represented by triangular surface meshes (Fig. 4E and F). Because the line segments constituting the skeletons of T-tubules often vary in length, the spheres along skeletons are non-equally distributed, resulting in non-uniformly “thickened” T-tubules. This problem, however, can be fixed by equally placing spheres along the skeletons. Another factor that causes the non-uniform thickness of “reconstructed” T-tubules is due to the varying curvature of skeletons from one region to others. Therefore, the variation of thickness shown in the current mesh model does not represent biologically the actual T-tubule anatomy, but it does provide an approximate model for future simulation.
While triangular surface meshes can be directly used in mathematical simulation using boundary element methods to model, for example, the propagation of membrane excitation along T-tubular branches, it is also in great demand to construct volumetric tetrahedral meshes and use finite element methods to simulate various biological activities. This strategy is especially useful for modeling Ca2+ mobilization within T-tubules and, perhaps more interestingly, simulating Ca2+ buffering and diffusion originated from T-tubules into the cytosol. To this end, we utilize the surface triangulation as seen in Fig. 4E to generate the tetrahedral meshes (Fig. 4G and H) using the constrained Delaunay triangulation as implemented in Tetgen (Si, 2004; Si and Gartner, 2005) and incorporated into our meshing tool (Yu et al., 2008). Here a large sphere is used to mimic the cell surface membrane and serve as a boundary for future simulation. The tetrahedral mesh is generated between this bounding sphere and the extracted T-tubular triangular mesh as shown in Fig. 4G. A close view of the area near T-tubules is shown in Fig. 4H, where T-tubular structures near the center of the picture (colored in cyan) are empty and surrounded by adaptive tetrahedra.
4. Discussion
4.1. Iso-value Estimation of T-tubules
In Section 2.4, we described how to build a pseudo-molecule given the extracted T-tubular structure, and how to construct an initial surface mesh from the Gaussian-blurred volume. The unanswered question is: how to find an appropriate iso-surface that matches the segmented T-tubule as well as possible? Apparently the isosurface is dependent on the iso-value and blobbyness chosen (we assume that the position and radius of each atom are known). In (Blinn, 1982), Blinn suggested that the default iso-value be set as 1, and the surfaces can change by adjusting the blobbyness B0. Following our previous work (Yu et al., 2008), we could also fix the blobbyness B0 (set as −0.5, for example) and adjust the iso-value to find the approximate isosurface.
Due to the variation of surface curvatures and non-uniform distribution of “atoms” near the boundary grids, it is difficult, if not impossible, finding an analytically represented iso-value that gives rise to an exactly matched surface. Apparently the iso-surface extracted using the sphere-packing method described above tends to be closer to the true surface at convex areas and farther away at concave areas. For simplicity, we consider only a planar surface region where the spheres or “atoms” are distributed uniformly in a 2D rectangular grid spaced by a unit of d in both X and Y directions. The question now becomes: given such a list of spheres with a constant radius (denoted by r0) and a fixed blobbyness B0, what is the value of F(x) at a point that is away from the plane by a distance of h, or in particular what is the value of F(0, 0, h)? We can show that (See Appendix A for details):
| (4) |
This is actually the threshold or iso-value that we use to extract initial surface meshes. For example, we know that h = 7.0 nm and r0 = 3.5 nm for the EM maps we considered in Section 3.1. The spacing distance between neighboring atoms is approximated by one-voxel size or 3.5 nm. The default blobbyness is set −0.5, as usually used in our molecular mesh generator. All these parameters together give rise to an iso-value of 1.402, which is the one we used to extract the initial surface from the segmented T-tubules as seen in Fig. 2 and Fig. 3.
From the extracted geometries of T-tubules, we can calculate their volumes, which in turn can be used to validate the iso-value estimation described above. The volume of a T-tubule can be calculated in two ways: from the voxels segmented or from the surface mesh generated. In the example shown in Fig. 1 or Fig. 2, the number of voxels corresponding to the segmented T-tubule is 66,176. Note that each voxel is equivalent to a cube of 3.5×3.5×3.5 nm3, which yields a total volume of 2,837,296 nm3 for this particular T-tubule. On the other hand, we can also calculate the volume enclosed by the extracted surface mesh (Fig. 2A). From the tetrahedral mesh inside this surface, we compute the sum of the volumes of all the tetrahedra and get a total volume of 2,867,207 nm3. Compared to the volume estimated from the segmented voxels, the volume calculated from the surface mesh is about 1.05% larger. This analysis quantitatively validates the iso-value determination as discussed above.
4.2. Iso-value Estimation of jSR
The estimation of iso-value for jSR is a little more complicated due to the lack of precise boundaries. However, we do have fairly accurate skeletons for jSR as shown in Fig. 1D. Given the segmented T-tubules, we can estimate the average distance from the skeletons of jSR to the boundaries of the corresponding T-tubules. Previous studies (Bers, 2001; Fabiato, 1985; Franzini-Armstrong et al., 1999; Langer and Peskoff, 1996) have suggested that the dyadic clefts span by an average distance of 10~15 nm between the membranes of T-tubules and neighboring jSR. We shall take the median of this range, which is 12.5 nm. For the example shown in Fig. 1, the average distance from skeletons of jSR to the nearby T-tubule is about 20.9 nm, which implies that the jSR surface should be away from the skeletons roughly by a distance of 20.9−12.5 = 8.4 nm. Note that the iso-surface of jSR, unlike that of T-tubules, is generated from a list of spheres lying along a one-dimensional curve. Therefore, we need a slightly different approximation of the iso-value for curvilinear features (see Appendix B for details):
| (5) |
The parameters here are basically the same as those for T-tubules as discussed in Section 4.1, except that h here should be set as 8.4. With these parameters, Equation 5 yields an iso-value of 0.582, which is a little smaller than that for T-tubules.
Because the average distance from the skeletons of jSR to the T-tubule is about 20.9 nm, we can approximate the thickness of jSR as follows: (20.9−12.5)×2 = 16.8 nm, where 12.5 nm is the average spanning distance of the dyadic clefts we assumed. On the other hand, we can also estimate the thickness of jSR based on its volumes. The total volume of jSR is 1,582,942 nm3, estimated from the tetrahedralization from the surface mesh in Fig. 2B. In addition, the total number of skeleton points (see yellow spheres on the jSR in Fig. 1F for illustration) is 7, 981. On average, each of these points occupies a surface area of 3.5×3.5 = 12.25 nm2. Therefore, the average thickness of SR can be estimated as 1,582,942/(7981×3.5£3.5) = 16.2 nm. This is close to the thickness estimated from the average spanning distance of the dyadic clefts, and confirms again that our iso-value determination and hence the iso-surface extracted are reasonably accurate.
4.3. Quantitative Analysis of Cell-Wide T-tubular Systems
Although the main goal of the present paper is to generate meshes from imaging data, the feature extraction alone may also be used to analyze the spatial distribution of T-tubular structures. Several recent studies have linked the T-tubule disorganization to the pathogenesis of heart failure (see (Brette and Orchard, 2007) for a review), suggesting that changes in the length variations of T-tubular branches might cause the desynchronization of CICR events. Therefore, achieving accurate geometric analysis of T-tubules in 3D space is significant to understand the structural contribution of membrane organelles and their changes to the contractile dysfunction of cardiomyocytes. From the extracted skeletons of T-tubules as seen in Section 3.2 and Fig. 4, we can analyze the branch lengths and orientations of T-tubules. As an example, we again cropped out a sub-volume from the T-PM data but doubled the size of the volume to 21.1 µm × 10.7 µm × 5.0 µm near the center of the cell. In our skeleton extraction method, each branch is represented by a number of short line segments. The length of the segments on average is about 70 nm, close to the pixel size (60 nm) in our experimental data. The length of each branch is measured by adding up the lengths of all segments lying on that branch. The orientation distribution of T-tubules is estimated by the orientation of each short line segment on the skeletons of T-tubules with respect to the longitudinal axis of the cell.
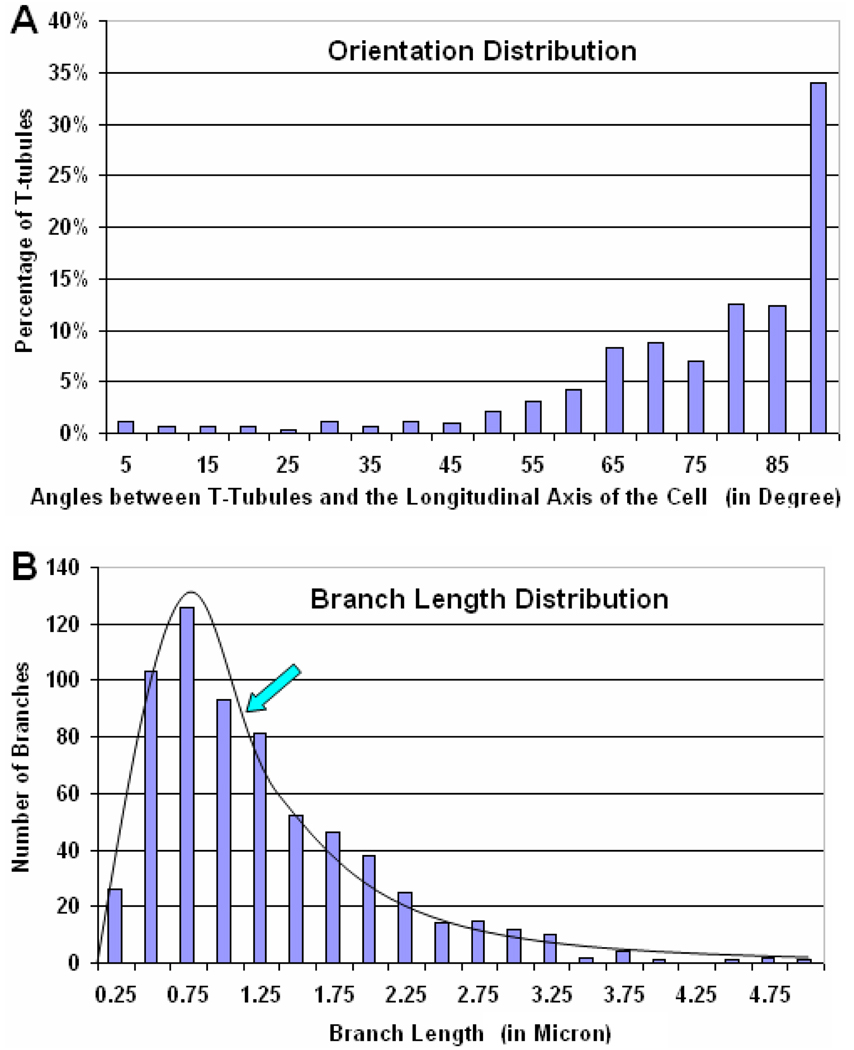
Fig. 5A shows the orientation distribution of T-tubules by percentages. The orientation of each line segment is represented by the angle between the segment and the longitudinal axis of the cell. Therefore, 90° corresponds to line segments parallel to the transverse plane of the cell. From the distribution shown in Fig. 5A, we can see that ~ 60% of the T-tubules in this particular example have orientations roughly in the transverse direction of the cell (corresponding to the three bars on the right in Fig. 5A). Since most T-tubules having such orientations are lying on or near the Z-disks of ventricular myocytes, our estimation of T-tubular orientations agrees well with previous studies (Soeller and Cannell, 1999). However, T-tubules can be oriented in arbitrary directions, forming a complicated three-dimensional network. In order to study how densely the T-tubules are connected to each other, we also calculated the histogram of T-tubular branch lengths as shown in Fig. 5B. There is a sharp increase from 0.25 µm to 0.75 µm, which then decreases rapidly to ~5.0 µm. The average length of T-tubular branches for this example is about 1.15 µm, as indicated by the arrow in Fig. 5B. The median length is about 1.06 µm. Note that the anisotropy of the original fluorescent data distribution does not seem to affect our geometric analysis much because of the skeleton representation used.
Figure 5.
Quantitative analysis of T-tubular systems using T-PM images. (A) The distribution of the orientation of T-tubules, which was calculated as the angle between each short line segment on the skeletons and the long axis of the cell. Most T-tubules have orientations roughly perpendicular to the longitudinal axis of the cell, implying that a majority of T-tubules lie on or near the Z-disks of ventricular myocytes. However, T-tubules can be in arbitrary orientation, forming a complicated three-dimensional network. (B) The distribution of T-tubular branch lengths. There is a sharp increase from 0.25 µm to 0.75 µm, which then decreases rapidly to ~5.0 µm. The average branch length of T-tubules in cardiomyocytes is about 1.15 µm, as indicated by the arrow. The median length is about 1.06 µm. The estimation of branch lengths indicates how densely the T-tubules are connected to each other.
4.4. Software Implementation and Resource
All the algorithms discussed here have been implemented in a combination of C and C++ programming languages. While the software packages developed can be compiled and run on a variety of computer operating systems, all results shown in the Results were generated on a Linux machine with a single processor, and the execution time for each of the algorithms varies from a few seconds up to one minute. We have made most of the software tools implementing these algorithms available online for free downloading under certain agreements. Specifically, the individual tools of image pre-processing (contrast enhancement and noise filtering) and feature extraction (segmentation and skeletonization) can be downloaded from the Computational Visualization Center (cvcweb.ices.utexas.edu/software/applications.php) at The University of Texas at Austin. The mesh generation tool, named Geometry-preserving Adaptive Mesher (or GAMer) (Yu et al., 2008), will be released as part of the finite element toolkit FeTK (www.fetk.org) (Holst, 2001) developed at The University of California, San Diego. Some of the image pre-processing and feature extraction code had been incorporated into a fast and scalable visualization tool called VolRover (cvcweb.ices.utexas.edu/software).
4.5. Automatic Segmentation: the Challenges and Future Work
Generally speaking, the problems of image pre-processing (noise filtering and contrast enhancement) and geometric modeling (mesh generation) are well-posed, meaning that the performance of the corresponding algorithms is often guaranteed (e.g., noise reduced, contrast enhanced, or mesh quality improved after each iteration of processing). However, the feature extraction from pixel-based gray-scale images is much harder to deal with. A small perturbation of image intensities may result in completely different features (boundaries or skeletons). In other words, the result of feature detection is very sensitive to the noise in the original image. In the framework described in Section 2, the skeletonization is based on the segmented (binary) images and hence easier to “predict” the results. Therefore, the real bottleneck of the image-based geometric modeling is the boundary segmentation from a gray-scale image. This is however not surprising − image segmentation has always been one of the fundamental but difficult problems in image processing and analysis.
Compared to the watershed method (Volkmann, 2002) or the traditional fast marching method (Sethian, 1996), our segmentation approach utilizes multiple sets of seed points and accordingly a number of contours compete with each other and deform to the most agreeable boundaries. The accuracy of the segmentation is generally affected by two important factors: the noise level and the manual selection of some seed points by the user. The image pre-processing can significantly reduce the noise as shown in Fig. 1C. However, some structures may be permanently “damaged” during the specimen preparation, imaging, or 3D reconstruction, and cannot be “recovered” by the pre-processing techniques. For example, some jSR on the right side of the T-tubule in Fig. 1C forms an “island” and the contours from the main jSR cannot reach there. This problem may be resolved by placing one (or more) new seed point within the “island”. In general, more sophisticated seed selection would result in better segmentation but require more manual work from the user. In our future work we will develop a user-friendly graphical interface, in which the user can interactively select seed points, run the segmentation, and visualize the results. When an input image has a high signal-to-noise ratio, it is also possible to select and classify the seeds automatically, thereby making the image-based geometric modeling fully automated. The multi-seeded segmentation approach can also be applied to images with a number of distinctive components (such as multilayered structures). One such example had been demonstrated in our recent work on subunit segmentation of viruses and ribosome (Baker et al., 2006; Yu and Bajaj, 2005).
4.6. Multiscale Simulation of E-C Coupling in Hearts
Although it is beyond the scope of the present paper, the ultimate goal of the image-based geometric modeling is realistic simulation of biological systems using various mathematical models. The simulation using the geometric models of T-tubules and jSR is being conducted at two levels. One is within a single dyad (or calcium release unit) from EM data to simulate the calcium-induced calcium release (CICR). Due to the random behaviors of calcium channelling and diffusion, and relatively small number of calcium ions involved in a single dyad, stochastic methods are more suitable at this scale by tracking the position of every single calcium ion. Being used for this purpose is the MCell tool (Stiles and Bartol, 2001), a Monte Carlo based stochastic simulation package developed at the Salk Institute (www.mcell.cnl.salk.edu). The other simulation problem of our interest is the global calcium dynamics at the cellular level, namely, modeling how calcium concentration changes in the whole cell or in a segment of the cell as a result of diffusion, buffering and re-uptake of calcium. At this scale, the stochastic behaviors become much less significant and hence a better way is to use a set of partial differential equations (PDE’s) to describe the continuous change of calcium concentration in the cell. The FeTK simulation tool (www.fetk.org) will be used to numerically solve the equations. Typically these numerical simulations can be conducted on a single processor within a reasonable time, but calculation of calcium diffusions may need more advanced parallel computation depending on the sizes of domains (meshes).
While the methodology described in the present paper primarily targets structures with detectable boundaries, non-membrane structures or structures with extremely noisy boundaries may still be identified and represented by their mass centers (Yu and Bajaj, 2003). For example, we can detect the centers of ryanodine receptors (RyR’s), given that their accurate boundaries may be difficult to extract in 3D reconstructed EM maps. These centers, together with the jSR membrane detected, can be used to determine the distribution (both locations and orientations) of RyR’s. We can then build a more realistic 3D model of calcium release units by fitting the cryo-EM map of RyR’s (Liu et al., 2005; Samso et al., 2005; Serysheva et al., 2007) into the electron tomographic map at a relatively lower resolution. On the other hand, the approaches and algorithmic details can also be extended to medical images such as CT-scanned heart data, making it possible to investigate structural analysis and functional simulation of heart failures from sub-cellular to whole organ levels.
Acknowledgments
We thank Dr. Anushka Michailova, Dr. Yuhui Cheng, Dr. Wilfred Li, Prof. Peter Arzberger, and Prof. Andrew McCulloch for helpful discussions. This work was supported in part by NSF Awards 0715146, 0411723, 0511766 and 0225630, DOE Awards DE-FG02-05ER25707 and DE-FG02-04ER25620, and supports from National Biomedical Computation Resource (http://nbcr.sdsc.edu/, P41 RR008605) and National Center for Microscopic and Imaging Research (http://ncmir.ucsd.edu/, P41 RR004050). M. Hoshijima was supported by American Heart Association Scientist Development Grant and Established Investigator Award. Work in McCammon’s group was supported by NSF (MCB-0506593), NIH (GM31749), HHMI, CTBP, W.M. Keck Foundation, and Accelrys, Inc..
Appendix
Appendix A: Iso-value Estimation for Planar Features
Let us assume that all the grids on a two-dimensional (or X–Y) plane be uniformly occupied by atoms and all the atoms have a fixed radius r0 and a constant blobbyness B0. From Equation (3) we know that the function value of F(x) at (0, 0, h) can be written as:
| (6) |
| (7) |
Note that:
| (8) |
Therefore (7) can be approximated by:
| (9) |
| (10) |
Equation (10) can be used to approximate the iso-value of the isosurface that is away from the layer of spheres by a distance of h. The error of such an approximation depends on the curvature of the local area on the surface and the way how the spheres are packed on the surface.
Appendix
Appendix B: Iso-value Estimation for Curvilinear Features
We assume that the curve be a straight line and all the grids on that line be uniformly occupied by atoms on a one-dimensional (or X) axis. Again, we assume that all the atoms have a fixed radius r0 and a constant blobbyness B0. Similar to Appendix A, we can estimate the function value of F̄(x) at (0, 0, h) as:
| (11) |
| (12) |
| (13) |
Equation (13) is the approximation to the iso-value in case of the curvilinear structures. The error of such an approximation mainly depends on the local curvature of the curve.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bajaj C, Wu Q, Xu G. ICES Technical Report: University of Texas at Austin; 2003a. Level-set based volumetric anisotropic diffusion for 3D image denoising. [Google Scholar]
- Bajaj C, Yu Z. Geometric processing of reconstructed 3D maps of molecular complexes. In: Aluru S, editor. Handbook Comput. Mol. Biol. Chapman and Hall/CRC Press; 2005. [Google Scholar]
- Bajaj C, Yu Z, Auer M. Volumetric feature extraction and visualization of tomographic molecular imaging. J. Struct. Biol. 2003b;144:132–143. doi: 10.1016/j.jsb.2003.09.037. [DOI] [PubMed] [Google Scholar]
- Baker M, Yu Z, Chiu W, Bajaj C. Automated segmentation of molecular subunits in electron cryomicroscopy density maps. J. Struct. Biol. 2006;156(3):432–441. doi: 10.1016/j.jsb.2006.05.013. [DOI] [PubMed] [Google Scholar]
- Barash D. A fundamental relationship between bilateral filtering, adaptive smoothing and the nonlinear diffusion equation. IEEE Trans. Pattern Anal. Mach. Intell. 2002;24:844–847. [Google Scholar]
- Bers D. Excitation-Contraction Coupling and Cardiac Contractile Force. 2nd Edition. Kluwer Academic Publishers: Dordrecht, The Nether-lands; 2001. [Google Scholar]
- Blinn J. A generalization of algegraic surface drawing. ACM Trans. Graph. 1982;1(3):235–256. [Google Scholar]
- Blum H. A transformation for extracting new descriptors of shape. In: Wathen-Dunn W, editor. Models for the Perception of Speech and Visual Form: MIT Press; 1967. pp. 363–380. [Google Scholar]
- Brette F, Orchard C. Resurgence of cardiac T-tubule research. Physiology (Bethesda) 2007;22:167–173. doi: 10.1152/physiol.00005.2007. [DOI] [PubMed] [Google Scholar]
- Caselles V, Lisani J, Morel J, Sapiro G. Shape preserving local histogram modification. IEEE Trans. Image Process. 1998;8:220–230. doi: 10.1109/83.743856. [DOI] [PubMed] [Google Scholar]
- Duncan B, Olson A. Shape analysis of molecular surfaces. Biopolymers. 1993;33:231–238. doi: 10.1002/bip.360330205. [DOI] [PubMed] [Google Scholar]
- Elad M. On the bilateral filter and ways to improve it. IEEE Trans. Image Process. 2002;11(10):1141–1151. doi: 10.1109/TIP.2002.801126. [DOI] [PubMed] [Google Scholar]
- Fabiato A. Time and calcium dependence of activation and inactivation of calcium-induced release of calcium from the sarcoplasmic reticulum of a skinned canine cardiac Purkinje cell. J. Gen. Physiol. 1985;85:247–289. doi: 10.1085/jgp.85.2.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franzini-Armstrong C, Protasi F, Ramesh V. Shape, size, and distribution of calcium release units and couplons in skeletal and cardiac muscles. Biophys. J. 1999;77:1528–1539. doi: 10.1016/S0006-3495(99)77000-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez R, Woods R. Digital Image Processing. Addison-Wesley Publishing Company. 1992 [Google Scholar]
- Grant J, Pickup B. A Gaussian description of molecular shape. J. Phys. Chem. 1995;99:3503–3510. [Google Scholar]
- Holst M. Adaptive numerical treatment of elliptic systems on manifolds. Adv. Comput. Math. 2001;15:139–191. [Google Scholar]
- Izu L, Means S, Shadid J, Chen-Izu Y, Balke C. Interplay of ryanodine receptor distribution and calcium dynamics. Biophys. J. 2006;91:95–112. doi: 10.1529/biophysj.105.077214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izu L, Wier WG, Balke C. Evolution of cardiac calcium waves from stochastic calcium sparks. Biophys. J. 2001;80:103–120. doi: 10.1016/S0006-3495(01)75998-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W, Baker M, Wu Q, Bajaj C, Chiu W. Applications of bilateral denoising filter in biological electron microscopy. J. Struct. Biol. 2003;144(1–2):114–122. doi: 10.1016/j.jsb.2003.09.028. [DOI] [PubMed] [Google Scholar]
- Jobson D, Rahman Z, Woodell G. Properties and performance of a center/surround retinex. IEEE Trans. Image Process. 1997;6:451–462. doi: 10.1109/83.557356. [DOI] [PubMed] [Google Scholar]
- Koh X, Srinivasan B, Ching H, Levchenko A. A 3D Monte Carlo analysis of the role of dyadic space geometry in spark generation. Biophys. J. 2006;90:1999–2014. doi: 10.1529/biophysj.105.065466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam L, Lee S, Suen C. Thinning methodologies - a compresensive survey. IEEE Trans. Pattern Anal. Mach. Intell. 1992;14:869–885. [Google Scholar]
- Langer G, Peskoff A. Calcium concentration and movement in the diadic cleft space of the cardiac ventricular cell. Biophys. J. 1996;70:1169–1182. doi: 10.1016/S0006-3495(96)79677-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Wang R, Zhang J, Chen S, Wagenknecht T. Localization of a disease-associated mutation site in the three-dimensional structure of the cardiac muscle ryanodine receptor. J. Biol. Chem. 2005;280(45):37941–37947. doi: 10.1074/jbc.M505714200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorensen W, Cline HE. Marching cubes: a high resolution 3D surface construction algorithm. Comput. Graph. 1987;21(4):163–169. [Google Scholar]
- Malladi R, Sethian J. A real-time algorithm for medical shape recovery. IEEE Int. Conf. Comput. Vision. 1998:304–310. [Google Scholar]
- Michailova A, DelPrincipe F, Egger M, Niggli E. Spatiotemporal features of calcium buffering and diffusion in atrial cardiac myocytes with inhibited sarcoplasmic reticulum. Biophys. J. 2002;83:3134–3151. doi: 10.1016/S0006-3495(02)75317-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palagyi K, Sorantin E, Balogh E, Kuba A, Halmai C, Erdohelyi B, Hausegger K. A sequential 3D thinning algorithm and its medical applications. In: Insana M, Leahy R, editors. Lecture Notes in Computer Science. Vol. 2082. 2001. pp. 409–415. [Google Scholar]
- Perkins G, Renken C, Song J, Frey T, Young S, Lamont S, Martone M, Lindsey S, Ellisman M. Electron tomography of large, multicomponent biological structures. J. Struct. Biol. 1997;120:219–227. doi: 10.1006/jsbi.1997.3920. [DOI] [PubMed] [Google Scholar]
- Pettersen E, Goddard T, Huang C, Couch G, Greenblatt D, Meng E, Ferrin T. UCSF Chimera - a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Pratt W. Digital Image Processing. 2nd Edition. A Wiley-Interscience Publication; 1991. [Google Scholar]
- Saetersdal T, Larsen T, Rotevatn S, Dalen H, Scheie P. Fibronectin and laminin in transverse tubules of cardiac myocytes studied by laser confocal microscopy and immunocytochemistry. Histochemistry. 1992;98:73–80. doi: 10.1007/BF00716997. [DOI] [PubMed] [Google Scholar]
- Samso M, Wagenknecht T, Allen P. Internal structural and visualization of tranmembrane domains of the RyR1 calcium release channel by cryo-EM. Nat. Struct. Mol. Biol. 2005;12(6):539–544. doi: 10.1038/nsmb938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanner M, Olson A, Spehner J. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Serysheva I, Chiu W, Ludtke S. Single-particle electron cryomicroscopy of the ion channels in the excitation-contraction coupling junction. Methods Cell Biol. 2007;79:407–435. doi: 10.1016/S0091-679X(06)79016-1. [DOI] [PubMed] [Google Scholar]
- Sethian J. A marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. 1996;93(4):1591–1595. doi: 10.1073/pnas.93.4.1591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Si H. Tetgen: a quality tetrahedral mesh generator and three-dimensional Delaunay triangulator. Tech. Rep. 9, Weierstrass Institute for Applied Analysis and Stochastics. 2004 (software download: http://tetgen.berlios.de) [Google Scholar]
- Si H, Gartner K. Meshing piecewise linear complexes by constrained Delaunay tetrahedralizations. 14th Int. Meshing Roundtable. 2005 [Google Scholar]
- Soeller C, Cannell MB. Examination of the transverse tubular system in living cardiac rat myocytes by 2-photon microscopy and digital imageprocessing techniques. Circ. Res. 1999;84:266–275. doi: 10.1161/01.res.84.3.266. [DOI] [PubMed] [Google Scholar]
- Stark J. Adaptive contrast enhancement using generalization of histogram equalization. IEEE Trans. Image Process. 2000;9:889–906. doi: 10.1109/83.841534. [DOI] [PubMed] [Google Scholar]
- Stiles J, Bartol T. Monte Carlo methods for simulating realistic synaptic microphysiology using MCell. In: Schutter E, editor. Computational Neuroscience: Realistic Modeling for Experimentalists. CRC Press; 2001. pp. 87–127. [Google Scholar]
- Tomasi C, Manduchi R. Bilateral filtering for gray and color images. IEEE Int. Conf. Comput. Vision. 1998:836–846. [Google Scholar]
- Volkmann N. A novel three-dimensional variant of the watershed transform for segmentation of electron density maps. J. Struct. Biol. 2002;138:123–129. doi: 10.1016/s1047-8477(02)00009-6. [DOI] [PubMed] [Google Scholar]
- Yu Z, Bajaj C. A gravitation-based clustering method and its applications in 3D electron microscopy imaging; 5th Int. Conf. Adv. Pattern Recognit; 2003. pp. 137–140. [Google Scholar]
- Yu Z, Bajaj C. A fast and adaptive algorithm for image contrast enhancement; IEEE Int. Conf. Image Process; 2004. pp. 1001–1004. [Google Scholar]
- Yu Z, Bajaj C. Automatic ultra-structure segmentation of reconstructed cryoem maps of icosahedral viruses. IEEE Trans. Image Process. 2005;14:1324–1337. doi: 10.1109/tip.2005.852770. [DOI] [PubMed] [Google Scholar]
- Yu Z, Holst M, Cheng Y, McCammon J. Feature-preserving adaptive mesh generation for molecular shape modeling and simulation. J. Mol. Graph. Model. 2008;26(8):1370–1380. doi: 10.1016/j.jmgm.2008.01.007. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Xu G, Bajaj C. Quality meshing of implicit solvation models of biomolecular structures. Comput. Aided Geom. Des. 2006;23(6):510–530. doi: 10.1016/j.cagd.2006.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]