Simultaneous Genotype Calling and Haplotype Phasing Improves Genotype Accuracy and Reduces False-Positive Associations for Genome-wide Association Studies

Abstract

We present a novel method for simultaneous genotype calling and haplotype-phase inference. Our method employs the computationally efficient BEAGLE haplotype-frequency model, which can be applied to large-scale studies with millions of markers and thousands of samples. We compare genotype calls made with our method to genotype calls made with the BIRDSEED, CHIAMO, GenCall, and ILLUMINUS genotype-calling methods, using genotype data from the Illumina 550K and Affymetrix 500K arrays. We show that our method has higher genotype-call accuracy and yields fewer uncalled genotypes than competing methods. We perform single-marker analysis of data from the Wellcome Trust Case Control Consortium bipolar disorder and type 2 diabetes studies. For bipolar disorder, the genotype calls in the original study yield 25 markers with apparent false-positive association with bipolar disorder at a p < 10⁻⁷ significance level, whereas genotype calls made with our method yield no associated markers at this significance threshold. Conversely, for markers with replicated association with type 2 diabetes, there is good concordance between genotype calls used in the original study and calls made by our method. Results from single-marker and haplotypic analysis of our method's genotype calls for the bipolar disorder study indicate that our method is highly effective at eliminating genotyping artifacts that cause false-positive associations in genome-wide association studies. Our new genotype-calling methods are implemented in the BEAGLE and BEAGLECALL software packages.

Introduction

Genome-wide association studies (GWAS) are playing an important role in the discovery of genetic regions and mechanisms contributing to common diseases.^1–4 GWAS use high-density oligonucleotide arrays to assay hundreds of thousands of single-nucleotide polymorphisms (SNPs) and copy-number variants (CNVs) in each individual. Genotype calls are typically made by using allele signal-intensity data from the arrays, without making use of correlation between nearby genetic markers. After exclusions of markers and samples with relatively poor-quality data, genotype-call accuracy for SNPs in GWAS can be ≥ 0.999; however, errors are not uniformly distributed across the genetic markers. For a subset of markers, the allele signal-intensity data do not form distinct, nonoverlapping clusters that correspond to the AA, AB, and BB genotypes, and these markers tend to have higher rates of missing (uncalled) genotypes and miscalled genotypes.

When genotype-error patterns and missing-genotype patterns are the same in cases and controls, the missing and miscalled genotypes cause a loss of power, but do not necessarily inflate the false-positive rate. However, in practice, genotype-error and missing-data patterns often differ between cases and controls because of differences in sample collection, processing, and storeage.^5,6 Case-control differences in genotype-error and missing-data patterns can cause false-positive association signals.^5–8 For example, in the Wellcome Trust Case Control Consortium (WTCCC) study, the investigators visually inspected plots of normalized allele signal intensities for approximately 100 markers per disease to identify false-positive associations caused by genotyping artifacts.⁷ Multilocus analysis has identified hundreds of highly significant associations (p < 2.5 × 10⁻⁷) in the WTCCC data, most of which appear to be due to genotyping artifacts.⁸ Large numbers of markers with relatively high levels of missing or miscalled genotypes are not unusual for genome-wide data sets,^7,9,10 particularly when whole-genome-amplified DNA is used.¹¹

Existing methods for detecting markers with high rates of miscalled genotypes for GWAS are not completely satisfactory. We review these existing methods, starting with the simpler methods that do not incorporate linkage disequilibrium (LD) information.

Two simple methods for detecting markers with high rates of miscalled genotypes are visual inspection of clustering on allele signal-intensity plots and data quality control (QC) filters. Visual inspection of clustering on allele signal-intensity plots is a valuable approach to detecting genotype error, but it can be applied only to a small subset of markers, such as the markers showing strongest association with a trait. Another approach to detecting markers with high rates of miscalled genotypes is to identify markers with a high proportion of missing or uncertain genotypes⁷ or markers with data showing deviation from Hardy-Weinberg equilibrium (HWE). Excluding markers identified by data QC filters can improve genotype accuracy, but it also throws away information and can result in missed association with a trait.⁸

Other methods for detecting and correcting genotype errors exploit LD. Intermarker correlation from LD is highly informative and can predict randomly masked genotypes from SNP arrays with > 0.98 accuracy.¹² LD-based methods typically employ a haplotype-frequency model for the population. The haplotype-frequency model gives an estimate of the frequency of each possible sequence of marker alleles on a chromosome. The model can be constructed from a reference panel, such as the HapMap,¹³ or from the called genotypes in the sample. Genotypes calls that result in unlikely allele sequences are flagged as possible genotype errors.

Hidden Markov models¹⁴ (HMMs) of haplotype frequencies have been used in detecting markers with high levels of genotype error and correcting miscalled genotypes. One approach is to incorporate an error model and estimate the error-model parameters for a genotype or for a marker.¹⁵ Another approach is to sequentially mask genotype calls and estimate the probability of all possible genotypes by using the haplotype-frequency model and remaining genotype data for the individual.^16,17 These HMM genotype-error detection and correction methods use existing genotype calls, not allele signal intensities, as input data. Consequently, they cannot make use of the relative evidence for each possible genotype call given by the allele signal-intensity data.

Kang et al.¹⁸ have described a novel extension of the Expectation-Maximization (EM) algorithm for inferring haplotype phase for small sets of tightly linked markers,^19–21 which incorporates genotype uncertainty when inferring haplotype phase. Although genotype calling was not the focus of the Kang et al. study, the resulting phased haplotypes implicitly determine SNP genotype calls. The authors use a multinomial model for haplotype frequencies, and for each marker, they use three t-distributions to model the distribution of the allele signal-intensity data (one t-distribution for each possible SNP genotype). For each marker, the three t-distributions determine three genotype likelihoods per sample, which give the relative evidence for each possible genotype call (AA, AB, and BB). Genotype uncertainty is incorporated into the EM algorithm for haplotype inference by the use of genotype likelihoods (instead of called genotypes) as input data for the EM algorithm.

Kang et al. did not use intermarker correlation to improve the estimation of the location and dispersion of the allele signal intensities corresponding to AA, AB, and BB genotypes. This advance was made by Yu et al.²² in their novel method for simultaneous estimation of allele signal-intensity model parameters and haplotype frequencies. Improved estimation of cluster location and dispersion parameters for allele signal-intensity data can increase genotype-call accuracy.

Both Kang et al. and Yu et al. employ a multinomial model for haplotype frequencies and estimate haplotype frequencies by using an EM algorithm. Multinomial models do not explicitly model biological processes, such as recombination and mutation, that give rise to the data, and computational constraints limit the number of markers that can be used with EM-based algorithms. Consequently, multinomial models generally cannot make full use of dense genotype data. Although sophisticated extensions, such as partition-ligation EM, extend the usefulness of the multinomial model, multinomial models for haplotype frequencies tend to provide less-accurate haplotype-phase inference than do methods based on HMMs.^23–25

In summary, existing methods for improving genotype data accuracy by using LD either do not make full use of the allele signal data because they reduce the data to genotype calls or do not make full use of the LD data because they use a multinomial model of haplotype frequencies.

In this work, we propose a novel method for simultaneous genotype calling and haplotype-phase inference. Our method makes full use of the LD data by employing an HMM model for population haplotype frequencies, and it makes full use of the allele signal-intensity data by incorporating genotype likelihoods instead of genotype calls. Posterior genotype probabilities are estimated by using the allele signal-intensity data and the population-haplotype-frequency model. The result is improved genotype-call accuracy and elimination of many false-positive associations that are caused by genotyping artifacts. We demonstrate that our method is computationally efficient and can be applied to large-scale data sets with hundreds of thousands of markers and thousands of samples.

Material and Methods

We present a general framework for simultaneous genotype calling and haplotype-phase inference. Our framework has two components: a genotype-calling module and a haplotype-phasing module. Using separate modules for genotype calling and haplotype phasing decouples these tasks, so that either module can be modified or replaced without changing the other module.

Our method is an iterative method. Each of the iterations consists of one run of the genotype-calling module followed by one run of the haplotype-phasing module. For this study, we have used three iterations. A graphical representation of our method is given in Figure 1. For each marker, the input data for the genotype-calling module are the allele signal intensities S and current estimates of genotype probabilities, (P(AA), P(AB), P(BB)), for each sample. For each marker, the output data from the genotype-calling module are the three genotype likelihoods, P(S|G = g) for g = AA, AB, BB, for each sample. The genotype likelihood P(S|G = g) is the estimated probability density of the observed allele signal intensity S if the true genotype is g. The genotype likelihoods from the genotype-calling module are the input data for the haplotype-phasing module. The output data from the haplotype-phasing module are updated estimated genotype probabilities that are used as input data (along with the allele signal intensities) for the genotype-calling module in the next iteration.

Figure 1.

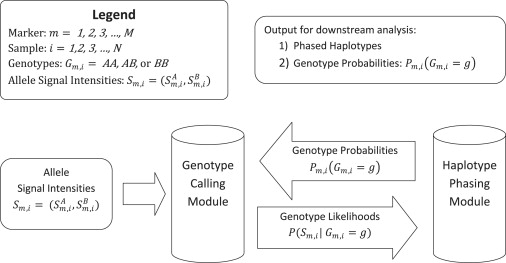
A Schematic of the Proposed Method for Simultaneous Genotype Calling and Haplotype-Phase Inference

Posterior genotype probabilities are produced by both the genotype-calling module and the haplotype-phasing module. For dense genotype data, we have found that posterior genotype probabilities from the haplotype-phasing module yield more accurate genotype calls than posterior genotype probabilities from the genotype-calling module. This is because the posterior genotype probabilities from the genotype-calling module are estimated by using allele signal intensities without making direct use of LD, but the posterior genotype probabilities from the haplotype-phasing module are estimated by using allele signal intensities and LD.

Genotype-Calling Module

Many SNP genotype-calling methods share a similar structure.²⁶ First, the allele signal-intensity data is normalized for reduction of chip-to-chip nonbiological variability.²⁷ For each marker, the normalized allele signal intensities for each sample are summarized by a univariate or multivariate statistic, and the parameters of the probability distribution of the summary statistics for samples with genotype g (g = AA, AB, or BB) are estimated. The probability distribution of the genotype (AA, AB, or BB) that maximizes the likelihood of a sample's summary statistic determines the genotype call for the sample.²⁶ In this study, we use the two-dimensional summary statistic S = (S^A, S^B) consisting of normalized A and B allele signal intensities, such as is used in the RLMM genotype-calling algorithm.²⁸ However, our implementation of the genotype-calling module will accept any summary statistic that can be modeled with a Gaussian or t distribution.

The genotype-calling module of our method extends this basic genotype-calling algorithm to accept current estimates of genotype probabilities, P(AA), P(AB), and P(BB), for each sample as input data. When the input genotype probabilities are informed by LD, the genotype probabilities can be used to improve estimates of the location and dispersion of the allele signal-intensity data corresponding to each genotype.

It is not uncommon for genotype-calling algorithms to use genotype calls from another method or from another data set to improve genotype-call accuracy^28,29 (see also the BRLMM White Paper in Web Resources). Prior to the initial iteration of our method, genotype probabilities informed by LD generally are not available, so for the first iteration of the genotype-calling module, we use genotype probabilities based on allele signal intensities that are obtained from another genotype-calling method. After the first iteration, the genotype-calling module uses updated genotype probabilities obtained from the haplotype-phasing module.

Some genotype-calling methods (e.g., CHIAMO⁷ and ILLUMINUS¹¹) produce genotype probabilities that can be used as input genotype probabilities for the genotype-calling module in the first iteration of our method. Other genotype-calling methods produce a called genotype and a quality score (e.g., GenCall and BIRDSEED²⁹). If genotype calls and quality scores (but not genotype probabilities) are available, we set a quality-score threshold so that quality scores that exceed the threshold represent high-confidence genotype calls. We create a temporary set of genotype probabilities by setting the three genotype probabilities equal to 0.333 for any genotype whose quality score is less than the threshold and by setting the genotype probability of the called genotype equal to 1.0 and the other two genotype probabilities equal to 0.0 for any genotype whose quality score is greater than or equal to the threshold. Then we perform a separate, preliminary run of the genotype-calling module using the temporary genotype probabilities as input data to produce updated genotype probabilities. In this preliminary run, the uninformative genotype probabilities corresponding to low confidence genotype calls are not used when modeling the allele signal-intensity data. The updated genotype probabilities produced by the preliminary run of the genotype-calling module are used as the genotype probabilities for the genotype-calling module in the first iteration of our method.

In this study we use CHIAMO⁷ and GenCall to obtain initial genotype probabilities for Affymetrix and Illumina data, respectively. We used a GenCall quality-score threshold of 0.2 when deriving initial genotype probabilities for Illumina data. Other genotype-calling methods, such as Birdseed²⁹ and Illuminus,¹¹ can also be used to initialize our method.

The algorithm that we used for estimating posterior genotype probabilities by using the allele signal-intensity data and genotype probabilities is described in Appendix 1.

Haplotype-Phasing Module

Our algorithm for the haplotype-phasing module employs the BEAGLE haplotype-phase-inference algorithm.^12,30 BEAGLE uses an HMM for the haplotype frequencies¹⁴ and performs haplotype-phase inference by alternating between a model-building step and a haplotype-sampling step. The original BEAGLE algorithm uses called genotypes as input data. Our algorithm for the haplotype-phasing module extends the BEAGLE algorithm to use genotype likelihoods instead of called genotypes as input data.

In the BEAGLE haplotype-phasing algorithm, each state of the HMM corresponds to a specific marker and is labeled with a single genotype (AA, AB, or BB). Many HMM states can correspond to a single marker. In the original BEAGLE haplotype-phasing method, the observed data for an individual are genotype calls, and the emission probability of the observed genotype is 1.0 if the observed genotype agrees with the genotype of the HMM state and 0.0 otherwise. In the extended BEAGLE algorithm, the observed data for an individual are the allele signal intensities, and the emission probability of the individual's observed signal intensities S for an HMM state labeled with genotype g is the genotype likelihood P(S|G = g) for the marker obtained from the genotype-calling module.

The computational efficiency of the BEAGLE haplotype-phasing algorithm depends on the extent to which the observed genotypes or genotype likelihoods constrain the possible haplotypes. Genotype likelihoods with value 0.0 constrain the possible haplotypes, and thus reduce the computational time. We have found that we can reduce computational time with negligible decrease in genotype accuracy by changing relatively small likelihoods to 0.0. This is accomplished by a user-defined parameter that sets the maximum permitted likelihood ratio (default = 5000). If the likelihood ratio for genotypes g₁ and g₂, P(S|G = g₁)/P(S|G = g₂), exceeds the maximum permitted likelihood ratio, then the smaller likelihood P(S|G = g₂) is set to 0.0. For the data sets examined in this paper, the default maximum permitted likelihood ratio of 5000 gave nearly optimal genotype accuracy.

Application to Multiple Cohorts

Many studies involve multiple cohorts from the same population that have been collected separately. For example, in the WTCCC data, there is a case cohort and two control cohorts.⁷ Differences in sample collection, handling, and storage can induce systematic intercohort differences in the distribution of allele signal data for the AA, AB, and BB genotypes,^5,6 which can bias genotype calls. When calling genotypes on multiple cohorts, our implementation of the genotype-calling module will automatically model the allele signal-intensity data for each cohort separately to accommodate intercohort differences in location and dispersion of allele signal-intensity data. For the haplotype-phasing module, all cohorts from the same population should be analyzed simultaneously.

Data Sets

We used autosomal genotype data from the BD, T2D, UKBS, and 58BC cohorts from the WTCCC study.⁷ The BD cohort has 1998 individuals diagnosed with bipolar disorder (MIM 125480). The T2D cohort has 1999 individuals diagnosed with type 2 diabetes (MIM 125853). The UKBS cohort has 1500 control individuals selected from a UK sample of blood donors, and the 58BC cohort has 1504 control individuals from the 1958 British Birth Cohort.³¹ We chose to use bipolar disorder case-control data because we wanted to analyze data for a disease that had few SNPs with replicated disease association.^7,32 Subsequently, we decided to call genotypes for the T2D cohort for a separate project, and we used these T2D genotype calls to evaluate genotype accuracy at SNPs with replicated association with type 2 diabetes. All four cohorts were genotyped on the Affymetrix GeneChip Human Mapping 500K Array (the Affymetrix 500K chip) by the WTCCC.⁷ We also use autosomal genotype data from the Illumina Infinium 550 SNP BeadChip (the Illumina 550K chip) that was generated by the Wellcome Trust Sanger Institute for 1438 individuals from the 1958 British Birth Cohort. There are 1400 individuals from the 1958 British Birth Cohort that are genotyped on both the Affymetrix 500K and Illumina 550K chips. The Affymetrix 500K chip has 490,032 autosomal markers, the Illumina 550K chip has 541,327 autosomal markers, and a subset of 82,981 autosomal markers is present on both the Affymetrix 500K and Illumina 550K chips.

Affymetrix 500K chip genotypes were called with the use of our method and two additional genotype-calling methods: CHIAMO⁷ and BIRDSEED²⁹ version 2 (incorporated in the Affymetrix Power Tools 1.10.2 release) with default options used. All CHIAMO calls were made by the WTCCC, with the use of the version of CHIAMO described in the WTCCC study.⁷ We used BIRDSEED to call genotypes for the 58BC cohort only. We used our methods to call genotypes for the bipolar disorder study (BD, 58BC, and UKBS cohorts), and we used the 58BC calls from the bipolar disorder study to evaluate genotype discordance rates. We also used our method to call genotypes for the type 2 diabetes study (T2D, 58BC, and UKBS cohorts) for a separate project, and we used these data to perform association tests at the 12 markers on the Affymetrix 500K chip with replicated association with type 2 diabetes that were described in Table 3 of the WTCCC's original study⁷ and Table 1 of the WTCCC's type 2 diabetes replication study.³³

Genotypes for the Illumina 550K chip for the 1958 British Birth Cohort were called with the use of our method and two additional genotype-calling methods: GenCall and ILLUMINUS.¹¹ The GenCall genotype calls were made by the Wellcome Trust Sanger Institute. We used ILLUMINUS with default options.

Data QC

For Affymetrix 500K data from the WTCCC study, we excluded the samples that were excluded in the WTCCC analysis: 130 BD samples, 75 T2D samples, 24 58BC samples, and 42 UKBS samples.⁷ We excluded from the Illumina 550K data for the 1958 British Birth Cohort 15 samples that had > 4% missing autosomal genotypes when called with the GenCall algorithm. Samples were excluded prior to genotype calling when our calling method was used, and after genotype calling (but prior to downstream analysis) when other calling methods were used.

We excluded markers that showed departure from HWE or that had high proportions of missing genotypes. Details of marker-exclusion criteria are given in Appendix 2. For Affymetrix data, the number of autosomal markers excluded was 34,328 for BIRDSEED, 30,586 for CHIAMO, 25,541 when three iterations of our method were used with bipolar disorder and control data, and 29,279 when three iterations of our method were used with type 2 diabetes and control data. For Illumina data, the number of autosomal markers excluded was 10,890 for GenCall, 9971 for Illuminus, and 6711 when three iterations of our method were used. Genotype accuracy for the nonexcluded markers tends to increase as the number of marker exclusions increases, so we calibrated the missing genotype filters so that our method had the disadvantage of having fewer excluded markers.

Results

For our method, genotype calls are made with the use of posterior genotype probabilities generated by the haplotype-phasing module. Because the haplotype-phasing module is implemented in the BEAGLE software package, for brevity we will occasionally refer to genotype calls made by our method as being made by BEAGLE.

Genotype Accuracy

Genotype-calling methods that use allele signal intensities, but not LD, are challenged when the allele signal intensities do not form distinct clusters, corresponding to the possible genotypes. Figure 2 displays allele signal intensities from the Affymetrix 500K array for marker rs4242382 for 1373 individuals from the 58BC cohort whose data passed QC filters (described in Material and Methods) and for which Illumina 550K array genotype data are also available. In the left panel of Figure 2, the genotype calls are from CHIAMO and use only allele signal intensities. In the right panel of Figure 2, the genotype calls are made with the use of our method and are based on both allele signal intensities and LD. In the left panel (CHIAMO), there are 73 uncalled genotypes, and there is a 3.8% discordance rate (50/1300) with genotype calls made from the Illumina 550K chip. In the right panel, there are two uncalled genotypes, and there is a 0.15% discordance rate (2/1371) with genotype calls made from the Illumina 550K chip. The Illumina 550K chip genotype calls from GenCall, Illuminus, and our method were identical for this marker.

Figure 2.

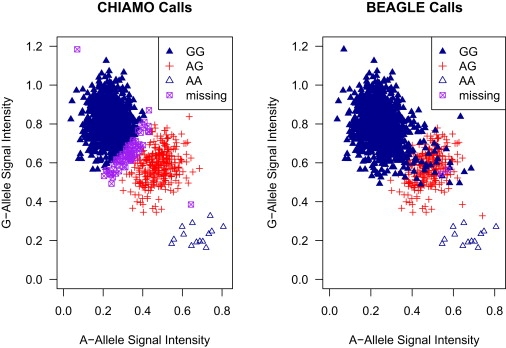
Allele Signal Intensities and Genotype Calls for Marker rs4242382

Affymetrix 500K chip allele signal intensities, CHIAMO genotype calls (left panel), and BEAGLE genotype calls (right panel) for marker rs4242382 for 1373 individuals from the 58BC cohort that were genotyped on the Affymetrix 500K chip and the Illumina 550K chip and passed genome-wide QC filters (see Material and Methods). Genotypes with CHIAMO posterior probability < 0.90 and BEAGLE posterior probability < 0.97 are labeled as missing. Genotype calls for these samples made with the use of Illumina 550K chip data have 96.2% concordance with CHIAMO genotype calls and 99.9% concordance with BEAGLE genotype calls.

Figure 2 illustrates two limitations of genotype calls based exclusively on allele signal intensities for a single marker. The first limitation is well-known: it is impossible to confidently assign genotypes to data points that lie in overlapping genotype clusters. In the left panel of Figure 2, there are 5.3% (73/1373) uncalled genotypes, and almost all of the uncalled genotypes are in the region where the major allele homozygote and heterozygote clusters overlap. The second limitation is that the allele signal-intensity data for a single marker may not provide enough information for an accurate estimation of the location or dispersion of the allele signal intensities for a given genotype. Note that CHIAMO (left panel) appears to have correctly identified the clusters in the allele signal data, but in fact, genotype calls made with the use of LD (right panel) and those made from Illumina data indicate that the dispersion of the major allele homozygote cluster is underestimated in the left panel. Recognition of this increased dispersion and the use of LD in the haplotype-phasing module prevented our method from miscalling dozens of major allele homozygote genotypes whose allele signal intensities are deep within the heterozygote genotype cluster.

We examined genotype-call accuracy for different genotype-calling methods for Affymetrix 500K and Illumina 550K data by using all autosomal markers that were genotyped on both chips. Genotype accuracy depends on the quality-score threshold required for calling a genotype. A stringent threshold leads to higher genotype accuracy and more uncalled genotypes, whereas a relaxed threshold leads to lower genotype accuracy and fewer uncalled genotypes. We show the trade-off between missing-data rates and genotype accuracy by plotting the missing-data proportion versus the genotype discordance rates for different values of the quality-score threshold used in calling genotypes.

When comparing the accuracy of genotype-calling methods for Affymetrix data, we computed discordance with > 105 million Illumina 550K chip reference genotypes that had estimated genotype probability ≥ 0.999995 when called with our method. Similarly, when comparing the accuracy of genotype-calling methods for Illumina data, we computed discordance with > 99 million Affymetrix 500K chip reference genotypes that had estimated genotype probability ≥ 0.999995 when called with our method. All discordance rates were calculated after the application of data QC filters that exclude markers and samples with poorer-quality data (see Material and Methods and Appendix 2).

Discordance rates between genotype calls from Affymetrix data and from Illumina data for the 1958 UK Birth Cohort are presented in Figure 3. For the evaluation of Affymetrix data, the comparison included three genotype-calling methods (BIRDSEED,²⁹ CHIAMO,⁷ and our method), and one hybrid method that used a combination of genotype calls from allele signal data and genotype imputation. Genotype imputation has the potential to provide more accurate genotype calls when the genotype call based on the allele signal data does not have high confidence (e.g., < 0.99 genotype probability). For the hybrid approach, we set all CHIAMO calls that had probability < 0.99 to missing, we used CHIAMO genotype calls for the nonmissing genotypes, and we imputed the sporadic missing genotypes by using BEAGLE 3.0.¹² Both the hybrid approach and our proposed method use the same haplotype-frequency model, but the hybrid approach does not make use of allele signal intensities at the imputed markers. We include the hybrid approach to illustrate the fact that imputation methods that use LD without using allele signal intensities at the imputed marker cannot be as accurate as genotype-calling methods that use both allele signal intensities and LD.

Figure 3.

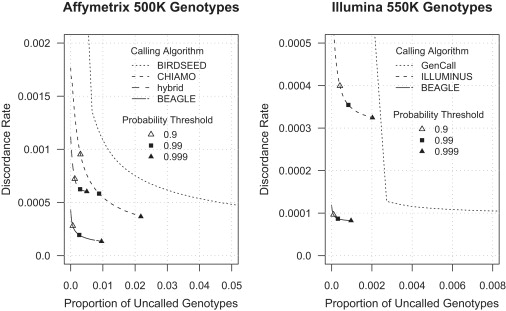
Genotype Discordance and Missing-Data Rates

Discordance rates for genotype calls for autosomal Affymetrix 500K chip data (left panel) and autosomal Illumina 550K chip data (right panel) are computed with the use of high-confidence genotype calls (probability > 0.999995) from the alternate platform. The genotype discordance rate and missing-data rate depend on the quality-score threshold required for calling a genotype. For each method and each possible calling threshold, the proportion of missing genotypes and the discordance rate for called genotypes was computed. The discordance and missing-data rates corresponding to calling thresholds of 0.9, 0.99, and 0.999 posterior genotype probability are shown for the genotype-calling methods that report genotype probabilities.

For Affymetrix data, the discordance rate for our method is at least a factor of seven smaller than the discordance rates for BIRDSEED and is approximately a factor of four smaller than the discordance rate for CHIAMO across the range of missing-genotype proportions for our method.

The hybrid strategy was effective at reducing missing-data rates relative to CHIAMO; however, it did not yield as accurate genotypes as CHIAMO did when a stringent calling threshold (>0.99 genotype probability) is used for CHIAMO calls. The discordance rate for the hybrid strategy is much higher than the discordance rate for our method because the hybrid strategy does not use the allele signal-intensity data when imputing missing genotypes.

For the evaluation of Illumina 550K chip genotype data, three programs were used: GenCall, Illuminus,¹¹ and our method. The discordance rate for our method was smaller than the discordance rates for ILLUMINUS and GenCall by a factor of four or more across the range of missing-genotype proportions obtained with our method. A sharp corner occurs in the GenCall discordance plot at the point where there is 0.0027 missing data and 0.00013 discordance, and this point corresponds to use of a GenCall score calling threshold of 0.1. Comparing the left and right panels of Figure 3 shows that the genotype accuracy for Illumina data is greater than that for Affymetrix data. Consequently, the increased accuracy for Illumina data provided by our method may be greater than shown in the right panel of Figure 3, because it is possible that the discordance in the right panel of Figure 3 is driven by genotype errors in the Affymetrix data.

We have used our method's genotype calls on the alternative platform as the reference genotypes when computing discordance rates in Figure 3. Figure S1, available online, shows that the smaller genotype discordance for our method's genotype calls is also evident when GenCall and CHIAMO genotype calls are used as reference genotypes. For Illumina data, the curves in Figure S1 are shifted up relative to those of Figure 3 because the CHIAMO reference genotypes in Figure S1 have a higher error rate than the corresponding BEAGLE reference genotypes shown in Figure 3.

The discordance rates in Figure 3 are averaged over all genotype calls. For the majority of SNPs on current high-density arrays, there is little scope for improved accuracy because the SNPs are called with high accuracy by existing genotype-calling methods. For example, there is perfect concordance (0% discordance) between the CHIAMO Affymetrix genotype calls and the GenCall Illumina genotype calls for 49% of the autosomal markers that passed the data QC filters and are present on both chips. Consequently, the average discordance rates in Figure 3 understate the improvement in genotype-call accuracy due to our method for “difficult” SNPs whose allele signal-intensity data does not form three nonoverlapping clusters. “Difficult” SNPs typically have higher missing genotype rates.⁷ Figure 4 shows the discordance rates for CHIAMO and BEAGLE Affymetrix genotype calls for the SNPs that passed the CHIAMO and BEAGLE data QC filters and have > 3% missing genotypes when called with CHIAMO. Cross-platform discordance is calculated with the use of BEAGLE calls for Illumina data. After excluding markers identified by the data QC filters used for each method, there are 4873 SNPs on the Affymetrix 500K chip that had > 3% missing genotype calls. For the SNPs with > 3% missing CHIAMO genotype calls, the discordance rate for BEAGLE genotype calls ranges from 15 to 88 times smaller than the discordance rate for CHIAMO genotype calls.

Figure 4.

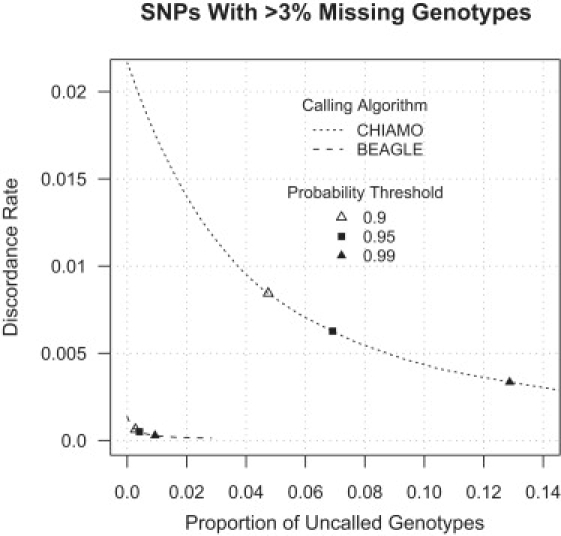
Genotype Discordance and Missing-Data Rates at SNPs with > 3% Missing CHIAMO Genotypes

Discordance and missing-data rates are given for CHIAMO and BEAGLE Affymetrix 500K chip genotype calls for the subset of SNPs with > 3% missing CHIAMO genotypes. Discordance rates are computed with the use of high-confidence (genotype probability > 0.999995) BEAGLE Illumina 550K chip genotype calls. The unfilled triangle, filled square, and filled triangle identify the discordance and missing-data rates corresponding to calling thresholds of 0.9, 0.95, and 0.99 posterior genotype probability.

Given that the cross-platform discordance rate is expected to be approximately equal to the sum of the genotype-error rates, the discordance rates in Figure 3 suggest upper bounds on the absolute genotype-error rates for the set of markers that are present on both the Affymetrix 500K and Illumina 550K chips. However, the discordance rates in Figure 3 may not reflect the genotype-error rate for markers that are found on one but not both of the Affymetrix and Illumina chips. There is evidence that the markers present on both chips tend to have more accurate genotypes than do markers that are unique to either chip. For the markers on the Affymetrix 500K chip, 5.3% of the markers that are not on the Illumina 550K chip and 4.7% of the markers that are on the Illumina 550K chip were excluded by the data QC filters for our method. For Illumina 550K chip markers, 1.34% of the markers that are not on the Affymetrix 500K chip and 0.70% of the markers that are on the Affymetrix 500K chip were excluded by the data QC filters for our method. Thus, the actual genotype-error rates for Affymetrix and Illumina data may be somewhat higher than the discordance rates presented here.

Most of the increased genotype accuracy obtained from our method is achieved by the first iteration. Improved modeling of allele signal data and use of increasingly stringent missing-data filters provide additional improvements in genotype accuracy in later iterations. For Affymetrix data, when the genotype-calling threshold is set to 0.333 so that there are no missing genotypes, the genotype discordance rate was 0.070%, 0.049%, and 0.043% when 1, 2, and 3 iterations of our method were used, respectively. For the Affymetrix 500K chip, the cumulative number of autosomal markers excluded by data QC filters prior to each iteration was 8663, 18,371, and 24,054 markers for iterations 1, 2, and 3, respectively. The data QC filters applied at each iteration are described in Appendix 2.

False Positives Due to Genotyping Artifacts

We evaluated the ability of our new methods to reduce false-positive associations due to differential genotype bias^5,6 by using WTCCC autosomal data from the BD, 58BC, and UKBS cohorts. We performed association analysis by using genotype calls from CHIAMO and those from our method and compared the results.

We performed single-marker association analysis by using PRESTO³⁴ and haplotypic analysis by using BEAGLE.³⁵ For each single marker (PRESTO) or haplotype cluster (BEAGLE), an allelic trend test and three genotype tests were performed, corresponding to recessive, overdominant, and dominant models. The minimum p value (minimized over the four tests) was recorded for each marker.

For the CHIAMO data, we used the WTCCC's calling threshold and set genotype calls with posterior probability < 0.9 as missing. In the supplemental data for the WTCCC study,⁷ the WTCCC reported that use of a calling threshold greater than 0.9 increased the false-positive rate on single-marker tests because of increased differential missingness. For the genotype calls from our method, markers with probability < 0.97 were set to missing, and we excluded markers that had ≥ 0.03 missing genotypes.

For the BEAGLE haplotypic analysis with CHIAMO genotype calls, we first phased WTCCC data and imputed missing data by using BEAGLE as described previously.⁸ For the haplotypic analysis with our method's genotype calls, we used the most likely phased haplotypes that are output by the haplotype-phasing module of our method.

Figure 5 presents quantile-quantile plots for the single-marker analysis and haplotypic analysis of the autosomal data for the WTCCC bipolar disorder and control cohorts. Four association-test statistics are plotted for each marker and for each haplotype cluster tested, corresponding to the allelic test and three genotypic tests (for recessive, overdominant, and dominant models). There is a pronounced inflation in the association-test statistics from CHIAMO calls as compared to BEAGLE calls for both the single-marker and haplotypic tests. For CHIAMO calls, there were 15 single-marker tests of association and 88 haplotypic tests of association for which the chi-square statistic was > 60. For BEAGLE calls, there were no tests of association with chi-square statistic > 60. The inflation factor for the single-marker analysis was 1.125 for CHIAMO calls and 1.102 for BEAGLE calls. The inflation factor is the ratio of the median observed allelic trend test statistic for markers with minor allele frequency ≥ 0.01 and the median of the chi-square distribution.

Figure 5.

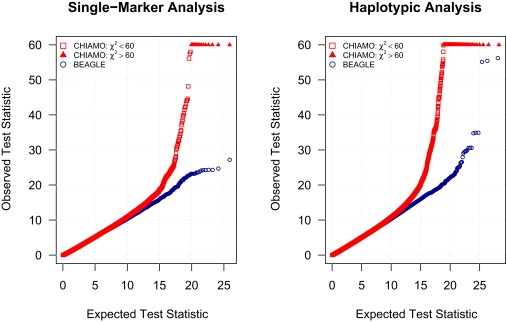
Quantile-Quantile Plots for Single-Marker and Haplotypic Analyses of Bipolar Disorder

Expected and observed association chi-square test statistics from analysis of CHIAMO genotype calls and BEAGLE genotype calls of WTCCC bipolar disorder and control data. An allelic test statistic and three genotypic test statistics, corresponding to dominant, overdominant, and recessive models, are computed for each marker (left panel) and each tested haplotype cluster (right panel).

There is also a striking reduction in extreme association-test statistics for the WTCCC type 2 diabetes and control cohorts when BEAGLE calls are used. Figure S2 contains quantile-quantile plots for the single-marker analysis of the autosomal data for the WTCCC type 2 diabetes and control cohorts when markers in three regions showing replicated association to type 2 diabetes are included (left panel) and excluded (right panel).

In Figure 6, we plot the minimum p value from the single-marker analysis of the bipolar disorder and control data for all markers that had an allelic or genotypic test p value < 0.0001 when genotype calls from CHIAMO or from our method were used. (The corresponding p value scatter plot for type 2 diabetes is presented in Figure S3.) The missing-data filters used with our method excluded a large number of markers that had small p values when called with CHIAMO. For CHIAMO calls, there are 64 markers with p value < 0.0001 that were excluded by the data QC filters for our method. In contrast, for our method's calls there are only five markers with p value < 0.0001 that were excluded by the WTCCC data QC filters.

Figure 6.

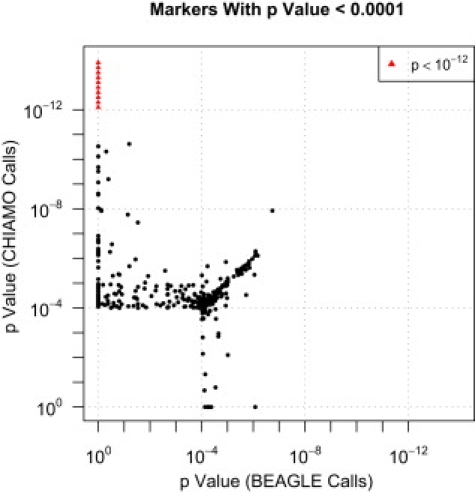
p Values from Single-Marker Analysis of WTCCC Bipolar Disorder and Control Data

The minimum p value from an allelic trend test and three genotypic tests (for dominant, overdominant, and recessive models) is calculated for each marker for CHIAMO and BEAGLE genotype calls. The p values from CHIAMO calls and BEAGLE calls are plotted with the use of a log scale for all markers with minimum p value < 0.0001 for one or both genotype-calling methods. p values for markers that were excluded by data QC filters for CHIAMO calls but not by those for BEAGLE calls are plotted along the line y = 1. p values for markers that were excluded by data QC filters for BEAGLE calls but not by those for CHIAMO calls are plotted along the line x = 1.

When we compared single-marker and haplotypic analysis of our method's genotype calls and CHIAMO's genotype calls for bipolar disorder, we found that our method produced far fewer associated markers and haplotype clusters. In the single-marker analysis, our method yielded 43% fewer associations at a 10⁻⁴ significance threshold (199 versus 350), 63% fewer associations at a 10⁻⁵ significance threshold (33 versus 89), 84% fewer associations at a 10⁻⁶ significance threshold (7 versus 45), and 100% fewer associations at a 10⁻⁷ significance threshold (0 versus 26). It should be noted that because of the WTCCC's postanalysis QC, the published WTCCC bipolar disorder analysis and the analysis of our genotype calls are in general agreement. The WTCCC visually inspected allele signal-intensity plots of associated markers to identify apparent false-positive associations caused by genotyping artifacts.⁷ Our method's improved genotype-call accuracy avoided many of the apparent false-positive associations that were filtered out in the WTCCC's postanalysis QC. For the CHIAMO genotype calls, 25 of the 26 markers with p < 10⁻⁷ were evidently determined to be false-positive associations by the WTCCC and were not reported in the WTCCC study.⁷ The one marker with p < 10⁻⁷ that was reported by the WTCCC to be associated with bipolar disorder (rs420259)⁷ also has a small p value when our method's genotype calls are analyzed. Marker rs420259 has a minimum p value of 1.2 × 10⁻⁸ under a recessive model when CHIAMO calls are used and has a minimum p value of 1.8 × 10⁻⁷ under a recessive model when our method's calls are used. At present, we are not aware of any studies that have replicated the association of marker rs420259 with bipolar disorder.³²

For the haplotypic analysis, our method yielded 79% fewer associations at a 10⁻⁵ significance threshold (63 versus 301), 92% fewer associations at a 10⁻⁶ significance threshold (12 versus 158), 94% fewer associations at a 10⁻⁷ significance threshold (6 versus 116), and 98% fewer associations at a 10⁻⁸ significance threshold (2 versus 82).

Only one of the three regions showing strongest association with bipolar disorder in a recent meta-analysis³² (a region on chromosome 1 containing a marker with meta-analysis p value = 2.0 × 10⁻⁷) showed evidence of association (p < 10⁻⁴) in the analysis using the CHIAMO or BEAGLE calls. For calls with our method, two of the 33 markers that were associated at the p < 10⁻⁵ level, 6 of the 63 haplotype clusters that were associated at the p < 10⁻⁵ significance threshold, and 3 of the 12 haplotype clusters that were associated at the p < 10⁻⁶ significance threshold are within this chromosome 1 region. The smallest p value observed in the analysis of our method's calls in this region was p = 2.6 × 10⁻⁷ at a haplotype cluster localizing to marker rs2987775.

The single-marker and haplotypic analysis of the WTCCC bipolar disorder data indicate that that our method is extremely effective at reducing false-positive association signals from differential genotype bias for both single-marker and haplotypic association tests. Our method's calls result in a large reduction in false-positive association signals relative to CHIAMO calls, even though our method excluded fewer markers (25,541 for our method versus 30,587 for CHIAMO).

Genotypes at Markers Associated with Type 2 Diabetes

We performed case-control association analysis for the 12 SNPs that were genotyped in the T2D, 58BC, and UKBS cohorts in the WTCCC study and are reported to have replicated association with type 2 diabetes susceptibility in the WTCCC's initial study or in the WTCCC's type 2 diabetes replication study.^7,33 We computed missing-data rates, discordance rates between genotype calls made with CHIAMO and BEAGLE, and p values by using genotype calls made by CHIAMO and BEAGLE (see Table 1). For 11 of the 12 markers, there is good concordance and low missing-genotype rates: < 3 discordant genotypes at each marker, < 13 missing genotypes for CHIAMO, and < 6 missing genotypes for our method. However, for marker rs5015480 (last row of Table 1), there are 126 (2.53%) missing genotypes for CHIAMO, 33 (0.68%) missing genotypes for our method, and 50 (1.06%) discordant genotypes among the 4712 genotypes that were called by both methods. Allele signal intensities and genotype calls for marker rs5015480 are shown in Figure S4. Marker rs5015480 was also genotyped on the Illumina 550K chip for a subset of 1373 samples from the 58BC cohort. The CHIAMO genotypes calls have a 1.8% discordance rate (23/1295) with the Illumina genotypes, and the BEAGLE genotype calls have a 0.074% discordance rate (1/1359) with the Illumina genotypes. This suggests that the genotypes and the less-significant p value from BEAGLE's genotype calls are likely to be more accurate for marker rs5015480.

Table 1.

Variants with Confirmed Association with Type 2 Diabetes

Marker	Missing Genotypes (%)		Discordance (%)	Allelic Test p Value
	CHIAMO	BEAGLE		CHIAMO	BEAGLE
rs7901695	0.19	0.12	0.02	6.7 × 10−13	1.8 × 10−12
rs4506565	0.12	0.00	0.0	5.7 × 10−13	9.2 × 10−13
rs5215	0.16	0.12	0.06	1.3 × 10−3	1.4 × 10−3
rs8050136	0.27	0.00	0.06	2.0 × 10−8	3.5 × 10−8
rs9939609	0.00	0.00	0.0	5.3 × 10−8	5.3 × 10−8
rs1801282	0.12	0.00	0.0	1.3 × 10−3	8.8 × 10−4
rs4402960	0.16	0.00	0.02	1.7 × 10−3	1.8 × 10−3
rs10946398	0.06	0.00	0.0	2.5 × 10−5	3.2 × 10−5
rs9465871	0.10	0.04	0.02	1.0 × 10−6	2.1 × 10−6
rs564398	0.19	0.00	0.06	3.2 × 10−4	2.2 × 10−4
rs10811661	0.04	0.08	0.02	7.5 × 10−4	6.0 × 10−4
rs5015480	2.53	0.68	1.06	5.4 × 10−6	2.1 × 10−5

Comparison of CHIAMO and BEAGLE genotype calls for 12 variants with confirmed association with type 2 diabetes, genotyped on 4862 samples that passed WTCCC data QC filters in the WTCCC T2D, 58BC, and UKBS cohorts.^7,33 CHIAMO genotypes with < 0.90 probability and BEAGLE genotypes with < 0.97 probability were not called (set as missing genotypes). Discordance rates are calculated with the use of genotypes called by both CHIAMO and BEAGLE. See the Results section for discussion of marker rs5015480.

Discussion

In this study, we have presented a general framework for simultaneous genotype calling and haplotype-phase inference. Genotype uncertainty in the allele signal-intensity data is incorporated in haplotype-phase inference, and population haplotype frequencies are used to improve statistical modeling of allele signal-intensity data. Posterior genotype probabilities are estimated with the use of both allele signal-intensity data and population haplotype frequencies.

We compared cross-platform discordance rates for some of the best existing genotype-calling methods and found that our method provides a marked improvement in genotype-call accuracy and missing-genotype rates. We postulate that the best methods that call genotypes for one marker at a time are extracting nearly all of the available information from the allele signal-intensity data for the marker and that the improved genotype-call accuracy from our method is due to the use of a population haplotype-frequency model.

Our methods can be used to call genotypes for a single cohort or for multiple cohorts that have intercohort differences in allele signal intensities. We have shown that analysis using our method's genotype calls eliminates a high proportion of the false-positive associations that are found in our analysis using the genotype calls from the WTCCC bipolar disease study.⁷ The WTCCC demonstrated that one effective method for eliminating false-positive associations due to genotyping artifacts is to visually inspect the allele signal intensities of all apparently associated markers. Indeed, almost all of the strongest associations reported by the WTCCC (that passed visual inspection of signal data) have been replicated in subsequent studies.^1,7,33,36,37 However, preventing false-positive associations with improved genotype calling is preferable to identifying false-positive associations after they have occurred.

Our framework employs a genotype-calling module and a haplotype-phasing module. We have provided methods and software implementation for each module. Many existing methods for genotype calling and haplotype phasing can also be adapted and used within the framework.

The algorithm of our genotype-calling module is relatively simple, and we expect that genotype-call accuracy can be improved by incorporating ideas from existing genotype-calling methods. For example, it may be beneficial to use different probability distributions to model homozygous and heterozygous genotypes, as is done in Illuminus.¹¹ Different normalization methods and summary statistics for allele signal-intensity data may also yield improved genotype calls.³⁸ In this study, we have used the same default parameters for both Affymetrix and Illumina data. Because Affymetrix and Illumina data have very different characteristics, it is possible that genotype-call accuracy can be further improved by tuning the parameters (e.g., degrees of freedom) separately for Affymetrix data and Illumina data.

Our implementation of the haplotype-phasing module has several advantages over possible alternative implementations. First, we use the computationally efficient, BEAGLE HMM for haplotype frequencies.¹² The BEAGLE model can accommodate large sample sizes, which yield more accurate haplotype-frequency models.³⁰ Second, our method uses the samples to build a population haplotype-frequency model and does not require a phased reference panel. Consequently, our method can be used when a reference panel is not available, has limited sample size, or is not genetically well matched to the samples. If phased or unphased genotype data for a reference panel are available for the population, our method can make use of this additional data. For very small sample sizes, we expect that genotype accuracy can be improved by including data from a reference panel when running the haplotype-phasing module, because the accuracy of the BEAGLE haplotype-frequency model tends to increase with sample size.³⁰

We have demonstrated that our method can be applied to large sample sizes and we have called autosomal genotypes from Affymetrix 500K chip data for 4800 individuals. It is possible to call genotypes for arbitrarily large sample sizes by randomly partitioning the total sample into subsamples and calling genotypes in each subsample separately.

For large samples (>1500 individuals), our method spends > 90% of its computation time in the haplotype-phasing module. The computation time for haplotype-phase inference is approximately quadratic in the number of samples. When performing genotype calling for 4800 individuals for the Affymetrix 500K chip autosomal genotypes, the total computation time for the 22 autosomes was approximately 60 days per iteration of our method. We parallelized by chromosome when calling genotypes with our method, and the maximum computation time for a chromosome was 5 days per iteration. Genotype calling could also be parallelized by overlapping chromosome segments to further speed up computation times. With current commercial rates for cloud computing (≤USD $0.40 per hr), the cost for three iterations of genotype calling for 4800 samples genotyped on the Affymetrix 500K chip is < USD $0.40 per sample. This cost is insignificant when compared to the total cost of genotyping for high-density arrays or the potential expense of investigating a false-positive association caused by a genotyping artifact. Furthermore, our method can salvage thousands of markers that would be excluded by standard data QC filters when genotype calls are made by using only allele signal intensities.

We plan to evaluate our methods in admixed and non-European populations in the future, and to extend our methods for calling genotypes to the X chromosome, to diallelic and multiallelic CNVs, and to related individuals.

Software Implementation

Our imputation and haplotype-inference methods are implemented in version 3.1 of the BEAGLE software package and in version 0.9 of BEAGLECALL, both of which are freely available. BEAGLE and BEAGLECALL are written in Java and run on all major computing platforms.

Appendix 1. A Genotype-Calling Algorithm that Incorporates LD-Based Estimates of Genotype Probabilities

In this appendix, we describe an algorithm for the genotype-calling module. The algorithm calls genotypes for a marker by using normalized allele-signal data and current LD-based estimates of genotype probabilities for that marker. In our algorithm, genotype probabilities specified as input data are used to estimate the probability of assay success for each individual and to estimate the parameters of the probability distributions that model the observed allele signal-intensity data. The genotype-calling method presented here generalizes to multiallelic markers; however, for simplicity we will assume that allele signal intensities are measured for only two alleles (A and B) and that the marker is diallelic with three possible genotypes (AA, AB, and BB). We assume that there are N samples, indexed by i (i = 1, 2, 3, … N). We first introduce some notation for equations in this appendix:

Observed Variables

• $S_i=\left(S_i^A,S_i^B\right)$ = normalized A and B allele signal intensities for the i-th sample.

Unobserved Variables

• G_i = the unobserved true genotype (AA, AB, or BB) for the i-th sample.

• Z_i = a Bernoulli variable indicating whether the genotype assay was successful (Z_i = 1) or unsuccessful (Z_i = 0) in the i-th sample. An unsuccessful genotype assay is uninformative for the true genotype.

Probabilities

• P_i (G_i = g) = current estimated probability that genotype G_i = g for the i-th sample.

• P(G = g) = population frequency of genotype g.

• P_i (Z_i = k) = probability that the genotype assay is successful (k = 1) or unsuccessful (k = 0) in the i-th sample. The algorithm for the genotype-calling module estimates this probability conditional on the signal intensities.

• P(Z = 1) = probability that the genotype assay is successful (k = 1) or unsuccessful (k = 0) in the population.

• f_g(S; λ_g) = probability density (parameterized by the vector λ_g) of the observed signal-intensity data S when the genotype assay is successful (Z = 1) and the true genotype is g.

• h(S) = probability density of the observed signal-intensity data S when the genotype assay is unsuccessful (Z_i = 0). We model h(S) as the uniform distribution in two dimensions with support equal to Cartesian product of the range of $S_i^A$ and the range of the $S_i^B$ for the marker.

We require $P_i\left(G_i=AA\right)+P_i\left(G_i=AB\right)+P_i\left(G_i=BB\right)=1$. We estimate the population genotype frequency of genotype g as $\widehat{P}\left(G=g\right)=\left(1/N\right){\sum }_{i=1}^N{P}_i\left(G_i=g\right)$, and we estimate the probability that an assay is successful and unsuccessful in the population as $\widehat{P}\left(Z=k\right)=\left(1/N\right){\sum }_{i=1}^N{P}_i\left(Z_i=k\right)$ for k = 0, 1.

We assume that the assay-success random variables Z and the true genotype G are independent. This assumption is not necessarily true. However, modeling the dependence of Z and G requires additional parameters (one parameter is required for each of the three possible genotypes). During the development of our method, we observed that increased genotype accuracy was obtained when we used fewer parameters and assumed independence of Z and G rather than dependence (data not shown).

Our genotype-calling module algorithm requires the normalized allele signal data S_i and current estimates of genotype probabilities P_i(G_i) for each sample as input, and returns the posterior genotype probabilities $P_i\left(G_i=g|S_i\right)$ and the genotype likelihoods $P_i\left(S_i|G_i=g\right)$ for the three possible genotypes (g = AA, AB, and BB) for each sample. After the initial iteration of our method, the input genotype probabilities $P_i\left(G_i\right)$ for the genotype-calling module are generated by the haplotype-phasing module (see Material and Methods). The genotype likelihoods $P_i\left(S_i|G_i=g\right)$ produced by the genotype-calling module are input data for the haplotype-phasing module.

We simultaneously estimate the assay-success probabilities $P_i\left(Z_i\right)$ for each individual and the parameters λ_g of the probability-density functions $f_g\left(S;{\lambda }_g\right)$ for the allele signal-intensity data when the genotype assay is successful. We start with an initial estimate of $P_i\left(Z_i\right)=c$ (default c = 0.997) and compute initial estimates of parameters λ_g for the probability densities of the signal data $f_g\left(S;{\lambda }_g\right)$ when the assay is successful. Then we iteratively update the estimates of λ_g and $P_i\left(Z_i\right)$. In each iteration, we first update the current estimate of the assay-success probabilities $P_i\left(Z_i\right)$ given the current parameters λ_g and we then update the current estimates of the parameters λ_g given the current estimates of the assay-success probabilities. A precise description of how these estimates are updated is given below. We stop when the estimate of the mean assay-success probability P(Z = 1) and the estimates of the components of the parameters λ_g converge (defined as a relative absolute change of < 0.001 between successive iterations), or when a specified maximum number of iterations have occurred (default maximum = 50 iterations).

Updating Assay-Success Probabilities P_i(Z_i)

We use $P\left(Z|S_i\right)$ as the updated estimate of the assay-success probability in the i-th sample $P_i\left(Z_i\right)$. The observed signal data, the current estimates of the parameters λ_g of the probability densities, the current estimate of the population assay-success probability P(Z = 1), and Bayes rule are used to estimate $P\left(Z|S_i\right)$:

$$P\left(Z=1|S_i\right)=\frac{P\left(Z=1,S_i\right)}{P\left(Z=1,S_i\right)+P\left(Z=0,S_i\right)}$$

Because G and Z are assumed to be independent, one can express P(Z, S) as

$$P\left(Z,S\right)=P\left(S|Z\right)P\left(Z\right)$$

$$=\sum _{g}P\left(S,G=g|Z\right)P\left(Z\right)$$

$$=\sum _{g}P\left(S|G=g,Z\right)P\left(G=g|Z\right)P\left(Z\right)$$

$$=\sum _{g}P\left(S|G=g,Z\right)P\left(G=g\right)P\left(Z\right)$$

and thus we estimate $P\left(Z=1,S_i\right)$ and $P\left(Z=0,S_i\right)$ as

$$\widehat{P}\left(Z=1,S_i\right)=\sum _g{f}_g\left(S_i|{\lambda }_g\right)P\left(Z=1\right)P_i\left(G_i=g\right)$$

and

$$\widehat{P}\left(Z=0,S_i\right)=\sum _{g}h\left(S_i\right)P\left(Z=0\right)P_i\left(G_i=g\right)=h\left(S_i\right)P\left(Z=0\right)\text{.}$$

Updating Parameters λ_g

We use the current estimates of the assay-success probabilities $P_i\left(Z_i\right)$ and genotype probabilities $P_i\left(G_i\right)$ to update the parameters λ_g of the probability-density functions $f_g\left(S;{\lambda }_g\right)$. In our approach, we assume that the probability density is parameterized by its moments, and we use a two-dimensional t distribution with a fixed number of degrees of freedom (df) (default = 5 df), parameterized by its mean vector and variance/covariance matrix. When the genotype assay is successful (Z = 1), the elements of the mean vector and variance/covariance matrix of the t distribution $f_g\left(S_i;{\lambda }_g\right)$ are

$$E\left[S^A|G=g,Z=1\right]$$

$$E\left[S^B|G=g,Z=1\right]$$

$$\mathrm{Var}\left(S^A|G=g,Z=1\right)=E\left[{\left(S^A\right)}^2\right|G=g,Z=1]-{\left(E\left[\left(S^A\right)|G=g,Z=1\right]\right)}^2\mathrm{Cov}\left(S^A,S^B|G=g,Z=1\right)$$

$$=E\left[\left(S^A{S}^B\right)|G=g,Z=1\right]-\left(E\left[S^A|G=g,Z=1\right]E\left[S^B|G=g,Z=1\right]\right)\mathrm{Var}\left(S^B|G=g,Z=1\right)=E\left[{\left(S^B\right)}^2|G=g,Z=1\right]-{\left(E\left[S^B|G=g,Z=1\right]\right)}^2$$

All of the expectations that define the mean and variance parameters of each t distribution can be represented as $E\left[\varphi \left(S\right)|G=g,Z=1\right]$ in which the function $\varphi \left(S\right)$ is $S_A,S_B,S_A^2,\left(S_A{S}_B\right)$ or $S_B^2$.

If G_i and Z_i were observed, we could estimate $E\left[\varphi \left(S\right)|G=g,Z=1\right]$ by using

$$\widehat{E}\left[\varphi \left(S\right)|G=g,Z=1\right]=\frac{\sum _{i=1}^N\varphi \left(S_i\right)I\left(G_i=g\right)I\left(Z_i=1\right)}{\sum _{i=1}^{N}I\left(G_i=g\right)I\left(Z_i=1\right)}$$

in which I() is an indicator function that is 1 if $G_i=g$ or $Z_i=1$ and 0 otherwise. Because G_i and Z_i are unobserved, we substitute the current estimate of the genotype probability $P_i\left(G_i=g\right)$ for $I\left(G_i=g\right)$ and we substitute the current estimate of the assay-success probabilities $P_i\left(Z_i=1\right)$ for $I\left(Z_i=1\right)$ to obtain the estimate:

$$\widehat{E}\left[\varphi \left(S\right)|G=g,Z=1\right]=\frac{\sum _{i=1}^N\varphi \left(S_i\right)P_i\left(G_i=g\right)P_i\left(Z_i=1\right)}{\sum _{i=1}^N{P}_i\left(G_i=g\right)P_i\left(Z_i=1\right)}$$

The current estimates of the moments $\widehat{E}\left[\varphi \left(S\right)|G=g,Z=1\right]$ determine updated estimates of the probability-density function parameters λ_g.

The estimated parameters λ_g and the estimated assay-success probabilities $P_i\left(Z_i\right)$ are used to estimate the likelihoods for each genotype g

$$P\left(S_i|G=g\right)=f_g\left(S_i|{\lambda }_g\right)P_i\left(Z_i=1\right)+h\left(S_i\right)P_i\left(Z_i=0\right)$$

and the likelihoods are used to estimate the posterior genotype probabilities:

$$P\left(G=g|S_i\right)=\frac{P\left(S_i|G=g\right)P\left(G=g\right)}{\sum _{\tilde{g}}P\left(S_i|G=\tilde{g}\right)P\left(G=\tilde{g}\right)}\text{.}$$

In some cases, the number of individuals with a genotype g is too small to allow accurate estimation of the parameters λ_g of the probability density $f_g\left(S_i;{\lambda }_g\right)$ describing the allele signal-intensity data for the genotype. For the analyses in this study, if the estimated number of individuals with a genotype g was < 5 (estimated from the $P_i\left(G_i\right)$), a uniform distribution was used in place of $f_g\left(S_i;{\lambda }_g\right)$. When g = AB, the support of the uniform distribution was equal to the Cartesian product of the ranges of the A and B allele signal intensities. When g = AA, the support of the uniform distribution was equal to the Cartesian product of the range of the A allele signal intensities and the range of the subset of B allele signal intensities that are less than the estimated mean B allele signal intensity of the BB genotype. Similarly, when g = BB, the support of the uniform distribution was equal to the Cartesian product of the range of the B allele signal intensities and the range of the subset of the A allele signal intensities that are less than the estimated mean A allele signal intensity of the AA genotype.

Appendix 2. Excluded Markers

When calling genotypes from allele signal data (without using LD), data QC filters are typically applied after making genotype calls. This is a sensible strategy because markers are called independently and incorrect genotype calls at one marker do not affect the accuracy of genotype calls at neighboring markers. However, for multilocus genotype-calling methods, markers with high rates of error introduce noise that may decreases genotype-call accuracy at neighboring markers. Thus, for multilocus methods, it may be advantageous to perform data-quality filtering prior to or during genotype calling. However, excluding markers with higher rates of genotype error can also have potential negative effects because information in the data set is also reduced.

During the development of our method, we found that it is necessary to apply an HWE filter before the first iteration of the method. When we omitted the HWE filter, many markers that would have been excluded by an HWE filter passed our missing-data filters and resulted in false-positive signals of association with bipolar disorder (data not shown). Applying an HWE filter at the end of multilocus genotype calling did not solve this problem. We conjecture that this is because the haplotype-phasing module infers haplotype phase under the assumption of HWE and that this reduces the departure from HWE somewhat without sufficiently improving genotype accuracy to eliminate the false-positive association. Applying an HWE filter prior to calling genotypes with our method was necessary for achieving the reduction in false-positive associations described in the Results section.

During development of our method, we also found that we obtained better results (improved genotype accuracy and fewer false-positive associations) by applying increasingly stringent missing-data filters prior to each iteration of the method, rather than applying data QC filters only prior to the first iteration (data not shown).

Genotype data QC filters were applied prior to each of the iterations of our method and after genotype calling for all other methods. For CHIAMO genotype data, we excluded the 30,586 autosomal markers that were excluded by the WTCCC in their analysis.⁷ Almost all (>99.5%) of the markers excluded by the WTCCC were excluded because of departure from HWE or a high proportion of missing genotypes. For genotype data from other genotype-calling methods, we excluded markers showing departure from HWE or having a high proportion of missing genotypes. The number of excluded markers depended on the genotype-calling method and the data source (Affymetrix 500K chip or Illumina 550K chip).

We excluded markers with HWE p value < 10⁻⁶ in controls or < 10⁻⁹ in cases. We chose a stricter HWE p value threshold for cases than for controls because disease-associated variants can cause departures from HWE in cases. We calculated exact HWE p values³⁹ by using the most likely genotype call obtained from the current estimate of genotype probabilities.

For BIRDSEED genotypes, we excluded markers with > 8% missing genotypes when using BIRDSEED's default 0.1 quality-score threshold. This missing-data filter for BIRDSEED was selected so that the number of excluded markers for BIRDSEED was similar to the number of excluded markers for CHIAMO. For GenCall, we excluded markers with > 3.5% missing genotypes when called with GenCall. For ILLUMINUS, we excluded markers with > 2% missing genotypes when genotypes with < 98% probability were set as missing.

For our method, we used increasingly stringent missing-data filters prior to each iteration. The missing-data filters operated on the current genotype probabilities that were the input data for the genotype-calling module. The missing-data filter that we used for our method depends on a single parameter β (0 ≤ β ≤ 1). We set all genotypes with probability < β to missing, and we excluded markers with > (1 - β) missing data. For Affymetrix bipolar disorder and control data, we used missing-data filters with β = 0.0, 0.96, 0.97 in iterations 1, 2, and 3, respectively. For Affymetrix type 2 diabetes and control data, we used missing-data filters with β = 0.9, 0.96, 0.97 in iterations 1, 2, and 3, respectively. For Illumina data, we used missing-data filters with β = 0.9, 0.98, 0.985 for iterations 1, 2, and 3, respectively. We applied the data QC filters for the third iterations (HWE filter and missing-data filter) before and after the third iteration of our method. Thus, before and after the third iteration of our method, for Affymetrix data we excluded markers with > 3% missing genotypes when genotypes with < 97% probability were set as missing, and for Illumina data we excluded markers with > 1.5% missing genotypes when genotypes with < 98.5% probability were set as missing.

Supplemental Data

Supplemental Data inclue four figures and can be found with this article online at http://www.cell.com/AJHG.

Web Resources

The URLs for data presented herein are as follows:

• Affymetrix Power Tools, http://www.affymetrix.com/partners_programs/programs/developer/tools/powertools.affx

• BEAGLE Genetic Analysis Package version 3.1, and BEAGLECALL version 0.9, http://www.auckland.ac.nz/∼browning/beagle/beagle.html

• BRLMM White Paper, http://www.affymetrix.com/support/technical/whitepapers/brlmm_whitepaper.pdf

• European Genotype Archive (repository of WTCCC genotype data), http://www.ebi.ac.uk/ega/page.php

• Illuminus, http://www.well.ox.ac.uk/∼tgc/illuminus_documentation.htm

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim

• Welcome Trust Case Control Consortium, http://www.wtccc.org.uk