Meta-Analysis of Genome-wide Association Studies with Overlapping Subjects

Abstract

Data from multiple genome-wide association studies are often analyzed together for the purposes of combining information from several studies of the same disease or comparing results across different disorders. We provide a valid and efficient approach to such meta-analysis, allowing for overlapping study subjects. The available data may contain individual participant records or only meta-analytic summary results. Simulation studies demonstrate that failure to account for overlapping subjects can greatly inflate type I error when combining results from multiple studies of the same disease and can drastically reduce power when comparing results across different disorders. In addition, the proposed approach can be substantially more powerful than the simple approach of splitting the overlapping subjects among studies, especially for comparing results across different disorders. The advantages of the new approach are illustrated with empirical data from two sets of genome-wide association studies.

Introduction

In the relatively brief but highly informative history of genome-wide association studies (GWAS),¹ meta-analysis (of individual participant data or summary results) has proven to be a crucial step. In many instances, the results of individual studies were unremarkable, and statistically compelling findings only emerged after aggressive data sharing. An excellent model is the discovery of risk loci for type 2 diabetes (MIM 125853).^2–5 Recognizing the need and benefits of data sharing, GWAS investigators have formed a large number of consortia and networks. Several papers have addressed statistical issues in the meta-analysis of GWAS data.^6–9

One important issue in GWAS meta-analysis that has received little attention is the overlap of study subjects, i.e., the appearance of the same subjects in multiple studies. The GWAS requirement for historically large samples—and its considerable expense—makes it desirable for individual studies to share control samples. This can occur by design, as with the Wellcome Trust Case Control Consortium (WTCCC),¹⁰ which genotyped ∼2000 cases from each of seven diseases and ∼3000 shared controls and thus essentially consisted of seven case-control studies with the same collection of controls. It can also occur when there is a paucity of available controls. For example, many psychiatric GWAS conducted in the United States have used controls ascertained and sampled by P.V. Gejman,¹¹ which are commonly referred to as the NIMH Gejman controls. The problem of overlapping controls will become more prominent as an increasing number of case-control studies are taking advantage of publicly available genotype data for large sets of population-based controls, such as the WTCCC and Gejman controls. There are also studies with overlapping cases, although such overlap tends to be less severe.

A simple approach to dealing with the problem of overlapping subjects is to split them among the studies such that each subject contributes only one record to meta-analysis. Unfortunately, this seemingly sensible approach has several drawbacks. First, there is a potential loss of efficiency, especially in cross-disorder comparisons (i.e., comparing results across different disorders). Second, there is generally no unique way to split the overlapping subjects, and the results of meta-analysis may depend appreciably on how the overlapping subjects are split. Third, splitting the overlapping subjects may exacerbate the bias caused by genotyping errors, as elaborated below. Fourth, splitting requires access to individual participant data, which may not be feasible in meta-analysis of summary results.

A more satisfactory approach is to use all of the records from all of the studies. This approach maximizes statistical efficiency, produces unique analysis results, and tends to be less affected by genotyping errors than the approach of splitting the overlapping subjects. (If an equal number of cases and controls are randomized to each genotyping plate, then the genotyping errors will tend to cancel out between the case and control groups. Splitting control samples will create unequal numbers of cases and controls on the plates such that the genotyping errors will not cancel out between the case and control groups if the directions or the magnitudes of the errors vary among the plates.) However, it is necessary to account for the fact that the observations from the overlapping subjects are not independent among studies. Failure to do so will inflate type I error when combining information from multiple studies of the same disease and reduce power when comparing results across different disorders, as will be demonstrated in this article.

In this article, we show how to properly adjust for the correlated observations of the overlapping subjects when all records are used in meta-analysis. The available data may consist of individual participant data (i.e., original phenotype, genotype, and covariate data) or meta-analytic summary results (i.e., parameter estimates and variance estimates). (Meta-analysis of individual participant data has been referred to as mega-analysis and joint analysis.) We demonstrate through simulation studies that the proposed approach preserves type I error and can be substantially more powerful than the approach of splitting the overlapping subjects, especially in cross-disorder comparisons. For meta-analysis of a single disorder, careful splitting of control samples yields statistical power similar to the proposed approach but still suffers from the bias caused by genotyping errors and the inherent variability of results. We evaluate various approaches with empirical data from the WTCCC study¹⁰ and the Genetic Association Information Network (GAIN)¹¹ and Clinical Antipsychotic Trials in Intervention Effectiveness (CATIE)¹² schizophrenia (MIM 181500) studies.

Material and Methods

Meta-Analysis of Individual Participant Data

Let Y denote the disease status (1 = disease, 0 = no disease) and X denote a set of explanatory variables. The explanatory variables represent the genotype score (or scores) of one or several SNPs and may also include covariates. Under the commonly used additive mode of inheritance, the genotype score is the number of minor alleles; under the dominant (or recessive) model, the genotype score indicates, by the values 1 versus 0, whether or not the subject has at least one minor allele (or two minor alleles). (All numerical results reported in this article are based on the additive model.) For an untyped SNP, the unknown genotype score may be replaced by the imputed genotype score. The covariates may include environmental factors and the principal components used to adjust for population stratification. It is natural to assume the following logistic regression model:

$$\text{Pr}\left(Y=1|X\right)=\frac{e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}X}}{1+e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}X}}\text{,}$$ (Equation 1)

where α is the intercept and β is a set of regression parameters on the log odds ratio scale.

All meta-analysis problems can be formulated through Equation 1. If we are interested in combining data from two case-control studies so as to make inference on a common genetic effect (without adjusting for covariates), then we simply set X = (G, S)^T, where G is the genotype score and S indicates, by the values 1 versus 0, whether the subject is from the first study; the regression parameter associated with G is the log odds ratio for the common genetic effect, whereas the regression parameter associated with S reflects the difference of the case-control ratios between the two studies. If we wish to compare the genetic effects between the two studies, then we define X = (G, S, G^∗S)^T, and the regression parameter associated with G^∗S is the difference of the log odds ratios between the two studies. It is straightforward to extend the formulation to more than two studies and to incorporate covariates into Equation 1.

Suppose that there is a total of n study subjects, counting the subjects as many times as they appear in the studies. For i = 1, …, n, let Y_i and X_i denote the values of Y and X on the ith subject. Let θ denote the collection of α and β. The “likelihood” for θ takes the form

$$L\left(\mathit{\theta }\right)=\prod _{i=1}^n\frac{e^{Y_i\left(\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i\right)}}{1+e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i}}\text{.}$$

The corresponding “score function” and “information matrix” are

$$U\left(\mathit{\theta }\right)=\sum _{i=1}^n\left(Y_i-\frac{e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i}}{1+e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i}}\right)\left[\begin{array}{c}1\\ X_i\end{array}\right],$$

and

$$I\left(\mathit{\theta }\right)=\sum _{i=1}^n\frac{e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i}}{{\left(1+e^{\mathit{\alpha }+{\mathit{\beta }}^{\text{T}}{X}_i}\right)}^2}\left[\begin{array}{c}1\\ X_i\end{array}\begin{array}{c}{X}_i^{\text{T}}\\ X_i{X}_i^{\text{T}}\end{array}\right],$$

respectively. The “maximum likelihood estimator” $\widehat{\mathit{\theta }}$ is the maximizer of L(θ) or equivalently the solution to the estimating equation U(θ) = 0.

We use the quotation marks for the likelihood and related quantities because L(θ) is not the correct likelihood when study subjects overlap. Although $\widehat{\mathit{\theta }}$ is not a genuine maximum likelihood estimator, we show in the Appendix that $\widehat{\mathit{\theta }}$ is a valid estimator of θ and that its variance can be estimated properly from the data. Specifically, $\widehat{\mathit{\theta }}$ is approximately normal with mean θ and variance-covariance matrix

$$V\left(\widehat{\mathit{\theta }}\right)=I^{-1}\left(\widehat{\mathit{\theta }}\right)\left\{I\left(\widehat{\mathit{\theta }}\right)+D\left(\widehat{\mathit{\theta }}\right)\right\}{I}^{-1}\left(\widehat{\mathit{\theta }}\right),$$ (Equation 2)

where

$$D\left(\mathit{\theta }\right)=\sum _{i=1}^n\sum _{j=1}^n{\delta }_{ij}{U}_i\left(\mathit{\theta }\right)U_j{\left(\mathit{\theta }\right)}^{\text{T}},$$

U_i(θ) is the ith summand in U(θ), and δ_ij takes the value 1 if i ≠ j but the ith and jth subjects are the same subject and takes the value 0 otherwise. If there are no overlapping subjects, then D(θ) = 0, so $V\left(\widehat{\mathit{\theta }}\right)$ reduces to $I^{-1}\left(\widehat{\mathit{\theta }}\right)$, which is the usual variance-covariance estimator of the maximum likelihood estimator.

We will refer to the approach described above as “sharing subjects,” in that all overlapping subjects are included in the meta-analysis as many times as they appeared in the studies. This is in contrast to the approach of “splitting subjects,” in which the overlapping subjects are divided among the studies such that every subject is used only once in the meta-analysis. We will refer to $V\left(\widehat{\mathit{\theta }}\right)$ and $I^{-1}\left(\widehat{\mathit{\theta }}\right)$ as the robust and naive variance-covariance estimators, respectively, in that the former properly accounts for the correlation of the observations from the same subject whereas the latter does not. Clearly, V(θ) = I⁻¹(θ) + I⁻¹(θ)D(θ)I⁻¹(θ), so I⁻¹(θ)D(θ)I⁻¹(θ) is the extra variance due to overlap.

Meta-Analysis of Summary Results

Suppose that there are K studies with potentially overlapping subjects. For k = 1, …, K, let ${\widehat{\mathit{\eta }}}_k$ be the estimator of a common genetic effect η from the kth study and let V_k be the corresponding variance estimator. For meta-analysis of K independent studies with such summary results, the well-known inverse-variance estimator of η is

$$\widehat{\mathit{\eta }}=\sum _{k=1}^K{w}_k{\widehat{\mathit{\eta }}}_k,$$ (Equation 3)

where $w_k=V_k^{-1}/{\sum }_{k=1}^K{V}_k^{-1}$; the variance of $\widehat{\mathit{\eta }}$ is estimated by ${\sum }_{k=1}^K{w}_k^2{V}_k$. When study subjects overlap, the optimal weights are no longer proportional to the inverse variances, and the variance of $\widehat{\mathit{\eta }}$ is no longer ${\sum }_{k=1}^K{w}_k^2{V}_k$. It can be shown that the optimal weights are

$$\left[w_1,\dots w_K\right]=e^{\text{T}}{\Omega }^{-1}/e^{\text{T}}{\Omega }^{-1}e,$$ (Equation 4)

where e is a K × 1 vector of 1’s and Ω is the (estimated) covariance matrix of $({\widehat{\mathit{\eta }}}_1,\dots ,{\widehat{\mathit{\eta }}}_K)$.¹³ Regardless of what the w_ks are, the variance of $\widehat{\mathit{\eta }}$ takes the form

$$\text{Var}\left(\widehat{\mathit{\eta }}\right)=\sum _{k=1}^K{w}_k^2{V}_k+2\sum _{k=1}^K\sum _{l=k+1}^K{w}_k{w}_l\text{Cov}\left({\widehat{\mathit{\eta }}}_k,{\widehat{\mathit{\eta }}}_l\right),$$ (Equation 5)

where Cov denotes covariance. For cross-disorder comparisons, the difference between the genetic effects of the kth and lth studies is simply estimated by ${\widehat{\mathit{\eta }}}_k-{\widehat{\mathit{\eta }}}_l$, and the corresponding variance is

$$\text{Var}\left({\widehat{\mathit{\eta }}}_k-{\widehat{\mathit{\eta }}}_l\right)=V_k+V_l-2\text{Cov}\left({\widehat{\mathit{\eta }}}_k,{\widehat{\mathit{\eta }}}_l\right)\text{.}$$ (Equation 6)

It is evident from Equation 5 and Equation 6 that failure to account for overlapping subjects will underestimate the true variation when making inference on a common genetic effect and will overestimate the true variation when comparing genetic effects across studies. We will refer to Equation 5 and Equation 6 as robust variance estimators in that they properly account for the correlations of the overlapping subjects.

To carry out the aforementioned analyses, we need to estimate the covariances or correlations of the ${\widehat{\eta }}_k$ s. We derive in the Appendix a simple correlation formula for case-control studies:

$$\text{Corr}\left({\widehat{\mathit{\eta }}}_k,{\widehat{\mathit{\eta }}}_l\right)\approx \left(n_{kl0}\sqrt{\frac{n_{k1}{n}_{l1}}{n_{k0}{n}_{l0}}}+n_{kl1}\sqrt{\frac{n_{k0}{n}_{l0}}{n_{k1}{n}_{l1}}}\right)/\sqrt{n_k{n}_l},$$ (Equation 7)

where n_k1, n_k0, and n_k (or n_l1, n_l0, and n_l) are, respectively, the number of cases, the number of controls, and the total number of subjects in the kth (or lth) study and n_kl0 and n_kl1 are, respectively, the numbers of controls and cases that overlap between the kth and lth studies. This formula also applies to the score tests. The approximation is accurate if the case-control status is independent of all explanatory variables in the model, which is true under the null hypothesis of no genetic association when no covariates are included in the analysis. The approximation may be inaccurate in the presence of strong genetic and/or covariate effects.

Results

Simulation Studies

We conducted simulation studies to compare the performance of the robust and naive variance estimators when sharing the overlapping subjects in the meta-analysis of individual participant data and to assess the efficiency loss of splitting the overlapping subjects. The first set of simulation studies was focused on combining results from multiple studies of the same disease. We simulated n₁ cases and n₀ controls from model 1 (i.e., the model given in Equation 1), in which X is the number of minor alleles of the test SNP. We created two studies with n₁/2 cases each, or with 3n₁/4 cases in one study and n₁/4 cases in the other. We considered various combinations of n₁ and n₀. For each configuration, we generated 10 million data sets. Each simulated data set was analyzed in two ways: sharing all of the n₀ controls between the two studies, and splitting the control samples between the two studies in a 1:1, 3:1, or 1:3 ratio. In either approach, we fit model 1 in which X consists of the genotype score (i.e., the number of minor alleles) and the study indicator, and we tested the null hypothesis that β = 0. The results reported below pertain to the choices of α = −3, β = 0 or 0.3, minor allele frequency (MAF) of 0.3, and nominal significance levels of 10⁻⁴ and 10⁻⁷ under β = 0 and β = 0.3, respectively. The results are similar for other choices of α, MAF, and nominal significance levels. Note that β = 0 and 0.3 correspond to odds ratios of 1 and ∼1.35.

The type I error rates of the joint association tests when the control samples are shared between the two studies are shown in Table 1 under the heading “Original Data.” Because the robust variance estimator accurately reflects the true variation of the odds ratio estimator (data not shown), the corresponding association test has proper type I error. (The slight conservativeness is a general phenomenon for Wald tests at extreme nominal significance levels and not a unique feature of the proposed method.) By contrast, the naive variance estimator seriously underestimates the true variation (data not shown), so the corresponding association test has grossly inflated type I error, especially under the first and fifth scenarios. The reason that the inflation of the type I error for the naive method decreases as the number of controls increases is because it can be shown from Equation 2 that the extra variance due to overlap is inversely proportional to n₀.

Table 1.

Type I Error Rates (×10⁴) of Association Tests at the Nominal Significance Level of 10⁻⁴ When Control Samples Are Shared in the Combined Analysis of Two Case-Control Studies

No. of Cases			Original Data		Summary Results
Study 1	Study 2	No. of Controls	Robusta	Naiveb	Robusta	Naiveb
1000	1000	1000	0.96	14.9	0.97	14.8
1000	1000	2000	0.95	7.4	0.96	7.4
1000	1000	3000	0.93	5.0	0.95	5.0
1000	1000	4000	0.96	3.7	0.96	3.7
1500	500	1000	0.97	11.3	0.96	11.2
1500	500	2000	0.97	5.5	0.96	5.5
1500	500	3000	0.95	3.8	0.94	3.8
1500	500	4000	0.96	2.9	0.97	2.9

^aRobust variance estimator used.

^bNaive variance estimator used.

The powers of the joint association tests under β = 0.3 when the control samples are shared versus split between the two studies are shown in Table 2 under the heading “Original Data.” (When the control samples are shared, the robust variance estimator is used.) When the control samples are split in the same ratio as the numbers of cases between the two studies, the two approaches have virtually the same power. When the control samples are split in a different ratio, however, sharing is considerably more powerful than splitting.

Table 2.

Powers of Association Tests at the Nominal Significance Level of 10⁻⁷ When Control Samples Are Shared or Split in the Combined Analysis of Two Case-Control Studies

			Original Data				Summary Results
No. of Cases				Splitting Controls
Study 1	Study 2	No. of Controls	Sharing Controlsa	1:1	3:1	1:3	Sharing Controlsa
1000	1000	1000	0.34	0.34	0.28	0.28	0.31
1000	1000	2000	0.73	0.73	0.66	0.66	0.71
1000	1000	3000	0.88	0.88	0.83	0.83	0.87
1000	1000	4000	0.93	0.93	0.90	0.90	0.93
1500	500	1000	0.32	0.28	0.33	0.15	0.31
1500	500	2000	0.72	0.66	0.73	0.43	0.72
1500	500	3000	0.87	0.83	0.88	0.63	0.87
1500	500	4000	0.93	0.90	0.93	0.75	0.93

^aRobust variance estimator used.

The next set of simulation studies was concerned with the comparison of odds ratios between different studies (i.e., cross-disorder comparison). We simulated two case-control studies with a set of common controls, the cases in the two studies representing two different disorders. The log odds ratios for the two studies were β₁ and β₂, and we were interested in testing the null hypothesis that β₁ = β₂. Other than potentially unequal odds ratios between the two studies, the simulation parameters were the same as in the first set of simulation studies. We set β₁ = β₂ = 0.3 under the null hypothesis and β₁ = 0 and β₂ = 0.5 under the alternative hypothesis. Note that the β value of 0.5 corresponds to an odds ratio of ∼1.65. Again, we generated 10 million data sets for each scenario and analyzed each simulated data set by sharing or splitting the control samples between the two studies. Whether the control samples were shared or split, we fit model 1 in which X consists of the genotype score, the study indicator, and their product. (The regression parameter associated with the product term corresponds to the difference between the log odds ratios of the two studies.)

The type I error rates for testing the null hypothesis that β₁ = β₂ when the control samples are shared in the analysis are displayed in Table 3 under the heading “Original Data.” Again, the robust variance estimator accurately reflects the true variation (data not shown) and thus yields proper type I error. The naive variance estimator overestimates the true variation (data not shown), so the corresponding test is too conservative.

Table 3.

Type I Error Rates (×10⁴) at the Nominal Significance Level of 10⁻⁴ for Testing Equal Odds Ratios When Control Samples Are Shared Between Two Case-Control Studies

No. of Cases			Original Data		Summary Results
Study 1	Study 2	No. of Controls	Robusta	Naiveb	Robusta	Naiveb
1000	1000	1000	0.95	0.001	1.65	0.001
1000	1000	2000	0.98	0.027	1.36	0.027
1000	1000	3000	0.99	0.091	1.25	0.091
1000	1000	4000	1.00	0.173	1.21	0.173
1500	500	1000	0.92	0.004	1.42	0.004
1500	500	2000	0.93	0.084	1.19	0.084
1500	500	3000	0.93	0.177	1.11	0.177
1500	500	4000	0.94	0.265	1.08	0.265

^aRobust variance estimator used.

^bNaive variance estimator used.

The powers against the alternative hypothesis that β₁ = 0 and β₂ = 0.5 when the control samples are shared versus split in the analysis are presented in Table 4 under the heading “Original Data.” When the control samples are shared, the use of the robust variance estimator yields a much more powerful test than the use of the naive variance estimator. Splitting the control samples results in substantial loss of power, especially when the total number of controls is small.

Table 4.

Powers of Detecting Unequal Odds Ratios at the Nominal Significance Level of 10⁻⁷ When Control Samples Are Shared or Split between Two Case-Control Studies

			Original Data					Summary Results
No. of Cases			Sharing Controls		Splitting Controls			Sharing Controls
Study 1	Study 2	No. of Controls	Robusta	Naiveb	1:1	3:1	1:3	Robusta	Naiveb
1000	1000	1000	0.93	0.30	0.11	0.05	0.05	0.95	0.30
1000	1000	2000	0.94	0.67	0.36	0.23	0.24	0.95	0.67
1000	1000	3000	0.94	0.78	0.53	0.40	0.41	0.95	0.78
1000	1000	4000	0.94	0.83	0.64	0.53	0.54	0.95	0.83
1500	500	1000	0.66	0.13	0.06	0.03	0.03	0.72	0.13
1500	500	2000	0.67	0.35	0.19	0.13	0.13	0.70	0.35
1500	500	3000	0.67	0.45	0.30	0.22	0.23	0.70	0.45
1500	500	4000	0.68	0.51	0.37	0.29	0.30	0.69	0.51

^aRobust variance estimator used.

^bNaive variance estimator used.

An important technical issue in GWAS is the possible presence of plate effects where there are important (but undetected) biases in the genotyping of some subjects. To assess the biases caused by splitting control samples in the presence of plate effects, we simulated a case-control study with 1920 cases and 1920 controls (i.e., 3840 subjects on 40 96-well plates) from model 1 with α = −3 and β = 0. We assumed that cases and controls were randomly assigned such that there was an equal number of cases and controls on each genotyping plate. We generated the genotypes for a test SNP with relatively low MAF independently of the case-control status. For $\tilde{n}$ cases and $\tilde{n}$ controls, each heterozygous genotype was miscalled as minor homozygous genotype with probability 0.1, and each major homozygous genotype was miscalled as heterozygous also with probability 0.1. (For a SNP with relatively low MAF, no minor homozygous genotypes may exist on a plate, so the clustering plots tend to mistakenly assign some heterozygous genotypes to minor homozygous genotypes and some major homozygous genotypes to heterozygous genotypes.) For the remaining $(n-\tilde{n})$ cases and $(n-\tilde{n})$ controls, all genotypes were called correctly. We assumed that the $\tilde{n}$ controls with potentially miscalled genotypes were involved in a second case-control study, which also randomized cases and controls to each plate. (If we share the overlapping control samples in the meta-analysis of such studies, the balance between cases and controls in each plate ensures that the expected genotype frequencies are the same between the case and control groups, which in turn ensures valid association testing. If we split the overlapping control samples, the resulting unequal numbers of cases and controls with genotyping errors within each study will yield unequal genotype frequencies between the case and control groups, which will inflate type I error.) We simulated 10 million data sets with $\tilde{n}$ = 96, 192, or 384 (i.e., one, two, or four plates) and MAF = 0.05 or 0.1. Table 5 shows the impact of splitting the overlapping control samples between the two studies on the association testing of the first study. When the overlapping control samples were shared in the analysis (such that no records were excluded) and the robust variance estimator was used, the type I error rates of the association tests were below the nominal significance level. When the overlapping control samples were split between the two studies such that a portion of the controls were excluded from the first study, the type I error rates were inflated, especially when the number of controls excluded was large.

Table 5.

Type I Error Rates (×10⁴) of Association Tests at the Nominal Significance Level of 10⁻⁴ When Different Proportions of the Controls with Potential Genotyping Errors Are Excluded

No. of Controls	Proportion Excluded	MAF = 0.05	MAF = 0.1
96	0	0.81	0.90
	1/2	1.26	1.13
	1	2.84	1.89
192	0	0.81	0.92
	1/2	2.39	1.77
	1	13.2	6.18
384	0	0.74	0.81
	1/2	7.99	4.34
	1	145.0	44.1

MAF denotes minor allele frequency.

All of the above simulation results pertain to the use of individual participant data. We also assessed the performance of the methods for meta-analysis of summary results. According to Equation 7, the correlation coefficients (between the estimated genetic effects of the two studies) for the eight scenarios shown in Tables 1–4 are 0.5, 0.333, 0.25, 0.2, 0.447, 0.293, 0.218, and 0.174. Under β = 0, the empirical correlation coefficients were found to be identical to the theoretical values up to the third decimal point. Under β = 0.3, the empirical correlation coefficients were estimated at 0.467, 0.307, 0.229, 0.182, 0.416, 0.269, 0.199, and 0.159, all of which are slightly below the theoretical values. Under β = −0.3, the empirical correlation coefficients were 0.524, 0.358, 0.273, 0.220, 0.471, 0.316, 0.239, and 0.192, all of which are slightly above the theoretical values.

The type I error rates and powers for meta-analysis of summary results are shown in Tables 1–4 under the heading “Summary Results.” For testing a common genetic effect, the type I error rates and powers based on summary results are nearly identical to those of individual participant data (see Table 1 and Table 2). For testing the equality of two odds ratios, meta-analysis of summary results based on the robust variance estimator had slight inflation of type I error and was slightly more powerful than meta-analysis of individual participant data based on the robust variance estimator because Equation 7 overestimates the correlation coefficients when the odds ratios are greater than 1 (see Table 3 and Table 4). Note that the two odds ratios were set to ∼1.35 under the null hypothesis of equal odds ratios. Meta-analysis of summary results based on the robust variance estimator had very accurate control of type I error when the two odds ratios were set to 1 instead of 1.35 (data not shown).

The last set of simulation studies was designed to assess the performance of meta-analysis of summary results when principal components are included in the model to adjust for population stratification. We simulated and analyzed data in the same way as before, except that the new model included a normally distributed covariate whose mean was the genotype score and whose variance was 1. We found that the actual correlations fluctuated slightly around the theoretical values determined by Equation 7 (data not shown). As shown in Table 6, the proposed method had good control of type I error even when the covariate effects were unusually strong.

Table 6.

Type I Error Rates (×10⁴) of Association Tests Based on Equations 4, 5, and 7 at the Nominal Significance Level of 10⁻⁴ in the Presence of Population Stratification

No. of Cases
Study 1	Study 2	No. of Controls	OR∗ = 1.35	OR∗ = 1.65	OR∗ = 2.23
1000	1000	1000	0.85	0.79	0.73
1000	1000	2000	0.92	0.89	0.89
1000	1000	3000	0.96	0.97	0.96
1000	1000	4000	0.94	1.00	1.04
1500	500	1000	0.88	0.86	0.82
1500	500	2000	0.94	0.93	0.93
1500	500	3000	0.96	0.97	1.01
1500	500	4000	0.95	1.01	1.05

Population stratification is represented by a normal covariate that is correlated with the genotype score of the test locus and whose odds ratio with the disease is denoted by OR^∗. OR^∗ is the increase in the odds of disease for every unit increase of the covariate value.

WTCCC Data

We considered GWAS data on rheumatoid arthritis (RA [MIM 180300]) and type 1 diabetes (T1D [MIM 222100]) from the WTCCC study.¹⁰ RA and T1D are both autoimmune disorders and are known to share common loci. The database contains 1860 subjects with RA, 1963 with T1D, and 2938 common controls. For the meta-analysis, we viewed the data as two case-control studies, one on RA and one on T1D, with completely overlapping controls.

The WTCCC reported eight SNPs that are significantly associated with RA, T1D, or both.¹⁰ For each of these eight SNPs, we performed the trend test and estimated the odds ratio under the additive model for both RA and T1D. The results are shown in Table 7. The first three SNPs are strongly associated with both RA and T1D, although the odds ratios appear to be quite different between RA and T1D for the second and third SNPs. The fourth SNP is more strongly associated with RA than with T1D. The results for the fifth SNP are almost identical between RA and T1D. The last three SNPs are significantly associated with T1D, but not with RA. We performed meta-analysis to formalize these statements.

Table 7.

Estimates of Odds Ratios and p Values of Trend Tests for Rheumatoid Arthritis and Type 1 Diabetes in the WTCCC Data

		RA			T1D
Chr	SNP	Est	SE	p Value	Est	SE	p Value
1p13	rs6679677	1.95	0.124	8.9 × 10−26	1.89	0.117	5.1 × 10−25
6(RA)	rs6457617	0.44	0.020	5.5 × 10−72	0.71	0.031	2.3 × 10−15
6(T1D)	rs9272346	0.72	0.032	4.7 × 10−14	0.27	0.015	9.1 × 10−122
7q32	rs11761231	0.81	0.036	2.4 × 10−6	0.91	0.039	2.8 × 10−2
10p15	rs2104286	0.80	0.039	7.1 × 10−6	0.81	0.038	1.1 × 10−5
12q13	rs11171739	0.99	0.042	8.6 × 10−1	1.33	0.055	1.3 × 10−11
12q24	rs17696736	1.13	0.048	3.5 × 10−3	1.39	0.058	3.4 × 10−15
16p13	rs12708716	0.97	0.043	4.5 × 10−1	0.79	0.035	7.4 × 10−8

The following abbreviations are used: RA, rheumatoid arthritis; T1D, type 1 diabetes; Est, estimate of odds ratio; SE, standard error estimate. p values shown are p values of trend test.

To combine the results on RA and T1D, we fit model 1 in which X = (G, S)^T, where G is the number of minor alleles of each SNP and S indicates, by the values 1 versus 0, whether the subject belongs to the RA case-control study or the T1D case-control study; the regression parameter associated with G is the common log odds ratio for RA and T1D. Thus, this analysis yields an estimate of a common odds ratio for RA and T1D and an overall trend test for the association of the SNP with the two diseases. The results are shown in Table 8 under the heading “Common Odds Ratio.” There is strong evidence of association for 5 of the 8 SNPs. Because of completely overlapping controls, the naive variance estimator substantially underestimates the true variation and the corresponding p values grossly exaggerate the degrees of statistical significance.

Table 8.

Meta-Analysis of Individual Participant Data for Rheumatoid Arthritis and Type 1 Diabetes in the WTCCC Data

		Common Odds Ratio					Ratio of Odds Ratios
			Robusta		Naiveb			Robusta		Naiveb
Chr	SNP	Est	SE	p Valuec	SE	p Valuec	Est	SE	p Valued	SE	p Valued
1p13	rs6679677	1.92	0.104	2.7 × 10−33	0.085	4.6 × 10−49	1.03	0.064	6.5 × 10−1	0.091	7.5 × 10−1
6(RA)	rs6457617	0.56	0.021	5.3 × 10−55	0.017	2.0 × 10−76	0.62	0.030	4.5 × 10−22	0.039	5.6 × 10−14
6(T1D)	rs9272346	0.47	0.019	6.5 × 10−82	0.016	3.3 × 10−109	2.61	0.154	6.8 × 10−60	0.185	6.6 × 10−42
7q32	rs1176123	0.86	0.031	3.6 × 10−5	0.026	1.1 × 10−6	0.89	0.043	1.7 × 10−2	0.055	6.3 × 10−2
10p15	rs2104286	0.81	0.032	8.5 × 10−8	0.027	3.4 × 10−10	0.99	0.053	8.6 × 10−1	0.067	8.9 × 10−1
12q13	rs11171739	1.15	0.040	6.5 × 10−5	0.034	2.4 × 10−6	0.75	0.035	3.6 × 10−10	0.044	1.0 × 10−6
12q24	rs17696736	1.26	0.044	7.7 × 10−11	0.037	1.5 × 10−14	0.81	0.038	9.0 × 10−6	0.049	5.5 × 10−4
16p13	rs12708716	0.87	0.032	2.1 × 10−4	0.027	1.3 × 10−5	1.23	0.060	3.0 × 10−5	0.077	1.1 × 10−3

Common odds ratio represents inference on a common odds ratio; ratio of odds ratios represents comparison of two odds ratios. The following abbreviations are used: Est, parameter estimate; SE, standard error estimate.

^aRobust variance estimator used.

^bNaive variance estimator used.

^cp value for testing no association.

^dp value for testing equal odds ratios.

To compare the strengths of association between RA and T1D, we fit model 1 in which X = (G, S, G^∗S)^T; the regression parameter associated with G^∗S is the difference of the log odds ratios between RA and T1D. Thus, this analysis yields an estimate of the ratio of the odds ratios between RA and T1D and the corresponding test for the equality of the two odds ratios. The results are shown in Table 8 under the heading “Ratio of Odds Ratios.” Based on the robust variance estimator, there is strong evidence that the effects of SNPs 2, 3, and 6 are different between RA and T1D, as well as moderate evidence that the effects of SNPs 7 and 8 are different between the two diseases. For this analysis, the use of the naive variance estimator greatly weakens the statistical evidence.

The results in Table 8 were obtained by sharing the controls in the meta-analysis. Figure 1 contrasts this approach with the approach of splitting the control samples in testing the equality of the two odds ratios. For the latter approach, we split the control samples equally between RA and T1D with three different random sequences. Splitting the control samples yields considerably less extreme p values than sharing the control samples. This phenomenon is consistent with the simulation results of Table 2. For some of the SNPs, the p values vary appreciably among the three random splits.

Figure 1.

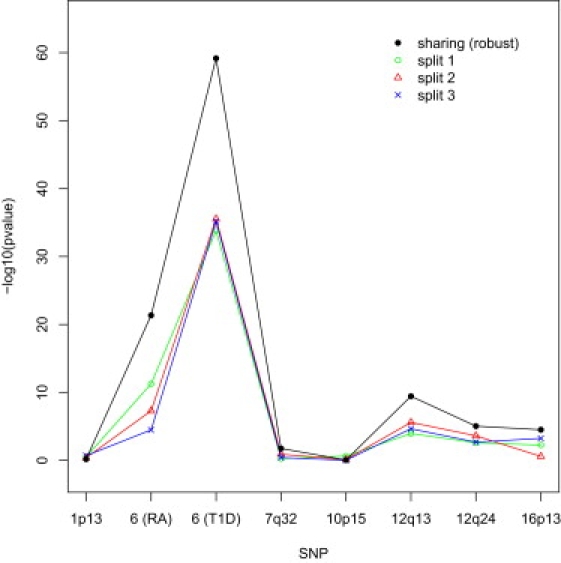
p Values for Testing Equality of Odds Ratios between Rheumatoid Arthritis and Type 1 Diabetes in the WTCCC Data When the Control Samples Are Shared or Split in the Analysis

The robust variance estimator is used when the control samples are shared in the analysis; three different random sequences are used to split the control samples. RA indicates rheumatoid arthritis; T1D indicates type 1 diabetes.

We also conducted meta-analysis of the summary results of Table 7 (pretending no access to individual participant data). According to Equation 7, the correlation between the genetic effects for RA and T1D is approximately 0.394. Given this correlation estimate, we used Equations 3–6 to perform the meta-analysis of summary results. The findings are reported in Table 9. The estimates of the common odds ratios and the corresponding standard error estimates are extremely close to their counterparts in Table 8, except for the third SNP. The estimates of the ratios of odds ratios are identical to their counterparts of Table 8; the corresponding standard error estimates are very close to their counterparts of Table 8, except for the first and third SNPs.

Table 9.

Meta-Analysis of Summary Results for Rheumatoid Arthritis and Type 1 Diabetes in the WTCCC Data

		Common Odds Ratio						Ratio of Odds Ratios
		Robusta			Naiveb				Robusta		Naiveb
Chr	SNP	Est	SE	p Valuec	Est	SE	p Valuec	Est	SE	p Valued	SE	p Valued
1p13	rs6679677	1.92	0.100	1.1 × 10−35	1.92	0.085	4.5 × 10−49	1.03	0.071	6.8 × 10−1	0.091	7.5 × 10−1
6 (RA)	rs6457617	0.57	0.021	7.2 × 10−52	0.57	0.018	2.3 × 10−73	0.62	0.030	4.8 × 10−22	0.039	5.6 × 10−14
6(T1D)	rs9272346	0.52	0.021	2.1 × 10−57	0.49	0.017	4.2 × 10−94	2.61	0.145	5.3 × 10−67	0.185	6.6 × 10−42
7q32	rs1176123	0.86	0.031	4.5 × 10−5	0.86	0.026	1.2 × 10−6	0.89	0.042	1.7 × 10−2	0.055	6.3 × 10−2
10p15	rs2104286	0.81	0.032	1.1 × 10−7	0.81	0.027	3.4 × 10−10	0.99	0.052	8.6 × 10−1	0.067	8.9 × 10−1
12q13	rs11171739	1.15	0.040	6.2 × 10−5	1.15	0.034	2.8 × 10−6	0.75	0.035	3.5 × 10−10	0.044	1.0 × 10−6
12q24	rs17696736	1.26	0.044	7.4 × 10−11	1.26	0.038	1.9 × 10−14	0.81	0.038	9.1 × 10−6	0.049	5.5 × 10−4
16p13	rs12708716	0.87	0.032	2.4 × 10−4	0.87	0.027	1.4 × 10−5	1.23	0.060	2.6 × 10−5	0.077	1.1 × 10−3

Common odds ratio represents inference on a common odds ratio; ratio of odds ratios represents comparison of two odds ratios. The following abbreviations are used: Est, parameter estimate; SE, standard error estimate.

^aRobust variance estimator used.

^bNaive variance estimator used.

^cp value for testing no association.

^dp value for testing equal odds ratios.

Schizophrenia Data

Our work was motivated by the presence of overlapping subjects in the Psychiatric GWAS Consortium.¹⁴ There are currently 17 schizophrenia studies in the consortium, with a total of 9387 cases, 12,301 controls, and 588 overlapping subjects. For this illustration, we considered two schizophrenia studies, the GAIN schizophrenia study¹¹ and the CATIE study,¹² and focused on the European-ancestry samples. There are 415 cases and 407 controls in the CATIE study and 1396 cases and 1442 controls in the GAIN study, with 199 controls appearing in both studies. Although the overlapping controls account for only ∼10% of the controls and 5% of all study subjects, the analysis results may depend appreciably on how the overlapping controls are handled.

We performed joint association tests for the CATIE and GAIN studies by sharing the 199 overlapping controls. We also considered four ways of splitting the overlapping control samples: (1) assigning all 199 controls to CATIE, (2) assigning all 199 controls to GAIN, (3) randomly assigning 99 controls to GAIN and 100 to CATIE, or (4) randomly assigning 29 controls to GAIN and 170 to CATIE. Option 4 yields equal case/control ratios between the two studies and should be the most efficient. Options 1 and 4 differ only by 29 subjects. Option 2 deviates the most from option 4 and is thus expected to yield the least significant results.

Figure 2 displays the p values of the trend tests for seven SNPs in a 0.4 Mb region on chromosome 7. The p values for sharing the control samples are based on the meta-analysis of individual participant data, but those of the meta-analysis of summary results are very similar. Even with 5% overlapping subjects, failure to account for correlated observations can cause considerable inflation of statistical significance: the p values based on the naive variance estimates are appreciably lower than those of the robust variance estimates. There are some noticeable differences between splitting control samples and sharing control samples (with the use of the robust variance estimator). As expected, the results for options 1 and 4 are very similar, and option 2 tends to yield the least significant results.

Figure 2.

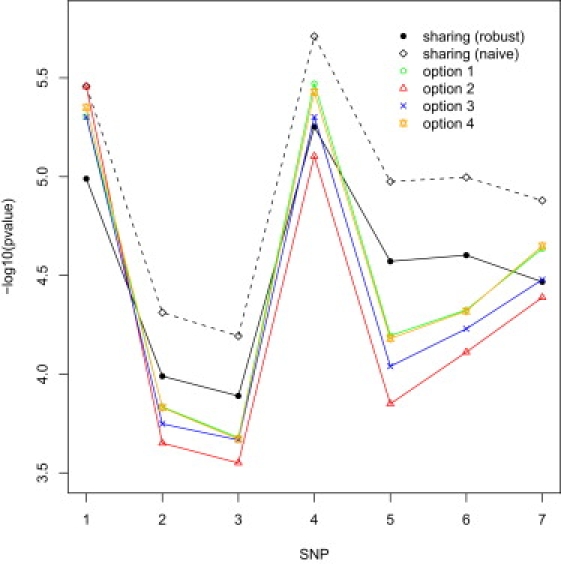
p Values of Joint Association Tests When the Overlapping Control Samples Are Shared or Split between the CATIE and GAIN Studies

“Sharing (robust)” and “sharing (naive)” pertain to the use of the robust and naive variance estimators when the overlapping control samples are shared in the meta-analysis. Under option 1, all 199 overlapping controls are assigned to CATIE; under option 2, all 199 overlapping controls are assigned to GAIN; under option 3, a total of 99 overlapping controls are randomly assigned to GAIN and 100 to CATIE; under option 4, a total of 29 overlapping controls are randomly assigned to GAIN and 170 to CATIE.

Discussion

There is a growing interest in the meta-analysis of GWAS data for the purposes of combining results from multiple studies of the same disease or comparing results across different disorders. It is common for the same subjects to appear in multiple studies of the same disease or related disorders. If subject overlap is ignored, the validity and efficiency of meta-analysis can be severely compromised. Specifically, there will be inflation of type I error in joint association testing and reduction of power in cross-disorder comparisons.

We have developed a very general framework to deal with overlapping subjects in GWAS meta-analysis. Its validity and efficiency have been clearly demonstrated with simulated and empirical data. The proposed approach is simple to implement and is computationally feasible for large GWAS. The relevant software is available at our website.

Our work covers both meta-analysis of individual participant data and meta-analysis of summary results. When there are no overlapping subjects, the two types of analysis have the same statistical efficiency.⁹ In the presence of overlapping subjects, the two types of analysis will still produce similar results, as shown in the Results section. Given access to individual participant data, one can account for the correlated observations of overlapping subjects in a very accurate manner through Equation 2. The correlation formula for meta-analytic summary results given in Equation 7 is asymptotically exact when there are no genetic or covariate effects and is a reasonable approximation even in the presence of strong covariate effects but may not be accurate when there are strong genetic effects. Thus, joint association testing of genetic effects based on this correlation formula is valid in the absence of covariates and approximately valid in the presence of covariate effects; however, the cross-disorder comparison may not have correct type I error if the odds ratios are equal across different disorders but are far away from 1. Thus, we recommend the use of Equation 2 when individual participant data are available and the use of Equation 7 when only meta-analytic summary results are available.

It is straightforward to perform meta-analysis of summary results. The optimal weights given in Equation 4 require special calculations. The usual weights based on inverse variances can be used instead. The efficiency gains due to the use of the optimal weights depend on the patterns of overlap among the studies. Regardless of the choices of the weights, it is important to account for the correlations of overlapping subjects through Equation 5 and Equation 7; otherwise, the validity of meta-analysis would be compromised.

Although we have focused our attention on case-control studies, the proposed approach can be applied to other types of studies. For a different study design, the regression model and the “likelihood” and related quantities will be different. However, the robust variance estimator given in Equation 2 is applicable to any parametric model as long as U_i is defined as the contribution of the ith study subject to the “score function.” For a quantitative trait in a cross-sectional study satisfying the linear regression model

$$Y_i=\alpha +{\beta }^{\text{T}}{X}_i+{\varepsilon }_i,$$

where ɛ_i is normal with mean 0 and variance σ², the “score function” for θ = (α, β, σ²) is

$$U\left(\mathit{\theta }\right)=\left[\begin{array}{l}\frac{1}{{\mathit{\sigma }}^2}{\Sigma }_{i=1}^n(Y_i-\mathit{\alpha }-{\mathit{\beta }}^{\text{T}}{X}_i)\hfill \\ \frac{1}{{\mathit{\sigma }}^2}{\Sigma }_{i=1}^n(Y_i-\mathit{\alpha }-{\mathit{\beta }}^{\text{T}}{X}_i)X_i\hfill \\ \frac{1}{2{\mathit{\sigma }}^4}{\Sigma }_{i=1}^n{(Y_i-\mathit{\alpha }-{\mathit{\beta }}^{\text{T}}{X}_i)}^2-\frac{n}{2{\mathit{\sigma }}^2}\hfill \end{array}\right]\text{.}$$

If the overlap of subjects occurs completely at random, then the analog of Equation 7 is

$$\text{Corr}\left({\widehat{\mathit{\eta }}}_k,{\widehat{\mathit{\eta }}}_l\right)\approx n_{kl}/\sqrt{n_k{n}_l},$$ (Equation 8)

where n_k and n_l are the numbers of subjects in the kth and lth studies, respectively, and n_kl is the number of overlapping subjects between the kth and lth studies. Unlike the situation of case-control studies, Equation 8 is accurate regardless of whether or not there are any genetic or covariate effects. When data on quantitative traits are collected from case-control rather than cross-sectional studies, the above formulas are approximately correct if the case-control status is included as a covariate in the linear regression.¹⁵

For making inference on a common odds ratio, one can achieve statistical efficiency that is comparable to that of the proposed approach by splitting overlapping subjects such that the case/control ratios are the same among all studies. For comparing odds ratios among studies, however, splitting overlapping subjects is always less efficient than the proposed approach. As demonstrated in Figure 1 and Figure 2, the results of meta-analysis may depend appreciably on how overlapping subjects are split. In addition, the splitting may need to be redone if new studies are added or cross-disorder comparisons are to be made. Furthermore, splitting control samples requires access to individual participant data, which are often difficult to obtain, and tends to induce biases in the presence of plate effects.

Overlapping subjects may be genotyped multiple times with the same or different GWAS platforms. Some of the NIMH Gejman controls have been genotyped four times, and the WTCCC controls have been genotyped at least twice. For the proposed approach, it is implicitly assumed that each study uses its own genotype calls. For the results shown in Figure 2, we used the genotype values from the CATIE study for the CATIE subjects and the genotype values from the GAIN study for the GAIN subjects. This strategy avoids the arbitrariness in deciding which set of genotypes to use and reduces the biases caused by (differential) measurement errors in case-control comparisons, especially if cases and controls were randomly assigned to genotyping plates.

Appendix

Meta-Analysis of Individual Participant Data

We adopt the notation of the main text. Because the mean of the estimating function U(θ) is 0, the corresponding estimator $\widehat{\mathit{\theta }}$ is consistent for θ. By the multivariate central limit theorem, n^−1/2U(θ) is asymptotically zero-mean normal with covariance matrix

$$B=\lim n^{-1}\left\{\sum _{i=1}^n{U}_i(\theta )U_i{(\theta )}^{\text{T}}+\sum _{i=1}^n\sum _{j=1}^n{\delta }_{ij}{U}_i(\theta )U_j{(\theta )}^{\text{T}}\right\},$$

where the limit is taken as n tends to ∞. It then follows from the Taylor series expansion that $n^{1/2}\left(\widehat{\mathit{\theta }}-\mathit{\theta }\right)$ is asymptotically zero-mean normal with covariance matrix A⁻¹B A⁻¹, where $A=\lim n^{-1}I\left(\mathit{\theta }\right)$. It is easy to show that $\lim n^{-1}{\sum }_{i=1}^n{U}_i\left(\mathit{\theta }\right)U_i{\left(\mathit{\theta }\right)}^{\text{T}}=\lim n^{-1}I\left(\mathit{\theta }\right)$. Thus, $B=\lim n^{-1}\left\{I\left(\mathit{\theta }\right)+D\left(\mathit{\theta }\right)\right\}$. Hence, the asymptotic covariance matrix of $n^{1/2}\left(\widehat{\theta }-\theta \right)$ can be consistently estimated by $n{I}^{-1}\left(\widehat{\mathit{\theta }}\right)\left\{I\left(\widehat{\mathit{\theta }}\right)+D\left(\widehat{\mathit{\theta }}\right)\right\}{I}^{-1}\left(\widehat{\mathit{\theta }}\right)$.

Although the main text of this article was focused on logistic regression models for case-control studies, the above derivations are very general, and the results apply to any phenotypes and any parametric models. The specific expressions for the U_i(θ)s and I(θ) are model dependent.

Meta-Analysis of Summary Results

The original data consist of (Y_ki, X_ki) (i = 1, …, n_k;k = 1, …, K), where Y_ki and X_ki are the disease status and the set of explanatory variables on the ith subject of the kth study. For the kth study, we fit the following logistic regression model:

$$\text{Pr}\left(Y_{ki}=1|X_{ki}\right)=\frac{e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}{1+e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}},$$

where α_k and β_k are the intercept and regression parameters. Denote the collection of α_k and β_k by θ_k. The maximum likelihood estimator of θ_k, denoted by ${\widehat{\theta }}_k$, is the root of the score function

$$U_k\left({\mathit{\theta }}_k\right)=\sum _{i=1}^{n_k}\left(Y_{ki}-\frac{e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}{1+e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}\right){\tilde{X}}_{ki},$$

where $\tilde{X}$ consists of 1 and X. By the maximum likelihood theory, ${\widehat{\mathit{\theta }}}_k$ is approximately normal with mean θ_k and covariance matrix I_k⁻¹(θ_k), where

$$I_k\left({\mathit{\theta }}_k\right)=\sum _{i=1}^{n_k}\frac{e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}{{\left(1+e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}\right)}^2}{\tilde{X}}_{ki}{\tilde{X}}_{ki}^{\text{T}}\text{.}$$

By the Taylor series expansion, ${\widehat{\mathit{\theta }}}_k-{\mathit{\theta }}_k\approx I_k^{-1}\left({\mathit{\theta }}_k\right)U_k\left({\mathit{\theta }}_k\right)$. Thus,

$$\text{Cov}\left({\widehat{\mathit{\theta }}}_k,{\widehat{\mathit{\theta }}}_l\right)\approx I_k^{-1}\left({\mathit{\theta }}_k\right)\text{Cov}\left\{U_k\left({\mathit{\theta }}_k\right),U_l\left({\mathit{\theta }}_l\right)\right\}{I}_l^{-1}\left({\mathit{\theta }}_l\right)\text{.}$$

It is easy to show that

$$\text{Cov}\left\{U_k\left({\mathit{\theta }}_k\right),U_l\left({\mathit{\theta }}_l\right)\right\}\approx \sum _{i=1}^{n_{kl}}\left(Y_{ki}-\frac{e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}{1+e^{{\mathit{\alpha }}_k+{\mathit{\beta }}_k^{\text{T}}{X}_{ki}}}\right)\left(Y_{li}-\frac{e^{{\mathit{\alpha }}_l+{\mathit{\beta }}_l^{\text{T}}{X}_{li}}}{1+e^{{\mathit{\alpha }}_l+{\mathit{\beta }}_l^{\text{T}}{X}_{li}}}\right){\tilde{X}}_{ki}{\tilde{X}}_{li}^{\text{T}},$$

where n_kl denotes the number of subjects who overlap between the kth and lth studies. (Without loss of generality, we arrange the data such that the first n_kl records pertain to the overlapping subjects.) Assume that the disease status is independent of all explanatory variables such that β_k = 0 (k = 1, …, K) and that any subject who appears in more than one study has the same disease status and same values of the explanatory variables across studies such that Y_ki = Y_li and X_ki = X_li for the n_kl overlapping subjects. Then

$$I_k\left({\mathit{\theta }}_k\right)=\frac{n_k{e}^{{\mathit{\alpha }}_k}}{{\left(1+e^{{\mathit{\alpha }}_k}\right)}^2}{n}_k^{-1}\sum _{i=1}^{n_k}{\tilde{X}}_{ki}{\tilde{X}}_{ki}^{\text{T}};$$

therefore,

$$I_k\left({\mathit{\theta }}_k\right)\approx \frac{n_k{e}^{{\mathit{\alpha }}_k}}{{\left(1+e^{{\mathit{\alpha }}_k}\right)}^2}H,$$

where H is the expectation of $\tilde{X}{\tilde{X}}^{\text{T}}$. By similar arguments,

$$\text{Cov}\left\{U_k\left({\mathit{\theta }}_k\right),U_l\left({\mathit{\theta }}_l\right)\right\}\approx \frac{n_{kl0}{e}^{{\mathit{\alpha }}_k+{\mathit{\alpha }}_l}+n_{kl1}}{\left(1+e^{{\mathit{\alpha }}_k}\right)\left(1+e^{{\mathit{\alpha }}_l}\right)}H\text{.}$$

Thus,

$$\text{Cov}\left({\widehat{\mathit{\theta }}}_k,{\widehat{\mathit{\theta }}}_l\right)\approx \left(n_{kl0}+\frac{n_{kl1}}{e^{{\mathit{\alpha }}_k+{\mathit{\alpha }}_l}}\right)\frac{\left(1+e^{{\mathit{\alpha }}_k}\right)\left(1+e^{{\mathit{\alpha }}_l}\right)}{n_k{n}_l}{H}^{-1}\text{.}$$

It follows that the correlation between the same components of ${\widehat{\mathit{\theta }}}_k$ and ${\widehat{\mathit{\theta }}}_l$ is

$$\left(n_{kl0}\sqrt{e^{{\mathit{\alpha }}_k+{\mathit{\alpha }}_l}}+\frac{n_{kl1}}{\sqrt{e^{{\mathit{\alpha }}_k+{\mathit{\alpha }}_l}}}\right)/\sqrt{n_k{n}_l}\text{.}$$

Note that $e^{{\mathit{\alpha }}_k+{\mathit{\alpha }}_l}\approx n_{k1}{n}_{l1}/\left(n_{k0}{n}_{l0}\right)$.

Web Resources

The URLs for data presented herein are as follows:

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for T1D, T2D, RA, and schizophrenia)

• Software implementing the new methods, http://www.bios.unc.edu/∼lin/software/MAOS/