Stereotactic Atlas-Based Depth Electrode Localization in the Human Amygdala

Abstract

Background

The efficacy of stereotactic neurosurgery procedures is critically dependent on the accuracy of the device placement procedure. The first step in this process involves correctly identifying the target location in three-dimensional brain space. In some clinical applications, this targeting process cannot be accomplished using MRI images of gross anatomical structures alone. The amygdala complex is a case in point, in that it consists of multiple histologically defined subnuclei with different functional characteristics.

Methods

In this report, we describe an elastic atlas brain-morphing method that projects amygdala subnuclear anatomical information onto the MRI volumes of individual subjects.

Results

The accuracy of this method was tested in 5 representative subjects using quantitative image-matching analytical techniques. The results demonstrate a high degree of intersubject variability in medial temporal lobe anatomy, and markedly superior anatomical matching performance by the elastic morphing method compared to Affine transformation.

Conclusion

Nonlinear elastic morphing technique provides superior performance on fitting atlas templates to individual brain. The strengths and limitations of this and other atlas morphing methods are discussed in the context of emerging functional neurosurgery applications.

Introduction

Deep brain stimulation (DBS) methods are used by neurosurgeons in a broad range of clinical applications [1]. One critical factor influencing the safety and efficacy of DBS treatment strategies is the ability to precisely localize electrode locations within the brain. A variety of anatomical and physiological mapping strategies have been employed to achieve this objective. The utility and applicability of these different approaches vary depending on what brain region is targeted. Some DBS implantation targets are clearly visible on structural MRI scans and demonstrate little anatomical variability across subjects. In these instances, it may be effective to choose targets directly from the patient's brain images, or use standard brain atlas information with linear adjustments for patient-specific scaling.

Existing localization methods are less well suited for DBS applications where the brain target cannot be identified clearly on MRI and the anatomy of the region varies significantly across subjects. This is the case with the human amygdala, which has become a brain site of interest for new DBS applications [2,3,4], and is also the focus of basic scientific investigations using depth electrodes [5, 6]. It is a large nuclear complex consisting of multiple subnuclei with different anatomical and functional properties. The results of experimental animal studies demonstrate that the effects of electrical stimulation vary depending on what amygdala subnuclei are activated [7,8,9,10]. In humans, these subnuclei cannot be identified using current MRI methods, and the intersubject variability in medial temporal lobe anatomy precludes the direct linear conformal transformation of anatomical information from an amygdala atlas onto a patient's brain images. In this report, we describe an atlas-based nonrigid transformation method that results in the customized transfer of anatomical information on amygdala subnuclei to the MRI volumes of individual subjects. This is a practical method for approximating subnuclear anatomy on the preimplantation MRI volume and to identify where electrodes are located within the amygdala complex after electrode implantation surgery. Although current clinical applications of DBS within the amygdala are limited, this method is well suited to current research protocols and may be useful in future clinical DBS applications specifically directed at modulating amygdala function.

Materials and Methods

This localization method was developed in the context of ongoing basic research investigations carried out in the University of Iowa Human Brain Research Laboratory (HBRL). Research subjects are neurosurgery patients who undergo stereotactic placement of amygdala depth electrodes as part of their evaluation and treatment for medically refractory epilepsy. Informed consent was obtained from all subjects and all HBRL research protocols have been reviewed and approved by the University of Iowa IRB and NIH review panels. The anatomical atlas used with this method provides a detailed map of the boundaries of the amygdala subnuclei, as determined in a single representative brain specimen [11]. With the exception of the first step in the localization process, all analytical procedures were carried out using custom-built software implemented in MATLAB (Mathworks Inc., MA, version 2008a). This software will be available on the HBRL website (under development) and each step in the procedure is described below.

Pre- and Postimplantation Image Acquisition

MRI volumes of the brain are obtained before and after electrode implantation in all subjects. Preimplantation images consist of structural T₁-weighted MRI volumes obtained with 3D magnetization-prepared rapid-acquisition gradient-echo (MP-RAGE) sequences (Siemens TIM Trio 3.0-tesla MRI with 12-channel head array coil, nonoverlapping contiguous coronal scan, 256 × 256 matrix with 1.0 mm slice thickness, 0.781 × 0.781 mm in-plane resolution with averaging of two complete imaging sequences, TE = 3.52 ms, TI = 1,100 ms, Flip angle = 10°). Following surgery, the postimplantation MRI volumes are obtained using the same protocol as the preimplantation study. The MRI volumes are converted so that they have cubic voxel dimensions of 0.781mm using cubic spline interpolation in the following analyses.

Aligning Pre- and Postimplantation MRI Volumes in the Atlas Space

The brain atlas of Mai et al. [11] provides a detailed histological demarcation of the medial temporal lobe structures including subnuclei of the amygdala. The spatial coordinate system used in the atlas, i.e. microscopic coronal plates oriented perpendicular to the anterior commissure (AC) and posterior commissure (PC) line, is based on the Talairach coordinate system with minor modifications. The first task is to align pre- and postimplantation MRI volumes in the atlas coordinate system. Pre- and postimplantation volumes are first coregistered using a rigid mutual information maximization algorithm that comes with Analyze software (version 8.1, AnalyzeDirect, KS). Next, both volumes are spatially aligned in AC-PC reference space using 2 landmark points, namely, the midpoints of the AC and PC by combining translation and rotation in 3 axes. Finally, brain size differences between the atlas brain and the subject's brain are corrected by applying piecewise linear scaling as originally defined in the 1988 Talairach and Tournoux atlas with 6 scaling factors [12]. For this process, users supply 8 landmark points within the preimplantation MRI volume (AC, PC, anterior and posterior borders, right and left borders, superior and inferior borders of the cerebral cortex) to delineate a bounding box. This bounding box is divided into 6 subvolumes as described by Talairach and Tournoux [12], and piecewise linear scaling transformations are applied to each of the subvolumes independently and resampled into the Talairach space. The same piecewise transformation was applied in postimplantation MRI volumes. This is necessary given the substantial interindividual variability of the brain size [13, 14]. Measurements in our subjects demonstrate the variability of brain sizes (table 1). After these processing steps, pre- and postimplantation volumes are in the same reference stereotaxic space as the one used in the atlas. Any point in the patient's brain volume can then be referenced with an x,y,z coordinate. The coordinates of the midpoint of the AC are assigned the values (x, y, z) = (0, 0, 0). In this study, the z-coordinate refers to the dorsoventral dimension andthe y-coordinate refers to the anteroposterior dimension. This is consistent with the nomenclature of plates in the atlas of Mai et al., with negative values along the y-axis being anterior to the AC and negative values along the z-axis being ventral to the AC.

Table 1.

Measurements of the subject's brain size

	Subject ID					Mean ± SD
	153	154	156	162	164	mm
AC-PC	27.3	26.6	25.0	26.6	27.3	26.6 ± 0.9397
Width	125.8	128.9	138.3	135.1	125.0	130.6 ± 5.8487
Length	168.9	167.2	160.2	192.9	162.5	170.3 ± 13.09
Height	110.7	109.4	112.5	114.8	109.4	111.4 ± 2.305

Measurements were done after the AC-PC line alignment, but before Talairach transformation using preimplantation MRI volumes.

Transferring Cytoarchitectural Boundary Information from the Atlas to the Subject Brain

Data from histologic studies of postmortem specimens demonstrate that while there is variability in the absolute volume in the amygdala complex and exact position of the complex relative to other brain structures across human subjects, the basic organizational pattern of subnuclei within the complex remains constant [15, 16]. This internal anatomic consistency within the nuclear complex provides the rationale for using an atlas-based approach to project histologic information from one representative subject onto the other human brains being studied.

Identifying Electrode Locations in Postimplantation Volumes

Depth electrode recording contacts create localized artifacts on the postimplantation imaging set that are readily identified. The center of each artifact is manually selected and a coordinate in the atlas space in the postimplantation volume is assigned for each electrode location. This location information is then transferred to the preimplantation volume in order to demonstrate the electrode locations on brain images that are not degraded by metal artifacts or other postsurgical changes. These high-quality distortion-free images facilitate comparative studies across subjects. The accuracy of this spatial localization transfer process is then assessed manually by inspecting anatomical features adjacent to contact locations in both MRI sets. In situations where the coordinate-based transfer process results in an imperfect anatomical match between two sets of images, manual adjustments are made to achieve the optimal localization match. This manual procedure is required because under some circumstances the coregistration process carried out using the three-dimensional (3D) AC-PC reference space coordinate system is not sufficiently accurate. Postsurgical changes can cause alterations in the exact spatial relationship between the AC-PC line and the brain region of interest.

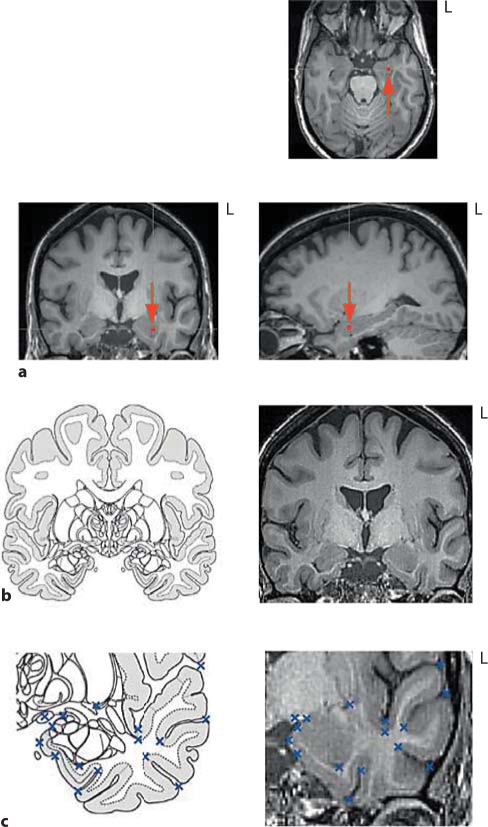
When the final contact locations are assigned to the preimplantation volume, locations can be depicted in a multiplanar image viewer (fig. 1a).

Fig. 1.

Method for transferring post-implantation electrode location information to the preimplantation image volume, and identifying matching control points for the atlas morphing procedure. a After Talairach transformation of both pre- and postimplantation MRI volumes were performed, an electrode location is identified and its coordinate (in this example, x = 25.0, y = 7.0, z = −14.8) is transferred onto the preimplantation MRI volume. Electrode locations are depicted with a dot (arrow). Agreement of the location between post- and preimplantation scans is confirmed using the multiplanar viewer by inspecting the relative position of the electrode location to nearby brain structures. b The atlas plate closest to the corresponding y-coordinate of the electrode contact is selected and paired with the appropriate patient coronal MRI image. c Both the atlas plate and MRI slice are cropped to confine the area of interest to the temporal lobe. Comparable control points are selected using matching anatomical landmarks in the atlas and patient images (shown as × marks).

Selection of Appropriate Microscopic Atlas Plate and Application of an Elastic Morphing

Since the subject's image data set is in the same spatial coordinate system as used in the atlas, and corrections have been made for brain size differences, the y-coordinate values from the patient brain image set can be used to select the coronal sections from the atlas that best match the patient brain coronal sections. Thus the y-value of an electrode contact location will be used to determine which section from the atlas best approximates the coronal brain slice containing that electrode contact.

Because of intersubject variability in medial temporal lobe anatomy, many of the temporal lobe anatomical features that are visible on the paired atlas and patient brain coronal sections match poorly when only simple linear conformal and Affine transformation methods are used. To address this deficiency, we use a more flexible nonlinear atlas-to-patient morphing technique that can manage unknown focal geometric deformations. This elastic deformation approach entails the use of 2D thin-plate spline (TPS) modeling, that is, general-purpose interpolants for labeled point data [17], with regularization parameters [18] (see Appendix). Landmark point-matching TPS modeling has been used for elastic image morphing for various purposes [17,19,20,21,22], and has been shown to perform better with image registration tasks than an optimal Affine transformation which leaves parallel lines parallel [18]. The regularization in the modeling ensures insensitivity to the subtle misplacement in control point selection while keeping flexible local deformation capabilities. Because we are focusing on the amygdala, MRI slices and the corresponding atlas sections are cropped so that they do not contain structures distant from the temporal region. Anatomical feature contrasts of the cropped MRI slices are enhanced using a Laplacian filtering method with a 3 × 3 Laplacian special mask. The registration procedure consists of two iterations of TPS warping. In the first stage, more than 10 control points are marked using side-by-side placement of the two corresponding images. Examples of the anatomical control points include; optic tract, semiannular sulcus, medial margin of uncus, limen insula, inferior boundary of insular sulcus, temporal horn of lateral ventricle, uncal notch, inferior margin of the putamen and collateral sulcus (fig. 1b, c). The resulting warped atlas plates are then overlaid onto the MRI images and control points are again selected from the image sets. A second and final warping procedure is then performed to further refine the anatomical match between the two image sets.

Performance Evaluation by Similarity Measures

We evaluated the performance of our atlas-to-patient coregistration procedure by comparing the results with those obtained using the Affine transformation method. Performances on representative brain sections were objectively determined using three similarity measures; normalized mutual information (NMI) [23,24,25], gradient cross-correlation (GCC) [26, 27] as well as normalized cross-correlation. We performed this evaluation on the coronal sections from all patient data sets having a y-coordinate value of +5.4 mm. This y-value was selected because in all cases this coronal plane traversed a central portion of the amygdala anterior to the hippocampus. The objective measures that were used to quantify and determine the statistical significance of the difference in performance between the two different methods were obtained from image features visible on the MRI. In all 5 patients, the entire amygdala complex appeared as a homogeneous structure on the MRI sections. Therefore, no information regarding subnuclear anatomy could be discerned from these images or used in the quantitive analysis.

Results

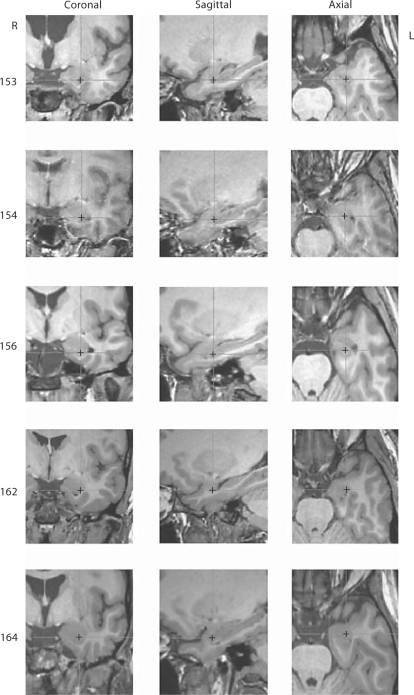
A total of 5 subjects with implanted medial temporal lobe depth electrodes were analyzed. We first sought to gain a qualitative understanding of the degree of intersubject variability in medial temporal lobe anatomy by examining each subject's coronal section having a y-value of 5.4. Additionally, a common test point (x, y, z) = (25.0, 5.4, −17.0) was depicted on each of these sections for the purpose of demonstrating the variable relationships that exist between a specific 3D coordinate and medial temporal lobe anatomy in all three planes (fig. 1). Inspection of the medial temporal lobe anatomy depicted on the representative coronal MRI images revealed significant intersubject variation in the size and shape of brain structures within this area of interest (e.g., medial temporal lobe boundary, size and shape of the inferior horn of lateral ventricle, and contour of the gray-white junction of the amygdala complex) (fig. 2). The magnitude of these differences was such that an Affine transformation of the atlas plate onto the patient coronal MRI sections resulted in clearly visible boundary mismatches in all cases, as depicted in figure 3. In contrast, our nonlinear elastic transformation method resulted in only minor mismatches of some gross anatomical features within the area of interest. The superiority of the elastic deformation method evident from a qualitative review of the images was confirmed to be statistically significant with all three of the quantitative measures that were used (table 2).

Fig. 2.

Image sets demonstrating intersubject variability in temporal lobe anatomy relative to a fixed 3D stereotactic coordinate. Multiplanar views are depicted of the left temporal lobe of 5 patients. In all image sequences, the cross indicates the location of the test point (x = 25, y = 5.4, z = −17.0). Marked variations are observed in the sizes and shapes of the amygdala, uncus, entorhinal cortex and ventricles, as well as the gyral patterns of the temporallobe.

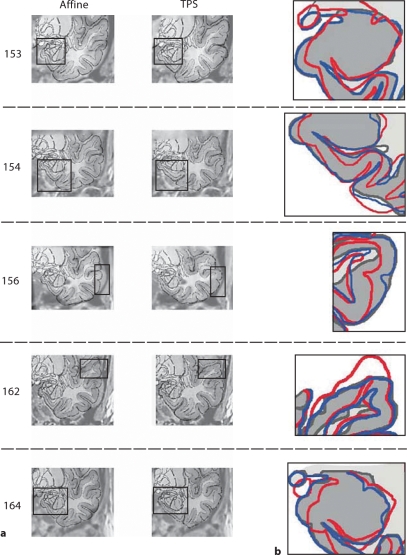
Fig. 3.

Comparison of atlas-to-patient MRI matching performance between the TPS elastic morphing method and the Affine transformation method (y = 5.4 mm). a Atlas features generated from the two different morphing methods are superimposed onto the patient MRI sections. Different regions of the temporal lobe are selected as areas of interest to demonstrate the range of variability observed in these different regions. b Mismatches in the selected areas of interest are graphically displayed using a line-drawing method. The gray matter on the patient's MRI section is shown in a uniform light gray color with darker gray lines demarcating anatomical boundaries and boarders (depicted as MRI in the figure). Morphed atlas features generated using the TPS method are superimposed on the patient-based image using blue lines (Atlas, TPS), and the features obtained using the Affine method are depicted with red lines (Atlas, Affine). The superior performance of the TPS method is reflected in the observation that the pattern of blue lines more closely approximates the patient's anatomy (gray lines) than does the pattern of red lines.

Table 2.

Performance measures of the atlas-to-patient coregistration methods

	Subject ID
	153	154	156	162	164
TPS
NMI	1.1940	1.1836	1.2170	1.2029	1.2556
NCC	0.7716	0.8182	0.7558	0.8424	0.8656
GCC	0.1932	0.1881	0.2155	0.1931	0.2654
Affine
NMI	1.1259	1.1700	1.1887	1.1725	1.2169
NCC	0.6958	0.7803	0.6259	0.6946	0.7761
GCC	0.1385	0.1603	0.0985	0.1661	0.1300

Three similarity measures were computed between the morphed atlas plate and subject's coronal MRI image at z = 5.4 mm. TPS elastic morphing of the atlas template is significantly superior to the Affine transform (normalized mutual information, NMI: p = 0.0166, normalized cross-correlation, NCC: p = 0.0080, and gradient cross-correlation, GCC: p = 0.0333; paired t test). Higher values indicate better fit with the atlas.

Discussion

Neurosurgeons have developed and employed a wide range of anatomical localization methods in order to improve the safety and efficacy of functional neurosurgical procedures. In this report, we describe a method for delineating amygdala subnuclear anatomy using nonlinear nonrigid atlas morphing techniques. This method was developed because borders of amygdala subnuclei cannot be visualized directly from current MRI acquisition techniques and previously described rigid atlas morphing approaches that are effective for some clinical applications are not well suited to the amygdala.

A variety of different atlas morphing methods have been developed for the purpose of transferring anatomical information contained within histologic atlases to the anatomy of specific patients. The most common approaches used, and the method that is incorporated into most current commercially available image guidance systems, involve rigid transformation (linear conformal transformation) of atlas feature. Rigid transformation methods involve translating and/or rotating atlas features in space without altering the shapes and contours of the structures being manipulated. The Affine transformation method is more complex in that the shape of atlas features can be altered to create ‘shear’ images of the area of interest. However, because the Affine alterations are constrained to linear manipulations that are applied to the entire area of interest, this method is incapable of addressing localized irregularities in the match between atlas and patient brain images. Given the individual variability that exists in human brain sizes and shapes [28, 29], nonlinear elastic deformations should in theory be superior to the rigid and Affine transformation [30, 31]. This is also true in terms of interhemispheric variability within a subject. Interhemispheric differences of structural boundary in the temporal lobe can be managed more precisely with nonlinear elastic deformations. In practice, however, the degree of variability of brain anatomy for a specific clinical or research application will influence whether the more computationally intensive elastic morphing methods are desirable or necessary.

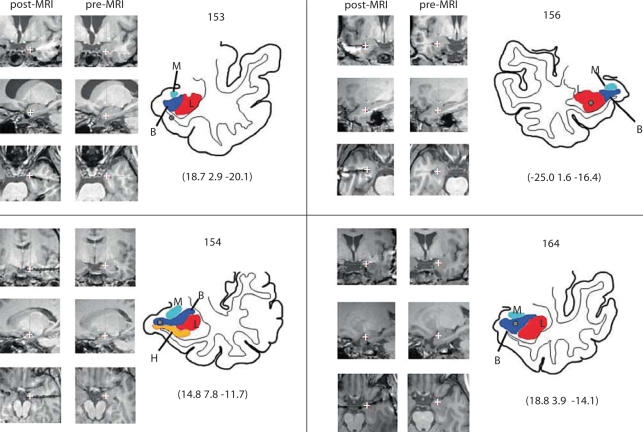
The challenges of atlas morphing are quite different in the amygdala compared to other subcortical structures such as the thalamus. The center point of the amygdala complex is a greater distance from standard midline reference structures (e.g., AC-PC line) and the size and shape of the amygdala appear to be more variable across subjects than the thalamus. The results of the current study objectively demonstrate that when the amygdala is targeted, an elastic deformation method is superior to a nonelastic transformation method such as the Affine transformation. The presence of multiple clearly identifiable anatomical reference features in close proximity to the amygdala make it particularly well suited to the elastic morphing method. Although superior matching of gross anatomical features has been demonstrated, we cannot directly and definitely prove that our approach achieves our primary objective of accurately delineating the subnuclei of the amygdala in individual patients. That could only be definitively proven if histologic data could be collected in our subjects. In the absence of such data, the results of this method represent an approximation of subnuclear boundaries. This atlas morphing method is designed to be used for both right and left amygdala cases, even though the atlas of Mai et al. is based on a left-hemisphere specimen. Whereas differences were noted for other temporal lobe structures such as the superior temporal gyrus, investigators to date have not reported any systematic differences in the gross or microscopic anatomy of the left and right amygdala of humans. It is for this reason that we believe it is acceptable to apply this atlas morphing method to both the left and right amygdala complexes. This is carried out by using a feature of the program that converts the left hemisphere atlas into a mirror image right-hemisphere atlas. This function was used in the right-sided case (subject 156) shown in figure 4.

Fig. 4.

Images demonstrating the sequence of steps used to depict the location of an amygdala electrode contact on post- and preimplantation MRI sections, and on a line drawing of the amygdala. Subnuclear boundaries derived from the atlas morphing method are overlaid on the line drawing. Four representative cases are shown. In each panel, the MRI sections in the left column are postimplantation axial, coronal and saggital images that pass through the center of the electrode contact metal artifact (white crosses). The electrode location information is transferred to the pre-implantation MRI volume and the accuracy of this step is confirmed by comparing the match of anatomical features, in all three reference planes, between the postimplantation (left column) and preimplantation (middle column) MRI sections in the brain region surrounding the contact. The anatomical line drawing is created by manually tracing the features of interest from the preimplantation image set, and projecting the morphed subnuclear atlas features onto the image. The Talairach coordinates for the contact location are reported below each line drawing. L (red in online version) = lateral nucleus, B (blue) = basolateral nucleus, M (lightblue) = medial nucleus of the amygdala, H (yellow) = hippocampus.

Recently, investigators have reported making significant progress in the development of population-based probabilistic human brain atlases that will provide objective, quantitative information regarding the variability of targeted brain structures [15,32,33,34]. This mapping approach has the potential to provide valuable, clinically relevant information when it is applied to the human amygdala in the future.

Other investigators have used MRI-based methods that make use of imaging algorithms that identify differences in cell packing density and connectivity within the thalamus to identify the boundaries of subnuclei [35,36,37]. We have conducted preliminary experiments using a double inversion-recovery MRI sequence which provides superior contrast between white and gray matter [38], and have not been able to identify amygdala subnuclei with this approach. Investigations are currently under way to determine whether these boundaries can be identified using diffusion tensor imaging methods. Additionally, the results of ongoing electrophysiologic studies will be examined for evidence of consistent across-subject correlations between physiologic findings and subnuclear electrode locations defined by this morphing method.

Conclusions

This paper has proposed the use of a histological atlas of the human brain and high-resolution MRI for the localization of implanted depth electrodes within the amygdala. Given large intersubject variability of size and shape of the temporal lobe structures, rigid and global transformation of the atlas shows large mismatch in the coregistration procedure. Using nonlinear TPS elastic morphing of the atlas template, superior coregistration performance could be achieved compared to linear Affine transformation.

Appendix

Thin-Plate Smoothing Spline Image Morphing

Details of the concept and method of TPS have been described elsewhere [17, 39]; therefore, only a brief summary is presented below.

TPS mapping f,given N control points (x_i, y_i) can be defined by the following equation;

$f(x,y)=a_i+a_{x}x+a_{y}y+\sum _{i=1}^N{w}_{i}U\left(\Vert \left(x_i,y_i\right)-\left((x,y)\right)\Vert \right)$

where U(r) = r²logr is the TPS kernel.

This can be solved analytically by least squares under landmark constraints, v = f(x_i, y_i), with positive regularization parameter λ, that results in thin-plate smoothing spline transformation.

$\left[\begin{array}{cc}k+N\lambda I& P\\ P^T& O\end{array}\right]\left[\begin{array}{c}w\\ a\end{array}\right]=\left[\begin{array}{c}v\\ o\end{array}\right]$

where K_ij = U(∣∣(x_i, y_i) – (x, y)∣∣), P_i = [1, x_i, y_i], a is the vector with elements [a₁a_xa_y], O and o are matrices of zeros and I is identity matrix.

If λ is 0, the matching of landmarks is exact. If λ is large (e.g. λ > 0.1), the resulted transformation is almost pure Affine without noticeable local deformation. We used intermediate values of 0.01.

Normalized Mutual Information

Marginal entropies of images A and B [H(A) and H(B)] and joint entropy [H(A,B)] were estimated from a joint histogram of two images with 256 bins.

NMI is defined as:

NMI(A, B) = [H(A) + H(B)]/H(A, B)

NMI does not rely on the pixel values of the images directly but on co-occurrence of the most probable values in the images.

Gradient Cross-Correlation (GCC)

Let Gx and Gy be estimates of first derivatives along the x- and y-directions of an image. These can be obtained by convolving images with Sobel operators (and its transpose) for each direction. Normalized cross-correlations between gradients (Gx and Gy) of two images (atlas plate and subject's MRI) are computed for each direction. GCC is the average of the normalized cross-correlations for each direction, and is sensitive to edge information. Maximum values of GCC were reported.