Revisiting the planarity of nucleic acid bases: Pyramidilization at glycosidic nitrogen in purine bases is modulated by orientation of glycosidic torsion

Abstract

We describe a novel, fundamental property of nucleobase structure, namely, pyramidilization at the N1/9 sites of purine and pyrimidine bases. Through a combined analyses of ultra-high-resolution X-ray structures of both oligonucleotides extracted from the Nucleic Acid Database and isolated nucleotides and nucleosides from the Cambridge Structural Database, together with a series of quantum chemical calculations, molecular dynamics (MD) simulations, and published solution nuclear magnetic resonance (NMR) data, we show that pyramidilization at the glycosidic nitrogen is an intrinsic property. This property is common to isolated nucleosides and nucleotides as well as oligonucleotides—it is also common to both RNA and DNA. Our analysis suggests that pyramidilization at N1/9 sites depends in a systematic way on the local structure of the nucleoside. Of note, the pyramidilization undergoes stereo-inversion upon reorientation of the glycosidic bond. The extent of the pyramidilization is further modulated by the conformation of the sugar ring. The observed pyramidilization is more pronounced for purine bases, while for pyrimidines it is negligible. We discuss how the assumption of nucleic acid base planarity can lead to systematic errors in determining the conformation of nucleotides from experimental data and from unconstrained MD simulations.

INTRODUCTION

From a structural point of view, the nucleic acid (NA) bases are usually regarded as planar and conformationally rigid units (1–3). This consideration comes from both ab initio calculations (4,5) and high-resolution X-ray and neutron diffraction studies on isolated bases (6–9). Although minute deformations in the local geometries of the bases have been experimentally observed, they have been considered to be insignificantly small and presumably equally distributed around mean values corresponding to planar geometry (8). As such, the observed deviations from planarity have been considered to be the result of experimental uncertainty. The only exception is the partial pyramidalization of the nucleobase amino groups, which was rather extensively studied in the past (10–12). In the past two decades, the idea of NA base rigidity and planar geometry has been generally accepted and implicitly merged into the schemes for both low-resolution X-ray and nuclear magnetic resonance (NMR) data interpretations, first via parameterization of the force field in the restrained molecular dynamics (rMD) simulation used for structure calculation (9), and second via the concept of the base and base-pair planarity restraints (13–23). The assumption of rigid, planar bases is also reflected in the direct interpretational schemes for the three-bond scalar coupling (³J) across the glycosidic bond (24,25), residual dipolar couplings (RDCs) (26) and auto- and cross-correlated relaxation rates (27–30). Recent quantum chemical (QM) calculations, however, suggest that all NA bases are highly flexible molecules and possess a nonplanar effective conformation (31–38). Nonetheless, the direct experimental evidence for NA base nonplanarity has been missing.

In 2000, Sklenar’s group noticed that the geometries of bases in crystal structures of DNA oligonucleotides deviated from planarity and that this property could be used to determine their relative orientations using RDCs (39). At that time, however, it was not obvious whether the observed deviations from planarity were real, i.e. resulting from intrinsic, real factors such as torsion angle strain in the five- and six-membered rings of NA bases, or an artifact coming from experimental uncertainty, low resolution, and/or the force field used in the course of structure refinement. More recently, indications of partial, intrinsic pyramidalization at N9 sites in purine (guanosine) bases have been observed during re-parameterization of the Karplus equation relating the three-bond, scalar coupling between C8 and H1′ nuclei (³J_C8-H1′) to the orientation of the glycosidic bond (χ) in DNA using both experimental (40) and theoretical data (41,42). The existence of systematic deviations from planar geometry in the 2′-deoxynucleotides has been challenged using the test of internal consistency of RDCs (26). The internal consistency test carried out for the RDCs measured for the 2′-deoxypyrimidines in the d(GCGAAGC) DNA hairpin indicated that RDCs were consistent with their planar geometries. However, for 2′-deoxypurines, the internal consistency, which presumes the planar base geometries, was severely broken when ²D(N7-H8) and ²D(N9-H8) were incorporated into the analysis (26). Altogether, these NMR experimental observations pointed out the possibility of intrinsic deviation from idealized, planar geometry in the NA bases, namely at N9 sites in 2′-deoxypurines.

As will be discussed in detail, the deviations from idealized, planar geometry of nucleobases have complex consequences and implications for interpretation of NMR and crystallographic data, as well as for possible improvement of the force fields currently used in the MD simulation of NAs. To address the issue of the existence of systematic deviations from idealized, planar geometry at N1/9 sites of NA bases, we performed an analysis of crystal structures of poly-nucleotides solved at atomic resolution (<1 Å) from the Nucleic Acid Database (NDB) (43) and ultra-high-resolution nucleoside and nucleotide structures deposited in the Cambridge Structural Database (CSD) (44). To gain detailed knowledge on the dependence of the geometry at the N1/9 sites on the local structure of nucleosides, i.e. glycosidic torsion angle and sugar pucker, we performed a series of QM calculations on 2′-deoxyadenosine and 2′-deoxycytidine. To assess the influence of the force field on the geometry at N1/9 sites, we further compared the solid state data obtained from ultra-high-resolution crystal structures with those extracted from 50 ns and 100 ns unrestrained molecular dynamics (MD) simulations of the bimolecular antiparallel d(G₄T₄G₄)₂ quadruplex structure and the d[GC(TCAG)₃TCGC].d[GCGA(CTGA)₃GC] duplex form, respectively.

MATERIAL AND METHODS

Analysis of crystallographic data

The NDB database (43) was searched for DNA oligonucleotide crystal structures having a resolution of 1.0 Å or better and R-values <0.2. The resolution, R-factors and NDB accession codes of the selected structures are listed in the Supplementary Data (Table S1). The CSD database (44) was searched for high-resolution structures of mononucleosides and mononucleotides using the program ConQuest (45). The sampling criteria were established based on both chemical and crystallographic considerations. Crystal structures containing transition metals were excluded from analysis. Only crystal structures with R-factor ≤0.06 were included in the analysis. The CSD accession codes along with the R-factors for the selected structures are listed in the Supplementary Data (Table S2).

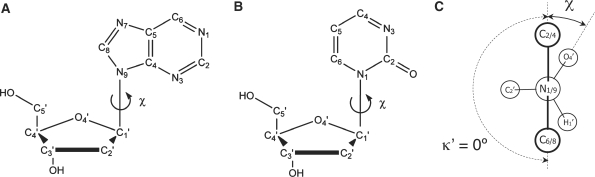
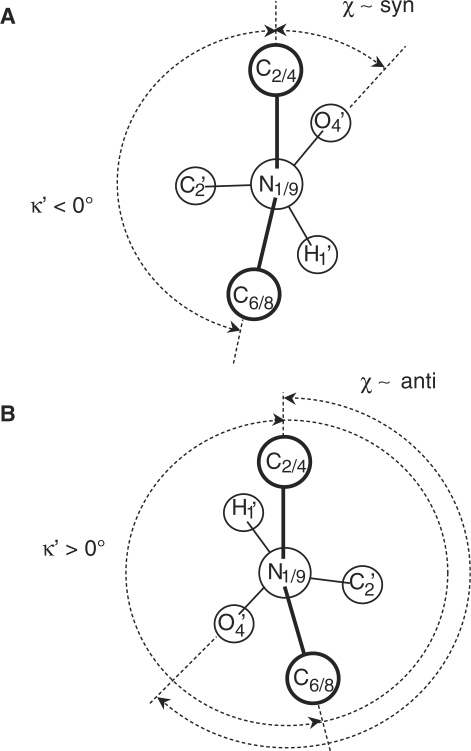
Deviations from planar geometry at the N1/9 sites were described using the improper torsion angle κ′, defined as κ′ = κ – 180°, where κ is the angle between the C2/4-N1/9-C1′ and N1/9-C1′-C6/8 planes in pyrimidine/purine NA bases, respectively (Figure 1). Currently used models for the hetero-aromatic NA bases assume that the κ′ amplitudes are normally distributed around 0° due to thermal motions of the atoms.

Figure 1.

Schematic structure of purine (A) and pyrimidine (B) nucleosides. Carbon and nitrogen atoms are labeled according to IUPAC nomenclature (75). The glycosidic torsion angle χ is defined by atoms O4′-C1′-N9-C4 and O4′-C1′-N1-C2 in purines and pyrimidines, respectively. There are two energetically favored regions of χ, syn and anti. In agreement with comparative studies of crystallographic data, the anti region is defined as 180° < χ < 280° and the syn region as 50° < χ < 80° (74). (C) Newman projection of the glycosidic torsion angle along the N1/9-C1′ axis. In idealized, planar geometries of purine and pyrimidine bases, the improper torsion κ′, defined as (C2-N1-C1′-C6)-180° in pyrimidines and (C4-N9-C1′-C8)-180° in purines and used as a descriptor of deviation from idealized structure within this study, equals 0°.

Glycosidic torsion angles (χ) (for definition see Figure 1) and κ angles were extracted from the crystal structures using the program NIH-XPLOR (46). The extracted geometrical parameters were characterized and compared using several statistical parameters: minimum [min(x)], maximum [max(x)], and median [med(x)] values. The mean [mean(x)] and standard deviation of the mean [stdev(x)] were estimates based on a normalized fit to the data using the program MATLAB (MathWorks, Inc.). Series of statistical tests were used to compare the mean, variance, and distribution of two different samples. The normality of the sample distributions was examined with the two-sided Lilliefor’s test as implemented in MATLAB. The modified Student’s t-test, as incorporated in the program Origin (OriginLab, Corp., USA), was employed to compare the means of the calculated magnitudes of the geometry parameters of the sample sets and also to determine whether two subgroups of structural parameters form separate classes.

MD simulations

The d[GC(TCAG)₃TCGC].d[GCGA(CTGA)₃GC] duplex starting structure was constructed in the standard B-like conformation using the Nucgen module of AMBER9. The starting structure of the bimolecular antiparallel d(G₄T₄G₄)₂ quadruplex was based on the X-ray structure (47). Both systems were embedded in octahedral water boxes using TIP3P (quadruplex) and SPC/E (duplex) water models. The quadruplex system was neutralized by addition of standard Na⁺ ions, which are also present in the central channel. The duplex system was simulated in the excess salt solution of 0.15 M KCl using Dang parameters (48) for K⁺ and Cl^– ions. MD simulations were performed with the Sander module of AMBER9. All simulations were carried out with parmbsc0 (49). The Particle Mesh Ewald (PME) method (50) was used for a correct treatment of electrostatic interactions. All simulations were run with the SHAKE algorithm (51) (with a tolerance of 0.0005 Å) to constrain covalent bonds involving hydrogens, with periodic boundary conditions, a 2-fs time step, and a temperature of 300 K (Berendsen temperature coupling algorithm with time constant of 0.2 ps) (52). Standard equilibration and production procedures were applied. The length of the MD simulations was 100 ns and 50 ns for the duplex and quadruplex systems, respectively. Analyses of resulting trajectories were performed with the Ptraj module.

QM calculations

The geometries of 2′-deoxyadenosine (dAde) and 2′-deoxycytidine (dCyt) were gradient optimized with the B3LYP exchange-correlation functional (53,54) and the 6-31G(d,p) atomic basis set. In the initial geometry optimization, the χ torsion angle was estimated to be close to either the syn or the anti minimum (the anti region was defined as 180° < χ < 280° and syn as 50° < χ < 80 °), and the sugar was adjusted to either C3′-endo (pseudo-rotation angle P (55) set to ∼20°) or C2′-endo (P about 160°). An unconstrained geometry optimization was then performed for each nucleoside. Starting from the optimized nucleosides with either the C2′- or the C3′-endo sugar pucker, a grid point geometry optimization of the nucleosides was carried out roughly varying the χ torsion angle by ∼30° in the interval 0°–360°. All calculations were performed with the Gaussian G03 program (56). For details on calculation procedure see (29,57)

RESULTS

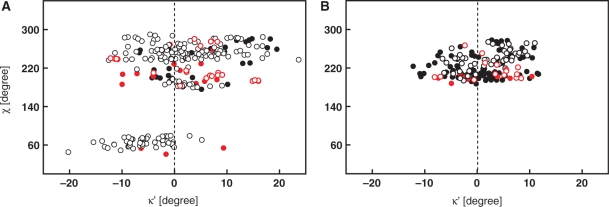
A total of 35 DNA and 23 RNA crystal structures were drawn from the NDB database based on the selection criteria. As many of the crystal structures contained more than one molecule in the asymmetric unit, the search yielded a total of 220 2′-deoxyguanosine, 65 guanosine, 140 2′-deoxyadenosine, 65 adenosine, 56 2′-deoxycytidine, 65 cytidine, 43 2′-deoxythymidine and 65 uridine ribonucleotides. The κ′ and the glycosidic torsion angle χ were extracted from the selected structures. Although the histogram for the κ′ angle in purines appeared to be unimodal (data not shown), the statistical analysis revealed significant differences between the mean values and variances of the κ′ angle distributions in syn and anti regions. The scattergrams in Figure 2 show mutual correlation of the improper torsion angles κ′ and the glycosidic torsion angles χ. Statistical analysis of the data on syn purines demonstrated that the population of the κ′ angles follows a normal distribution at 5% significance level with a mean value of –5.6°. In anti purines, the κ′ angle values follow a normal distribution centered at 3.1°. For anti purines, the scattergram further indicated two distinct sets of κ′ torsion angles (Figure 2A). The first lies in the low-anti region of χ (∼200°), the typical region for A- and Z-DNA or RNA. The second one lies in the high-anti region of χ (∼250°), typical for B-DNA like structures. In the low-anti region, 160° < χ < 230°, the κ′ torsion values were normally distributed about the mean value of +1.2°. In the high-anti region, 230° < χ < 270°, the κ′ values were found to be normally distributed about the mean value of +3.1°. Although the frequency distributions for the high-anti and low-anti subsets appeared to be distinct, at the 5% level of significance, the means of these samples were indistinguishable according to the two-sided Lilliefor’s test.

Figure 2.

Scattergrams of κ′ improper angles in the purine (A) and pyrimidine (B) nucleotides extracted from ultra-high-resolution structures of both DNA and RNA oligonucleotides deposited in the NDB versus glycosidic torsion angle χ. Black filled circles stand for 2′-deoxyadenosine (A) and 2′-deoxycytidine (B). Black open circles denote 2′-deoxyguanosine (A) and 2′-deoxythymidine (B). In an analogous way, the red filled and open circles stand for guanosine and adenosine residues in (A) and for cytidine and uridine residues in (B).

In contrast to purines, no data matching selection criteria on the syn pyrimidines are available in the NDB databases. In the anti pyrimidines, the κ′ angles followed a normal distribution at the 5% level of significance with the mean centered at 0.9°. The statistical descriptors of κ′ as extracted from the NDB are summarized in Table 1.

Table 1.

Statistics of κ′ in purine and pyrimidine bases derived from X-ray structures of RNA/DNA oligonucleotides deposited in the Nucleic Acid Database (NDB) and from purine (pu) and pyrimidine (py) (deoxy)-ribonuclesides/(deoxy)- ribonucleotides deposited in the Cambridge Structural Database (CSD)

	C2/4-N1/9-C1′-C6/8-180 (κ′) (deg)
	Base type	χ	No. of points	Min.	Max.	Median	Mean (SD)	P-vala
NDB	pu	syn	54	−20.2	9.3	−6.0	−5.4 (5.4)	0.342
		anti	208	−12.6	23.7	2.3	3.1 (7.1)	0.267
	py	syn	–	–	–	–	–	–
		anti	183	−12.2	11.7	0.3	0.91 (5.0)	0.223
CSD	pu	syn	29	−20.5	13.7	−2.6	−3.6 (7.2)	0.672
		anti	97	−13.2	18.2	2.2	2.1 (6.5)	0.225
	py	syn*	10	−8.7	6.4	−2.4	−2.6 (5.1)	0.397
		anti	268	−8.2	20.3	0.9	0.9 (5.3)	0.127

^aP-value for the Lilliefor’s statistic when the means were estimated from the sample (for details cf. MATLAB, MathWorks, USA).

*Insufficient amount of available data for performing reliable statistical analysis.

Mean and standard deviations (SD) were estimates based on a normalized fit to the data.

Minimum (min), maximum (max) and median were calculated from the data set with extreme values excluded from the analysis.

In agreement with comparative studies of crystallographic data, the anti region was defined as 180° < χ < 280° and the syn region as 50° < χ < 80° (74).

For distribution histograms of the κ′ in purine and pyrimidine bases derived from X-ray structures of RNA/DNA oligonucleotides deposited in the NDB and from purine and pyrimidine (deoxy)- ribonuclesides/(deoxy)-ribonucleotides deposited in the CSD see Supplementary Data, Figure S1.

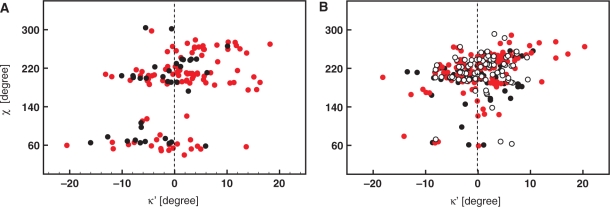
To allow assessment of the effect of secondary structure and the effect of overall NA topology on the local geometry at N1/9, we complemented the analysis on oligonucleotides with an analogous analysis performed on isolated nucleosides and nucleotides extracted from the CSD database. Importantly, the structures selected from CSD were mostly refined without any interference from empirical force fields contrary to the NDB data. Therefore, the comparison of NDB and CSD results allows in principle an estimate of the influence of the force field on nonplanarity at the N1/9 sites. The search in the CSD database yielded a total of 36 (2′-deoxy)guanosine, 99 (2′-deoxy)adenosine, 74 (2′-deoxy)cytidine, 139 (2′-deoxy)thymidine and 77 uridine nucleosides/nucleotides. Figure 3A shows scattergrams in which the improper torsion angles κ′ for purine residues are plotted against the glycosidic torsion angle χ. In the anti region, the κ′ values follow a normal distribution at the 5% significance level with a mean of +2.1°. In the syn region, the normally distributed κ′ values of purine residues are centered at −3.6°. In contrast to the NDB, the CSD also contains information on syn pyrimidines. Unfortunately, the relatively small number of syn pyrimidines (10) found in the CSD did not allow reliable statistical analysis. In the anti region, the κ′ values of the pyrimidines follow a normal distribution with a mean value of +0.9° (Figure 3B). The statistical descriptors of κ′ as extracted from the CSD are summarized in Table 1.

Figure 3.

Scattergrams showing improper torsion κ′ as a function of glycosidic torsion angle χ in purine (A) and pyrimidine (B) nucleosides/nucleotides deposited in CSD. Black filled circles stand for 2′-deoxyadenosine (A) and 2′-deoxycytidine (B). Black open circles denote 2′-deoxyguanosine (A) and 2′-deoxythymidine (B). In an analogous way, the red filled and open circles stand for guanosine and adenosine residues in (A) and for cytidine and uridine residues in (B).

Altogether, the analysis of the X-ray data revealed pyramidalization at the N1/9 sites of NA bases. The magnitudes of pyramidalization as extracted from ultra-high-resolution structures of oligonucleotides from the NDB quantitatively agree with the magnitudes extracted from ultra-high-resolution structures of isolated nucleosides and nucleotides drawn from the CSD. Both NDB and CSD data show inversion of pyramidalization at N1/9 sites upon re-orientation of the glycosidic bond from the syn to the anti region of χ.

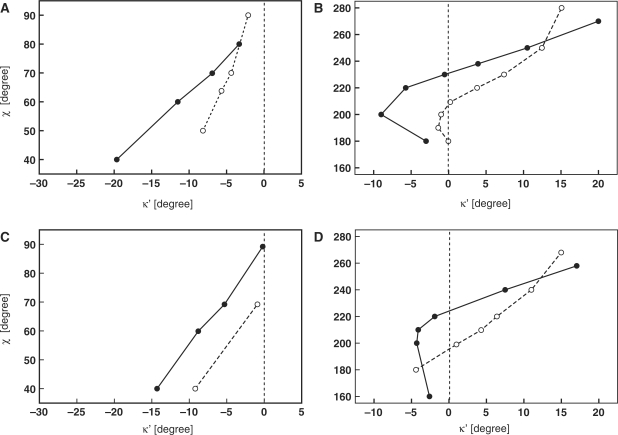
To gain a detailed picture of how the improper torsion κ′ depends on the local geometry of a nucleoside, we performed a series of QM calculations. The dependence of κ′ on the χ torsion was calculated for both the 2′-deoxyadenosine and the 2′-deoxycytidine with the sugar puckering in the C2′-endo and C3′-endo conformations (Figure 4). The QM calculations suggest that the deviations from planar geometry at N9 depend on the glycosidic torsion angle and the sugar ring conformation. Over the entire syn region, the values of the κ angle were always smaller than 180°, regardless of the sugar pucker. The QM calculations predict larger deviations from planarity for the syn purines with the C3′-endo sugar pucker than for those having the C2′-endo sugar pucker. In the anti region, the situation is more complicated. According to the QM calculations, pronounced deviations from planarity at N9 corresponding to κ angles larger than 180° might be expected in B-DNA like structures, i.e. for purines with the C2′-endo sugar conformation with 240° ≤ χ ≤ 270°. In A-DNA/RNA like structures, i.e. for purine bases where 180° ≤ χ ≤ 230° and with the C3′-endo sugar conformation, the QM calculations indicated only minute deviations from planarity (0° < |κ′| < 1.5°). However, compared to the high-anti region of χ, the QM calculations predicted κ′ angles with opposite sign in the low-anti region.

Figure 4.

Calculated dependence of the κ′ angle on glycosidic torsion angle and sugar pucker for syn (A) and anti (B) 2′-deoxyadenosine and for syn (C) and anti (D) 2′-deoxycytidine. Solid and dashed lines correspond to calculated dependencies for C2′-endo and C3′-endo nucleosides, respectively.

MD predicts inverse pyramidalization at N9 as compared to X-ray and QM data

Even ultra-high-resolution X-ray structures in the NDB might be biased by the force field parameterization used during structure refinement. As such, the observed pyramidalization at the N1/9 nitrogen could simply be an artifact from the force field used for refining the structure from low X-ray data rather than a real structural deformation. To verify how Cornell’s force field (49,57), one of the most widely used force fields both for structure simulations of NAs and for restrained MD refinement of NAs from both NMR and X-ray data (22,23), treats the planarity of nucleobases at the N1/9 sites, we have analyzed 100 ns and 50 ns of unrestrained MD trajectories calculated for the DNA duplex and the quadruplex, in explicit solvent. The κ′ angles extracted from unrestrained MD simulations of the DNA duplex and the quadruplex are given in Table 2. In all MD simulations, χ and κ′ angles followed a normal distribution at 5% significance level. Along the 50-ns MD trajectory of the DNA quadruplex, the κ′ angles in the anti purines with C2′-endo sugars were distributed around the mean value of −3.4°. In the syn purines with C2′-endo sugars, the κ′ angles were found to have an inverse pyramidalization at N9 with κ′ being centered at +2.5°.

Table 2.

Comparison of κ′ angles for purine (pu) and pyrimidine (py) bases as determined by statistical analysis of crystallographic data (NDB and CSD), quantum chemical calculations (QM) and 100-ns unrestrained molecular dynamics simulation of d[GC(TCAG)₃TCGC].d[GCGA(CTGA)₃GC] (MD^duplex) and d(G₄T₄G₄)₂ (MD^quadruplex)

Base type	χ	C2/4-N1/9-C1′-C6/8 - 180 (κ′) (deg)
		CSDa	NDBb	QM	cMDduplex	dMDquadruplex
Pu	syn	−3.6 ± 7.2	−5.4 ± 5.4	−8.0e	n.a.	2.5 ± 9.5
	anti	2.1 ± 6.5	3.1 ± 7.1	8.8f	−3.3 ± 10.2	−3.4 ± 9.4
Py	syn	−2.6 ± 5.1	n.a.	−3.8g	n.a.	n.a.
	anti	0.9 ± 5.3	0.91 ± 5.0	8.5h	0.9 ± 8.2	n.a.

^aMean values for torsion angle χ in purine and pyrimidine bases were 62.3° and 62.5° in syn and 209° and 222.5° in anti region, respectively.

^bMean values for torsion angle χ in purine and pyrimidine bases were 65.3° and n.a. in syn and 249.5° and 213.5° in anti region, respectively.

^cMean values for torsion angle χ in anti purine and pyrimidine nucleotides were 253.0° and 241.4°, respectively.

^dMean values for torsion angle χ in syn and anti purines were 52.0° and 246.9°, respectively.

^eFor χ = 52.0°, C3′-endo sugar conformation.

^fFor χ = 246.9°, C2′-endo sugar conformation.

^gFor χ = 60.0°, C3′-endo sugar conformation.

^hFor χ = 243.0°, C2′-endo sugar conformation.

The 100-ns unrestrained MD simulation of the DNA duplex provided results consistent with the MD simulation of the quadruplex (Table 2), suggesting that the observed deviations of nucleobases from planarity are independent of the DNA topology. In anti 2′-deoxypyrimidines with C2′-endo sugars, the κ′ angles were equally distributed around +0.9°. In anti purine bases with C2′-endo sugars, the MD simulation predicted the κ′ angle to be centered on –3.3°. Although Cornell’s force field generated pyramidalization of glycosidic nitrogens, which is compatible with experimental data, the predicted pyramidalization is of opposite sign compared to that observed in the X-ray structures and/or predicted by QM calculations.

DISCUSSION

To gain information on the geometry at the glycosidic nitrogen N1/9 in purine and pyrimidine nucleosides, we performed statistical analysis on ultra-high-resolution structures of both DNA and RNA oligonucleotides selected from the NDB. Statistical analysis of the crystallographic data revealed that in the oligonucleotides, the NA bases possess effective nonplanar geometry at N1/9, indicating partial, intrinsic pyramidalization of the glycosidic nitrogen. In addition, the data indicate that reorientation of the glycosidic torsion angle from the syn to the anti region is correlated with the stereo-inversion of the pyramidalization at N1/9 sites (Figure 5). One may ask whether the observed deformation from idealized, planar geometry is an intrinsic property of the nucleoside or whether it is a numerical artifact depending on actual parameterization of the force field employed during structure refinement. To answer this question, we complemented the analysis of the X-ray structural data from the NDB with the more accurate data on isolated nucleosides and nucleotides from the CSD. The structures were selected from the CSD because they were mostly refined without any or with only minute restraints or constraints compared to the NDB data. In addition, the CSD data for isolated nucleosides/nucleotides allowed assessment of the effect of secondary structure and overall NA topology on the local geometry at N1/9. The statistical analysis of the mononucleoside and mononucleotide structures selected from CSD almost quantitatively agrees with all the trends calculated for the data from the NDB database, namely the pyramidalization of N1/9 sites and the stereo-inversion of the pyramidal configuration upon re-orientation of the glycosidic bond. Comparison of the NDB and the CSD data suggests that the stereo-inversion effect originates from intrinsic sources and is imposed neither by the force field nor by the secondary NA structure (Table 2). The analysis of CSD structures indicated that the pyramidalization at N1 in pyrimidines was less pronounced than the pyramidalization at N9 in purines. The QM calculations indicated that structural deformations at N1/9 sites depend not only on the orientation of the glycosidic bond, but also on the conformation of the sugar ring. It follows that different representative geometries at N9 might be expected for, e.g. A-, B-, or Z-DNA-like structures. Strikingly, the geometries obtained with unrestrained MD simulation showed pyramidalization at N1/9 sites despite the fact that standard geometries in the force field are planar (8,9). However, while the absolute magnitudes of deformation indicated by the MD simulation were fully consistent both with the statistical analysis of crystallographic data and with QM calculations, the MD simulation predicted inverse pyramidalization at N9 sites. This finding points most probably to the inappropriate parameterization of Cornell’s force field and suggests that in the course of structure refinement, this force field might be in conflict with experimental data relating to nucleobase geometries.

Figure 5.

Newman projection of the glycosidic torsion angle along the N1/9-C1′ axis showing representative κ improper torsion angles in syn (A) and anti (B) regions, respectively.

From the physical–chemical point of view, the finding of the pyramidalization of the glycosidic nitrogen in hetero-aromatic ring is not surprising. It has been known for quite a time that (hyper)-aromaticity can be maintained even in systems deviating profoundly from planarity (58–62). QM calculations suggest that NA bases possess a notable degree of conformational flexibility despite their aromatic character (32–37). The transition of the heterocycle from a planar equilibrium geometry to a nonplanar structure with an endocyclic torsion angle of ±20° results in an energy increase of <2.8 kcal/mol (34). In analogy to [n](2,7) pyrenophanes (60), one could regard pyramidalization of the glycosidic nitrogen as a result of the interplay between the tendency of the five/six-membered rings of NA bases to gain stability via pi-electron delocalization, requiring planar arrangement, and counteracting forces involving mechanical stress in the form of angular strain.

The pyramidalization of the glycosidic nitrogen represents very fundamental structural property of NA bases. In that respect, our findings of systematic deviations from planar geometry at N1/9 sites, as a function of the local geometry of a nucleoside, directly points to holes in several schemes for interpretation of experimental X-ray and NMR data on NA. The largest impact of these findings can most probably be expected to be in regard to the schemes used in NA structure determination using NMR spectroscopy. The assumption of planarity at the N1/9 sites is directly reflected in interpretation of the ³J_C6/8–H6/8, three-bond scalar couplings assigned to the glycosidic bond orientation (24,25). Deviation from planar geometry at the N1/9 site directly modulates phase shift of the respective Karplus parameterizations. Our results indicate that the phase shift is not constant over the whole χ range, but rather depends on both χ and sugar pucker. Statistical analysis of X-ray data suggests that the currently established parameterizations for ³J_C8–H8 couplings, which assume a planar geometry of purine bases, overestimate the χ torsions on average by about −5.5° and +3.5° in syn and anti regions, respectively (Table 2). This conclusion is supported by the fact that incorporating deformations at N1/9 sites results in improved agreement between experimental ³J_C8–H8 couplings and those back-predicted based on corrected parameterization (Z.Vokacova et al., in preparation). The re-parameterization of the Karplus equation for three-bond scalar coupling constants across the glycosidic bond, accounting for deformations at N1/9 sites and motional averaging by κ′, will be published elsewhere (Z.Vokacova et al., in preparation). It is noteworthy that the estimated error in χ due to the varying phase shift in respective Karplus parameterizations is comparable to the typical error (∼0.15 Hz) due to experimental uncertainty in determination of ³J_C8–H8 (40).

Identical corrections to those proposed for the ³J_C6/8–H1′ couplings may be required for interpretation of the cross-correlated rates between N1/9 chemical shift anisotropy and C6/8-H1′dipole–dipole interaction (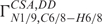) (27). 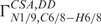values are typically evaluated in terms of the conformation of the glycosidic torsion angle using Karplus-like parameterizations (27,29). Again, the established parameterization strictly relies on the assumption of planar, idealized geometry at N1/9 sites. An estimated error due to pyramidalization at the N9 site for determination of χ torsion with the 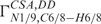using the established parameterizations (27) is again comparable to that coming from uncertainty of the cross-correlated relaxation rate measurements.

The finding of systematic deviations from planarity at N9 sites of purine bases also has consequences for the evaluation of RDCs measured in NA bases. During refinement of NA structure using RDC data, experimentalists often observe conflicts between covalent geometry imposed by the force field and experimental RDC data via notable deformations in bond length as well as bond and improper torsion angles in the resulting NA structure (63,64). As a consequence, artificially high force constants preserving the expected geometry usually have to be applied in order to prevent unreliable deformations of the covalent structure in the course of NA structure refinement (63–68). These conflicts point to either inconsistency between experimental RDC data and force fields or inconsistency within RDC data. To avoid problems connected with inconsistency of RDC data, Zidek et al. (26) proposed an internal consistency test allowing exclusion of incompatible RDC data prior to structure calculation. The test presupposes that only three frequencies corresponding to the second-rank tensorial interactions (such as RDC, anisotropic chemical shielding and quadrupolar interaction) can be measured independently in a rigid, planar NA base. Additional frequencies can be directly predicted, as they are linear combinations of independent frequencies assigned to the three in-plane dipoles. The internal consistency test carried out in the d(GCGAAGC) DNA hairpin indicated the RDCs for cytosines being consistent with their planar geometries. However, for 2′-deoxypurines, the internal consistency was severely broken when ²D_N7–H8 and ²D_N9–H8 were involved in the analysis (26). One of the plausible explanations is that the observed inconsistencies resulted from underestimation of some experimental errors in the ²D_N7/9–H8 data. Another explanation, which is consistent with our findings, is that the inconsistencies reflect a faulty definition of the imidazole geometry in purines, namely, the out-of-plane deviation of the H8-N7/9 interaction vectors.

Besides direct interpretational schemes for NMR observables given above, one should be also aware of potential problems arising from the use of planarity restraints imposed on NA bases in the course of structure refinement using NMR data. The nonexperimental planarity restraints, including restraining of the improper torsion κ′, are usually used together with experimental data for NA structure calculation to prevent undesirable deformations in the covalent structure of NA. Paradoxically, the observation of systematic deviations from planarity at N1/9 sites almost justifies the use of planarity restraints when using Cornell’s force field for NA structure determination. Considering that unrestrained MD simulation provides pyramidalization at N9 of opposite chirality than in the experiment, the planarity restraints might diminish potential conflicts between experimental data and the force field.

Statistical analysis of X-ray data showed that in the course of refining a model, crystallographers are confronted with what is apparently a much larger than expected deviation from planarity in an isolated NA base. The question is asked whether such an apparent anomaly is possible. Here, we showed that substantial deviation can be tolerated, with a standard deviation for the κ angle of up to 7° around the mean value, which depends on base type and orientation of the glycosidic torsion angle.

As stated above, the κ angle reflects an important and frequently used stereochemical restraint, the base planarity restraint, applied in the course of NMR and low-resolution crystal structure determination. Considering in general the data presented here, the single target value used in current refinement programs should be regarded as a rather crude simplification, which does not match with really preferred values. This suggests that the planarity of bases during rMD simulation should not be tightly restrained to the predefined values used in appropriately parameterized force fields. Analogous findings of basic stereochemical constraints, such as peptide bond planarity or bond angles, violating ideal values in proteins have recently attracted a great deal of attention and evoked discussion of possible revision of basic stereochemical restraints (69–73). As the outcome of vigorous discussion, Karplus et al. (74) has proposed that the “context dependence of stereochemistry can be transformed from frustrating reality that limits the accuracy of protein modeling to a feature that can instead increase modeling accuracy.” At least in the protein community, there is a tendency to move beyond a ‘single target value’ paradigm to an ‘ideal geometry function’ paradigm in which each restraint target value varies depending on the local geometry. Currently, there are attempts to develop a set of empirical conformation dependent ‘ideal geometry functions’ for backbone bond angles and lengths that can be incorporated into refinement software (74). The same initiative would be more than welcome in NA refinement protocols, as imperfections in basic stereochemical restraints seem to be more pronounced than in proteins.

This and other recent studies on important geometrical parameters of NA bases, such as the nonplanarity of the amino-group (10–12), and of proteins, such as deviations from planarity of the peptide bond (71) and bond angles violating ideal values (69,70), clearly indicate that we still lack knowledge of fine details of the geometry of basic units of biomolecules. During this study, we also attempted to characterize representative structures of individual NA bases using ultra-high-resolution data from both CSD and NDB databases. We could extract some general trends, such as notable nonplanarity of six-membered rings of both pyrimidine and purine bases and pseudo-correlation among individual endocyclic torsion angles (for illustration see Supplementary Data, Figure S2). However, in contrast to the geometry at N1/9 sites, the extent of nonplanarity and its sense with respect to the average NA base plane depends on the primary sequence and the secondary and tertiary structure of the oligonucleotide. At present, there is not enough ultra-high-resolution data available to perform a reliable analysis of these structural factors.

Undoubtedly, more investigation will be needed to reveal representative geometries of NA bases in sufficient detail with respect to their sequential and structural environments. Ultra-high-resolution structures of NAs and the use of second-rank tensorial interactions such as RDCs clearly offer a chance for systematic analysis of NA base geometries in sufficient detail.

Assumptions regarding the planarity of NA bases have historically been very deeply rooted within the biochemistry and molecular and structural biology communities. Textbooks have often reproduced these assumptions as fact. Although the generally accepted paradigm of base planarity may have been in agreement with the available experimental data 10–20 years ago, the planarity concept is in conflict with many of the most recent high-precision NMR and ultra-high-resolution X-ray data. Advances in instrumentation and methodology, in both X-ray crystallography and NMR spectroscopy, now allow us to obtain structural information with a very high precision and at impressive resolutions. This fact highlights our need to revise the concept of planarity.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

The Ministry of Education of the Czech Republic (MSM6007665801 to S.F.-T., AVOZ50040507, AVOZ50040702, LC06030 to N.S. and J.S.); the Grant Agency of the Czech Academy of Sciences of the Czech Republic (KAN200100801 to L.T., IAA400040802 to N.S. and J.S., IAA400550701 to V.S.); and the Grant Agency of the Czech Republic (203/09/1476 to N.S. and J.S.); Human Frontier Science Program (HFSP) Young Investigator's Grant (to V.S.). Funding for open access charges: University of South Bohemia, Ceske Budejovice, Czech Republic.

Conflict of interest statement. None declared.