High Efficiency, Low Distortion 3D Diffusion Tensor Imaging with Variable Density Spiral Fast Spin Echoes (3D DW VDS RARE)

Abstract

We present an acquisition and reconstruction method designed to acquire high resolution 3D fast spin echo diffusion tensor images while mitigating the major sources of artifacts in DTI - field distortions, eddy currents and motion. The resulting images, being 3D, are of high SNR, and being fast spin echoes, exhibit greatly reduced field distortions. This sequence utilizes variable density spiral acquisition gradients, which allow for the implementation of a self-navigation scheme by which both eddy current and motion artifacts are removed. The result is that high resolution 3D DTI images are produced without the need for eddy current compensating gradients or B₀ field correction. In addition, a novel method for fast and accurate reconstruction of the non-Cartesian data is employed. Results are demonstrated in the brains of normal human volunteers.

1. Introduction

The motivation for acquiring high spatial resolution, three-dimensional (3D) diffusion tensor (DT) magnetic resonance (MR) images is not only the ability to produce images with finer spatial resolution of the tissue, as in anatomical imaging, but also to overcome both the partial volume effects of intravoxel multiple fibers distributions while mitigating the effects of SNR loss due to both diffusion weighting and the reduction in voxel volume size. The diffusion weighted signal from a voxel in the human brain is an admixture of the microscopic diffusion weighted signals from the often highly complex microstructure of neural tissue (Basser and Pierpaoli, 1996). The larger the voxel volume, the more complex the signal, and the more difficult it is to discern the microstructure from the signal, which is typically the goal of diffusion tensor imaging (DTI). However, reducing the voxel volume also reduces the signal-to-noise (SNR) in a method already signal starved because of its dependence on signal attenuation as the measure of interest.

The acquisition of high resolution, low distortion diffusion tensor (DT) images in the human brain is a problem that exhibits the classic interplay of trade-offs in MR imaging (MRI). All clinical diffusion-weighted imaging using whole-body gradient sets generates significant eddy currents which need to be corrected or compensated to preserve diagnostic image quality. Generation of significant diffusion weighting requires the application of large diffusion encoding gradients which in turn generate both eddy current induced phase shifts, and motion induced phase and data shifts that further distort the images (Anderson and Gore, 1994). Both of these effects vary with the diffusion gradient orientation. The diffusion weighting gradients can be modified to cancel the major component of an exponential eddy current field (Reese et al., 2003), but this lengthens the echo time, thus reducing the SNR. Furthermore, the effectiveness of these pulses is predicated on the eddy currents being well described by a single exponential decay, which is known not to be the case (S. Hinks, private communication). Motion induced phases can be alleviated by acquiring data with a single shot method such as echo planar imaging (EPI), but this then limits the attainable resolution because the extent of k-space that can be sampled is severely limited by T₂^* relaxation. Moreover, the sensitivity of EPI to off-resonance effects, coupled with the long echo times required to fit in the diffusion weighting gradients, results in significant distortions in regions of the brain near air or bone interfaces. Resolution can be increased by employing a multi-shot technique but phase discrepancies from eddy currents and motion result in data inconsistencies between interleaves that produce severe artifacts.

The acquisition time can be significantly reduced by the use of fast spin echoes, but these require great phase stability throughout the echo train to maintain the CPMG condition, which can be compromised by phase errors due to eddy currents produced by, or motion within, the diffusion weighting gradients preceding the echo train. Extending this to three dimensions (3D) only makes matters worse as now phase stability is required over not only the echo train but for the volume encoded interleaves as well.

Despite these competing effects, in this paper we present an acquisition and reconstruction method designed to acquire high resolution 3D fast spin echo diffusion tensor images while mitigating the major sources of artifacts in DTI - eddy currents and physiological motion. The fast spin echo acquisition makes efficient use of each excitation by covering substantial amounts of k-space and exhibits greatly reduced field distortions compared to EPI acquisitions. The acquisition is a modification of the previously report three-dimensional (3D) fast spin echo spiral acquisition (Wong et al., 2000) to include diffusion weighting gradients and variable density spiral acquisition gradients, which allow for the implementation of a self-navigation scheme by which both eddy current and motion artifacts are greatly reduced with little penalty in efficiency. Reconstruction of the non-Cartesian data is implemented by a recently introduced iterative method. The result is that high resolution 3D DTI images are produced without the need for eddy current compensating gradients nor field correction. In addition, a novel method for fast and accurate reconstruction of the non-Cartesian data is employed. High spatial resolution fractional anisotropy (FA) and principal-eigenvector colored maps are demonstrated in the brains of normal human volunteers.

2. Acquisition

2.1. 3D Fast Spin Echo

The pulse sequences is based on the 3D fast spin echo using a stack of spirals previously introduced by Wong (Wong et al., 2000) with the addition of diffusion weighting and variable density spiral readout gradients. The pulse sequence diagram for a single excitation is shown in Figure 1. The z encoding is applied as a function of the echo train, and thus the number of slices is constrained to be an integer number (N_zs) of the echo train length (ETL). The sequence acquires N_zs excitations, and thus spans the range of k_z, for each of N_i interleaves in order, all for a single diffusion encoding direction. In this way eddy current effects from the diffusion encoding gradients are relatively consistent for an acquired volume.

Figure 1.

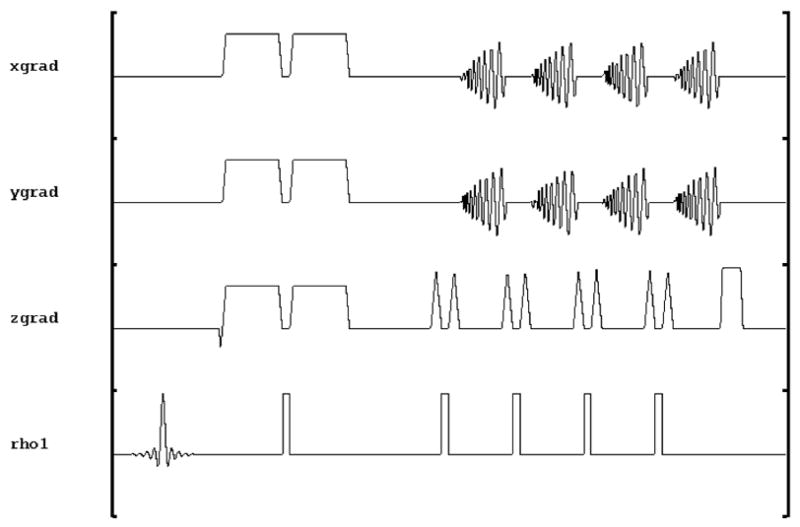
3D Variable Density Spiral Fast Spin Echo diffusion weighted pulse sequence.

Note that a single spin echo Stejskal-Tanner (Stejskal and Tanner, 1965) diffusion encoding strategy is shown. Both this standard diffusion weighting scheme and the dual spin echo preparation (Reese et al., 2003) which has become ubiquitous in DTI as method of reducing eddy current effects, were implemented. As we show below, however, our eddy current correction in the reconstruction obviates the need for the dual spin echo. Elimination of the dual spin echo can significantly reduce the minimum TE, which is advantageous in studies involving tissues with short T2’s, such as muscle. Consequently, dual echo preparation is no longer implemented by our sequence.

2.2. Variable Density Spiral (VDS) acquisition

A variable density spiral (VDS) k-space trajectory was used in order to oversample the low k-space frequencies for estimation of the phase errors, and because they are intrinsically less sensitive to motion (Liao et al., 1997). The variable density spiral was generated using the analytic spiral design of Kim (Kim et al., 2003), where for a system with gradient g and slew rate s = ġ ≡ dg/dt, the k-space trajectory as a function of the time t dependent parameter τ and the number of turns n for an image with field of view FOV and matrix size N is given by

$$k(\tau )=A{\tau }^{\alpha }{e}^{i2\pi n\tau }$$ (1)

where A = N/(2 FOV) and

$$\tau =\{\begin{array}{ll}{\left(\frac{s}{A{\omega }^2{\beta }_1^2}\right)}^{{\beta }_1/2},\hfill & 0\le t\le min(T_{s2\alpha },T_{es})\hfill \\ {\left(\frac{g}{A\omega {\beta }_2}\right)}^{{\beta }_2/2},\hfill & 0\le t\le t_{\mathit{end}}\hfill \end{array}$$ (2)

where

$$\begin{array}{l}{\beta }_1\equiv {(\alpha /2+1)}^{-1}\\ {\beta }_2\equiv {(\alpha +1)}^{-1}\end{array}$$ (3)

where τ(t) ∈ [0, 1]. The transition time from slew-rate limited to amplitude-limited region is denoted T_s2α and T_es is the ending time of the slew-rate limited region, and t_end is the time at the completion of the spiral. All gradients are expressed in units of rad/(cm-sec). This trajectory has previously been used for self-navigated interleaved spirals for DTI (Li et al., 2005; Liu et al., 2004). In the current implementation the magnetization was rewound after each shot by the addition of a numerically generated refocusing trajectory segment. This was applied coincidentally with the slice encoding gradients in order to minimize the echo spacing.

3. Reconstruction

Reconstruction of data acquired on a (variable density) spiral trajectory requires the inversion of data sampled on a non-Cartesian grid with a non-uniform density in k-space. This is a well known problem that requires both a theoretical formulation of the proper inversion, and an efficient and accurate numerical scheme to perform it. Both have been the subject of much investigation in relation to the reconstruction of non-uniformly spaced MRI data (Desplanques et al., 2002; Fesler and Sutton, 2003; Hoge et al., 1997; Jackson et al., 1991; Meyer et al., 1991; Pipe and Menon, 1999; Sedarat and Nishimura, 2000; Van der Walle et al., 2000). In this paper we employ the numerical method developed by (Inati and Greengard, 2006), with a slightly different, but ultimately equivalent, theoretical formulation.

The goal of MRI is to reconstruct the effective spin density ρ(x) from a finite number of data samples s_j, j = 1, …, n of the form

$$s_j(\mathit{k})=\int \rho (\mathit{x})e^{i{\mathit{k}}_j·\mathit{x}}d\mathit{x}+{\eta }_j$$ (4)

with a noise term, η_j. Although the data are clearly in the Fourier domain, reconstruction of ρ(x) cannot simply be accomplished by inverse Fourier transformation because we only have a finite number of samples and these are contaminated by noise. While inverse Fourier transformation is often a good approximation if the data are evenly and densely sampled (as is the case, for example, in standard Cartesian MR experiments), this is actually never precisely the case, and the present sampling scheme emphasizes the necessity for understanding the proper formulation of the estimation of ρ(x).

Eqn 4 can be written in compact form as (Inati et al., 2005; Van der Walle et al., 2000)

$$\mathit{s}=\mathcal{H}\mathit{\rho }$$ (5)

where ℋ maps the spin density (i.e., image space) to the signal (i.e., k-space). This can be solved by least squares to find the best estimate ρ̂(x)of the spin density:

$$\widehat{\mathit{\rho }}=\mathit{Ps}$$ (6)

where P is the projection operator that maps the signal onto the space spanned by the operator ℋ. P is also called the pseudo-inverse of ℋ and is given by

$$\mathit{P}={\mathcal{H}}^{†}{(\mathcal{H}{\mathcal{H}}^{†})}^{-1}$$ (7)

where † denotes the Hermitian conjugate. The complexity of solving Eqn 7 hinges on the invertibility of the matrix B ≡ ℋℋ^† in P, which is dependent upon the eigenstructure of B, which for the Fourier problem of Eqn 4 is given by

$$B_{ij}=\text{sinc}({\mathit{k}}_i-{\mathit{k}}_j)$$ (8)

where sinc(k) ≡ sin(πk)/(πk) and $\text{sinc}(\mathit{k})={\displaystyle \prod _l^n}\text{sinc}(k_l)$ where n is the dimension of k. Thus in the present problem sinc(k) = sinc(k_x) sinc(k_y) sinc(k_z) thus

$$B_{ij}=\text{sinc}(\mathrm{\Delta }{k}_x)\text{sinc}(\mathrm{\Delta }{k}_y)\text{sinc}(\mathrm{\Delta }{k}_z)$$ (9)

where Δk ≡ k_i − k_j.

In Cartesian sampling schemes B is diagonal and the problem simplifies greatly. However, in non-Cartesian schemes, nearly coincident points can produce very small eigenvalues which make B poorly conditioned and its invertibility problematic. This has led to a significant amount of research on practical and robust methods of reconstruction. However, it can be shown (Inati et al., 2005) that the pseudo-inverse solution Eqn 6 is approximately equal to the weighted Fourier reconstruction

$$\widehat{\mathit{\rho }}=\sum _m{w}_m{s}_m{e}^{-2\pi i{\mathit{k}}_m·\mathit{r}}$$ (10)

where the weights w_m are given by

$$w_m=\frac{1}{{\sum }_n{\text{sinc}}^2({\mathit{k}}_m-{\mathit{k}}_n)}$$ (11)

The direct computation of Eqn 10, while straightforward, takes 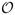(N²) and so can be prohibitively expensive for long trajectories, since each point must be summed over all other points. However, it can be calculated in 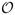(N log N) using the fast sinc² transform (Greengard et al., 2006). The image (Eqn 6) can then be reconstructed using fast non-uniform Fourier transform (Greengard and Lee, 2004). Furthermore, it can be shown (Inati and Greengard, 2006) that the approximation to the pseudo-inverse (Eqn 6) given by the weighted Fourier reconstruction (Eqn 10) can be improved upon via a simple iterative scheme:

$$\begin{array}{l}{\widehat{\mathit{a}}}_0=0\\ {\widehat{\mathit{s}}}_j=B{\widehat{\mathit{a}}}_j\\ {\widehat{\mathit{a}}}_{j+1}={\widehat{\mathit{a}}}_j+W(\widehat{\mathit{s}}-{\widehat{\mathit{s}}}_j)\\ \widehat{\mathit{\rho }}=\sum _m{a}_{N,m}{e}^{-2\pi i{\mathit{k}}_m·\mathit{r}}\end{array}$$ (12)

where W = Diag(w_m) is the diagonal matrix of weights. The application of the sinc matrix B is accomplished via the fast sinc transform (Greengard et al., 2006), and the final sum is calculated using the non-uniform fast Fourier transform (Greengard and Lee, 2004). Typically, only a small number of iterations (<10) are required to achieve convergence. This iterative approximate pseudo-inverse method is stable with respect to noise.

This reconstruction method was implemented in a parallel fashion on a linux cluster using standard MPI programming tools. Parallelization was performed over the coil dimension so that reconstruction for data collected in the 8-channel head coil took the same time as that over a single coil. This parallel implementation of the fast iterative non-uniform FFT method (Inati and Greengard, 2006) allowed reconstruction and phase correction of 32 slice, 32 direction, N_i=4, matrix = 128 ×128 variable density spiral data for 8 channels in ≈ 12.3 min. Further optimization is possible and is currently underway.

It should be noted that, while we take a standard point of view of reconstruction as far as solving the least squares problem, and the algorithm looks standard on the surface, the specific implementation details are novel. Our weights formula produces an approximate pseudo-inverse very accurately and allows us to use a very simple iteration scheme without needing to impose any additional regularization term. Prior to this work, the components of the reconstruction method had only been applied to synthetic data and had only been published in abstract form (Inati and Greengard, 2006; Inati et al., 2005). This is the first publication applying this method to real data. The application of the fast sinc algorithm to MR image reconstruction is also novel.

4. Sources of error

There are two major sources of error in multi-shot diffusion weighted sequences: eddy currents, produced by the diffusion weighting gradients, and subject motion. Both of these produce inconsistencies between the shots that result in artifacts in the reconstructed images.

4.1. Eddy current induced errors

Eddy currents are generated in the magnet by the rapidly changing magnetic fields of the diffusion gradients being turned on and off. These, in turn, generate non-linear spatially and temporally varying magnetic fields across the subject. This is a well-known problem in diffusion weighted imaging (Bastin, 1999; Calamante et al., 1999; Horsefield, 1999; Jezzard et al., 1998). In practice, these residual fields alter the area of the diffusion gradients very little but induce spatially and temporally varying residual fields across the sample (Reese et al., 2003). The standard model for eddy currents for an MR imaging system (Reese et al., 2003) is that n gradient transitions, the i’th of which occurs at time ξ_i, generates a magnetic field that decays exponentially according to

$$B^{\mathit{eddy}}(\mathit{x},t)=\mathrm{\Delta }B(\mathit{x})\sum _{i=1}^n\sum _{j=1}^m{c}_j{e}^{({\xi }_i-t)/{\lambda }_j}$$ (13)

where the {λ_j} are the m decay constants that are assumed to characterize the system and {c_j} are the amplitudes of each of these components. If the simplification is made that the system is dominated by a single exponential λ (and a single amplitude c), and that the field ΔB(x) is linearly varying in space, and that ΔB is equal and opposite for gradient transitions that are equal and opposite, then Eqn 13 reduces to (Reese et al., 2003)

$$B^{\mathit{eddy}}(\mathit{x},t)=(\mid \mathrm{\Delta }B\mid ·\mathit{x})\sum _{i=1}^{n}c{e}^{({\xi }_i-t)/\lambda }$$ (14)

This characterization of the system by a single decay time is amenable to the creation of a sequence of diffusion weighting gradients whose transitions cancel out the eddy current fields produced at the transitions. The two gradient pulses surrounding the 180° refocussing pulse is replaced by a dual spin echo - a pair of 180° pulses, each surrounded by gradient pulses with widths chosen to minimize the eddy current induced fields (Reese et al., 2003). Unfortunately, this method is predicated on the accurate characterization of a system by a single eddy current time constant λ, which is known not to be the case (Dr. Scott Hinks, private communication.). However, for single shot EPI methods it is adequate to eliminate a significant amount of distortion. But for fast spin echo schemes in which phase coherence between shots is critical, this is not sufficient as their decay during the echo train produces spatially and temporally varying phases per echo.

4.2. Motion induced errors

Motion of the subject during the imaging process also produces spatially and temporally dependent changes in the data that produce artifacts in reconstructed images. There are two major classes of motion that we are concerned with in human brain imaging: gross head motion during scanning and much more complex, though lower amplitude motion of the brain due to cardiac and cerebral spinal fluid (CSF) pulsations. It can reasonably be assumed that the phases due to motion are generated on a significantly longer timescale than the echo train duration, so are effectively constant from echo to echo. For simple rigid body motion during the application of diffusion weighting gradients, it is well-known (Anderson and Gore, 1994) that translational motion produces a constant signal phase and rotational motion causes a shift in k-space, or, equivalently, a constant and linear phase in image space. Even so, gross head motion during acquisition will produce phase variations in between data acquisitions periods, causing phase inconsistencies. Motion of the brain itself within the skull due to cardiac and CSF pulsations is not rigid body motion, and thus the phases produced in image space have a non-linear spatial variations (Enzmann and Pelc, 1992). Our model for motion induced phase variations incorporates both sources, and is therefore modeled as slowly and non-linear spatially varying.

5. Correction of eddy current and motion induced phase errors

Our basic hypothesis about the structure of the errors due to eddy currents and motion is that they produce spurious phases at every data acquisition period, since the eddy current phases vary as a function of echo number and the motion phases vary across echo train number. The spatial variation of these phases is hypothesized to vary non-linearly but slowly across the image volume and temporally across all acquisitions, but are assumed to be constant during each acquisition. Because the phases are of low spatial frequency, they can be estimated from the central portion of k-space, and removed in image space. This method, introduced by Miller (Miller and Pauly, 2002, 2003), has been used previously to correct for phase artifacts in slice-selective DTI experiments (Liu et al., 2004). This method has the advantage that it can correct for low order non-linear phase variations due to both eddy currents and motion without the necessity for separately modeling the distinct effect produced by either source. However, the problem is more complicated in 3D imaging because there are phase variations in the additional phase encoding direction as well. However, this can be accounted for by recognizing that the b=0 image serves as a reference phase image (Tyszka and Frank, MRM 2009): In the absence of diffusion encoding pulses it is absent the eddy current and motion induced phases that contaminate the diffusion encoded images. In addition, the reference phase account for phase variations between coils in a multichannel array, thus allowing the phase correction to be done independently for each coil. This then allows an efficient parallel computing implementation of the reconstruction, which is important because we are using an iterative, non-uniform FFT reconstruction that can be time consuming. Therefore, the phase correction scheme for each interleave consists of the following steps:

1. Create reference low spatial frequency 3D image phase map ϕ_ref from the central portion of the b=0 data by applying a 2D Fermi filter in k-space, then performing a 2D non-uniform FFT at each z-encoding step back to image space.

2. Create low spatial frequency 3D image phase map ϕ_l from the central portion of the current interleave l by applying a 2D Fermi filter in k-space, then performing a 2D nonuniform FFT at each z-encoding step back to image space.

3. For each interleave l, perform 2D transform at each z-encoding step to image space

4. Multiply image space data for interleave l by e^{−i(ϕl − ϕref)}

5. Add up all interleaves to create final image

6. Transform over z

This procedure is shown schematically in Figure 2. Low frequency images are generated by applying a 2D fermi filter in k-space. The radius and width of the Fermi filter are 0.1 and 0.01 of the k-space matrix size, respectively.

Figure 2.

Schematic of the phase correction algorithm. A represent the complex image data from a single interleave, and ${\displaystyle \sum _l}A(l)$ means the sum over all interleaves.

k-space changes due to diffusion weighting

Estimation of motion-related errors from k-space data is problematic in diffusion weighted imaging where the image amplitudes are modulated by the diffusion weighting, as this causes both amplitude and phase variations in k-space. This is easy to understand from basic Fourier properties: the k-space amplitude determines the image amplitude and the k-space phase determines the location. Conversely, amplitude variations at a particular location in image space cause a phase in k-space dependent upon where in the image the amplitude varies. This is illustrated for a numerical phantom in Figure 3. However, because the spatial variations of the diffusion weighted regions in the brain are primarily of high spatial frequency (white matter tracts), the resulting phase variations tend to be high frequency in character, and thus as long as the estimation of phases is done from the low frequency phases, this is not a problem.

Figure 3.

Numerical phantom simulation of k-space magnitude and phase changes due to diffusion. The phantom is composed of a disk (a head) plus and an arc (a white matter bundle). k-space magnitude images are scaled for better visibility. In the top row is an arc of image intensity (a) as an idealized model for a white matter region in the brain, and its k-space magnitude (b) and phase (c). The Fourier structure exhibits strong radial and angular variations consistent with the spatial frequency content and object location and amplitude. In the bottom row, the image intensity from the top row is combined with a uniform disk, used to represent an idealized uniform brain. The magnitude and phase variations, formed from the superposition of the top and bottom rows, exhibit strong radial and angular variations produced by the image intensity modulations in the arc. Thus variable density spiral phase estimation methods that rely on the central portion of k-space must be careful not to remove phase variations due to diffusion weighting, which would then alter the location and magnitude of the diffusion modulated image intensities.

This has two major implications. First, we are using the b=0 image as a reference phase to correct the diffusion weighted images. But the k-space phase of the diffusion weighted images is not the same as that of the b=0 images because its intensities have been modulated. However, if these modulations are of high spatial frequency, then using the low frequency phase of the b=0 is still viable. This brings about the second point: the parameters of the fermi filter are important. Restricting its width to too small a portion of the central region of k-space does not capture enough structure to eliminate the artifactual phases, but allowing two many high spatial frequencies can let in high frequency phase modulations from modulated intensities. This is exacerbated by the fact that we are reconstructing single interleaves, which are undersampled beyond the critical radius of the variable density spiral.

6. Diffusion data analysis

High angular resolution data in the the current study were analyzed using the standard Gaussian model of diffusion which can be reduced to the estimation of a real, symmetric 3×3 diffusion tensor from whose eigen decomposition can be constructed the mean diffusivity (MD) and fractional anisotropy (FA) (Basser, 1994). The eigen decomposition as performed using the program 3dDWItoDT of the AFNI suite of programs (Cox, 1996) which guarantees the positivities of the eigenvalues. All computations and display were performed within the AFNI Diffusion Plugin being developed at the Center for Scientific Computation in Imaging (http://csci.ucsd.edu).

7. Methods

All human brain images were acquired in normal human subjects, with approval from the Humans Subject Committee at UC San Diego, on a GE Signa 3T Clinical Scanner (GE Healthcare, Waukesha, WI) using an 8-channel phased array head radio-frequency coil (GE Healthcare, Waukesha, WI). Three volunteer studies (two males and one female) were conducted using 3D DW VDS RARE.

Axial images were acquired of a normal human volunteer in a region that extended from the genu and splenium of the corpus callosum to the ventral frontal cortex, a region prone to severe susceptibility induced distortions. 3D DW VDS RARE images were acquired with parameters were ETL = 4, nz = 16, N_i = 16. The repetition time, TR, was 1000 ms, the Stejskal-Tanner preparation echo time was 80 ms and the CPMG echo spacing was 11.6 ms. The effective total echo time was 80 ms, with the first CPMG echo assigned to the center of the k_z dimension. Total scan time was approximately 14 min. For comparison, DT images were also acquired with a commercial 2D echo planar imaging (EPI) sequence with parameters of 5000 msec TR; 88.4 msec TE; 2 NEX; and scan time of 2:30. Both sequences were acquired with a field of view was 23 cm with a 128×128×16 matrix size with 1.8mm³ isotropic resolution, and diffusion encoding was achieved with a single spin echo Stejskal-Tanner preparation at a b-value of b=1000 s/mm² and 12 isotropically distributed diffusion encoding directions.

8. Results

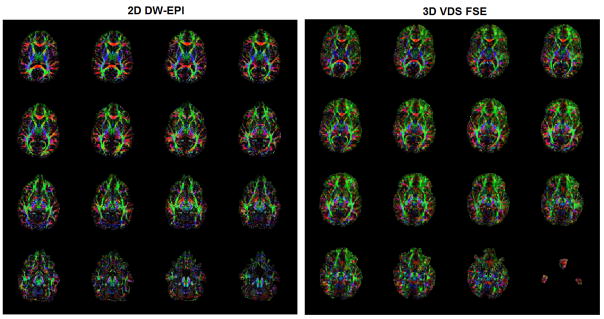
While the non-linear phase correction scheme corrects for both eddy current and motion related errors, application to a spherical phantom (where there is no subject motion) allows the demonstration of the algorithm on only eddy current induced errors, as shown in Figure 4. The efficacy of the phase correction method in a real data set is demonstrated graphically in Figure 5. In Figure 6 is shown the uncorrected and corrected diffusion weighted images from a single location but three different diffusion encoding directions. The b=0, mean diffusivity, fractional anisotropy, and directional colormaps images for the two sequences are shown in Figure 7. A comparison of the FA maps of the two sequences for all 16 slices is shown in Figure 8. The directions of the fibers expressed in the colormaps are commensurate with the previously published results (e.g. (Jellison et al., 2004)). Of particular note is the consistency in areas where motion artifacts dominate in multi-shot techniques, such as anterior limb and posterior limb of the internal capsule, and the existence of fibers in the frontal regions of the 3D VDS-FSE DTI images, which are highly distorted in the 2D EPI images and show fewer fibers. Comparison with the EPI acquisition reveals that the significant distortion in the frontal region characteristic of EPI data is not present in the 3D DW VDS RARE DTI sequence. The high SNR of this sequence allows the flexibility to significantly shorten the total acquisition time by reducing the repetition time. For example, in Figure 9 is shown a comparison between the mean diffusivity and fractional anisotropy from with TR = 1.0 sec, as in the previous images, with an acquisition with TR = 0.5 sec, which thus took half the time. The measured SNR values in the splenium are 26.5 for EPI and 120 for 3D DW VDS RARE. The scan time for VDS was 834 sec. and that for EPI was 150 sec, giving a relative SNR efficiency of 3D DW VDS RARE to EPI of (120/sqrt(843)) / (26.5/sqrt(150)) = 1. 92.

Figure 4.

Correction of eddy current induced phase errors. Coefficient of variance of the signal intensity across diffusion directions is shown in a spherical phantom before (left) and after (right) application of the phase correction algorithm. Since this is a phantom, there are no motion effects, and thus all errors are primarily due to eddy currents.

Figure 5.

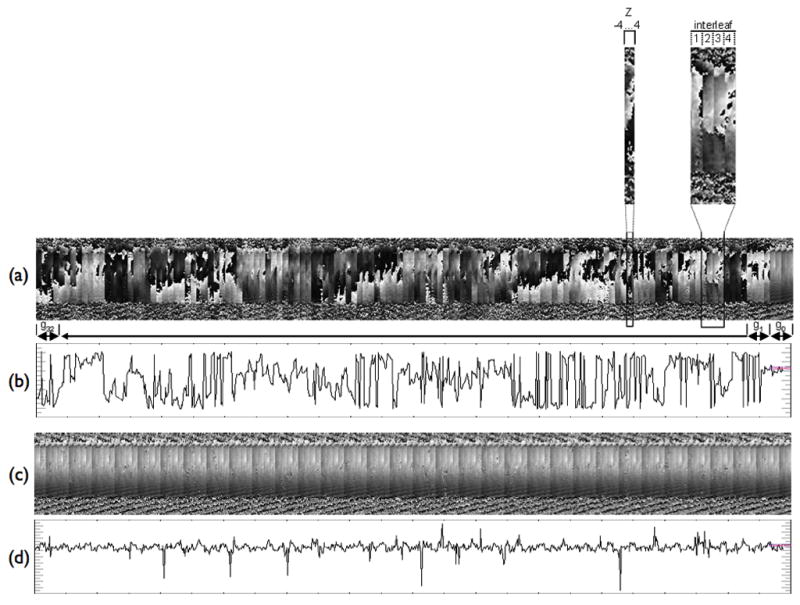
3D self-navigated phase correction over z-encoding, interleaves, and diffusion directions. The image phase for blocks of z-encodings from z=−4,…,+4, within N_i=4 interleaves, for 32 different diffusion encoding directions. (a) Uncorrected images; (b) A single line through (a) shows an example of the phase variations. (c) Corrected images; (d) A single line through (c) shows a significant reduction of the phase variability. Only the results from a single coil are shown. The non diffusion weighted images (b=0) are the block of 4 interleaves the right hand side.

Figure 6.

Uncorrected (top) and corrected (bottom) diffusion weighted images from a single location but three different diffusion encoding directions.

Figure 7.

Comparison of DTI parameter maps between (top) product 2D DW-EPI sequence and (bottom) 3D DW VDS RARE. (Acquisition parameters are listed in the text.) The MD maps are scaled from 0 to 2 um²/ms and FA maps are scaled from 0.1 to 0.7. The existence of lateral callosal fibers in these maps is an indication of the integrity of the data.

Figure 8.

Comparison of FA parameter maps for all 16 slices between (left) product 2D DW-EPI sequence and (right) 3D DW VDS RARE. The ventral frontal and temporal regions are significantly better in the VDS than in the EPI. The most inferior image in the 3D VDS FSE is distorted because it is in the transition band of the slab selection.

Figure 9.

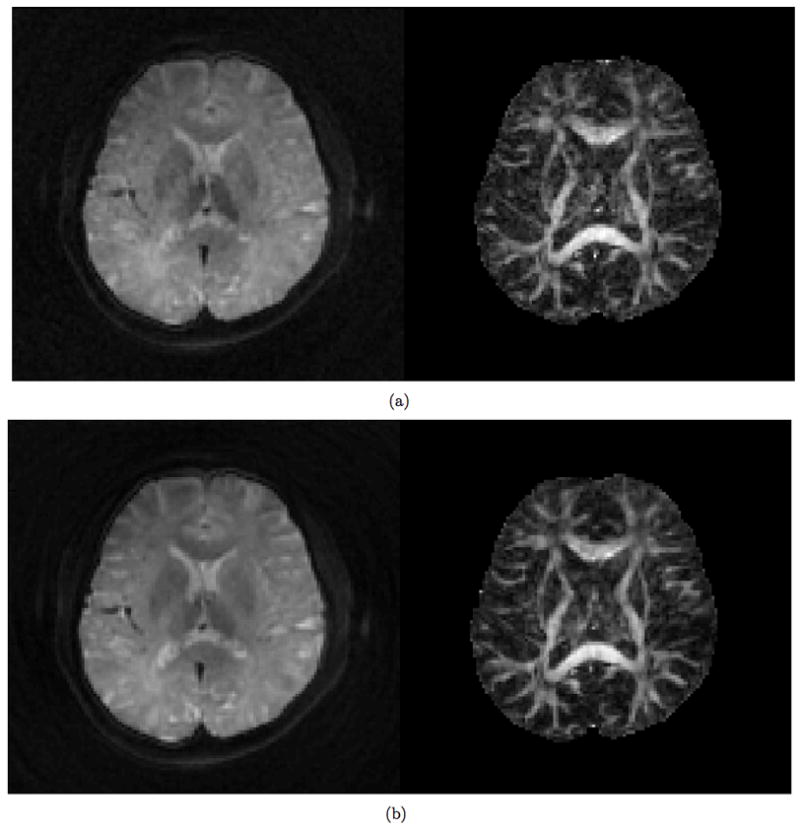
Comparison of 3D DW VDS RARE mean diffusivity (left) and FA (right) images at (a) TR = 0.5s and (b) TR = 1.0 s.

9. Discussion and Conclusion

Diffusion tensor imaging has the potential to provide important information on tissue structures and indeed has found utility in a wide range of areas of scientific research. However, in its application to living subjects it is most often implemented in a single-shot EPI method, which has the advantage of being insensitive to subject motion, but is limited in spatial resolution and prone to severe distortions due to field inhomogeneities. The sensitivity of single shot EPI methods to eddy currents causes image distortions that can either be corrected in post-processing (Jezzard et al., 1998) or by reducing the effects of the primary eddy current decay component with a dual spin echo preparation (Reese et al., 2003). However, single shot methods pose limitations on the spatial resolution, so recent work has focussed on multi-shot methods for high resolution including radial fast spin echo methods (Pipe et al., 2002; Trouard et al., 1999) and interleaved variable density spirals (Li et al., 2005; Liu et al., 2004). The current work is a natural extension of these methods to three dimensions, which offers the typical advantages of 3D MR methods over these 2D methods: high resolution and better signal-to-noise, along with the disadvantages: increased sensitivity to phase inconsistencies (e.g. (Frank et al., 1993)). The primary advantages over the conventional EPI method which are higher SNR efficiency, isotropic 3D PSF and low distortion due to off-resonance effects. Estimation and removal of phase errors required for multishot methods is achieved in the PROPELLER (Pipe et al., 2002) and TurboPROP (Pipe and Zwart, 2006) by collecting several lines through the central region of k-space. Spiral acquisitions are able to more efficiently sample this region in a single variable density spiral, thus allowing each echo to be corrected. Moreover, spiral offer the possibility of optimizing the trajectory to modify the trade-off between the coverage of the central region of k-space and the time required to do so. This type of optimization is the focus of ongoing work in our lab.

The sequence described here allows application-dependent trade-offs between spiral length, echo spacing, echo train length, number of z-encodings, slice thickness, and number of diffusion directions. For example, a small number of interleaves (N_i=4) allowed for a short acquisition time, which, when combined with a short echo train length (ETL=4), helps preserve SNR by reducing the effects of T₂ decay affected by the rather long echo spacing of ≈ 35 ms. Conversely, for imaging of an excised dog heart, with large air-filled ventricles and short myocardial T₂, the number of interleaves was set very high (N_i=32), reducing the echo spacing to ≈ 5 ms. In the present paper we have focused on demonstrating the feasibility of the sequence and have therefore collected data of reasonably high spatial resolution and only moderate angular resolution (12 direction). However, one application of particular interest that this sequence will facilitate is the acquisition of data that has both high spatial (~.5 mm) and angular (~60 directions) resolution for the purpose of investigating complex tissue microstructure in regions such as the ventral frontal and temporal white matter and brain stem (Frank, 2001, 2002). Because the sequence is a fast spin echo, distortions due to B₀ field inhomogeneities can be greatly reduced, thus facilitating the acquisition of DTI data in regions of the brain near air and bone interfaces. Moreover, this eliminates the need for field map acquisitions and distortion correction in post-processing.

The central issue in the feasibility of these interleaved methods is the ability to correct for the phase errors induced by both motion and eddy currents, and all of these methods using the low frequency phase information to make these corrections. While earlier work focused on rigid body models and correction in k-space, it has become clear that the phase structure is more complicated but can still be reasonably estimated using an image-based method where these artifacts are manifest as low spatial frequency. These can be removed in 2D imaging either by directly removing the phase of the low resolution reconstruction or by use of a dual spin echo in combination with an iterative rephasing scheme (Liu et al., 2004). The difficulty with the extension to 3D imaging is that there is an inherent phase structure of the data due to the 3D encoding that is susceptible to phase errors, so that phase error generate not only misregistration of the spiral interleaves, but phase encoding errors as well, thus providing an efficient mechanism for image distortions. However, we have shown that by using the non-diffusion weighted (i.e., b=0) image as a reference phase, a robust phase correction scheme can be implemented. However, this is predicated on the stability of the b=0 images. Main field drifts that compromise fat suppression pulses, for example, would cause phase variations that could interfere with the correction scheme. Our results indicate that this is not a significant problem to first order, but will be investigated in future work. One interesting consequence of our correction scheme is that, because our phase model is rather general and the correction is carried out for every acquisition period, the residual eddy current phases produced by the diffusion weighting gradients are significantly reduced and thus appear to obviate the need for a dual spin echo preparation. This allows the acquisition of images with a significantly shorted echo time, which facilitates studies in tissues with short T₂’s, such as muscle. Nevertheless, imaging of short T₂ tissues and high b-value DTI due present an intrinsic limitation to the phase correction method: As the SNR decreases, the phase correction becomes more problematic. Determining the range of b-values that provide reasonable results for any particular tissue type is a complicated question that is currently under investigation. Typical primary eddy current decay constants on clinical scanners are on the order of 50 ms (Reese et al., 2003), which is significantly longer than the 11 ms echo spacing used in this study. Eddy currents with time constants on the order of the CPMG echo spacing will be more difficult to correct using our approach.

The post-processing required in our method does introduce a significant computational burden. Because of the necessity of performing an iterative, non-Cartesian reconstruction for each echo, for each interleave at each z-encoding step for each coil for each diffusion encoding step, the number of reconstructions is often quite large. All of the reconstruction is done off-line on a Linux cluster with 72 nodes. Our current implementation of the reconstruction has been parallelized only over coils, which still gives a significant improvement in reconstruction time when using our 8-channel head array coil. For example, for the data shown above with parameters 128 × 128 × 16 with ETL = 4, nz = 16, N_i = 16 and 12 diffusion encoding directions, the reconstruction time is ≈ 7 min. While this is a reasonable amount of time, there are nevertheless significant improvements in performance that can be made by further parallelization.

The implemented sequence described here does not include compensation for non-CPMG components arising from inaccurate initial phasing of the transverse magnetization at the start of the CPMG echo train (Bastin and Le Roux, 2002; Le Roux, 2002). Any phase modulation of the echo train by non-CPMG components was mitigated by per-echo phase correction during reconstruction, as described in Section 5 above. Residual amplitude modulation of the echo train by non-CPMG components was not compensated by refocusing pulse phasing although significant ghosting artifacts in the z dimension were not observed in practice (Fig 6). The addition of quadratic phasing of the refocusing pulses to address amplitude modulation effects should be considered, particularly if longer echo trains are employed (Bastin and Le Roux, 2002; Le Roux, 2002). In addition to non-CPMG effects, T2-relaxation modulation of the echo train is inevitable but represents a less significant source of artifacts for the sequence implementation described here. The Stejskal-Tanner diffusion preparation has an echo time of 80 ms, which deemphasizes short T₂ components that would undergo significant blurring in the z dimension. Assuming a white matter T₂ relaxation time of 70 ms (Stanisz et al., 2005), and a total delay between the first and final (fourth) spiral readouts of 50ms, the T₂-decay modulated point spread function FWHM can be estimated crudely as √3/ π (50 ms / 70 ms) = 0.4 voxels in the k_z-dimension (Haacke et al., 1999). The use of longer echo trains is therefore not recommended for in vivo DTI.

DTI methods based on steady state free precession (SSFP) are a natural avenue of investigation for 3D implementations due to their relative efficiency for 3D acquisitions and large diffusion sensitivity. Such methods have been developed for musculoskeletal applications (Miller et al., 2004) and for imaging fixed tissue (McNab et al., 2009) but are problematic for in vivo brain imaging because of their strong sensitivity to motion. A segmented SSFP sequence with diffusion-weighted driven equilibrium preparation has been proposed for 3D acquisitions, but was found to be sensitive to physiological motion induced phase effects and non-diffusion-weighted signal contamination, complicating accurate diffusion measurements in vivo (Jeong et al., 2003). Volume localized diffusion-weighted EPI techniques such as that proposed in (Jeong et al., 2006) offer significantly improved susceptibility gradient tolerance compared to conventional DW-EPI at the expense of spatial coverage and are best suited to spinal cord applications. 3D DTI using radial acquisitions tends to be less efficient because a radial acquisition covers a significantly reduced portion of k-space than a spiral (Jung et al., 2009). This reduces the accuracy of motion and eddy current phase estimation at each shot since only a few central points of k-space are acquired. Radial imaging can be approximated with our implemented sequence by requesting many short spirals, allowing the user to optimize the trajectory based on preference and application.

The most significant difference between our method and the alternatives is the use of 3D volumetric acquisition which makes efficient use of sequence dead time by combining spiral readouts with CPMG echo train generation. PROPELLER has significantly lower SNR efficiency (SNR/sqrt(Time)) than VDS-RARE which is comparable to TurboPROP. 3D diffusion acquisition methods provide higher SNR and thin contiguous slices (Jeong et. al., MRM 2006, Jung et. al. JMRI 2009). Recent work by both Porter (Porter and Heidemann, 2009) and Holdsworth (Holdsworth et al., 2008) have utilized segment readout 2D EPI sequences to reduced geometric distortions. The blurring of spiral acquisitions in the presence of off-resonance frequencies, rather than the distortions created in EPI (Noll et al., 1992; Yudilevich and Stark, 1987), produce somewhat less “sharp” looking images, but are advantageous in that they reduce the mismatch between the images and the true anatomical geometry (Glover and Lai, 1998). The preliminary data in Figure 9 suggests the potential for making good use of the enhanced SNR provided by the 3D nature of the acquisition to significantly reduce the TR. In addition, time savings can be gained by optimizing the trajectory. Determining the trajectory that enables estimation of the motion and eddy current phases in the minimal amount of time would allow reduction of the echo spacing, and a subsequent reduction in the TR. The data in Figure 89was suboptimal because it a 90° flip angle was used (future experiments will employ the Ernst angle), but the point is clear non-the-less: There is some trade-off between the total imaging time and the eventual “detectability” of regions of anisotropy. Assessment of this “diffusion SNR per unit time” is ultimately an experimental and statistical issue that we will address in the near future. Total imaging time is always at a premium in DTI, so future work will always include attempts to shorten the acquisition time.

There are several areas of future investigation for improvement of the method presented here. The most obvious is the extension to true 3D trajectories in order to be able to self-navigate motion in all directions. Additionally, while the self-navigation inherently corrects for a significant component of the eddy current variations between echoes, it should be noted that in our acquisition scheme each echo contains a different k-space line in z (slice encoding) but we do phase correction in a hybrid space which is image space in x-y plane and k-space in the z direction. The correction is done in the hybrid space because we do not have a navigator through z direction. Therefore, if there are echo-to-echo phase variations in z-direction, this will introduce echo-to-echo magnitude variation as well as phase variations in the z directional k-space which would produced variations not remedied by our correction method. Furthermore, the reduction of field inhomogeneities by the use of fast spin echoes does not mean that such effects are eliminated. The investigation of inhomogeneity corrections in spiral imaging is an active area of research that will find use in the future development of our method. Further refinements are possible by taking into account the change in b-value and the diffusion direction with motion between the individual spirals. This effect is currently ignored and results in, effectively, and “average” b-value and direction for any nominal set of these, where the averaging occurs over the different motions that occur during the different spiral segments.

Our primary motivation for the current work is our need to investigate the structure of white matter in certain disorders that affect the ventral frontal, temporal WM and the brain stem, where distortions in EPI acquisition can be severe. In addition to the desire to probe particular regions of the brain with more specificity, it is also well known that the greater the spread of fiber orientations with a voxel, the more difficult it is to interpret the diffusion weighted signal (e.g., (Frank, 2001, 2002)), and thus a method for acquiring high spatial resolution also serves to reduce this loss of information. However, because the neural fibers producing the diffusion anisotropy are always much smaller than the imaging resolution, there will always be orientation averaging. This then requires a high angular resolution DTI acquisition and subsequent analysis to disentangle the signal (Frank, 2001, 2002). In this paper we have shown a method that allows the efficient acquisition of both high spatial resolution, high SNR efficiency compared to other RARE-based sequences, diffusion weighted data with significantly reduced field distortions, without the need for either distortion correction or a dual spin echo for eddy current compensation.

List of Symbols

MRI

magnetic resonance imaging

DT

diffusion tensor

DTI

diffusion tensor imaging

DST

diffusion simulation tractography

MD

mean diffusivity

FA

fractional anisotropy

ETL

echo train length

nz

number of slices

SNR

signal to noise ratio

T₂

transverse relaxation time constant

EPI

echo planar imaging

VDS

variable density spiral

esp

echo spacing

N_i

number of interleaves

b

b-factor

k

spatial frequency

g

gradient

s

slew rate

n

number of spiral turns

N

matrix size

A

N/2 \fov - amplitude factor for VDS trajectory

t

time

τ

VDS time dependent parameter

T_s2α

transition time from slew-rate limited to amplitude-limited region for VDS

T_es

ending time of the slew-rate limited region for VDS

t_end

is the time at the completion of the VDS

α

VDS parameter

β₁

VDS parameter

β₂

VDS parameter

x

spin position

s

signal

ρ

spin density

η

noise

ℋ

mapping from image space to signal space

P

projection operator (pseudo-inverse of \mathcal{H})

i

imaginary unit

e

Euler’s number or Napier’s constant

π

pi

sinc

sinc function

†

Hermitian conjugate

w

weights

â

estimated Fourier coefficient

W

weight matrix

FFT

fast fourier transform

MPI

message passing interface

ΔB

field variations from eddy currents

λ

eddy current decay constants

ξ

gradient transition times

c

eddy current expansion coefficient

CSF

cerebrospinal fluid

ϕ_ref

reference low frequency phase map

ϕ_l

low frequency phase map for interleave l