Abstract
Children with poor arithmetic fact mastery (n = 45) at the end of third grade were compared to grade-level peers with good arithmetic fact mastery (n = 60) in competencies related to reading and mathematics. Children were assessed longitudinally across second and third grades. When predictor variables such as IQ were held constant, the poor fact mastery and good fact mastery groups performed at about the same level and progressed at a comparable rate on math story problems and on broad reading achievement. The groups also progressed at a comparable rate on broad math achievement, although children with poor fact mastery performed at a significantly lower level. Children with poor fact mastery showed remarkably little growth on timed number facts during the study period, despite normal growth in other areas of mathematics. Deficits in fact mastery are highly persistent and appear to be independent of reading and language abilities.
Keywords: Mathematics, Learning disabilities, Cognitive development
Young children show uneven patterns of competencies in mathematics. In particular, some children cannot master basic arithmetic facts despite relatively strong problem-solving skills (Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Hanich, 2000; Jordan & Montani, 1997). Deficits related to mastery, or fast retrieval, of arithmetic facts is a key characteristic of children with mathematics difficulties (MD) who are good readers (Geary, Hamson, & Hoard, 2000, 1999; Hanich et al., 2001; Jordan, Hanich, & Kaplan, in press). In contrast, children with both MD and reading difficulties (RD) are characterized by weaknesses in problem solving as well as in arithmetic fact mastery.
Speed of processing numerical information appears to be a particular problem for children with MD only. Jordan and Montani (1997) presented children with MD only and children with MD/RD with number facts and math story problems, both in timed and in untimed conditions. All the problems involved addition or subtraction operations. On the timed condition, children were required to answer orally presented problems within 3 s. Relative to children with normal mathematics achievement, children with MD only were strong on untimed conditions but not on timed conditions. When given enough time, MD only children successfully represented the problems and employed verbal counting methods. Children with MD/RD performed worse than normally achieving children on untimed as well as on timed tasks. They inaccurately represented problems and made numerous counting mistakes, even in the absence of time constraints.
It has been suggested that number fact deficits are associated with general weaknesses in processing speed (Bull & Johnston, 1997) and in linguistic processes related to representing phonological information and retrieving information from long-term semantic memory (Ashcraft, 1992; Geary, 1993). If number facts are encoded in terms of their phonemic features, then there should be a connection between number fact mastery and word-level reading, which also depends on phonological representation (Miles, 1993; Robinson, Menchetti, & Torgesen, 2002). However, the presence of normal reading skills in children with MD only—who are characterized by number-fact weaknesses—and strong number-fact skills in children with word reading difficulties (i.e., RD only; Hanich et al., 2001) suggests a more fundamental, number-based explanation of fact retrieval deficits. For example, difficulties in manipulating nonverbal representations, such as a number line, may limit rapid processing of addition and subtraction number facts (Cohen, Dehaene, Cohochon, Lehericy, & Naccache, 2000).
In the present study, we focused specifically on children who have difficulties mastering addition and subtraction facts, rather than children with MD overall. We examined two groups of children: children with poor fact mastery and children with good fact mastery. For the purpose of this investigation, we defined fact mastery as the ability to compute an addition or subtraction number fact in 3 s or less (Hanich et al., 2001; Jordan & Montani, 1997). Although children may meet this criterion by retrieving a fact from memory, it is also possible for them to use a covert calculation shortcut, such as 5 + 5 = 10 so 5 + 6 = 11 (Baroody, 1999; Cohen et al., 2000; Siegler & Stern, 1998). Group classification was based on fact mastery at the end of third grade. To assess stability and growth, however, we assessed children’s performance on the same number facts task longitudinally at four time points, starting in the fall of second grade. Previous cross-sectional work (Ostad, 1997, 1999) suggests that number fact deficits in children are tenacious. But the participants in these studies appeared to have general intellectual impairments, and it is not clear whether they exhibited broad delays in mathematics or whether some had more specific weakness in fact mastery.
To provide information about growth in other areas of mathematics as well as in reading, we measured children’s performance on a standardized diagnostic test of broad math and reading achievement, on an untimed number combinations task, and on a verbal math story problems task over the same four time points. We also assessed children’s word reading speed to determine whether children with poor fact mastery are slower than children with good fact mastery in reading words as well as answering number facts. Finally, measures of oral vocabulary and IQ (verbal and nonverbal) gave us additional data about children’s cognitive functioning.
If deficiencies in fact mastery have a verbal basis then children with poor fact mastery should show deficiencies, relative to children with good fact mastery, in reading (particularly on a timed word reading task), vocabulary, and verbal problem solving. If, instead, nonverbal weaknesses underlie such deficits, then children with poor fact mastery should show relative weaknesses in nonverbal problem solving. If poor fact mastery is a reflection of general intellectual impairments, then children with poor fact mastery should show delays in both verbal and nonverbal processes and their growth between second and third grades should be generally slow in most areas.
Finally, we explored the relation between skill and growth in addition and subtraction to skill and growth in multiplication. We assessed the multiplication skills of a subset of children with good fact mastery and poor fact mastery over three time points between third and fourth grades. We examined multiplication speed as well as accuracy. Evidence from neurological studies points to a dissociation between multiplication and addition/subtraction (Cohen et al., 2000). Adults with severe dyslexia, apahasia, and acalculia—as a result of lesions in the left perisylvan area of the brain—perform better on addition and subtraction facts than on multiplication facts. Cohen et al. maintain that multiplication facts are solved by accessing a table of rote verbal associations whereas addition and subtraction facts are solved through manipulation of nonverbal number representations.
Because a main question of our study relates to skill growth, we used growth curve modeling to analyze the longitudinal data. Growth curve modeling provides an estimate of the average level of number fact competency at any time point as well as the average growth rate over time in the outcomes for the sample (Raudenbush & Bryk, 2002). It also provides an estimate of the average rate of acceleration in growth and is flexible enough to deal with nonequidistant measurements. Growth curve modeling allowed us to predict individual levels and growth by IQ, ethnicity, income, and gender as well as by the two fact mastery groups (i.e., good fact mastery and poor fact mastery).
Method
Participants
Participants were 105 third graders. Children were drawn from a pool of 180 children who participated in a three-year longitudinal study on the development of mathematical thinking. We selected children who, at the end of third grade, scored either in the bottom quartile (i.e., at or below the 25th percentile) or in the third quartile (i.e., between the 51st and 75th percentiles) on a measure of number-facts skill (i.e., forced retrieval of number facts, which is described in Materials and procedure). There were 45 children with poor fact mastery and 60 children with good fact mastery. Descriptive data for both groups of children, related to gender, ethnicity, parental income level, and third-grade math and reading achievement are presented in Table 1.
Table 1.
Descriptive information for participants, by fact mastery skill
| Group | N | M/F | Percent ethnic minority | Percent low SES | Percent special education | Reading composite percentile scores | Mathematics composite percentile scores |
|---|---|---|---|---|---|---|---|
| Poor fact mastery | 45 | 20/25 | 60 | 44 | 20 | 46 (25) | 34 (26) |
| Good fact mastery | 60 | 32/28 | 50 | 50 | 7 | 54 (24) | 52 (26) |
Note. Standard deviations are shown in parentheses. Children identified as ethnic minority were primarily African American (85%). Low income was determined by eligibility for the subsidized lunch program at school.
Materials and procedure
Each child was given the following tasks four times, twice in second grade and twice in third grade: forced retrieval of number facts; calculation of arithmetic combinations; math story problems; math achievement; and reading achievement. (Although a wide range of tasks was given to children as a part of the larger investigation, we only report findings from tasks that were relevant to the concerns of the present study.) All children were tested individually in their schools by one of several female experimenters who were thoroughly trained in the test procedures. Forced retrieval of number facts, calculation of arithmetic combinations, and math story problems were given in January and April of second grade and in November and May of third grade. The achievement tests were given in October/November and in May of second grade and in October/November and in April/May of third grade. The occurrence of nonequidistant measurement occasions is explicitly incorporated in the growth curve model estimation.
Forced retrieval of number facts
This task is based on a method developed by Russell and Ginsburg (1984) and Jordan and Montani (1997). The experimenter read eight number facts to the child, one at a time (i.e., 4 + 2; 9 + 4; 7 + 9; 3 + 8; 6 − 4; 13 − 9; 16 − 7; and 11 − 8). Each fact was also printed on a separate card and shown to the child at the same time the problem was read. The child was told to answer right away or to indicate that he or she would need more time. Immediately after the problem was read, the experimenter started timing. If the child did not answer correctly within 3 s or indicated that he or she would need more time, the item was marked wrong. To minimize the possibility of children using a simple “number-after” rule to derive an answer within 3 s, we did not use n + 1 combinations. Although a child still may have used a strategy other than direct retrieval to get the answer (Siegler & Stern, 1998; Jordan et al., in press), performance level on the forced retrieval task depends on fast mental processing. Internal reliability, using coefficient α, is 0.70.
Calculation of arithmetic combinations
In this task, the child was read a series of addition and subtraction combinations, but this time children were told to use any method they wanted to figure out the answer and were given as much time as they needed. (We used the term “combinations” for this task rather than “facts” because facts may suggest that retrieval is necessary for reaching solutions rather than application of calculation strategies, such as counting.) A printed version was presented as each problem was read and kept in full view of the child during problem solving. The problems were 9 + 8, 3 + 6, 5 + 6, 8 + 7, 9 − 3, 17 − 9, 1 − 5, and 15 − 8. In addition to recording the answer on each problem, the experimenter noted whether the child used his or her fingers to reach solutions. Internal reliability for calculation of arithmetic combinations, using coefficient α, is 0.66.
Math story problems
Ten math story problems were read to each child, ranging from simple to complex (Carpenter & Moser, 1984; Riley & Greeno, 1988; Riley, Greeno, & Heller, 1983). The experimenter presented the child with a written version of the problem as it was read and kept it in front of the child until the problem was solved. Four types of math story problems were given: change problems (e.g., Nina had 9 pennies. Then she gave 3 pennies to Anthony. How many pennies does Nina have now?), combine problems (e.g., Emily has 3 pennies. John has 6 pennies. How many pennies do they have altogether?), compare problems (e.g., Dennis has 7 pennies. Molly has 5 pennies. How many pennies does Dennis have more than Molly?), and equalize problems (e.g., Claire has 4 pennies. Ben has 9 pennies. How many pennies does Claire need to get to have as many as Ben?). All problems involved answers under 10. Children were told to solve the problems any way they wanted and were given a container of play pennies during the activity. Internal reliability for math story problems, using coefficient α, is 0.72.
For all children, order of task presentation was calculation of arithmetic combinations, math story problems, and forced retrieval of number facts.
Math and reading achievement
Math and reading achievement was assessed with the Woodcock–Johnson Psycho-Educational Battery—Revised (WJ; Woodcock & Johnson, 1990), a standardized battery with high reliability and validity (Hanich et al., 2001). Forms A and B were alternated throughout the four test sessions. The WJ Broad Mathematics Composite includes calculation and applied problems subtests. The WJ Broad Reading Composite is comprised of letter-word identification and passage comprehension subtests.
Other measures
Children also were given tests of IQ (January of third grade), word recognition speed (January of second grade), and oral vocabulary (January of second grade).
IQ was assessed with the Wechsler Abbreviated Scale of Intelligence (WASI; Weschler, 1999). The WASI yields verbal, performance (nonverbal/spatial), and full-scale IQ scores. Vocabulary and Similarities subtests comprise the verbal scale and Block design and Matrix Reasoning comprise the performance scale. All internal reliability estimates for the three IQs scales exceed 0.90. The correlation between the WASI and the Wechsler Intelligence Scale for Children—III is 0.87.
Oral vocabulary was assessed with the Peabody Picture Vocabulary Test—III (PPVT; Dunn & Dunn, 1997). The PVVT, a standardized measure, tests receptive word knowledge. Internal reliability, using coefficient α, is 0.95.
Children also were given the Test of Word Reading Efficiency (TOWRE; Torgesen, Wagner, & Rashotte, 1999) Form A, Sight Word Efficiency. The Sight Word Efficiency subtest assesses the number of printed words that can be read accurately in 45 s. It is a standardized measure with internal consistency of 0.93.
A multiplication task was given to children in the fall and spring of third grade. Additionally, a subset of the same children (40 with poor fact mastery and 54 with good fact mastery) was assessed on the multiplication task in the fall of fourth grade. This subset was used in the data analyses. The multiplication task consisted of 10 problems presented in the following order: 4 × 1; 7 × 8; 4 × 4; 2 × 3; 6 × 6; 3 × 5; 9 × 7; 3 × 6; 7 × 2; and 4 × 6. At the same time each fact was read aloud by the examiner a printed fact was presented. To estimate solution time, the experimenter began timing the child with a stopwatch immediately after reading the problem. As soon as children began stating their answer, the experimenter stopped timing. If the child answered before the experimenter finished reading the problem a time of 0 was recorded. If a child gave an answer but then wanted to think some more and answer again, the experimenter restarted the stopwatch. If the child stated a second answer after the original answer, the experimenter made a best estimate of how many additional seconds the child took. Response times were recorded for each multiplication fact. Although the stopwatch was marked in units of 0.1 s, times of 0.5 or greater were rounder up to the nearest whole number and times less than 0.5 were rounded down.
Results
We begin by describing the main analytic methodology for this paper—growth curve modeling. Growth curve modeling is a procedure that has been advocated for many years by researchers such as Tisak and Meredith (1990), Rogosa, Brandt, and Zimowski (1982), Muthén (1991), Willett (1988), and Willett and Sayer (1994) for the study of intra-individual differences in change. Growth curve modeling captures intra-individual differences in rates of growth and estimates the average initial level and average rate of growth taken to be estimates of the growth parameters in the population.
Growth curve modeling can be specified from two rather distinct perspectives. First, conventional growth curve modeling can be specified as a special case of multilevel modeling (Raudenbush & Bryk, 2002). In this context, the level-1 model consists of intra-individual differences in growth over time. The level-1 parameters consist of individual intercepts and slopes that can be modeled at level-2, or the individual level of analysis. The intercept parameters represent the outcomes at time t = 0, and this can be chosen to be at any point in the study. For this investigation, the intercept represents the outcome of interest for a particular student at the end of third grade. In addition to the linear rate of growth, a quadratic term can be added to the model that captures the acceleration or de-acceleration in the rate of growth over time. For this paper, we estimate both the linear and quadratic growth rates. Time-varying predictors can be included in the level-1 model, although they are not be used in the present study.
At level-2, individual differences in the intercepts and slopes can be modeled as functions of time-invariant individual characteristics. For this study, the time invariant predictors of the individual intercepts and slopes are gender, income, ethnicity, and IQ. These time invariant predictors are coded so that the average end-of-third grade score and average rate of growth are with respect to majority girls with average IQ who are not participating in a free or subsidized lunch program.
Growth curve modeling via the multilevel modeling perspective is a powerful and natural way of modeling growth. The popularity of the multilevel approach toward modeling growth notwithstanding, research by Muthén (1991) and Willett and Sayer (1994) has shown how conventional growth curve modeling can also be modeled as a special case of the general structural equation modeling (SEM) framework (Jöreskog, 1973). In this case, growth curve modeling is specified as a highly restricted factor analytic model where the factor loadings are fixed to yield the intercept and rate of growth, and the factors are then interpreted as latent randomly varying growth factors. In the case of simple two-level growth curve models, the HLM and SEM perspectives yield identical results. For this paper, we estimate growth curve models from the structural equation modeling perspective utilizing the software program AMOS (Arbuckle, 1999).
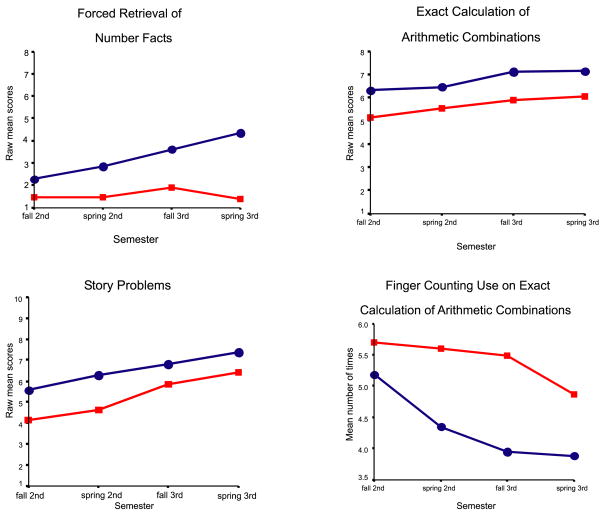
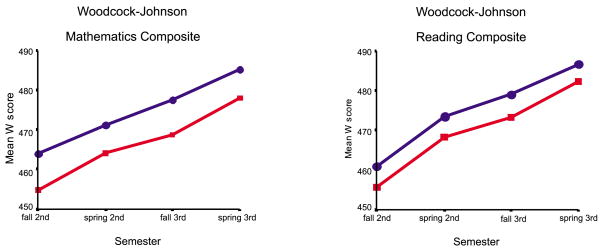
Growth curve analyses were performed on forced retrieval of number facts, calculation of arithmetic combinations (frequency of finger strategies as well as accuracy), math story problems, WJ Broad Mathematics, and WJ Broad Reading. Raw scores were used in all analyses with the exception of the WJ achievement tests, where W-scores (i.e., Rasch-scaled scores) were used. The average empirical growth trajectories by fact mastery group for the math tasks are shown in Fig. 1 and for the WJ achievement tests in Fig. 2.
Fig. 1.
Average empirical growth trajectories on mathematics tasks, by fact mastery skill. (Points represent the mean raw scores for each task.) (▨) poor fact mastery; (●) good fact mastery.
Fig. 2.
Average empirical growth trajectories on Broad Mathematics and Broad Reading Composites of the WJ, by fact mastery skill. (Points represent the mean W-scores for each scale.) (▨) poor fact mastery; (●) good fact mastery.
The analytic strategy that we followed is similar to block entry multiple regression analysis. We were interested in the added contribution of predictor variables over and above a simple baseline growth curve model. Thus, for each task, three growth curve models were computed: (1) Baseline model, which provides estimates of the slope and intercept; Table 2; (2) Model 1, which adds the effects of children’s fact mastery group; Table 3; and (3) Model 2, which adds the effects of time-invariant predictor variables (i.e., gender, income, ethnicity, and IQ; Table 4). In Model 2, boys, minority students, and students participating in the subsidized lunch program were dummy coded 1 and IQ was centered on the sample mean. Model 2 tests whether the differences in growth parameters as function of the fact master group are moderated by student background demographic characteristics. The parameters of each model reflect children’s growth over the period of the study (accounting for the nonequidistant measurement occasions). As noted above, we included linear and quadratic models in the analyses, although we focus our discussion on linear models because there was only one task that showed a significant acceleration (quadratic) effect.
Table 2.
Baseline model: Growth curve results for mathematics tasks and achievement tests
| Forced retrieval of number facts | Calculation of arithmetic combinations | Finger counting strategy use on calculation of arithmetic combinations | Math story problems | WJ mathematics composite | WJ reading composite | |
|---|---|---|---|---|---|---|
| Intercept | 3.09* | 6.69* | 4.33* | 6.96* | 481.78* | 484.64* |
| Slope | 0.02 | −0.00 | −0.01 | 0.07 | 1.20* | 0.93* |
| Variance (intercept) | 1.88* | 1.37* | 5.06* | 3.88* | 74.58* | 136.52* |
| Variance (slope) | 0.01* | 0.00 | 0.02* | 0.01* | 0.06 | 0.07 |
| R (int. slope) | 0.63* | 0.05 | 0.49* | 0.47* | 0.16 | −0.35 |
| Acceleration variable | −0.00 | −0.00 | 0.00 | −0.00 | 0.00 | −0.03* |
Note. p < .05.
Table 3.
Model 1: Growth curve results for mathematics tasks and achievement tests with effects of fact mastery skill
| Forced retrieval of number facts | Calculation of arithmetic combinations | Finger counting strategy use on calculation of arithmetic combinations | Math story problems | WJ mathematics composite | WJ reading composite | |
|---|---|---|---|---|---|---|
| Intercept | 4.35* | 7.18* | 3.93* | 7.36* | 484.99* | 486.56* |
| Slope | 0.10* | −0.00 | 0.07 | 0.05 | 1.20* | 0.86* |
| Variance (intercept) | 0.22 | 1.03* | 4.64* | 3.67* | 61.62* | 131.31* |
| Variance (slope) | 0.00* | 0.00 | 0.02* | 0.01* | 0.06 | 0.07 |
| R (int. slope) | 0.12 | 0.02 | 0.48* | 0.54* | 0.25 | −0.34 |
| Acceleration variable | −0.00 | −0.00 | 0.01* | −0.00 | 0.00 | −0.03* |
| Intercept on group | −2.95* | −1.14* | 0.96 | −0.93* | −7.47* | −4.50 |
| Slope on group | −0.19* | −0.00 | −0.19 | 0.03 | −0.01 | 0.19 |
| Acceleration on group | −0.00 | 0.00 | −0.01* | −0.00 | −0.00 | 0.01 |
Note. p < .05.
Table 4.
Model 2: Growth curve results for mathematics tasks and achievement tests with effects of fact mastery skill and time-invariant predictors
| Forced retrieval of number facts | Calculation of arithmetic combinations | Finger counting strategy use on calculation of arithmetic combinations | Math story problems | WJ mathematics composite | WJ reading composite | |
|---|---|---|---|---|---|---|
| Intercept | 4.28* | 7.07* | 4.37* | 7.43* | 484.62* | 489.33* |
| Slope | 0.10* | 0.00 | 0.07 | 0.04 | 1.23* | 0.77* |
| Variance (intercept) | 0.20 | 0.81* | 3.57* | 2.33* | 35.38* | 87.78* |
| Variance (slope) | 0.00* | 0.00 | 0.01* | 0.01* | 0.03 | 0.06 |
| R (int. slope) | 0.10 | 0.00 | 0.46 | 0.57* | −0.06 | −0.37 |
| Acceleration variable | −0.00 | −0.00 | 0.01* | −0.00 | 0.00 | −0.03* |
| Intercept on group | −2.91* | −1.03* | 0.78 | −0.46 | −5.37* | −2.22 |
| Slope on group | −0.19* | −0.01 | −0.21* | 0.03 | −0.01 | 0.18 |
| Acceleration on group | −0.00 | 0.00 | −0.01* | −0.00 | −0.01 | 0.01 |
| Intercept on gender | −0.01 | −0.49 | −1.29* | −0.83* | −2.59 | −3.82* |
| Slope on gender | 0.01 | −0.01 | 0.03 | −0.05 | 0.03 | 0.14 |
| Intercept on ethnicity | 0.06 | 0.77* | 0.21 | 0.60 | 2.56 | 2.09 |
| Slope on ethnicity | 0.01 | 0.03 | −0.02 | 0.05 | 0.14 | −0.03 |
| Intercept on income | 0.07 | −0.16 | 0.21 | −0.13 | −0.11 | −4.85* |
| Slope on income | −0.02 | −0.02 | −0.01 | 0.01 | −0.24* | 0.07 |
| Intercept on IQ | 0.01 | 0.04* | −0.07* | 0.10* | 0.49* | 0.55* |
| Slope on IQ | 0.00 | −0.00 | −0.01* | 0.00 | 0.01 | 0.00 |
Note. p < .05.
Forced retrieval of number facts
We present a thorough description of the results for the forced retrieval of number-facts task. This description is intended to help the reader interpret results for subsequent tasks, which are presented in a similar format but with less detail.
The average intercept and average slope on forced retrieval of number facts for the total sample are shown in the baseline model in Table 2. The average intercept representing the average raw score at the end of third grade was 3.09 (out of 8) and the average growth was 0.02 points over two years.
The effects of adding children’s fact mastery group to the growth curve model are summarized in Model 1 in Table 3. In this model, the slope and intercept refer to children with good fact mastery (dummy coded 0). The average raw score at the end of third grade for children with good fact mastery was 4.35 and the slope was 0.10. As expected, children with poor fact mastery had significantly lower scores at the end of third grade than children with good fact mastery (intercept). Regarding growth rate, children with poor fact mastery, on average, achieved at a slower rate than children with good fact mastery. Children with poor fact mastery showed almost no growth in fact mastery during the test period whereas children with good fact mastery showed steady, incremental growth (see Fig. 1).
The effects of time-invariant predictors of gender, ethnicity, income, and IQ are shown in Model 2 of Table 4. In this model, the average slope and average intercept refer to nonminority girls with average IQs with good fact mastery. The average intercept for this group is 4.28 and the slope is 0.10. None of the predictor variables were significant predictors of either the intercept or slope. As in Model 1, children with poor fact mastery had significantly lower scores at the end of third grade and achieved at a significantly slower rate than children with good fact mastery.
Calculation of arithmetic combinations
Holding predictor variables constant (Model 2 in Table 4), children with poor fact mastery ended third grade with significantly lower calculation of arithmetic combinations scores than children with good fact mastery. There were no differences in growth rate. IQ and ethnicity were significant predictors of the intercept, favoring children with higher IQ scores and minority children. There were no significant predictors of the slope.
Frequency of finger use on calculation of arithmetic combinations
There was no group effect in the frequency with which fingers were used at the end of third grade (Model 2 in Table 4). However, there was a group significant group effect on the acceleration of the growth rates. Children with good fact mastery decelerated more rapidly in finger use than children with poor fact mastery, who did not start tapering off until the third time point (i.e., early third grade; see Fig. 1). Gender and IQ were significant predictors of finger counting at the end of third grade. Girls used their fingers more often than boys and children with lower IQ scores used their fingers more often than children with higher IQ scores. IQ was also a significant predictor of the slope, indicating that children with higher IQs decline more in finger counting more than do children with lower IQs.
Math story problems
Controlling for predictor variables (Model 2 in Table 4), there were no significant group effects on the slope or the intercept. It should be noted, however, that children with good fact mastery had significantly higher scores than children with poor fact mastery without the predictors (see Model 1 in Table 3 and Fig. 1). Gender and IQ were significant predictors of the intercept, favoring girls and children with higher IQ scores. There were no significant predictors of the slope.
Math achievement
Holding predictor variables constant (Model 2 in Table 4), there was a significant group effect on the intercept. Children with good fact mastery had significantly higher WJ math scores at time 4 than children with poor fact mastery. There were no significant group differences in growth rate. IQ was a significant predictor of the intercept, favoring children with higher IQ scores. Income was a significant predictor of growth rate, with low-income children achieving at a slower rate than middle-income children.
Reading achievement
Considering predictors (Model 2 in Table 4), there were no significant group effects on the slope or the intercept for WJ reading achievement. Gender, income, and IQ were significant predictors of end of third grade scores, but not of the rate of growth over the study. Girls, children with higher IQ scores, and middle-income children program ended third grade with higher WJ reading achievement than boys, children with lower IQs and low-income children, respectively.
Summary of growth curve analyses
Holding predictors constant, children with good fact mastery had higher scores at the end of third grade than children with poor fact mastery in forced retrieval of number facts, calculation of arithmetic combinations, and WJ math achievement but not in reading achievement or math story problems. Children with good fact mastery achieved at a faster rate than their counterparts with poor fact mastery on forced retrieval of number facts and decelerated more quickly in finger use on arithmetic combinations. IQ predicted performance at the end of third grade on all of the tasks, except forced retrieval of number facts, and predicted the slope on finger counting. Gender predicted performance on math story problems (favoring girls), reading achievement (favoring girls), and frequency of finger counting (favoring boys), while income (favoring middle income) predicted reading achievement and ethnicity (favoring minorities) predicted calculation of arithmetic combinations at the end of the third grade.
Verbal and nonverbal competencies
The mean verbal and performance IQ (WASI) scores, oral vocabulary (PPVT) scores, and word reading speed (TOWRE) scores, are presented in Table 5. On Performance IQ, children with good fact mastery scored significantly higher than children with children with poor fact mastery, F (1, 103) = 10.45, p < .01. Children with good fact mastery and poor fact mastery did not differ in Verbal IQ, oral vocabulary or word reading speed, all language-based measures.
Table 5.
Scores on verbal IQ, performance IQ, PPVT, and TOWRE, by fact mastery skill
| Group | WASI verbal IQ | WASI performance IQ | PPVT | TOWRE |
|---|---|---|---|---|
| Poor fact mastery | 93.18 (12.01) | 87.38 (10.28) | 91.80 (11.59) | 97.60 (11.02) |
| Good fact mastery | 94.43 (10.66) | 94.25 (11.14) | 92.80 (12.74) | 100.32 (10.64) |
Note. Standard deviations are shown in parentheses.
Multiplication accuracy and speed
Only children who completed the multiplication task all three times (i.e., fall and spring of third grade and fall of fourth grade) were included in the longitudinal analysis. The mean multiplication scores and response times (by fact mastery group) are shown in Table 6. Taking predictors into account (Model 2 of Table 7), there was a significant effect of group on the intercept (favoring children with good fact mastery) but not on the slope. Children with good fact mastery performed more accurately than children with poor fact mastery but both groups progressed at about the same rate. There also were significant intercept effects for ethnicity (favoring minority children) and IQ (favoring children with higher IQs). A significant effect of the intercept on gender indicated that girls achieved at a faster rate than boys on multiplication. Estimates of response times (see Table 6) indicated that on average children in both fact mastery groups took a long time (i.e., >7 s) to answer the multiplication problems.
Table 6.
Mean number correct and mean response times on multiplication task, by fact mastery skill
| Group | Fall third grade |
Spring third grade |
Fall fourth grade |
|||
|---|---|---|---|---|---|---|
| Number correct | Response time | Number correct | Response time | Number correct | Response time | |
| Poor fact mastery | 1.65 (2.47) | 7.75 (6.37) | 4.65 (2.98) | 9.01 (6.87) | 5.35 (2.64) | 7.94 (4.49) |
| Good fact mastery | 2.19 (2.17) | 8.70 (5.54) | 6.04 (2.61) | 8.70 (4.83) | 6.46 (2.11) | 7.64 (4.30) |
Note. Standard deviations are shown in parentheses.
Table 7.
Multiplication growth curve results
| Effect | Maximum likelihood estimates |
||
|---|---|---|---|
| Baseline modela | Model 1b | Model 2c | |
| Intercept | 5.99* | 6.46* | 6.53* |
| Slope | 0.30* | 0.32* | 0.38 |
| Variance (intercept) | 5.69* | 5.39* | 3.79* |
| Variance (slope) | 0.02* | 0.02* | 0.03* |
| R (int. slope) | 0.84* | 0.85* | 0.59* |
| Intercept on group | −1.13* | −0.96* | |
| Slope on group | −0.04 | −0.06 | |
| Intercept on gender | −0.78 | ||
| Slope on gender | −0.10* | ||
| Intercept on ethnicity | 1.18* | ||
| Slope on ethnicity | 0.08 | ||
| Intercept on income | −0.38 | ||
| Slope on income | −0.02 | ||
| Intercept on IQ | 0.06* | ||
| Slope on IQ | −0.00 | ||
Baseline model: no fact mastery groups and no predictor variables.
Model 1: fact mastery groups (good fact mastery as reference group) and no predictor variables.
Model 2: fact mastery groups and time-invariant predictor variables (gender, ethnicity, income year 1, full-scale IQ).
p < .05.
Discussion
We compared children who at the end third grade showed poor mastery of addition and subtraction facts to their grade level counterparts who showed good fact mastery. We looked at development across second and third grades in selected numerical competencies as well as in broad math and reading achievement. Children’s word reading speed and general language and nonverbal abilities also were measured.
Our findings revealed that, when predictor variables of IQ, gender, income level, and ethnicity were held constant, children with poor fact mastery performed as well as children with good fact mastery on math story problems and on broad reading achievement at the end of third grade. Moreover, children with good fact mastery and poor fact mastery progressed at about the same rate in these areas during the course of the study. Children with poor fact mastery and good fact mastery also progressed at a comparable rate on calculation of arithmetic combinations (where time limits were not imposed) and on broad math achievement, although children with poor fact mastery performed at a lower level in these areas. In contrast, children with poor fact mastery showed remarkably little growth on timed number facts during second and third grades; their performance in the middle of second grade was about the same as their performance at the end third grade. However, children with good fact mastery, contrast, achieved at a steady rate on timed number facts throughout the study period. The poor fact mastery group’s relatively slow decline in finger use, which serves as a back-up strategy when answers cannot be derived automatically or through mental manipulations (Siegler & Jenkins, 1989), is a further indication of the persistence of fact retrieval deficits (Ostad, 1997, 1998).
Are fact mastery deficiencies a manifestation of a core weakness in verbal processes, a weakness that is common to reading and mathematics difficulties? Our findings did not reveal a link between deficits in fact mastery and word-level reading. In fact, children with poor fact mastery performed as well as children with good fact mastery on a test of word reading speed and a test of broad reading (that took into account word-level processes as well as comprehension). Number facts do not appear to be primarily encoded in terms of their phonemic features, as suggested by other work (Geary, 1993, 1994). Children with poor fact mastery also performed as well as children with good fact mastery in verbal IQ, story problem solving (when IQ was taken into account), and receptive vocabulary, indicating relatively strong verbal facility more generally.
The good fact mastery group showed a significant advantage over the poor fact mastery group on a measure of nonverbal IQ, which assessed children’s abilities to manipulate blocks to produce a stimulus design and to recognize and complete patterns. This finding supports the Cohen et al. (2000) assertion that weaknesses in accessing and manipulating nonverbal representations limit rapid processing of addition and subtraction number facts more than difficulties in language. Investigation of whether skill at and rate of learning nonverbal numerical abilities (e.g., pattern recognition, estimation, nonverbal calculation) in early childhood predict later difficulties in learning addition and subtraction facts would further explicate this issue.
A multiplication task was given to a subset of the study participants to examine skill and growth in addition and subtraction in relation to skill and growth in multiplication. It has been suggested that skill in multiplication depends on cognitive processes that are different from those needed for addition and subtraction (Cohen et al., 2000). That is, skill with multiplication facts relies on the ability to access verbal associations learned by rote whereas skill with addition and subtraction relies more heavily on facility in manipulating nonverbal number representations (as discussed above). Because multiplication is not typically taught until third grade, we started assessing children’s multiplication skill in third grade and continued into fourth grade. We found that across third and fourth grades, children with poor fact mastery performed worse than children with good fact mastery on the multiplication tables, although both groups progressed at a similar rate. (These data parallel our findings on the untimed calculation of addition and subtraction combinations task.) Our estimates of response times indicated that, even in fourth grade, most children took a relatively long time to answer (i.e., averaging over 7 s for both groups). Our accuracy and response time data suggest that multiplication facts were hard for all fourth graders and that children most likely used computational strategies (e.g., adding) to reach solutions rather than rote retrieval. Although the present findings do not support the rote verbal access hypothesis, group differences in accuracy may become attenuated with increased drill and practice on the multiplication tables. Moreover, an examination of performance and growth on a “forced retrieval” multiplication task in middle elementary school, like the one we used for addition and subtraction in the present study, might reveal more disassociations between addition/subtraction and multiplication fact mastery.
Overall, our study suggests that deficits in addition and subtraction fact mastery can be reliably identified in second grade, that they are highly persistent, and that they occur even when we hold predictor variables, such as IQ, constant. Children with poor fact mastery, as a group, do not show relative difficulties in reading and language but do show weaknesses in nonverbal reasoning. Potential markers of fact retrieval deficits should be explored in preschool, kindergarten, and first-grade children. Whether specific interventions related to accessing and manipulating representations on a number line can boost retrieval growth trajectories of children with fact retrieval deficits is an open question. It also is important to consider whether mastery of number facts leads to increased performance levels in broad math achievement. Previous work indicates that automaticity with lower-level number skills increases the ability to acquire and sustain general mathematical competence (Bahrick & Hall, 1991).
Acknowledgments
This study was supported by a grant from the National Institute of Child Health and Human Development (HD36672). We greatly appreciate the generosity of the children and teachers who participated in this project.
References
- Arbuckle JL. AMOS 4.0 Users’ Guide. Chicago: Smallwaters Inc; 1999. [Google Scholar]
- Ashcraft MH. Cognitive arithmetic: A review of data and theory. Cognition. 1992;44 doi: 10.1016/0010-0277(92)90051-i. [DOI] [PubMed] [Google Scholar]
- Baroody A. Children’s relational knowledge of addition and subtraction. Cognition and Instruction. 1999;17:137–175. [Google Scholar]
- Bahrick HP, Hall LK. Lifetime maintenance of high school mathematics content. Journal of Experimental Psychology: General. 1991;120:22–33. [Google Scholar]
- Bull R, Johnston RS. Children’s arithmetical difficulties: Contributions from processing speed, item identification and short-term memory. Journal of Experimental Child Psychology. 1997;65:1–24. doi: 10.1006/jecp.1996.2358. [DOI] [PubMed] [Google Scholar]
- Carpenter TP, Moser JM. The acquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education. 1984;15:179–202. [Google Scholar]
- Cohen L, Dehaene S, Cohochon F, Lehericy S, Naccache L. Language and calculation within the parietal lobe: A combined cognitive, anatomical and fMRI study. Neuropsychologia. 2000;38:1426–1440. doi: 10.1016/s0028-3932(00)00038-5. [DOI] [PubMed] [Google Scholar]
- Dunn LM, Dunn LM. Peabody picture vocabulary test. 3. Circle Pines, MN: American Guidance Service; 1997. [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association; 1994. [Google Scholar]
- Geary DC, Hamson CO, Hoard MK. Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability. Journal of Experimental Child Psychology. 2000;77:236–263. doi: 10.1006/jecp.2000.2561. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Hamson CO. Numerical and arithmetical cognition: Patterns of functions and deficits in children at risk for a mathematical disability. Journal of Experimental Child Psychology. 1999;74:213–239. doi: 10.1006/jecp.1999.2515. [DOI] [PubMed] [Google Scholar]
- Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology. 2001;93:615–626. [Google Scholar]
- Jordan NC, Hanich LB. Mathematical thinking in second-grade children with different types of learning difficulties. Journal of Learning Disabilities. 2000;33:567–578. doi: 10.1177/002221940003300605. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with co-morbid mathematics and reading difficulties. Child Development. doi: 10.1111/1467-8624.00571. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Montani TO. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997;30:624–634. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
- Jöreskog KG. A general method for estimating a linear structural equation system. In: Goldberger AS, Duncan OD, editors. Structural equation models in the social sciences. New York: Academic Press; 1973. pp. 85–112. [Google Scholar]
- Miles TR. Dyslexia: The pattern of difficulties. 2. London: Whurr; 1993. [Google Scholar]
- Muthén B. Analysis of longitudinal data using latent variable models with varying parameters. In: Collins L, Horn J, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington: American Psychological Association; 1991. pp. 1–17. [Google Scholar]
- Ostad SA. Developmental differences in addition strategies: A comparison of mathematically disabled and mathematically normal children. British Journal of Educational Psychology. 1997;67:345–357. doi: 10.1111/j.2044-8279.1997.tb01249.x. [DOI] [PubMed] [Google Scholar]
- Ostad SA. Developmental progression of subtraction strategies: A comparison of mathematically normal and mathematically disabled children. European Journal of Special Needs Education. 1999;14:21–36. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2. Thousands Oaks, CA: Sage; 2002. [Google Scholar]
- Riley MS, Greeno JG. Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction. 1988;5:49–101. [Google Scholar]
- Riley MS, Greeno JG, Heller JI. Development of childrens’ problem-solving ability in arithmetic. In: Ginsburg HP, editor. The development of mathematical thinking. New York: Academic Press; 1983. pp. 153–196. [Google Scholar]
- Robinson CS, Menchetti BM, Torgesen JK. Toward a two-factor theory of one type of mathematics disabilities. Learning Disabilities Research and Practice. 2002;17:81–89. [Google Scholar]
- Rogosa DR, Brandt D, Zimowski M. A growth curve approach to the measurement of change. Psychological Bulletin. 1982;90:726–748. [Google Scholar]
- Russell RL, Ginsburg HP. Cognitive analysis of children’s mathematics difficulties. Cognition and Instruction. 1984;1:217–244. [Google Scholar]
- Siegler RS, Jenkins E. How children discover new strategies. Hillsdale, NJ: Erlbaum; 1989. [Google Scholar]
- Siegler RS, Stern E. Conscious and unconscious strategy discoveries: A microgenetic analysis. Journal of Experimental Psychology: General. 1998;127:377–397. doi: 10.1037//0096-3445.127.4.377. [DOI] [PubMed] [Google Scholar]
- Tisak J, Meredith W. Longitudinal factor analysis. In: von Eye A, editor. Statistical methods in longitudinal research. Vol. 1. New York: Academic Press; 1990. pp. 125–149. [Google Scholar]
- Torgesen JK, Wagner R, Rashotte C. Test of word reading efficiency. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- Weschler D. Wechsler abbreviated scale of intelligence. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- Willett JB. Questions and answers in the measurement of change. In: Rothkepf E, editor. Review of research in education. Washington, DC: American Educational Research Association; 1988. pp. 345–422. [Google Scholar]
- Willett JB, Sayer AG. Using covariance structure analysis to detect correlates and predictors of individual change over time. Psychological Bulletin. 1994;116:363–381. [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock–Johnson Psycho-Educational Battery—Revised. Allen, TX: DLM Teaching Resources; 1990. [Google Scholar]