Mechanisms of Direct Radiation Damage in DNA, Based on a Study of the Yields of Base Damage, Deoxyribose Damage, and Trapped Radicals in d(GCACGCGTGC)₂

Abstract

Dose–response curves were measured for the formation of direct-type DNA products in X-irradiated d(GCACGCGTGC)₂ prepared as dry films and as crystalline powders. Damage to deoxyribose (dRib) was assessed by HPLC measurements of strand break products containing 3′ or 5′ terminal phosphate and free base release. Base damage was measured using GC/MS after acid hydrolysis and trimethylsilylation. The yield of trappable radicals was measured at 4 K by EPR of films X-irradiated at 4 K. With exception of those used for EPR, all samples were X-irradiated at room temperature. There was no measurable difference between working under oxygen or under nitrogen. The chemical yields (in units of nmol/J) for trapped radicals, free base release, 8-oxoGua, 8-oxoAde, diHUra and diHThy were G_total(fr) = 618 ± 60, G(fbr) = 93 ± 8, G(8-oxoGua) = 111 ± 62, G(8-oxoAde) = 4 ± 3, G(diHUra) = 127 ± 160, and G(diHThy) = 39 ± 60, respectively. The yields were determined and the dose–response curves explained by a mechanistic model consisting of three reaction pathways: (1) trappable-radical single-track, (2) trappable-radical multiple-track, and (3) molecular. If the base content is projected from the decamer’s GC:AT ratio of 4:1 to a ratio of 1:1, the percentage of the total measured damage (349 nmol/J) would partition as follows: 20 ± 16% 8-oxoGua, 3 ± 3% 8-oxoAde, 28 ± 46% diHThy, 23 ± 32% diHUra, and 27 ± 17% dRib damage. With a cautionary note regarding large standard deviations, the projected yield of total damage is higher in CG-rich DNA because C combined with G is more prone to damage than A combined with T, the ratio of base damage to deoxyribose damage is ~3:1, the yield of diHUra is comparable to the yield of diHThy, and the yield of 8-oxoAde is not negligible. While the quantity and quality of the data fall short of proving the hypothesized model, the model provides an explanation for the dose–response curves of the more prevalent end products and provides a means of measuring their chemical yields, i.e., their rate of formation at zero dose. Therefore, we believe that this comprehensive analytical approach, combined with the mechanistic model, will prove important in predicting risk due to exposure to low doses and low dose rates of ionizing radiation.

INTRODUCTION

Damage to DNA by the direct effect occurs through two routes. One is by direct ionization of the DNA. The other is by ionization of that portion of the solvent shell that is tightly bound to the DNA and rapid transfer of that damage to the DNA. Although the latter is physically an indirect effect, by transferring holes and electrons created in the DNA solvation shell to the DNA, the initial DNA lesions are indistinguishable from those formed directly in the DNA. The effect due to electron and hole transfer from the solvation shell to DNA has been termed the “quasi-direct” effect (1). The damage created by both routes is collectively called “direct-type” damage (2), distinguishing it from “indirect-type” damage that is due to reactions with hydroxyl radicals and aqueous electrons. Information on the direct effect is optimized by studying DNA in the solid state.

There is a wealth of information on free radicals trapped in solid-state DNA and DNA components (3, 4). Considerably less is known about end-product formation in DNA by the direct effect. Two studies have led the effort to link the free radical chemistry with end-product yields. Swarts et al. determined the release of unaltered base in freeze-dried salmon sperm DNA (5). Unaltered base release is directly coupled to deoxyribose (dRib) damage (6, 7); consequently it was possible to report the yields of dRib damage as function of DNA hydration (Γ). In a sequel, this group reported the yields of base damage due to the oxidative pathway (8). Later studies measured free base release (fbr) (9, 10) and strand break products (11–13) in oligo-deoxynucleotides and single-strand breaks (SSBs), double-strand breaks (DSBs), and base damage in plasmid DNA (14–16). The plasmid system is exquisitely sensitive and permits measurement of SSBs and DSBs at low doses, 0.1–5 kGy.

Previous work using analytical chemistry to measure end products, with the exception of the work on free base release (9, 10), has relied on data obtained at high doses, typically greater than 10–20 kGy. The reported yields were based on extrapolation of linear fits to the high-dose points. Because chemical yields are defined as the rate of increase in product at zero dose, it is important that the yields based on extrapolation be verified at low dose. Using techniques such as HPLC and GC/MS, this is quite difficult because the product to parent ratio is between 1:1000 and 1:10,000 at low doses. To overcome this unfavorable ratio, it is necessary to collect data at high doses. However, this poses a problem that is revealed in EPR studies.

The sensitivity of EPR is unusually high, and because it detects only paramagnetic species (free radicals in this case), the large background of undamaged DNA (which is diamagnetic) does not hinder detection. It is well established that the concentration of radicals trapped at low temperatures (4 K to 77 K) enters into dose saturation around 10 kGy. Divergence from a linear response begins somewhere between 5 and 10 kGy (17, 18). Dose saturation is particularly obvious in DNA because about 90% of the radicals are trapped by the bases and these radicals have a particularly high cross section for destruction. The deoxyribose-centered radicals, making up the other 10%, have a low cross section for destruction, and therefore the concentration of deoxyribose radicals increases linearly to unusually high doses, ~500 kGy (17, 18). The EPR data make it clear that, in solid-state DNA, single-track chemistry accounts for effectively all of the trapped radicals at doses below 5 kGy. Above 10 kGy, a mixture of single-track and multiple-track chemistry occurs. If data are collected at doses above 10 kGy, it becomes necessary to consider the contribution of multiple-track chemistry. Only by doing so can the mechanisms of damage formation be fully understood.

The strength of EPR, detecting only free radicals, is also a weakness. If damage occurs that does not pass through a trappable free radical intermediate, that damage is said to be EPR silent. If an EPR-silent pathway exists, it should be observed by comparing the chemical yields of product with free radical precursors. The extent that end-product yield exceeds trapped radical yield is the chemical yield of damage that has no observable free radical precursor. Mechanistically, we view this as product formed between energy deposition and thermalization, entailing predominantly reactions that occur within a spur of ionizations. This pathway is referred to as “molecular”, referring to molecular products such as H₂ for which there is no scavengeable free radical precursor (19).

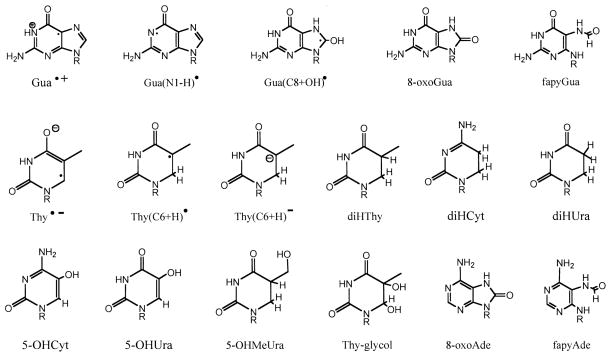
In this work, we measured the chemical yields of direct-type products by collecting data at doses low enough to obtain an improved measure of the slope at zero dose. We also investigated the role of various reaction pathways, including the molecular pathway, in product formation. We applied combination of techniques, EPR, HPLC and GC/MS, to well-defined solid-state samples of DNA. The DNA was the oligodeoxynucleotide, d(GCACGCGTGC)₂, known to crystallize in the A-form, and it was studied as polycrystalline powder and as films. EPR was used to measure free radical trapping at 4 K. HPLC was used to measure free base release and strand break products. GC/MS was used to measure four major base damage products: 8-oxoGua, 8-oxoAde, diHUra and diHThy. For the notation and structures of these and other compounds discussed below, see Fig. 1. Primarily because of very low product background in unirradiated d(GCACGCGTGC)₂, it was possible to collect data at low doses and obtain improved measurements of the chemical yield of the base damage products.

FIG. 1.

Chemical structures and abbreviations used in this paper.

MATERIALS AND METHODS

Film Preparation

The oligodeoxynucleotide, d(GpCpApCpGpCpGpTpGpC), was purchased from Ransom Hill, where it was desalted by reverse-phase chromatography. We refer to this palindromic oligomer, in which the 3′ phosphate is absent, as d(GCACGCGTGC)₂. Without further purification, d(GCACGCGTGC)₂ was dissolved in Omnipur nuclease-free water (Merck) to give 3–7 μg of oligomer/μl solution. The DNA concentration was determined by measuring the absorbance at 260 nm using a 20-μl aliquot diluted 50 times. Films were prepared in two distinct ways. One was by placing 20–85-μl drops onto Teflon petri dishes. The other was by drawing solution into silylated suprasil-quartz capillary (1.5 mm outer diameter) open at both ends (20). In both cases, evaporation inside a sealed container was governed by a much larger volume of saturated NaOH, presumed to maintain a relative humidity of 8% at room temperature. Clear pliable films reached steady-state weights in 1–2 weeks using the Teflon dishes and 3–4 weeks using the quartz tubes. Under these conditions, it is assumed that the hydration level of the DNA is 2.5 mol water per mol nucleotide. The film weights, 200–400 μg, were measured with a Cahn C-30 Microbalance to an accuracy of ±1 μg. DNA content of the films varied between 60–66% across all sample sets; within any given data set (the data used for one dose–response curve), the DNA content varied by 1–3%. There was no distinguishable difference in the results obtained from films prepared on Teflon plates or in suprasil-quartz tubes.

Crystallization

Crystalline d(GCACGCGTGC)₂ was prepared following the method of Ban and Sundaralingam (21). Polycrystalline material was harvested by methods described previously (22). The calculated water content of these crystals is Γ = 14 (23).

Irradiation

X irradiation was performed under air at room temperature for base-damage product analysis by GC/MS and free base release by HPLC. Irradiation was under nitrogen or oxygen in the analysis of strand break products by HPLC. For EPR measurements, irradiation and measurement was at 4 K under vacuum. The X-ray source was a Varian/Eimac OEG-76H tungsten-target tube operated at 70 keV and 20 mA, and the X-ray beam was filtered by 40-μm-thick aluminum. At room temperature, the dose rate was 2.2 kGy/min to the sample container. Attenuation by the wall of containers decreased the dose at the sample by 50% in the case of the Teflon-grown film contained in a 1.5-ml screw-cap (with siliconized o-ring) tube and by 52% in the case of film contained in a quartz capillary. For EPR measurements, the dosimetric methods were described previously (24); the dose rate to the samples contained within quartz capillaries was 24 kGy/h.

EPR

The concentration of radicals trapped at 4 K was measured using a Q-band (35 GHz) Varian E-12 EPR spectrometer operating at a nominal microwave output of 20 mW attenuated by 50 db and using a ruby standard mounted inside the EPR cavity. Free radical yields were determined as described by Purkayastha (18).

HPLC

A Waters Alliance^™ HPLC with a 2690 solvent system was used for quantifying free base release and strand break products. For free base release measurements, separation was by a Phenomenex Columbus C-18 reverse-phase column (4.6 × 250 mm, 5 μm, 110 Å pore size) at 30°C using 40 mM ammonium acetate (pH 6.8) as a mobile phase and by applying a linear gradient 0.9–10% of acetonitrile over 25 min. As described previously (10), the unaltered bases were detected with a Waters 996 photodiode array detector by their absorbance at 254 nm and quantified against uracil as an internal standard.

For strand break products, the samples were treated at room temperature only, i.e., under conditions that reveal primarily prompt strand breaks and not alkaline-labile strand breaks. Separation was done on a Dionex DNA Pac PA-100 4 × 250-mm strong anion-exchange column as described previously (13).

GC/MS

After irradiation and storage for 4–8 h at room temperature, the films were dissolved in nuclease free water at a mass ratio of 1:1. Subsequent DNA hydrolysis, derivatization and data acquisition closely followed the methods described previously (8). Key steps and differences are given here.

DNA hydrolysis was performed on freeze-dried samples prepared with a known addition of internal standards (6-azathymine, 8-azaadenine, thymine-α,α,α,6-d₄, diHUra-U-¹³C-U-¹⁵N, diHThy-α,α,α,5,6,6-d₆, 5-OHMeUra-α,α-d₂-1,3-¹⁵N, 5-OHCyt-2-¹³C-1,3-¹⁵N, Thy-glycol-α,α,α,6-d₄, 8-oxoAde-8-¹³C-6,9-¹⁵N₂, 8oxoGua-4,5,6,8-¹³C₄, fapyAde-[5-formyl-¹³C]-diamino-¹⁵N₂, fapyGua-4,5,6-¹³C₃-[5-formyl-¹⁵N]) to d(GCACGCGTGC)₂. Hydrolysis was by 88% formic acid for either 90 min or 30 min; the longer time was used to detect primarily 8-oxoGua, 8-oxoAde, diHUra and diHThy, and the shorter time was used to detect primarily fapyGua and fapyAde. Subsequently, the samples were freeze dried and then held under vacuum for 5 or more days. Hydrolyzed d(GCACGCGTGC)₂ was trimethylsilylated by adding 120 μl of degassed N,O-bis(tri-methyl-silyl)trifluoroacetamide (BSTFA) with 1% tri-methylchlorosilane (TMCS)/5:1 acetonitrile + pyridine/butanethiol (10:4:1) to the freeze-dried samples and then holding the samples under dry nitrogen gas (O₂ < 100 ppm) in a sealed chamber at 22°C for 60 min.

GC/MS, working under selected ion monitoring (SIM), was used to quantify base products. The instrument was the one used previously, a Hewlett-Packard 5890B GC with a Hewlett-Packard 5970B MSD. See ref. (8) for instrument settings and run conditions. Base damage products were quantified using isotope dilution methods. A careful calibration scheme minimized artifacts that arise during hydrolysis and derivatization.

To test the quantitative accuracy of the three major base products, 8-oxoGua, diHUra and diHThy, known amounts of the authentic product where added to d(GCACGCGTGC)₂ and then analyzed by the procedure described above in analyzing X-irradiated d(GCACGCGTGC)₂. The recovery of the authentic compounds was 97 ± 9% for 8-oxoGua, 117 ± 14% for diHUra, and 111 ± 15% for diHThy, where the standard deviations are based on 13 measurements. These recovery values were used to adjust the measured yields of product. For example, the yield of 8-oxoGua is reported in Table 4 as 1.03× (1.0/0.97) the measured yield.

TABLE 4.

Parameters in Eq. (4) Used to Fit the Dose–Response Curves for Major Products in d(GCACGCGTGC)₂ Irradiated at Room Temperature Given as a Weighted Average over N Experiments

Product	k1 nmol/J	±SDa	k2 nmol/J	±SD	k3 1/MGy	±SD	k4 1/MGy	±SD	G(P) nmol/J	±SD	N
8-oxoGua	101	49	10	12	12	12	100	140	111	62	6
8-oxoAde	2	2	2	2	0	0	77	37	4	3	3
diHUra	99	139	28	21	11	14	190	130	127	160	6
diHThy	36	52	3	8	4	2	59	120	39	60	5
Free base									93	15

Note. Examples for fits to one data set are shown in Fig. 8.

^aCalculated using standard statistical procedure: for (A ± a)/(B ± b) = (D ± d), where A/B = D, then d = D × [(a/A)² + (b/B)²]^1/2.

Chemical Yields

For the films, the chemical yields were based on a target mass consisting of d(GpCpApCpGpCpGpTpGpC) plus 9 ${\text{NH}}_4^{+}$ counter ions and 9 × 2.5 water molecules. For the crystalline samples, the yields were based on the entire sample mass, for which the calculated level of water is 14 waters per nucleotide (23). Not accounted for in the crystalline samples is an unknown concentration of Co²⁺ as an impurity. The impurity arose because the crystal growing solutions contained cobalt hexamine and its presence was indicated by color, ranging from pale yellow to dark orange, depending on the level of Co²⁺ incorporation.

RESULTS AND ANALYSIS

Trapped Free Radicals at 4 K

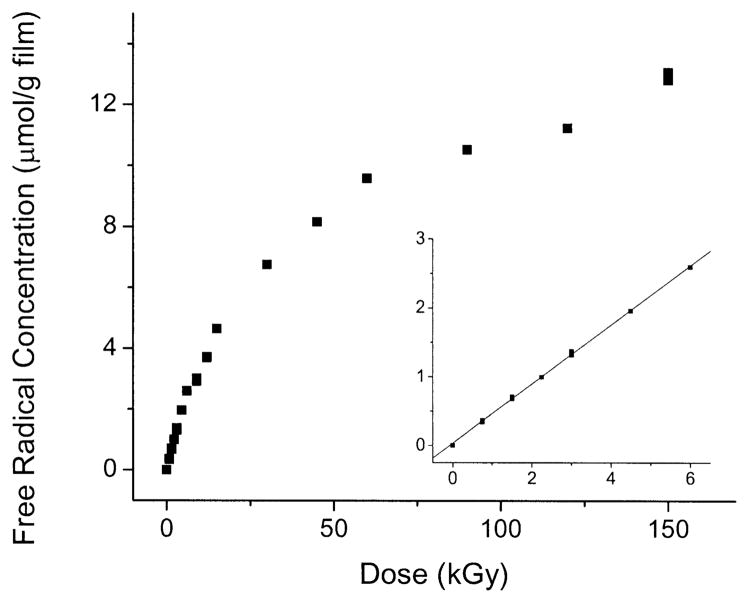
The concentration of free radicals trapped in films of d(GCACGCGTGC)₂, X-irradiated and observed at 4 K, increased linearly from 0 to 6 kGy, as shown in Fig. 2. At higher doses, the rate of change decreased until a lower, approximately linear, rate of change was maintained. The slope at zero dose was used as a measure of the chemical yield for total free radicals, G_total(fr), trapped by the oligomer. G_total(fr) is given in Table 1. The total complement of radicals consists, to a very good approximation, of radicals formed by one-electron oxidation of deoxyribose, one-electron oxidation of purines, and one-electron reduction of pyrimidines (3, 4, 14, 18, 25). Based on a considerable body of information on radical trapping by DNA (3, 4, 14, 18, 25), the value of G_total(fr) is the sum of the respective yields for each of these constituents, G_dRib(fr) = G_Pur(fr) + G_Pyr(fr). Each of these component yields can be estimated. These estimates are given in Table 1; they were calculated as follows.

FIG. 2.

Dose–response curves for free radicals trapped in d(GCACGCGTGC)₂ film X-irradiated and measured at 4 K. The inset shows the low-dose region and the line, fitted to the data ≤6 kGy, from which the chemical yield reported in Table 1 was determined.

TABLE 1.

The Measured Chemical Yield of Total Free Radicals, G_total(fr), Trapped by d(GCACGCGTGC)₂ X-Irradiated and Observed at 4 K

	Yield (nmol/J)	Standard deviationsa (nmol/J)	Percentage of total
Gtotal(fr)	618	±60	100
GdRib(fr)	62	±10	10
Gbase(fr)	556	±70	90
Gpyr(fr)	309	±30	50
Gpur(fr)	247	±100	40

Notes. The yields for trapping by deoxyribose, bases, pyrimidines and purines are calculated from the percentages in the last column as described in the text.

^aThe SD for G_total(fr) was calculated from the straight-line fit to the low-dose points shown in Fig. 2. SD for the remaining yields, which were calculated from G_total(fr) were calculated from the SD of G_total(fr).

The first step of the calculation is to divide G_total(fr) into two components, G_dRib(fr) and G_base(fr), where G_base(fr)= G_Pyr(fr) + G_Pur(fr). These two components are determined from the bimodal nature of this dose–response curve (18). The dose response for the base radicals is characterized by a large chemical yield, G_base(fr), and a large cross section for radiation destruction, k_base. Thus, if base radicals could be viewed in isolation, the dose–response curve would rise sharply, bend over around 10 kGy, and then flatten to zero slope at higher doses. The dose response of the deoxyribose radicals is characterized by a small yield, G_dRib(fr), and small destruction constant, k_dRib. The dose response of sugar radicals in isolation is described by a curve that is linear, has a small slope, and remains linear until dose saturation sets in at unusually high doses, >500 kGy (18, 26). Thus the slope for total radical concentration in the high-dose range, 100–500 kGy, is largely dictated by G_dRib(fr). By extending the dose–response curve out to very high doses, ~1 MGy, it is possible to partition the dose–response curve into these two components (18). Due to a lack of high-dose data on d(GCACGCGTGC)₂, accurate partitioning could not be done; instead we took advantage of results obtained previously. Partitioning done on plasmid DNA gives G_sugar(fr) = 9–11% of G_total(fr) (14), and for a series of crystalline oligodeoxynucleotides, the fraction due to G_sugar(fr) had a wider variation, 10–20% (18). Because the former measurements are more robust than the latter, and because they are in good agreement with those of Shukla et al. (27), we assume here that G_dRib(fr) = 10% of G_total(fr). G_base(fr) is then obtained from G_total(fr) − G_dRib(fr).

The second step is to divide G_base(fr) into its two components, G_Pyr(fr) and G_Pur(fr). This entails three assumptions. One, there exists a 1:1 stoichiometry between radicals formed by one-electron oxidation and one-electron reduction, giving G_ox(fr) = G_red(fr) = 0.5G_total(fr). Two, one-electron reduction occurs exclusively at the pyrimidines; this gives G_Pyr(fr) = G_red(fr) = 0.5G_total(fr). Three, one-electron oxidation results in radical trapping only by deoxyribose and the purine bases. The value of G_Pur(fr) is the difference between 0.5G_total(fr) and G_dRib(fr). The last column in Table 1 recasts this set of assumptions in terms of percentages.

Free Base Release

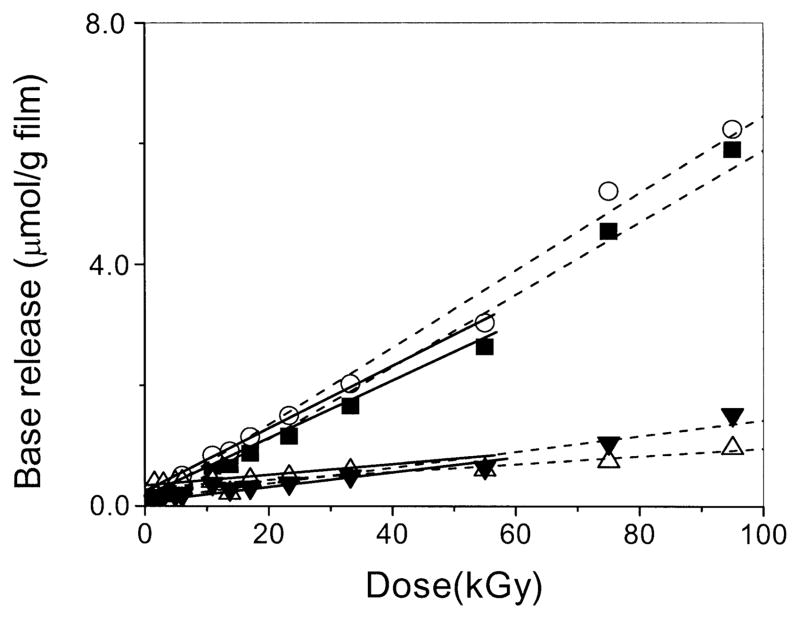
The dose–response curves for release of each of the four bases from d(GCACGCGTGC)₂ films irradiated at room temperature are shown in Fig. 3. As reported for the d(CGCGCG)₂ films (10), the dose response for each base is linear from 0 to 80 kGy. Because the background levels of the bases are very small, the curves pass very close to the origin. We consider the yield of total base release to provide a fairly accurate measure of the yield of deoxyribose damage. This has been shown to be the case for the indirect effect (6, 7), and it appears to hold for the direct effect (5, 9). This linearity therefore corroborates the above analysis of the trapped free radical dose response in which the deoxyribose radical component is considered to be linear from zero to high dose.

FIG. 3.

Dose–response curves for the release of cytosine (■), guanine (○), thymine (△) and adenine (▼;) from d(GCACGCGTGC)₂ films X-irradiated at room temperature under air. The broken lines show the linear fit from 0–95 kGy, and the solid lines show the linear fit to the data <60 kGy. There was no statistically significant difference between the slopes of these two fits, demonstrating that high-dose points remain in line with low-dose points. The slope of the latter was used to determine the chemical yields reported in Table 2.

The yields of free Gua, Cyt, Ade, Thy and their sum are reported in Table 2. The sum, G(fbr) = 93 ± 8 nmol/J, is discussed further below. Given that the ratio of bases in this decamer is G:C:A:T = 4:4:1:1, the releases of Gua, Ade and Cyt are within one standard deviation of what would be predicted if the base exerts no influence on the damage resulting in the release. The release of thymine, on the other hand, is below the yield expected, raising the possibility of a dependence of deoxyribose damage on sequence context as observed previously (10).

TABLE 2.

The Chemical Yields of Unaltered Free Base Released from d(GCACGCGTGC)₂ X-Irradiated at Room Temperature

	Yield		Ratio: G value in column 1 divided by G value listed below
Free base	nmol/J	SDa	G(Gua)	SDb	G(Cyt)	SD	G(Ade)	SDb	G(Thy)	SDb
Gua	41	6	1.0	0.2	1.0	0.2	5.1	1.5	10.3	5.3
Cyt	40	3			1.0	0.2	5.0	1.4	10.0	5.2
Ade	8	2					1.0	0.4	2.0	1.1
Thy	4	2							1.0	0.7
Total free base released	93	8	0.44	0.08	0.43	0.07	0.09	0.02	0.04	0.02

^aCalculated from the straight-line fits shown in Fig. 3.

^bThe SD for the ratios were calculated using (A ± a)/(B ± b) = (D±d), where A/B = D, then d = D × [(a/A)² + (b/B)²]^1/2.

Strand Break Products

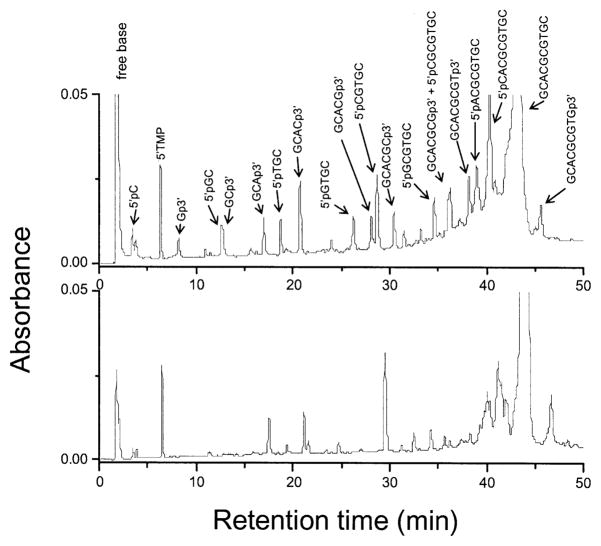
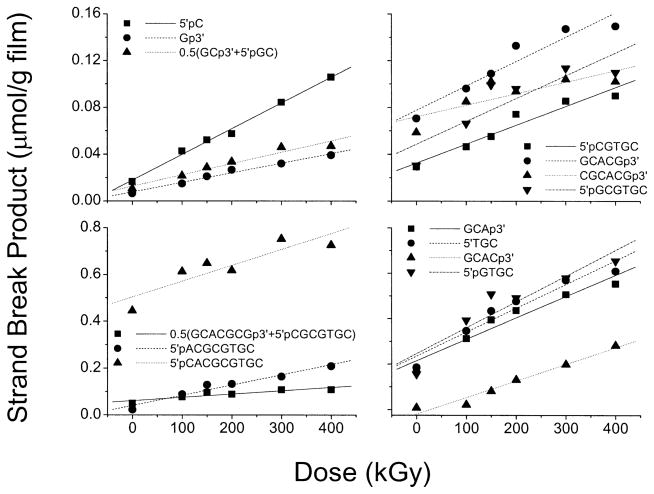
The concentrations of products due to prompt strand breaks in d(GCACGCGTGC)₂ films were measured by ion exchange HPLC. A chromatogram taken after a 540-kGy dose is compared with the zero-dose background in Fig. 4. The dose–response curves for 16 out of the 18 products being monitored are given in Fig. 5. The background levels for many of the products were significant, as is reflected in the non-zero intercepts with the vertical axis. The plots display the same qualities as those reported for a series of other oligodeoxynucleotides (11–13). In all cases, the minimum dose required to detect product above the background level is ~50 kGy. One might be concerned, therefore, that the use of only high-dose data makes it uncertain whether these dose–response curves are linear across the entire dose range, particularly at low dose (0–10 kGy). There are three reasons why the assumption of linearity is likely to be valid. First, the data extrapolate to zero at zero dose (11–13). Second, the presumed deoxyribose radical precursors do not dose saturate, as discussed above. Third, free base release, which is tightly coupled to the strand break reaction, is clearly linear at low dose [Fig. 3 and ref. (10)]. Therefore, these slopes, even though they are determined from high-dose points, are assumed to be reasonable measures of the chemical yields for each strand break product.

FIG. 4.

HPLC profile of d(GCACGCGTGC)₂ film X-irradiated at room temperature under N₂. The doses were 540 kGy (upper panel) and 0 kGy (lower panel). Separation was by a Dionex DNA Pac PA-100 4 × 250-mm strong anion-exchange column at 60°C using 50 mM Tris (pH 10.22) as a mobile phase and applying a linear NaCl gradient (0.1–1 M NaCl over 40 min). Detection was at 260 nm and quantification was against 5′-TMP as an internal standard.

FIG. 5.

Dose–response curves for strand break products containing either 3′ or 5′ phosphate end groups analyzed by HPLC of d(GCACGCGTGC)₂ film X-irradiated at room temperature under N₂. An example of a chromatogram is shown in Fig. 4. The yields given in Table 3 are calculated from the slopes of the lines fitted to the data. As noted in Table 3, the peaks from two of the long-chain products could not be resolved. Two pairs of products, GCp3′/5′pGC and GCACGCGp3′/5′pCGCGTGC, ran together; for each pair, half of the peak intensity was assigned to each product.

Only products terminated in either 3′- or 5′-phosphate were measured in our strand break analysis, the yields of which are presented in Table 3. Within the rather wide limits of the standard errors, there was neither a difference between samples irradiated under O₂ or N₂ nor a difference between samples prepared as films or crystalline. The lack of resolution of some of the elution peaks either prevented measurements on some products or required estimates, as detailed in the table footnotes. Because of the missing products, the SSB yield cannot be obtained by simply summing over the measured strand break products. However, an estimate obtained by using the yield of the products related by sequence symmetry to fill in the missing information is given at the bottom of Table 3. This rough estimate gives an SSB yield of 40–60 nmol/J. This is notably lower than G(fbr), an observation we return to in the Discussion.

TABLE 3.

The Yields of 3′- and 5′-Phosphate Strand Break Products Produced in d(GCACGCGTGC)₂ X-Irradiated at Room Temperature

Yield (nmol/J)									Yield (nmol/J)
Crystalline		Film		Film					Film		Film		Crystalline
Air	SDa	O2	SD	N2	SD	3′-Phosphate product	Lost dRib	5′-Phosphate product	N2	SD	O2	SD	Air	SD
N/Ab		N/A		N/A		N/A	1	5′pCACGCGTGC	7.5	2.1	19.2	4.1	4.4	0.6
9.8	1.7	13.5	1.9	6.9	0.5	Gp3′	2	5′pACGCGTGC	5.4	0.7	9.7	1.3	3.4	0.3
6.0	1.7	7.5	2.4	5.0	1.1	GCp3′	3	5′pCGCGTGC	3.6	0.9	5.8	1.7	2.9	0.7
4.2	0.9	6.8	1.3	2.2	0.3	GCAp3′	4	5′pGCGTGC	3.2	0.9	7.2	1.4	1.8	0.3
4.6	1.3	4.4	0.8	1.8	0.2	GCACp3′	5	5′pCGTGC	3.5	0.4	5.6	0.5	4.5	0.9
2.9	0.6	7.4	1.3	3.9	0.6	GCACGp3′	6	5′pGTGC	2.4	0.5	6.1	1.2	0.2	0.0
3	0.5	4.9	0.9	1.5	0.6	GCACGCp3′	7	5′pTGC	3.7	0.5	9.5	1.8	4.2	0.9
2.4	0.4	5.8	1.7	3.6	1.7	GCACGCGp3′	8	5′pGC	5.0	1.7	7.5	1.7	6.0	1.7
2.7	0.3	N/Dc		N/D		GCACGCGTp3′	9	5′pC	6.9	0.5	13.5	1.9	11.6	3.2
N/D		N/D		N/D		GCACGCGTGp3′	10	N/A	N/A		N/A		N/A
36	3.0	50	4.2	25	2.2		Measured total strand breaks		41	2.4	37	16	39	3.9
							Average of measured total SSBsd		33	3	43	6	37	5
							Estimated total SSBse		41		63		42

Note. The yields shown in italics are for products that co-elute with another product, GCp3′ and 5′pGC, GCACGCGp3′ and 5′pCGCGTGC. In both cases, the yield was estimated by dividing the co-eluting peak in half.

^aCalculated from straight-line fits in Fig. 5.

^bNot applicable because damage of terminal sugar creates no short chain product.

^cNot determined because the product peak could not be resolved.

^dAverage based on one half of the sum of 3′- and 5′-phosphate products.

^eTotal SSBs estimated by using the yield of 3′ (5′) product for those cases where the 5′ (3′) product was not determined.

Base Damage Products

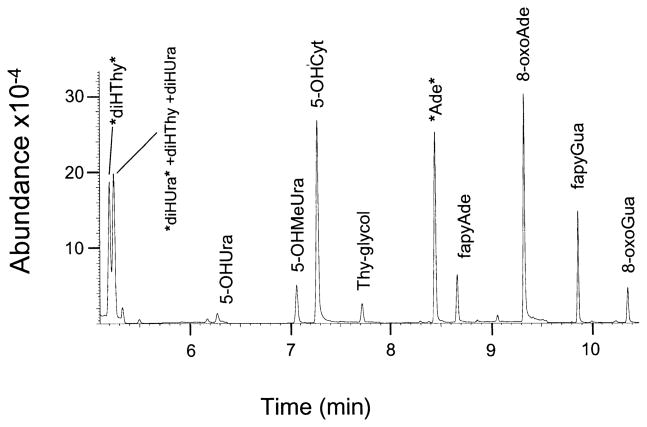
Our GC/MS analytical method used selected ion monitoring techniques that were optimized for quantifying 10 base damage products. A gas chromatogram of the products and internal standards is shown in Fig. 6. The abbreviations used for the products are given in Fig. 1. Note that the actual elutant is the trimethylsilylated derivative of the product, not the product itself.

FIG. 6.

GC/MS chromatogram of the trimethylsilylated authentic compounds representing the group of direct-type base end products quantified in this work. The labels *diHThy* and *diHUra* are the isotopically labeled forms of diHThy and diHUra, respectively, and the label *Ade* represents the internal standard, 8-azaadenine.

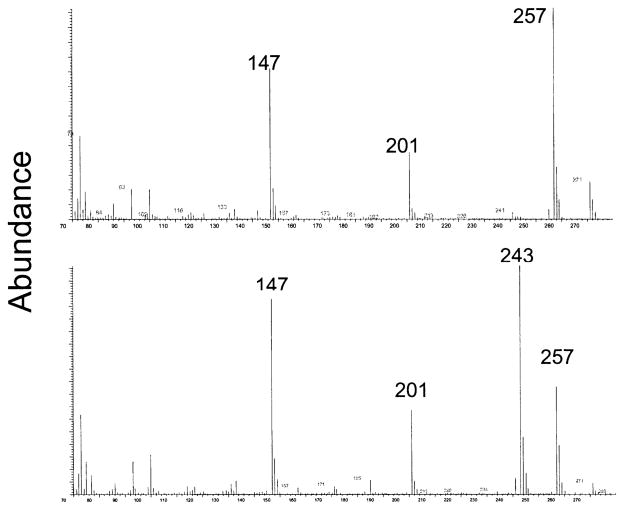
Examples of mass spectra for the diHUra and diHThy derivatives are shown in Fig. 7. Quantification of diHUra used the ion fragments at 243 m/e against the internal standard line at 249 m/e. For diHThy, the ion fragment was at 257 m/e and internal standard line was at 263 m/e. As can be seen in Fig. 7, diHUra presents an ion fragment at 257 m/e as well. When quantifying diHThy, in the presence of diHUra, it was necessary to subtract out the fraction of the 257 m/e line assignable to diHUra. diHThy was the only product reported on here that required this type of correction for overlapping ion fragments.

FIG. 7.

Mass spectrum of the trimethylsilylated forms of two authentic compounds, diHThy (upper panel) and diHUra (lower panel). diHThy is the only product of those being measured in this work using SIM for which the representative ion at 257 m/e is coincident with a minor ion from another co-eluting product, in this case an ion fragment from diHUra at 243 m/e. Therefore, as explained in the Materials and Methods, quantification of diHThy requires a correction based on the measured amount of diHUra in the sample.

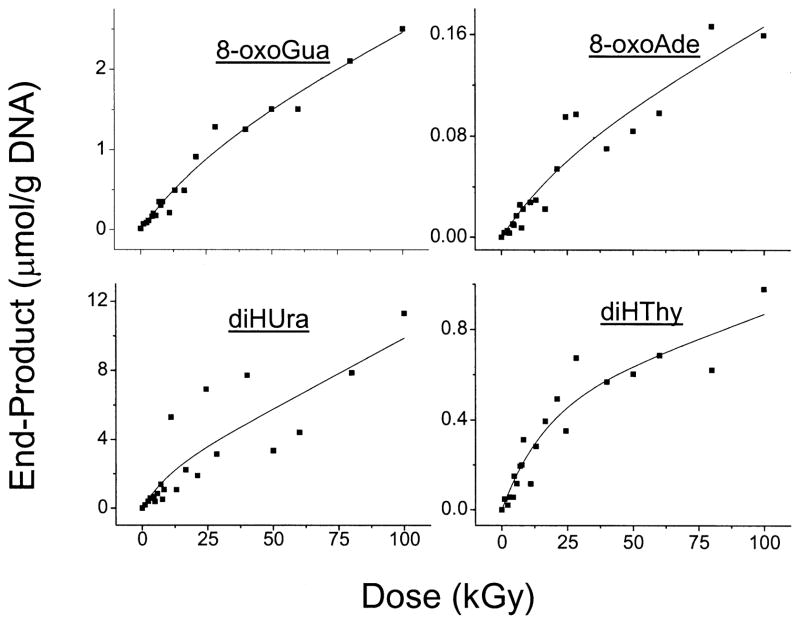
Of the 10 products being monitored, four, 8-oxoGua, 8-oxoAde, diHUra and diHThy, gave yield measurements with standard errors of ~100% or less. Dose–response curves for these four, all from the same experiment, are shown in Fig. 8. The yields of these products, presented in Table 4, were calculated by the formalism presented in the next subsection.

FIG. 8.

Dose–response curves for four base end products derived from d(GCACGCGTGC)₂ films X-irradiated at room temperature under air. The data shown in all four panels were collected in the same experiment, in which all of the films were irradiated, hydrolyzed, derivatized and then analyzed by GC/MS. The curves shown were derived from a non-linear least-squares fit to Eq. (4). A statistical average of the parameters determined from these other similar fits is given in Table 4.

Due to high background levels of fapyGua and fapyAde, the measurement of product yields was not possible at low doses, <14 kGy. For example, because the background of fapyGua was 4–6 μmol/J, a yield of fapyGua comparable to that of 8-oxoGua (~100 nmol/J) would not have been measurable. Four other products, 5-OHCyt, 5-OHUra, 5-OHMeUra and Thy-glycol, gave low yields with standard errors ranging from 200% to 5000%. Because of these uncertainties, they are not included in the analysis below.

There was no significant effect of oxygen on product formation. Dose–response measurements were made in the high-dose range (>20 kGy) with samples irradiated under nitrogen instead of air with no observable effect (data not shown). Also, a comparison of irradiated samples dissolved in deaerated and aerated solutions showed no significant difference in the dose response over the entire dose range. Experiments confined mainly to the high-dose range were performed on crystalline d(GCACGCGTGC)₂, and these showed the expected levels of 8-oxoGua but no significant yields of diHUra and diHThy. We presumed that the loss of dihydropyrimidine products was due to the presence of Co²⁺ in the crystal lattice. But since the concentration of Co²⁺ in the crystals is unknown (it is present in the lattice as an impurity) and because quantities of crystalline material were limited, we did not investigate this effect further.

Mechanistic Model for Describing Product Dose Response

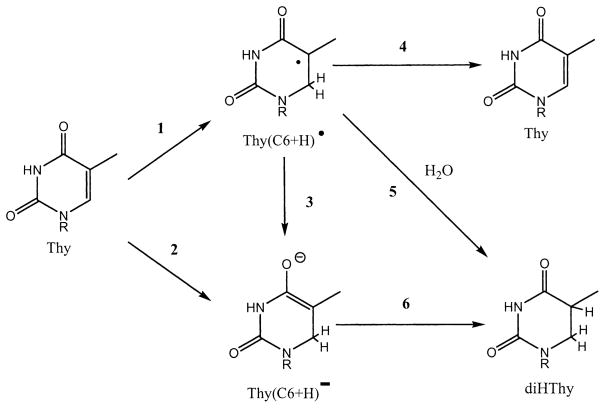
In Fig. 9, the reaction pathways used in the model are illustrated for the specific case where the end product is diHThy and the parent molecule is thymine. In reaction 1, thymine is one-electron reduced and then protonated to give the trappable radical Thy(C6+H)^•. The precursor to Thy(C6+H)^• is Thy^•−, which is efficiently trapped at 4 K. The conversion of Thy^•− to Thy(C6+H)^• has been observed by others when DNA irradiated at 77 K was warmed to 140–200 K (17, 28). For samples irradiated at room temperature, it is Thy(C6+H)^• that is assumed to accumulate. In reaction 3, one-electron reduction of Thy(C6+H)^• gives the diamagnetic product Thy(C6+H)^•. It may protonate in the film, or upon dissolution, give diHThy as shown in reaction 6. Competing with reaction 3 is the radiation destruction reaction 4, which leads to a non-radical product, typically a back reaction to Thy. Another reaction pathway to formation of Thy(C6+H)^• entails a two-electron reduction of Thy, as indicated in reaction 2. From our EPR measurements on d(GCACGCGTGC)₂, we can estimate the yield of Thy^•− at 4 K, but the yield of Thy(C6+H)^• is not known. The three pathways leading to diHThy formation are generalized to include all of the detected end products using the notation shown in Fig. 10.

FIG. 9.

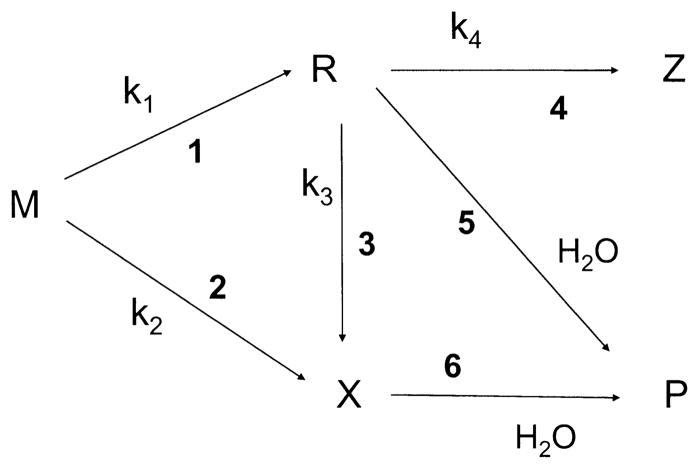
Mechanistic model employed in the analysis of dose–response curves for direct-type DNA products. Three pathways are shown, beginning with ionization of parent molecule M and ending with formation of product P. The intermediates are trappable radical R and diamagnetic damage precursor X. Z represents a side product, which will predominantly be the same as M, being formed by a back reaction from R.

FIG. 10.

A specific example of the mechanistic model shown in Fig. 9, based on Thy ≡ M and diHThy ≡ P.

Each of the three distinct pathways shown in Fig. 10 begin with ionization of the parent molecule M. In the major pathway, M can give a trappable radical R by reaction 1 and, upon solvation of the sample, R gives the end product P by reaction 5. In a minor pathway, M can go directly to a diamagnetic precursor X by reaction 2, which may be identical to P or, by reaction 6, X may give P upon solvation of the sample. The high-dose pathway requires interaction between a pre-existing radical, R, and another radiation track. In this case R is converted, by one-electron oxidation/reduction, to either X by reaction 3 or the side product Z by reaction 4. Most often Z ≡ M; i.e., R is returned to the parent state. We call these three pathways “trappable-radical single-track” (1 and 5), “molecular” (2 and 6), and “trappable-radical multiple-track” (1, 3 and 6).

The dose dependence for the formation of product P by these three pathways can be described by a system of differential and algebraic equations for R, X and P:

$$\text{dR}/\text{dD}={\text{k}}_1-({\text{k}}_3+{\text{k}}_4)\text{R}$$ (1)

$$\text{dX}/\text{dD}={\text{k}}_2+{\text{k}}_3\text{R}$$ (2)

$$\text{P}=\text{R}+\text{X}$$ (3)

Solution of this system of equations can be expressed in a form

$$\begin{array}{l}\text{P}=[{\text{k}}_4{\text{k}}_1/{({\text{k}}_3+{\text{k}}_4)}^2]\{1-exp[-({\text{k}}_{\text{3}}+{\text{k}}_4)\text{D}]\}\\ +[{\text{k}}_3{\text{k}}_1/({\text{k}}_3+{\text{k}}_4)]\text{D}+{\text{k}}_2\text{D},\end{array}$$ (4)

where the indexes of formal reaction rates k_j match the reaction numbers in Fig. 9. According to this solution, the maximum concentration of R in solid films is expressed in the form

$${\text{R}}_{max}={\text{k}}_1/({\text{k}}_3+{\text{k}}_4).$$ (5)

Furthermore the model predicts that the low-dose slope of P as a function of D is given by

$$G(\text{P})={\text{k}}_1+{\text{k}}_2,$$ (6)

and the slope at high dose, S_high(P), is given by

$${\text{S}}_{\text{high}}(\text{P})={\text{k}}_2+{\text{k}}_3{\text{R}}_{max}.$$ (7)

If S_high(P) is extrapolated to zero dose, the intercept, HD_inter(P), is

$${\text{HD}}_{\text{inter}}(\text{P})=({\text{k}}_4/{\text{k}}_1){\text{R}}_{max}^2.$$ (8)

Fitting the experimental data using four adjustable parameters (k₁, k₂, k₃ and k₄) produced the parameters given in Table 4. Although the least-squares error for any given fit is relatively small, the standard deviation (SD) between separate experiments is large. We performed six experiments for this analysis, but not all of these gave data that could be analyzed for each product. The number of experiments, N, used to calculate the SD is given in the last column. An example of the fit to each of the four base products, all for the same experiment, are given by the curves shown in Fig. 8.

DISCUSSION

The dose–response curves for products derived from deoxyribose damage were distinctly different from the curves for products derived from base damage. Deoxyribose damage was linear from zero to very high doses, ~90 kGy for base release (see Fig. 3) and ~500 kGy for stand break products (Fig. 5). Base damage was not linear (Fig. 8); the slope in the 0–10-kGy range was about twice that of the slope in the 20–90-kGy range. The linearity found for dRib damage correlates with the linearity observed for the radicals trapped by deoxyribose (18, 29). Likewise, the lack of linearity in base damage is similar to the lack of linearity observed for radicals trapped by the bases, which enter into dose saturation at ~10 kGy (18, 29). As discussed further below, these correlations support the previously proposed mechanism of end-product formation where the reaction proceeds through free radical intermediates (4, 8, 30). We have labeled this the trappable-radical single-track pathway.

If the only reaction pathway giving rise to direct-type base damage is the trappable-radical single-track pathway, then the dose–response curve would be expected to dose saturate at low doses (5–10 kGy) in a manner parallel to that observed for the precursor radicals (18). That this does not happen is evidence of at least one other pathway. Given the substantial evidence (17, 18, 31) that track-track interactions become prevalent at doses between 5 and 10 kGy, it follows that precursor radicals, such as T(C5+H)^• in Fig. 9, are undergoing one-electron oxidation or reduction. It has been assumed that a radical produced by reduction, such as T(C5+H)^•, is oxidized so as to lead back to the parent. The fact that k₄ is much larger than k₃ for diHThy in Table 4 supports that assumption. Indeed, this is true for each of the base products listed in Table 4. However, with the exception of 8-oxoAde, k₃ is not zero. (The 8-oxoAde data, for reasons discussed below, was not robust enough to calculate k₃.) Simply, k₃ combined with k₄ are the only parameters that simulate a bend in the response curve; if they are zero, the curve generated by Eq. (4) is straight. We conclude, therefore, that base end products are formed by a trappable-radical multiple-track pathway at high doses. In the case of the dihydropyrimidines, this entails two one-electron reductions. In the case of the 8-oxo-purines, this entails two one-electron oxidations. Although the accumulation of base end product has a quadratic dependence on dose at very low dose, it will have a distinctly linear appearance at high dose, with a slope given by Eq. (6). But the slope at high dose is not the chemical yield, and while the intercept of the high-dose slope, Eq. (7), is non-zero, it would be difficult to detect a non-zero intercept in cases where the background obscures data collection at doses below 10 kGy, as was the case in the study of salmon sperm DNA (5).

Based on the logic of the preceding paragraph, the linear dose response found for free base release and strand break products means that k₃ is zero, and deoxyribose damage therefore does not entail a multiple-track reaction pathway. Knowing this, one can then ask if the trappable-radical single-track pathway accounts for all of the damage. For d(GCACGCGTGC)₂, it appears that it does not. The calculated yield of deoxyribose radicals, 62 ± 10 nmol/J, falls short of the yield of free base release, 93 ± 8 nmol/J. This shortfall of ~30 nmol/J is smaller than that observed for SSBs in plasmid DNA (60 nmol/J) (14) and free base release in d(CGCGCG)₂ (80 nmol/J) (10). [As a caveat, we note that the base release for d(GCACGCGTGC)₂ was performed on room temperature-irradiated samples and the above comparison assumes that base release is the same for samples irradiated at 4 K. This assumption is based on the previously observed lack of an effect of sample temperature during irradiation for free base release in d(CGCGCG)₂.] As proposed previously, we hypothesize that this shortfall is due to two one-electron oxidations of the deoxyribose, an example of the molecular pathway. In the case of the chemical yield of deoxyribose damage, the molecular pathway is comparable to the trappable-radical single-track pathway.

Projection to DNA with a CG:AT Ratio of 1:1

If the GC:AT ratio is projected from the 4:1 ratio of the oligomer to a 1:1 ratio, the chemical yield of total damage would decrease from 374 nmol/J for the oligomer to 349 nmol/J for DNA with a 1:1 GC:AT ratio. The decrease in yield is due to the decreased percentage of CG, a consequence of CG being more prone to direct damage than AT. In DNA with a 1:1 base ratio the damage would partition as follows: 20 ± 16% 8-oxoGua, 3 ± 3% 8-oxoAde, 28 ± 46% diHThy, 23 ± 32% diHUra, and 27 ± 17% dRib damage. Using free base release to calculate dRib damage, the ratio of base damage to deoxyribose damage would be ~3:1.

Using these percentages to calculate expected yields for DNA with a GC:AT of 1:1, comparison can be made with previous results on freeze-dried salmon sperm DNA, Γ = 2.5, γ-irradiated under N₂ (5, 8, 32). To make the comparison, the values from these studies were increased by 10% to account for the 10% excess salt included in the target mass. For salmon sperm DNA, the yields, in units of nmol/J, for 8-oxoGua, 8-oxoAde, diHThy, diHUra and free base release were 111 ± 16, 1.5 ± 0.2, 28 ± 11, 17 ± 3, and 80 ± 3, respectively. The respective values projected from the decamer results are 69 ± 38, 10 ± 10, 79 ± 100, 98 ± 150, and 93 ± 8. One should expect reasonable agreement in free base release yields, as seen here, because this measurement is insensitive to the dose range employed. That is, high-dose data up to ~90 kGy give the same results as low-dose data due to the extended linearity of free base release (Fig. 3). The salmon DNA yields for 8-oxoAde, diHThy and diHUra were lower than the values projected from the decamer. This is also expected because these values were based on high-dose data, and the lack of linearity results in a lower apparent yield. The comparison of 8-oxoGua yields does not fit these expectations. We suggest that this stems from the gentler derivatization conditions employed in the current work, which reduced fortuitous oxidation of guanine to a greater extent than in the earlier work.

The Two Major Base Reduction Products

The findings here and in previous studies (8, 32) indicate that the yield of diHUra is comparable to the yield of diHThy. Based on EPR studies, electron trapping by DNA at 4 K is distributed between cytosine and thymine in a 4:1 ratio (33, 34). However, at higher temperatures (120–180 K), the excess electrons are thermally mobilized, escaping from cytosine and dropping into a deeper trap at thymine (35). As a result, the free radical distribution at higher temperatures is dominated by the relatively stable Thy(C6+H)^• (17). Therefore, if the dihydropyrimidines are formed exclusively by the trappable-radical single-track pathway, one would expect G(diHThy) ≫ G(diHUra). As explained below, the finding that the projected values are similar to one another can be attributed at least in part to the molecular pathway providing an additional route for dihydropyrimidine formation.

Our model attributes the yield of end product, G(P), to the sum of k₁ and k₂. The contribution of the molecular pathway is reflected by k₂. For diHUra k₂ is ~20% of G(P), whereas for diHThy it is ~10%. The model indicates, therefore, that the molecular pathway plays a larger role in diHUra formation. We offer a conjecture on why this may occur, which is based on a key difference between the radicals formed by one-electron reduction of cytosine and thymine. The difference is that proton transfer to the former is thermodynamically more favorable than for the latter (36, 37). Thus the cytosine radical anion, rapidly neutralized by proton transfer, may undergo one-electron reduction more readily than the thymine radical anion. If cytosine is more prone to double reduction within a spur, then the molecular pathway would contribute more to G(diHUra) than it would to G(diHThy).

Two Base Oxidation Products

Oxidation of the two purines, Gua and Ade, are two of the three sites from which statistically significant yields of oxidation products were identified, the third being deoxyribose. Gua, given that it has the lowest oxidation potential, is expected to be the major site of hole capture within the base stack (36, 37). This is also predicted from EPR studies, which show the precursor to 8-oxoGua (38), one-electron oxidized Gua [Gua(N1-H)^•], dominates the population of radicals produced by electron loss (28, 39). The results given in Table 4, however, suggest that Ade is also an effective hole trap. Extrapolating to a 1:1 ratio of GC:AT, the yields of 8-oxoGua and 8-oxoAde would be G(8-oxoGua) = 69 ± 38 nmol/J and G(8-oxoAde) = 10 ± 10 nmol/J. The yield of 8-oxoAde accounts for ~15% of the combined yields. This is somewhat surprising given that there is no evidence to date that adenine is able to compete with guanine with respect to hole trapping.

The mechanism of 8-oxo-purine formation is of interest, particularly for 8-oxoGua, which has been studied extensively. The mechanism proposed by Cullis and coworkers (38) is widely accepted for fully hydrated DNA. By this mechanism, OH⁻ adds to the guanine radical cation, Gua^•−, to yield the Gua(C8+OH)^•, which upon subsequent oxidation forms 8-oxoGua. But the decamer films contain only ~2.5 waters per nucleotide. Because these waters are presumed to be tightly bound to the backbone phosphate, it seems unlikely that they react with the guanine radical cation to produce the Gua(C8+OH)^• in the solid phase. Further, the formation of 8-oxoGua in these films shows no difference, within our limits of error, between films irradiated under O₂ and N₂ and no difference for films dissolved in water that was deoxygenated or not. Therefore, we suggest that in the absence of water, 8-oxoGua formation proceeds through an intermediate X, as in Fig. 9, where X is formed by two one-electron oxidations and when the sample is solvated X reacts to give 8-oxoGua.

Products Derived from Deoxyribose Oxidation

The yield of strand break products, G(sb products) = 41–63 nmol/J, is significantly less than the yield of free base release, G(fbr) = 93 ± 8 nmol/J. This is expected for two reasons. One is that some unknown fraction, presumably a small fraction, of the SSBs result in strand break fragments containing sugar fragments (11, 12). The chromatograms consistently show relatively small peaks that could be due to such fragments, and these are not included in the analysis. The other is that deoxyribose damage initiated by loss of hydrogen from C1′ results in free base release and a stable strand containing deoxyribonolactone (40, 41). Under the conditions used here, the C1′ pathway would yield free base but no cleavage products. C1′ damage appears to account for a large fraction, up to 30%, of the deoxyribose damage through the indirect effect (41, 42). If this high percentage were to hold true for the direct effect, it would account for much of the gap between G(fbr) and G(sb) products found here for films of the decamer.

Balance between Products Initiated by One-Electron Oxidation and Reduction

If one considers only the major products, one would expect the oxidation products to roughly balance against the reduction products. The yield for all the oxidation products detected (8-oxoGua, 8-oxoAde and dRib-damage represented by fbr) was 208 ± 80 nmol/J and the yield for all the reduction products detected (diHUra and diHThy) was 166 ± 220 nmol/J. Within the rather large error limits, there is balance.

It should be noted, however, that there is an imbalance for radicals trapped in salmon testes DNA γ-irradiated at 77 K; the radicals produced by reduction exceed those produced by oxidation by ~1.4:1.0 (28). The authors suggested that hole-hole combination reactions, occurring within the spur, might account for the observed radical imbalance. This suggestion is consistent with our model and findings. Two important consequences of hole-hole recombination, which is the molecular pathway (reaction 2 in Figs. 9 and 10), are (1) a reduction in the yield of trapped radicals produced by one-electron oxidation and (2) the formation of end products derived from double oxidation, i.e., 8-oxoGua and 8-oxoAde. Because the trapped radicals are, according to the model, presumed to go forward to the same products, the loss of trapped precursor radicals does not mean there will be a corresponding loss of product.

Balance between the Yield of Trapped Radicals at 4 K and Stable End Products

Ideally for this analysis, yields of the intermediate radical, R in Fig. 10, would be determined. In the absence of this determination, one can obtain a rough estimate of what the yield of R is likely to be from the yield of trapped radicals at 4 K. Based on previous work on oligodeoxynucleotides, annealing samples irradiated at 4 K to room temperature reduced the 4 K radical yield by 70–90% and irradiation at room temperature gave radical yields comparable to the yields obtained by annealing to room temperature (43, 44). Thus an estimate of the radical yields at room temperature will be 10–30% of the 4 K yield of 610 nmol/J, giving 60–180 nmol/J. The total product yield was 374 ± 300 nmol/J. In spite of the large errors, once again this raises the point that the yield of trappable radicals appears insufficient to account for the yield of end product.

There are Other Damage Pathways

We want to emphasize that the mechanistic model proposed here is not meant to cover all of the pathways that lead to direct-type damage in DNA. For example, strand breaks are formed by the dissociative electron attachment of low-energy electrons (45), and radical formation on deoxyribose, need not come from direct ionization of the DNA backbone or hole transfer from the solvation shell; it can occur by way of electronic excited states of the purine radical cations (46–48). But we do suggest that the proposed model provides an explanation for the dose–response curves of the more prevalent end products. While the quantity and quality of the data fall considerably short of proving the hypothesized model, the model does explain the data in a way consistent with these new results and with our current understanding of radical reactions in solid-state DNA. We do not know of any other published model that does so.

CONCLUSIONS

1. The chemical yields and dose–response curves were measured for 8-oxoGua, 8-oxoAde, diHUra, diHThy and deoxyribose damage (as judged by free base release) produced from dry d(GCACGCGTGC)₂ by the direct effect at room temperature. The yields were determined and the dose–response curves explained by a mechanistic model consisting of three reaction pathways: trappable-radical single-track, trappable-radical multiple-track, and molecular.

2. The chemical yields of the five products are G(fbr) = 93 ± 8, G(8-oxoGua) = 111 ± 62, G(8-oxoAde) = 4 ± 3, G(diHUra) = 127 ± 160, and G(diHThy) = 39 ± 60. If the base content is projected from the decamer’s GC:AT ratio of 4:1 to a ratio of 1:1, the percentage of the total measured damage (349 nmol/J) would partition as follows: 20 ± 16% 8-oxoGua, 3 ± 3% 8-oxoAde, 28 ± 46% diHThy, 23 ± 32% diHUra, and, 27 ± 17% dRib damage.

3. The projected yield of total damage is higher in CG-rich DNA because both C and G are prone to damage relative to A and T.

4. The ratio of base damage to deoxyribose damage is ~ 3:1.

5. The projected yield of diHUra is comparable to the yield of diHThy.

6. The projected yield of 8-oxoAde is not negligible.

7. The projected yield of trappable deoxyribose radicals is insufficient to account for the total yield of deoxyribose damage (measured by free base release).

8. It appears that the yield of trappable base radicals may be insufficient to account for the total yield of base product.

9. Within the limits of large standard errors, there is a balance between products derived from electron loss and electron gain.