Scaling Aspects of Block Co-Polymer Adsorption on Curved Surfaces from Nonselective Solvents

Abstract

In this paper, we have developed a geometric-based scaling model that describes the adsorption of diblock copolymer chains from good solvents and θ-solvents onto reactive surfaces of varying curvatures. To evaluate the impact of particle size on the adsorption process, we probed the adsorption of poly(styrene-bmethymethacrylate) (PS-PMMA) diblock copolymers from solvents with different degrees of selectivity on aluminum oxide (Al₂O₃) surfaces belonging to particles of different sizes. When the adsorbed PMMA layer is dense enough (in the case of a θ-solvent for the PMMA block), our results show good correlation between the theory and experimental results, pointing to the formation of a PMMA adsorption layer and a brushlike PS layer. Conversely, when adsorption occurs from a nonpreferential solvent, particularly on particles with high curvature, the PMMA adsorption layer at the surface becomes less dense and the grafted PS moiety exhibits a transitional morphology consisting of several layers of increasingly sparsely spaced blobs.

1. Introduction

The adsorption of polymeric chains onto various substrates has been the subject of extensive research in recent years.^1–13 This process is governed by a competition between the adsorption energy per polymer segment in contact with the substrate,^13–15 the loss of conformational entropy due to chain confinement on the surface,^16,17 and the interactions between the polymer and the solvent.^1,2,18–21 Of particular interest is the adsorption of polymers on metallic or metal oxide nanoparticles upon their formation. The adsorbed polymer chains act as steric and hydrophobic barriers that prevent the aggregation of the metallic clusters beyond an equilibrium size, thus imparting a stabilizing effect to the nanoparticles. Hence, polymer adsorption plays a major role in the control of particle size during polymer-mediated particle synthesis,^22–29 and on the characteristics of the particle suspensions in the polymer solutions.^22–29

It has been shown, both theoretically and experimentally,^30–33 that the characteristics of the adsorbed polymer layer are strongly dependent on the radii of the substrate particles. In our previous article,³³ we have developed a simple model that was based on scaling arguments,^34–38 to describe the adsorption of a polymer from a good solvent onto particles of different sizes. Our work incorporated results obtained from adsorption experiments into the scaling model that we developed and thus probed the validity of the model and its predictive capability. To highlight the specific role that the size of the adsorbing particle imparts on the extent of polymer adsorption, we limited ourselves to one type of polymer and followed its adsorption on surfaces that differed only in the magnitude of their curvature, i.e., from flat surfaces to very small particles, but consisted of the same chemical makeup. Our fundamental premise was that the details of the segment-level chemistry was independent of surface curvature, and therefore, the variations of the amount of polymer adsorbed and the density of contact points between the polymer and the surface of the particles must be a result of the variations in particle sizes, i.e., of surface curvature.

In this previous work, we established three different regimes of adsorption of polymer chains onto the surfaces of metal particles: (a) when the particle radius was much larger than the radius of gyration of the polymer, the adsorption was similar to adsorption on a flat metal surface; (b) when the particle size was of the order of magnitude of the radius of gyration of the polymer, the adsorption scaled linearly with the curvature of the particle; (c) when the radius of the particle was of the same order of magnitude as the thickness of the adsorbed layer, the number of adsorbed polymer chains was constant.

The adsorption of polymers on both flat and curved substrates also serves to modify the chemical properties of the surfaces according to the chemical nature of the polymer, the extent and nature of the particle/polymer interfacial interactions, and the resulting morphology of the adsorbed layer. As previously shown, the curvature has a notable effect on the substrate coverage by the polymer, specifically the density of the anchoring points of the polymer on the surface. Although curvature considerations provided insight into the amount of polymer adsorbed, they did not explain the deviations from the homogeneous self-similar structure of the adsorption layer.^34–36,38 To supply additional degrees of freedom that would enable the control of structural properties of the adsorbed layer, we have extended our work to systems that include block copolymers having blocks with dissimilar chemical features. In this case, polymer adsorption will be governed by the specific interfacial interactions of each block with each other, with the surface and with the solvent.

In this article, we present theoretical models in concert with experimental results regarding the adsorption of block copolymers onto metallic particles of different sizes. As in our previous work, the experimental setup consisted of suspensions of Al₂O₃ particles in solution of block copolymers, poly(methymethacry-late-b-styrene), PMMA-PS diblock, and solvents with different degrees of selectivity. More specifically, we present results for the adsorption of the PMMA-PS from two different solvents: (a) a solvent that is good for the PS block but is a θ-solvent for the PMMA block; (b) a solvent that is good for both the PS and PMMA monomers. The highly complex case in which the solvent was a bad solvent for the PS monomers and a good solvent for the PMMA monomers will be discussed separately.

The substrate in our experiments (i.e., adsorbing agent) was monodispersed Al₂O₃ particles with controllable radii. As previously shown, there was a preferential affinity of the PMMA block to the Al₂O₃ surface as compared to that of the PS block. The mechanism of the PMMA chemisorption results in the formation of a coordination bond between the methyl methacrylate (MMA) segments and Al⁺³ sites on the surface. Although the PMMA block exhibits a strong total adsorption on the surface,³³ the interaction strength of an individual monomer, whether a methylmethcrylate or a styrene, is weak (i.e., smaller than the thermal energy k_BT) in the limit of the definition by deGennes.³⁴ The fundamental premise of our approach was that the details of the chemistry concerning the segment-level adsorption mechanism of PMMA and PS on aluminum oxide surfaces is independent of surface curvature, because the Kuhn length of the segment rigidity is at least 1 order of magnitude smaller than the size of the smallest particles probed.^39,40 The solvents used in this work are toluene, a good solvent for the PS block, and a θ-solvent for the PMMA block, and cyclohexanone, a good solvent for both the PMMA and PS blocks. Both these cases fall into the category of adsorption of block copolymers from nonselective solvents.

Theoretical mean field and scaling methods have been employed to analyze adsorption of block copolymers from nonselective solvents for flat as well as for spherical surfaces.^{1,5,34–36,41,42} These studies suggested the formation of a bilayer structure comprising a self-similar anchor layer, i.e., the PMMA block, and a brush comprised of the unadsorbed block, i.e., the PS block. The dimensions and concentrations of these layers are controlled to a large extent by the relative size of the blocks. These results were further confirmed by numerical studies regarding the adsorption of short copolymers.^43–45

In the current work, we extend the geometric-based scaling of the adsorption of homo-polymers to diblock copolymers, as a generalization of our previous work.³³ We employ the experimental results described in this work to develop an interpolation equation that describes diblock copolymer adsorption on spherical particles. In accordance with the increase in the complexity of the chemical composition from one to two different monomeric species, we will use two, rather than one, independent geometrical correction factors. Our results show good correlation between the theory and the result for the case when the adsorbed polymers are dense enough, i.e., when the solvent is a good solvent for PS block and a θ-solvent for the PMMA block. However, in the case when the adsorption layer is dilute, we are suggesting a different model, as expressed in the results for the case in which the solvent is a good solvent for both blocks.

2. Experimental Section

2.1. Materials

Cyclohexanone, chlorobenzene (spectral grade), 2-ethoxy ethanol (spectral grade), and toluene (spectral grade) were purchased from Fisher Scientific and were used without further preparation. Block copolymers (BCP) of PS-b-PMMA of varying molecular weights and varying compositions were purchased from Polymer Source Inc.: PS₂₅₃₀₀-b-PMMA₂₅₉₀₀, PS₄₇₀₀₀-b-PMMA₂₈₀₀₀₀, PS₇₁₃₀₀-b-PMMA₁₁₂₀₀,PS₉₆₀₀₀-b-PMMA₁₂₈₃₀₀, PS₁₀₁₁₀₀-b-PMMA₁₆₅₈₀₀, PS₁₆₆₂₀₀-b-PMMA₄₂₀₀₀, PS₂₀₁₅₀₀-b-PMMA₁₅₂₀₀₀, and PS₂₆₀₀₀₀-b-PMMA₆₃₅₀₀, with PDI ranging from 1.06 to 1.13. Homopolymers of PS and PMMA of various molecular weights were purchased from Alfa Aesar, with PDI values ranging from 1.04 to 1.12. A summary of the various polymers used is given in Table 1. Alumina nanoparticles were purchased from different sources (Nanophase Technologies, NanoScale, Reade) depending on the availability of the desired size

TABLE 1.

Summary of the Various Adsorption Experiments Performed with PS-PMMA Diblock Copolymers with Various Molecular Weights and Different Block Mass Ratios onto Alumina Surfaces from Different Selective and Nonselective Solvents; Cyclohexanone Is a Common Good Solvent for Both PS and PMMA and Toluene Is a Good Solvent for PS and a θ-Solvent for PMMA

${\stackrel{‒}{M}}_w$ of PS block (g/mol)	${\stackrel{‒}{M}}_w$ of PMMA block (g/mol)	total ${\stackrel{‒}{M}}_w$ (g/mol)	PDI
71 300	11 200	82 500	1.12
25 300	25 900	51 200	1.06
166 200	42 000	208 200	1.07
260 000	63 500	323 500	1.07
96 000	128 300	224 300	1.06
201 500	152 000	353 500	1.09
101 100	165 800	266 900	1.13
47 000	280 000	327 000	1.09

2.2. Experimental Procedure

2.2.1. Preparation of Initial System Mixtures

Forty-five milliliters of cyclohexanone, which is a common good solvent for both the PS and the PMMA blocks (b.p.155.65 °C, density 0.9478 g/cm³), was introduced into a 100 mL Erlenmeyer flask and placed on a Thermolyne Mirak stirring hotplate with the temperature set to 70 °C. A magnetic stirrer was dropped into the flask and began spinning at the pre-set speed of 200 RPM. 0.603 g of PS₁₀₁₁₀₀-b-PMMA₁₆₅₈₀₀ were poured into the flask, to form a 1.25 vol % diblock copolymer solution. After the polymer was completely dissolved, the stirrer was removed. 0.05 g of alumina (Al₂O₃) nanoparticles (Nanophase Technologies, D_avg = 37 nm, density 3.97 g/cm³) were measured and kept in weighing paper. The flask was agitated on a Scientific Industries Vortex-2 Genie vortex with a setting of 8 to 10. While the mixture was swirling continuously the alumina was slowly poured into the flask. Mixing continued for 5 min. The flask was covered with laboratory film and stored in a fume hood for 24 h. Similar experiments were performed with the other diblock copolymer (BCP) molecular weights and compositions, keeping the same polymer volume fraction in all solutions, and other sizes of the alumina particles, i.e., D_avg = 4 nm, D_avg = 97 nm, and D_avg = 400 nm.

Experiments on flat alumina surfaces were performed by first depositing a 1000 Å layer of aluminum onto previously washed Si wafers by electron beam evaporation, using an instrument equipped with a multisample holder mounted on a rotating carriage to ensure even deposition. The thickness of the metal film was measured with a quartz crystal monitor. Immediately upon removal from the evaporator, the freshly prepared aluminum substrates were immersed in a 1.25 vol % cyclohexanone solution of the BCP at 70 °C, similarly to the procedure described previously. The time lapse from the opening of the sample holder of the evaporator and the complete immersion of the samples in the BCP solution was on the average less than 10 min. This allowed the formation of an amorphous native oxide layer on the aluminum surface.^20,22 The BCP solutions with the immersed metal oxide substrates were allowed to mix vigorously for 5 min and then stored at room temperature for 24 h. Excess, unadsorbed polymer was removed by repeated washing with cyclohexanone, to generate a stable, chemisorbed BCP film.

2.2.2. Characterization of Alumina Particle Size

Transmission electron microscopy (TEM) was used to determine size and distribution of original particles for all polymer suspensions. TEM samples were obtained by placing a small droplet of the reacted solution containing the polymer-coated metal oxide particles onto a Formvar coated copper TEM grid from Ted Pella. The grid rested on a thin piece of tissue paper so that the liquid will drain into the paper leaving a very thin film on the grid itself. The TEM analysis was performed on a JEOL 4000 EX high-resolution electron microscope with an operating voltage of 200 keV.

2.2.3. Characterization of the Adsorbed Diblock Copolymer Layer

Thermo gravimetric analysis (TGA) was conducted to measure the amount of adsorbed polymer. TGA samples were prepared by centrifuging each of the BCP nanocomposite mixtures using Fisher Scientific Centrific model 228 centrifuge at 10 000–15 000 RPM for 12–17 min. The capped particles formed a solid mass at the bottom of the vial and excess polymer and solvent solution were removed. The remaining particles were washed with solvent and the vial was shaken using a Scientific Industries Vortex-2 Genie vortex for 1 min to remove any excess unbound polymer from the particles. The suspension was centrifuged again and this process was repeated 3–4 times. The particles were placed onto a TGA platinum pan and the data was collected using a TA Instruments Inc. TGA model 50 at a ramp rate of 10 °C/min to 600 °C.

The fundamental premise in this work was that the PMMA block is considerably more reactive than the PS block toward the alumina surface. Hence, because the adsorption process occurred from solvents that were either good for both blocks or good preferentially for the weaker block, i.e., PS, the predominant, if not exclusive, chemisorbed species on the surface of the particles would be the PMMA block, i.e., only the PMMA block will reactively anchor to the surface. The associated PS block would be present on the surface as well, but only as an unadsorbed or physisorbed associated moiety. The thermal degradation of adsorbed polymers is directly related to the strength of the interaction between the polymer chains and the substrate, and, to a lesser degree, the film thickness.⁴⁶ Thus, the degradation profile of a polymer mixture (whether in bulk or on a substrate), is given by the appropriately weighted profile of the components.^46–49 This linear superposition of thermal profiles is valid in cases in which the polymers do not interact with each other, such as PS and PMMA, and hence, each adsorbed layer exhibits a thermal profile that is governed by the individual properties of each polymer system. The TGA profiles of PS and PMMA differ significantly, either as adsorbed films or as free-standing thin films, thereby enabling us to probe the composition of the adsorbed films on the surface of the alumina particles. Therefore, the TGA profile expected in our case would consist of a combination of the characteristic thermal decomposition profiles of adsorbed PMMA on alumina and free thin PS films. These characteristic thermal decomposition profiles were separately obtained from samples containing either PMMA-coated alumina nanoparticles or free-standing thin films of PS. In order to determine the actual composition of our samples, the experimental TGA profile was matched with a synthetic TGA profile constructed from a linear combination of the Al₂O₃-PMMA profile and the free PS profile.²⁹ The expected mass ratios between the chemisorbed PMMA moiety and the associated PS brush moiety should match the ratios between the molecular weights of the two blocks. Table 2 summarizes the experimental mass ratios obtained for the case of BCP adsorption from a common good solvent, which were used to calculate the polymer coverage and the density of anchoring points of the BCP on the surface of the alumina particles.

TABLE 2.

Summary of the Experimental Mass Ratios Obtained for the Case of Diblock Copolymer Adsorption from a Common Good Solvent, Which Were Used to Calculate the Polymer Coverage and the Density of Anchoring Points of PS-PMMA Copolymers on the Surface of the Alumina Particles

${\stackrel{‒}{M}}_w$ of PS block (g/mol)	${\stackrel{‒}{M}}_w$ of PMMA block (g/mol)	theoretical wPMMA of PMMA block (%)	experimental wPMMA of PMMA block (%)
71 300	11 200	13.5	11.8
25 300	25 900	50.6	49.7
166 200	42 000	20.1	18.5
260 000	63 500	19.6	18.7
96000	128300	57.2	56.3
201500	152000	42.9	41.1
101100	165800	62.1	60.5
47000	280000	85.6	86.8

FTIR was used to identify the bonding between the polymer chains and nanoparticles in the various Al₂O₃–BCP systems that we explored. The sample cell was placed inside a Nicolet Instrument Corporation Nexus 870 FT-IR spectrometer sample compartment, and after the latter was sealed and purged for at least 15 min, background spectra were taken and assigned for use on subsequent spectra acquisitions. The vials containing the centrifuged capped particles were shaken using a Scientific Industries Vortex-2 Genie vortex to initiate their re-suspension in a hydrocarbon solvent. Using Nicolet OMNIC 5.2a software the spectra of the capped metal oxide particles were compared against previously recorded spectra of PMMA solutions or PMMA thin films, to highlight peaks that are unique to the capped particles.

Determination of polymer layer thickness on the flat alumina samples was performed using a J. A. Woollam Co. Inc. Variable Angle Spectroscopic Ellipsometer (VASE). Prior to the adsorption process, the optical parameters of the bare metal oxide layer and the refractive index of a spin-coated (nonadsorbing) BCP film were determined. The polymer film thickness at various different points on the substrate and for two different angles of incidence was determined to be ~ 85 Å ± 9 Å. The BCP film was thin enough to see the photoemission signal and/or avoid distortions of the vibrational band shapes that depend on the thickness and refractive index of the sample.

2.3. Calculation of Anchoring Density

The adsorption of the PMMA block onto the Al₂O₃ surface occurs via the interaction of the ester group with the Al⁺³ centers, resulting in the formation of a metal-bonded carboxylate group. FTIR may be employed to follow the changes that occur in the absorbance spectra of the PMMA block as a result of these interactions. The change in the characteristic ratio between the 1687 cm⁻¹ absorption band, corresponding to the asymmetric stretch of the COO⁻ group,^4,9,10 as compared to the 1734 cm⁻¹ carbonyl peak for the adsorbed PMMA, {COO⁻}/{C=O} = {E₁₆₈₇}/{E₁₇₃₄}, provides the relative concentration of the reacted COO⁻ group.^4,9,10,28 The conformation polymer rearrangement upon adsorption generate a change of the ratio of the 1156 and 1171 cm⁻¹ bands, corresponding to the cooperative symmetric and asymmetric stretches of the C–O and C–C bonds of the polymer backbone. The total number of PMMA segments that have anchored to the surface can be calculated from the fraction of the segments containing the bonding group (COO⁻) that is also experiencing the conformational change, multiplied by the total number of monomers in the sample and divided this by the total number of chains, as follows^28,33

$$\frac{N_{\mathrm{anchors}}}{N_{\mathrm{chains}}}=\frac{E_{1687}}{E_{1734}}\frac{E_{1156}}{E_{1171}}\frac{N_{\mathrm{monomers}}}{N_{\mathrm{chains}}}$$ (1)

Note that the number of chains in the sample (i.e., the number of PMMA chains, which by definition is equal to the total number of BCP chains) is given by the following expression

$$N_{\mathrm{chains}}=\frac{M_{\mathrm{sample}}{w}_{\mathrm{PMMA}}{N}_{\mathrm{A}}}{{\stackrel{‒}{M}}_{{\mathrm{W}}_{\mathrm{PMMA}}}}$$ (2)

where M_sample is the mass of the sample, w_PMMA is the mass fraction of the chemisorbed PMMA block as determined from TGA analysis, and ${\stackrel{‒}{M}}_{{\mathrm{w}}_{\mathrm{PMMA}}}$ is the weight average molecular weight of the PMMA block.

The anchoring density of the PMMA block on the surface of the alumina particles is given by the number of anchoring segments divided by the total surface area of the particles in the sample. TGA data were used to calculate the number of alumina particles in the sample and their resulting surface area, according to the following expression

$$A_{particles}=\frac{M_{sample}\cdot w_{particles}}{\underset{N_{particles}}{\underbrace{d\cdot \left(\frac{4\pi }{3}\right){\left(\frac{{\stackrel{‒}{D}}_{particles}}{2}\right)}^3}}}\cdot 4\pi {\left(\frac{{\stackrel{‒}{d}}_{particles}}{2}\right)}^2$$ (3)

where w_particles is the mass fraction of the alumina particles as determined from TGA measurements, d is the density of the alumina nanoparticles (supplied by the manufacturers), and ${\stackrel{‒}{D}}_{\mathrm{particles}}$ is the average diameter of the alumina particles as determined from TEM measurements. The surface density of the chains adsorbed on the aluminum oxide particles, η, is given by

$$\frac{N_{\mathrm{chains}}}{A_{\mathrm{particles}}}=\frac{w_{\mathrm{PMMA}}{N}_{\mathrm{A}}d{\stackrel{‒}{D}}_{\mathrm{particles}}}{6w_{\mathrm{particles}}{\stackrel{‒}{M}}_{{\mathrm{w}}_{\mathrm{PMMA}}}}$$ (4)

Combining eqs 1 and 4 gives the density of anchoring points per unit area of oxide nanocluster surface (in units of nm²), σ.

3. Theoretical Methods

3.1. Curvature Effects for Homopolymer Adsorption

Theoretical models based on scaling arguments^34–36 and mean field approaches give a detailed description of the equilibrium structure of the adsorption layer. The main results that we have used in our work are as follows: (a) The monomer density ϕ-(z) (where z is the vertical distance from the surface), has a self-similar structure. This self-similarity is manifested in the correlation length scaling law³⁴

$$\xi \left(\varphi \left(z\right)\right)\approx z\Rightarrow \varphi ={(a∕z)}^{4∕3}$$ (5)

where a denotes the typical size of the monomer.

(b) The coverage, i.e., the number of monomers in the adsorption layer per nm² is a constant³⁴

$$\Gamma ={\int }_0^{\infty }{a}^{-3}\varphi \left(z\right)=\mathrm{const}.$$ (6)

The surface coverage is independent of the polymer length or of the bulk concentration of the solution. The effort to extend the theoretical solution to adsorption on small spherical particles has shown that the self-similarity character of the adsorption layer has prevailed also for the spherical geometry.^33,50–53 However the coverage of the surface can be reduced substantially with the decrease of the particles radii.^53,54

However, in our recent work that was based on experimental results,³³ we have obtained a quantitative scaling rule for the homopolymer adsorption, that could be characterized by the following behavior: In the small particle limit, R < aN^1/2, the coverage was constant (i.e., no dependency on the radius or on the degree of polymerization). In the medium particle regime, which spanned between the limits aN^1/2 < R < CaN^3/5 (where C was a constant on the order of 2–5), the coverage scaled as: Γ ~ L/R, where L was a typical width of the adsorption layer. The large particle limit again gave the flat surface coverage.

In this paper, we will employ an interpolation formula that will describe a unified coverage expression for the medium to large particle adsorption regimes. We have chosen the sigmoid form because our previous work has indicated a sharp transition between the two size regimes

$$\Gamma \left(R\right)={\Gamma }_{\mathrm{flat}}\left[1-\exp \left(-\frac{{\alpha }_{1}R}{L}\right)\right]$$ (7)

where α₁ is an empirical constant and Γ_flat is the coverage on a flat surface. We would like to emphasize that the exponential form that we have chosen is empirical. We do not have experimental evidence that can predict the true behavior of the coverage at the turnover from a flat surface to a sphere with a small radius. Equation 7 seems to retain the experimental behavior only in the trivial regions of very large and very small radii of the adsorbing particles. In the next subsection, we adapt this expression for a block copolymer, rather than for the hompolymer case for which this formalism has been originally developed.³³ The justification for this adaptation will emerge from our experimental results, which demonstrate the same behavior of the adsorbed block as that of the adsorbed homopolymer.

3.2. Curvature Effects for Block Copolymers Adsorption

Adsorption of diblock copolymers shows a much richer behavior due to the extra degrees of freedom associated with these systems. The higher variability in the block copolymers adsorption is due to the incompatibility between the two blocks, the difference in solubility, and the strength of the interactions of the two monomers with the surface.

In this work, we have probed the adsorption of the PMMAPS diblock copolymer from a either a good or a θ-solvent. The first adsorption experiment was performed from a solvent that was good for the PS block and a θ-solvent for the PMMA. The second adsorption experiment was performed from a solvent that was good for both blocks. The analysis of the experimental results that we have obtained relied on the mean field formalism that was developed for the adsorption from a nonselective good solvent for flat surfaces,^53,54 and hence, we will give a short overview of the formalism.

A polymer with degree of polymerization N is made of two blocks: block A, the anchor block that can undergo adsorption onto the surface; and block B, the buoy block.^{41,42,55–61} This block does not interact with the surface and is repelled from the surface due its incompatibility with block A. The degrees of polymerization of the two blocks are N_A and N_B, respectively. The adsorption layer, shown in Figure 1, is made of two distinct layers: (a) first layer, an anchor layer containing a semidilute solution of block A featuring a self-similar structure; (b) second layer, a buoy layer consisting of a brushlike structure of the B blocks. The widths of these layers are L_A and L_B, respectively.

Figure 1.

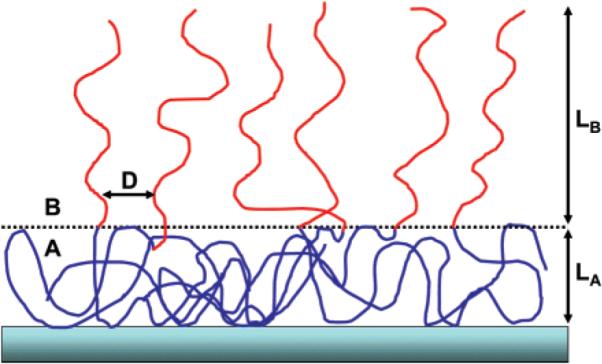
Schematic description of the adsorption of diblock copolymers from a nonselective solvent. The first layer, i.e., the anchor layer, includes only the anchor A blocks. This layer has a self-similar structure. Each block can interact with the surface through the reactive anchoring of many monomers in that block, as dictated by the interplay of the loss in entropic energy and the gain in energy due to the favorable interactions between the adsorbing monomers and the surface. The second layer, i.e., the buoy layer, consists of a brush of the B blocks that are grafted through their edge to the anchor layer. L_A and L_B denote the thickness of the two layers and D is the typical distance between the chains that make up the brush.

The free energy per surface site of the adsorption layer, Fa²/k_BT, consists of three interaction terms: A surface monomer interaction term, an anchor layer term, and a buoy term. The first term is simply −δ_sAϕ_s, where δ_sA is the interaction strength between the surface and monomer A and ϕ_s is the volume fraction of monomers A in the first layer from the surface. The second term that gives the energy stored in the anchor layer is given by^42,53,54

$${\int }_0^{\infty }\frac{a^2}{6}\left[{\left(\frac{\mathrm{d}\Psi }{\mathrm{d}z}\right)}^2+\frac{{\nu }_{\mathrm{A}}}{2}{\Psi }^4\right]\frac{\mathrm{d}z}{a}$$ (8)

where Ψ² = ϕ and ν_A is the solvation volume of monomer A.

When the blocks density is much higher than the brush critical density, the last term of the surface free energy is given by⁶²

$$\left(\frac{3}{2}\right)\sigma {\left(\frac{L_{\mathrm{B}}}{N_{\mathrm{B}}a}\right)}^2+\left(\frac{1}{2}\right){\nu }_{\mathrm{B}}{N_{\mathrm{B}}}^2{\sigma }^2$$ (9)

where σ is the density of the blocks B in the buoy layer (which is equal, by definition, to the density of blocks A in the anchor layer). Using energy minimization, the coverage of the surface can be recovered as follows⁴²

$${\Gamma }_{\mathrm{A}}={\sigma }_{\mathrm{A}}{N}_{\mathrm{A}}=\left(\frac{a}{6b{\nu }_{\mathrm{A}}}\right)\left[1-\left(\frac{\beta }{N_{\mathrm{A}}^{1∕3}}\right)f\left(\frac{{\nu }_{\mathrm{A}}}{{\nu }_{\mathrm{B}}}\right)\right]$$ (10)

where f is a scaling function that depends on the ratio of the excluded values of both types of monomers, b is a typical length measure of the order of few monomers length and β = (N_B/N_A)^1/2.⁴² For the remainder of the paper, we will use the correction coefficient $\gamma =\beta ∕N_{\mathrm{A}}^{1∕3}$.

In this formalism, there is no reference to the entropic contribution to the coverage. Increasing the curvature generates an increase in the available conformation space for the adsorbed polymers and hence, should result in an increase in the number of adsorbed polymer chains. However, in our experiment, we observed the opposite, i.e., the coverage decreased with the increasing of the curvature, and therefore, we concluded that the entropic contribution was negligible.

The first term in eq 10 describes the surface coverage of block A, which is similar to that of a homopolymer of type A (and independent of block B). The second term is a correction term due to the existence of the second block forming the brush. The origin of this term is the “buoyancy energy” originating from the second layer, which increases the total energy of the adsorption layer and hence decreases the ability of the surface to attract polymers. It should be mentioned that the quality of the solvent for the monomer A is expressed here through the excluded volume parameter ν_A and hence, this result is valid for both good and θ-solvents.

Adsorption on a spherical geometry will cause a change in the density expression for the buoy layer. In a similar manner to the polymer density that has been shown for star polymers (having an intrinsic spherical geometry), we can relate the sphere radius of the adsorbing particle to the adsorption layer height and density function of the polymer brush via the expression⁶³

$${\left[\left(\frac{L_{\mathrm{B}}}{R}\right)+1\right]}^{5∕3}=1+\left(\frac{k{N}_{\mathrm{B}}a}{R}\right){\left(\frac{{\nu }_{\mathrm{B}}\sigma }{a_{\mathrm{k}}}\right)}^{1∕3}$$ (11)

where k is a constant with an order of unity and a_k is the Kuhn length in the block B.

For the case of a high degree of polymerization in the brush polymer (L_B/R ≫ 1 and N_Ba/R ≫ 1), this latter expression is reduces to the relation ${\sigma }_{\mathrm{R}}=(L_{\mathrm{B}}^2∕R^2){\sigma }_0$, where σ₀ = (L_B/N_Ba)³ is the surface density of a brush on a flat surface.^38,64 On the basis of this result, we define an effective brush density as follows

$${\sigma }_{eff}=\left(\frac{R^2}{{L_{\mathrm{B}}}^2}\right){\sigma }_{\mathrm{R}}$$ (12)

This expresses the effective contribution of the brush to the correction term of eq 10 in the limit of a long B block, or only for the limit of L_B > R. In the case when R is much larger than L_B (almost flat surface) one expects to retrieve the result for a flat surface, or σ_eff = σ_R.

One can again interpolate the results between the two regions of curvature and derive the following second geometrical correction factor

$${\sigma }_{eff}=\left[1-\exp \left(-\frac{{\alpha }_2{R}^2}{{L_{\mathrm{B}}}^2}\right)\right]{\sigma }_{\mathrm{R}}$$ (13)

The constant α₂ can be empirically found experimentally. It is important to note that because of eq 12, the correction factor in the exponent depends on (R/L_B)², as opposed to its linear dependence shown in eq 7. As with eq 7, we would like to emphasize that this form of the geometrical factor has been chosen only to give the correct behavior in both the small and large radii limits of the adsorbing particle. We do not have enough results to give an exact mathematical formalism of the behavior of the surface density of the adsorbed blocks.

By introducing the two geometrical factors (eq 7 and eq 13) into the expression of the planar coverage (eq 10), we find the following expression for the surface coverage on a spherical geometry

$${\Gamma }_{\mathrm{A}}=\left[1-\exp \left(-\frac{{\alpha }_{1}R}{L_{\mathrm{A}}}\right)\right]\left(\frac{a}{6b{\nu }_{\mathrm{A}}}\right)\times \left\{1-\left[1-\exp \left(-\frac{{\alpha }_2{R}^2}{{L_{\mathrm{B}}}^2}\right)\right]\left(\frac{\beta }{N_{\mathrm{A}}^{1∕3}}\right)f\left(\frac{{\nu }_{\mathrm{B}}}{{\nu }_{\mathrm{A}}}\right)\right\}$$ (14)

We have chosen this form of eq 14 regarding the coverage because we expect that the contribution to the correction in total energy from the buoy layer (expression in the curly parenthesis) will contribute a smaller scale perturbation than the anchor layer.

We would like to emphasize that this formula is valid for adsorption of block copolymers from θ and good solvents or a combination of both. We refer to this as the semi-selective solvent case. Moreover, the above formalism is based on the assumption that the degree of polymerization N is very large. Subsequently, we will use the above equation to interpret the experimental results in the appropriate limits.

4. Results and Discussion

4.1. Adsorption from a Semiselective Solvent

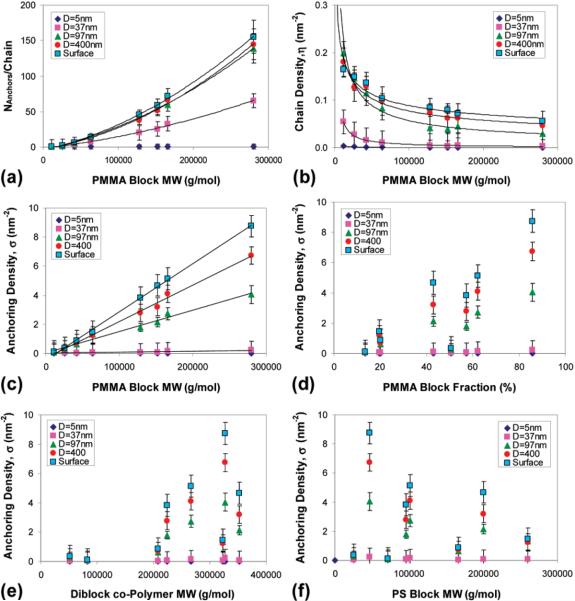
Two different characterization methods have yielded two types of experimental data: (a) The number of anchoring points (i.e., surface-bound monomers) per PMMA block adsorbed on the cluster surface was obtained from FTIR experiments according to eq 1, and shown in Figure 2a; (b) the number of adsorbed polymer chains per unit area of cluster surface (in units of nm²), η, was obtained from TGA experiments according to eq 4, and shown in Figure 2b. The combination of these two independent experiments yielded the density of the number of anchoring points per unit area of particle surface (in units of nm²), σ, and shown in Figure 2c. Note that σ exhibited a linear dependence on the molecular weight of the PMMA block, but showed no dependence on the mass fraction of the PMMA block (Figure 2d), the total molecular weight of the polymer (Figure 2e), or the molecular weight of the PS block (Figure 2f). On the basis of these experimental results, we have calculated the coverage Γ_A of the adsorbing particles with different radii and for diblock copolymers with different ratios of the block degrees of polymerization. The results are summarized in Table 3. The columns are organized according to the correction parameter $\gamma =\beta ∕N_{\mathrm{A}}^{1∕3}$.

Figure 2.

Experimental results of the adsorption of PS-PMMA diblock copolymers onto alumina surfaces from a solvent that is good for PS and a θ–solvent for PMMA. (a) The number of anchoring points (i.e., surface-bound monomers) per PMMA block adsorbed on the cluster surface as a function of the molecular weight of the PMMA block; (b) the number of adsorbed polymer chains per unit area of cluster surface (in units of nm²) as a function of the molecular weight of the PMMA block; (c) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the molecular weight of the PMMA block; (d) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the mass fraction of the PMMA block in the polymer; (e) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the total molecular weight of the polymer; (f) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the molecular weight of the PS block in the polymer.

TABLE 3.

Summary of the Coverage Data for the Adsorption of Diblock Copolymers from a Good Solvent for PS and a θ-Solvent for PMMA Calculated from the Experimental Results Shown in Figure 2 and Using the Two Geometric Correction Factors in Eq 14; Columns Marked by a Star Represent the Cases of “Short Polymers” as Explained in the Text

	γ
	0.03	0.07	0.08	0.10	0.16*	0.25	0.28	0.54*
NA (NPMMA)	2800	1658	1283	1520	259	635	420	112
NB (NPS)	452	972	923	1938	243	2500	1598	686
Davg = 5 nm	0.36	0.48	0.39	0.31	0.47	0.39	0.44	0.43
Davg = 37 nm	9.7	7.5	5.6	5.8	7.3	6.6	6.8	6.1
Davg = 97 nm	81.4	75.8	53.0	60.0	37.8	52.7	48.0	22.3
Davg = 400 nm	130.5	103.0	94.0	95.0	32.9	62.3	54.1	20.2
surface	157.5	119.0	108.0	121.0	38.5	65.8	57.2	18.4

From the results in Table 3, we can make the following remarks:

(a) For the case of small particles D_avg = 5 nm (R < R_G^1/2) the coverage seems to be independent of the correction parameter. This reflects the fact that an adsorption of a small particle does not perturb the non adsorbed block and that only few polymers will be adsorbed.

(b) On the basis of our observations regarding the adsorption of homopolymer on curved surfaces, as indicated by eq 7, we expect to obtain the following relationship between the surface coverage and the radius of the adsorbing particles

$$\frac{{\Gamma }_{\mathrm{A}}\left(R_1\right)}{{\Gamma }_{\mathrm{A}}\left(R_2\right)}\approx \frac{R_1}{R_2}$$ (15)

From the rows in Table 3, we note the following average behavior (average performed over the columns)

$$\begin{array}{c}\hfill \langle {\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=97)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=37)\rangle \approx 9.0\hfill \\ \hfill \langle {\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=400)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=97)\rangle \approx 1.5\hfill \\ \hfill \langle {\Gamma }_{\mathrm{A}}\left(\mathrm{surface}\right)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=400)\rangle \approx 1.1\hfill \end{array}$$

This is different than the behavior expected from our previous studies. Based on this, we can conclude that the transition between the flat surfacelike behavior to medium curvature-like behavior occurs at a radius of approximately R ≈ 50 nm (D_avg ≈ 100 nm), which is considerably smaller than the transition radius that we found in the case of homopolymer adsorption (R ≈ 200 nm or D_avg ≈ 400 nm). This difference may originate from the correction term that is quite large for the case of a semi-selective solvent (ν_B/ν_A is very large for this case). Alternatively, it may indicate that in a θ-solvent, the adsorption of homopolymers onto a spherical particle is dictated by a correcting factor [1 − exp(−α₁R²/L²)] rather than the corresponding factor in eq 14.

(c) From the columns of Table 3, we can see that an increase in the correction parameter γ will usually cause a decrease in the coverage Γ_A, in accordance with eq 14. The exceptions to this behavior are in the columns that represent short polymers. We assume that this deviation originated from the decrease of the incompatibility of the two blocks for short polymers.⁶³ This will strongly perturb the two layers adsorption structure (shown in Figure 1).

(d) In each row of Table 3, the surface coverage decreased from left to right, due to the increase in the correction parameter γ. Also from Table 3, we can see that the larger the adsorbent (particle) size D_avg, the larger is also the decrease in coverage. The relationship between the rows (across the columns) is shown in the following expression

$$\frac{{\Gamma }_{R1}\left({\gamma }_1\right)-{\Gamma }_{R1}\left({\gamma }_2\right)}{{\Gamma }_{R2}\left({\gamma }_1\right)-{\Gamma }_{R2}\left({\gamma }_2\right)}>1\text{for}{R}_1>R_2\text{and for}{\gamma }_1>{\gamma }_2$$ (16)

This means that the larger the R, the larger the correction to the surface coverage, again in accordance with eq 14.

In summary, we found that for the correct limits of long polymers (high N), eq 14 gave a good qualitative prediction of the experimental results. A higher power of N_A in the correction factor γ in eq 14 may give a better match. Also, it is possible that a better approximation for the geometrical factor (eq 7) may be [1 − exp(−α₁R²/L²)]. One expects that calculations based on scaling arguments rather than on a mean field approach, would reveal the proper structure of eq 14.

4.2. Adsorption from a Nonselective Good Solvent

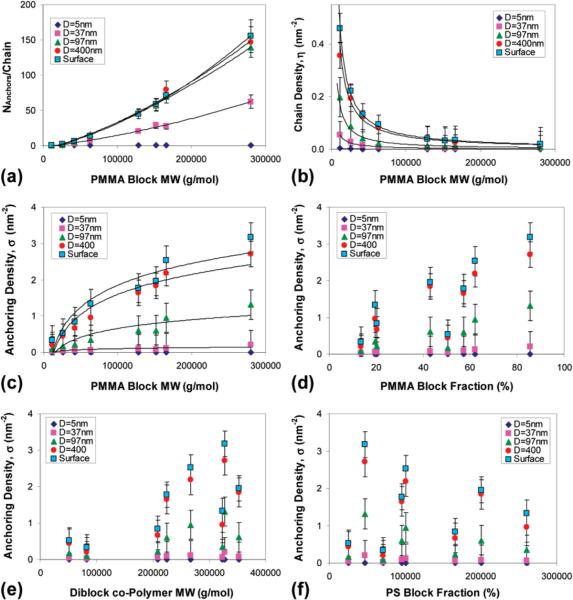
As in the previous experiment, the number of anchoring points per PMMA block adsorbed on the particle surface (Figure 3a) and the number of adsorbed polymer chains per unit area of particle surface (Figure 3b) were used to calculate the density of the number of anchoring points per unit area of particle surface (in units of nm²), σ, and shown in Figure 3c. Note that also in this case, σ exhibited a dependence (albeit nonlinear) on the molecular weight of the PMMA block, but showed no dependence on the mass fraction of the PMMA block (Figure 3d), the total molecular weight of the polymer (Figure 3e), or the molecular weight of the PS block (Figure 3f). A summary of the experimental results for this case is given in Table 4. As in the previous case, we can formulate the following observations:

Figure 3.

Experimental results of the adsorption of PS-PMMA diblock copolymers onto alumina surfaces from a solvent that is good for both the PS and PMMA blocks. (a) The number of anchoring points (i.e., surface-bound monomers) per PMMA block adsorbed on the cluster surface as a function of the molecular weight of the PMMA block; (b) the number of adsorbed polymer chains per unit area of cluster surface (in units of nm²) as a function of the molecular weight of the PMMA block; (c) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the molecular weight of the PMMA block; (d) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the mass fraction of the PMMA block in the polymer; (e) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the total molecular weight of the polymer; (f) the number of anchoring points per unit area of particle surface (in units of nm²) as a function of the molecular weight of the PS block in the polymer.

TABLE 4.

Summary of the Coverage Data for the Adsorption of Diblock Copolymers from a Good Solvent for Both the PS and the PMMA Blocks (i.e., Nonpreferential Solvent) Calculated from the Experimental Results Shown in Figure 3 and Using the Two Geometric Correction Factors in Eq 14; Columns Marked by a Star Represent the Cases of “Short Polymers” as Explained in the Text^a

	γ
	0.03	0.07	0.08	0.10	0.16*	0.25	0.28	0.54*
NA (NPMMA)	2800 :	1658	1283	1520	259	635	420	112
NB (NPS)	452	972	923	1938	243	2500	1598	686
Davg = 5 nm	0.4	0.5	0.4	0.3	0.4	0.4	0.5	0.4
Davg = 37 nm	9.3	7.0	5.6	4.2	7.4	5.6	6.8	6.1
Davg = 97 nm	26.5	22.6	16.4	16.2	22.8	13.9	17.5	22.3
Davg = 400 nm	51.6	45.6	47.1	48.5	50.3	51.3	52.1	40.2
surface	57.2	58.7	50.1	50.3	57.3	60.0	55.7	51.6

^aThe results for N_A = 420 seem to give results that are marginal between long and short polymers.

(a) Constant behavior for the 5 nm particles.

(b) From the rows in Table 4, we observe the following average behavior (average performed over the columns)

$$\begin{array}{c}\hfill \langle {\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=97)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=37)\rangle \approx 3.0\hfill \\ \hfill \langle {\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=400)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=97)\rangle \approx 3.0\hfill \\ \hfill \langle {\Gamma }_{\mathrm{A}}\left(\mathrm{surface}\right)∕{\Gamma }_{\mathrm{A}}(D_{\mathrm{avg}}=400)\rangle \approx 1.1\hfill \end{array}$$

This is in accordance to the behavior expected from our previous studies (involving homopolymers), as predicted by eq 7 for the medium particle size limit.

(c) The decrease in coverage, Γ_A, from left to right in the rows of Table 4 is consistent with eq 14, indicating that the larger the correction factor, the larger the decrease in the coverage.

(d) The relationship between the rows (across columns) regarding the change in coverage for different radii of the adsorbing particles (shown in Figure 5) is shown as follows

$$\frac{{\Gamma }_{R1}\left({\gamma }_1\right)-{\Gamma }_{R1}\left({\gamma }_2\right)}{{\Gamma }_{R2}\left({\gamma }_1\right)-{\Gamma }_{R2}\left({\gamma }_2\right)}<1\text{for}{R}_1>R_2\text{and for}{\gamma }_1>{\gamma }_2$$ (17)

This means that the larger the R, the smaller is the correction to the surface coverage, implying that the second geometric correction is not valid in this case. The source of the incompatibility with eq 14 stems from the initial assumption that the brush formed by the polystyrene block is a dense brush, given that N_B is large, or D ⪡ R_G, where D is the typical distance between two grafted B blocks. However, a careful observation of the coverage data in Table 4 shows that the polymer density, particularly for the small particles (R = 37 and R = 97), is larger by only a small factor than the critical brush transition density, defined as $D_{\mathrm{critical}}^{-2}={\eta }_{\mathrm{critical}}=R_{\mathrm{G}}^{-2}$.^38,64 Taking the Kuhn length of the blocks to be 0.5–0.8 nm,^39,40,65 we get that R_G/D for the small particles is on the order of 2–6. This ratio increases for the larger adsorbing particles, since for larger particles, η is larger. Hence, for the smaller particles having a lower coverage, the adsorbed block copolymer resides on the surface with a morphology between a two-dimensional layer (bubblewrap-like) and a stretched-out (brush-like) configuration, which can be referred to as the quasibrush configuration.^62,66

Figure 5.

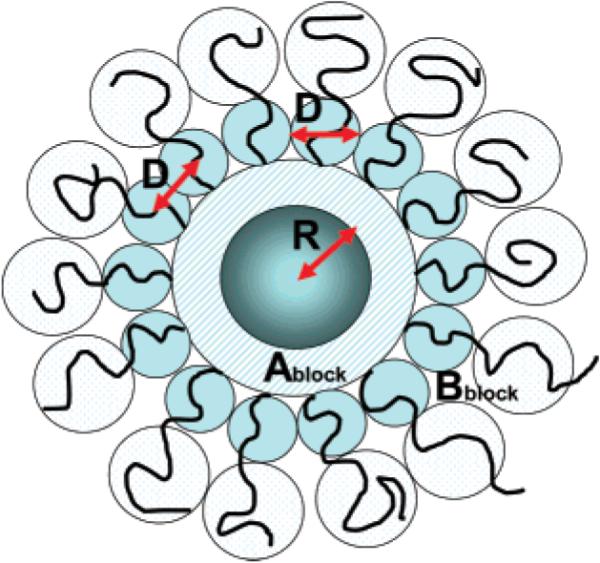
Schematic description of the discrete blobs model representing the case of a dilute PS buoy layer that is only marginally above the pancake-brush transition. The first adsorption layer is made of a melt of A monomers (PMMA). The second layer is made the B blocks (PS) that are arranged in two shells of bubbles. The diameter of a typical bubble, D, is of the same order as the typical distance between the B blocks.

To explain the quasibrush case, we will employ the blobs model,^50,52 schematically shown in Figure 4. The block that is protruding into the brush is confined to a series of blobs, each having a diameter D (this diameter is considered to be the same as the typical distance between two grafted blocks). On a small adsorbing particle, η_A (which is also equal to η_B) is small, because there are only a few layers of blobs that will be formed on the surface. Increasing N_A will cause a decrease in the density η_A. This will increase the radius of the brush blobs up to a limit where a complete shell of brush blobs could no longer be accommodated on a highly curved particle (small R). Hence, the expected buoyancy energy of the brush will abruptly decrease.

Figure 4.

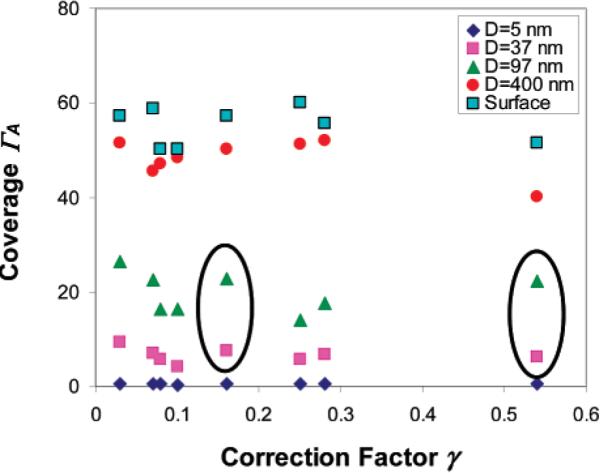
Plot of the polymer coverage as a function of the correction factor γ. The particular cases of low molecular weight polymers, for which the second geometric correction factor in eq 14 is not valid, are circled.

The larger the R, the larger is also the surface coverage Γ_A, due to the geometrical factor described in eq 7, and consequently, the larger is the number of shells in the brush. For a multishell layer, the correction due to the removal of a shell will be diminishingly small and eq 14 will be valid again in this limit (long brush limit.) The outcome of this behavior is that for short brushes, the increase in the correction parameter γ will lead to a larger correction term in eq 14 and a larger decrease in the number of adsorbed polymers, in accordance with the experimental results in Table 4. We would like to mention that our results hint that the dependence of the coverage on the degrees of polymerization is not exactly monotonic but seems to indicate some small oscillatory behavior (Table 4). Although this result is not unequivocally proven (due to the margin of errors in the experiment), we can nevertheless view it as an extra validation of the small number of the sparsely spaced blobs model.

5. Conclusions

In this paper, we generalized our geometric-based scaling model and applied it in order to explain certain experimental results regarding the adsorption of block copolymers onto particles with various sizes. The experimental setup consisted of suspensions of Al₂O₃ particles in solutions of poly(styrene-b-methymethacrylate) (PS-PMMA) diblock copolymers and solvents with different degrees of selectivity. More specifically, we probed the validity of our generalized model on two adsorption scenarios: (a) Adsorption from a solvent that is good for the PS block but is a θ-solvent for the PMMA block; (b) adsorption from a nonpreferential solvent, i.e., a solvent that is good for both the PS and PMMA blocks. Because of the increase in the complexity of the chemical composition from one to two different monomeric species, we developed an interpolation equation that took into consideration both the curvature of the adsorbing surfaces and the two different solvent systems, and hence introduced two, rather than one, independent geometrical correction factors to the classical adsorption equation. Our results show good correlation between the theory and the results obtained for the case when the adsorbed polymers are dense enough, i.e., when the solvent is a good solvent for PS block and a θ-solvent for the PMMA block, generating a PMMA adsorption layer and a brushlike layer in which the PS chains are stretched out. Conversely, when adsorption occurs from a nonpreferential solvent, the larger the particle size, the smaller the correction to the surface coverage, implying that the second geometric correction is not valid. This was particularly obvious for diblock copolymers with low-molecular-weight blocks. This can be explained by the fact that when the PMMA adsorption layer at the surface becomes less dense, the grafted PS moiety exhibits a transitional morphology between a brush-like layer and bubblewrap-like layer.

These observations have important implications regarding the surface properties of polymer-coated metal and metal oxide substrates. In particular, the stratification of the adsorbed polymer layer in the case of the adsorption of diblock copolymers on curved substrates may impart specific functionality and chemical reactivity to such particles. These properties may prove crucial in a variety of applications where the use of such surface-tailored particles is being contemplated.