Recent Developments in the Methods and Applications of the Bond Valence Model

1. Introduction

The bond valence model was described comprehensively in my 2002 book, The Chemical Bond in Inorganic Chemistry: The Bond Valence Model,(1) where references to earlier work can be found. The present paper reviews the work that has been published since then, specifically covering the years 2000 to 2007 inclusive with some coverage of 2008. Coverage is comprehensive except for one area: the use of bond valences for routine validation of newly determined crystal structures. Since there are many thousands of examples of this use, it would be tedious to include them all and it would defeat the purpose of this review. A few examples are given by way of illustration.

Different authors often use different terms to describe the same concept. A consistent set of names is used in this review but where an author uses a different term this is included in parentheses at the point where it is first referenced. A glossary of terms is included and this has cross references to alternative names as well as to the equations in the text that are used to define the terms.

The first part of this review (sections 1−4) sets the context for the later discussion. It briefly outlines the historical background of the model and rehearses its theorems, emphasizing both their simplicity and their limitations. The second part (sections 5−13) reviews advances that have been made in the methodology and techniques during the review period, whereas the third part (sections 14−26) describes the applications of bond valences in a variety of different disciplines. It ends with a short assessment of the opportunities for further development of the model (section 27).

In the theoretical development of the model presented here, certain terms are used with precise meanings which may differ from those used in other models. These terms are defined below with the caveat that the definitions apply only to the bond valence model as described here. Other models may define the same terms differently. Terms in italics in the following list are also defined in the list. (Names in parentheses are alternative names used in papers referenced in this review.)

• Accessible volume: The volume of a crystal that is accessible to a mobile ion. It comprises the volume lying within ΔV of the surface on which the bond valence sum of the conducting ion is equal to its atomic valence. The relative volume of the conducting path, F, is the ratio of the accessible volume to the total volume of the crystal (section 24).

• Anion: An ion with a negative atomic valence. In any compound the anions always have a larger electronegativity than the cations. In the ionic model an anion is treated as a point charge with magnitude equal to its valence.

• Anion bonding strength, L_b (Lewis base strength): The anion valence divided by a typical coordination number, V_a/⟨N⟩. For this purpose, the coordination number of oxygen is taken as four. Since the atomic valence of an anion is negative, L_b is also a negative number.

• Atom: The smallest indivisible unit of elemental matter. It has properties of valence, average coordination number, and electronegativity which depend on its oxidation state.

• Atomic valence, V_i: For cations the atomic valence is positive and is equal to the number of valence electrons used in bonding. For anions it is negative with a magnitude equal to the number of electron holes in the valence shell. The valence of ion or atom i is used to define the stoichiometry of the compounds it forms and is often equated with its oxidation state.

• Average bond length, R_av: Average of the observed bond lengths of the bonds formed by a particular ion.

• Average coordination number, ⟨N⟩_o: The coordination number of a cation when coordinated by oxygen, averaged over all its compounds. This is used as a measure of the size of the ion.

• Bond: In the ionic model, a chemical bond is defined as existing between a cation and anion if and only if they are linked by bond flux. Such localized bonds are not found in compounds with partially filled conduction bands (metals).

• Bond discrepancy index: The difference between the experimental and theoretical valences of a bond.

• Bond flux: The electrostatic flux linking a cation to a neighboring anion when the ions are replaced at their observed positions by point charges.

• Bond length, R: Distance between the nuclei of two bonded atoms.

• Bond network: A formal description of the topology of a structure in which ions are linked by bonds. It is often represented by a graph where the nodes represent the ions and links represent the bonds.

• Bond type: Bonds of the same type share the same bond valence parameters. Bonds having the same terminal ions usually belong to the same type.

• Bond valence: A generic term that includes bond flux, theoretical bond valence and experimental bond valence.

• Bond valence deficiency: See residual valence.

• Bond valence parameters, R₀, b, N: Empirically determined parameters in eq 26 (or eq 25) used to calculate experimental bond valences from the observed bond lengths. Commonly these are R₀, the notional length of a bond of unit valence, and b, the softness parameter (see section 7.3).

• Bond valence sum, V_s: The sum of experimental bond valences incident at a given ion.

• Bonding strength: See cation bonding strength or anion bonding strength.

• Cation: An ion with a positive atomic valence. In any polar compound the cations always have a smaller electronegativity than the anions. In the ionic model a cation is treated as a point charge equal to its valence.

• Cation bonding strength, L_a,, (Lewis acid strength): The valence of the cation divided by its average coordination number to oxygen, V_c/⟨N⟩_o. Since the valence of a cation is positive, the cation bonding strength is also positive.

• Classical valence, V: The same as the atomic valence. The classical valence was assigned to account for observed stoichiometries.

• Conduction path: In ionic conductors, the conduction paths form a percolation network which is defined by the accessible volume.

• Coordination number, N: The number of bonds formed by an ion.

• Discrepancy factor, d_i: The difference between the observed bond valence sum around ion i and its atomic valence, V_i (see also bond discrepancy index). It is defined in eq 42.

• Electric capacitor, C: Two equal and opposite charges linked by electrostatic flux. In physical capacitors the charges reside on conducting plates separated by an insulator.

• Electronegativity, χ: Ratio of the valence of a cation to its average coordination numberV_c/⟨N⟩_o (eq 8). It is numerically equal to the cation bonding strength. In the bond valence model it is simpler and more convenient to define the electronegativity in terms of other quantities used in the model. Although the numerical value given by this definition differs from that of other scales, it orders the ions is the same way as the more traditional scales.

• Experimental bond valence, S, (Apparent valence): The bond valence obtained from the observed bond length using the empirical correlation expressed by the bond valence parameters.

• Global instability index, G: The root-mean-square deviation of the experimental bond valence sums from the atomic valence (eq 44). The deviations are averaged over all the atoms in the formula unit. This measures the degree of failure of the valence sum rule.

• Ideal bond length: The bond length calculated from the theoretical bond valence.

• Ion: An atom defined by both its element and its atomic valence. It is sometimes treated as carrying a charge equal to its atomic valence.

• Ionic valence: Synonym for atomic valence. In this review it does not refer to a type of valence that is complementary to a covalent valence. Neither of the terms covalent valence (covalency) or ionic valence (as the complement of covalent valence) are used in this review except when reporting work in which the term is used in this traditional sense.

• Lewis acid strength, L_a: See cation bonding strength.

• Lewis base strength, L_b: See anion bonding strength.

• Pauling bond strength, S_p: The atomic valence of a cation divided by its observed coordination number (eq 1).

• Polar bond: A localized bond between two ions with different electronegativities.

• Polar compound: A compound containing polar bonds.

• Residual valence: The atomic valence remaining after the bond valence of some or all the bonds formed by the ion have been subtracted.

• Theoretical bond valence, s: The bond fluxes (or valences) calculated using the Kirchhoff network eqs 9 and 13, based on the assumption that all the bonds are of equal weight, that is, the bond capacitances are all equal.

• Total Lewis acid strength, U_a: Sum of the Lewis acid strengths of the bonds expected for a simple or complex ion, a positive number.

• Total Lewis base strength, U_b: Sum of the Lewis base strengths of the bonds expected for a simple or complex ion, a negative number.

• Valence, V: An atomic property used to determine the allowed stoichiometries. The rules that determine the valence are described under atomic valence.

• Valence vector: A vector, normally having the magnitude of the bond valence and the direction of the bond.

• Valence unit, vu: This is equivalent to one electron unit in the atomic valence, or an electron pair in the bond valence.

1.1. The Four Heuristic Principles

Principle of maximum symmetry: A system in equilibrium adopts the highest symmetry consistent with the constraints acting on it (eq 3).

Electroneutrality principle: The sum of all atomic valences (ionic charges) in a system is zero, (eq 4).

Principle of local charge neutrality: In an equilibrium condensed phase each ion arranges itself so that it is surrounded by ions of opposite charge, that is, there is no local build up of charge, (eq, 5).

Equal valence principle: Consistent with the valence sum rule and other constraints which may apply, in an equilibrium structure each atom distributes its valence as equally as possible between the bonds it forms, (eq 6).

1.2. Theorems and Rules

Compressibility rule, (equal valence rule), (valence matching rule): The bond valence sum around each cation in a compound increases by the same amount under the application of hydrostatic pressure, (eq 60).

Distortion theorem; Keeping the bond valence sum constant, the average bond length in a coordination sphere increases the more the individual bond lengths deviate from their average. Alternatively: keeping the average bond length constant, the bond valence sum increases for a given ion the more its individual bond lengths deviate from their average, (eq 35, see also eq 43).

Equal valence rule: This name is used for two different rules, the loop rule, and in section 20, the compressibility rule.

Local charge neutrality rule: The electroneutrality principle applies locally to small clusters of ions (eq 5).

Loop rule, (Equal valence rule): The valence sum around a loop in the bond network is zero (eq 13). It can be derived(2) from the equal valence principle in cases where the only constraint is the valence sum rule.

Short range order rule: The most likely short-range ordering of ions are those that most closely conform to the valence sum rule.

Valence matching rule: Bonds will normally only form between a cation and an anion if 0.5 < |L_a/L_b| < 2 and will be most stable if |L_a| = |L_b| where L_a is the bonding strength of the cation and L_b is the bonding strength of the anion, (eq 16). See also section 11. In section 20, this term is also used for the compressibility rule.

Valence sum rule: The sum of bond valences around any atom should be equal to the atomic valence, (eq 5).

Valence vector sum rule: The sum of valence vectors around any ion is ideally zero, (eq 45). This rule applies when ion is at the center of its coordination sphere. It is not expected to apply when electronic or steric distortions are present.

2. Background

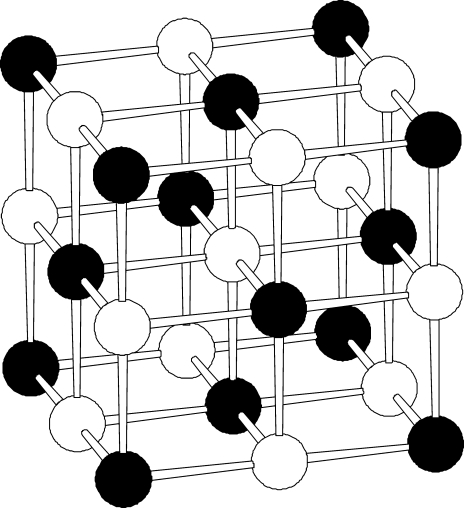
In 1911, it was shown that the sodium atom in crystals of sodium chloride has six nearest chlorine neighbors. This required rethinking the contemporary model of chemical bonding that held that the number of chemical bonds formed by an atom was equal to its atomic valence. An alternative model for describing inorganic compounds was therefore developed by Born, Landé, and Madelung during breaks from designing ordinance for the German army during the First World War. They proposed that the sodium atoms should be considered as cations carrying a single positive charge (as had been demonstrated in electrolysis experiments) and that the chlorine atoms should be considered anions carrying a single negative charge. According to classical physics, an array of such charges is unstable and collapses to a point, so to prevent this from happening, Born and his colleagues introduced a repulsive potential to keep the atoms apart. The equilibrium state of such a system is one in which each cation is surrounded by anions and each anion is surrounded by cations as observed in the structure of NaCl (Figure 2). Although the subsequent development of quantum mechanics has shown that this ionic model is an unrealistic description of chemical bonding, the model has proved to be remarkably robust and successful in describing chemical structure (atomic arrangements), so that even though it does not give a good description of the physical forces that bind the atoms into solids and liquids, it can be used to make good predictions of the positions the atoms occupy. However, it suffers from one important limitation—for reasons given below, it cannot be applied to bonds that are formed between atoms with the same electronegativity. This unfortunately excludes C−C and C−H bonds and therefore large parts of organic chemistry.

Figure 2.

Portion of the bond network of an NaCl crystal. Black ions are Na⁺, light ions are Cl⁻.

There are a number of reasons for the success of the ionic model. It is simple and involves only classical physics, making it more accessible than quantum mechanical models. It is robust because the empirically fitted repulsive potential automatically takes account of most of the complicating factors of the model, and because of this robustness, the model has proven as successful as quantum mechanical calculations in predicting the structures of compounds with polar bonding. Because of its simplicity, it provides many insights that are lost in the complex calculations associated with the more physically rigorous theories.

Over the last half century, the ionic model has been developed in two different directions: one follows the traditional physics approach of seeking the structure with the lowest potential energy, the other exploits the chemist’s description of localized bonds. Both approaches are based on the same set of assumptions, but they give complementary pictures of the structure of condensed matter. The physics-based two-body potential model is widely used to simulate the structures of solids and liquids and to study their dynamics while the chemistry-based bond valence model is used to describe and analyze structures using the familiar terminology of chemical bonds. This review surveys the advances made in the bond valence model since the beginning of the current century.

In 1929 using the ionic model, Pauling(3) analyzed a number of the mineral structures that had been determined during the previous decade and proposed his much-quoted five rules governing the structures of minerals. The most important of these is the second rule, the principle of local charge neutrality. In this he suggested that the negative charge, V_a, on each anion is neutralized by the positive charges on its neighboring cations. He assigned to each bond a Pauling bond strength, S_p, given by eq 1.

where V_c is the valence (or formal charge) of the cation and N_c is its coordination number, that is the number of first-neighbor anions that surrounded the cation. His electrostatic valence rule, eq 2, states that the sum of the bond strengths received by each anion tends to compensate the valence of the anion.

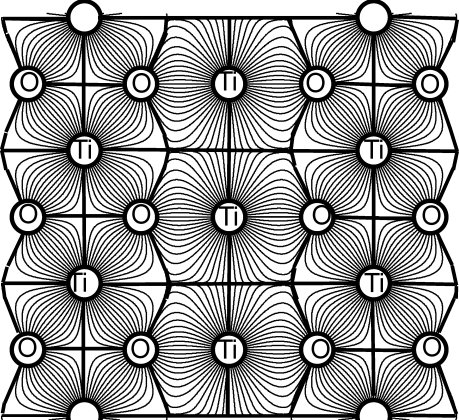
This rule implies that the cations and anions arrange themselves in such a way as to provide local charge neutrality. The idea was expressed in a more visual form by Bragg,(4) who suggested that the electric field could be represented by Faraday’s lines of field (electrostatic flux) and that the observed arrangements of ions in a crystal corresponds to an arrangement that keeps the field lines as short as possible. A picture of the flux lines lying in the (110) plane of rutile (TiO₂) is shown in Figure 1. We now recognize that Pauling’s bond strength and Bragg’s electric flux lines were early attempts to estimate what is today called the bond valence; the limitation of the technology of structure determination at that time did not allow for a better definition. Consequently, eq 2 is usually only approximately true.

Figure 1.

Bond fluxes in the (110) plane of rutile, TiO₂. Copyright 1999 International Union of Crystallography. Reproduced with permission from ref (9).

During the 1930s and 1940s, while chemists looked to quantum mechanics to solve the problem of chemical bonding, mineralogists exploited Pauling’s rules to help them understand the increasingly complex mineral structures they were discovering, but while these rules were useful in understanding mineral structures, they were more heuristic than quantitative. It was not until the 1950s and 1960s that the ionic model was further developed with the aid of the newly available computers that could calculate the potential energy of every atom pair in the crystal. At the same time, with the improvement in the quality of crystal structure determination, Baur(5) pointed out that there was a strong correlation between the length of a bond and Pauling’s concept of its strength. The term bond valence was introduced by Donnay and Allmann(6) to describe a bond strength derived from its measured bond length, leaving the term Pauling bond strength to refer to the estimate of the bond valence derived from the coordination number using eq 1. When summed around the anions and cations, the bond valences were found to reproduce the atomic valences (ionic charges) more accurately than Pauling bond strengths.^7,8 Determination of this correlation for different bond types (ion pairs), and the discovery that these correlations were robustly transferable between different crystals, followed soon after, In this way the bond valence model provided a more quantitative picture of chemical structure than was possible with Pauling’s second rule.

As shown in section 3, if one calculates the flux lines that represent the electrostatic field in the ionic model of a crystal, one finds that they do indeed link neighboring cations and anions, showing that the Coulomb field of the ionic model can be decomposed into localized regions that correspond closely to the classical idea of a chemical bond as shown in Figure 1. Further, my colleagues and I(9) have shown that the total flux linking two ions is equal to the bond valence determined from the bond lengths. The bond valence model thus provides a rational for the classic chemical model of localized bonds, at least for acid−base bonds, that is, those that have a cation at one end and an anion at the other. As the bond valence model gives a good description of the structure of water, it also provides a simple description of the chemical structure of aqueous solutions, which opens up its use in fields ranging from mineralogy to biology as described in later sections of this review.

The bond valence model preserves many of the traditional concepts of chemistry, such as atom, bond, cation, anion, electronegativity and valence, but it gives them precise definitions (see the glossary in section 1). Although expressed entirely in terms of nearest neighbor interactions (i.e., bonds), the model gives a complete description of the Coulomb field, including the repulsive electrostatic forces between like-charged ions and the long-range interactions that make the two-body potential model computationally intensive. Both of these effects are correctly described by the localized bonds of the bond valence model.

Since the turn of the century, there has been in interest in exploiting the complementary character of the two-body and bond valence models; the two-body potential model is used to simulate a structure which can then be analyzed and interpreted using the bond valence model. Quantum mechanical simulations can also be analyzed in the same way, with the satisfying result that all three models are found to agree with the observed structures.

Gibbs et al.(10) have recently published a review which gives a more complete account of the development of the concepts of chemical bonding particularly with reference to the crystal chemistry of minerals. Some of the original papers in this field have recently been reproduced in the Landmark Papers series of the Mineralogical Society of Great Britain and Ireland.(11)

3. Theoretical Derivation of the Bond Valence Model

This section provides a mathematical derivation of the theorems of the bond valence model. It is included here to emphasize the underlying assumptions of the model whose possibilities and limitations are often misunderstood in the papers reviewed below. It outlines the aspects of the model needed to appreciate the ideas described in the literature surveyed.

The physical entities involved in the cohesion of solids are nuclei and electrons, but these do not lead naturally to unique definitions of the traditional chemical concepts of atom, bond, valence, and ion. Even though there are no precise and generally accepted definitions of these terms, they do refer to useful chemical concepts which we impose on the patterns of nuclei and electron densities that we observe in solids and liquids. Within the bond valence model, these terms are given exact definitions that may differ from those used in other models or from the reader’s intuitive sense of their meaning. For example, there is no natural definition of an atom in a condensed phase since the electron density is a continuous finite function with no natural boundaries between the nuclei. Different definitions of the word atom are found in the Atoms in Molecules (AIM) approach of Bader(12) and in the bond valence model. In Atoms in Molecules, an atom is defined by the topological properties of the electron density and the charge on the atom depends on the number and arrangement of its neighbors, while in the bond valence model an atom is defined as having a fixed charge (or valence) regardless of where it is found. The terms used in the bond valence model are precisely defined in section 1 and are used in this sense throughout this review. Section 1 also includes a summary of the principal theorems of the model. Because the bond valence model is a version of the ionic model, ionic terminology is used throughout the review, but without implying that the bonds necessarily have any ionic character. In this model, the ionic or covalent character of a bond is irrelevant.

A couple of useful heuristic principles underlie the theorems of the bond valence model. They describe properties of the minimum energy solution of the ionic model when it is developed using two-body potentials, but they do not appear naturally in the bond valence model and must be introduced explicitly. The most important of these principles is the principle of maximum symmetry.

One justification for this principle is that any symmetry element will be an extremum in the potential energy. Energy minima will therefore tend to be found on symmetry elements. It follows that equilibrium structures will tend to adopt high symmetry unless prevented from doing so by some symmetry-breaking constraint.

Next in importance is the electroneutrality principle.

This principle, taken together with the observed stoichiometries of compounds, is what allows valences to be assigned to atoms. Consequently, it restricts the chemical compositions for which the bond valence model can be used. For example, many metallic and organic compounds do not satisfy this principle and therefore cannot be described by the model.

The next two principles follow from the previous two. The principle of local charge neutrality is the basis of Pauling’s second rule and the valence sum rule developed below.

This principle follows from the electrostatic properties of the ionic model as shown below. A fourth heuristic is the equal valence principle.

This principle is a special case of the principle of maximum symmetry. A more formal theoretical justification for this is suggested in section 6.

The bond valence model describes the structures of compounds containing polar bonds, that is bonds between atoms of different electronegativity. In each bond, the atom with the smaller electronegativity is called the cation and that with the larger electronegativity is called the anion. Cation and anion are formal labels that do not imply any particular type of physical bond nor do they imply the physical transfer of charge between atoms. The discussion of the physical origin of chemical bonding is in any case beyond the scope of the bond valence model.

The valences, V, of cations and anions are derived from the observed stoichiometries of compounds which satisfy the electroneutrality principle.

where the sum is over all atoms in the formula unit. In practice, this means that the cation valence is equal to the number of its valence-shell electrons used in bonding (often called the formal oxidation state) and the anion valence is the negative of the number of holes in the valence shell. Cations are therefore assigned a positive valence and anions are assigned a negative valence.

In the bond valence model, the electronegativity, χ, is defined by eq 8.

where V_c is the cation valence and ⟨N⟩_o is its average coordination number when bonded to oxygen. ⟨N⟩_o is used here as a measure of the size of the ion.(13) Although the numerical values in this scale differ from other electronegativity scales, the order in which the main group elements occur is similar to other scales. The advantage of this particular definition is that it is defined using the concepts of the bond valence model, it is simple to calculate, and it is numerically equal to the cation bonding strength defined in eq 14 below. It allows atoms to be identified as cations or anions, since the anions all have a higher electronegativity than any of the cations.

The ionic model is generated by replacing the cations and anions by point charges equal to their valences, and allowing these charges to interact in three-dimensional space. According to electrostatic theory, the electrostatic (or Coulomb) energy of such an array of point charges is minimized by having the cations surrounded by anions and anions surrounded by cations corresponding to the principle of local charge neutrality. However such an array is unstable and collapses to a point unless there is a repulsive potential to prevent the charges from coalescing. The combination of the attractive electrostatic potential and an appropriate repulsive potential results in the ions coming to equilibrium in a structure that depends on the nature of the repulsive potential. If this potential is appropriately chosen, the equilibrium arrangement of the point charges can be made to replicate the observed arrangement of the ions. For a given cation−anion pair, these potentials are found to be more-or-less transferable between compounds.

The ionic model is usually applied by searching for the arrangement of ions that minimizes the energy calculated from the electrostatic and repulsive potentials. However, the bond valence model takes a different approach, exploiting the properties of the electrostatic field rather than the electrostatic potential. The electrostatic field provides a local description which is easy to visualize using Faraday’s lines of field as shown in Figure 1. Each field line starts at a cation and ends at a neighboring anion. A bond is then defined as occurring between a cation and an anion if and only if they are directly linked by Faraday field lines. The number of such lines is proportional to the electrostatic flux which can be used as a direct measure of the strength of the bond and which will later be identified with the bond valence. Since the electrostatic flux is equal to the charges that it links (Gauss’ law), it follows that the sum of all the bond fluxes around any ion is equal to its ionic charge or valence. Therefore if the bond valence, s_ij, is set equal to the bond flux, the sum of bond valences around any ion, i, is equal to its valence, V_i. This is expressed in eq 9, the valence sum rule, which is the central equation of the bond valence model and follows from the above definition.

Calculating the bond flux is not trivial and in any case requires an exact knowledge of the structure.(6) It is not therefore particularly useful in prediction or analysis, but it provides a powerful way of visualizing the bond valence whose properties will now be developed into a more user-friendly model.

The topology of a structure in the bond valence model can be represented by a bond network in which ions are represented by the nodes of a graph and bonds by the links between them. This graph is generated by replacing the bond flux linking two ions by a single link representing the presence of a bond. The graph of such a network is described as bipartite, meaning that the graph contains two kinds of nodes, cations and anions, and every link (bond) has a cation at one end and an anion at the other as shown for a portion of a crystal of NaCl in Figure 2. Such a bond is referred to here as a polar bond, and the bipartite restriction necessarily follows from treating ions as charged atoms and defining a bond as the electrostatic flux linking them. A bipartite graph only contains loops with even numbers of bonds since an odd-membered loop necessarily has at least one bond between two cations or between two anions. Many of the theorems of the model (such as the valence sum rule given in eq 9) depend on this condition, which thus defines the principal limitation of the model.

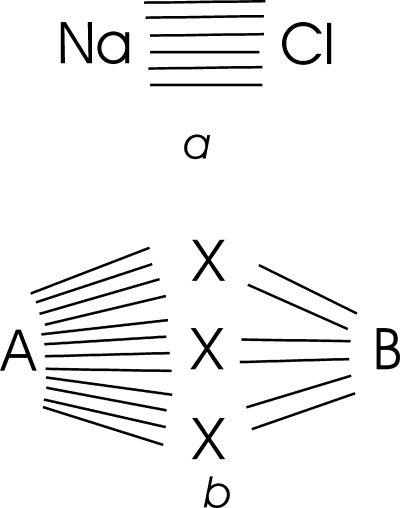
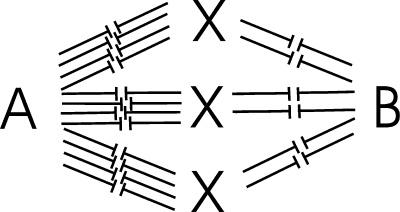
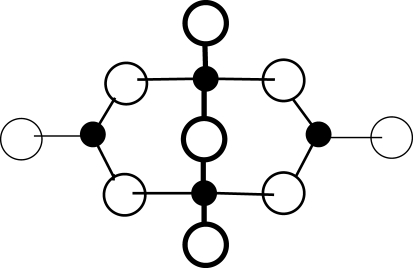
If, as is usual, a compound containing polar bonds forms a crystal, the bond network is infinite, but it is possible to extract from this infinite network a finite bond network comprising a single formula unit. Bonds must be broken when such a formula unit is extracted from the infinite network, but the broken bonds can all be relinked internally within the extracted unit, retaining all the nearest neighbor topological relationships between the ions and the bonds as shown in Figure 3a for NaCl and Figure 3b for ABX₃ perovskite whose structure is shown in Figure 21. Such finite bond graphs are similar to the schematic diagrams frequently used to display the structure of organic molecules, but while for organic molecules such diagrams often represent the geometric arrangement of the atoms in the molecule, the finite bond graph of a crystal is necessarily more abstract and cannot be made to conform to Euclidian geometry.

Figure 3.

Finite bond graphs for (a) NaCl (c.f. Figure 2) and (b) perovskite (c.f. Figure 21).

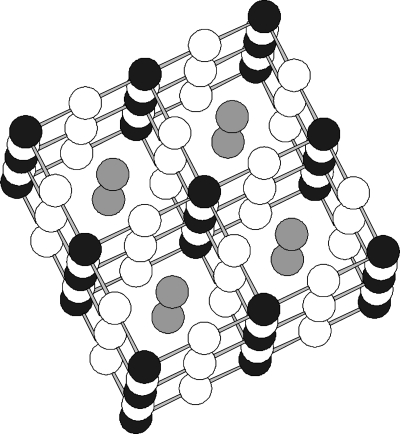
Figure 21.

Group of eight unit cells of the cubic perovskite structure ABX₃. The B cations (black) are octahedrally coordinated by X anions (white). The octahedra are linked through shared corners to form a cubic network. The A cations (gray) occupy the centers of the cubes formed by the linked octahedra.

The bond valence model can be extended by noting that in the ionic model a chemical bond is an electric capacitor since it consists of two equal and opposite charges linked by electrostatic flux. Bonds in the bond network can therefore be formally replaced by electric capacitors, thereby converting the bond network into an equivalent capacitive electric circuit as shown for the perovskite structure in Figure 4.

Figure 4.

Finite bond graph for perovskite as a capacitive electric circuit based on Figure 3b. According to the principle of maximum symmetry, the capacitors are all identical.

This allows the bond fluxes, which are equal to the charges on the capacitor plates, to be calculated from the atomic valences (charges) using the two Kirchhoff circuit laws appropriate to a capacitive circuit.

Law 1: The sum of all capacitor charges Q_ij at a node is equal to the charge on the node (in this case the atomic charge, V_i). This is equivalent to the valence sum rule given in eq 9,

and Law 2: The sum of all the potentials around any loop in the graph is zero.

The potential P_ij across a capacitor C_ij is related to the charge Q_ij on the capacitor by eq 12.

The only unknown in these equations is C_ij, the capacitance of the ijth bond. Unless there is an a priori reason for making one bond different from another, one can invoke the equal valence principle and assume that in an equilibrium structure every bond has the same capacitance, in which case C cancels and the equations can be solved for Q_ij, the charge (or flux) associated with the bond, which is the same as the bond valence. It is found in practice that the assumption of equal capacitances is fully justified except in the presence of the electronic anisotropies or the steric constraints discussed in section 8.

The bond valence obtained from the Kirchhoff laws is called the theoretical bond valence, s, and has been shown(9) to be the same as the bond flux, except in those aforementioned cases discussed in section 8.

The Kirchhoff laws can be recast in a form appropriate to the bond valence model by replacing the charge on the ion by the atomic valence, V_i, and the bond charge Q_ij by the theoretical bond valence, s_ij. The first law is then the valence sum rule given in eq 9. By definition, this law is exactly obeyed by both the bond fluxes and the theoretical bond valences under all circumstances. Assuming that all the capacitances are equal, Kirchhoff’s second law then becomes:

This is known as the loop rule or the equal valence rule and it, too, by definition is obeyed by the theoretical bond valences, but not necessarily by the bond fluxes which are derived from the observed structure and may be subject to the constraints described in section 8. The presence of these constraints can, in principle, be modeled by assigning bond capacitances that are not all equal though in practice this is not usually feasible. A program, BONDVAL, for solving the bond network equations is available from Orlov.^14,15

The usefulness of this derivation of the bond valence model lies in the fact that the bond fluxes, and also the theoretical bond valences when electronic and steric constraints are not present, correlate well with the observed bond lengths. These correlations are described in more detail in section 7. Here it is sufficient to note that the parameters describing this correlation are transferrable between bonds of the same type, that is, bonds having the same pair of terminal ions, and they can be used to calculate experimental bond valences, S, from the observed bond lengths, or alternatively can be used to calculate ideal bond lengths from theoretical bond valences, s. It is this correlation, which corresponds to the repulsive potential of the traditional ionic model, that provides the link between the theorems of the bond valence model and the structures of real compounds.

There are extensions to this model that increases its power. The average coordination number, ⟨N⟩_o, that a cation adopts with oxygen is a useful, if arbitrary, measure of the size of the cation(13) but it is a choice with a number of advantages. It can be determined to sufficient accuracy (one decimal place) by averaging over a random set of known structures and is therefore typical of the coordination numbers found in stable oxides. The ratio of the valence of the cation, V_c, to its average coordination number is called the cation bonding strength (or Lewis acid strength), L_a, (eq 14) as it is equal to the valence expected for a typical bond formed by the cation in oxides. It is also the same as the electronegativity defined in eq 8.

An anion bonding strength (or Lewis base strength), L_b, equal to the valence of a typical bond formed by the anion, is defined in the same way (eq 15) by taking the average coordination number, ⟨N_a⟩, of O²⁻ to be four. Corresponding values can be found for other anions.

L_a and L_b, which are defined as positive and negative respectively, can also be defined for complex ions in the same way as for simple ions. Some complex ions or molecules can simultaneously act as both a Lewis acid and a Lewis base and so can have both a cation and an anion bonding strength. For example, water acts as a Lewis base through O²⁻ and as a Lewis acid through H⁺. A selection of cation and anion bonding strengths is given in Table 1.

Table 1. Selected Bonding Strengths.

Cation bonding strength (Lewis acid strength) and electronegativity in valence units from ref (1)
symbol	average observed coordination number	bonding strength	remarks
Cs+	9.2	0.109
Tl+	3−9	0.11−0.33	Lone pair
Rb+	8.0	0.124
K+	7.9	0.126
Na+	6.4	0.156
H2O	2	0.2	Bonding through H
Ca2+	7.3	0.274
Mg2+	6.0	0.334
Al3+	5.3	0.57
Nb5+	6.1	0.82	d0 element
Si4+	4.0	1.00
Mo6+	4.9	1.23	d0 element
P5+	4.0	1.25
C4+	3.0	1.33
S6+	4.0	1.5
N5+	3.0	1.67
Cl7+	4.0	1.75

Anion bonding strength (Lewis base strength) in valence units
symbol	coordination number	bonding strength	remarks
ClO4−	12	−0.08
NO3−	9	−0.11
Br−	8	−0.12
VO3−	7	−0.14	Polymeric tetrahedral coordination
Cl−	6	−0.17
SO42−	12	−0.17
Oxalate	12	−0.17
MoO42−	12	−0.17
H2O	2	−0.2	Through O
CO32−	9	−0.22
F−	4	−0.25
PO43−	12	−0.25
SiO32−	7	−0.29	Chain
Si2O76−	19	−0.32
BO33−	9	−0.33
SiO44−	12	−0.33
BO45−	12	−0.42
O2−	4	−0.50

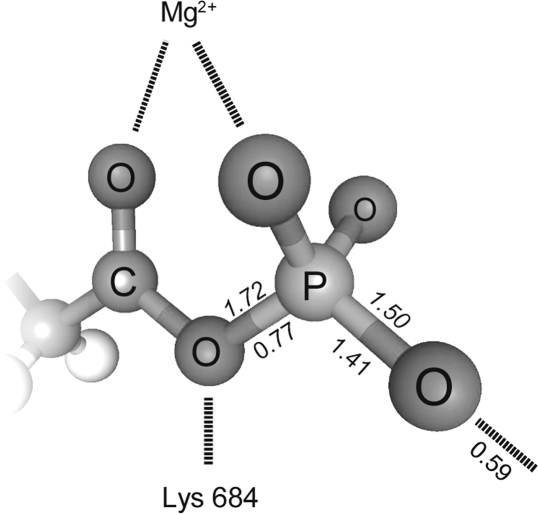
Since the anion and cation bonding strengths are both estimates of the valence of the bond formed between them, it follows that the most stable bonds will be formed when they are the same. In practice it is found that for most observed bonds the two bonding strengths differ by less than a factor of 2. This is known as the valence matching rule, eq 16.

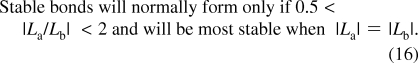This rule explains why a compound formed from two well matched but weakly bonding ions, such as Cs⁺ and ClO₄⁻ is more stable than a compound formed from two stronger, but mismatched, ions, such as Na⁺ and SiO₄⁴⁻ or Na⁺ and O²⁻. A stable structure is defined here as one that cannot rearrange itself into a structure with a better matching of the bonding strengths, either because the matching is already good or because there is no mechanism to achieve a better matched arrangement. A few complexes such as NO₃⁻ (|L_a/L_b| = 3.3) or ClO₄⁻ (|L_a/L_b| = 3.5) with very poor valence matches exist only because there is no mechanism for them to rearrange to form a more stable compound, but when such complexes are presented with the opportunity to rearrange by being mixed with, for example, C⁴⁺ that is better matched to O²⁻ they can do so explosively as the strain energy is released.

In addition to determining which compounds are likely to form and which of these will be more stable, the valence matching rule allows one to predict the likely products of a chemical reaction. It is particularly useful in exploring reactions with water (e.g., solubility and hydration complexes in solids and liquids). Since many important reactions occur in aqueous solutions, the bond valence model and the valence matching rule have applications in many branches of chemistry. Applications of these ideas are found in a number of places in this review, particularly in sections 11 and 25.

Compounds in which |L_a| = |L_b| also satisfy Pauling’s electrostatic valence rule exactly since the Pauling bond strength is the same as the cation bonding strength in the case where N_c in eq 1 is the same as ⟨N_c⟩ in eq 14.

4. Relationship between Structural Models

The physics (two-body potential) and the chemistry (bond valence) versions of the ionic model have advantages and disadvantages that are surprisingly complementary. Both contain a complete description of the electrostatic interactions between the cations and anions, including the long-range effects which are mediated in the bond valence model by application of the valence sum rule around all the intermediate ions. The two-body potential model seeks an arrangement of the ions that minimizes a single variable (the energy), while the bond valence model requires the valence sum rule (and the equal valence rule) be obeyed around each ion in the system. This larger number of restrictions makes the bond valence model much more robust and less sensitive to the choice of repulsive potential, which is represented in this model by the bond-valence−bond-length correlation discussed in section 7.

In spite of the larger number of constraints in the bond valence model, there are problems in using it for modeling and these are discussed in section 12. The two-body potentials are better for simulating structures, but a bond valence analysis of the results can be a useful check on their validity. Rossano et al.,(16) for example, used a bond valence analysis to improve the potentials in their two-body potential simulation. A valence analysis need not be confined to analyzing classical simulations; it can also be applied to quantum mechanical simulations, as well as to structures determined experimentally. Bickmore et al.(17) used a bond valence analysis to correct the bond lengths obtained from their density functional theory calculation. Bond valences give chemical insights that are not readily derived from energy-based models; section 8 shows how they can be used to decide if variations in bond lengths arise from the bond topology, from the steric strains resulting from having to fit the atoms and bonds into Euclidian space, or from anisotropic electronic effects. It is the only model that does not need to know the positional coordinates of the ions, hence it can be used to examine structures that cannot exist because they are impossible to map into three-dimensional space. Its strength lies in its use for conceptual modeling, where only imagination and a pocket calculator are required.

Because both the bond valence and the two-body potential models are derived from the ionic model, both are restricted to structures with bipartite bond graphs, that is, structures in which all the bonds are formed between a cation and an anion. Quantum mechanical models, on the other hand, are not so restricted, and further, quantum mechanical models give a correct physical description of the electron density associated with the bond, but like the two-body potential model, most of the insights into the structure are hidden in the complex calculations. Fortunately at the point where the models can be compared, density functional calculations, two-body potential models and bond valence analysis are all found to agree with observation. There are many examples where bond valences have been used to analyze or confirm simulations obtained by two body potentials,^16,18,19 density functional theory,^{17,19−21,12,23} or other quantum methods.^24,25

5. Theoretical Basis of the Bond Valence Model

The success of the empirical bond valence model has given rise to a number of attempts to find a secure basis for it in physical theory, an endeavor that for the most part has met with indifferent success. My current attempt, described in section 3 above, is only one in a continuing series. It is more rigorous, but less physical, than most.

Mohri(26) has published a derivation from an approximate electron density model. He assumes that each bond involves the same number of electrons and that the valence of a bond is proportional to its electron density. He therefore divides the number of electrons by the volume they occupy, taken to be proportional to the cube of the bond distance after those parts of the distance that lie within the atom cores have been subtracted. Using the sum of the cation radii, r, as a measure of the sizes of the cores, the space occupied by the bonding electrons is (R − r),(3) where R is the bond length. This leads to eq 17.

where s is the valence of a bond of length R and s′ is the valence of a bond of length R′. He shows that this equation can be reduced to eqs 25 and 26 which are commonly used to describe the bond-valence−bond-length correlation. He includes a number of worked examples.

In a subsequent paper Mohri(27) looked for a quantum mechanical quantity that gives the classical bond orders for covalent, that is, nonpolar, bonds, one that also obeys the valence sum rule and that correlates with the bond length. Using molecular orbital theory, he derives Okada bond orders from a Lewis electron pairs approach to spin-coupling matrix theory. After various approximations, the Okada bond orders are shown to be the same as Mayer bond orders(28) (though derived in a different way) as given by eq 18.

where P is the density matrix and r and s refer to atomic orbitals. He calls B the covalent bond order and shows, with many examples, that the sum of B_ij around any given atom is a constant which he defines as the atomic valence. In many cases Mohri’s atomic valences are numerically the same, or very close to, the classical atomic valence. In two subsequent papers^29,30 he applies the covalent bond order model to the hydrogen bond, X−D−H···A−Y, in the first paper showing that the sum of Mayer bond orders around H is 1.0 regardless of whether the atom A is present or not. In the second paper, he considers how the electrostatic field generated by X and Y affects the molecular orbitals in a way that leads to alternating bond strengthening and weakening. His arguments are given in terms of the electrostatic potential energies, but they can as easily be expressed in terms of bond fluxes.

Gibbs and his colleagues^10,31 have explored the relationships between structure properties (chiefly the bond lengths) and the topological properties of the electron density. Among the correlations they give is one which shows a linear relationship between the bond valence, s, and the electron density at the bond critical point, ρ. For Si−O bonds they show that:

The fact that the electron density at the bond critical point is numerically almost equal to the bond valence is a welcome simplification though it remains to be seen whether this relationship holds for other bond types. The experience of Howard and Lamarche(32) described in section 13 is not promising. They show that correlations that work for C−C bonds do not always work so well for heteroatomic bonds.

6. Bond Valence as a Measure of Energy

There is no rigorous way of deriving energy from the bond flux or bond valence in order to obtain bond energies. Nor is it possible to measure the energy of a bond since any experiment in which a bond is broken is followed by a relaxation of all the other bonds in the system; all that can be measured in such an experiment is the total energy of this process.

However, it would be useful if we could convert valence to energy. It should be possible to find some correspondence since a bond in the ionic model is equivalent to a capacitor as described in section 3, and if the capacitance is known, the stored electrostatic energy can be calculated. However, calculating the capacitance of a bond runs into trouble because the point charges representing the atoms constitute mathematical singularities.

Although a rigorous evaluation of the capacitance is not possible, the capacitiance can be estimated since it will be approximately the same as that of a flat plate capacitor of dimensions similar to those of the bond. The capacitance, C, of such a device is given by eq 20.

where A the area of each of the plates and d their separation. The area of the plates can be approximated by surrounding the cation with a sphere of radius, r, equal to 1 Å and dividing its surface area by the cation coordination number, N, viz: 4πr²/N. The separation, d, of the plates can conveniently be set to 1 Å.

The energy stored in a capacitor carrying a charge Q is:

Substituting for C gives:

Recognizing that Q is equal to the bond flux, and hence the bond valence, s, we can substitute s for Q and inserting numerical values for r and d, and 6 for N, eq 22 becomes:

where k has been written for 1/(4πε₀). This can be abbreviated to:

where a is equal to 7 eV vu⁻². Given the crude nature of the approximations, this value can only be considered an order of magnitude.

This equation can be compared with a number of experimental indications of the link between energy and bond valence. As mentioned in section 22.6, Etxebarria, et al.(33) show that the change in the calculated energy of SrBa₂Ta₂O₉ as it is distorted along various soft normal modes correlates quantitatively with the square of the global instability index, G², as shown in eq 24 with a equal to 0.5 Ry vu⁻² (6.8 eV vu⁻², 656 kJ mole⁻¹ vu⁻² or 157 kcal mole⁻¹ vu⁻²).

The close agreement between the estimated and this measured values of a is fortuitous given the approximations involved in the derivation of eq 24, but work by others suggests that this relationship may have some validity.

Adams(34) shows that in ionic conductors the activation energy for migration of the mobile ion in eV is equal to 2ΔV, where ΔV is the half-width (in vu) of the volume accessible to the mobile ion as described in more detail in section 10. Adams shows these as a linear correlation between activation energy and ΔV in Figure 6 of his paper, but they can also be fitted by eq 24 over the range of his measurements. The equation also fits the correlation between the energy of a hydrogen bond and the valence of the weak H···O bond given in Figure 7 in my earlier work.(35) The energies of N−H···N bonds given by Majerz and Olovsson(25) are also in agreement.

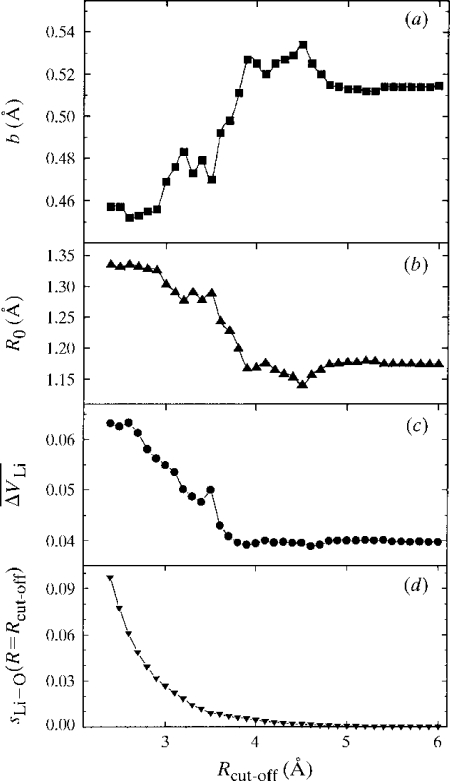
Figure 6.

Consequences of different choices for the cutoff radius, R_cutoff, on the values of the bond valence parameters, R₀ and b, for Li−O bonds. (a) Refined value of R₀, (b) refined value of b, (c) average difference between the atomic valence and the bond valence sum calculated with the bond valence parameters refined at this cutoff, (d) bond valence at the cutoff calculated with the corresponding bond valence parameters. Copyright 2001 International Union of Crystallography. Reproduced with permission from ref (79).

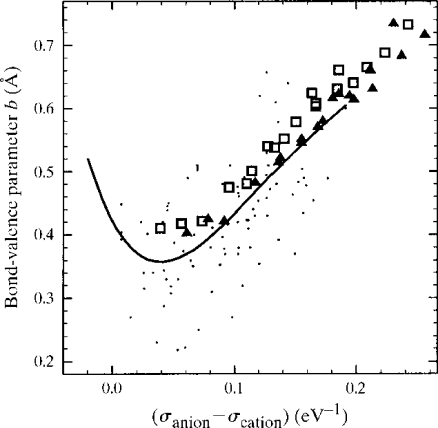
Figure 7.

Refined value of b as a function of the difference in softness between the anion and the cation calculated using eq 32. Squares are alkali halides, triangles are alkali chalcogenides, dots represent values taken from the literature. The line is a fit to the dots. All distances out to at least 6 Å were used. Copyright 2001 International Union of Crystallography. Reproduced with permission from ref.(79)

If eq 24 is valid, it provides some justification for the equal valence rule (eq 6). At equilibrium the energy is a minimum, therefore Σs_i² must also be a minimum under the constraint that Σs_i is held constant. This condition is achieved when all the values of s_i are the same. This is the underlying assumption of the equal valence rule.

Although the identification of the energy with the square of the valence is promising, much more work needs to be done to understand how this relation should be used.

7. The Bond Valence−Bond Length Correlation

7.1. Introduction

The correlation between bond valence and bond length has been known for some time.^7,8 Preiser et al.(9) showed that a good correlation exists between the observed bond length and the bond flux, which is not surprising given that the bond flux is calculated using the same observed atomic positions as are used to calculate the bond length. More usefully they showed that the bond length also correlates with the theoretical bond valence, s, calculated using the valence sum and loop rules given in eqs 9 and 13. The only exceptions are for the cases discussed in section 8 below where electronic asymmetries or steric strains are present. A knowledge of the bond-valence−bond-length correlation allows experimental bond valences, S, to be calculated from observed bond lengths. This in turn allows experimentally determined structures to be validated against the bond valence rules such as the valence sum rule. Alternatively, ideal bond lengths can be calculated from the theoretical bond valences if these are known.

Determining this correlation is not straightforward since the expected bond valence can only be reliably predicted in a limited number of cases. Calculating the bond fluxes would give the expected bond valences, but no general software is available for this nontrivial calculation. Theoretical bond valences are easy to calculate, but can only be used where electronic or steric effects are absent. Since the asymmetry of the hydrogen bond is a steric effect (see section 21), it is impossible to determine theoretical bond valences for any structure with hydrogen bonds, thus eliminating the large and important group of hydrated structures. Indirect methods must therefore be used.

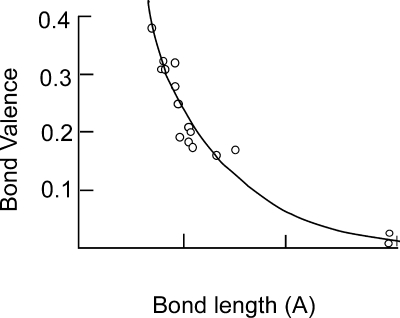
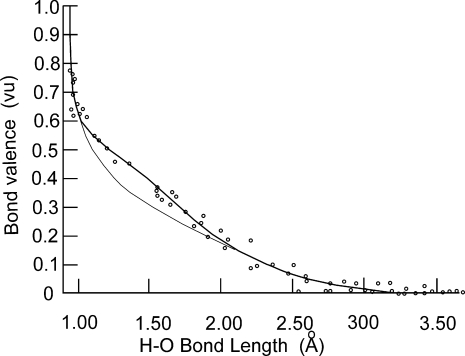
The bond-valence−bond-length correlation for Ca−O bonds shown in Figure 5 is typical. The points in this figure are determined from bond fluxes calculated for observed structures, and the line, which is the fit to these points, can be expressed either graphically as in this case, or algebraically. The graphical representation can show all the nuances in the correlation, and in certain cases, such as the correlation for the H−O bond type shown in Figure 19, the graphical representation is required, but since the majority of bond types show a limited range of observed bond lengths, a simple two parameter algebraic equation such as 25 or 26 is sufficient.

or

where S is the experimental bond valence, R the observed bond length, and R₀ and b or N are fitted bond valence parameters. R₀, which represents the nominal length of a bond of unit valence, depends on the sizes of the atoms forming the bond. N or b measures the softness of the interaction between the two atoms. Equation 26 is now the most widely used relation, and an accumulated table of values of R₀ and b, culled from the literature, is available on the web.(33) A number of programs³⁶⁻³⁸ are available for calculating bond valences. Values of bond valence parameters reported during the period covered by this review are given in Table 2, The value of b is found to lie between 0.3 and 0.6 Å but because of the limited range of experimental bond lengths its precise value is not easy to determine. For this reason a value of 0.37 Å is frequently assumed although recent work discussed in section 7.3 shows that significantly different values should be used for some bond types.

Figure 5.

Bond-valence−bond-length correlation for Ca−O bonds. The circles represent the bond fluxes calculated for a number of observed bonds. The line is calculated using eq 26 with R₀ = 1.967 Å and b = 0.37 Å. Reproduced from Figure 3.1 (p. 27) from “The Chemical Bond in Inorganic Chemistry: the Bond Valence Model” by Brown, David (2002) by permission of Oxford University Press.

Figure 19.

Bond-valence−bond-length plot for O−H bonds. The points plot the valence against the observed bond lengths for a number of accurately determined hydrogen bonds. The thick line is a fit to these points, the thin line is an interpolation of the correlation that would be expected if the repulsion strain between the terminal O²⁻ ions were absent. Reproduced from Figure 7.1 (p.77) from “The Chemical Bond in Inorganic Chemistry. The Bond Valence Model” by Brown, David (2002). By permission of the Oxford University Press.

Table 2. Table of Bond Valence Parameters, R₀ and b in eq 26, Reported since 2000^a.

cation	anion	r0	bb		sourcec	reference	remarkd
La	3+	O	2.148	0.37	CD	44
Ce	3+	O	2.116	0.37	CD	44
Pr	3+	O	2.098	0.37	CD	44
Nd	3+	O	2.086	0.37	CD	44
Sm	3+	O	2.063	0.37	CD	44	c.f. R0 = 2.055 below
Eu	3+	O	2.038	0.37	CD	44
Gd	3+	O	2.031	0.37	CD	44
Lu	3+	O	1.947	0.37	CD	44
La	3+	N	2.260	0.37	CD	45
Ce	3+	N	2.254	0.37	CD	45
Pr	3+	N	2.215	0.37	CD	45
Nd	3+	N	2.201	0.37	CD	45
Sm	3+	N	2.176	0.37	CD	45
Eu	3+	N	2.161	0.37	CD	45
Gd	3+	N	2.146	0.37	CD	45
Tb	3+	N	2.130	0.37	CD	45
Dy	3+	N	2.124	0.37	CD	45
Ho	3+	N	2.118	0.37	CD	45
Er	3+	N	2.086	0.37	CD	45
Tm	3+	N	2.082	0.37	CD	45
Yb	3+	N	2.064	0.37	CD	45
Lu	3+	N	2.046	0.37	CD	46
Ce	4+	O	2.074	0.37	CD	46
Sm	2+	O	2.126	0.37	CD	46	c.f. R0 = 2.116 below
Eu	2+	O	2.102	0.37	CD	46
Yb	2+	O	1.989	0.37	CD	46
Ce	4+	N	2.179	0.37	CD	46
Sm	2+	N	2.267	0.37	CD	46
Eu	2+	N	2.165	0.37	CD	46	average
Eu	2+	N	2.075	0.37	CD	46	a
Eu	2+	N	2.228	0.37	CD	46	b
Yb	2+	N	2.092	0.37	CD	46	average
Yb	2+	N	1.967	0.37	CD	46	a
Yb	2+	N	2.127	0.37	CD	46	b
La	3+	Cl	2.545	0.37	CD	46
Ce	3+	Cl	2.538	0.37	CD	46
Pr	3+	Cl	2.521	0.37	CD	46
Nd	3+	Cl	2.512	0.37	CD	46
Sm	3+	Cl	2.481	0.37	CD	46
Eu	3+	Cl	2.468	0.37	CD	46
Gd	3+	Cl	2.457	0.37	CD	46
Tb	3+	Cl	2.437	0.37	CD	46
Dy	3+	Cl	2.407	0.37	CD	46
Ho	3+	Cl	2.399	0.37	CD	46
Er	3+	Cl	2.385	0.37	CD	46
Tm	3+	Cl	2.381	0.37	CD	46
Yb	3+	Cl	2.376	0.37	CD	46
Lu	3+	Cl	2.361	0.37	CD	46
La	3+	S	2.632	0.37	CD	46
Ce	3+	S	2.593	0.37	CD	46	interpolated
Pr	3+	S	2.569	0.37	CD	46	interpolated
Nd	3+	S	2.559	0.37	CD	46
Sm	3+	S	2.538	0.37	CD	46
Eu	3+	S	2.509	0.37	CD	46
Gd	3+	S	2.507	0.37	CD	46	interpolated
Tb	3+	S	2.489	0.37	CD	46
Dy	3+	S	2.475	0.37	CD	46	interpolated
Ho	3+	S	2.461	0.37	CD	46	interpolated
Er	3+	S	2.449	0.37	CD	46	interpolated
Tm	3+	S	2.437	0.37	CD	46	interpolated
Yb	3+	S	2.453	0.37	CD	46
Lu	3+	S	2.414	0.37	CD	46	interpolated
La	3+	C	2.231	0.37	CD	46	π bonded to C
Ce	3+	C	2.209	0.37	CD	46	π bonded to C
Pr	3+	C	2.172	0.37	CD	46	π bonded to C
Nd	3+	C	2.161	0.37	CD	46	π bonded to C
Cm	3+	C	2.143	0.37	CD	46	π bonded to C
Eu	3+	C	2.135	0.37	CD	46	π bonded to C
Gd	3+	C	2.118	0.37	CD	46	π bonded to C
Tb	3+	C	2.078	0.37	CD	46	π bonded to C
Dy	3+	C	2.073	0.37	CD	46	π bonded to C
Ho	3+	C	2.061	0.37	CD	46	π bonded to C
Er	3+	C	2.058	0.37	CD	46	π bonded to C
Tm	3+	C	2.047	0.37	CD	46	π bonded to C
Yb	3+	C	2.008	0.37	CD	46	π bonded to C
Lu	3+	C	1.999	0.37	CD	46	π bonded to C
Cr	2+	O	1.739(21)	0.37	CD	47
Cr	3+	O	1.708(7)	0.37	CD	47
Cr	5+	O	1.762(14)	0.37	CD	47
Cr	6+	O	1.793(7)	0.37	CD	47
Cr	2+−4+	O	1.724	0.37	CD	47	Use for unknown oxidation state
Sn	2+	N	2.058(20)	0.37	CD	48
Sn	4+	N	2.042(35)	0.37	CD	48
Sn	all	N	2.058(20)	0.37	CD	48	Use for unknown oxidation state
Sn	2+	S	2.423(23)	0.37	CD	48
Sn	4+	S	2.392(11)	0.37	CD	48
Sn	all	S	2.391(14)	0.37	CD	48	Use for unknown oxidation state
Sm	2+	O	2.116(21)	0.37	CD	49	c.f. R0 = 2.126 above
Sm	3+	O	2.055(13)	0.37	CD	49	c.f. R0 = 2.063 above
Ce	3+	O	2.121(13)	0.37	CD	50
Ce	4+	O	2.068(12)	0.37	CD	50
Ce	all	O	2.094	0.37	CD	50	Use for unknown oxidation state
Sb	3+	O	1.955(13)	0.37	CD	51
Sb	5+	O	1.912(12)	0.37	CD	51
Sb	all	O	1.934	0.37	CD	51	Use for unknown oxidation state
Cd	2+	O	1.875(13)	0.37	CD	52
Cd	2+	N	1.951(15)	0.37	CD	52
Cd	2+	S	2.279(7)	0.37	CD	52
Cd	2+	Cl	2.216(17)	0.37	CD	52
Cd	2+	Br	2.334(7)	0.37	CD	52
Cd	2+	I	2.525(7)	0.37	CD	52
Mo	all	O	1.879*	0.305	I	57
Mo	2+	O	1.834*	0.37	I	53
Mo	4+	O	1.856*	0.37	I	53
Mo	5+	O	1.878*	0.37	I	53
Mo	6+	O	1.900*	0.37	I	53
Mo	all	O	1.879*	0.30	I	53
Mo	2+	O	1.762	0.40(2)	I	85	R0 fixed by Mo2O7
Mo	3+	O	1.762	0.35(1)	I	85	R0 fixed by Mo2O7
Mo	4+	O	1.762	0.34(2)	I	85	R0 fixed by Mo2O7
Mo	5+	O	1.762*	0.30(1)	I	85	R0 fixed by Mo2O7
Mo	6+	O	1.762	0.27(2)	I	85	R0 fixed by Mo2O7
Mo	7+	O	1.762*	0.26(1)	I	85	R0 fixed by Mo2O7
V	2+	O	1.724(8)*	0.37	I	54
V	all	O	1.788	0.32	I	54
Fe	4+	O	1.780(10)*	0.37	I	54
Fe	all	O	1.795	0.30	I	54
Pb	2+	F	2.036	0.382	I	56	R0 from gas phase
Pb	2+	Cl	2.447*	0.40	I	56	R0 from gas phase
Pb	2+	Br	2.598*	0.40	I	56	R0 from gas phase
Pb	2+	I	2.804*	0.386	I	56	R0 from gas phase
Pb	2+	O	1.963	0.49	ID	76
Tl	1+	O	1.927	0.50	ID,CD	77
W	all	O	1.896	0.28		55
Tc	3+	O	1.768*	0.37	CD	75
Tc	4+	O	1.841*	0.37	CD	75
Tc	5+	O	1.859*	0.37	CD	75	6-coordination
Tc	5+	O	1.870*	0.37	CD	75	5-coordination
Tc	6+	O	1.955*	0.37	CD	75
Tc	7+	O	1.909	0.37	ID,CD	75
Mn	3+	F	1.666	0.36	ID	67
NH4	1+	Cl	2.619(10)	0.372(20)	ID	66	b may be 0.37
NH4	1+	F	2.129(10)	0.372(20)	ID	66	b may be 0.37
NH4	1+	O	2.219(10)	0.372(20)	ID	66	b may be 0.37
NH4	1+	O	2.223(10)	0.372(20)	CD	66	b may be 0.37
B	3+	O	1.371	0.37	I	62	global average
B	3+	F	1.289	0.37	I	62
B	3+	S	1.815	0.37	I	62
B	3+	N	1.482	0.37	I	62
B	3+	P	1.920	0.37	I	62
P	5+	O	1.615	0.37	I	62
C	4+	O	1.407*	0.37	I	62
Si	4+	O	1.622	0.37	I	62
Cu	1+	C	1.716	0.37	CD	68
Cu	2+	C	1.716	0.37	CD	68
Cu	3+	C	1.844*	0.37	CD	68
Cu	1+	N	1.571	0.37	CD	68	Depends of coordination of N
Cu	2+	N	1.713	0.37	CD	68	Depends of coordination of N
Cu	3+	N	1.768*	0.37	CD	68	Depends of coordination of N
Cu	1+	O	1.567	0.37	CD	68
Cu	2+	O	1.655	0.37	CD	68
Cu	1+	P	1.844	0.37	CD	68
Cu	2+	P	2.053*	0.37	CD	68
Cu	1+	S	1.834	0.37	CD	68
Cu	2+	S	2.024	0.37	CD	68
Cu	3+	S	2.078	0.37	CD	68
Cu	1+	Cl	1.840	0.37	CD	68
Cu	2+	Cl	1.999	0.37	CD	68
Cu	1+	As	1.856	0.37	CD	68
Cu	1+	Se	1.900*	0.37	CD	68
Cu	2+	Se	2.124*	0.37	CD	68
Cu	1+	Br	1.967	0.37	CD	68
Cu	2+	Br	2.134	0.37	CD	68
Cu	1+	I	2.153	0.37	CD	68
Cu	2+	I	2.36*	0.37	CD	68
Nb	4+	Cl	2.236*	0.37		69	Based on eq 5 in ref (41)
Nb	4+	N	2.004*	0.37		69	Based on eq 5 in ref (41)
Bi	3+	Br	2.567*	0.421	I	78	From gas and solid BiBr3
Sb	5+	O	1.908*	0.409	I	84
Mo	3+	O	1.789	0.418	ID	124	5.5 Å cutoff
Mo	4+	O	1.724	0.562	ID	124	6.5 Å cutoff
Mo	5+	O	1.848	0.482	ID	124	5.5 Å cutoff
Mo	6+	O	1.912	0.405	ID	124	5.0 Å cutoff
Mo	2+	S	2.072	0.422	ID	124	5.5 Å cutoff
Mo	3+	S	2.062	0.519	ID	124	6.0 Å cutoff
Mo	3+	F	1.738	0.427	ID	124	5.5 Å cutoff
Mo	2+	Cl	2.052	0.441	ID	124	5.5 Å cutoff
Mo	3+	Cl	2.089	0.501	ID	124	6.0 Å cutoff
Mo	4+	Cl	2.128	0.558	ID	124	6.5 Å cutoff
Mo	3+	Br	2.191	0.541	ID	124	6.0 Å cutoff
Li	1.+	O	1.174	0.590	ID	130	6.0 Å cutoff
Li	1+	N	1.15	0.631	ID	130	6.5 Å cutoff
Li	1+	O	1.172	0.515	ID	79	6 Å cutoff
Na	1+	O	1.560	0.483	ID	79	6 Å cutoff
K	1+	O	1.973	0.422	ID	79	6 Å cutoff
Rb	1+	O	2.057	0.425	ID	79	7 Å cutoff
Cs	1+	O	2.298	0.403	ID	79	7 Å cutoff
Li	1+	S	1.507	0.632	ID	79	6 Å cutoff
Na	1+	S	1.831	0.621	ID	79	6 Å cutoff
K	1+	S	2.171	0.571	ID	79	7 Å cutoff
Rb	1+	S	2.301	0.552	ID	79	7 Å cutoff
Cs	1+	S	2.515	0.735	ID	79	7 Å cutoff
Li	1+	Se	1.530	0.515	ID	79	7 Å cutoff
Na	1+	Se	1.879	0.660	ID	79	7 Å cutoff
K	1+	Se	2.257	0.624	ID	79	7 Å cutoff
Rb	1+	Se	2.402	0.581	ID	79	7 Å cutoff
Cs	1+	Se	2.657	0.546	ID	79	7 Å cutoff
Li	1+	Te	1.734	0.717	ID	79	7 Å cutoff
Na	1+	Te	2.052	0.684	ID	79	7 Å cutoff
K	1+	Te	2.393	0.662	ID	79	7 Å cutoff
Rb	1+	Te	2.460	0.616	ID	79	8 Å cutoff
Cs	1+	Te	2.736	0.617	ID	79	8 Å cutoff
Li	1+	F	1.101	0.501	ID	79	6 Å cutoff
Na	1+	F	1.426	0.475	ID	79	6 Å cutoff
K	1+	F	1.847	0.422	ID	79	6 Å cutoff
Rb	1+	F	2.957	0.418	ID	79	6 Å cutoff
Cs	1+	F	2.196	0.411	ID	79	7 Å cutoff
Li	1+	Cl	1.342	0.661	ID	79	6 Å cutoff
Na	1+	Cl	1.694	0.603	ID	79	6 Å cutoff
K	1+	Cl	2.087	0.552	ID	79	6 Å cutoff
Rb	1+	Cl	2.244	0.540	ID	79	7 Å cutoff
Cs	1+	Cl	2.505	0.481	ID	79	7 Å cutoff
Li	1+	Br	1.534	0.665	ID	79	7 Å cutoff
K	1+	Br	2.100	0.625	ID	79	7 Å cutoff
Rb	1+	Br	2.327	0.579	ID	79	7 Å cutoff
Cs	1+	Br	2.515	0.538	ID	79	7 Å cutoff
Li	1+	I	1.673	0.723	ID	79	7 Å cutoff
Na	1+	I	1.969	0.688	ID	79	7 Å cutoff
K	1+	I	2.320	0.641	ID	79	7 Å cutoff
Rb	1+	I	2.467	0.631	ID	79	7 Å cutoff
Cs	1+	I	2.695	0.608	ID	79	8 Å cutoff

^aThose for hydrogen bonds are given in Table 6. All distances in Å.

^b* fewer than 10 structures used

^cCD from structures in the Cambridge Structural Database. ID from structures in the Inorganic Crystal Structure Database. I from selected inorganic structures.

^da for acetonitrile, bidentate pyrazol, and triethanolatoamine ligands. b for all other ligands not in a.

7.2. Determinations of Conventional Bond Valence Parameters

The widespread use of bond valences for checking new crystal structures has spawned a cottage industry devoted to the determination of bond valence parameters. Sometimes such determinations arise out of a need to know bond valence parameters that have not yet been determined or for which the tabulated parameters may not be reliable, but there are also some systematic studies of groups of related bond types.

The normal method for determining bond valence parameters is to look for values of R₀ and b that ensure the valence sum rule is obeyed in a reasonable selection of accurate structure determinations. This rule is key to the process as the bond valence parameters are designed to reflect the assumption, described in section 3, that the bond valence sum rule should always be obeyed, that is to say the valence sum rule is used to normalize the valences. The only places where such normalization is not appropriate are certain cases where steric strain results in all the bonds around a given ion being stretched or compressed as discussed in section 8.3. Typically a large set of well-ordered and accurately determined structures containing the given bond type is selected from either (or both) the Cambridge (organic) Crystallographic Database(39) or the Inorganic Crystal Structure Database.(40) Wherever possible, all of the bonds formed by the central cation will be of the same bond type, for example, CaO_n. In some cases, a starting set of bond valence parameters is refined by least-squares to minimize the difference between the atomic valence of the central cation and the bond valence sums. Care is needed as R₀ and b are strongly coupled if the available bonds have valences very different from 1.0 vu. If only one coordination number is present, b will always refine to infinity though the final paragraph of section 7.3 suggests a way around this difficulty. A more usual approach(41) is to assume that b is equal to 0.37 Å and solve for R₀′ in eq 27 which is readily derived from eqs 9 and 26:

Here V is the valence of the cation and R_j the length of the j^th bond in the coordination sphere of the cation. This function is available in the DOS program VALENCE.^36,42 The result is a set of values of R₀′, one for each of the cation environments in the set of structures. Ideally the values of R₀′ should all be the same, though in practice experimental uncertainties in the bond lengths will cause some deviation. If the values of R₀′ show a systematic variation with, say, coordination number or oxidation state, a different value of b should be tried until the systematic variation is removed (if this is possible) though this step is frequently omitted. Section 7.3 shows that failure to refine the value of b can lead to an apparent breakdown in the valence sum rule if the parameters are used uncritically. The value of b that shows the least variation in the values of R₀′, together with the corresponding average value, R₀ = ⟨R₀′⟩, are then taken as the bond valence parameters for all bonds of this type. The bond valence sums calculated with these parameters usually lie close to the cation valence. However, in many of the studies reviewed below it has become customary for some of the outliers to be removed from the test set before averaging R₀′. Even though the practice of ignoring outliers is rarely justified by the authors, the resulting bond valence parameters are probably valid. Their validity should be tested by checking that the valence sum rule is also is obeyed around the anions, but such checks, if performed, are rarely reported. The bond valence parameters reported in the studies reviewed here are listed in Table 2.

Recently, Sidey(43) has proposed a method for determining R₀ and b simultaneously by rewriting eq 26 as a linear equation in ln(S) and R. It is shown as eq 28 for regular coordination in which all bonds have the same length. Here R_S is the observed bond length and V/N has been written for S, where V is the valence and N the coordination number, of the central ion.

Over the range in which eq 26 is a valid approximation, a plot of R_S against ln(V/N) yields a straight line of slope b and intercept R₀. If the coordination is irregular, V/N is the average bond valence, but according to the distortion theorem, the average bond length is slightly greater than R_S. The correction needed to recover the correct value of R_S from the average is discussed in section 8.1. Even though this correction (eq 35) depends on b, it is of the order of 0.1 Å so an approximate value of b based on uncorrected average bond lengths is sufficiently accurate. For a given value of N, R_S can be replaced by the average of several corrected average bond lengths, and since N is always an integer, eq 28 gives rise to a small number of equations any two of which can be solved analytically. A graphical plot not only gives immediate values for the bond valence parameters but also information about their scope and accuracy. No bond valence parameters have so far been published using this method, but it is so simple and powerful that it is likely to become standard in the next few years.

In a series of three papers, Trzesowska et al.⁴⁴⁻⁴⁶ report a systematic evaluation of the bond valence parameters for the rare earth cations bonded to the anions O²⁻, C⁴⁻, N³⁻, S²⁻, and Cl⁻ using structures taken from the Cambridge Structural Database.(39) Using the same database, Palenik and his colleagues⁴⁷⁻⁵² have produced a series of studies to determine the best values of R₀ for the bonds formed by many transition metals. They also discuss specific cases where the bond valence sum differs from the expected value, often indicating an error in the determination or interpretation of the crystal structure. In all of these studies the value of b was held fixed at 0.37 Å. Hu and his colleagues⁵³⁻⁵⁶ have done the same for a variety of cations in inorganic compounds. In some cases they varied b to produce parameters that could be used for any oxidation state, or they set R₀ to the length of the single bond found in the gas phase as noted in Table 2.

Zocchi(57) has reviewed the many bond valence parameters that have been proposed for Mo−O bonds in a variety of oxidation states. From 149 well determined structures containing MoO₆ octahedra, he removed six that had bond valence sums greater than 6.025 vu and from the remainder he selected eight coordination polyhedra that contained Mo in well-defined oxidation states between 3+ and 6+. These he refers to as reference polyhedra. He fitted a single set of bond valence parameters (R₀ and b) to give bond valence sums that agree well with the assigned oxidation states in the eight reference polyhedra, and showed that better agreement was achieved with b equal to 0.305 Å rather than 0.37 Å. In a subsequent paper(58) using only six reference polyhedra he obtained what he claimed were even better values of R₀ and b even though they differed only in the fourth decimal place. In further papers⁵⁹⁻⁶¹ he presents bond valence parameters determined using a bizarre graphical method that even he admits lacks any basis in logic. The parameters he reports for different elements in different oxidation states and different coordination numbers look reasonable, but are determined to a precision (10⁻⁴) that is hardly warranted by the differences between the atomic valences and the bond valence sums shown in his graphs.

In their study of the nonlinear optical properties of borates Yu and Xue(62) have determined the bond valence parameters of various B−O bond types. They divided the B−O bonds according to the type of polyion in which they are found and determined R₀ (with b fixed at 0.37 Å) for each kind of polyion, finding differences of up to 0.014 Å between the averages, ⟨R₀′⟩; polyanions with the most rings having a smaller R₀. Only the global average R₀ for B−O bonds is shown in Table 2. In other papers, Yu and colleagues⁶³⁻⁶⁵ have determined R₀ values for H−O bonds. Somewhat confusingly, their recommended values are themselves functions of the H−O bond length as described more fully in section 21 that deals with hydrogen bonds.

García-Rodriguez et al.(66) have determined bond valence parameters for bonds between the ammonium ion and O²⁻, F⁻ and Cl⁻, noting that NH₄⁺ often behaves like an alkali metal. In addition to R₀, they refined b to 0.372 Å, essentially the same as the value of 0.37 Å usually assumed. Exceptionally, they used structures from both the Cambridge Structural Database(39) and the Inorganic Crystal Structure Database,(40) though they found no bonds to F⁻ or Cl⁻ in the Cambridge database.

Urusov(67) reports bond valence parameters for Mn³⁺−F bonds as part of his study, described in section 8.1, of the Jahn−Teller distortions found around Mn³⁺, while Shields et al.(68) decided to determine the best bond valence parameters for a range of Cu bonds in order to explore how useful the bond valence model would be in determining the oxidation states of transition metal atoms in the Cambridge Structural Database(39) as discussed in section 15. In the process they discovered that different bond valence parameters are needed for Cu−N bonds depending on the coordination number of N, though they report these only for four-coordinate Cu. While they list different values of R₀ for Cu in different oxidation states, they claim that it would be possible to find a single value of R₀ for all oxidation states if the value of b were allowed to deviate from 0.37 Å. Henke(69) was interested in bond valence parameters for Nb⁴⁺−Cl bonds of which not many examples are known so he calculated R₀ for b equal to 0.37 Å using the procedure described by Brown and Altermatt(41) for estimating unknown values of R₀.

Several papers provide bond valence parameters for hydrogen bonds and these are discussed in section 21 and reported in Table 6.

Table 6. Bond Valence Parameters, R₀ and b in Å in eq 26, for Hydrogen Bonds.

cation	anion	r0	b		sourcea	reference	remarks
H	1+	O	0.781	0.56	ID	178
H	1+	O	0.957	0.35		213	From gas and symmetrical bond length
H	1+	O	0.925	0.40	I	213
H	1+	O	0.870	0.457		124	4.0 Å cutoff, b determined from softness
H	1+	O	0.790	0.37	I	65	For s > 0.5 vu, see Section 21
H	1+	O	1.409	0.37	I	65	For s < 0.5 vu, see Section 21
H	1+	F	0.708	0.558		124	4.5 Å cutoff, b determined from softness
H	1+	Cl	1.336	0.53	ID	178
H	1+	S	1.192	0.591		124	5.5 Å cutoff, b determined from softness
H	1+	N	1.014	0.413		25	From gas and symmetrical bond length

^aCD from structures in the Cambridge Structural Database. ID from structures in the Inorganic Crystal Structure Database. I from selected inorganic structures.

Although they did not determine any bond valence parameters, Keller and Krämer(70) exploited a related idea. If one has two isostructural compounds, one containing A and X ions, the other containing B and X ions, the difference between the A–X and B–X bond lengths should be equal to the difference, d_AB, between the ionic radii of A and B, since the X anion is common to both. Empirical ionic radii for cations in various coordination numbers have been tabulated by Shannon and Prewitt^71,72 so the value of d_AB is easy to determine. To compare this difference with that expected in real compounds, one can rewrite eq 26 as eq 29.

If the crystals containing the A−X and B−X bonds are isostructural, the value of s is the same for both and b will likely also be the same. In this case the difference between R_AX and R_BX is equal to the difference between R_0AX and R_0BX, the final term on the right-hand side of eq 29 canceling out. Thus, as shown in eq 30 the difference in the bond valence parameters, D_AB, should be equal to the difference in the ionic radii, d_AB.

Since no real bond lengths are involved in the comparison of D_AB with d_AB, these two numbers should be the same whether or not any isostructural compounds actually exist.

Keller and Krämer then checked whether these two quantities really are the same. They wrote a program RADDIF to search the database of bond length parameters(36) and a database of Shannon’s ionic radii.^71,72 Since for any given pair of cations A and B, R₀ values are available for several different X, and in some cases different values of R₀ for the same X, it is possible, as they show in the case of A = Na⁺ and B = K⁺, to calculate as many as eighteen independent values for the same D_AB and eight independent values for the same d_AB depending on the number of radii given for different coordination numbers.

Choosing AB atoms that are adjacent to each other in the same column of the periodic table, they found that individual values of D and d generally agree with each other apart from a few egregious outliers which on inspection are found to be problematic, for example, R₀ was fitted to different values of b. Further they found that the average values of D and d agreed with each other as long as A and B had the same valence as required by eq 30.

In a second paper(73) they checked the bond length changes in KBi₆O₉X, BiOX and BiSX as X is changed from F⁻ to Cl⁻, from Cl⁻ to Br⁻ and from Br⁻ to I⁻, and found that some of the changes do not agree with the predictions of the earlier paper. In each case bismuth has a valence of +3 and the question arises whether the lone pair is responsible for the differences. They analyze each structure in some detail. In structures where there are mixed anions, the anions with the largest valence (in this case O²⁻ and S²⁻) will form strong bonds and these are responsible for dictating the form of the observed structure. The anions with lower valence (in this case the halogen ions) will be left to absorb the steric strain, thus accounting for the lack of conformity. The Bi³⁺ ions show different degrees of stereoactivity in the different structures which influences how they behave as the halogen ions are changed. Though not mentioned by the authors, the assumption that b is the same for all halogens bonded to a lone pair cation is clearly one that needs to be examined as discussed in section 8.2.2.

Incidentally, eq 30 suggests an easy way to check for erroneous values of R₀. For most cations, values of R₀ are available with b = 0.37 Å for several different anions. Checking the differences between the values of R₀ for two cations, A and B, bonded to the same anion, X, should quickly isolate any value that is an outlier. Brese and O’Keeffe(74) used this idea, though expressed differently, when they predicted values of R₀ for rare or unknown bonds.

In their study of bonds to the artificial element technetium, Wester and Hess(75) made use of structural information from all available sources including EXAFS experiments. They determined the bond valence parameters using the conventional method described above, but because there are so few examples of known structures containing Tc, they confirmed their results using eq 31 which is readily derived from eq 30, again under the assumption that b will be the same for all oxidation states.

Here the subscripts 1 and 2 refer to the same ion in different oxidation states. If R₁ and R₂ are chosen as the average bond lengths (if known), and s₁ and s₂ the corresponding bond valences, then eq 31 can be solved for R₀₂ in terms of R₀₁. In this way the relative values of R₀ for different valence states assigned by the normal procedure were confirmed. However the results are limited in their reliability since both methods use the same input information and the number of cation environments is statistically small, all oxidation states except Tc⁷⁺ being represented by only one or two examples.

7.3. Is the Value of b Constant?

A number of studies suggest that in certain cases, such as cations with lone electron pairs, the value of the bond valence parameter b should be significantly larger than 0.37 Å. Krivovichev and Brown(76) found a value of 0.49 Å for Pb²⁺−O bonds and a similar value was found by Locock and Burns(77) for Tl⁺−O bonds. Sidey(78) reported a value of 0.42 Å for the Bi³⁺−Br bond and Hu(56) found values between 0.38 and 0.40 Å for Pb²⁺ halides, though both these latter studies are suspect as they set R₀ equal to the single bond length in the gas phase which, for reasons discussed below, is likely to lead to values for b that are too low.

In a seminal paper Adams^38,79 demonstrated that there is no unique value for b for a given bond type since its value depends on the arbitrarily chosen maximum bond length, the cutoff distance beyond which two ions are no longer considered as bonded. Since the valence drops off exponentially with distance in eq 26, it has always been assumed that including bonds to the second and higher coordination spheres would make little difference to the bond valence sum. Adams however has shown that bond valence parameters determined using both the first and second coordination spheres were significantly different from those determined using the first coordination sphere alone. To see how the choice of bond cutoff distance might affect the bond valence parameters, he selected a set of accurate crystal structures containing Li−O bonds from the Inorganic Crystal Structure Database(40) and used this set in a series of least-squares refinements of R₀ and b using different cutoff distances. Specifically, he found that as the cutoff distance increases, the value of b increases and the value of R₀ decreases as shown in Figure 6a and 6b. Adding the third and fourth coordination spheres, however, makes no further change to the parameters. Figure 6c shows that the larger the bond-length cutoff, the more closely the valence sum rule is obeyed until at a cutoff distance of 4 Å is reached. Beyond this, in the case of Li−O bonds, the average difference between the valence sum and atomic valence remains constant at 0.04 vu, down from the value of 0.06 vu when only the first coordination sphere is included. Figure 6d shows that only when cutoff distance is set to 4 Å do the bond valences at the cutoff truly reach a negligible value. The value of the cutoff used by Brown and Altermatt,(41) and followed by most subsequent authors, corresponds, for Li−O bonds, to a bond valence of 0.04 vu (2.66 Å). Adams’ results, summarized in Table 3, show that the bond valence parameters need to be matched to the calculation in which they are used. Fortunately most published bond valence parameters are determined using only the first coordination sphere with a cutoff of around 3 Å and this, for the most part, is also where they are used. The bond valence parameters determined by Adams for the alkali metal chalcogenides and halogens are shown in Table 2 and can be found in the accumulated online bond-valence parameter list.(36)

Table 3. Values of R₀ and b in Å for Li−O Bonds using Different Cut-Off Distances.

R0	b	cut-off	ΔVa	remarks
1.466	0.37	2.67	0.07	R0 fitted to assumed value of b, ref (41)
1.33	0.44	2.67	0.06	Refined by least-squares, ref (79)
1.1525	0.515	4.2+	0.04	Refined by least-squares, ref (79)

^aΔV is the mean deviation of the bond valence sum from the atomic valence of Li⁺.

Since b represents the apparent softness of the interaction between the cation and anion, Adams^79,80 further explored the relationship between b and the atomic softness parameter, σ, for alkali metal halides and chalcogenides, He used values of b determined with cut-offs between 6 and 8 Å and σ for cations defined by Parr and Pearson.(81)

where IE is the ionization energy and EA is the electron affinity of the ion. For the anions, he used an empirical softness that increases linearly with the anion radius. He showed that the value of b depends on the difference between the anion and cation softness, rather than on their sum. This accords with the observation that hard cations tend to bond to hard anions and soft cations to soft anions. Where the cation and anion have the same softness, Adams showed that b has a value close to 0.37 Å but that this value increases to 0.7 Å as the difference in the softness exceeds 0.2 eV⁻¹ as shown in Figure 7. The alkali metal softness increases from 0.04 to 0.12 eV⁻¹ in going from Li⁺ to Cs⁺ while the anion softness increases from 0.14 to 0.29 eV⁻¹ in going from F⁻ to Te²⁻. Online information about Adams’ bond valence parameters is available, together with a discussion of hardness and softness, at ref (38).

Those who routinely determine bond valence parameters have taken little notice of this work. As mentioned above, the majority take b to be a universal constant with the value of 0.37 Å. There are, however, some exceptions. A number of studies describe fixing R₀ and varying b. Such a procedure may give adequate parameters as long as the bond lengths extend over only a limited range, but it could lead to poor bond valences for very long or very short bonds since the value of R₀ is sensitive to the choice of b and vice versa.

In their study of the stability of LnOCl structures, Hölsa et al.(82) chose bond valence parameters for the Ln−O bonds by holding R₀ fixed at the value of 2.172 Å, given for La−O bonds by Brese and O’Keeffe,(74) and refining b to 0.33 Å, which value they subsequently assumed would apply to all the other lanthanides. Their justification for this was that the value of 0.37 Å was derived from fits to more ionic bonds while the bonds in the LnOCl compounds were more covalent, a conclusion based on the correlation between bond valence and covalency suggested by Brown and Shannon.(83) However, as the covalency and bond valence increase together, the influence of the covalency should have been captured in the original fitting of b. Further, the value of 2.172 Å which they chose for R₀ was originally fitted on the assumption that b was equal to 0.37 Å. Changing b requires that R₀ also be recalculated.

Sidey(78) obtained bond valence parameters for Bi³⁺−Br bonds by comparing the bond lengths in gaseous and solid BiBr₃. He argued that because the bond valence can be assigned unambiguously in these materials, viz: 1.0 and 0.5 vu for the gas and solid respectively, the parameters he derives are more reliable and more physically meaningful, but this not only overlooks the unknown experimental uncertainties in the reported bond lengths of the two forms of BiBr₃, but assumes that eq 26 correctly describes the bond-valence−bond-length correlation over the whole range from 1.0 to 0.5 vu and beyond. Sidey et al.(84) later determined parameters for Sb⁵⁺−O using the single bonds in Sb₂O₅ and distances from eight other crystals. He showed that the new values give significantly better valence sums than the previously reported values. The same method was used by Majerz and Olovsson(25) to obtain bond valence parameters for N−H bonds as discussed in more detail in section 21. Hu(56) adopted the same approach in his studies of Pb²⁺ halides discussed in section 8.2.2. Urusov(85) used a related technique when seeking to improve on the published bond valence parameters of Mn−O bonds in oxidation states ranging from 2+ to 7+. He first noted the length of 1.762 Å for the bridging bond in Mn₂O₇ where the bond valence must be 1.00 vu. He therefore set R₀ to this value for all oxidation states, and for each oxidation state he took the distances (averaged if necessary) of bonds of known valence as a second fixed point, which allowed him to determine values of b which he found increased monotonically from 0.26 Å for Mn⁷⁺ to 0.40 Å for Mn²⁺. He does not provide any confirmation that these values give better bond valence sums than others in the literature, and the method can be criticized on several grounds. It makes the questionable assumption that gas phase and solid state bond lengths follow the same correlation and that a simple equation such as eq 26 can provide a good fit to the bond-valence−bond-length correlation over a wide range of bond lengths. It also overlooks the fact that the bridging bond in P₂O₇⁴⁻, which might be expected to be similar to that in Mn₂O₇, has, for reasons that are not clear, an experimental bond valence significantly larger than the expected value of 1.0 vu.

While it is reasonable to suppose that the valence of the bond to a terminal F⁻ or Cl⁻ in the gas phase is 1.0 vu, it is less clear that its length will correspond to the value of R₀ required in eq 26. Such an assumption implies that eq 26 gives a correct description of the bond-valence−bond-length correlations over the whole range from the minimum observed value to 1.0 vu. It is not easy to test this assumption as one can only check the correlation over the range in which bond lengths are observed. In most cases the reported values of R₀ are less than the single bond length found in the gas phase. There are several possible reasons for this. The different techniques used in measuring gases and solids may be sampling different distances, or it may be that there is an intrinsic difference between the true terminal bonds found in gases and those found in solids which are, strictly speaking, never terminal. But the most likely reason is that the two-parameter exponential function in eq 26 is not flexible enough to express the complex bond-length−bond-valence correlation over more than a limited range. This is certainly true for H−O bonds where the correlation, shown in Figure 19, has been traced over its full range. If R₀ is set equal to the gas phase distance, it is likely too large and the corresponding value of b will be too small. In most cases the parameters determined in these studies have not been fully tested to see how well they reproduce the valence sum rule.

Urusov(67) has used eq 39, derived from the distortion theorem, eq 35 in section 8, as an alternative method of determining b. This would be an appropriate method to use for cations that appear in distorted environments, but with only one coordination number. Although a couple of examples are given in section 8, this method still requires some refinement. It could well form part of a needed study to determine the proper b parameters (and the corresponding values of R₀) to use in analyzing first-coordination sphere distances.

7.4. Alternative Expressions for the Bond Valence

Valach(86) describes the correlation between bond valence and bond length using the five-parameter function shown in eq 33.

This is obtained from a Taylor expansion of the molecular orbital overlap matrix. However, he determined the parameters (a₁, a₂, a₃, a₄, a₅) empirically as (−4.86, 15.42, −1.83, −5.85, −10.80) for Cu−O bonds and (−0.91, 2.46, 0.23, 0.85, 5.12) for Cu−N bonds fitted to a large number of structures taken form the Inorganic Crystal Structure Database.(40) The Cu−O correlation agrees closely with that given by Brown(87) except that it becomes negative for R > 3.07 Å. The correlation for Cu−N bonds has a different shape with an inflection point at 2.10 Å, becoming negative for R > 2.78 Å. Valach analyzes, as have others before him, how the constancy of the bond valence sum at Jahn−Teller distorted Cu²⁺ ions results in the correlation of the lengths of the four short and two long Cu–X bonds (X = O²⁻, N³⁻). He postulates that distances for which eq 33 yields negative values of S should not be considered as bonds.

Mohri(26) derived the bond-valence - bond-length correlation shown in eq 34 from his bonding electron density model described in section 5,

Here r is the sum of the cation and anion core radii, which he took to be the same as the Shannon ionic radii.^71,72S₀ is a reference bond valence and R₀ the corresponding bond length. This expression is based on identifying the bond valence with a notional calculation of the electron density in the bond region. The only variables in this equation are S and R and Mohri provides values for the constant terms for a number of different bond types. He also shows, that with suitable approximations, eq 34 can be used to derive both eqs 25 and 26, and that the bond valence parameters he gives for eq 34 agree with those provided by Brown and Altermatt(41) for eq 26. In view of the discussion of the value of b in section 7.3 it is of interest to note that the values he derives in this way for b range from 0.26 to 0.51 Å (the latter for P⁵⁺-S bonds).

Although the correlation between bond valence and bond length is normally expressed using eq 26 because of the relative invariance of b, eq 25 is equally effective in expressing the correlation and is still sometimes used. It has been used, for example, by Albuquerque et al.(88) in their calculation of ligand field parameters described in section 18, as well as by Grinberg et al.(89) in their study of Pb(Ti,Zr)O₃ perovskites described in section 22.3. Grinberg et al. initially adopted the parameters for eq 25 published by Brown(87) but found it necessary to change the values of R₀ from 2.044 to 2.021 Å for Pb²⁺−O, 1.950 to 1.937 Å for Zr⁴⁺−O and 1.804 to 1.846 Å for Ti⁴⁺−O, in order to compensate for the steric strain that stretches the Ti⁴⁺−O bonds and compresses the others in this compound. Locock and Burns(77) suggest that for bond types that show a wide range of distances, as found for example around cations with lone electron pairs (section 8.2.2), a more complex equation than either eq 25 or 26 might be needed as suggested in section 7.3.

7.5. What is the Maximum Length of a Bond?

A facile answer to this question has been provided by Valach(86) in section 7.4 above, but a more profound discussion is given in the paper by Adams(79) described in section 7.3. Section 24 describes modeling the structures of glasses which requires the calculation of bond valences for distances that extend beyond the first coordination sphere since this sphere is not well-defined in amorphous materials. As discussed in section 7.3 the value of the bond valence parameters vary with the cutoff distance used, that is, the distance selected as the maximum length of a bond. To reach the point at which the bond valence parameters no longer depend on the choice of cutoff distance it is necessary to include all the Li−O distances (for example) out to 4.0 Å, corresponding to a bond valence of 0.003 vu. This could therefore be taken as the maximum length of a Li−O bond, although when analyzing crystal structures it is more convenient and more relevant to include only the first coordination sphere.

Some support for the importance of second neighbors is given by the bond flux calculations of Preiser et al.(9) who found that, although most of the flux in the ionic model of a crystal terminates on atoms in the first coordination sphere, a small proportion sometimes finds its way to the ions in the second coordination sphere. These tertiary bonds do not exert much influence on the structure, but do make a small contribution to the valence sum. Adams(79) points out that while the higher cutoff distance is important for glass studies, for most other applications one need only consider the first coordination sphere. In either case it is important to use the appropriate bond valence parameters.

7.6. van der Waals Radii

Nag et al.(90) propose a method for determining the van der Waals radii for transition metals by assuming that any interatomic distance that corresponds to a valence of 0.01 vu would represent a van der Waals interaction. They use Pauling’s van der Waals radii for the anions, combined with the bond lengths predicted for bonds of 0.01 vu, to calculate van der Waals radii for all the d block elements. The numbers they obtained are similar to those published by Batsanov(91) but it is not obvious how one might confirm these values by measuring the van der Waals radius of a transition metal ion, and the authors do not give any suggestions for how these radii might be used.

7.7. Differences between Structures in ICSD and CSD

Values of R₀ for b equal to 0.37 Å determined using structures of transition metal complexes in the Cambridge Crystallographic Database(39) usually show small differences from those determined using the Inorganic Crystal Structure Database.(40) The differences (inorganic−organic) shown in Table 4 range from −0.02 to +0.05 Å, showing a slight tendency for values derived from organic compounds to be smaller, but as the differences are comparable to the differences observed between the values of R₀ obtained by different authors using the same database, they are probably not significant as can be seen by comparing the different bond valence parameters for the same bond type shown in Table 2.

Table 4. Differences in the Values of R₀ in Å (for b = 0.37 Å) derived from Organic and Inorganic Compounds.

	R0(inorg)−R0(org)	reference
Ln3+−O	−0.004 to +0.054	41, 44
Ln3+−S	−0.005 to +0.031	41, 46
Ln3+−Cl	−0.021 to +0.005	41, 46
Sb3+−O	+0.018	51
Sb5+−O	+0.030	51
Cd2+−O	+0.024	52
Cd2+−S	+0.030	52
Cd2+−Cl	−0.002	52
NH4+−O	−0.014	66

8. Distorted Ion Environments

8.1. Introduction

Bond valences are particularly useful in discussing atomic environments in which the bonds have different lengths, even more so when the environment contains different kinds of ligands. One may be tempted to compare the average bond lengths between two different cation environments, but this could be misleading even when the ligands are all the same, because the average bond length itself is a function of the degree of distortion. These difficulties disappear if the bond lengths are first converted to bond valences since the valence sum rule holds regardless of the nature of the ligands or the degree of distortion.

It has long been recognized^1,92 that the average bond length will increase with increasing distortion as expressed by the distortion theorem, eq 35.

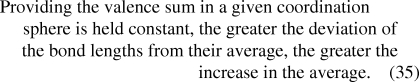There are several proofs of this theorem but its validity can be seen from an inspection of the curvature of the bond-valence−bond-length curve shown in Figure 8. Urusov(93) repeats the proof originally provided by Allmann(92) and then proceeds to examine the quantitative implications of the theorem. He expands the increase in the average bond length, ΔR_a, as the sum of a Taylor series in the deviations of the individual bond lengths from their average. He shows that if the mean square bond deviation, δ₂, is less than 0.05 Ų, the increase in average bond length is proportional to δ₂.

where b is the bond valence softness parameter. For more distorted environments an additional term in the mean cube deviation, δ₃, has to be added, showing that the increase in average bond length depends not just of the degree of distortion as measured by δ₂ but also on the nature of the distortion as reflected in δ₃. Urusov offers a number of worked examples, in particular looking at the effects of the crystal field distortions around Cu²⁺, showing that the more long bonds and fewer short ones there are in a distorted octahedron, the larger will be the increase in the average bond length for a given value of δ₂. This observation suggests a possible reason why the environment of Cu²⁺ always contains two, not four, long bonds even though both are allowed by the Jahn−Teller theorem. For small distortions eq 36 can be used to calculate the increase in average bond length, but for larger deviations one needs to know how the different bond lengths are distributed.

Figure 8.

Bond-valence−bond-length curve illustrating the distortion theorem by showing how the average bond length increases from 2.56 to 2.62 Å as the valences of two hypothetical bonds change from 0.2 vu to 0.1 and 0.3 vu, that is, at constant bond valence sum.

Hunter et al.(94) have provided a striking example of the distortion theorem. The addition of 10% of the smaller Sn⁴⁺ ion to the tetragonal structure of yttrium-doped zirconia results in a shortening of the four short (Zr,Sn)−O bonds. To compensate, the four long bonds are increased by a larger amount, resulting in an increase in the average bond length and an expansion of the unit cell. In this case the distortion theorem leads to the counterintuitive result that substituting a smaller impurity ion causes the crystal to expand.

Lalik(95) has pointed out that the distribution of bond lengths can be compared with a probability distribution and that a good measure of the size of such a distortion is given by the entropy, ΔH, of Shannon and Weaver’s information theory.(96)

Here s_j is the valence of an individual bond, s₀ is the average bond valence, V is the atomic valence and A is a scaling factor, which is equal to 1/ln 2 if the entropy is measured in bits of information. Brown(97) subsequently proposed that the increase in the average bond length would itself provide a useful measure of the size of a distortion, and this is easily calculated using a modification of eq 37, namely:

where N is the coordination number and b the bond valence softness parameter. One advantage of using ΔR_a is that it is, in principle, measurable. Both these expressions have the advantage that they can be used even when the ligands are different.

As mentioned in section 7.3, eq 36 can be used as an alternative way to determine b, one that is complementary to the methods described in section 7.3, since:

and all the terms on the right-hand side of this equation are known. This method would be particularly useful for cations that are known with only one coordination number but are normally found with distorted environments. Two studies which hold promise for such a determination were published by Urusov^67,98 who examined the crystal field distortion in Mn³⁺O₆ and Mn³⁺F₆ octahedra. He shows that in both cases the linear approximation of eq 36 holds for the majority of Mn³⁺ environments, but as the scatter in the values of ΔR_a is large; the correlation coefficient is typically only 0.7. As a result b is not well-defined and the values of b calculated from the reported slopes, 0.38(3) Å for Mn³⁺−O bonds and 0.50(6) Å for Mn³⁺−F bonds are not significantly different. Part of the scatter is likely caused by the bond valences not adding up exactly to 3.0. Renormalizing the valences in these structure so that the sum is exactly 3.0 for all coordination spheres might reduce the scatter and lead to more accurate values of b.

There are three main reasons why the environment of an atom may be distorted: (1) the bonds in the bond graph may not be topologically equivalent, (2) one or more atoms may have an electronic structure that is intrinsically anisotropic, or (3) steric strains may result from the need to stretch or compress bonds when mapping the ideal bond lengths of the bond graph into three-dimensional space. Distortions related to the topology of the bond graph are already included in the calculation of the theoretical bond valences described in section 3 and represent the normal distortions that arise from the way the atoms are linked. The electronic anisotropies and steric effects are discussed in the following sections 8.2 and 8.3 respectively.

8.2. Electronic Distortions

8.2.1. Introduction

According to the Jahn−Teller theorem, a system with a degenerate electronic ground-state will distort if such a distortion can remove the degeneracy. There are three well studied cases of this kind of distortion: the stereoactive lone pairs associated with main group cations in lower valence states, for example, S⁴⁺ and As³⁺, the so-called ‘second-order Jahn−Teller effect’ found around octahedrally coordinated transition metals with a d⁰ or d¹ configuration, for example, V⁵⁺, and the crystal field effect, commonly referred to as the ‘Jahn−Teller distortion’, found around octahedrally coordinated Cu²⁺ and Mn³⁺. Each of these is discussed in turn. A fourth source of electronic anisotropy is found in compounds such as the polyiodine complexes that involve large soft elements. Bond valence methods have not yet been applied to these latter compounds and they are not discussed further in this review.

8.2.2. Lone-Pair Distortions

Main group cations are sometimes found in states in which two, or occasionally four or even six valence electrons do not take part in bonding but form chemically inert lone electron pairs. According to the traditional VSEPR description, if the cation lies at the center of its coordination sphere the lone pair is centered on the nucleus as shown schematically by the dotted circle in Figure 9a. Alternatively, if the cation has three, four or five strong bonds all on the same side, its coordination environment is described as a tetrahedron or octahedron with the lone pair occupying a vacant apex. In solids there are usually three or four longer secondary bonds surrounding the position of the lone pair as shown by the dashed lines in Figure 9b.

Figure 9.

Electronic distortion shown by lone electron pairs (dashed spheres). (a) Lone pair is nonstereoactive and (b) lone pair is stereoactive.

The bond valence model suggests an alternative description of this effect. The presence of the lone pair in the valence shell results in the cation being soft, that is, having more than one possible ground state, each stabilized by a different environment (c.f. the discussion of softness in section 7.3). The result is that lone-pair cations can adopt a variety of different states each with its own cation bonding strength (Table 1), allowing them to adopt states which match the bonding strength of their environment. For example, Tl⁺ has a lone electron pair and can adopt any bonding strength between 0.11 and 0.33 vu, in contrast to Rb⁺, a cation of the same size and valence, which has a bonding strength of only 0.12 vu. Thus in TlNO₃ where the nitrate ion has an anion bonding strength of −0.11 vu, Tl⁺ behaves like Rb⁺, adopting an undistorted environment of nine Tl−O bonds of 0.11 vu each. However, unlike Rb⁺, Tl⁺ can also bond to BO₃³⁻ with an anion bonding strength of −0.33 vu. In Tl₃BO₃, each Tl⁺ ion forms only three bonds to borate anions, each bond having a valence of 0.33 vu. With only three primary Tl−O bonds, there is plenty of room in the coordination sphere for the lone pair which thus becomes stereoactive. Usually some weaker secondary bonds are also present and intermediate cases with smaller distortions are also known.

In 1996 Wang and Liebau(99) observed, that using the tabulated bond valence parameters of Brese and O’Keeffe,(74) the valence sum rule is not always obeyed around atoms with lone pairs, the valence sum being larger the greater the distortion. Krivovichev(100) also noted a high bond valence sum around those O²⁻ ions that form primary bonds to four surrounding Pb²⁺ cations with stereoactive lone pairs. He interpreted this as indicating that the O²⁻ ion is compressed by an encapsulating rigid tetrahedron of Pb²⁺ ions, but such an explanation implies some unusual kind of bonding between the Pb²⁺ ions. Later, Krivovichev and Brown(76) showed that there was an alternative explanation; the valence sum rule can be preserved around the oxygen if a different set of bond valence parameters is chosen, in particular they suggested, that for Pb²⁺−O bonds, b in eq 26 should be increased from 0.37 to 0.49 Å. An equally large value of b (0.50 Å) was found by Locock and Burns(77) for Tl⁺−O bonds. Hu(56) found smaller values, 0.38 to 0.40 Å for Pb²⁺ halides, as did Sidey(78) (0.42 Å) for the Bi³⁺−Br bond, though, as discussed in section 7.3, these values for b are probably too small. On the other hand, Jensen et al.(48) showed that, contrary to the claims of Wang and Liebau described above, the valence sum rule is obeyed around Sn²⁺ using b equal to 0.37 Å.

Wang and Liebau^101,102 followed their first paper with others which showed that the increase in the bond valence sum with distortion is a characteristic of all the lone-pair cations when bonded to a single kind of anion. They suggest that the excess in the bond valence sum is a real chemical effect which indicates the presence of additional bonding electrons. In the cetineites, a series of Sb³⁺-containing minerals, Liebau(103) suggest that these additional electrons are responsible for the observed semiconductivity. Wang and Liebau do not, however, explain where these additional electrons come from or why they should be involved only in distorted cation environments. The additional electrons are unlikely to be part of the electron core, and the well localized lone pair found in the more distorted environments would be even less likely to contribute to the bonding than the symmetrical lone pair found in the undistorted cases. In all their work Wang and Liebau assumed that b has the value of 0.37 Å, though they suggest that this should be checked. Sidey,(104) in a critique of Liebau and Wang’s work, points out the importance of fitting both R₀ and b to the valence sum rule, and he suggests that if Liebau and Wang were to do this they would find that the effect they describe disappears.

Further study of the bond valences around lone-pair cations is needed. Wang and Liebau’s explanation of the failure of the valence sum rule is not convincing and is not compatible with the use of the valence sum rule as a normalizing condition for the bond valences. The indications are that the failure of the valence sum rule is attributable to the use of the wrong value of b. The discussion in section 7.3 makes it clear that b cannot be taken as a universal constant and that a value of around 0.5 Å is likely more appropriate. This is consistent with the soft character of these cations described above. Only when it is impossible to find fully transferrable bond valence parameters that satisfy the valence sum rule should it be necessary to look for alternative explanations (c.f. section 8.3).

As described in more detail in section 9, Zachara(105) has defined valence vectors, in which valences are treated as vectors pointing along the direction of the bond. He shows that for most cations the sum of the valence vectors will be zero, but for cations with lone pairs the vector sum will represent a vector that can be used to localize the lone pair, an idea that is worth pursuing.

8.2.3. d⁰ Cations

Transition metals with a d⁰ or d¹ electron configuration are found to prefer coordination environments that lack a center of symmetry. This is a result of the filled pπ orbitals on the ligands mixing with the empty dπ orbitals on the central cation, leading to an accidentally degenerate ground state when the cation is in a centrosymmetric environment, sometimes referred to as a second order Jahn−Teller effect. These cations therefore prefer either the noncentrosymmetric tetrahedral coordination or an octahedral coordination with the cation strongly displaced from its center. This tendency increases as the increasing formal charge on the cation lowers the energy of the vacant d orbitals until with Cr⁶⁺ even a distorted octahedral coordination is no longer possible. Cr⁶⁺ is found only in tetrahedral coordination even though there is enough space in its coordination sphere for the additional two ligands.

There have been fewer applications of the bond valence model to this kind of distortion in the period covered by this review, though Kunz and Brown(106) pointed out that the distortions are larger, and the application of bond valences less controversial, than for other types of electronic anisotropy. Guevarra et al.(107) show that Ca(Nb_0.76Ti_0.24)O_3.33 has a perovskite structure broken into slabs separated by a layer of Ca²⁺ ions. Bond network arguments suggest that the octahedra at the surface of the slabs should be more distorted than those at the center of the slab. The X-ray diffraction pattern was able to show that the Nb⁵⁺ ions favors the more distorted octahedra at the surfaces of the slabs while Ti⁴⁺ favors the less distorted octahedra at the centers, an arrangement one would also expect from their relative charges. The authors calculated the bond valences in order to confirm this distribution but interestingly found that the bond valence sums at all the octahedral sites are 5.0 vu when calculated with the bond valence parameters for Nb⁵⁺−O and 4.0 vu when calculated with those for Ti⁴⁺−O, meaning that in this example the bond valence sums around the cations cannot distinguish between Nb⁵⁺ and Ti⁴⁺. The authors did not check the bond valences sums around the O²⁻ ions which would likely have resolved the ambiguity, an application that would apply to any case of antisite disorder. Descriptions of other examples of d⁰ distortions in perovskites can be found in section 22.

A more thorough bond valence analysis of ordering, this time of O²⁻ and F⁻ in Nb₃O₅F₅ and related compounds, was performed by Brink et al.(108) who were able to use electron and X-ray diffraction results and bond valence arguments to assign not only the average occupancy of each of the four anion sites, but also show that they were locally ordered.

Noting that the nonlinear optical properties of compounds containing the anion NbOF₅²⁻ have potential applications, Poeppelmeier and his collaborators^109,110 have examined a number of structures, mostly containing the NbOF₅ group as a ligand in a transition metal complex. They set themselves two tasks, the first is to find the conditions under which the complex anion NbOF₅²⁻ is ordered, that is, the O²⁻ ion occupies a single well-defined site; the second is to predict which of these ordered structures will crystallize in a noncentrosymmetric space group. They consider that the distortion observed around the Nb⁵⁺ ion in KNa(NbOF₅) and CsNa(NbOF₅) can be decomposed into a primary distortion that results from the electronic anisotropy, and a secondary distortion that arises from the topology of the bond network between the NbOF₅²⁻ anion and its nearest neighbor cations (Na⁺ and either K⁺ or Cs⁺). The primary distortion consists of a displacement of Nb⁵⁺ toward O²⁻ and away from the trans-F⁻ anion (because O²⁻ has a larger bonding strength than F⁻). This results in the trans-F⁻ ligand being more weakly bound to Nb⁵⁺, causing it to form stronger bonds to the alkali metals. They argue that the F⁻ ions occupy sites with a positive electrostatic potential created by the neighboring alkali metals, and that the trans-F⁻ ion is directed to the site with the highest such potential. They also compare the experimental bond valences in KNa(NbOF₅) and CsNa(NbOF₅) with the theoretical bond valences; the experimental bond valences reflect both kinds of distortion while the theoretical bond valences reflect only the secondary distortion, but from these one can extract information about the primary electronic distortion. Both types of distortion are found to be greater in the K⁺ crystals which are also the only ones that crystallize in a space group without a center of symmetry.

8.2.4. Crystal Field Effects

Distortions caused by crystal field effects, commonly referred to as ‘Jahn−Teller distortions’ because they were the first to be explained using the Jahn−Teller theorem(111) have long constituted an active field of study, often to the neglect of other much larger distortions. Crystal field effect distortions are found around octahedrally coordinated Cu²⁺ and Mn³⁺, each of which has an odd number of electrons occupying a degenerate d electronic state of e_g symmetry. The degeneracy is removed by a tetragonal distortion in which two axial bonds become longer and the four equatorial bonds shorter. Valach(86) has added his name to the long list of those who have demonstrated that the lengths of the two long bonds around octahedral Cu²⁺ correlate inversely with the lengths of the four short bonds, a natural consequence of the valence sum rule, and Urusov(93) used the distortion around Cu²⁺ to illustrate his analysis of bond distortions as discussed in section 8.1. Recent interest has focused more on Mn³⁺ because of the large magnetoresistive properties of materials such as (La,Sr)MnO₃ that result from an interplay between the magnetic and structural properties of Mn³⁺ and Mn⁴⁺. As part of this work Urusov^67,98 has examined the distortions in Mn³⁺O₆ and Mn³⁺F₆ octahedra, but otherwise bond valences appear not to have been used much in this area during the review period.

8.3. Steric Distortions and the Global Instability Index

Bond valence parameters are chosen to normalize the bond valences by ensuring that, on average, they obey the valence sum rule. Ideal bond lengths determined from the theoretical bond valences calculated using eqs 9 and 13 are required to obey this rule by definition. However, there are occasions when these ideal bond lengths must be strained if the structure is to be mapped into three-dimensional space. The classic example of such a steric effect is the strained cubic perovskite structure described more fully in section 22. Compounds with this structure have the formula ABX₃ (X = O²⁻, F⁻, Cl⁻, A and B are any suitable cations) and all atoms occupy special positions as shown in Figure 21. The structure has only one adjustable parameter, namely the lattice constant, a. This must be chosen to satisfy two equations, 40 and 41, that relate a to the ideal lengths, R, of both the A–X and B–X bonds.

These two conditions cannot in general be satisfied simultaneously by a single value of a, so that in the crystal one set of bonds will be compressed and the other will be stretched. The cation with the compressed bonds will have an experimental bond valence sum larger than its atomic valence and the cation with the stretched bonds will have a sum that is smaller. This pattern, with some ions having valence sums that are too large and others having valence sums that are too small, is characteristic of steric bond strain. Similar steric strain can be found if the ideal repeat distances in different parts of a structure are incommensurate, so that the crystal can only have translational symmetry if one part of the structure is stretched and another part compressed. Steric strain is also found where atoms are forced too close together. The classic example of this is the hydrogen bond where contact between the two terminal atoms in a symmetrical hydrogen bond causes the O−H bonds to stretch as described in section 21. One important consequence of this is that the H⁺ ion moves off-center according to the distortion theorem in the form given in eq 43 below.

Not all steric strain results in the failure of the valence sum rule. The preferred method by which a crystal relaxes is to maintain the valence sum rule by compensating for the compression of some bonds by lengthening other bonds in the same coordination sphere, that is, by relaxing the equal valence rule constraint (eq 6). Only when the strain requires that all the bonds formed by an ion be stretched or compressed will the valence sum rule fail. When this happens, a convenient measure of the strain experienced by an ion, i, is the discrepancy factor, d_i: the difference between the bond valence sum, Σ_jS_ij, and the atomic valence, V_i:

If d_i is positive, the bonds around the ion are compressed, if it is negative, they are stretched. Using the distortion theorem (eq 35) one can predict that:

The degree to which the structure as a whole is strained is measured by the global instability index, G, which is the root-mean-square value of the discrepancy factors averaged over the N atoms of the formula unit:

In stable, well determined structures G is usually less than 0.1 vu. Values between 0.1 and 0.2 vu indicate a strained structure. Correctly determined structures with G greater than 0.2 vu are rare. If a large value of G is the result of steric strain, both positive and negative values of d_i will be found, otherwise one should look for some other cause, such as an incorrect structure determination or the use of inappropriate bond valence parameters as in the example of LnCoO₃ described below.

The program SPuDS, which was written by Lufaso and Woodward^112−114 to predict the structures of perovskites, is a striking example of the use of the global instability index. For a given composition, SPuDS generates the most common distortions of the cubic perovskite structure, and refines each by minimizing G. The distortion with the lowest G is usually found to predict the observed structural parameters within 1%. SPuDS is described more fully in section 22.2. Section 22 also includes other examples of the use of the global instability index in perovskites.

The lanthanides are another fertile field for the use of the global instability index since G changes systematically in the lanthanide series of isostructural compounds. Alonso et al.(115) determined the structure of a series of LnCoO₃ perovskites where Ln = Pr³⁺ and Tb³⁺−Lu³⁺. These compounds show a variety of interesting magnetic phenomena, but at room temperature all the members of this series, except possibly PrCoO₃, contain the d⁷ cation, Co³⁺, in a low spin state. The crystals adopt an orthorhombic distortion of the perovskite structure in the space group Pbnm with the tilt angle of the CoO₆ octahedron increasing from from 11° for PrCoO₃ to 17° for LuCoO₃ which contains the smaller Lu³⁺ cation. As the distortion from the ideal perovskite structure increases, G also increases from 0.15 vu for PrCoO₃, to 0.205 vu for LuCoO₃, in agreement with the increased difficulty in synthesizing the Tm³⁺, Yb³⁺, and Lu³⁺ members. Although for steric strains one expects a mixture of overbonded and underbonded ions, the discrepancy factors (eq 42) reported in this paper are all positive. An examination of the bond valence parameters used shows that if the authors had used R₀(Co³⁺−O) value of 1.637 Å given by Wood and Palenik(116) rather than the value 1.70 Å reported by Brese and O’Keeffe,(74) the discrepancy factor around Co³⁺ would have dropped from +0.2 to −0.2 vu. It is noteworthy that although PrCoO₃ has the lowest G in the series studied, indicating a stable structure, LaCoO₃, which should be even less strained, crystallizes in a trigonal structure.

Several authors report the changes in G as the radius of the lanthanide cation is reduced. Hölsa et al.(82) show that in tetragonal LnOCl (Ln = La³⁺−Nd³⁺, Sm³⁺−Ho³⁺, Y³⁺) G is 0.09 vu for LaOCl and decreases slowly as the radius of Ln decreases, reaching a minimum of close to 0.08 vu for Gd³⁺, then increasing rapidly to 0.11 vu for Ho³⁺ and 0.14 vu for Y³⁺. For even smaller Ln the tetragonal structure becomes unstable relative to the hexagonal structure with YOCl crystallizing in both structures. In (Ln,Sr)₂CoO₄ with the La₂NiO₄ structure Sánchez-Andujar and Señaris-Rodriguez(117) found that G was equal to 0.08 vu for La₂CoO₄ but increased rapidly through Nd₂CoO₄ to a value of 0.18 vu for Gd₂CoO₄. Presumably beyond Gd³⁺ the La₂NiO₄ structure becomes unstable. Substituting Sr²⁺ apparently reduces G, but the authors do not give any values.

SrBi₂Ta₂O₉ is a much-studied ferroelectric Aurivilius phase with the space group A2₁am at room temperature. Between 600 and 750 K it undergoes a phase transition to a paraelectric phase in the space group I4/mmm. The room temperature structure with varying degrees of substitution of Pr³⁺ for Sr²⁺ up to 15% has been determined by Mata et al.(118) using Rietveld powder X-ray diffraction. They note an increase in G from 0.18 to around 0.22 vu as the Pr³⁺ content is increased. However, given the quality of the structure determination, the changes they observe in the bond valences are barely significant and do not vary in any systematic way. One could however conclude that the 15% limit of Pr³⁺ solubility is related to G reaching the upper stability limit. A more significant study of this material was published by Perez-Mato et al.(119) They undertook a detailed ab initio analysis of the paraelectric to ferroelectric phase transition at around 700 K and conclude that the transition involves the simultaneous freezing out of no less than three separate soft phonons. They explored the energy landscapes of each of these soft modes using first principles methods, but the global instability indices, G, calculated for structures deformed by one or more of the normal modes gave insights into the roles that each of the different modes play. Together they lower G from 0.27 vu in the I4/mmm paraelectric phase to around 0.21 in the ferroelectric phase. The high value of G in the paraelectric phase is indicative of an unstable structure, suggesting that the high symmetry is dynamic and that viewed at a local level the structure is still distorted.

More interestingly, in a second paper Perez-Mato and colleagues(33) show that G² quantitatively reproduces the change in potential energy of each soft phonon as a function of its amplitude with 1.0 vu² corresponding to 0.5 Ry or 6.8 eV, an observation whose significance is considered more fully in section 6. However, they found that G² did not track the potential energy of the stable modes as well. The authors point out that minimizing G does not, in this compound, lead to the observed equilibrium structure, even though a structure can be found with G as small as 0.03 vu. Clearly there are other factors at play; the authors suggest that it might be the neglect of anion−anion and cation−cation repulsions. There are other possibilities. The equal valence principle (eq 6) suggests that in addition to the requirement of adjusting the bond lengths to satisfy the valence sum rule, there is a competing tendency for the valence to distribute itself as uniformly as possible among the various bonds. This may result in the strain relaxing only until G reaches the stability limit of 0.2 vu, at which point further relaxation only leads to a greater violation of the equal valence rule.

Perovskite-like structures in the series A₅B₄O₁₅, with A = Ba²⁺, La³⁺; B = Nb⁵⁺, Ti⁴⁺, were determined by neutron powder diffraction by De Paoli et al.(120) The three compounds with compositions between Ba₅Nb₄O₁₅ and (Ba₃La₂)(Nb₂Ti₂)O₁₅ crystallize with the same structure in space group P3̅m1. It contains three crystallographically distinct A sites and two B sites with A1 and A2 giving rise to highly overbonded Ba²⁺ ions (bond valence sum ≈ 2.5 vu). Such a large overbonding would indicate these as the most likely sites for substitution of the smaller La³⁺ ion, particularly as the Ba²⁺ bond valence sum calculated at these sites increases with increasing La³⁺ substitution. However, the Rietveld refinement suggests that La³⁺ substitutes only on the A2 site. The overbonding on this site is characteristic of steric strain, but although the authors report values of G ranging from 0.31 to 0.57 vu it appears that these have been incorrectly calculated by not including the whole formula unit. When the calculation is done correctly, G is closer to 0.2 vu. A more careful calculation of G for these structures is needed before one can confirm the authors’ claim that this strain is responsible for (Ba₂La₃)(NbTi₃)O₁₅ adopting a different structure with G = 0.24 vu in space group P3̅c1.

Xue and He(121) make a different use of the discrepancy and global instability indices in their studies of the nonlinear optical material LiNbO₃. The properties of this compound can be changed by doping with various divalent or trivalent cations. To determine whether these dopants occupy the Li or the Nb site, they calculated the discrepancy factor, d, (eq 42) for each dopant on each site, assuming that the site remains unrelaxed. They showed that substitution occurs at the site at which the dopant has the smallest value of d. The actual picture that emerges is a little more complicated because the as-grown LiNbO₃ has some Nb⁴⁺ ions occupying Li sites. Using d_Nb to indicate the value of d calculated when the dopant is placed on the Nb site, they found that if d_Nb < d_Li, but both values are small, the dopant first replaces the Nb⁴⁺ on the Li sites before replacing Nb⁵⁺ on the Nb sites. G tends to increase with doping and at some critical value the substitution changes from the Nb⁴⁺-on-Li-site to Nb⁴⁺-on-Nb⁵⁺-site. Other uses of bond valences made by Xue and collaborators are described in sections 18 and 19.

Taguchi and colleagues^122,123 report G as part of the routine characterization of new perovskite-related materials, showing that G lies well within the acceptable levels.

A novel use of the global instability index is to produce a map showing possible locations of hydrogen atoms. This work by Adams and colleagues(124) is more fully described under valence maps in section 10 and hydrogen bonds in section 21.

Finally Zhao et al.(125) describe the use of a modification of the global instability index, calculated with only the valence sums around the cations, in modeling the structures of perovskites under pressure. This work is reported in section 20. Other uses of the global instability index can be found in other sections of this review.

9. Bond Valence Vectors

As shown in section 3 the bond valence is derived from the electrostatic field of the ionic model. It therefore has a directional character, and to capture all the information in the Coulomb field it is necessary to take this character into account. The flux lines leaving a spherically symmetric ion are themselves spherically symmetric at the point where they leave the ion so that their vector sum must be zero. This gives rise to three additional conditions that must be satisfied in a condensed phase, namely the sums of each of the three orthogonal components of the vector sum of the flux must be zero.

This idea has been invoked at various times in the past. The flux lines that link an ion to one of its neighbors can be added together vectorially to produce a single bond valence vector. Brown^13,126 Wang and Liebau,(99) Lufaso and Woodward,(112) Müller et al.(127) and Palenik et al.(128) have all made use of this idea in one form or another, but only recently have Harvey et al.(129) proposed the valence vector sum rule as a formal hypothesis.

The usual caveats apply to this statement, namely that the hypothesis is not necessarily obeyed in the presence of noncentrosymmetric distortions resulting from the electronic or steric anisotropies discussed in section 8.

Palenik et al.(128) examined a series of rare earth complexes, all with the same pentacoordinated ligand, but with varying numbers of coordinated nitrate and water groups. From a qualitative examination they noted that the variations in bond lengths in these complexes could be understood by assuming that the bond valence was equally distributed in all directions of three-dimensional space.

Quantitative applications of the valence vector rule requires a definition for the valence vector. Calculating this exactly is not straightforward as the flux lines forming a bond are neither straight nor parallel. Consequently two different approximations have been proposed. The simplest and most common approach is to associate the magnitude of the bond valence with a vector lying along the direction of the bond. Müller et al.(127) adopted this definition while exploring how to use bond valences to determine the identity of cations in protein structures, described in more detail in section 26. To ensure that no bonds had been missed when they calculated the bond valence sum, they checked that the valence vector sum was close to zero, tacitly assuming that the valence vector rule would be valid. Only if this sum was less than 0.2 vu were they satisfied that no significant bonds had been missed.

Lufaso and Woodward(112) used bond valence vectors in their program SPuDS for predicting the structures of ABX₃ perovskites as described in section 22.2. In certain low symmetry perovskites the position of the A cation is not fixed by symmetry, but they found that they could correctly predict its position by moving it to the point at which its valence vector sum is zero. This corresponds to placing it at a minimum in the valence map (section 10) which is the most symmetric point within a distorted bonding environment.

Harvey et al.(129) carried out a systematic examination of the valence vector hypothesis and found that the valence vector sum was typically around 0.05 vu when calculated around the Group 12 cations they were studying. This is less than the difference, 0.10 vu, they typically found between the (scalar) bond valence sum and the atomic valence in the same compounds. These observations provide strong support for the hypothesis. The main thrust of their paper, however, was to show that when a chelating ligand formed several bonds to a cation, the valence vectors of these bonds could themselves be added to give a single vector that represented the total bonding from the ligand as a whole. Replacing several bonds with a single vector, they were able to describe the chelating of an octahedrally coordinated cation in terms of just two or three valence vectors. The near-zero valence vector sum in these complexes indicates that not only the individual bonds, but also the complex ligands, arrange themselves in a regular manner. When just two chelating ligands were present the angle between their valence vectors was close to 180° and when three chelating ligands were present their valence vectors were close to being coplanar as illustrated in Figure 10.

Figure 10.

Schematic representation of a three-ligand seven-coordinated complex and its reduction to a simple planar pseudotrigonal description using the valence vector model. Copyright 2006 International Union of Crystallography. Reproduced with permission from ref (129).

Zachara(105) proposed a different way to approximate the magnitude of the bond valence vector. As in the previous definition, he chose the direction to be parallel to the bond, but rather than assigning a magnitude equal to the bond valence, that is, the total flux connecting the bonded ions, he took the magnitude to be equal to the normal flux crossing a plane perpendicular to the bond direction, which he showed can be approximated by eq 46.

where S is the bond valence, V is the cation valence and v is the valence vector. He examined CO₃²⁻ anions from organic compounds, some of which are constrained by being part of a ring. Like Harvey et al.(129) he also found that the average valence vector sum is close to 0.05 vu except when the O−C−O angles are constrained by being part of a four- or six-membered ring. As expected five-membered rings have valence vector sums close to zero since they are not strained. Zachara showed that for collinear two-coordination the valence vector sum calculated according to eq 46 is identically zero regardless of how asymmetric the bonding, that is, it is zero around H⁺ in any linear hydrogen bond, but as the bond angle decreases from 180° the valence vector sum increases. For three-coordination, a zero valence vector sum implies a unique set of O−C−O angles, and he shows that the observed angles are better reproduced using eq 46 than using the traditional definition.

Zachara(105) also examined the valence vector sums around N³⁺, P³⁺, and S⁴⁺ cations which have a stereoactive pair of nonbonding valence electrons (the lone electron pairs discussed in section 8.2.2). He assumed that the lone pairs can be treated as pseudoanions having a valence of −2 but with no atomic core. Treated this way, the cations N³⁺ and P³⁺ would have a valence of +5 and S⁴⁺ a valence of +6, and one would expect the pseudobond between the cation and lone pair to have a valence of 2. Calculating the valence vector sum using only the bonds to the real ligands yields a nonzero vector whose negative should represent the valence vector to the lone pair pseudoanion, For a large number of compounds containing N³⁺ and P³⁺ he finds the magnitudes of the valence vector sums cluster around 1.15 vu while for S⁴⁺ they cluster around 1.29 vu. Using eq 46 it can be shown that these correspond to valences of pseudobonds of around 1.78 vu for N³⁺ and P³⁺ and 1.87 vu for S⁴⁺. Although the ideal bond valence is 2.0 vu, smaller values are expected if the lone pair is not fully stereoactive. Using Zachara’s figures the stereoactivity of the lone pairs in N³⁺ and P³⁺ are 89%, and the lone pair in S⁴⁺ is 94%, expressed. Zachara ascribes the deficiency to the overlap between the lone pair and the core, which is another way of saying the same thing. It would be interesting to see how these measures compare with the valence vector sum calculated using the traditional definition described earlier, and what sums would be found around some of the heavier ions such as Tl⁺ and Pb²⁺ in which the lone pairs show a full range of stereoactivity.

The properties of the valence vector, particularly its different definitions, deserve to be more fully explored. Potential uses have been hinted at in the above studies but there are other possibilities. The valence vector hypothesis, eq 44, provides three further constraints on the geometry of each atom in addition to the valence sum rule, suggesting that the four constraints together could be used in structure modeling as described in section 12, at least in cases where the ions were expected to be spherically symmetric. The hypothesis also implies constraints on the angles between bonds, another application that is worthy of further examination.

10. Valence Maps and Ionic Conduction

The idea of a bond valence map was originally proposed as a method of locating the positions of very light ions such as Li⁺ in the presence of heavy ions such as W⁶⁺. The bond valence sum that a Li⁺ ion would have if it were placed at an arbitrary position in the crystal is first calculated. If the valence sum happens to be 1.0 vu, the location is a possible site for the Li⁺ ion. Moving this notional Li⁺ ion systematically through all points in the unit cell generates a valence map in which any point on the map having a value of 1.0 vu represents a possible location for Li⁺. The map requires few computing resources since one only needs to calculate the distances from each point in the unit cell to nearby anions. These distances are then converted to bond valences which are summed to give the valence-map value at that point. Many of the possible locations for the cation also happen to be minima, the points where the bond valence vectors sum to zero as described in section 9. The only correction that has to be made is to block positions that are already occupied by a cation by introducing short-range cation−cation ‘valences’ to ensure the map has a large value in the neighborhood of existing cations.(130)

While valence maps are still used to locate light atoms, a more important application is the mapping of diffusion paths in ionic conductors. Schindler et al.(131) have used valence maps to help locate Na⁺ and Li⁺ ions in the solid solution compound (Na, Li)V₃O₈ and to determine why LiNa(V₃O₈)₂ is a better ionic conductor than either LiV₃O₈ or NaV₃O₈. They calculated the valence maps for Li⁺ and for Na⁺ in the presence of the V₃O₈⁻ anions and found broad regions in the structure where valences were close to 1.0 vu for both cations. Analysis of these regions helped to locate the positions of the two cations and showed that those positions were linked by narrow paths in which the valence was small but significantly greater than 1.0 vu. They assumed that the larger the valence at the passes between the alkali metal sites, the higher would be the activation energy for conduction. In all three phases the valence at the pass for Na⁺ was greater than 3 vu, too high to allow Na⁺ to be mobile. For Li⁺ the picture was different. In LiV₃O₈ the highest valence along the conduction path was 1.8 vu but in LiNa(V₃O₈)₂ it was reduced to 1.4 vu. Because it is not necessary for an ion to be present in the crystal in order to calculate its valence map, they were able to show that in NaV₃O₈ the passes for Li⁺ conduction had dropped to 1.3 vu. They surmise that the activation energy for Li⁺ in LiV₃O₈ is too high for easy conduction, but that adding Na⁺ expands the space between the anions, making diffusion of Li⁺ easier. There can be no conduction without Li⁺, but Li⁺ cannot conduct without the presence of Na⁺, explaining why the highest conduction is found when both ions are present. These results should be compared with the opposite effect observed in mixed-alkali glasses discussed in section 24.

Levi et al.(132) used essentially the same idea to locate the positions of the Mg²⁺ ions in the intercalated chevral phase MgMo₆Se₈ and to discuss its possible diffusion paths. However, rather than calculate a valence map they calculated the valence sum at several possible sites that the Mg²⁺ ion might occupy during diffusion.

The traditional way of presenting valence maps is to draw contour maps in sections through the structure. Such a map can be generated using the program VALMAP written by González-Platas et al..(133) An alternative display developed by Adams and Swensson^134,135 shows a three-dimensional picture of the surfaces that define the regions accessible to the mobile ion. Ideally the ions would lie on the locus of points having a value equal to the valence of the mobile ion, V₀. In practice the ion may be displaced slightly from these points providing the difference in valence is small, that is, the mobile ions might be found anywhere in the accessible volume, the region whose valence sum satisfies expression 47.

Adams and Svensson(136) use values of ΔV lying between 0.05 and 0.2 vu for light atoms at room temperature; the choice is not critical providing the value is large enough to allow percolation.

Since the valence map may possibly include values less than V₀ − ΔV as well as values larger than V₀ + ΔV, the accessible volume may form shells around low-valence cavities as well as sheets, rods or islands. A conduction path will only exist if the accessible regions are linked into a continuous volume running through the structure. The percolation point can be found by gradually increasing the value of ΔV until the conduction threshold is reached. There is a rough correlation between this value of ΔV and the activation energy for conduction. If the limiting step is migration, the activation energy in eV is numerically equal to 2ΔV in vu (but see also section 6 which suggests that energy should be proportional to the square of the valence). If the limiting step is defect creation, the activation energy is usually somewhat smaller.(34) When comparing activation energies of different ions in crystals, ΔV at percolation can be scaled by dividing it by the square root of the reduced mass.(137) Adams(138) illustrates the conduction paths drawn for different choices of ΔV in several different ion conducting crystals, one dramatic example being the unlikely ion conductor Sc₂(WO₄)₃. The high charge on the Sc³⁺ ion makes it an improbable candidate for the mobile ion and the O²⁻ anions are likely to remain firmly attached to W⁶⁺. The conduction paths however show that neither Sc³⁺ nor O²⁻ are the conducting species; it is the WO₄²⁻ anions that follow a broad conduction path. In a molecular dynamics simulation of crystalline layers of BaF₂ and CaF₂ Adams and Tan(138) were able to show that it is the disorder of the F⁻ ions in the interface region between the BaF₂ and the CaF₂ layers that is responsible for opening up better conduction paths than exist in either BaF₂ or CaF₂ alone.

One of the best known ionic conductors is AgI which comes in a number of different phases. α-AgI is the highest temperature phase and the best ionic conductor. Its conduction paths are shown in Figure 11. β-AgI has the wurtzite structures and the conduction of Ag⁺ ions via interstitial sites was the subject of a detailed paper by Lee et al.(140) They use valence maps to show that there are three possible pathways—the octahedral cavities link into conducting chains along the c axis when ΔV is 0.082 vu, when ΔV is 0.114 vu the tetrahedral cavities link through the octahedral cavities to form chains in the ab plane, and when ΔV is 0.125 vu the tetrahedra link directly to each other. Adams(31) also reports similar studies of a number of Ag⁺ containing crystals including Ag₄P₂O₇, Ag₅IP₂O₇, Ag₈W₄O₁₆, Ag₈I₄V₂O₇, RbHg₄I₅ and Ag₂HgI₄. Adams has extended this work to ion conduction in glasses as described in section 24.

Figure 11.

The Ag⁺ conduction paths in the unit cell of α-AgI with ΔV = 0.05 vu. Reproduced with permission from ref (135), copyright 2000 by American Physical Society.

Valence maps have been used by Cabana et al.(130) to locate possible Li⁺ sites in potential electrode materials such as Li₁₀CrN₄O₂, and Adams^141,142 reports their use to plot the conduction paths in Li₄GeS₄, (La,Li)TiO₃ and LiMn₂O₄.

Thangadurai et al.(143) noted poor valence sums around Li⁺ and O²⁻ in the determinations of the garnet-like structures reported for Li₅La₃Nb₂O₁₂ and Li₅La₃Ta₂O₁₂. Two determinations of the Nb⁵⁺ compound had global instability indices, G (eq 44), of 0.31 and 0.22 vu. respectively. Rietveld methods were unable to give accurate positions for the light ions in the presence of the heavy ions, so Thangadurai et al. refined the structure by minimizing the global instability index, G. The coordinates they report have G = 0.03 vu, though as reported in section 8.3 the correct structure is not necessarily the one with the smallest value of G if there are strong violations of the equal valence rule (eq 6). In this revised structure percolation occurs when ΔV is around 0.1 vu.

Ouerfelli et al.(144) calculated the bond valence sums along the lowest valence path of Na⁺ in two phases of Na₂Fe₂(AsO₄)₃. The low temperature phase I has the garnet structure, and as expected from the poor ionic conduction of this phase, the maximum valence along the conduction path is 1.65 vu. On the other hand the high temperature phase II, which has a nasicon-like structure, has a conduction path between the two Na2 sites which hardly deviates from the value of 1.0 vu. The path between Na1 and Na2 in this phase has a maximum valence of 1.68 vu and is unlikely to conduct.

Producing valence maps for H⁺ leads to an ambiguity because of the asymmetry of hydrogen bonds. Symmetry dictates that the minimum in the valence map will occur at the mid point between the donor and acceptor anions, but it will have a value considerably less than 1.0 vu. The accessible volume will therefore not be found at the minimum, but at the place where the valence map has a value of 1.0 vu. Again by symmetry, there are two such regions, one close to the donor anion, the other close to the acceptor anions, but the valence map itself cannot distinguish which of the two anions is the donor. To locate the donor one must also look at the valence sum around the terminal anions. In their study of proton conductors, Adams et al.(124) treated this problem in an elegant manner by calculating a map for H⁺ that plots the global instability index, G (eq 43), rather than the valence sum at H⁺. If the positions of all the ions apart from the hydrogen are fixed, the only contributions to G that change as H⁺ is moved through the crystal are those of the H⁺ ion itself and the anions to which it is bonded. Only when the H⁺ ion is placed close to the donor anion will all the valence sums have their expected value and when this happens, G will be a minimum. They tested the method on the structures of Ca(HSeO₃)₂·H₂O and Cs₂(HSO₄)(H₂PO₄) using the G map to refine the location of the H⁺ ions. They then showed that H⁺ percolation could occur in H_0.95MoO₃ for values of G less than 0.2 vu.

Other examples of the use of valence maps are give in section 24 which deals with ion conducting glasses. A full discussion of the determination and interpretation of valence maps in amorphous systems can be found there.

11. The Valence Matching Rule

The valence matching rule, eq 16, states that cations and anions will form stable bonds only if they have similar bonding strengths, that is, the bonding strength (Lewis acid strength, L_a in eq 14) of the cation should be similar in size to the bonding strength (Lewis base strength, L_b in eq 15) of the anion. The reason for this is that both bonding strengths are estimates of the valence of the bond that forms between them. If the two ions are mismatched, either one or both must adjust to form a bond with a valence that differs from its bonding strength. It is generally found that in stable compounds the magnitudes of L_a and L_b do not differ by more than a factor of 2. Values of L_a and L_b for a selection of ions are given in Table 1.

Pauling’s electrostatic valence rule, eq 2, is an early form of the valence matching rule. Providing the same coordination number is used, the Pauling bond strength is the same as the cation bonding strength, and when Pauling’s electrostatic valence rule is exactly obeyed, L_a and L_b have equal magnitudes. Deviations from Pauling’s rule are reflected in the degree of mismatch between L_a and L_b.

In a paper describing the different ternary and quaternary compounds that adopt an ordered form of the NaCl structure, Mather et al.(145) point out that the most commonly encountered compounds, namely those with the formulas ABO₂, A₂BO₃ and A₅BO₆, are those that exactly satisfy the Pauling electrostatic valence rule (eq 2). For each of these formulas, several different orderings are observed depending on the relative charges and sizes of the A and B cations. Compounds such as A₃BO₄ that only approximately obey Pauling’s electrostatic valence rule are found less frequently since the cation coordination sphere has to be distorted if the valence sum rule is to be obeyed. This favors the incorporation of cations that have intrinsic electronic distortions of the kind described in section 8.2, distortions such as those found in main group ions with lone electron pairs or in transition metals with a d⁰ configuration, since the electronic distortion helps stabilize the distortions induced by the bond network. The A₃BO₄ structure is also more likely to be adopted by compounds that contain ordered arrangements of three different cations.

Chlorite minerals are sheet silicates which contain octahedrally coordinated Mg²⁺ and Al³⁺ as well as tetrahedral Al³⁺ and Si⁴⁺ ions. Pauling’s electrostatic valence rule was used by Lee et al.(146) to explore which cations can occur in adjacent octahedra within a layer.

One consequence of the valence matching rule is that water, and sometimes other molecules, can play an important role in stabilizing a structure. Water molecules coordinated to a cation can act as valence transformers by reducing the cation’s bonding strength to match the bonding strength of the anion. For example, the cation bonding strength of Mg²⁺, L_a, is 2/6, that is, 0.33 vu, and the anion bonding strength of SO₄²⁻, L_b, is −2/12, that is, −0.17 vu (taking the average coordination number of O²⁻ to be four). The ratio of these two values is 2 and therefore MgSO₄, while allowed by the valence matching rule, is at the limit of its stability. When magnesium sulfate is prepared from solution, six water molecules bind to the Mg²⁺ cation and act as transformers since the coordination number of the hydrated ion, Mg(H₂O)₆²⁺, is 12, one bond being formed by each of the 12 H⁺ ions. The cation bonding strength of Mg(H₂O)₆²⁺ is therefore 2/12, that is, 0.17 vu, a perfect match for the sulfate anion. As a result when MgSO₄ crystallizes from solution it forms the hydrate using six water molecules as transformers for a perfect valence match. The normal compound formed from solution is not the hexahydrate but the heptahydrate, Mg(H₂O)₆SO₄(H₂O), with the extra water molecule serving as a space filler rather than a transformer. Water of crystallization can therefore perform two distinct roles, as a transformer to provide valence matching and as a filler of a space that would otherwise remain as a void.

In a series of papers Hawthorne and Schindler and their colleagues^131,147,148 have used the valence matching rule to understand the structures and properties of complex minerals. A convenient and readable summary of this work can be found at ref.(149) Their approach(147) is to divide the ions in a mineral into two components, a structural unit, usually anionic, in which the atoms are strongly bound to each other, and an interstitial complex, usually cationic, which is only weakly bound to the structural unit. They assign an anionic bonding strength (Lewis base strength, L_b) to the structural unit, and a cationic bonding strength (Lewis acid strength, L_a) to the interstitial component, and show how the ions that form the interstitial component are selected in order to provide a good valence match to the structural unit.

The bonding strengths are normally calculated by dividing the formal charge (valence) of an ion or group of ions by the coordination number as shown by eqs 14 and 15. However, for the structural unit and the interstitial component of a complex mineral, neither the formal charge nor the coordination number are trivial to determine because the structural unit is usually complex and may act simultaneously as a Lewis acid through some atoms such as H⁺ and as a Lewis base through others. Its net charge, V, is the sum of its total Lewis acid strength, U_a, and its total Lewis base strength, U_b, (U_b being a negative number) as shown in eq 48.

The net charge is therefore positive if U_a is larger than U_b and negative if it is smaller. While V is known from the chemical composition of the complex ion, U_a and U_b are not. Since the structural unit is generally anionic, the Lewis acid function is normally expressed through hydrogen bonds, which allows U_a to be estimated as 0.2 times the number of hydrogen ions on the surface of the structural unit (see section 21). Equation 48 then allows U_b to be calculated. The base strength of the structural unit is then given by eq 49 derived from eq 15.

where N_b is the number of Lewis base bonds formed by the structural unit. Note that V is a negative number if the structural unit is an anion, so the presence of Lewis acid functions such as H⁺ ions on the structural unit enhances U_b. In this equation N_b is not known a priori, so Hawthorne and Schindler devised an empirical method to estimate it. They calculate the residual valence (i.e., charge deficiency) per anion of the structural unit, C_b, (inappropriately called the average basicity in their earlier papers) from eq 50.

where n_a is the total number of simple anions (e.g., O²⁻ ions) in the formula of the structural unit. C_b represents the average residual valence that each anion in the structural unit has available for bonding to the interstitial component, but not all of these anions will be close enough to the surface of the structural unit to be able to form bonds to the interstitial component. However, Hawthorne and Schindler note that C_b and the observed average external coordination number, N_b, are strongly correlated in known structures. This correlation is shown in Figure 12 and is expressed in eq 51.

Figure 12.

Average observed coordination number (⟨NB⟩ = N_b) of anions plotted against the residual valence (CDA = C_b) for (a) borates, (b) uranyl minerals, and (c) sulfates. Copyright 2008 Oldenbourg Wissenschaft Verlag GmbH. Reproduced with permission from ref (149).

From Figure 12 the correlation coefficient, k, is seen to be around five.

Substituting N_b back into eq 49 gives the anion bonding strength, L_b, of the structural unit. However, eq 51 is not exact so the resulting anion bonding strengths can only be estimated within ±25%.

Hawthorne and Schindler then consider the cation bonding strength (Lewis acid strength) of the interstitial component. In the absence of water molecules the cation bonding strength is the same as that of the individual cations themselves. The presence of water can modify the cation bonding strength depending on the number of bonds each water molecule forms to the cations within the interstitial component. Where the water O²⁻ forms only one bond with a cation, the water acts as a transformer, with the hydrogen bonds having a valence half that of the bond to the cation. Where the water forms two such bonds, the hydrogen bonds have the same valence as the bonds to the cation and the water acts as a space filler, merely extending the existing bonding network.

For each potential compound, Hawthorne and Schindler draw graphs of the cation bond strength of the interstitial component as a function of the number of transformer water molecules as shown in the top half of Figure 13. A different curve is needed depending on the valence and coordination number of the cations present. The lower part of Figure 13 shows the same graph overlain by a shaded bar representing the range of possible matching anion bonding strengths, |L_b|, of the structural unit.

Figure 13.

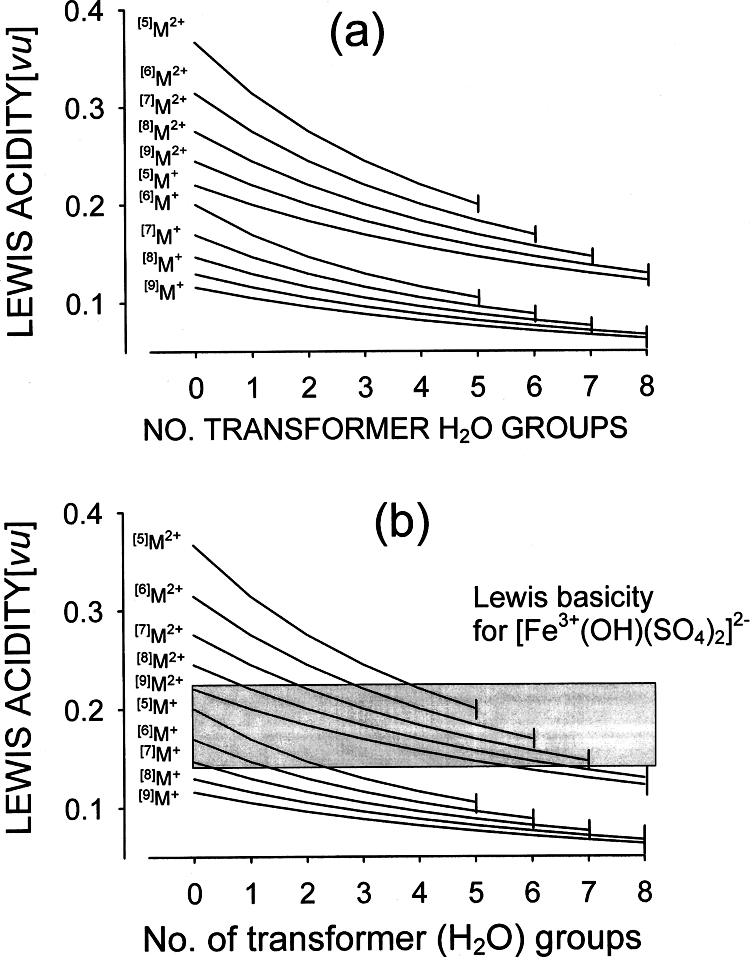
(a) Lewis acid strength of Fe²⁺ plotted against the number of transformer water molecules; (b) same as (a) but with the range of basicities of the structural unit superimposed. Copyright 2008 Oldenbourg Wissenschaft Verlag GmbH. Reproduced with permission from ref (149).

The region where the structural unit bar overlaps with the cation bonding strength curves indicates the region where the valence matching rule holds. The compositions of the interstitial components that satisfy this rule can then be read off. In this way Hawthorne and Schindler were able to account for the many different compositions found for borate, uranyl and sulfate minerals.

Finally they define a bond valence distribution factor which is the ratio of the number of receptor anions on the structural unit divided by the number of bonds formed by the interstitial component (modified to take account of OH groups that link between structural units). This number correlates well with the total number of water molecules present (transformer and nontransformer water), allowing the total composition be predicted.

Echigo and Kimata(150) examined the differences between thallium and rubidium oxalate, in order to determine what role the lone pairs of Tl⁺ play in the structure. Since Rb⁺ is about the same size as Tl⁺, they assumed that any difference must be caused by the lone pair. Much of their discussion revolves around the role of the water molecule in the Rb⁺ crystal which is absent Tl⁺ oxalate. They argue that this is a transformer water, but the cation bonding strength, L_a, of Rb⁺ is 0.124 vu (Table 1), and the anion bonding strength, L_b, of the oxalate is −0.17 vu, are sufficiently similar that no transformer is needed. As expected the water molecule forms two bonds to Rb⁺ and so is strictly a space filler. The lone electron pair in Tl⁺ oxalate performs the same function, occupying a similar position in the structure.

Becker(151) examined the structure of borate anions in relation to the cations present. After extracting all the borate structures from the Inorganic Crystal Structure Database,(40) he eliminated all the hydrates (to avoid the complexities faced by Hawthorne and Schindler) and the structures in which the counterion had L_b ≥ 1.0 vu, such as Si⁴⁺, P⁵⁺ etc. since these would dominate the structure leaving the B³⁺ ions in a secondary role. In this way he was left with a tractable collection of compounds in which boron would determine the nature of the structure.

Rather than comparing L_b of the borate anion with L_a of the cations, Becker looked only at the bonding strengths of the cations, using them to infer the bonding strengths of the various kinds of borate anions. He calculated the cation bonding strengths using eq 14 with ⟨N_c⟩_o set equal to the average coordination numbers of the cations observed in his sample of borates. Becker’s values of the cation bonding strengths are similar to, or slightly larger than, the tabulated bonding strengths(1) shown in Table 1.

Boron forms both three-coordinated (BO₃³⁻, L_b equal to −0.33 vu) and four-coordinated (BO₄⁵⁻, L_b equal to −0.42 vu) polyhedra and these are frequently condensed to form one of thirty nine different finite polyanions, or infinite chain, ring or sheet polyanions. Becker plots the boron:cation ratio against the cation bonding strength and generally finds a positive correlation but with significant spread. The bonding strengths of the different kinds of borate anions are best seen in the range of bonding strengths of their counterions, shown plotted as a function of the cation radius in Figure 14.

Figure 14.

Cation radii in borates in Å plotted against the cation Lewis acid strength. The lines show the different trends for (a) infinitely polymerized borates, (b) finitely polymerized borates and (c) unpolymerized borates. Adapted from ref (146). Copyright 2001 Oldenbourg Wissenschaft Verlag GmbH. Adapted with permission from ref (151).

Since the radius and the coordination number of the cation are expected to be correlated, it is not surprising that for a given type of polyanion there is a good negative correlation between the radius and the bonding strength of the cation but the regression lines are shifted according to the bonding strength of the different kinds of polyanion. Isolated BO₃³⁻ and BO₄⁵⁻ anions crystallize with counterions having bonding strengths in the range 0.33 to 0.50 vu, finite polyanions in the range 0.25 to 0.33 vu while polyanions that form chains, rings and frameworks crystallize with counterions having bonding strengths less than 0.25 vu. Becker finally provides systematic tables showing which borate structures are allowed and which are not. Not all the predicted structures are known, but all the known structures are among those he predicts.

Grice(152) took a somewhat similar approach in his analysis of the calcium silicate carbonates though in this case he compares the anion bonding strengths of the various silicate anions with that of CO₃²⁻. The carbonate anion has a bonding strength of −0.22 vu (Table 1), and because of the large valence of the C−O bond (1.33 vu), it does not lend itself to forming condensed polyions. Silicates on the other hand, which have Si−O bonds of 1.00 vu, readily condense to form disilicates, Si₂O₇⁶⁻ and more complex polyanions, mostly infinite in one or more directions. The bonding strengths of silicates range from zero (for SiO₂) to −0.33 vu for SiO₄⁴⁻. The bonding strength of Ca²⁺ is 0.27 vu and hence is well matched to both silicates and carbonates. Fine tuning of the Ca²⁺ bonding strength is achieved by changing its coordination number. For example, with SiO₄⁴⁻ (L_b equal to −0.33 vu) and Si₂O₇⁶⁻ (L_b equal to −0.32 vu), the silicate and carbonate components separate into different layers, the silicate layer includes seven-coordinate Ca²⁺ (L_a equal to 2/7 or 0.29 vu) and the carbonate layer includes eight-coordinate Ca²⁺ (L_a equal to 2/8 or 0.25 vu). Condensed silicates that form ring and finite islands have bonding strengths in the range −0.20 to −0.29 vu and in these compounds the carbonate and silicate components are intermixed since they both have bonding strengths similar to Ca²⁺. Sheet and other highly condensed silicates have bonding strengths lower than −0.20 vu and here the carbonate and silicate components are again separated, because sheet silicates naturally form silicate layers, forcing other components into the intersheet layers.

The application of the valence matching rule to Cd₄In₁₆S₃₅⁻¹⁴ by Li et al.(153) is described in section 15.

Zhao et al.(125) use the term ‘valence matching rule’ in connection with their study of perovskites under pressure, but as reported in section 20, they use it to describe a different phenomenon.

12. Modeling

Most techniques for modeling structures are based on finding the arrangement of atoms that has the lowest energy, where the energy is calculated using either the classical ionic two-body potential model or a quantum mechanical model such as density functional theory.(154) The energy function that is minimized in this process is called the cost function and may include additional terms whose values are expected to be a minimum for the correct structure. A variation on these methods is molecular dynamics in which kinetic energy is added to the model so as to monitor how the structure evolves over time at any given temperature.

The cost function often includes chemical constraints such as bond angles and anion−anion separations, though these tend to be added in an ad hoc manner. A more elegant approach is to include constraints corresponding to the various rules of the bond valence model. According to the valence sum rule, the square of the discrepancy factor, d_i, (eq 42) which measures the difference between the atomic valence, V_i, and the corresponding bond valence sum, Σ_jS_ij, has the expectation value of zero and can therefore be introduced directly into the cost function.^136,155 Although the valence sum rule is readily included in the cost function, finding a way to include the equal valence rule is more problematic, with the result that no modeling of this kind has so far been based only on bond valence constraints.

The standard approach to simulations of condensed matter structure start by placing a finite number of atoms in a box using cyclic boundary conditions. The size of the box determines the density of the material to be modeled, and if a crystal structure is being simulated, the box must be commensurate with the unit cell, so that the cyclic boundary conditions match the translational symmetry of the crystal. However, when modeling liquids and glasses, one has to be careful to avoid introducing unwanted translational symmetry and the larger the size of the box the better, limited only by the time required for the simulation.

Adams and Swenson^134,135,156 have included the bond valence sum rule in their reverse Monte Carlo analysis of ionic conduction in crystals and glasses. In this method a structure is optimized using a cost function based on the difference between a calculated and an experimental X-ray or neutron diffraction pattern. For noncrystalline materials the diffraction pattern contains no Bragg peaks and whole-pattern fitting is needed. In this case reverse Monte Carlo fitting can produce a large number of possible structures that minimize the cost function, but many do not represent chemically reasonable structures. Swenson and Adams therefore included a number of chemical constraints, such as requiring the cations to have coordination numbers similar to those found in the Inorganic Crystal Structure Database,(40) and requiring strongly bonding cations such as B³⁺ and W⁶⁺ to remain bonded to the number of O²⁻ ions indicated by nuclear magnetic resonance measurements. In addition they required the valence sum rule to be obeyed. Bond valence sums are also used in the program RMCProfile.(157)

Unlike methods based on a real-space cost function, the reverse Monte Carlo method using the whole diffraction pattern produces a snapshot of what the local structure of the compound might typically look like at the temperature of the experimental measurement. Figure 15 shows the ionic conduction paths found in such a simulation of the crystal α-AgI. This should be compared with Figure 11 which shows the conduction paths in α-AgI calculated using the atomic coordinates of the published crystal structure. The conduction paths shown in Figure 11 conform to the crystal symmetry and represent a time- and space-averaged structure, those in Figure 15 shows how a randomly chosen portion of the structure might appear at some particular instant when the atoms are thermally displaced from their mean positions. The reverse Monte Carlo method is ideally suited to studying glasses, liquids and other amorphous structures where there is no crystallographic symmetry. Applications of this method to the modeling of glass structures is described in section 24 and examples of the use of the valence maps and G-maps in modeling the positions of light atoms can be found in section 10. Using the bond valence model, Adams and Swenson^80,141 explored a number of properties of mobile ions including diffusion and electrical conduction.

Figure 15.

Ag⁺ conduction paths in α-AgI modeled at 525 K using the reverse Monte Carlo method. In contrast to Figure 11 which shows the conduction paths in the time and space averaged structure that conforms to the space group symmetry, this figure shows the localized paths at a specific hypothetical point and at a particular time with the atoms displaced from their average positions by thermal motion. Reproduced with permission from ref (135). Copyright 2000 by the American Physical Society.

Grinberg and colleagues(158) used bond valences in a different way when examining the complex ferroelectric materials described in section 22.3. The desirable electrical properties of the perovskite Pb(Ti,Zr)O₃ can be attributed to the electronic anisotropies present in all three of the cations causing them to move away from the centers of their coordination spheres; Pb²⁺ has a stereoactive lone pair as described in section 8.2.2, and Ti⁴⁺ and Zr⁴⁺ show the distortion characteristic of a d⁰ configuration as described in sections 8.2.3. A consequence of this distortion is that the O²⁻ ion that forms a strong bond with one cation will tend to form a weak bond with the neighboring cation, thus ensuring that the directions of the distortions are strongly correlated. Grinberg et al.(89) started by using density functional theory to simulate the cooperative distortions of Pb²⁺, Ti⁴⁺ and Zr⁴⁺ in various configurations of three different compositions of Pb(Zr,Ti)O₃. They^20,159,160 used these results, which established the energy landscape of the system, to create an equivalent classical two-body potential model for use in molecular dynamics. With 22 fitted parameters, this cost function had four different terms which were designed to reflect, respectively, the Coulomb energy, the bond valence sum rule, a short-range repulsion (to keep atoms apart) and an angular function designed to maintain a more or less rigid octahedron around the Zr⁴⁺ and Ti⁴⁺ ions. The reason why both a Coulomb term and a bond valence sum term were needed is discussed in section 22.3. This composite function reproduced the density-functional-theory energy sufficiently well that the authors could carry out molecular dynamics calculations on the system. For example, Shin et al.(161) used this function to examine the movement of ferroelectric domain walls by the application of a polarizing field in PbTiO₃ and BaTiO₃.

The valence sum rule is sometimes used to check the simulations produced by two-body potential models. When Rossano et al.(16) calculated bond valences to check their molecular-dynamic simulation of a glass of composition CaFeSi₂O₆, they found that the average valence sum around Si⁴⁺ was too large (4.66 vu) while that around Ca²⁺ was too small (0.86 vu) as shown in simulation 1 in Table 5.

Table 5. Average Bond Valence Sums and Standard Deviations (in Valence Units) around Classes of Atoms in Two Molecular Dynamics Simulations of a Calcium Iron Silicate Glass^a.

	simulation 1		simulation 2
atom	average	standard deviation	average	standard deviation
Si	4.66	0.20	4.26	0.24
O	2.00	0.24	1.94	0.17
Ca	0.87	0.14	1.43	0.20
Fe	1.77	0.19	1.70	0.22

^aSimulation 1 shows the bond valence sums after the calculation with the original potential function. Simulation 2 shows the bond valence sums after the potential function was refined.(16)

This could be the result of using inappropriate bond valence parameters, but the parameters for Ca−O, Fe−O and Si−O bonds are all well-known. The authors therefore assumed that the problem lay with their potentials, noting that such potentials are often context sensitive and need to be fine-tuned to the particular system being examined. After they had revised their potentials by fitting distances to those found by wide-angle X-ray scattering, the valence sums (shown as simulation 2) were greatly improved, though still rather low for Ca²⁺. They suggest that bond valences can be used to check, and if necessary improve, the interatomic potentials used in such simulations. They note along the way that the initial poor simulation resulted in a significant difference between the bond valence sums around the bridging (2.20 vu) and nonbridging (1.89 vu) O²⁻ ions but that this difference disappeared when the corrected potentials were used.

A number of authors using density functional theory have used the bond valence model to validate their results. Launay et al.(21) used density functional theory to simulate the structures of VOXO₄ (X = P or As) and LiVOSO₄, and confirmed that the simulated structures obeyed the valence sum rule. Alavi and Thompson(22) used bond valences to check the hydrogen bond distances in a density functional theory modeling of gas phase hydroxyammonium nitrate as described in section 21, and in their study of the interface between phyllosilicate-mineral surfaces and water, described in section 25.3, Bickmore et al.(17) used bond valences to show that density-functional-theory bond lengths were likely around 0.01−0.02 Å too short. They also quoted the distortion theorem (theorem 34) to warn of the dangers of comparing average bond lengths around cations whose coordination spheres are significantly distorted. These authors used bond valences to analyze their predicted geometries and to show that they satisfy the requirements of the valence sum rule. Later they(19) showed that the valence sum rule is obeyed by their density-functional-theory simulation of hydrated ions in liquid water as described in section 25.3.

It might seem surprising, given the very different assumptions underlying the quantum and ionic models, that bond valences can be used to validate density-functional-theory simulations, but ultimately all chemical models are based on the notion that the closer two atoms approach each other, the more electrons will be found in the bonding region.

A more restricted, but equally impressive, example of the use of bond valences in modeling is the program SPuDS written by Lufaso and Woodward^112−114 to predict the distortions found in perovskite materials. The modeling is restricted to certain key structural parameters, but these are adjusted so as to minimize the global instability index, G. Described in more detail in sections 9 and 22.2, SPuDS is remarkably successful in predicting the correct structure for most perovskite-type compounds.

Using bond valence rules to mimic energy terms in cost functions fails to exploit the unique feature of the model, namely it ability to describe a structure using only nearest neighbor interactions. There are several possible ways in which this approach might be realized, most of which have not yet been fully explored. In one such approach,(1) a bond network is first constructed using the valence matching rule. The theoretical bond valences, hence the ideal bond lengths, are determined using the network eqs 9 and 13. The resulting network is mapped onto a compatible space group and the coordinates of the atoms are chosen to reproduce the ideal bond lengths. A unique feature of this approach is that the geometry is determined without the use of atomic coordinates which means that it is possible to model structures which cannot be mapped into three-dimensional space.

Although the network equations can be used to determine the theoretical bond valence, there are occasions when the solution contains a negative bond valence. To circumvent this situation, Rutherford(162) has suggested a different way of solving the bond network. He retains the valence sum rule (eq 9) but suggests an alternative to the loop rule (eq 13) for expressing the equal valence rule. He exploits the symmetry of the finite bond graph, such as one of those shown in Figure 3, by considering the irreducible representations of the automorphism group of the bond graph to create a solution space in which the theoretical bond valences can be found.

Urusov(163) has developed a method for embedding the bond network in crystallographic space. This he calls the Extended Bond Valence Method. He divides an infinitely connected structure into polyhedral clusters, that is, formula units corresponding to finite bond graphs, which he then expresses as a series of plausible structural formulas based on a listing of the Wyckoff sites that might be occupied, each such site having its own element symbol and coordination number. The various possible bond networks (expressed as connectivity matrices) corresponding to each structural formula are then explored. Urusov postulates that the bond graphs most likely to be found are those that satisfy the following three conditions:

• 1.The structure should satisfy (more or less) the Pauling electrostatic valence rule (eq 2) for each anion. The most favorable topology corresponds to eq 2 being obeyed for every anion since it gives a perfect match between the anion and cation bonding strengths. This condition is equivalent to the valence matching rule discussed in section 11.
• 2.The structure should have a small distortion index, D (eq 52) corresponding to the equal valence principle. This measures the extent to which the individual bond valences differ from the average around the cation.
  

  where ⟨ ⟩ indicates an average taken over all the bonds in the polyhedral cluster and s_ij is the theoretical bond valence calculated for the chosen bond network using eqs 9 and 13. Large distortions, say with D greater than 0.2 vu, are not favored. If eq 2 is exactly obeyed, D will also equal zero since no distortion of the cation environment is needed if the valence match is perfect.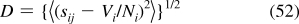
• 3.The linkedness, L, of the topology, is defined as the fraction of the anions that link two or more different cations. This must have a value close to its maximum of 1.0 to ensure that all parts of the structure are connected.

With this equipment, Urusov examined in some detail the possible topologies of Al₂SiO₅, pointing out that his three criteria are favorable for the three observed structures (kyanite: Pauling’s rule obeyed exactly, D = 0 vu, L = 0.8; andalusite: Pauling’s rule approximately obeyed, D = 0.08 vu, L = 0.8; and sillimanite: Pauling’s rule approximately obeyed, D = 0.08 vu, L = 0.8). The observed bond lengths agree satisfactorily with those predicted using the network eqs 9 and 13.

A different and as yet untried approach to structure simulation is closer to the classical simulation methods but exploits the bond valence description of local structure. It is based on finding the best location for each ion within its local environment. Each ion has three positional coordinates that need to be determined but the valence sum rule provides only one constraint, so that at this level the problem is underdetermined. What is missing is the constraint implied by the equal valence rule. This can be provided by the valence vector sum rule, eq 45, which states that the sum of the valence vectors around each atom is zero when the atom is at the center of its coordination environment. Confining the atom to this point introduces three additional constraints since the sum of each of the vector components must also be zero. There are now four constraints on each atom, the valence sum rule being a hard constraint, and the valence vector sum rule (eq 44) providing three somewhat softer constraints. The problem is now overdetermined but can be solved using an appropriate optimization. Although the valence vector sum rule applies strictly only to ions with spherical symmetry, ions susceptible to electronic distortions might be modeled by having a nonzero target for the magnitude (and possibly direction) of the valence vector sum. A simulation technique based on a separate cost function for each atom is conceptually different from the current simulation methods and would provide a useful addition to the suite of structure simulation models.

13. Homopolar Bonds

Although the theorems of the bond valence model are restricted to compounds with bipartite bond graphs, that is, compounds containing polar bonds as described in section 3, it has long been noted that bond lengths and bond valences (or bond orders) are correlated in most, if not all, types of bond. This relation is well-known for C−C bonds where the bond length is routinely used as a measure of the bond order, that is, the number of electron pairs presumed to form the bond. However, since the bond graphs for such compounds are not necessarily bipartite, the theorems of the bond valence model developed in section 3, in particular the valence sum rule, will not in general apply; there are some nonbipartite bond graphs for which it is mathematically impossible to assign a set of bond valences that obey the valence sum rule around all the atoms. Nevertheless, it is appropriate to mention such work in this review because of its close relationship with the bond valence model.

Mayer bond orders(28) have been used in a number of theoretical studies of organic molecules. In many cases the bond graphs of such molecules are not bipartite and the studies usually focus on isolated molecules, ignoring the intermolecular interactions, such as hydrogen bonds, found in crystals. Lendvay(164) has fitted the bond order correlations to eq 26 and found parameters, R₀ and b (in Å), similar to those used to describe the bond valence correlation, namely 1.54 and 0.37 for C−C, 1.43 and 0.38 for C−O and 1.08 and 0.26 for C−H respectively. The values for C−C bonds are identical to those given in the accumulated list of bond valence parameters(36) and the values of C−O bonds are similar. No bond valence parameters have been reported for C−H bonds. Lendvay(165) has also shown that these bond orders obey a bond order sum rule for some simple reaction pathways.

Mayer bond orders have been adapted to the Atoms in Molecules definition of an atom(12) by Cioslowski and Mixon(166) making use of atomic overlap matrices. More recently Howard and Lamarche,(32) in a seminal paper, explored ways in which these bond orders might be obtained from properties that can be determined experimentally so as to avoid the theoretical calculations implicit in the earlier definition. They first tried eq 26 with bond order replacing the bond valence and found that, while it worked well for C−C bonds as had been pointed out much earlier by Pauling,(167) it did not work so well for other bonds. They then examined the correlation, noted by Bader(12) between the bond orders and the electron density at the bond critical point, but found the agreement worse, particularly for the C−P bonds in which π bonding is important. Howard and Lamarche finally found good agreement between the theoretically calculated bond orders, n, of Cioslowski and Mixon and the properties of the electron density using more complex expressions such as that given in eq 53.

Here ρ is the electron density at the bond critical point (the point of minimum electron density on the line of steepest descent connecting the two bonded atoms), λ₃ is its second derivative along the direction of the bond and λ₁₂ is the sum of the two second derivatives perpendicular to the bond. They chose values for the constants a, b, c, and d for C−X (X = C, O, N, S and P) bonds to match the bond orders of Cioslowski and Mixon.

Tsirelson et al.(168) subsequently revised these parameters, extending the list of bond types to include N−O, N−N and several bonds to H. They compare the bond orders calculated using the Cioslowski and Mixon method with those calculated from the electron density, both theoretical and experimental. The sum of the bond orders (atomic valence index) are generally less than the atomic valence, sometimes significantly so. The discrepancy arises in part because, as Howard and Lamarche carefully point out, these are covalent bond orders and do not measure the total bonding between the atoms, but Tsirelson and co-workers suggest that the difference might also represent the residual (free) valence available for forming external bonds. Both explanations are speculative but suggest that the difference may have some chemical significance. In the absence of a clear definition of how the strength or order of a bond is decomposed into ionic and covalent components it is difficult to relate these results to bond valences, which do not recognize this distinction.

Although this work is not directly related to the bond valence model, it does draw attention to the similarity between bond valences and the concept of bond order currently used in organic chemistry. C−X bonds, where X is not C or H, are technically polar since C and X have different electronegativities, and for these bonds the bond valence model can be used. A simple blending of the concepts of the two fields is therefore a desirable goal. However, although it is clear that bond length and bond order (or bond valence) are correlated for all bonds, the rules of the bonds valence model can only be applied if the bond graph is bipartite as defined in section 3.

Hughes and Wade(169) report that the entropy of metal−metal bonds in M_x(CO)_y cluster molecules correlates with the bond length according to eq 25 with N = 4.6, similar to the values found for the correlation between bond-valence and bond-length.

Trömel and Hübner^170−174 have explored the structures of the elements, particularly the metals, making use of eq 26 to determine bond valences, assuming that the resulting valences will obey the valence sum rule. Initially they explored the metallic elements, many of which crystallize with the close-packed face-centered cubic structure. They define an atomic volume, v_A, which, when summed over all the atoms in the crystal, is equal to the total volume of the crystal. Values of v_A vary according to the particular structure even for the same element, but they can be separated into a reduced volume, v_D, which is an intrinsic property of the element, and a packing density, q, which is a specific property of the structure.

Trömel and Hübner assumed that the face-centered cubic structure (or the body-centered cubic structure for those metallic elements that adopt this form) represents the densest possible packing arrangement. They defined the reduced volume, v_D, of an atom as the volume of its atom-centered Voronoi, or Frank-Kasper, polyhedron in its most densely packed phase. The Voronoi polyhedron is formed when a crystal is partitioned into atom-centered fragments by planes that perpendicularly bisect the lines joining neighboring atoms. Since each face-centered cubic cell contains four atoms, the reduced volume of each atom is just one-quarter of the volume of the unit cell (half the volume of the unit cell in the case of the body-centered cubic structure). Trömel and Hübner assume that two atoms are bonded if their Voronoi polyhedra share faces (which they call the geometric coordination). In the face centered cubic structure each atom forms 18 bonds (12 short and 6 long) and in the body centered cubic structure they form 14 bonds (8 short and 6 long).

Assuming that the face-centered and body-centered cubic structures both represent the densest packing, that eq 26 describes the relation between bond length and bond valence (Bindungsgrad), and that the valence sum rule holds for both the face-centered and body-centered cubic packings, they derive eq 55 for the softness bond valence parameter, b, in terms of a_D, the characteristic distance of an atom, defined as (v_D)^1/3.

The values reported for b range from 0.30 Å for Be−Be bonds to 0.72 Å for Cs−Cs bonds. Equation 55 allows the values of b to be calculated with high precision, but it is based on the assumption that if a metallic element were to crystallize in both the face-centered and body-centered cubic forms, both forms would exactly obey the same valence sum rule.

Many metals are known with more than one structure, and values of a_D can be calculated for each using eq 56 obtained by substituting eq 55 into eq 26 and eliminating b.

Here the summation is over the observed bond lengths, R_i, in a given geometric coordination sphere. Trömel and Hübner found that the values of a_D, hence v_D, calculated for the different structures in which a given element can crystallize were remarkably similar, thus justifying eq 54 and allowing the packing density, q, to be found.

They also derive eq 57.

which allows the valence, V₂, of element 2 to be determined if the valence, V₁, of element 1 is known. Most of the atomic valences calculated in this way lie within 0.05 vu of the expected integer, though for a few, such as Ti⁴⁺ and Zr⁴⁺ with V = 3.5 vu, nonintegral values are found.

Once the atomic valences are known from eq 57 and the values of b are known from eq 55, eq 27 can be used to determine R₀. The resulting bond valence parameters are listed in Table 2 of ref (173). They are not listed in Table 2 of the present review as they are not suitable for routine structure checking unless the same procedures are followed, that is, they must be used only for bonds between two atoms of the same element in coordination environments defined by the Voronoi polyhedra. In any case metallic elements do not form bipartite bond graphs.

Trömel and Hübner^171,175 subsequently extended their work on metallic elements to nonmetallic elemental structures with similar results. Here it was found that the values of v_D were not always the same for a given element. For example the diamond structure of α-Sn has v_D = 24.66 ų and an atomic valence of 4 vu, but the metallic β-Sn has v_D = 25.47 ų and atomic valence of only 3.73 vu. Similarly four-coordinated carbon in diamond with v_D = 4.10 ų has a valence of 4 but three-coordinate carbon in graphite has v_D = 3.69 ų which corresponds to a valence of 5 vu. Trömel(175) finds that the lengths predicted for multiple C−C bonds, calculated using bond valence parameters based on eq 55, deviate from those observed, but he attributes the difference to the additional bonds included in the geometric coordination. An examination of the many different high pressure structures of Si show that the values of v_D all lie on a smooth curve in which v_D decreases monotonically with pressure, even though values of v_A vary from one high-pressure structure to another.

It is not clear what significance is to be attached to the various quantities that are calculated using this procedure. Even though the assumptions on which the value of b is based (eq 55) can be questioned, the determination of a structure-independent atomic volume and a characteristic length for each element is impressive, and the calculated atomic valences and values of b seem highly plausible, even if their meaning in a metallic context is not clear. It will be interesting to see how far this approach can be taken.

14. Structure Validation

By far the greatest use of the bond valence model is for checking and validating newly determined structures containing polar bonds. The literature contains several thousand examples of the routine use of the bond valence sums as a check on the correctness of crystal structures. Only a couple of representative examples are included here.

The valence sum rule (eq 9) is the most frequently used theorem of the model. Compliance with this rule is taken as a validation of a structure determination. It is also used to confirm or determine the oxidation states of cations where this is uncertain. More rarely are bond valences used to understand why some bonds have been lengthened and others shortened, and most of these cases are discussed in other sections.

A typical example of the use of bond valences for checking a structure determination can be found in a recent paper by Nfor et al.(176) who used bond valences to check the coordination of O²⁻, S²⁻ and N³⁻ to Cu²⁺ in (acetato-κO)(2-acetylpyridine 4-methylthiosemicarbazonato-κ³-N,N′,S)copper(II) monohydrate. This paper, which illustrates that the model can be used with metal-organic complexes, describes the use of the valence sum rule in detail and shows that the sum of the bond valences around the Cu²⁺ ion is equal to 1.94 vu, a value that is satisfactorily close to the expected value of 2.00 vu.

The valence sum rule has been incorporated into the X-ray single crystal refinement program TOPAS Academic in order to ensure that when the highly disordered β-La₂Mo₂O₉ structure was refined the Mo−O and La−O bonds were chemically reasonable.(177) It is also used in other structure determination and analysis programs but could be introduced more widely.

Sometimes validation of a new structure requires the determination of suitable bond valence parameters. Sidey et al.(84) determined the structure of Hg₂Sb₂O₇ using powder diffraction and showed that the results gave good bond valence sums and a global instability index, G (eq 44), of 0.07 vu, though they found it necessary to redetermine the bond valence parameters for Sb⁵⁺–O bonds to give the value shown in Table 2. The paper in which Malcherek and Schlüter(178) reported the structure of Cu₃MgCl₂(OH)₆ used bond valences to analyze the hydrogen bonding, but only after they had determined the bond valence parameters for O−H···Cl bonds. These values are shown in Table 6.

An anomalously low bond valence sum of 1.49 vu around one of the borate O²⁻ ions in Zn₄O(BO₃)₂, together with its unexpected partial occupancy, raised the suspicion of Delahaye et al.(179) that the reported structure was probably wrong. This led them to redetermine the structure and show that the formula should be written Zn₆O(OH)(BO₃)₃.

The Web site SoftBV(38) provides an introduction to bond valences and gives the user an opportunity to check a structure in SHELX or CIF format. VaList(37) is another program that calculates bond valences and bond valence sums for a list of bond lengths supplied by the user in CIF, GSAS or FULLPROF format.

15. Assigning Charge Distribution

Bond valences provide an excellent, and often the only, way to assign oxidation states, particularly in a mixed valence compound, or to determine the distribution of different cations over different sites.

Shields et al.(68) tested the ability of bond valences to automatically assign oxidation states to metal ions in the structures of complexes found in the Cambridge Structural Database.(39) They report a success rate of 88% in a test sample of four-coordinate Cu complexes and a virtually complete success when this was combined with a system of ligand templates. They used the program OXQUEST which also used by Harris et al.(180) to prepare a classified library of molecular geometry for metal complexes. They found they could use bond valence sums to distinguish between high and low spin complexes. For example, the high spin Fe²⁺ ions in six coordinate Fe(II) pyridine complexes had bond valence sums close to 2.0 vu but using the same parameters, low spin compounds had sums that clustered around 5 vu.

Van Smaalen and Lüdecke(181) and Bernert et al.(182) describe an X-ray analysis of α′-NaV₂O₅, the low temperature version of a structure that consists of vanadate ladders running along the b axis of the Pmmn cell. The sides of the ladders consist of edge sharing VO₅ square pyramids which are linked by V−O−V rungs. At room temperature all the V ions are equivalent and their bond valence sum of 4.57 vu is consistent with the expected formal valence of 4.5 vu. As expected, the structure gives a single vanadium nuclear magnetic resonance signal. Below room temperature two nuclear magnetic resonance signals are seen, but the compound develops a superstructure with six crystallographically unique V ions occupying three crystallographically distinct ladders in the space group Fmm2. The question that interested these investigators was how six distinct V ions could give rise to only two nuclear magnetic resonance signals. The two groups came to different conclusions. Van Smaalen and Lüdecke(181) found that in one ladder the bond valence sums remain at 4.58 vu indicating a continued mixed occupancy, but the other two ladders show alternating V⁴⁺ and V⁵⁺ ions with bond valence sums of 4.22 and 4.99 vu in one ladder and 4.27 and 4.97 vu in the other. Bernert et al.(182) undertook a new refinement and came to a different conclusion about the charge distribution. In their analysis, in which they carefully customized the bond valence parameters to the compound and temperature of the analysis (15 K), they concluded that one chain contained only V^4.6+ ions, while the other two chains contained V^4.6+ ions alternating with V^4.1 ions, an arrangement which they point out agrees more closely with the two signals seen in the nuclear magnetic resonance.

In addition to determining atomic valences, bond valences can be used to determine how the residual valence of a polyatomic ion is distributed over the simple ions that form its surface. The residual valence (or external charge) is the valence of an ion remaining after the valences of all the internal bonds have been satisfied. In the case of S₂I₄(AsF₆)₂ reported by Brownridge et al.(183) the cation is S₂I₄²⁺ and the residual valence on each of the I⁺ ions was determined by summing the valences of the bonds between each I⁺ ion and its F⁻ ligands.

One charge distribution that has always fascinated scientists is that found in compounds with mixed Fe²⁺ and Fe³⁺ states such as the spinel Fe₃O₄. At higher temperatures all the Fe ions have bond lengths corresponding to the same nonintegral oxidation state, but below a transition, known as the Verwey transition, the different oxidation states tend to freeze out on particular sites. Karen et al.(184) examined the charge ordering in the perovskite-related compound EuBaFe₂O₅ as a function of temperature using high resolution powder X-ray diffraction and Mössbauer spectroscopy. The structure determination showed that above 256 K all the Fe ions had bond valence sums of 2.5 vu. Immediately below this temperature the Fe ions split into two groups, one with a bond valence sum close to 3.0, the other close to 2.0 vu, but below this temperature they settled at 2.88 and 2.10 vu respectively. The Mössbauer results on the other hand showed almost complete separation into Fe²⁺ and Fe³⁺ below 256 and a partial separation between 256 and 299 K. The interpretation is that the Mössbauer measurements are looking at individual Fe ions, showing that above 299 K each ion has an oxidation state of +2.5. Between 299 and 256 K the ions move toward oxidation states of either 3+ or 2+, but there is no long-range ordering, so the effect is not seen in the bond valence sums calculated using the space and time averaged structure measured by the diffraction experiments. Below 256 K each Fe ion has an integral oxidation state and these show long-range order. However, the ordering is not perfect and does not extend beyond defects such as a missing O²⁻ ion except just below the point where the long-range order breaks down. This example shows how the bond valence model can be used in combination with other techniques to elucidate the changes taking place in a structure, in particular how the model can be used to distinguish local ordering from global ordering.

Robinson et al.(185) used bond valences to decide on the distribution of Fe²⁺ and Fe³⁺ ions at the interface between hematite, Fe³⁺₂O₃, and the isostructural ilmenite, Fe²⁺TiO₃. In this structure the cations are octahedrally coordinated with the octahedra linked into pairs through a shared face. Robinson et al. used bond valences to argue that the Fe³⁺ in the contact layer shares a face with the Ti⁴⁺ in ilmenite and that Fe²⁺ in the contact layer shares a face with the Fe³⁺ in hematite. Even though this arrangement appears to be counterintuitive a Monte Carlo simulation produced the same result.

Li et al.(153) used the valence matching rule (eq 16) described in section 11 to rationalize the distribution of Cd²⁺ and In³⁺ ions in the Cd₄In₁₆S₃₅¹⁴⁻ anion. This complex ion consists of a pyramidal-shaped extract from the cubic sphalerite structure of CdS with both Cd and S in 4-fold coordination. The bonds that are broken in the process of extracting this ion ensure that the S²⁻ ions on the surface have coordination numbers less than four, but there is one four-coordinated S²⁻ ion at the center of the complex. The bonding strengths, L_b (eq 15), of the four-, three- and two-coordinated S²⁻ ions are −0.50, −0.67, and −1.00 vu respectively and the bonding strengths, L_a (eq 14) of four-coordinated In³⁺ and Cd²⁺ are 0.75 and 0.50 vu respectively. According to the valence matching principle Cd²⁺ is the preferred cation for bonding to the central four-coordinated S²⁻ ion while In³⁺ is the preferred cation for bonding to the surface S²⁻ ions. This distribution was confirmed from an examination of the bond lengths, equivalent to checking the experimental bond valence sums.

Valach et al.(186) used bond valences to discover if the Cu−Cu distance in a copper-acetate-structure analog represents a real bond. Using eq 33, they calculated the bond valence sums around Cu²⁺ in tetrakis(2-iodobenzoato)bis(caffeine)dicopper(II) which has two copper ions separated by 2.704 A completing the octahedral coordination around each Cu²⁺ ion. They found that the sum of the valences of the four Cu−O and one Cu−N bond was 2.05 vu. As this was equal to the atomic valence (formal oxidation state) normally assumed for copper in these compounds, they concluded that the Cu−Cu distance made no contribution to the valence sum and therefore no Cu−Cu bond existed. This argument however is circular because if a Cu−Cu bond existed, it would involve the unpaired d electrons on the two Cu ions. These are, however, considered as belonging to the cores of Cu²⁺ ions. One could alternatively consider the core as d⁸ with the unpaired ninth d electron contributing to a δ bond between the two Cu ions. In this case the Cu would have to be assigned an oxidation state of 3+ and the Cu³⁺ ions would be linked by an electron pair bond of valence 1.0. This is a problem where bond valences are unable to shed any light.

16. Structure Analysis

In their exploration of wide-angle convergent-beam electron-diffraction as a specialist tool for structure determination, Tabira and Withers(187) examined the structures of the spinels MgCr₂O₄ and NiAl₂O₄, the former known to be a normal spinel (tetrahedral Mg²⁺ and octahedral Cr³⁺) and the latter suspected of being an inverse spinel (tetrahedral Al³⁺ and octahedral Al³⁺ and Ni²⁺). The convergent-beam electron diffraction was used to determine the free positional parameter, u, of the O²⁻ ion and bond valences were used to infer whether the spinel was normal or inverted. The graph in Figure 16a shows how the bond valence sums around the three ions in MgCr₂O₄ change as u is varied. The correct value for u, 0.262, can be read off as the point at which all three ions have their expected valence sums. For NiAl₂O₄ the degree of inversion depends on the value of u. Figure 16b shows that if the crystal is a normal spinel u would be around 0.265 since this gives a bond valence sum of 2 around tetrahedral Ni²⁺ and 3 around octahedral Al³⁺, but if it is an inverse spinel u would be 0.253 with a bond valence sum of 3 around tetrahedral Al³⁺ and 2.5 around the mixed octahedral site. The convergent-beam electron-diffraction experiment measured u as 0.255, confirming that this material has the expected inverted-spinel structure.

Figure 16.

Variation in the bond valence sums (AV) as a function of the O²⁻ parameter, u, of each of the ions in the spinels MgCr₂O₄ (top) and NiAl₂O₄ (bottom). The predicted value of u is the one which gives the bond valence sums for each ion that correspond to their atomic valence. With kind permission of Springer Science + Business Media from Phys. Chem. Miner. “Cation ordering in NiAl₂O₄ spinel by a 111 systematic row CBED technique” 27 (1999) 112, Tabira and Withers, Figure 4.

Tabira et al.(18) used three different methods to determine the free atomic positional coordinate, x, in a series of pyrochlores. As in the previous study they obtained the experimental value using wide-angle convergent-beam electron-diffraction and compared this with the values obtained using the two-body potential model and the bond valence model. As before they plotted the bond valence sums that would be found for a range of values of x for the four extreme compositions they examined: La₂Zr₂O₇, Sm₂Zr₂O₇, Sm₂Ti₂O₇ and Er₂Ti₂O₇. From this graph they could then find the value of x that gave a valence sum of 3.0 vu around La³⁺ or Sm³⁺ and 4.0 vu around Zr⁴⁺ or Ti⁴⁺. Each compound thus gave two estimates of x which were found to differ by less than 0.005, with their average differing by less than 0.005 from the observed value, corresponding to an accuracy of around 0.05 Å. The values of x from the two-body potential model differed systematically by 0.007 from the observed values, a discrepancy the authors attribute to antisite disorder.

An interesting use of the bond valence sums was made by Chiang et al.(188) in their study the Preyssler anion. This polyphosphotungstate ion is built around a ring of five linked PO₄ tetrahedra. Arranged symmetrically above and below this ring are two polytungstate double rings, each double ring consisting of one ring containing ten, the other five, W⁶⁺ ions respectively, to give a formula P₅W₃₀O₁₁₀¹⁵⁻. A 5-fold axis runs down the central channel which contains an exchangeable cation as well as some weakly coordinated water molecules. Chiang et al. describe EXAFS measurements at the absorption edges of the exchangeable central cations Sr²⁺, Am³⁺, Eu³⁺, Sm³⁺, Y³⁺, Th⁴⁺, and U⁴⁺ which show that the cation forms five short and five long bonds to the O²⁻ ions lining the channel. The small changes in these distances as the cation is changed indicates that the Preyssler ion is quite rigid. The EXAFS distances were used to calculate bond valences. For Sr²⁺ the valence sum was 2.89 vu, considerably higher than the expected value of 2.00 vu, indicating that Sr²⁺ is highly compressed, but all the other cations gave valence sums that were too low by between 0.24 vu (Am³⁺) and 0.83 vu (for U⁴⁺). Bonds to the coordinated water molecules may account for some of this difference, but even when these are taken into account, the cation-O bonds are still stretched as indicated by the ability of the Preyssler anion to stabilize lower oxidation states and shift redox potentials.

17. Incommensurate Structures

Related to the problem of finding the distribution of charges (valences) between the ions described in section 15, is the problem of describing aperiodic crystals. These are crystals comprising two components with incommensurate repeat distances in one or more directions, or in which the atomic positions or occupancies are modulated by a wave with a wavelength that is incommensurate with the lattice parameters. Such crystals do not have a true translational symmetry and no two unit cells are the same, making the description of the crystal chemistry more complex. The method most frequently adopted to describe these structures is to define atomic coordinates in four or more dimensions. Three of these are used to define a real-space basis set of lattice parameters and the others are used to describe a second repeat length along one or more of the basis directions. Van Smaalen(189) has provided an introduction to the supersymmetry description of such structures in which he points out that while the bonding environment, hence the individual bond valences, around any given ion will depend on where it appears in the crystal, the sum of the bond valences always equals the atomic valence at all points where the ion can be found.

An example of such an application is given in the paper of van Smaalen et al.(190) in which they report the crystal structure of Na_xCuO₂ with x = 1.58, 1.60, and 1.62. The structure consists of CuO₂ chains of edge-sharing CuO₄ squares running parallel to chains of Na⁺ ions. In Na_1.6CuO₂ the Na⁺ chain is commensurate with the CuO₂ chain, but in the other two compositions it is incommensurate. Van Smaalen et al. found that even though every Na⁺ ion is bonded to a different arrangement of O²⁻ ions, its valence sum remained within 0.1 vu of the expected value of 1.0 vu, regardless of where the Na⁺ ion appears in the crystal. However, the presence of Na⁺ requires a reduction in the oxidation state of Cu, but since each Cu has a different number of Na⁺ second neighbors, the valence sums around Cu are modulated by a wave whose wavelength is equal to the repeat distance of the Na⁺ ion lattice. The Cu valence sums form a wave centered at 2.45 vu with an amplitude of around 0.3 vu, The authors interpret this as representing a sequence of Cu²⁺ and Cu³⁺ ions with integral valences arranged in a way that most closely matches the amplitude of the valence sum modulation.

Isobe et al.(191) have analyzed the composite ladder and chain structure of Ca₁₄Cu₂₄O₄₁. This contains chains of corner sharing CuO₄ squares as one component and ladders of edge sharing CuO₄ squares as the second component. In both cases the 5-coordination of the Cu ions is completed by an O²⁻ ion of the other component. Since the repeat distances in the chains and ladders are in the ratio of √2 they are incommensurate and each component is modulated by a wave with the lattice spacing of the other component. The average valence of the Cu ions is 2.25 indicating the presence of electron holes (relative to Cu²⁺) in both the chains and the ladders. A bond valence analysis of the oxidation state of the Cu ions indicates that the holes are localized in a way that follows the modulation. The authors interpret the results to show that at low temperatures (5 K) the holes have all migrated from the ladders to the chains, and they discuss the implications of this for the magnetic and electric properties of the compound.

Tamazyan et al.(192) solved the two-dimensional modulated structure of GdS_1.82 and were faced with the task of presenting the results of their five-dimensional refinement in a chemically meaningful way. Figure 17 shows maps of the modulations of the bond valence sums around Gd and S as a function of the two additional coordinates, allowing the reader to get a much clearer picture of this complex structure. These maps show that the valence sum around S varies by less than 0.1 vu while that around Gd varies by ±0.3 vu.

Figure 17.

Modulation of the bond valence sums in GaS_1.82 around Ga (top, contour interval 0.1 vu) and S (bottom, contour interval 0.05 vu) as a function of the two additional dimensions. Solid lines are positive contours, broken lines are negative. Over the whole crystal the environments around Ga and S will sample all of the regions shown in this diagram. Copyright 2003 International Union of Crystallography, Reproduced with permission from ref (192).

18. Chemical Properties

Xue et al.(193) used bond valences to calculate notional electronegativities using eq 58.

where r_i is the covalent radius of atom i, Δχ_ij is the difference in electronegativity of atoms i and j, and β = 0.085 Å. Using the bond valence parameters of Trzesowska et al.(44) (Table 2) they calculated the ideal values of R_ij for all the Ln⁺³–O bonds with coordination numbers from 6 to 12. With these distances and tabulated covalent radii, and taking the electronegativity of oxygen as 3.5, they used eq 58 to produce a table of electronegativities for each of the lanthanide atoms in each of six different coordination numbers. The electronegativities they obtained decreased with coordination number and increased with the atomic number of the lanthanide, the smallest for 12-coordinate La³⁺ is 0.445 and the largest for 6-coordinate Lu³⁺ is 3.031. The authors did not compare these values with any other scale nor did they comment on why the electronegativity should vary with coordination number. It is not clear how the authors intend these values to be used.

Bhuvaneswari et al.(194) used bond valences in an unconvincing interpretation of the Raman and infrared spectra of Li_xNiVO₄ (x = 0.8−1.2). They assume that each V−O bond gives rise to its own vibrational frequency which can be used to determine the corresponding bond valence. From these they deduce that the valence sum at V is 5.2 vu in each of the three samples they examined.

Buttrey(195) has determined the structures of several bismuth molybdates to find out how they function as catalysts for the oxidation of olefins. He noted that the bond valence sums around Bi³⁺ and the O²⁻ ions that were bonded only to Bi³⁺ were typically too high by around 0.3 vu which he considered the source of their catalytic ability. However, the structures were mostly determined by powder X-ray diffraction which, given the large number of electrons on the Bi³⁺ ion, does not allow the O²⁻ positions to be determined with sufficient accuracy for a meaningful application of the bond valence model. This could explain why there is not much consistency between the reported catalytic power and valence sums. Furthermore, the large Bi−O bond valences are likely the result of using bond valence parameters with b of 0.37 A, which as shown in sections 7.3 and 8.2.2, is probably too small for an ion with a lone electron pair.

Albuquerque et al.(88) described a rather tortuous process for calculating ligand field parameters for lanthanide coordination complexes. The approximation they use for calculating the overlap integral in terms of the bond lengths has the same form as eq 25, indicating that the overlap integrals are proportional to the bond valences. This allows them to use the valence sum rule as one of the constraints in the determination of the charge factor for each of the ligands. With this constraint they are able to calculate the ligand field levels for three Eu³⁺ complexes within a few percent providing not more than two different kinds of ligating atoms are present.

19. Physical Properties

Xue and colleagues have published a large number of papers describing what they call the ‘chemical bond method’ of predicting nonlinear optical properties from crystal structures. The underlying model described by Xue and Zhang^196,197 assumes that the optical properties of the crystal can be calculated by summing the corresponding properties of the constituent bonds. Inconsistent notation makes it difficult to follow the description of their model, but it appears that they take the bond valence as a measure of the number of electrons in the bond, a key term in the theory. Xue et al.^198,198,200 studied the nonlinear optical properties of LiNbO₃, making the assumption, that since the wavelength of visible light is large compared to interatomic distances, it is satisfactory to treat impurities as if the crystal were composed of mixed domains of LiNbO₃ + M_xNbO₃. They explore the influence of M = Mg²⁺, Zn²⁺ and In³⁺, using bond graphs like those shown in Figure 3 to help assign the bond valences. In later papers^121,201 they develop a more sophisticated model with oxygen defects and some Nb⁴⁺ occupying Li⁺ sites. They explore the distribution of the impurity atoms by calculating the discrepancy factor (eq 41) around each unrelaxed impurity atom when placed on either the Li or Nb site and assume that the site with the lowest discrepancy factor is the likely site for the impurity as described in more detail in section 8.3. Xue and Ratajczek(202) applied the same model to a hydrated sodium selenate while Xue et al.(197) applied it to LiB₃O₅, LiCsB₆O₁₀ and CsB₃O₅. In a separate study, Yu and Xue(62) divided all the borates into classes based on the topology of their bond graph, and for each class they fitted individual values of the bond valence parameter R₀ as described in section 7.3. They showed that there is a weak relationship between the value of R₀ they determine and the largest component of the nonlinear optical tensor.

Adams and Swenson(137) have shown that the nuclear magnetic resonance chemical shift of Na⁺ and Li⁺ in their oxyacid salts correlates with the valence of the bonds formed by the O²⁻ ligands to cations other than the central Na⁺ or Li⁺, weighted by the inverse of the bond valence softness parameter b.

Newville(203) has proposed using bond valences as a constraint or restraint in interpreting XAFS spectra. These spectra give mutually independent values for the bond length and coordination number around the activated cation. In fact the bond length and coordination number are highly correlated: the larger the coordination number the longer the bond. This correlation is captured by the valence sum rule which can consequently be used as a constraint in the interpretation of the XAFS spectrum, ensuring that the refined bond length and coordination number are appropriately related.

A desire to understand thermoluminescence in Li₂B₄O₇:X (X = Cu²⁺ or Mn²⁺) following annealing in reducing and oxidizing atmospheres led Holovey and colleagues^204,205 to use bond valences to determine which O²⁻ ion is the most labile and likely to be removed during reduction. The B₄O₇²⁻ network consists of two BO₃ triangles and two BO₄ tetrahedra corner-linked into an eight-membered ring which is bridged by the shared fourth O²⁻ ion of the BO₄ groups as shown in Figure 18. They note that while the bond valence sums around most of the ions are very close to the atomic valence, that for the oxygen atom that links the two tetrahedra in the cluster is significantly low (1.70 vu) which led them to speculate that this is the oxygen that is lost, converting the tetrahedral BO₄ groups to triangular BO₃. Charge balance would be achieved by the reduction of Cu²⁺ (or Mn²⁺) to Cu⁺ (or Mn⁺) and Li⁺ to Li⁰ as needed. Apart from noting that the sample turned gray after reduction, they offer little experimental evidence in support of this plausible explanation.

Figure 18.

Structure of the B₄O₇²⁻ ion. Open circles represent O²⁻, filled circles represent B³⁺. The central O²⁻ is proposed to be the labile anion.

20. Pressure

Brown et al.(206) developed a classical model based on an electrostatic attraction and an exponential repulsion between the ions, to predict the effect of pressure on the lengths of individual bonds, deriving eq 59 for the bond compressibility, β.

Here R is the equilibrium bond length, g a geometric factor of order 1 related to the area supported by the bond, k is a dimensional constant equal to 23 nN.Ų, b is the bond valence softness parameter and q is the effective charge on the ions forming the bond. Empirically q is found to equal to (8S/3)^3/2, where S is the bond valence. They found reasonable agreement with the observed compressibilities of a number of high symmetry binary compounds, though they noted deviations associated with bond softness. There was also good agreement with the observed compressibilities of individual bonds measured using single crystal diffraction. The few cases where the agreement failed could be understood in terms of steric effects specific to the structure.

A different and simpler approach has been reported in a number of papers by Angel and colleagues^{125,207−210} who analyzed the structural changes in a series of compounds with the perovskite structure. These have the formula ABO₃ where A is a cation that occupies a 12-coordinate site and B a cation that occupies an octahedral site (see Figure 21). Perovskites make an excellent test-bed for exploring the effects of pressure on structure as the two cations, A and B, are expected to have different compressibilities, resulting in a change in their relative size as the pressure is increased. Since the structure of low-symmetry perovskites is sensitive to the relative sizes of the cations, small changes in bond length are easily detected.

Angel and colleagues hypothesized that the rate of change of the valence sums with pressure, dV_s/dP, would be the same for both cations in a perovskite structure, even if the bond compressibilities of the two cations were different, that is:

This they call the ‘equal valence rule’ and later the ‘valence matching rule’, though both these terms are used in the present paper with different meanings (see the glossary in section 1). Here I refer to eq 60 as the compressibility rule. They demonstrate(208) that this rule holds for a number of 2:4 perovskites (such as CaSnO₃) as well as for 3:3 perovskites (such as GdFeO₃) with coefficients in the range of 0.02 to 0.03 vu GPa⁻¹. In a later paper(125) they show that the compressibility rule is obeyed by an ab initio simulation of MgSiO₃ at 120 GPa. This shows an increase in the bond valence sum around Si⁴⁺ from 3.81 (at zero pressure) to 5.60 vu, and around Mg²⁺ from 2.31 to 4.13 vu, in both cases the change is 1.80 vu corresponding to a compressibility coefficient of 0.015 vu.GPa⁻¹.

Using the compressibility rule and making the approximation that the bonds in a given coordination sphere have a similar length, R, they derive eq 61.

where

Here β is the compressibility of the bond, N is the coordination number of the cation and V_s is the bond valence sum. In cases where a cation forms bonds with widely different lengths, the bonds must be grouped according to length and the contribution of each group to M calculated separately.

If (dV_s/dP) is the same for both cations, it follows from eq 61 that

and since M can be calculated from eq 61, the ratio of the compressibilities of A and B can be found.

As part of this study Zhao et al.(208) initially looked at perovskites with the orthorhombic GdFeO₃ structure (space group Pbnm), a distortion of the cubic aristotype caused by the framework of corner linked FeO₆ octahedra twisting so as to distort the environment of Gd³⁺ according to the prediction of the distortion theorem (eq 35). If the 12-coordinated A cation is more compressible than the 6-coordinated B cation, A will shrink faster than B so one would expect the twisting distortion to increase. On the other hand if B is more compressible than A, the twisting distortion would be reduced, possibly leading to a phase change to the cubic aristotype at high enough pressure. Whether the distortion increases or decreases depends, according to eq 63, on the ratio of the relative values of M, and from eq 62, M is dominated by the bond valence sum, V_s, of the cation, with the length, R, of the bonds playing a lesser role. For compounds with divalent A and tetravalent B, such as CaSnO₃, M_A/M_B < 1 indicating that A is the more compressible, but if A and B are both trivalent, the valences are the same and the ratio is determined by the bond lengths. In the perovskite structure R_A = √2 R_B (at least approximately) and M_A/M_B > 1. The 2:4 perovskites will therefore become more distorted under pressure while 3:3 perovskites will become less distorted, a prediction which the authors have verified. They point out, however, that this approach is unlikely to work in compounds containing cations with electronic anisotropies such as those with stereoactive lone electron pairs discussed in section 8.2.2, or cations that can flip from a high spin to a low spin configuration under pressure. The results are also unlikely to work in cases where the symmetry is dynamic, that is, where the local symmetry is lower than the macroscopic symmetry of the crystal because atoms are moving between macroscopically equivalent sites.

M_A (or M_B) will, in general, be different for a given cation in different compounds because the size of the space available to A depends also on the size of B. This changes both R and the bond valence sum. In CaGeO₃, the Ge⁴⁺ cation is relatively small, so although Ca²⁺ is still small enough to cause the compound to adopt the CaSnO₃ structure, the distortion of the framework is relatively small and M_A/M_B is closer to 1.0 than in CaZrO₃ where the larger Zr⁴⁺ ion makes the distortion more pronounced. The consequence is that the change in distortion with pressure is larger in CaZrO₃ than in CaGeO₃ and consequently CaZrO₃ has the lower bulk modulus.

In another paper(207) these authors apply the same analysis to LaAlO₃ which is also based on a twisted framework of AlO₆ octahedra, but this time with trigonal symmetry (space group Rc). In this case the Al−O bonds are on average more compressible than the La−O bonds, so that application of pressure reduces the distortion. However, the La−O bonds are not all the same length; there are three bonds at 2.54 Å, six at 2.68 Å and three at 2.82 Å. The three longest (and weakest) La−O bonds are highly compressible (3.47 × 10⁻³ GPa⁻¹) while the other nine La−O bonds all have compressibilities that are less than that of the Al−O bonds (1.78 × 10⁻³ GPa⁻¹). Because the long bonds are weak and make little contribution to the effective compressibility, La³⁺ can be regarded as nine-coordinated.

In a later paper(125) they explore the possibility of predicting the evolution of the structures of the GdFeO₃ perovskites as a function of pressure. They note that the lattice parameters can be accurately measured at high pressure using X-ray powder diffraction but the positions of the atoms in the unit cell are more difficult to determine. Using the change in lattice parameters as a guide, they propose looking for a structure model that satisfies eq 60 and also gives a minimum value for the global instability index, G (eq 44), here calculated using only the cations. They model the changes in two stages, first reducing the cell size while holding the atomic coordinates fixed, then allowing the coordinates to relax to increase or decrease the degree of twist.

A theoretical analysis of the effect of pressure on the charge distribution in YBa₂Cu₃O₇ reported by Mohammedizadah and Akharan(211) is described in section 22.6.

21. Hydrogen Bonding

Hydrogen bonding continues to attract interest, chiefly because of its vital importance in all disciplines of science, but also because of its unusual properties which do not fit comfortably into traditional models of chemistry. Unlike most cations which tend to be found in regular environments, the H⁺ ion is normally found strongly displaced from the midpoint of its coordination sphere, forming one short and one or more long bonds. The short donor bond, X−H, and the long acceptor bond. H···Y, when taken together, are referred to here as a hydrogen bond and are represented by X−H···Y in chemical diagrams. In some texts the term ‘hydrogen bond’ is restricted to the H···Y linkage, but this tends to emphasize the difference in character between the X−H and H···Y bonds. In the bond valence model both bonds have the same character, and which atom, X or Y, acts as donor depends on which has the largest bonding strength.

The asymmetry in the hydrogen bond arises because of the strong repulsion between the terminal X and Y ions when H⁺ is placed symmetrically between them.(1) The symmetric hydrogen bond is therefore strained with the X···Y distance determined more by the repulsion between the X and Y ions than by the expected lengths of the X−H and H−Y bonds. The result is that placing H⁺ at the center of the hydrogen bond causes the X−H and H−Y bonds to be stretched, and according to the corollary to the distortion theorem given in eq 43, the H⁺ ion moves off-center, giving rise to the typical asymmetric hydrogen bond. By including the X···Y repulsion, the bond valence model is able to account quantitatively for the geometries of hydrogen bonds observed in different chemical contexts.(1) Bonds shorter than those found in ice are frequently referred to as ‘strong hydrogen bonds’, but this is a misnomer since the energy gained by making the bond shorter and more symmetric is more than balanced by the strain energy required to bring the X and Y ions closer together. Such bonds can only be stabilized by a gain in energy elsewhere in the structure. The strongest hydrogen bond, that is, the one with the lowest energy, is the unconstrained bond found in ice with a donor O−H bond of around 0.8 vu and an acceptor H···O bond of around 0.2 vu. Because hydrogen bonds that are more symmetric than this are stretched by the repulsion between X and Y, the X−H and H···X bonds are in tension and are constrained to be linear, that is, the X−H···Y angle is 180°, and eq 26 no longer strictly applies as can be seen from an inspections of the bond-valence - bond-length correlation for H−O bonds shown in Figure 19. Symmetric hydrogen bonds are only found where there are chemical constraints strong enough to supply the additional strain energy. Long (weak) hydrogen bonds are not strained and the longer they are, the more bent they are likely to be. Although the application of the bond valence model to hydrogen bonding accounts for its geometry and simplifies the analysis of hydrogen bonded structures, most studies in the review period confined themselves to applying the valence sum rule at the H⁺ ion, and in most of these cases defined the bond-valence - bond-length correlation in a way that successfully conceals the presence of strain in the symmetric bonds.

Mohri^29,30 has analyzed a number of hydrogen bonded systems using orbital theory and compared the results to the bond valence model. Further details of this work can be found in section 5.

Hydrogen bonding in organic chemistry has recently been reviewed by Steiner and Saenger(212) who described briefly the valence sum rule around H⁺ in the last section. In the often-encountered case where H⁺ forms only two bonds, a strong X−H bond and a weak H···Y bond, application of the valence sum rule around H⁺ results in a unique relationship between R_XH and R_HY, the lengths of the two bonds formed by H⁺. With the help of eq 26, this relationship can be derived from the form of the valence sum rule given in eq 64.

The locus of the R_XH versus R_HY graph is sometimes described as a reaction coordinate for the notional hydrogen transfer reaction X−H···Y_X···H−Y. Because of the simplicity of this result, many studies restricted their analysis to two-coordinated H⁺ even when more than one weak bond may be present and eq 64 strictly no longer applies.

The reaction coordinate can be displayed in two different ways, either by plotting R_XH against R_HY, or using Steiner plots like the one shown in Figure 20 with the coordinates q1 and q2 defined by eqs 65 and 66.

and

Figure 20.

Example of a Steiner plot. See text for details. Copyright 2003 American Chemical Society. Reproduced with permission from Picazo, O.; Alkorta, I.; Elguero, J. J. Org, Chem.2003, 68, 7485.

The quantity q1, which can be positive or negative, represents the asymmetry of the bond, with the symmetric bond (q1 = 0) being shown in the middle of the diagram. q2 is equal to the sum of the two bond lengths, which for linear bonds, is just R_XY; for bent bonds q2 > R_XY.

Most studies plot the measured, or quantum-mechanically calculated, reaction coordinates of the H⁺ ion together with the locus of reaction coordinates derived from the valence sum rule, eq 64. However, the position of this locus depends on the bond-valence - bond-length correlation used. The points in Figure 19 plot the experimentally derived H−O bond-valence - bond-length correlation reported in accurate neutron diffraction studies. The heavy line is a graphical (nonanalytic) fit to these points. The light line shows an estimate of the true correlation that would be expected if the X···Y repulsion were not present. These lines clearly show that neither eq 25 nor eq 26 is able to give a correct description of the relationship over the whole valence range from 0 to 1.0 vu. Over the range of the donor O−H bonds b is equal to 0.28 Å, while over the range of the acceptor H···O bond b is equal to 0.59 Å. Between these extremes, in the region where the O···O repulsion dominates, b is equal to 0.94 Å.(36)

Most workers in the field choose to ignore, or are unaware of, the strained nature of the symmetric hydrogen bond and assume that eq 26 with a single set of parameters can be used to cover the whole range of X−H and H···Y distances. A customary approach is to choose bond valence parameters that fit the spectroscopic single bond length for a valence of 1.0 and half the X···X distance of a symmetric hydrogen bond for a valence of 0.5. Except as noted, these bond valence parameters, together with the valence sum rule of eq 64, generate a line that more or less correctly describes the bond lengths in the ranges where most hydrogen bonds are observed but it fails to reveal the subtleties associated with the strain in the symmetric hydrogen bond which can be seen in Figure 19. Various bond valence parameters proposed for hydrogen bonds during the review period are listed in Table 6. It is interesting to note the wide range of values assigned to these parameters by different people, reflecting the inability of an equation as simple as eq 26 to provide an adequate description of the correlation.

Olovsson(24) compared the reaction coordinate calculated using the bond valence model with the quantum mechanical energy fields for idealized X−H···X hydrogen bonds (X = F⁻, Cl⁻, N³⁻ and O²⁻). In each case he found the two methods of calculation, bond valence and quantum mechanics, gave identical reaction coordinates within the limitations of the study. However, the bond valence reaction coordinate gives only the relation between the lengths of the X−H and H···X bonds with no indication of the location of the energy minimum. In a follow up paper, Majerz and Olovsson(25) explore N−H···N hydrogen bonds in more detail, comparing the predictions of the quantum mechanical and bond valence models with real structures. From the Cambridge Structural Database(39) they selected a number of examples of molecules or pairs of molecules in which the two N³⁻ ions are chemically equivalent. Unfortunately they were forced to use structures determined by X-ray diffraction which does not accurately locate the H⁺ ions. From quantum mechanical optimizations of the respective molecules they calculate the energy field for various arrangements of the N−H and H···N bonds close to the reaction coordinate and plot the resulting energy field which they compare with the bond valence prediction. They used bond valence parameters, given in Table 6, determined by fitting the bond lengths to the bond valences at 1.0 and 0.5 vu as described above. For intermolecular hydrogen bonds the minimum energy reaction pathway follows closely the locus of points corresponding to the valence sum rule. Typically they find two minima in the energy field arranged symmetrically along the reaction pathway. However, for intramolecular hydrogen bonds the situation is different. Instead of following the bond valence reaction pathway, the energy minima lie on the straight line that is expected when the N···N distance is held fixed by the rest of the molecule. They also found that the energy field is usually not symmetric. In these cases the reaction pathways predicted by the valence sum rule and the quantum mechanical energy field are different, but to the extent that the experimentally measured H⁺ ions were located, they appear to be close to the point where the valence sum rule and the energy reaction pathway intersect. Although this is the position of minimum energy along the valence reaction pathway, it is not necessarily the position of the absolute energy minimum. It appears that the bond valence model supplies some additional restraint that is missing from the energy calculation of these constrained systems.

A similar study has been reported by Grabowski(213) using structures determined by neutron diffraction taken from the Cambridge Structural Database.(39) Neutron diffraction gives more accurate positions for the hydrogen and deuterium atoms than X-ray diffraction. Like Olovsson, Grabowski chose the bond valence parameters for O−H bonds by fitting to the distances corresponding to bond valences of 1.0 and 0.5, but he later revised them after noting that the weaker observed hydrogen bonds deviated significantly from the bond valence reaction coordinate. He also used density functional theory to calculate the geometries of hydrogen bonds between water and several organic molecules, mostly carboxylates, and found that deuterium lay on the same reaction path as hydrogen but formed a weaker (i.e., a more asymmetric) bond.

Grabowski and Pogorzelska(214) were curious to know why a small number of the hydrogen bonds in the Cambridge Structural Database had unusually short O−H bonds (<0.9 Å). They used ab initio methods on model systems and concluded that the energy of these short bonds is high and therefore they must be stabilized by ‘interatomic forces in the crystal’ which they did not specify. They do not appear to have checked the original reports to see if they offered some explanation for the short distances.

In a later paper Palusiak and Grabowski(215) examined the hydrogen bonding between methoxybenzene and various hydrogen bond donors such as H₂O, NH₂CH₃, HF in a variety of simple hydrocarbons. They chose accurately determined X-ray diffraction structures from the Cambridge Structural Database(39) as there were no neutron diffraction studies available. To compensate for the systematic and random errors, the lengths of the X−H distances were fixed to their presumed correct value, ranging from 0.947 Å for F−H bonds to 1.090 Å for C−H bonds. The observed geometries agreed with density functional theory calculations, and bond valences were calculated for the two methoxybenzene C−O bonds using the theoretically calculated geometries. Bond valence parameters for the C−O bonds were chosen to fit the simulation with no hydrogen bond present on the assumption, which hardly seems justified, that each C−O bond must have a valence of 1.0 vu. However, the two bonds have different lengths so different values of R₀ (1.419 and 1.366 Å, b = 0.37 Å) were used for the two bonds. The valence of the H···O bond accepted by the bridging O²⁻ was calculated by subtracting the sum of the bond valences of the two observed C−O bonds from 2.0, the valence of the O²⁻ ion. The resulting H···O bond valences were found to correlate linearly with the hydrogen bond energy, though the bond valences estimated this way were an order of magnitude smaller than expected for the observed H···O distances.

Alavi and Thompson(22) used Steiner plots to validate density functional theory calculations of a variety of configurations of monomeric and dimeric NH₂OH.HNO₃ and found that the calculated hydrogen bond geometries lay exactly on a modified Steiner plot calculated with b = 0.343 Å, indicating that the bond valence model can be used to describe acid−base bonds in the gas phase.

Determining the bond valence parameters for X−H bonds by fitting the bond lengths observed for valences of 1.0 and 0.5 vu ensures that the experimental point corresponding to a symmetric bond lies on the reaction coordinate that satisfies eq 64 even though such a bond is strained. While the resulting correlation is satisfactory for many purposes, it ignores the small strain that characterizes symmetric hydrogen bonds and so fails to reveal the very interaction that drives the asymmetry. This strain has however been noticed by Limbach and colleagues(216) in a careful and detailed study of the H/D isotope effect in symmetric N−H−N bonds, their aim being to see if the isotope effect could distinguish between a symmetric hydrogen bond in which the H⁺ ion occupies a single potential well at the center of the bond and one in which it dynamically occupies the two symmetrically arranged minima of a double-well potential. They prepared Steiner plots with bond valence parameters (R₀ = 0.992, b = 0.404 Å) chosen to fit the calculated geometries of the N−H···N bond in the hydrogen dicyanide anion. When they plotted the experimental N···N distances, q2, for the hydrogen bispentacarbonylcyanochromium anion they found that q2 for the symmetric bonds was around 0.03 Å longer than expected. As this discrepancy was comparable to the measured isotope effect, it could not be ignored. The authors attributed this strain to anharmonic zero point vibrations of H⁺ and D⁺ which could well be a natural consequence of the repulsion between the two N³⁻ ions. They applied a four-parameter empirical corrections to the calculated valences to flatten the Steiner curve at the symmetric bond. They describe the Ubbelohde isotope effect in which D⁺ is displaced by more than the corresponding H⁺ ion as noted also above by Grabowski. By a suitable choice of parameters for their correction function, they were able to model both the increase in R_NN resulting from the increased displacement of D⁺ relative to H⁺, as well as the decrease in R_NN when D⁺ replaces H⁺ at the center of the bond (the inverse Ubbelohde effect). It follows that if H⁺ statistically occupies both minima of a double-well potential, substituting D⁺ will increase R_NN, but if it is in a single well at the center of the bond, substituting D⁺ will decrease R_NN. Similar bond valence corrections for N−H···O bonds, reported in a second paper by Limbach et al.,(217) showed a larger maximum strain of around 0.1 Å at zero q1 (for H−N, R₀ = 0.992, b = 0.385 Å, for H−O, R₀ = 0.942, b = 0.371 Å). This paper also discussed the application of these results to nuclear magnetic resonance. In subsequent papers, Limbach and colleagues^218−220 have used their modified valence sum rule to interpret nuclear magnetic resonance chemical shifts and coupling constants using the expression in eq 67 in which A, B and C are empirical constants.

Xue and colleagues⁶³⁻⁶⁵ required bond valences for the hydrogen bonds occurring in the borate structures that they were studying. Like others, they fixed b at 0.37 Å but they noted that it was necessary to use two different values of R₀: R_0s to be used for the donor O−H bond (s > 0.5 vu) and R_0w to be used for the acceptor H···O bond (s < 0.5 vu). As this introduces a second R₀ variable, eq 27 must be supplemented by an additional condition in order to uniquely determine both R_0s and R_0w. They explored two ways of introducing this condition. The first was to note that, for a linear hydrogen bond at equilibrium, the O−H and H···O bonds must exert equal and opposite forces on the H⁺ ion. They assumed that these forces could be approximated by a Coulomb expression in which each of the anions was assigned an effective charge equal to its atomic valence reduced by the valence of the bond in question. This, combined with the valence sum rule at H⁺, provided the right number of conditions to solve for both R_0s and R_0w. The alternative approach, appears to involve dividing the O−H and H···O distances into radii whose ratio is equal to the golden mean, 1.618, and to use these to determine R_0s and R_0w though the details of this process are difficult to follow and the justification for assuming that the golden mean was relevant is not convincing. They determined values for R_0s and R_0w for each hydrogen bond found in borate structures in the Inorganic Crystal Structure Database.(40) They noticed that there is a linear correlation between the O−H (and H···O) bond lengths, R_OH (R_HO), and the individual values they determine for R_0s (and R_0w), and based on the Coulomb force calculation, they(63) proposed the bond valence parameters given in eqs 68 and 69.

and

Xue and colleagues point out that these parameters should be used only with structures determined by X-ray diffraction unless an appropriate correction is made, since the structures in the sample set were all determined in this way. They(64) compare the bond valences calculated using eqs 66 and 67 with similar equations derived from their golden mean model, as well as with others reported in the literature. Because X-ray diffraction gives shorter O−H bonds than neutron diffraction, eqs 68 and 69 give smaller valences for the donor bonds than other parameter sets, but they also give significantly larger valences for the weak bonds. Their use of recursive relations such as eqs 66 and 67 seem somewhat counterproductive, particularly when the dependence of R₀ on R can probably be eliminated by a better choice of b, a possibility that the authors apparently did not consider. The idea of using more than one set of valence parameters to describe the full range of O−H bond valences from 0 to 1.0 vu is not new, and the valences calculated using eqs 68 and 69 most nearly match those calculated using the three-parameter sets of Brown.(1) The physical basis for the derivation of R_0s and R_0w shows perhaps more imagination than sound science and the recursive eqs 68 and 69 seem counterproductive, but the results may well be serviceable though not simple to apply.

Adams et al.(124) take a different approach to hydrogen bonding. Their interest is to track possible hydrogen atom locations in hydrogen ion conductors for which they find it necessary to use bond valence parameters based on cutoff distances as high as 6 Å. They first chose b using eq 32 relating b to the relative softnesses of the two ions as proposed by Adams.(79) They then fitted R₀ against 244 well-determined and ordered neutron-diffraction structures from the Inorganic Crystal Structure Database.(40) They present their results in plots of O−H bond lengths and O−H bond valences against O−O distances. Since all the H−O distances out to 4 Å were calculated, the sample included the distances from the OH group to other O²⁻ ions in the same XO_nOH complex. These involve O−H···O angles less than 90° and O···O distances as small as 2.4 Å. In other studies such distances are usually excluded as not constituting a bond, but the interaction is arguably important in the context of this study. Adams and his colleagues also plot the frequencies of the O−H stretching vibrations against O···O distances and against ΔS. the difference between S_OH and S_HO. The latter shows a linear relationship (with some scatter) for ΔS < 0.7 vu (strained and normal hydrogen bonds). For ΔS > 0.7 vu (weak hydrogen bonds) the O−H frequency is constant. This is consistent with the observation that for weak hydrogen bonds, the donor O−H bond valence is constant because there are usually several acceptor H···O bonds whose valences taken together sum to around 0.15 vu leaving a constant 0.85 vu for the O−H bond whose frequency is being measured.

22. Perovskites

22.1. Introduction

The many compounds having the formula ABX₃ that crystallize in structures derived from the simple cubic perovskite structure are popular subjects of study, as much for the rich palette of electrical and magnetic properties they display as for the light they shed on the structural chemistry of solids. Because of the simplicity and high symmetry of the cubic arisotype structure, these compounds prove to be an ideal workbench for exploring steric constraints and the influence of magnetism and electronic anisotropies. The bond valence model has been used in many different ways to model and analyze the complex interactions found in this simple structure type.

The aristotype of the perovskite family is the simplest of all ternary structures having the formula ABX₃. It consists of a cubic cell of length 4 Å (see Figure 21) with B cations at the cell corners octahedrally surrounded by X anions at the midpoints of the cell edges. The X anions link adjacent BX₆ octahedra into a three-dimensional network. The A cation is in the center of the cell and it bonds to twelve X anions.

The interesting structural chemistry of perovskite arises because the cubic structure has only one free parameter, the length of the unit cell, which cannot in general be chosen in a way that allows both the A−X and the B−X bonds to adopt their ideal lengths, R_AX and R_BX, unless their ratio is exactly equal to √2. This ratio is expressed by the tolerance factor, t:

Only when t is equal to 1.0 is it possible for the A-X and B-X bonds to adopt their ideal lengths in the cubic aristotype structure. For all other values of t, one of the cations will occupy a cavity that is too small (the bonds will be shorter than expected) and the other will occupy a cavity that is too large (the bonds will be longer than expected). Some degree of compression or stretching of the environments of these atoms is possible, but if the tolerance factor lies outside this limit, the distortion theorem (eq 42) predicts that the environment of the cation in the oversized cavity will distort. Thus if t is greater than 1.0 the B cation is in the oversized cavity and will tend to move off-center within its octahedron, which is why B in these cases is usually a d⁰ or d¹ cation such as Ti⁴⁺ with an inherent tendency to favor a noncentrosymmetric environment as discussed in section 8.2.3. If t is less than 1.0 it is the A cation that is in the oversized cavity and the distortion in this case is achieved by a rotation of the octahedra in the BX₃ framework, shortening some A−X bonds and lengthening others, in effect twisting the framework in order to reduce the effective coordination number of A.

There are a large number of ABX₃ compounds that adopt the perovskite structure or one of its derivatives. X is usually O²⁻ or F⁻, but other anions are possible. When X = O²⁻, the A and B cations can have valences of +1 and +5, +2 and +4, or +3 and +3 respectively. When X = F⁻ the A and B cations must have the valences +1 and +2. The perovskites are often grouped according to the valences of their cations, since the members of each group tend to have similar properties. For convenience the groups are referred to by the symbols 1:5, 2:4, 3:3 and 1:2 respectively. The cation B must be one that can adopt six-coordination and A is a cation that normally adopts a larger coordination number, generally between eight and twelve, depending on the nature of the twists in the BX₃ framework. This allows a large number of cations to appear on either the A or the B site. Perovskite-type compounds are known with two or more different A atoms and two or more different B atoms (AA′BB′X₆), and many important perovskite-related compounds are composed of alternating perovskite and rock-salt layers. Other combinations of atomic valence and coordination number can be accommodated by incorporating anion or cation vacancies. Bond valences are particularly suited to the analysis of these systems since the theoretical bond valences are simple to calculate and can be used to separate the effects of chemical, steric and anisotropic electronic influences on their structure and properties.

22.2. Systematic Studies

A systematic bond valence study of perovskites was undertaken by Zhang et al.(221) They downloaded 376 entries of ABO₃ compounds from the Inorganic Crystal Structure Database,(40) of which 232 (62%) crystallized in one of the perovskite structures. The structures adopted by the remaining 144 compounds were not stated, but a survey of the Supporting Information deposited with their paper shows that most contained B cations that are not found in octahedral coordination. For each of the 376 compounds included in their database they used bond valences to determine the ideal bond lengths the structures would have if the compound crystallized in the simple cubic perovskite structure. These were used to calculate the tolerance factor, t (eq 70), and the global instability index, G, (eq 44). The values of t in this sample ranged from 0.82 to 1.14 and the values of G ranged between 0 and 1.2 vu, much larger than the 0.2 vu upper limit expected for a stable structure. One of the strengths of the bond valence model is that it can be used to examine the properties of compounds that do not, or even cannot, exist. It is not surprising to find that G covers such a wide range given that fewer than two out of three of the compounds crystallize with a perovskite-related structure and only a small fraction of these crystallize in the cubic aristotype. The purpose of this study was to discover the stability fields for different perovskite groups in terms of the A-O and B-O distances, but the numbers the authors report reveal some interesting facts about the series. Almost all of the compounds that adopt a perovskite structure have t less than 1.06 and almost all of the nonperovskite compounds have t greater than 1.06. An examination of the Supporting Information shows that the perovskites with t greater than 1.0 usually have B cations with anisotropic electronic structures (lone electron pairs or d⁰ distortions) that stabilize the expected steric distortions. Figure 22 shows a plot of G versus t in which the 1:5, 2:4 and 3:3 compounds lie on different curves. Assuming that the cubic aristotype structure will only be found if G is less than 0.20 vu (section 8.3), Figure 22 shows that 1:5 compounds will adopt the cubic perovskite structure for t lying between 0.93 and 1.05. For 2:4 compounds this range narrows to 0.97 to 1.02 while for 3:3 compounds the cubic structure will only be found for t between 0.98 and 1.01, though few 3:3 compounds have t as large as this.

Figure 22.

Global instability index, G, plotted against the tolerance factor, t, for all known ABO₃ compounds assuming that each adopts the cubic perovskite structure. The 3:3 compounds lie on the solid line, the 2:4 compounds lie on the dash line and the 1:5 compounds lie on the dotted line. The horizontal line at G = 0.2 vu represents the upper stability limit of the cubic strncture. Adapted from ref (221). Copyright 2007 International Union of Crystallography. Reproduced with permission.

The majority of the perovskites have t less than 1.0 and much effort has been applied to analyzing the different modes of twisting that the octahedral framework adopts in order to provide a distorted environment for the A cation. Since each octahedron has three independent axes around which it can twist, and in some cases adjacent octahedra can twist in the same or in opposite directions, there are as many as fifteen possible modes of distortion, first enumerated by Glazer(222) in 1972. These are the basis of the popular program SPuDS written by Lufaso and Woodward.^112−114 Starting with the composition and a knowledge of only the bond valence parameters of the A-X and B-X bonds, this program calculates the global instability index, G, for the ten most commonly observed twist modes. Each of these twist structures is optimized by changing the twist angle to minimize G, and using the zero valence vector rule (eq 44) to position those A ions whose location is not defined by symmetry. SPuDS is able to predict the structure in most cases with remarkable accuracy, giving lattice parameters and bond lengths within one or two percent of the observed values. SPuDS is widely used to identify the cations that will form a material with a desired set of properties. It also provides a good starting model for further refinement against X-ray and neutron diffraction patterns.

22.3. Single Perovskites

One of the more studied series of perovskite compounds is Pb(Zr,Ti)O₃ which contains varying proportions of Zr⁴⁺ and Ti⁴⁺ on the B site. PZT, as it is generally known, is of technological importance as a relaxor ferroelectric, a character that is driven in part by the natural tendencies of the all three of its cations to undergo electronic distortions as Pb²⁺ has a lone electron pair and Ti⁴⁺ and Zr⁴⁺ have d⁰ configurations (section 8.2). Grinberg and Rappe and their colleagues^89,158,223 modeled this system using density functional theory with clusters of 6 to 8 cells having various distributions of Zr⁴⁺ and Ti⁴⁺ cations. They observed that all the structures they predict obey the valence sum rule (eq 9), giving confidence in the validity of the results obtained from both density functional theory and the bond valence model. They then used molecular dynamics to look at phase boundary migration and the order−disorder (ferroelectric-paraelectric) transition.^20,161,224 This approach is based on the two-body potential model, for which they constructed an energy function that mimics the energy from density functional theory. In addition to the usual two-body potential terms (Coulomb potential and a short-range repulsive potential), their energy function contains an angular constraint and the bond valence sum rule. It has a large number of fitted parameters, but it leads to good agreement with many experimental measurements. They found that the bond valence sum constraint was essential to a good simulation, even though this term duplicates the functions of the Coulomb and short-range repulsion terms. The reason why the model only worked when the valence sum rule was included is somewhat subtle. The tolerance factor for PbTiO₃ is close to 1.00, meaning that a cubic crystal would normally be expected. However, because of the electronic distortions expected around both Pb²⁺ and Ti⁴⁺, the distortion theorem (eq 35) leads to the prediction that the coordination spheres of both cations will be larger than they would be if the crystal adopted the undistorted cubic structure. If the structure is modeled using the predicted cubic lattice constants then the modeled structure would show no distortion, but if it is performed using the larger observed lattice constants, the bond valence sum at the central point of each coordination sphere will be smaller than the atomic valence. To achieve their correct valence sum the cations must be displaced from the center of their coordination sphere. Requiring the correct valence sums around the anions ensures that these displacements are correctly correlated.

The system PbTiO₃−PbZrO₃ shows two principal phases: in the Ti⁴⁺ rich region the crystal adopts a tetragonal structure in space group P4mm with Pb²⁺ displaced along the 4-fold axis, that is, the cubic [001] direction, but in the Zr⁴⁺ rich region it adopts the rhombohedral space group R3m with Pb²⁺ displaced along the 3-fold axis, that is, along the cubic [111] direction. Glazer et al.(225) point out that as neither space group is a subgroup of the other, the transition between these two phases should be first order, which appears not to be the case. They found in reviewing previous work on this transition that there was an intermediate monoclinic phase whose space group, Pm, is a subgroup of both the tetragonal and the rhombohedral phases. They propose that in the rhombohedral phase, in addition to the long-range order of the displacement of the Pb²⁺ ion along [111], there is also a displacement of Pb²⁺ ions perpendicular to [111] that shows only short-range order. As the transition to the tetragonal phase is approached, this short-range order becomes long-range and changes the space group to Pm. Moving into the tetragonal phase, the order again becomes short-range until the displacement settles in the [001] direction. As evidence for this they point out that Pb²⁺ in the rhombohedral phase has an atomic displacement ellipsoid in the shape of a disk flattened perpendicular to [111] as well as the low bond valence sum of 1.82 vu. According to the distortion theorem (eq 44) a low valence sum suggests that the average structure displays less distortion than is found locally, that is, the distortion around Pb²⁺, which would lead to the correct valence sum, is partially disordered and is averaged out in the observed crystal structure.

Page et al.(226) investigated the ordering of N³⁻ in the BaTaO₂N perovskite. Bragg reflections showed that the crystal is cubic, but bond valence arguments suggest that a cis arrangement of the N³⁻ ions is favored as this places the strong Ta−N bonds to one side of the Ta⁵⁺ coordination sphere, which is more compatible with the expected electronic distortion. This arrangement leads to a simpler structure that agrees with the neutron diffraction pair distribution and density functional theory.

Yoon and colleagues^227,228 measured the dielectric properties of (Pb_1-xCa_x)(Mg_0.33Ta_0.67)O₃ and (Al_0.5Ta_0.5)_1-x(Mg_0.33Ta_0.67)_xO₄ as a function of x. They noticed that as the Ca²⁺ content of the former compound increases, the polarization of the atom on the A site decreases but not as quickly as the simple mixing would suggest. Over this range the compound, which has a tolerance factor of 0.94, adopts the cubic aristotype structure and the Ca²⁺ bond valence sum decreases from 1.57 to 1.48 vu. They took this to indicate that the more underbonded the Ca²⁺ ion is, the more room it has for movement, hence the decrease in polarization was not as large as expected. Somewhat similar results were found for the Al³⁺ compound. This group^229,230 makes similar routine use of bond valence sums in their work on dielectric materials.

The work of Angel and collaborators on the effect of pressure on single perovskites is reported in section 20, and that of Alonso et al.(115) on LaCoO₃ is reported in section 8.3.

22.4. Double Perovskites

The double perovskites, AA′BB′O₆, in general have two different A cations and two different B cations, though in some cases all the A cations (or all the B cations) are the same. If the two A cations have similar charges and sizes they are likely to be randomly distributed over the A and A′ sites, and the same holds for the B cations. However, if their chemical properties are sufficiently different, the cations tend to order. The normal ordering of the B cations takes the form of a rock-salt pattern with each O²⁻ ion bonded to one B and one B′ cation, an arrangement that gives good valence sums around the O²⁻ anions without the need to distort the environment of either B or B′. For intermediate cases. the ordering may be partial, giving rise to places where antiphase boundaries appear.

(Na,K)BiTi₂O₆ is a relaxor ferroelectric, favored because it contains no toxic lead. Shuveava et al.(231) examined this system and found using EXAFS that the lone electron pair distortion around Bi³⁺ (section 8.2) is much larger than the distortion reported in the neutron diffraction study. In the neutron study the valence sum is only 2.38 vu, compared to 2.90 or 3.13 vu for the EXAFS study. This suggests that the distortion is disordered. Locally Bi³⁺ shows its full distortion with a valence sum close to the expected value of 3,0, but the direction of this distortion varies from one Bi³⁺ ion to another, so that when averaged over the whole crystal the distortion appears to be small or even absent. As the averaging tends to move the cation closer to the center of its coordination sphere, its valence sum will necessarily be too small. Thus a low valence sum may be a useful indication of disorder.

Knapp and Woodward(232) used bond valences to analyze the interactions between the cations in Na⁺La³⁺BB′O₆, where B and B′ are two cations on the B site having an average atomic valence of 4+. The two A site cations, Na⁺ and La³⁺ are sometimes ordered into Na⁺ and La³⁺ layers. Given the very large difference in atomic valences, the rock salt ordering, which keeps the La³⁺ cations well separated, would appear to be more favorable. Knapp and Woodward therefore constructed the bond graph for the layer structure to see if this would provide any insight as to why a layered ordering was preferred. This graph contains three different kinds of O²⁻ anions, All six oxygen anions of the formula unit form one bond each to B and B′. Four form two bonds each to Na⁺ and La³⁺, but of the remaining two, the O²⁻ ion that points into the Na⁺ layer forms four bonds to Na⁺, and the other forms four bonds to La³⁺. The former is therefore underbonded since the Na−O bonds are expected to have a valence of only 0.08 vu, and the latter is overbonded since the La−O bonds are expected to have a valence of 0.25 vu. The overbonding and underbonding can only be relieved if either B or B′ is able to distort by moving away from the La³⁺ layer toward the Na⁺. Knapp and Woodward examined several BB′ pairs such as Mg²⁺W⁶⁺, Mg²⁺Te⁶⁺ and Sc³⁺Nb⁵⁺ as well as cases where B and B′ were both Zr⁴⁺ or Ti⁴⁺. The compounds containing W⁶⁺ and Nb⁵⁺, that is, d⁰ elements with a strong electronic tendency to be displaced from the center of their coordination sphere, showed a significant tendency for the A cations to order in layers, compared to Te⁶⁺ which shows no such tendency. This synergy allows the d⁰ element distortion to stabilize the layer ordering of the A cations and vice versa.

Nakade et al.(122) reported the structures and other properties of a number of perovskites in the Ca(Mn,Ti)O₃ series. They showed that the global instability index, G, (eq 43) increases from 0.02 to 0.10 vu as the manganese content is increased from zero to 70%. Like many other perovskites, this series of compounds shows some reduction in oxygen content from 3.0 to 2.9 as the exchangeable Mn content increases, indicating the presence of Mn³⁺.

Zhang et al.(233) explored the substitution of V³⁺ for Fe³⁺ in the partially ordered double perovskite Sr₂FeMoO₆. The use of X-ray and neutron powder diffraction provided two constraints on the relative occupation numbers of the three cations Fe³⁺, Mo⁵⁺ and V³⁺ over the B and B′ sites, but this is insufficient to uniquely determine their values. The authors therefore carefully examined the valence sums for each of the three cations when placed on each of the two sites for V³⁺ substitutions ranging from 3 to 10%. From these, and considerations of possible electronic anisotropies, they deduce that V³⁺ preferentially occupies the B′ site, displacing Mo⁵⁺ to the B site. For all compositions studied the global instability index, G, was close to 0.12 vu.

The compound Sr₂MgMoO₆ has two B ions that differ markedly in both size and valence. Bernuy-Lopez et al.(234) showed that Mg²⁺ and Mo⁶⁺ adopt the rock-salt ordering as expected. The valence sum around Sr²⁺ is close to 2.00 vu but that around Mg²⁺ is high (2.46 vu) and that around Mo⁶⁺ is low (5.53 vu). Surprisingly this compound does not adopt either the R3̅ or P2₁/n structure predicted by SPuDS (G = 0.00009 and 0.00030 vu respectively) but a structure in the space group P4/mmc with a predicted G of 0.021 vu. The authors attribute this to the electronic distortion around the d⁰ cation Mo⁶⁺, although the distortion they report is small. The solution to this problem may be found in the observation, discussed above for Bi³⁺, that the local environment of Mo⁶⁺ could be significantly different from that reported for the average crystal structure as a result of disorder, twinning or dynamic distortion.

Ting et al.(235) used a bond valence analysis to deduce that Ba₂InNbO₆ should have Fm3̅m symmetry but that the Sr²⁺ and Ca²⁺ analogs would crystallize in the more distorted P2₁/n space group. Later they(236) report a similar analysis on the triple perovskite A₃CoNb₂O₉.

The work of Di Paoli et al.(120) on A₅B₄O₁₅ with A = Ba²⁺, Ln³⁺; B = Nb⁵⁺, Ti⁴⁺ is described in section 8.3.

22.5. Triple Perovskites

The triple perovskites may contain up to four different cations and these may or may not be ordered. A typical example, CaCu₃Ti₄O₁₂, adopts a structure in space group Im3̅ with a unit cell 2 × 2 × 2 times the size of the simple perovskite cell. The two A cations are found at the corners and center of the cubic unit cell and six A′ cations on the face and edge centers. Figure 21 shows a 2 × 2 × 2 perovskite cell.

Božin et al.(237) made diffraction measurements on the same compound at a range of temperatures from 30 to 290 K to find the source of its unusually large dielectric constant. They noted that while the Ca−O distance increased with temperature, the Cu−O and Ti−O distances were nearly constant. They therefore decided to model the structure using SPuDS, assuming that the Cu−O and Ti−O bonds, being relatively strong, did not change with temperature, but that the weaker Ca−O bonds, which show significant thermal expansion, needs to be modeled with temperature-dependent bond valence parameters. They also assumed that the square planar coordination around Cu²⁺ would hold the twist angle constant. At the lowest temperatures Cu²⁺ is slightly overbonded (compressed) while Ca²⁺ is underbonded. Increasing the effective temperature by increasing the bond valence parameter, R₀, of the Ca−O bond, increased its ideal length so that the degree of underbonding diminished. At 260 K SPuDS predicted that the Cu²⁺ and Ca²⁺ bond valence sums would both be equal to 2.00 vu and the fit between the A and A′ sites would be exact (G = 0.0 vu). They conclude that the large dielectric constant below 260 K is caused by the ease with which the Ca²⁺ ion can be moved by an external field within its oversized cavity.

CaCu₃Ga₂Ru₂O₉ adopts the same structure as CaCu₃Ti₄O₉ with Ga³⁺ and Ru⁵⁺ disordered over the B sites. Byeon et al.(238) point out that while the bond valence sum at Cu²⁺ is close to 2.0 vu in CaCu₃Ti₄O₉ and in Ga³⁺ compounds in which the Ru⁵⁺ is substituted by Sb⁵⁺, Nb⁵⁺ and Ta⁵⁺, in the GaRu compound itself the bond valence sum of Cu is 2.31 vu. They argue that this represents a change in the oxidation state of Cu from 2+ to 2.31+ and implies a reduction in the oxidation state of Ru from 5+ to 4.53+. Because of the disorder between Ga and Ru on the B site, one cannot get a direct measure of the valence sum around Ru but it can be estimated at 4.43 vu, which is close to the expected value.

In another study, Lufaso(113) explored the distortions found in the structures of Ba₃BB′₂O₉ perovskites with B = Mg²⁺, Zn²⁺ and Ni²⁺, and B′ = Nb⁵⁺ and Ta⁵⁺. He related these distortions to the dielectric constants. Since these perovskites all have a tolerance factor, t > 1, the twisting deformations are not expected, but with B and B′ underbonded, that is, occupying a cavity that is too large, out-of-center distortions of B or B′ can be expected. Further, Nb⁵⁺ and Ta⁵⁺ are d⁰ cations for which such distortions are favored (section 8.2.3). Lufaso modified the program SPuDS (section 22.2) by allowing for nonrigid octahedra, so that he could predict ideal structures with distorted octahedral bonding in the observed space group (P3m1) of A₃BB′₂O₉ structures. The resulting ideal structure was then used as a starting point in the refinement of the five structures whose X-ray and neutron powder diffraction patterns Lufaso had measured. Two significantly different determinations of the structure of the remaining compound, Ba₃ZnTa₂O₉, were already in the literature. Because the two O²⁻ ions are topologically distinct, SPuDS predicts that three B′-O bonds will be short and three will be long, producing the out-of-center distortion that would be expected for a d⁰ cation. Thus, as is frequently found, the topological and electronic distortions are mutually supportive. In spite of this, the experimental values of G are relatively high, ranging from 0.16 vu (for ZnTa) to 0.24 vu (for NiNb), suggesting that some of these compounds are close to their limit of stability. Lufaso also explored various dielectric properties of these compounds and showed that there is a good correlation between the bond valence sum at the B²⁺ site and the temperature coefficient of the resonant frequency. This can be understood from the observation that the B²⁺−O bonds expand more with temperature than the B′⁵⁺−O bonds and, since they are underbonded and more easily displaced within their cavity, they will contribute more strongly to the polarizability.

22.6. Layered Perovskites

Usually included in discussions of perovskites are compounds composed of layers of perovskite structure alternating with rock-salt layers. The layered structure results in these compounds typically having tetragonal or lower symmetry based on an aristotype in either space group P4/mmm or I4/mmm.

The simplest of the layered perovskites is La₂CuO₄ in which one LaO rock-salt layer alternates with one LaCuO₃ perovskite layer. This structure is adopted by CaSmCoO₄ and CaGdCoO₄ which were studied by Taguchi et al.(122) who calculated their global instability indices to be 0.07 and 0.06 vu respectively.

The compound SrBa₂Ta₂O₉ is a technologically important ferroelectric used in the construction of nonvolatile computer memories. It consists of defect perovskite SrTa₂O₆ layers alternating with defect rock-salt Ba₂O₃ layers. The application of bond valences to the study of this compound is described in section 8.3.

The most famous of the layered perovskites are the copper oxide superconductors which continue to be the subject of study. The effects of pressure on the original copper superconductor, YBa₂Cu₃O₇, were modeled by Mohammadizadeh and Akhavan.(211) They note that it is necessary to allow the bond valence parameters to vary when examining structures under pressure, which means renormalizing the parameters to ensure that the valence sums (on average) are equal to the atomic valences. Normally this would be done by allowing R₀ to decrease, but Mohammadizadeh and Akhavan chose instead to keep R₀ constant and reduce b, arguing that since these two parameters are empirically fitted they are without physical significance. Further, while R₀ has to be redetermined for each bond type separately, it should be possible to use the same value of b for all bond types at a given pressure. This argument is fallacious because although these parameters may have no physical significance, they do have a mathematical significance, and the effect of pressure is to decrease b for bonds with valences less than 1.0 vu, but to increase b for bonds with larger valence. Mohammadizadeh and Akhavan tested this method against published measurements of the structure up to pressures of 0.7 GPa and then applied it to structures modeled by ab initio methods using the observed lattice parameters at 5 and 10 GPa. The bond valence parameter b was found to change from 0.37 Å at zero pressure to 0.325 Å at 10 GPa.. As the valence sums at 10 GPa did not apparently add up to zero (which should be mathematically impossible), Mohammadizadeh and Akhavan assumed that the coordinates of one of the oxygen ions was in error. After adjustment a consistent picture appeared with the valence of Cu1 dropping from 2.26 to 2.22 vu in going from 0 to 10 GPa, while that of Cu2 increased from 2.18 to 2.22 vu. The mechanism of charge transfer is the movement of the apical O²⁻ ion, and this motion accounts for the anomalous behavior of dT_c/dP. However, the changes in the structure are less than the standard uncertainty in the experimental work, and the authors’ arbitrary adjustment of a nonconforming parameter throws considerable doubt on the significance of the results.

Wu et al.(239) calculated bond covalency in four members of the series HgBa₂Ca_n-1Cu_nO_2n+2-ó using a method based on dielectric properties and bond valences. They point out that not only is the maximum superconducting temperature, T_c, found for the n = 3 member of this series, but the n = 3 member also tends to have bond covalencies and bond valences that are either a maximum or a minimum within the series. They do not explain the significance of these observations except to speculate that the Cu−O and Hg−O bond covalencies might be ‘important in governing the superconducting temperature’.

23. Minerals

In a recent issue of Zeitshcrift fur Kristallographie devoted to a discussion of mineralogy, Hawthorne and Schindler(149) review their recent in-depth studies of weak bonding in oxy-salt minerals. They point out that, unlike laboratory-prepared samples in which the starting materials are carefully measured out in stoichiometric quantities, natural minerals crystallize from a solution that contains a large number of chemical species. These combine to form a variety of different complexes in the solution, some of which will condense together to form a mineral crystal when the conditions are right. Under the wide range of conditions found in the earth’s crust many different kinds of minerals will be formed. It is not surprising that this can produce structures that might not be easily prepared under laboratory conditions. Because of the complexity of the growth conditions and the complexity of the resulting structures, it is difficult if not impossible to predict which structures will be formed, but that does not prevent us from analyzing the known complex mineral in order to understand why they might have formed.

At the beginning of the review period Schindler et al.(240) reported a study of vanadium minerals, and subsequently Schindler and Hawthorne(147) published a detailed approach to the analysis of complex minerals which is described in more detail in section 11. In this approach they divide each mineral structure into a strongly bonded structural unit, usually anionic, and a more weakly bonded interstitial complex, composed of low-valence cations and water molecules, which provides the cationic component. They then use the valence matching principle (eq 16) to determine what combination of cations and water molecules are best matched to the bonding requirements of the structural unit. Together with various colleagues they illustrate this approach with a comprehensive examination of hydrated borate,^241,242 uranyl^148,243 and sulfate minerals,(244) showing that they can separate out the mineral compositions that are allowed from those that are unlikely to be found. As described in section 25 they show how their approach using the bond valence model can be used to study the surfaces, the morphologies and the growth and dissolution of minerals.

Uvarova et al.(245) determined the structure of a new mineral, nickelalumite NaAl₄(SO₄)(H₂O)₁₅, from Kyrgyzstan. Using the Schindler and Hawthorne approach described in section 11 they determined that the structural unit is a cation with a bonding strength of 0.167 vu which is compatible with an anionic interstitial component that contains SO₄²⁻, NO₃⁻, or VO₃⁻ but is not compatible with a component that contains SiO₄⁴⁻, BO₃³⁻, PO₄³⁻, or BO₄⁵⁻.

Because minerals are formed from a soup of different ions, it is quite common for cation sites in a structure to be occupied by more than one type of cation, frequently by several. One of the tasks confronted by mineralogists is to decide whether or not cations occupying a group of such sites are arranged in an ordered manner. Two types of order have been recognized; long-range and short-range order. If a site is occupied by two cations that differ significantly in valence or size, they are more likely to show long-range order. Two such cations alternating between adjacent sites will result in local charge neutrality and there will be no local build up of excess positive or negative charge (valence). The alternation may remain coherent over a long distance, making it visible in the X-ray diffraction pattern as a superstructure, representing a cell two or more times larger than the subcell that would be expected if the site was randomly occupied.

However, if the two cations have similar valences and are similar in size, the driving force for long-range order will be weak. In this case the diffraction experiments will reveal only the subcell and the average occupancy of each cation site. In the absence of diffraction evidence for long-range order, it is customary to assume that the cations are distributed over the sites in a random manner, but in minerals in which several such cation sites are found clustered close to each other, some arrangements of cations will result in a local concentration of positive or negative valence and will therefore be less likely to occur than arrangements that satisfy the local charge neutrality rule (eq 5). The result is the creation of short-range order preferred local arrangements of cations that may be different in different unit cells. To help unravel the short-range order which is not revealed by diffraction experiments, Hawthorne et al.(246) invoked the principle of local charge neutrality in the form of the short-range order rule, eq 71.

They applied this idea to the study of short-range order in amphiboles which have the generic formula AB₂C₅T₈O₂₂W₂. Here A is a vacancy, an alkali metal or (rarely) an alkaline earth, B and C are cations of higher valence capable of occupying the four octahedral M sites, T is a tetrahedral cation such as Si⁴⁺ or Al³⁺ and W is an anion such as O²⁻, OH⁻ or a halogen. They used the shift of the O−H stretching frequency (where present) to give clues to the occupation of the adjacent M1 and M3 sites and then applied the short-range order rule by assuming that the bond valence sums around the O5, O6 and O7 ions will be close to 2.00 vu. Subsequently Hawthorne et al.(247) used these ideas to explore the short-range order in an amphibole from the Bear Lake diggings in Ontario.

Tourmaline is another crystal capable of incorporating many different cations. It has the generic formula XY₃Z₆(T₆O₁₈)(BO₃)₃V₃W where X, Y and Z are cations that occupy octahedral sites, T are cations (Si⁴⁺ or Al³⁺) that occupy a tetrahedral site, B is a boron ion in a trigonal site, and V and W are anions such as O²⁻, OH⁻ or F⁻. The structure is trigonal with X, W and B³⁺ lying on 3-fold axes and with T₆O₁₈ forming a ring of six tetrahedra around this axis. Many short-range order combinations of cations are possible on the X, Y and Z sites, and Hawthorne(248) has used the bond-valence sums to explore which of these are most likely to be stable. Starting with W, which forms three bonds to Y cations, he shows that if W is O²⁻, then the Y-W bonds must have an average valence of 0.67 vu, but if W is F⁻ or OH⁻, then Y-W bonds must have an average valence of only 0.33 vu, or slightly larger in the case of OH⁻. This puts restrictions on which cations can occupy the Y site and this in turn restricts the cations that can occupy the adjacent Z sites. A similar analysis can be carried out around the V anion which forms two bonds to Z and one to Y. Using these ideas, Hawthorne exhaustively examined all the likely combinations of different cations on the different sites, and used the predicted bond lengths to list twenty seven possible stable end-member compounds and eighteen that he considered unstable.

Another example of the use of bond valences to assign short-range order can be found in the work on Nb₃O₅F₅ by Brink and colleagues(108) discussed in section 8.2.3.

Bosi and Lucchesi(249) explored the relationships between the bond lengths, site occupancies, distortions and twist angles of 127 different tourmalines and compared these with the ideal bond lengths calculated from the bond network using the Kirchhoff equations (eq 9 and 13). They confirmed that the observed bond lengths were close to the ideal values, though they covered a smaller range, indicating that the tourmaline structure lacks the flexibility to accommodate the full range of expected distances. The result is that the Y site tends to be underbonded when occupied by cations that form shorter bonds but it satisfies the valence sum rule when occupied by cations that form longer bonds, while the Z site tends to be overbonded when occupied by cations that form longer bonds but it satisfies the valence sum rule when the ideal bonds are short. The B−O bond lengths show little variation and are about 0.003 Å longer than predicted.

Lee et al.(146) applied the short-range order rule to determine the favorable cation distributions in chlorite, a layered silicate, using Pauling bond strengths (eq 1) in place of bond valences. Because the Pauling bond strength is only an approximation to the bond valence, the valence sum rule is only approximately obeyed; sums around O²⁻ can range from 1.6 to 2.4 vu. However, as discussed in section 3, bond topologies in which the sum of the Pauling bond strength are exactly equal to the anion valences are particularly stable since the valence matching rule (eq 16) is exactly obeyed for these topologies. Lee and colleagues summed the Pauling bond strengths around the crystallographically distinct O²⁻ ions in chlorite for various possible distributions of cations over the different octahedral sites, and assumed that the closer the Pauling bond strength sum of a given distribution was to 2.00 vu, the more likely this distribution is to be found.

Garnets have the generic formula A₃B₂T₃O₁₂ with A in an 8-coordinate site, B in an octahedral site and T in a tetrahedral site of a cubic crystal. Rodehorst et al.(250) explored the structures and thermal expansions of compositions along the join of spessartine, Mn₃Al₂Si₃O₁₂, and grossular, where the Mn²⁺ is replaced by Ca²⁺. They note that Ca²⁺ has a lower bonding strength (0.274 vu) than Mn²⁺ (0.34 vu) which suggests that Ca−O bonds should be more ionic than the Mn−O bonds. However, in grossular Ca²⁺ is overbonded which the authors speculate may indicate that the Ca−O bonds here are more covalent, but they eventually conclude, correctly, that the overbonding probably has more to do with Ca²⁺ being in a cavity that is too small.

In a more recent paper examining the bond valence sums around the lanthanide cations in the Li₃Te₂Ln₃O₁₂ garnets, Liebau and Wang(251) note that Li⁺ is overbonded, indicating that the Li−O bonds are in compression, while Te⁶⁺ and Ln³⁺ are both underbonded, indicating that they occupy cavities that are too large. Such steric strains are expected in a high-symmetry structure like garnet. They also note that as the atomic number of Ln³⁺ increases, the Ln³⁺ bond valence sums decrease, while the Li⁺ and Te⁶⁺ sums increase, as would be expected as the size of Ln³⁺ decreases. Finally they observe that the plot of the bond valence sum of Ln³⁺ against its atomic number bears a remarkable similarity to the corresponding plot of the third ionization energy of Ln³⁺ ions, both showing an increase between Eu³⁺ and Gd³⁺. However, the size of this increase in valence is comparable to the estimated standard uncertainty. Not surprisingly, echos of this variation are also seen in the valence sums around Li⁺ and Te⁶⁺. This effect is not observed in a corresponding series of Ln³⁺ chelates in which the Ln³⁺ cation is compressed (overbonded), leading to the suggestion that this ionization-energy effect is only revealed when the Ln³⁺ cation has the space available to display it. Assuming the correlation is real, it is not clear if it is a direct electronic interaction or if it is transmitted through changes in the size or shape of the cation.

Lavina et al.(252) have examined the substitution of V³⁺ for Cr³⁺ in the normal spinel MgCr₂O₄ finding that substitution increased not only the size of the octahedral site as expected, but also the tetrahedral site. They measured the size of this effect using the global instability index, G (eq 44), which increased from 0.08 vu for MgCr₂O₄ to 0.16 vu for MgV₂O₄, a somewhat larger increase than expected.

24. Glasses

Glasses and amorphous materials differ from crystals in having no long-range order. The structure of a crystal is characterized by the contents of a single unit cell that represents the contents of each unit cell in the crystal averaged over time and space. Such a structure conforms to the macroscopic crystal symmetry given by the space group, even though it is well understood that locally at any given instant the atoms will be displaced from their average position by thermal motion, defects or disorder. An instantaneous snapshot of the atoms in a crystal does not, therefore, show the full macroscopic symmetry of the crystal and the loss of this symmetry makes it difficult to see the average structure in such a view. This difference is quite dramatic and can be seen by comparing the ion conduction paths calculated for the average unit cell of α-AgI shown in Figure 11 with those shown in Figure 15 based on a snapshot picture obtained by Adams and Swenson(135) using a reverse Monte Carlo simulation (section 12). Figure 11 shows the full crystal symmetry, Figure 15 is hardly recognizable as the same structure. The description of the structure of a glass necessarily corresponds more to the latter picture, since without any translational symmetry, space averaging of the structure leads to a featureless diagram. The conduction paths in a silver iodide molybdate glass are shown in Figure 23.

Figure 23.

A 2 Å thick slice through a silver iodide molybdate glass showing the Ag⁺ conduction pathways. Light parts correspond mainly to I⁻−, the dark parts to O²⁻-coordinated, Ag⁺. Reproduced with permission from ref (135), copyright 2000 by American Physical Society.

Since each snapshot simulation gives a different picture, the view is not reproducible, or put another way, every part of the glass sample has a different structure which is continually varying in time as a result of thermal motion. Therefore while a crystal can be characterized by its atomic structure, this is not true for a glass. One has to look for other descriptors that can be meaningfully averaged. One such is the set of bond lengths for a given bond type. Not all bonds of a given type will have the same length in the glass, but they will all belong to the same distribution whose average and standard deviation can, in principle, be determined by examining the atomic structures in many different parts of the glass sample, but at present the only way of doing this is by simulating the structure using, for example, the reverse Monte Carlo method. This uses as the cost function the difference between the calculated and observed X-ray or neutron diffraction pattern of the glass as described in section 12. However, not all the structures that match the diffraction pattern are chemically plausible, so it is necessary to include some chemical restraints in the cost function. These can be in the form of closest-approach distances between rigid complexes such as MoO₄, or in the form of the valence sum rule. This technique is the basis of much of the work of Adams and Swenson.^134,135,156

Modeling glasses differs from modeling crystals in another way. The ions in a glass will not always find themselves in their optimum environment and it may be necessary to consider bonds to neighbors more distant than are typically found in a crystal where the atoms are relatively densely packed. For this reason, bond valence - bond length parameters determined using a larger cutoff distance are used as described in section 7.3. Equation 26 can still be used, but the standard bond valence parameters that have been fitted to the first coordination sphere will not give good bond valence sums if bonds to more distant atoms are included. For this reason, Adams and Swenson^79,124 determined bond valence parameters fitted to distances out to 4, 6, or even 8 Å for use in their simulations.

Bond valences were used to check the correctness of the simulated structures of glasses as described in section 12, giving support to the principle of local charge neutrality (eq 5) which implies that the bond valence theorems will apply around individual ions as well as around the average atoms positions found in crystal structure determinations. In a series of papers^{135,137,156,253,254} Adams and Swenson describe the use of valence maps to locate the ion conduction paths in glasses. Section 10 shows how their valence maps display surfaces that enclose the regions in the structure that are accessible to the conducting ion, namely those places where the valence sum of a conducting ion would lie between V − ΔV and V + ΔV, where V is the atomic valence of the conducting ion and 2ΔV defines the width of the conducting path. When ΔV is small, the accessible volume is localized at the possible positions the ion could occupy, but as ΔV is increased the accessible volume increases until the localized positions merge to form a percolation network. For ionic conductors this typically occurs when ΔV is around 0.2 vu.

In their work on crystals, Adams and Swenson noted that the activation energies for the conduction of ions in glasses of different composition correlate with the value of ΔV at the percolation limit, indicating that the activation energy was related to the height of the valence barrier that the ions have to cross. In glasses, however, ΔV depends on the local structure; in some simulations it will be larger than in others. Adams and Swenson found that a more uniform property of the glass is the proportion, F, of the total volume of the glass that is accessible to the conducting ion. However, not all of this volume contributes to the conduction, since even at percolation, some parts of the accessible volume remain localized and disconnected from the conduction network. Some of these isolated regions will be occupied by ions that remain localized and do not contribute to the conduction. Adams and Swenson(156) found that the percentage of the Ag⁺ ions that occupy the conduction path in silver iodide tungstate glasses increases with F, reaching 40% when F is equal to 0.08. They^134,135 found that the activation energy and the logarithm of the conductivity were both linear functions of F^1/3, the activation energy dropping to zero when 45% of the material lies within the accessible volume. They set ΔV to 0.05 vu for these calculations, but showed that the results were not sensitive to the choice of ΔV, provided the same value was used for all simulations. For bonds with a large value of the softness bond valence parameter, b, the bond-valence−bond-length graph is flatter and the accessible volume correspondingly larger, accounting for the higher conductivity of soft ions such as Ag⁺ and I⁻.(129) Adams(142) has given a useful short review of the application of valence maps to the study of ionic conduction in crystals and glasses.

In mixed iodide-oxide glasses there had been speculation that the conduction path would be lined with I⁻ ions as silver iodide was known to be good ion conductor. Swenson and Adam’s^{134,135,141,156} simulations showed that this was not the case, at least in silver iodide phosphate glasses. In their simulations they found the conduction path was lined with both I⁻ and O²⁻ ions, and both are involved in the long-range migration of Ag⁺. The mobility was measured using simulated diffusion and conduction, dividing the conduction path into a fine grid of points and allowing Ag⁺ ions to hop randomly from grid point to neighboring grid point within the conduction path. They validated the resulting diffusion pattern by showing that the distance an ion moves from its starting point is proportional to the square root of the time taken.

After working through several Ag⁺ iodide and oxide glasses, Adams and Swenson^{136,255−258} turned their attention to another problem of conducting glasses: the mixed alkali effect: the observation that conducting glasses containing two different alkali metal ions are poorer conductors than either of the glasses containing only one kind of conducting ion. The samples they chose to study were (Li,Na)PO₃ and (Li,Rb)PO₃ where the conduction in the sample containing equal amounts of Li⁺ and Rb⁺ was 6 orders of magnitude smaller than the conduction in either LiPO₃ or RbPO₃. They(80) used F to compare the conductivities, σ, and activation energies, E₀, of the different compositions and found that they had to modify F by multiplying it by m^1/2 where m is the mass of the conducting ion. The modified relationships for the conductivity and activation energy are given in eqs 72 and 73.

where A, B, C, and D are fitted empirical constants. They simulated the structures of a number of glass compositions between LiPO₃ and RbPO₃, and using eqs 72 and 73 they were able to closely match the measured conductivities and activation energies. The reason for the mixed alkali effect was revealed by these conduction paths. Each type of cation has its own conduction path adapted to its own bonding requirements. In the single alkali glasses these provide an uninterrupted path for the mobile cation to move through the sample, but in the mixed alkali glasses these paths intersect and block each other, causing a decrease in the relative volume of the conduction path. This behavior is the opposite of the mixed alkali effect in crystalline LiNa(V₃O₈)₂ discussed in section 10.

Another tool that this group^136,257 used to characterize the conduction paths is their fractal dimensionality, d. This they calculated using the relationship in eq 74.

where n(R) is the average number of grid points within the same connected cluster out to a distance of R. They(256) found that for the single alkali glasses d rose from about 2 at R = 2 Å to an asymptotic value of 3 as R increased beyond 7 or 8 Å. However for LiRb(PO₃)₂, d remained well below 2 for all values of R. By10 Å it had fallen to 1.3 and was still dropping. These results are interpreted as meaning that on a length scale of 2 Å all the conducting paths appear as two-dimensional sheets as one would expect, but on a longer scale the conduction path in the single alkali glasses expands in all three dimensions, reaching into all parts of the sample, but in the mixed alkali glasses many of the paths are blocked from achieving percolation by the second alkali ion and their fractal dimension therefore drops as R becomes larger.

Molecular dynamics calculations(257) on sodium silicate glasses, revealed that even though the alkali metal ions migrated along the conduction paths, the other ions in the glass did not migrate during the period of the simulation, which was admittedly quite short. There were small time-dependent changes in the conduction path corresponding to thermal fluctuations, but the paths themselves were stable over longer intervals. Further, the conduction paths were found to be independent of the temperature of the molecular dynamics simulation. The increased conduction at high temperature does not therefore arise from an increase in the volume of the conduction path, but only from the higher kinetic energy of the mobile ions, which allows them to move beyond the boundaries of the conduction path as the temperature is increased. This suggests that changes in temperature can be simulated by increasing ΔV so that the conduction path corresponds to the actual volume accessible to the ion at the given temperature. Changing the thickness of the conduction path was found to increase its fractal dimensionality. Changing ΔV from 0.2 to 0.4 vu corresponds roughly to a change in temperature from 300 to 400 K in this example.

Having developed the techniques for simulating glass structures using reverse Monte Carlo methods and analyzing the results using, inter alia, bond valence methods, Hall, Adams and Swenson^258,259 compared the conduction paths in a series of M₂B₄O₇ glasses (M = Ag⁺, Li⁺, Na⁺) doped respectively with AgI, LiCl, and NaCl. The aim was to discover the reason for the large difference in ion conductivity between the Ag⁺ and Na⁺ doped glasses, They found that in the silver glass the iodide and oxide parts of the structure were well mixed with I⁻ preferentially lining the conduction paths. The Li⁺ doped glass, and particularly the Na⁺ doped glass, were inhomogeneous with the borate and oxychloride components tending to separate on an intermediate length scale (∼5 Å). In all cases the fractal dimensions of the conduction path at large distances was 3 but because the Cl⁻ ions were confined to the halide rich regions in the Li⁺ and Na⁺ glasses, the conduction paths necessarily involved more bonding to O²⁻. In this study the authors compared the pair-distributions of the conduction paths with similar pair distributions calculated using the reverse Monte Carlo method in which the cost function contained only chemical restraints, that is, the difference between the observed and calculated scattering patterns were omitted. Three types of chemical restraint were used; hard sphere atomic radii, fixed B−O bond networks, and bond valence restraints. None of these gave good agreement with the realistic pair distribution calculated using the experimental scattering pattern, but the network and bond valence simulations gave the best agreement. This indicates that more work needs to be done to define chemical constraints, including bond valence constraints, that can successfully be used in a stand-alone simulation.

The work of Farges and colleagues(16) on Ca,Fe silicate glasses is described in section 12. Later work by the same group^260−262 used EXAFS and XANES to explore the influence of Mo⁶⁺ and Nb⁵⁺ on silicate magmas. They discovered that Mo⁶⁺ occurs as MoO₄²⁻ and they used bond valences to argue that while the observed (MoO_4-xS_x)²⁻ ion was a reasonable species to expect, the bonding strength of tetrahedral Mo⁶⁺ (1.5 vu) was too large to bond to impurities such as F⁻, Cl⁻, or H₂O, and the bonding strength of MoO₄²⁻ (0.17 vu) was too weak to bond directly to Si⁴⁺ or Al³⁺. Mo⁶⁺ is therefore unable to act as a network modifier and is uninfluenced by the impurities that are typically found in magmas. The situation is different for Nb⁵⁺ which is found in octahedral coordination, usually distorted. This gives Nb⁵⁺ an average bonding strength of 0.83 vu but with a wide variation around this average because of the tendency, described in section 8.2.3, for octahedral Nb⁵⁺ to distort. This value allows it to bind to F⁻ and Cl⁻ as well as possibly H₂O. Nb−O−Si and Nb−O−Al linkages are also possible if Na⁺ or other alkali is present to bring the valence sum around the bridging O²⁻ up to 2 vu. Nb⁵⁺ is found to have a marked effect on magmas, making them much less viscous by breaking up the aluminosilicate framework, Similar arguments apply to Sn⁴⁺. Strongly bonding cations such as Mo⁶⁺ and W⁶⁺ form complexes that cannot bond to the polymerized SiO₄ or AlO₄ tetrahedral network but more weakly bonding cations such as Sn⁴⁺ with a bonding strength of 0.68 vu can.

25. Interfaces

25.1. Introduction

Surface chemistry is important in fields as varied as catalysis, corrosion, mineralogy, soil sciences and biology. It is also an area in which bond valences are making a unique contribution. Different kinds of interfaces, e.g., solid-vacuum and solid−liquid, require different treatments, but since the principle of local charge neutrality (eq 5) is expected to apply at all points in the system, the same rules of the bond valence model apply to the bonding on each side of the interface as well as across the interface itself, even though the composition, structure and physical properties of the two phases may be different.

25.2. Solid-Vacuum Interfaces

Bond valences have not been used much to examine the interface between solids and vacuum but the method was used by Ruberto et al.^23,263 who examined the vacuum surfaces of α-Al₂O₃ and κ-Al₂O₃. α-Al₂O₃ is the stable corundum form of alumina in which all Al³⁺ ions are octahedrally coordinated, and κ-Al₂O₃ is one of several metastable forms in which some Al³⁺ ions are tetrahedrally coordinated. Ruberto et al. initially found that Pauling’s second rule (eq 2) is exactly obeyed by corundum, indicating that it is a stable structure. The rule is not, however, exactly obeyed by κ-Al₂O₃ but the deviations from Pauling’s rule were unable to distinguish between the many candidate models of the structure. Ruberto et al.’s primary tool was density functional theory, but they checked their results using bond valences. Using their theoretically refined structure of bulk κ-Al₂O₃ they obtained bond valence sums of 2.91 vu for octahedral and 2.82 vu for tetrahedral Al³⁺ ions. These are close to the charges obtained from the quantum calculation. However, Ruberto et al. assume that this is the amount of charge physically transferred from Al³⁺ to the O²⁻ ions and hence is the charge that should be used to calculate the surface charge on the unrelaxed surface. In their density functional analysis, they allow the surface to relax, finding that the relaxation reaches through the full ten layers of their simulation. The structure of κ-Al₂O₃ lacks a center of symmetry and the charge on the surface should make the crystal unstable, but they found that this was not the case in their simulation. The result is consistent with the local charge neutrality rule which predicts that any surface charge will be removed by relaxation. Application of the valence sum rule around all the ions in this structure shows that there is a relative shift in the centers of gravity of the cation and anion lattices that is just sufficient to cancel the surface charge. This shift corresponds to the polarization of the medium that extends through the system causing the bonds on one side of the cations to be shorter than those on the other. This also explains why in the density functional calculation the relaxation extended through the simulated layer.

25.3. Interfaces between Solids and Aqueous Solution

Interfaces between solid and aqueous solution have been studied for well over a century but during the period under review the model used to describe this interface has been gradually evolving from one based on a macroscopic viewpoint to one based on a microscopic bond valence picture. The present review follows this transition in some detail because it is instructive to see the differences in the two approaches and the difficulties encountered when the way ahead is not clear. The section starts with a brief description of the macroscopic model that postulates a surface charge on the solid and an equal and opposite charge induced in the solution. Hiemstra and van Riemsdijk introduced the bond valence model as a way of calculating the size of this surface charge from the structure of the solid. Their model has been used by many workers, but also criticized, in particular by Bickmore and his collaborators, who have striven for a more complete microscopic picture of the surface based on the bond valence model. Finally Schindler and Hawthorne and colleagues have adopted a purely bond valence approach based on the principle of local charge neutrality (eq 5) in which the macroscopic assumption of a charged surface is finally dropped. A brief review of Hiemstra and van Riemsdijk’s MUSIC model has been provided by Bourikas et al.(264) who also describe the potentiometric titration measurements that provide the major experimental input.

The first theory to describe the interface between a solid and an aqueous solution was introduced in the nineteenth century by Helmholtz and was expressed in macroscopic terms. It was assumed that a cleaved solid surface would carry a residual charge, depending on how the cleavage occurred, and that when immersed in an aqueous solution, this charge would be neutralized by oppositely charged ions in the solution migrating to the surface. Since the ions on the surface of the solid and those in the solution remain distinct, the two layers of charge cannot approach closer than 1 or 2 Å and the interface can be represented by a capacitor having two layers of equal and opposite charge. The attractive force bonding the liquid to the solid is thus the electrostatic force between the two plates of the equivalent capacitor. This is called the diffuse double layer model (DDL), diffuse because the concentration of ions in the solution would drop off gradually as the distance from the surface increases. The goal of this model was to find values for the charges and capacitance that would correctly reproduce the observed titration results.

Over the last couple of decades Hiemstra and van Riemsdijk^265,266 have attempted to predict the charge on the surface layer from a knowledge of the atomic structure of the solid surface. They note that the surface is not flat and homogeneous as assumed in the classical model, but contains terminating anions of different basicity. In aqueous solution, the surface layer of the solid is terminated with O²⁻ anions since any bare cation at the surface would attract and bind O²⁻ ions from the water to complete its coordination sphere. Each terminal O²⁻ ion may in turn attach one or more H⁺ ions depending on its basicity and the pH of the solution. Since the crystal structure of the solid is usually known, it is possible to identify which O²⁻ ions are the most likely terminators. Not all will be chemically equivalent and, depending on the number and strength of the M−O bonds (where M is a cation in the solid), the terminating O²⁻ ions will have a greater or lesser ability to attract H⁺ ions. This led Hiemstra and van Riemsdijk to propose the MUlitiSIte Complexation (MUSIC) model. They assumed that the charge carried by an individual surface ion would be equal to its residual bond valence, that is, the unsatisfied valence remaining on the terminating anion after the requirements of the M−O and O−H bonds have been satisfied. The larger the residual valence the greater the basicity of the O²⁻ ion and the greater its ability to attract another proton. They defined the residual valence (the degree of underbonding), U, of a terminating O²⁻ ion using eq 75.

where V is the atomic valence of the O²⁻ ion (−2.0 vu), s_MO is the valence of an M–O bond (of which there may be more than one), s_D is the average valence of a donor O−H bond (assumed to be 0.8 vu), s_A is the average valence of an acceptor bond (assumed to be 0.2 vu), m is the number of hydrogen bonds donated by the terminal O²⁻ ion (1 for an OH group, 2 for an OH₂ group), and n is the number of hydrogen bonds accepted by the same ion. The number of donor bonds is chosen as part of the model, and Hiemstra and van Riemsdijk proposed that the number of acceptor bonds be chosen so as to bring the total number of hydrogen bonds, m + n, to two when O²⁻ is part of a surface and three when it is part of a hydrated metal complex in solution. These numbers are based on the questionable assumption that since O²⁻ has four valence orbitals it can form four bonds. The best choice for n has been the subject of some debate, in part because the definitions above are not always self-consistent. Further, the assumption that U represents the contribution of the terminal ion to the layer charge indicates a misunderstanding of the bond valence model, since in a description of the correct structure, U should by definition be zero if eq 75 includes all the bonds formed by the O²⁻ ion. One could argue that the right-hand side of eq 75 gives a description of the bonding around the unrelaxed terminating O²⁻ ion and that U represents the residual valence before relaxation. For this reason U might correlate with the pK_a of the anion as seems to be confirmed by subsequent studies.

In spite of these conceptual problems, as well as the uncertainty about the choice of n, the model has been used by many workers. If U is negative, the O²⁻ ion is underbonded and has an ability, proportional to the magnitude of U, to form an additional donor hydrogen bond. If U is positive, that is, the O²⁻ ion is overbonded, it will have a tendency to lose H⁺ ions rather than gain them. According to Hiemstra and van Riemsdijk, the residual valence, U, is proportional to the pK_a of the ion as shown in eq 76.

where they propose that A should be equal to 19.8 vu⁻¹. They originally recommended setting the bond valence, s_MO, in eq 75 to the Pauling bond strength (eq 1), but in more recent work it has been calculated from either the observed distances in the bulk crystal or the distances obtained from simulations of the relaxed surface.

In 1996 Hiemstra and van Riemsdijk(266) extended the MUSIC model to include hydrated cations and complex anions attached to the surface. Univalent ions are only weakly bonding and generally do not stick to the surface. For this reason these weakly bonding ions are used as the electrolytes in surface experiments. Ions with larger valences have larger bonding strengths and can bind to the surface in one of two ways. Oxyanions, such as PO₄³⁻, or hydrated cations, such as Fe(H₂O)₆³⁺, can form outer-sphere complexes in which they hydrogen-bond to the terminating O²⁻ or OH⁻ ions, but they can also form inner-sphere complexes in which an intervening water molecule is eliminated and the cation, or the central atom of an oxyanion, is bonded directly to a terminating O²⁻ ion of the solid. The presence of an inner-sphere complex adds an additional charged layer to the macroscopic model: the three layers being the surface of the solid, the inner-sphere complex layer, and the outer-sphere complex layer. The macroscopic version of this model thus requires three layers, equivalent to two capacitors in series. This is known as the triple diffuse layer model (TDL) as shown in Figure 24.

Figure 24.

(a) Outer sphere complexes hydrogen bonded to the surface and the equivalent diffuse double layer capacitor. (b) Inner sphere complexes directly bonded to the surface and the equivalent diffuse triple layer capacitor.

Calculating the charge on these three layers is the challenge that persuaded Hiemstra and van Riemsdijk to introduce the Charge Distribution version of the MUSIC model, CD-MUSIC. This version allows them to assign charges to each of these layers under the constraint that the total charge must be zero. In this model Pauling bond strengths are calculated for the M′−O bonds formed by the M′ cation of the inner-sphere complex. These bond strengths are used to reduce the residual charge (valence) of the terminating O²⁻ ion of the solid, since it represents the valence used for forming the M′−O bond. The charge on the outer side of the inner-sphere plane is then determined by reducing the valence (i.e., −2.00 vu) of the terminating inner-sphere O²⁻ ions by 1.00 vu for each bonded H⁺ ion and by the Pauling bond strength of any M′−O bonds.

Hiemstra et al.(267) use this model to show that CO₃²⁻ and SeO₃²⁻ must form bidentate inner-sphere complexes on goethite, α-FeOOH, bonding to the surface through two O²⁻ ions, by arguing that all the alternative models have unrealistic charge distributions (i.e., residual valence distributions). In later papers^268−270 they estimate the charge distributions for various inner-sphere (hydr)oxyanions on goethite surfaces, replacing the Pauling bond strengths by bond valences calculated from the relaxed bond lengths determined using density functional theory. They point out that the relaxed structure should lead to a more realistic charge distribution, but conclude that this charge distribution is not particularly sensitive to changes in the bond length. Tadanier and Eick(271) have modified the program FITEQL to incorporate the charge distribution requirements of the CD-MUSIC model.

The phyllosilicates are minerals composed of strongly bonded silicate sheets that are only weakly bound to each other. In the presence of aqueous solutions the sheets separate and the minerals form clays, an important component of soil. One of these minerals, montmorillonite, was the subject of studies by Tournassat et al.(272) who compared the ability of two models to explain their titration results: the MUSIC model and a model by Baeyens and Bradbury that uses two pK_as and three complexation sites. The Baeyens and Bradbury model required nine fitted parameters, and while it generally followed the experimental results, the fit was much better for the MUSIC model with only four fitted parameters. Using bond lengths taken from the literature, Tournassat et al. used eqs 73 and 74 to predict the pK_a for 27 different O²⁻ sites, though they considered that only seven of these were relevant to their calculations. As they were unsure how the seven values of m + n should be chosen, they treated three of them as fitted parameters along with the relative amounts of the two topologically different chains that appear on the surface of these crystals.

Zhang et al.(273) in a thorough exploration of the attachments of different ions on the (110) surface of the rutile form of TiO₂, used a wide range of experimental techniques as well as density functional theory and molecular dynamics, not only to show that most of the strongly bonding cations formed inner-sphere complexes, but also to determine the locations of these cations on the surface. They used the MUSIC model to estimate the pK_a of the surface using bond valences calculated from the relaxed bond lengths of their model. They point out that even small difference in the lengths of surface bonds can give rise to significant differences in the computed pK_as, which appears to contradict the findings Hiemstra et al. quoted above.

Machesky et al.(274) used eqs 73 and 74 in their study of the effects of temperature on the protonation of surfaces of rutile, but to confirm that these equations worked, they first calculated the pK_a values for twenty different hydrated complexes of cations. They used Pauling bond strengths defined in eq 1, but instead of using Hiemstra and van Riemdijk’s integral coordination numbers, N_c, derived from the ionic radii, they used the average observed coordination numbers tabulated by Brown(13) and found these gave better predictions of the pK_a with the constant A in eq 76 set equal to 21.7(4) vu⁻¹. Using the reduction in the hydration numbers at higher temperatures observed in spectroscopic measurements and molecular dynamics calculations for five different hydrated cations, they generated the expected hydration numbers for their twenty different species at 250 C and showed that the drop in coordination number correlates with the smaller values of pK_a measured at this temperature. For this correlation, A in eq 76 was set equal to 16.4(3) vu⁻¹.

Having shown that a good correlation exists between U and pK_a for hydrated complexes, Machesky et al. then applied the same ideas to the surface of rutile with the same satisfactory results. Their calculations predict two pK_a values for the (110) surface: 6.72 for the O²⁻ ion bonded to a single Ti⁴⁺ cation and 4.76 for the O²⁻ bonded to two Ti⁴⁺ cations. The average of these two values agrees well with the observed value of 5.4. By 250 C this value had dropped to 4.2.

In a later paper by Vlcek et al.(275) this group applied the same techniques to the surface of cassiterite, α-SnO₂, which is isostructural with rutile. In this paper they focused on the hydrogen bonding expected for different uncomplexed surface states. As a typical starting state for their molecular dynamics simulations they assumed that the terminating O²⁻ anion bonded to one Sn⁴⁺ cation was protonated but the terminating O²⁻ anion bonded to two Sn⁴⁺ cations was not. They found that the bridging =O²⁻ accepted a strong hydrogen bond (0.35 vu) and that the terminal −OH⁻ group accepted an average of 1.2 hydrogen bonds. They found that eqs 75 and 76, used with valences calculated from the bond lengths of their model (slightly adjusted), gave a correct prediction for the pK_a (4.4), whereas the use of the Sn−O distances observed in the crystal led to the significantly different value of 3.88. Although the difference between the bond lengths in the crystal and in the relaxed model was only around 0.05 Å, this corresponds to a difference in bond valence of around 0.1 vu.

Rustad(276) carried out molecular dynamics simulations on a large dumbell-shaped complex cation, Al₃₀O₈(OH)₅₆(H₂O)₂₆¹⁸⁺, which consists of two Al₁₃O₄(OH)₂₄(H₂O)₁₂⁷⁺ units connected by a neck of AlO₆ octahedra. The simulation indicated that the O²⁻ ions in the neck were the most susceptible to deprotonation. While simulations of the surface in vacuum and solution showed that most Al−O bond length were the same as those measured in the crystal, the bonds from Al³⁺ to the active functional O²⁻ ions in neck neck were shorter in the crystal than in either of the simulations. Rustad used the MUSIC model to calculate the pK_a using the observed crystalline bond lengths. He found that while the MUSIC model correctly identified the O²⁻ anions with the highest acidity in the simulations, it ranked them in a different order.

Yoon et al.(277) and Johnson et al.,²⁶⁷⁸ in a study of how the oxalate ion (⁻O₂CCO₂⁻) binds to boehmite (γ-AlOOH) and corundum (α-Al₂O₃) surfaces, used bond valence arguments to show why a surface Al³⁺ cation that forms three bonds within the corundum crystal and two to a bidentate oxalate ion does not complete its octahedral coordination by attaching an OH⁻ ion or an H₂O molecule. They also assign charges to the solid surface and inner-sphere complex layers based on bond valences and the expected covalency of the bonds, an exercise that shows the confusion caused by references to ionicity and covalency which are irrelevant to the application of the bond valence model.

In an important series of papers Bickmore and collaborators^17,19,279 have criticized the relative inflexibility of the MUSIC model and have used bond valences to address these shortcomings. They argue that the Pauling bond strengths defined in eq 1 should not be used in eq 75 because Pauling bond strengths are rational numbers and bear little relation to the real structure. They also pointed out the inconsistent rules for determining the number of acceptor hydrogen bonds. Further, the correct bond valences require a knowledge of the relaxed structure which can be predicted from simulations. However, such simulations should include all the species found at the surface, including the water molecules of the adjacent solution. For this reason the often-used density functional theory simulations of surfaces in vacuum may not be suitable for modeling solid-solution interfaces. Further, the relaxed structure is not static since protonating or deprotonating one terminating O²⁻ anion causes all the neighboring bonds to relax. This means that the proton affinity of a given terminating O²⁻ anion depends on the protonation state of its neighbors.

They(17) start by directing their attention to the surfaces that form the edges of the sheets in phyllosilicates such as pyrophyllite. The flat surface of the sheets are relatively inert and the interesting chemistry occurs at the edges. They first used density functional theory to model the crystal structure of a sheet, checking their calculations against the bond valence sums. Finding that the modeled bond valences were systematically about 0.1 vu too high, they increased their predicted bond lengths to compensate. They then used density functional theory to model the edge surfaces of the sheet. Neutral surfaces were generated by attaching the appropriate number of H⁺ ions in a variety of different ways. Bond valences calculated from the relaxed bond lengths were used to determine the residual valence, U, before the acceptor bonds were included, that is, using eq 75 with n set to zero. Equation 74 then gave pK_a values in the right range, but Bickmore et al. were still concerned about the inconsistent way in which the MUSIC model adds hydrogen bonds to match the expected number of O²⁻ orbitals, as well as the inability of the model to take account of the change in pK_a that occurs when a neighboring O²⁻ ion is protonated. In a second paper Bickmore et al.(279) followed up this work with a study using relaxed surfaces as the basis for calculating the bond valences. After reviewing early methods of predicting pK_a values of the terminating O²⁻ ions they point out that if the valence sum rule is to be obeyed, the residual valence, U, is what will be used to form the acceptor bonds and therefore the acceptor bonds should not be included in eq 75. Before trying this out on solid surfaces, they tested it on a variety of protonated oxycomplexes, MO₄, and hydrated cations, MAq₆. They obtained bond valences for the relaxed complexes by applying eq 26 to the M−O bond lengths calculated with density functional theory. They then calculated anion bonding strengths, L_b, for these complexes using eq 77.

where U is the residual valence calculated from eq 75 with n set to 0, and n in eq 77 is chosen to ensure that the total coordination number of the terminating O²⁻ is four. (Note that U and L_b are negative numbers). Bickmore et al. show the major predictor of the pK_a is not the residual valence, U, but the bonding strength (L_b, Lewis base strength) of the terminating O²⁻ ion calculated using eq 77. However, to achieve agreement within one logarithm unit of the measured pK_a they found it necessary to include an ionicity factor, I, for the M−O bonds, defined in eq 78.

where χ_M and χ_O are the Allred(265) electronegativities of their respective atoms. Bickmore et al. used eq 79 to fit the pK_a to the bonding strength and ionicity, where the constant f has a value close to 60, h has a value close to 18 and g is variable, with values ranging between 5 and 50 depending on whether the pK_a was being predicted for triangular oxyanions, tetrahedral oxyanions, octahedral hydrated cations or surfaces.

These values show that L_b is the most important determinant of the pK_a but ionicity is also a factor. The variations in the value of g led them to propose that there must be a further factor that affects the calculation of the pK_a, possibly related to the shape of the molecule or surface. While they show that a shape factor is plausible they do not suggest how it might be calculated.

The pK_a predicted by eq 79 is the intrinsic pK_a which is derived from the apparent (or observed) pK_a by making an electrostatic correction for the work needed to bring the proton to the potential of the terminating O²⁻ ion. Bickmore et al. speculate that the ionicity term in eq 79 is needed to compensate for the commonly used and relatively crude electrostatic correction based on a point charge model.

With success in predicting the pK_a of complexes in solution, they then applied the method to the surfaces of gibbsite, AlOOH, and cristobalite, SiO₂. They modeled a solid-vacuum interface using density functional theory but without imposing crystallographic symmetry. In the case of gibbsite this resulted in topologically equivalent terminating O²⁻ ions having bonding strengths ranging from 0.02 to 0.28 vu.

Resolving the variability of the size of the electrostatic correction was taken up in another paper by Bickmore et al.(19) On this occasion Bickmore and colleagues calculated the bond lengths of carbonate, silicate and phosphate ions in water using ab initio molecular dynamics with standard pseudopotentials correlated against the bond valence model. Using these bond lengths, they calculated the bond valences, S, which they averaged over the various configurations and time steps of the simulation to check the validity of the Hiemstra and van Riemsdijk assumptions. They first confirmed that the valence sums calculated around all the O²⁻ ions are close to 2.00 vu which not only gives confidence in the simulation but suggests that the bond valence model gives a good description of the local bonding in liquids. They then calculated the residual valence, U, for each terminating O²⁻ ion using eq 75 with n set to zero. They set the value of s_D equal to the valence they calculated for the O−H donor bonds. These they found ranged from 0.71 to 0.83 vu, close enough to the value of 0.80 vu assumed by Hiemstra and van Riemsdijk. The residual valences, U, range from 0.0 to 0.94 vu, values that must be matched by the total valences of the accepted hydrogen bonds. The average number of such bonds corresponding to n in eq 75 ranges from 0.72 to 3.5. Although not pointed out by Bickmore et al., their Table 4 shows a clear difference between the number of acceptor bonds formed by OH⁻ (m = 1) and O²⁻ (m = 0) ions, with n equal to 1.3 for OH⁻ and 2.9 for unprotonated O²⁻ ions. These numbers should be compared to the values of 2.0 and 3.0 respectively assumed by Hiemstra and van Riemsdijk and the value of 1.2 found for OH⁻ ions in the molecular dynamics calculations of Vlcek et al.(275) mentioned above.

Bickmore et al. then calculate the anion bonding strengths, L_b, using eq 77 with n set to 2 and 3 for OH⁻ and O²⁻ ions respectively, and found a good correlation between L_b and the valence of the strongest accepted hydrogen bond, s_A^max, over the range from 0.04 to 0.38 vu. This range should be compared with the value of s_A (0.2 vu) assumed by Hiemstra and van Riemsdijk. It is of interest to note the s_A^max is just under twice 0.2 vu as required by the valence matching rule (eq 16).

These results confirm that the bond valence model can be used to describe the complex (hydr)oxyanion simulations, that although the acceptor hydrogen bond valences cover a wide range of acceptable values, the strongest acceptor bond in each case has a valence close to the anion bonding strength derived from a realistic residual valence. Apart from the relatively wide range of values observed in the simulations for s_A and the lower value of n for OH⁻ groups, Hiemstra and van Riemsdijk’s estimates used in eq 75 are seen to be reasonable first approximations.

In this work Bickmore and his colleagues moved closer to a fully microscopic view of the surface based on the bond valence model. They are no longer concerned with the charged surface of the solid except to convert the observed pK_a to the intrinsic pK_a. They recognize that the bonds linking the solid and the solution are the hydrogen bonds accepted by the terminating O²⁻ ions, and consequently these bonds should not be included when calculating the residual valence; rather it is the residual valence that determines the number and strength of the acceptor bonds. They make use of the model’s ability to account for changes in the environment of neighboring ions. More importantly they recognize that the pK_a is not determined by the residual valences, U, of the terminating O²⁻ per se, but by the anion bonding strengths of eq 77 since these take into account the number of acceptor bonds that the terminating O²⁻ ions can form.

In a discussion of the morphology, growth and dissolution of mineral crystals, Schindler, Hawthorne and colleagues(281) adopt a more complete bond-valence approach to interface chemistry. They note that the principle of local charge neutrality (eq 5) requires that the valence sum rule be observed around each ion in the system, whether in the solid, in the solution or in the interface itself. This shifts the emphasis from concern over the differences between the solid and solution, to their similarity; the same set of chemical rules apply to all the atoms regardless of where they are found. The difference between the solid and solution arises from the difference in their composition, not from any difference in the chemical rules the ions obey. The water molecules are linked to each other by hydrogen bonds that behave in the same way as those that attach the water molecules to the solid, and the bonds formed by ions in solution obey the same rules as the bonds formed by the ions in the solid. In this view, the adhesion between the solid and the liquid is supplied by chemical bonds that are no different from other bonds in the system; it is no longer necessary to invoke a double charge layer to account for this adhesion.

Schindler, Hawthorne and their collaborators(281) point out, that in the absence of inner sphere complexes, the bonding between the solid and the solution does not depend on the number of H⁺ ions attached to the solid, but on the total number of hydrogen bonds linking the solid to the solution. Since the acceptor bond is the one that would be cleaved if the solution were removed, the strength of the bonding between solid and solution is determined by all the acceptor H···O links regardless of whether the H⁺ ion is attached to the solid or to the solution,. The H⁺ ion will lie closer to the anion with the greater bonding strength, and which one that is depends on the relative anion bonding strengths of the water molecule in the solution and the terminating O²⁻ ion in the solid at the pH of the measurement. The total number of hydrogen bonds thus determines the strength of the water-surface adhesion; the position of the H⁺ ion within the bond determines the surface chemistry. Where the terminating O²⁻ anion of the solid is a hydrogen bond donor (e.g., an OH⁻ group) the solid behaves as a Lewis acid, forming a hydrogen bond through its H⁺ cation, but where the terminating O²⁻ anion is an acceptor it behaves as a Lewis base. Most OH⁻ groups act as both an acid and base simultaneously. The OH⁻ group has a cation bonding strength, L_a, of 0.2 vu and the O²⁻ anion has an anion bonding strength, L_b, given by eq 77. The total bond valence linking the solid to the liquid is therefore given by the sum of the bonding strengths of all the hydrogen bonds, donor and acceptor alike, as shown in eq 80.

where L_a is summed over the donor-, and L_b is summed over the acceptor-bonds formed by the surface. The larger this sum, the stronger the binding between the solid and liquid. The net bond valence, on the other hand, is given by eq 81

The net bond valence would be the charge remaining on the surface if the H···O bonds were cleaved and the solution removed without relaxing the surface. At the point of zero charge (pzc) the net bond valence is zero, that is, |ΣL_a| is equal to |ΣL_b| and the number of acid and base functions are approximately equal. Increasing the pH of the solution changes the donor hydrogen bonds on the solid surface into acceptor bonds, and the net bond valence of eq 81 becomes negative.

If the solution pH is set equal to pK_pzc, then the measured pK_a is the same as the intrinsic pK_a for this surface, but if the pH is decreased, for example, by adding HCl, then the concentration of H⁺ ions (strictly H₃O⁺) is increased which forces more H⁺ ions onto the surface, turning surface acceptors into surface donors and thus increasing the net valence of the surface. In the double layer model this corresponds to a placing a positively charged layer on the solid which, in the solution, will attract the negative layer that is responsible for the electrostatic correction needed to obtain the intrinsic pK_a from the measured pK_a. Hawthorne and Schindler consider that the increased number of donor bonds on the surface attracts the Cl⁻ ions in the solution since these are good hydrogen bond acceptors. Thus Schindler et al. make the correction using eq 82.

where pK_a^meas is the measured value, [acid] and [base] are the concentrations of the acid and base functions on the surface of the solid.

Schindler et al. point out that the total bond valence of eq 80 tends to be smaller near the point of zero charge and larger as the surface becomes more basic or acidic.

Schindler et al.^{243,281−284} then applied these ideas to the growth, morphology and dissolution of sheet-like uranyl minerals containing strongly bonded linear uranyl (O=U=O)²⁺ cations (S_UO ≈ 1.65 vu) oriented perpendicular to the sheets. The uranyl cations are linked by O²⁻ anions lying in the plane of the sheet, each forming two or three weaker bonds to the U⁶⁺ ions (S_UO ≈ 0.54 vu). Each U⁶⁺ cation forms four, five or six (usually five) equatorial U−O bonds to the in-plane O²⁻ anions perpendicular to the strong uranyl group. Because the primary surface of the sheet is composed of the strongly bonded (and therefore weakly basic) O²⁻ anions of the uranyl group, they form only acceptor hydrogen bonds to the water molecules and thus contribute little of interest to the surface chemistry. Schindler et al. therefore focused their attention on what happens at the edges of the layers or at the steps and kinks found on the primary surface since these are the place where the chemical reactions are most likely to occur. They assumed that the edges would be defined by the strongly bonded chains that can be traced in different directions within the sheets and that the properties of these edges would be determined by the basicity of the O²⁻ anions that terminate the edge. They further assumed, that since the natural minerals are grown from aqueous solution, the observed crystal faces would be those with the lowest growth rate in solution. To predict the growth rates of different possible surfaces they turned to bond valences.

As a starting point they used the MUSIC model to calculate the relative basicity of the terminating O²⁻ ions since eq 75 treats the donors and acceptors equally. As the lengths of the equatorial U−O bonds are found to vary over a relatively wide range, Schindler et al. generated a model system in which all the (equatorial) U−O bonds are assumed to have a valence of 0.5 vu while the donor and acceptor hydrogen bonds are assigned valences of 0.8 and 0.2 vu respectively. The coordination number of O²⁻ is taken as four with m being determined by the choice of the structural model being studied, being zero for an unprotonated species, one for a hydroxyl group, two for a water molecule and three for a hydronium ion. They recognize that this model does not give a true picture of the structure, but it does order the different terminating O²⁻ anions according to their basicity. When these numbers are substituted into eq 75, Schindler et al. obtain residual valences, U, which vary from +0.32 to −0.52 vu, positive values representing Lewis acidity. When substituted into eq 76 these give notional pK_as for the surface anions that range from −9 to +18. Although these extreme values are quite unrealistic, they can be used to decide which terminating O²⁻ ions will be permanently protonated, which will be permanently unprotonated and what distribution of donor and acceptor bonds one would expect at the interface of a solution with a pH close to 7.

A more realistic measure of the basicity of the relevant terminating O²⁻ ions can then found by calculating their anion bonding strength, L_b, using eq 83.

Note that L_b is negative, and V is −2.0 for O²⁻. The numerator is the residual valence before the acceptor bonds are added, that is, the valence that remains unsatisfied after the U−O and donor O−H bonds have taken their share. The denominator is the number of acceptor bonds needed to bring the coordination number of the O²⁻ ion up to four, N_UO being the number of bonds the O²⁻ ion forms to U⁶⁺. As expected, the anion bonding strength determined using eq 83 correlates with the pK_a. From the valence matching rule (eq 16) one expects the surface anions to form bonds with solution cations having a bonding strength in the range |L_b|/2 to 2|L_b| and this is the valence that each acceptor bond would have to supply. Ideally one would expect the acceptor valence to be close to 0.2 vu with an acceptable range from 0.1 to 0.4 vu.

The crystal will dissolve fastest when UO₂O_aq complexes can be removed from the surface, that is, when the bonds that bind these complexes to the surface become weaker. This can occur if the bridging O²⁻ ions attract H⁺ ions from the solution since this will weaken the U−O bonds. Thus dissolution will be enhanced when the terminating O²⁻ anions have a high base strength or the pH is low. Similarly growth is greatest when the preformed hydrated uranyl complexes in the solution are able to eliminate water or OH⁻ when they bond to the terminating O²⁻ anions having the largest anion bonding strength. Thus the relative growth rates of different edges can be determined and the crystal morphology predicted. Edges with low total and low net bonding strengths are the slowest growing and tend to dominate in the final crystal morphology.

25.4. Comment

The bond valence model and the diffuse double layer model are both developed from the traditional ionic picture. The diffuse double layer model allows one to rationalize the experimental observations by describing the electrostatic interaction across the surface in terms of the force attracting the two plates of a capacitor. In the bond valence model all the electrostatic effects are incorporated into the bonds themselves and the adhesion between solid and solution is found by ensuring that the valence sum rule is obeyed around each atom in the system.

The above description of how the classical electrostatic model is in the gradual process of transforming into the microscopic bond valence model illustrates some of the problems that accompany a changing paradigm, particularly the complications that arise when hybrid approaches are constructed out of models whose incompatible assumptions are not fully appreciated. The classical double diffuse layer model was based on the notion that a crystal would cleave by breaking the ionic bonds along a plane, leaving a (negative) charge equal to the valence of the broken bonds on the solid surface. As this surface is brought into contact with the solution, a matching (positive) charge is provided at the interface by the solution. No other relaxation of either the solid or the solution is assumed and the bonding between the solid and solution is expressed explicitly as the electrostatic attraction between the two planes. The strength of the original MUSIC model was that it recognized that different surface atoms would have different base strengths but it failed to realize that charged surfaces are incompatible with Pauling’s(2) principle of local charge neutrality that is the basis of the bond valence model. A key step in the transition toward a true microscopic model was the realization that n in eq 75 should be set to zero. The transformation will be complete when the last vestige of the surface charge is removed from the model.

26. Biological Systems

Because bond valences are ideal for discussions of bonding in aqueous solutions, they should be ideal for discussing reactions in molecular biology. The main reason why they have not been more widely used in this field is that the crystal structures of proteins do not usually provide bond lengths with sufficient accuracy for meaningful use of the valence sum rule and other bond valence theorems. However in a short review Cachau and Podjarny(285) mention bond valences as one of the models that can be used to analyze high resolution protein structures, those determined at resolutions better than 1.0 Å. They quote(286) as an example the structure of human aldose reductase-inhibitor complex determined at a resolution 0.66 Å, accurate enough to reveal the reciprocal relationship between the lengths of the C−O and C−N peptide bonds.

One way around the problem of low accuracy is to use bond valences to analyze model compounds. Harding(287) has surveyed small molecules from the Cambridge Structural Database,(39) looking at the bonding around a number of the metal atoms commonly found in proteins. She used bond valences to point out that the longer bonds, those with lengths out to 3 Å, particularly around Cu²⁺ and Zn²⁺, contribute significantly to the valence sum around the metal atom and should not be ignored in the analysis of protein structures.

An alternative approach is to examine a statistically significant number of well determined protein structures since this allows one to determine whether the experimental uncertainties are sufficiently small to allow some of the bond valence rules to be used. This was the approach taken by Müller et al.(127) who examined the bonding around Ca²⁺, Mg²⁺, Na⁺, and K⁺ in two groups of protein structures, those that had been determined with a resolution of better than 1.5 Å and those that had been determined with a resolution between 1.5 and 1.8 Å. Since the structure refinement of a protein by X-ray diffraction cannot easily distinguish between Na⁺, Mg²⁺, and water, or between K⁺ and Ca²⁺, particularly if the site is not fully occupied, they calculated the bond valence sums around all the metal atoms (and some anions) using the bond valence parameters for Ca−O bonds, weighting each bond by the occupation number of the ligand. In structures at the highest resolution, the bond valence sums were found to cluster around 2.1 vu with a standard deviation of around 0.5 vu if the metal atom really was Ca²⁺. The slightly high value of this sum relative to the expected value of 2.0 vu probably arises from the choice of 3.5 Å as the cutoff distance for including a bond in the sum (see for example the discussion in section 7.5).

For the other metal ions the Ca-valence sum, that is, the bond valence sum calculated using the Ca−O bond valence parameters, is not expected to yield the correct atomic valence. The Ca-valence sum around Mg²⁺ was found to be close to 4.4 vu, for Na⁺ 1.5 vu and for K⁺ it was 0.7 vu, values that can be used to identify a cation. Since the environment of these ions is often disordered, and some ligands may have been missed in the determination of the structure, Müller et al. calculated the valence vector sum as described in section 9, arguing that since the metals examined were all expected to have spherically uniform environments, the valence vector sum should be close to zero if the coordination sphere were complete. Conversely a large valence vector sum would indicate a coordination sphere missing one or more of its ligands. They noted that the structures determined at resolutions better than 1.5 Å had reasonable bond valence sums and rarely had valence vector sums greater than 0.2 vu. However those with resolutions in the range 1.5 to 1.8 Å had a wide scatter of valence vector sums (0.0 - 0.8 vu) and Ca-valence sums that deviated by up to 50% from the expected value, though those structures with valence vector sums less than 0.2 vu generally had reliable Ca-valence sums. This suggests that any metal in a protein structure that has a valence vector sum less than 0.2 vu is likely to have a Ca-valence sum that can be used to determine what cation occupies the given site. Their frequency tables suggest that there are some examples where the reported structures have misidentified a Ca²⁺ ion as Mg²⁺.

Where bond valences can be determined, they are able to reveal details of the reaction mechanisms of enzymes, since it becomes possible to see how the close approach of a cation to a potential ligand in one part of the protein can result in a chain of alternating strengthened and weakened bonds which results in the weakening of the bond that is about to be cleaved.

Cheng et al.(288) used difference-Fourier-transform infrared methods with isotopic substitution to estimate bond valences from the stretching frequencies using eq 84 which they had developed earlier for P−O bonds.

Here ν is the root-mean-square observed stretching frequency in wave numbers. They were interested in studying how the β,γ P−O−P bond is cleaved at the active site of the GTPase enzyme RAS as GTP is converted to GDP. They measured the stretching frequencies of the terminal P−O bonds of GTP and GDP, comparing the frequencies in the enzyme bound complexes with those in Mg-GDP and Mg-GTP. Although the differences were smaller than the uncertainties in the absolute values of the bond valences, the authors make the point that the differences are significant. They then use these valences to predict bond lengths and angles and to support arguments that suggest why the γ-phosphate group can be hydrolyzed.

Barth and his colleagues^289−291 used the same method to study the sarcoplasmic reticulum Ca²⁺-ATPase whose job is to transport Ca²⁺ ions against a concentration gradient in muscle. The original Ca-bound enzyme, Ca2E1, is phosphorylated by ATP to form Ca2E1P. This form then releases the Ca²⁺ to form E2P which rapidly hydrolyzes, releasing the phosphate. Barth et al. were interested to know why E2P is much more rapidly hydrolyzed than Ca2E1P, a feature essential to ensuring the rapid relaxation of the muscle. Using acetylphosphate as a reference material they measured the C=O and P−O(terminal) stretching vibrations under a variety of different conditions. They then used valences of the P−O bonds obtained using eq 84 to estimate the bond lengths, and from these and the force constants, they estimated the bond energies which allowed them to predicted the rate of hydrolysis.

The arrangement of the phosphate and carboxyl groups in the protein is shown in Figure 25 which also shows the estimated bond lengths and bond valences. In the reference acetylphosphate in aqueous solution, they estimate that the terminal P−O bonds have a valence of 1.34 vu corresponding to a P−O bridging bond valence of 0.97 vu. The C−O bonds would then have a valence of 1.03 vu and the C=O bond a valence of 1.97 vu, assuming that the bridging O²⁻ formed only bonds to P and C. For the -PO₃ group attached to the carboxyl group of asp³⁵¹ the terminal P−O bonds are stronger with an average valence of 1.41 vu leaving the bridging P−O bond with a valence of only 0.77 vu. The total residual valence on the terminal bonds of the phosphate group is thus reduced from 2.00 vu in the reference compound to 1.77 vu in the enzyme bound compound. The result is, that compared to the acetylphosphate reference material, 0.22 vu of residual valence has been transferred from the phosphate ions to the carboxyl O²⁻ ions in the protein. Lys⁶⁸⁴ lies close to the bridging O²⁻ ion and may supply some of this, and a Mg²⁺ ion lies in a position that allows it to bond to the C=O oxygen. A bond valence description thus shows that the weak external bonding to the phosphate group combined with the external bonding to the carboxyl O²⁻ ions results in a weakening of the P−O(bridging) bond, thus facilitating the rapid hydrolysis. In the Ca2Ed1P state the P−O(terminal) bonds are not as strong as in E2P (1.39 vu), so that P−O(bridging) is stronger and the phosphate does not significantly hydrolyze. Although this analysis does not give the full picture of the enzyme reactivity, it shows how bond valences provide a simple and quantitative framework for discussing likely mechanisms of enzyme reactivity even in the absence of experimental bond valences.

Figure 25.

Acetyl phosphate group in E2P showing the bonding of the Mg²⁺ ion. The numbers above the bonds are the lengths in Å, the numbers below are the bond valences. Copyright 2004 American Society for Biochemistry and Molecular Biology. Reproduced with permission from ref (289).

27. Outlook

The main advance in the bond valence model during the review period has been the extension of its underlying principle of local charge neutrality from crystals, where its consequences have been known for some time, to amorphous materials and liquids. The papers reviewed here show that the bond valence model applies to individual atoms and bonds wherever they are found, as shown by the concordance of the bond valence model with the simulations using density functional, two-body potential and molecular dynamics calculations for amorphous materials, and all these techniques are found to agree with experiment. This realization opens up new fields for the application of bond valences to glasses, liquids and solutions and points the way to a unified view of acid−base chemistry in different phases and across phase boundaries. The model uses the traditional language of chemistry to explore the structure and properties of acid−base compounds, and holds the promise that we will soon be able to simulate structures using chemical rather than physical concepts. There are several areas in which the model is ripe for development:

The continued application of the model to the evaluation of new crystal structures has focused attention on the need to improve the correlation between bond-valence and bond-length. During the early development of the model it was sufficient to use a simple relation such as eq 25 or 26 to represent this correlation. Either of these equations works well as long as they are used over a relatively small range of bond lengths. Extending this range to describe both the harder short bonds as well as the softer long ones requires a more complex expression. Little attention has so far been directed to this problem, with the result that parameters that have been fitted to match wide ranges of bond lengths are likely to prove inadequate for detailed studies (sections 7.3 and 7.4).

Several recent studies have focused on the proper value for the softness parameter, b, in eq 26. While the frequently assumed value of 0.37 Å works for many bonds, values of up to 0.5 Å and higher appear to be more appropriate for bonds involving softer ions. We need a systematic reexamination of the assigned values of b to follow up on the pioneering work of Adams(79) (section 7.3).

The concept of bond valence (or bond order) and its correlation with bond length appears to be a general phenomenon that extends well beyond the restriction to bipartite bond graphs assumed in section 3. While there is no guarantee that the rules of the bond valence model will apply to nonbipartite graphs, the presence of such a correlation in all compounds with localized bonds, suggests that similar rules may apply to organic molecules, though so far these have proved elusive (section 13).

The tentative identification of a relationship between bond valence and energy implies that it might be possible to overcome one of the principle weaknesses of the bond valence model, namely its inability to quantify energy. It is a topic that deserves further study, though if such a relationship exists, it is likely to be more complex than suggested in section 6.

The bond valence model has not yet been used to simulate structures though it has been used to validate simulations produced using the two-body potential and quantum mechanical models. However the bond valence rules do provide sufficient constraints to allow for such simulations. The valence sum rule would be easy to apply, as well as the valence matching rule which is required to ensure correct coordination numbers. The equal valence rule is more problematic but can probably be applied via the valence vector sum rule. If the details can be worked out, the bond valence model would not only allow the constraints of a simulation to be established in terms of chemical concepts, but it would provide insights into the modeling process that are not available in other simulation techniques (section 12).

Another area with potential for advancement is the use of the model in the study of phase transitions. The properties of materials change discontinuously across phase boundaries and at phase transitions, whether these be between two solids or a solid and a liquid. The change in properties at a phase boundary is not the result of a change in the rules of structural chemistry, but rather a change in the constraints, such as composition or order, under which those rules operate. Because bond valences provide a unified description of structure across the whole system, they help to highlight the constraints that are the real driving force for the transition (section 25).

In short, the work covered in this review shows that the potential of the bond valence model is far from exhausted. When fully developed the model will complement the current energy-based methods of predicting structure by providing an equally powerful description based on the traditional chemical concepts of atoms and bonds. The insights it provides and its inherent simplicity will not only commend itself to chemists, but will result in a more quantitative approach to the description of the chemical structures of acid−base compounds.

Biography

David Brown was born in London in 1932 and spent the Second World War years in Montreal, returning to England to complete his education. After graduating with a BSc from King’s College London, he studied with Jack Dunitz at the Royal Institution, London and the ETH, Zurich, graduating with a PhD in 1959 as a novice solver of crystal structures. His post doctoral years were spent with Howard Petch setting up neutron diffraction at the newly opened nuclear reactor at McMaster University. Here he developed an interest in the structure of inorganic solids, an area that at that time was much neglected except by mineralogists. Solid state physicists were mostly interested in crystals with cubic symmetry, preferably containing only one kind of atom, and inorganic chemists were preoccupied with the chemistry of transition metal complexes. One reason for the neglect of inorganic compounds was the lack of an effective model for the systematic description their structure, hence his interest in addressing this need.

In 1962 he became a member of the Physics Department at McMaster University where interdisciplinary contact was encouraged. The atmosphere being congenial, he remained there for the rest of his career, interacting with local chemists such as Gillespie and Bader. His first decade was spent searching for the topic that would be the focus his research, but in order to recognize it he needed to gain much more experience in structural chemistry and crystallography. It was not until 1971 that Bob Shannon, arriving at McMaster on a year’s leave from duPont, introduced him to Donnay and Allmann’s extension of Pauling’s electrostatic valence concept. Together with Shannon, he enlarged and simplified their approach, showing that a correlation between bond valence and bond length could be found for all bond types. They showed that bond valences had many uses, ranging from validating newly determined structures to understanding the reasons why similar bonds often had different lengths. Much of Brown’s subsequent career has been spent exploring the implications of this model, showing how it can be used to predict and analyze crystal structures. Thirty years later, he brought these ideas together as a coherent theory of the structural chemistry of polar bonds in his 2002 book ‘The Chemical Bond in Inorganic Chemistry’.(1)

Because the development of the model required systematic studies of crystal structures, he developed an interest in the retrieval of crystallographic information. In the 1960s, compilations of crystals structures, such as Structure Reports, were woefully out of date. To remedy this, between 1969 and 1981, he published an annual bibliography of inorganic crystal structures indexed by the bonds present. Bond Index to the Determination of Inorganic Crystal Structures (BIDICS) was designed as a stop gap until, together with Guenter Bergerhof of Bonn, he was able to establish the Inorganic Crystal Structure Database,(40) allowing him to retrieve any inorganic crystal structure in machine readable form. In 1978, as an adjunct to the database, he also proposed a common crystallographic file structure to make it easier to distribute crystallographic information in electronic form, but it was not until 1990 that the International Union of Crystallography adopted the award-winning Crystallographic Information Framework (CIF). For 15 years as chair of the committee responsible to the Union for overseeing this project, he has been heavily involved in both its establishment and development.

In 1996 he retired from teaching and has spent much of his time subsequently trying to understand what makes the bond valence model so successful and how it relates to the more physical quantum mechanical descriptions of structure and bonding. His evaluation of the work reviewed in this article is colored by the perspective he has gathered on these questions.

His work was supported by the encouragement of his wife, the late Mariana Paterson, and his three daughters.

In the paragraph following eq 28, the average bond valence was incorrectly referred to as V/R. It has been corrected to V/N. The paper originally posted to the web on September 3, 2009, and was reposted on September 24, 2009.