Interindividual Variation in Functionally Adapted Trait Sets Is Established During Postnatal Growth and Predictable Based on Bone Robustness

Abstract

Adults acquire unique sets of morphological and tissue-quality bone traits that are predictable based on robustness and deterministic of strength and fragility. How and when individual trait sets arise during growth has not been established. Longitudinal structural changes of the metacarpal diaphysis were measured for boys and girls from 3 mo to 8 yr of age using hand radiographs obtained from the Bolton-Brush collection. Robustness varied ∼2-fold among boys and girls, and individual values were established by 2 yr of age, indicating that genetic and environmental factors controlling the relationship between growth in width and growth in length were established early during postnatal growth. Significant negative correlations between robustness and relative cortical area and a significant positive correlation between robustness and a novel measure capturing the efficiency of growth indicated that coordination of the subperiosteal and endocortical surfaces was responsible for this population acquiring a narrow range of trait sets that was predictable based on robustness. Boys and girls with robust diaphyses had proportionally thinner cortices to minimize mass, whereas children with slender diaphyses had proportionally thicker cortices to maximize stiffness. Girls had more slender metacarpals with proportionally thicker cortices compared with boys at all prepubertal ages. Although postnatal growth patterns varied in fundamentally different ways with sex and robustness, the dependence of trait sets on robustness indicated that children sustained variants affecting subperiosteal growth because they shared a common biological factor regulating functional adaptation. Considering the natural variation in acquired trait sets may help identify determinants of fracture risk, because age-related bone loss and gain will affect slender and robust structures differently.

INTRODUCTION

Although bone geometry is an important determinant of strength,(1) the relationship between morphological traits and fracture risk remains complex. Many studies showed that having slender bones (narrow relative to length) is a key risk factor for fractures in the elderly,(2–6) military recruits,(7) young adult athletes,(8) and children.(9) However, other studies showed that having wide bones increases fracture risk.(10,11) An important but overlooked factor that may contribute to this descrepancy is the natural variation in skeletal growth patterns that results in individuals acquiring unique sets of adult traits. Because the trait set a person acquires during growth is the set they take through the aging process,(12) a better understanding of how these trait sets arise during growth should advance our understanding of the relationship between bone morphology and fracture risk.

Recent studies showed that adults acquire trait sets that are predictable based on external bone size and that involve interactions among morphological and tissue quality traits. For adult long bones, percent cortical area and tissue stiffness (matrix mineralization) are inversely related to robustness, such that slender bones tend to show a greater percent cortical area and tissue stiffness compared with robust bones.(13–15) Likewise, wider corticocancellous structures have proportionally less cortical bone and lower trabecular density (lower vBMD), whereas narrow structures have proportionally greater cortical bone and higher trabecular density (higher vBMD).(12,16) Although these trait interactions make sense from an engineering perspective, the range of trait sets that can be considered to be functionally adapted for individuals within a population is not known. Current methods of assessing skeletal growth do not take a person's predisposition to a robust or slender skeleton into consideration.(17,18) Furthermore, how these naturally occurring trait sets affect the ability of adaptive processes to maintain strength with aging has not been established. Clearly, this is an important question to resolve, because age-related bone loss and gain will affect bone strength differently depending on whether the structure is narrow or wide. Consequently, the variation in growth patterns leading to unique adult trait sets may result in individuals fracturing for different structural and/or tissue quality reasons, thereby contributing to the complex relationship between bone geometry and fracture risk.

Although the development of human long bone has been well studied for boys and girls of different races,(19,20) these and other studies reported temporal changes in skeletal traits in terms of population averages and rarely showed how growth patterns varied among individuals within these populations.(21) Thus, the age during growth when these trait interactions compensate for the interindividual variation in bone robustness remains unclear. Prior work in inbred mouse strains provided insight into this problem showing that functionally adapted trait sets arise early during postnatal growth.(15) Studying the development of trait interactions within the range of functionally adapted structures will provide new insight into the biological factors that differentially affect subperiosteal expansion from those that affect functional adaptation. Taking a person's predisposition to slender or robust bones into consideration is important for advancing our ability to determine how genetic and environmental factors and prophylactic treatment regimens affect the development of bone strength.

We propose to build on prior developmental studies by using a novel systems approach that determines when functionally adapted trait sets arise during human skeletal growth. We used the interindividual variation in robustness (cross-sectional size/length) as a model for examining the compensatory nature of the skeletal system. The variation in skeletal robustness poses a particularly important challenge for biological processes to establish mechanical function during growth because bone length and width contribute to overall stiffness and strength in opposite ways.(22) Based on studies examining trait interactions for adult bone,(12,14) we postulated that the functional adaptation process during growth varies in fundamentally different ways among individuals and results in the acquisition of specific sets of traits that are predictable based on bone robustness. Because homeostatic buffering mechanisms control the amount of phenotypic variation that can be expressed in a population,(23) we expected that genetically heterogeneous individuals would not show random trait sets but rather a narrow range of functionally adapted sets of traits. Finding a consistent pattern of trait sets across a population is important, because it would imply that individuals within this population express variants affecting subperiosteal growth but share a common biological control regulating functional adaptation. Longitudinal changes in the structure of the second metacarpal diaphysis were measured for boys and girls from 3 mo to 8 yr of age. Hand radiographs were obtained from the Bolton-Brush collection,(24) a longitudinal database curated by the School of Dental Medicine at Case Western Reserve University (Cleveland, OH, USA). The radiographs, which were acquired in Cleveland, OH, circa 1930, allowed us to examine compensatory changes in morphology but not mineralization.

MATERIALS AND METHODS

Sample population

Digitized posteroanterior (PA) radiographs (512 dpi) of the nondominant hand and wrist for 37 white girls and 32 white boys were selected at six time points from the Bolton-Brush Collection, which contains longitudinally collected hand radiographs for children growing up in Cleveland, OH, circa 1930. Time points included 3 mo, 9 mo, 2 yr, 4 yr, 6 yr, and 8 yr, corresponding to the earliest stages of postnatal and childhood growth. Body weight and height data were also included. Radiographs that were degraded or missing were replaced by radiographs from the adjacent time point, if available. This resulted in a few individuals being examined for only four to five time points and several individuals being examined beyond 8 yr of age. A total of 377 digitized radiographs were analyzed.

Bone morphology

Morphological traits were quantified using LabVIEW Vision Builder (National Instruments, Austin, TX, USA). Outer diameter, marrow diameter, and cortical thickness were measured at 30%, 50%, and 70% along the length of the second metacarpal, as well as an exclusive measurement taken at the location of minimum shaft thickness (∼50–55% of shaft length). For human metacarpals, measurements at the minimum shaft thickness are as reliable as those taken at the midshaft, and these regions are homologous throughout the period of growth.(25–27) Because the distal end of the second metacarpal consists of a nonossified growth plate during postnatal growth, metacarpal length (Le) was measured from the proximal end to the most distal ossified end along the midshaft axis (i.e., proximal edge of growth plate). Manual point-to-point measurements of outer and inner bone widths had an average CV of 1.61%.

Total cross-sectional area (Tt.Ar), cortical area (Ct.Ar), and marrow area (Ma.Ar) of the second metacarpal were calculated using a circular approximation.(19,28–30) Tt.Ar assesses overall shaft size, and changes in Tt.Ar over time indicate the biological activity occurring at the subperiosteal surface. Likewise, changes in Ma.Ar indicate expansion or infilling at the endocortical surface. Ct.Ar provides an estimate of the amount of bone. Tt.Ar was calculated using the formula π(B.Dm/2)², where B.Dm is the outer diameter of the metacarpal. Similarly, Ct.Ar was calculated by subtracting Ma.Ar from Tt.Ar, using the formula π(B.Dm/2)² − π(Ma.Dm/2)², where Ma.Dm is the marrow cavity diameter. Cortical thickness (Ct.Th) was measured by averaging medial and lateral cortical thicknesses. Polar moment of inertia (Jo), which is a measure of tissue distribution that is proportional to bending and torsional stiffness, was calculated as π[(B.Dm⁴ – Ma.Dm⁴)/32]. Third ray length and hand breadth were measured as additional indices of body size. Third ray length was measured from the proximal end of the third metacarpal to the distal phalangeal edge. Distal hand breadth was measured from the most distal medial edge of the second metacarpal to the most distal lateral edge of the fifth metacarpal. Sex-specific differences in morphological traits were determined at each age using a Student's t-test.

Covariation

Measures assessing the relationship between traits included robustness, defined as Tt.Ar/Le, and the relative cortical area (RCA), defined as Ct.Ar/Tt.Ar. Robustness measures the relationship between growth in width (Tt.Ar) and growth in length (Le). Tt.Ar was used to measure growth in width because the amount of bone deposited during subperiosteal expansion increases by the square of width (i.e., area). Relative cortical area (RCA), a measure of the relative amount of bone, assesses the relationship between periosteal and endocortical expansion. A linear regression analysis showed that Tt.Ar increased linearly with Le over time for all individuals in the study population (R² > 0.90–0.99, p = 0.001–0.01). Likewise, Ct.Ar increased linearly with Tt.Ar over time for all individuals (R² = 0.85–0.99, p = 0.001–0.03). A least squares regression was conducted between robustness and RCA at each age to test the hypothesis that variants leading to slender bones were compensated by proportional increases in RCA. A partial regression analysis was conducted to confirm that robustness correlated with RCA when the effects of body size (body weight, hand breadth, third ray length) were taken into consideration.

Interindividual variation in growth patterns

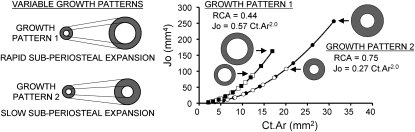
A new method of analysis was developed that uses data across growth rather than single age groups to further test whether variation in robustness is associated with coordinated changes in marrow expansion. This analysis involves regressing the polar moment of inertia, Jo, against cortical area, Ct.Ar, using the data measured at all ages. Because Jo (a measure of the distribution of bone) and Ct.Ar (a measure of the amount of bone) depend on bone width raised to the fourth and second powers, respectively, variation in the relative movement of the subperiosteal and endocortical surfaces results in quantitative differences in the Jo versus Ct.Ar curves. The relationship between Jo and Ct.Ar is nonlinear and can be fit using a power law regression, y = Ax^B (GraphPad Software, LaJolla, CA, USA). For simplicity, we set the y-intercept equal to zero. Because the exponent, B, was similar among individuals, regressions were conducted with a fixed value for B allowing the scaling coefficient, A, to be used as a measure of differences in the Jo versus Ct.Ar curves. Higher values for A reflect a more structurally efficient growth pattern, because a structure with greater Jo for a given Ct.Ar uses less bone mass to achieve the same resistance to torsional and bending loads. The constant A can thus be regarded as a measure of the structural efficiency of growth.

The effect of variable growth patterns (i.e., the relative expansion of the subperiosteal and endocortical surfaces) on the Jo versus Ct.Ar curves is shown in Fig. 1. Structures growing with the same relative subperiosteal and endocortical expansion rates (i.e., similar relative cortical area) show identical Jo versus Ct.Ar curves, regardless of the final size of the structure. Consequently, if all individuals in a population grow with the same RCA values (or random RCA values), the constant A will not correlate with measures of external bone size (e.g., Tt.Ar, Width). However, if the movements of the subperiosteal and endocortical surfaces are coordinated such that all individuals in a population share a common biological constraint (e.g., Ct.Ar increases at the same rate over time), the constant A will correlate significantly with external bone size.

FIG. 1.

Variation in subperiosteal expansion relative to endocortical expansion leads to differences in the relationship between polar moment of inertia, Jo, and cortical area, Ct.Ar. Idealized cylindrical structures growing with the same relative expansion rates of the outer and inner surfaces (i.e., same relative cortical area, RCA = Ct.Ar/Tt.Ar) show identical Jo vs. Ct.Ar curves, regardless of the rate of external growth or the adult size. Growth patterns that differ in RCA follow different Jo vs. Ct.Ar curves. The relationship between Jo and Ct.Ar can be modeled as a power-law regression (y = Ax^B), where the constant, A, becomes a measure of the structural efficiency of growth when the exponent, B, is held fixed.

Because this is a nontraditional analysis, we confirmed the theoretical relationships using a computer model that simulated diaphyseal growth for 35 individuals from 3 mo to 8 yr of age. For the simulation, body size and bone length were held fixed allowing subperiosteal and endocortical expansion rates to be the only variable quantities. The first simulation allowed both subperiosteal expansion rate and endocortical expansion rate to vary randomly. Subperiosteal expansion rates were constrained to generate random cross-sectional bone sizes between the minimum and maximum values measured for the Bolton-Brush data set. To ensure that marrow area did not exceed total area, endocortical expansion rate was calculated as the subperiosteal expansion rate times a random number between 0 and 1. This simulation represented “uncoordinated” growth between the subperiosteal and endocortical surfaces resulting in a population showing random combinations of Tt.Ar and Ma.Ar. A second simulation allowed subperiosteal expansion rate to vary randomly similar to the first simulation, but constrained (i.e., coordinated) endocortical expansion rate so all structures had the same age-related increase in Ct.Ar. A third simulation allowed subperiosteal expansion rate to vary randomly similar to the first two simulations but constrained endocortical expansion rate so all structures had the same age-related increase in Jo.

We used this analysis to test whether subperiosteal and endocortical surfaces move in a coordinated manner across the Bolton-Brush study population. The constant A was calculated from the Jo versus Ct.Ar curves for each individual and regressed against the corresponding robustness (Tt.Ar/Le) and RCA values measured at 8 yr of age using least-squares linear regression analysis. We calculated 95% CIs and tested whether the slopes of the regressions were significantly different from zero, which would be expected if bone surface expansions were uncoordinated.

RESULTS

Sex-specific differences in morphological traits

Anthropometric traits for girls and boys were compared at each age to assess sex-specific differences in body size and metacarpal morphology (Table 1). Body weight and height increased rapidly during the first year of life and increased more slowly from 2 to 8 yr, as expected. The age-related increases observed for Le, Tt.Ar, Ct.Ar, and Jo were similar to those observed for body weight and height. Despite the height and weight differences between boys and girls, metacarpal length (Le) was not different between sexes (p > 0.10), except for a small (∼4%) difference at 2 yr. Both total cross-sectional area (Tt.Ar) and Jo were significantly greater for boys at all ages, and this resulted in boys showing greater robustness, Tt.Ar/Le, compared with girls at all ages. For girls, the smaller Tt.Ar was accompanied with smaller Ma.Ar from 9 mo to 8 yr. Although girls showed a 26% smaller cortical area (Ct.Ar; p < 0.0004) at 3 mo of age, Tt.Ar and Ma.Ar changed in such a way that Ct.Ar did not differ between girls and boys after 9 mo of age. The similarity in Ct.Ar combined with the differences in Tt.Ar resulted in girls showing greater relative cortical area, RCA, compared with boys after 2 yr of age (p < 0.04). Thus, sex-specific differences in robustness and RCA were apparent postnatally and resulted from differences in transverse expansion and not longitudinal growth.

Table 1.

Variation in Body Weight, Body Height, and Morphology of the Second Metacarpal Diaphysis for Boys and Girls From 3 mo to 8 yr of Age

Trait	Sex	3 mo	9 mo	2 yr	4 yr	6 yr	8 yr
Weight (kg)	F	5.7 ± 0.6	8.7 ± 1.0	11.9 ± 1.3	15.7 ± 1.8	20.4 ± 3.0	26.6 ± 4.5
	M	6.2 ± 0.7	9.6 ± 1.1	13.1 ± 1.5	17.5 ± 2.4	22.0 ± 3.1	27.5 ± 3.5
Height (mm)	F	589 ± 21	697 ± 24	852 ± 29	1017 ± 50	1160 ± 46	1278 ± 55
	M	603 ± 26	712 ± 29	868 ± 34	1047 ± 56	1178 ± 45	1297 ± 50
Le (mm)	F	17.7 ± 1.1	21.8 ± 1.7	27.6 ± 1.5	33.6 ± 2.4	38.6 ± 2.6	42.9 ± 2.8
	M	18.1 ± 1.5	21.9 ± 2.0	28.8 ± 2.5	34.6 ± 2.4	39.2 ± 3.0	43.2 ± 3.4
B.Dm (mm)	F	3.12 ± 0.30	3.75 ± 0.30	4.52 ± 0.45	5.05 ± 0.44	5.46 ± 0.49	5.97 ± 0.56
	M	3.48 ± 0.26	4.08 ± 0.40	5.06 ± 0.54	5.44 ± 0.48	5.82 ± 0.62	6.32 ± 0.63
Ma.Dm (mm)	F	1.89 ± 0.36	2.53 ± 0.30	2.77 ± 0.45	2.71 ± 0.53	2.74 ± 0.60	2.80 ± 0.64
	M	2.06 ± 0.37	2.85 ± 0.42	3.52 ± 0.51	3.16 ± 0.55	3.16 ± 0.58	3.19 ± 0.65
Ct.Th (mm)	F	0.62 ± 0.13	0.61 ± 0.11	0.88 ± 0.20	1.17 ± 0.17	1.36 ± 0.21	1.58 ± 0.20
	M	0.71 ± 0.13	0.62 ± 0.11	0.77 ± 0.15	1.14 ± 0.16	1.33 ± 0.21	1.56 ± 0.22
Tt.Ar (mm2)	F	7.7 ± 1.4	11.1 ± 1.8	16.2 ± 3.2	20.2 ± 3.5	23.6 ± 4.2	28.2 ± 5.3
	M	9.5 ± 1.5	13.1 ± 2.6	20.3 ± 4.3	23.4 ± 4.2	26.9 ± 5.6	31.6 ± 6.3
Ct.Ar (mm2)	F	4.9 ± 1.0	6.1 ± 19	10.0 ± 2.6	14.2 ± 2.3	17.4 ± 2.9	21.7 ± 3.5
	M	6.1 ± 1.0	6.7 ± 1.5	10.4 ± 2.6	15.3 ± 2.5	18.8 ± 3.9	23.3 ± 4.4
Ma.Ar (mm2)	F	2.9 ± 1.1	5.1 ± 1.2	6.2 ± 2.0	6.0 ± 2.2	6.2 ± 2.7	6.5 ± 2.9
	M	3.4 ± 1.1	6.5 ± 1.9	9.9 ± 2.7	8.1 ± 2.8	8.1 ± 2.8	8.3 ± 3.4
Jo (mm4)	F	8.4 ± 2.9	15.9 ± 5.1	36.8 ± 15.1	60.3 ± 19.6	84.0 ± 28.6	123.0 ± 43.2
	M	12.8 ± 4.0	21.4 ± 8.7	51.7 ± 22.3	89.0 ± 32.2	108.4 ± 44.7	152.6 ± 59.3
RCA	F	0.63 ± 0.10	0.54 ± 0.07	0.62 ± 0.10	0.71 ± 0.08	0.74 ± 0.08	0.78 ± 0.07
	M	0.65 ± 0.09	0.51 ± 0.08	0.51 ± 0.08	0.66 ± 0.08	0.70 ± 0.07	0.74 ± 0.08
Tt.Ar/Le (mm)	F	0.44 ± 0.08	0.51 ± 0.08	0.59 ± 0.12	0.60 ± 0.11	0.61 ± 0.11	0.66 ± 0.12
	M	0.52 ± 0.06	0.60 ± 0.09	0.70 ± 0.12	0.68 ± 0.11	0.68 ± 0.12	0.73 ± 0.12

Bold indicates p < 0.05 between girls and boys at each age (Student's t-test). Data are shown as mean ± SD.

Interindividual variation in robustness

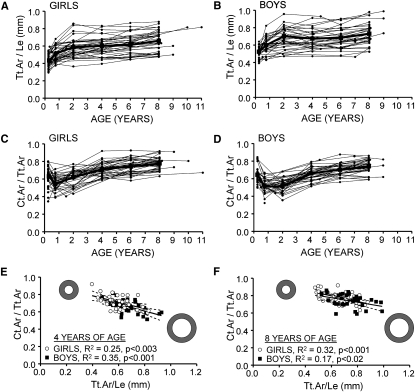
Robustness (Tt.Ar/Le), which was normally distributed for boys and girls at each age (p > 0.10, Kolmogorov-Smirnov test), varied widely among individuals and showed an average CV of 16.9%. For each individual, robustness increased rapidly during the first year of life and plateaued after 2 yr of age (Figs. 2A and 2B). Robustness measured at 3 mo was a significant predictor of robustness measured at 8 yr of age for both girls (R² = 0.36, p < 0.0001) and boys (R² = 0.26, p < 0.004). Robustness at 2 yr of age explained 57% (p < 0.001) and 76% (p < 0.001) of the variation in robustness at 8 yr of age for girls and boys, respectively, indicating that the interindividual variation in robustness was largely established by that time in both sexes.

FIG. 2.

Robustness (Tt.Ar/Le) of the second metacarpal diaphysis varied widely among (A) girls and (B) boys and was established largely by 2 yr of age. Variation in RCA (Ct.Ar/Tt.Ar) of the second metacarpal diaphysis as a function of age for (B) girls and (C) boys. Ct.Ar/Tt.Ar correlated negatively with robustness (Tt.Ar/Le) at nearly all ages including (D) 4 and (E) 8 yr of age. The 95% CIs for the regressions are shown as dashed lines.

To determine how slender bones were compensated morphologically, the relative cortical area (Ct.Ar/Tt.Ar) was regressed against robustness at each age. RCA, which varied widely among boys and girls, decreased during the first year of life and then increased steadily thereafter for both sexes, as expected (Figs. 2C and 2D). RCA correlated negatively with robustness for girls and boys at each age (Figs. 2E and 2F). The regressions were significant (p < 0.05) for boys at 9 mo and at 4, 6, and 8 yr of age (R² = 0.15–0.35). For girls, the regressions were significant at 4, 6, and 8 yr of age (R² = 0.25–0.32). A partial regression analysis confirmed that the negative correlation between RCA and robustness was significant when the effects of body size were removed.

Interindividual variation in growth patterns

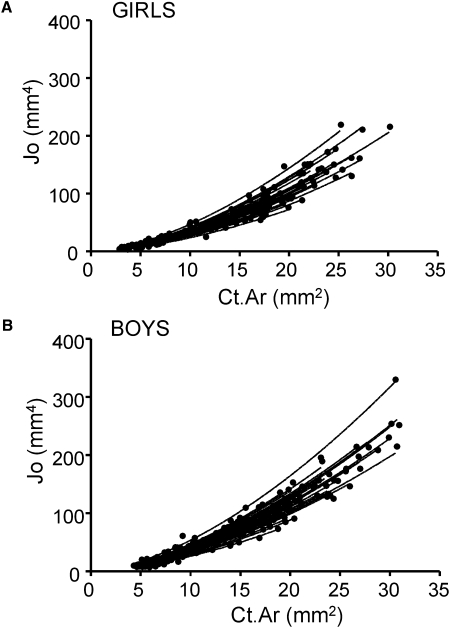
To test whether growth patterns varied with robustness in a consistent manner across the study population, Jo was regressed against Ct.Ar using data collected at all ages for each individual. The interindividual variation in growth patterns resulted in widely varying Jo versus Ct.Ar curves for both sexes (Figs. 3A and 3B), which confirmed that there were differences in the relative expansion of the subperiosteal and endocortical surfaces among individuals during growth. The exponent, B (1.62 ± 0.18), calculated from the power-law regression Jo = ACt.Ar^B showed little variation among individuals and was similar for boys and girls (p < 0.25, t-test). Setting the exponent, B, to the average of all individuals did not affect the Jo versus Ct.Ar regressions (average R² > 98%). The average value for A was significantly (p < 0.002) greater for boys (0.91 ± 0.14) compared with girls (0.81 ± 0.12), indicating that the metacarpal diaphyses of boys grew on average in a more structurally efficient manner compared with girls. The constant A did not correlate with body weight or bone length (R² < 0.07, p > 0.1) at 8 yr of age for either girls or boys.

FIG. 3.

Variable postnatal growth patterns from 3 mo to 8 yr of age lead to wide variation in the relationship between polar moment of inertia, Jo, and cortical area, Ct.Ar, measured at the midshaft of the second metacarpal for (A) girls and (B) boys.

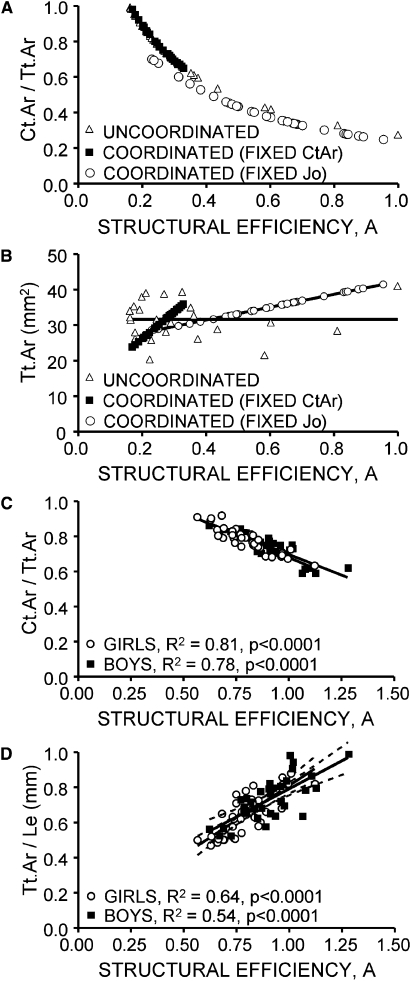
To determine whether variation in bone growth patterns correlated with measures of bone morphology, the constant A was regressed against Tt.Ar/Le and RCA measured at 8 yr of age for both the computer simulation (Figs. 4A and 4B) and the Bolton-Brush study population (Figs. 4C and 4D). The simulated growth patterns showed negative (nonlinear) correlations between A and RCA measured at 8 yr (Fig. 4A). However, only the coordinated simulations showed a significant correlation between A and Tt.Ar (which is equivalent to Tt.Ar/Le) at 8 yr, as expected (Fig. 4B). For the Bolton-Brush study population, the constant A correlated negatively with RCA (R²_Girls = 81%, R²_Boys = 78%, p < 0.0001) for both sexes (Fig. 4C), which was expected given the results of the computer simulation. Importantly, A correlated positively with robustness for both sexes (R²_Girls = 64%, R²_Boys = 54%, p < 0.0001), indicating that expansion of the subperiosteal surface relative to the endocortical surfaces was not random but highly coordinated across this study population, as hypothesized (Fig. 4D). The slopes and intercepts were not different between boys and girls (p > 0.3, ANCOVA), and there was substantial overlap in the 95% CIs for the regression slopes (girls: 0.58–0.99; boys: 0.42–0.85). The positive slope between A and robustness and the negative slope between A and RCA together indicated that growth patterns leading to a robust phenotype were associated with reduced RCA, whereas growth patterns leading to a slender phenotype were associated with increased RCA.

FIG. 4.

(A) A computer model simulating growth of circular cylinders with the same length showed that RCA (Ct.Ar/Tt.Ar) decreased with the structural efficiency parameter, A, regardless of whether subperiosteal and endocortical surface movements were coordinated or uncoordinated. (B) The computer simulation also showed a strong positive correlation between the structural efficiency parameter, A, and bone size (Tt.Ar) measured at 8 yr of age only when the relative movements of the outer and inner surfaces were coordinated by constraining all cylinders to have the same age changes in cortical area, Ct.Ar, or polar moment of inertia, Jo. (C) The relative cortical area (RCA = Ct.Ar/Tt.Ar) of the second metacarpal diaphysis measured at 8 yr of age for boys and girls correlated negatively with the structural efficiency parameter, A, measured across growth from the Jo vs. Ct.Ar curves. (D) Robustness (Tt.Ar/Le) measured at 8 yr of age correlated positively with the structural efficiency parameter, A, for both boys and girls. The 95% CIs are shown as dashed lines.

The structural efficiency constant, A, differed between the simulated and actual growth patterns because the constant A increases as the exponent B decreases. Varying the choice of B from B = 1.5 to B = 1.7 so that it spanned the mean value for the study population affected the magnitude of A but did not affect the significance of the correlations shown in Fig. 4D (data not shown). The simulation idealized bone growth patterns resulting in an exponent of B = 2.0, whereas the exponent B for the study population was much lower (1.62), resulting in larger values for the constant A.

To determine whether the coordinated movements of the subperiosteal and endocortical surfaces resulted from a constraint limiting the amount of bone (Ct.Ar) or the distribution of bone (Jo/R ∼ structural stiffness) across the study population, a partial regression analysis was conducted between Tt.Ar/Le and Ct.Ar and between Tt.Ar/Le and Jo/R with the effects of body weight removed. For girls and boys, the slope of the correlation between the Jo/R-BW residuals (R² = 0.84–0.86) and the Tt.Ar/Le-BW residuals was significantly greater (p < 0.0001, ANCOVA) than the slope between the Ct.Ar-BW residuals and the Tt.Ar/Le-BW residuals (R² = 0.62–0.65). This analysis indicated that slender and robust diaphyses were constructed with approximately the same amount of tissue relative to body weight, suggesting that the coordinated movements of the subperiosteal and endocortical surfaces resulted from a constraint regulating the amount of diaphyseal bone (Ct.Ar) that could be used to grow functional structures. However, the small but significant positive slope of the Ct.Ar-BW residuals versus the Tt.Ar/Le-BW residuals indicated that this constraint was not perfect and that individuals with slender bones relative to body size tended to have slightly less cortical area compared with individuals with robust bones relative to body size.

Slender versus robust growth patterns

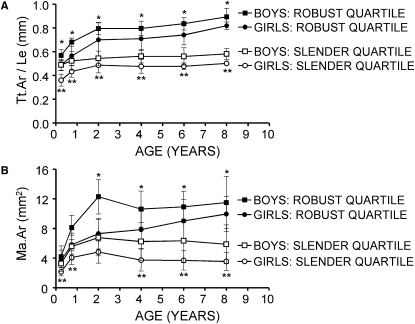
To determine how the growth patterns differed between children with the most slender metacarpals from children with the most robust metacarpals, body size, and morphological trait values were compared across growth for the eight to nine children showing the smallest and largest quartiles for Tt.Ar/Le measured at 8 yr of age. Male and female data were analyzed separately by a mixed-model ANOVA (repeated-measures two-way ANOVA). Individual comparisons were made by posthoc t-tests and corrected for multiple comparisons (p < 0.008). The mixed model ANOVA showed significant effects because of age (p values ranged from 0.0001 to 0.02) and robustness quartile (p values ranged from 0.0001 to 0.0003) for both TtAr/Le and MaAr, as expected. This was true for both males and females. Body weight and height did not differ significantly between the slender and robust groups at any age for boys and girls (p > 0.1; data not shown). Likewise, metacarpal length did not differ between slender and robust groups at any age for girls and boys (p > 0.3; data not shown), indicating that differences in robustness resulted from variation in transverse expansion and not longitudinal growth. An examination of Tt.Ar/Le across growth (Fig. 5A) showed that the boys and girls with slender metacarpals at 8 yr of age also had significantly more slender metacarpals at 3 mo of age (p < 0.008), indicating that measurable differences in robustness were apparent shortly after birth. Tt.Ar/Le increased 39.6% from 3 mo to 2 yr of age for boys with the most robust metacarpals, whereas Tt.Ar/Le increased only 11.2% for boys with the most slender metacarpals. This indicated that a key factor differentiating slender from robust growth patterns for boys was the amount of subperiosteal expansion from 3 mo to 2 yr of age. Girls, on the other hand, did not show large differences in the percent increase in Tt.Ar/Le from 3 mo to 2 yr, indicating that the difference at 3 mo was a primary factor differentiating robust from slender phenotypes. The change in marrow area during postnatal growth also varied with sex and between robustness quartiles (Fig. 5B). The primary differentiating feature for boys was the amount of marrow expansion from 3 mo to 2 yr: Ma.Ar increased 192.2% for boys with robust metacarpals but only 107.2% for boys with slender metacarpals, a 2-fold difference. Ma.Ar decreased (i.e., infilled) thereafter for both robustness groups. Girls also showed rapid increases in Ma.Ar (i.e., expansion) from 3 mo to 2 yr. However, the primary differentiating feature for girls was found after 2 yr of age: Ma.Ar increased (expanded) for girls with robust bones but decreased (infilled) for girls with slender bones. This analysis showed that growth patterns were fundamentally different between sexes and between robustness quartiles.

FIG. 5.

(A) Robustness (Tt.Ar/Le) and (B) marrow area (Ma.Ar) of the second metacarpal diaphysis change over time differently for boys and girls in the most robust quartile compared with those in the most slender quartile. Quartiles were assessed using data at 8 yr of age. Error bars are SD. *p < 0.008 for boys and **p < 0.008 for girls (t-tests corrected for multiple comparisons).

DISCUSSION

Variation in robustness is compensated morphologically during postnatal growth

Recent work showed that compensatory (functional) interactions among skeletal traits during growth was responsible for adult mice acquiring unique sets of traits that were important for overall stiffness and strength.(13–15) In this study, variation in robustness of the second metacarpal diaphysis was used as a model to study how and when these compensatory trait interactions arise during postnatal growth in the human skeleton. We examined radiographs from the Bolton-Brush Collection because selection methods biased the inclusion of healthy children from economically stable homes.(24) Thus, we expected that all skeletal structures would be functionally adapted to support physiological loads. This allowed us to identify the range of functionally adapted structures and the associated growth patterns in a population. Examination of longitudinal changes in the structure of the second metacarpal from 3 mo to 8 yr of age showed that growth patterns varied in fundamentally different ways between boys and girls and with the degree of robustness. The longitudinal changes in morphological traits were entirely consistent with previous studies.(19,21,31,32)

Prior work established that movements of the subperiosteal and endocortical surfaces are coordinated during growth(19) to adapt cross-sectional morphology with physiological loading demands.(20,33–35) Because these studies reported population-averaged growth patterns, it was unclear whether growth patterns would vary in a consistent manner among individuals in response to naturally occurring variants affecting external bone size. These data provided new insight into the coordination that occurs between bone surfaces during growth. The significant negative correlations between Tt.Ar/Le and RCA after 4 yr of age (Figs. 2E and 2F) and the significant positive correlation between Tt.Ar/Le and the structural efficiency parameter, A, measured across growth (Fig. 4D) indicated that coordination of the relative movements of the subperiosteal and endocortical surfaces was consistent across the population. This coordination was responsible for generating sets of traits that were predictable based on bone robustness. Boys and girls with robust metacarpal diaphyses had proportionally thinner cortices (i.e., lower RCA), whereas boys and girls with slender diaphyses had proportionally thicker cortices (i.e., higher RCA). These results indicated that variation in robustness was compensated morphologically during postnatal growth. It will be important to extend the current analyses to a larger, contemporary population to establish normative ranges for robustness and covariation, and to determine how ethnic background and environmental conditions impact the functional adaptation of trait sets.

Because variable growth patterns resulted in unique total areas and marrow areas by 8 yr of age, the resulting compensatory interactions allowed multiple functional sets of traits to exist within the study population. These results strongly argue that a “one size fits all” paradigm does not adequately characterize the impact of variation in skeletal growth patterns on the development of bone strength. For example, a comparison of the largest and smallest robustness quartiles showed that the magnitude and direction of the temporal changes in marrow area varied with sex and robustness (Fig. 5). For girls with robust metacarpals, the marrow space expanded across growth, whereas the marrow space infilled for girls with slender metacarpals. This indicated that the relative amount of osteoblastic and osteoclastic activity on the endocortical surfaces varied with robustness. Therefore, responses to prophylactic treatment to strengthen bone may vary with sex, robustness, and the timing of treatment.

Variation in robustness is established by 2 yr of age

Identifying the mechanisms responsible for morphological variation is not only of interest to evolutionary biologists and anthropologists,(36,37) but also to orthopedists, endocrinologists, and biomedical engineers who want to predict how genetics and environment impact the development of bone strength. In our study population, robustness (Tt.Ar/Le) was normally distributed and varied ∼2-fold among individuals, consistent with prior work.(31) Robustness is not a single trait but instead represents the amount of subperiosteal expansion (Tt.Ar) relative to longitudinal growth (Le). Consequently, variation in robustness arises when genetic or environmental factors differentially affect the activities of chondrocytes directing longitudinal growth and the relative activities of osteoblasts and osteoclasts directing growth in width. Although the biological factors regulating endochondral growth overlap with those regulating subperiosteal expansion, the factors that regulate the ratio of these orthogonally directed growth processes are not understood fully.(22) The large narrow sense heritability(38,39) suggests that much of the variation in robustness can be attributed to genetic factors. Prior work showed that variation in robustness can also be attributed to environmental factors such as climatic conditions and activity level.(36)

A comparison of the largest and smallest robustness quartiles indicated that the genetic and environmental factors defined the variation in subperiosteal expansion relative to longitudinal growth by 2 yr of age. The primary aspects of growth that differentiated slender from robust phenotypes were the magnitude of robustness at 3 mo of age and the change in robustness from 3 mo to 2 yr of age, consistent with prior work.(31) For both males and females, robustness increased from 3 mo to 2 yr and stabilized despite the large amount of overall growth that occurred from 2 to 8 yr. Because robustness is a key risk factor for fractures throughout life,(2,6,8,9,40,41) it will be important to identify the global and local factors operating from birth to 2 years that differentiate robust from slender phenotypes. Furthermore, because robustness may change during and after puberty, it will also be important to determine whether the patterns established at 2 yr hold through 18 yr. Given that robustness is determined early and seems to be relatively fixed during postnatal growth, early knowledge of a child's metacarpal robustness may be predictive of fracture risk in later life.

Morphological integration establishes a narrow range of trait sets for the study population

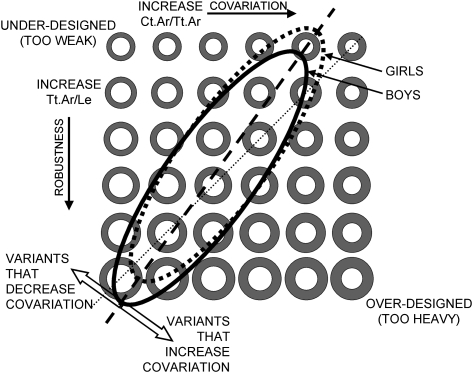
The biological factors responsible for coordinating subperiosteal and endocortical surface movements during growth remain unknown. Covariation among traits, also known as morphological integration,(42) is thought to arise during growth as traits develop together or are subject to a common stimulus, such as mechanical forces or hormones.(43) The mechanism that mediates the interplay between genetically varying traits and environmental stimuli may be a by-product of natural selection(44) or an emergent property of developmentally stable gene networks.(45) Because the normal function of complex systems can arise from different combinations of traits,(46) developmentally determined covariation in bone may result in a genetically heterogeneous population showing a limited range of functionally adapted sets of traits, depending on the number of variables involved. Based on these results, we constructed a schematic diagram showing the range of trait sets for this white population at a single age (Fig. 6). Given that covariation was similar between sexes, the range of trait sets for boys and girls was shown as overlapping but with girls showing a more slender set of traits. This schematic also shows how genetic or environmental variants may impact the development of functionally adapted structures. Given an individual's skeletal robustness, variants that move the trait set perpendicular to the dashed line would be expected to lead to underdesigned (weak) or overdesigned (bulky) structure. This may be viewed as variation in covariation (RCA) superimposed on variation in robustness (Tt.Ar/Le).

FIG. 6.

Schematic showing the large number of trait sets that could be exhibited by a genetically heterogeneous population at a single age. The different combinations of total area, Tt.Ar, and marrow area, Ma.Ar, shown vary according to robustness (y-axis) and relative cortical area (x-axis). The study population showed a fairly narrow range of trait sets, which is shown by the overlapping ellipses for boys and girls.

Once norms are established for these sets of traits in different populations, it may be possible to search for genetic or environmental variants that move an individual out of this phenotypic range or to determine how medical treatment moves an individual within this phenotypic range. Comparing populations based on their range of acquired sets of traits rather than the population averages will advance our ability to determine how ethnic background(18) and activity level(47) affect specific aspects of morphology (e.g., robustness versus functional adaptation). Additionally, establishing norms for sets of traits will help determine whether having a wide femoral neck combined with a thin cortex, a risk factor for femoral neck fractures,(11) results from growth or is a consequence of aging.(12)

Finding a narrow range of trait sets suggested that these genetically heterogeneous individuals used a common biological control to establish and maintain mechanical function of the second metacarpal when faced with variants affecting robustness. The correlation between robustness and RCA observed among the white children is consistent with the variation observed previously between various study populations(36) and among various hominoid mandibles.(48) This suggested that the biological controls buffering the interindividual variation in robustness are similar to those that buffer variation in robustness between sexes, across ethnic backgrounds, and throughout the skeleton.

Analysis of the Jo versus Ct.Ar curves (Figs. 3 and 4) and the partial regression analysis between Ct.Ar and Tt.Ar/Le suggested that the coordination between subperiosteal and endocortical expansion resulted from a biological constraint imposed on the amount of bone (i.e., Ct.Ar) that could be used to build mechanically functional structures. This constraint, which has recently been reported in the adult skeleton,(12) is a key factor explaining why the trait sets were not random but highly ordered across the study population. Coordination between surface movements makes intuitive sense from an engineering perspective and is consistent with the theory that bone maximizes stiffness using minimum mass(49) or a common set point.(50) Currey and Alexander(49) suggested that bone adapts to achieve an optimal value of K (ratio of inner to outer diameter), and further work suggested that variation in K is an indication of variation in the type of habitual loading.(51) However, our data indicated that K, which is inversely related to RCA, varied with robustness for individuals with presumably similar habitual loading patterns. A limitation of this morphological compensation is that adding bone to the endocortical surface to compensate for a slender phenotype has limited mechanical benefit.(14) The partial regression between J/R and Tt.Ar/Le showed that slender bones remain at a structural disadvantage compared with robust bones despite the strong compensatory response. This is an important finding of this study. Although we were not able to measure mineralization, we suspect that slender bones relative to body size would also have greater mineralization as a secondary level of compensation.(13,14,52–56) This may be tested in future studies using measuring techniques such as pQCT.(17)

The trait interactions reported in this study seem to result from an interplay between genetic background and Wolff's Law. Prior work examining the mouse skeleton could not determine whether variation in subperiosteal expansion among inbred mouse strains was affected directly by genetic background or was a compensatory response to genetic variants affecting marrow expansion.(15) This study, which examined longitudinal changes in human bone traits using a finer resolution of time points, may provide insight into this relationship. In the human skeleton, variation in metacarpal robustness was apparent very early during postnatal growth and preceded the age-dependent changes in marrow area. These results suggested that variation in robustness is influenced largely by genetic background and variation in marrow expansion results largely from functional adaptation. These associations would need to be confirmed in additional work. Furthermore, future studies can determine whether different loading environments impair or improve the covariation of traits, given a person's predisposition to bone robustness. Taking variation in robustness into consideration will provide a more refined understanding of whether growth patterns or prophylactic treatments lead to the development of a strong, fracture resistant skeleton.

Second metacarpal is a model to observe covariation during ontogeny

In 1960, Barnett and Nordin(57) first suggested radiogrametry of the second metacarpal as a method for determining overall bone health by measuring cortical and marrow thickness. Our results and those of others(58) support a similar notion: the development of bone strength can be assessed in a pediatric cohort using radiographs by measuring the movement of bone surfaces over time. Although the metacarpal is non–weight bearing, the second metacarpal is integral to hand movements that characterize early fine motor milestones like grasping, crawling, and hand-to-hand transfer,(59–61) and its use is later expanded to include exercise and sports.(62,63) As such, the metacarpal maintains multiple muscle attachments to both intrinsic and extrinsic muscles of the hand(64,65) and is integral to fine and powerful manipulation.(66) These data suggest that these forces are sufficient to establish mechanically functional structures in individuals showing a wide range in robustness through compensatory changes in morphology. Variation in robustness of the second metacarpal has been correlated with robustness at other skeletal sites, including weight-bearing bones like the femur and tibia.(36) Similar compensatory responses have been reported in other bones, namely the femur(12,13,54,67,68) and tibia.(14,55,56,69) Finally, measures of structure and mass at the metacarpal have been shown to be significant predictors of fracture risk at other skeletal sites, including the hip(70–72) and vertebrae,(73,74) suggesting that knowledge of the development and maintenance of metacarpal morphology has relevance to fracture prevention.

The results showed that variation in robustness, a critically important strength trait, was determined by 2 yr of age, indicating that the biological factors controlling the relationship between subperiosteal expansion and longitudinal growth were established during postnatal growth. We confirmed that acquired sets of traits varied with sex but were predictable based on robustness. The results suggested that individuals within this population share a common biological control that buffered genetic and environmental factors affecting external bone size relative to body size by allowing certain trait sets to exist without loss of mechanical function. Studies searching for determinants of fracture risk across a population should consider this natural variation in acquired sets of traits, because age-related bone loss and gain will differentially affect slender and robust structures.