Differential quantum tunneling contributions in nitroalkane oxidase catalyzed and the uncatalyzed proton transfer reaction

Abstract

The proton transfer reaction between the substrate nitroethane and Asp-402 catalyzed by nitroalkane oxidase and the uncatalyzed process in water have been investigated using a path-integral free-energy perturbation method. Although the dominating effect in rate acceleration by the enzyme is the lowering of the quasiclassical free energy barrier, nuclear quantum effects also contribute to catalysis in nitroalkane oxidase. In particular, the overall nuclear quantum effects have greater contributions to lowering the classical barrier in the enzyme, and there is a larger difference in quantum effects between proton and deuteron transfer for the enzymatic reaction than that in water. Both experiment and computation show that primary KIEs are enhanced in the enzyme, and the computed Swain-Schaad exponent for the enzymatic reaction is exacerbated relative to that in the absence of the enzyme. In addition, the computed tunneling transmission coefficient is approximately three times greater for the enzyme reaction than the uncatalyzed reaction, and the origin of the difference may be attributed to a narrowing effect in the effective potentials for tunneling in the enzyme than that in aqueous solution.

Although the dominant factor in enzyme catalysis is the lowering of the quasiclassical free energy barrier of the enzymatic reaction in comparison with the uncatalyzed process (1–3), quantum mechanical tunneling has been recognized to also play a role in enzymatic hydrogen transfer reactions (2, 3). An intriguing, yet unanswered, question is whether enzymes have evolved to enhance tunneling to accelerate the reaction rate because quantum effects on rate acceleration are much smaller than hydrogen bonding and electrostatic stabilization of the transition state (1, 4, 5). Nevertheless, a small factor of two in rate enhancement can have important physiological impacts. Although it appears straightforward to address this question by comparing the enzymatic and the uncatalyzed reaction in solution, the difficulty is to design a model system that mimics exactly the same enzymatic reaction and mechanism. The present study examines the structure of nitroalkane oxidase (NAO) complex with nitroethane and kinetic isotope effects at the primary and secondary sites for the enzymatic and the uncatalyzed reaction. The computational findings are consistent with experimental data, suggesting that there is a differential tunneling effect for the proton transfer reaction in NAO and in water. Analysis of tunneling paths reveals that the enzyme reduces both the free energy of activation and the width of the effective potential, resulting in enhanced proton tunneling in the active site.

The flavoenzyme NAO catalyzes the conversion of nitroalkanes to nitrite and aldehydes or ketones (Fig. S1) (6). The α-proton abstraction of the small substrate nitroethane by Asp-402 is rate-limiting, which is accelerated by a factor of 10⁹ over the uncatalyzed reaction between nitroethane and acetate ion in water (7).

Interestingly, the deuterium kinetic isotope effects (KIEs) are noticeably greater for the enzymatic reaction (9.2) than that in water (7.8) (see refs. 7, 8). Although tantalizing, the relatively small difference in the observed KIEs is not sufficient to conclude that there is a greater tunneling contribution in the enzymatic process than that of the uncatalyzed reaction in water. A number of experimental and theoretical studies suggested that the extent of tunneling was the same in several enzymes as in model reactions in solution (2, 9, 10), whereas other experiments showing differential tunneling behaviors may be attributed to different reaction mechanisms (2, 11–13). Nuclear tunneling cannot be measured directly, and the best experimental diagnostic of tunneling is through measurement of kinetic isotope effects (14). Klinman and coworkers showed that the presence of tunneling can be revealed indirectly by a potentiated Swain-Schaad exponent in the secondary KIEs (2, 15, 16). However, computational studies can shed light on the extent of nuclear quantum effects (NQE), including both zero-point energies and tunneling contributions (3, 17). The proton transfer reaction between nitroethane and Asp-402 catalyzed by NAO (18, 19) provides an excellent opportunity for a comparative study because the enzymatic process (Fig. S1) can be directly modeled by the reaction of nitroethane and acetate ion in water (Scheme 1). Nitroalkanes represent a prototypical system for the study of carbon acidity, which exhibit surprisingly slow deprotonation rates compared with their high acidities (20); this phenomenon has been termed as the nitroalkane anomaly (21, 22).

Scheme 1.

Proton abstraction of nitroethane by acetate ion in water.

We employ a coupled free-energy perturbation and umbrella-sampling simulation technique in Feynman centroid path integral calculations (PI-FEP/UM) to describe the NQE (23). Moreover, we adopt a combined quantum mechanical and molecular mechanical (QM/MM) method to represent the potential energy surface (22, 24). Thus, both the electronic structure of the reacting system and the nuclear dynamics are treated quantum mechanically. In our approach (23), we follow a two-step procedure (25) in which we first carry out Newtonian molecular dynamics simulations to determine the classical mechanical potential of mean force (PMF) along the reaction coordinate for the proton transfer reaction between nitroethane and Asp-402. Then, atoms that are directly involved in the proton transfer reaction are quantized, and the configurations sampled in molecular dynamics simulations are used in path-integral simulations by constraining the centroid positions of the quantized particles to the classical coordinates. This double (quantum and classical) averaging procedure is formally exact (23, 25–28), which yields the QM-PMF as a function of the centroid reaction path (29, 30). In PI-FEP/UM, the ratio of the quantum partition functions for different isotopes, which yields the KIEs, is obtained by free-energy perturbation from a light isotope mass into a heavier one within the same centroid path-integral simulation (23), avoiding the difference between two free-energy barriers with greater fluctuations than the difference itself for the two isotopic reactions. Consequently, the PI-FEP/UM method is unique in that it yields accurate results on computed KIEs, including secondary KIEs that are not possible by other path-integral simulation methods (23, 31). The method has been demonstrated in a series of studies of chemical reactions in solution and in enzymes (22, 31, 32).

Results

Crystal Structure and Computational Model of the Michaelis Complex.

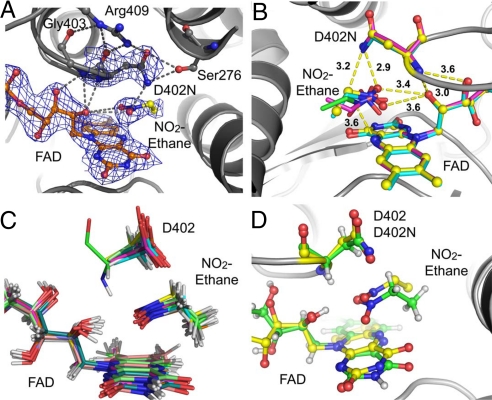
We have determined crystal structures of NAO complexes with a series of nitroalkanes (33) including nitroethane, which is reported here (Fig. 1A). The data collection and refinement statistics are provided in Table S1. The experiment was designed to provide a crucial validation of the computational method because the Michaelis complex (MC) structure is typically not available for an enzyme system, and a computational model must be constructed before simulations can be carried out. Thus, we have performed separate experimental and computational investigations of the NAO·nitroethane complex and compared the results after each study was completed.

Fig. 1.

The crystal structure of the D402N-nitroethane complex. The active site is in subunit D (A) and the superposition of the substrate configurations from all four active sites are in the asymmetric unit cell (B). The 10 computational models are shown in C, and the comparison between the crystal structure for the D402N nitroethane complex (carbon atoms in yellow) and one of the computational models (carbon in green) is displayed in D. The 2mF_o – ΔF_c electron density map (2.4-Å resolution) is shown with 1.5 sigma contours (see ref. 33). The atoms are colored by atom type with the exception of the FAD (carbon atoms in orange) and nitroethane (carbon atoms in yellow).

We used the NAO isosteric D402N mutant to trap the MC for crystallographic analysis because it is not active with neutral nitroalkanes (34). The 2.4-Å resolution cocrystal structure with nitroethane demonstrates that the mutation does not significantly perturb the active site. The electron density maps are consistent with nitroethane located above the FAD re-face (Fig. 1A). In the crystal structure, the oxygen atoms of the R-NO₂ moiety form hydrogen bonds with the ribityl 2′-OH group (3.4 and 3.7 Å). This hydrogen bonding network places the nitroethane, C_α, directly “below” the side chain of Asn-402. Slightly different substrate orientations are observed in each of the four subunits in the crystal structure of the D402N nitroethane complex (Fig. 1B). The variability likely results from a combination of real enzyme-substrate binding effects and the modest resolution of the crystal structure. For comparison, the crystal structures with the substrates 1-nitrohexane or 1-nitrooctane demonstrate similar complexes, but with less binding orientation variability (33). Thus, nitroethane exhibits the most active site variability in the D402N complex, which correlates well with the lower k_cat/K_m value relative to the longer chain nitroalkane substrates (7, 8). This rate difference is consistent with the shorter substrate exhibiting less potential hydrophobic interactions with the enzyme than the longer chain substrates.

On the computational side, we used the 2.07-Å resolution crystal structure of the oxidized wild-type NAO, complexed with the inhibitor spermine [Protein Data Bank (PDB) ID code 2C12] (19), to construct the MC model. We replaced spermine by nitroethane and randomly generated 10 orientations in the active site with the C_α atom placed ≈3.5 Å from the Asp-402 side-chain oxygen atoms (Fig. S2). These structures were minimized, followed by 100 ps of hybrid QM/MM simulations; nine of the 10 structures converged to a unique conformation within the first 25 ps, whereas the 10th structure also reoriented after 50 ps (Fig. 1C). The MC structure is characterized by hydrogen bonding interactions of the nitro group with the ribityl 2′-OH group and the Asp-402 amide group, in close agreement with the D402N·nitroethane X-ray structure. The average distance between the C_α atom of nitroethane and the N5 atom of the isoalloxazine ring is ≈3.6 Å. Fig. 1D shows the superimposed structures from X-ray diffraction and from molecular dynamics simulations; the agreement is excellent, suggesting that our simulation procedure can reasonably sample the conformational subspace of the substrate in the present system.

Potential of Mean Force.

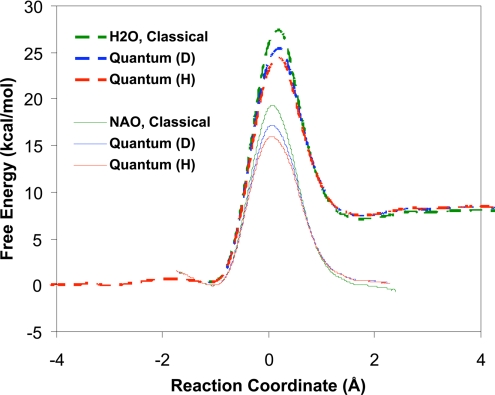
The centroid (quantum mechanical) PMFs from PI-FEP/UM simulations for the nitroethane-deprotonation reaction in NAO (Fig. S1) and in water (Scheme 1) are shown in Fig. 2, and the computed free energies of activation are listed in Table 1. The reaction coordinate is defined as the difference between the breaking (donor–proton) and forming (acceptor–proton) bond distances (Scheme 1). In the Feynman path-integral representation (23, 27, 28), the centroid positions of the discrete paths of quantized particles are used to specify the reaction coordinate (29, 30). The present PI-FEP/UM method allows for accurate KIE determination by free energy perturbation between different isotopic masses within a single simulation rather than separate calculations for different isotopic reactions (23).

Fig. 2.

Computed classical (green) and quantum potentials of mean force for the proton (H) in red and deuteron (D) in blue abstraction of nitroethane by Asp-402 in nitroalkane oxidase (solid curves) and by acetate ion in water (dashed curves). The reaction coordinate is defined as the difference between the distances of the transferring proton (or deuteron) and the donor carbon atom and acceptor oxygen atom. The centroid coordinates are used in path-integral simulations.

Table 1.

Computed classical mechanical (ΔG_cm^≠) and quantum mechanical (ΔG_qm^≠) free energies of activation, total nuclear quantum effects (ΔΔG_qm^≠), and the tunneling transmission coefficient (κ) and dominant tunneling energy (ΔΔG_tunn^≠) for the deuteron (D) and proton (H) transfer reactions between nitroethane and acetate ion in water and in nitroalkane oxidase enzyme

Reaction	ΔGcm≠	ΔGqm≠ (D)	ΔGqm≠ (H)	ΔΔGqm≠ (D)	ΔΔGqm≠ (H)	ΔΔGtunn≠ (H)	κ
H2O	27.4	25.5	24.4	−1.9	−3.0	−0.14	1.3
NAO	19.3	17.2	15.9	−2.1	−3.4	−0.74	3.5

Free energies are given in kcal/mol and tunneling transmission coefficient is unitless.

Fig. 2 shows that the computed free energies of activation are 15.9 and 24.4 kcal/mol for the enzymatic and the uncatalyzed proton transfer reaction in water, respectively, which are in good accord with the corresponding experimental results (14.0 and 24.8 kcal/mol) (7). Consequently, we estimate that NAO stabilizes the transition state of the proton abstraction by 8.5 kcal/mol from computation or 10.8 kcal/mol from experiment. The computed free energy of reaction in water (7.1 kcal/mol) (22) is also in accord with experiment (5.2 kcal/mol) (20), and the computed free energy of reaction yields a pK_a of 9.9 for nitroethane compared with experiment (8.6) (35). In the enzyme, the relative free energies of the MC and the product complex are nearly identical, indicating that the acidity of nitroethane is enhanced to a value similar to that of Asp-402. Overall, the structural and free-energy results demonstrate that the present QM/MM and path integral methods can provide an adequate description of the uncatalyzed reaction in water and in NAO, allowing us to further analyze kinetic data.

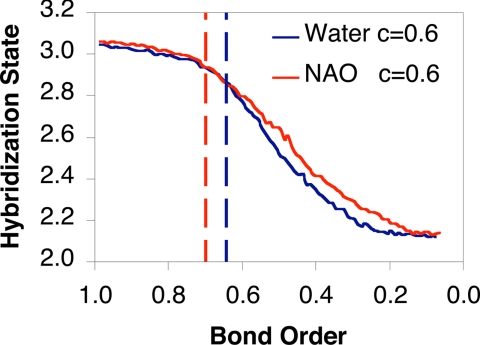
The slow deprotonation rate of a nitroalkane in water has been rationalized based on the principle of nonperfect synchronization in that product stabilization by solvation lags behind the progress of the reaction coordinate (20). Computational studies have shown that there is little charge delocalization at the transition state in the gas phase and that the C_α rehybridization is only 10% at the transition state for aqueous reaction (Fig. 3) (22). The lack of redistribution of the anionic charge into the nitro group results in poor solvation at the transition state and an increased free-energy barrier. Fig. 3 compares the progress of the rehybridization at the C_α center as a function of the C_α–Η bond order for the aqueous and enzymatic reactions. Evidently, there is no appreciable difference in rehybridization state in the two environments; the enzymatic process even shows somewhat slower geometrical rearrangement than the reaction in water. The similarity in the reaction progress demonstrates that the observed difference in KIE is not due to change in the reaction mechanism.

Fig. 3.

Hybridization state of the C_α atom of nitroethane as a function of the Pauling bond order (n = n₀ exp[(r₀-r_C-H)/c], where c = 0.6 for transition structure and r₀ is the equilibrium bond length) for the breaking C_α–H bond as an indicator of the reaction progress in the enzyme (red) and in water (blue). The C_α–H bond order changes from one to zero in the deprotonation reaction as the C_α atom changes from an sp³ tetrahedral structure into an sp² planar configuration. The locations of the transition state are indicated by the vertical dashed lines.

Kinetic Isotope Effects.

The computed primary and secondary KIEs for the nitroethane deprotonation reaction in water and in the enzyme are listed in Table 2, along with the total KIEs that have been determined for the perdeuterated substrate nitroethane at the C_α position (7). In PI-FEP/UM simulations, the computed NQE includes both zero-point energies and nuclear tunneling, and their contributions to the computed KIEs are not separable (23). Thus, it is useful to use semiclassical methods (36) to estimate the tunneling transmission coefficient to gain an understanding of the origin of NQE in NAO catalysis. Consequently, we have used the ensemble-averaged variational transition state theory (EA-VTST), developed previously (3, 17, 37) and successfully applied to a variety of enzyme systems (3, 17), to separate tunneling from the overall quantum effects. The results are listed in Table 1, in addition to the phenomenological free energy that lowers the classical barrier due to tunneling, ΔΔG_tunn^≠ (H).

Table 2.

Computed primary (1°) and secondary (2°) kinetic isotope effects, and computed and experimental total deuterium isotope effects for the proton abstraction of nitroethane in NAO and in water

1°	kHH/kDH	kHH/kTH	kDD/kTD
H2O	6.63 ± 0.31	13.0 ± 1.0	2.17 ± 0.04
NAO	8.36 ± 0.58	18.1 ± 2.4	2.38 ± 0.05
2°	kHH/kHD	kHH/kTH	kDD/kDT
H2O	1.340 ± 0.132	1.375 ± 0.183	1.096 ± 0.048
NAO	1.213 ± 0.150	1.229 ± 0.209	1.050 ± 0.025
kHH/kDD	Calc.	Expt.
H2O	8.3 ± 1.1	7.8 ± 0.1
NAO	10.1 ± 1.4	9.2 ± 0.4

Subscripts and superscripts are used to specify the rate constant for isotope substitutions at the primary and secondary position, respectively.

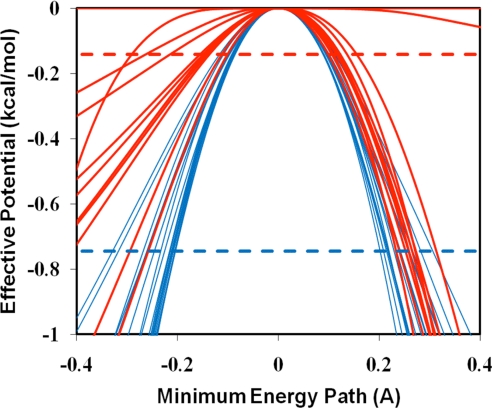
Fig. 4 depicts the effective potentials (36) that include zero-point energy of all bound vibrations except that corresponding to the reaction coordinate for the proton transfer process in water and in NAO. In these calculations, the minimum-energy reaction paths were determined starting from each transition state with the surrounding solvent and protein coordinates fixed at the configurations in the transition state ensemble that had been determined during the free-energy simulations (17, 37). In Fig. 4, we show the reaction paths used to obtain the average tunneling transmission factors. The average tunneling energies for the deprotonation reactions in water and in the enzyme are depicted as horizontal lines. Fig. 4 shows that the minimum-energy paths have broad distributions, which overlap between reaction paths for the enzymatic reaction (blue) and the uncatalyzed process (red); however, it is clear that the effective potentials for the enzymatic reaction paths are more narrowly distributed than those for the reactions without the catalyst. In Fig. 4, the mass-weighted minimum-energy path in angstrom per atomic mass unit is used to represent the reaction coordinate.

Fig. 4.

Effective potentials (including zero-point energies) for the proton abstraction of nitroethane by Asp-402 in nitroalkane oxidase (blue) and by acetate ion in water (red). The reaction coordinate is the mass-weighted distance from the transition state in angstrom per atomic mass unit. The horizontal dashed lines indicate average dominant tunneling energies.

Discussion

Fig. 2 shows the classical and quantum mechanical PMF for the proton and deuteron deprotonation reactions in water and in the enzyme, which are obtained from Newtonian molecular dynamics simulations and Feynman path-integral calculations. With the inclusion of NQE in the latter simulations (23), the computed free energies of activation for the deuteron and proton transfer reactions between nitroethane and acetate ion in water are, respectively, 1.9 and 3.0 kcal/mol lower than the corresponding “classical” barrier (Table 1). Similar NQE has been found in other enzymatic reactions and the corresponding uncatalyzed reactions (3). In the enzyme, we found that NQEs are slightly enhanced over the uncatalyzed reaction, lowering the classical barrier by 2.1 and 3.4 kcal/mol for deuteron and proton transfer to Asp-402. The results emphasize the importance of including NQE in enzyme kinetics modeling to obtain accurate rate constants (3, 17). Moreover, we note that the difference in the free-energy barrier between the two isotopic processes is also increased in the enzyme compared with that in solution. The dominant factor for the enzymatic rate enhancement is transition-state stabilization by the enzyme with important contributions from the 2′-OH group of the flavin cofactor in comparison with the uncatalyzed process in aqueous solution. The stabilization effect is indicated by the difference in barrier height from classical molecular dynamics simulations (Fig. 2). The contributions to transition-state stabilization from hydrogen bonding interactions in the active site and the effects of the flavin cofactor will be reported later; we focus the present study on NQE in catalysis, which has not been quantified previously (3), albeit, its contribution to the rate enhancement is relatively small.

Experimentally, the proton transfer of nitroethane to a carboxylate base shows a modest increase in KIE from 7.8 in water to 9.2 in NAO (7). For comparison, the computed KIEs from PI-FEP/UM simulations are slightly higher than the experimental data shown in Table 2, but the relative increase from water to the enzyme is reproduced. The individual primary and secondary KIEs have not been measured experimentally because the rate-limiting step is no longer the proton transfer reaction for larger nitroalkane substrates, whereas there is no stereoselectivity for the small substrate nitroethane (7). From path-integral and free-energy perturbation simulations, we find that the enzymatic process has greater primary KIEs than the corresponding reaction without the catalyst in water. The difference in KIE is consistent with the free energy results shown in Fig. 2 and Table 1, where the enzymatic reaction has somewhat greater NQE than that of the uncatalyzed reaction. However, the secondary KIEs are smaller in NAO than in water. Interestingly, the product of the primary and secondary deuterium KIEs in water yields a value of 8.9, somewhat greater than the computed value of 8.3 for the perdeuterated substrate (7, 31), suggesting that there is slight deviation from the rule of geometric mean. For the enzymatic reaction, the rule of geometric mean is followed.

The finding of a larger KIE for the proton transfer reaction in the NAO enzyme than that in water, both from PI-FEP/UM simulations and from experiments, suggests that there is differential NQE between the catalyzed and uncatalyzed reactions. However, the total quantum effect does not distinguish between nuclear tunneling and zero-point effect. A diagnostic approach that has been proposed by Klinman to assess the involvement of tunneling contributions in enzymatic reactions (2, 15) is the use of the mixed Swain-Schaad exponent, which describes the relationship between the H/T secondary KIE when the primary position is occupied by hydrogen with that of D/T when the primary position has deuterium. A value that is greater than the semiclassical limit of 3.3 is typically attributed to the presence of tunneling (2). Using the data in Table 2, we obtained Swain-Schaad exponents of 3.5 and 4.3 for the proton abstraction of nitroethane in water and in NAO, respectively. Thus, according to this criterion, hydrogen tunneling is not significant for the uncatalyzed reaction in water, whereas it is enhanced in the enzymatic process. Importantly, this difference suggests that there is differential hydrogen tunneling in the catalyzed and uncatalyzed reactions.

To further assess tunneling effects, we used EA-VTST to separate tunneling from the overall NQE (3, 17, 37). The computed tunneling transmission coefficients in Table 1 are 1.3 and 3.5 for the uncatalyzed and NAO-catalyzed process, respectively, implying that differential tunneling effects accelerate the proton abstraction rate by a factor of 2.7 in catalysis. Analyses of the dynamic trajectories correspond to the minimum-energy reaction path with the inclusion of zero-point energy from all bound vibrations except the degree of freedom corresponding to the reaction coordinate (36, 37). An ensemble of reaction paths has been obtained, starting from the transition-state ensemble generated during the umbrella sampling simulation (3), and the results in Fig. 4 show that the origin of enhanced tunneling may be attributed to changes in the adiabatic potential energy surface for the proton transfer reaction in going from aqueous solution into the enzyme active site. Fig. 4 depicts the effective potentials of the proton transfer trajectories for the reactions in water and in NAO. We found that the effective potentials have a tighter and narrower distribution in the enzyme environment than that in aqueous solution, leading to greater average tunneling contributions for the proton transfer between nitroethane and Asp-402. On average, the tunneling paths for the enzymatic reaction is 0.6 kcal/mol lower than that for the uncatalyzed reaction in water from the saddle point of the effective potential (Fig. 4 and Table 1). Of course, tunneling is also influenced by the barrier height. In the present study, the effects of barrier height are considered in that the minimum energy reaction paths shown in Fig. 4 are obtained from the transition state ensemble. The difference in NQE is a relatively small factor in catalysis in comparison with the overall barrier reduction (8.5 kcal/mol); however, the key finding of the present study is that there is an unambiguous contribution from nuclear quantum effects to the enzymatic rate enhancement in the NAO-catalyzed proton transfer reaction.

The presence of quantum tunneling in enzymatic processes was shown in the hydride transfer reaction catalyzed by alcohol dehydrogenase (15). To assess tunneling contributions to catalysis, it is rare that a reaction in water can be compared with the same reaction catalyzed by an enzyme in sufficient detail (2, 12). In the present study, we present overwhelming evidence demonstrating quantitatively differential NQE that contributes to catalysis in NAO: We found that the overall NQE has a greater contribution to lowering the classical barrier in the enzyme, and there is a larger difference in quantum effects between proton and deuteron transfer for the enzymatic reaction than the uncatalyzed one. Both experiment and computation show enhanced primary KIEs in the enzyme over that in water. The mixed Swain-Schaad exponent for the enzymatic reaction is greater than the semiclassical limit without tunneling, and it is exacerbated relative to that in the absence of the enzyme. Employing an entirely different computational method and theory, we found that the tunneling transmission coefficient is approximately three times greater for the enzyme reaction than the uncatalyzed reaction. In addition, the origin of the difference may be attributed to a narrowing effect in the effective potentials for tunneling in the enzyme than that in aqueous solution. One may argue that the rate acceleration due to hydrogen tunneling is a small factor in NAO catalysis in comparison with the much larger and dominating effect of the lowering of the quasiclassical free energy barrier; however, small rate enhancement can still be physiologically significant for an enzyme with a relatively slow rate. Significantly, the present work demonstrates that differential quantum tunneling contributions, albeit small, are used by the nitroalkane oxidase enzyme in catalysis.

Methods

Molecular Dynamics Free-Energy Simulations.

The PMF was obtained from a series of 35 umbrella sampling simulations for the reaction in water and 17 in the enzyme (4). Periodic boundary conditions were used along with the particle mesh-Ewald method (38) for the uncatalyzed reaction in a box of ≈30 × 30 × 30 ų. Stochastic boundary molecular dynamics were used on one active site of the tetrameric enzyme with a solvation sphere of 24 Å (39). Each umbrella sampling window included at least 100 ps of equilibration followed by 100 ps of averaging at 25 °C. Because these simulations were performed using Newtonian molecular dynamics simulations, the computed free-energy changes correspond to the classical mechanical PMF (3). The QM-PMFs were obtained using a double averaging procedure by centroid path-integral simulations on configurations saved during the umbrella sampling (23, 25, 26). In essence, the centroid path-integral simulations yield the free energy difference between the classical mechanical and the quantum mechanical PMFs (23, 25, 26). To evaluate the KIEs, the centroid path-integral simulations were carried out for the light isotopic reactions, and the ratio of the partition function between two isotopic reactions was determined by free-energy perturbation theory from the light mass into a heavier one (25). A unique feature of our PI-FEP/UM method is that highly accurate KIEs, including secondary KIEs, can be obtained because a single set of simulations is performed (23, 31). In contrast, two separated simulations are needed in other approaches to obtain the quantum mechanical PMFs, one for each isotopic reaction, and the statistical fluctuations in the computed free energy barriers are typically larger than the free energy difference, especially for secondary KIEs. Although a reasonable estimate can be obtained for primary isotope effects, it is very difficult to yield meaningful results for secondary KIEs before the development of the PI-FEP/UM method. To our knowledge, secondary KIEs have not been reported for enzymatic reactions from path-integral simulations. In the present study, we quantized the donor (C_α) and acceptor (O) heavy atoms and the α-protons of nitroethane along with atoms directly connected to them. Each quantized particle was represented by 32 beads, and convergence was validated by using 8, 16, and 64 beads (27, 28). We used a bisection sampling technique (27) in all centroid path-integral simulations and a total of 10⁵ free-particle configurations were sampled in each system.

For the combined QM/MM potential (24), we used a semiempirical model that has been specifically parameterized for the proton transfer reaction between nitroethane and acetate ion to reproduce experimental or ab initio data at the Gaussian-3 (G3) level of theory (22). Consequently, the quality of such a specific reaction model (22, 31) is comparable with ab initio calculations at the G3 level. The calibration was done only for the reaction in the gas phase, i.e., the intrinsic performance of the QM model, and the performance of the QM/MM potential was validated for the solution phase reaction (31).

Ensemble-Averaged Variational Transition-State Theory.

In EA-VTST calculations (3, 17, 37), we used the microcanonically optimized multidimensional tunneling path, in which the small curvature tunneling and large curvature tunneling paths are optimized, to determine the tunneling coefficient and the dominant tunneling energy (40, 41). The transition-state ensemble was obtained during the free-energy simulations for determining the PMF, and the tunneling transmission coefficient for the enzyme was averaged over 19 reaction trajectories. The mass-weighted minimum-energy path, corresponding to the steepest descent path in isoinertial coordinate of the reactants, which are nitroethane and the side chain of Asp-402 or an acetate ion, was optimized for each transition-state configuration in which the surrounding solvent and protein atoms are kept frozen. The effective adiabatic potential (Fig. 4) for locating the transition state and for computing the tunneling transmission coefficient was obtained by adding the zero-point vibrational energy of the reactants to the potential energy. All simulations were carried out using the program CHARMM (c34a1) (42) and POLYRATE (43) along with the CHARMM22 force field (44) and the TIP3P model for water (45).

Additional Details.

For details of the crystal structure determination, see Table S1. For details of initial enzyme–substrate configurations used in MC optimization, see SI Text. In addition, all input scripts, topology, parameter, and coordinate files are available upon request from the corresponding authors.