Spectrally-resolved Bioluminescence Tomography with the Third-order Simplified Spherical Harmonics Approximation

Abstract

Bioluminescence imaging has been extensively applied to in vivo small animal imaging. Quantitative three-dimensional bioluminescent source information obtained by using bioluminescence tomography can directly and much more accurately reflect biological changes as opposed to planar bioluminescence imaging. Preliminary simulated and experimental reconstruction results demonstrate the feasibility and promise of bioluminescence tomography. However, the use of multiple approximations, particularly the diffusion approximation theory, affects the quality of in vivo small animal-based image reconstructions. In the development of new reconstruction algorithms, high-order approximation models of the radiative transfer equation and spectrally-resolved data introduce new challenges to the reconstruction algorithm and speed. In this paper, a SP₃-based (the third-order simplified spherical harmonics approximation) spectrally-resolved reconstruction algorithm is proposed. The simple linear relationship between the unknown source distribution and the spectrally-resolved data is established in this algorithm. A parallel version of this algorithm is realized, making BLT reconstruction feasible for the whole body of small animals especially for fine spatial domain discretization. In simulation validations, the proposed algorithm shows improved reconstruction quality compared with diffusion approximation-based methods when high absorption, superficial sources and detection modes are considered. In addition, comparisons between fine and coarse mesh-based BLT reconstructions show the effects of numerical errors in reconstruction image quality. Finally, BLT reconstructions using in vivo mouse experiments further demonstrate the potential and effectiveness of the SP₃-based reconstruction algorithm.

1. Introduction

Bioluminescence imaging has become an indispensable imaging modality in preclinical research (Ntziachristos et al. 2005)(Weissleder 2002). It is extensively applied and is an efficient tool for in vivo small animal research. Usually, in bioluminescence imaging, bioluminescence probes (such as luciferase gene) are used to label the specified biological targets. The photons emitted by bioluminescence probes are detected after they are scattered and partly absorbed within the small animal body. Therefore, when using planar bioluminescence imaging, the collected surface photon distribution does not accurately and directly reflect the biological target activity (Virostko et al. 2007). The acquisition of three dimensional bioluminescence source information (that is bioluminescence tomography (BLT)) becomes necessary for improved observation of biological phenomena.

Previous work on bioluminescence tomography has demonstrated its potential in simulations and experimental reconstructions. However, when performing BLT reconstructions on small animals, several approximations and assumptions can lead to poor bioluminescence source localization (Virostko et al. 2007). Single wavelength and mixed spectral BLT reconstructions produce poor results especially when bioluminescence sources are located far from the animal surface. On the other hand, the use of spectrally resolved information in whole-body small animal reconstruction violates the assumptions of the diffusion approximation theory in some cases (such as high absorption tissues, void-like domains, small tissue geometries and so on). A priori information and high-order approximations to the radiative transfer equation (RTE) need to be further investigated to improve BLT reconstruction. Anatomical information and relevant optical properties (Alexandrakis et al. 2005)(Lv et al. 2007), spectrally-resolved measurements (Kuo et al. 2004)(Chaudhari et al. 2005)(Alexandrakis et al. 2005)(Cong & Wang 2006)(Dehghani et al. 2006), and the spatial distribution of surface photons (Cong et al. 2005) are validated and extensively applied in reconstructions. BLT reconstructions employing direct RTE models and high order approximations need to be further developed (Klose et al. 2005)(Klose & Beattie 2008). With respect to the heterogeneous tissue characteristics and high-order approximation models in small animals, spectrally-resolved BLT reconstruction becomes costly in speed and even impossible to achieve in terms of the memory requirements of sequential execution. In this context, parallel execution mode makes BLT reconstruction feasible.

BLT reconstructions can be realized by establishing an objective function and minimizing the discrepancies between the surface measurements and the computed photon density. Similarly, as in statistical reconstruction in positron emission tomography (PET), a source basis function-based reconstruction has been developed (Alexandrakis et al. 2005). In this method, each point or element in the discretized domain is treated as a bioluminescence source. The boundary photon density information is collected as source basis functions and then the corresponding optimization is performed to obtain the reconstruction results. Source basis functions (such as the system response P matrix in PET) can be calculated prior to source reconstruction using deterministic or Monte Carlo methods, allowing for a reduction in reconstruction time. However, since virtually all of the bioluminescence photons are scattered during their propagation, and the boundary photon density is sensitive to propagation domain changes (Alexandrakis et al. 2006), precalculating source basis functions will affect the reconstruction quality to a certain degree. Moreover, during the reconstruction, “forward projection” and “back-projection” are time-consuming. Another method is to determine the direct linear relationship between the unknown source distribution and the boundary photon density (Cong et al. 2005). Although matrix inversion calculations need to be performed, the obtained least-square (LS) problem based on the linear relationship facilitates a solution to the BLT problem and reduces the reconstruction time.

In this work, a spectrally-resolved reconstruction algorithm is developed using the third-order simplified spherical harmonics (SP₃) approximation. A linear relationship between the unknown source distribution and the measurable boundary flux is established. To handle the data storage and process problems of sequential execution, the relevant data matrices are operated in distributed mode. Parallel execution is performed during the entire reconstruction, making BLT reconstruction feasible especially on the fine mesh of the domain. Validation of the simulation in the cases of high absorption domain, superficial source positions and single- and multi-view data acquisitions shows the effectiveness of the proposed algorithm. BLT reconstructions on coarse and fine mesh demonstrate the effects of domain discretization on reconstruction quality and the necessity of selecting a suitable fine mesh. Experimental BLT reconstructions further show the potential of the SP₃-based reconstruction algorithm for practical bioluminescence imaging. In the next section, we present the SP₃-based spectrally-resolved BLT algorithm. In the third section, we evaluate the performance of the proposed method with respect to several factors discussed above. In the final section, we discuss relevant issues and conclude this paper.

2. Formulation

2.1. Spectrally resolved BLT reconstruction with the SP₃ approximation

2.1.1. SP₃ approximation

The radiative transfer equation (RTE) comes from the energy conservation principle (Vo-Dinh 2002). In the RTE, some wave phenomena such as polarization and interference are ignored. When the surface optical signals are collected in bioluminescence imaging, the light source is generally assumed to be invariant. Therefore, the steady-state RTE in 3D is used for the wavelength λ (Klose et al. 2005):

$$\begin{array}{l}\widehat{\mathbf{s}}·\nabla \psi (\mathbf{r},\widehat{\mathbf{s}},\lambda )+({\mu }_s(\mathbf{r},\lambda )+{\mu }_a(\mathbf{r},\lambda ))\psi (\mathbf{r},\widehat{\mathbf{s}},\lambda )\\ ={\mu }_s(\mathbf{r},\lambda ){\int }_{4\pi }p(\widehat{\mathbf{s}},{\widehat{\mathbf{s}}}^{\prime })\psi (\mathbf{r},{\widehat{\mathbf{s}}}^{\prime },\lambda )\text{d}{\widehat{\mathbf{s}}}^{\prime }+S(\mathbf{r},\widehat{\mathbf{s}},\lambda )\end{array}$$ (1)

where ψ(r, ŝ, λ), μ_a(r, λ), μ_s(r, λ), and S(r, ŝ, λ) are the radiance, absorption coefficient, scattering coefficient, and bioluminescence source respectively; p(ŝ, ŝ′) is the scattering phase function and gives the probability of a photon scattering anisotropically from the incoming direction ŝ′ to the outgoing direction ŝ. Generally, the Henyey-Greenstein (HG) phase function is usually used to characterize this probability (Ishimaru 1997):

$$p(cos\theta )=\frac{1-g^2}{4\pi {(1+g^2-2gcos\theta )}^{3/2}}$$ (2)

where g is the anisotropy parameter; cos θ denotes the scattering angle and is equal to ŝ·ŝ′ when we assume that the scattering probability only depends on the angle between the incoming and outgoing directions. The HG phase function is easily expanded by the Legendre polynomial and is therefore convenient for numerical computation. After a series of deductions in the planar geometry with the spherical harmonics methods (P_N), the 3D SP₃ approximation is obtained by replacing the 1D diffusion operator with its 3D counterpart (Klose & Larsen 2006):

$$\{\begin{array}{l}-\nabla ·\frac{1}{3{\mu }_{a1}(\lambda )}\nabla {\varphi }_1(\lambda )+{\mu }_a(\lambda ){\varphi }_1(\lambda )-(\frac{2}{3}{\mu }_a(\lambda )){\varphi }_2(\lambda )=S(\lambda )\hfill \\ -(\frac{2}{3}{\mu }_a(\lambda )){\varphi }_1(\lambda )-\nabla ·\frac{1}{7{\mu }_{a3}(\lambda )}\nabla {\varphi }_2(\lambda )+(\frac{4}{9}{\mu }_a(\lambda )+\frac{5}{9}{\mu }_{a2}(\lambda )){\varphi }_2(\lambda )=-\frac{2}{3}S(\lambda )\hfill \end{array}$$ (3a,3b)

where μ_an = μ_s(1 − gⁿ) + μ_a(n = 1, 2, 3); and ϕ_i(i = 1, 2) are the composite moments relevant to the Legendre moments. The Legendre moments can be obtained by expanding ψ with the P_N approximation. Detailed deductions are described in (Klose & Larsen 2006). We use

$$R_n={\int }_0^{1}R(\omega ){\omega }^n\text{d}\omega$$ (4)

to depict the effect of reflectivity in different angular moments on the SP_N approximation. Since there are no external sources present in bioluminescence imaging, the corresponding boundaries are given (Klose & Larsen 2006):

$$\{\begin{array}{l}(\frac{1+B_1}{3{\mu }_{a1}(\lambda )})\mathbf{v}·\nabla {\varphi }_1(\lambda )-(\frac{D_1}{{\mu }_{a3}(\lambda )})\mathbf{v}·\nabla {\varphi }_2(\lambda )=-(\frac{1}{2}+A_1){\varphi }_1(\lambda )+(\frac{1}{8}+C_1){\varphi }_2(\lambda )\hfill \\ -(\frac{D_2}{{\mu }_{a1}(\lambda )})\mathbf{v}·\nabla {\varphi }_1(\lambda )+(\frac{1+B_2}{7{\mu }_{a3}(\lambda )})\mathbf{v}·\nabla {\varphi }_2(\lambda )=(\frac{1}{8}+C_2){\varphi }_1(\lambda )-(\frac{7}{24}+A_2){\varphi }_2(\lambda )\hfill \end{array}$$ (5a,5b)

The coefficients A₁, …, D₁, …, A₂, …, D₂ can be found in (Klose & Larsen 2006). Furthermore, the exiting partial current J⁺ is obtained at each boundary point r:

$$\begin{array}{l}{J}^{+}(\lambda )=(\frac{1}{4}+J_0)({\varphi }_1(\lambda )-\frac{2}{3}{\varphi }_2(\lambda ))-(\frac{0.5+J_1}{3{\mu }_{a1}(\lambda )})\mathbf{v}·\nabla {\varphi }_1(\lambda )\\ +\frac{1}{3}(\frac{5}{16}+J_2){\varphi }_2(\lambda )-(\frac{J_3}{7{\mu }_{a3}(\lambda )})\mathbf{v}·\nabla {\varphi }_2(\lambda )\end{array}$$ (6)

where the coefficients J₀, …, J₃ can also be found in (Klose & Larsen 2006). Note that SP₁ (the diffusion equation) can be obtained correspondingly by setting ϕ₂ = 0. When the optical data at the discretized wavelength λ_k is collected in an experiment, the general equation form for Eqs. 3a and 3b is followed to describe the proposed reconstruction algorithm

$$-\nabla ·{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)\nabla {\varphi }_i({\lambda }_k)+{\mathcal{C}}_{i,{\varphi }_1}({\lambda }_k){\varphi }_1({\lambda }_k)+{\mathcal{C}}_{i,{\varphi }_2}({\lambda }_k){\varphi }_2({\lambda }_k)={\mathcal{S}}_i({\lambda }_k)(i=1,2)$$ (7)

2.1.2. Reconstruction method

In the frame of the finite element analysis, after applying the Gauss divergence theorem and considering Robin boundary conditions (Eqs. 5a–5b), we get the following equation for BLT reconstruction:

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}\left\{{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)\nabla {\varphi }_i({\lambda }_k)·\nabla v+[{\mathcal{C}}_{i,{\varphi }_1}({\lambda }_k){\varphi }_1({\lambda }_k)+{\mathcal{C}}_{i,{\varphi }_2}({\lambda }_k){\varphi }_2({\lambda }_k)]v\right\}\text{d}\mathrm{\Omega }\\ +{\int }_{\partial \mathrm{\Omega }}\left\{-{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)[f_{\mathbf{v}·{\varphi }_i}({\varphi }_1({\lambda }_k))+f_{\mathbf{v}·{\varphi }_i}({\varphi }_2({\lambda }_k))]v\right\}\text{d}\partial \mathrm{\Omega }-{\int }_{\mathrm{\Omega }}{\mathcal{S}}_i({\lambda }_k)v\text{d}\mathrm{\Omega }\end{array}$$ (8)

The function f_v·ϕ_i(·) can be obtained through solving the boundary equations (5a–5b), and expressed by the linear combination of ϕ₁(λ_k), ϕ₂(λ_k).

When the reconstruction domain Ω is discretized as a volumetric mesh T, the space of the linear finite element V is introduced on T, satisfying V ⊂ H¹(Ω). In that case, ϕ_i(λ_k) and S_i(λ_k) are approximated as:

$$\{\begin{array}{l}{\varphi }_i(\mathbf{r},{\lambda }_k)\approx {\sum }_{p=1}^{N_{\mathcal{P}}}{\varphi }_{i,p}({\lambda }_k)v_p(\mathbf{r})\hfill \\ S_i(\mathbf{r},{\lambda }_k)\approx {\sum }_{p=1}^{N_{\mathcal{P}}}{s}_{i,p}({\lambda }_k)v_p(\mathbf{r})\hfill \end{array}$$ (9a,9b)

where ϕ_i,p(λ_k) and s_i,p(λ_k) are the discretized values at a discretized point p when using the basis function v_p(r); N^P is the total number of discretized points on the entire domain. Considering Equ. 8 and the SP₃ approximation, for a volumetric element τ_e, we have

$$\left[\begin{array}{ll}{m}_{1{\varphi }_1}({\lambda }_k)\hfill & m_{1{\varphi }_2}({\lambda }_k)\hfill \\ m_{2{\varphi }_1}({\lambda }_k)\hfill & m_{2{\varphi }_2}({\lambda }_k)\hfill \end{array}\right]\left[\begin{array}{l}{\varphi }_{1,{\tau }_e}({\lambda }_k)\hfill \\ {\varphi }_{2,{\tau }_e}({\lambda }_k)\hfill \end{array}\right]=\left[\begin{array}{ll}{b}_{1{\varphi }_1}({\lambda }_k)\hfill & \hfill \\ \hfill & b_{2{\varphi }_2}({\lambda }_k)\hfill \end{array}\right]\left[\begin{array}{l}{s}_{1,{\tau }_e}({\lambda }_k)\hfill \\ s_{2,{\tau }_e}({\lambda }_k)\hfill \end{array}\right]$$ (10)

where

$$m_{i{\varphi }_j}({\lambda }_k)=\{\begin{array}{ll}\begin{array}{l}{\int }_{{\tau }_e}\{{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)\nabla v_p·\nabla v_q+{\mathcal{C}}_{i,{\varphi }_i}({\lambda }_k)v_p{v}_q\}\text{d}\mathbf{r}\\ -{\int }_{\partial {\tau }_e}{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)f_{\mathbf{v}·{\varphi }_i}(v_p)v_q\text{d}\mathbf{r}\end{array}\hfill & \text{if}i=j\hfill \\ {\int }_{{\tau }_e}{\mathcal{C}}_{i,{\varphi }_j}({\lambda }_k)v_p{v}_q\text{d}\mathbf{r}-{\int }_{\partial {\tau }_e}{\mathcal{C}}_{i,\nabla {\varphi }_i}({\lambda }_k)f_{\mathbf{v}·{\varphi }_i}(v_p)v_q\text{d}\mathbf{r}\hfill & \text{if}i\ne j\hfill \end{array}$$ (11)

and

$$b_{i,{\varphi }_i}({\lambda }_k)={\int }_{{\tau }_e}{v}_p{v}_q\text{d}\mathbf{r}$$ (12)

After assembling all the submatrices, we get

$$\left[\begin{array}{ll}{M}_{1{\varphi }_1}({\lambda }_k)\hfill & M_{1{\varphi }_2}({\lambda }_k)\hfill \\ M_{2{\varphi }_1}({\lambda }_k)\hfill & M_{2{\varphi }_2}({\lambda }_k)\hfill \end{array}\right]\left[\begin{array}{l}{\varphi }_1({\lambda }_k)\hfill \\ {\varphi }_2({\lambda }_k)\hfill \end{array}\right]=\left[\begin{array}{ll}B\hfill & \hfill \\ \hfill & B\hfill \end{array}\right]\left[\begin{array}{l}{S}_1({\lambda }_k)\hfill \\ S_2({\lambda }_k)\hfill \end{array}\right]$$ (13)

By inverting the matrix at the left side of Equ. 13, we have

$$\{\begin{array}{l}{\varphi }_1({\lambda }_k)=({IM}_{1{\varphi }_1}({\lambda }_k)-\frac{2}{3}{IM}_{1{\varphi }_2}({\lambda }_k))·B·S({\lambda }_k)\hfill \\ {\varphi }_2({\lambda }_k)=({IM}_{2{\varphi }_1}({\lambda }_k)-\frac{2}{3}{IM}_{2{\varphi }_2}({\lambda }_k))·B·S({\lambda }_k)\hfill \end{array}$$ (14a,14b)

where IM_iϕj(λ_k) are the submatrices of the inverse matrix IM(λ_k) corresponding to M_iϕj (λ_k). Note that the matrix at the left side of Equ. 13 is considered as the entire one when the inversion is performed. After we remove the rows in matrices $({IM}_{1{\varphi }_1}({\lambda }_k)-\frac{2}{3}{IM}_{1{\varphi }_2}({\lambda }_k))·B$ and $(I{M}_{2{\varphi }_1}^{-1}({\lambda }_k)-\frac{2}{3}{IM}_{2{\varphi }_2}({\lambda }_k))·B$ corresponding to the boundary measurable discretized points, we use Eq. 6 to get

$$\begin{array}{l}{J}^{+,b}({\lambda }_k)={\beta }_1({\lambda }_k){\varphi }_1^b({\lambda }_k)+{\beta }_2({\lambda }_k){\varphi }_2^b({\lambda }_k)\\ =({\beta }_1({\lambda }_k)G_1({\lambda }_k)+{\beta }_2({\lambda }_k)G_2({\lambda }_k))·S({\lambda }_k)\\ =G({\lambda }_k)S({\lambda }_k)\end{array}$$ (15)

where β₁(λ_k) and β₂(λ_k) can be calculated based on Eq. 6; G₁(λ_k) and G₂(λ_k) are the corresponding matrices after the operation of rows removing in Eqs. 14a and 14b. When the surface optical data at K wavelengths are collected, we get

$$J^{+,b}=\mathcal{A}S$$ (16)

where

$$J^{+,b}=\left[\begin{array}{c}{J}^{+,b}({\lambda }_1)\\ ⋮\\ J^{+,b}({\lambda }_k)\\ ⋮\\ J^{+,b}({\lambda }_K)\end{array}\right],\mathcal{A}=\left[\begin{array}{c}{\gamma }_{1}G({\lambda }_1)\\ ⋮\\ {\gamma }_{k}G({\lambda }_k)\\ ⋮\\ {\gamma }_{K}G({\lambda }_K)\end{array}\right]$$ (17)

Generally, A is considered as an ill-conditioned matrix because of the ill-posed problem of BLT. The surface measured data J^+,m corresponding to J^+,b will likely lead to a reconstruction failure when solving Eq. 16 directly due to the noise. We can though solve the bound-constrained least squares problem

$$\underset{0<S<S^{\mathit{sup}}}{min}\mathrm{\Theta }(S):{\left|\right|\mathcal{A}S-J^{+,m}\left|\right|}^2+\delta \eta (S)$$ (18)

where S^sup is the upper bound of the source density; δ the regularization parameter; and η(·) the penalty function.

By minimizing the objective function Θ(S), BLT reconstruction is possible. Since the least square problem easily obtains the Hessian matrix, several types of Hessian matrix based optimization algorithms have been adopted to obtain good reconstructions (Cong et al. 2005)(Lv et al. 2007). However, these methods require a significant amount of memory during the optimization procedure, especially when fine discretization at the whole-body level of small animals is used in the reconstruction. In addition, when computing the search direction, it is necessary to invert the Hessian matrix, a time-consuming process that severely affects the speed of BLT reconstruction. One solution to this is to use a quasi-Newton method. Generally, this method builds up an approximate Hessian matrix through the use of gradients and iterative algorithms. This approximate matrix is obtained in real-time by vector-vector multiplications and is easy to invert, saving memory and time requirements. Here, the limited memory variable metric bound constrained quasi-Newton method (BLMVM) is used for BLT reconstruction. The detailed algorithm is found in (Benson & Moré 2001).

2.2. Parallel implementation

When the reconstruction domain is discretized into N^P points, the SP₃-based BLT reconstruction needs to process a 2N^P × 2N^P matrix compared with a N^P × N^P matrix in diffusion approximation-based reconstructions. The computational complexity of the matrix inversion is O(N³). Therefore, the computation burden is increased remarkably in the SP₃-based reconstruction. Although computer hardware technology is rapidly improving, it is very difficult to process a matrix that has a very large number of elements. In addition, sequential execution is severely time-consuming. Time analysis of the simulation of photon propagation using the SP_N approximation has shown a significant reduction in time when using a parallel implementation (Lu & Chatziioannou 2009).

To make this reconstruction algorithm possible, a fully parallel version was developed. All of the components in the reconstruction were parallelized, including the FEM-based matrix assembly, the matrix inversion, and the BLMVM-based optimization. To perform the parallel reconstruction and reduce the load imbalance problem, a multilevel k-way partitioning method was used to perform the partitioning after the input of the volumetric mesh (Karypis & Kumar 1998). This method achieves improved performance by reducing the dimensions of the mesh, partitioning it into a smaller size, and refining it back to the original.

3. Results

3.1. Simulation verifications

Ever since the BLT concept was proposed in 2003 (Wang et al. 2003), a number of possible research scenarios have been investigated which use liquid or solid optical phantoms (Gu et al. 2004)(Cong et al. 2005)(Dehghani et al. 2006)(Kuo et al. 2007) as well as real mouse subjects (Wang et al 2006)(Kuo et al. 2007). There are though significant differences between real mice and optical phantoms, and the differences between them need to be addressed. One important factor is the optical properties at the time of the experiment. Table 1 shows a comparison of the optical properties between mouse muscle and a commercial mouse-shaped phantom fabricated by Caliper Life Sciences (Hopkinton, Massachusetts, USA). Three wavelengths (580, 620, 660nm) are commonly used for spectrally-resolved data acquisition in luciferase-based bioluminescence imaging. The optical properties of mouse muscle were derived using Bevilacqua’s method (Bevilacqua et al. 1999). One parameter of interest is the ratio of ${\mu }_s^{\prime }$ and μ_a. Generally, if the ratio of these parameters is larger than 10.0, it can be said that the corresponding optical domain has high-scattering characteristics. In this case, the diffusion approximation is considered to be suitable for successfully modeling the photon propagation. However, this ratio for mouse muscle is much lower compared with that of the mouse-shaped phantom, as shown in Table 1. Even if the wavelength is 660nm, the ratio is just 11.3. Another important parameter is the mean free path $(1/({\mu }_s^{\prime }+{\mu }_a))$. The diffusion approximation tends to fail if the depth of the bioluminescence source is less than one or even several (typically two) mean free paths. In this case, the reconstruction localization and quantity is significantly affected (Virostko et al. 2007). The data in Table 1 demonstrates that the actual mouse muscle has a longer mean free path when compared with the mouse-shaped phantom.

Table 1.

Optical properties of mouse muscle compared to a mouse-shaped phantom

	Real mouse muscle			Mouse phantom
Wavelength	580nm	620nm	660nm	580nm	620nm	660nm
μa(λk)[mm−1]	0.463	0.107	0.08	0.038	0.006	0.004
${\mu }_s^{\prime }({\lambda }_k)[m{m}^{-1}]$	0.975	0.922	0.902	1.82	1.66	1.46
${\mu }_s^{\prime }({\lambda }_k)/{\mu }_a({\lambda }_k)$	2.1	8.6	11.3	47.9	276.7	339.5
$1/({\mu }_s^{\prime }({\lambda }_k)+{\mu }_a({\lambda }_k))$	0.69	0.97	1.02	0.54	0.60	0.68

In recent years, several groups have attempted to develop multiview-based data acquisition systems for BLT based on CCD camera (Kuo et al. 2005)(Wang et al. 2006). Multiview-based data are very useful since the photon distribution can be obtained more accurately. However, more efficient methods of combining the data from multiple views need to be developed. In addition, one distinct advantage of bioluminescence imaging is its ability to achieve high throughput. This is usually limited in multiview-based data acquisitions. Therefore, single view measurements and new reconstruction methods should be further investigated for BLT reconstruction. Adaptive mesh evolution-based reconstruction methods are being developed to improve BLT reconstruction quality and speed (Lv et al. 2006), but the selection of an optimal initial coarse mesh is always a critical and sometimes problematic step. Furthermore, sequential executions limit reconstructions on fine meshes, especially for large volume domains. It is therefore necessary to explore reconstruction differences when using meshes with different discretized scales.

Monte Carlo (MC) methods can produce accurate simulation results and also avoid the inverse crime problem. However, these methods are severely time-consuming. To accelerate simulations, MPI-based parallel MC codes has been developed based on the Molecular Optical Simulation Environment (MOSE) (Li et al. 2004) in order to perform spectrally resolved simulations. The simulation reconstruction domain was based on the mouse-shaped phantom. To acquire the shape of the phantom, an Imtek microCAT system (Siemens Preclinical Solutions, Knoxville, TN) was used. The commercial software Amira 3.0 (Mercury Computer Systems, Inc. Chelmsford, MA) was used to convert the CT images into a tetrahedral-based finite element volumetric mesh. About 2/3 of the entire phantom was selected for mesh generation. Two volumetric meshes (called Fine mesh and Coarse mesh) were obtained with different discretized scales. The average element diameter of the Coarse mesh and Fine mesh were 2.0mm and 1.5mm respectively. Note that the memory cost of the inverse matrix at the single wavelength was about 1.6GB when SP₃-based BLT reconstruction was performed on the Fine mesh.

In the simulation settings, a solid spherical source with 1.0mm radius was placed at different deep positions in a MC simulation, that is (4, −3, 0), (4, −3, 5), and (4, −3, 10) (Unit: mm). A total of 10⁷ photons at each wavelength were tracked due to the high absorption coefficient of the selected domain. The distance of the first source from the bottom flat boundary of the phantom was about 7mm. The distance of the third source from the top curved boundary was about 2mm. These source settings were suitable for verifying the effects of the mean free path and different source locations from the reconstructed results. The regularization parameter δ is difficult to be selected in advance. Furthermore, it is difficult to quantify the reconstructed results due to the use of the regularization term. Spectrally-resolved measurements as a priori information were used to help obtain a unique and stable BLT solution. To fully verify the effect of this information and evaluate the performance of the SP₃ approximation, we set δ to “0” in the entire reconstruction. All the reconstructions were performed on a cluster of 27 nodes (2 CPUs of 3.2GHz and 4 GB RAM at each node).

3.1.1. Multiview-based reconstructions on the Fine mesh

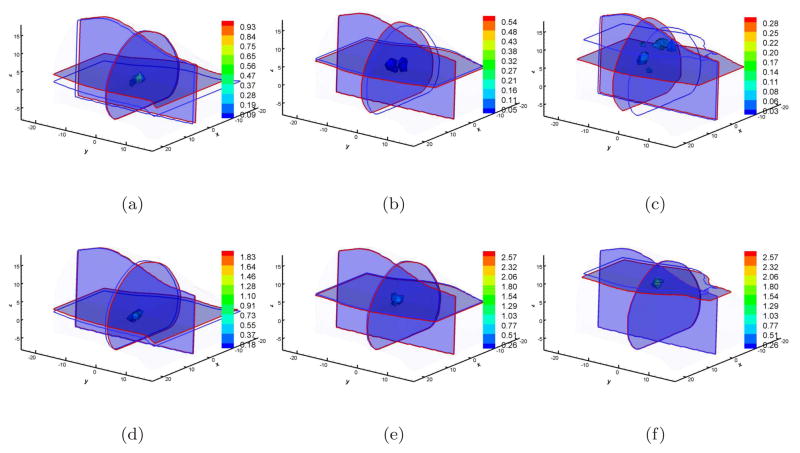
In the first case, we just considered multiview-based BLT reconstructions on the Fine mesh since this setting can produce adequate information with minimal discretized numerical errors. Figure 2 shows the reconstructed results based on the DA and SP₃ approximations. When 10 CPUs were used, the reconstruction time was 1, 592sec and 4, 001sec corresponding to DA and SP₃ approximation when the source was at (4, −3, 5). The effect of the mean free path was evaluated first. When multiview measured data was used, the source at (4, −3, 10) was the most superficial among the three sources. From Figure 2(c), it is apparent that it is almost impossible to reconstruct this source accurately. The reconstructed values are distributed and the center position offset is 7.2mm as shown in Table 2. The reason leading to such large errors most likely is that the diffusion approximation cannot accurately describe photon propagation when the source is very superficial. The counterpart reconstruction based on the SP₃ approximation is shown in Figure 2(f). The reconstructed results more accurately reflect the real source information not only in the position offset (0.8mm) but also in the distribution. Furthermore, Figures 2(a) and 2(d) display the reconstructed results when the source was placed at (4, −3, 0). The source was reconstructed well based on both DA and SP₃ approximation. The difference was that the reconstructed position offsets were 2.4mm and 1.1mm corresponding to DA and SP₃ approximation. The mean free path and high absorption should contribute to this difference since the source was about 7mm away from the boundary. The deepest source reconstructions for multiview data acquisitions are shown in Figures 2(b) and 2(e). The reconstructed position offsets are 1.9mm and 0.5mm for DA and SP₃ approximation respectively. Another important problem is that the DA-based results show a reconstruction artifact, severely affecting the reconstruction quality.

Figure 2.

Multiview-based reconstruction comparisons between DA and SP₃ approximation on the Fine mesh. Figures (a), (b), and (c) are the DA-based reconstruction results when the source was located at (4, −3, 0), (4, −3, 5), and (4, −3, 10) respectively (Unit: mm). Figures (d), (e), and (f) are the counterparts with the SP₃-based reconstruction. Cross-sections with blue and red boundaries are the center position of the actual and reconstructed sources respectively. The volumetric mesh denotes reconstructed values larger than 10% of the reconstructed maximum.

Table 2.

Source reconstructed position comparisons between DA and SP₃ approximation. (FM: Fine mesh, Multiview; CM: Coarse mesh, Multiview; FS: Fine mesh, Single view; Reconstruction: the center position of reconstructed source; Relative Errors: the absolute distance between the reconstructed and actual positions at X-, Y-, and Z-axis directions; Distance: the absolute distance between the reconstructed and actual positions)

		DA
		Reconstruction	Relative Errors	Distance
FM	(4, −3, 0)	(2.8, −2.6, 2.0)	(1.2, 0.4, 2.0)	2.4
	(4, −3, 5)	(4.1, −4.8, 4.4)	(0.1, 1.8, 0.6)	1.9
	(4, −3, 10)	(3.2, −8.3, 5.2)	(0.8, 5.3, 4.8)	7.2
CM	(4, −3, 0)	(5.9, −4.0, 2.1)	(1.9, 1.0, 2.1)	3.0
	(4, −3, 5)	(2.8, −4.4, 4.2)	(1.2, 1.4, 0.8)	2.0
	(4, −3, 10)	(5.2, −1.8, 8.4)	(1.2, 1.2, 1.6)	2.3
FS	(4, −3, 0)	(4.4, −2.2, 14.2)	(0.4, 0.8, 14.2)	14.2
	(4, −3, 5)	(3.7, −3.5, 14.0)	(0.3, 0.5, 14.0)	14.0
	(4, −3, 10)	(4.6, −2.6, 11.0)	(0.6, 0.4, 1.0)	1.2
		SP3
		Reconstruction	Relative Errors	Distance
FM	(4, −3, 0)	(3.7, −2.2, 0.7)	(0.3, 0.8, 0.7)	1.1
	(4, −3, 5)	(4.1, −2.6, 4.7)	(0.1, 0.4, 0.3)	0.5
	(4, −3, 10)	(3.9, −3.2, 9.2)	(0.1, 0.2, 0.8)	0.8
CM	(4, −3, 0)	(5.1, −2.2, 0.2)	(1.1, 0.8, 0.2)	1.4
	(4, −3, 5)	(3.7, −1.3, 4.7)	(0.3, 1.7, 0.3)	1.7
	(4, −3, 10)	(3.7, −4.0, 7.9)	(0.3, 1.0, 2.1)	2.3
FS	(4, −3, 0)	(3.7, −2.6, 0.5)	(0.3, 0.4, 0.5)	0.7
	(4, −3, 5)	(4.2, −3.2, 5.5)	(0.2, 0.2, 0.5)	0.6
	(4, −3, 10)	(4.6, −1.3, 7.9)	(0.6, 1.7, 2.1)	2.8

3.1.2. Multiview-based reconstructions on the Coarse mesh

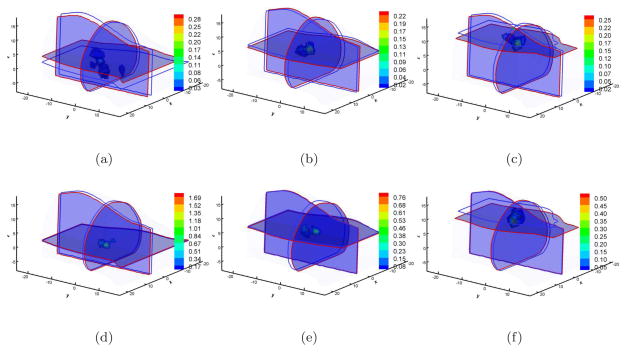
In FEM-based photon propagation simulations, the simulation error is bound by C₁h^C₂, where h is the largest element diameter; C₂ is related to the degree of the basis function and the singularity of the problem; and C₁ reflects other factors (Zienkiewicz & Craig 1986). The element diameter has a significant effect in the forward simulation precision. However, its effect in BLT reconstructions should be further investigated. When the Coarse mesh is used, the reconstructed results are shown in Figure 3 and the reconstructed center position information is also summarized in Table 2. As a whole, the reconstructed results become inferior compared with those on the Fine mesh. One observation is that the reconstructed results cover larger regions as is obvious after comparing the results in Figures 2 and 3. The second observation is that almost all the reconstructions have artifacts. The third observation is that the reconstructed position errors become larger than those on the Fine mesh, as shown in Table 2. One exception is that the reconstructed position offsets were 7.2mm and 2.3mm on the Fine mesh and Coarse mesh respectively with diffusion approximation when the source was at (4, −3, 10). Since regularization methods were not used in the reconstruction, one possible explanation was that the condition number of the matrix A on Coarse mesh was smaller than that on the Fine mesh, reducing the sensitivity of the measurement noise to model errors. However, SP₃-based BLT reconstructions show good results despite the fact that reconstruction artifacts exist. With respect to the Coarse mesh and SP₃ approximation, reconstruction methods with adaptive mesh evolution strategy improve BLT reconstruction quality.

Figure 3.

Multiview-based reconstruction comparisons between DA and SP₃ approximation on the Coarse mesh. Figures (a), (b), and (c) are the DA-based reconstruction results when the source was located at (4, −3, 0), (4, −3, 5), and (4, −3, 10) respectively. Figures (d), (e), and (f) are the counterparts with SP₃-based reconstruction. Cross-sections with blue and red boundaries are the center position of actual and reconstructed sources respectively. Volumetric mesh denotes the reconstructed values larger than 10% of the reconstructed maximum.

3.1.3. Single view-based reconstructions on the Fine mesh

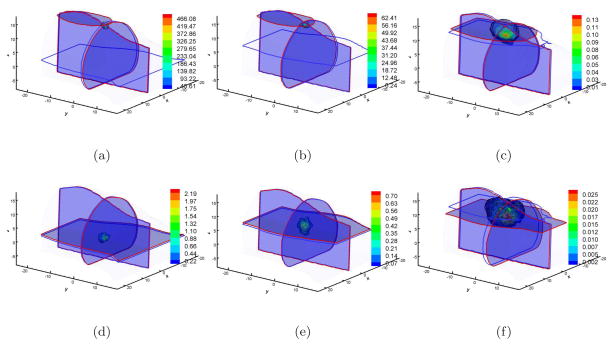
Another BLT reconstruction investigation was based on single view data collection because of the facile implementation and the high throughput potential. In this case, we assume that the side used for data acquisition is the bottom flat surface of the mouse. Regarding the domain discretization errors, Fine mesh was used for BLT reconstructions. The reconstructed results are shown in Figure 4. With respect to the bottom surface, the most superficial source was at (4, −3, 0). Its distance from the detection surface was about 7mm, which is much larger than the mean free path. We could acquire a similar source reconstruction localization with multiview data acquisition when the SP₃ approximation was used, as shown in Figure 4(d) and Table 2. However, DA-based reconstruction could not localize the bioluminescence source (Figure 4(a) and Table 2). Since the same volumetric mesh and synthetic measured data were used in BLT reconstructions, the reasonable explanation is that model errors of the diffusion approximation are more sensitive than the SP₃ approximation to the noise in MC-based synthetic data. When the source was at (4, −3, 5), the DA-based reconstruction produced similar results (Figure 4(b)) with the source at (4, −3, 0). We could also obtain good reconstruction with the SP₃ approximation as shown in Figure 4(e). The difference of the reconstructed results between the above source settings is that the reconstructed source distribution was enlarged when the source was at (4, −3, 5). The reconstruction became sharper when the source was localized at (4, −3, 10), which is shown in Figure 4(f). The localization errors of the latter two sources were 0.6mm and 2.8mm respectively, as shown in Table 2. Note that the distance between the sources and the measured surface were about 12mm and 17mm. The maximal diameter of the mouse volume is about 25mm. Therefore, a single view data acquisition could be suitable for real mouse geometries with the SP₃ approximation.

Figure 4.

Single view-based reconstruction comparisons between DA and SP₃ approximation on Fine mesh. Figures (a), (b), and (c) are the DA-based reconstruction results when the source was located at (4, −3, 0), (4, −3, 5), and (4, −3, 10) respectively. Figures (d), (e), and (f) are the counterparts with SP₃-based reconstruction. Cross-sections with blue and red boundaries are the center position of actual and reconstructed sources respectively. Volumetric mesh denotes the reconstructed values larger than 10% of the reconstructed maximum.

3.1.4. Quantitative BLT reconstructions

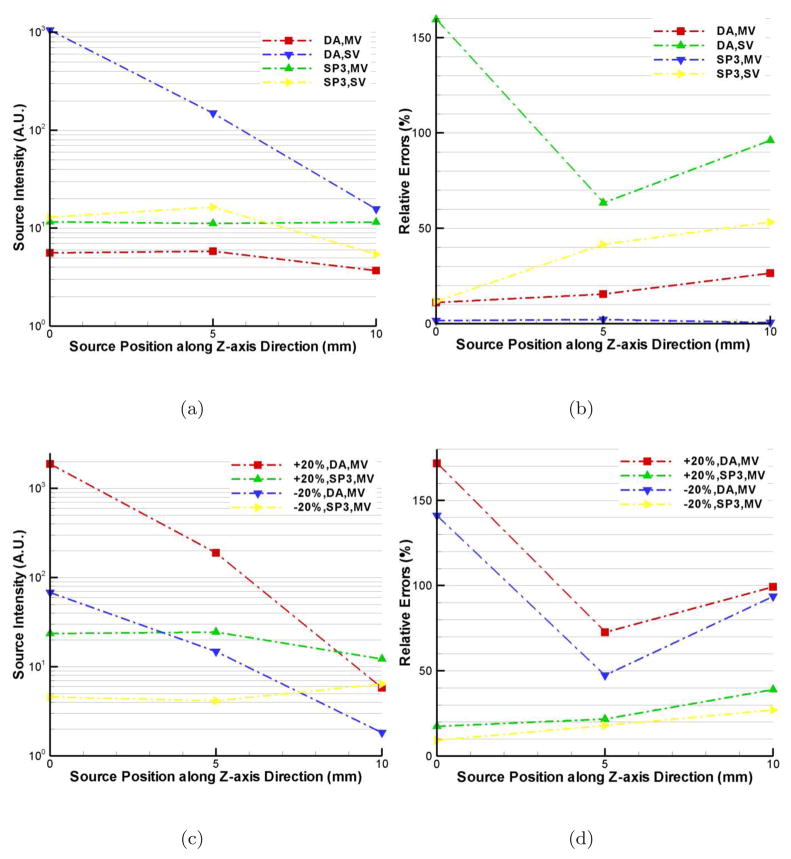
Quantitative BLT reconstruction means that the reconstructed source intensities are consistent when the same source is placed at different locations, especially at different depths. Compared with planar bioluminescence imaging, quantitative reconstruction is another important advantage of BLT besides the 3D source localization. In this case, we just show the reconstructed source intensities, obtained by integration over the entire reconstruction domain. The relative errors (RE) between different deep positions are calculated by |S_r − S_ar|/S_ar, where S_r and S_ar are the reconstructed source intensity and the average of three source reconstructions. Figure 5(a) shows the DA and SP₃ reconstructed results. Compared with the multiview (MV) data acquisition, single view-based (SV) reconstructed source intensities have larger deviations. However, the SP₃-based SV reconstructions are much better than the DA-based counterparts. The maximal REs are 21% and 11% for DA- and SP₃-based MV reconstructions. Note that the reconstructed intensities with the sources at (4, −3, 0) and (4, −3, 5) were more consistent compared with those at (4, −3, 10). The effect of the mean free path most likely is the key factor here. This phenomenon is more distinct when the ±20% errors in optical property are considered in SP₃-based MV BLT reconstructions, as shown in Figure 5(c). However, these reconstructions have much better performance compared with the DA-based counterparts. From Figure 5(d), we see that the maximal REs are 170% and 40% for the DA- and SP₃-based reconstructions.

Figure 5.

Quantitative BLT reconstruction comparisons between DA and SP₃ approximation on Fine mesh. Figures (a) and (c) are the absolute reconstructed source intensity respectively without and with optical property errors, which are obtained by integration over the entire domain. Figures (b) and (d) are the relative errors corresponding to Figures (a) and (c).

3.2. Experimental reconstructions

To further verify the SP₃-based reconstruction algorithm, living mouse experiments were performed on a Maestro 2 in vivo imaging system (CRI, Woburn, Massachusetts). This system uses a cooled CCD camera and a liquid crystal tunable filter (LCTF) to acquire spectrally-resolved data. To simulate a bioluminescence source, a calibrated luminescent bead (Mb-Microtec, Bern, Switzerland) was used with an emission spectrum similar to that of a firefly luciferase-based source (Kuo et al. 2007)(Klose & Beattie 2008). In this bead, tritium is used to excite phosphor that generates photons, making it a very stable source. Its dimensions are 0.9mm in diameter and 2.5mm long. Figure 6(a) shows a SKH1-hr hairless mouse (Charles River, San Diego, CA) used in this experiment. Before performing the experiments, the mouse was anesthetized and the bead was surgically inserted into the mouse body. When the filter bandpass width was set to 20nm, the optical data at two wavelengths (600 and 660nm) was collected from a dorsal view. The exposure time for each wavelength was 5min to obtain high signal-to-noise ratio (SNR). After finishing the optical signal acquisition, the mouse was imaged using the microCAT system to obtain X-ray CT images. These CT images were used to generate the volumetric mesh for image reconstruction through a commercial software package (Amira). The same software was also used to register the volumetric mesh and the mouse photograph for measured data mapping.

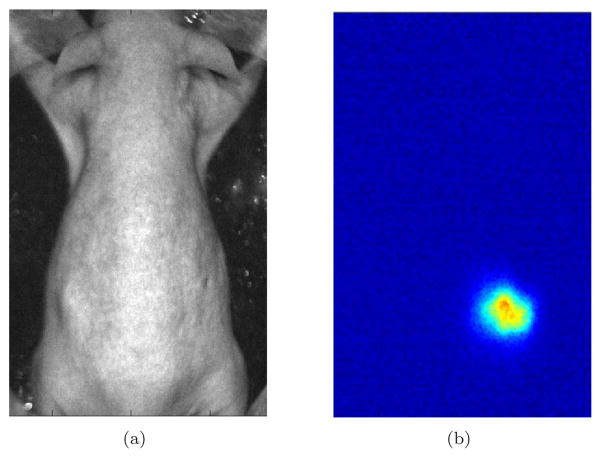
Figure 6.

(a) The photograph of the hairless mouse for bioluminescence imaging; (b) The acquired optical data at 660nm corresponding to (a).

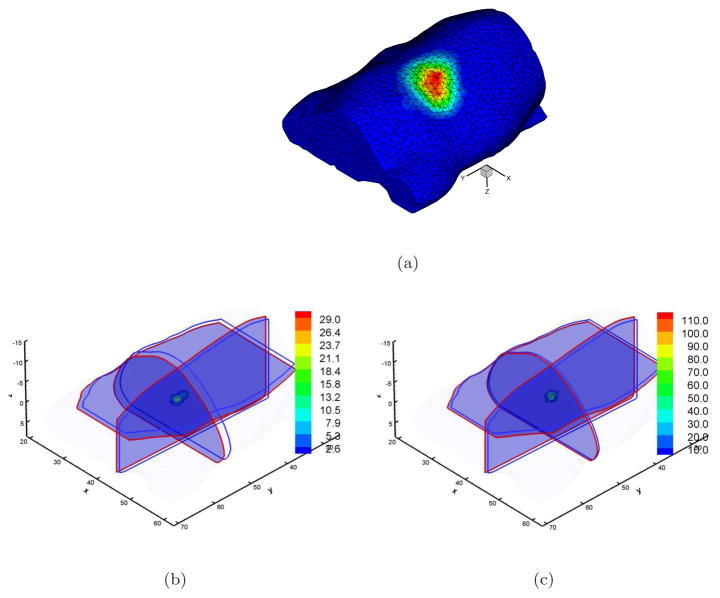
Figure 7(a) shows the volumetric mesh used in this reconstruction and the mapped photon distribution on the mouse surface. This mesh has the average element diameter of 1.5mm and contains 9, 193 discretized points and 44, 333 tetrahedral elements. Regarding the signal quality and the differences of the measured data at different wavelengths, two wavelengths were used to perform BLT reconstruction. Since it is difficult to distinguish other organs besides lung and bone using CT images, while the photon propagation region is almost totally comprised of muscle, the corresponding optical properties at 660nm shown in Table 1 (μ_a: 0.187 and ${\mu }_s^{\prime }$: 0.929 at 600nm (Virostko et al. 2007)) were used in reconstruction. The tritium source was easily distinguished in CT images and we could confirm that the actual position of the source was (44.6, 50.2, −4.9). Figures 7(b) and 7(c) show the reconstructed results corresponding to DA- and SP₃-based algorithms. The center positions of the reconstructed sources are (43.7, 52.0, −3.8) and (43.7, 50.7, −4.2) respectively. Although both of them are very close to the actual source position, the reconstructed localization with the SP₃-based reconstruction is more precise. However, there is little difference between the experimental reconstructions and the simulations especially regarding the DA-based reconstruction. The key factor is that the measured view on the curved surface of the mouse is wider compared with the flat surface measurement of the source, resulting additional measurement information in the experimental reconstruction. Another reason is that the distance between the tritium source and the top surface is about 8mm, making the source deep with respect to the mean free path. In addition, the complexity of in vivo mouse tissues also introduces some effects in the reconstructed results when only the optical property of the muscle is used. However, the experimental reconstructions show the potential of the proposed SP₃-based reconstruction algorithm especially when the regularization method is not used in the reconstructions. This further demonstrates the source uniqueness in BLT reconstructions when sufficient a priori information is used.

Figure 7.

Single view experimental BLT reconstructions with DA- and SP₃-based algorithms. Figures (a) shows the volumetric mesh and the mapped photon distribution. Figures (b) and (c) are the reconstructed results corresponding to DA and SP₃ methods. Cross-sections with blue and red boundaries are the center position of actual and reconstructed sources respectively. Volumetric mesh denotes the reconstructed values larger than 10% of the reconstructed maximum.

4. Discussions and conclusion

In this paper, a SP₃-based spectrally-resolved BLT reconstruction algorithm is developed. The strategy of establishing the simple linear relationship between the unknown source variable and the boundary measured data is introduced for the SP₃ high-order approximation. Parallel execution of the proposed algorithm makes possible and accelerates the reconstruction of sources in the whole-body of a mouse on a fine discretization domain. Simulation reconstruction comparisons between DA- and SP₃-based algorithms show the effectiveness and numerical stability of the developed algorithm, with respect to superficial source settings, single view-based data acquisitions and quantitative BLT reconstruction. Experimental real mouse BLT reconstructions further show the possibility and potential of the SP₃-based algorithm for practical BLT applications.

In BLT, several approximations and assumptions have significantly affected the performance of bioluminescence source reconstructions. Four types of bioluminescence reporters can be used currently, that is luciferase enzymes from firefly (FLuc), click beetle (CBRLuc), Renilla reniformis (hRLuc), and more recently Gaussia princeps (GLuc). The spectrum range of these luciferases are about 400–750nm (Zhao et al. 2005). Even if BLT is used at 660nm, in vivo tissues such muscle, skin and liver (Virostko et al. 2007) show high absorption characteristics. Due to the high scattering assumption of tissues, the diffusion approximation theory has been extensively applied in optical imaging. The comparisons between DA- and SP₃-based reconstructions have shown that high-order approximations to the RTE can bring much better numerical stability and reconstruction quality. Note that the diffusion approximation has a significant adverse effect in BLT reconstruction quality when the source is very close to the animal surface, something that is not being considered currently, but is often the case in biological in vivo experiments. The proposed algorithm significantly improves BLT reconstructions in this case.

Another important assumption is that the mouse is optically homogeneous. The optical properties between different organs of in vivo mice are very different. Multiple BLT reconstructions have shown that the knowledge of the heterogeneous geometry and optical properties are necessary for improved BLT reconstruction. Although preliminary surface flux comparisons with MC methods have shown that SP_N approximations provide slight improvement compared with the DA in heterogeneous cases, fully parallel FEM reconstruction framework in the proposed algorithm is also suitable for second-order self-adjoint approximation formulas to the RTE. Future work will explore more precise approximation models to improve BLT reconstruction.

In conclusion, we have developed a fully parallel BLT reconstruction algorithm with high-order approximations to the RTE compared with DA. Simulation and experimental reconstruction verifications demonstrated that BLT reconstructions using the proposed algorithm acquire good source localization and quantity and better numerical stability and efficiency. Further research will focus on real mouse experiments with disease models and the relevant bioluminescence probes (Loening et al. 2007) for the recently developed Optical-PET (OPET) system (Douraghy et al. 2008).

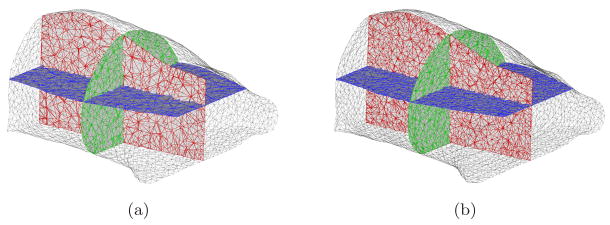
Figure 1.

The volumetric meshes used in simulation validations. Figure (a) and (b) are Coarse mesh and Fine mesh, with average element diameters of 2.0mm and 1.5mm respectively. The surface and total discretized points of the Coarse mesh are 2, 598 and 5, 102 respectively and the counterparts on the Fine mesh are 4, 287 and 10, 293.