Performance of Prewhitening Beamforming in MEG Dual Experimental Conditions

Abstract

This paper presents an analysis on the performance of the prewhitening beamformer when applied to magnetoencephalography (MEG) experiments involving dual (task and control) conditions. We first analyze the method’s robustness to two types of violations of the prerequisites for the prewhitening method that may arise in real-life two-condition experiments. In one type of violation, some sources exist only in the control condition but not in the task condition. In the other type of violation, some signal sources exist both in the control and the task conditions, and that they change intensity between the two conditions. Our analysis shows that the prewhitening method is very robust to these nonideal conditions. In this paper, we also present a theoretical analysis showing that the prewhitening method is considerably insensitive to overestimation of the signal-subspace dimensionality. Therefore, the prewhitening beamformer does not require accurate estimation of the signal subspace dimension. Results of our theoretical analyses are validated in numerical experiments and in experiments using a real MEG data set obtained during self-paced hand movements.

I. Introduction

ONE MAJOR problem with magnetoencephalography (MEG) measurements is that the measured MEG data contain not only signals from brain regions of interest, but also large interfering magnetic fields generated from spontaneous brain activities all over the brain. Such background interference degrades the quality of source reconstruction results, and often makes interpreting the results difficult. Such background interference is sometimes referred to as brain noise or physiological noise.

A common strategy for extracting the signal of interest from measurements overlapped with a large amount of interference is to design experiments with dual (control and task) conditions. Subtraction between the reconstruction results obtained under these two conditions is a common procedure to reconstruct signal sources of interest [1]. (This subtraction is often performed as a part of calculating pseudo-t statistics, which is used for statistically evaluating the source configuration difference between the two conditions.) However, when the source reconstruction is performed with adaptive spatial filter methods [2]-[4], such subtraction-based methods cannot effectively remove the influence of the background interference [5]. This is because the influence of the background activity is not simply additive. It involves spatial blur and source location bias, as will be shown in our computer simulation in Section V.

Recently, we have proposed a novel prewhitening method suitable for reconstructing sources from evoked measurements overlapped with large background interference [6]. The goal of this paper is to show that the prewhitening method can also be effective for measurements involving task and control conditions. We first analyze the prewhitening method’s robustness to two types of violations of the prerequisites for the prewhitening method that may arise in real-life two-condition experiments. We refer to these two types violations as the control-only source scenario and the modulating source scenario in this paper. In the control-only-source scenario, some sources appear only in the control measurements and that they do not appear in the task measurements. In the modulating-source scenario, some signal sources of interest exist both in the control and the task measurements, and they change intensity between the two conditions. In real-life measurements, one or both of these scenarios may arise. In this paper we demonstrate that the prewhitening method is still effective under these scenarios.

This paper also presents an analysis on the influence caused by the overestimation of the signal subspace dimensionality, and it shows that the method is considerably insensitive to such overestimation. Therefore, the accurate determination of the signal subspace dimension is not essential for implementing the prewhitened beamformer, and an intentionally large value can be used for the signal subspace dimension.

Section II briefly reviews the prewhitening method that has already been proposed in [6]. Section III presents our theoretical analysis on the method’s performance under two realistic scenarios with dual-condition experiments. Section IV shows the effects of overestimation of the signal subspace dimension. The arguments in Sections III–IV are validated first by numerical experiments in Section V and by an application to real MEG data collected during self-paced finger flection in Section VI. Throughout this paper, plain italics indicate scalars, lower-case boldface italics indicate vectors, and upper-case boldface italics indicate matrices. The eigenvalues are numbered in decreasing order.

II. Prewhitening Beamforming Under an Ideal Scenario

We use a model for measurements b(t) expressed as

$$\mathit{b}\left(t\right)={\mathit{b}}_s\left(t\right)+{\mathit{b}}_I\left(t\right)+\mathit{n}\left(t\right)$$ (1)

where b_s(t) is the magnetic field generated by signal sources of interest, b_I(t) is the magnetic field generated by background activity, and n(t) is the additive sensor noise. These vectors are M × 1 column vectors where M is the number of sensors. The covariance matrix of the measurements is denoted R such that R = 〈b(t)b^T(t)〉 where 〈·〉 indicates an expectation operator. We define the covariance matrix of the signal magnetic field as R_s, such that ${\mathit{R}}_s=\langle {\mathit{b}}_s\left(t\right){\mathit{b}}_s^T\left(t\right)\rangle$. We assume that the signal is low rank, i.e., the rank of R_s is Q, which is smaller than M, the number of sensors. We also define the interference-plus-sensor-noise covariance matrix R_i+n, such that R_i+n = 〈[b_I(t) + n(t)][b_I(t) + n(t)]^T〉. Note that this R_i+n is a positive definite matrix, because we assume that the sensor noise is the white Gaussian noise uncorrelated between different channels. Under the assumption that the signal source activity is uncorrelated with the background interferences and sensor noise, the relationship

$$\mathit{R}={\mathit{R}}_s+{\mathit{R}}_{i+n}$$ (2)

holds. In the conventional (nonprewhitened) minimum-variance spatial filter, the source power reconstruction Φ̂(r) is obtained using this covariance matrix R such that

$$\widehat{\Phi }\left(\mathit{r}\right)=\langle \widehat{s}{(\mathit{r},t)}^2\rangle =\frac{1}{{\mathit{l}}^T\left(\mathit{r}\right){({\mathit{R}}_s+{\mathit{R}}_{i+n})}^{-1}\mathit{l}\left(\mathit{r}\right)}$$ (3)

where l(R) is an M × 1 column vector representing the sensor lead field in the estimated source direction¹ at location r. Equation (3) indicates that the influence of the additive interference is not simply additive, but it affects the final source-reconstruction results through R_i+n in a highly nonlinear manner. The influence actually involves spatial blur and source location bias, as will be shown in our computer simulation in Section V.

We next explain the prewhitening method of estimating the signal covariance matrix R_s; the method was first reported in [6]. We here assume the ideal scenario, in which control-state measurements b_c(t) contain only the interference and sensor noise, i.e.,

$${\mathit{b}}_c\left(t\right)={\mathit{b}}_I\left(t\right)+\mathit{n}\left(t\right)$$

and the interference-plus-noise covariance matrix R_i+n can be obtained from such control-state measurements. Namely, defining the covariance matrix from the control measurements as R_c, i.e., ${\mathit{R}}_c=\langle {\mathit{b}}_c\left(t\right){\mathit{b}}_c^T\left(t\right)\rangle$, the relationship

$$\begin{array}{cc}\hfill \text{Control}:& {\mathit{R}}_c={\mathit{R}}_{i+n},\hfill \\ \hfill \text{Task}:& \mathit{R}={\mathit{R}}_s+{\mathit{R}}_{i+n}\hfill \end{array}$$ (4)

holds. To estimate the signal covariance matrix, we first calculate the prewhitened measurement covariance matrix $\tilde{\mathit{R}}$, which is defined as $\tilde{\mathit{R}}={\mathit{R}}_c^{-1∕2}{\mathit{RR}}_c^{1∕2}$. Thus, from (4), we have the relationship

$$\tilde{\mathit{R}}={\mathit{R}}_c^{-1∕2}{\mathit{R}}_s{\mathit{R}}_c^{-1∕2}+\mathit{I}={\tilde{\mathit{R}}}_s+\mathit{I}$$ (5)

where

$${\tilde{\mathit{R}}}_s={\mathit{R}}_c^{-1∕2}{\mathit{R}}_s{\mathit{R}}_c^{-1∕2}.$$ (6)

We define the eigenvalues and eigenvectors of an M × M matrix ${\tilde{\mathit{R}}}_s$ as γ₁, . . . , γ_M and u₁, . . . , u_M. Since R_s is a positive semidefinite matrix with rank Q and ${\mathit{R}}_c^{-1∕2}$ is a nonsingular matrix, ${\tilde{\mathit{R}}}_s$ is also a positive semidefinite matrix with rank Q. Thus, the eigenvalues γ₁, . . . , γ_Q are positive and the other eigenvalues γ_Q+1, . . . , γ_M are zero. (Here, we assume that the eigenvalues are ordered in a decreasing manner.) Namely, we have

$${\tilde{\mathit{R}}}_s=\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T.$$ (7)

Therefore, the eigendecomposition of $\tilde{\mathit{R}}$ can be expressed as

$${\tilde{\mathit{R}}}_s=\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T+\mathit{I}=\sum _{j=1}^Q({\gamma }_j+1){\mathit{u}}_j{\mathit{u}}_j^T+\sum _{j=Q+1}^M{\mathit{u}}_j{\mathit{u}}_j^T.$$ (8)

The above equation indicates that the Q largest eigenvalues of $\tilde{\mathit{R}}$ are greater than 1 and the corresponding eigenvectors are the same as those for the nonzero eigenvalues of ${\tilde{\mathit{R}}}_s$. The eigenvalues of ${\tilde{\mathit{R}}}_s$ greater than 1 are referred to as the signal-level eigenvalues and their corresponding eigenvectors as the signal-level eigenvectors. Equation (8) indicates that it is possible to retrieve ${\tilde{\mathit{R}}}_s$ from the signal-level eigenvalues and their corresponding eigenvectors of $\tilde{\mathit{R}}$. That is, defining a matrix U_S as U_S = [u₁ , . . . , u_Q], the signal covariance matrix, R_s, can be obtained using

$$\begin{array}{cc}\hfill {\mathit{R}}_c^{1∕2}{\mathit{U}}_S{\mathit{U}}_S^T(\tilde{\mathit{R}}-\mathit{I}){\mathit{R}}_c^{1∕2}& ={\mathit{R}}_c^{1∕2}\left[\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T\right]{\mathit{R}}_c^{1∕2}\hfill \\ \hfill & ={\mathit{R}}_c^{1∕2}{\tilde{\mathit{R}}}_s{\mathit{R}}_c^{1∕2}={\mathit{R}}_s.\hfill \end{array}$$ (9)

In actual cases, the covariance matrices R and R_c are unknown, and instead we should use the sample covariance matrices, which are obtained using

$$\widehat{\mathit{R}}=\frac{1}{K}\sum _{k=1}^K\mathit{b}\left(t_k\right){\mathit{b}}^T\left(t_k\right){\widehat{\mathit{R}}}_c=\frac{1}{K}\sum _{k=1}^K{\mathit{b}}_c\left(t_k\right){\mathit{b}}_c^T\left(t_k\right)$$ (10)

where t₁, . . . , t_K are the time points contained in a certain time window. We define $\widehat{\tilde{\mathit{R}}}$ such that $\widehat{\tilde{\mathit{R}}}={\widehat{\mathit{R}}}_c^{-1∕2}\widehat{\mathit{R}}{\widehat{\mathit{R}}}_c^{-1∕2}$. Using (9), the estimate of the signal covariance matrix ${\tilde{\mathit{R}}}_s$ can be obtained using

$${\widehat{\mathit{R}}}_s={\widehat{\mathit{R}}}_c^{1∕2}{\widehat{\mathit{U}}}_S{\widehat{\mathit{U}}}_S^T(\widehat{\tilde{\mathit{R}}}-\mathit{I}){\widehat{\mathit{R}}}_c^{1∕2}$$ (11)

where Û_S = [û₁, . . . , û_Q], and û₁, . . . , û_>Q are the signal-level eigenvectors of $\widehat{\tilde{\mathit{R}}}$. Given the estimate of the signal covariance matrix R̂_s, a reasonable estimate of the signal-plus-sensor-noise covariance matrix, R̂_s+n, can be obtained using

$${\widehat{\mathit{R}}}_{s+n}={\widehat{\mathit{R}}}_s+\mu \mathit{I}$$ (12)

where μ is the regularization constant that should be set close to the variance of the sensor noise ${\sigma }_0^2$. (Actually, since the noise variance ${\sigma }_0^2$ is unknown, an appropriate value of μ should be determined from the measured data, and some empirical methods, such as that of using the minimum-eigenvalue of R, are employed to determine μ.) Consequently, using the minimum-variance spatial filter, the prewhitening source power reconstruction free from the influence of the background activity, can be obtained using

$$\widehat{\Phi }\left(\mathit{r}\right)=\frac{1}{{\mathit{l}}^T\left(\mathit{r}\right){\widehat{\mathit{R}}}_{s+n}^{-1}\mathit{l}\left(\mathit{r}\right)}=\frac{1}{{\mathit{l}}^T\left(\mathit{r}\right){({\widehat{\mathit{R}}}_s+\mu \mathit{I})}^{-1}\mathit{l}\left(\mathit{r}\right)}.$$ (13)

III. Prewhitening Beamforming Under Nonideal Scenarios

In this section, we analyze the performance of the prewhitening method under two kinds of nonideal scenarios that may arise in real-life task and control-type measurements. In the scenario argued first, there are some sources that appear only in the control state and do not appear in the task state. Such sources are called the control-only sources in this paper, and this scenario is referred to as the control-only-source scenario. In the scenario argued next, the signal sources of interest are active in the control state as well as in the task state but they change their intensities between the two states. Such sources are called the modulating sources in this paper, and this scenario is referred to as the modulating-source scenario.

A. Control-Only Source Scenario

In the control-only-source scenario, we assume that there are P sources that exist only in the control state and do not appear in the task state. We also assume that the observed signal space is still low-rank, i.e., Q+P < M. When such control-only sources exist, the control state measurements b_c(t) can be expressed as

$${\mathit{b}}_c\left(t\right)={\mathit{b}}_I\left(t\right)+\mathit{n}\left(t\right)+{\mathit{b}}_{\Delta }\left(t\right)$$ (14)

where b_Δ(t) indicates the magnetic field generated by control-only sources. The covariance matrix relationships are then expressed as

$$\begin{array}{cc}\hfill \text{Control}:& {\mathit{R}}_c={\mathit{R}}_{i+n}+{\mathit{R}}_{\Delta }\hfill \\ \hfill \text{Task}:& \mathit{R}={\mathit{R}}_s+{\mathit{R}}_{i+n}\hfill \end{array}$$ (15)

where

$${\mathit{R}}_{\Delta }=\langle {\mathit{b}}_{\Delta }\left(t\right){\mathit{b}}_{\Delta }^T\left(t\right)\rangle .$$ (16)

In deriving (15), we assume that the activity of control-only sources is uncorrelated with the interference and sensor noise. Using (15), we have

$$\mathit{R}={\mathit{R}}_s+{\mathit{R}}_c-{\mathit{R}}_{\Delta }$$ (17)

and thus

$$\tilde{\mathit{R}}={\tilde{\mathit{R}}}_s+\mathit{I}-{\tilde{\mathit{R}}}_{\Delta }$$ (18)

where ${\tilde{\mathit{R}}}_{\Delta }={\mathit{R}}_c^{-1∕2}{\mathit{R}}_{\Delta }{\mathit{R}}_c^{-1∕2}$. Since R_δ is a nonnegative definite matrix with rank P and ${\mathit{R}}_c^{-1∕2}$ is a nonsingular matrix, ${\tilde{\mathit{R}}}_{\Delta }$ is a nonnegative definite matrix with rank P. Thus, ${\tilde{\mathit{R}}}_{\Delta }$ is decomposed as

$${\tilde{\mathit{R}}}_{\Delta }=\sum _{j=1}^P{\beta }_j{\mathit{v}}_j{\mathit{v}}_j^T$$ (19)

where β_j, (j = 1, . . . , P) are P nonzero eigenvalues of ${\tilde{\mathit{R}}}_{\Delta }$, and v_j are the corresponding eigenvectors. Substituting (7) and (19) into (18), we have

$$\tilde{\mathit{R}}=\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T+\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T+\sum _{j=1}^P(1-{\beta }_j){\mathit{v}}_j{\mathit{v}}_j^T.$$ (20)

When the control-only sources are well separated from the signal sources of interest, the relationship

$$\mathit{span}\{{\mathit{v}}_1,\dots ,{\mathit{v}}_P\}\perp \mathit{span}\{{\mathit{u}}_1,\dots ,{\mathit{u}}_Q\}$$ (21)

approximately holds. Under this assumption, we will show that a set of vectors

$$\{{\mathit{u}}_1,\dots ,{\mathit{u}}_Q,{\mathit{d}}_1,\dots ,{\mathit{d}}_{M-P-Q,},{\mathit{v}}_1,\dots ,{\mathit{v}}_P\}$$ (22)

are the eigenvectors of $\tilde{\mathit{R}}$, where {d₁, . . . , d_{M - P - Q}} are the orthonormal basis set of the subspace $\mathcal{S}$, which is defined as $\mathcal{S}=\mathit{span}\{{\mathit{u}}_{Q+1},\dots ,{\mathit{u}}_M\}\bigcap \mathit{span}\{{\mathit{v}}_{P+1},\dots ,{\mathit{v}}_M\}$.

We first show that the relationship

$$\tilde{\mathit{R}}{\mathit{u}}_i=({\gamma }_i+1){\mathit{u}}_i(i=1,\dots ,Q)$$ (23)

holds. That is, we show that the vectors u_i (where i = 1, . . . , Q) are the eigenvectors of $\tilde{\mathit{R}}$ and their corresponding eigenvalues are γ_i + 1. To show this, we calculate the right multiplication of u_i (i = 1, . . . , Q) to $\tilde{\mathit{R}}$, and using (20) this multiplication results in

$$\begin{array}{cc}\hfill \tilde{\mathit{R}}{\mathit{u}}_i=\left(\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T\right){\mathit{u}}_i& +\left(\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{u}}_i\hfill \\ \hfill & +\left(\sum _{j=1}^P(1-{\beta }_j){\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{u}}_i.\hfill \end{array}$$ (24)

The first term in the right-hand side becomes γ_iu_i. The second term becomes u_i, because the relationship

$$\left(\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{u}}_i={\mathit{u}}_i$$ (25)

holds. The validity of (25) is shown in the Appendix. The third term in the right-hand side of (24) vanishes due to the orthogonality assumption in (21). Therefore, we can derive the relationship in (23), i.e., we can show that the vectors u_i (where i = 1, . . . , Q) are the eigenvectors of $\tilde{\mathit{R}}$.

Next, we show that the relationship

$$\tilde{\mathit{R}}{\mathit{d}}_i={\mathit{d}}_i(i=1,\dots ,M-P-Q)$$ (26)

holds. That is, we show that the vectors d_i (i = 1, . . . , M - P - Q) are the eigenvectors of $\tilde{\mathit{R}}$ and the corresponding eigenvalues are equal to 1. To show this relationship, we calculate the right multiplication of d_i to $\tilde{\mathit{R}}$, which is equal to

$$\begin{array}{cc}\hfill \tilde{\mathit{R}}{\mathit{d}}_i=\left(\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T\right){\mathit{d}}_i& +\left(\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{d}}_i\hfill \\ \hfill & +\left(\sum _{j=1}^P(1-{\beta }_j){\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{d}}_i.\hfill \end{array}$$ (27)

Since d_i is orthogonal to both the subspace spanned by u_j (j = 1, . . . , Q) and that spanned by v_j (j = 1, . . . , P), the only nonzero term in the right-hand side is the second term, which is equal to d_i, because d_i ∈ span {v_P+1, . . . , v_M}. Thus, we have proved (26).

Finally, we calculate the right multiplication of v_i (i = 1, . . . , P) to $\tilde{\mathit{R}}$, which produces that

$$\begin{array}{cc}\hfill \tilde{\mathit{R}}{\mathit{v}}_i=\left(\sum _{j=1}^Q{\gamma }_j{\mathit{u}}_j{\mathit{u}}_j^T\right){\mathit{v}}_i& +\left(\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{v}}_i\hfill \\ \hfill & +\left(\sum _{j=1}^P(1-{\beta }_j){\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{v}}_i.\hfill \end{array}$$ (28)

On the right-hand side, the first term becomes zero due to the orthogonality assumption in (21) and the second term becomes zero due to the orthogonality relationship between the signal and the noise subspaces. Thus, we have

$$\tilde{\mathit{R}}{\mathit{v}}_i=(1-{\beta }_i){\mathit{v}}_i.$$ (29)

Therefore, v_i (i = 1, . . . , P) are eigenvectors of $\tilde{\mathit{R}}$ and the corresponding eigenvalues are 1 - β_i. We can also show that these eigenvalues are positive but less than 1, i.e., 0 < 1 - β_j < 1, although we do not include the proof here. In summary, we have shown that the vectors

$$\{{\mathit{u}}_1,\dots ,{\mathit{u}}_Q,{\mathit{d}}_1,\dots ,{\mathit{d}}_{M-P-Q,},{\mathit{v}}_P,\dots ,{\mathit{v}}_1\}$$

are the eigenvectors of $\tilde{\mathit{R}}$. The corresponding eigenvalues, in a decreasing order, are

$${\gamma }_1+1,\dots ,{\gamma }_Q+1,\underset{M-Q-P}{\underbrace{1,\dots ,1}},1-{\beta }_P,\dots ,1-{\beta }_1.$$ (30)

Here, the largest Q eigenvalues γ₁ + 1, . . . , γ_Q + 1 are greater than 1, and therefore, (9) is still effective at retrieving R_s, even when the control-only sources exist.

In general, however, the subspace angle between span{u₁, . . . , u_Q} and span{v₁, . . . , v_P} may not be so large and the assumption that these two subspaces are orthogonal may not be satisfied. In such cases, (23) is changed to

$$\tilde{\mathit{R}}{\mathit{u}}_i=({\gamma }_i+1){\mathit{u}}_i+\sum _{j=1}^P(1-{\beta }_j)\left({\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{u}}_i.$$ (31)

This equation shows that u_i (i = 1, . . . , Q) is no longer the eigenvector of $\tilde{\mathit{R}}$ and the second term on the right-hand side of (31) indicates the error term. Thus, if the relationship

$$({\gamma }_i+1)⪢\mid \sum _{j=1}^P(1-{\beta }_j){\mathit{v}}_j^T{\mathit{u}}_i\mid$$ (32)

holds, the error term is negligibly smaller than the first term, and u_i are still approximately the signal-level eigenvectors of $\tilde{\mathit{R}}$. Conversely, when the error term is not small, the signal-covariance estimate obtained from (9) could be erroneous.

B. Modulating-Source Scenario

We next examine the modulating-source scenario. We define the covariance matrix of the signal activity in the control state as ${\mathit{R}}_s^{\prime }$. Then we have the relationship

$$\begin{array}{cc}\hfill \text{Control}:& {\mathit{R}}_c={\mathit{R}}_s^{\prime }+{\mathit{R}}_{i+n},\hfill \\ \hfill \text{Task}:& \mathit{R}={\mathit{R}}_s+{\mathit{R}}_{i+n}.\hfill \end{array}$$ (33)

Thus, we have

$$\mathit{R}={\mathit{R}}_s-{\mathit{R}}_s^{\prime }+{\mathit{R}}_c.$$ (34)

We consider a general case where some signal sources have their intensities greater in the control state than in the task state, but others have their intensities smaller in the control state than in the task state. The power of the jth signal source in the task and the control conditions are denoted, respectively, ${\sigma }_j^2$ and ${\left({\sigma }_j^{\prime }\right)}^2$. We assume that the signal sources with j = 1, . . . , Q_p have the relationship of ${\sigma }_j^2>{\left({\sigma }_j^{\prime }\right)}^2$, and that the signal sources with j = Q_p+1, . . . , Q have the relationship ${\left({\sigma }_j^{\prime }\right)}^2>{\sigma }_j^2$. Therefore, defining ${\left(\Delta {\sigma }_j\right)}^2=\mid {\sigma }_j^2-{\left({\sigma }_j^{\prime }\right)}^2\mid$, we have

$${\mathit{R}}_s={\mathit{R}}_s^{\prime }+{\mathit{D}}_p-{\mathit{D}}_n$$ (35)

where

$${\mathit{D}}_p=\sum _{j=1}^{Q_p}{\left(\Delta {\sigma }_j\right)}^2\mathit{l}\left({\mathit{r}}_j\right){\mathit{l}}^T\left({\mathit{r}}_j\right)$$ (36)

$${\mathit{D}}_n=\sum _{j=Q_p+1}^Q{\left(\Delta {\sigma }_j\right)}^2\mathit{l}\left({\mathit{r}}_j\right){\mathit{l}}^T\left({\mathit{r}}_j\right).$$ (37)

Therefore, we have

$$\mathit{R}={\mathit{D}}_p-{\mathit{D}}_n+{\mathit{R}}_c$$ (38)

and thus

$$\tilde{\mathit{R}}={\tilde{\mathit{D}}}_p+\mathit{I}-{\tilde{\mathit{D}}}_n$$ (39)

where

$${\tilde{\mathit{D}}}_p={\mathit{R}}_c^{-1∕2}{\mathit{D}}_p{\mathit{R}}_c^{-1∕2}{\tilde{\mathit{D}}}_n={\mathit{R}}_c^{-1∕2}{\mathit{D}}_n{\mathit{R}}_c^{-1∕2}.$$

Because both ${\tilde{\mathit{D}}}_p$ and ${\tilde{\mathit{D}}}_n$ are the positive semidefinite matrices, (39) is in principle the same as (18), and exactly the same arguments hold as those in Section III-A. Therefore, we can estimate D_p by using

$${\tilde{\mathit{D}}}_p={\widehat{\mathit{R}}}_c^{-1∕2}{\widehat{\mathit{U}}}_S{\widehat{\mathit{U}}}_S^T(\widehat{\tilde{\mathit{R}}}-\mathit{I}){\widehat{\mathit{R}}}_c^{1∕2}$$ (40)

where Û_S = [û₁, . . . , û_Qp] is a matrix containing Q_p eigenvectors of ${\widehat{\mathit{U}}}_S=[{\widehat{\mathit{u}}}_1,\dots ,{\widehat{\mathit{u}}}_{Q_p}]$. We can estimate D_n by changing the role of R̂ and R̂_c. That is, we first calculate ${\widehat{\tilde{\mathit{R}}}}_c$ such that ${\widehat{\tilde{\mathit{R}}}}_c={\widehat{\mathit{R}}}^{-1∕2}{\widehat{\mathit{R}}}_c{\widehat{\mathit{R}}}^{-1∕2}$, and then obtain an estimate of D_n using

$${\tilde{\mathit{D}}}_n={\widehat{\mathit{R}}}^{1∕2}{\widehat{\mathit{U}}}_S^c{\left({\widehat{\mathit{U}}}_S^c\right)}^T(\widehat{\tilde{\mathit{R}}}-\mathit{I}){\widehat{\mathit{R}}}_c^{1∕2}.$$ (41)

In the equation above, ${\widehat{\mathit{U}}}_S^c$ is defined as ${\widehat{\mathit{U}}}_S^c=[{\widehat{\mathit{u}}}_1^c,\dots ,{\widehat{\mathit{u}}}_{Q_n}^c]$, which is a matrix containing Q_n (where Q_n = Q - Q_p) signal-level eigenvectors of ${\widehat{\tilde{\mathit{R}}}}_c$. The prewhitening method in which the roles of R̂ and R̂_c are reversed is referred to as the “flipped” prewhitening method in this paper. Therefore, the sources that are stronger in the task state than in the control state can be reconstructed using

$${\widehat{\Phi }}_p\left(\mathit{r}\right)=\frac{1}{{\mathit{l}}^T\left(\mathit{r}\right){({\widehat{\mathit{D}}}_p+\mu \mathit{I})}^{-1}\mathit{l}\left(\mathit{r}\right)}.$$ (42)

The sources that are stronger in the control state than in the task state can be reconstructed using the flipped prewhitening, i.e.,

$${\widehat{\Phi }}_n\left(\mathit{r}\right)=\frac{1}{{\mathit{l}}^T\left(\mathit{r}\right){({\widehat{\mathit{D}}}_n+\mu \mathit{I})}^{-1}\mathit{l}\left(\mathit{r}\right)}.$$ (43)

IV. Overestimation of Signal-Subspace Dimensionality

The prewhitening method requires us to determine Q, the dimension of the signal subspace of R (or the rank of R_s). This determination is usually performed by counting the number of distinctively large eigenvalues of data covariance matrix R̂. In actual MEG measurements, however, it is often problematic to accurately determine Q because the eigenvalue spectrum does not have a clear separation between these two subspaces. Here, we presents an analysis on the influence caused by the overestimation of the signal subspace dimensionality, and we show that the prewhitening method is very insensitive to such over-estimation. Therefore, the accurate determination of Q is not needed and we can use an intentionally large Q to implement the prewhitening method.

In the following, we discuss the influence caused when the dimension of the signal-subspace of $\tilde{\mathit{R}}$ is overestimated. We assume the ideal scenario in this section. Let us assume that the signal subspace dimension is overestimated as Q + Q_ε and define U_ε as U_ε = [u_Q+1, . . . , u_Q+Qε]. Ideally, the prewhitened data covariance matrix, $\tilde{\mathit{R}}$, has Q signal-level eigenvalues greater than 1 and M - Q eigenvalues equal to 1. Therefore, according to (9), the overestimation of Q does not affect the signal covariance estimate R̂_s because the relationship ${\mathit{U}}_{\epsilon }{\mathit{U}}_{\epsilon }^T(\tilde{R}-I)=0$ holds. However, the prewhitened covariance matrix $\tilde{\mathit{R}}$ is usually estimated from finite time samples, and in such cases, the noise-level eigenvalues are generally not equal to 1. We denote the noise-level eigenvalues of the estimated prewhitened covariance matrix $\widehat{\tilde{\mathit{R}}}$ as δ_j + 1 and assume δ_j ≥ 0 for j = Q + 1, . . . , Q_ε. Then, the estimated signal covariance matrix, R̂_s, is expressed in this case as

$$\begin{array}{cc}\hfill {\widehat{\mathit{R}}}_s& ={\widehat{\mathit{R}}}_c^{1∕2}[{\widehat{\mathit{U}}}_S{\widehat{\mathit{U}}}_S^T+{\widehat{\mathit{U}}}_{\epsilon }{\widehat{\mathit{U}}}_{\epsilon }^T](\widehat{\tilde{\mathit{R}}}-\mathit{I}){\widehat{\mathit{R}}}_c^{1∕2}\hfill \\ \hfill & ={\widehat{\mathit{R}}}_c^{1∕2}\left[\sum _{j=1}^Q{\gamma }_j{\widehat{\mathit{u}}}_j{\widehat{\mathit{u}}}_j^T\right]{\widehat{\mathit{R}}}_c^{1∕2}+{\widehat{\mathit{R}}}_c^{1∕2}\left[\sum _{j=Q+1}^{Q+Q_{∊}}{\delta }_j{\widehat{\mathit{u}}}_j{\widehat{\mathit{u}}}_j^T\right]{\widehat{\mathit{R}}}_c^{1∕2}.\hfill \end{array}$$ (44)

The second term on the right-hand side of the above equation indicates the error term caused by the overestimation. The error term, R̂_ε, is expressed as

$${\widehat{\mathit{R}}}_{\epsilon }={\widehat{\mathit{R}}}_c^{1∕2}\left[\sum _{j=Q+1}^{Q+Q_{∊}}{\delta }_j{\widehat{\mathit{u}}}_j{\widehat{\mathit{u}}}_j^T\right]{\widehat{\mathit{R}}}_c^{1∕2}=\sum _{j=Q+1}^{Q+Q_{∊}}{\delta }_j{\stackrel{‒}{\mathit{u}}}_j{\stackrel{‒}{\mathit{u}}}_j^T$$ (45)

where ${\stackrel{‒}{\mathit{u}}}_j={\widehat{\mathit{R}}}_c^{1∕2}{\widehat{\mathit{u}}}_j$.

Let us define the signal and noise subspaces of the measuremnt covariance matrix R, as ε_S and ε_N, i.e.,

$${\epsilon }_S=\mathit{span}\{{\mathit{e}}_1,\dots ,{\mathit{e}}_Q\}{\epsilon }_N=\mathit{span}\{{\mathit{e}}_{Q+1},\dots ,{\mathit{e}}_M\},$$

where e_j is the jth eigenvector of R_s. Then, assuming that ${\stackrel{‒}{\mathit{u}}}_j={\sum }_{j=1}^M{\alpha }_{j,i}{\mathit{e}}_i$, we can expand R̂_s using e_j such that

$${\widehat{\mathit{R}}}_{\epsilon }=\sum _{i=1}^Q\Delta {\lambda }_i{\mathit{e}}_i{\mathit{e}}_i^T+\sum _{i=Q+1}^M\Delta {\lambda }_i{\mathit{e}}_i{\mathit{e}}_i^T$$ (46)

where $\Delta {\lambda }_i={\sum }_{j=Q+1}^{Q+Q_{∊}}{\delta }_j{\alpha }_{j,i}^2(i=1,\dots ,M)$. On the righthand side of (46), the first term is the signal subspace component and the second term is the noise subspace component. To obtain the source reconstruction in (13), we need to calculate the signal-plus-sensor-noise convariance matrix. The estimate of the signal-plus-sensor-noise convariance matrix, R̂_s+n, is in this case given by

$$\begin{array}{cc}\hfill {\widehat{\mathit{R}}}_{s+n}& ={\mathit{R}}_s+{\mathit{R}}_{\epsilon }+\mu \mathit{I}\hfill \\ \hfill & =\sum _{i=1}^Q({\lambda }_i+\mu ){\mathit{e}}_i{\mathit{e}}_i^T+\sum _{i=Q+1}^M(\mu +\Delta {\lambda }_i){\mathit{e}}_i{\mathit{e}}_i^T\hfill \end{array}$$ (47)

where λ_i is the ith eigenvalue of R_s, and we assume that λ_i ≫ Δλ_i for i = 1, . . . , Q.

The equation above indicates that the influence of the over-estimation is mainly an increase of the regularization constant. The regularization in the minimum variance beamformer, known as diagonal loading, has been widely used and a significant increase of the regularization constant is known to cause a spatial blur in the reconstruction results [5]. Therefore, the overestimation of the signal subspace dimension should cause a spatial blur. However, the blur should not be large if Q_ε and the resultant Δλ_i are small. In Section V, examples are presented in which the prewhitening method can still provide successful reconstruction, even when the signal subspace dimension is significantly overestimated. In the analysis presented in this section, we assume the ideal scenario. Considering the fact that large eigenvalues are the same in the ideal and the nonideal scenarios, it is obvious that the arguments here are also valid for the nonideal scenarios.

V. Computer Simulation

A. Data Generation

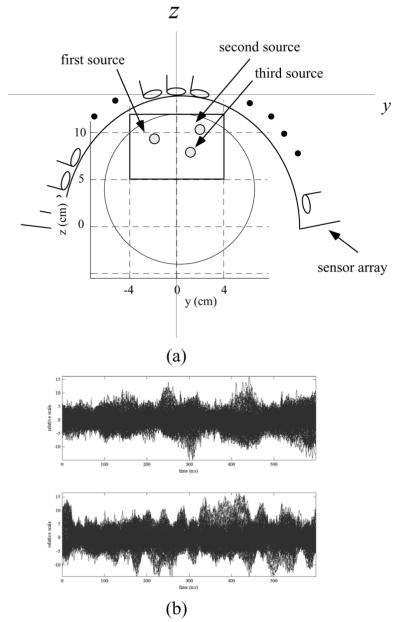
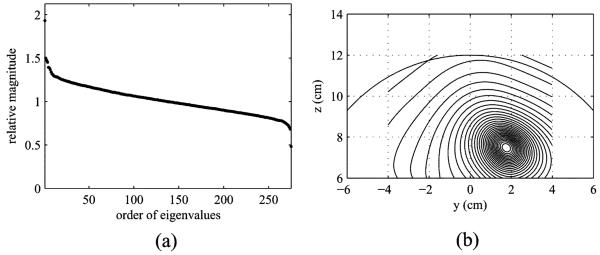
A computer simulation was performed to demonstrate the validity of the arguments in the preceding sections. In our experiments, we used a sensor alignment of the 275-sensor array from the Omega™ (VMS Medtech, Coquitlam, Canada) neuromagnetometer. Three sources were assumed to exist on a single plane (x = 0 cm), and their (y,z) coordinates were (−2.1,9.5) cm, (2.6,10.5) cm, and (1.4,7.5) cm, respectively. The source-sensor configuration and the coordinate system are depicted in Fig. 1(a). The spherical homogeneous conductor model [10] with the sphere origin set as (0,0,4) cm was used for the forward calculation. The powers of the three sources were set equal in the sensor-domain, i.e., the relationship, ${\sigma }_1^2{\mid \mid \mathit{l}\left({\mathit{r}}_1\right)\mid \mid }^2={\sigma }_2^2{\mid \mid \mathit{l}\left({\mathit{r}}_2\right)\mid \mid }^2={\sigma }_3^2{\mid \mid \mathit{l}\left({\mathit{r}}_3\right)\mid \mid }^2$, held where r_j, ${\sigma }_j^2$, and l(r_j) were the location, the power, and the lead field vector of the jth source, respectively. Multiepoch measurements were simulated.

Fig. 1.

(a) Source-sensor configuration and the coordinate system used in the numerical experiments. The plane at x = 0 cm is shown. The small filled circles indicate the locations of the three sources. The large circle indicates the boundary of the sphere used for the forward calculations. The center of the sphere was set to (0,0,4) cm. (b) Representative examples of the generated single-epoch data ${\mathit{B}}_c^{\left(\ell \right)}$ (upper panel), and B^(ℓ) (lower panel).

Each epoch had two sets of data: the task and the control data sets. The task and the control data sets in the ℓth epoch are denoted B^(ℓ) and ${\mathit{B}}_c^{\left(\ell \right)}$, respectively, and they are expressed as B^(ℓ) = [b^(ℓ)(t₁, . . . , b^(ℓ)(t_K)], and ${\mathit{B}}_c^{\left(\ell \right)}=[{\mathit{b}}_c^{\left(\ell \right)}\left(t_1\right),\dots ,{\mathit{b}}_c^{\left(\ell \right)}\left(t_K\right)]$, where K is the number of time points. Since K was set at 600 in our computer simulation, B^(ℓ) and ${\mathit{B}}_c^{\left(\ell \right)}$ resulted in 275 × 600 spatio-temporal data matrices. To calculate B^(ℓ)(t_k) and ${\mathit{b}}_c^{\left(\ell \right)}\left(t_k\right)$, we assumed uncorrelated sinusoidal time courses for the three sources; the source time course for the jth source and for the ℓth epoch is expressed as $s_j^{\left(\ell \right)}\left(t_k\right)={\sigma }_j\sin (2\pi A_j(t_k-t_1)∕\left(\Delta T\right)+{\theta }_j^{\left(\ell \right)})$, where ΔT is the time window equal to t_K - t₁, and the constant A_j controls the frequency, which was set at 6.3 for the first source, 9.1 for the second source, and 13.1 for the third source. The phase offset ${\theta }_j^{\left(\ell \right)}$ was generated using the random number between 0 and 2π, and different random number was used for ${\theta }_j^{\left(\ell \right)}$ depending on j, ℓ, and the two conditions. We therefore simulated induced source activities, which are elicited by the stimulus but not phase-locked to it.

B. Simulation for the Control-Only-Source Scenario

We first check the performance of the prewhitening method under the existence of a control-only source. In this computer simulation, the first source is the control-only source, and the second and the third sources are the signal sources, which appear only in the task state. Namely, ${\mathit{b}}_s^{\left(\ell \right)}\left(t\right)$ contains the magnetic field from the second and the third sources, and ${\mathit{b}}_{\Delta }^{\left(\ell \right)}\left(t\right)$ contains the magnetic field from the first source. Real spontaneous MEG was used as the interference ${\mathit{b}}_I^{\left(\ell \right)}\left(t\right)$, and the signal-to-interference ratio (SIR) was set equal to 0.3. That is, values of the source power ${\sigma }_2^j,(j=1,2,3)$ were determined in order for the SIR defined as $\sqrt{{\sum }_{k=1}^{K,}{\mid \mid {\mathit{b}}_s^{\left(\ell \right)}\left(t_k\right)\mid \mid }^2∕{\sum }_{k=1}^K{\mid \mid {\mathit{b}}_I^{\left(\ell \right)}\left(t_k\right)\mid \mid }^2}$ to be equal to 0.3. A total of 96 epochs of ${\mathit{B}}_c^{\left(\ell \right)}$ and B^(ℓ) (ℓ = 1, . . . , 96) were generated. The representative examples of ${\mathit{B}}_c^{\left(\ell \right)}$ and B^(ℓ) are shown in Fig. 1(b). The sample covariance matrices R̂_c and R̂ were calculated using ${\widehat{\mathit{R}}}_c={\sum }_{\ell =1}^{L_e}{\mathit{B}}_c^{\left(\ell \right)}{\left({\mathit{B}}_c^{\left(\ell \right)}\right)}^T∕\left(L_{e}K\right)$ and $\widehat{\mathit{R}}={\sum }_{\ell =1}^{L_e}{\mathit{B}}^{\left(\ell \right)}{\left({\mathit{B}}^{\left(\ell \right)}\right)}^T∕\left(L_{e}K\right)$ where L_e indicates the number of epochs, which is equal to 96 in this computer simulation. The total covariance matrix was calculated for later use, using

$${\widehat{\mathit{R}}}_{\text{total}}=\frac{1}{L_{e}K}\sum _{\ell =1}^{L_e}({\mathit{B}}^{\left(\ell \right)}+{\mathit{B}}_c^{\left(\ell \right)}){({\mathit{B}}^{\left(\ell \right)}+{\mathit{B}}_c^{\left(\ell \right)})}^T.$$ (48)

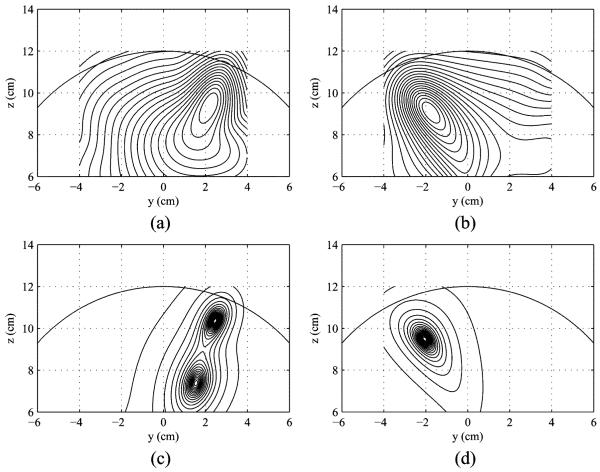
The conventional beamformer source reconstruction was performed for the control and the task data, using ${\widehat{\Phi }}_C\left(\mathit{r}\right)=1∕\left[{\mathit{l}}^T\left(\mathit{r}\right){\widehat{\mathit{R}}}_c^{-1}{\mathit{l}}^T\left(\mathit{r}\right)\right]$ and Φ̂(r) = 1/ [l^T(r)R̂⁻¹l^T(r)] where Φ̂_C(r) and Φ̂_C(r) are the source power reconstruction for the control and the task states, respectively. The results are shown in Fig. 2(a) and (b). These results contain severe blur due to the interference inherent in the task and the control data. The source reconstruction was next performed with the prewhitening estimate of the signal covariance matrix R̂_s, using (13). The prewhitening estimate of R_Δ, R̂_Δ, was also obtained from the flipped prewhitening method using ${\widehat{\tilde{\mathit{R}}}}_c={\widehat{\mathit{R}}}^{-1∕2}{\widehat{\mathit{R}}}_c{\widehat{\mathit{R}}}^{-1∕2}$, and the source reconstruction was performed using (13) with R̂_s replaced by R̂_Δ. The results of prewhitening and flipped prewhitening source reconstructions are shown in Fig. 2(c) and (d). Compared to the results in Fig. 2(a) and (b), the results in Fig. 2(c) and (d) show that the signal and the control-only sources were reconstructed at the correct locations with much higher spatial resolution, demonstrating that the prewhitening method is still effective in the control-only-source scenario.

Fig. 2.

Results of the source reconstruction experiments simulating the control-only-source scenario. (a) Results of conventional reconstruction for the task condition, Φ̂(r). (b) Results of conventional reconstruction for the control condition, Φ̂_C(r). (c) Results of the prewhitening source reconstruction. (d) Results of the flipped prewhitening source reconstruction.

C. Simulation for the Modulating-Source Scenario

In this computer simulation, the intensity of the first source was decreased by 30% from the control to the task conditions, while the intensity of the third source was increased by 30% from the control to the task conditions. The intensity of the second source remained the same between the two conditions. The SIR was set equal to 0.3.

The existing method of processing this type of data calculates the following pseudo-F image[3], such that F(r) = (Φ̂(_r) - Φ̂(_C(r))/Φ̂(_r), where Φ̂_C(r) and Φ̂(r) are obtained using Φ̂_C(r) = w^TR̂_cw, and Φ̂(r) = w^TR̂w, and where the beamformer weight is obtained using

$$\mathit{w}=\frac{{\widehat{\mathit{R}}}_{\text{total}}^{-1}\mathit{l}\left(\mathit{r}\right)}{{\mathit{l}}^T\left(\mathit{r}\right){\widehat{\mathit{R}}}_{\text{total}}^{-1}\mathit{l}\left(\mathit{r}\right)}.$$ (49)

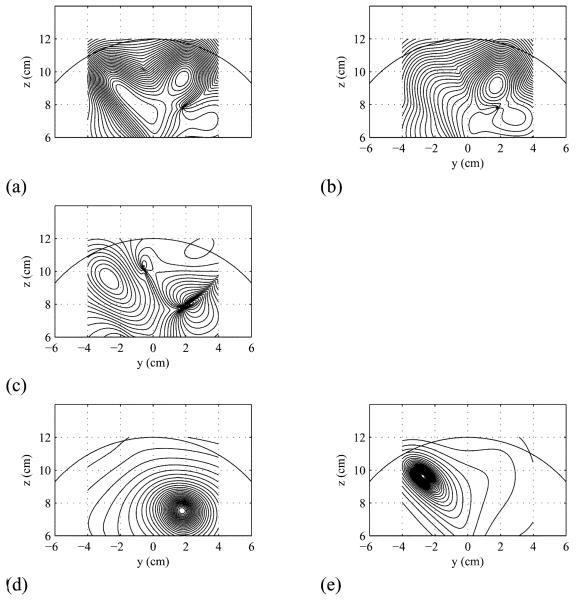
In the above expression, the total covariance matrix R̂_total is calculated using (48). The results of calculating Φ̂(r), Φ̂_C(r) and F (r) are shown in Fig. 3(a)-(c), respectively. In the pseudo-F image in (c), the third source forms a positive peak, and the first source forms a negative peak. Although these peaks are blurred and the peak locations are biased, the pseudo-F image F (r) can at least detect these two sources. Next, the methods of prewhitening and flipped prewhitening source reconstruction were performed, and the results are shown in Fig. 3(d) and (e). In these results, the signal source and the control-only source form clear peaks around the correct locations of these sources, although a small bias of the reconstructed source location can be observed, particularly for the third source.

Fig. 3.

Results of the source reconstruction experiments simulating the modulating-source scenario. (a) Results of conventional reconstruction for the task condition, Φ̂(r). (b) Results of conventional reconstruction for the control condition, Φ̂_C(r). (c) Results of calculating the pseudo-F image F (r). (d) Results of applying the prewhitening source reconstruction. The signal subspace dimension was set to 15. (e) Results of the Flipped prewhitening source reconstruction.

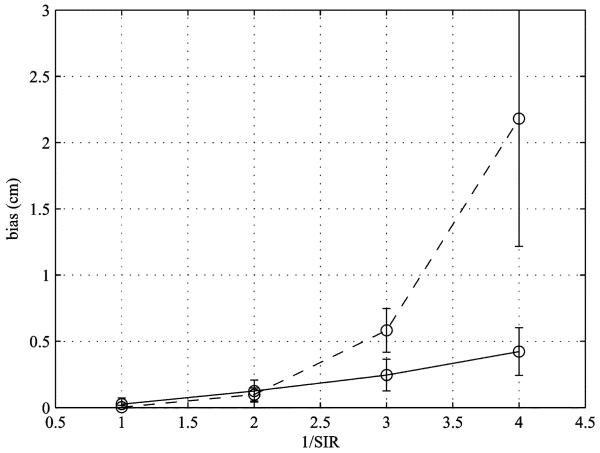
To compare the source localization biases for the pseudo-F and the prewhitening results, we performed a Monte Carlo-type computer simulation in which 40 data sets, each containing B^(ℓ) and ${\mathit{B}}_c^{\left(\ell \right)}(\ell =1,\dots ,L_e)$, were generated and 40 sets of reconstruction results were obtained. In each set of the results, the distance between the peak location and the true location of the third source was calculated as the source locatization bias. The mean and the standard deviation of the 40 sets of the source-bias results are plotted for four SIR values in fig. 4. (The values of 1/SIR were set to 1, 2, 3, and 4.) According to these results, the amount of the source bias is almost the same for the prewhitening and pseudo-F results when the SIR is moderately high (1/SIR ≤ 2). However. When the SIR is low (1/SIR > 2), the prewhitening results have a significantly smaller source bias. These results demonstrate the effectiveness and superiority of the prewhitening method in the modulating-source scenario.

Fig. 4.

Results of the Monte Carlo-type computer simulation performed to estimate the amount of the source localization bias. The mean of the 40 sets of the calculated distance between the true and the estimated locations of the third source are plotted for four SIR values. The solid line represents the average source localization bias for the prewhitening beamforming, and the broken line represents that for the pseudo-F method. The error bars indicate ±1 standard deviation.

Finally, we show the robustness of the prewhitening method to the overestimation of the signal-subspace dimension Q. The eigenvalue spectrum of $\widehat{\tilde{\mathit{R}}}$ for obtaining the results in Fig. 3(d) is shown in Fig. 5(a). This spectrum indicates that there is no clear separation between the noise- and the signal-level eigen-values, and there should be some ambiguity when determining the signal subspace dimension. When obtaining the results in Fig. 3(d), the signal subspace dimension was set to 15. The reconstruction results obtained with the signal subspace dimension set to 30 are shown in Fig. 5(b). Results almost identical to those in Fig. 3(d) were obtained in spite of the fact that the signal subspace dimension was significantly overestimated in this case.

Fig. 5.

(a) Eigenvalue spectrum of $\widehat{\tilde{\mathit{R}}}$ used for reconstruction in Fig. 3(d). (b) The results of the prewhitening source reconstruction obtained with the signal subspace dimension set to 30.

VI. Experiment

The effectiveness of the prewhitening method is further demonstrated using real MEG data collected during finger flection. The measurement was performed using the 275-channel Omega-275™ whole-cortex biomagnetometer installed at the Biomagnetic Imaging Laboratory, University of California, San Francisco. Here, a subject was asked to press a button with his right-index finger every 3–4 s. The onset of the movement was indicated by a button press and defined as the time-origin. A total of 200 epochs were acquired at a 1-kHz sampling rate.

We set two time windows for covariance matrix estimation: the first from 1000–1300 ms, and the second from −300–0 ms. The fourier transforms of the ℓth epoch data in the first and the second time windows are respectively denoted ${\mathit{g}}_1^{\left(\ell \right)}\left(f\right)$ and ${\mathit{g}}_2^{\left(\ell \right)}\left(f\right)$. The frequency-domain sample covariance matrices for the first and the second time windows, Ω̂₁ and Ω̂₂, are obtained using

$${\widehat{\Omega }}_{\iota }=\sum _{f\in F_w}\sum _{\ell =1}^{200}{\mathit{g}}_{\iota }^{\left(\ell \right)}\left(f\right){\left({\mathit{g}}_{\iota }^{\left(\ell \right)}\left(f\right)\right)}^T$$ (50)

where l = 1 and 2. In this equation, ℓ is the epoch index and the notation ${\sum }_{f\in F_w}$ indicates the summation over a specific frequency band F_w, and F_w was set to the beta-band region between 15 and 25 Hz inour experiments. In these experiments, Ω̂₁ and Ω̂₂ were used as the task and the control covariance matrices.

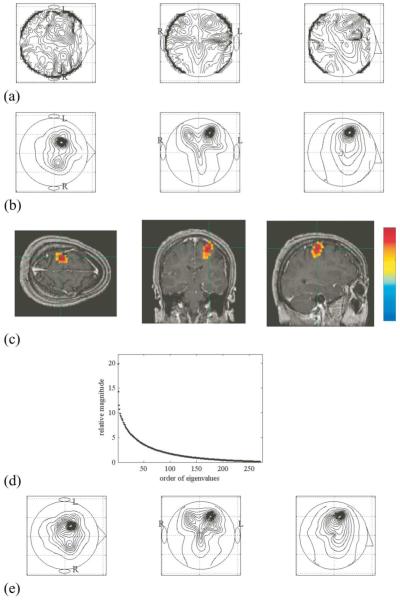
It is well-known that the intensity of the magnetic field in the beta-band spectral region decreases preceding and during the button-press finger movements [11]. Therefore, these measurements represent the modulating-source scenario where signal sources are present both in the task and control conditions but modulated in their amplitudes. First, we calculated the pseudo-F map F (r) with the results shown in Fig. 6(a). Although the Pseudo-F map was able to detect source activities in the left temporal region, the results are considerably blurry. We next applied the prewhitening source reconstruction and the results are shown in Fig. 6(b). We can see that the proposed method can reconstruct a clear, localized source in the left temporal region. The MRI overlay of these results in shown in Fig 6(c). The overlay shows that the center of the reconstructed activity is located in contralateral hand-cortex. The results in Fig. 6(b) and (c) demonstrate the effectiveness of the prewhitening source reconstruction for this data set.

Fig. 6.

Results of the source reconstruction experiment using hand-motor MEG data. The maximum-intensity projections of (a) the pseudo-F results F(r) and (b) the prewhitening results. The left, middle, and the right columns, respectively, show the maximum intensity projections of the 3-D reconstruction onto the axial, coronal, and sagittal planes. The uper-case letters L and R show the left and the right hemispheres. The signal subspace dimension was set to 15. (c) MRI overlay of the prewhitening source reconstruction results in (b). (d) The eigenvalue spectrum of $\widehat{\tilde{\mathit{R}}}$ used for reconstructing the results in (b). (e) the results of the pewhitening source reconstruction obtained with the signal subspace dimension set to 25.

We again check the sensitivity of the prewhitening method to the overestimation of the signal subspace dimension. The eigenvalue spectrum of $\widehat{\tilde{\mathit{R}}}$ is shown in fig. 6(d). We can see that there is no clear separation between the noise and the signal level eigenvalues and that there would be some abiguity when determining the signal-subspace dimension. When obtaining the results in Fig. 6(b), the signal-subspace dimension was set to 15. (This value was determined by our computer algorithm that detects a point where the spectrum starts to rise above th noise slope.) The reconstruction results obtained with the dimension set at 25 are shown in Fig. 6(e). These results are almost identical to those in Fig. 6(b), demonstrating that results from the prewhitening method are largely insensitive to the overestimation of the signal subspace dimension.

Biographies

Kensuke Sekihara received the M.S. and Ph.D. degrees from the Tokyo Institute of Technology, Tokyo, Japan, in 1976 and 1987, respectively.

From 1976 to 2000, he worked with Central Research Laboratory, Hitachi, Ltd., Tokyo. He was a Visiting Research Scientist at Stanfrod University, Stanford, CA from 1985 to 1986, and at Basic Development, Siemens Medical Engineering, Erlangen, Germany from 1991 to 1992. From 1996 to 2000, He worked with “Mind Articulation,” a research project sponsored by the Japan Science and Technology Corporation. He is currently a Professor at the Department of Systems Design and Engineering, Tokyo Metropolitan University, Tokyo. His research interests include neuromagnetic source reconstruction and statistical signal processing, especially its application to functional neuroimaging.

Dr. Sekihara is a member of IEEE Medicine and Biology Society and the IEEE Signal Processing Society.

Kenneth E. Hild, II (M’90-SM’05) received the B.S. and M.Sc. degrees in electrical engineering, with emphasis in signal processing, communications, and controls, from the University of Oklahoma, Norman, in 1992 and 1996, respectively, and the Ph.D. degree in electrical engineering from the University of Florida, Gainesville, in 2003, where he studied information-theoretic learning and blind source separation in the Computational NeuroEngineering Laboratory. Dr. Hild has also studied biomedical informatics at Stanford University, Palo Alto.

From 1995 to 1999 he was employed at Seagate Technologies, Inc., where he served as an Advisory Development Engineer in the Advanced Concepts group. From 2000 to 2003 he taught several graduate-level classes on adaptive filter theory and stochastic processes at the University of Florida. He is currently employed at the Biomagnetic Imaging Laboratory in the Department of Radiology, University of California at San Francisco, where he is applying variational Bayesian techniques for biomedical signal processing of encephalographic and cardiographic data.

Dr. Hild is a member of Tau Beta Pi, Eta Kappa Nu, and the International Society for Brain Electromagnetic Topography.

Sarang S. Dalal was born in Hayward, CA, in 1978. He received the B.S. degree in biomedical engineering, with a concentration in electrical engineering and a minor in psychology, from The Johns Hopkins University, Baltimore, MD, in 2000 and the Ph.D. degree in bioengineering, jointly with the University of California, San Francisco (UCSF) and the University of California, Berkeley in the laboratory of Dr. Srikantan Nagarajan, in 2007.

His research interests include neuromagnetic source reconstruction, time-frequency analyses, cortical connectivity, and auditory/language processing. He is currently a Postdoctoral Scholar with the Mental Processes and Brain Activation Lab, INSERM U821, Bron, France.

Dr. Dalal is a member of the IEEE Engineering in Medicine and Biology Society. He received the Young Investigator Award from the International Conference on Biomagnetism in 2004, the Ruth L. Kirschstein National Research Service Award from the National Institute on Deafness and Other communication Disorders, and the Chateaubriand Fellowship from the Embassy of France in the U.S.

Srikantan S. Nagarajan (S’90-M’91-SM’07) received the M.S. and Ph.D. degrees in biomedical engineering from Case Western Reserve University (CWRU), Cleveland, OH.

His research career began at the Applied Neural Control Laboratory, CWRU. After graduate school, he did a postdoctoral fellowship at the Keck Center for Integrative Neuroscience, University of California, San Francisco (UCSF), under the mentorship of Drs. Michael Merzenich and Christoph Schreiner. Subsequently, he was a tenure-track faculty member in the Department of Bioengineering, University of Utah. Currently, he is the Director of the Biomagnetic Imaging Laboratory, an Associate Professor in Residence in the Department of Radiology, and a member in the UCSF/University of California, Berkeley Joint Graduate Program in Bioengineering. His research interests are in the area of neural engineering where his goal is to better understand dynamics of brain networks involved in processing, and learning, of complex human behaviors such as speech, through the development of functional brain imaging technologies.

Appendix

This appendix presents the proof of (25). We first point out that the following relationship holds:

$$\mathit{span}\{{\mathit{u}}_1,\dots {\mathit{u}}_Q\}\bigcap \mathit{span}\{{\mathit{v}}_1,\dots {\mathit{v}}_P\}=\varnothing$$ (51)

where ∅ indicates the empty set. Although we do not provide the formal proof, it is easy to prove this relationship. Because this relationship holds, we can then show u_j (j = 1, . . . , Q) ∈ span{v₁, . . . , v_p}. That is, u_j (j = 1, . . . , Q) belongs to the complementary subspace of span{v₁, . . . , v_p}, which is equal to span{v_Q+1, . . . , v_M}, i.e., u_j ∉ span{v_Q+1, . . . , v_M}. Therefore, because ${\sum }_{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T$ is the projector onto sapn{v_Q+1, . . . , v_M}, the application of this projector to u_i results in

$$\left(\sum _{j=P+1}^M{\mathit{v}}_j{\mathit{v}}_j^T\right){\mathit{u}}_j={\mathit{u}}_i,$$

which is (25).