The Influence of the Phonological Neighborhood Clustering-Coefficient on Spoken Word Recognition

Abstract

Clustering coefficient—a measure derived from the new science of networks—refers to the proportion of phonological neighbors of a target word that are also neighbors of each other. Consider the words bat, hat, and can, all of which are neighbors of the word cat; the words bat and hat are also neighbors of each other. In a perceptual identification task, words with a low clustering coefficient (i.e., few neighbors are neighbors of each other) were more accurately identified than words with a high clustering coefficient (i.e., many neighbors are neighbors of each other). In a lexical decision task, words with a low clustering coefficient were responded to more quickly than words with a high clustering coefficient. These findings suggest that the structure of the lexicon, that is the similarity relationships among neighbors of the target word measured by clustering coefficient, influences lexical access in spoken word recognition. Simulations of the TRACE and Shortlist models of spoken word recognition failed to account for the present findings. A framework for a new model of spoken word recognition is proposed.

Several models of spoken word recognition view the mental lexicon as a collection of arbitrarily ordered phonological representations, and the process of lexical retrieval as a special instance of pattern matching (e.g., TRACE: McClelland & Elman, 1986; Shortlist: Norris, 1994). In these accounts, acoustic-phonetic input activates several phonological word-forms “…which are roughly consistent with the bottom-up input” (Norris, 1994; pg. 201). The candidate words then compete among each other (in some cases via an inhibitory mechanism among activated word-forms) until the activation level of one candidate exceeds that of the other candidates, indicating that a representation that best (though not necessarily correctly) matches the input has been found.

Although this perspective of the mental lexicon has advanced our understanding of spoken word recognition and other related processes, it is not the only way to view the mental lexicon. Indeed, an early model of word recognition proposed by Forster (1978; page 3) suggested that: “[a] structured information-retrieval system permits speakers to recognize words in their language effortlessly and easily.” The idea that the lexicon may not be a collection of arbitrarily ordered phonological representations, but may instead be structured in such a way to influence the process of spoken word recognition can also be found in a more recent model of spoken word recognition—the neighborhood activation model (Luce & Pisoni, 1998; page 1)—which assumes “…that similarity relations among the sound patterns of spoken words represent one of the earliest stages at which the structural organization of the lexicon comes into play.” If the phonological representations in the mental lexicon are structured rather than arbitrarily ordered, it is important to determine how the lexicon is structured, and, more importantly, how that structure might influence processing.

One way to examine the structure of a complex system is with the tools of network science. The tools of network science have been applied to many complex systems found in the real world (e.g., the World Wide Web) to help researchers model the structure of such systems, and better examine the influence of that structure on the processes occurring in that system. For example, Montoya and Solé (2002) created a network representing the animals in an ecosystem (as nodes in the network), and the predator-prey relationship among those animals (as directed links between relevant nodes) to examine how the extinction of a given species might affect the rest of the ecosystem.

Recent analyses using the tools of network science have also provided some insight regarding the structure of the mental lexicon (e.g., Steyvers & Tenenbaum, 2005; Vitevitch, 2008). Vitevitch (2008) constructed a network from approximately 20,000 English words in which nodes in the network represented phonological word-forms, and (unweighted, undirected) links between nodes represented phonological similarity between words (using the one-phoneme metric used in Luce & Pisoni, 1998). Figure 1 shows a small portion of this network. Vitevitch (2008) found that the network of phonological word-forms in English had several unique structural features: (1) a large highly interconnected component, as well as many islands (words that were related to each other—such as faction, fiction, and fission—but not to other words in the large component) and many hermits, or words with no neighbors; the largest component exhibited (2) small-world characteristics (“short” average path length and, relative to a random graph, a high clustering coefficient; Watts & Strogatz, 1998), (3) assortative mixing by degree (a word with many neighbors tends to have neighbors that also have many neighbors; Newman, 2002), and (4) a degree distribution that deviated from a power-law. Note that the same constellation of features was also found in phonological networks of Spanish, Mandarin, Hawaiian, and Basque (Arbesman, Strogatz, & Vitevitch, submitted).

Figure 1.

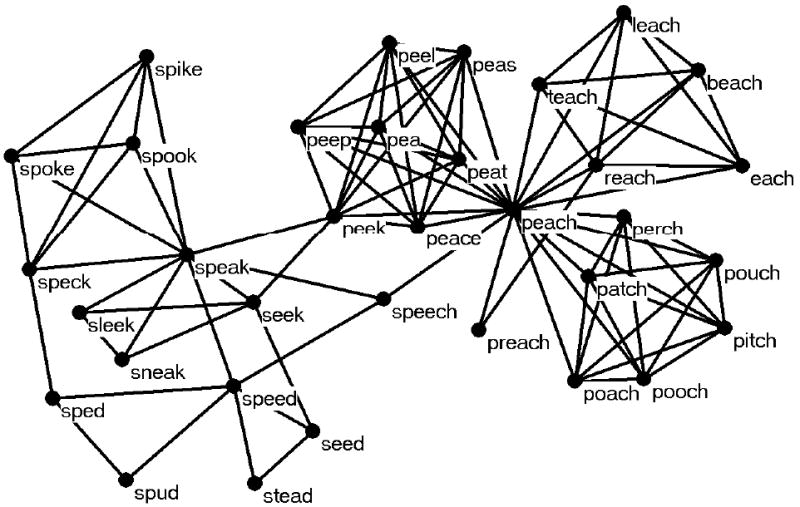
A portion of the phonological network examined in Vitevitch (2008). Depicted are the word speech, phonological neighbors of speech, and the phonological neighbors of those neighbors.

The network analyses by Arbesman et al. (submitted) and Vitevitch (2008) lend some support to the idea that phonological representations in the mental lexicon may be structured in some non-arbitrary way. Indeed, if phonological word forms in the mental lexicon were an arbitrary collection of representations, one would have expected the network analysis of the lexicon to yield measures comparable to a random network rather than a small-world network, no mixing by degree, and a degree distribution that resembled a normal distribution, instead of the constellation of features observed in Vitevitch (2008).

If phonological representations in the mental lexicon are indeed structured in some way, how might this organization influence processing? Consider, for example, that network simulations by Kleinberg (2000) found that a small-world structure afforded rapid search through what may appear to be a large system (i.e., the network contains many nodes). Given this finding, it is not unreasonable to hypothesize that—despite the tens of thousands of words contained in the mental lexicon—the small-world structure observed in the mental lexicon may contribute to the rapid and efficient nature of the lexical retrieval process.

The structure of a network is also commonly characterized by a measure called the degree distribution. Degree refers to the number of links that a node has, and the degree distribution refers to the number of nodes that have many links, the number of nodes that have few links, etc. Several network analyses have demonstrated that the degree of a node can be used to successfully navigate through and rapidly retrieve information from very large systems (Simsek & Jensen, 2008; see also Griffiths, Steyvers & Firl, 2007). In a network model of phonological word-forms in the mental lexicon (Vitevitch, 2008), degree would correspond to the number of words that sound similar to a given word. In the spoken word recognition literature, this measure is referred to as the density of the phonological neighborhood (Luce & Pisoni, 1998). A word like cat, which has many neighbors (e.g., at, bat, mat, rat, scat, pat, sat, vat, cab, cad, calf, cash, cap, can, cot, kit, cut, coat), is said to have a dense phonological neighborhood, whereas a word, like dog, that has few neighbors (e.g., dig, dug, dot, fog) is said to have a sparse phonological neighborhood (n.b., each word has additional neighbors, but only a few were listed for illustrative purposes). Much psycholinguistic research has demonstrated the influence of neighborhood density on spoken word recognition (e.g., Cluff & Luce, 1990; Goldinger, Luce, & Pisoni, 1989; Luce & Pisoni, 1998; Vitevitch, 2002a, 2003; Vitevitch & Luce, 1999; Vitevitch & Rodríguez, 2005; Vitevitch, Stamer & Sereno, in press) and other language processes (e.g., Storkel, Armbruster & Hogan, 2006; Vitevitch, 1997, 2002b; Vitevitch & Stamer, 2006).

The influence of neighborhood density (i.e., degree) on language processing is not only consistent with a structural account of the mental lexicon, but it can also be accounted for by current models of spoken word recognition such as TRACE (McClelland & Elman, 1986) and Shortlist (Norris, 1994), which view the mental lexicon as a collection of arbitrarily ordered phonological representations. Indeed, the field has learned much about language processing from such models. However, given the evidence that the lexicon may be structured in a non-arbitrary way (Arbesman et al., submitted; Steyvers & Tenenbaum, 2005; Vitevitch, 2008; see also Albert & Barabási, 2002; Batagelj, Mrvar & Zaveršnik, 2002; Ferrer i Cancho & Solé, 2001b, Motter et al., 2002; Wilks & Meara, 2002; Wilks, Meara & Wolter, 2005), and that structural organization can influence processing (Kleinberg, 2000), it is important to examine how the structure based on phonological similarity might affect the process of lexical retrieval. Specifically, in the present experiments, we focused on how similarity among the neighbors, a measure referred to in network science terms as the clustering coefficient (e.g., Watts & Strogatz, 1998), affects the recognition of the target word.

It is important to note the difference between the measures of phonological neighborhood density and clustering coefficient. Consider for example, the word badge, which has among its phonological neighbors the words budge, bag, bad, bat, back, ban, and batch. Simply counting the number of neighbors a word has gives us the measure known as neighborhood density. To assess the clustering coefficient of the word badge, one must consider the extent to which the neighbors are similar to each other. Notice that bag, bad, bat, back, ban and batch are not only neighbors of the word badge, but are also neighbors of each other. The clustering coefficient, therefore, measures the proportion of phonological neighbors that are also neighbors of each other.

A word with a large proportion of neighbors also being neighbors of each other is said to have a high clustering coefficient, whereas a word with (an equal number of neighbors but) a small proportion of neighbors also being neighbors of each other is said to have a low clustering coefficient. The words log and badge are used as examples of words with low and high clustering coefficient, respectively. As illustrated in Figure 2, both words have 13 phonological neighbors and thus the same neighborhood density. Note that there are fewer interconnections among the neighbors of the word log (i.e., low clustering coefficient) than for the neighbors of the word badge (i.e., high clustering coefficient). Clustering coefficient is an important network parameter to investigate due to its critical role in transmission dynamics within the network (Read & Keeling, 2003; Newman, 2003). For example, computational analyses by epidemiologists suggest that differences in clustering coefficient influence how quickly and how widespread diseases infect (and re-infect) people in networks that model social interactions (Keeling, 2005).

Figure 2.

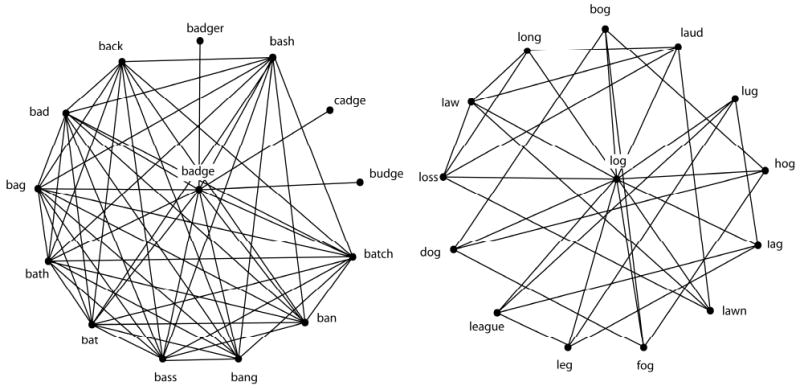
The left panel represents a word with a higher clustering coefficient (badge), whereas the right panel represents a word with a lower clustering coefficient (log). Note that both words have the same number of phonological neighbors.

In an interesting analogue designed to experimentally examine the influence of network structure on disease transmission dynamics, Naug (2008) measured the food transfer interactions of honeybees as a function of food quality (high versus low concentrations of sucrose in a feeding solution). As honeybees transfer food mouth-to-mouth, this approach offered an ideal (if not unique) way to model the route an orally transmitted pathogen might spread through a network of social contacts. Germane to the present study, Naug found that transmission of a pathogen tended to be contained in a smaller region of the network in conditions with high clustering coefficients, resulting in a few nodes with high amounts of contagion. In contrast, the pathogen tended to be more broadly dispersed across the network in conditions with low clustering coefficients, resulting in a large number of nodes with a lower amount of the contagion.

The relevance of pathogen transmission and honeybees to spoken word recognition is evident if one extracts the basic principles of network structure and processing found in the work of Naug (2008), and applies those principles to a network of phonological word-forms over which activation spreads.¹ When the lexicon is viewed as a network—comprised of nodes representing phonological word-forms and links connecting words that are phonological neighbors, as in Vitevitch (2008)—the structure found among the neighboring words (i.e., the clustering coefficient) could disperse (or contain) the spread of activation in the network, making it easier (or more difficult) to retrieve a given word from the lexicon. By examining a different aspect of lexical structure, namely the clustering coefficient, we might gain important insight into how the structure of the lexicon influences spoken language processing.

Consider, first, a word with a low clustering coefficient, or few neighbors being neighbors of each other. As the incoming acoustic-phonetic signal activates a target word and phonologically related words, the partially activated neighbors will not only transmit some activation back to the target word, but they will also disperse that activation to other words elsewhere in the network. With activation being distributed to other parts of the network (i.e., the lexicon), many representations will become slightly activated, but only one item—the target word—will be highly activated as a result of receiving some amount of spreading activation from its neighbors and being stimulated most consistently and directly by the acoustic-phonetic input. With only the target word being highly activated, retrieval of that item from the lexicon and recognition of that word will be trivial (i.e., rapid and efficient).

Now consider a word with a high clustering coefficient, or many neighbors being neighbors of each other. In this case, the incoming acoustic-phonetic signal will again activate a target word and phonologically related words. However, for words with a high clustering coefficient, the partially activated neighbors will not only transmit activation back to the target word (as occurred in words with low clustering coefficient), but the neighbors will spread activation amongst the other phonologically related neighbors of the target word rather than dispersing it to other words in the lexicon that are less similar to the target. With the spread of activation reverberating amongst the neighbors—essentially containing activation within the phonological neighborhood—the target word will no longer “stand out” from the neighbors, which are also now highly activated, making it difficult to retrieve an item from the lexicon quickly and without error. The present studies used two standard psycholinguistic tasks to examine these predictions, which were derived from studies of networks in other contexts.

Experiment 1

The present experiment used a conventional task in psycholinguistics, the perceptual identification task, to examine how the inter-connective relationships among the phonological neighbors (i.e., the clustering coefficient) might influence processing of a target word. In the perceptual identification task, participants are asked to identify a stimulus word that is presented in a background of white noise. Although numerous psycholinguistic studies have examined the influence of phonological neighborhood density on various language related processes, none of these previous studies examined how the relationship among the neighbors of the target word might influence processing. It is important to note that it is not the intent of the authors to find yet another lexical characteristic that must be controlled in psycholinguistic experiments (Cutler, 1981). Rather we are simply using the perspective and tools of network science to explore a fundamental assumption about word-forms in the mental lexicon, namely, that they are organized in a non-arbitrary way (Vitevitch, 2008). In the present experiments we examined the influence of lexical structure, as measured by the clustering coefficient, on the process of spoken word recognition. Current models of spoken word recognition are silent in predicting how the relationship among the neighbors of the target word might influence processing. However, based on the results of a network experiment by Naug (2008), we predicted that words with a low clustering coefficient should be identified more accurately than words with a high clustering coefficient.

Method

Participants

Thirty native English speakers were recruited from the pool of Introductory Psychology students enrolled at the University of Kansas. The participants received partial credit towards the completion of the course for their participation. All participants were right-handed with no reported history of speech or hearing disorders. None of the participants in the present experiment took part in the other experiment that is reported here.

Materials

Seventy-six English monosyllabic words were used as stimuli in this experiment. A male native speaker of American English (the second author) produced all of the stimuli by speaking at a normal speaking rate and loudness in an IAC sound attenuated booth into a high-quality microphone. Isolated words were recorded onto a digital audiotape at a sampling rate of 44.1 kHz. The digital recordings were then transferred directly to a hard-drive via an AudioMedia III sound card and Pro Tools LE software (Digidesign). The pronunciation of each word was verified for correctness. Each stimulus word was edited using SoundEdit 16 (Macromedia, Inc.) into an individual sound file. The amplitude of the individual sound files was increased to their maximum without distorting the sound or changing the pitch of the words by using the Normalization function in SoundEdit 16. The same program was used to degrade the stimuli by adding white noise equal in duration to the sound file. The white noise was 24 dB less in amplitude than the mean amplitude of the sound files. Thus, the resulting stimuli were presented at a +24 dB signal to noise ratio (S/N).

All stimuli consisted of three phonemes in a consonant-vowel-consonant structure. Half of the stimuli had high clustering coefficients and half had low clustering coefficients. These stimulus words and their lexical characteristics are listed in Appendix A and further described below.

Clustering coefficient

The clustering coefficient (C) measured the probability that the neighbors of a given node were also neighbors of each other. The clustering coefficient for each stimulus was obtained by using the Pajek computer program (Batagelj & Mrvar, 1988) to analyze the 19,340 lexical entries in Nusbaum, Pisoni, and Davis (1984). To calculate the clustering coefficient, count the number of edges between neighbors of a vertex, and divide that value by the number of possible edges that could exist among the neighbors. Putting these network analysis terms into terms more familiar to psycholinguists, a vertex is equivalent to a word-form, and an edge exists between two vertices if those vertices are phonologically similar to each other. The clustering coefficient is, therefore, the number of relationships that exist among the neighbors compared to the number of connections that could exist among the neighbors if they were all interconnected to each other.

The clustering coefficient, C, has a range from 0 to 1. When C = 0, none of the neighbors of a target node are neighbors of each other, and when C = 1, every neighbor of a target word is also a neighbor of all of the other neighbors of a target word. Two groups of words were selected for the present study. Selection of the stimulus items from this larger set of words was not random, as various constraints, described below, had to be met. The selected words with a higher clustering coefficient had a mean clustering coefficient value of .350 (SEM = .007), and words with a lower clustering coefficient had a mean clustering coefficient value of .250 (SEM = .005). The difference between the two groups of stimuli was statistically significant, F (1, 74) = 144.464, p < .0001). In addition to being selected such that the two groups of words differed significantly in clustering coefficient, the two groups of words were selected such that they were equivalent in subjective familiarity, word frequency, neighborhood density, spread of the neighborhood, number of neighbors formed in a given phoneme position, neighborhood frequency, and phonotactic probability.

Subjective familiarity

Subjective familiarity was measured on a seven-point scale (Nusbaum, et al., 1984). Words with a higher clustering coefficient had a mean familiarity value of 6.908 (SEM = .029) and word with a lower clustering coefficient had a mean familiarity value of 6.956 (SEM = .015, F (1, 74) = 2.145, p > .050). The mean familiarity value for the words in the two groups indicates that all of the words were highly familiar.

Word frequency

Word frequency refers to how often a word in the language is used. Average log word frequency (log-base 10 of the raw values from Kučera & Francis, 1967) was 1.327 (SEM = .120) for the higher clustering coefficient words, and 1.431 (SEM = .100) for the lower clustering coefficient words (F (1, 74) = .441).

Neighborhood density

Neighborhood density was defined as the number of words that were similar to a target word. Similarity was assessed with a simple and commonly employed metric (Greenberg & Jenkins, 1967; Landauer & Streeter, 1973; Luce & Pisoni, 1998). A word was considered a neighbor of a target word if a single phoneme could be substituted, deleted, or added into any position of the target word to form that word. For example, the word cat has phonological neighbor words like _at, scat, mat, cut, cap. Note that cat has other neighbors, but only a few were listed for illustration. The neighborhood density values for the higher and lower clustering coefficient words were 20.658 neighbors (SEM = .934) and 21.553 neighbors (SEM = 1.188) respectively (F (1, 74) = .351).

Spread of the neighborhood (P)

The spread of the neighborhood refers to the number of phoneme positions (or letter positions, as in Johnson & Pugh, 1994) in a word that form a neighbor (Vitevitch, 2007). Consider the words mop (/mɑp/) and mob (/mɑb/). When a single phoneme is substituted in all three phoneme-positions of the word mop, phonological neighbors are formed (e.g., hop, map, mock). However, when a single phoneme is substituted into the word mob, phonological neighbors are formed by only two phoneme-positions (e.g., rob, m*b, mock); no real word in English is formed when a single phoneme is substituted in the medial position of the word mob. In the examples above, the word mop would have a spread of 3 (P = 3), because three phoneme positions produce a phonological neighbor, whereas the word mob would have a spread of 2 (P = 2), because two phoneme positions produce a phonological neighbor.

The phonological spread of the stimuli was assessed using N-Watch (Davis, 2005). Words with a high clustering coefficient had a mean spread (P) of 2.89 (SEM = .05) and words with a low clustering coefficient also had a mean spread (P) of 2.97 (SEM = .026, F (1, 74) = 1.925, p = .17).

Number of neighbors formed in a given phoneme position

We also used N-Watch (Davis, 2005) to compare the number of neighbors formed in each phoneme position in each word; recall that the two conditions did not differ on the overall number of neighbors (i.e., neighborhood density). The number of neighbors formed in the first position of the words was 6.18 (SEM = .54) for words with high clustering coefficient, and 6.26 (SEM = .485) for words with low clustering coefficient. This difference was not statistically significant (F (1, 74) < 1). The number of neighbors formed in the medial (vowel) position of the words was 4.58 (SEM = .446) for words with high clustering coefficient, and 5.53 (SEM = .430) for words with low clustering coefficient. This difference was not statistically significant (F (1, 74) = 2.34, p = .13). The number of neighbors formed in the final position of the words was 5.42 (SEM = .454) for words with high clustering coefficient, and 5.32 (SEM = .277) for words with low clustering coefficient. This difference was not statistically significant (F (1, 74) < 1).

Neighborhood frequency

Neighborhood frequency is the mean word frequency of the neighbors of the target word. Words with a higher clustering coefficient had a mean log neighborhood frequency value of 1.024 (SEM = .208), and words with a lower clustering coefficient had a mean log neighborhood frequency value of 1.025 (SEM = .203, F (1, 74) < .0001).

Phonotactic probability

The phonotactic probability was measured by how often a certain segment occurs in a certain position in a word (positional segment frequency) and by the segment-to-segment co-occurrence probability (biphone frequency; Vitevitch & Luce, 1998; 2005). The mean positional segment frequency for higher and lower clustering coefficient words was .139 (SEM = .005) and .143 (SEM = .007, F (1, 74) = .222), respectively. The mean biphone frequency for higher and lower clustering coefficient words was .006 (SEM = .001) and .006 (SEM = .001, F (1, 74) = .383), respectively. These values were obtained from the web-based calculator described in Vitevitch and Luce (2004).

Duration

The duration of the stimulus sound files was equivalent between the two groups of words. The mean overall duration of the sound files was 528 ms (SEM = 14.423) for the stimuli with higher clustering coefficients and 523 ms (SEM = 16.704) for the stimuli with lower clustering coefficient (F (1, 74) = .061). The mean onset duration, including the silence from the beginning of the sound file to the onset of the stimulus, was 11 ms (SEM = 1.107) for the stimuli with higher clustering coefficient and 9 ms (SEM = .771) for the stimuli with lower clustering coefficient (F (1, 74) = 1.427, p > .050). The stimulus duration, measured from the onset to the offset of the stimulus excluding any silence before and after the stimulus in the sound files, had a mean value of 506 ms (SEM = 14 ms) for the stimuli with higher clustering coefficient and a mean value of 503 ms (SEM = 16) for the stimuli with lower clustering coefficient (F (1, 74) = .022).

Distribution of phonemes

Given that the white noise used in the perceptual identification task does not mask all phoneme types equivalently, we describe in the present section how various phonemes were distributed among the stimuli in the two clustering coefficient conditions. The following consonants appeared in equal numbers in each condition in the onset position: /b, d, f, g, k, l, m, p, r, s, w/.

The following vowels appeared in the words with a lower clustering coefficient (with the number of occurrence in parentheses): æ (3), ᴵ (4), ᶷ (1), ᶺ (2), ᵅ (1), i (3), ᵅu (1), e (2), ᵓ (5), u (2), ɝ (3), ᵅᴵ (5), ε (5), o (1). The words with a higher clustering coefficient had the following vowels (with the number of occurrence in parentheses): æ (5), ᴵ (4), ᶷ (3), ᶺ (5), ᵅ (1), i (8), ᵅu (2), e (2), ᵓ (2), u (1), ɝ (2), ᵅᴵ (3). A chi-square analysis shows that there was no statistically significant difference in the distribution of vowels between the two conditions (Χ² = 13.711, df = 13, p = .395).

For the consonants in the final position of the words, the words with low clustering coefficient had 11 fricatives, and the words with high clustering coefficient had 12 fricatives in the final consonant position of the words. A chi-square analysis shows that this difference was not statistically significant (Χ² = .062, df = 1).

As sibilant fricatives, /s, ∫, z, and ʒ/, are louder than non-sibilant fricatives, /f, θ, v, ð, and h/, a balanced distribution of sibilant and non-sibilant fricatives in the final consonant position is important. The following sibilant fricatives appeared in final consonant position of the words with low clustering coefficient (with the number of occurrence in parentheses) —/s (6), ∫ (1), z (1), and ʒ (0)/; words with high clustering coefficients—/s (3), ∫ (2), z (2), and ʒ (0)/. The following non-sibilant fricatives appeared in final consonant position of the words with a lower clustering coefficient (with the number of occurrence in parentheses) —/f (1), θ (0), v (2), ð (0), h (0)/; words with high clustering coefficient—/f (1), θ (2), v (2), ð (0), h (0)/. A chi-square analysis shows that the distribution of sibilant and non-sibilant fricatives was not statistically different in the two conditions (Χ² = .524, df = 1).

In the final consonant, there were also approximately equal numbers of voiced (/z, ʒ, v, ð/) and voiceless fricatives (/s, ∫, f, θ/) in the two conditions— 4 and 3 voiced fricatives in high and low clustering coefficient condition respectively and 8 voiceless fricatives in both conditions. A chi-square analysis shows that the distribution of voiced and voiceless fricatives was not statistically different in the two conditions (Χ² = .1, df = 1). Given the overall similarities in the distribution of constituent phonemes in the two conditions, it is more likely that any difference observed in the perceptual identification task is due to the difference in the independent variable (i.e., clustering coefficient) than to any difference in the distribution of phonemes in the two conditions.

Procedure

Participants were tested individually. Each participant was seated in front of an iMac computer running PsyScope 1.2.2 (Cohen et al., 1993), which controlled the presentation of stimuli and the collection of responses.

In each trial, the word “READY” appeared on the computer screen for 500 ms. Participants then heard one of the randomly selected stimulus words imbedded in white noise through a set of Beyerdynamic DT 100 headphones at a comfortable listening level. Each stimulus was presented only once. The participants were instructed to use the computer keyboard to enter their response (or their best guess) for each word they heard over the headphones. They were instructed to type “?” if they were absolutely unable to identify the word. The participants could use as much time as they needed to respond. Participants were able to see their responses on the computer screen when they were typing and could make corrections to their responses before they hit the RETURN key, which initiated the next trial. The experiment lasted about 15 minutes. Prior to the experiment, each participant received five practice trials to become familiar with the task. These practice trials were not included in the data analyses.

Results and Discussion

For the perceptual identification task, accuracy rates were the dependent variable of interest. A response was scored as correct if the phonological transcription of the response matched the phonological transcription of the stimulus. Misspelled words and typographical errors in the responses were scored as correct responses in certain conditions: (1) neighboring letters in the word were transposed, (2) the omission of a letter in a word was scored as a correct response only if the response did not form another English word, or (3) the addition of a single letter in the word was scored as a correct response if the letter was within one key of the target letter on the keyboard. Responses that did not meet the above criteria were scored as incorrect.

The mean accuracy rate for words with higher clustering coefficient was 58% (sd = 8.4) whereas the mean accuracy rate for words with lower clustering coefficient was 72% (sd = 8.2). Repeated-measures analysis of variance (ANOVA) was performed for accuracy rates between the two groups of words. The words with lower clustering coefficient had a significantly higher accuracy rate than the words with higher clustering coefficient, F₁ (1, 29) = 50.925, p < .0001. This observed difference is considered a large effect (d = 1.566) and has a high probability of being replicated (p_rep = .996; Killeen, 2005).

Although the current design of the present study renders analyses that treat items as a random factor (F₂) inappropriate, we report this analysis to maintain the current conventions of psycholinguistic research.² The discussion of the theoretical implications of our findings will be based on the results of the only appropriate analyses, namely, the analyses that treat participants as a random factor (F₁). When collapsed across participants, items with higher clustering coefficient had a mean accuracy rate of 58% (sd = 29.0), whereas items with lower clustering coefficient had a mean accuracy rate of 72% (sd = 27.5). A one-way ANOVA showed that the difference between the two groups of words was statistically significant (F₂ (1, 74) = 4.558, p = .036).

The results of Experiment 1 showed a robust influence of the clustering coefficient on spoken word identification, suggesting that the clustering coefficient influences spoken word recognition. In the perceptual identification task, words with fewer interconnected neighbors (i.e., a low clustering coefficient) were identified more accurately than words with the same number of neighbors, but with more of those neighbors being interconnected with each other (i.e., a high clustering coefficient). The present results support the hypothesis that listeners are sensitive to the clustering coefficient of target words, a measure derived from the analyses of network science and applied to phonological word-forms in the mental lexicon (Vitevitch, 2008). In addition to the number of phonological neighbors, the present finding shows that the phonological relationship among the neighbors also influences the processing of a target word. This further demonstrates the importance of understanding how the structural organization of phonological word-forms in the lexicon can influence language processing. Similar structural characteristics might also influence processing among semantic representations in the lexicon (e.g., Nelson, Bennett, Gee, Schreiber, & McKinney, 1993; Nelson & Zhang, 2000).

Experiment 2

Experiment 1 provided strong evidence to support the hypothesis that the clustering coefficient influences the recognition of spoken words. However, we wished to perform another experiment to bolster this empirical foundation. The purpose of the present experiment was to further examine the effects of the clustering coefficient on spoken word recognition by employing another task that emphasizes the activation of lexical representations in memory—the auditory lexical decision task. Although the degraded stimuli in the auditory perceptual identification task is somewhat akin to the input we normally get in the real world (i.e., a signal produced by an interlocutor amidst a background of environmental sounds), it is important to demonstrate that the influence of the clustering coefficient on processing generalizes to stimuli that are not degraded in any way. The use of stimuli that are not degraded would also minimize the possibility that participants responded to the stimuli using some sort of sophisticated guessing strategy, which might occur in tasks using degraded stimuli (Catlin, 1969; Hasher & Zacks, 1984).

The auditory lexical decision task has proven quite useful in examining the influence of many variables—including phonological neighborhood density, phonotactic probability, and neighborhood frequency—on spoken word processing (e.g., Luce & Pisoni, 1998; Vitevitch & Luce, 1999). In this task, participants are presented with either a word or a nonword (without any white noise) over a set of headphones. Participants are asked to decide as quickly and as accurately as possible whether the given stimulus is a real word in English or a nonsense word.

In addition to using stimuli that are not degraded, the lexical decision task also allows reaction time data to be assessed. Reaction times provide us with a means for investigating the time course of spoken word recognition, and may reveal an effect of the clustering coefficient on the temporal aspect of spoken word recognition.

Based on the results of Experiment 1, we predicted that words with a high clustering coefficient would be responded to less accurately in the lexical decision task than words with a low clustering coefficient. Furthermore, we predicted that words with a high clustering coefficient would be responded to more slowly than words with a low clustering coefficient, reflecting detriments in processing in the reaction times.

Method

Participants

Forty-five native English speakers were recruited from the pool of Introductory Psychology students enrolled at the University of Kansas. The participants received partial credit towards the completion of the course for their participation. All participants were right-handed with no reported history of speech or hearing disorders. None of the participants in the present experiment took part in Experiment 1.

Materials

The same 76 word stimuli that were used in Experiment 1 were used in the present experiment. A list of 76 phonotactically legal nonwords with the same word length (as measured by the number of phonemes and syllables) as the word stimuli was constructed by replacing the first phoneme of a real word with another phoneme. For example, the nonword ‘baith’ /beθ/ was formed by replacing /f/ in ‘faith’/feθ/ with /b/. The base words from which the nonwords were created were not words in the stimulus list. The nonwords did, however, have the same distribution of phonemes in the onset position as the stimuli.

The nonwords were recorded by the same male speaker in the same manner and at the same time as the real word stimuli that were used in Experiment 1. The same method for digitizing the word stimuli was used for the nonwords in the present experiment. This procedure eliminated possible cues to the lexical status of the stimuli that might be induced by different recording characteristics for the words and nonwords.

Duration

The mean overall duration of the sound files for the nonword stimuli was 536 ms (SEM = 10.279), which was not different from the mean overall duration of the sound files for the word stimuli (F (1, 150) = .450). The stimulus duration, measured from the onset to the offset of the stimulus excluding any silence before and after the stimulus in the sound files, had a mean value of 520 ms (SEM = 10) for the nonword stimuli. The word and nonword stimuli did not differ in stimulus duration either (F (1, 150) = 1.070, p > .050).

Procedure

Participants were tested individually. Each participant was seated in front of an iMac computer connected to a New Micros response box. As in Experiment 1, PsyScope 1.2.2 (Cohen et al., 1993) was used to control the randomization and presentation of stimuli, and to collect responses.

In each trial, the word “READY” appeared on the computer screen for 500 ms. Participants then heard one of the randomly selected words or nonwords through a set of Beyerdynamic DT 100 headphones at a comfortable listening level. Each stimulus was presented only once. The participants were instructed to respond as quickly and as accurately as possible whether the item they heard was a real English word or a nonword. If the item was a word, they were to press the button labeled ‘WORD’ with their right (dominant) hand. If the item was not a word, they were to press the button labeled ‘NONWORD’ with their left hand. Reaction times were measured from the onset of the stimulus to the onset of the button press response. After the participant pressed a response button, the next trial began. The experiment lasted about 20 minutes. Prior to the experimental trials, each participant received ten practice trials to become familiar with the task. These practice trials were not included in the data analyses.

Results and Discussion

Reaction times and accuracy rates were the dependent variables of interest. Only accurate responses to the word stimuli were included in the analysis of reaction times. Reaction times that were too rapid or too slow (i.e. below 500 ms and above 2000 ms) were considered outliners and were excluded from the analysis; this accounted for less than 1% of the data.

Repeated measures analysis of variance (ANOVA) was used to analyze the reaction times and accuracy rates. Words with a high clustering coefficient (mean = 900 ms, sd = 86.6) were responded to more slowly than words with a low clustering coefficient (mean = 888 ms, sd = 82.1). Although the difference in reaction time between the two groups of words is considered a small effect (d = .142), the difference was nevertheless statistically significant (F₁ (1, 44) = 6.468, p = .015), and has a high probability of being replicated (p_rep = .938; Killeen, 2005).

For the accuracy rates, the influence of clustering coefficient approached statistical significance (F₁ (1, 44) = 4.037, p = .051). Words with a higher clustering coefficient were correctly responded to 91.6% of the time (sd = 5.7) whereas words with a lower clustering coefficient were correctly responded to 93.3% of the time (sd = 4.2).

The manner in which stimuli were selected for the present study renders analyses that treat items as a random factor (F₂) inappropriate; however, we report these analyses to maintain the conventions of current psycholinguistic research. The items in the high clustering coefficient condition had a mean reaction time of 908 ms (sd = 83), whereas items in the low clustering coefficient had a mean reaction time of 890 ms (sd = 93). Although the means in the items analysis are in the same direction as those in the analysis treating participants as a random variable, the difference between the means was not statistically significant (F₂ (1, 74) = .771, p = .383). Similarly, the mean accuracy rates in the analysis treating items as a random factor were also in the same direction as the accuracy rates in the analysis treating participants as a random variable (high clustering coefficient mean = 91.3%, sd = 11.0; low clustering coefficient mean = 93.3%, sd = 10.0), but were not statistically significant (F₂ (1, 74) = .560, p = .457).

Even though Raaijmakers (2003) has demonstrated that “items analyses” actually do not provide such information, “items analyses” that do not reach conventional levels of statistical significance are often interpreted as indicative that a few “odd” items are responsible for the effect observed in analyses treating participants as a random variable. To more directly address the possibility that a few “odd” items were responsible for the observed effect, we conducted the following supplemental analysis.

If a few “odd” items were responsible for the observed effect, then one might expect to see the (numerically) faster reaction time responses for low clustering coefficient words compared to high clustering coefficient words to disappear or reverse when the items are randomly split into two groups of high and low clustering coefficient words, as the “odd” item would only affect half of the data. In the present case, when half of the high and low clustering coefficient words were randomly separated into two lists (List A and List B, for ease of discussion), the numerical advantage in reaction time for low over high clustering coefficient words was still found in both lists.

In List A, the items in the low condition had a mean reaction time of 869 (sd = 101.92), whereas items in high condition had a mean reaction time of 899 (sd = 95.47; F_A (1, 36) < 1). In List B, the items in the low condition had a mean reaction time of 911 (sd = 81.78), whereas items in the high condition had a mean reaction time of 917 (sd = 70.06; F_B (1, 36) < 1). Although neither of these analyses is statistically significant, both lists of randomly assigned stimuli (each containing half of the high C and half of the low C words) show the expected result: low clustering coefficient words were responded to (numerically) faster than high clustering coefficient words. If the result observed in the participant analysis were due to a few “odd” items, it is unlikely that both lists of randomly separated items would continue to show the expected result.

Significant effects of the clustering coefficient on lexical decision time were found in the present experiment. Words with more interconnected neighbors (i.e., a higher clustering coefficient) were responded to more slowly than words with fewer interconnected neighbors (i.e., a lower clustering coefficient). Although the influence of the clustering coefficient on the accuracy rates in the lexical decision task only approached statistical significance in the present experiment, a trend in the predicted direction was observed. Words with fewer of their neighbors also being neighbors of each other (i.e., a lower clustering coefficient) tended to be recognized more accurately than words with many interconnected neighbors (i.e., a higher clustering coefficient).

The results of the present experiment suggest that the clustering coefficient not only affects the accuracy of word recognition (as demonstrated in Experiment 1), but also affects the time-course of lexical access. This is important because accuracy rates obtained in a perceptual identification task may only reflect the end product of the spoken word recognition process and could be biased by post-perceptual guessing strategies (Marslen-Wilson, 1987). Instead, the lexical decision time is an immediate measure of processing activities, which may be less susceptible to post-perceptual biases. In addition, results from the present experiment showed that the effects of the clustering coefficient on spoken word recognition are not restricted to degraded stimuli. Therefore, the influence of the clustering coefficient on spoken word recognition is not likely to be due to participants simply using a sophisticated guessing strategy when presented with degraded stimuli.

General Discussion

The “new” science of networks enables researchers in a variety of fields to analyze the structure of complex systems, and to examine the influence of that structure on the processes occurring in that system (Watts, 2004). Using these tools, Vitevitch (2008) found that phonological word-forms in the mental lexicon were organized in a non-arbitrary way (see Steyvers & Tenenbaum, 2005 for evidence that semantic representations in the mental lexicon are also organized in a non-arbitrary way and that the structure influences processing). The goal of the present study was to investigate how the structure that Vitevitch (2008) observed in the lexicon influences the process of spoken word recognition. To this aim, the clustering coefficient of the stimuli, which measures the proportion of phonological neighbors of a target word that are also neighbors of each other, was examined. In Experiment 1, the results of an auditory perceptual identification task showed that words with a lower clustering coefficient (i.e., few interconnected neighbors) were identified more accurately than words with a higher clustering coefficient (i.e., many interconnected neighbors). In Experiment 2, the effect of clustering coefficient was observed in a lexical decision task such that words with a lower clustering coefficient were responded to more quickly than words with a higher clustering coefficient. Thus, the clustering coefficient influences the accuracy as well as the speed of spoken word recognition.

The results obtained in the present set of experiments are consistent with the prediction derived from previous network simulations and experiments examining the dynamics of disease transmission (e.g., Naug, 2008). Just as a social network with a high clustering coefficient “traps” a pathogen in a local region of the network and causes continued re-infection, regions of the phonological network with high clustering coefficient “trap” activation in a local region of the lexicon, thereby increasing the difficulty of discriminating a target word from its similar sounding neighbors. In contrast, in regions of the phonological network with low clustering coefficient, activation was distributed more widely, to all the words in the network, enabling the target word to “stand out” from its closest competitors and be effectively recognized. The present results generalize to the cognitive domain previous observations regarding the influence of network structure on processing. Finally, the present work illustrates how the tools of network science can be used to ask new questions in cognitive psychology.

Given that current models of spoken word recognition can account for the influence of the number of phonological neighbors on processing, one might ask if a structured lexicon—as shown via analyses with the tools of network science (e.g., Vitevitch, 2008)—is really necessary to account for the present results which showed that the relationship among the neighbors influences processing. Said another way, can current models of spoken word recognition account for the influence that the clustering coefficient has on spoken word recognition. In the following sections we consider how three current models of spoken word recognition— NAM, TRACE, and Shortlist—account for the present findings. Recall that none of these models of spoken word recognition (explicitly) represent the lexicon as a structured system. Rather, they all view the mental lexicon as an arbitrarily ordered collection of representations. After considering how current models of spoken word recognition (fail to) account for the observed results, we will conclude with a framework to guide the future development of a new model of spoken word recognition.

NAM

Luce and Pisoni (1998) developed the neighborhood activation model (NAM) to account for the influence of the structural organization among representations in the mental lexicon on spoken word recognition. Although Luce and Pisoni acknowledge the importance of a structured lexicon and its influence on processing, the global structure of the lexicon is not explicitly modeled in NAM (cf., Vitevitch, 2008). Rather, NAM offers a single mathematical expression to predict the probability of correctly identifying a target word based on several parameters (described in more detail below).

It is assumed in NAM that spoken input activates a set of acoustic-phonetic patterns in memory according to the degree of similarity between the spoken input and the patterns. The more they are similar, the higher the level of activation is. The acoustic-phonetic patterns that correspond to words in memory activate a system of word decision units which monitor several sources of information including the acoustic-phonetic pattern activation to which the units correspond (i.e. activation of the target word), the overall level of activity in the system of units (activation of the target and all its neighbors), and higher levels of information (e.g., frequency of the target and neighbor words). As the processing of spoken input continues, the decision units continuously compute decision values based on the neighborhood probability rule to determine the probability of identification of the stimulus word (see Equations 1-7 in Luce & Pisoni, 1998). Once the decision value surpasses the criterion, the word is recognized. The neighborhood probability rule (summarized in Equation 1 below)

$$(\frac{\mathit{\text{SWP}}\ast \mathit{\text{Fre}}{q}_s}{(\mathit{\text{SWP}}\ast \mathit{\text{Fre}}{q}_s)+\sum ({\mathit{\text{NWP}}}_j\ast \mathit{\text{Fre}}{q}_{N_j})})$$ (1)

takes into account the activation level of the acoustic-phonetic pattern (SWP), the sum of neighbor word probabilities (NWPjs, i.e., the overall level of activity in the decision system) and frequency information. Neighborhood density and word frequency effects are accounted for in the decision stage of processing in NAM via the neighborhood probability rule. When the input word has a high number of confusable and high frequency neighbors, the sum of neighbor word probabilities (Σ(NWP_j * Freq_Nj)) would be high and thus the probability of recognizing the input word would be low. In contrast, when the input word has a small number of confusable and low frequency neighbors, the sum of neighbor word probabilities would be low and thus the probability of recognizing the input word would be high.

Although the neighborhood probability rule assesses local structure in the lexicon by considering the number of related words in the phonological neighborhood of the target word, it does not take into account other information regarding the structure of the phonological neighborhood, namely the clustering coefficient. In Equation (1) there is no variable that represents the interconnectivity among the neighbors. Like TRACE and Shortlist, NAM has a two-stage process of activation and decision. However, in NAM, the competition among lexical candidates does not involve any inhibitory links among them. This means activation of one decision-unit will not directly affect the activation of another decision-unit, but it will influence the output decision through its influence on the overall activation of the whole decision system. Thus, in order for NAM to account for the clustering coefficient effect found in this study, a variable representing the interconnectivity among the neighbors may need to be included in the neighborhood probability rule (perhaps in the sum of neighbor word probabilities, Σ(NWP_j * Freq_Nj)) so that the total activation of the system would increase with higher interconnectivity among the neighbors. This will decrease the probability of correctly recognizing the input stimulus (i.e., result in a slower reaction time) when a word has a higher clustering coefficient. However, the detail of what variable to add in the rule and whether the modified NAM would be able to model the results observed in the present study is at present unclear.

It is also unclear if considering only the local structure of the lexicon is sufficient to account for the influence that the other aspects of lexical structure observed by Vitevitch (2008) may have on the process of spoken word recognition. If a new parameter must be added to the neighborhood probability rule to account for the influence on processing of each aspect of lexical structure, the simplicity and parsimony of the original mathematical expression is lost. Instead, it may be more parsimonious to reconsider the fundamental assumption that underlies other models of spoken word recognition; the lexicon may not be an unstructured, arbitrarily ordered collection of representations. By instead viewing the mental lexicon as a structured system, we can begin to examine, as we did in the present set of experiments, how that structure might influence lexical processing. Before reconsidering the fundamental assumption that underlies many models of spoken word recognition, we examined whether TRACE and Shortlist—two models of spoken word recognition that assume the lexicon is an arbitrarily ordered collection of representations—could account for the results of the present set of experiments.

TRACE

The TRACE model of spoken word recognition, developed within the interactive activation framework, consists of several levels of individual processing units representing features, phonemes, and words (McClelland & Elman, 1986). Feature units are connected to phoneme units, and phoneme units are connected to word units. Connections between units within the same level are fully interconnected and inhibitory, whereas connections between units in different levels are facilitatory and bidirectional. Units influence each other in proportion to their activation levels and the weights associated with their connections. When input is presented to TRACE, activation levels of consistent units increase through the excitatory connections between layers of nodes.

Given the complexity of the TRACE model, verbal exploration of its inner workings is not sufficient to determine whether the model would be able to account for the results observed in the present set of studies (Lewandowsky, 1993). Therefore, we used jTRACE (Strauss, Harris, & Magnuson, 2007), a Java reimplementation of TRACE, to simulate the recognition of words varying in clustering coefficient. From the monosyllabic words with three phonemes in the “initial_lexicon” in jTRACE, we selected 28 words with “high” and 28 words with “low” clustering coefficient. (Pajek was again used to compute the clustering coefficient for the words in initial_lexicon.) The words and their lexical characteristic are listed in Appendix B. Words with a high clustering coefficient had a mean value of .509, and words with a low clustering coefficient had a mean value of .193 (F (1, 54) = 47.68, p < .0001). However, the two groups of words were equivalent in neighborhood density (F (1, 54) < 1). As information regarding frequency of occurrence was not modeled in the original TRACE model, measures of word frequency, neighborhood frequency, and phonotactic probability are irrelevant in this simulation. The same parameter values used in TRACE II by McClelland and Elman (1986) were used in this simulation. Each stimulus word was then input and run for 180 cycles.

If TRACE (as implemented in jTRACE) can account for the influence of the clustering coefficient on word recognition as observed in the present study, then the maximum activation level of words with lower clustering coefficients should be greater than the maximum activation level of words with higher clustering coefficients. Furthermore, the maximum level of activation for words with lower clustering coefficients should be reached with fewer time steps than the maximum activation level of words with higher clustering coefficients. A one-way ANOVA showed that there was no significant difference in maximum activation levels for words with higher clustering coefficient (mean = .55, sd = .010) and words with lower clustering coefficient (mean = .55, sd = .004; F (1, 54) = 2.012, p = .16). Words with higher clustering coefficient reached maximum activation on average in the 105^th cycle (sd = 16.28) and words with lower clustering coefficient reached maximum activation on average in the 99^th cycle (sd = 17.98); this difference also was not significant (F (1, 54) = 1.294, p = .26). Although the architecture of TRACE is flexible enough to account for many effects in spoken word recognition (e.g., McClelland & Elman, 1986; see also the review in Strauss et al., 2007), the results of the present simulation suggest that it is not able to account for the influence of clustering coefficient on spoken word recognition that was observed in the present study.

Shortlist

Another current model of spoken word recognition is Shortlist (Norris, 1994; for other instantiations of Shortlist see Norris & McQueen, 2008; Scharenborg, ten Bosch, Boves & Norris, 2003). Shortlist contains a layer of phoneme nodes and a layer of word nodes with one-way excitatory connections from the phoneme layer to the word layer. Thus, Shortlist has an entirely bottom-up architecture with a recurrent network generating a set of candidate words that are roughly consistent with the bottom-up input. The activation of each candidate word is determined by its degree of similarity with the phonemic input. In the lexical level of Shortlist, overlapping words inhibit each other in proportion to the number of phonemes they have in common, and they compete with each other for recognition.

To determine if Shortlist could account for the results of the present study we again used jTRACE (Strauss, Harris, & Magnuson, 2007) to simulate the recognition of words varying in clustering coefficient. In this case, however, the parameter controlling feedback from the lexical units to the phoneme units was set to zero to create the feed-forward processing found in Shortlist.³ The same lexicon and stimuli used in the TRACE simulation were used in the Shortlist simulation, and performance was again assessed via the maximum activation level of words and the number of time steps required to reach that maximum activation level. A one-way ANOVA showed that there was no significant difference in maximum activation levels for words with higher clustering coefficient (mean = .55, sd = .009) and words with lower clustering coefficient (mean = .55, sd = .007; F (1, 54) = .621, p = .43). Words with higher clustering coefficient reached maximum activation on average in the 98^th cycle (sd = 3.92), as did words with lower clustering coefficient (sd = 3.91); this difference was not significant (F (1, 54) = .010, p = .92). Just like TRACE, Shortlist was not able to account for the influence of clustering coefficient on spoken word recognition that was observed in the present set of experiments.

Framework for a new model of spoken word recognition

The work of Arbesmen et al. (submitted) and Vitevitch (2008) suggest that phonological word-forms in the mental lexicon are organized in a non-arbitrary way. More important, the results of the present experiments suggest that certain characteristics of this structure influence spoken language processing. Specifically, words with a lower clustering coefficient were recognized more quickly and more accurately than words with a higher clustering coefficient. Although many current models of spoken word recognition can account for the influence that the number of phonological neighbors a target word has on recognition, it is not clear that they can account for the influence that the interconnectivity among the phonological neighbors exerts on spoken word recognition.

We recognize the difficulty in making definitive statements based on the results of only two experiments (and the null-results obtained in two simulations), so we will not be so presumptuous as to propose a new model of spoken word recognition at present. We will, however, consider the analogy that underlies many current models of spoken word recognition, and propose an alternative analogy, which might not only account for the results of the present set of experiments but also serve as a framework for a new model of spoken word recognition.

Many current models of spoken word recognition view the mental lexicon as a collection of arbitrarily ordered phonological representations, and the process of lexical retrieval as a special instance of pattern matching. From this cauldron of lexical soup the representation of a word-form that best matches the acoustic input somehow bubbles up to the top to be retrieved, beating out other competitors. That is, current models of spoken word recognition account for various effects (such as neighborhood density effects) not because of some explicit structure in the lexicon, but simply due to the amount of evidence the acoustic-phonetic input provides a given word-form (or word-forms). Although this simple approach has provided language researchers with much insight into the process of spoken word recognition, it may be time to consider an alternative approach. For example, it is unclear how listeners are able to process nonwords—something that, by definition, does not have a representation in the lexicon—when this arbitrarily ordered lexical soup will always produce the best matching lexical representation for retrieval (see Vitevitch & Luce, 1998; 1999; 2005 for one approach to this problem, and Scharenborg et al., 2003 for another). Given the alternative that the lexicon might be ordered in some non-arbitrary way (Arbesmen et al., submitted; Vitevitch, 2008), language researchers might gain new insight into spoken word recognition by viewing the lexicon as a structured collection of information and the process of spoken word recognition as a search process through that structured information.

Although Forster (1978) proposed a (verbal) model of lexical retrieval based on a similar premise, the model he described was reminiscent of the (now somewhat antiquated) card catalog system commonly used in libraries. In the library card catalog system, one could access a book via one of three sets of cards based on the subject, title, or author of the book. Each set of cards was organized alphabetically. Once the card representing the desired book was found, the “address” indicating the location of the book in the library was given in the form of the Dewey Decimal Classification number (or the Library of Congress Classification number), enabling one to retrieve the desired book from the library. In Forster's (1978) model of lexical retrieval, one could access a word via one of three access files based on orthographic, phonological or semantic/syntactic characteristics of the word. Each access file was ordered based on the frequency of occurrence of the words. Once the access code representing the word that was read, heard, or desired for production was found, a “pointer” indicated the location of that word in the master lexicon, enabling one to retrieve the desired word from the mental lexicon.

It is interesting to note that Forster (1978) went to great lengths to illustrate that not all structures were well suited for describing how the mental lexicon might be organized, and how that structure might influence the process of lexical retrieval (i.e., the decision tree for a direct access lexicon). Like Forster (1978), we do not believe that just any structure will suffice to describe how phonological word-forms are organized in the mental lexicon. (See Vitevitch, 2008 for the characteristics that describe the structure found among phonological word-forms in the mental lexicon.) In contrast to Forster (1978), however, we suggest a more contemporary analogy to describe the structure of the lexicon, and the process of search and retrieval from the lexicon: the World Wide Web (WWW) and an Internet search engine.

Just as TRACE, Shortlist, and NAM allow for the activation of multiple competitors that match to varying degrees the incoming acoustic-phonetic input, navigating the directed graph often used to represent the WWW with search engines such as Google also result in not a single entity, but a list of entities that match the initial query with varying degrees of relevancy. Recursive algorithms such as PageRank (Page, Brin, Motwani & Winograd, 1998) efficiently order the results of that search based on the location of each entity in the (very large) graph structure representing the WWW (see Griffiths, Steyvers, and Firl, 2007 for evidence of a similar algorithm accounting for performance in a semantic fluency task). Search algorithms like those used to retrieve information from the WWW might also be involved in the retrieval of word-forms from a lexical network.

Epidemiologists understanding of disease transmission greatly increased when the assumption that all individuals had an equal chance of infection (i.e., mean-field models) was replaced by the assumption that social interaction resembled a structured network (Read & Keeling, 2003). Perhaps Psycholinguists and other cognitive scientists can increase their understanding of spoken language processes by re-considering, in light of the evidence presented in Vitevitch (2008), the assumption that the mental lexicon is an arbitrary collection of representations. Examining other aspects of lexical organization—through experiments and through mathematical analyses—will help us better understand the structure of the lexicon, and how that structure influences various aspects of spoken language processing.

Appendix A

High Clustering Coefficient Words
Stimulus Word	Clustering Coefficient	Fam.	log Word Freq.	ND	log NF	Pos. Seg. Freq.	Biphone Freq.
bash	0.333	6.50	0.00	24	0.82	0.138	0.0079
bath	0.397	7.00	1.42	17	1.26	0.138	0.0069
bib	0.359	6.83	0.30	13	1.25	0.173	0.0064
bull	0.321	7.00	1.15	13	1.43	0.135	0.0031
bug	0.308	7.00	0.60	26	0.8	0.108	0.0047
dot	0.342	7.00	1.11	26	1.06	0.178	0.0050
dig	0.368	6.92	1.00	17	1.19	0.166	0.0187
dish	0.455	7.00	1.20	12	1.22	0.156	0.0164
dug	0.359	7.00	1.20	22	0.83	0.109	0.0037
feel	0.338	7.00	2.33	30	1.06	0.152	0.0046
full	0.457	7.00	2.36	15	1.45	0.131	0.0026
foul	0.404	7.00	0.70	17	1.00	0.130	0.0010
gang	0.400	7.00	1.34	15	0.65	0.117	0.0070
gain	0.367	7.00	1.87	25	1.22	0.151	0.0042
gum	0.425	7.00	1.15	16	0.93	0.115	0.0067
call	0.311	7.00	2.27	26	1.16	0.183	0.0060
case	0.355	6.75	2.56	22	1.14	0.201	0.0050
lag	0.311	6.58	0.48	27	0.73	0.131	0.0073
leaf	0.387	7.00	1.08	25	0.9	0.086	0.0033
leap	0.331	6.83	1.15	30	0.93	0.103	0.0039
lease	0.339	6.92	1.00	27	1.02	0.145	0.0042
leave	0.342	7.00	2.31	26	0.76	0.089	0.0038
look	0.419	7.00	2.60	17	1.21	0.098	0.0013
lose	0.331	6.50	1.76	17	1.00	0.076	0.0031
lull	0.314	6.25	0.30	15	0.66	0.147	0.0064
love	0.327	6.67	2.37	11	0.91	0.097	0.0030
math	0.314	7.00	0.60	15	1.23	0.144	0.0111
mall	0.312	7.00	0.48	24	1.27	0.147	0.0044
meal	0.354	7.00	1.48	28	0.92	0.163	0.0047
mouse	0.352	7.00	1.00	14	0.93	0.146	0.0017
perk	0.307	6.83	0.00	22	0.72	0.163	0.0061
pearl	0.314	7.00	0.95	21	0.98	0.183	0.0045
ring	0.316	7.00	1.69	23	1.04	0.158	0.0203
ripe	0.316	6.92	1.15	20	0.93	0.122	0.0034
seal	0.338	7.00	1.23	31	1.20	0.208	0.0055
size	0.318	7.00	2.14	12	1.29	0.157	0.0041
weak	0.307	7.00	2.49	22	0.93	0.106	0.0030
wire	0.355	7.00	1.62	22	0.86	0.133	0.0035
Low Clustering Coefficient Words
Word	Clustering Coefficient	Fam.	log Word Freq.	ND	log NF	Pos. Seg. Freq.	Biphone Freq.
beach	0.261	7.00	1.83	18	1.04	0.091	0.0028
bead	0.225	7.00	0	26	1.22	0.121	0.0044
beat	0.237	7.00	1.83	33	1.28	0.149	0.0045
bush	0.133	7.00	1.15	6	0.83	0.069	0.0015
boot	0.240	7.00	1.11	32	0.91	0.139	0.0039
dog	0.286	7.00	1.88	8	0.82	0.086	0.0016
dead	0.272	7.00	2.24	24	1.25	0.163	0.0108
deck	0.279	7.00	1.36	20	1	0.178	0.0142
debt	0.262	7.00	1.11	28	1.36	0.191	0.012
fat	0.267	7.00	1.78	28	1.37	0.192	0.0093
fell	0.267	6.83	1.96	30	1.29	0.193	0.0114
fate	0.266	6.92	1.56	29	1.47	0.142	0.0049
gas	0.251	7.00	1.99	19	0.86	0.184	0.0104
goat	0.240	7.00	0.78	26	0.91	0.141	0.0056
gull	0.229	6.67	0	21	0.75	0.139	0.0062
cough	0.255	7.00	0.85	11	1.1	0.129	0.0031
couch	0.194	7.00	1.08	9	0.62	0.11	0.0021
lock	0.230	7.00	1.36	31	0.93	0.148	0.0052
log	0.282	6.73	1.04	13	1.28	0.069	0.0024
lose	0.331	7.00	1.93	19	1.14	0.129	0.0026
ledge	0.235	6.83	0.78	18	0.82	0.118	0.0056
lick	0.220	6.75	0.48	32	1.04	0.184	0.0148
lip	0.249	7.00	1.26	29	0.81	0.167	0.0111
live	0.257	7.00	2.25	15	0.94	0.154	0.0093
lime	0.261	6.92	1.11	23	0.97	0.118	0.0047
luck	0.249	7.00	1.67	26	0.88	0.127	0.0037
miss	0.217	7.00	2.41	23	0.91	0.232	0.0251
merge	0.236	6.92	1.00	11	0.65	0.093	0.0021
mood	0.257	7.00	1.57	17	1.03	0.117	0.0024
mile	0.275	6.75	1.68	28	0.95	0.165	0.0051
pass	0.239	7.00	1.95	24	0.96	0.243	0.0158
purse	0.240	7.00	1.15	19	0.96	0.188	0.0066
rhyme	0.243	7.00	0.60	25	0.94	0.134	0.0031
rise	0.276	7.00	2.01	21	1.05	0.105	0.0029
sause	0.222	7.00	1.30	10	1.25	0.198	0.0022
save	0.264	7.00	1.79	22	1.01	0.155	0.0033
word	0.269	7.00	2.44	19	1.29	0.083	0.003
wide	0.265	7.00	2.10	26	1.06	0.093	0.0041

Note: Fam. is Familiarity; ND is neighborhood density; NF is neighborhood frequency; Pos. Seg. Freq. is position segment frequency (a measure of phonotactic probability); Biphone Freq. is biphone frequency (a measure of phonotactic probability).

Note: Fam. is Familiarity; NF is neighborhood frequency; Pos. Seg. Freq. is position segment frequency (a measure of phonotactic probability); Biphone Freq. is biphone frequency (a measure of phonotactic probability).

Appendix B

High Clustering Coefficient Words in jTRACE
Word	Clustering Coefficient	Neighborhood Density
lig	1.0000	2
tub	1.0000	2
rˆS	0.3333	3
pul	1.0000	3
pˆt	0.5000	4
rut	0.5000	4
sˆk	0.5000	4
did	0.4000	5
dip	0.4000	5
lid	0.4000	5
tul	0.4000	5
ark	0.4000	5
bar	0.4000	6
dat	0.4000	6
Sut	0.4000	6
Sˆt	0.4000	6
tar	0.4000	6
sis	0.6667	6
lat	0.3810	7
sil	0.3939	8
sik	0.3929	8
sid	0.3611	9
sit	0.2889	10
blu	1.0000	2
dru	0.5000	4
dˆk	0.5000	4
gat	0.6000	5
par	0.3214	8
Low Clustering Coefficient Words in jTRACE
Word	Clustering Coefficient	Neighborhood Density
lup	0.0000	2
Rˆb	0.0000	2
Tri	0.0000	3
bˆs	0.3333	3
kˆp	0.1667	4
gad	0.1667	4
rab	0.1667	4
ril	0.1000	5
rad	0.2000	5
kru	0.3000	5
gru	0.3000	5
lˆk	0.3000	5
lak	0.1333	6
dil	0.2000	6
rid	0.2000	6
tru	0.2000	6
but	0.2667	6
pap	0.2667	6
bit	0.1905	7
kap	0.1429	8
Sit	0.2500	8
Sat	0.2778	9
pat	0.2000	10
bab	0.0000	3
klu	0.3333	3
dal	0.3333	3
kip	0.1905	7
lip	0.1905	7

Note: Words are in the phonological transcriptions used in jTRACE.