Function-based Intersubject Alignment of Human Cortical Anatomy

Abstract

Making conclusions about the functional neuroanatomical organization of the human brain requires methods for relating the functional anatomy of an individual's brain to population variability. We have developed a method for aligning the functional neuroanatomy of individual brains based on the patterns of neural activity that are elicited by viewing a movie. Instead of basing alignment on functionally defined areas, whose location is defined as the center of mass or the local maximum response, the alignment is based on patterns of response as they are distributed spatially both within and across cortical areas. The method is implemented in the two-dimensional manifold of an inflated, spherical cortical surface. The method, although developed using movie data, generalizes successfully to data obtained with another cognitive activation paradigm—viewing static images of objects and faces—and improves group statistics in that experiment as measured by a standard general linear model (GLM) analysis.

Introduction

Aligning functional neuroanatomy across multiple subjects is a crucial precursor for the statistical analysis of group data in functional neuroimaging studies and, more generally, for developing models of brain organization that are representative of a population. Current methods for anatomical alignment rely on anatomical features that can be identified with high-resolution structural magnetic resonance imaging (MRI) scans. The most common technique is Talairach normalization (Talairarch and Tournoux 1988)—a three-dimensional (3D) piecewise affine registration technique based on a small number of anatomical landmarks. A more powerful technique uses the curvature of cortical folding to align cortical neuroanatomy, represented in a two-dimensional (2D) manifold (Fischl, Sereno, and Dale 1999; Fischl, Sereno, Tootell, et al. 1999; Argall et al. 2006). Basing cortical registration on curvature produces superior alignment of the major sulci and gyri of the cortex, as compared with 3D volumetric registration (Fischl, Sereno, and Dale 1999; Argall et al. 2006).

Functionally defined regions, however, are not consistently located relative to anatomical landmarks on the cerebral cortex. For example, the location of the visual motion area, MT, can vary across individuals by more than 2 cm after Talairach normalization (Watson et al. 1993) and can either be in the inferior temporal sulcus or the lateral occipital sulcus (Tootell et al. 1995). Moreover, the primary visual cortex, area V1, can vary in size by as much as 2-fold across different subjects’ brains (Rademacher et al. 1995; Dougherty et al. 2003). Consequently, methods for intersubject alignment based on anatomy can afford only approximate intersubject registration of the center and extent of functional cortical areas.

The functional anatomy of the human brain also has a regular organization at a finer spatial scale than that of cortical areas. Functional areas mostly subtend 1 cm² of the cortical surface or more. Topographic maps within cortical areas, however, can exist at a much finer spatial scale. The separation of representations in V1 for nearby retinotopic locations is on a millimeter scale (Sereno et al. 1995). At an even finer level of organization, the representation of a single retinotopic location consists of topographically organized maps of stimulus orientation (Bartfeld and Grinvald 1992; Vanduffel et al. 2002). Similar topographic maps exist in other sensory cortices, such as tonotopy in auditory cortex and somatotopy in somatosensory cortex. In higher-order visual areas within the lateral occipital and ventral temporal (VT) cortices, different object categories evoke distinct patterns of activity, suggesting the existence of within-area topographies that reflect object features (Haxby et al. 2001).

Between-subject alignment of anatomy based on functional response is possible with CARET software (Van Essen et al. 2001). This method relies on landmarks that are drawn on the surface by the operator. Consequently, this method is limited by the number of landmarks that can be identified and does not attempt to align within-area topography.

We decided to investigate whether cortical functional anatomy could be better aligned based on local variations in functional response to a complex stimulus that are common across subjects. In contrast to previous approaches and proposals (Van Essen et al. 2001; Mazziotta et al. 2001a, 2001b), our method attempts to find the optimal alignment of all cortical points, whose spacing is defined by the size of voxels in the imaging grid—a “complete correspondence code”—that relates every cortical point in an individual's brain to a corresponding cortical point in the brains of other individuals. This approach incorporates more locally defined functional information than simple alignment of the centers of functionally defined areas that are identified with functional localizers (e.g., Van Essen et al. 2001). Thus, the long-term goal of our method development project is to align not only the centers of functional areas but also the borders of these areas and some aspects of within-area topography.

In this report, we present an algorithm for aligning cortical functional anatomy across subjects based on patterns of neural activity evoked by cognitive and perceptual tasks. Our method employs algorithms for intersubject cortical alignment that were developed originally for anatomy-based cortical alignment in the 2D manifold of an inflated, spherical cortical surface (Fischl, Sereno, and Dale 1999; Fischl, Sereno, Tootell, et al. 1999). We use functional magnetic resonance imaging (fMRI) time-series as indices of local functional response profile. The fMRI time-series were obtained while subjects watched a feature movie, Raiders of the Lost Ark, and while subjects participated in an experiment on face and object perception. Previous work suggests that neural activity during a movie viewing is synchronized across subjects in a large percentage of the cerebral cortex, presumably reflecting a broad spectrum of perceptual and cognitive processes (Hasson et al. 2004; Bartels and Zeki 2004a, 2004b). Perception of still images of faces and objects evokes neural activity primarily in early visual cortices and in the extrastriate cortices of the ventral object vision pathway (Puce et al. 1996; Kanwisher et al. 1997; Haxby et al. 1999, 2001; Ishai et al. 1999, 2000). Activity in VT cortex that is evoked by face and object perception reveals a few areas that respond preferentially to some categories, such as faces and houses (Kanwisher et al. 1997; McCarthy et al. 1997; Epstein and Kanwisher 1998; Downing et al. 2001), and category-related variation on a finer scale than that defined by these areas (Haxby et al. 2001; Hanson et al. 2004). Our procedure uses anatomy-based alignment as the initial condition. We then use our new method of function-based alignment to further warp the cortical surface. Whereas the anatomy-based alignment maximizes correspondence of indices of cortical curvature, our method maximizes correspondence of functional time-series for each cortical node.

We derive independent warps based on each half of the time-series data collected while subjects watched the movie. We also derive warps based on time-series data collected while subjects participated in the face and object perception experiment. The validity of the warps is then tested by applying them to the data sets that were not used in their derivation, such as the other half of the movie or the face and object perception experiment.

The results demonstrate that our algorithm improves the registration of functional architecture across subjects, as indexed by cross-validating generalization to movie-viewing data and by generalization to data from the face and object perception experiment. Generalization across experiments indicates that the warps that our algorithm generates have general validity that extends beyond the specifics of the experimental paradigm that was used to generate the warps.

Materials and Methods

Data Acquisition

Subjects

Ten healthy young subjects (5 men, mean age = 23 years) participated in 2 fMRI studies. All subjects gave written informed consent.

Movie Stimulus

In the first fMRI study, subjects watched Raiders of the Lost Ark. Movie viewing was divided into 2 sessions. In the first session, subjects watched the first 55:03 of the movie. After a short break, during which subjects were taken out of the scanner, the second 55:30 of the movie was shown. Subjects were instructed simply to watch and listen to the movie and pay attention. The movie was projected with an LCD projector onto a rear projection screen that the subject could view through a mirror. The sound track for the movie was played though headphones using an air conduction system.

Face and Object Stimuli

In the second fMRI study, subjects viewed static pictures of 4 categories of faces (human female, human male, monkeys, and dogs) and 3 categories of objects (houses, chairs, and shoes). Images were presented for 500 ms with 2000-ms interstimulus intervals. Sixteen images from one category were shown in each block and subjects performed a one-back repetition detection task. Repetitions were different pictures of the same face or object. Blocks were separated by 12-s blank intervals. One block of each stimulus category was presented in each of 8 runs.

fMRI Image Acquisition

Blood oxygen level–dependent images were obtained with echoplanar imaging using a Siemens Allegra head-only 3T scanner (Siemens, Erlangen, Germany) and head coil.

For the movie study whole brain volumes of 48, 3-mm thick sagittal images (time repetition [TR] = 3000, time echo [TE] = 30 ms, flip angle = 90, 64 × 64 matrix, field of view [FOV] = 192 mm × 192 mm) were obtained every 3 s continuously through each half of the movie (1101 volumes for part 1, 1110 volumes for part 2).

For the faces and objects study, we obtained images of brain volumes consisting of 32, 3-mm thick axial images (TR = 2000, TE = 30 ms, flip angle = 90, 64 × 64 matrix, FOV = 192 mm × 192 mm) that included all of the occipital and temporal lobes and all but the most dorsal parts of the frontal and parietal lobes. One hundred and ninety-two volumes were obtained in each of 8 runs.

Structural MRI Image Acquisition

High-resolution T₁-weighted Magnetization-prepared Rapid Acquisition Gradient-echo (MPRAGE) images of the entire brain were obtained in each imaging session (TR = 2500 ms, TE = 4.3 ms, flip angle = 8°, 256 × 256 matrix, FOV = 256 mm × 256 mm, 172 1-mm thick sagittal images). Additional T₁-weighted MP–RAGE images were available for some subjects from unrelated experimental sessions. These images were used to create models of the cortical surface (see below).

fMRI Data Preprocessing

Movie fMRI Data

Preprocessing of the movie fMRI data began with correcting between-scan head movements (3dVolreg in AFNI, Cox, http://afni.nimh.nih.gov), then reducing extreme values (3dDespike in AFNI). Movement-related artifacts were reduced further by regressing the time-series data against the motion parameters that were calculated in the motion-correction step (3dDeconvolve in AFNI). We then calculated the residuals around the model of movement-related signal changes. The data were then low- and high-pass filtered to remove temporal variation with frequencies higher than 0.1 Hz and lower than 0.00667 Hz (3dFourier in AFNI). High-pass filtering removes low temporal frequency changes with periods longer than 150 s. Low pass filtering temporally smoothes fluctuations with frequencies higher than the hemodynamic response function. Global variations in signal were factored out by first calculating the mean whole brain intensity for each time point then regressing the time series against the whole brain means (3dmaskave then 3dDeconvolve in AFNI). The residuals around variation that correlated with whole brain means were used for the analysis of between-subject synchrony of neural activity. By removing the effect of global variation, the data reflects only local variation (Hasson et al. 2004). The data were not smoothed spatially.

Face and Object fMRI Data

Preprocessing of the visual categories fMRI data began with correcting between-scan head movements (3dVolreg in AFNI, Cox, http://afni.nimh.nih.gov), then reducing extreme values (3dDespike in AFNI). In the next step, we removed the mean, linear and quadratic drifts from each time series and further reduced movement-related artifacts by regressing the time-series data against the motion parameters that were calculated in the motion-correction step (3dDeconvolve in AFNI). We then calculated the residuals around the calculated model of signal changes that could be related to these factors. The data were further preprocessed in the same way as the movie data (low- and high-pass filtering, removal of global variation effects).

Mean response to each category was calculated using multiple regression with 7 regressors, one for each category (3dDeconvolve in AFNI). The β-weights for each regressor were used as indices of response magnitude for subsequent group analysis of the difference between responses to faces and responses to objects using t-tests (see below).

Building a Model of the Cortical Surface from the Structural MRI

The structural T₁-weighted MRI images for each subject were brought into alignment (minctracc in MINC, Collins, http://www.bic.mni.mcgill.ca) then averaged. This produces a high-quality, low noise image. The cortical surface was then extracted from the intensity-normalized, segmented 3D image as a tessellated triangular mesh, then inflated to a sphere and registered to a spherical atlas (recon-all in FreeSurfer, Fischl, http://surfer.nmr.mgh.harvard.edu). Extraction of the cortical surface begins with automated alignment of the 3D brain image to the Talairach atlas (Talairarch and Tournoux 1988) using affine transformations. The initial sphere, therefore, is a Talairach-normalized representation of cortical anatomy. The registered spherical meshes provide a 2D (spherical) coordinate system for comparing cortices across subjects at about 1-mm resolution (about 160 000 nodes per hemisphere). To further simplify comparison between subjects and reduce the number of nodes to about 40 000 per hemisphere, the meshes were resampled using standard numbering, uniformly on the sphere, at 2-mm resolution (MapIcosahedon in SUMA, Saad, http://afni.nimh.nih.gov/afni/suma). The new meshes provide a standard ordering for comparing cortices across subjects.

Placing fMRI Data on the Cortical Surface

Functional data were placed on the cortical surface by first registering structural images obtained during the experiment, which were already in alignment with functional data, with the high-resolution structural images used to create the cortical surfaces (3dvolreg in AFNI). Functional data recorded at locations falling on or between corresponding inner and outer (pial) cortical mesh nodes were then averaged and associated with that standard mesh node number (3dVol2Surf in SUMA). The time course at each cortical node was an average of voxels across the thickness of the cortex. The voxels averaged for any given cortical node lay along a line connecting corresponding mesh nodes in the inner (white matter–gray matter boundary) and outer (pial) surfaces, and extending 1 mm on either side. This line traversed from one to 3 voxels. We used 2-mm spacing of cortical nodes as a compromise between voxel size (3 mm linearly) and the roughly 1-mm spacing in the nodes recovered by FreeSurfer. One-mm spacing was too computationally expensive. However, 3-mm spacing would undersample voxels in some locations. Associated with each standard mesh node number within the 2-mm resolution mesh (36 002 nodes), then, is a functional time-series for each subject on the cortex, aligned anatomically.

Function-based Registration Approach

Our approach is to employ the whole fMRI time-series data (that corresponds to some standard experiment, e.g., movie viewing) as a feature vector that represents the functionality of the corresponding point on the cortical surface. Using anatomical alignment as initialization, the algorithm iteratively optimizes a warp field for each subject that maximizes the intersubject correlation of functional time-series, subject to a pair of regularization constraints that preserve the cortical topology of each subject. Thus, we view the functional registration algorithm as a fine-tuning of the anatomical alignment. In regions where there is negligible activity detected by the fMRI scan, the algorithm will have no incentive to apply a warp, resulting in the preservation of the anatomical alignment. Moreover, instead of basing alignment on functionally defined areas, whose location is usually defined as the center of mass or the local maximum response, the alignment is based on patterns of response as they are distributed spatially both within and across cortical areas (Haxby et al. 2001). In other words, the alignment is based on a complete correspondence code (Blanz and Vetter 2003) that relates every cortical point in an individual's brain to a corresponding cortical point in the brains of other individuals. The proposed method is implemented on a standard 2D representation (inflated and projected onto a standard spherical surface, as described in the previous section) of the cortical surface. Registration is thus performed on a spherical surface, not a Euclidean grid.

Deformation Model

Intersubject registration requires nonrigid warp models that can account for local deformations. Here, we employ a dense deformation approach, where each mesh node is allowed to move independently of its spatial neighbors. Regularization terms incorporated in the objective function ensure that the warps respect the surface topology and minimize the distortion of distances between neighboring cortical nodes.

The dense deformation approach typically requires a local (point) similarity measure, the gradient of which determines the direction of the move (warp) of the corresponding point. When dealing with data sets that have a small number of values at each point/voxel (e.g., convexity, sulcal depth, curvature or T₁-weighted MR images that display structural information, beta maps that summarize the response to various stimuli in a controlled experimental paradigm, etc.) computing a point-wise similarity between the 2 data sets is usually only possible by making use of a local neighborhood around the point of interest or the whole image. In the case of fMRI, however, we have much richer information at each point: long time-series (typically of length 100–2000). We used this information to compute a local (point-wise) alignment measure, the gradient of which can be used to drive the warp locally. Because computation time and memory are valuable resources, we investigated the fast-to-compute Pearson correlation measure r between the 2 time-series as an index of similarity.

Warp Regularization

There are many approaches to regularize a nonlinear spatial warp (see Modersitzki 2003, for a detailed treatment). The main goal is to avoid overfitting by penalizing unexpected warps. Typically, invertibility and smoothness are the 2 main characteristics imposed on a spatial warp. In the triangulated (mesh-like) representation of the cortical surface, smoothness is related to the preservation of internode distances. Invertibility, on the other hand, can be achieved by avoiding folds of the mesh.

Following Fischl, Sereno, and Dale (1999), we investigated a folding penalty and metric distortion penalty (precise definitions of these terms can be found in Online Supplemental Material). The folding penalty effectively prevents the introduction of folds in the warped mesh, rendering the final warp invertible. The metric distortion penalty, on the other hand, favors transformations that preserve internode distances. The influence of both of these terms is determined by their relative weights that are input parameters to our algorithm.

Our current approach to regularize the warp was favored over alternative methods due to its flexibility and relative ease of implementation. Furthermore, it has previously been successfully applied to registration problems (Fischl, Sereno, and Dale 1999). There is, however, very limited scientific evidence that would justify any other regularization. For instance, as we discussed in the Introduction, the areas of some well-studied functional regions can vary significantly across individuals, whereas we have very limited knowledge about intersubject variability of other functional regions. This suggests that strongly imposing the preservation of internode distances may be too strict for functional registration. Thus, in our implementation we put a small weight on the metric distortion penalty term.

Implementation

The cortical surface is represented with a regularized triangulation, which is stored as a list of mesh nodes. For each subject i, each mesh node v contains a spatial position 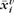, experimental time-series 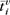, a list of neighboring nodes N_v, and belongs to a list of mesh triangles T_v. In the regularized mesh, all interneighbor distances are the same d₀, and all triangles have the same area A₀.

The functional registration algorithm modifies the time-series and spatial positions of the floating subject mesh nodes only. This is stored as a warp field, which can be added to the original spatial positions to interpolate the new time-series. (The warp field is in spherical coordinates, because the mesh nodes are only allowed to move on the spherical surface, conforming to the 2D topology of the cortex.)

The algorithm attempts to maximize $E_{\text{T}}=E_{\text{c}}-\mathrm{\lambda }{E}_{\text{f}}-\mathrm{\beta }{E}_{\text{m}}$with respect to the warp field parameters of each cortical node, where E_c is the total node-wise intersubject correlations (i.e., the alignment measure), E_f is the folding penalty term, and E_m is the metric distortion penalty. λ and β are scalar weights that determine the influence of the regularization terms. Each node is allowed to move independently, and the optimization is done using gradient-ascent with a line search, as implemented in MATLAB's Optimization Toolbox.

The algorithm can be summarized with the following update equation:

where γ(t) is a time-varying step size.

Note that gradient-ascent is guaranteed to find a local optimum of the objective function, but not necessarily the global optimum. In an attempt to improve the capture range of the algorithm, and avoid local optima, the algorithm uses a multiresolution strategy, in which the functional data of each subject are represented at multiple spatial resolutions. Alignment is performed first on fMRI time-series data smoothed to 6 mm spatial resolution, followed by alignment on data smoothed to 4-mm resolution. The final warp is then calculated based on unsmoothed data.

Group-Wise Registration

We register a group of N > 2 subjects together by developing an atlas, or group template, that represents the average of the population. Selecting an individual subject as the atlas may fail to sufficiently capture the variability of functional response across the group. On the other hand, selecting the average of the group as the atlas might blur the location of functionally defined cortical areas. For these reasons, we develop the atlas iteratively during the registration process through a sequence of pair-wise registrations. In each pair-wise registration, the brain of an individual subject is functionally aligned to the current estimate of the group atlas.

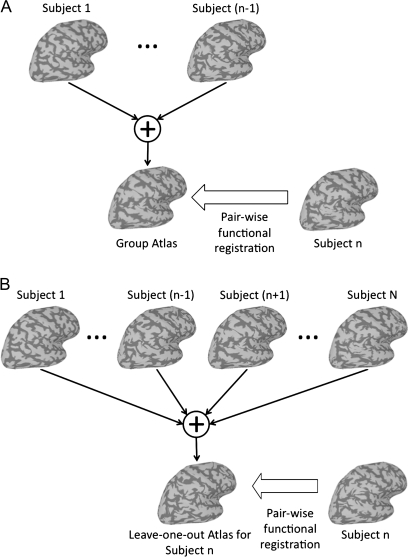
When the functional registration begins, the group of subjects is in anatomical alignment. An atlas defined as the group average of functional response is undesirable due to the variability in anatomical location of functional areas across subjects. Hence, the functional data of an individual subject is selected as the initial group atlas. The alignment then proceeds by sequentially registering the remaining subjects to the group atlas using the pair-wise functional registration algorithm described above. After each registration, the group atlas is refined by averaging the functional data of the subjects that have been functionally normalized. Thus, subject n, 2 ≤n ≤N, is registered to the average of subjects 1 through (n − 1). This procedure is illustrated in Figure 1A.

Figure 1.

(A) The first step for developing a group atlas. First, one subject's functional data is aligned to that of another. The mean time-series at each cortical node is calculated for these 2 subjects. The functional data for the third subject is aligned to the mean data for the first 2 subjects, and the mean time-series at each cortical node is calculated for these 3 subjects. The functional data for each additional subject is added to the atlas in the same way, by first aligning the functional data then calculating the group mean time-series for each cortical node. (B) The atlas is further refined by iteratively realigning each subject's functional data to its leave-one-out atlas, that is, the mean time-series for all of the other functionally normalized subjects. After each pair-wise registration, all subjects’ warps are renormalized so that the average location of all individual subject nodes warped to each atlas node is the anatomical location of that node in standardized spherical cortical space. This is done to prevent universal (across subjects) drifts in the warps (see Online Supplemental Material for details).

After one pass through this process, the group atlas represents an average of functional response from the group. However, the initial selection of an individual to represent the group can potentially introduce bias into the alignment procedure. To address this concern, we run several additional passes through the group in which each subject's warp field is refined by functionally (pair-wise) registering it to its leave-one-out atlas, defined as the average of all of the other functionally normalized subjects in the group. This procedure is illustrated in Figure 1B. After each pair-wise registration, all subjects’ warps are renormalized so that the average location of all individual subject nodes warped to each atlas node is the anatomical location of that node in standardized spherical cortical space. This is done to prevent universal (across subjects) drifts in the warps (see Online Supplemental Material for details).

Validation Testing

The output of the functional registration algorithm are warps—sets of changes in spherical coordinates $(\mathrm{\Delta }{\mathrm{\varphi }}_{i,j},\mathrm{\Delta }{\mathrm{\theta }}_{i,j})$ required to functionally align each node i in subject j‘s cortical mesh (the standardized, anatomically registered spherical mesh as provided by FreeSurfer and SUMA described above) to a group functional template—for a given experiment such as movie viewing. How warps generalize from training data from which the warps are derived, such as one half of the movie, to test data, such as the other half of the movie or the faces and objects experiment, provides a key test of warp validity. The validation procedure was as follows. Data from the test experiment was placed on the existing standardized, anatomically registered spherical meshes for each subject (3dVol2Surf in SUMA). Warps from the training experiment were applied to each mesh node. Functional data at each new warped to location was assigned via interpolation. Time-series test data was correlated at each node before and after functional warping, for each subject versus the template formed by all other subjects. A significant increase in correlation would provide support for warp validity. When test data consisted of regressor β-weights, as in the general linear model (GLM) analysis of the faces and objects experiment, a significant increase in the magnitude of t-tests of selected contrasts after functional warping would provide further support for warp validity. Finally, warp validity was tested by examining the effects of warps on the between-subject overlap of functionally defined regions of interest, namely the fusiform face area (FFA) (Kanwisher et al. 1997) and the parahippocampal place area (PPA) (Epstein and Kanwisher 1998). Each subject's FFA nodes were determined as the cortical nodes in VT cortex that responded significantly more strongly to faces than to objects (P < 0.0001). The PPA nodes of each subject were determined as the cortical nodes in VT that responded significantly more strongly to houses than to both small objects and faces (P < 0.0001 for both contrasts).

Results

Improved between Subject Correlations on Cross-Validation

As the starting point for function-based alignment, we used anatomy-based alignment that uses local cortical curvature as an index of gyral anatomy to align the cortex (FreeSurfer, Fischl, http://surfer.nmr.mgh.harvard.edu). This procedure begins with normalization to the Talairach stereotaxic brain atlas (Talairarch and Tournoux 1988) as the initialization point. As a further test of validity, we also applied function-based alignment using Talairach normalization as the initialization point (next section). In this section, however, anatomic registration refers to the full procedure of Talairach normalization plus curvature-based alignment.

Mean correlation was calculated at each cortical point for all pairings of each subject versus the mean time-series of the other 9 subjects. The correlations were performed on time-series data at 72 004 anatomically corresponding cortical points (36 002 points per hemisphere). We calculated 2, independent warps of cortical anatomy that were based on the data sets obtained while subjects watched the first half (P1 warp) and the second half (P2 warp) of the movie, respectively. For cross-validation of these functional registrations, we then applied the P2 warp to the data from the first half of the movie and vice versa and calculated the correlations again for comparison with the initial values. In the first half of the movie, mean correlation improved from +0.066 to +0.086 with functional registration based on the P2 warp. Note that the signal variance in this analysis of unsmoothed data is a small portion of total variance. The enhancement of between-subject alignment was evident in the number of cortical points with significant correlations (r > 0.1, P < 0.01 after correction of df for temporal autocorrelation) in the positive tail of the distribution, with a 25.9% (SD = 2.4%) increase from 19 776 to 24 899 (t(9) = 34.0, P < 10⁻¹⁰). In the second half of the movie, mean correlation improved from +0.068 to +0.088 with functional registration based on the P1 warp. The number of significant correlations increased by 25.6% (SD = 2.8%) from 20 435 to 25 670 (t(9) = 28.5, P < 10⁻⁹).

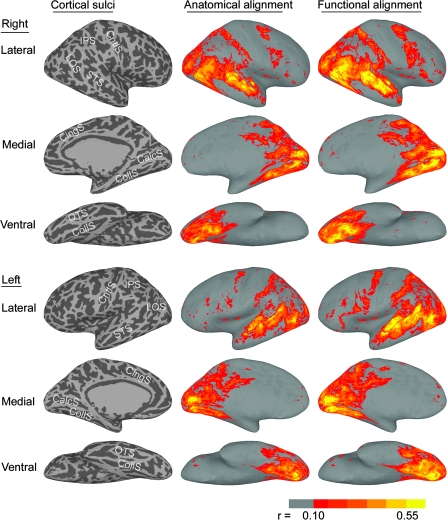
Figure 2 demonstrates visually the effect of applying the P2 warp to the first half of the movie (see Supplemental Figure 1 for images of the application of the P1 warp to the second half of the movie). The strength of correlations and the area occupied by significant correlations (r > 0.10, P < 0.01) have increased noticeably. Highly correlated nodes tend to be in posterior cortices, especially in the superior temporal, VT, and lateral occipital cortices, as well as in parietal and premotor cortices. Motor and somatosensory cortices near the central sulcus show little or no between-subject synchrony. Uncorrelated areas also appear in locations similar to the “default” (Gusnard and Raichle 2001) or “intrinsic” system (Golland et al. 2007).

Figure 2.

Generalization to the first half of the movie. The images in the left column show the sulcal anatomy for the inflated cortical surfaces (IPS—intraparietal sulcus; LOS—lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS—cingulate sulcus; CalcS—calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus). The images in the middle column show the mean correlation of each subject with the other 9 subjects for corresponding nodes after anatomical cortical registration. The images in the right column show mean correlations after applying the warps to these nodes that maximized functional similarity in the second half of the movie (cross-validation test). The effect of applying the warps based on the first half of the movie to the data from second half of the movie was highly similar (see Supplemental Fig. S1). Correlations less than +0.10 (P < 0.01) are not shown.

The increases in between-subject correlations in the training data, in other words the effect of applying a warp to the data that were used to produce that warp, were substantially greater, as expected. In the first half of the movie, the non–cross-validated increase in mean correlation was from +0.066 to +0.109, with a 59% increase in the number of significant correlations. In the second half of the movie, non–cross-validated increase in mean correlation was from +0.068 to +0.112, with a 60% increase in the number of significant correlations. The shrinkage with cross-validation is an index of how much overfitting occurred in the derivation of warps, a source of error that could be improved with further refinements of our method.

Direct Comparison of Anatomic-Curvature–based and Function-based Alignment Starting with the Same Initialization

The results reported above were for function-based registration using anatomic normalization based on cortical curvature as the initialization point. We reasoned that optimal use of our method should start with the optimal anatomic alignment. This comparison, however, does not index the power of function-based alignment versus anatomic-curvature–based alignment when both are calculated using the same initialization point. Curvature-based alignment using Freesurfer begins with Talairach normalization of the 3D brain image before identifying the cortical surface and warping that surface based on gyral anatomy (curvature). For a direct comparison of the power of anatomic-curvature–based alignment and function-based alignment, we recalculated the warp fields based on functional response for each subject using the same Talairach-normalized surfaces as the initialization point. We used the same cross-validation procedure to evaluate the results, namely applying the P1 warp to the data from the second half of the movie. Anatomic-curvature–based alignment, relative to Talairach normalization, increased the number of significant correlations by 17.6% (SD = 8.0%). By contrast, function-based alignment, using Talairach alignment as the initialization point, increased the number of significant correlations over Talairach alignment alone by 32.6% (SD = 3.5%). This difference was highly significant (t(9) = 5.1, P < 10⁻³). As expected, function-based alignment starting with anatomic-curvature–based alignment produced a significantly, larger increase in the number of significant correlations than did function-based alignment starting with Talairach normalization. Relative to Talairach normalization, function-based normalization using anatomic-curvature–based normalization as the starting point increased the number of significant correlations by 47.8% (SD = 7.7%). The number of significant correlations after function-based alignment initialized with curvature-based alignment was significantly greater than that initialized with Talairach normalization (t(9) = 6.14, P < 10⁻³). The recommended procedure for applying our method, therefore, uses anatomic-curvature–based alignment as the starting point for function-based alignment.

Cross-Validation to Visual Perception Experiment

Increased between-Subject Correlations for Full Time-Series

We also applied our functional alignment algorithm to the data from a block design study of face and object recognition. Between-subject correlations for the full time-series were significant for 9.4% of cortical nodes (SD = 1.9%) after anatomic-curvature–based alignment. Of nodes in VT cortex, 29.2% (SD = 4.8%) showed significant between-subject correlations. After functional registration, based on the warps derived from response to the movie, the number of significant correlations increased by 17.5% (SD = 3.5%) in the whole brain and by 15.7% (SD = 2.1%) in VT cortex (t(9) = 16.2, P < 10⁻⁷ and t(9) = 24.2, P < 10⁻⁸, respectively).

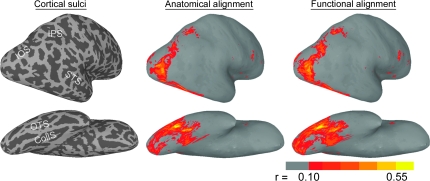
Figure 3 shows the effect of functional registration on the number of between-subject correlations for the full time-series from the face and object perception experiment. The increase in correlations is evident in the visual cortices—VT, ventral and dorsal occipital, posterior parietal—and a small locus in inferior frontal cortex. The extent of VT cortex that showed significant correlations for the visual experiment time-series was highly similar to that in the movie data, but, unlike in the movie data, we did not find large areas of significant correlations in the lateral occipitotemporal cortex, in the superior temporal sulcus, or in the parietal and premotor cortices.

Figure 3.

Generalization to a face and object perception experiment—between-subject correlations. The images on the left show the sulcal anatomy for the inflated cortical surfaces of a representative subject (IOS—intraoccipital sulcus; IPS—intraparietal sulcus; STS—superior temporal sulcus; OTS—occipitotemporal sulcus; CollS—collateral sulcus). The images in the middle show between-subject correlations in posterolateral and ventral views of the right hemisphere (r > 0.1, P < 0.01) after anatomical registration. The images on the right show between-subject correlations after functional registration based on a cortical warp derived from the first half of the movie data. The lateral view has been turned to enhance the view of posterior occipital and parietal cortex.

Enhanced t-Test Contrast for Faces versus Objects

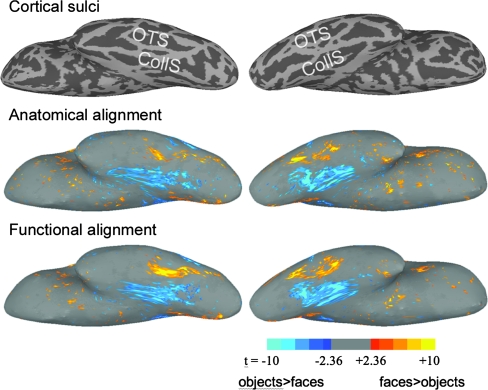
Between-subject correlations of the full time-series from the face and object perception experiment reflect shared variance due to both general visual responses as well as category-specific responses. In order to examine whether functional registration based on neural activity evoked by watching a movie increased the alignment of category-specific cortical topographies, we also performed a GLM analysis on the contrast between responses to faces and to nonface objects across subjects. We calculated a t-test at each node, testing whether the contrast between the response to faces versus objects (mean β for face responses—mean β for object responses) was significant. The number of cortical nodes that showed significantly different responses to faces and objects (|t| > 2.36, P < 0.05), increased by 14.0% in the whole brain from 3980 nodes (5.5% of cortex) after anatomy-based registration to 4539 nodes (6.3% of cortex) after function-based registration based on the warps from part 1 (4527 nodes) or part 2 (4550 nodes) of the movie data. In VT cortex, the number of cortical nodes that showed significantly different responses to faces and objects increased by 31.8% from 631 (23.8% of VT cortex) to 832 (31.1% of VT cortex). The increases in mean absolute value of t-tests for both warps (based on parts 1 and 2 of the movie) were highly significant in both hemispheres (t[36 001] > 6 in all cases, P < 10⁻¹⁰).

Figure 4 shows the effect of functional registration on the detection of cortical nodes in ventral occipitotemporal cortex that showed a significantly different response to faces and houses across subjects.

Figure 4.

Generalization to a face and object perception experiment—GLM group analysis. The left images show the t-statistic between 10 subjects after anatomically aligning betas for faces (red to yellow) versus objects (dark to light blue) contrast (right hemisphere). The right images show the t-statistic after further aligning the betas using functional warps from the first half of the movie. Absolute t-values less than 2.36 (P > 0.05) are not shown.

Improved Alignment of Functionally Defined Areas

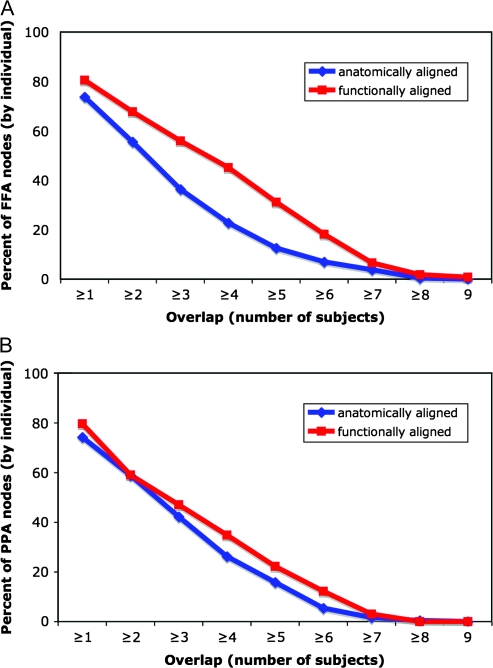
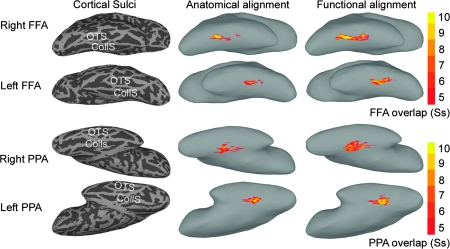
As a further test of the effect of functional alignment on conventional statistics, we identified 2 areas in VT cortex that are defined by differential response to different visual object categories—the FFA (Kanwisher et al. 1997) and the PPA (Epstein and Kanwisher 1998). The FFA and PPA were identified in each subject based on data from the face and object perception experiment after anatomic-curvature–based alignment and after functional alignment based on Part 1 of the movie. For each individual FFA and PPA, the number of cortical nodes that also were identified as the FFA or PPA in other subjects was counted. After anatomic alignment, a mean of 22.8% (SD = 6.1%) of each subject's FFA overlapped with 4 or more other subjects’ FFA. Functional alignment nearly doubled the portion of the FFA showing this amount of overlap to 45.2% (SD = 7.4%) (P < 10⁻⁶). Functional alignment also improved overlap for the PPA, albeit to a lesser extent (26.2 ± 10.0% to 34.8 ± 13.8%, P < 0.01). The percentage of nodes showing different levels of overlap for the FFA and PPA are shown in Figure 5. The locations of FFA and PPA nodes that overlapped for 5 or more subjects are shown in Figure 6.

Figure 5.

The effect of functional alignment on the overlap of 2 functionally defined regions—the FFA and the PPA—across subjects. The graphs show the average portion of an individual subject's FFA (Panel A) and PPA (Panel B) that overlaps with the same functional region in other subjects for different amounts of overlap.

Figure 6.

Illustration of the location and amount of overlap of 2 functionally defined regions—the FFA and the PPA—across subjects. Only nodes that were identified for 5 or more subjects are shown. The images that illustrate PPA overlap are tipped to provide a better view of this region that is located more medially than the FFA. The images on the left show the locations of sulci in these inflated cortex images (OTS—occipitotemporal sulcus; CollS—collateral sulcus). The images in the middle column show overlap among subjects after alignment based on sulcal anatomy. The images on the right show overlap among subjects after functional alignment based on a warp derived from the movie data.

Warping Functional Neuroanatomy based on the Face and Object Perception Study

We also tested whether our functional normalization method worked if the basis was functional brain responses during the face and object perception experiment. We derived a warp based on between-subject correlations for the face and object study time-series and applied that warp to the data from the first and second halves of the movie. Functional normalization based on the face and object data increased the number of cortical nodes with significant correlations in the first half of the movie by 5.9% (SD = 1.1%, t(9) = 17.2, P < 10⁻⁷) and in the second half of the movie by 5.5% (SD = 0.8%, t(9) = 22.0, P < 10⁻⁸). Improvement of between-subject correlations after normalization based on the face and object perception data was most evident in ventral occipitotemporal cortex, but we also observed small improvements in parietal and lateral temporal cortices. Whereas the number of significant correlations in VT cortex increased by 10.5% (SD = 2.8%), the number of significant correlations outside of VT cortex increased by a significantly smaller proportion (5.2%, SD = 0.9%, t(9) = 5.4, P < 10⁻³).

Discussion

Warps generated from the movie data generalized well not only to new movie data but also to a visual face and object perception experiment consisting of the presentation of static images of objects and faces. Mean intersubject correlations of the functional time-series increased significantly, over anatomical alignment alone, in every generalization test of the cortical warps based on neural responses recorded while watching the movie. The extent of cortex that showed correlated response to the movies across subjects was 28% of total cortex based on anatomical alignment alone and increased to 35% of total cortex based on functional alignment.

The cortices that showed improved alignment after functional alignment were primarily in occipital, temporal, and parietal areas that are associated with visual and auditory perception. Of particular interest is the large cortical area in the superior temporal sulcus, extending for nearly the entire length of this structure, which showed increased synchrony (Fig. 1). These cortices are known to be polysensory (Beauchamp et al. 2004) and to play an important role in action understanding and social cognition (Allison et al. 2000; Haxby et al. 2000; Gobbini et al. 2007). Functional alignment, also improved detection of between-subject synchrony in premotor and inferior frontal cortices. In general, the cortical areas that showed between-subject synchrony agree well with the findings of Hasson et al. (2004; Golland et al. 2007).

In a direct comparison of function-based alignment and anatomic-curvature–based alignment using the same initial condition, namely Talairach-based alignment, function-based alignment resulted in between-subject synchrony in a significantly larger extent of cortex, providing a clear quantitative index of the advantage of function-based alignment. Whereas curvature-based alignment increased the number of cortical locations having significant between-subject synchrony by 19%, function-based alignment resulted in an increase of 33%. As expected, function-based alignment initialized with Talairach alignment was not as effective as function-based alignment initialized with curvature-based alignment, indicating that our algorithm is more likely to settle into a suboptimal local minimum with a less optimal initialization point. The recommended procedure for applying our method, therefore, is to use anatomic-curvature–based alignment as the starting point.

Functional alignment based on the movie data also had a large effect on between-subject synchrony of local brain activity during a face and object perception experiment, with an 18% increase in the number of nodes with significant correlations. Moreover, this increased synchrony reflected category-specific functional topographies. Functional registration increased the number of cortical nodes that showed a significant difference between responses to faces and objects by 14% in the whole brain and by 32% in VT cortex. In addition to improving group statistics for identifying face-selective cortex in the fusiform gyrus (ventral view), function-based alignment also improved detection of face-selective cortex in the superior temporal sulcus, an area that is known to play an important role in the representation of facial expression, eye gaze, and social cognition (Allison et al. 2000; Haxby et al. 2000; Gobbini et al. 2007). Functional alignment based on the movie also increased overlap across subjects of 2 VT areas that are defined by selective responses to faces and houses, namely the FFA and the PPA.

Our method shows that a better map of the functional organization of cortex that is general across subjects can be derived using both anatomical and functional data than maps that are derived based only on anatomical data. This map preserves the topology of cortex in that it does not allow folding. It is, therefore, a rubber-sheet warping of individual subject topography. Penalty terms for warping distance insure that loci in an individual subject's brain are never warped more than 3 cm to locations in the template brain, a distance that is consistent with reports on the variability of the locations of functional loci (e.g., Watson et al. 1993; Dougherty et al. 2003). The anatomy of the template brain is meaningful, because each location in the template brain is the mean location of the cortical loci in individual brains that were warped to that location.

Functional alignment based on neural activity evoked by watching a movie clearly enhanced the GLM group statistics in the unrelated experiment on face and object perception, indicating that our method may be of general utility for functional neuroimaging research on a wide range of sensory, perceptual, and cognitive functions. Further work is needed to determine whether other fine-grained functional cortical topographies, such as retinotopy and somatopy, can also be better aligned using this method.

Our method also worked well when based on time series from the more controlled experiment on face and object perception. Due to the limited range of perceptual and cognitive operations that are associated with viewing still images of a restricted number of categories, the associated neural activity involves a smaller portion of the cerebral cortex. With anatomical alignment, the extent of cortex that showed significant between-subject correlations for response to the face and object stimuli was 34% of the extent of cortex that showed significant correlations for response to the movie. As expected, warps generated from the face and object perception experiment improved functional normalization in less cortex than did warps generated from the movie data. Functional normalization based on the face and object experiment was most effective for increasing the number of significant between-subject correlations in VT cortex, presumably because this focused experiment preferentially activated cortex in the ventral object vision pathway.

These results show clearly that the neural response while watching a movie provides more information about the functional architecture of the cerebral cortex than does the neural response during a more limited, controlled experiment, and that this information can be used effectively for function-based alignment of cortical anatomy. The range of perceptual and cognitive states that are evoked while watching a movie undoubtedly plays the major role in the efficacy of this procedure. An action movie, such as Raiders of the Lost Ark, also may be especially effective in engaging the attention of subjects and may be more useful for subjects with uncertain compliance, such as children and clinical populations. Further investigations are required to determine the extent to which functional alignment based on movie data generates warps that are consistent with controlled experiments in other cognitive domains.

It is possible that function-based normalization based on neural activity evoked by more controlled experiments could be more effective for a specific functional region. In our study, however, the warps based on the face and object experiment data did not align VT cortex, as indexed by the increase in between-subject correlations while watching the movie, better than did the warps based on data from watching the other half of the movie. The key question is whether a single, optimal warp exists for the cerebral cortex or for sectors of the cerebral cortex—or will overlapping topographic maps for different functions be aligned optimally by different warps. The generalization of the movie-based warp to the face and object data suggest that a single resampling warp can be effective for many different functional topographies, but the optimality and uniqueness of this warp are not established.

Our results show that 2 functionally defined regions, the FFA and the PPA, are better aligned across subjects using warps based on the movie data. Further work is necessary to determine if other functionally defined regions, such as retinopically defined early visual areas, the visual motion area MT, and auditory areas, are also better aligned. Of even greater interest is the question of whether within-area topographies, such as retinotopy and tonotopy, are better aligned across subjects. Some topographies have a spatial scale finer than that of conventional fMRI, such as orientation-selectivity in early visual cortex, but, nonetheless, can be detected with fMRI using multivariate pattern analysis (e.g., Haynes and Rees 2005; Kamitani and Tong 2005). These topographies, however, lose their structure when undersampled into a 2- or 3-mm imaging grid and, therefore, cannot be aligned with rubber-sheet warping of the cortex.

We are making the MATLAB software for our algorithm available for download (www.csbmb.princeton.edu/funcnorm). Although we believe that function-based alignment will be a useful preprocessing step for a broad spectrum of fMRI studies, there are several reasons why the algorithm is not yet ready for routine use:

• 1. Further work is necessary to optimize the method. Shrinkage on cross-validation, and the sensitivity of the method to initialization, indicates that our algorithm does not find a unique, optimal solution. Further refinement is necessary to insure that the method finds an optimal or near-optimal warp that is consistent and replicable.

• 2. We have not established the optimal stimulus for our algorithm. A different movie or a variety of selected movie clips may prove better. For focused investigations of specific brain systems, carefully designed stimuli within that domain may be better. Setting the movie that we selected for this initial report as the standard may not be the best choice.

• 3. We have not developed a functional template brain that is based on the alignment of a large number of brains of subjects who have watched the same movie. It also is unclear whether such a template will work well across scanners, scanner field strengths, and laboratories. Consequently, each laboratory would have to develop its own in-house brain template.

• 4. Finally, our method is costly in terms of scanner time. The results we present here derive warps based on nearly one hour of fMRI data for each subject. Consequently, use of this method would require an additional scanning session for each subject.

The use of our method as a preprocessing step to improve statistics does not affect the degrees of freedom for statistical analyses if the warps are based on unrelated data, such as those obtained while subjects view a movie. If functional alignment of data is based on data from the same experiment, extreme care must be taken to insure that the data used to derive the warp are not part of the data that are analyzed. Such an application would involve standard split-half or leave-one-out data folds.

It is important to note that all of these analyses were performed on data with minimal spatial smoothing. The data were resampled to 2-mm spacing on the cortical mesh, which is below the intrinsic spatial resolution of 3 mm in the functional EPI images. Group analyses of fMRI data, including conventional GLM analyses and between subject correlations for movie data (Hasson et al. 2004), typically smooth the data spatially to compensate for misaligned functional anatomy, using filters with a full width at half maximum of 6–12 mm. By contrast, our method allows us to overcome misaligned functional anatomy without spatial smoothing and without the resulting loss of high spatial frequency features of functional topographies.

Conclusion

In summary, our results indicate that functional registration based on neural activity while watching a movie is a further refinement beyond anatomical registration, and cross-validates both to the other half of the movie and to another experiment entirely. On cross-validation, the extent of cortex that shows correlated time courses of neural activity while watching a movie increased by 26% after function-based alignment. The warp based on time courses of activity while watching a movie also increased the sensitivity of group statistical analysis for an experiment on visual perception of still images of faces and objects, suggesting that it also may enhance the sensitivity for investigations of many other perceptual and cognitive functions. Thus, the method that we introduce here may be useful for a wide range of applications in functional neuroimaging research. Moreover, the vector field for warping can be used as an index of the similarity of functional architectures in different individuals, with potential for investigating the effect of development, experience, and clinical disorders on cortical functional anatomy.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.

Funding

National Institute of Mental Health (grant no. 5R01MH075706).