Manipulating stimulated coherent anti-Stokes Raman spectroscopy signals by broad-band and narrow-band pulses

Abstract

A transition-amplitude based representation of heterodyne detected coherent anti-Stokes Raman signals is used to separate them into a parametric component that involves no change in the material and dissipative processes associated with various transitions between states. Qualitatively different contributions from the two processes are predicted for the signal generated by an overlapping narrow (picosecond) and broad-band (femtosecond) pulse.

INTRODUCTION

Coherent anti-Stokes Raman spectroscopy (CARS) is a four wave mixing technique widely used since the early days of nonlinear optics,^{1, 2, 3, 4, 5} which shows narrow two-photon ω₁−ω₂ resonances (Fig. 1). The technique provides a powerful spectroscopic tool for probing molecular vibrations and for imaging applications.^{6, 7} Time domain femtosecond techniques with pulse shaping enhance the degree of control over the signals.^{8, 9, 10, 11, 12, 13, 14}

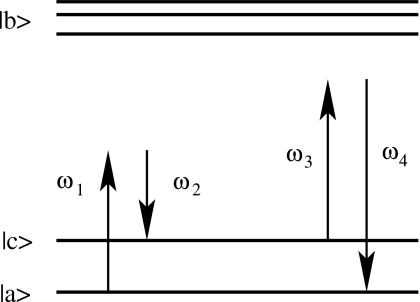
Figure 1.

The molecular levels and the relevant optical transitions in a CARS process.

All third order nonlinear optical techniques, such as CARS, are commonly described in terms of the third order optical susceptibility χ⁽³⁾, obtained from a perturbative expansion of the density matrix.¹⁵ For clarity we first consider frequency-domain heterodyne-detected (i.e., stimulated) CARS, where a molecule is coupled to four optical modes with complex field amplitudes that are defined using E(r,t)=∑_jE_j exp(ik_jr_j−iω_jt)+c.c. This will allow us to introduce the basic ingredients which will be used later to describe multimode broad-band time-domain CARS as superpositions of the frequency domain signals. Time translation invariance requires that the mode frequencies satisfy

$${\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4=0.$$ (1)

The signal obtained by measuring mode ω_i will be denoted S_i. There are four possible signals:³

$$S_1=-\frac{4\pi }{\hslash }\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\chi }^{\left(3\right)}\left(-{\omega }_1;{\omega }_4,-{\omega }_3,{\omega }_2\right)\right],$$ (2)

$$S_2=-\frac{4\pi }{\hslash }\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\chi }^{\left(3\right)}\left(-{\omega }_2;{\omega }_3,-{\omega }_4,{\omega }_1\right)\right],$$ (3)

$$S_3=-\frac{4\pi }{\hslash }\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\chi }^{\left(3\right)}\left(-{\omega }_3;{\omega }_2,-{\omega }_1,{\omega }_4\right)\right],$$ (4)

$$S_4=-\frac{4\pi }{\hslash }\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\chi }^{\left(3\right)}\left(-{\omega }_4;{\omega }_1,-{\omega }_2,{\omega }_3\right)\right].$$ (5)

While Eqs. 2, 3, 4, 5 provide a useful recipe for computing the various signals, it is not obvious from these expressions what is really happening in the material in the course of the χ⁽³⁾ process. The CARS signal is composed of two different types of processes: Resonant processes, where the molecule makes transitions between different electronic or vibrational states, and parametric processes, which involve an exchange of photons between various field modes but ultimately leave the molecule in its initial state. Separating the two will be one of the goals of this paper. One recipe used to accomplish this goal is to write $\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\chi }^{\left(3\right)}\right)=\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }\right)\mathfrak{R}{\chi }^{\left(3\right)}+\mathfrak{R}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }\right)\mathfrak{I}{\chi }^{\left(3\right)}$, identifying the first term with the parametric process and the second as the contribution of resonant processes.⁶ We shall show that this applies in some cases but is not generally valid.

The physical interpretation becomes more transparent when we examine the material system directly. In frequency-domain heterodyne experiments the molecule is prepared in a nonequilibrium steady state involving the molecule and the four modes of the radiation field and undergoes transitions between states. Such transitions can be described using scattering theory,¹⁶ and their flux is recast in the form

$$J_{fi}=\pi {\mid T_{fi}\mid }^2\delta \left({\omega }_{\text{opt}}-{\omega }_{fi}\right),$$ (6)

where ω_opt denotes the energy supplied by the optical modes (which is some combination of the mode frequencies ω_j, see below), and T_fi is a transition amplitude connecting the initial and final states. ℏω_fi=E_f−E_i is the energy difference between the initial and final states of the molecule. To first order in the radiation matter interaction T_fi=−Eμ_fi and Eq. 6 becomes the Fermi Golden rule. Photon counting statistics is also recast in this form.¹⁷ Spontaneous Raman signals, where ω₁ is absorbed and ω₂ is emitted, are given by the celebrated Kramers–Heisenberg (KH) formula, which coincides with Eq. 6 when T is calculated to second order,¹⁸

$$S_{\text{KH}}\left({\omega }_1,{\omega }_2\right)={\mid {\mathcal{E}}_1\mid }^2{\mid \sum _b\frac{{\mu }_{cb}{\mu }_{ba}}{{\omega }_1-{\omega }_{ba}}\mid }^2\delta \left({\omega }_1-{\omega }_2-{\omega }_{ca}\right).$$ (7)

The KH form implies that the molecule undergoes a transition from state a to state c, at a steady state rate given by Eq. 7.

Pump-probe signals, which involve only two field modes, were recently recast in terms of T matrix elements.¹⁹ Here we extend this approach to the more general four mode case of stimulated CARS signals. The CARS signal is recast in terms of transition amplitudes and the parametric and dissipative components of the signals are identified. In addition, certain linear combinations of optical signals are shown to be equal to material fluxes, and are therefore purely dissipative. The expressions for the dissected CARS signals are then used to study the signal from a strong narrow-band pulse with a weaker overlapping broad-band pulse. In this case the resonant and parametric processes make very different contributions to the overall signal, which are analyzed in detail. This application, which demonstrates the usefulness of the transition amplitudes representation, is the main result of this paper.

In Sec. 2 we define the minimal model of frequency domain CARS, a molecule with three relevant levels interacting with four field modes and give the standard expressions for the optical signals in terms of the nonlinear susceptibility χ⁽³⁾. In Sec. 3 the signals are recast in term of transition amplitudes and dissected into their dissipative and dispersive components. These results are extended to pulses of arbitrary shape and used to analyze the signal from a specific pulse configuration in Sec. 4 The resonant and parametric processes make qualitatively different contributions to the overall signal. Finally, some implications of the results are discussed in Sec. 5.

STIMULATED CARS SIGNALS

In this section we define the model and derive expressions for the various CARS signals. The model for the interacting molecule, with relevant states as well as the couplings to the electromagnetic field, is depicted in Fig. 1. a and c are vibrational states belonging to the ground electronic state whereas b is an electronically excited state. The levels a and c are resonantly coupled by two possible Raman processes, with ω₁−ω₂=ω₄−ω₃≃ω_ca. The system is described by the Hamiltonian^{3, 4, 5}

$$\mathcal{H}={\mathcal{H}}_s+{\mathcal{H}}_f+{\mathcal{H}}_{\text{int}},$$ (8)

with the molecular part,

$${\mathcal{H}}_s=\hslash {\omega }_a\mid a⟩⟨a\mid +\hslash {\omega }_b\mid b⟩⟨b\mid +\hslash {\omega }_c\mid c⟩⟨c\mid ,$$ (9)

and the field part,

$${\mathcal{H}}_f=\sum _{i=1}^4\hslash {\omega }_i{\widehat{a}}_i^{†}{\widehat{a}}_i.$$ (10)

Within the rotating wave approximation, the dipole coupling between the laser field and the molecule is given by

$${\mathcal{H}}_{\text{int}}={\left(\frac{2\pi {\omega }_1}{\Omega }\right)}^{1∕2}{\widehat{a}}_1{e}^{-i{\omega }_{1}t}{\mu }_{ba}\mid b⟩⟨a\mid +{\left(\frac{2\pi {\omega }_2}{\Omega }\right)}^{1∕2}{\widehat{a}}_2{e}^{-i{\omega }_{2}t}{\mu }_{bc}\mid b⟩⟨c\mid +{\left(\frac{2\pi {\omega }_3}{\Omega }\right)}^{1∕2}{\widehat{a}}_3{e}^{-i{\omega }_{3}t}{\mu }_{bc}\mid b⟩⟨c\mid +{\left(\frac{2\pi {\omega }_4}{\Omega }\right)}^{1∕2}{\widehat{a}}_4{e}^{-i{\omega }_{4}t}{\mu }_{ba}\mid b⟩⟨a\mid +h.c.,$$ (11)

which corresponds to the transitions depicted in Fig. 1. We had suppressed the dependence on the photon momentum to simplify the notation.

To set the stage we first present the various CARS signals in the standard χ⁽³⁾ form. In practice, one only needs to calculate the S₄ signal explicitly. All other signals can be obtained from it using various symmetries of the system.

The optical signal, defined as the (integrated) rate of change of the number of photons in the ith mode, is given by

$$S_i\equiv \int dt\frac{d}{dt}\left[\text{Tr}{\widehat{a}}_i^{†}{\widehat{a}}_i\widehat{\rho }\left(t\right)\right].$$ (12)

Equations 2, 3, 4, 5 for the signals can be derived from Eq. 12 using the method outlined in Refs. ^{20, 19}. The contributions to χ⁽³⁾ can be represented by closed time loop (CPTL) diagrams. The calculation of χ⁽³⁾ in terms of amplitudes representing the wave function in Hilbert space requires pathways on the Schwinger loop involving both forward and backward time evolutions.²⁰

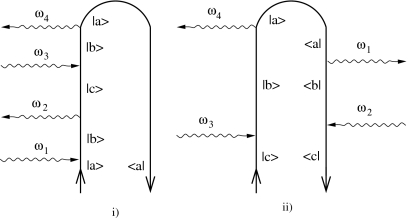
The CPTL diagrams, which correspond to the two processes contributing to the signal [Eq. 5] are depicted in Fig. 2. In (i) the system is excited out of the ground state a, while in (ii) it is excited out of state c. The loop diagrams can be read according to the rules given in Refs. ^{19, 20} leading to

$${\chi }^{\left(3\right)}\left(-{\omega }_4;{\omega }_1,-{\omega }_2,{\omega }_3\right)=-\frac{{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{cb}\mid }^2}{{\hslash }^3}\left[\frac{P\left(a\right)}{\left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_{ba}+i\eta \right)\left({\omega }_1-{\omega }_2-{\omega }_{ca}+i\eta \right)\left({\omega }_1-{\omega }_{ba}+i\eta \right)}+\frac{P\left(c\right)}{\left({\omega }_3-{\omega }_4+{\omega }_1-{\omega }_{bc}-i\eta \right)\left({\omega }_3-{\omega }_4-{\omega }_{ac}-i\eta \right)\left({\omega }_3-{\omega }_{bc}+i\eta \right)}\right].$$ (13)

Substitution in Eq. 5 gives

$$S_4=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\mid {\mu }_{ab}\mid }^2{\mid {\mu }_{bc}\mid }^2\left(\frac{P\left(a\right)}{\left({\omega }_4-{\omega }_{ba}+i\eta \right)\left({\omega }_1-{\omega }_2-{\omega }_{ca}+i\eta \right)\left({\omega }_1-{\omega }_{ba}+i\eta \right)}+\frac{P\left(c\right)}{\left({\omega }_3-{\omega }_{bc}+i\eta \right)\left({\omega }_2-{\omega }_{bc}-i\eta \right)\left({\omega }_2-{\omega }_1-{\omega }_{ac}-i\eta \right)}\right)\right],$$ (14)

where we further used Eq. 1 to replace some frequency combinations by more compact ones.

Figure 2.

CPTL representation of χ⁽³⁾(−ω₄;ω₁,−ω₂,ω₃) contributing to the S₄ signal. (i) and (ii) represent the two terms in Eq. 13, respectively. The interaction with the detected mode (ω₄) is chronologically the last.

The other signals can be calculated using the same method, or more simply by noticing that they are physically equivalent to S₄ under permutations of certain field modes, and of the states a and c. The signal S₃ can be obtained from S₄ by interchanging modes 1 and 2, modes 3 and 4, and states a and c,

$$S_3=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\mid {\mu }_{ab}\mid }^2{\mid {\mu }_{bc}\mid }^2\left(\frac{P\left(a\right)}{\left({\omega }_1-{\omega }_{ba}-i\eta \right)\left({\omega }_4-{\omega }_{ba}+i\eta \right)\left({\omega }_1-{\omega }_2-{\omega }_{ca}-i\eta \right)}+\frac{P\left(c\right)}{\left({\omega }_2-{\omega }_{bc}+i\eta \right)\left({\omega }_3-{\omega }_{bc}+i\eta \right)\left({\omega }_2-{\omega }_1-{\omega }_{ac}+i\eta \right)}\right)\right].$$ (15)

The signals S₁ and S₂ can be obtained from S₄ and S₃ in an even simpler way. One notices that the modes 1 and 4, and similarly 2 and 3, play the similar roles for these pairs of signals. Therefore, exchanging the field modes 1 and 4, as well as 2 and 3, will transform the S₄ into S₁ and S₃ to S₂. The remaining signals are given by

$$S_1=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\mid {\mu }_{ab}\mid }^2{\mid {\mu }_{bc}\mid }^2\left(\frac{P\left(a\right)}{\left({\omega }_4-{\omega }_{ba}+i\eta \right)\left({\omega }_4-{\omega }_3-{\omega }_{ca}+i\eta \right)\left({\omega }_1-{\omega }_{ba}+i\eta \right)}+\frac{P\left(c\right)}{\left({\omega }_2-{\omega }_{bc}+i\eta \right)\left({\omega }_3-{\omega }_{bc}-i\eta \right)\left({\omega }_3-{\omega }_4-{\omega }_{ac}-i\eta \right)}\right)\right]$$ (16)

and

$$S_2=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\mid {\mu }_{ab}\mid }^2{\mid {\mu }_{bc}\mid }^2\left(\frac{P\left(a\right)}{\left({\omega }_1-{\omega }_{ba}+i\eta \right)\left({\omega }_4-{\omega }_{ba}-i\eta \right)\left({\omega }_4-{\omega }_3-{\omega }_{ca}-i\eta \right)}+\frac{P\left(c\right)}{\left({\omega }_3-{\omega }_{bc}+i\eta \right)\left({\omega }_3-{\omega }_4-{\omega }_{ac}+i\eta \right)\left({\omega }_2-{\omega }_{bc}+i\eta \right)}\right)\right].$$ (17)

DISSECTING CARS SIGNALS INTO MATERIAL AND PARAMETRIC FLUXES

Each of the signals given by Eqs. 14, 15, 16, 17 has contributions from two different types of physical processes: (i) parametric processes, which involve an exchange of photon between different field modes but ultimately leave the molecule in its initial state, and (ii) resonant dissipative processes, which involve molecular transitions from one state to another. The two types of processes play different roles and the ability to separate their contributions can be used to improve and analyze various measurements.

The different roles played by the parametric and resonant components become clear when χ⁽³⁾ is recast in terms of products of transition amplitudes. These transition amplitudes describe processes where the molecule makes specific transitions through interactions with given field modes. For instance, $T_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right)={\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mu }_{cb}{\mu }_{ba}{\left({\omega }_1-{\omega }_{ba}+i\eta \right)}^{-1}\equiv {\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right)$ corresponds to a second order transition in which the molecule first makes a transition a→b, by absorbing a photon from mode 1, and then makes another transition b→c, emitting a photon into mode 2. The dressed transition amplitudes T are given by products of the bare amplitudes, $\tilde{T}$, and the field amplitudes. All relevant transition amplitudes for the present application are listed in Appendix A.

Written in terms of bare transition amplitudes, resonant processes assume a generalized KH form. They are proportional to a product of two transition amplitudes, one of which is complex conjugated, between the same pair of states, multiplied by a δ-function expressing conservation of molecule+field energy. Parametric processes, in contrast, are described in terms of a single transition amplitude, T_aa, where the system starts and ends in the same state. This representation is not unique since (the imaginary part of) a linear combination of such transition amplitudes is connected to resonant transitions via the optical theorem. The latter states that the probability missing in a state must be balanced by transitions from that state to other states.

We shall partition the S₄ signal [Eq. 14] into its parametric and resonant components in two steps. First, the terms in Eq. 14 are brought into a form which is proportional to diagonal transition amplitudes ${\tilde{T}}_{\nu \nu }^{\left(4\right)}$ plus additional resonant terms. The term proportional to P(a) already has the desired form. The term proportional to P(c) can be brought to a similar form by writing (ω₃−ω_ba+iη)⁻¹=(ω₃−ω_bc−iη)⁻¹−2πiδ(ω₃−ω_bc), and then by taking the complex conjugate of the term with three advanced Green functions. In the second step, each of the terms with three retarded Green functions $\left(\sim {\tilde{T}}_{\nu \nu }^{\left(4\right)}\right)$ is rewritten as a sum of a symmetric and antisymmetric contributions. (The symmetry is with respect to the order of interactions with the field modes.) The optical theorem is then applied to the symmetric combination, recasting it as a sum over resonant processes. The antisymmetric part is identified as the parametric process. This second step is sketched in Appendix B.

The signal finally takes the form

$$S_4=S_{4,\text{par}}+S_{4,\text{dis}},$$ (18)

where

$$S_{4,\text{par}}=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }\right)\left[P\left(a\right)\mathfrak{R}{\tilde{T}}_{aa}^{\left(4\right)}\left(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1\right)+P\left(c\right)\mathfrak{R}{\tilde{T}}_{cc}^{\left(4\right)}\left(-{\omega }_2,{\omega }_1,-{\omega }_4,{\omega }_3\right)\right],$$ (19)

and

$$S_{4,dis}=-\frac{2{\pi }^2}{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\left\{P\left(a\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_2,-{\omega }_3,{\omega }_4\right){\tilde{T}}_{ba}^{\left(1\right)\ast }\left({\omega }_1\right)+c.c.\right]\delta \left({\omega }_1-{\omega }_{ba}\right)+P\left(a\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_3,-{\omega }_2,{\omega }_1\right){\tilde{T}}_{ba}^{\left(1\right)\ast }\left({\omega }_4\right)+c.c.\right]\delta \left({\omega }_4-{\omega }_{ba}\right)+P\left(a\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right){\tilde{T}}_{ca}^{\left(2\right)\ast }\left(-{\omega }_3,{\omega }_4\right)+c.c.\right]\delta \left({\omega }_1-{\omega }_2-{\omega }_{ca}\right)+P\left(c\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_4,-{\omega }_1,{\omega }_2\right){\tilde{T}}_{bc}^{\left(1\right)\ast }\left({\omega }_3\right)+c.c.\right]\delta \left({\omega }_3-{\omega }_{bc}\right)-P\left(c\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_1,-{\omega }_4,{\omega }_3\right){\tilde{T}}_{bc}^{\left(1\right)\ast }\left({\omega }_2\right)+c.c.\right]\delta \left({\omega }_2-{\omega }_{bc}\right)-P\left(c\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{ac}^{\left(2\right)}\left(-{\omega }_1,{\omega }_2\right){\tilde{T}}_{ac}^{\left(2\right)\ast }\left(-{\omega }_4,{\omega }_3\right)+c.c.\right]\delta \left({\omega }_2-{\omega }_1-{\omega }_{ac}\right)\right\}.$$ (20)

The other signals can be treated in a similar manner. For S₃ we get

$$S_3=S_{3,\text{par}}+S_{3,\text{dis}},$$ (21)

where

$$S_{3,\text{par}}=\frac{4\pi }{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\mathfrak{I}\left({\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4\right)\left[P\left(c\right)\mathfrak{R}{\tilde{T}}_{cc}^{\left(4\right)}\left(-{\omega }_3,{\omega }_4,-{\omega }_1,{\omega }_2\right)+P\left(a\right)\mathfrak{R}{\tilde{T}}_{aa}^{\left(4\right)}\left(-{\omega }_1,{\omega }_2,-{\omega }_3,{\omega }_4\right)\right],$$ (22)

and

$$S_{3,\text{dis}}=-\frac{2{\pi }^2}{{\hslash }^4}\delta \left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_4\right)\left\{P\left(c\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_4,-{\omega }_1,{\omega }_2\right){\tilde{T}}_{bc}^{\left(1\right)\ast }\left({\omega }_3\right)+c.c.\right]\delta \left({\omega }_3-{\omega }_{bc}\right)+P\left(c\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_1,-{\omega }_4,{\omega }_3\right){\tilde{T}}_{ba}^{\left(1\right)\ast }\left({\omega }_2\right)+c.c.\right]\delta \left({\omega }_2-{\omega }_{bc}\right)+P\left(c\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{ac}^{\left(2\right)}\left(-{\omega }_1,{\omega }_2\right){\tilde{T}}_{ac}^{\left(2\right)\ast }\left(-{\omega }_4,{\omega }_3\right)+c.c.\right]\delta \left({\omega }_2-{\omega }_1-{\omega }_{ac}\right)+P\left(a\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_3,-{\omega }_2,{\omega }_1\right){\tilde{T}}_{ba}^{\left(1\right)\ast }\left({\omega }_4\right)+c.c.\right]\delta \left({\omega }_4-{\omega }_{ba}\right)-P\left(a\right)\left[{\mathcal{E}}_1^{\ast }{\mathcal{E}}_2{\mathcal{E}}_3^{\ast }{\mathcal{E}}_4{\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_2,-{\omega }_3,{\omega }_4\right){\tilde{T}}_{ba}^{\left(1\right)\ast }\left({\omega }_1\right)+c.c.\right]\delta \left({\omega }_1-{\omega }_{ba}\right)-P\left(a\right)\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right){\tilde{T}}_{ca}^{\left(2\right)\ast }\left(-{\omega }_3,{\omega }_4\right)+c.c.\right]\delta \left({\omega }_1-{\omega }_2-{\omega }_{ca}\right)\right\}.$$ (23)

The expressions for S₁ and S₂ can be obtained from S₄ and S₃ by exchanging the field modes, as was discussed in Sec. 2. However, we will only make use of S₄ and S₃ in the following application.

An alternative approach for computing the dissipative signals is based on examining molecular fluxes. These are defined as the rates of change of the population in the molecular states,

$${\mathcal{J}}_{\nu }\equiv \int dt\frac{d}{dt}\left[\text{Tr}\mid \nu ⟩⟨\nu \mid \widehat{\rho }\left(t\right)\right],$$ (24)

with ν=a,b,c. Conservation of probability implies J_a+J_b+J_c=0, which follows from ${\sum }_{\nu }\mid \nu ⟩⟨\nu \mid =\widehat{1}$ in the molecular Hilbert space.

It is possible to relate the molecular fluxes J_ν to combinations of optical signals S_i. This is done by comparing the Heisenberg equation of motion $\frac{d}{dt}{\widehat{a}}_{i,H}^{†}{\widehat{a}}_{i,H}=\left(i∕\hslash \right)\left[{\mathcal{H}}_{\text{int}},{\widehat{a}}_{i,H}^{†}{\widehat{a}}_{i,H}\right]$ with $\frac{d}{dt}{\mid \nu ⟩}_H{⟨\nu \mid }_H=\left(i∕\hslash \right)\left[{\mathcal{H}}_{\text{int}},{\mid \nu ⟩}_H{⟨\nu \mid }_H\right]$. For the interaction Hamiltonian 11, this gives

$${\mathcal{J}}_a=S_1+S_4,$$ (25)

$${\mathcal{J}}_c=S_2+S_3,$$ (26)

$${\mathcal{J}}_b=-\sum _{i=1}^4{S}_i.$$ (27)

Equations 25, 26, 27 express the rate of change of molecular populations in terms of combinations of optical signals. This connection is important since optical signals are usually measured in order to study material properties. Equations 25, 26, 27 enforce conditions on the parametric part of the various optical signals. For instance, Eq. 25 means that S_1,par+S_4,par=0. This can be verified using Eq. 19, and noting that S_1,par is obtained from it by exchanging field modes 1 and 4, and similarly modes 3 and 2. (The factor of $\mathfrak{I}{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}$ changes its sign under this operation while the rest is left unchanged.) The combinations of signals [Eqs. 25, 26, 27] are purely dissipative and better suited for molecular interpretation.

APPLICATION TO SIGNALS GENERATED BY A NARROW AND A BROAD-BAND PULSE

Signals driven by pulses of arbitrary bandshape can be readily computed as superpositions of the frequency-domain results presented earlier. To that end we need to switch from the discrete mode expression Eq. 18 [or Eq. 21] to a description allowing for a continuous distribution of frequencies. This is done by replacing E_i$\left[{\mathcal{E}}_i^{*}\right]$ with ε(ω_i)∕2π [ε^∗(ω_i)∕2π=ε(−ω_i)∕2π] and integrating over all frequencies except the one corresponding to the frequency dispersed signal. [ε(ω) is the bandshape of the optical field.] We then have

$$S_4\left({\mathcal{E}}_i\right)\to S\left({\omega }_4\right)=\frac{1}{{\left(2\pi \right)}^4}\int d{\omega }_{1}d{\omega }_{2}d{\omega }_3{S}_4\left(\epsilon \left({\omega }_i\right)\right).$$

We now apply the results of Sec. 3 to a specific pulse configuration and show that the resonant and parametric processes lead to distinct components of the signal. The results presented below demonstrate the usefulness of dissecting the signal into its dissipative and dispersive components.

In recent experiments^{8, 10, 11, 14} molecules were driven by an overlapping broad-band femtosecond and narrow-band picosecond pulse (depicted in Fig. 3)

$$\epsilon \left(\omega \right)=\tilde{\epsilon }\left(\omega \right)+2\pi {\mathcal{E}}_0{\delta }_{\Delta }\left(\omega -{\omega }_0\right)+2\pi {\mathcal{E}}_0^{\ast }{\delta }_{\Delta }\left(\omega +{\omega }_0\right),$$ (28)

where $\tilde{\epsilon }\left(\omega \right)$ is the band shape of the broad-band pulse, and E₀ is the amplitude of the narrow-band pulse, centered at ω₀. δ_Δ(ω) is a slightly broadened δ-function, of width Δ, describing the shape of the narrow pulse. The narrow-band pulse is strong, so that high-order interactions with it dominate the measured signal. The signal is given by two interactions in the narrow-band and two with the broad-band and we assume that there are no electronic resonances in the frequency range covered by the pulses.

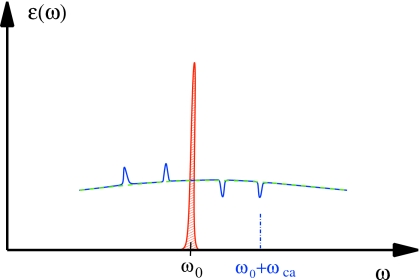
Figure 3.

The pulse configuration [Eq. 28] consists of a broad-band pulse (dashed-green line) and a narrow-band pulse (red-filled line) centered at ω₀. Raman resonances at ω₀±ω_ca modulate the broad pulse envelope (blue-solid line).

Due to the Raman interactions with the narrow-band pulse the measured signal shows a series of Raman peaks at frequencies ω₀±ω_νν^′ where ω_νν^′ are vibrational transition frequencies of the molecules. The resulting signal is also depicted heuristically in Fig. 3

In the following we analyze the signal using Eqs. 18, 21, which dissect it into its components. For clarity, we assume a single active vibrational mode, leading to one positive and one negative Raman peak.

The signal outside the frequency range of the narrow-band pulse has two regions, (ω>ω₀ and ω<ω₀), which will be treated separately. In each region the signal frequency corresponds to a different detection mode out the four discrete modes of Sec. 3 We assume Δ⪡ω_ca. Typically Δ is a few cm⁻¹ whereas the resonant frequency ω_ca∼1000 cm⁻¹.

For ω>ω₀ the signal is obtained by taking Eq. 18 for S₄, replacing the discrete modes by integrals over the pulse band-shape, and identifying these as belonging to either the narrow or broad-band pulse, and then performing some ofthe integrations with the help of the δ-functions. The narrowness of the peak at ω₀ allows to make further approximations, leading to a simple form of the signals. Details of the derivation and a general expression are given in Appendix C. Assuming a very narrow band, Eqs. C1, C2 give

$$S\left(\omega >{\omega }_0\right)=S_{\text{par}}\left(\omega >{\omega }_0\right)+S_{\text{dis}}\left(\omega >{\omega }_0\right),$$ (29)

with

$$S_{\text{par}}\left(\omega {\omega }_0\right)\simeq \frac{1}{\pi {\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{cb}\mid }^2\left[\frac{P\left(c\right)}{\left({\omega }_0-{\omega }_{bc}\right)\left(2{\omega }_0-\omega -{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left({\omega }_0-{\omega }_{ba}\right)\left(\omega -{\omega }_{ba}\right)}\right]\mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left(2{\omega }_0-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\int d{\omega }_3{\delta }_{\Delta }\left({\omega }_3-{\omega }_0\right)\mathfrak{R}\frac{1}{\omega -{\omega }_3-{\omega }_{ca}+i\eta },$$ (30)

and

$$S_{\text{dis}}\left(\omega {\omega }_0\right)\simeq -\frac{1}{{\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{cb}\mid }^2\left[P\left(a\right)-P\left(c\right)\right]{\delta }_{\Delta }\left(\omega -{\omega }_{ca}-{\omega }_0\right)\left\{\frac{1}{{\left({\omega }_0-{\omega }_{bc}\right)}^2}{\mid \tilde{\epsilon }\left({\omega }_0+{\omega }_{ca}\right){\mathcal{E}}_0\mid }^2+\frac{1}{\left({\omega }_0-{\omega }_{ba}\right)\left({\omega }_0-{\omega }_{bc}\right)}\mathfrak{R}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_0-{\omega }_{ca}\right)\tilde{\epsilon }\left({\omega }_0+{\omega }_{ca}\right)\right]\right\}.$$ (31)

Equation 31 describes the Raman resonance for ω>ω₀ for a single vibrational mode and shows a single vibrational transition. Extension to the multimode case is straightforward and would result in additional Raman peaks. This should be contrasted with the parametric part of the signal, Eq. 30, which is not restricted to a narrow frequency range. Instead, it is given by the long range function of ω, ∫dω₃δ_Δ(ω₃−ω₀)R(ω−ω₃−ω_ca+iη)⁻¹. Additional vibrational or solvent modes would result in parametric contribution in all frequencies. The solvent contributions often dominate the parametric signal.

The derivation of the signal for ω<ω₀ is done along similar lines. The main difference is that the frequency of interest must be the lower one in a Raman pair, and therefore corresponding to S₃ instead of S₄. The derivation is sketched in Appendix C. For a very narrow band, Eqs. C3, C4 give

$$S\left(\omega <{\omega }_0\right)=S_{\text{par}}\left(\omega <{\omega }_0\right)+S_{\text{dis}}\left(\omega <{\omega }_0\right),$$ (32)

with

$$S_{\text{par}}\left(\omega <{\omega }_0\right)\simeq \frac{1}{\pi {\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{cb}\mid }^2\left[\frac{P\left(c\right)}{\left({\omega }_0-{\omega }_{bc}\right)\left(\omega -{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left({\omega }_0-{\omega }_{ba}\right)\left(2{\omega }_0-\omega -{\omega }_{ba}\right)}\right]\mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left(2{\omega }_0-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\int d{\omega }_4{\delta }_{\Delta }\left({\omega }_4-{\omega }_0\right)\mathfrak{R}\frac{1}{{\omega }_4-\omega -{\omega }_{ca}+i\eta },$$ (33)

and

$$S_{\text{dis}}\left(\omega <{\omega }_0\right)\simeq \frac{1}{{\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{cb}\mid }^2\left[P\left(a\right)-P\left(c\right)\right]{\delta }_{\Delta }\left(\omega +{\omega }_{ca}-{\omega }_0\right)\left\{\frac{1}{{\left({\omega }_0-{\omega }_{ba}\right)}^2}{\mid \tilde{\epsilon }\left({\omega }_0-{\omega }_{ca}\right){\mathcal{E}}_0\mid }^2+\frac{1}{\left({\omega }_0-{\omega }_{ba}\right)\left({\omega }_0-{\omega }_{bc}\right)}\mathfrak{R}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_0-{\omega }_{ca}\right)\tilde{\epsilon }\left({\omega }_0+{\omega }_{ca}\right)\right]\right\}.$$ (34)

Equation 34 shows a positive Raman resonance at the frequency ω=ω₀−ω_ca, as expected. Note that the Raman peak in Eq. 31 was negative.

Equations 31, 34 are quite similar, except for an overall sign. They only differ by two factors appearing in the pump-probe terms. Since the vibrational transition frequency is much smaller than electronic transition frequencies, ω_ca⪡ω_ba, it is justified to use ω₀−ω_ba≃ω₀−ω_ca as long as ω₀ is tuned far from the electronic resonances. This means that as long as the field amplitude $\tilde{\epsilon }$ varies slowly on the scale of vibrational transition frequencies, so that $\mid \tilde{\epsilon }\left({\omega }_0+{\omega }_{ca}\right)∕\tilde{\epsilon }\left({\omega }_0-{\omega }_{ca}\right)\mid -1⪡1$, the magnitude of the Raman peaks at ω>ω₀ and ω<ω₀ is essentially the same and the resonant part of the signal is antisymmetric around ω₀. The parametric contribution, in contrast, is not antisymmetric even when the above approximations are valid.

We now discuss the relative magnitudes of the parametric and dissipative contributions to the signal assuming that $\tilde{\epsilon }$ is constant in the frequency regime of interest. We can write

$$\mathfrak{R}\left({\mathcal{E}}_0^{\ast 2}{\tilde{\epsilon }}^2\right)={\mid {\mathcal{E}}_0\tilde{\epsilon }\mid }^2\text{cos}\varphi ,$$ (35)

$$\mathfrak{I}\left({\mathcal{E}}_0^{\ast 2}{\tilde{\epsilon }}^2\right)={\mid {\mathcal{E}}_0\tilde{\epsilon }\mid }^2\text{sin}\varphi .$$ (36)

The phase ϕ controls the magnitude of the parametric and dissipative processes. When ϕ=π∕2 or 3π∕2 the parametric part of the signal takes its maximal value, while it vanishes for ϕ=0 or π. In addition, the two dissipative terms in Eq. 31 or Eq. 34 interfere constructively when ϕ=0 and destructively when ϕ=π.

The narrow peak at ω₀ is assumed to have a Gaussian bandshape,

$${\delta }_{\Delta }\left(\omega \right)=\frac{1}{\sqrt{2\pi {\Delta }^2}}{e}^{-{\omega }^2∕2{\Delta }^2}.$$ (37)

The transition frequencies are chosen as ω_ba=20 000 cm⁻¹, ω_ca=1000 cm⁻¹, and ω_bc=19 000 cm⁻¹. The narrow peak is assumed to be centered at ω₀=10 000 cm⁻¹ and to have width of Δ=10 cm⁻¹. Finally, we take η=1 cm⁻¹.

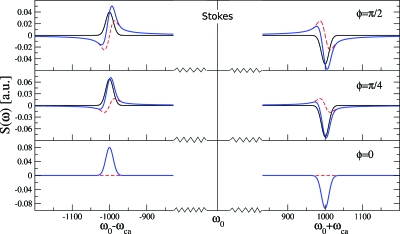
The different contributions to the signal in the vicinity of the Raman peaks (ω₀±ω_ca) are depicted in Fig. 4 for various values of ϕ, as indicated. The dissipative process presented in Fig. 4 is an a→c transition, namely, a Stokes process.

Figure 4.

The Stokes contributions to the CARS signal from processes starting at state a for various values of ϕ, as indicated. The dissipative part of the signal (solid-dark line) given by Eqs. 31, 34, the parametric part (dashed line) given by Eqs. 30, 33, and their sum (thick-blue line). The dissipative part of the signal corresponds to a Stokes process, namely, the transition a→c. The width of the signals is determined by Δ, the width of the narrow-band peak. Including the anti-Stokes contribution would reduce the signal without changing the lineshapes.

To understand the relative magnitude of the parametric and dissipative contributions, we note that the parametric signal is proportional to sin ϕ. By comparison, in each of the region of the Raman peaks depicted in Fig. 4, the dissipative part of the signal is proportional to A+B cos ϕ, with A,B of order unity. (The precise values are immaterial for the following qualitative argument.) Therefore, the parametric process give maximal contribution to the signal when ϕ=π∕2 [Fig. 4(i)] or ϕ=3π∕2. Interestingly, the dissipative process is composed of two contributions which can either interfere constructively (ϕ=0) or destructively (ϕ=π). At ϕ=0 [Fig. 4(iii)] only the dissipative signal contributes. Moreover, its contribution is relatively strong. At ϕ=π both the dissipative and dispersive contributions are suppressed.

The above considerations show that it is possible to control the relative contributions of dissipative and dispersive processes to the signal by tuning the phase difference between the narrow-band and broad-band pulses. It should be noted that the parametric contribution may include contributions from additional modes (not included in our simplified model). However, these are expected to be featureless on the scale of Δ, the width of the peaks.

DISCUSSION

Time-domain CARS measurements are traditionally interpreted in terms of vibrational coherences and represented by double sided Feynman diagrams for the density matrix in Liouville space. That representation allows to naturally incorporate vibrational dephasing. The close time path loop representation used here is more suitable for frequency domain measurements and for describing parametric processes. Vibrational dephasing (which is not discussed here) will require performing ensemble averages over products of amplitudes and is less transparent in this picture. Both representations are exact but highlight different aspects of the process.

In this paper we showed that the loops can be broken into products of two transition amplitudes. One represents forward propagations and its complex composite is time reversed. This representation was used to study the signal resulting from a combination of a narrow (picosecond) and a broad-band (femtosecond) pulse. Such measurements have a mixed time and frequency domain characteristics and can be described by both types of diagrams. We demonstrated that this representation naturally separates the contributions from dissipative and dispersive processes.

The dissipative signal consists of a series of (pairs of) Raman peaks with opposite signs. These peaks were shown to be antisymmetric around the narrow-band pulse. That is, equal in magnitude, but with opposite overall sign, independent of the overall phase difference between the pulses. The dispersive part of the signal breaks this symmetry.

It is interesting to compare the present dissection of the signal, which is based on transition amplitudes, and the method used in Ref. 6. For the part of the signal which is proportional to P(a), χ⁽³⁾ turns out to be equal to the bare transition amplitude ${\tilde{T}}_{aa}^{\left(4\right)}$ (frequency arguments omitted from brevity). In this case, using

$$\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{aa}^{\left(4\right)}\right)=\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }\right)\mathfrak{R}{\tilde{T}}_{aa}^{\left(4\right)}+\mathfrak{R}\left({\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }\right)\mathfrak{I}{\tilde{T}}_{aa}^{\left(4\right)},$$

and the optical theorem yields identical results to those of Ref. 6.

Interestingly, the part of χ⁽³⁾ proportional to P(c) is not equal to the bare transition amplitude ${\tilde{T}}_{cc}^{\left(4\right)}$. (More precisely, to its complex conjugate.) They differ by a term whose contribution to the (dissipative part of the) signal S₄ is

$$\delta \left({\omega }_3-{\omega }_{bc}\right)\mathfrak{R}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{\ast }{\mathcal{E}}_3{\mathcal{E}}_4^{\ast }{\tilde{T}}_{bc}^{\left(3\right)\ast }\left({\omega }_4,-{\omega }_1,{\omega }_2\right){\tilde{T}}_{bc}^{\left(1\right)}\left({\omega }_3\right)\right].$$

As long as the product of bare transition amplitudes is real both methods of dissecting the signal give the same results. This means that these recipes differ only when ${\tilde{T}}_{bc}^{\left(3\right)\ast }\left({\omega }_4,-{\omega }_1,{\omega }_2\right){\tilde{T}}_{bc}^{\left(1\right)}\left({\omega }_3\right)$ becomes imaginary, that is, when there is an additional resonance.

By inspecting Eq. 20 for the dissipative signal, written in terms of transition amplitudes, we can identify the molecular transitions involved. Focusing on the second order Raman transitions, we see that the ∼P(a) contribution includes a factor of ${\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right){\tilde{T}}_{ca}^{\left(2\right)\ast }\left(-{\omega }_3,{\omega }_4\right)+c.c$. This allows to associate this signal withinterference between two pump-probe processes, involving modes 1, 2 and 3, 4, respectively. The molecular transition generating this signal is from state a to c through b. This is obviously a Stokes process. This is amusing, as this is the resonant part of the so-called coherent anti-Stokes Raman spectroscopy. The “CARS” acronym is more suited for the description of the parametric part of the signal. Similar considerations show that the resonant Raman signal proportional to P(c) is an anti-Stokes process.

APPENDIX A: TRANSITION AMPLITUDES FOR THE MODEL OF FIGURE 1

The transition amplitudes required for the calculation of CARS signals for the level scheme of Fig. 1 are listed below:

$${\tilde{T}}_{ba}^{\left(1\right)}\left({\omega }_1\right)={\tilde{T}}_{ba}^{\left(1\right)}\left({\omega }_4\right)={\mu }_{ba},$$ (A1)

$${\tilde{T}}_{bc}^{\left(1\right)}\left({\omega }_2\right)={\tilde{T}}_{bc}^{\left(1\right)}\left({\omega }_3\right)={\mu }_{bc},$$ (A2)

$${\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_2,{\omega }_1\right)=\frac{{\mu }_{cb}{\mu }_{ba}}{{\omega }_1-{\omega }_{ba}+i\eta },$$ (A3)

$${\tilde{T}}_{ca}^{\left(2\right)}\left(-{\omega }_3,{\omega }_4\right)=\frac{{\mu }_{cb}{\mu }_{ba}}{{\omega }_4-{\omega }_{ba}+i\eta },$$ (A4)

$${\tilde{T}}_{ac}^{\left(2\right)}\left(-{\omega }_1,{\omega }_2\right)=\frac{{\mu }_{ab}{\mu }_{bc}}{{\omega }_2-{\omega }_{bc}+i\eta },$$ (A5)

$${\tilde{T}}_{ac}^{\left(2\right)}\left(-{\omega }_4,{\omega }_3\right)=\frac{{\mu }_{ab}{\mu }_{bc}}{{\omega }_3-{\omega }_{bc}+i\eta },$$ (A6)

$${\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_2,-{\omega }_3,{\omega }_4\right)=\frac{{\mu }_{bc}{\mu }_{cb}{\mu }_{ba}}{\left({\omega }_4-{\omega }_3-{\omega }_{ca}+i\eta \right)\left({\omega }_4-{\omega }_{ba}+i\eta \right)},$$ (A7)

$${\tilde{T}}_{ba}^{\left(3\right)}\left({\omega }_3,-{\omega }_2,{\omega }_1\right)=\frac{{\mu }_{bc}{\mu }_{cb}{\mu }_{ba}}{\left({\omega }_1-{\omega }_2-{\omega }_{ca}+i\eta \right)\left({\omega }_1-{\omega }_{ba}+i\eta \right)},$$ (A8)

$${\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_4,-{\omega }_1,{\omega }_2\right)=\frac{{\mu }_{ba}{\mu }_{ab}{\mu }_{bc}}{\left({\omega }_2-{\omega }_1-{\omega }_{ac}+i\eta \right)\left({\omega }_2-{\omega }_{bc}+i\eta \right)},$$ (A9)

$${\tilde{T}}_{bc}^{\left(3\right)}\left({\omega }_1,-{\omega }_4,{\omega }_3\right)=\frac{{\mu }_{ba}{\mu }_{ab}{\mu }_{bc}}{\left({\omega }_3-{\omega }_4-{\omega }_{ac}+i\eta \right)\left({\omega }_3-{\omega }_{bc}+i\eta \right)},$$ (A10)

$${\tilde{T}}_{aa}^{\left(4\right)}\left(-{\omega }_1,{\omega }_2,-{\omega }_3,{\omega }_4\right)=\frac{{\mid {\mu }_{cb}{\mu }_{ba}\mid }^2}{\left({\omega }_4-{\omega }_3+{\omega }_2-{\omega }_{ba}+i\eta \right)\left({\omega }_4-{\omega }_3-{\omega }_{ca}+i\eta \right)\left({\omega }_4-{\omega }_{ba}+i\eta \right)},$$ (A11)

$${\tilde{T}}_{aa}^{\left(4\right)}\left(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1\right)=\frac{{\mid {\mu }_{cb}{\mu }_{ba}\mid }^2}{\left({\omega }_1-{\omega }_2+{\omega }_3-{\omega }_{ba}+i\eta \right)\left({\omega }_1-{\omega }_2-{\omega }_{ca}+i\eta \right)\left({\omega }_1-{\omega }_{ba}+i\eta \right)},$$ (A12)

$${\tilde{T}}_{cc}^{\left(4\right)}\left(-{\omega }_3,{\omega }_4,-{\omega }_1,{\omega }_2\right)=\frac{{\mid {\mu }_{ab}{\mu }_{bc}\mid }^2}{\left({\omega }_2-{\omega }_1+{\omega }_4-{\omega }_{bc}+i\eta \right)\left({\omega }_2-{\omega }_1-{\omega }_{ac}+i\eta \right)\left({\omega }_2-{\omega }_{bc}+i\eta \right)},$$ (A13)

$${\tilde{T}}_{cc}^{\left(4\right)}\left(-{\omega }_2,{\omega }_1,-{\omega }_4,{\omega }_3\right)=\frac{{\mid {\mu }_{ab}{\mu }_{bc}\mid }^2}{\left({\omega }_3-{\omega }_4+{\omega }_1-{\omega }_{ba}+i\eta \right)\left({\omega }_3-{\omega }_4-{\omega }_{ac}+i\eta \right)\left({\omega }_3-{\omega }_{bc}+i\eta \right)}.$$ (A14)

APPENDIX B: SEPARATING THE DISSIPATIVE AND PARAMETRIC CONTRIBUTIONS

In this appendix we sketch the steps needed to separate the contribution to the optical signal S₄ which is proportional to $\mathfrak{I}\left[{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1)\right]$ into its resonant and parametric parts. [The first term in the right hand side of Eq. 14, which is written in terms of the transition amplitude A12.] While we discuss the signal S₄ and processes starting and ending at state a the same considerations would apply to other signals as well as for other diagonal transition amplitudes.

The transition amplitude above represents a four-photon process a→b→c→b→a where a photon from mode 1 is absorbed first, then a photon is emitted into mode 2, and a photon is absorbed from mode 3 and finally a photon is emitted into mode 4. The model discussed here allows also for a time reversed process which starts by absorbing a photon from mode 4, then emitting into mode 3, absorbing from mode 2 and finally emitting into mode 1. The contribution to the signal can be written in a form which takes into account both processes

$${\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1)=T_{\mathit{sym}}+T_{\mathit{as}},$$ (B1)

where

$$T_{\mathit{sym}}=\frac{1}{2}[{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1)+{\mathcal{E}}_1^{*}{\mathcal{E}}_2{\mathcal{E}}_3^{*}{\mathcal{E}}_4{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_1,{\omega }_2,-{\omega }_3,{\omega }_4)]$$ (B2)

$$T_{\mathit{as}}=\frac{1}{2}[{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1)-{\mathcal{E}}_1^{*}{\mathcal{E}}_2{\mathcal{E}}_3^{*}{\mathcal{E}}_4{\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_1,{\omega }_2,-{\omega }_3,{\omega }_4)].$$ (B3)

This separation is meaningful since T_sym and T_as turn out to correspond to resonant and parametric contributions to the signal.

Eq. 1 can be used to show that ${\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1)={\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_1,{\omega }_2,-{\omega }_3,{\omega }_4)$. This allows to write T_as as

$$T_{\mathit{as}}=i\mathfrak{I}\left({\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}\right){\tilde{T}}_{aa}^{\left(4\right)}(-{\omega }_4,{\omega }_3,-{\omega }_2,{\omega }_1),$$ (B4)

whose imaginary part appears in Eq. 19. This contribution is identified as a parametric process.

T_sym is the sum of the two possible pathways to make a fourth order transition starting and ending at a. It can be recasted as a contribution from resonant terms using the optical theorem

$$2\mathfrak{I}{T}_{\mathit{sym}}=-\pi [{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{ba}^{\left(1\right)}\left({\omega }_1\right){\tilde{T}}_{ba}^{\left(3\right)*}({\omega }_2,-{\omega }_3,{\omega }_4)+\mathit{c.c.}]\delta ({\omega }_1-{\omega }_{ba})-\pi [{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{ba}^{\left(3\right)}({\omega }_3,-{\omega }_2,{\omega }_1){\tilde{T}}_{ba}^{\left(1\right)*}\left({\omega }_4\right)+\mathit{c.c.}]\delta ({\omega }_4-{\omega }_{ba})-\pi [{\mathcal{E}}_1{\mathcal{E}}_2^{*}{\mathcal{E}}_3{\mathcal{E}}_4^{*}{\tilde{T}}_{ca}^{\left(2\right)}(-{\omega }_2,{\omega }_1){\tilde{T}}_{ca}^{\left(2\right)*}(-{\omega }_3,{\omega }_4)+\mathit{c.c.}]\delta ({\omega }_1-{\omega }_2-{\omega }_{ca}).$$ (B5)

Eq. B5 recast the imaginary part of a fourth order forward (a→a) scattering amplitude as a sum over all processes leaving the initial state.

Substitution of Eq. B4 [Eq. B5 respectively] in Eq. 14, with the help of Eq. B1, result in the ∼P(a) terms of Eq. 19 [Eq. 20]. The ∼P(c) terms are obtained by first bringing the term to a similar form and then repeating the above steps, as discussed in Sec. 3.

APPENDIX C: DERIVATION OF EQUATIONS 29, 30, 31, 32, 33, 34

In this appendix we derive the expressions for the dissipative and parametric components of the signal considered in Sec. 4. We start with the signal at ω>ω₀ obtained by two interactions with the narrow-band pulse and two interactions with the broad-band pulse. Note that more interactions with the narrow-band pulse can only affect the signal at frequencies which overlap with that pulse (or are very close to it), so we can discard this possibility. Contributions to the signal with either one, or no interactions with the narrow-band pulse may be readily separated out using their different functional dependence on E₀. The result of all these considerations is that the signal frequency must play the role of the larger frequency in a pair of modes, which can be chosen as ω₄, with ω₃ as a mode in the narrow-band pulse. As a result the signal in this case is described by S₄, Eq. 18. [Similarly, the case ω<ω₀ would lead us to identify the measured frequency as the lower frequency in the Raman pair and use Eq. 21 instead.]

We are yet to identify ω₁ and ω₂ with frequencies of the broad-band and narrow-band pulses. Since we consider the signal which scale as ${\mathcal{E}}_0^2$ one of these modes should be taken from the narrow-band pulse. This allows for two different contributions: (i) ω₂ in the narrow-band pulse, which forces ω₁≃ω>ω₀ and (ii) ω₁ in the narrow band pulse with ω₂<ω₀. The first contribution is a pump-probe process while in (ii) there are contributions from both sides of the narrow-band pulse.

This leads to

$$S_{\text{par}}\left(\omega {\omega }_0\right)=\frac{1}{\pi {\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{bc}\mid }^2\left\{\int d{\omega }_{2}d{\omega }_3{\mid {\mathcal{E}}_0\mid }^2{\delta }_{\Delta }\left({\omega }_3-{\omega }_0\right){\delta }_{\Delta }\left({\omega }_2-{\omega }_0\right)\mathfrak{I}\left[{\tilde{\epsilon }}^{\ast }\left({\omega }_2-{\omega }_3+\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\left[\frac{P\left(c\right)}{\left({\omega }_3-{\omega }_{bc}\right)\left({\omega }_2-{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left(\omega -{\omega }_3+{\omega }_2-{\omega }_{ba}\right)\left(\omega -{\omega }_{ba}\right)}\right]\mathfrak{R}\frac{1}{\omega -{\omega }_3-{\omega }_{ca}+i\eta }+\int d{\omega }_{1}d{\omega }_3{\delta }_{\Delta }\left({\omega }_1-{\omega }_0\right){\delta }_{\Delta }\left({\omega }_3-{\omega }_0\right)\mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_1+{\omega }_3-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\left[\frac{P\left(c\right)}{\left({\omega }_3-{\omega }_{bc}\right)\left({\omega }_1+{\omega }_3-\omega -{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left({\omega }_1-{\omega }_{ba}\right)\left(\omega -{\omega }_{ba}\right)}\right]\mathfrak{R}\frac{1}{\omega -{\omega }_3-{\omega }_{ca}+i\eta }\right\},$$ (C1)

and

$$S_{\text{dis}}\left(\omega {\omega }_0\right)=-\frac{1}{{\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{bc}\mid }^2\left[P\left(a\right)-P\left(c\right)\right]\left\{\int d{\omega }_2\frac{1}{\left({\omega }_2-{\omega }_{bc}\right)\left(\omega -{\omega }_{ba}\right)}\mathfrak{R}\left[{\tilde{\epsilon }}^{\ast }\left({\omega }_2+{\omega }_{ca}\right)\tilde{\epsilon }\left(\omega \right)\right]{\mid {\mathcal{E}}_0\mid }^2{\delta }_{\Delta }\left({\omega }_2-{\omega }_0\right){\delta }_{\Delta }\left(\omega -{\omega }_{ca}-{\omega }_0\right)+\int d{\omega }_1\frac{1}{\left({\omega }_1-{\omega }_{ba}\right)\left(\omega -{\omega }_{ba}\right)}\mathfrak{R}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_1-{\omega }_{ca}\right)\tilde{\epsilon }\left(\omega \right)\right]{\delta }_{\Delta }\left({\omega }_1-{\omega }_0\right){\delta }_{\Delta }\left(\omega -{\omega }_{ca}-{\omega }_0\right)\right\}.$$ (C2)

Equations C1, C2 are quite general. However, the presence of the broadened δ-function in Eqs. C1, C2, which is a result of the narrow-band pulse, allows to make further approximations.

We assume that the pulse envelope $\tilde{\epsilon }\left(\omega \right)$, as well as the nonresonant factors of the form (ω^′−ω_ba)⁻¹, arising from transitions to and from state b, are slowly varying functions of the frequency on the scale of Δ. We can then replace some of the frequency variables in the slowly varying factors, whose range is limited by the broadened δ-functions, with ω₀. For example, in the second factor of Eq. C1, $\mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_1+{\omega }_3-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\simeq \mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left(2{\omega }_0-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]$. Consistent application of this approximation simplifies the expressions considerably and allows to perform some of the remaining integrations.

This approximation also allows to neglect one of the parametric contributions as it is typically small when compared to the other. This results from the fact that $\tilde{\epsilon }\left({\omega }_2-{\omega }_3+\omega \right)\tilde{\epsilon }\left(\omega \right)\simeq {\mid \tilde{\epsilon }\left(\omega \right)\mid }^2$ which is real. Since it is the imaginary part of this factor which appears in Eq. C1, we conclude that this term is subdominant as long as ${\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left(2{\omega }_0-\omega \right)\tilde{\epsilon }\left(\omega \right)$ does not turn out to be a real number too. The latter case would require a more careful analysis. Since it is not a typical case, we do not consider it here. Application of the narrow pulse approximation results in Eqs. 30, 31.

The signal for ω<ω₀ can be calculated similarly. Here ω must correspond to the lower frequency in a Raman pair. As a result it should be identified with ω₃ of Sec. 3, and S₃ [Eq. 21] should serve as a starting point for the calculation. Repeating the above steps, we find

$$S_{\text{par}}\left(\omega <{\omega }_0\right)=\frac{1}{\pi {\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{bc}\mid }^2\left\{\int d{\omega }_{1}d{\omega }_4{\mid {\mathcal{E}}_0\mid }^2{\delta }_{\Delta }\left({\omega }_1-{\omega }_0\right){\delta }_{\Delta }\left({\omega }_4-{\omega }_0\right)\mathfrak{I}\left[{\tilde{\epsilon }}^{\ast }\left({\omega }_1+\omega -{\omega }_4\right)\tilde{\epsilon }\left(\omega \right)\right]\left[\frac{P\left(c\right)}{\left({\omega }_1+\omega -{\omega }_4-{\omega }_{bc}\right)\left(\omega -{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left({\omega }_4-{\omega }_{ba}\right)\left({\omega }_1-{\omega }_{ba}\right)}\right]\mathfrak{R}\frac{1}{{\omega }_4-\omega -{\omega }_{ca}+i\eta }+\int d{\omega }_{2}d{\omega }_4{\delta }_{\Delta }\left({\omega }_4-{\omega }_0\right){\delta }_{\Delta }\left({\omega }_2-{\omega }_0\right)\mathfrak{I}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_2+{\omega }_4-\omega \right)\tilde{\epsilon }\left(\omega \right)\right]\left[\frac{P\left(c\right)}{\left({\omega }_2-{\omega }_{bc}\right)\left(\omega -{\omega }_{bc}\right)}-\frac{P\left(a\right)}{\left({\omega }_4-{\omega }_{ba}\right)\left({\omega }_2+{\omega }_4-\omega -{\omega }_{ba}\right)}\right]\mathfrak{R}\frac{1}{{\omega }_4-\omega -{\omega }_{ca}+i\eta }\right\},$$ (C3)

and

$$S_{\text{dis}}\left(\omega <{\omega }_0\right)=\frac{1}{{\hslash }^4}{\mid {\mu }_{ba}\mid }^2{\mid {\mu }_{bc}\mid }^2\left[P\left(a\right)-P\left(c\right)\right]\left\{\int d{\omega }_1\frac{1}{\left({\omega }_1-{\omega }_{ba}\right)\left(\omega -{\omega }_{bc}\right)}\mathfrak{R}\left[{\tilde{\epsilon }}^{\ast }\left({\omega }_1-{\omega }_{ca}\right)\tilde{\epsilon }\left(\omega \right)\right]{\mid {\mathcal{E}}_0\mid }^2{\delta }_{\Delta }\left({\omega }_1-{\omega }_0\right){\delta }_{\Delta }\left(\omega +{\omega }_{ca}-{\omega }_0\right)+\int d{\omega }_2\frac{1}{\left(\omega -{\omega }_{bc}\right)\left({\omega }_2-{\omega }_{bc}\right)}\mathfrak{R}\left[{\mathcal{E}}_0^{\ast 2}\tilde{\epsilon }\left({\omega }_2+{\omega }_{ca}\right)\tilde{\epsilon }\left(\omega \right)\right]{\delta }_{\Delta }\left({\omega }_2-{\omega }_0\right){\delta }_{\Delta }\left(\omega +{\omega }_{ca}-{\omega }_0\right)\right\}.$$ (C4)

Using the narrowness of δ_Δ(ω) to make further approximations results in Eqs. 33, 34.