Simulation of large x-ray fields using independently measured source and geometry details

Abstract

Purpose: Obtain an accurate simulation of the dose from the 6 and 18 MV x-ray beams from a Siemens Oncor linear accelerator by comparing simulation to measurement. Constrain the simulation by independently determining parameters of the treatment head and incident beam, in particular, the energy and spot size.

Methods: Measurements were done with the treatment head in three different configurations: (1) The clinical configuration, (2) the flattening filter removed, and (3) the target and flattening filter removed. Parameters of the incident beam and treatment head were measured directly. Incident beam energy and spectral width were determined from the percent-depth ionization of the raw beam (as described previously), spot size was determined using a spot camera, and the densities of the flattening filters were determined by weighing them. Simulations were done with EGSnrc∕BEAMnrc code. An asymmetric simulation was used, including offsets of the spot, primary collimator, and flattening filter from the collimator rotation axis.

Results: Agreement between measurement and simulation was obtained to the least restrictive of 1% or 1 mm at 6 MV, both with and without the flattening filter in place, except for the buildup region. At 18 MV, the agreement was 1.5%∕1.5 mm with the flattening filter in place and 1%∕1 mm with it removed, except for in the buildup region. In the buildup region, the discrepancy was 2%∕2 mm at 18 MV and 1.5%∕1.5 mm at 6 MV with the flattening filter either removed or in place. The methodology for measuring the source and geometry parameters for the treatment head simulation is described. Except to determine the density of the flattening filter, no physical modification of the treatment head is necessary to obtain those parameters. In particular, the flattening filter does not need to be removed as was done in this work.

Conclusions: Good agreement between measured and simulated dose distributions was obtained, even in the buildup region. The simulation was tightly constrained by independent measurements of parameters of the incident beam and treatment head. The method of obtaining the input parameters is described, and can be carried out on a clinical linear accelerator.

INTRODUCTION

Traditional dose calculation algorithms yield doses from megavoltage photon beams that may be in clinically significant disagreement with measurement, for example, in inhomogeneous media.¹ With the increasing use of precision dose delivery techniques and image guided radiotherapy to improve the accuracy of patient setup and account for target motion, this error can become a dominant source of error in treatment planning. Dose calculation with Monte Carlo simulation in principle can reduce this error,² but there have been two hurdles to widespread adoption of Monte Carlo treatment planning in the clinic. Historically, the slow speed of the calculation was a major obstacle, but with the development of faster Monte Carlo codes and faster hardware, the calculation speed is now less of an issue. Commissioning a Monte Carlo treatment planning system remains a difficulty. In order to use Monte Carlo codes to calculate the dose to a patient, knowledge of the fluence map at the exit of the treatment head is required.

The most accurate and detailed method of obtaining the fluence for Monte Carlo-based treatment planning is to simulate the treatment head with Monte Carlo code.² In this method, simulation details are adjusted to achieve a good match between calculation and measured dose distributions and other quantities. Difficulties with this method are that the details of the treatment head are typically proprietary, and even if they are provided by the manufacturer, are subject to manufacturing tolerance, adjustment following installation [e.g., Siemens linear accelerators (linacs) are often tuned to give desired dose distributions], and even errors in the values provided.^{3, 4} Parameters such as the energy of the incident beam and its lateral size are typically either nominal or not specified. Furthermore, certain dose measurements have similar sensitivity to changes in different parameters, making it impossible to determine the correct parameter to adjust to match the measurement. For example, lowering the energy of the beam, decreasing the lateral size (spot size), and increasing the separation between the target and flattening filter all increase the off-axis ratio. Previous works^{5, 6} have taken the energy and spot size to be free parameters, allowing both to vary to obtain the best match to measured dose distributions. The use of redundant free parameters makes it difficult to ensure that source and geometry details used in the simulation are accurate.

In this paper, the treatment head of a Siemens Oncor linac operating in x-ray mode was simulated. Key parameters of the source and treatment head were determined independently of each other. This included parameters to which the dose distribution is sensitive, namely, the energy of the incident beam (determined previously⁷), its lateral size, and the flattening filter density and position. Measurements and simulations were done with the flattening filter both in and removed.⁸ Jaws and multileaf collimator (MLC) were set to their widest setting of 40×40 cm² (open field) to reduce scatter. The simulated dose distributions in water were compared to measured values. Aside from the removal of the flattening filter, which is not required to determine the linac parameters, the methods presented here may be followed without mechanical modification of the linac, and hence are readily applicable in the clinic.

METHOD AND MATERIALS

Measurement of dose distributions

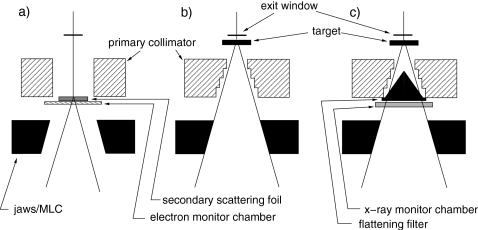
A Siemens Oncor linac, not used for clinical treatment, operating at nominal energies of 6 and 18 MV, was used. The jaws and MLC were opened to their largest setting, 40×40 cm². The linac was operated in three configurations, shown in Fig. 1. One was with the treatment head in the clinical configuration, and the beam tuned to give dose distributions matching those of the clinical linacs of the same model at our institution. Another configuration was with the flattening filters, compensator (18 MV only), and monitor chamber removed.⁸ The linac was run using the same beam parameters (energy, beam peaking, and dose per pulse) as for the full clinical beam. It was run in open loop (no dose rate feedback loop) with no monitor chamber. At 18 MV, additional beam steering is provided that is changed dynamically with beam angle, based on the readings of the monitor chamber. With no monitor chamber in the beam, the dynamic steering gain was adjusted so that the steering current was the same as it was for the clinical beam. The dynamic steering current was monitored at the console during the measurements and observed to be constant at 110 mA, with short-term fluctuations in the measured value of around 5 mA that had negligible effect on dose distributions.

Figure 1.

Configurations of the treatment head. (a) Electron mode with no foil in the primary foil slot. (a) X-ray mode with the flattening filters, 18 MV compensator, and monitor chamber removed. (c) Full clinical x-ray mode.

A third configuration, with the target and flattening filter removed, was used to determine the energy of the primary beam, as reported earlier.⁷ To do so easily, the linac was run in electron mode with no primary scattering foil in the beam. The only components in the beam path were the exit window, secondary electron scattering foil, and electron monitor chamber. This configuration was set entirely via the console, and did not require repositioning of any treatment head components. Beam parameters were set to their x-ray values, except beam current (INJI) and pulse frequency (PRFP), which were lowered to avoid recombination effects in the ion chamber. Note that these beams are referred to here by their nominal accelerating voltages of 6 and 18 MV, even though they were electron beams.

Dose was measured with an ion chamber in a Wellhöfer WP700 water tank. A Scanditronix–Wellhöfer CC13 with an inside diameter of 6 mm was used for lateral profile scanning and as the reference detector. The effective points of measurement were taken as the scanning software default values of 1.8 and 2.0 mm above the center of the chamber for 6 and 18 MV, respectively, the 0.2 mm difference at 18 MV from the value in the TG-51 protocol⁹ value making negligible difference for the lateral profiles. Following the recommendation of McEwen et al.,¹⁰ percent-depth doses were measured with a Roos parallel plate ion chamber (PTW N34001), to take advantage of its flat front surface and well-defined effective point of measurement. Based on the manufacturer’s specification of the electron density of the front wall and the ICRU-37 (Ref. ¹¹) stopping powers of the wall material, the effective point of measurement of the Roos chamber was taken to be 1.15 mm below the top surface of the chamber. Accuracy and positioning reproducibility for the depth dose measurements was within 0.3 mm.⁷ The water was at 100 cm from the nominal source position (SSD), and the scan depth was at least 40 cm. The chamber carriage was aligned with the water surface at the four corners within 0.5 mm.

Horizontal dose profiles were measured inplane (in the direction of the waveguide), crossplane (perpendicular to the direction of the waveguide), and both diagonal directions, with the collimator at 0°. Diagonal profiles were measured with secondary collimators fully open to obtain dose at the maximum off-axis distance inside the field and to determine the position of the primary collimator, which collimates the beam to 50 cm diameter at 100 cm from the source.¹²

For the purposes of comparison with simulations, measured profiles were averaged over the length of equal-sized bins. Bin sizes were the same as for the simulations, and were 0.2 cm along the beam axis in the buildup region and 0.5 cm elsewhere.

DETERMINATION OF LINAC PARAMETERS

Collimator rotation axis

The origin of the detector coordinate system in the plane perpendicular to the beam axis was on the collimator rotation axis. The inplane and crossplane coordinates of the collimator rotation axis were found by scanning the detector under the distal scraper of the 10×10 cm² electron applicator with the collimator at 0° and 180°. The collimator rotation axis is at the midpoint of the penumbrae formed by the same part of the scraper for the two opposite collimator rotations. The detector was scanned in air at 97 cm SSD, 2 cm below the scraper, in the inplane and crossplane directions at both collimator angles. With the flattening filter in, the axis of rotation was determined using the 12 MeV electron beam. With the flattening filter removed, the 6 MV x-ray beam was used (still with the applicator) because with the x-ray monitor chamber removed and placed on top of a jaw, linac components may have been damaged if the linac were switched to electron mode.

Spot size

The lateral size of the primary beam, or spot size, was determined using a spot camera¹³ consisting of alternating layers of lead and Mylar. The average layer thickness was 0.28 mm, and the length of the camera was 20 cm, such that only x rays traveling nearly parallel to the layers pass through the camera. The camera was placed on the block tray, with its proximal end 36 cm from the target. A diode, oriented such that the normal to the surface of the diode was perpendicular to both the beam axis and the slits, was scanned in air below the camera. A second diode placed below the camera was used as a reference. A Gaussian function was fit to the measured profile to extract the width.

To account for the broadening of the measured profile with distance from the target, Lutz et al.¹³ considered a point source and a single slit of width s. X rays from a point source may travel in a straight line through the slit when the slit, as measured from its center, is a distance b from the beam axis, where

$$b=s\frac{d_1+d_2+d_3}{d_2}-\frac{s}{2}$$ (1)

and d₁, d₂, and d₃ are the distance between source and camera, the length of camera, and the distance between camera and detector. The geometry is shown in the inset to Fig. 2. Therefore, a broadening proportional to the target-detector distance is expected. In general, the width of the measured profile is given by the convolution of the spot size and the broadening function. For a Gaussian spot profile, the measured profile width w may be approximated by

$$w^2=w_s^2+b^2\approx w_s^2+a^2{\left(d_1+d_3\right)}^2,$$ (2)

where w_s is the spot size and a is approximately s∕d₂.

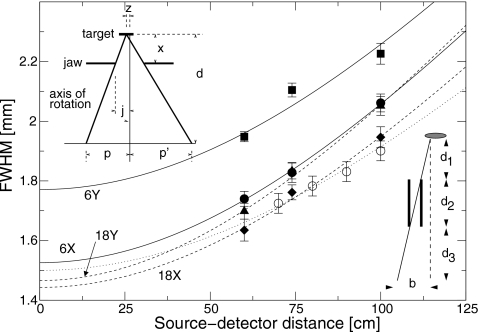
Figure 2.

Full width at half maximum (FWHM) of profile under the spot size camera as a function of distance between the target and the detector. Squares: 6 MV, inplane; circles: 6 MV, crossplane; triangles: 18 MV, inplane; diamonds: 18 MV, crossplane. Open circles are simulated results using a 14 MeV photon beam with a spot size of 1.5 mm FWHM. Lines are fits to Eq. 2. Solid lines, 6 MV; dashed lines, 18 MV; dotted line, simulated results. The left inset shows a schematic drawing of a single slit of the spot camera. The right inset shows the variables used in the determination of the position of the beam spot at the x-ray target.

In order to verify Eq. 2, the spot camera was simulated using the EGSnrc∕BEAMnrc Monte Carlo code (described below). A component module was written to model the spot camera. The phase-space was recorded at the exit of the spot camera, and 14 MeV photons were transported various distances in vacuum from the camera. The photons were binned by position, and a Gaussian was fit to the distribution. Results for a simulated camera with a geometry similar to the actual camera are shown in Fig. 2. A source of x rays with a Gaussian profile of FWHM 1.5 mm, and a Gaussian distribution of angles with FWHM of 3°, was used. The profile widths were fit to Eq. 2, yielding a spot size of 1.50±0.01 mm, in agreement with the spot size used in the simulation. This confirmed that the actual spot size is determined accurately from the measurements using Eq. 2.

The spot camera was characterized by measuring profile widths for different target-detector distances. A clinical Siemens Oncor linac, tuned such that the dose distributions matched those of the linac used in the present study to within 1%, was used. The spot camera was placed on the block tray, and the detector was scanned at 60, 74, and 100 cm from the source. Profile widths for the 6 and 18 MV inplane and crossplane directions are shown in Fig. 2. The broadening coefficient [a in Eq. 2] was found to be 0.0139±0.0005, with the uncertainty representing the standard deviation of the four measurements.

For the linac on which the dose measurements presented here were done, the spot profiles were measured at 100 cm from the source. The measured profile width and broadening equation above were used to deduce the spot size at the target.

Primary beam energy, spectral distribution, and beam divergence

The method used to determine the primary beam energy, spectral distribution, and beam divergence was published previously.⁷ The target, flattening filter, compensator, and monitor chamber were removed from the treatment head. This was accomplished by running the linac in electron mode and selecting the empty primary foil slot via the console. Dose distributions in a water phantom were measured. The energy and width of the Gaussian energy distribution used for the incident beam were varied in the simulations to match measurement. Determination of the beam divergence required comparisons of measurement and simulation with the target reinserted.

Spot position

The position of the primary spot was determined using two methods. One method of determining the spot position used the position of the primary collimator, determined from photographs (described below). The penumbrae of the diagonal scans were formed by the primary collimator. The spot position was chosen such that the simulated positions of the penumbrae matched the measured values. The second method used the penumbra of a jaw, measured with the jaw positioned at different collimator angles. The measurement is shown schematically in Fig. 2 (where a thin, totally absorbing jaw is assumed). The jaw was a distance x from the target, and the edge of the jaw was a distance j from the collimator rotation axis. Let the spot be offset from the collimator rotation axis by a distance z as shown. A CC13 chamber was scanned in air a distance d=97 cm from the target. Neglecting scatter, the penumbrae for the two collimator rotations were distance p and p^′ from the collimator rotation axis. Consideration of similar triangles leads to an equation for z,

$$z=\frac{p^{\prime }-p}{2\left(\frac{d}{x}-1\right)}.$$ (3)

Points p and p^′ were taken to be where the dose dropped to 50% of its value on the central axis, and x was taken to be the midpoint of the jaw or MLC. The measurement was done using both banks of each of the jaws and MLC, for a total of four independent measurements of the spot position in each of the inplane and crossplane directions. The field size in the direction of the scan was 5 cm. In the perpendicular direction, it was set to 40 cm to reduce scatter. The spot position in each plane was determined as the average of the four measurements.

The second method of determining the spot position used the position of the primary collimator, determined from photographs (described below). The penumbrae of the diagonal scans were formed by the primary collimator. The spot position was chosen such that the simulated positions of the penumbrae matched the measured values.

Beam angle

The angle of the incident beam in the inplane and crossplane directions was determined from the position of the spot and the position of the bremsstrahlung peak, measured with the flattening filter removed. The bremsstrahlung peak was measured in water, with SSD 100 cm, at depths ranging from 1.5 to 40 cm. A polynomial consisting of quadratic and fourth-power terms was fit to the central region of the peak to determine the peak position. The beam angle (in radians) was taken to be the difference between the spot position and the bremsstrahlung peak position linearly extrapolated to 97 cm from the nominal source position, divided by the distance between the two along the beam axis.

Treatment head geometry

The treatment head geometry was based on the manufacturer’s specification. Several of the parameters were determined or verified independently. The thickness of the exit window was determined earlier,⁷ based on measurements of the profile with only the exit window in the beam path.

The positions of the primary collimators (one for 6 MV and one for 18 MV) along the beam axis were taken to be as specified by the manufacturer. The specification was verified by direct measurement to within 2 mm with the flattening filters and monitor chamber removed. The offsets of the primary collimators from the collimator rotation axis were determined by two methods. One method was to take digital photographs with the flattening filters and monitor chamber removed. Crosshairs were attached to the edge of the jaws closest to the target, within 0.5 mm of the collimator rotation axis. A digital camera was mounted on a tripod on the treatment couch, with the lens 86 cm from the target. The camera was positioned on the beam axis using the room lasers. Photographs were taken with the collimator, and thus the crosshairs, at the four cardinal angles. Both the camera and the primary collimator remained in the same position for each photograph. The collimator rotation axis was determined as the average position of the crosshairs in the four photographs, and the position of the primary collimator was determined relative to the collimator rotation axis. The second method used the spot position, as determined from the penumbra cast by the jaw. The penumbrae of the diagonal scans are cast by the primary collimator. Measurement of the positions of the penumbrae allowed determination of the primary collimator position.

The target position along the beam axis was determined from the width of the diagonal profiles. Because the field is collimated in the diagonal directions by the primary collimator when the jaws are wide open,¹² the field size depends on the distance between the target and the primary collimator. With the position of the primary collimator determined as described above, the remaining variable to obtain the measured width of the diagonal profiles was the position of the target. The target positions that minimized the discrepancies between measured and simulated penumbra in the diagonal profiles were chosen. The target position was allowed to be different with the flattening filters in and out, and for the different energies. The distance from the target to the primary collimator was verified to within 2 mm by direct measurement. The target material was simulated as specified.¹⁴

The position of the flattening filter along the beam axis relative to the primary collimator was taken to be as specified. The flattening filter was bolted to the primary collimator with a centering ring with a beveled edge, which allows it to be moved in the lateral directions but not along the beam axis. The position was verified within 2 mm by direct measurement. The lateral positions in the simulations were adjusted until both the position of the dips in the center of the profiles and the asymmetry matched the measured values. The position of the 6 MV flattening filter was compared to that obtained from digital pictures, using the same method as for the primary collimator. The position of the 18 MV flattening filter was not determined from photographs because the compensator blocked the view of the flattening filter. Removing the compensator would likely have changed the position of the flattening filter because both the compensator and flattening filter were attached to the primary collimator with the same centering ring and bolts.

The material of the flattening filter was specified by the manufacturer, according to an ASTM specification. However, the density of the type of steel used was not given in that specification. To determine the density, the flattening filters were weighed and their volumes determined using CAD software and the engineering drawings. Because of the irregular shape of the flattening filters, their volumes were not easily measured. The relatively large diameters and small volumes made the submersion technique imprecise. Instead, the measured flattening filter dimensions were used as a second check on the manufacturer’s specification. The densities of the two flattening filters were found to be 7.84 g∕cm³, a reasonable value for the material.

At 18 MV, there is a compensator downstream of the flattening filter. The thickness of the compensator changes in the plane of the waveguide to compensate for the asymmetric incident beam. This compensator was simulated as a flat slab and the incident beam used in the simulations was symmetric. This component had the same density as the flattening filters, 7.84 g∕cm³, as verified by direct measurement.

The monitor chamber, 18 MV absorber, jaws, and MLC were simulated as specified by the manufacturer. Positions of the jaws and MLC were set to match the inplane and crossplane profile edges. Because these components move in an arc, the vertical positions of these components were determined using the measured lateral positions and a spreadsheet provided by the manufacturer.

SIMULATION

Simulations of the treatment head were done using the EGSnrc (version 1.40 of July 24, 2008) (Ref. ¹⁵) and BEAMnrc code (version 1.104 of July 24, 2008).¹⁶ The water phantom was simulated using the EGS user code MCRTP.¹⁷ A water phantom of size 60×60×60 cm³ and voxel size 0.5×0.5×0.5 cm³ was used, except in the first 3 cm, where the voxel size along the beam axis was 0.2 cm. To improve statistical uncertainty, simulated results were averaged over three voxels in each of the two directions perpendicular to the profile or percent-depth dose curve. Transport parameters were based on those of Refs. ^{18, 8} except that uniform bremsstrahlung splitting with a factor of 100 was used, and Russian roulette of secondary particles was on. Triplet production was on.

The BEAMnrc code had previously been modified locally to allow for a horizontal translation of component modules.¹⁹ Further modifications were made here to allow for more asymmetry. Source 19, which models a beam with an elliptical Gaussian profile, was modified to allow the incident beam to be offset from the axis of rotation. The BEAMnrc component module used for simulation of the flattening filter and primary collimator, FLATFILT, was modified to allow the lateral position of the flattening filter to be offset from the primary collimator. This was required because the flattening filters in the linac could be moved in the lateral direction relative to the primary collimator (on Siemens linacs, the flattening filter is inside the primary collimator).

Simulated percent-depth dose curves were normalized such that the dose at 10 cm depth agreed with the measured dose.

RESULTS

Simulation inputs

The values of the parameters used in the simulation are given in Table 1. The energies of the incident beams, their spectral widths, and the beam divergences were determined previously.⁷ The energies of the 6 and 18 MV beams were found to be 6.51±0.15 and 13.94±0.2 MeV, respectively, with only the exit window in the beam path. The full widths of the spectra at half maximum were 20±4% and 13±4% at 6 and 18 MV, respectively. Measurements and simulations in configuration A of Fig. 1 (with no target or flattening filter), using the above parameters of the incident beam, were compared. For the nominally 6 MV beam, the simulations agreed with measurement, but at 18 MV, the measured depth at which the ionization fell to 50% of its maximum value I₅₀ was 0.07 cm greater than the simulated I₅₀. This difference is approximately equal to the uncertainty in the measurement, taking into account the uncertainty in detector positioning, stopping power of water, and uncertainty of the effective point of measurement for the Roos chamber in electron beams.²⁰ The value of 14.12 MeV, determined with the secondary foil in the beam path, was used in the simulations. This was reasonable because the measurements of the energy with the secondary foil in place were made concurrently with the measurements on the photon beams, whereas the measurements with only the exit window in the beam path were made several months previously.

Table 1.

Parameters of the treatment head and the incident beam used in the simulations. X and Y denote the crossplane and inplane directions, respectively. Negative Y is away from the gun, and negative X is to the left when facing the gantry. Spot positions, primary collimator and flattening filter lateral positions, and jaw (Y) and MLC (X) positions are relative to the collimator rotation axis, and are the displacement of the object. The jaw and MLC positions are the positions extrapolated to 100 cm SSD. Target position is relative to the manufacturer’s specification. Where two uncertainties are listed, the first applies to the 6 MV beam and the second to the 18 MV beam.

Nominal energy	6 (FF out)		6 (FF in)		18 (FF out)		18 (FF in)		Uncertainty
Plane	X	Y	X	Y	X	Y	X	Y
Energy (MeV)	6.51				14.12				0.15∕0.2
Spectral width (FWHM) (%)	20				13.2				4
Divergence (deg)	0				0				0.2∕0.1
Spot size (FWHM) (mm)	1.4	2.1	1.4	2.1	1.2	1.6	1.2	1.6	0.1
Beam angle (mrad)	1.0	−1.0	0.8	−1.1	0.8	0.7	0.8	0.6	0.5
Spot position (mm)	−0.1	0.5	0.0	0.6	0.0	0.3	0.0	0.4	0.5
Target position along beam axis (mm)	−0.4		−0.5		−0.3		−0.4		0.1
Primary collimator lateral position (mm)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.5
Flattening filter lateral position (mm)	⋯	⋯	0.0	0.6	⋯	⋯	0.1	0.4	0.1
Flattening filter density (g∕cm3)	7.84				7.84				⋯
Jaw∕MLC positions (cm)	−20.1	−20.0	−20.1	−20.1	−20.0	−19.9	−20.0	−19.9	0.1
Jaw∕MLC positions (cm)	20.1	19.9	20.1	19.8	20.0	19.8	20.0	19.8	0.1

The thickness of the exit window and the beam divergences were determined earlier,⁷ and the results summarized here. With only the exit window in the beam, simulated lateral profiles that used the manufacturer-specified exit window and zero beam divergence were 2–3 cm narrower than measured. Good matches could be obtained by increasing the exit window thickness by up to 100%, or by using a beam divergence of 2°–3°. Such large divergences are unphysical, and led to incorrect profiles with the target in place. Comparisons of measurement to simulation with the target in place led to determination of beam divergences of 0.0°±0.2° at 6 MV and 0.0°±0.1° at 18 MV. It was found that increasing the thickness of the cooling water layer by 100% would reproduce measured profiles. This increase might result from the inner metal layer bowing into the evacuated waveguide.

With the spot camera in place, profile widths were measured at 100 cm from the target and found to be 2.0 and 2.5 mm for the 6 MV crossplane and inplane profiles, and 1.8 and 2.1 mm for the 18 MV crossplane and inplane profiles. Correcting for the broadening of the beam with distance from the target yielded spot sizes of 1.4 and 2.1 mm for the crossplane and inplane directions of the 6 MV beam, and 1.2 and 1.6 mm for the crossplane and inplane directions of the 18 MV beam. These values were twice as large as those found by Jaffray et al.²¹ for a Siemens KD2 linac, but the difference in size width between the inplane and crossplane directions was similar. This is reasonable, as the spot size is expected to be different for different machines. There was good agreement between simulated and measured profile widths with the spot camera in the beam, showing that the uncertainty of the measurement was given by the uncertainties in the measured profile widths and the fit. This uncertainty was 0.1 mm.

Determination of the spot positions and primary collimator lateral positions were related. Using the penumbra of a jaw or MLC, the spot position was determined to be 1.0±0.3 mm from the collimator rotation axis in the inplane direction, and −0.2±0.3 mm in the crossplane direction, for both energies. The uncertainty is the standard deviation of multiple measurements, done on different days and with different water tank rotations. One source of uncertainty in the measured spot position was the uncertainty in the distance between the target and the effective jaw or MLC. The jaws and MLC are nearly 8 cm thick, and the position along this thickness that corresponded to the 50% position in the penumbra was uncertain and depended on spot position. The effective position of the jaw or MLC was taken to be the midpoint of the jaw or MLC. A 4 cm uncertainty in the effective jaw∕MLC position led to a 10% uncertainty in the spot position, which was small compared the variation from measurement to measurement. With these spot positions and the measured penumbrae of the diagonal scans, the primary collimator was 0.5±0.3 mm from the collimator rotation axis in the inplane direction, and −0.2±0.3 mm in the crossplane direction.

By taking photographs at various collimator rotations, the primary collimator was determined to be 0.0±0.5 mm from the collimator rotation axis in both the inplane and crossplane directions. The uncertainty was dominated by the uncertainty in the angle of the camera, which was estimated using the position of the primary collimator relative to the center of the photograph. The center of the primary collimator was within 40 pixels of the center of the photographs, which corresponded to 4 mm. The distance between the camera and the crosshairs was eight times the distance between the crosshairs and the primary collimator. Assuming the displacement of center of the primary collimator in the photograph results from a tilt in the camera, as opposed to a shift, gives an error of 0.5 mm in the determination of the position of the collimator position. These positions of the primary collimator, and the measured penumbrae of the diagonal scans, yielded spot positions 0.0±0.5 mm from the collimator rotation axis in the crossplane direction, at both energies. In the inplane direction, the spots were between 0.3 and 0.6±0.5 mm from the collimator rotation axis at both energies. The uncertainties follow from the uncertainty in the position of the primary collimator.

The two methods of determining the spot position and primary collimator position resulted in spot and primary collimator positions, which are within the combined uncertainties of each other. In the crossplane direction, both the spot and the primary collimator were within 0.5 mm of the collimator rotation axis. In the inplane direction, the spot positions were between 0.3 and 1.0 mm from the collimator rotation axis, toward the gantry, depending on the method of measurement. The sum of the uncertainties of the two methods was 0.8 mm, greater than the difference between the values. Furthermore, using either of the two sets of values in the simulations did not change the simulated results. In Table 1, parameter values determined from the photographs of the primary collimator are tabulated.

The measured beam angles were up to 1.1 mrad in absolute value, which was at 6 MV in the inplane direction. At 18 MV, the angle in the inplane direction was 0.6 mrad. In the crossplane direction, the angles were near 0.8 mrad. The uncertainty in determining the beam angle resulted from the uncertainty in determination of the spot position, as described above. The uncertainty in determination of the bremsstrahlung peak was less than 0.5 mm, as verified by measuring at different distances from the target. These uncertainties in position corresponded to an uncertainty in the angle of 0.5 mrad. These angles corresponded to a maximum of a 1.0 mm shift in the bremsstrahlung peak at 100 cm from the target, relative to the spot position. The beam angles and spot positions correspond to a bremsstrahlung peak at 100 cm from the target within 1 mm of the collimator rotation axis, including the crossplane direction.

The target position along the beam axis was found to vary between 0.3 and 0.5 mm closer to the exit window than the manufacturer’s specification, even though it was the same target for all beams. The difference from the specification is reasonable because the target can be easily moved by 1 mm. The difference for the different beam energies is physically possible as different primary collimators are used for the two energies.

The positions of the flattening filters were found to be within 0.06 mm of the spot position. This is a result of the profiles having an asymmetry (difference in doses at 10 cm off-axis in either direction) of less than 0.8%.

The distance of the secondary collimators from the collimator rotation axis, projected to 100 cm SSD, were up to 2 mm different from their nominal settings of 20 cm. This machine was not used clinically, therefore, a 2 mm error in secondary collimator position was acceptable. The individual MLC leaves were aligned to 1 mm, verified with the light field. The positions with the flattening filters in and out and for the two energies were the same to within 1.5 mm, showing that the positions were repeatable. As with the determination of the primary collimator position, the accurate determination of the position of the jaws and MLC depended on an accurate determination of the spot position.

DOSE DISTRIBUTIONS

6 MV

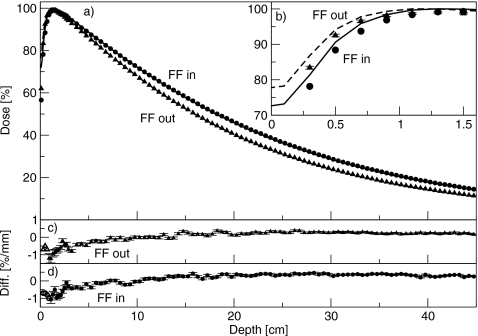
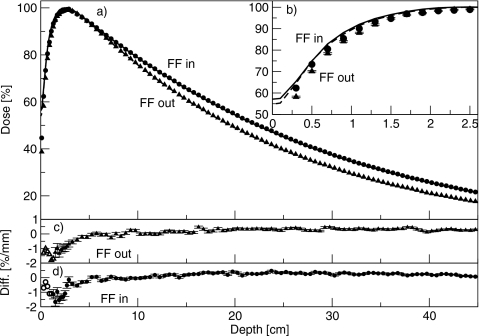
Figure 3 shows the percent-depth dose curves for the 6 MV beam, with and without the flattening filter in place. The inset shows the buildup region. The percent doses at 10 cm depth were 72.1% with the flattening filter in place, and 67.8% with the flattening filter removed. At depths greater than d_max, the simulations agreed with measurement to better than 0.5%. At shallower depths, the simulated dose was less than the measured dose. With the flattening filter removed, the discrepancy was 1.5%, or 0.5 mm, at 0.5 cm depth, and 1.4%, or 3 mm, at 1.1 cm depth. At all depths, the difference was less than or equal to the least restrictive of 1.5%∕1.5 mm. With the flattening filter in place, the discrepancy was 1.6%, or 0.5 mm, at 0.5 cm depth, and 1.1%, or 1.8 mm, at 1.1 cm depth. At all depths, the difference to agreement was equal to or less than 1.5%∕1.5 mm.

Figure 3.

(a) Percent-depth dose curves for the 6 MV beam, with and without the flattening filter. Lines are measured data and points are simulated data. Triangles are with the flattening filter out, and circles are with the flattening filter in. (b) Same results showing the comparison in the buildup region. Measured data are averaged over 0.2 cm and plotted at the center of the bin. Solid line is with the flattening filter in, and dashed lines are with the flattening filter removed. (c) and (d) Difference between simulated and measured results with the flattening filter out and in, respectively. Filled symbols (with error bars) represent a difference in percent, and open symbols (without error bars) represent a difference in millimeters.

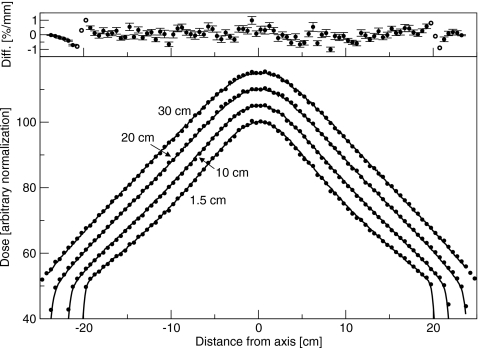
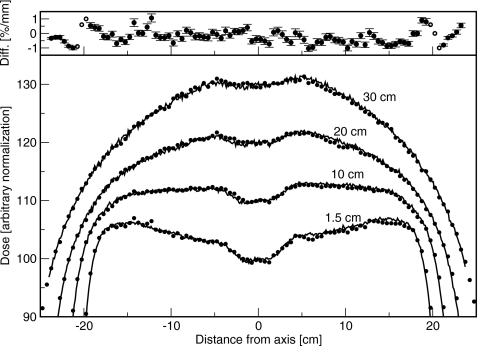
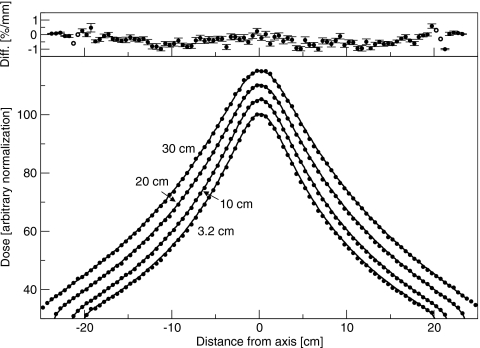
Crossplane profiles without the flattening filter are shown in Fig. 4. The difference between simulated and measured doses is less than 1%. With the flattening filter out, the measured inplane profile at d_max (not shown) was 1.5% greater at 15 cm off-axis away from the gun than toward the gun. This difference was not simulated, and resulted in a discrepancy between measurement and experiment of less than 1%. With the flattening filter in place, crossplane results are shown in Fig. 5, and agreement between simulation and measurement better than 1% was obtained both inplane and crossplane. The dip in the center of the profile was correct, and the off-axis ratio was correct. The asymmetry in the inplane scans observed with the flattening filter out was, with the flattening filter in place, indistinguishable from an offset in the flattening filter position.

Figure 4.

Crossplane profiles measured for the 6 MV beam with the flattening filter out. Normalization is arbitrary. Depths are 1.5, 10, 20, and 30 cm. Lines are measured and points are simulated. Top: Difference between simulated and measured results. Solid circles represent a difference in percent, and open circles represent a difference in millimeters.

Figure 5.

Crossplane profiles measured for the 6 MV beam with the flattening filter in. Normalization is arbitrary. Depths are 1.5, 10, 20, and 30 cm. Lines are measured and points are simulated. Top: Difference between simulated and measured results. Solid circles represent a difference in percent, and open circles represent a difference in millimeters.

Overall, the agreement was within 1.5%∕1.5 mm. Neglecting the buildup region, agreement was within 1%∕1 mm.

18 MV

At 18 MV, simulations were also in good agreement with the measured dose distributions. Percent-depth dose curves are shown in Fig. 6, with the buildup region shown in the inset. The percent doses at 10 cm depth were 78.8% with the flattening filter in place, and 75.7% with the flattening filter removed. Agreement at depths greater than 5 cm was better than 0.5%. In the buildup region, the simulated dose was again less than the measured dose. With the flattening filters removed, at 0.5 cm depth, the discrepancy was 2.7%, corresponding to a position difference of 1.0 mm. At 1.1 cm depth, the discrepancy was 3.9%, and the distance to agreement was 1.8 mm. At all depths the agreement was within 2%∕2 mm. With the flattening filters in place, at 0.5 cm depth, the difference in dose was 2.6%, or 0.3 mm. At 0.9 cm depth, the discrepancy was 1.6% or 1.1 mm. The largest disagreement, at 1.5 cm depth, was 1.7% or 1.8 mm. At all depths, agreement was with 2%∕2 mm. Within 1 cm of the surface, the disagreement between simulation and measurement was greater with the flattening filter out than with it in.

Figure 6.

Percent-depth dose curves for the 18 MV beam, with and without the flattening filter. Lines are measured data and points are simulated data. Triangles are with the flattening filter out, and circles are with the flattening filter in. (b) Same results, showing the comparison in the buildup region. Measured data are averaged over 0.2 cm and plotted at the center of the bin. Solid line is with the flattening filter in, and dashed lines are with the flattening filter removed. (c) and (d) Difference between simulated and measured results with the flattening filter out and in, respectively. Filled symbols represent a difference in percent, and open symbols represent a difference in millimeters.

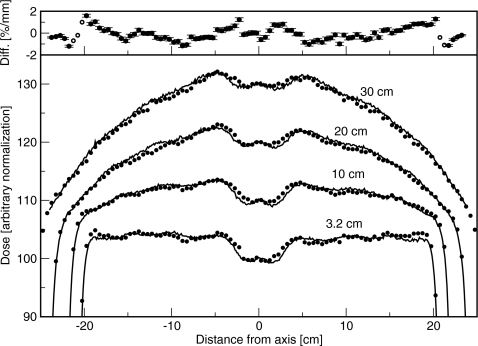
Crossplane profiles with the flattening filter out are shown in Fig. 7. The difference between simulated and measured doses was less than 1%. In the inplane direction, where the focusing of the bending magnet results in an incident beam spectrum or intensity that changes along the spot profile, the measured profiles were asymmetric. The dose on the side away from the gun was 1.6% greater than the dose on the side toward the gun, at 15 cm off-axis. This asymmetry was not simulated, resulting in a disagreement with measurement of 0.8%. For the clinical beam, with the flattening filter in place, simulated doses agreed with measured doses to within 1.5%∕1.5 mm. Crossplane profiles are shown in Fig. 8. The asymmetry in dose on either side of the collimator rotation axis, resulting from placing the flattening filter in a different position than the spot, was simulated correctly. The largest disagreements were just inside the field edge, and at the edge of the dip in the center. The asymmetry in the inplane profile with the flattening filter removed was not present because it was corrected in the measurement by the compensator. Furthermore, any asymmetry in the simulated profiles was accounted for by shifting the flattening filter.

Figure 7.

Crossplane profiles measured for the 18 MV beam with the flattening filter out. Lines are measured and points are simulated. Normalization is arbitrary. Depths are 3.2, 10, 20, and 30 cm. Lines are measured and points are simulated. Top: Difference between simulated and measured results. Solid circles represent a difference in percent, and open circles represent a difference in millimeters.

Figure 8.

Crossplane profiles measured for the 18 MV beam with the flattening filter in. Lines are measured and points are simulated. Normalization is arbitrary. Depths are 3.2, 10, 20, and 30 cm. Lines are measured and points are simulated. Top: Difference between simulated and measured results. Solid circles represent a difference in percent, and open circles represent a difference in millimeters.

Overall, the agreement between measured and simulated was to within 2%∕2 mm. Except for the buildup region, agreement was within 1.5%∕1.5 mm. In the buildup region, the discrepancy was 2%∕2 mm with the flattening filter either removed or in place.

DISCUSSION

Simulations of the x-ray beams of a Siemens Oncor linac operating at 6 and 18 MV have been presented. Agreement to the 1.5%∕1.5 mm level has been obtained, except in the buildup region. There, the differences were 2%∕2 mm at 18 MV with the flattening filters either removed or in place, and 1.5%∕1.5 mm with the flattening filter either removed or in place at 6 MV. The 6 MV profiles and 18 MV profiles with the flattening filter removed agreed to within 1%∕1 mm. Parameters which have the largest effect on dose distributions are the energy of the incident beam, the spot size, and the density and relative position of the flattening filter. These parameters have been measured independently of each other, resulting in a strongly constrained simulation. This is unlike previous works by other authors, where the energy and spot size were both taken to be free parameters.

The 18 MV compensator was simulated as a flat slab, although its thickness changes along the inplane direction. The intent of the compensator is to compensate for an asymmetry in the incident beam. In this work, the incident beam was taken to be symmetric, thus the compensator could be taken to be flat. The consequences of this approximation can be seen in the inplane profile scans with the flattening filter out because the compensator was also removed. The difference between the doses on either side of the collimator rotation axis was 1.5% at 6 MV and 1.6% at 18 MV. Using the average thickness of the compensator produced simulated doses which were incorrect by 0.8%. These differences were sufficiently small that the asymmetry in the incident beam was not simulated.

Historically, on Varian linacs, there has been a large shortfall in simulated dose, as compared to measured dose, in the buildup region.^{3, 5, 22, 23, 24, 25} The discrepancy is up to 26% on Varian linacs.³ For Siemens linacs, the discrepancy was 6±1% at 6 MV and 0±1% at 18 MV.²² Chibani and Ma³ ascribed much of the discrepancy on Varian linacs to an incorrect geometry of the primary collimator. A second source of the discrepancy was an incorrect effective point of measurement for a cylindrical chamber.²⁶ McEwen et al.^{10, 27} found that with the correct effective point of measurement, correct linac geometry, and correct parameters of the incident beam, the BEAMnrc∕EGSnrc codes are capable of agreeing to measured data within 0.2 mm. In the present work, simulated doses were less than the measured doses. At both 6 and 18 MV, the discrepancy was larger with the flattening filter out than with the flattening filter in. With the flattening filter out, the discrepancy was 2%∕2 mm for both energies, and with the flattening filter in, the discrepancy was 1.5%∕1.5 mm at 18 MV and 1%∕1 mm at 6 MV. We note that Bruggmoser et al.²⁸ found the effective point of measurement for the Roos chamber to be 1.5 mm, 0.35 mm greater than that used here. Using this value would reduce the discrepancy between measurement and simulation.

The difference in doses in the buildup region suggests that there are electrons or low energy photons not present in the simulation. In comparison to benchmark measurements with no flattening filter, simulation codes underestimate the fluence near 5 MeV by 10% while closely matching measured data above 5 MeV.¹⁸ Low energy photons are removed by the flattening filter, so a discrepancy in the fluence of low energy photons could be observed with the flattening filter removed but masked with the flattening filter present. This is consistent with the comparison of measurement to simulation at 18 MV in Fig. 6. In the simulations of the 18 MV beam, the electrons contributed 15% of the dose at the surface (averaged over 0–2 mm depth) with the flattening filter out, and 28% with the flattening filter in. A change in the simulated electron fluence would therefore have a larger effect on the simulated dose with the flattening filter in, than with the flattening filter out.

Various sources of asymmetry have been included in the model. The lateral positions of the spot and primary collimator and the angle of the beam were measured and set to their measured values in the simulation. The lateral positions of the flattening filters were allowed to vary, and were determined from simulation. As discussed above, the asymmetry in the fluence distribution of the primary beam was sufficiently small that it could be ignored. The remaining asymmetries were in the position of the primary collimator, which only changes the positions of the penumbrae in the diagonal scans and the positions of the flattening filters. In commissioning a linac, the flattening filters are positioned such that the beam is acceptably flat. In these measurements, the asymmetry was 0.7%. This nearly symmetric beam is in contrast to electron beams measured on the same linac, which are strongly asymmetric.¹⁸

Removal of the flattening filters provided a second check on the simulations, but did not yield new information (aside from the density of the flattening filters). In principle, there are several advantages to removing the flattening filter. There was no uncertainty in the simulations relating to the scattering of x rays in the flattening filter. The energy of the incident beam can be determined in a straightforward manner because with no flattening filter, dose distributions are independent of spot size, flattening filter density, and position of the target relative to the flattening filter. However, the energy of the incident beam was determined directly in this work, and without mechanical alteration of the treatment head, from the percent-depth ionization curve of the raw electron beam. In the clinic, removal of flattening filters is not undertaken lightly. Simulation of linacs in which the flattening filter density is not known can still be done as described here, by determining the incident beam energy from the raw beam percent-depth ionization curve. The density of the flattening filter is then the only variable remaining, and can be chosen to be a reasonable value for the material that gives good agreement with the measured data.

Varying the position of the target along the beam axis changes the off-axis ratio because the distance between the target and flattening filter changes. Other parameters, such as the energy and spot size, also affect the off-axis ratio, so the off-axis ratio is not an effective method of determining the target position. The value specified by the manufacturer is subject to adjustment in the field by a couple of millimeters. The position of the penumbra in the diagonal scans only depends on the distance between the target and primary collimator, to which the flattening filter is bolted. Knowledge of this distance, plus the position of the primary collimator as specified by the manufacturer, is sufficient to constrain the simulation.

Previous simulations of Siemens x-ray beams include those of Sheikh-Bagheri and Rogers²² in 2002, who showed percent-depth doses, and Faddegon et al.¹⁴ The former work compared simulated to measured percent-depth dose curves. For the 6 MV beam, the authors found that simulations overestimated the dose in the buildup region by 6±1%. For the 18 MV beam, measurements and simulation agreed to within 1%. In Ref. 14, agreement to 1% was obtained for profiles and percent-depth dose curves, except in the buildup region where the simulations underestimated the dose. The present work has the advantages over previously published simulations of Siemens linacs of: Much greater precision in the Monte Carlo simulations; direct determination of simulation parameters, especially the energy and spot size; consideration of asymmetry; measurement and simulation of diagonal profiles, and percent-depth dose to 45 cm depth; and measurement and simulation with the flattening filters removed. The result is a strongly constrained simulation.

CONCLUSIONS

A Siemens Oncor treatment head has been simulated, and the simulated dose distributions compared to measurements. Key simulation input parameters were determined independently. An agreement between measured and simulated dose distributions has been obtained to the 1.5%∕1.5 mm level, except in the buildup region. The simulated dose in the buildup region, with or without the flattening filter, was 1.5%∕1.5 mm less than measured at 6 MV, and 2%∕2 mm less than measured at 18 MV. Simulated profiles matched measured profiles to within 1%∕1 mm for the 6 MV beams with and without the flattening filter, and the 18 MV without the flattening filter. With the flattening filter in place, the 18 MV profiles agreed with 1.5%∕1.5 mm. The parameters of the treatment head and incident beam used in the simulation were measured as independently as possible, in contrast to other works, where parameters were determined through a minimization procedure. The incident beam energy was determined from the percent-depth ionization curve of the raw beam and the spot size was determined with a spot camera. The measurements did not require mechanical modification of the treatment head, and may thus be carried out on clinical linacs. Removal of the flattening filters provided a second check, but was not necessary to determine the linac parameters.

The phase-space files determined in this work will be useful for benchmarking beam models and calculating doses to patients. Work to evaluate the accuracy of the phase-space files in the presence of patient-specific beam modifiers such as secondary collimators and wedges is underway.