The Effect of Chemical Information on the Spatial Distribution of Fruit Flies: I Model Results

Abstract

Animal aggregation is a general phenomenon in ecological systems. Aggregations are generally considered as an evolutionary advantageous state in which members derive the benefits of protection and mate choice, balanced by the costs of limiting resources and competition. In insects, chemical information conveyance plays an important role in finding conspecifics and forming aggregations. In this study, we describe a spatio-temporal simulation model designed to explore and quantify the effects of these infochemicals, i.e., food odors and an aggregation pheromone, on the spatial distribution of a fruit fly (Drosophila melanogaster) population, where the lower and upper limit of local population size are controlled by an Allee effect and competition. We found that during the spatial expansion and strong growth of the population, the use of infochemicals had a positive effect on population size. The positive effects of reduced mortality at low population numbers outweighed the negative effects of increased mortality due to competition. At low resource densities, attraction toward infochemicals also had a positive effect on population size during recolonization of an area after a local population crash, by decreasing the mortality due to the Allee effect. However, when the whole area was colonized and the population was large, the negative effects of competition on population size were larger than the positive effects of the reduction in mortality due to the Allee effect. The use of infochemicals thus has mainly positive effects on population size and population persistence when the population is small and during the colonization of an area.

Electronic Supplementary Material

The online version of this article (10.1007/s11538-008-9327-0) contains supplementary material, which is available to authorized users.

1. Introduction

Many studies indicate that animal aggregation is a general phenomenon in ecological systems (Parrish and Edelstein-Keshet, 1999;Wertheim et al., 2005). Forming an aggregation can be beneficial to individuals as a result of overcoming difficulties that are associated with low population densities, such as finding a mate (Parrish and Edelstein-Keshet, 1999; Wertheim et al., 2005) or overcoming resource resistance (Wertheim et al., 2002, 2005). In addition, protection from predators is considered to give important selective advantage to group membership of individuals (Krebs and Davies, 1997; Wertheim et al., 2005). However, aggregations can also involve costs. At large group sizes, individuals compete for resources or suffer density-dependent predation and disease (Parrish and Edelstein-Keshet, 1999; Wertheim et al., 2005).

Animal aggregations can arise when individuals respond behaviorally to the presence of conspecifics and actively search for each other. This is possible only if individuals release information on their whereabouts, either deliberately or involuntarily as a result of their activities. Conspecifics that receive this information can exploit it to adjust their behavior. The cues that are concerned in such information conveyance can be visual, auditory, tactile, or chemical. In insects, as in many other animals, chemical information conveyance is of profound importance (Bell and Cardé, 1984, 1995; Cardé and Minks, 1997; Schoonhoven et al., 2005). The chemicals involved in the chemical information conveyance are termed info- or semiochemicals, and can influence both intra- and interspecific interactions (Dicke and Sabelis, 1988).

The chemicals that specifically induce group formation are termed aggregation pheromones. The chemical composition of aggregation pheromones and attraction of insects to them has been studied in great detail (Bartelt et al., 1985; Schaner et al., 1987; see also Wertheim et al., 2005). In addition, the searching behavior of insects in odor plumes has been studied in the laboratory and in the field (Cardé, 1984; Murlis et al., 1992; Bell et al., 1995) and mathematical models for odor plumes and plume tracing models for individual insects or autonomous robots have been developed (Sutton, 1953; Yamanaka et al., 2003; Farrell et al., 2002). These studies focus on short term behavioral responses of individual insects. However, no studies have been reported on the long term effects of infochemical use and its effect on spatial population dynamics.

In this paper, we study the implications of infochemical use on population dynamics of a single species in a spatial context, by adopting a spatio-temporal approach that incorporates odor dispersal and organismal responses. We use Drosophila melanogaster as a model organism. Drosophilid fruit flies breed in various ephemeral substrates like decaying materials, fermenting fruits, fungi, and sap streams. Therefore, the place where an adult emerges from its pupa often contains no food anymore. Thus, the life of adult fruit flies generally starts with the task of locating a suitable substrate where they can eat, mate, and where females can oviposit. Chemical attraction toward fermentation products produced by microorganisms that live on food sources and aggregation pheromones emitted by recently mated adult female fruit flies play a directive role in the selection of these substrates (Hutner et al., 1937; West, 1961; Bartelt et al., 1985; Wertheim, 2001). Moreover, the combination of aggregation pheromone with food odors is more attractive than food odors alone (Bartelt et al., 1985).

The use of aggregation pheromones can only evolve when individuals benefit from clustering. This situation can occur when an Allee effect plays a role, which is the phenomenon that for smaller populations the per capita growth rate is lower than for intermediate population sizes due to lower reproduction or higher mortality (Allee, 1931). In D. melanogaster, its aggregation pheromone induces aggregated oviposition. The presence of adults prior to larval development increases the amount of food that is present for the larvae; adults (especially females) vector a diversity of yeasts and inoculate the resource with these yeasts during their presence (Morais et al., 1995). Furthermore, Wertheim et al. (2002) showed that increased adult densities prior to larval development reduced fungal growth. It is known that strong fungal growth can cause a high mortality in fruit fly larvae (Rohlfs et al., 2005; Rohlfs, 2006). Adult aggregation thus has a positive effect on larval survival by altering the suitability of the resource. Forming aggregations is not only beneficial. Rohlfs and Hoffmeister (2003) show that the survival from egg to adulthood for Drosophila subobscura is hump shaped, with low survival not only at low population numbers, but also at high population numbers. Thus, there also is a risk in aggregation. At high local population densities, larval survival decreases due to competition (Wertheim et al., 2002; Hoffmeister and Rohlfs, 2001).

Etienne et al. (2000, 2002) studied how the Allee effect, scramble competition, and nondirected dispersal affected population dynamics of D. melanogaster. They found that local instability in population numbers could be balanced by dispersal. In reality, the dispersal of fruit flies is not random, but directed by the response to infochemicals. We investigate to what extent the presence of infochemicals, specifically food odors and aggregation pheromone, affect the spatial distribution of a fruit fly population and whether infochemical-directed dispersal can balance local population instability. Furthermore, we investigate the positive and negative effects of the use of infochemicals on population numbers, by addressing larval mortality due to Allee effect and competition and the net effect on population numbers. We expect the use of infochemicals to promote population persistence in a heterogeneous unpredictable environment in space and time, where colonization and recolonization after local extinction are important processes.

2. Description of the model

Odor distribution and the insects’ responses are by definition spatial processes. Therefore, a spatio-temporal model is the most appropriate approach to gain insight into the effect of infochemicals on population dynamics.

2.1. Dispersal of fruit flies and population dynamics

The reproductive life of female fruit flies generally starts with searching for a suitable resource. When they find a resource they settle to feed, mate, and oviposit. Thereafter, they leave the resource to search for another suitable resource. To model these different activities, we divided the adult population density P into three activity states: a searching state S (with fly density P _S), in which individuals fly in the air and use infochemicals that are present in the air to find a suitable resource, the moment they find a resource and land they come into a settled state R (with fly density P _R), in which individuals spend time on a resource, and a moving state M (with fly density P _M), in which individuals actively fly away from the resource. In our model, the total adult population remains constant within a generation; there is no adult immigration, emigration, or mortality. Furthermore, we only modeled the adult females. In Drosophila melanogaster, adult males produce the aggregation pheromone (cis-vaccenyl acetate) and transfer it to females during mating (Bartelt et al., 1985). Recently mated females then emit the aggregation pheromone. The amount of aggregation pheromone emitted by males is very small compared to the amount that the females emit. In addition, Bartelt et al. (1985) showed that both sexes respond similarly to the aggregation pheromone. We, therefore, assumed that the distribution of females gives a good representation of the distribution of the whole fruit fly population and that the adult female population dynamics could be modeled satisfactorily without considering the adult males.

2.1.1. Dispersal of fruit flies

The dispersal of searching fruit flies (S) is random in the absence of infochemicals. In the presence of infochemicals, however, the movement of searching fruit flies is usually directed toward the source of the odor. We assume that D. melanogaster only uses a concentration gradient to find the odor source and that dispersal can be modeled with a two-dimensional chemotaxis model for the redistribution of flies.

Powell et al. (1998) gave a general format for chemotactic movement in biology. We used this format to model the population responses toward a concentration gradient of the food odor (F) and aggregation pheromone (A)

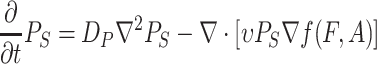where P _S is the density of the searching Drosophila population, ν is the attraction constant of the infochemicals, f is the effective sensory index of D. melanogaster with respect to F and A (see below), and D _P is the dispersal constant of the searching population.

2.1.1.1. Sensory index

Bartelt et al. (1985) showed two important features concerning the responses of D. melanogaster toward food odors (blend of fermentation products and yeast odor) and its aggregation pheromone: (1) the aggregation pheromone is only attractive when food odors are present; (2) D. melanogaster is about four times more attracted to the combination of food odors and its aggregation pheromone than to food odors alone. A description of the response of D. melanogaster to infochemicals that is consistent with these findings is:

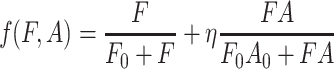, where F and A are the food odors and aggregation pheromone, respectively; F ₀ and A ₀ are the corresponding half saturation values, and η represents the attraction ratio of food odor in combination with aggregation pheromones (F + A) relative to the attraction to food odor alone (F).

2.1.1.2. Leaving the resource

While the movement of searching fruit flies is directed by infochemicals, the movement away from the resource by the moving fruit fly population (M) in the model is not considered to be affected by the presence of food odors and aggregation pheromone. The movement of the moving population is described by ring-random dispersal, where fruit flies first actively fly away from the resource and then distribute randomly (see (9)). We chose this type of dispersal to achieve that a large part of the moving population actually does leave the resource. Without first flying away from the resource, the largest part of the fruit flies would remain on the resource.

2.1.2. Population dynamics

2.1.2.1. Within-generation dynamics

The total adult population is held constant within a generation, and there is no migration over the boundaries of the spatial domain (reflecting boundary conditions). However, the distribution of individuals over the three activity states does change over time (Fig. 1). When a searching individual finds a resource (R) it settles on the resource with settlement probability λ (min⁻¹). Settled individuals leave the resource at a constant rate, the patch leaving probability, α ₁ (min⁻¹). A moving individual that has left the resource starts searching again with a probability α ₂ (min⁻¹). The distribution of the resources (i.e., yeast-infected apples) and local within-generation population dynamics in each point in space (x, y) (see Section 2.4) are described by the following equations

,

,

.

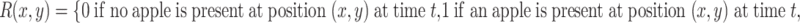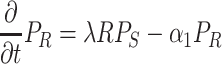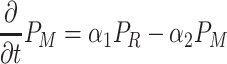Fig. 1.

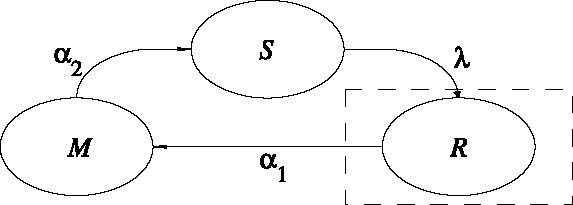
Schematic representation of the population dynamics. The total population is divided into three activity states, S the searching part of the population, R the settled part of the population, M the moving part of the population, with λ, α ₁ and α ₂ the transition rates. The dashed block represents a resource.

From hereon, we refer to yeast-infected apples simply as apples. Values for the parameters used are given in Table 1. For more details on how these values are arrived at, we refer to the companion paper (de Gee et al., 2008).

Table 1.

The model parameters involved in the short time dynamics and their values. For dimensionless parameters, the “–” sign is used.

Name	Description	Value	Units
D P	Dispersion coefficient of at random moving fruit flies	0.058	m2 min−1
α 1	Rate of settled fruit flies leaving the resource	0.002	min−
α 2	Rate of moving fruit flies that start searching for resources	0.5	min{−1}
λ	Settlement rate of searching fruit flies	0.25	min{−1}
ρ	Velocity of movement away from the resource	1	m min−1
F 0	Saturation parameter for food odors	10	ng m−
A 0	Saturation parameter for aggregation pheromones	0.04	ng m−2
D I	Dispersion rate of infochemicals	1	m2 min−1
μ(720)	Loss rate of infochemicals in a 12 hours period (measured from the moment of production)	0.025	min−1
μ(5)	Loss rate of infochemicals in a 5 minutes period (measured from the moment of production)	0.171	min−1
θ F	Food odor production by the resource	2	ng apple−1 min−1
θ A	Aggregation pheromone production by settled fruit flies	0.83	ng fly−1 min−1
ω	Evaporation rate of liquid aggregation pheromone	4.10−4	min
ν	Attraction towards infochemicals	5D P	−
κ	Relative strength of movement towards infochemicals compared to random dispersal	5	−
η	Attraction ratio of food odor together with aggregation pheromones relative to the attraction to food odor alone	2.51	−
ξ	Fecundity of the settled population	0.0083	min−1
ϕ	Sex ratio of the larvae (fraction of females)	0.5	−
L A	Number of larvae per apple at which 50% survives the Allee effect	25	−
L C	Number of larvae per apple at which 50% survives competition	250	−
c A	Slope sigmoid survival curve modeling the Allee effect	0.088	−
c C	Slope sigmoid survival curve modeling the competition	0.044	−

2.1.2.2. Between-generation dynamics: reproduction

Adult females that have settled on a resource (R) deposit ξ eggs per minute on average. The cumulative number of eggs (L) on each resource item after 3 days (in generation n) determines whether larvae develop successfully into adults (4). The percentage of the larvae on one substrate that survives depends on the number of larvae present, survival is best for intermediate numbers of larvae. When there are only a small number of larvae on an apple, a fraction dies due to the Allee effect, while mortality due to competition plays a role when there are many larvae present. Of the surviving larvae, a fraction ϕ is female and these constitute the next female adult generation.

.

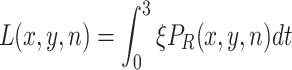The number of larvae becoming adult females in the next generation P(x, y, n + 1) depends on the survival probabilities for the Allee effect (s _A(L)) and for competition (s _C(L)) in the following way

with

,

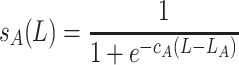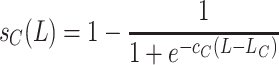, where P(x, y, n + 1) denotes the newly emerged adult females that start searching immediately (S). The graphs of these functions are sigmoid curves with values between 0 and 1. The functions s _A(L) and s _C(L) are increasing and decreasing, respectively, the parameters c _A and c _C affect the slope of this increase or decrease and L _A and L _C are the number of larvae at which the survival rate is 50%.

2.2. Infochemical distribution

D. melanogaster responds to food odors (F) and its aggregation pheromone (A). In this model, we assume that there is no wind and that these odors thus diffuse randomly, with an equal probability to go in all directions. Odor diffusion is a much faster process than the dispersal of adult fruit flies. In addition, odor diffusion is a 3-dimensional process, while we model in two dimensions. We, therefore, introduced a loss term to represent odor matter that gets out of reach of the searching population by diffusion in the vertical direction (see also our companion paper by de Gee et al., 2008). Aggregation pheromone is not excreted in a gaseous form, but as a fluid accompanying the eggs. We, therefore, divide the aggregation pheromones in two phases: a liquid form on the resource that slowly evaporates (A _R), and a gaseous form (A) that is detectable for the searching fruit flies in the air. The distribution of food odors and aggregation pheromone can thus be modeled by

,

,

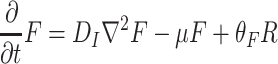, respectively, where D _I is the diffusion constant of the infochemicals, μ is the average loss rate of the infochemicals in the z-direction, the value of this loss rate is dependent on the average time used. For more details on odor loss, we refer to the companion paper (de Gee et al., 2008). As dispersal and loss are mainly driven by atmospheric turbulence, these parameters have the same value for both food odors and aggregation pheromone. Furthermore, θ _F and θ _A are the production rates of the food odor by the resource (R) and the aggregation pheromone by the settled population (P _R), respectively, and ω is the odor release rate by evaporation.

2.3. Integro-difference equation (IDE) approach

The model derived contains spatial dispersion of fruit flies and odors. Therefore, the system of ordinary differential equations that result after spatial discretization is stiff. This means that it contains a range of different timescales; while we are interested in the process at the slowest timescale, the fastest time scale may control the numerical stability of explicit methods for solving this system of ordinary differential equations. In our case, this situation is aggravated by the fact that the odor distribution is a much faster process than the dispersal of fruit flies. Therefore, simple explicit integration methods are unsuitable because of a small step size, while on the other hand, the nonlinearity of the model impedes the use of implicit integration methods. For this reason, we chose the integro-difference approach (as in Neubert et al., 1995; Powell et al., 1998 and Etienne et al., 2002), which treats the dispersion as a separate process that can be solved analytically. This approach is effective because it allows us to take large time steps in accordance to the slow process, without running into any stability problems. In this approach, dispersal and population dynamics (e.g., reproduction) are treated as two distinct phases; we model odor and fruit fly dispersal separate from adult population dynamics.

The dispersal of the population is calculated by taking the convolution product of the population density and the dispersal probability function. We take dispersal to be described by one of the following two-dimensional probability density functions or dispersal kernels (8) and (9). Random dispersal, used for modeling the dispersal of the searching population and for odor diffusion, is described by

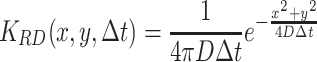, where Δt is the time step taken and D is the dispersal constant of the fruit flies (D _P) or the diffusion constant of the infochemicals (D _I). Ring random dispersal, used to model the moving population, is described by

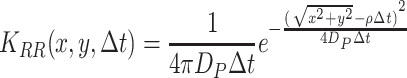, where ρ is the velocity of the displacement away from the resource.

The random dispersal kernel above, models the diffusion of the odor that is already present in the system. During each time step, odor is produced by the resources and released into the air. The dispersal of the produced odor is calculated by taking the convolution product of the odor produced per minute and a dispersal probability function for a continuously producing source. The distribution of the produced odor is described by (10),

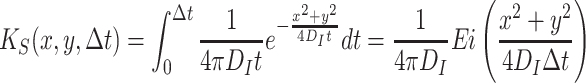, where Ei is the exponential integral.

The infochemicals direct the movement of the searching population toward the odor source. The spatial distribution of searching fruit flies, resulting from (1), can according to Powell et al. (1998), be approximated in discrete time by

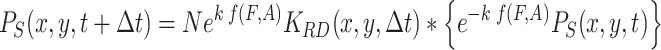, where K _RD is the random dispersal kernel for the population of fruit flies and N a normalization constant. The “*” denotes the convolution operator over all spatial coordinates, i.e.,

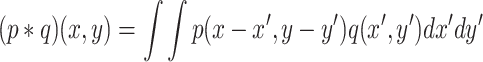. In (11), chemotaxis is modeled as a diffusion process. Diffusion is the movement of materials from an area with a high density to an area with a low density until equilibrium is reached. We can model movement toward the attractive source by artificially reducing the population density, with a stronger reduction for a more attractive spot. As diffusion occurs from high densities to low densities, the reduced population diffuses toward the attractive source, because the population density is—artificially—low at and around the source.

Equation (11) is best interpreted when it is read from the right to the left. It describes how the population at time t is first multiplied by a factor that contains the sensory index of the species and the attraction ratio κ (= ν/D _P). This multiplication amounts to rescaling the population density. It strongly decreases the population density at points with a high odor concentration (combination of food odor and aggregation pheromone), while the density remains approximately the same where odor concentration is low. The dispersal is now directed toward the points with a low—rescaled—population density. After dispersal, the rescaled population is scaled back with the inverse of the above mentioned factor. This results in a strong increase of the population density in points with a high odor concentration. In this way, dispersal with a bias directed toward the infochemicals is modeled. However, this dispersal is not completely mass-conservative when using numerical approximations. Therefore, the dispersal step is finalized by normalization. To this end, we multiply the resulting density after chemotactically driven diffusion by such a number N that the total number of searching fruit flies is preserved.

2.3.1. Attractiveness to infochemicals

The dimensionless ratio κ = ν/D _P is a measure for the relative strength of the chemical attraction (ν) as compared to the random dispersal (D _P). If there is no chemical attraction, then the movement is at random and κ = 0. On the other hand, a strong influence of the chemical attraction in comparison to the random dispersion corresponds to high values of κ. In that case, the movement is directed toward the odor source.

2.4. Simulation

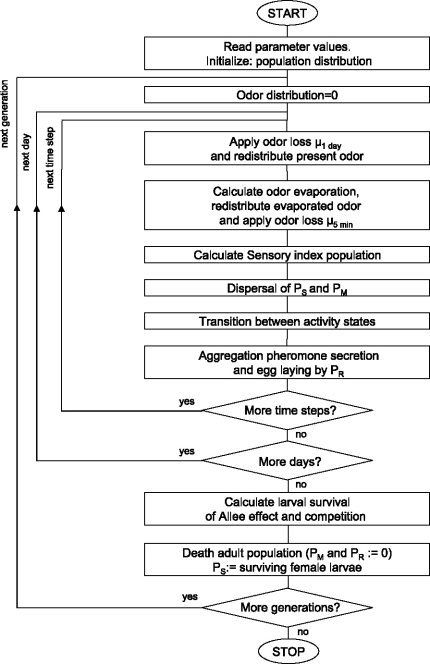
We considered a square spatial domain with reflecting boundary conditions for the population of fruit flies, and absorbing boundaries for the infochemicals. The reflecting boundary conditions for the flies represent a closed system (they cannot escape). On the other hand, the infochemicals can freely pass through the boundaries, never to come back: this is modeled by the absorbing boundary condition. We ran simulations for one generation, consisting of 3 dispersal days (short term population dynamics) and 10 generations of 3 dispersal days (long term population dynamics). Because evaporation is temperature dependent, odor evaporation during the night is much smaller than during the day. Also, the activity of yeasts, the main producers of the attractive fermenting fruit smell, is temperature dependent. We, therefore, assume that during the night no odor is produced. Furthermore, we assume that fruit flies do not reproduce or disperse during the night. Therefore, we modeled 12 hours per day. We discretized each dispersal day in steps of 5 minutes of dispersal by adult females followed by population dynamics (i.e., by settlement on resource, reproduction, patch leaving, or start of searching behavior) (Fig. 2).

Fig. 2.

Flow chart of the processes in the model. In our model, the time step, Δt, is 5 min. We simulated 1 generation in the short term simulation and 10 generations in the long term simulation. Each generation consisted of 3 days.

2.4.1. Short term (one generation) simulation

To study the basic distribution patterns of fruit flies in a two-dimensional environment where infochemicals are present or absent, we ran three simulations, one “control” simulation where no odors were present, one simulation where only food odors were present “F”, and a simulation where both food odors and aggregation pheromone were present “F + A”. We simulated the dispersal of fruit flies on a spatial domain of 30 m × 30 m. It is divided into 256 × 256 cells with a diameter of 0.117 m. The factor 256 is not essential for the design of the experiments, nor does it influence the results essentially; however, it enhances the efficiency of the numerical computations because powers of 2 allow use of the fast Fourier transform for the convolutions.

2.4.1.1. Initial distribution of resources

We are interested in spatial differences due to aggregation. We, therefore, divided the domain in four quadrants. Each quadrant contained 9 resource patches of 1 m² clustered in one block (of 5 m × 5 m), with an interpatch distance of 1 m (Fig. 3a). The blocks were situated 6.5 m from the boundaries of the domain. The distance between two adjacent blocks was 7 m. The initial resource density was 5 apples m⁻², evenly distributed over the block (like apple-sauce).

Fig. 3.

The set-up of the domain with spatial dimensions of the (a) short term simulation, size 30 m × 30 m, with 4 blocks of 9 clustered resources with resource density of 5 apples m⁻², and the (b) long term simulation, size 90 m × 90 m, with 36 blocks containing randomly distributed apples with resource density of 5 apples m⁻². The release point of the initial population is denoted with ×.

2.4.1.2. Initial adult distribution

To study whether aggregation occurs at resources with a higher initial density, we unevenly divided 800 adults (P ₀) over the four quadrants. We situated 500 females in the lower left quadrant and 100 females in each of the other three quadrants. The fruit flies were released near the center of the domain. The release points were situated 2.5 m from the nearest resource. The distance between the release points in the center was 3.5 m.

2.4.1.3. Larval survival

At the end of the generation, the larval survival is calculated. We assessed the number of larvae that successfully developed into an adult female. In addition, to determine the costs and benefits of the use of infochemicals, we also assessed the number of larvae that did not survive due to the Allee effect or due to competition, and calculated mortality rates for both effects separately.

2.4.1.4. Statistics

To calculate the degree of aggregation of the population, we use k a measure of the amount of clumping, given by

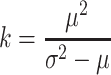, where μ is the mean and σ ² the variance of the negative binomial distribution (Southwood and Henderson, 2000). The smaller the value of k, the greater the extent of aggregation, whereas for k → ∞(i.e., in practice k × 8), the distribution approaches a Poisson distribution, i.e., is virtually random. The value of k is influenced by the size of the sampling unit. In our model, we use same-sized units. Thus, we are able to use this measure to compare the degree of aggregation for the different treatments of availability of infochemicals.

To test the effects of infochemical use on settlement and on larval survival, we used the G-independence test on the number of settled and moving fruit flies for each treatment or on the number of larvae that survived or died for each treatment (Sokal and Rohlf, 1981).

The short term simulation is also used for a sensitivity analysis. For more details on the sensitivity analysis, we refer to our companion paper (de Gee et al., 2008).

2.4.2. Long term (ten generations) simulation

To study the long term population dynamics, we modeled a fruit fly population in an unpredictable heterogeneous environment. D. melanogaster cannot survive the winter in the natural climate of the Netherlands. Therefore, we simulated only one breeding season, consisting of 10 discrete generations. We model discrete nonoverlapping generations of 3 days each. These days consist of 12 dispersal hours, divided in time steps of 5 minutes (Fig. 2). The larval development was lumped, and computed at the end of the generation. For the long term simulation, we considered a domain of 90 m × 90 m, divided into 512 × 512 square cells, each with a diameter of 0.176 m. We ran three simulations, one “control” simulation where no odors were present, one simulation where only food odors were present “F”, and a simulation where both food odors and aggregation pheromone were present “F + A”.

2.4.2.1. Initial adult and resource distribution

We introduced 2,000 fruit flies (P ₀) in one single cell in the center of the domain. This domain contains 36 resource blocks of 5 m × 5 m (Fig. 3b). The resource blocks were situated 17.5 m from the boundaries of the domain. The distance between two adjacent blocks was 5 m. The initial resource density was 1 apple m⁻². To study at which spatial scale effects take place, we looked at the population dynamics at a large spatial scale, i.e., the four quadrants of the domain (each containing 9 resource blocks), at an intermediate spatial scale, i.e., the resource blocks and 2.5 meter around the blocks, and at a small spatial scale, i.e. individual apples. For the simulation at the largest spatial scale, we used two additional resource densities, 5 and 10 apples m⁻² to study whether the spatial dynamics of the fruit fly population depends on resource availability.

To mimic the natural situation, the apples were placed randomly each generation, with each grid cell in the block containing either one apple or no apple (3a). Outside the resource blocks, the cells were empty. The total amount of apples per quadrant of the domain was fixed (for example, when the initial resource density is 1 apple m⁻², a quadrant contains 9 (blocks) × 25 (m²) × 1 (apple m⁻²) = 225 apples), but as they were placed randomly over the resource blocks, there were differences in the amount of apples per resource block.

We ran the simulations at the largest spatial scale three times, with a different starting point of the random number generator, to verify the consistency of the results.

2.4.2.2. Statistics

We used linear mixed models to test the effect of the use of infochemicals on the mortality due to the Allee effect (%), mortality due to competition (%), and larval survival (%) in the first five generations (during the population expansion). This method is especially suitable for data, where the measurements are correlated in time. In the model, we took “generation” as repeated measurement, and “treatment”, “generation”, and “treatment × generation” as fixed effects. We tested the model for four different covariance structures, compound symmetry (CS), first-order autoregressive (AR(1)), heterogeneous first-order autoregressive (ARH(1)), and an unstructured covariance matrix (UN). The unstructured covariance matrix was the best model for the data (it had the lowest AIC). For these statistics, we used SAS 9.1.

2.5. Parameter values

We used the parameter values as given in Table 1. For more details on how these values are arrived at, we refer to the companion paper (de Gee et al., 2008).

3. Results

3.1. Short term (one generation) simulation

In our model, the infochemicals affect, as expected, the spatial distribution of the fruit flies. When both food odors and aggregation pheromone are present (F + A), the distribution of the total population (P _S + P _R + P _M) over the quadrants after one generation is significantly different from the control situation where no chemical information is present (χ ²₍₃₎ = 150.64, p < 0.0005) or where only food odors are present (F, χ ²₍₃₎ = 115.59, p < 0.005). This can also be seen if we look at the measure for clustering: k changes from 47.73 (control) to 23.52 (F) to 2.16 (F + A) with increasing availability of chemical information. Increasing the chemical information present thus causes the population to distribute less randomly. This indicates that aggregation occurs when both food odors and aggregation pheromones are present (F + A) (Fig. 4).

Fig. 4.

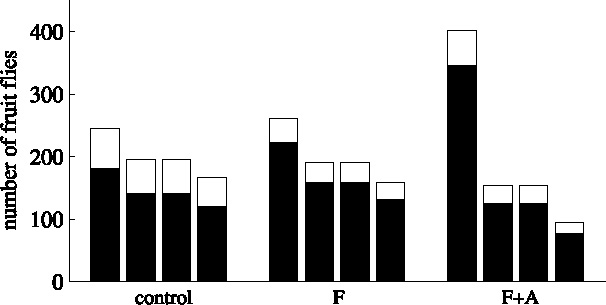
The distribution over the quadrants of the total fruit fly population, subdivided in settled (black part) and moving (white part) fruit flies, after one generation, for the simulations: without chemical information present (control), with only food odors present (F) and with both food odors and aggregation pheromone present (F + A). Within a treatment, the first bar depicts the quadrant with the highest initial adult population. The second and third bar depict the quadrants positioned adjacent to it, and the fourth bar depicts the quadrant positioned opposite to it.

We have also compared the distribution of settled fruit flies (P _R) over the four quadrants (Fig. 4, lower part bars). The distributions of the settled populations for both F + A and F turns out to be significantly different from the control situation (χ ²₍₇₎ = 216.97 (F + A), χ ²₍₇₎ = 51.93 (F), both p < 0.0005). For the settled fruit fly population, the clumping parameter k changes from 43.31 (control) to 21.50 (F) to 1.96 (F + A). The distribution of settled fruit flies when both food odors and aggregation pheromone are present differs also significantly from the distribution with only food odors (χ ²₍₇₎ = 116.97, p < 0.0005). The different distribution, combined with the lower value for the clumping measure, indicates that the availability of aggregation pheromone indeed mediates aggregation.

The percentage of the total adult population that settled on the resources after one generation is higher when chemical information is present. For the quadrant with the highest initial density, the settlement increases from 73.8% in the control situation without infochemicals, to 85.0% (F, G = 4.84, p < 0.05) and 86.3% (F + A, G = 7.63, p < 0.01) when infochemicals are present. Food odors and pheromone thus are able to guide more fruit flies toward the resources.

At the end of the generation, the larvae did not suffer from competition (0% mortality), but instead a high mortality due to the Allee effect occurred. This was the case for all treatments. When both food odors and aggregation pheromone could be used (F + A), the mortality due to the Allee effect in the quadrant with the highest initial density significantly decreased from 84.1% mortality in the control situation and 81.6% for the situation where food is present (F) to 58.8% for F + A (G = 172.1539 (control), G = 159.5866, (F), both p < 0.0005). No significant effect is observed in the quadrants with the lower initial population density. As expected, this positive effect is density dependent. When more fruit flies are present, aggregation on the resources can better prevent mortality due to the Allee effect. At the same time, no negative effects, like higher mortality due to competition, are observed. By decreasing the mortality in the quarter with the highest initial density, the presence of both food odors and aggregation pheromones thus have an overall positive effect on population numbers. As a result, the total number of larvae that survive go up from 677 (control) and 854 (F) to 1757 new adults (F + A) in the whole domain in the next generation.

3.2. Long term (ten generations) simulation

3.2.1. Large spatial scale: quadrants of the domain

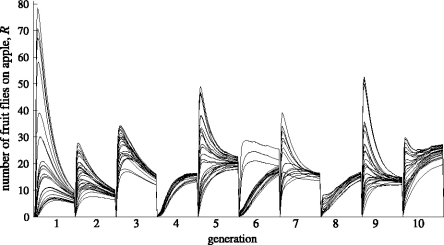
The effect of infochemicals on the distribution of the modeled fruit flies depends on resource density. All simulations show a strong increase in population numbers in all 4 quadrants in the first five generations (Fig. 5). In these generations, the population is expanding, both spatially and numerically. Because more apples can provide more food for the larvae, the total number of fruit flies increases faster for higher resource density. The presence of infochemicals had a positive effect on population numbers. The mortality due to the Allee effect was significantly lower when infochemicals were present for all resource densities (p < 0.0001 for both F and F + A). However, at a resource density of 1 apple m⁻² the presence of infochemicals also caused higher mortality due to competition (p < 0.0001 for both F and F + A) (Fig. 6a). Even though the increase in mortality due to competition was larger than the decrease in mortality due to the Allee effect, the number of offspring that survived was higher in the presence of infochemicals. Thus, the presence of food odors and aggregation pheromone had a net positive effect on population numbers.

Fig. 5.

The dynamics of the total number of fruit flies in the 4 quadrants of the domain (each line represents one quadrant) during 10 generations, when no chemical information is present (control), only food odors are present (F) or both food odors and aggregation pheromones are present (F + A), for the resource densities of 1 apple m⁻² (a–c) and 10 apples m⁻² (d–f). The apples were randomly distributed per resource block. The initial fruit fly population P ₀ = 2,000 was situated in one cell in the center of the domain. The attraction towards infochemicals was κ = 5 and η = 2.51.

Fig. 6.

Larval mortality due to the Allee effect (solid lines) and competition (dotted lines) for (a) all generations, and (b) focused at the Allee effect from the fifth generation onwards, for the control simulation without odors (•), for the simulation with only food odors (▪), and for the simulation with both food odors and aggregation pheromone present (♦), for resource density 1 apple m⁻². Note the scale difference of the y-axes.

In the first 5 generations, during population growth, there was a significant trend in time, i.e., the mortality due to the Allee effect decreased significantly and mortality due to competition increased significantly (both p < 0.0001) (Fig. 6a). This was the case for all treatments (control, F and F + A) and for all simulated resource densities. The fixed factor “generation × treatment” interaction was also significant (p < 0.0001) for the mortality due to the Allee effect and due to competition, indicating that even though the mortality in all treatments show a trend in time, the mortality due to the Allee effect remained significantly lower and the mortality due to competition remained significantly higher when infochemicals were present than when fruit flies could not respond to odors.

The population dynamics from the sixth generation onwards is influenced by the resource density. At a resource density of 1 apple m⁻² large fluctuations in population numbers between generations can be seen for all treatments (Fig. 5a–5c). At this resource density, a relatively large number of fruit flies in one generation is generally followed by much lower number in the next generation. Food odors and aggregation pheromone influence the recovery of the population. When no chemical information is present, a high mortality due to competition (>80%) is usually followed by a slow increase in population numbers due to higher mortality due the Allee effect in the following generation (Fig. 6b). When infochemicals are present, the population increases much faster after a local population crash, because the mortality due to the Allee effect in the following generation is lower when infochemicals were present (Fig. 6b). This was consistent in all repetitions. Attraction toward infochemicals, and thereby decreasing the mortality due to the Allee effect, thus seems to have a stabilizing effect at this resource density. Despite this stabilizing effect the local population dynamics are inherently unstable at this resource density. The fluctuations are in the same order of magnitude as the mean population density.

At a resource density of 10 apples m⁻², the presence of infochemicals increases spatial variation in population numbers, but also the variation between generations (Fig. 5d–5f). The attraction toward food odors and aggregation pheromone results in a more aggregated distribution. Where the number of eggs produced at the apples exceeds the local larval carrying capacity more often, which results in higher mortality due to competition (83–87%). At a resource density of 10 apples m⁻², the increase in variation between generations (for F + A) did not affect the overall stability and persistence of the population. The fluctuations are much smaller than the mean population density. However, also when fruit flies could not respond to infochemicals, the larval carrying capacity was exceeded considerably. The mortality due to competition varied between 80 and 85%. Generally, for mortality between 80–85%, the population size remained constant, the population decreased when mortality is higher than 85% and increased when mortality is lower than 80%.

At a resource density of 5 apples m⁻², the population dynamics show a combination of the dynamics at higher and lower resource densities. The dynamics show large fluctuations, and there is more spatial variation when chemical information is present (ancillary material: spatial distribution mortality due to Allee effect and competition for control simulation and F + A).

3.2.2. Intermediate spatial scale: on and around resource patches

At the scale of resource blocks, the effect of infochemicals in the first five generations is dependent on the distance between the resource block and the initial population. Infochemicals have a positive effect on the survival of the population at the resources close to the initial population. Infochemicals attract more fruit flies toward the resources, and thus reduce the Allee-effect-dependent mortality. However, arresting more fruit flies at resources close to the initial population also implies that fewer fruit flies dispersed to more remote resources, resulting in a higher mortality due to the Allee effect at resources further on. In addition, the stronger attraction toward resources close to the release point also causes overcrowding at these resources, and thus higher mortality from competition. However, the positive effect of locally reducing the mortality due to the Allee effect has a greater effect on total population numbers than the negative effect of increased competition. At the large scale, we have found that infochemicals have a net positive effect on the population numbers by decreasing the mortality due to the Allee effect in the first four generations. From the fifth generation on, the negative effects of increased competition have a larger effect on population size than the positive effects of a decrease in mortality due to the Allee effect.

3.2.3. Small spatial scale: individual apples

Figure 7 depicts the long term population dynamics of the total population per apple in block one of quadrant one when both food odors and aggregation pheromone are present. At the smallest simulated scale of individual apples, the population dynamics in the first four generations exhibits a similar pattern for all apples in one resource block. However, there exists variation in the number of fruit flies present per apple. From the fifth generation on, the population dynamics vary between apples. This variation is mainly caused by differences in the number of fruit flies present in the beginning of the generation. In an area where relatively more fruit flies survived the previous generation, generally, the number of fruit flies on an apple decreased, while apples in an area with low numbers of fruit flies at the start of the generation generally attracted fruit flies. The fruit flies thus tend to distribute more evenly at the end of the generation (for instance look at generation 5 or 9 in Fig. 7). This can imply that fruit flies are more attracted to intermediate concentrations of aggregations pheromones than to high concentrations. If this is the case, this would be a good strategy since the survival curve of the larvae is hump-shaped, with the highest survival at intermediate larval densities (Rohlfs and Hoffmeister, 2003).

Fig. 7.

The dynamics of the total number of fruit flies depicted per apple for the resource block closest to the initial population, during 10 generations when both food odors and aggregation pheromone are present (F + A) at resource density 1 apple m⁻².

4. Conclusion and discussion

We developed a spatio-temporal model for the dispersal of food odors and aggregation pheromone and the responses of a fruit fly population to these infochemicals. In this model, we divided the population in three activity states: individuals could be searching for a resource, be settled on a resource or moving away from a resource. We studied the effect of the presence or absence of food odors and aggregation pheromone on the spatial distribution of a fruit fly population. Furthermore, we investigated the positive and negative effects of the use of infochemicals on population numbers, by looking at larval mortality due to an Allee effect and competition and the net effect on population numbers. We showed that the presence of infochemicals affects the spatial distribution of a modeled fruit fly population. The short term simulations showed that infochemicals guide the flies toward the resources. As expected, aggregation pheromone in combination with food odors caused a higher settlement than food odors alone. Furthermore, the presence and use of infochemicals positively affected the net larval survival (in numbers), by decreasing mortality due to an Allee effect during the colonization of the domain. The effect of infochemicals depended on the distance from the initial population. In accordance to field data of Wertheim et al. (2002), infochemicals attracted more fruit flies toward the resources close to the release point and hereby positively influenced population numbers in the next generation by reducing the mortality due to the Allee effect at these resources.

The use of infochemicals has both positive and negative effects on population size. During the colonization of the domain the positive effects, of a decreased mortality due to the Allee effect, are larger than the negative effects of an increased mortality due to competition, resulting in a stronger population growth when infochemicals are present. After the colonization of the domain and the strong population growth, the negative effect of increased competition is not balanced by a reduced mortality due to the Allee effect anymore, resulting in higher population numbers when no infochemicals are present.

The effect of infochemicals also interacted with the resource density. At a low resource density (1 apple m⁻²), the presence of chemical information increases the resilience of the system, because it reduces the mortality due to the Allee effect after a population decline due to competition. At high resource densities, the presence of infochemicals increases both spatial and “between-generation” variation, causing large amplitude variations in population sizes. However, due to the higher population densities, these variations pose no threat for population persistence.

The study of Etienne et al. (2002) showed that local instability could be balanced by dispersal and suggested that attraction to infochemicals could be a stabilizing factor for population persistence. Although the population was inherently unstable at a low resource density (1 apple m⁻²), our long term simulation indeed showed that infochemicals increased population’s resilience, by decreasing the mortality due to the Allee effect after a local population crash, and thus promoted population persistence. Looking at population dynamics at a smaller scale, local instability (at the scale of recourse blocks) in our model was also balanced by dispersal. Apples within a resource block showed similar population dynamics. However, at the scale of resource blocks there was variation in dynamics. This was mainly caused by initial differences in population density due to the rate of colonization and the differences in resource density between generations.

In our long term simulation, the initial population was released from one point in the center of the domain. This is typical for a field experiment but very unrealistic for the natural situation. Drosophila melanogaster cannot survive the winter in the natural climate of the Netherlands. Therefore, at the beginning of the season, no natural fruit fly population is present in orchards. Adult D. melanogaster overwinter in human constructions (Boulétreau-Merle et al., 2003). They recolonize the orchards from the boundaries in spring. During recolonization, locating the resources, and thus guidance of the fruit flies by infochemical information is important. By placing the initial population in the center of the domain, close to suitable substrates, the results we found for the growth of the population that could not use infochemicals is probably much better than in the natural situation where the fruit flies had to recolonize the area. In the latter situation, population size is small and the population is also distributed more randomly. Therefore, mortality due to the Allee effect plays a more prominent role. Our results could thus be an underestimation of the positive effect of infochemicals of reducing the mortality due to the Allee effect during population growth. Still, we showed that even under these favorable conditions, the use of chemical information had a positive effect on population numbers during the colonization of the domain. We plan to study the role of infochemicals on long term population dynamics when fruit flies have to re-colonize an orchard in the future.

Studies of Kellogg et al. (1962) and Frye et al. (2003) show that for D. melanogaster visual cues are essential to locate the horizontal position of an odor source. In our model, D. melanogaster can only use chemical information to find a resource. They use a concentration gradient to find the odor source. This works sufficiently while the odor concentration is lower than the saturation level. However, the moment the odor concentration reaches saturation level our simulated fruit flies cannot locate the resource anymore and start to disperse randomly. In addition, in our model, settlement is dependent on the odor concentration above a resource. As we model in 2D, it is not possible to determine whether the odor originated from that resource or another resource nearby. Yet, an experimental study showed that Drosophila melanogaster is able to follow an odor trace to its source (Budick and Dickinson, 2006). Both saturation and the inability to localize the actual odor source could be an explanation for the even distribution of fruit flies over the apples within a resource block we found in our small scale simulation. As both effects could cause a more even distribution, the negative effects of aggregation, in particular, higher mortality due to competition, could be underestimated. However, more competition would also result in lower population numbers. In that case, the positive effect of infochemicals by decreasing mortality due to the Allee effect is again more important.

The use of infochemicals thus has not solely positive effects. Infochemicals guide fruit flies toward the resources and thereby can have a positive effect on population numbers by decreasing the mortality due to the Allee effect. On the other hand, when too many fruit flies are attracted, the carrying capacity of an apple can be exceeded which will result in a higher larval mortality due to competition for food. Hoffmeister and Rohlfs (2001) experimentally showed that fruit flies often misjudge the carrying capacity of resources and not only aggregate their eggs when confined to a limited amount of resource items (when it would be appropriate) but also when resources are not a limiting factor. They gave as a possible explanation that ample supply of food patches is not found in nature, and thus that the reproductive success of fruit flies is mainly determined by their opportunities of producing clutches (i.e., locating patches) rather than optimal egg-laying decisions. In a low maintenance orchard in the Netherlands, the density of apples on the orchard floor is 0–6 apples m⁻² (Wertheim et al., 2006). This is comparable with our simulation with 1 apple m⁻². In this simulation, infochemicals indeed had a positive effect on the resilience of the population.

A mechanism by which aggregation can be advantageous is that at high population densities individuals can experience a diluted risk of attacks by their natural enemies (Parrish and Edelstein-Keshet, 1999; Wertheim et al., 2005). Rohlfs and Hoffmeister (2004) indeed show that risk of parasitism can decrease with increasing larval density. The most important natural enemies of Drosophila in temperate regions are their larval parasitoids (Janssen et al., 1988). Wertheim et al. (2006) found that the overall percentage of parasitism in the field by Leptopilina spp. on Drosophila species in apples was 22%. The percentage of apples that contained Leptopilina was even higher, namely 67%. Leptopilina spp. use the same odors as fruit flies (i.e., food odors and D. melanogasters’ aggregation pheromone) to find their hosts (Wiskerke et al., 1993; Wertheim et al., 2003). Parasitism could have a stabilizing effect on the population dynamics of the fruit flies, by decreasing population growth, and thus decreasing the probability of over-aggregation at low resource densities. We suggest that a reduced risk of parasitism in higher larval densities in combination with the use of aggregation pheromones promotes persistence of the host-parasitoid interaction. In future research, we investigate the role of infochemicals in spatial host-parasitoid interactions.

In nonsocial arthropods, hundreds of species belonging to more than ten different orders are known to use aggregation pheromones (Wertheim et al., 2005). Many of these are pest species. Wertheim et al. (2005) found that generally there is a connection between aggregation pheromones usage and food exploitation. Knowing the effects of the use of infochemicals on spatial population dynamics of the pest species, if possible in combination with the dynamics of its natural enemy, may lead to novel insights for biological control. Many animal species (but also plant species) suffer from a decrease in growth rate at small population sizes, known as the Allee effect. In these species, the ability to use chemical information, especially aggregation pheromones, enhances population persistence. We found that infochemicals mainly had a net positive effect on population size and population persistence in situations where resources are scarce or difficult to find or when the (local) population of fruit flies is small. This is the case in spring when the natural population that overwintered in shelters recolonizes an orchard. We showed that aggregation promotes population resistance during colonization of the domain and, for low resource densities, also for recolonization after a local population crash. Aggregation then decreases the mortality due to the Allee effect. At high resource densities and large population numbers, the use of aggregation pheromones had a net negative effect on population numbers. However, for the persistence of a population the reduction of the larval mortality due to the Allee effect at low population densities was of great importance. At the same time, the negative effect of infochemicals on population numbers due to increased competition at large population size did not have a negative effect on population persistence. Overall, the use of food odors and aggregation pheromones enhances the persistence of a fruit fly population.