How to work with a subgroup analysis

Surgical practice should principally be based on evidence originating from high-quality data such as randomized controlled trials (RCTs). Whereas these studies mostly investigate general and representative patient populations, clinical decisions most often depend on individual patient characteristics. To concede to the need of individually based guidelines, many RCTs report analyses on specific subgroups of patients.^1,2 The main aim of a subgroup analysis is to identify either consistency of or large differences in the magnitude of treatment effect among different categories of patients. Determining whether the observed overall treatment effect is different across certain subgroups may justly provide some patients with its benefits and protect others from its harm.

Irrespective of its practical potentials, subgroup analysis must be conscientious in design, reporting and interpretation. Many stringent methodological criteria apply but are far from always fulfilled.² Consequently, inferences drawn may wrongfully direct management of certain patient groups. In fact, the definition of a subgroup analysis is equivocal in that authors use the term to indicate tests that estimate differences in treatment effect within subgroups (a subgroup effect) and between subgroups (an interaction; Table 1).

Table 1.

Conceptual difference between within- and between-subgroup tests

Subgroup	Group, outcome percentage		Subgroup effect (relative risk reduction)
	Treatment	Control
Category 1	34	40	0.15	↕
Category 2	22 ↔	42	0.48
Category 3	25	35	0.29

The horizontal arrow indicates a within-subgroup test. The results of this test are called a subgroup effect. In our example, the test is performed for every subgroup using a χ² test. The vertical arrow indicates a between-subgroup interaction test. The results of this test are called an interaction. It is not performed in our example.

The purpose of this article is to consider criteria for sound subgroup analyses in RCTs, assuming good underlying methodological quality of the main trial (i.e., randomization, assessor blinding, etc.).³ A clinical scenario, based on a recent RCT in orthopedic surgery, will practically support the theoretical statements throughout the text.

Clinical scenario

A 25-year-old woman keeps returning to your practice with recurrent anterior dislocations of her shoulder. Since her initial dislocation more than 3 years ago, she has had 3 recurrent dislocations and several subluxations of her shoulder. On the second dislocation, you tried a different method of reduction and immobilized her shoulder for a longer time, but unfortunately this did not prevent another redislocation. You noticed that some patients in your practice with dislocated shoulders did not have any recurrences, despite receiving exactly the same treatment. So you asked yourself, “What makes this patient different from the others?”, and you searched the literature to find an answer. Age of the patient^4–6 and duration of immobilization^7,8 might explain the difference in recurrence, but the data remain largely inconclusive. You recall a colleague discussing immobilization of the shoulder in external rotation (ER) rather than the usual internal rotation (IR) as a great method to reduce recurrences. You decide to expand your search to identify the best available evidence on shoulder position.

Literature search

To find out if internal rotation immobilization has ever been compared with another immobilization method, you search the available literature. You perform a comprehensive search⁹ using the following search terms: “immobilization AND dislocation AND shoulder AND young patient.” Because you only want reliable and valid evidence, you limit your search with “randomized controlled trials (RCT).” This search yields 4 articles. As you review their titles, you notice that the first one contains “immobilization in external rotation reduces the risk of recurrence.”¹⁰ As you had come up with the ER yourself and the title suggests that the recurrence risk is reduced by this method, you expect it to help you with your decision for your young patient with the dislocated shoulder. You retrieve the article for further evaluation while consulting guidelines to assess surgical RCTs.³

Summary of the appraised article

The study by Itoi and colleagues¹⁰ was designed to compare immobilization in ER with immobilization in IR after initial anterior dislocation of the shoulder. The authors hypothesized that immobilization in ER would decrease the recurrence rate. From a total of 198 patients with a mean age of 37 years, 94 patients were randomly assigned to immobilization (up to 3 days after reduction) in IR and 104 to immobilization in ER for 3 weeks. The primary outcome assessed was a recurrent dislocation or subluxation of the shoulder, and the minimum follow-up period was 2 years.

A total of 74 patients in the IR group and 85 in the ER group were included in the authors’ analysis, which was enough to attain power of 80% to detect a difference of 0.3 in the ratio of effectiveness (the necessary sample size was 42 patients in each group). The treatment adherence rate was significantly higher in the external rotation group (p = 0.013).

The authors compared rates of the primary outcome between the 2 treatment groups using the χ² test. They also compared recurrence rates between subgroups based on different ages (≤ 20, 21–30, 31–40 and ≥ 41 yr) and based on when the immobilization was started (first, second or third day). Significance of subgroup tests was set at the 0.05 level.

Intention-to-treat analysis revealed that the recurrence rate was 42% in the IR group and 26% in the ER group (p = 0.033). In the subgroup of patients aged 21–30 years, the recurrence rate following immobilization in ER was significantly lower than immobilization in IR (p = 0.037). No significant differences were found in the other age groups. The authors also reported a significant within-subgroup difference in recurrence rates associated with immobilization on day 1 (p = 0.024) but not in rates associated with immobilization on days 2 and 3.

The users’ guide

Using previously proposed rules,^11–16 the subgroup analysis in the RCT of the clinical example can now be examined on a point-by-point basis (Box 1). Although the example is a nonoperative one, similar guidelines can be applied to RCTs on operative interventions.

Box 1.

Users’ guide for a randomized controlled trial employing a subgroup analysis in surgery^11–16

Design

• Was the subgroup analysis based on a rational indication?

• Was the subgroup analysis predefined or was it carried out post hoc?

• Was the subgroup analysis one of a small number?

• Did the power calculation account for between-subgroup treatment effects?

• Were subgroup definitions based on prerandomization patient characteristics?

• Was randomization stratified for important subgroup variables?

Analysis

• Were interaction tests used for assessing subgroup treatment effect interactions?

• Were the significances of treatment effect interactions adjusted for multiplicity?

• Were the subgroups checked for comparability of prognostic factors?

Reporting

• Are all performed subgroup analyses reported?

• Are subgroup analyses reported as relative risk reductions?

• Does the emphasis of the discussion and conclusion remain on the overall treatment effect?

Applicability

• Is the subgroup difference consistent across other studies?

• Is the subgroup effect or interaction clinically important?

• Are the patients in the subgroup comparable to my patients?

• Is the between-subgroup treatment effect clinically important?

Design

Was the subgroup analysis based on a rational indication?

The first step in evaluating a subgroup analysis is to determine its logical sense. In line with the main RCT analysis (i.e., comparing the primary outcome between the treatment and control groups), a sensible rationale should be the basis of every subgroup analysis. When undertaken without any clinical explanatory background, no subgroup analysis will attain practical utility, no matter how significant the results are.¹¹ So when are subgroup analyses rationally justified? Patient groups that are expected to have different treatment effects compared with the general trend may be analyzed as separate groups, but only if explained by differences in risk of attaining a certain outcome or by differences in pathophysiology.¹² For example, it may be advantageous for low-risk patients to be investigated separately since potentially harmful interventions could be of no benefit to them. Especially in surgical trials in which mortality is a frequently measured outcome, it is of great importance that patients with a high mortality risk will be recognized and analyzed separately. As for subgroups based on pathophysiology, differences in underlying disease mechanisms could induce heterogeneity in treatment effect and therefore justify a subgroup analysis. The report by Itoi and colleagues¹⁰ explains that the subgroup of patients younger than 30 years was chosen because of previously demonstrated increased risk for redislocation in this group. However, it does not provide a rationale for analyzing this subgroup for treatment–control differences in secondary outcomes (compliance, sports participation, shoulder stiffness). Results would have made more sense if the authors had expressed evidence-based hypotheses that secondary outcomes would particularly decrease in this age group. Similarly, they did not justify their subgroup analysis based on the delay between dislocation and immobilization.

Was the subgroup analysis predefined or was it carried out post hoc?

Subgroup analyses that are performed to test hypotheses generated before the study has started should be clearly distinguished from those identified after the main trial analyses are performed.¹⁴ Post hoc analyses are encountered often because unexpected results might lead to a wide scale of new hypotheses. Such analyses are generated by the trial data rather than the data being tested, and they should be regarded as unreliable unless they can be replicated by other studies.¹² However, post hoc observations are not automatically invalid and can have important clinical consequences.

Besides predefining the subgroup variables, the expected direction (the same or the opposite direction as the overall treatment effect) and the magnitude of the subgroup effects should be reported at the beginning of the trial.¹² Also, the exact definitions and categories of the subgroup variables should be predefined. This will avoid post hoc definitions or interpretations that suit the authors’ conclusions and retroactively fit the data. For example, the results of a certain subgroup analysis can become statistically significant when an alternative definition is used.¹³

In the study by Itoi and colleagues,¹⁰ both the subgroups based on the immobilization day and the subgroups based on age were predefined. However, in the description of the statistical analysis in the methods section, they state that they analyzed a subgroup of patients aged 30 years or younger and that they categorized age in 4 subgroups, but they do not define the subgroups in that section. In the discussion section, the authors report the results for a subgroup of patients aged 30 years or younger, but they analyzed 2 different groups under the age of 30 individually, of which the results were significant in the subgroup of patients aged 21–30 years. This illustrates the importance of exact predefined definitions of the subgroup categories.

Was the subgroup analysis one of a small number?

The chance of falsely obtaining significant subgroup effects and interactions (i.e., type 1 errors) increases quite dramatically when many subgroup analyses are performed.¹⁷ For subgroup effects, false-positive results are found in 1 subgroup in 7%–66% of trial simulations. For interactions, the rate of false-positive results is stable at 5% of the number of tests performed.^14,18 To minimize the risks of chance and sampling error, the subgroup analyses should be restricted.

The number of subgroup analyses is the product of the number of subgroups and the number of outcomes analyzed. Therefore, the outcome measures used to compare subgroups should be limited to the primary outcome of the main trial and secondary outcomes that are unique to specific subgroups. In addition, the number of subgroups should be limited. For example, it may be preferable to divide the total sample based on age into 2 groups (≤ 50 and > 50 yr) instead of multiple groups (e.g., 0–10, 11–20, 21–30, 31–40 yr). This may prevent subgroups from becoming too small, thereby reducing the chance of false-negative results. In addition to the methodological setbacks, conducting too many subgroup analyses will result in confusion for both readers and authors. Exhausting subgroup analyses distract readers from the key message concerning the observed overall effect. Additionally, it is hard for authors to discuss their results in a well-organized and clear manner.

Itoi and colleagues¹⁰ basically repeat their main effect analyses on their subgroup of patients aged 30 years and younger. Adding to the complexity, they further subdivide this subgroup based on the delay between dislocation and immobilization. In fact, this is a double subgroup analysis, which should certainly be interpreted cautiously.

Did the power calculation account for between-subgroup treatment effects?

The power of a trial is the ability to detect a difference between 2 groups if one truly exists and is positively correlated with the magnitude of the treatment effect and the sample size of the study.

Generally, the sample size of a trial is just large enough to detect an overall treatment effect with a power of 80%. It is very unlikely for these trials to detect subgroup effects or interactions because subgroups always include fewer patients than the main treatment groups. Consequently, subgroup analyses are frequently underpowered, which means there is a greater probability of false-negative results.^11,13 For a subgroup analysis to be reliable, the trial power calculation should have accounted for the subgroups. For detection of interactions of the same size and with the same power as the overall effect, the sample sizes should be inflated 4-fold.¹⁸ However, interaction effects are considerably smaller than overall treatment effects. This means that even larger sample sizes are needed, and these are very unlikely to achieve in practice. Therefore, it would be more reliable to look at the overall results of a study than the apparent effect observed within a subgroup.

In the study by Itoi and colleagues,¹⁰ the sample size was calculated for a power of 80% to detect an overall effect, but this calculation did not account for subgroups. Because the authors applied the same statistical test for each within-subgroup analysis, they would have needed the same number of patients in each subgroup as the number calculated for the overall treatment groups (42 patients for each group) to reach a similar power for each subgroup analysis. As the sample size needed for a certain power is also dependent on the estimated effect size, the subgroups should have contained even more patients to detect a smaller effect than the overall effect. Except for the immobilization with IR and ER on day 1 subgroups, none of the other subgroups contained a sufficient number of patients, which means that the probability of false-negative (nonsignificant) results was large for all these subgroups. The results from the subgroup analyses are therefore probably not valid, and the conclusion about the absence of treatment effect should be questioned.

Were subgroup definitions based on prerandomization patient characteristics?

A variable by which a subgroup is defined should not be affected by treatment response. Thus, only disease characteristics obtained before randomization and independent patient characteristics (e.g., age, sex, tumour grade) can be used to subdivide the main analysis. If subgroups are based on outcome-dependent data, an observed interaction may be simply the result of one subgroup that had a better prognosis rather than being truly caused by the treatment. For example, comparing compliant to noncompliant patients is invalid since compliance is related to prognosis.¹⁹ In operative trials, a patient’s “compliance” with an assigned procedure more often refers to whether he or she has refused the allocated treatment and has crossed over to another intervention. Comparing treatment effects for patients who did and did not crossover would cause misleading results. After all, crossover patients have significantly different prognostic characteristics than patients who receive the treatment to which they were randomly assigned.²⁰ In their recent trial investigating the efficacy of operative compared with nonoperative treatment of lumbar disk herniation, Weinstein and colleagues²⁰ found that patients who crossed over to surgery had lower incomes and worse baseline symptoms than those who underwent nonoperative treatment. Additionally, patients who crossed over to nonoperative care were older, had less pain and experienced less disability.

For a subgroup analysis to be clinically applicable, surgeons need to know what types of patients are going to benefit from a type of treatment before they decide on a treatment option. Itoi and colleagues¹⁰ specified their subgroups by patient age and by the day immobilization was started. These variables cannot have been influenced by the effect of immobilization in any way.

Was randomization stratified by important subgroup variables?

In the design of a trial with predefined subgroups, stratification of randomization by important subgroup variables should be considered.¹² Stratified randomization leads to a greater similarity between treatment groups with regard to prognostic factors that influence treatment effect and can reduce the chance of both type I and II errors.²¹ It is especially beneficial for trials with a small sample size in which the risk for an imbalance between prognostic factors and for type I errors is very large. Because subgroups usually are of limited size, it cannot be assumed that prognosis at baseline is similar among subgroups unless randomization was stratified.²² However, when the size of the subgroup is sufficiently large, the chance of subgroup incomparability might be small even though randomization was not stratified.

When stratification of randomization is based on subgroup variables, it is more likely that treatment assignments within subgroups are balanced, making each subgroup a small trial. Because randomization makes it likely for the subgroups to be similar in all aspects except treatment, valid inferences about treatment efficacy within subgroups are likely to be drawn.²³ In post hoc subgroup analyses, the subgroups are often incomparable because no stratified randomization is performed.²² Additionally, stratified randomization is desirable since it forces researchers to define subgroups before the start of the study.²¹

In the study by Itoi and colleagues,¹⁰ no stratified randomization for subgroup variables was performed. They compared the mean age and other patient characteristics for statistical significance between the 2 treatment groups postrandomization. However, they did not compare the groups with regard to the age categories and the day immobilization was started.

In trials comparing 2 operative interventions, surgical skill may be of major importance in determining treatment results.³ When no stratification by surgeon has occurred, subgroups may be incomparable with respect to the surgeon’s operating skill. For example, in an RCT comparing stentless and stented bioprostheses for aortic valve disease, Narang and colleagues²⁴ defined 2 subgroups by preoperative left ventricular ejection fraction (< and ≥ 50%). Despite the small sample size (n = 62), the randomization was not stratified by surgeon. In the subgroup with an ejection fraction less than 50%, stentless bioprostheses had a favourable effect on the left ventricular ejection fraction and the effective aortic orifice area. However, this difference may have been due, by chance, to stentless operations having been performed by more skilled surgeons than stented procedures.

Analysis

Were interaction tests used for assessing between-subgroup treatment effect interactions?

One should not question whether a treatment is efficacious in subgroup 1 and subgroup 2 separately (both subgroup effects), but if treatment efficacy differs between subgroup 1 and 2 (an interaction; Table 1) The former is investigated by simple tests as used for the main analysis (e.g., a Student t test or a χ² test), and the latter is investigated by a formal test of interaction. The most frequently used formal interaction tests include the Mantel–Haenszel technique and regression models.²⁵ Although they have a standard 5% type I error rate, they are likely to be under-powered.¹⁸ This may be one of the reasons why still 37% of RCTs report only subgroup effects.²

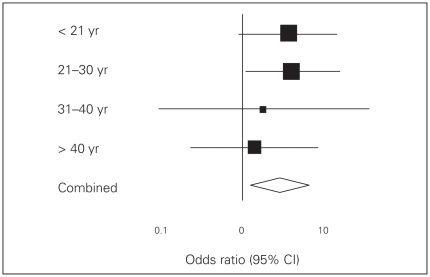
To illustrate the misleading nature of testing for separate subgroup effects, we can use the analysis of treatment effect subdivided by age in the study by Itoi and colleagues.¹⁰ Figure 1 displays a comprehensive overview of the subgroup data presented in their report. The vertical line indicates similar risks of dislocation recurrence between the ER and IR groups. An odds ratio (OR) greater than 1 favours immobilization in the ER group.

Fig. 1.

Forest plot of the results of the age-based subgroup analysis by Itoi and colleagues.¹⁰ CI = confidence interval.

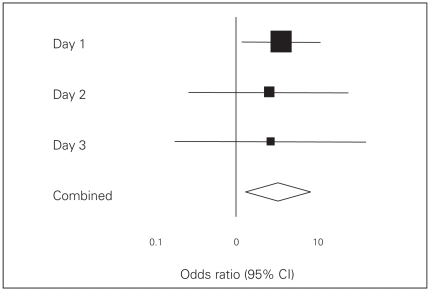
The authors tested the difference in recurrence rate in each subgroup with a χ² test to find a significant effect in the subgroup of patients aged 21–30 years. Because the other groups were too small, the ORs were not significant. Yet, ORs were greater than 1 in all subgroups, as can be seen by the position of the black squares in Figure 1. Furthermore, the 95% confidence intervals (CIs) are wide. In fact, they all overlap, suggesting that the treatment effects do not differ between subgroups. It would thus be invalid to conclude that external mobilization is better, particularly (as the authors did) in patients aged 21–30 years. The same comments apply to their subgroup analysis by day of immobilization (Fig. 2).

Fig. 2.

Forest plot of the results of the subgroup analysis on the day of immobilization by Itoi and colleagues.¹⁰ CI = confidence interval.

Using an interaction test would not have been appropriate here since the sample size is probably too small for adequate power. Rather, a careful description of the subgroup effects, emphasizing the similarity of patterns across all subgroups, would have been more representative of the underlying truth.

Were the significances of treatment effect interactions adjusted for multiplicity?

As mentioned earlier, the greater the number of subgroup analyses performed, the greater the probability of a positive finding caused by chance alone. Therefore, the significance of within-subgroup treatment effects should be adjusted for multiplicity when multiple subgroup analyses are performed simultaneously.¹²

A commonly used method for adjusting is dividing the overall significance level by the total number of subgroup analyses, also called the Bonferroni method. For example, in a study with a significance level of 0.05 and 10 subgroup analyses, the significance level for each subgroup analysis would be 0.005. However, some statisticians state that significant results are rarely observed after adjustment with the Bonferroni method.²⁶ Therefore, other methods for p value adjustment have been proposed. However, the complexity of these methods makes them fall beyond the scope of the present article.

In the study by Itoi and colleagues,¹⁰ no adjustments for multiplicity were made, as the p value was set at the 0.05 level for all subgroup analyses.

Were the subgroups checked for comparability of prognostic factors?

In most subgroup analyses, the randomization is not stratified for subgroup variables. As mentioned above, the chance of incomparability of subgroups is reduced by stratifying randomization for subgroup variables. However, imbalances regarding prognostic factors may still be present after stratified randomization owing to chance.¹⁵ Therefore, it is important to check the subgroups for comparability of prognostic factors after randomization, especially for the factors that are expected to bias the treatment effect. If an imbalance in prognostic factors between the subgroups exists, the investigators of the study should describe it explicitly to warn readers to be cautious with the interpretation of the results. If possible, the subgroup analysis should be adjusted for important prognostic factors (e.g., with regression techniques).

Reporting

Are all performed subgroup analyses reported?

The validity of a subgroup analysis depends to a great extent on how many other subgroup analyses were performed but not reported.¹² As stated in our guidelines for analysis, the probability of a positive finding due to chance increases when multiple analyses are performed simultaneously. Often, the investigators deliberately report only the significant analyses. In this case, the reader might falsely conclude that there is a difference in treatment effect because they consider the results to be fairly reliable when they are not.

Are subgroup analyses reported as relative risk reductions?

In general, there are 2 ways to report the magnitude of an observed treatment effect. The absolute risk reduction is the difference in the absolute risk for a certain outcome between the patient group with and without the treatment, whereas the relative risk reduction gives an estimate of the proportion of risk that is removed by the treatment.

It would be favourable to use relative risk reductions when describing subgroup effects, because they tend to be more similar across risk groups than absolute risk reductions.^27,28 When patients have a low baseline risk, the absolute risk reduction after treatment can never be of a substantial magnitude, whereas the absolute risk reduction in a high-risk group is often very large after treatment. However, since the high-risk group has a high baseline risk, the relative risk reduction could still be similar in the low-risk group. So, based on absolute risk reductions, one would conclude more easily that there is a difference in treatment effect between 2 subgroups, although no difference in relative risk reduction actually exists.

In the article study by Itoi and colleagues,¹⁰ both the relative and absolute risk reductions are reported for the dislocation recurrence rate in the subgroup of patients aged 30 years or younger. No risk reductions are reported for the subgroups based on day of immobilization, but a calculation can be made by the reader using the recurrence percentages from the table.

Does the emphasis of the discussion and conclusion remain on the overall treatment effect?

Early in the discussion of their results, Itoi and colleagues¹⁰ interpret that starting immobilization on day 1 led to better results than days 2 and 3. In addition, they state that patients aged 30 years or younger particularly benefitted from immobilization in ER. Textually, the subgroup findings receive more attention than the overall result. This is surprising because the main study finding is the topic of most of the discussion. If there had been no significant overall treatment effect, subgroup findings might have merited more emphasis. In the conclusion the authors again pay attention to a subgroup finding, influencing their main statement unjustly.

Irrespective of particular methodological limitations as described by the above criteria, subgroup analyses should not affect a trial’s conclusion since they are exploratory in nature. Still, subgroup results are used in more than 25% of RCTs to support the conclusion.²

Applicability

Is the subgroup difference consistent across other studies?

When a subgroup interaction effect is consistent across other studies, it becomes far more credible than when it is observed in a single study.^11,16 The best index to its credibility would be the consistency in a systematic review of the relevant literature with a high level of evidence. Reproducibility of a subgroup treatment effect might contribute even more to the validity of a subgroup analysis than the significance of the effect.¹² That is, an anticipated subgroup interaction effect might be more believable when it is underpowered but reproducible, than an unanticipated effect that is highly significant but not consistent across other studies.

However, comparisons of subgroup analyses across studies should be performed with caution for 2 reasons.¹¹ First, many subgroup analyses are small in size and therefore underpowered, making the results unreliable. Second, studies almost always differ is their designs, populations, interventions and outcomes, thereby making them incomparable to one another.

Itoi and colleagues¹⁰ reported that the recurrence rate of shoulder dislocation was much higher among young patients. However, they did not note that the ER immobilization had better treatment effects than IR immobilization in other studies involving patients aged 30 years or younger. Regarding the subgroup effect associated with the day on which immobilization was started, there were also no other studies with similar findings mentioned.

Is the subgroup effect or interaction clinically important?

To decide whether an observed subgroup effect or interaction is clinically important, one should first judge whether the subgroup analysis was performed based on a rational indication.

Second, a subgroup effect or interaction is only clinically important when the treatment studied is frequently administered to patients.

Also, the subgroup variables, including demographic variables, comorbid conditions, tumour grade or severity of deformity, should be commonly used so that results from subgroup analyses can easily be applied to common patient populations.

The outcomes in which the differences in treatment effect are represented should be clinically important too. In the clinical scenario presented earlier, you would not be as interested in a difference of treatment effect on level of sports as you would be in a difference in effect on recurrence rate of dislocation.

Further, the magnitude of the subgroup effect or interaction can contribute to its importance. For example, when a certain subgroup of patients experiences far fewer complications after a treatment, that treatment method may be extended to patients with less severe conditions. Also, if there is an overall treatment effect and a very small difference in treatment effects between subgroups is observed, the treatment may still be applied to all subgroups, even if the difference is statistically but not clinically significant.

Are the patients in the subgroup comparable to my patients?

Although a subgroup may seem comparable to your own patients at first sight, it is necessary to look critically at the subgroup patients’ characteristics before applying the findings into practice. Since a randomized controlled trial uses very stringent inclusion and exclusion criteria, the patients from the trial sample are almost never similar to your patients. Differences could include comorbidities, cointerventions and several patient demographic characteristics. A subgroup analysis should make it easier to judge the applicability of trial results. However, when applying the results of a subgroup analysis, the inclusion and exclusion criteria of the total sample should be kept in mind.

In the clincial scenario of the 25-year-old woman with an initial anterior shoulder dislocation, the results of Itoi and colleagues’¹⁰ subgroup analysis of patients aged 21–30 years could be applied if the woman meets the inclusion criteria of the total sample from which the subgroup was derived; she should have presented within 3 days after the dislocation and should have had no associated fractures of the shoulder.

Discussion

After reading the article by Itoi and colleagues,¹⁰ you conclude that immobilization in ER would reduce the risk of a recurrent dislocation of the shoulder for your 25-year-old patient. However, you drew this conclusion based on the overall study results, since it was a well-conducted RCT with sufficient power to detect an overall treatment effect. You consider the results of the subgroup analyses to be unreliable, since they were performed without a proper interaction test and were underpowered to detect a difference in treatment effect. Thus, you infer no difference between patients younger and older than 30 years and treat them all with immobilization in ER instead of IR.

Conclusion

As targeting therapy is increasingly used in clinical practice, surgeons encounter many subgroup analyses in the literature. In this article, we provided guidelines for the design, analysis and reporting of subgroup analyses in RCTs. When these guidelines are not followed, subgroups may not be as comparable to one another as the main treatment groups and may be analyzed using incorrect statistical tests. Also, subgroup analyses may often yield false-negative and false-positive results and receive too much attention compared with the main analysis. As such, subgroup results have too much weight in study conclusions and thus in routine surgical practice. However, subgroup analyses can result in improved precision in assigning treatments, provided the discussed criteria have been taken into account.

Before applying the results into clinical practice, one should question to what extent the patients from the subgroup are comparable to the target population and whether the findings are clinically important.