Abstract
Background/Objective:
It is suspected that the speed of the motion of the spinal cord under static compression may be the cause of spinal cord injury (SCI). However, little is known about the relationship between the speed of the motion of the spinal cord and its stress distributions. The objective was to carry out a biomechanical study of SCI in patients with ossification of the longitudinal ligament without radiologic evidence of injury.
Methods:
A 3-dimensional finite element spinal cord model was established. After the application of static compression, the model underwent anterior flexion to simulate SCI in ossification of the longitudinal ligament patients without radiologic abnormality. Flexion of the spine was assumed to occur at 1 motor segment. Flexion angle was 5°, and flexion speeds were 0.5°/s, 5°/s, and 50°/s. Stress distributions inside of the spinal cord were evaluated.
Results:
Stresses on the spinal cord increased slightly after the application of 5° of flexion at a speed of 0.5°/s. Stresses became much higher at a speed of 5°/s and increased further at 50°s.
Conclusions:
The stress distribution of the spinal cord under static compression increased with faster flexion speed of the spinal cord. High-speed motion of the spinal cord under static compression may be one of the causes of SCI in the absence of radiologic abnormality.
Keywords: Spinal cord injuries, Cervical spine, Myelopathy, Ossification of the posterior longitudinal ligament, Finite element method, Biomechanics, SCIWORA (Spinal Cord Injury Without Radiographic Abnormality)
INTRODUCTION
Ossification of the posterior longitudinal ligament (OPLL) is a well-known cause of myelopathy and is generally considered to be slow and progressive. However, minor trauma, such as falls and impacts to the head, in patients with OPLL can result in acute spinal cord injury (SCI) without radiologic evidence of abnormality. Some authors have reported cervical cord injury in OPLL patients without radiologic bone abnormality (1,2). Mihara reported 10 cases of cervical cord injury in patients with OPLL (2). None had radiologic bone abnormality, and 6 suffered only very minor trauma. One was a flexion injury with no bony pincers mechanism or buckling of the ligamentum flavum. In some of these cases, additional compressions may not have impacted upon the spinal cord. The velocity of spinal cord flexion under compression may therefore become a cause of SCI. In this report, we simulate flexion injury in patients with SCI and evaluate the influence of spinal cord flexion velocity on SCI using a 3-dimensional finite element method (3D FEM).
METHODS
3D FEM Model
A standard solid model with a nonlinear component was used to simulate the viscoelasticity of the spinal cord. Linear elastic elements (Ee), nonlinear elastic elements (Ec), and a viscous element (C) were connected to form a time-dependent material response. Elastic parameters and viscous coefficients were determined mathematically using data obtained from tensile tests of fresh bovine spinal cord. The constitutive equation needed for the FEM calculation in this model was established previously, and the details are described elsewhere in the literature (3).
Elastic parameters and viscous coefficients were determined mathematically using data obtained by the tensile test of bovine spinal cord. To determine the mechanical properties of the gray and white matter, the data obtained by the tensile stress strain curve and stress relaxation under various strain rates were used. The mechanical property of the pia mater was obtained from the literature (4).
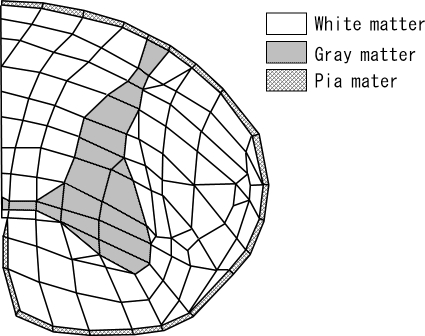
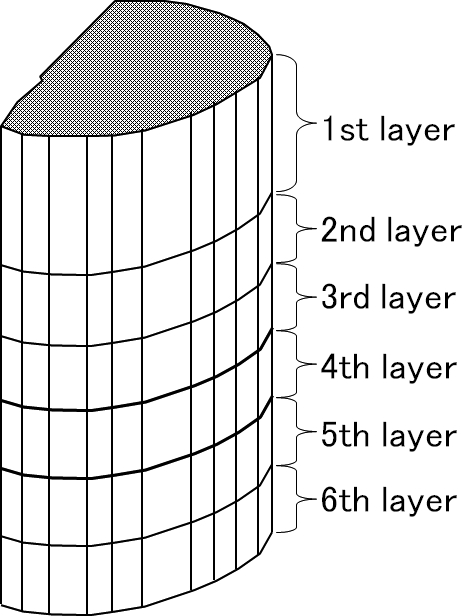
A 3D-FEM spinal cord model was developed consisting of gray matter, white matter, and pia matter (Figure 1). To simplify calculations, the model consisted of 1 motion segment. The spinal cord model was at the level of upper vertebra, intervertebral disk, and upper half of lower vertebra and was assumed to be of segmental type OPLL. The spinal cord of upper vertebral level was composed of the first, second, and third layers, and the fourth layer was the intervertebral disk level. The fifth and sixth layers were the upper half of the lower vertebral level. The spinal cord close to the center of rotation was sliced into thin layers to observe the stress distributions minutely (Figure 2). By assuming the spinal cord to be symmetric, the left half model was established to simplify calculations. The total number of isoparametric 20-node elements was 780, and the total number of nodes was 3,643 (3).
Figure 1.
Cross-sectional views of stress distributions after 5° of flexion in the 0.5°/s model.
Figure 2.
Cross-sectional views of stress distributions after 5° of flexion in the 5°/s model.
Static Compression Model
For simulation of segmental OPLL, anterior static compression was applied to the first, second, third, fifth, and sixth layers of the model, and stress distributions in each layer of the spinal cord were computed. The degree of compression was 20% of the anteroposterior diameter of the spinal cord. As a simulation of OPLL compression, the rigid plate parallel to the coronal plane compressed the anterior surface of the spinal cord. The spinal cord was supported from behind by the rigid body along the posterior border of the spinal cord, simulating lamina.
Flexion Model Simulating SCI Without Radiographic Abnormality
To evaluate the influence of flexion speed on SCI without radiographic abnormality, the spinal cord model under static compression was flexed anteriorly. Anterior flexion was considered to exclude the bony pincers mechanism and anterior slack of the ligamentum flavum that occurred in extension and also compressed the spinal cord. Thus, the influence of flexion speed could be evaluated independently. Static compression was first applied to the model. The compression condition was the same as for the static compression model above. Nodes of the spinal cord model at the fifth and sixth layers and in contact with the anterior compressing plane and posterior supporting plane were restrained from anteroposterior deformation. Next, anterior flexion was applied to the spinal cord model. The enforced displacement was applied to the nodes of the spinal cord model at the first, second, and third layers in contact with the anterior compressing plane and posterior supporting plane. Flexion was set at 5° to simulate a light injury. The angular velocities of the flexion were 0.5°/s, 5°/s, and 50°/s. One second is needed for 5° of flexion at 5°/s. This motion velocity is considered within the range of normal physiologic movement. To study the effect of the differences in angular velocity, 2 other velocities were also chosen. One was 0.5°/s, which was one tenth of the velocity and considered to be slow compared with 5°/s. The other was 50°/s, which was 10 times the velocity and considered to be fast compared with 5°/s. Nodes of the fourth layer corresponding to the intervertebral disk level were not restrained.
The stress distributions in each slice of the spinal cord model were calculated using the von Mises stress criterion.
RESULTS
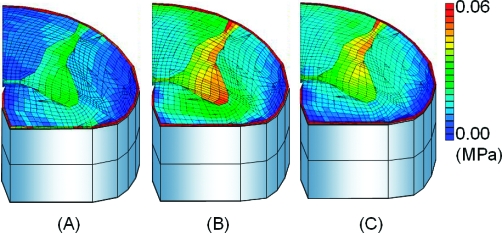
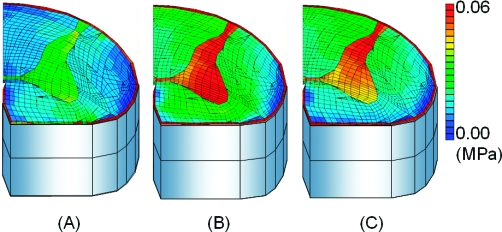
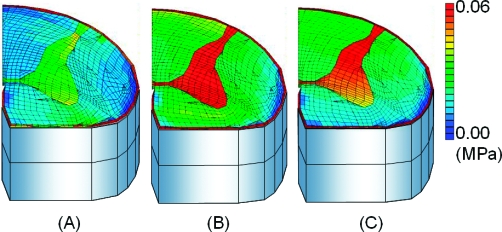
After the application of 5° of flexion at 0.5°/s, stresses of the spinal cord increased and were concentrated in gray matter. The stress of the uncompressed layer at the intervertebral disk level was higher than the upper and lower vertebral level (Figure 3). After the application of 5° of flexion at 5°/s, the stresses in the spinal cord became much higher than those observed at 0.5°/s (Figure 4). After the application of 5° of flexion at 50°/s, stresses in the spinal cord increased above those seen at 5°/s (Figure 5). The highest stress distributions were observed at the fourth layer. The fourth layer of the intervertebral disk level was the motion level, and the highest distributions were observed at all angle velocities.
Figure 3.
Cross-sectional views of stress distributions after 5° of flexion in the 50°/s model. (A) Upper vertebral level (third) layer. (B) Flexed disk level (fourth) layer. (C) Lower vertebral (fifth) layer.
Figure 4.
Cross-sectional views of stress distributions after 0.5°/s. (A) Upper vertebral level (third) layer. (B) Flexed disk level (fourth) layer. (C) Lower vertebral (fifth) layer.
Figure 5.
Cross-sectional views of stress distributions after 5°/s. (A) Upper vertebral level (third) layer. (B) Flexed disk level (fourth) layer. (C) Lower vertebral (fifth) layer.
The difference in stress distributions between 5°/s and 50°/s was smaller than the difference observed between 0.5°/s and 5°/s.
DISCUSSION
OPLL disease is a well-known cause of cervical myelopathy. Okano reported that one quarter of cases showed aggravation during a mean follow-up period of 6 years, whereas the remainder did not change (5). However, it is also known that OPLL myelopathy can present or can aggravate neurologic symptoms shortly after a minor trauma without radiologic abnormality (e.g., fall, head impact). In a retrospective study of OPLL patients with myelopathy, Matsunaga et al (6) reported that trauma was the cause of onset of myelopathy in 24 of 184 patients (13%). These authors studied patients with OPLL and without myelopathy. In this prospective study, 70 of 368 patients (19%) developed myelopathy during the follow-up period, and 9% developed trauma-induced myelopathy (6). Several other authors have also reported a link between minor trauma and the onset or aggravation of myelopathy (7–10).
Inward bulging of the ligamentum flavum during hyperextension was proposed by Taylor (11) as a cause of SCI without radiologic abnormality. On the other hand, Penning (12) proposed the bony pincers mechanism in cervical extension as a cause of cervical myelopathy. Both theories have so far been considered as the cause of SCI without radiologic abnormality.
However, patients with OPLL and myelopathy include some cases whose onset is thought to be due to flexion injury or minor trauma. In such cases, inward bulging of the ligamentum flavum or the bony pincers mechanism may not have occurred. Henderson et al (13) described how flexion could stretch the spinal cord, leading to its deformation and the generation of injurious shear and strain in the constituent axon. Therefore, we investigated whether high-speed motion of the spinal cord under compression by OPLL might cause neurologic deterioration in these patients.
The finite element method has recently been used for the study of SCI. Ichihara et al (14) used a finite element model and analyzed stress distribution under compression. They described a detailed computer simulation method and used a well-established, although 2-dimensional, model. In contrast, a more physiologic 3D model was used in the present study and allowed us to add motion to the spinal cord.
Conditions were established in a simulation model to evaluate the effect of flexion velocity of the spinal cord on minor trauma in patients with OPLL. First, a flexion model was used to exclude additional compression by ligamentum flavum or posterior listhesis of the vertebra. Second, to simulate minor trauma, the flexion angle was set at 5° so that it was within the normal range of motion. Third, to compare the stress distributions of the spinal cord in relation to the velocity of the flexion, 3 different velocities (0.5°/s, 5°/s, and 50°/s) were applied to the model.
The stress distribution increased progressively as the flexion velocity increased from 0.5°/s to 5°/s and from 5°/s to 50°/s. The difference in stress distributions at speeds of 5°/s to 50°/s was not as large as the difference observed at 0.5°/s to 5°/s.
Additional and clinically relevant data were obtained from this simulation. At any velocity, the highest stress distributions were observed at the fourth layers, compromising the disk levels. Thus, when additional compression was not applied to the spinal cord, spinal cord motion was considered to be an important factor for injury. This is the reason the edge or noncontinuous portion of the OPLL is often the responsible level of the myelopathy induced by OPLL.
CONCLUSIONS
We investigated whether the motion velocity of the spinal cord itself could be a cause of neurologic deterioration in patients with OPLL after minor trauma without radiologic abnormality. The motion velocity of the spinal cord under static compression might become a cause of SCI. We studied the effect of flexion velocity of the spinal cord in patients with OPLL myelopathy using 3D-FEM simulation. The stress distribution of the spinal cord under static compression increased progressively after an increase in the angler velocity of flexion of the spinal cord. However, the increased stress distribution did not correlate linearly with the increase in speed of flexion velocity. We conclude that in patients with OPLL, the motion velocity of the spinal cord under static compression may induce SCI without radiologic abnormality.
REFERENCES
- Ueta T, Shiba K, Katsuki M. Mechanism of injury and instability of cervical cord injuries without radiological remarkable XP evidence of injury [in Japanese] Rinsho Seikeigeka. 1989;24:483–490. [Google Scholar]
- Mihara K, Torigoshi T, Konishi H. Cervical spinal cord injury with ossification of the posterior longitudinal ligament [in Japanese] Seikeigeka to Saigai Geka. 1991;40:763–765. [Google Scholar]
- Kato Y, Kataoka H, Ichihara K. Biomechanical study of cervical flexion myelopathy using a three-dimensional finite element method. J Neurosurg Spine. 2008;8(5):436–441. doi: 10.3171/SPI/2008/8/5/436. [DOI] [PubMed] [Google Scholar]
- Tunturi AR. Elasticity of the spinal cord, pia and denticulate ligament in the dog. J Neurosurg. 1978;48:975–979. doi: 10.3171/jns.1978.48.6.0975. [DOI] [PubMed] [Google Scholar]
- Okano T, Sakou T, Taketomi E, Matsunaga S, Ijiri K, Iwao S. Natural history of ossification of posterior longitudinal ligament [in Japanese] J West Jpn Res Soc. 1994;20:83–86. [Google Scholar]
- Matsunaga S, Sakou T, Hayashi K, Ishiduo Y, Hirotsu M, Komiya S. Trauma-induced myelopathy in patients with ossification of the posterior longitudinal ligament. J Neurosurg. 2002;97(2 suppl):172–175. doi: 10.3171/spi.2002.97.2.0172. [DOI] [PubMed] [Google Scholar]
- Fujimura Y, Nakamura M, Toyama Y. Influence of minor trauma on surgical results in patients with cervical OPLL. J Spinal Disord. 1998;11(1):16–20. [PubMed] [Google Scholar]
- Katoh S, Ikata T, Hirai N, Okada Y, Nakauchi K. Influence of minor trauma to the neck on the neurological outcome in patients with ossification of the posterior longitudinal ligament (OPLL) of the cervical spine. Paraplegia. 1995;33(6):330–333. doi: 10.1038/sc.1995.74. [DOI] [PubMed] [Google Scholar]
- Kawai S, Saika M. Ossification of the posterior longitudinal ligament: clinical results [in Japanese] Kotsu Kansetsu Jintai. 1990;3:567–572. [Google Scholar]
- Saika S, Kawai S, Sunago M. Cervical myelopathy due to OPLL induced by minor trauma [in Japanese] Seikeigeka to Saigai Geka. 1988;36:794–796. [Google Scholar]
- Taylor AR. The mechanism of injury to the spinal cord in the neck without damage to the vertebral column. J Bone Joint Surg Br. 1951;33-B(4):543–547. doi: 10.1302/0301-620X.33B4.543. [DOI] [PubMed] [Google Scholar]
- Penning L. Some aspects of plain radiolography of the cervical spine in chronic myelopathy. Neurology. 1962;12(8):513–519. doi: 10.1212/wnl.12.8.518. [DOI] [PubMed] [Google Scholar]
- Henderson FC, Geddes JF, Vaccaro AR, Woodward E, Berry KJ, Benzel EC. Stretch-associated injury in cervical spondylotic myelopathy: new concept and review. Neurosurgery. 2005;56(5):1101–1113. [PubMed] [Google Scholar]
- Ichihara K, Taguchi T, Sakuramoto I, Kawano S, Kawai S. Mechanism of the spinal cord injury and the cervical spondylotic myelopathy: new approach based on the mechanical features of the spinal cord white and gray matter. J Neurosurg. 2003;99(3 suppl):278–285. doi: 10.3171/spi.2003.99.3.0278. [DOI] [PubMed] [Google Scholar]