Abstract
This study tested a dynamic field theory (DFT) of spatial working memory and an associated spatial precision hypothesis (SPH). Between three and six years of age there is a qualitative shift in how children use reference axes to remember locations: 3-year-olds’ spatial recall responses are biased toward reference axes after short memory delays, whereas 6-year-olds’ responses are biased away from reference axes. According to the DFT and the SPH, quantitative improvements over development in the precision of excitatory and inhibitory working memory processes lead to this qualitative shift. Simulations of the DFT in Experiment 1 predict that improvements in precision should cause the spatial range of targets attracted toward a reference axis to narrow gradually over development with repulsion emerging and gradually increasing until responses to most targets show biases away from the axis. Results from Experiment 2 with 3- to 5-year-olds support these predictions. Simulations of the DFT in Experiment 3 quantitatively fit the empirical results and offer insights into the neural processes underlying this developmental change.
Within the domain of spatial cognitive development, there is a rich body of research that has identified what is changing as children develop a host of spatial cognitive skills (Plumert & Spencer, 2007). For example, beginning around one year of age there is a transition from coding locations primarily egocentrically to coding locations allocentrically (Acredelo, 1978; Bremner & Bryant, 1977). A second example comes from work by DeLoache and colleagues (e.g., DeLoache, 2000; DeLoache, Miller, & Rosengren, 1997; see also DeLoache, 2004, for a review). These researchers have demonstrated that 2.5-year-olds have difficulty using information about the location of an object in a scale model to find a corresponding object in a large room. Three-year-olds, by contrast, succeed in the same task when they acquire dual representation—an understanding that something can be an object in and of itself and refer to the location of another object in another space. We also know that spatial memory becomes more precise over development between 3 and 11 years, leading to smaller spatial memory errors and less variability in memory responses (e.g., Huttenlocher, Newcombe, & Sandberg, 1994; Plumert, Hund, & Recker, 2007; Schutte & Spencer, 2002; Spencer & Hund, 2003). These examples highlight that developmental changes in spatial cognition can take on both a qualitative and quantitative flavor. Critically, however, there are few cases in the spatial cognitive domain where we understand the mechanisms underlying developmental change (Plumert & Spencer, 2007; Spencer, Simmering, Schutte, & Schöner, 2007). The present paper moves in this direction by focusing on one particular case study—the development of spatial memory.
Remembering the locations of objects is fundamental to successful interaction with the world. Nevertheless, the complexity of many real-world situations can often make it difficult to remember where objects are when they are out of view. One strategy for reducing this complexity is to capitalize on the fact that richly structured contexts are naturally carved into smaller spatial regions—the desk by the window, the shelves by the door, the cabinet across the room. Anchoring memory to these smaller regions can enrich our encoding of locations and can support accurate memory for locations when we need to find hidden objects.
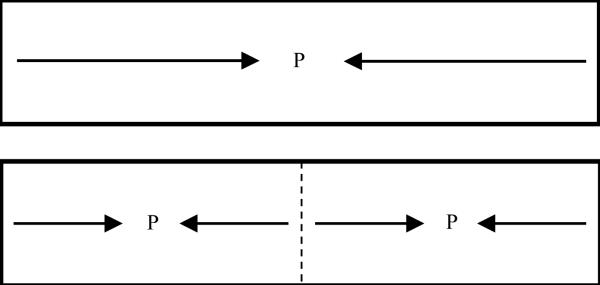
Given the complexity of real-world settings, researchers have often probed children’s ability to remember locations using relatively simple spatial recall tasks. Use of such tasks has revealed that spatial memory undergoes dramatic changes in the first few years of life, particularly with regard to how children anchor memories to the perceived structure of the task space. In a innovative set of experiments, Huttenlocher and colleagues (1994; Newcombe, Huttenlocher, Drummey, & Wiley, 1998) found that early in development there is a transition in how children remember locations relative to the edges and symmetry axes of a rectangular space. Children’s spatial memory abilities were tested using a sandbox task in which the experimenter buries a toy in a long, narrow sandbox, there is a delay, and then the child is allowed to search for the toy. Huttenlocher and colleagues found that between 6 and 10 years of age, there is an inversion in the direction of recall errors: children 6 years of age and younger make errors toward the midline axis of the sandbox, whereas children 10 years of age and older make errors away from the midline axis and toward the center of each half. Figure 1 shows a schematic of these biases. The fact that these biases completely reverse direction suggests a major shift in how children anchor spatial memories to the structure of the task space.
Figure 1.
Schematic of memory biases in the sandbox task. Arrows indicate the direction of memory biases. The dashed line indicates the midline axis of the sandbox, and P’s indicate the location of the CA model prototypes.
The dominant account of this transition in the literature is grounded in a formal theory of spatial recall—the category-adjustment model (CA model) (Huttenlocher, Hedges, & Duncan, 1991; Huttenlocher et al., 1994). According to the CA model, people represent locations in memory at two levels of detail. They represent fine-grained information—the direction and distance of a location from a reference point. In addition, they represent information about the category in which the target is located. A category is a region that is bounded by either visible boundaries (e.g., the edges of a table) or “mentally imposed” reference axes (e.g., the midline symmetry axis of the sandbox). These boundaries and the most prototypical member of the category—the center of the category (see P’s in Figure 1)—are represented in memory. At recall, people combine their fine-grained representation of the location and categorical information. Under conditions of uncertainty (e.g., after a memory delay), people weight prototypical information more heavily. This weighting results in errors that are biased away from category boundaries and toward spatial prototypes (see the P’s in Figure 1).
According to Huttenlocher and colleagues (1994), the transition in geometric categorization over development reflects a change in children’s ability to subdivide space (see also Sandberg, 1999). Specifically, young children treat large, homogeneous spaces as one category with a prototype at the center (see Figure 1, top panel). As a result, children’s responses at recall are biased toward the prototype at the center of the space. Older children and adults, however, subdivide large spaces into two categories with spatial prototypes at the centers of the left and right categories (see Figure 1, lower panel). Thus, older children and adults’ responses are biased away from the midline of the task space and toward prototypes to the left and right.
Although this account explains performance before and after the transition, the CA model says little about how the transition occurs or what is happening across this developmental transition. This leaves us with a host of unanswered questions. For instance, the CA model does not specify how children go from treating large spaces as one category to subdividing the same spaces into two categories. Moreover, this model fails to predict whether the developmental transition is an all-or-none shift from categorizing space using one category to using two categories versus a more gradual transition where children vacillate between use of one and two categories. Finally, the CA model says little about the mechanisms that underlie this developmental transition, that is, the processes that give rise to changes in geometric category use.
In addition to these theoretical questions, there has not been any detailed empirical examination of the transition in geometric categorization. Huttenlocher and colleagues found that the transition occurred between 6 and 10 years of age in the sandbox task (Huttenlocher et al., 1994). Spencer and colleagues (Schutte & Spencer, 2002; Spencer & Hund, 2002; Spencer & Hund, 2003) also documented the transition using a similar spatial memory task. In this task children had to remember the location of a spaceship-shaped target on a large, homogeneous table. Spencer and colleagues found a developmental shift in geometric biases between 3 and 6 years of age (Schutte & Spencer, 2002; Spencer & Hund, 2002; Spencer & Hund, 2003). Critically, all of these studies have probed changes in spatial memory across a broad age range and none have investigated the developmental course of the transition in detail.
The current paper tests whether a new theory of spatial cognition, the Dynamic Field Theory, can capture the detailed developmental course of the transition in geometric categories. The DFT is a dynamic systems approach to spatial cognition instantiated in a particular type of neural network called a dynamic neural field (DNF) which is made up of several layers or fields of neurons one of which is a spatial working memory field. Neurons within this field interact with each other according to a local excitation/lateral interaction function. Specifically, when a neuron is excited it activates nearby neurons and, through an inhibitory field, inhibits neurons that are far away. Through these excitatory and inhibitory interactions the field is able to maintain a peak of activation. Spencer and colleagues (2007; see also Simmering, Schutte, & Spencer, 2008) recently demonstrated that this dynamic neural field model of spatial recall can capture both the early and later endpoints of the transition in geometric biases without recourse to a change in spatial subdivision per se. Rather, changes in the stability of working memory processes as well as changes in children’s ability to use perceived reference frames to anchor the memory of a target location to available perceptual cues result in the transition in geometric biases.
What specific modifications were needed in the model to capture the endpoints of the transition? To accomplish this goal, Spencer et al. (2007) implemented a central developmental hypothesis—the spatial precision hypothesis. According to the SPH, neural interactions become stronger and more precise over development, that is, excitatory interactions become stronger and narrower (i.e., more precise) with an increase in the strength of inhibitory interactions as well (Schutte, Spencer, and Schöner, 2003; Simmering, Schutte, & Spencer, 2008; Spencer et al., 2007; for related ideas, see Westermann & Mareschal, 2004; Mareschal et al., 2007). Figure 2, created using the interaction function equations from Schutte et al. (2003), illustrates this hypothesis. Figure 2 displays different developmental interaction profiles relative to one neuron, x. When neuron x is activated, it excites neurons that code for nearby locations and inhibits neurons that code for locations far away. Early in development excitation is broad and weak and inhibition is also weak (see light grey bold line in Figure 2). Later in development, excitation is strong and precise and inhibition is also strong (see black bold line in Figure 2). Schutte and colleagues (2003) proposed that interaction changes quantitatively over development (see lines in Figure 2), and they tested several predictions generated from this proposal with 2- to 6-year-old children using a sandbox task. All predictions were confirmed, and the data were quantitatively fit using the SPH. Importantly, the changes in neural interaction captured by this developmental hypothesis should also have consequences for how locations are remembered near reference frames and developmental changes in geometric biases. The goal of this report is to probe these consequences using simulations of the DFT and empirical tests of model predictions.
Figure 2.
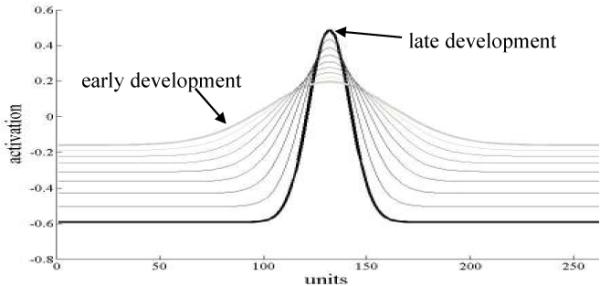
Modulation of interaction function over development created using the interaction function equations from Schutte, Spencer, and Schöner, 2003.
In Simulation Experiment 1 of the present paper, we take the basic account of the endpoints of the transition in geometric biases proposed by Spencer and colleagues and ask whether the step-by-step changes in neural interaction specified by the SPH generate novel predictions regarding the nature of this developmental transition. This is indeed the case. Quantitative manipulation of the precision of neural interactions in the model generated a set of detailed predictions regarding how biases toward/away from midline would change, as well as predicting changes in variability over development. In Experiment 2, we tested these predictions with 3-to 5-year-olds. Results from Experiment 2 generally supported the predictions of Experiment 1, except the bias away from midline did not emerge exactly at the spatial locations predicted by the model. In Simulation Experiment 3, we examined whether the model could capture the specific pattern of bias away from midline over development, which was indeed the case. In the general discussion, we consider the implications of these findings for the DFT and CA accounts of geometric biases, as well as for our understanding of the development of spatial cognition more generally. We contend that the present paper offers the first neurally-grounded theory of the mechanisms underlying changes in spatial cognitive development in early childhood.
Simulation Experiment 1
The Dynamic Field Theory (DFT) of spatial cognition (Schutte, Spencer, & Schöner, 2003; Spencer, Smith, & Thelen, 2001; Spencer & Schöner, 2003; Spencer, Simmering, & Schutte, 2006) captures children’s and adults’ performance in a variety of spatial working memory (SWM) tasks (Schutte & Spencer, 2002; Schutte et al., 2003; Spencer et al., 2006; Simmering, Spencer, & Schöner, 2006). Previously, we used this theoretical framework to account for developmental changes in perseverative errors in a sandbox task (Schutte et al., 2003), as well as categorical biases that emerge as the result of verbal and motor responses (Spencer et al., 2006). Here we build on a new account that captures the endpoints of the developmental transition in geometric biases. This new account relies on two novel insights: (1) that geometric biases result from bias away from perceived reference frames rather than toward spatial prototypes (see Spencer & Schöner, 2003; Spencer et al., 2007), and (2) that developmental changes in spatial working memory can be captured by quantitative changes in the precision of neural interactions that underlie working memory (Edin et al, 2007; Schutte, Spencer, & Schöner, 2003; Simmering et al., 2008; Spencer et al., 2007). In the sections below, we begin by describing the basic theory. Then we discuss how it captures biases away from a reference axis, and, finally, how the model captures developmental changes in geometric biases.
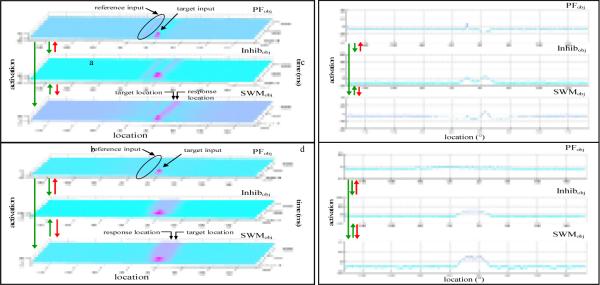
The DFT is a dynamic systems approach to spatial cognition instantiated in a particular type of neural network called a dynamic neural field (DNF). Simulations of our particular DNF model of spatial recall are shown in Figure 3. Figure 3a shows the model using “adult” parameters, and Figure 3b shows the model using young “child” parameters (e.g., 3-year-olds). Each simulation models a single trial in a simple spatial memory task used in Schutte & Spencer (2002) (see Figure 8). In this task, the participant sees a spaceship-shaped target appear on a large, black table top. The target turns off, and following a short delay the computer says “go”. The participant then places a small rocket-shaped marker at the remembered target location. Critically, young children show systematic biases toward the midline symmetry axis in this task (see 0° line in Figure 8 inset), while older children and adults show biases away from the midline axis.
Figure 3.
Adult (a) and child (b) simulations of the Dynamic Field Theory. Panels represent: perceptual field [PFobj]; inhibitory field [Inhibobj]; excitatory working memory field [SWMobj]. Arrows represent interaction between fields. Green arrows represent excitatory connections and red arrows represent inhibitory connections. In each field, location is represented along the x-axis (with midline at location 0), activation along the z-axis, and time along the y-axis. The trial begins at the back of the figure and moves forward. Time slices from the end of the delay for the adult model (c) and the child model (d)
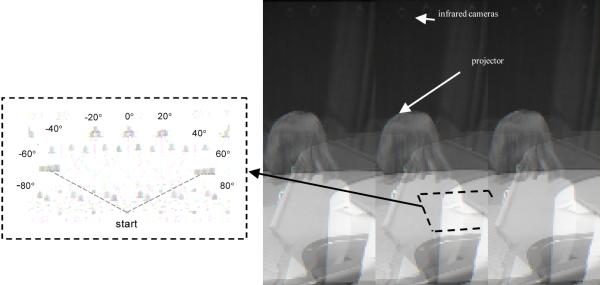
Figure 8.
Apparatus used for spaceship task. Inset shows sample target locations relative to the starting point. Targets are projected onto the table from beneath and responses are recorded using an Optotrak movement analysis system. Note that the lights in the room are turned on for the photograph. During the experiment the lights were dimmed, and the table appeared black.
The model is made up of several layers (or fields) of neurons. In each layer, the neurons are lined up along the x-axis according to their “preferred” locations, that is, the locations for which they fire maximally. The activation of each neuron is on the y-axis, and time is on the z-axis. The top layer in each panel is the perceptual field, PFobj. This field captures perceived events in the task space, such as the appearance of a target, as well as any stable perceptual cues in the task space, such as the midline reference axis. This layer sends excitation to both of the other layers (see green arrows). The third layer, SWMobj, is the working memory field. This field receives weak input from perceived events in the task space and stronger input from the perceptual field. The SWM field is primarily responsible for maintaining a memory of the target location through self-sustaining activation—a neurally plausible mechanism for the maintenance of task-relevant information in populations of neurons (Amari, 1989; Amari & Arbib, 1977; Compte, Brunel, Goldman-Rakic, & Wang, 2000; Trappenberg, Dorris, Munoz, & Klein, 2001). The second layer, Inhibobj, is an inhibitory layer that receives input from and projects inhibition broadly back to both the perceptual field and the working memory field. Note that the layered structure shown in Figure 3 was inspired by the cytoarchitecture of visual cortex (see Douglas & Martin, 1998). Note also that the full model includes longer-term memory layers that we will not consider here, because they do not affect the hypotheses we are testing (for an overview of the full model, see Spencer et al., 2007).
The working memory field, SWMobj, is able to maintain an activation pattern because of the way neurons interact with each other. Specifically, neurons that are sufficiently activated (rising above zero activation from a negative resting level) excite neurons that code for locations that are close by, and—through the Inhibobj layer—inhibit neurons that code for locations that are far away. The result is an emergent form of local excitation/lateral inhibition which sustains activation in working memory in the absence of inputs from the perceptual layer (see Amari, 1989, Amari & Arbib, 1977, Compte, Brunel, Goldman-Rakic, & Wang, 2000, for neural network models that use similar dynamics).
Considered together, the layers in Figure 3 capture the real-time processes that underlie performance on a single spatial recall trial. At the start of the trial, the only activation in the perceptual field is at the location associated with the perceived reference axis (see highlighted reference input in Figure 3a). This is a weak input and is not strong enough to generate a self-sustaining peak in the SWM field, though it does create an activation peak in the perceptual field (PFobj). Note that this input to the model is assumed to be generated by relatively low-level neural processes that extract symmetry using the visible edges of the task space (for evidence that symmetry axes are perceived as weak lines, see Li & Westheimer, 1997). We have not included the visible edges in simulations of the model because they are quite far from the target locations probed in our experiments. Given that neural interactions in the DFT depend on metric separation, these additional inputs far from the targets would have negligible consequences.
The next event in the simulation in Figure 3a is the target presentation. This event creates a strong peak in PFobj (see target input in Figure 3a) which drives up activation at associated sites in the SWM field (SWMobj). When the target turns off, the target activation in PFobj dies out, but the target-related peak of activation remains active in SWMobj. In addition, activation from the reference axis continues to influence PFobj because the reference axis is supported by readily available perceptual cues (see peak in PFobj during the delay).
Central to the DFT account of geometric biases is how the reference-related perceptual input affects neurons in the working memory field during the delay. Figure 3c shows a time slice of the SWMobj field at the end of the delay. As can be seen in the figure, the working memory peak has slightly lower activation on the left side. This lower activation is due to the strong inhibition around midline created by the reference-related peak in PFobj (see highlighted reference input in Figure 3a & 3c). The greater inhibition on the left side of the peak in SWM effectively “pushes” the peak away from midline during the delay, that is, the maximal activity in SWM at the end of the trial is shifted to the right of the actual target location (for additional behavioral signatures of these inhibitory interactions, see Simmering et al., 2006). Note that working memory peaks are not always dominated by inhibition as in Figure 3c. For instance, if the working memory peak were positioned very close to or aligned with midline (location 0), it would be either attracted toward or stabilized by the excitatory reference input. This hints at how the DFT accounts for developmental changes in geometric biases.
A simulation of the model with “child” parameters is shown in Figure 3b. This simulation is the same as the adult simulation in Figure 3a, except the interaction among neurons within each field and the projections between the fields have been scaled according to the spatial precision hypothesis: the neural interactions within the SWMobj and PFobj fields are weaker (relative to the adult parameters), the widths of the projections between the fields are broader, and the excitatory and inhibitory projections are weaker (for a more detailed discussion see below). As can be seen in Figure 3b, these changes in interaction result in a broader peak in the SWMobj field. Additionally, the reference input is broader and weaker to reflect young children’s difficulty with reference frame calibration, that is, their ability to stably align and re-align egocentric and allocentric reference frames (see Spencer et al., 2007). The result of these changes is that neural interactions in PFobj are not strong enough to build a reference-related peak during the delay. Consequently, SWMobj is only influenced by the broad excitatory input from detection of midline in the task space and the SWMobj peak drifts toward the reference axis instead of away from the axis.
The simulations in Figure 3 demonstrate that the spatial precision hypothesis and the DFT can capture the general pattern of geometric biases in early development and later development, but what is happening between these two points in time? We examined this in the present simulation experiment by parametrically scaling the parameters related to the spatial precision hypothesis to generate a set of predicted behavioral changes during the period between 3 and 6 years.
Method and Results for Simulations of Developmental Endpoints
All simulations were conducted using MATLAB software. The simulations used a 10 s delay, and we ran 100 simulations to each target location for each parameter set. The target locations were 0°, 10°, 20°, 30°, 40°, 50°, and 60° from the reference axis. For specifics of the model and a complete list of parameters see the appendix and Table A1 (see also Spencer et al., 2007; Simmering et al., 2008).
Table A1. Parameter values for Experiment 1 simulations.
| Layer | τ | h | self- excitation |
excitatory projection(s) |
inhibitory projection(s) |
reference input |
target input |
|---|---|---|---|---|---|---|---|
| u (PF) | 80 | −7 | cuu = 1.645 | cuv = 1.21 | cref = 13.31 | ctar = 45 | |
| σuu = 3.0 | σuv = 4.7 | σref = 1.0 | σtar = 3 | ||||
| kuv = 0.05 | |||||||
| v (Inhib) | 10 | −12 | cvu = 4.55 | ||||
| σvu = 5.0 | |||||||
| cvw = 2.2 | |||||||
| σvw = 6.0 | |||||||
| w (SWM ) | 80 | −5 | cww = 2.793 | cwu = 1.75 | cwv = 0.759 | [all inputs scaled by cs = 0.2] |
|
| σww = 5 | σwu = 3 | σwv = 43.32 | |||||
| kwv = 0.05 | |||||||
|
| |||||||
| developmental scaling parameters (from ‘youngest’ to ‘oldest’ parameter setting) |
dev_cuu = 0.57 | dev_cv = 0.046 | dev_cref = 0.475 | ||||
| dev_cww = 0.505 | dev_σv = 3.51 | dev_σref = 46.0 | |||||
| dev_cuu = 0.5855 | dev_ cv = 0.224 | dev_cref = 0.54 | |||||
| dev_cww = 0.614 | dev_σv = 3.37 | dev_σref = 26.65 | |||||
| dev_cuu = 0.6165 | dev_cv = 0.386 | dev_cref = 0.61 | |||||
| dev_cww = 0.724 | dev_σv = 3.18 | dev_σref = 15.42 | |||||
| dev_cuu = 0.663 | dev_cv = 0.534 | dev_σref = 0.69 | |||||
| dev_cww = 0.824 | dev_σv = 2.94 | dev_σref = 8.92 | |||||
| dev_cuu = 0.725 | dev_cv = 0.667 | dev_σref = 0.76 | |||||
| dev_cww = 0.9 | dev_σv = 2.62 | dev_σref = 5.16 | |||||
| dev_cuu = 0.8025 | dev_cv = 0.789 | dev_σref = 0.84 | |||||
| dev_cww = 0.952 | dev_σv = 2.21 | dev_σref = 2.99 | |||||
| dev_cuu = 0.8955 | dev_cv = 0.9 | dev_σref = 0.92 | |||||
| dev_cww = 0.981 | dev_σv = 1.68 | dev_σref = 1.73 | |||||
| dev_cuu = 1.0 | dev_cv = 1.0 | dev_σref = 1.0 | |||||
| dev_cww = 1.0 | dev_σv = 1.0 | dev_σref = 1.0 | |||||
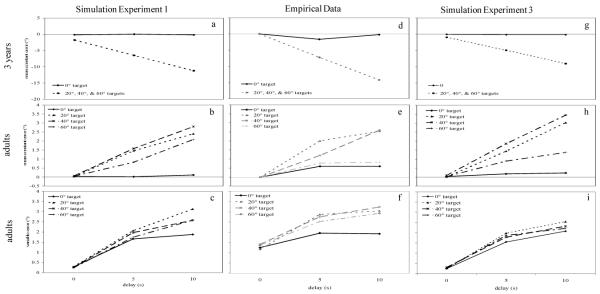
Our first task in the present report was to move from the qualitative simulations of development in Figure 3 to quantitative simulations of the endpoints of the transition in geometric biases. We began by finding a set of parameters that matched the pattern of error adults make in our spatial recall task using data from Spencer and Hund (2002). We examined fits of the model for both mean directional error (constant error) and within-subject standard deviations (variable error) to each target (0-60°) over 0, 5, and 10 s delays. Figure 5 shows the model data (left panels) and the behavioral data (center panels) (Spencer & Hund, 2002). Examination of constant error confirmed that the models’ errors increased as delay increased for targets 20°, 40°, and 60° (the targets for which we had behavioral data), and errors were comparable in magnitude to the behavioral data. Additionally, errors to the 0° target remained near zero. Variable error for the adults increased over delay (Figure 5c) and was similar to the variable error from Spencer and Hund (2002) (see Figure 5f). Variability was lowest to the 0° target in both the model and the data from Spencer and Hund. Thus, we were able to successfully model the adult data in quantitative detail for these target locations.
Figure 5.
Panels on the left show simulation results for Experiment 1 including (a) mean constant error over delays for parameter set 1, the 3-year-old model, (b) mean constant error over delays for parameter set 8, the adult model, and (c) standard deviation over delays for the adult model. Panels in the center show mean constant error for (d) 3-year-old children from Schutte and Spencer (2002) and (e) adults from Spencer and Hund (2002). Panel (f) shows standard deviations (variable error) for the adults from Spencer and Hund (2002). Panels on the right show mean constant error over delay for Experiment 3 for (g) parameter set 1, the 3-year-old model, and (h) parameter set 6, the adult model, and (i) standard deviations over delay for parameter set 6.
We then implemented the spatial precision hypothesis by scaling the strength of local excitation, the strength and width of the reference input, and the strength and width of the inputs between the fields. We increased the various width parameters and decreased the various strength parameters until we fit the 3-year-old data from Schutte and Spencer (2002), showing biases toward midline for all targets to the left and right of this axis. The parameter values are given in Table A1.
Figures 5a and 5d show the model data (left panels) and the behavioral data (center panel) for the 0° target and mean error collapsed across the 20°, 40°, and 60° targets (Schutte & Spencer, 2002). Note that Schutte and Spencer (2002) did not find a difference between responses to the 20°, 40°, and 60° targets for 3-year-olds, so we collapsed across these targets. As can be seen in the figure, errors toward midline (i.e., negative directional errors) increased as delay increased for the 3-year-old model, providing a good match to the behavioral data. Additionally, errors to the 0° target remained near zero. Thus, by scaling parameters related to the spatial precision hypothesis, we were able to successfully model 3-year-olds’ performance in quantitative detail.
Implementation of the SPH During the Developmental Transition
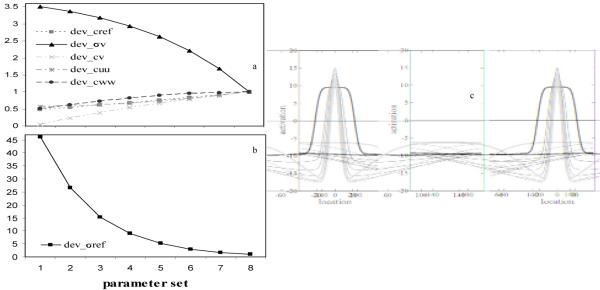
To examine the behavior of the model during the transition, we scaled parameters linked to the SPH between the 3-year-old and adult parameter values used above yielding eight total parameter sets. The parameter values for each set are given in Table A1. The criteria we used for determining the scaling parameters were the following: parameters had to be scaled in a smooth, gradual manner, and each parameter set needed to show the right qualitative behaviors across target locations, that is, (1) successfully build a peak in SWM when the target turned on, (2) maintain this peak in SWM during the 10 s delay, and (3) hold onto the peak in SWM without forming a second peak associated with the midline reference frame (which can occur if the reference input is too salient).
To meet these criteria, we scaled the width of the reference axis input exponentially, and the strength of the reference axis input using a negative exponential function. The width and strength of projections from the inhibitory layer (Inhibobj) to the SWMobj and PFobj layers were also scaled using a negative exponential function. The strength of excitatory connections within the PFobj layer was scaled using the following linear equation:
Where n is the number of the parameter set (i.e., 1–8), and dev_ cuu is the value of the scaling parameter (see appendix and Table A1). The strength of excitatory connections within SWMobj was scaled smoothly such that strength increased more rapidly for the initial parameter sets, and more gradually for the later parameter sets. This differential scaling was needed to maintain stable peaks in SWMobj across all parameter sets. Figure 4 shows the developmental trajectories of the parameters showing that all of the parameter values fell on smooth curves. Note that scaling the parameters in other ways, including scaling all of the parameters linearly, violated one or more of the criteria listed above (e.g., the peak died during the delay or two peaks formed—one at the target and one at midline).
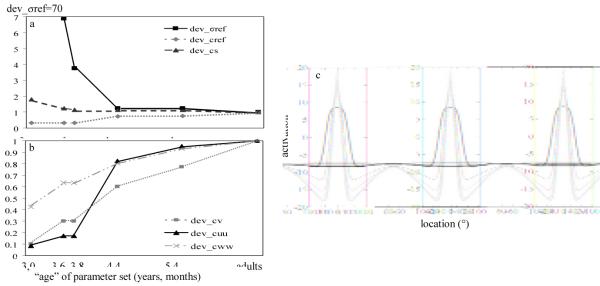
Figure 4.
Panels (a) and (b): Developmental scaling parameters for parameter sets 1 through 8. Panel (c): Developmental changes in the self-sustaining peaks in the SWM field as a result of changes in spatial precision parameters from early in development (black bold line) to later in development (light gray bold line).
The resultant effect on self-sustaining peaks in the SWM field can be seen in Figure 4c. Figure 4c shows a time-slice of the activation peak at the end of the delay for each parameter set when the target was presented at 0°. Note that noise was not included in these exemplary simulations to highlight differences in peak structure across parameter sets. The peak in the 3-year-old model is broader and weaker (see black, bold line) than the peak in the adult model (see light gray, bold line). As the parameters are scaled, the peak becomes narrower and stronger (see black to light gray lines). Thus, the scaling replicated the central aspects of the SPH, that is, peaks in SWM became more precise over development.
Although we scaled the parameter values to maintain target peaks, the target peaks still died out on a few trials, particularly in the context of the strong noise we needed to capture the variability present in children’s responses. Note that a similar effect occurs in our experimental data as well (see discussion of perseverative errors in Experiment 2). These trials were removed from analysis. Overall, 2.5% of trials (138 trials out of a total of 5600 trials) were removed (parameter set 1: 6.6%, parameter set 2: 0%, parameter set 3: 1%, parameter set 4: 2.7%, parameter set 5: 4.7%, parameter set 6: 4.3%, parameter set 7: 4.3%, parameter set 8: 0%).
Results of Developmental Simulations
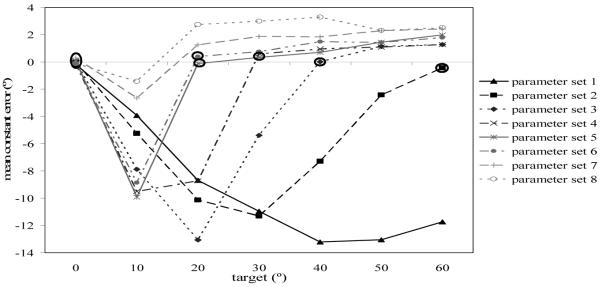
The constant error at each target location for each parameter set at the end of the delay is shown in Figure 6. Negative errors are toward the reference axis and positive errors are away from the reference axis. Two things are clear in the figure. First, the bias toward the reference axis gradually reduced, with the targets furthest from the axis showing the reduction in bias first. Second, repulsion from the reference axis emerged and gradually spread to all but the 10° target. To determine which data points were significantly different from 0 error, we performed t-tests on the errors to each target for each parameter set. The data points that are not significantly different from 0 error are circled in the figure. As can be seen in the figure, as the parameters scaled up for each target location except 0° and 10°, the bias toward the reference axis reduced until the target was not significantly biased, and then a significant bias away from the reference axis emerged first at far targets and then gradually increased and spread to all targets except 10°. Note that the performance of the model at 10° was not realistic, particularly for the adult parameters. Adults in our task show biases away from midline at 10°, while the model shows slight attraction toward midline at 10° (see, e.g., Simmering & Spencer, 2007). This poor fit reflects practical constraints in our numerical simulations. The size of the fields used here (397 units) was too small to achieve repulsion at the 10° target and larger fields produce prohibitively slow simulation times (the current simulator required 3 hours to run a complete set of simulations for one parameter set). Thus, we excluded simulation data for the 10° target in subsequent analyses of the model’s behavior.
Figure 6.
Mean constant error from simulation Experiment 1 for each parameter set to each target at the 10 s delay. Parameter set 1 is the 3-year-old model (black line), and Parameter set 8 is the adult model (light gray, dotted line with circular markers). The values that are not significantly different from 0 error are circled.
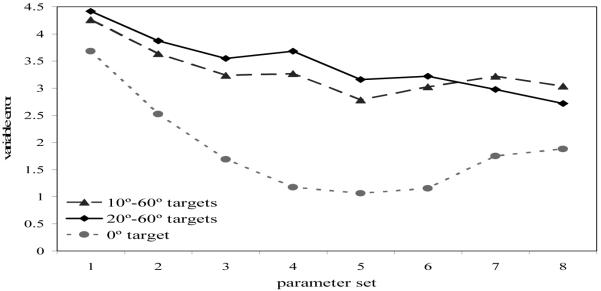
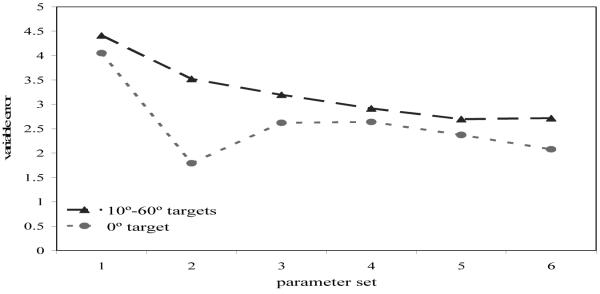
To examine changes in response variability, we computed the standard deviation of responses to each target location for each parameter set. We then averaged the standard deviations across the 20° to 60° targets for each parameter set (see Figure 7). Note that we computed response variability to 0° separately because results from previous studies show that responses to targets aligned with reference frames are accurate with low variability, while responses to non-0° targets show comparable performance (see Spencer & Hund, 2002; Engebretson & Huttenlocher, 1996). As can be seen in Figure 7, there was a reduction in variability over development in the model even though the noise strength was constant across simulations. Figure 7 also shows that variability at the 0° target was lower than at the other target locations for all parameter sets. Although over development there is most likely a decrease in noise, the results here demonstrate that even without varying noise, there is a robust increase in the stability of SWM over development in the model, consistent with results from Spencer and Hund (2003). This is important because it shows a link between changes in spatial recall biases and reductions in variability—as SWM becomes more stable, geometric biases change and WM is less influenced by random fluctuations.
Figure 7.
Mean variable error (standard deviation) for parameter sets 1 (3-year-old model) to 8 (adult model) for the 0° target (light gray, dotted line), the 10°–60° targets (dark gray, dashed line), and the 20°–60° targets (black, solid line).
Discussion
The first goal of this simulation experiment was to determine whether the model could quantitatively fit the time-dependent pattern of error from studies of adults’ spatial recall abilities. The model successfully captured the pattern of error for the adults with reasonable quantitative precision. This was the case for both mean responses as well as response variability. Most critically, the adult model was biased away from midline at all but the 10° target locations. Additionally, the model successfully captured adults’ reduced variability at 0° and the increase in variability over delays. It is not clear whether the CA model can capture either aspect of response variability. According to the CA model, response variability should be high near midline because on some trials participants are likely to mis-categorize the target. This is not the case empirically. Moreover, because the CA model is not a process model, there is no mechanism to produce an increase in variance over delays.
How does the DFT capture these two effects? The reduction in variability for targets aligned with a reference axis emerges in the DFT through coupling between the perceptual and working memory fields and sustained reference-related input to these layers during the delay. These two factors help keep working memory peaks stably aligned with the continuously available perceptual structure in the task space (i.e., the table’s edges and symmetry axis). The increase in variability over delays is a natural product of the dynamics in the model: as peaks “drift” in the context of noise, there is an increase in variance over delays due to stochastic fluctuations in how quickly peaks drift over delays on different trials.
In addition to capturing the adults’ data, the second goal of our simulations was to quantitatively capture the other endpoint of development, the 3-year-olds’ data (Schutte & Spencer, 2002), by scaling parameters related to the spatial precision hypothesis. The model was able to quantitatively match the 3-year-old data: the lateral targets (20°, 40°, and 60°) were biased toward midline, and the bias increased as delay increased. Additionally, mean error to the 0° target was smaller. Although previously the DFT has been used to qualitatively capture the spatial recall performance of adults and 3-year-olds (e.g., Schutte & Spencer, 2002; Simmering, Schutte, & Spencer, 2008; Spencer et al., 2007), this is the first time the DFT has been used to quantitatively model the spatial recall performance of these age groups. Critically, the DFT captured the performance of 3-year-olds in a manner directly analogous to parameter changes implemented in Schutte et al. (2003) to capture young children’s performance in a sandbox task.
The third goal of this simulation experiment was to derive a set of developmental predictions by scaling the neural interaction parameters linked to the spatial precision hypothesis between the young child and adult settings. Results of these simulations led to three predictions about how spatial working memory performance should change over development. First, during the transition, the spatial region across which targets are biased toward the reference axis will narrow. This occurs as reference-related inputs to the model become narrower and more precise, that is, as children’s perception of the midline reference axis becomes more precise. The narrowing of peaks in SWM also contributes here, because narrower peaks are less likely to overlap with the excitatory reference input near midline.
Second, the model predicts that as inhibition increases over development, repulsion away from the reference axis should emerge and become stronger. Early in development, reference-related inhibition is not strong enough to cause significant repulsion from the midline axis (see Figure 6, black line). With increasing inhibition, however, repulsion effects gradually increase until the majority of targets are biased away from midline (see, e.g., parameter set 8 in Figure 6).
The third prediction is that variability will decrease over development. It is important to note that the decrease in variability in our simulations occurred even though the amount of noise in the model remained constant across all parameter settings. We acknowledge that this is a relatively weak prediction since most accounts of development would expect noise to decrease. Nevertheless, the prediction is important because changes in recall biases and reductions in variability arise from the same dynamic processes in the model—changes in the stability of working memory peaks. Consequently, if we were to see changes in recall biases that were not accompanied by reductions in variability, this would violate model predictions. We tested these three predictions empirically in Experiments 2a and 2b.
Experiment 2a
The goal of Experiment 2 was to test the predictions of the DFT about the nature of the developmental transition in geometric effects. We tested these predictions using a spaceship game (see Figure 8). In this task the child sat at a large table. A spaceship-shaped target was projected onto the table, there was a delay, and then the child moved a small rocket to the remembered target location. Prior research has demonstrated that 3-year-olds show attraction toward the midline axis in the spaceship task for targets as far as 80° from midline (Schutte & Spencer, 2002; see also, Huttenlocher et al., 1994). Six-year-olds, 11-year-olds, and adults, by contrast, are repelled from midline for targets as close as 10° (Spencer & Hund, 2002; Spencer & Hund, 2003; see also, Huttenlocher et al., 1994). Thus, we know that in the spaceship task the transition in geometric biases occurs between 3 and 6 years of age, so we tested three age groups—3-, 4-, and 5-year-olds.
Method
Participants
Thirty-seven 3-year-olds (M = 3 years, 6.2 months, SD = .43 months, range = 3 years, 5.3 months to 3 years, 7.2 months), 33 4-year-olds (M = 4 years, 3.9 months, SD = 1.35 months, range = 4 years, 1.5 months to 4 years, 7.2 months) and 33 5-year-olds (M = 5 years, 3.2 months, SD = 1.5 months, range = 4 years, 11.2 months to 5 years, 5.8 months) participated in this experiment. Seventeen children participated that were not included in the final analyses for the following reasons: 6 children (1 3-year-old, 2 4-year-olds, and 3 5-year-olds) only participated in one session due to scheduling conflicts, 8 children (7 3-year-olds and 1 4-year-old) stopped playing the game early, two 3-year-olds did not understand the game, and one 3-year-old did not have enough trials following initial data analysis (see below for details). The dropout rate for the 3-year-olds is higher than is ideal (although it is comparable to previous studies, see Schutte et al., 2003). It is important to note, however, that most children did not have difficulty understanding and playing the game. Rather, 3-year-olds had difficulty attending to the game long enough to complete the number of trials required to test the detailed predictions of the DFT. Children participated in two sessions that were generally scheduled within a week of each other. Children received a small gift following each session. The parents of all participants gave informed consent.
Apparatus
Participants sat at a large table. The table top was a rear projection screen with an arc removed from one side (see Figure 8). The participant’s chair was positioned within the arc. A video projector positioned below and to the rear of the table projected images onto the table’s surface. The display size was 4′ by 3′ (.91 m by 1.22 m) with a resolution of 1024 × 768 pixels. The room lights were dimmed and black curtains were hung along the walls to the front and sides of the table and across the ceiling. This prevented reflections from appearing on the tabletop that could be used as reference points. A yellow dot was projected along the midline axis of the table 15 cm from the front edge. This was the starting point for each trial. A rocket ship 5.5 cm high and 2 cm in diameter sat on this dot. Participants used the rocket to indicate where “spaceships” were hiding. A computer controlled the type and timing of all stimuli presented in the experiment using customized software. Prerecorded messages were played through two speakers on either side of the table. These messages led participants through the game and gave feedback after each trial.
Participants’ movements of the rocket were recorded at 150 Hz using an optical-electronic motion analysis system (Optotrak, Northern Digital, Inc.). This system tracks small (radius = 3.5 mm), individually pulsed infrared emitting diodes (IREDs) within a specified 3-D volume with better than 1 millimeter precision. One IRED was attached to the tip of the rocket to track participants’ responses as they moved the rocket from the starting position to the remembered location.
Procedure
At the start of the first session, the experimenter played a warm-up game on the floor with the child to teach the child the basics of the task. The child was told that he/she was going to play a game to help “Buzz Lightyear” find his lost spaceships. The experimenter gave the child the toy rocket and then showed the child two flashcards, one with a spaceship on it and one with a star. The experimenter pointed out the spaceship card and placed both cards face down on the floor. When the experimenter said “go”, the child was encouraged to place the rocket on top of the spaceship card. The warm-up game was played until the child successfully found at least two spaceships in two different locations.
Next, the child was told he/she was going to play the game on the special “spaceship table”, and the child and parent moved over to the experimental table to start the task. The session began with demo trials to help the child learn the game. These trials were identical to the test trials except the experimenter performed the task. The experimenter controlled the number of demo trials. Generally, children required only one demo; however, demo trials were repeated if a child did not attend to a complete demo trial or was not willing to participate following the first demo trial.
Each trial began when the computer said, “Let’s look for a spaceship.” Following a random pretrial delay, a spaceship was illuminated for 2 s in one of two possible target locations (see below). The child’s task was to move the rocket from the starting location to where the spaceship was hiding when the computer said “go, go, go.” If the participant moved the rocket before the “go” signal, the computer gave a verbal warning such as, “Don’t forget to wait for the go.” After each trial, the target was re-illuminated for 1.5 s so the child could compare the actual location with the location of the rocket (i.e., the remembered location). The child received verbal and visual feedback from the computer based on whether he/she found the spaceship (the distance between the response and the target was < 3 cm), was close to the spaceship (the response-target distance was > 3 cm and < 5 cm), or was not so close (the response-target distance was > 5 cm). For each spaceship the child found, he/she received verbal feedback, a picture of Buzz and/or his friends was displayed on the table, and the child received a star, which was also displayed on the table. When the response-target distance was between 3 cm and 5 cm, the child received both verbal feedback and a picture of Buzz. When the response-target distance was greater than 5 cm, the child received only verbal feedback, such as “Nice try. We’ll get it next time.” The parent or guardian was instructed not to talk during a trial or give any signal that would help the child find the spaceship, but was asked to give positive feedback after each trial.
Design
Participants were randomly assigned to one of three conditions. In each condition, children recalled the locations of two targets (one on each trial) separated by 80° relative to the start location (see Figure 8). We chose to use only two target locations with an 80° separation in order to minimize the interaction between the memory of the current target and the longer-term memory of the other target (see Schutte and Spencer, 2002; Schutte, Spencer, & Schöner, 2003). To further minimize this potential interaction, the targets were on opposite sides of midline. This was necessary to isolate geometric effects from longer-term memory effects. For instance, if a response is biased toward midline, these precautions ensure that the bias is toward midline and not toward another target (i.e., a perseverative error, see Schutte & Spencer, 2002; Schutte et al., 2003) because the other target was very far away and on the other side of the reference axis. The target counter-clockwise from midline was always near midline (inner target), and the target clockwise from midline was always far from midline (outer target). The target locations across the three conditions were: −10° and 70°, −20° and 60°, and −30° and 50° from midline (see Figure 8). Note that all of these target locations were closer to midline than to the outer edges of the table. Delays of 0, 5, and 10 s were used. For the 4- and 5-year-olds there were 48 test trials divided evenly between two experimental sessions—8 trials to each target at each delay. Children completed 6 practice trials at the start of each session. For the 3-year-olds, there were 36 test trials divided evenly between the two experimental session—6 trials to each target at each delay. Three-year-olds completed 2 practice trials at the start of each session. It was necessary to reduce the number of trials for the 3-year-olds, because 3-year-olds were not able to attend to the game as long as the 4- and 5-year-olds.
Children participated in two sessions that were each approximately 20 minutes long. The two sessions were identical except the warm-up game was not played before the second session. Which target appeared on each trial and the order of the delays were randomized. Participants were encouraged to complete all the trials during each session; however, during some sessions, children stopped playing the game early (for details, see below).
Method of analysis
Optotrak data and customized software were used to identify a starting and ending location for each trial. The start of the movement was defined as the first data frame in a trial with a tangential velocity > 2 cm/s. This “resting level” criterion was used by Hund and Spencer (2003) and Schutte and Spencer (2002) to distinguish low-level noise from the movement of the hand/rocket. The end of the movement was identified by searching backwards from the end of the trial to the last frame that had a velocity less than 2 cm/s and a z-coordinate value (vertical dimension) less than 8 cm and greater than 3 cm (recall that the rocket was 5.5 cm high). A z-coordinate greater than 8 cm meant the rocket was still in the air above the table. A z-coordinate less than 3 cm meant the rocket had fallen over.
After the start and end locations were selected, the computer calculated the directional error for each trial. Specifically, the computer calculated the angle between the line connecting the start location and the target location and a line connecting the start location and the ending location. Negative directional errors indicate errors toward midline relative to the target direction and positive errors indicate errors away from midline relative to the target direction.
All trials that were not within 2 standard deviations of the median error for each target at each delay were checked manually for computer selection mistakes using an interactive version of the automated analysis software. In addition, trials for which the computer could not find valid start or end locations were also checked manually. The interactive software allowed us to manually edit the start and end locations. All manual selections, however, were required to meet the starting and ending criteria outlined above.
After manually inspecting the data, all trials that did not meet the start and end criteria listed above were eliminated. This resulted in a total of 94 trials being removed across all participants (3-year-olds: 70 trials [5% of trials]; 4-year-olds: 16 trials [1% of trials]; 5-year-olds: 8 trials [0.5% of trials]). In addition, inspection of the data revealed that on several trials children made large errors. A majority of these errors were in the direction of the opposite target.
We examined two possible explanations for these large errors. The first possible explanation was that children made perseverative errors, that is, they responded to a just-previous target rather than to the target on the current trial (see Schutte et al., 2003). A second possibility was that children made “mirror image” errors, that is, they responded to the target location on the opposite side of midline (e.g., a response to 30° when the target was at −30°). To examine these possibilities, we inspected data to the −20° and −30° targets for the 3-year-olds because this age group made the largest errors. We computed the number of trials where the response was within ±5° of the mirror image target (e.g., within the spatial region 15° to 25° to the right of midline for the −20° target) versus when the response was beyond the mirror image location and closer to the perseverative target. Results of this analysis revealed 8 mirror image responses and 34 perseverative responses. Thus, children’s large errors were primarily due to perseverative biases (note that similar results were obtained when we restricted the spatial range for what qualified as a perseverative response to ±5° of the perseverative target).
Inclusion of perseverative errors in the analyses could result in a false bias toward midline, because the other target was always on the opposite side of midline. To isolate geometric biases from these perseverative errors, we removed all trials from the overall data analysis with an error greater than 50° and in the direction of the non-cued target and analyzed these trials separately (see Results for further details). Recall that the targets were separated by 80°. Thus, a 50° error meant the response was closer to the incorrect target than the correct target. Note that trials with errors greater than 50° that were not in the direction of the other target were removed from all analyses. There were only 2 trials removed for this reason across all participants.
Following removal of invalid trials and separation of trials with errors greater than 50°, 3-year-olds completed an average of 30 trials (SD = 5.26), 4-year-olds completed an average of 45 trials (SD = 5.00), and 5-year-olds completed an average of 47 trials (SD = .98). One 3-year-old had at least one cell without any valid trials; thus, data from this child were not included in the final analyses. The median error to each target at each delay was computed for each participant. We refer to this as directional error below. Variable error was computed by calculating the standard deviation of responses to each target at each delay for each participant.
Results
Directional error
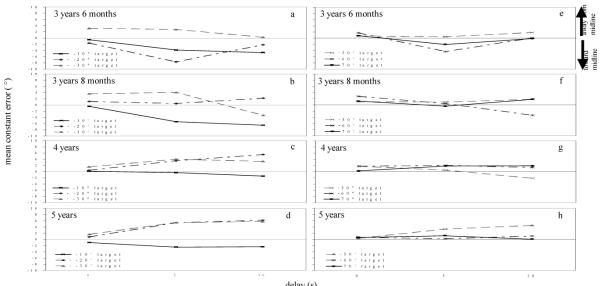
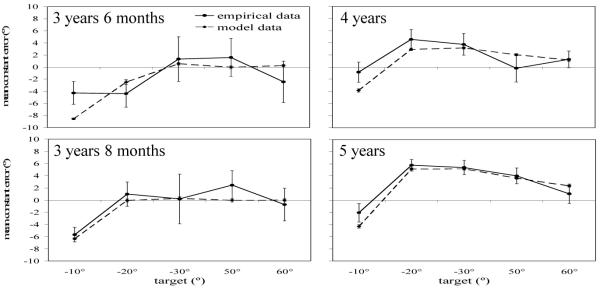
Mean directional error across participants for each target at each delay is shown in Figure 9. Data from the inner targets (−10°, −20°, and −30°) are in the left column and data from the outer targets (50°, 60°, and 70°) are in the right column. Positive errors indicate errors away from midline, and negative errors indicate errors toward midline. As can be seen in Figure 9a, as delay increased, 3-year-olds’ responses were biased toward midline at −10° and −20° and were not biased at −30°. In contrast, 4- and 5-year-olds’ responses to −20° and −30° were biased away from midline and this bias increased as delay increased (Figure 9b, c). Four- and 5-year-olds’ responses to the −10° target, however, were relatively accurate over delays (Figure 9c). Errors to the outer targets were generally near zero for all ages, with the exception of the 5-year-olds’ responses to the 50° target (Figure 9f) which were biased away from midline over delay.
Figure 9.
Mean error in Experiment 2a across age groups (3 years, 6 months; 4 years; 5 years) & 2b (3 years, 8 months) to the inner targets near midline (left panels: −10°, solid line; −20°, dot-dashed line; −30°, dashed line) and the outer targets far from midline (right panels: 50°, dashed line; 60°, dot-dashed line; 70°, solid line). Positive errors are toward the midline reference axis, and negative errors are away from the midline reference axis.
Mean directional error was analyzed in a 4-way ANOVA with Condition (−10°/70°, −20°/60°, −30°/50°) and Age (3, 4, 5) as between-subjects factors and Target (inner, outer) and Delay (0 s, 5 s, 10 s) as within-subjects factors. There was a main effect of Age, F(2,94) = 4.93, p < .01, η2 = .10. There was also a significant Delay x Age interaction, Wilks’ Λ = .82, F(4,186) = 4.78, p = .001, η2 = .09. Tests of simple effects revealed that the 3-year-olds were biased significantly toward midline over delays, F(2,72) = 3.15, p < .05, η2 = .08 (0 s: M = .63, 5 s: M = −2.74, 10 s: M = −.87). In contrast, the 4-year-olds’ bias did not change significantly over delays, F(2,64) = .66, n.s., η2 = .02 (0 s: M = .92, 5 s: M = 1.82, 10 s: M = 1.31), and the 5-year-olds were biased significantly away from midline over delays, F(2,64) = 6.82, p < .01, η2 = .18 (0 s: M = .52, 5 s: M = 2.20, 10 s: M = 2.55). There was also a main effect of Condition, F(2,94) = 4.79, p = .01, η2 = .09, and a marginal Target x Condition interaction, Wilks’ Λ = .94, F(2, 94) = 3.06, p = .052, η2 = .06. Tests of simple effects revealed a significant effect of Condition for the inner targets, F(2,100) = 6.74, p = .005, η2 = .12, but not the outer targets, F(2,100) = .31, n.s., η2 = .01. Thus, errors to the three outer targets were similar, while errors to the inner targets differed depending on the target. The −10° target was biased slightly toward midline (M = −1.84), the −20° target was relatively accurate (M = 1.16), and the −30° target was biased away from midline (M = 3.11).
A central goal of this experiment was to test the predictions that the region across which targets are attracted toward midline narrows over development while inhibitory effects (repulsion from midline) should emerge and become stronger over development. To test these predictions directly, planned comparisons (t-tests versus zero error) were conducted on the directional error collapsed across 5 and 10 s delays for each target and age separately. All t-tests were two-tailed given the predicted changing nature of attraction and repulsion.
Mean error for each age at each target location is given in Table 1. Three-year-olds’ responses to the −10° target were biased significantly toward midline, t(11) = −2.28, p < .05, and responses to the −20° target were biased marginally toward midline, t(13) = −1.96, p = .07. Responses to the other targets were not significantly biased toward or away from midline. Four-year-olds’ responses to the −20° target were biased significantly away from midline, t(9) = 2.83, p < .05, and their responses to the −30° target were biased marginally away from midline, M = 3.73, t(9) = 2.10, p = .07. Responses to the other targets were not biased significantly. Five-year-olds’ responses to the −20° target were biased significantly away from midline, t(10) = 6.08, p < .001, as were their responses to the −30° target, t(10) = 4.57, p = .001, and the 50° target, t(10) = 3.11, p = .01. Responses to the other target locations were not biased significantly. These results are consistent with the predicted effects, although repulsion first emerged in the model at targets far from midline.
Table 1. Mean error in Experiments 2a and 2b across 5 and 10 s delays for each age group at each location.
| Location | ||||||
|---|---|---|---|---|---|---|
| Age | −10° | −20° | −30° | 50° | 60° | 70° |
| 3 years, 6 months |
−4.27** | −4.38* | 1.34 | 1.60 | −2.44 | −1.73 |
| 3 years, 8 months |
−5.68** | .97 | .18 | 2.44 | −.73 | .33 |
| 4 years | −.83 | 4.56** | 3.73* | −.19 | 1.26 | 1.71 |
| 5 years | −2.04 | 5.77** | 5.40** | 4.01** | 1.07 | −.09 |
p < .05
p = .07
Individual differences
The analyses of directional error generally support the predictions of the DFT. It is important, however, to determine whether the results reflect the performance of individual participants or are the result of variable performance across participants. Variability across participants could yield the result that half of the children are biased toward midline and half are biased away from midline. The small directional errors (and associated non-significant t-tests) at some of the close target locations presented previously might reflect this state of affairs. It is also possible, however, that children were, in fact, consistently accurate. To evaluate these alternatives, we examined individual differences within each age group by classifying each child as being biased toward midline, away from midline, or unbiased at the inner targets. We used the inner targets only because responses to these targets changed the most dramatically across ages.
The classification scheme was based on each child’s directional error, collapsed across the 5 and 10 s delays. In particular, we computed the standard error across all of the inner targets for each age group. This standard error was then used to compute the critical mean error necessary, based on the t-distribution, for each target to be significantly biased toward or away from midline for each age group. The value of each child’s constant error at the inner target was compared to this critical value. If a child’s error was greater than the critical value and the error was positive, the child was classified as being biased away from midline. If a child’s error was greater than the critical value and the error was negative, the child was classified as being biased toward midline. If a child’s error was less than the critical error, the child was classified as unbiased. Note that we used the standard error across all children within each age group because it provided the best estimate of the variability of performance at each age, that is, this estimate was based on the largest N possible for each age group.
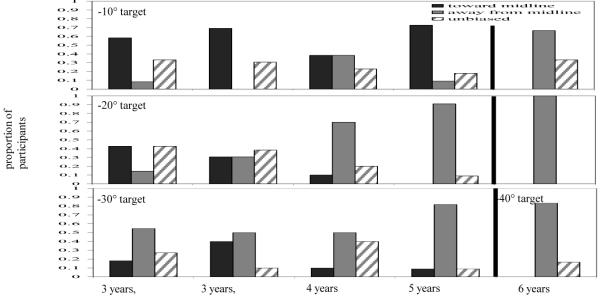
The proportion of children in each classification group at each age for each inner target can be seen in Figure 10. In addition, data from 6-year-olds from Spencer and Hund (2003) were reanalyzed using the same analysis method. These data are shown for comparison. As can be seen in the figure, at −10° more than half of 3- and 5-year-olds were biased toward midline while about one-third of the 4-year-olds were biased toward midline and one-third were biased away from midline. In contrast, the majority of the 6-year-olds were biased away from midline. At −20°, the number of children biased away from midline systematically increased as age increased. About half of the 3-year-olds were biased toward midline and the other half were unbiased, with just a few children biased away from midline. In contrast, the majority of the 4-, 5-, and 6-year-olds were biased away from midline. At −30°, the majority of children at all ages were biased away from midline, although there were quite a few 3- and 4-year-olds categorized as unbiased.
Figure 10.
Proportion of children classified as biased toward midline (black bars), away from midline (gray bars), or not biased (striped bars) in Experiment 2a (3 years, 6 months; 4 years; 5 years) and Experiment 2b (3 years, 8 months) at each of the inner targets (−10°, −20°, −30°). Data from 6-year-olds from Spencer and Hund (2003) are shown for comparison. Note that the 6-year-olds children responded to targets at 10°, 20°, and 40° from midline (not 30°).
These results are consistent with the mean directional error t-tests and provide additional information about the nature of the transition. First, there are individual differences regarding when children move through the transition. This can be clearly seen in the 3-year-old data at 20° with the same number of children biased toward midline as are biased away. Second, these data are consistent with the idea that the transition is not an “all-or-none” transition. For example, a majority of the 3-year-olds were biased away from midline at 30° and toward midline at 10°. Similarly, there are a number of 5-year-olds showing attraction toward midline at −10°, even though repulsion is the dominant pattern for this age group. Although longitudinal studies are necessary to confirm a gradual transition, this pattern points toward a gradual developmental transition that depends both on age and the target location probed.
Variable directional error
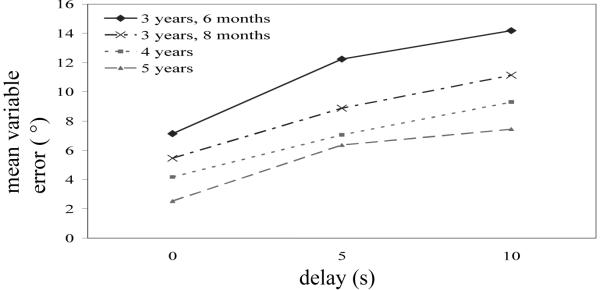
Previous research with older children found that variability in directional responses increased as delay increased and that variability decreased as age increased (Hund & Spencer, 2003; Spencer & Hund, 2003). As can be seen in Figure 11, this study replicated these findings with younger age groups. Mean variable directional error was analyzed in a 4-way ANOVA with Condition ( −10°/70°, −20°/60°, −30°/50°) and Age (3, 4, 5) as between-subjects factors and Target (inner, outer) and Delay (0 s, 5 s, 10 s) as within-subjects factors. There was a main effect of Delay, Wilks’ Λ = .36, F(2,91) = 81.88, p < .001, η2 = .64 (0 s: M = 4.62, 5 s: M = 8.55, 10 s: M = 10.31). As can be seen in Figure 11, as delay increased all three age groups became significantly more variable. There was also a main effect of Age, F(2,92) = 29.81, p < .001, η2 = .39. As age increased, variability decreased (3-year-olds: M = 11.19, 4-year-olds: M = 6.84, 5-year-olds: M = 5.45).
Figure 11.
Mean variable error over delay in Experiment 2a (3 years, 6 months; 4 years; 5 years) and 2b (3 years, 8 months) for the four age groups.
Perseverative error analyses
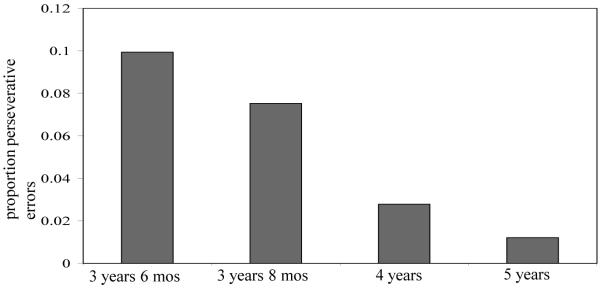
Errors that were greater than 50° and in the direction of the incorrect target were classified as perseverative errors (see Schutte & Spencer, 2002) and analyzed separately. This resulted in the removal of 184 trials out of 4333 total trials. For the 3-year-olds, the number of trials with perseverative errors ranged from 0 to 10 per participant. For the 4-year-olds the number ranged from 0 to 6 per participant, and for 5-year-olds the number ranged from 0 to 2 trials per participant. Figure 12 shows the mean proportion of each participant’s trials that were classified as perseverative errors at each age. As can be seen in the figure, the proportion of perseverative errors decreased as age increased. The proportion of perseverative errors to each target was analyzed in a repeated measures ANOVA with Target as a within-subjects factor and Condition and Age as between-subjects factors. There was a significant Age main effect, F(2,94) = 28.07, p < .001, η2 = .37, confirming that perseverative errors decreased significantly as age increased (see Figure 12).
Figure 12.
Mean proportion of perseverative errors per participant in Experiment 2a for Experiment 2a (3 years, 6 months; 4 years, 5 years) and Experiment 2b (3 year, 8-month-olds).
Discussion
The goal of Experiment 2a was to test a set of predictions of the DFT about the developmental course of the transition in geometric biases. Results generally supported the DFT’s predictions and provide preliminary evidence that the transition in geometric bias is gradual over development and depends on the target locations probed, with the bias toward midline decreasing and the repulsion from midline emerging and spreading. The one difference relative to the model was that repulsion first emerged at 20° in the data, while in the model repulsion emerged at targets further from midline.
The individual differences analyses also pointed toward a gradual transition. At −20°, the majority of 3-year-olds were biased toward midline while the majority of 4-year-olds were biased away from midline. This suggests that children’s spatial memory abilities have changed qualitatively by 4 years, 4 months—but only for this particular location. In particular, the 4- and 5-year-olds were not biased away from midline at −10°. Rather, the transition in performance linked to this location occurred between 5 and 6 years.
The model also predicted that as stability increases over development there should be a decrease in variable error. We examined two indexes of stability: variable error and perseverative errors. As age increased there was a decrease in the variability of children’s responses, consistent with previous research with older children (Spencer & Hund, 2003; see also Plumert & Hund, 2001). The second index of stability was the proportion of perseverative errors. As age increased, the proportion of perseverative errors decreased. According to Thelen et al. (2001), perseverative errors in infancy occur when target-generated peaks in working memory decay away during memory delays. If we extend this to older ages, the proportion of perseverative errors provides an index of how stably peaks are maintained in SWM. Specifically, destabilization of the peak state in the DFT (e.g., due to noise fluctuations) can result in the disappearance of the peak during the delay. When this happens, the model must re-build a peak at the “go” signal based on long-term memory traces of previously responded-to locations (for details, see Spencer et al., 2007). In such cases, the model—and young children—will respond to the location that is most active in longer-term memory. In the case of children in our experiment, the most active location in longer-term memory on some trials was the other target location yielding a perseverative error. Thus, the data reported here show that over development, peaks in SWM are more likely to self-sustain during the delay and less likely to spontaneously de-stabilize.
Overall, results offer support for the predictions from Simulation Experiment 1. To probe these model predictions further, we collected data from an intermediate age group to determine whether the performance of this age group would fall squarely between the performance of younger and older children as predicted by the gradual, continuous changes specified by the model and the spatial precision hypothesis. Thus, in Experiment 2b we tested children who were between 3 years, 6 months and 4 years, 4 months. Based on results from the present experiment, we expected that these children would be biased toward midline at −10° and not biased at −20°. In addition, the indexes of stability (variable error and perseverative error) should fall in between the performance of 3- and 4-year-olds from the present experiment.
Experiment 2b
Methods
Participants
Thirty-six 3-year-olds (M = 3 years, 8.8 months, SD = .56 months, range = 3 years, 7.8 months to 3 years, 10.1 months) participated in this experiment. Fourteen children also participated, but their data were not included in the final analyses for the following reasons: 9 children stopped playing the game early, one child was not included due to experimenter error, two children were missing data following initial analyses (see below for details), and two children did not understand the game. All other participant details were the same as in Experiment 2a.
Apparatus, Procedure, and Design
The apparatus, procedure, and design were the same as in the 3-year-old condition of Experiment 2a.
Methods of Analysis
The Method of Analysis was the same as in Experiment 2a. Trials that did not meet the start or end criteria were removed from analysis (64 trials; 5.1% of trials), and trials with errors in the direction of the other target that were greater than 50° were removed from the overall analysis and analyzed separately (139 trials; 11.6% of trials). In addition, there was one trial with an error greater than 50° that was not in the direction of the other target (cued target: −10°). This trial was removed. Following removal of invalid trials and separation of perseverative errors, 2 children had at least one cell without any valid trials. Data from these children were not included in the final analyses. Following removal and sorting of trials, 3-year-olds completed an average of 31 trials (SD = 5.9).
Results
Directional error
The mean directional error for the inner targets (−10°, −20°, and −30°) at each delay are shown in Figure 9b, and data for the outer targets (50°, 60°, 70°) at each delay are shown in Figure 9f. As can be seen in the figure, responses to the −10° target were biased toward midline while responses to −20° and −30° were accurate. Responses to the outer targets were near zero with the exception of responses to the 60° target which were biased toward midline at the long delay. Mean directional error was analyzed in a 3-way ANOVA with Condition (−10°/70°, −20°/60°, −30°/50°) as a between-subjects factor and Target (inner, outer) and Delay (0 s, 5 s, 10 s) as within-subjects factors. There was a significant Delay x Target x Condition interaction, Wilks’ Λ = .73, F(4,64) = 2.68, p > .05, η2 = .14. Tests of simple effects revealed a significant Delay x Condition interaction for the inner targets, F(4,66) = 2.84, p < .05, η2 = .15, but not for the outer targets, F(4,66) = 1.63, n.s., η2 = .09. Additional analyses of delay at each of the inner targets revealed a significant delay effect to the −10° target, F(2,24) = 6.69, p = .005, η2 = .36, but not to the −20°, F(2,24) = .43, n.s., η2 = .03, or −30° target, F(2,18) = 2.62, n.s., η2 = .23. Therefore, over delay the −10° target was biased toward midline, while the other targets were not biased.
As in Experiment 2a, planned comparisons were conducted comparing directional error collapsed across 5 and 10 s delays to zero error (see Table 1). Responses to the −10° target were biased significantly toward midline, M = −5.68, t(12) = −4.70, p = .001. Responses to the other targets were not significantly biased (−20°: M = .97, −30°: M = .18, 50°: M = 2.44, 60°: M = −.73, 70°: M = .34). This differs from the younger 3-year-olds in Experiment 2a who were biased toward midline at both −10° and −20°. It also differs from the 4-year-olds who were accurate at −10° and significantly biased away from midline at −20°.
To examine age differences across experiments directly, the older 3-year-olds in Experiment 2b were compared to the younger 3-year-olds and 4-year-olds in Experiment 2a by conducting two repeated-measures ANOVAs with Target and Delay as within-subjects factors and Age and Condition as between-subjects factors. Only significant Age effects (i.e., Experiment effects) are reported. There were no significant Age effects in the ANOVA comparing the younger and older 3-year-olds. There was a significant Age x Delay interaction in the ANOVA comparing the older 3-year-olds and the 4-year-olds, F(2,126) = 3.51, p < .05, η2 = .05. Over delay the older 3-year-olds were biased slightly toward midline (0 s: M = 1.56, 5 s: M = .03, 10 s: M = −1.22), while the 4-year-olds were biased slightly away from midline (0 s: M = .99, 5 s: M = 1.93, 10 s: M = 1.42).
Individual Differences
Using the same methods as in Experiment 2a, we classified each child as being biased toward midline, away from midline, or unbiased. The proportion of children in each classification group for the −10° target can be seen in Figure 10, upper panel. The majority of 3 years, 8-month-olds were biased toward midline at −10°. There were also a number of children who were unbiased. This is comparable to the performance of 3 years, 6 months in Experiment 2a. The proportion of children in each classification group for the −20° target can be seen in Figure 10, center panel. About one-third of older 3-year-olds were biased toward midline, one-third were biased away from midline, and one-third were unbiased. Considered in the context of data from Experiment 2a, this resulted in a linear decrease in the proportion of children biased toward midline as age increased, and a linear increase in the proportion of children biased away from midline as age increased. Finally, the proportion of children in each classification group for the −30° target can be seen in Figure 10, lower panel. Here, about half of the older 3-year-olds were biased toward midline and half were biased away from midline. Therefore, at both −20° and −30°, the 3 years, 8-month-olds showed transitional behavior.
Variable Directional Error
Variable error is shown in Figure 11 (gray, dot-dash line). As can be seen in the figure, variable error increased as delay increased. In addition, the magnitude of 3 years, 8-month-olds’ variable error was in between the 3 years, 6-month-olds and 4-year-olds from Experiment 2a. Variable error was analyzed in a repeated measures ANOVA with Condition (−10°/70°, −20°/60°, −30°/50°) and as a between-subjects factor and Target (inner, outer) and Delay (0 s, 5 s, 10 s) as within-subjects factors. The only significant effect was a Delay main effect, Wilks’ Λ = .42, F(2,30) = 20.84, p > .001, η2 = .58.
Older 3-year-olds’ variable error was compared directly to the younger 3-year-olds’ and 4-year-olds’ variable error by conducting two repeated-measures ANOVAs with Target and Delay as within-subjects factors and Age and Condition as between-subjects factors. Only significant Age effects are reported. There was a significant Age main effect in the ANOVA comparing the younger and older 3-year-olds, F(1,64) = 9.13, p < .01, η2 = .13. There was also a significant Age main effect in the ANOVA comparing the older 3-year-olds and 4-year-olds, F(1,60) = 6.22, p < .05, η2 = .09. Thus, the systematic decrease in variable error over development evident in Figure 11 was statistically reliable.
Perseverative Error Analyses
Three years, 8-month-olds made 86 perseverative errors out of a total of 1201 trials. The number of perseverative error trials ranged from 0 to 14 per participant. The mean proportion of perseverative errors per participant can be seen in Figure 12. As can be seen in the figure, the mean proportion of perseverative errors for the older 3-year-olds was in between the mean proportion of perseverative errors for the younger 3-year-olds and 4-year-olds from Experiment 2a. The mean proportion of 3 years, 8-month-olds’ perseverative errors to each target was analyzed in a repeated measures ANOVA with Target as a within-subjects factor and Condition as a between-subjects factor. There were no significant effects.
Discussion
Experiment 2b further tested the gradual, continuous nature of the predictions of the DFT and the spatial precision hypothesis. Specifically, we tested whether an age in between 3 years, 6 months and 4 years, 4 months would show an intermediate pattern of error relative to Experiment 2a. Results supported this prediction. Children 3 years, 8 months of age were biased toward midline at −10° and not biased at −20° or −30°. This pattern is more advanced than the younger 3-year-olds who were biased toward midline at −10° and −20°, and less advanced than the 4-year-olds who were biased away from midline at −20° and not biased at −10°.
Individual differences at −20° provided particularly dramatic evidence of the gradual nature of the developmental transition predicted by the DFT. Recall that in the previous experiment, the majority of the 3 years, 6-month-olds were biased toward midline or unbiased while the majority of the 4-year-olds were biased away from midline at −20°. In the present experiment, a third of the older 3-year-olds were biased toward midline, a third were biased away from midline, and a third were unbiased. Thus, across experiments there was a linear increase in the number of children biased away from midline at −20° as age increased.
Beyond the change in geometric effects, results of this experiment also provide further support for the prediction of increased stability in SWM over development (see also Thelen et al, 2001; Spencer & Hund, 2003). Across Experiments 2a and 2b there was a linear decrease in the number of perseverative errors as age increased. There was also a systematic decrease in variable error over development.
Although data from Experiments 2a and 2b are generally consistent with the predictions of our model, the exact pattern of attraction and repulsion across ages did not match the simulations. Specifically, in the simulations, the 60° target was the first target to show significant repulsion from midline, and then repulsion gradually spread inward to the targets closer to midline. In children’s responses, however, repulsion first emerged at 20° and then spread outward to the other targets. The goal of Experiment 3 was to examine whether the DFT can capture this specific pattern of biases across targets and ages.
Simulation Experiment 3
The goal of Simulation Experiment 3 was to determine whether the DFT and the spatial precision hypothesis can quantitatively match the pattern of errors observed in Experiment 2. Results of Experiment 2 were in general agreement with predictions of the DFT, but the emerging bias away from midline over development did not fit the exact pattern the model exhibited. There were two primary differences. First, the model was initially biased away from midline at the 50° and 60° targets and then spread to the targets that were closer to midline. Children, however, were initially biased away from midline at 20° and then the bias spread to the other targets. The second difference is that the model showed significant bias toward midline at targets close to this axis when repulsion first emerged at 50° and 60°. This is not the case with children: children whose responses were biased away from midline at 20° were not significantly biased toward midline at any location.
The pattern of error in children’s responses suggests a modification in how the SPH is implemented: the fact that repulsion first emerged at 20°—the same target location where adults show maximal repulsion (see Spencer & Hund, 2002)—suggests that the width of inhibition is not changing over development. Increasing the strength of inhibition without manipulating the width over development should result in repulsion that first emerges near the reference axis and then spreads to the outer targets as the strength of inhibition increases.
In Simulation Experiment 3 we tested the DFT and SPH by trying to match the pattern of errors from Experiment 2. We did this by manipulating the same developmental parameters as in Experiment 1 with the exception of leaving the width of the inhibitory projections the same across development.
Method and Results for Simulations of Developmental Endpoints
The methods for the simulations were the same as in Simulation Experiment 1 except that the number of simulations was increased to 200 trials to each target location for each parameter set to ensure that the subtle effects we were attempting to capture were robust effects in the model. As in Experiment 1, we began by quantitatively modeling the adult data from Spencer and Hund (2002). In our effort to quantitatively fit data from Experiment 2 with consistent changes in the direction of parameters across development, we had to slightly modify the adult parameters used previously. Although the parameter values used for the adult model were slightly different than in Experiment 1 (see Table A2), the results were similar (see Figure 5h and 5i).
Table A2. Parameter values for Experiment 3 simulations.
| Layer | τ | h | self- excitation |
excitatory projection(s) |
inhibitory projection(s) |
reference input |
target input |
|---|---|---|---|---|---|---|---|
| u (PF) | 80 | −7 | cuu = 1.90 | cuv = 1.206 | cref = 16.638 | ctar = 45 | |
| σuu = 3.0 | σuv = 5.7 | σref = 0.8 | σtar = 3 | ||||
| kuv = 0.05 | |||||||
| v (Inhib) | 10 | −12 | cvu = 4.7 | ||||
| σvu = 5.0 | |||||||
| cvw = 2.2 | |||||||
| σvw = 6.0 | |||||||
| w (SWM) | 80 | −6.5 | cww = 3.296 | cwu = 1.75 | cwv = 0.757 | [all inputs scaled by cs = 0.2] |
|
| σww = 5 | σwu = 3 | σwv = 35 | |||||
| kwv = 0.05 | |||||||
|
| |||||||
| developmental scaling parameters (from ‘youngest’ to ‘oldest’ parameter setting) |
dev_cuu = 0.0866 | dev_cv = 0.1003 | dev_cref = 0.32 | ||||
| dev_cww = 0.4237 | dev_σref = 75.0 | ||||||
| dev_cs = 2.0 | |||||||
| dev_cuu = 0.1732 | dev_cv = 0.3008 | dev_cref = 0.32 | |||||
| dev_cww = 0.6356 | dev_σref = 6.875 | ||||||
| dev_cs = 1.2 | |||||||
| dev_cuu = 0.1732 | dev_cv = 0.3008 | dev_cref = 0.32 | |||||
| dev_cww = 0.6356 | dev_σref = 3.75 | ||||||
| dev_cs = 1.15 | |||||||
| dev_cuu = 0.8225 | dev_cv = 0.5985 | dev_σref = 0.72 | |||||
| dev_cww = 0.8051 | dev_σref = 1.25 | ||||||
| dev_cs = 1.15 | |||||||
| dev_cuu = 0.9524 | dev_cv = 0.7719 | dev_σref = 0.76 | |||||
| dev_cww = 0.9322 | dev_σref = 1.25 | ||||||
| dev_cs = 1.15 | |||||||
| dev_cuu = 1.0 | dev_cv = 1.0 | dev_σref = 1.0 | |||||
| dev_cww = 1.0 | dev_σref = 1.0 | ||||||
| dev_cs = 1.0 | |||||||
Next, we fit the 3-year-old data from Schutte and Spencer (2002) using the implementation of the SPH from Experiment 1, with the exception that we did not scale the widths of the connections between fields. Thus, we scaled the width of the reference input as well as the strength of this input into the perceptual and working memory fields; the strength of local excitation in the perceptual and working memory fields; and the strength of the connections from the inhibitory field to the perceptual and working memory fields. We increased the width of the reference input and decreased the various strength parameters until the model showed biases toward midline for all targets to the left and right of this axis (see Figure 5g). The parameter values are given in Table A2. As Figure 5 shows, we were able to capture the performance of 3-year-olds with the simplified version of the SPH.
Implementation of the SPH During the Developmental Transition
To examine the behavior of the model during the transition, we scaled the parameters between the 3-year-old and adult parameter values. Our goal was to produce a total of 6 parameter sets each of which fit one of the age groups. The parameter values for each set are given in Table A2. In addition to fitting the pattern of error in the data, each parameter set needed to meet the same criteria that were used in Experiment 1: (1) successfully build a peak in SWM when the target turned on; (2) maintain this peak in SWM during the 10 s delay; and (3) hold onto the peak in SWM without forming a second peak associated with the midline reference frame.
We examined several parameter sets en route to the final values. In fact, we ran simulations for over 80 different parameter sets in order to fully explore the parameter space (note that each set took approximately 18 hours to simulate for a total of over 1440 hours of simulation time). Of the parameter sets tested, some did not meet the criteria listed above. For example, increasing the strength of inhibitory connections too much, dev_cv, resulted in working memory peaks that would not sustain during the delay for some target locations. Some parameter sets met the above criteria and displayed the basic qualitative pattern—decreasing bias toward midline over development and the emergence of repulsion from midline that increased over development—but had errors that were either too large or too small. For example, increasing the strength of the excitatory connections, dev_cww, within the working memory field, SWMobj, often resulted in errors that were too large. In summary, although it is likely that the final parameter set described below is not the only parameter set that would offer a good fit to the empirical data, we are confident that only a very limited number of parameter sets will reach the level of fit we obtained. In our experience, there are simply too many constraints to think otherwise, including constraints in (a) the DFT and how collections of parameters constrain one another (effectively limiting the number of “free” parameters), (b) how the model must operate on each trial to perform the spatial recall task, and (c) the empirical data that includes estimates of both mean directional error and response variability at each target location and each age.
The parameter values that met the above criteria and provided the best fit are in Table A2 and are graphed in Figure 13a and b. Note that because we were matching the behavioral data we did not attempt to scale the parameters smoothly, but many of the parameters ended up falling on relatively smooth curves. A primary question is whether the resultant effect on the self-sustaining peaks would show the properties proposed by the SPH—broad, weaker peaks early in development with little inhibition and stronger, more precise peaks later in development with stronger inhibition. This was indeed the case. As can be seen in Figure 13c, a WM peak in the 3-year-old model is broader and weaker (see black bold line) than the peak in the adult model (see light gray, bold line). As the parameters are scaled, the peak becomes narrower and stronger (see black to light gray lines). Thus, the scaling replicated the central aspects of the SPH, that is, peaks in SWM become stronger and more precise over development.
Figure 13.
Panels (a) and (b) show the developmental scaling parameters used in Experiment 3 for each age group modeled. Note that dev_σref was set to 70 for the youngest 3-year-old model (3,0). Panel (c) shows developmental changes in the activation profile of self-sustaining peaks in the SWM field as a result of changes in spatial precision parameters from early in development (black bold line) to later in development (light gray bold line).
As in Experiment 1, the target peaks still died out on a few trials so these trials were removed from analysis. Overall, 0.3% of trials (23 trials out of a total of 8400 trials) were removed (parameter set 1: 0%, parameter set 2: 0%, parameter set 3: 0%, parameter set 4: 0.6%, parameter set 5: 0.001%, parameter set 6: 1.0%).
Results of Developmental Simulations
The constant error at each target location at the end of the delay for parameter sets 2 to 5 is shown in Figure 14, dashed lines. The data from Experiment 2 are shown for comparison (Figure 14, solid lines). As can be seen in the figure, the data from the model match the data from Experiment 2 quite closely, that is, the pattern of attraction/repulsion from midline over development fits the empirical data. Most critically, repulsion first emerges for the 4-year-old model at the 20° and 30° targets—the precise locations where repulsion first emerged in the empirical data. Due to the relatively limited number of neurons we used in the model, fits to the 10° target are the least accurate, but even the 10° target in these simulations behaves similarly to results from Experiment 2.
Figure 14.
Mean constant error from Experiment 3 simulations (dashed lines) and mean constant error from Experiment 2 (solid lines) for each age group. Error bars are standard error of the mean for the data from Experiment 2.
Why did repulsion first emerge at 20° in the model? This was due to how inhibition changed over development. Initially inhibition was only strong enough to cause peaks in working memory to be repelled near 20°—the place where inhibition from the reference peak substantially overlapped inhibition from the working memory peak. When targets were farther from midline inhibition overlapped, but was too weak to cause peaks in working memory to drift systematically over delays. As inhibition strengthened over development, the spatial range across which inhibitory overlap could cause delay-dependent drift increased and working memory peaks farther from midline showed this effect.
As in Experiment 1, we examined response variability by computing the standard deviation of responses to each target location for each parameter set. We then averaged the standard deviations across the 10° to 60° targets for each parameter set (see Figure 15). As can be seen in Figure 15, there was a reduction in variability over development in the model which is consistent with the results from Experiment 2 and Spencer and Hund (2003). Additionally, variability at the 0° target was lower than at the other target locations for all parameter sets (see Figure 15) which is consistent with results of Spencer and Hund (2003).
Figure 15.
Variable error (standard deviation) for parameter sets 1 (3-year-old model) to 6 (adult model) for the 0° target (light gray, dotted line) and the 10°–60° targets (dark gray, dashed line).
Overall, the standard deviations are much lower than the empirical values from Experiment 2. This is not surprising, given that we did not change the level of noise from the level used for the adult simulations. It is reasonable to assume that the level of noise would be higher for younger children. We attempted to reach the 3-year-olds’ level of variability by scaling the strength of the noise. Although this did increase response variability in the model, there was an upper limit: we could not obtain the level of variability observed in 3-year-olds’ responses because at high levels of noise, the model could no longer maintain a peak in the SWM field. It is likely that the high variability seen in young children’s responses reflects multiple noise sources. For instance, children must maintain their ego position relative to the table in order to correctly map the required motor response onto a location in the task space. Three-year-olds tend to be rather antsy in laboratory tasks; thus, it is likely that some of the variance in their responses reflects mis-estimation of ego position that accumulates during each trial. Similarly, 3-year-olds are easily distracted and may temporarily lose their focus on task-relevant details. None of these extraneous factors are included in our model. Although variability in the model was not at a 3-year-old level, the model did show a decrease in variability over development. This establishes that changes in the precision of neural interactions in the model contribute to the stability of peaks as well as the size and direction of response errors.
One advantage of quantitatively modeling a developmental change is using the model to generate hypotheses for future work. We were able to capture the developmental change by changing the precision of neural interaction in the model, but can we learn anything from the specific parameter changes? Examination of the parameter changes in Figure 13 reveals that some parameter changes were relatively gradual, while others changed more dramatically over development. For the parameters related to the reference axis input, the largest changes occurred between the 3 years and 3 years, 6 months parameter sets (see Figure 13a). In contrast, for the parameters related to neural interaction in the perceptual and spatial working memory fields, the largest changes occurred between the 3 years, 8 months and 4 years, 4 months models (see Figure 13b). This suggests that changes in the perception of the midline symmetry axis may precede dramatic changes in how the target is remembered and actively anchored to perception of the reference frame during the memory delay. Therefore, future work should examine the connection between perception of reference axes and the precision of spatial memory, using, for instance, tasks that probe perception of the midline symmetry axis directly.
In summary, the model did a good job quantitatively modeling a complex pattern of results over development. Importantly, these fits were obtained without any changes in the width of projections between the fields. Only changes in the reference input and the strength of local excitation and lateral inhibition were required. As we discuss below, these changes in neural interactions are consistent with known changes that occur during brain development, effectively grounding the transition in geometric biases in well-documented neural mechanisms.
General Discussion
The purpose of this study was to test a set of predictions of the DFT about the developmental course of the transition in geometric effects. Simulations of the DFT in Experiment 1 were used to generate a set of hypotheses about the transition which were tested empirically in Experiment 2. Results from the empirical study found that the age range during which the transition in geometric effects occurred was protracted, and depended on the target location probed. Table 2 shows the direction of bias for each target at each age. As can be seen in the table, results supported the prediction that over development the range of attraction toward midline narrows. In addition, data from the experiments supported the prediction that over development inhibition emerges and becomes stronger; however, the location at which inhibitory biases first emerged at 4 years, 4 months of age was not consistent with model simulations. Thus, in Simulation Experiment 3 we attempted to quantitatively fit results from Experiment 2 with a simpler implementation of the spatial precision hypothesis. Simulation results showed a good match to the empirical findings. Specifically Experiment 3 was able to capture the data by changing the strength of connections between the fields and not changing the widths of neural interaction.
Table 2. Pattern of memory biases over development.
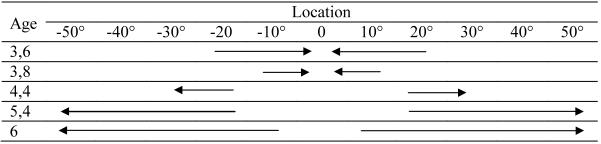
|
Results from Experiment 2 also supported the predicted increase in stability over development. This was evident in analyses of variable error and perseverative errors. DFT simulations predicted a decrease in the variability of responses over development. The model also demonstrated that early in development peaks may not always sustain at the target location. Specifically, the target peaks did not sustain in every simulation, even though we chose scaling parameters that would sustain target peaks in a maximum number of trials. Results of Experiment 2 suggest that in some instances young children had difficulty sustaining a peak in working memory, and when the peak did not sustain, responses were dominated by longer-term memory.
Thus, overall results from Experiment 2 provide preliminary support for the prediction that the transition in geometric effects is gradual, protracted, and depends on the specific target location probed. It is important to emphasize that this work is only a first step and needs to be followed by longitudinal studies that seek stronger evidence that the developmental transition is gradual within individual subjects. We note, however, that this presents some real challenges. In the present study, each child responded to only 2 targets on either side of midline. This ensured that results were not caused by known developmental changes in recall biases toward items in long-term memory built up across trials (see Schutte et al., 2003). In a longitudinal study, one would have to factor such long-term memory processes into the design and control for the practice effects that arise by asking children to repeatedly respond to the same targets. In this context, the cross-sectional design used here has some merit because it precisely controlled for known influences on spatial working memory. That said, it is only through the combined strengths of cross-sectional and longitudinal designs that we can get a full picture of the nature of the developmental transition in geometric biases.
Implications for Dynamic Systems Theory
The results of these experiments supported two key insights of dynamic systems theory: qualitative developmental transitions can arise from quantitative changes in underlying parameters and behavior is the result of soft-assembly in a multiply-determined system (for discussion, see Spencer & Perone, in press). One of the central insights of dynamic systems theory is that bifurcations (i.e., transitions) from one stable attractor state to another over development can be due to quantitative changes in an underlying variable (see, e.g., Elman et al., 1996; Thelen & Smith, 1994; van der Maas & Molenaar, 1992; van Geert, 1998). According to the spatial precision hypothesis, the developmental transition in geometric effects is such a case: seemingly qualitative changes result from quantitative changes in neural interactions.
A central question, however, is whether the transition in geometric effects is a qualitative or quantitative developmental transition. The dominant explanation of this transition provided by the CA model, characterized the transition as a qualitative change—children transition from using one category to a re-conceptualization of space and the use of two categories. Although, previous research supported this proposal (Huttenlocher et al., 1994; Schutte & Spencer, 2002; Spencer & Hund, 2003), this research only tested children prior to the transition and children post transition. Several researchers (e.g., Adolph et al., in press; Newcombe & Learmonth, 1999; Thelen & Smith, 1994) have argued that qualitative transitions only appear qualitative because of the resolution of the data (see also, Fischer & Paré-Blagoev, 2000). When age samples are widely separated, as they were in the previous studies, transitions can appear qualitative. When viewed at a finer scale, qualitative transitions can appear more quantitative. This study has shown that the transition in geometric effects is not an all-or-none qualitative change as previous research suggested. Rather, the transition is more quantitative in nature with the region attracted toward midline narrowing and the region repelled from midline expanding (see Table 2).
There is, however, a clear qualitative component to the transition in geometric effects. Rather than just the region of attraction toward midline narrowing, repulsion emerges over development. Before 4 years, 4 months of age there is not enough inhibition to bias targets away from midline. Strong inhibition first emerges at −20° at around 4 years of age. This causes a qualitative change in behavior—a bias away from midline. After that, inhibition continues to change quantitatively, and, as the strength of inhibition increases, targets further out are also repelled from midline. Thus, both attractive and repulsive effects emerge from a quantitative change in the precision of neural interactions. Future work using a longitudinal design will be needed to track individual children during the time of the transition to determine the detailed time course of changes in neural precision as children move step-by-step from attraction to repulsion.
Implications for the CA Model
According to the CA model, the transition in geometric effects is a transition in children’s ability to subdivide space into two categories (Huttenlocher et al, 1994). What are the implications of our findings for the CA model? Can the CA model account for the details of the pattern of error we observed?
If there is a prototype at midline—as is suggested by the biases toward midline early in development—biases should be smaller near midline and larger further out (Huttenlocher & Lourenco, 2007). Although data from 3-year-olds are generally consistent with this proposal (see Schutte & Spencer, 2002), data from children closer to the developmental transition are not. For instance, 3 years, 6-month-olds’ biases toward midline were larger at locations near midline and not significantly biased further out (see Experiment 2). It is not clear how the CA model would explain this pattern of error. Similarly, it is not clear how this model would explain the initial emergence of biases away from midline at −20° followed by the expansion of the repulsion effect across a range of target locations over development.
These empirical details highlight a primary limitation of the CA model in the context of the present report: this model does not explain how development occurs. According to the CA model, children’s ability to impose categories increases with age (Huttenlocher & Lourenco, 2007), but the model does not tell us anything about the processes that give rise to subdivision or how they change over development. Thus, in our view, the present study presents a major challenge to the dominant theory of geometric biases. We see no clear way that this model can account for the pattern of error predicted a priori by the DFT.
In this context, we think it is time to reconsider the concepts introduced by the CA model nearly two decades ago. There are now a growing number of ways in which data from spatial recall tasks are not consistent with the details of the CA model, but are consistent with the DFT. For instance, we highlighted in Simulation Experiment 1 that children and adults show lower variability when responding to targets aligned with a midline symmetry axis (see also, Engebretson & Huttenlocher, 1996)—a pattern consistent with the DFT but not the CA model (for extensive discussion, see Baud-Bovy, 2008). Similarly, spatial recall responses are systematically biased relative to longer-term memories built-up from trial-to-trial (see, e.g., Schutte et al., 2003; Spencer & Hund, 2002; Spencer & Hund, 2003), yet there is no concept in the CA model to account for such effects (Huttenlocher et al., 2004). Finally, the CA model does not provide an adequate account of the complex pattern of developmental changes predicted by the DFT and tested in the present report.
Some of these differences in specificity arise because the DFT and CA model live at different levels: the CA model lives at the level of computational theory, while the DFT lives at the level of process, grounded in neural principles. Although we have sometimes described these two theories as complementary in nature (see Spencer & Hund, 2002), real differences between the theories have emerged over time that can be directly tied to the fact that the DFT moves concepts to the level of process. The DFT specifies changes in recall responses over delay (both constant and variable error); it specifies how patterns of responses should change from trial-to-trial; and it specifies what is changing over development to yield predictable and empirically robust changes in how perceived reference axes affect SWM. Although there can certainly be conceptual coherence when theories live at different levels, we contend that the DFT and CA model are much less coherent than they once appeared.
The DFT, for example, presents a conceptually related, but different view of “category boundaries.” In our theory, “boundaries” are always anchored to visible structure (see Simmering, Peterson, et al., 2008), for instance, the edges of a table and the symmetry axes they specify (for similar ideas, see Schiano & Tversky, 1992). Consequently, there are real constraints regarding when geometric biases should arise, and how variations in perceptual cues should systematically alter—and in some cases, destroy—geometric biases. We demonstrated this recently by showing that adults are unable to mentally impose a category boundary in otherwise empty space (Simmering & Spencer, 2007). Is this view of “boundaries” fundamentally different than the view proposed by Huttenlocher et al. (1991)? At one level, the answer is no: both theories have been used to model geometric biases near visible edges and symmetry axes, and perceptual cues that divide space into regions have played a fundamental role in the concepts used by Huttenlocher, Newcombe, and colleagues for decades (for a general review, see Newcombe & Huttenlocher, 2000). At another level, the answer is yes because the DFT specifies the origin of boundary effects (for further discussion, see Spencer et al., 2007), this theory can capture—in detail—the pattern of constant and variable errors near boundaries, and this theory places constraints on when boundary effects should and should not occur in both early and later development.
Given that the time-dependent interaction between perceptual and working memory processes in the DFT produces both stability along an axis and geometric biases to the left and right of an axis, there is no need for spatial prototypes. Thus, a second point of contrast between models is that the CA model posits represented prototypes, and the DFT does not. That said, the longer-term memory mechanism in the DFT (a form of Hebbian learning; see Spencer et al., 2007; Spencer, Dineva, & Schöner, in press) can create a prototype-like pull toward the center of a spatial region if participants are asked to remember targets in that region of space. Critically, however, this mechanism differs fundamentally from a spatial prototype because non-prototype-like behaviors can also emerge: biases away from the center of a spatial region can arise if targets are asymmetrically distributed near an axis (see Spencer & Hund, 2002), responses are sensitive to trial-to-trial variations in target placement (e.g., Schutte et al., 2003), and responses vary with the frequency of occurrence of each target (Spencer & Hund, 2003). Note that recent extensions of the category adjustment ideas move in a related direction, but the concepts remain at the level of computational theory (see Cheng et al., 2007; Huttenlocher et al., 2000).
The points of contrast above raise an important question: does the CA model account for phenomena that the DFT does not? This question is difficult to evaluate at present. The concepts of boundaries and spatial prototypes have been applied to many phenomena. For instance, Sandberg, Huttenlocher, and Newcombe (1996) showed a complex pattern of developmental change when children’s performance was probed in single vs. two-dimensional spatial recall tasks. In our view, these data are consistent with a two-dimensional implementation of the DFT, but it is our task to show how. Similarly, CA model concepts have been applied to tasks that ask children to learn both about the spatial locations of objects as well as which objects go where (see, Plumert, Hund & Recker, 2007). Although we have extended the DFT to address working memory for non-spatial features and how objects might be actively maintained in working memory (Johnson, Spencer & Schöner, in press), we have yet to explore the application of dynamic neural fields to these specific examples in development. Thus, our overall evaluation is that there are similarities between the DFT and CA model, but the DFT provides a more detailed, accurate, and complete account of spatial recall and the development of this cognitive ability.
Development in the Dynamic Field Theory
By implementing a central developmental hypothesis, the spatial precision hypothesis, in a dynamic neural field model, we were able to capture the predicted pattern of bias during the transition in geometric effects. This is now the second paper that uses the DFT and SPH to quantitatively model a developmental change in spatial memory. Schutte et al. (2003) used the DFT and SPH to quantitatively model developmental changes in experience-dependent biases in spatial memory. The fact that the same theory and the same developmental hypothesis have now quantitatively captured two different classes of spatial memory biases is impressive and lends strong support for both the DFT and the SPH.
There are differences between the architectures used in Schutte et al. (2003) and the present paper. In the present paper, we used a new architecture which takes neural grounding to a deeper level. Although both models represent locations in space using a population of spatially-tuned neurons consistent with cortical neurophysiology (e.g., in motor cortex: Georgopoulos, Kettner, & Schwartz, 1988; Georgopoulos, Taira, & Lukashin, 1993; in premotor cortex: di Pellegrino & Wise, 1993; in prefrontal cortex: di Pellegrino & Wise, 1993; Wilson, Scalaidhe, & Goldman-Rakic, 1993), the model in Schutte et al. (2003) combined inhibitory and excitatory connections in one field. By contrast, the multi-layered model used here is more consistent with the multi-layered structure of visual cortex (see Douglas & Martin, 1998; for related network models, see Tanaka, 2000; Compte et al., 2000). Such ties to neurophysiology are exciting, because they raise the possibility of testing the model using neurophysiological techniques. Indeed, several studies have demonstrated that dynamic fields can be directly estimated through single-cell recording studies (e.g., Bastian, Riehle, Erlhagen, & Schöner, 1998; Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999). Several reaction time predictions of a dynamic field model of motor planning have been tested in this way (Bastian et al., 1998; Erlhagen et al., 1999).
Although ties to neurophysiology provide important grounding, we emphasize that the DFT is a functional model of behavior. We highlighted this aspect in the present report, showing how the multi-layered architecture used here opens the door to study new behaviors not previously addressed within our framework. In particular, the 3-layer architecture is needed to specify how perceptual-like processes and working memory processes come together in real time—an issue that was not addressed in Schutte et al. (2003).
The different architectures used across studies raises the question of whether the current architecture can capture the experience-dependent biases modeled in Schutte et al. (2003). Schutte et al. showed that biases toward a longer-term memory (LTM) of an “A” location when children remembered a nearby “B” location decreased as age increased and as the distance between A and B increased. The simulations in Experiments 1 and 3 did not include any inputs from a longer-term memory process. Therefore, to confirm that the current version of the model can capture the effects from Schutte et al., we ran a set of simulations with a target at 40° and a Gaussian LTM input centered at 20°, 30°, 50°, or 60°. The same LTM input in was used in all simulations.
Figure 16 shows the difference between mean directional error from 50 simulations with LTM input and 50 simulations without LTM input for each parameter set. Even though the LTM input was identical across parameter sets, the influence of this input varied depending on the parameter set and the distance of the LTM input from the target location. Specifically, as the “age” of the model (i.e., parameter set) increased, bias toward the LTM input decreased. In addition, this change over age depended on the separation between the LTM input and the target location. The three younger parameter sets (1–3) showed robust biases toward the LTM input across all separations, while the three older parameter sets (4–6) only showed robust biases with a 10° separation (i.e., when LTM was centered at either 30° or 50°). Overall, these results demonstrate that the current model behaves in a manner consistent with results from Schutte et al. (2003).
Figure 16.
Difference in mean directional error to a 40° location when the model responded with no LTM input and LTM input centered at 20°, 30°, 50°, or 60° for parameter sets 1–6 from Experiment 3. Negative difference scores reflect relatively more counterclockwise error (toward 20° and 30°), while positive difference scores reflect relatively more clockwise error (toward 50° and 60°).
Despite changes in the architecture, the basic assumptions of the model used here and in Schutte et al. and the developmental hypothesis implemented remain the same. In both papers, developmental changes in spatial memory were captured by quantitative changes in the precision of neural interaction. Thus, the DFT has successfully captured two developmental changes in SWM—in quantitative detail—in addition to qualitative aspects of performance in other spatial memory and spatial discrimination tasks (Schutte & Spencer, 2002; Simmering, Schutte, & Spencer, 2008; Spencer et al., 2007), as well as developmental changes in novel noun generalization in early childhood (Samuelson, Schutte, & Horst, in press).
Although this degree of generalization is impressive, there are, of course, several other aspects of children’s spatial recall performance that remain to be explained. One result that appears consistent with our theory comes from Huttenlocher and colleagues (1994). These researchers found that even young children show biases away from a midline axis when spatial recall is measured in a small geometric space (a small rectangle on a piece of paper; see also, Spencer, Simmering & Schutte, 2006). A smaller scale geometric space should have more salient and precise symmetry cues. Implementing this in our model using a stronger and more precise reference input produces stronger reference-related inhibition and narrower reference-related excitation. These changes produce reliable biases away from midline in our model with parameter values that produced attraction toward midline in the present study (see Schutte & Spencer, 2009). Therefore, the DFT is able to explain why the age at which children show reference-related repulsion depends on the size of the geometric space.
This result highlights that developmental changes in performance in our model emerge from a complex interplay between the system’s “intrinsic” dynamics and the details of the task. This raises a fundamental question: does our model actually provide a mechanism for how developmental changes occur? The spatial precision hypothesis offers an explanation for what is changing over development and, further, that changes in neural interaction should arise from continuous processes over a developmental time scale. But how do these changes in neural interaction occur?
Given that the DFT has strong ties to neurophysiology (for further discussion, see Spencer, Dineva & Schöner, in press), we can look for answers to how changes in neural interaction occur by examining neurophysiological changes in the brain over development (for a more extensive discussion, see Simmering, Schutte & Spencer, 2008). Prefrontal cortex (PFC) is still developing during the time of the transition in geometric effects (Gogtay, et al., 2004; Rakic, 1995; Sowell, Thompson, Tessner & Toga, 2001), and pruning of synapses and myelination are still occurring (Huttenlocher, 1990; Sampaio & Truwit, 2001). It is possible that these neurophysiological changes underlie changes in spatial precision over development. For example, Edin and colleagues (2007) examined neurophysiological changes related to the development of working memory by implementing changes related to synaptic pruning, synaptic strengthening, and myelination in a neural network model of visuospatial working memory. These researchers then used the model to generate five developmental predictions about BOLD signals. They compared predictions the network made to BOLD signals measured with fMRI in 13-year-olds and adults, and found that neural interactions with “higher contrast” over development effectively captured developmental changes in BOLD signals. Higher contrast in their model consisted of strengthening connections both within and between regions which yielded more precise patterns of neural activation. Thus, the most effective developmental hypothesis in their simulation and fMRI study mirrored the changes captured by our implementation of the spatial precision hypothesis in Experiment 3.
An example of a similar proposal is the representation acuity hypothesis proposed by Westerman and Mareschal (2004) to explain the development of visual object processing. According to the representation acuity hypothesis, the transition from processing object parts to processing objects as wholes is the result of the narrowing of receptive fields in visual cortex. This narrowing of receptive fields is conceptually similar to the increase in the precision of neural interactions in the DFT. The present paper shows, however, that such narrowing can be an emergent result of strengthening excitatory and inhibitory interactions among layers of neurons in cortical fields.
Although these explanations of what is changing at the level of the brain are exciting, this simply shifts the developmental question to another level of description, leaving the question open as to what motivates the change in cortex. It is likely that these cortical changes are regulated by complex interactions among a host of factors from the genetic level to the level of large-scale interactions among populations of neurons in different cortical areas. It is also likely that these changes are massively experience-dependent (see Johnson, 1999, for a review). Given that the changes we made to the model in Simulation Experiment 3 involved only changes in the strength of excitatory and inhibitory interactions among layers, it is easy to imagine that such changes could arise from a simple Hebbian process that strengthens cortical connections as a function of experience. Future research will need to probe whether such a process can indeed give rise to the types of parameter changes we implemented in Experiment 3 as the network is given experience in different spatial tasks.
Conclusion
The DFT predicted that the transition in geometric biases would be gradual with the area that is biased toward midline narrowing and the repulsion from midline emerging and expanding. The predictions were supported by behavioral evidence from an initial cross-sectional study. Taken together, the simulation and behavior experiments presented here bring us closer toward understanding the processes underlying the development of spatial working memory. Although detailing the processes that underlie development is clearly a daunting challenge, the empirical and theoretical work reported here provides a critical first step as we move toward a more mechanistic understanding of how developmental transitions arise within the domain of spatial cognition.
Acknowledgments
This research was supported in part by NIMH F31 MH066595 awarded to Anne R. Schutte, and NSF HSD 0527698 awarded to John P. Spencer. We would like to thank Larissa Samuelson and Gregor Schöner, as well as two anonymous reviewers, for their comments on this work. We would also like to thank the children and parents who participated in this research.
Appendix
Model Equations
Activation in the perceptual field, PF (u), was governed by the following equation:
| (1) |
where is the rate of change of the activation level for each neuron across the spatial dimension, x, as a function of time, t. The constant τ sets the time scale of the dynamics (Erlhagen & Schöner, 2002). The current activation in the field is u(x, t) . This component is negative so that activation changes in the direction of the resting level hu . The excitation / lateral inhibition interaction profile is defined by self-excitatory projections, , and inhibitory projections from the Inhibitory layer (Inhib; v), . These projections are defined by the convolution of a Gaussian kernel with a sigmoidal threshold function.The Gaussian kernel was specified by:
| (2) |
with strength, c, width, σ, and resting level, k. The level of activation required to enter into the interaction was determined by the following sigmoid function:
| (3) |
where β is the slope of the sigmoid. The slope determines whether neurons close to threshold (i.e., 0) contribute to the activation dynamics with lower slope values permitting graded activation near threshold to influence performance, and higher slope values ensuring that only above-threshold activation contributes to the activation dynamics. This field also receives reference input, S ref ( x, t ) and target input, S tar ( x, t ). These inputs are gaussian inputs with associated widths, σref and σtar, and strengths, cref and ctar. The final input to the field is spatially correlated noise, , (see Schutte, Spencer, & Schöner, 2003, for a discussion of spatially correlated noise)
The second layer of the model, Inhib (v), is specified by the following equation:
| (4) |
As with PF (u), v(x, t) is the rate of change of the activation level for each neuron across the spatial dimension x, as a function of time, t. The constant τ sets the time scale, v(x,t) is the current activation in the field, hv set the resting level of the field. Inhib (v) receives activation from both PF (u), and SWM(w), . These projections are defined by the convolution of a Gaussian kernel with a sigmoidal threshold function using the same equations as the interaction in PF (u). As in PF (u), the final input to the field is spatially correlated noise, .
The SWM layer (w) is governed by the following equation:
| (5) |
where w(x,t) is the current activation in the field, and hw is the resting level. SWM receives self excitation, , lateral inhibition from Inhib, , and input from PF, . SWM also receives direct reference input, S ref ( x, t ) and target input, S tar ( x, t ) , scaled by cs. The final input to the field is spatially correlated noise, .
Model parameters
The size of the fields used in all simulations was 397 units with 1.2 units equal to 1 degree. For all simulations, noise strength was set to .135, and noise width—the spatial spread of noise—was set to 1. Additionally, for all simulations the strength and width of the target input were set to 45 and 3 respectively. The remaining parameters used in Experiment 1 are given in Table A1, and the parameters used for the simulations in Experiment 3 are given in Table A3.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/journals/xhp.
Contributor Information
Anne R. Schutte, University of Nebraska-Lincoln
John P. Spencer, University of Iowa
References
- Acredolo LP. Development of spatial orientation in infancy. Developmental Psychology. 1978;14:224–234. [Google Scholar]
- Adolph KE, Robinson SR, Young JW, Gill-Alvarez F. What is the shape of developmental change? Psychological Review. doi: 10.1037/0033-295X.115.3.527. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amari S. Dynamical stability of formation of cortical maps. In: Arbib MA, Amari S, editors. Dynamic interactions in neural networks: Models and data. Springer; New York: 1989. pp. 15–34. [Google Scholar]
- Amari S, Arbib MA. Competition and cooperation in neural nets. In: Metzler J, editor. Systems Neuroscience. Academic Press; New York: 1977. pp. 119–165. [Google Scholar]
- Bastian A, Riehle A, Erlhagen W, Schöner G. Prior information preshapes the population representation of movement direction in motor cortex. NeuroReport. 1998;9:315–319. doi: 10.1097/00001756-199801260-00025. [DOI] [PubMed] [Google Scholar]
- Baud-Bovy G. Manuscript submitted for publication. 2008. Comments on the category adjustment model and the oblique effect. [Google Scholar]
- Bremner JG, Bryant PE. Place versus response as the basis of spatial errors made by young infants. Journal of Experimental Child Psychology. 1977;23:162–171. doi: 10.1016/0022-0965(77)90082-0. [DOI] [PubMed] [Google Scholar]
- Cheng K, Shettleworth SJ, Huttenlocher J, Rieser JJ. Bayesian integration of spatial information. Psychological Bulletin. 2007;133:625–37. doi: 10.1037/0033-2909.133.4.625. [DOI] [PubMed] [Google Scholar]
- Compte A, Brunel N, Goldman-Rakic PS, Wang XJ. Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cerebral Cortex. 2000;10:910–923. doi: 10.1093/cercor/10.9.910. [DOI] [PubMed] [Google Scholar]
- DeLoache JS. Dual representation and young children’s use of scale models. Child Development. 2000;71:329–338. doi: 10.1111/1467-8624.00148. [DOI] [PubMed] [Google Scholar]
- DeLoache JS. Becoming symbol-minded. Trends in Cognitive Science. 2004;8:66–70. doi: 10.1016/j.tics.2003.12.004. [DOI] [PubMed] [Google Scholar]
- DeLoache JS, Miller KF, Rosengren KS. The credible shrinking room: very young children’s performance with symbolic and non-symbolic relations. Psychological Science. 1997;8:308–313. [Google Scholar]
- di Pellegrino G, Wise SP. Visuospatial versus visuomotor activity in the premotor and prefrontal cortex of a primate. Journal of Neuroscience. 1993;13:1227–1243. doi: 10.1523/JNEUROSCI.13-03-01227.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas R, Martin K. Neocortex. In: Shepherd GM, editor. The Synaptic Organization of the Brain. Oxford University Press; New York: 1998. pp. 459–509. [Google Scholar]
- Erlhagen W, Bastian A, Jancke D, Riehle A, Schöner G. The distribution of neuronal population activation (DPA) as a tool to study interaction and integration in cortical representations. Journal of Neuroscience Methods. 1999;94:53–66. doi: 10.1016/s0165-0270(99)00125-9. [DOI] [PubMed] [Google Scholar]
- Edin F, Macoveanu J, Olesen P, Tegner J, Klingberg T. Stronger synaptic connectivity as a mechanism behind development of working memory-related brain activity during childhood. Journal of Cognitive Neuroscience. 2007;19:750–760. doi: 10.1162/jocn.2007.19.5.750. [DOI] [PubMed] [Google Scholar]
- Elman JL, Bates EA, Johnson MH, Karmiloff-Smith A, Parisi D, Plunkett K. Rethinking Innateness: A Connectionist Perspective on Development. MIT Press; Cambridge, MA: 1996. [Google Scholar]
- Engebretson PH, Huttenlocher J. Bias in spatial location due to categorization: Comment on Tversky and Schiano. Journal of Experimental Psychology: General. 1996;125:96–108. doi: 10.1037//0096-3445.125.1.96. [DOI] [PubMed] [Google Scholar]
- Erlhagen W, Schöner G. Dynamic field theory of movement preparation. Psychological Review. 2002;109:545–572. doi: 10.1037/0033-295x.109.3.545. [DOI] [PubMed] [Google Scholar]
- Fischer KW, Paré-Blagoev J. From individual differences to dynamic pathways of development. Child Development. 2000;71:850–853. doi: 10.1111/1467-8624.00192. [DOI] [PubMed] [Google Scholar]
- Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, Nugent TF, III, Herman DH, Clasen LS, Toga AW, Rapoport JL, Thompson PM. Dynamic mapping of human cortical development during childhood through early adulthood. Proceedings of the National Academy of Sciences. 2004;101:8174–8179. doi: 10.1073/pnas.0402680101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kettner RE, Schwartz AB. Primate motor cortex and free arm movements to visual targets in three-dimensional space. II. Coding of the direction of movement by a neuronal population. Journal of Neuroscience. 1988;8:2928–2937. doi: 10.1523/JNEUROSCI.08-08-02928.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Taira M, Lukashin A. Cognitive neurophysiology of the motor cortex. Science. 1993;260:47–52. doi: 10.1126/science.8465199. [DOI] [PubMed] [Google Scholar]
- Hund AM, Spencer JP. Developmental changes in the relative weighting of geometric and experience-dependent location cues. Journal of Cognition and Development. 2003;4:3–38. [Google Scholar]
- Huttenlocher J, Hedges LV, Corrigan B, Crawford LE. Spatial categories and the estimation of location. Cognition. 2004;93:75–97. doi: 10.1016/j.cognition.2003.10.006. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Hedges LV, Duncan S. Categories and particulars: Prototype effects in estimating spatial location. Psychological Review. 1991;98:352–376. doi: 10.1037/0033-295x.98.3.352. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Hedges LV, Vevea JL. Why do categories affect stimulus judgment? Journal of Experimental Psychology: General. 2000;129:220–241. doi: 10.1037//0096-3445.129.2.220. [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Lourenco SF. Using spatial categories to reason about location. In: Plumert JM, Spencer JP, editors. The Emerging Spatial Mind. Oxford University Press; New York, NY: 2007. [Google Scholar]
- Huttenlocher J, Newcombe N, Sandberg EH. The coding of spatial location in young children. Cognitive Psychology. 1994;27:115–147. doi: 10.1006/cogp.1994.1014. [DOI] [PubMed] [Google Scholar]
- Huttenlocher PR. Morphometric study of human cerebral cortex development. Neuropsychologia. 1990;28:517–527. doi: 10.1016/0028-3932(90)90031-i. [DOI] [PubMed] [Google Scholar]
- Johnson JS, Spencer JP, Schöner G. Garzón F, Laakso A, Gomila T, editors. Moving to higher ground: The dynamic field theory and the dynamics of visual cognition. New Ideas in Psychology. 2008;26:227–251. doi: 10.1016/j.newideapsych.2007.07.007. Dynamics and Psychology [special issue] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson MH. Cortical plasticity in normal and abnormal cognitive development: Evidence and working hypotheses. Development and Psychopathology. 1999;11:419–437. doi: 10.1017/s0954579499002138. [DOI] [PubMed] [Google Scholar]
- Li W, Westheimer G. Human discrimination of the implicit orientation of simple symmetrical patterns. Vision Research. 1997;37:565–572. doi: 10.1016/s0042-6989(96)00166-6. [DOI] [PubMed] [Google Scholar]
- Mareschal D, Johnson MH, Sirois S, Spratling M, Thomas M, Westermann G. Neuroconstructivism, Vol. I: How the brain constructs cognition. Oxford University Press; Oxford, UK: 2007. [DOI] [PubMed] [Google Scholar]
- Newcombe NS, Huttenlocher J. Making space: The development of spatial representation and reasoning. MIT Press; Cambridge, MA: 2000. [Google Scholar]
- Newcombe N, Huttenlocher J, Drummey A, Wiley J. The development of spatial location coding: Place learning and dead reckoning in the second and third years. Cognitive Development. 1998;13:185–200. [Google Scholar]
- Newcombe NS, Learmonth A. Change and continuity in early spatial development: Claiming the “radical middle”. Infant Behavior & Development. 1999;22:457–474. [Google Scholar]
- Plumert JM, Hund AM. The development of memory for locations: What role do spatial prototypes play? Child Development. 2001;72:370–384. doi: 10.1111/1467-8624.00284. [DOI] [PubMed] [Google Scholar]
- Plumert JM, Hund AM, Recker KM. Organism-environment interaction in spatial development: Explaining categorical bias in memory for location. In: Plumert JM, Spencer JP, editors. The Emerging Spatial Mind. Oxford University Press; New York: 2007. pp. 25–52. [Google Scholar]
- Plumert JM, Spencer JP, editors. The Emerging Spatial Mind. Oxford University Press; New York: 2007. [Google Scholar]
- Rakic P. The development of the frontal lobe: A view from the rear of the brain. In: Jasper HH, Riggio S, Goldman-Rakic PS, editors. Advances in neurology: Vol. 66. Raven Press; New York, NY: 1995. pp. 1–8. [PubMed] [Google Scholar]
- Sampaio RC, Truwit CL. Myelination in the developing human brain. In: Nelson CA, Luciana M, editors. Handbook of Developmental Cognitive Neuroscience. MIT Press; Cambridge, MA: 2001. pp. 35–44. [Google Scholar]
- Samuelson LK, Schutte AR, Horst JS. The dynamic nature of knowledge: Insights from a Dynamic Field Model of children’s novel noun generalization. Cognition. doi: 10.1016/j.cognition.2008.10.017. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandberg EH. Cognitive constraints on the development of hierarchical spatial organization skills. Cognitive Development. 1999;14:597–619. [Google Scholar]
- Sandberg EH, Huttenlocher J, Newcombe NS. The development of hierarchical representation of two-dimensional space. Child Development. 1996;67:721–739. [PubMed] [Google Scholar]
- Schiano DJ, Tversky B. Structure and strategy in encoding simplified graphs. Memory and Cognition. 1992;20:12–20. doi: 10.3758/bf03208249. [DOI] [PubMed] [Google Scholar]
- Schutte AR, Spencer JP. Generalizing the dynamic field theory of the A-not-B error beyond infancy: Three-year-olds’ delay- and experience-dependent location memory biases. Child Development. 2002;73:377–404. doi: 10.1111/1467-8624.00413. [DOI] [PubMed] [Google Scholar]
- Schutte AR, Spencer JP. The influence of perceptual structure on a developmental transition in spatial working memory. 2009. Manuscript submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schutte AR, Spencer JP, Schöner Testing the dynamic field theory: Working memory for locations becomes more spatially precise over development. Child Development. 2003;74:1393–1417. doi: 10.1111/1467-8624.00614. [DOI] [PubMed] [Google Scholar]
- Simmering VR, Peterson C, Darling W, Spencer JP. Location memory biases reveal the challenges of coordinating visual and kinesthetic reference frames. Experimental Brain Research. 2008;184:165–178. doi: 10.1007/s00221-007-1089-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmering VR, Schutte AR, Spencer JP. Becker S, editor. Generalizing the dynamic field theory of spatial cognition across real and developmental time scales. Brain Research. 2008;1202:68–86. doi: 10.1016/j.brainres.2007.06.081. Computational Cognitive Neuroscience [special issue] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmering VR, Spencer JP. Carving up space at imaginary joints: Can people mentally impose arbitrary spatial category boundaries? Journal of Experimental Psychology: Human Perception and Performance. 2007;33:871–894. doi: 10.1037/0096-1523.33.4.871. [DOI] [PubMed] [Google Scholar]
- Simmering VR, Spencer JP, Schöner G. Reference-related inhibition produces enhanced position discrimination and fast repulsion near axes of symmetry. Perception and Psychophysics. 2006;68:1027–1046. doi: 10.3758/bf03193363. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Tessner KD, Toga AW. Mapping continued brain growth and gray matter density reduction in dorsal frontal cortex: Inverse relationships during postadolescent brain maturation. Journal of Neuroscience. 2001;21:8819–8829. doi: 10.1523/JNEUROSCI.21-22-08819.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, Dineva E, Schöner G. Moving toward a unified theory while valuing the importance of the initial conditions. In: Spencer JP, Thomas MS, McClelland JL, editors. Toward a Unified Theory of Development: Connectionism and Dynamic Systems Theory Re-Considered. Oxford University Press; New York: in press. [Google Scholar]
- Spencer JP, Hund AM. Prototypes and particulars: Geometric and experience-dependent spatial categories. Journal of Experimental Psychology: General. 2002;131:16–37. doi: 10.1037//0096-3445.131.1.16. [DOI] [PubMed] [Google Scholar]
- Spencer JP, Hund AM. Developmental continuity in the processes that underlie spatial recall. Cognitive Psychology. 2003;47:432–480. doi: 10.1016/s0010-0285(03)00099-9. [DOI] [PubMed] [Google Scholar]
- Spencer JP, Perone S. Defending qualitative change: The view from dynamical systems theory. Child Development. 2008;79:1639–1647. doi: 10.1111/j.1467-8624.2008.01214.x. [DOI] [PubMed] [Google Scholar]
- Spencer JP, Schöner G. Bridging the representational gap in the dynamic systems approach to development. Developmental Science. 2003;6:392–412. [Google Scholar]
- Spencer JP, Simmering VR, Schutte AR. Toward a formal theory of flexible spatial behavior: Geometric category biases generalize across pointing and verbal response types. Journal of Experimental Psychology: Human Perception and Performance. 2006;32:473–490. doi: 10.1037/0096-1523.32.2.473. [DOI] [PubMed] [Google Scholar]
- Spencer JP, Simmering VR, Schutte AR, Schöner G. What does theoretical neuroscience have to offer the study of behavioral development? Insights from a dynamic field theory of spatial cognition. In: Plumert JM, Spencer JP, editors. The Emerging Spatial Mind. Oxford University Press; New York: 2007. pp. 320–361. [Google Scholar]
- Spencer JP, Smith LB, Thelen E. Tests of a dynamic systems account of the A-not-B error: The influence of prior experience on the spatial memory abilities of two-year-olds. Child Development. 2001;72:1327–1346. doi: 10.1111/1467-8624.00351. [DOI] [PubMed] [Google Scholar]
- Tanaka S. Roles of intracortical inhibition in the formation of spatially tuned delay-period activity of prefrontal cortical neurons: Computational study. Progress in Neuro-psychopharmacology & Biological Psychiatry. 2000;24:483–504. doi: 10.1016/s0278-5846(00)00088-9. [DOI] [PubMed] [Google Scholar]
- Thelen E, Schöner G, Scheier C, Smith LB. A dynamic field theory of infant perseverative reaching errors. Behavioral and Brain Sciences. 2001;24:1–86. doi: 10.1017/s0140525x01003910. [DOI] [PubMed] [Google Scholar]
- Thelen E, Smith LB. A dynamic systems approach to the development of cognition and action. MIT Press; Cambridge, MA: 1994. [Google Scholar]
- Trappenberg TP, Dorris MC, Munoz DP, Klein RM. A model of saccade initiation based on the competitive integration of exogenous and endogenous signals in the superior colliculus. Journal of Cognitive Neuroscience. 2001;13:256–271. doi: 10.1162/089892901564306. [DOI] [PubMed] [Google Scholar]
- van der Maas HLJ, Molenaar PCM. Stagewise cognitive development: An application of catastrophe theory. Psychological Review. 1992;99:395–417. doi: 10.1037/0033-295x.99.3.395. [DOI] [PubMed] [Google Scholar]
- Van Geert P. A dynamic systems model of basic developmental mechanisms: Piaget, Vygotsky, and beyond. Psychological Review. 1998;105:634–677. [Google Scholar]
- Westermann G, Mareschal D. From parts to wholes: Mechanisms of development in infant visual object processing. Infancy. 2004;5:131–151. doi: 10.1207/s15327078in0502_2. [DOI] [PubMed] [Google Scholar]
- Wilson FAW, Scalaidhe SP, Goldman-Rakic PS. Dissociation of object and spatial processing domains in primate prefrontal cortex. Science. 1993;260:1955–1958. doi: 10.1126/science.8316836. [DOI] [PubMed] [Google Scholar]