A practical guide to the staggered herringbone mixer

Abstract

An analytical model of mixing in the staggered herringbone mixer (SHM) was derived to estimate mixing parameters and provide practical expressions to guide mixer design and operation for a wide range of possible solutes and flow conditions. Mixing in microfluidic systems has historically been characterized by the mixing of a specific solute system or by the redistribution of flow streams; this approach does not give any insight into the ideal operational parameters of the mixer with an arbitrary real system. For Stokes-flow mixers, mixing can be computed from a relationship between solute diffusivity, flow rate, and mixer length. Confocal microscopy and computational fluid dynamics (CFD) modeling were used to directly determine the extent of mixing for several solutes in the staggered herringbone mixer over a range of Reynolds numbers (Re) and Péclet numbers (Pe); the results were used to develop and evaluate an analytical model of its behavior. Mixing was found to be a function of only Pe and downstream position in the mixer. Required mixer length was proportional to Log(Pe); this analytical model matched well with the confocal data and CFD model for Pe < 5×10⁴, at which point the experiments reached the limit of resolution. For particular solutes, required length and mixing time depend upon Re and diffusivity. This analytical model is applicable to other solute systems, and possibly to other embodiments of the mixer, to enable optimal design, operation, and estimation of performance.

Introduction

Microfluidics

Microfluidic systems are defined as those in which at least one of the dimensions is smaller than a millimeter. They have the advantages of small sample/reagent volumes, and can afford exquisite process control and reproducibility. These properties make such systems ideal for a myriad of applications such as immuno- and nucleic acid-based assays,^{2, 3} cell and tissue cultures,⁴ and micro-prep chemistries.^5-7 These common techniques often require mixing of solutes ranging from small buffer components to very large molecules such as polymers or DNA. When designing or operating a device, it is crucial to understand such parameters as the necessary length of time or required length of mixer to achieve homogeneity, and how varying the solutes or flow rates may affect them.

The small dimensions of the channels generally constrain the flow to the laminar regime, with adjacent fluid layers flowing parallel in a smooth and straight channel for an infinite length. The Reynolds number, Re, describing the relative importance of inertia and viscosity in fluid movement, is typically near or below 1. Depending on the nature of the solutes, the Péclet number, Pe, a measure of convective versus diffusive solute motion, is considerably higher, ranging from 10³ to 10⁶. Solute movement occurs only by diffusion and, for the scales of typical microchannels under practical flow conditions, mixing is often prohibitively slow. In unperturbed flow, the length of channel required for diffusive mixing is on the order of wPe.⁸ Disruption of this flow to reduce the length scales for diffusion, thereby improving mixing, can be achieved by a range of strategies with differing qualities and requirements,^{5, 9-13} but the ideal choice is largely dependent upon the application. Chaotic advection mixers, such as the staggered herringbone mixer (SHM)¹ are widely used, due to their efficiency and simple fabrication and operation.

Mixing

On the microscale, mixing is movement of solute between fluid elements, and takes place only via diffusion between fluid layers. Mixers reduce the time necessary for this process by redistributing the fluids, decreasing the necessary length for diffusion and increasing the probability for solute transport between fluids.

Mixing can be assessed in a variety of ways, but most do not lend themselves to practical applications. Examination of the fluid motion alone provides solute-independent information, and many such measures and techniques exist. The increase of entropy in a fluid is a general measure of mixing quality,^{14, 15} Poincaré sections¹⁶ and linked twist maps¹⁷ provide qualitative pictures of the process, Lyapunov exponents are a classic quantitative measure,¹⁸ and computational fluid dynamics (CFD) modeling enables consideration of the redistribution of streamlines¹⁹ and of reduction of striation thickness.²⁰ However, though they can identify a good mixer, these methods do not readily give information for application of the mixer. A number of techniques for optimization of geometry have also been developed and utilized,^{19, 21, 22} but they are also not directly applicable to quantitation of mixing. Chemical reactions provide a direct measure of mixing in a device,²³ but testing with a range of solutes is difficult. Confocal microscopy, on the other hand, can provide concentration profiles from a variety of fluorescent or Raman-active solutes,²⁴ enabling measurement of actual mixer function under variety of conditions. Such data can then be analyzed by autocorrelation,²⁵ compared to the mixing cup concentration,²⁶ or evaluated by “mixing index”²⁷ or other measures of homogeneity, and compared to data generated by modeling to observe mixing over a range of Re and Pe. Analysis of the behavior of a particular mixer by such measures as vortex index²⁷ or development of scaling relationships²⁸ can enable extrapolation of mixer performance over an even wider range. A versatile expression of function from such analysis would be an invaluable tool for designing and using the mixer.

Though some systems are more complex, with interactions between solutes and different requirements of proximity between solutes or evenness of concentration, the analysis presented here simply considers the mixing of a stream containing a uniform concentration of a single, independent solute with an identical stream of buffer flowing side-by-side. This study uses the coefficient of variation (CV) as a common descriptor of mixing. By quantifying the degree of variability in the concentration, the CV tracks the solutes that have not moved between fluids. Similarly, the analytical model presented here assesses mixing by the probability that solutes have not diffused sufficient distance (L_d) to cross the interface between the two fluid streams (L_i). As the fluids mix, both values approach zero, enabling comparison of the measures.

Direct CFD modeling yields vast amounts of information about fluid motion and solute behavior, but modeling even a simple system can extremely challenging. As mixing progresses, the interface may stretch exponentially, resulting in exponential increases in the complexity of the problem.²⁹ Such difficulties become even more significant at high Pe, as the sharper interfaces require extremely small meshing.²⁶ Even with powerful computers and efficient software, solutions may not be attainable for the desired experimental conditions. Streamline and particle tracing ignores the problem of diffusion entirely, but the results are non-ideal, often with no data near the low-flow walls,³⁰ though backtracking alleviates this problem.³¹ Monte Carlo methods may also be used to estimate concentration profiles at particular locations in a channel.²⁸ In the absence of convenient symmetries, a 3D mixing channel may be reduced to a 2D model as a moving reference frame¹⁰ or to a lid-driven model for some Stokes-regime mixers,³² though these also may require approximations that limit their accuracy. To predict mixing over a wider range of Pe than is permitted by direct CFD modeling, this study uses the information generated by a direct 3D CFD model of the mixer to develop the simpler analytical model.

The Staggered Herringbone Mixer

The SHM has attracted significant attention since its debut from the Whitesides group in 2002,¹ largely because it is simple, elegant, and readily manufactured. It consists of a rectangular channel with “herringbone grooves” in one or more walls of the channel (Figure 1). In the Stokes flow regime, where viscous forces dominate, these grooves cause transverse flow in the channel,³³ resulting in two counter-rotating vortices along the channel length. The vertices of the grooves are offset to approximately one third of the way across the channel width, and each set of herringbones alternates with a complementary set, mirrored across the centerline of the channel, to create a full mixing cycle. This alternation reorients the flow periodically, disrupting the relatively untouched elliptic points in each of the vortices to dramatically improve mixing.¹⁷ The effects of individual half-cycles approximate lid-driven duct flow, a non-chaotic process,³⁴ but the reorientation of the circulating flow produces chaotic mixing.

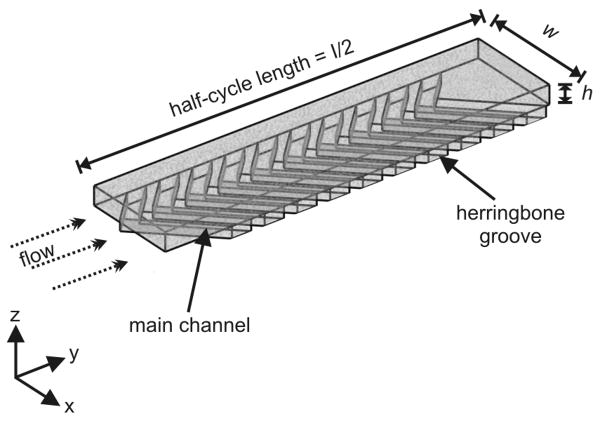
Figure 1.

One half-cycle of the SHM, with a channel cross-section of w × h and 10 herringbones with points offset 1/3 of the way across the channel. Each half-cycle alternates with a complementary unit, in which the herringbones are offset to the opposite side of the midline, to complete a full mixing cycle. COMSOL models were segmented into half-cycle units 1.7 mm in length, with an 80 μm × 410 μm channel cross-section, and herringbones 85μm wide along the flow axis and recessed 50 μm into the channel floor. The device used for confocal experiments featured a 56 μm × 392 μm cross section, with herringbones 90 μm wide and 36 μm deep. Seven full cycles were modeled or imaged.

Not only is the SHM simple to fabricate and operate, it is also an efficient mixer for continuous flow. Fluid is redistributed over the entire channel cross section, significantly reducing Taylor dispersion¹ and resulting in a nearly uniform residence time distribution.^{20, 32} Numerous studies have included the SHM in device design,^{3, 6, 7} analyzed geometric effects on performance,^{21, 33} and assessed improvements to the design, ^{25, 35, 36} though none of these adequately addresses operational parameters. This work aims to produce a simple analytical model of an SHM, using information from a CFD model, to enable prediction of crucial information such as ideal flow rates, required mixer length, and mixing time for arbitrary solutes.

The Analytical Model

The asymmetry of the SHM design makes it difficult to model by conventional CFD methods, though the periodicity can be used to segment the mixer into smaller, more easily modeled units. An analytical model, such as the one developed here, would enable easy prediction of behavior at longer mixer lengths and larger values of Pe than direct CFD modeling.

Dominance of viscous forces in the function of the SHM produces flow behavior that is similar over a range of flow rates. This reduces the number of flow rates that must be modeled to characterize the mixer. The absence of significant inertial forces suggests that the configuration of streamlines—and any interfaces—will depend only upon the downstream position in the mixer. Mixing, the movement of a solute between fluid elements, is then a relationship between residence time, the diffusivity of the solute, and position. The near-uniform residence time distribution of the SHM^{20, 32} reduces this list of key factors to simply flow rate, diffusivity, and position—or just Pe and downstream position, l. The configuration of the fluids at a given point in the mixer may be determined by the more sophisticated CFD modeling, and this information combined with equations of diffusion to develop an analytical model of mixing.

Consider two side-by-side inputs of solute and buffer at a particular distance along the mixer channel, when the fluids may be twisted and folded into thin layers. For mixing to occur, the solute in each volume element must diffuse into the other fluid. Displacement by diffusion follows a normal distribution centered at zero, but the mean magnitude in one dimension, L̂_d, is $\sqrt{2Dt}$. The probability that the distance which a solute in an arbitrary volume element has diffused, L_d, not exceeding a particular distance a is

$$P(L_d<a)=\frac{1}{2}[1+\text{erf}(\frac{a}{{\widehat{L}}_d\sqrt{2}})]$$ Equation 1

When diffusing away from the interface between the two fluids, the solute will eventually encounter another, more distant interface (Figure 2, a-2). If a given layer is assumed to be flat and of thickness b, the mean minimum distance to an interface, L̂_i, will be b/4. If the solute in an arbitrary volume element must travel a in one direction, the mean distance to the other interface would be 4L̂_i−a, and the resultant 2-sided probability function during mixing can be approximated as

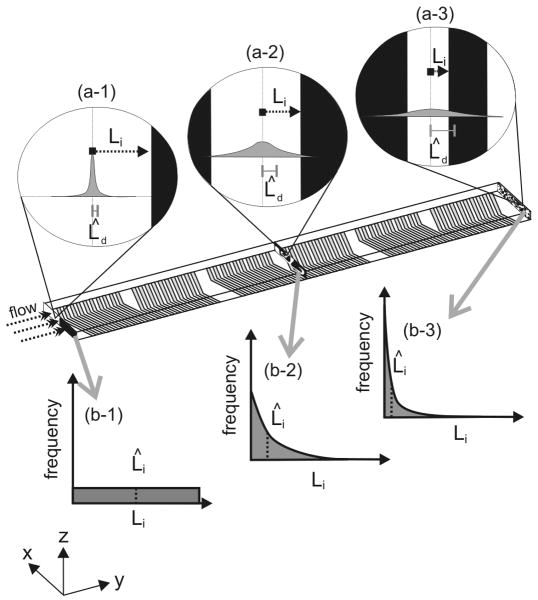
Figure 2.

Illustration of mixing behavior of two fluids in the SHM. Each infinitesimal volume element of the fluid is a particular distance, L_i, from the interface, and the solute originally contained in the volume diffuses a distance, L_d, toward or away from the interface. Initially, the solute is unlikely to have diffused far (a-1), and the side-by-side inputs give a uniform distribution of L_i (b-1). As fluid moves down the mixer, the solute is likelier to have traveled farther (a-2 and a-3). The fluid is stretched and folded into increasingly thin layers (a-2 and a-3) similar to a baker's transformation, except the complexity of the rotational flows and reorientations cause L_i to adopt an exponential distribution (b-2 and b-3). Mixing results from increasing the mean diffusion distance, L̂_d, and decreasing the mean distance to an interface, L̂_i.

$$P(-(4{\widehat{L}}_i-a)<{\widehat{L}}_d<a)=\frac{1}{2}[\text{erf}(\frac{a}{{\widehat{L}}_d\sqrt{2}})+\text{erf}(\frac{4{\widehat{L}}_i-a}{{\widehat{L}}_d\sqrt{2}})]$$ Equation 2

Likewise, the minimum distance to the interface from this particular volume element, L_i, varies. Unlike an ideal lamination mixer, which results in uniform layering, a chaotic mixer produces a distribution of layer thicknesses (Figure 2, b-1 through b-3). Before mixing begins, the fluids are of a single thickness with the interface half way across the channel width, w/2. The distribution of L_i is uniform from 0 to w/2, the position of the pre-mixing interface, and, as fluid moves down the mixer, this distribution evolves to a delta function at 0 for infinite mixing, suggesting that L_i may follow an exponential distribution

$$p(L_i=a)=A{e}^{\frac{-a}{{\widehat{L}}_i}}$$ Equation 3

Combining the distributions for L_d and L_i (Equations 2 and 3), and integrating over all a during mixing (where L̂_d > L̂_i) yields

$$P(L_d<L_i)=\frac{1}{2}\text{erf}(2\sqrt{2}\stackrel{{\widehat{L}}_i}{}/\underset{{\widehat{L}}_d}{})\approx 1.60\stackrel{{\widehat{L}}_i}{}/\underset{{\widehat{L}}_d}{}$$ Equation 4

Because this measures the likelihood that a solute has not crossed the interface, and it varies from 1 to 0 as mixing proceeds, it will be of similar magnitude and trend to the CV, and the two values will be comparable, particularly as the system approaches infinite mixing. If uniform residence time is assumed, the mixing equation can be restated as a function of only l, the mixer position in cycles, and Pe

$$P(L_d<L_i)\approx 1.60\sqrt{\frac{Pe}{\text{wld}}}{\widehat{L}}_i$$ Equation 5

Given an expression for L̂_i as a function of mixer position, this relationship should hold true for any Stokes-regime mixer.

Mixing in the SHM was modeled by COMSOL Multiphysics 3.3a software, and compared to experimental data from confocal microscopy. The COMSOL model results were then analyzed in MATLAB to extract the distance to the interface, and the information was used to develop and test the analytical model described above. Despite inherent approximations and experimental imprecision, this analytical model, the COMSOL model, and confocal experiments show remarkable agreement.

Experimental

Mixer design and fabrication

The SHM design was based upon the work of Stroock et al.¹ The master mold was created by 2-layer photolithography on a 3″ silicon wafer (Silicon Sense, Nashua, NH) with SU-8 photoresist (Microchem, Newton, MA), and passivated with (1H, 1H, 2H, 2H-perfluorooctyl)tricholorosilane (Alfa Aesar, Ward Hill, MA). Devices were fabricated from Sylgard 184 polydimethylsiloxane (PDMS) (Dow Corning, Midland, MI), bonded to #1-½ 24 mm × 60 mm glass cover slips (VWR, Westchester, PA), following treatment by oxygen plasma (oxygen pressure 30 psi, flow rate 3-5 SCFH, 600W) in a Plasma Preen II-973 (Plasmatic Systems Inc., North Brunswick, NJ). The ports, consisting of 3/32″ × 1/32″ silicone tubing (Cole-Parmer, Vernon Hills, IL) embedded in pads of PDMS, were plasma bonded over holes in the PDMS. Samples were loaded via 1/16″ × 0.010 fluorinated ethylene propylene (FEP) tubing (Upchurch Scientific, Oak Harbor, WA) from two 1 ml gas-tight glass syringes (Hamilton Company, Reno, NV) driven by a model 22 syringe pump (Harvard Apparatus, Holliston, MA).

Channel dimensions were determined from confocal images of fluorescein-filled devices. The main channel measured 392 μm ± 4 μm in width (w) and 56 μm ± 2μm in height (h). Herringbone grooves were 90 μm ± 2μm wide along the channel axis and were recessed 36μm ± 2μm into the floor of the channel, for a total depth of 92 μm. The grooves met the walls at a 45° angle and came to a 90° point one-third of the way across the channel width to form the herringbone, and were spaced 145 μm center-to-center along the channel length in half-cycles of 10. Each half-cycle alternated with one mirrored across the center of the channel, such that the point was on the opposite side, to complete a full cycle, and 7 of these 3.5 mm mixing cycles were positioned along each of three 25 mm passes of the channel, creating a total of 21 mixing cycles over 75 mm of channel.

Confocal microscopy

Devices were imaged on a Zeiss LSM510 laser scanning microscope (Carl Zeiss Inc., Oberkochen, Germany) at the Nanotech User Facility at the University of Washington, using a 488 nm Argon laser and a 20× Plan-Apochromat objective and a 57 μm pinhole, for a pixel resolution of 0.90 μm × 0.90 μm × 1.50 μm. The mixer was taped to the stage, and reinforced with pieces of acrylic along the long sides to minimize flexing.

Mixing was assessed for each of three solutes with buffer: fluorescein (MW 0.4 kDa), and fluorescein-conjugated dextrans of MW 40 kDa and 2000 kDa (Invitrogen Corp, Carlsbad, CA) (D = 5×10^-9 m²/s, 5×10^-10 m²/s, and 5×10^-11 m²/s, respectively, calculated from published relationships).³⁸ All solutions were diluted to 10 μM with fluorescein content in 0.05 M sodium borate buffer, pH 8.5 (Pierce, Rockford, IL). The fluorescent sample was injected into the device on one side with an equal flow of buffer on the other to visualize the position and relative motion of the two fluid streams in the channel. Flow rates were varied from 3 μl/min to 300 μl/min (Re = 1.2×10^-1 − 1.2×10¹, Pe = 8.33×10² − 8.33×10⁵). The full data stacks were 461.4 μm (x) × 196.6 μm (y) × 175.5 μm (z) (502 × 214 × 117 pixels) to capture the full region. Slices orthogonal to the channel axis (x-z plane) were extracted from the image stacks using Zeiss AIM software (Carl Zeiss Inc., Oberkochen, Germany) in a location just upstream of the following half-cycle. The images were converted to grayscale, and device dimensions and fluorescence intensity were measured in ImageJ (NIH, Bethseda, MD),³⁷ and further data analysis was completed in Excel 2000 (Microsoft Corp., Redmond, WA). For fluorescence data, only the central 350μm × 45μm (389 × 49 pixels) of the channel was measured to reduce edge effects.

COMSOL modeling

Modeling was completed on a Dell Precision 490 workstation (Dell Inc., Round Rock, TX) with 9GB RAM and dual Xeon 5150 processors (Intel Corp., Santa Clara, CA), running Windows ×64 (Microsoft Corp., Redmond, WA). CFD modeling was completed using COMSOL Multiphysics 3.3a (COMSOL Inc., Stockholm, Sweden).

The model was drawn to 410 μm main channel width (w), 80 μm channel height (h), with 50 μm groove depth (130 μm total), and herringbones 85 μm wide along the y axis (Figure 1). The models used the incompressible flow (Navier-Stokes, NS) and convection-diffusion (CD) application modes of the Chemical Engineering module. The density and viscosity were set to those of water at 25°C, and flow was fully developed at the inlet.

CFD modeling of 3-dimensional fluid and solute motion is computationally demanding, and both memory and processor speed limit the resolution and complexity of the model. To attain micron-level resolution using the desktop workstation, the problem was divided into smaller segments, either 3 herringbone segments for flow rate evaluation or a series of 10 herringbone half-cycles for the complete model of mixing. To further reduce the complexity of the problem, NS and CD solutions were computed separately for each unit in the complete model. Velocity and concentration were defined to have particular profiles at the inlet of each segment, and were allowed to exit passively at the outlet via a p = 0 condition in NS simulations, or convective flux for CD. Velocity and concentration profiles at outlets were exported and used as inlet conditions for the following segment to produce the complete model of mixing.

To evaluate the dependence of fluid motion on Re, flow rate analyses were completed on short mixer segments, which consisted of 3 herringbones in a 700 μm channel length. The main body of the channel was set to a maximum mesh element size of 15 μm, while the mesh in the groove volumes was set to 10 μm, resulting in 1.76×10⁵ elements. This meshing scheme optimized solution time and accuracy; for such a complex model, even small increases in mesh density dramatically increased solution time, but previous tests showed that fluid motion in the herringbones, |v|/u, changed only approximately 1% per tenfold increase in mesh elements (not shown). The problem had 8.1×10⁵ degrees of freedom, and 19 flow rates between 5 nl/s and 50 μl/s (Re = 1.4×10^-2 − 1.4×10²) were tested using the NS application mode only.

The complete model of flow and diffusion was segmented into half-cycles (10 herringbones over a 2 mm length, Figure 1) to reduce the degrees of freedom and enable faster solutions and more detailed models. Three NS models were computed: the first half-cycle, and an “even” half cycle and an “odd” half-cycle for all successive units. Velocity at the inlet for the first half-cycle was defined as fully developed flow at 30 μl/min (Re = 1.4), while successive half-cycles used the velocity profile from the outlet of a complementary half-cycle. The NS problems were meshed as for the short models described above, resulting in 2.8×10⁵ mesh elements and 1.3×10⁶ degrees of freedom. The three NS solutions were used to model solute behavior using the CD mode for all 14 half-cycle units of the model. The first unit had a smoothed step-function concentration change from 0 to 1 as input. Concentration data was then exported from the outlet of each half-cycle and applied at the inlet of the following half-cycle. To enable convergence at higher Pe and reduce errors near the fluid interface, two methods predefined by COMSOL, streamline artificial diffusion (Petrov-Galerkin/Compensated, tuning parameter 0.25) and adaptive meshing (single iteration, increase number of elements by 1.1), were also used. The initial mesh had a 20 μm maximum element size, 1.6×10⁵ elements, and 2.4×10⁵ degrees of freedom, and 7.2×10⁵ degrees of freedom following adaptive refinement. Models corresponding to Pe = 6.25×10¹ – 3.10×10⁶ were generated.

Concentration and concentration gradient data were exported from the outlet of each half-cycle in a uniform grid with 2.5 μm spacing for analysis in Excel, or 1.0 μm spacing for MATLAB.

MATLAB Analysis

To express a mixer performance as a function only of l and Pe, it is necessary to quantify fluid configuration along the mixer length, specifically, the minimum distance from any point to the interface between the two input fluids, L_i. To determine distance to the interface, COMSOL model data was evaluated in MATLAB R2007a (The Mathworks Inc., Matick, MA). The data generated at Pe = 6.25×10⁴ was used to obtain the most distinct interface possible without significant processing errors, which occur near sharp interfaces. The algorithm identified the interface as local maxima in concentration gradient. For a point to be stored, the concentration also had to be between 0.25 and 0.75 to exclude any aberrant maxima resulting from processing errors. Each point in the channel section was then compared to the interface locations to compute minimum distance, L_i. This process was repeated for each half-cycle modeled in COMSOL.

For each dataset, a histogram of L_i was compiled, and evaluated in Excel to determine a fit to the distribution, and analyze the evolution of the distribution as mixing proceeded down the channel and trends in the mean, L̂_i.

Results and discussion

Flow rate dependence of mixer function (COMSOL model)

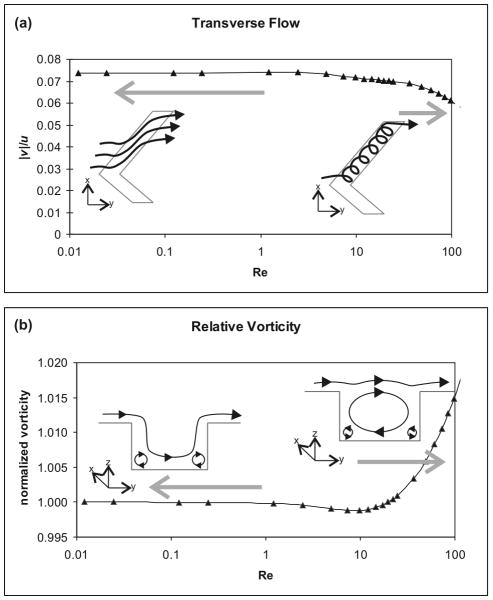
Because the SHM functions by causing transverse flow elements in the channel, the relative magnitude of such flow horizontal across the channel, $\stackrel{\left|v\right|}{}/\underset{u}{}$, was examined as a measure of mixer performance in the short 3-herringbone NS model of flow. Vorticity, the curl of the velocity vector, was also quantified and normalized to flow rate. As expected in a Stokes-regime mixer, the fluid behavior was constant below 1 μl/s (Re = 2.7) for both measures (Figure 3). Flow separation in the grooves, resulting in a significant increase in vorticity and a decrease in transverse flow, occurred above 10 μl/s (Re = 27). Visualization of streamlines (illustrated in Figure 3, a, data not shown) revealed the fluid smoothly entering and exiting the grooves in the channel at low flow rates, and the development of vortices in the grooves, which themselves reduced the relative volume of fluid moved across the channel, at high flow rates. In the transition between these two flow regimes, a small decrease in vorticity occurred, suggesting the breakdown of small eddies in the corners of the grooves before they are reversed in direction by the formation of the larger vortex seen at high flow (illustrated in Figure 3, b). Despite these changes, the effect on bulk fluid behavior was small, and the fluid configuration from a single NS solution should be accurate at up to 5 μl/s (Re = 14). Changes remained relatively minor at up to 15 μl/s (Re = 36), though the backpressure for such flow is relatively high, with the model predicting around 3×10⁴ Pa for a full device, and declining performance would be seen at higher flow rates. This is a marked contrast to the estimated limit of Re = 100 in the original description of the SHM.¹

Figure 3.

Flow rate behavior of the SHM, with illustrations of fluid motion. (a) The relative magnitude of transverse flow induced by the herringbone grooves was relatively stable Re < 1, but decreased as recirculation within the herringbones developed, resulting in substantially degrading performance for Re > 36. (b) The total vorticity was scaled to flow rate and normalized to reflect the relative magnitude over a range of flow rates. Illustrations depict a projection along the length of the groove. A slight dip in relative vorticity above Re = 1 revealed the dissolution of minor eddies in the corners of features before larger vortices were established in the herringbone grooves at Re > 10.

Mixing in the SHM (COMSOL model versus confocal measurements)

Mixing performance was evaluated by both the confocal experiments and the COMSOL model using both NS and CD application modes. Despite minor differences in dimensions between the COMSOL model and the experimental device, the proportions for each remained in the optimum range for such mixers,^{20-22, 32, 33} and did not have significant impact on qualitative appearance of the flow. As expected for a Stokes-flow mixer and predicted by the short model of flow rate, both the COMSOL models and the confocal measurements showed that interface position did not change significantly with flow rate over the range tested (Re < 14). Images with similar values of Pe also showed good correspondence, both within each method (not shown) and between the two techniques (Figure 4, a and b).

Figure 4.

(a) Confocal micrograph showing a cross-section of the 56 μm × 392 μm channel perpendicular to flow and downstream of cycle 1.5, with 40kDa dextran mixing with buffer at 30 μl/min (Pe = 8.33×10⁴). The image has been adjusted to show the tendrils of fluid. (b) Surface plot of COMSOL model in the same location of the mixer, using D = 5×10^-11 m²s^-1 at 30 μl/min (Pe = 6.25×10⁴) in the 80 μm × 410 μm channel. (c) Plot of points from the exported COMSOL data identified by the MATLAB algorithm as part of the interface.

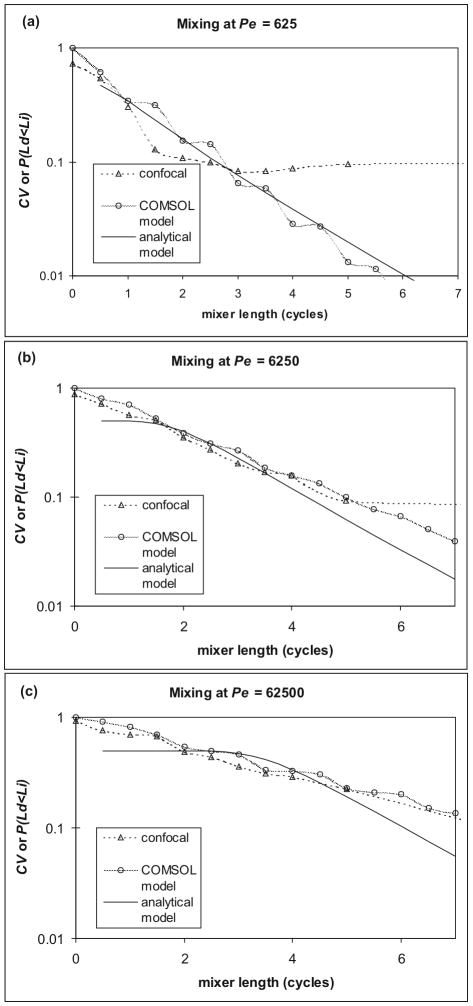
As mixing progressed, CV decreases from 1 to 0 (Figure 5). The COMSOL data showed an exponential decay, with a slope dependent upon Pe. An apparent oscillation in the data was an artifact of processing, as the mean concentration showed similar variation. If such an oscillation were due to the segmented construction of the model, the expected period would be one full cycle, rather than the one and one-half seen at higher Pe. The confocal data did not show this variation, and showed similar exponential behavior until reaching baseline at CV = 0.08. The primary contributor to this baseline is non-uniform intensity due to edge effects in the channel. To minimize this effect, only the central region of the channel was analyzed. Further reduction of the measurement region would reduce data accuracy, and averaging techniques would exacerbate any overstatement of mixing due to unstable flow from the syringes at low flow rates but would not alleviate spatial variation near the channel walls.

Figure 5.

Comparison of confocal mixing data (triangles, dashed line) to COMSOL (circles, shaded line) and analytical (solid line) models at Pe = 6.25×10² (a), Pe = 6.25×10³ (b), and Pe = 6.25×10⁴ (c). Confocal and COMSOL were quantified by CV, while the analytical model refers to P(L_d<L_i); both are plotted on the same axis. Confocal data reached baseline just below CV = 0.1, which is particularly evident at low Pe. COMSOL models oscillated slightly during the exponential decline due to processing errors. While confocal and COMSOL appeared to give a pure exponential decline, the analytical model predicted a Pe-dependent length with little change in mixing, followed by an exponential decline of P(L_d<L_i) with a Pe-independent slope. The noise and resolution limits of the confocal and COMSOL data may have obscured such behavior.

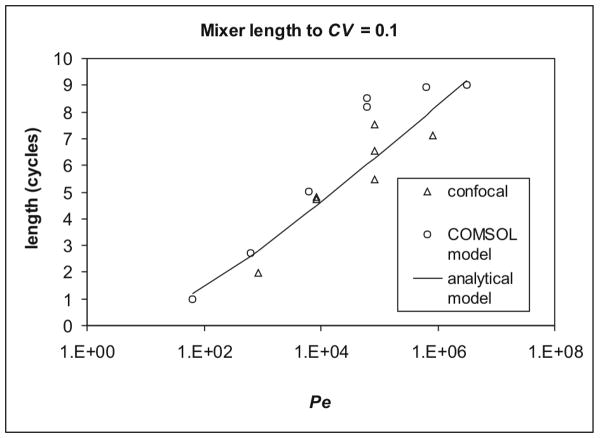
One of the most valuable pieces of information in device design is the required length of a mixer. To match the data range available from confocal experiments, the cutoff considered for mixing was CV = 0.1, and the mixer length necessary to achieve this threshold, l_0.1, was extracted from the mixing traces. Estimates of l_0.1 were similar between the COMSOL models and confocal data (Figure 6). Some spread could be seen in replicates in the confocal data, taken with different combinations of solute and flow rate to achieve the same Pe, due to the unstable flow at low flow rates. This variation in interface position resulted in slightly lower estimated mixing distances overall for confocal than predicted by COMSOL. For both methods, l_0.1 appeared to increase linearly with Log(Pe), as predicted,¹ until Pe reached 6.25×10⁵, when it leveled off. However, fluid layering thinner than the minimum resolution (0.9 × 1.5μm pixel size for confocal, 2.5μm mesh size for COMSOL) could not be distinguished. Furthermore, each technique also overstated diffusion near the interface: the unstable flow in the confocal experiments, and the artificial diffusion in COMSOL, which would have overwhelmed thin layers and native diffusion. This indicates that direct measurement or modeling of mixing is currently limited to Pe < 6.25×10⁵. To extend such experiments to higher Pe, significant improvements in resolution for confocal microscopy or finer meshing in COMSOL would be required.

Figure 6.

Required length of mixer to reduce CV < 0.1, or P(L_d<L_i) < 0.1 for the analytical model, by Pe. Multiple data points were replicates with a different flow rate and solute combination, and spread in the confocal data (triangles) was due to syringe stepping, which caused greater apparent mixing at low flow rate. Both the confocal data and COMSOL model (circles) flattened out at Pe > 6.25×10⁴, though the analytical model (line) suggested a near-perfect logarithmic relationship. This difference was likely due to the noise and resolution limits of the confocal measurements and COMSOL modeling.

Analytical model (from MATLAB processing of COMSOL data)

To complete the analytical model, the decay of mean minimum distance to the interface, L̂_i, along the length of the mixer, l, was extracted from the COMSOL data. The MATLAB code successfully identified the interface in the exported COMSOL model data without significant gaps or discontinuities in most (Figure 4, c). However, before the first half-cycle, too few points were marked, and beyond 4 cycles, when a significant number of points were selected relative to the sample size (approximately 1 point in 7), and the layer thickness approached the COMSOL mesh size of 2.5μm. Histograms of L_i appeared to follow an exponential distribution for all data sets, and quantile-quantile plots of the data with exponential models confirmed a good fit (R = 0.98 ± 0.02, not shown).

The repeating nature of the mixer suggested exponential behavior with respect to mixer length, which is also a hallmark of chaotic mixing.³⁹ L̂_i decreased exponentially with mixer length from cycles 1 to 4, L̂_i = 19.7e^−0.55l (R² = 0.994, not shown). However, the utility of the MATLAB algorithm was limited before the first half-cycle, when too few points were marked, and beyond 4 cycles, when a significant number of points were selected relative to the sample size (approximately 1 point in 7) and the layer thickness approached the COMSOL mesh size of 2.5μm. When the empirical expression for L̂_i was combined with Equation 5, the mixing relation became

$$P(L_d<L_i)=0.027\sqrt{\frac{Pe}{l}}{e}^{-0.55l}$$ Equation 6

For a cutoff at P(L_d<L_i) = 0.1, this gave Pe ≈ 13.6l_0.1e^1.1(l_0.1) (Figure 6), identical in form to the relation found previously.¹ Despite the mixed form, this could be approximated as the direct logarithmic relation without significant deviation at low Pe suggested by other studies.^{1, 28}

$$l_{0.1}=1.73\text{Log}(Pe)-2.16({\text{R}}^2=0.998)$$ Equation 7

Though this matched the l_0.1 data from confocal and COMSOL modeling relatively well, the slope was shallower than expected, particularly in light of the errors in the data tending to overstate mixing. The determining factor in the slope was the development of L̂_i, which may have been less accurate, due to the coarseness of the grid spacing and COMSOL data, inaccuracies in the MATLAB algorithm, or the relatively small data range used.

Despite the good correspondence between the derived analytical model and the confocal and COMSOL results for required length, the derived model did not match the individual mixing traces for CV vs. l generated by COMSOL and confocal, particularly at higher Pe (Figure 5). While Log(CV) decreased linearly with mixer position in both the COMSOL and confocal data for all l and Pe, this model (Equation 6) predicted a relatively flat region at early l, followed by a linear decrease in Log(P(L_d<L_i)). Furthermore, the model predicted that the final slope of the decay is independent of Pe, while the slopes of the COMSOL and confocal data varied with Pe. This was not, however, an artifact of comparing CV to P(L_d<L_i), a probability of diffusion, as the same Pe-independent slope behavior has been found by analysis of non-uniformity of concentration in another chaotic micromixer.²⁸ The reason for a delay in the onset of an exponential decay is scale: the fluid layering must reach a scale comparable to diffusion distance before appreciable mixing can occur.²⁸ The noise and resolution may have obscured this in the COMSOL and confocal data, and the segmented construction of the COMSOL models could have interfered. Nevertheless, this analytical model appears to be a reasonably accurate predictor of mixer performance.

Practical Implications

The ideal design and operational parameters for the SHM depend upon the specific application. For a given solute, the mixer may be run at a higher flow rate to achieve faster mixing time, but a slower rate may be required to reduce the required channel length or accommodate other inline processes or pressure concerns. The COMSOL model suggested a simple estimate for pressure drop, with k = 33 Pa/cycle for this particular mixer.

$$p=kl\text{Re}$$ Equation 8

As noted by the models, though fluid motion may be similar over the Stokes regime below Re = 15, flow rate does affect mixer function. For the experimentalist, this model yielded several equations of practical importance for this device.

$$l_{0.1}=1.73[\text{Log}(\text{Re})-\text{Log}(\text{D})]-\text{11.8}\text{cycles}$$ Equation 9

$$t_{0.1}=0.46{\text{Re}}^{-\text{1}}[\text{Log}(\text{Re})-\text{Log}(\text{D})-\text{36}\text{.4}]\text{s}$$ Equation 10

For a solute with D = 5×10^-11 m²/s, such as 40kDa dextran, mixing at 2 μl/s (Re = 5.6) would produce CV < 0.1 in 0.34 s after 7.5 cycles of mixing, while doubling the flow to 4μl/s would nearly halve the time to 0.18 s but only require an additional half-cycle of length. However, the increased flow rate and increased length more than double the required backpressure, from 1.4×10³ Pa to 3.0×10³ Pa, so care must be taken in choice of flow rate. For the ranges of diffusivities and flow rates used in this paper, CV < 0.1 would generally be achieved in approximately 100 ms – 1s, in fewer than 12 cycles of mixing (40 mm). CV < 0.1 is not a sufficiently stringent requirement for many applications. However, the curve of l_mix will simply shift left by one unit of Log(Pe) for every two unit reduction in target Log(CV), and mixing time will increase by an amount proportional to Re^-1.

For some applications, however, the overall device may require a specific combination of flow rate and length, such that the fluid may not be fully mixed at the end of the mixer. The actual mixing time may still be calculated based on the final fluid configuration at the end of the mixing units, and it is independent of Re.

Flow constraints may require a channel of different dimensions than those used in this paper, and variations in photolithography may cause masters made from the same mask to differ slightly. As the confocal images and COMSOL slices showed (Figure 4, a and b), minor changes in dimensions and aspect ratios do not have a large impact on the mixing performance, though calculations of Re and Pe must be adjusted to accurately reflect the channel. There is an optimum range of parameters for SHM design,^{20-22, 32, 33} and varying within those ranges will not have significant impact on mixer function, but major changes in aspect ratio, angles, or the number of grooves in a half-cycle will alter the transport of fluid across the channel and the mixing efficiency. Such modifications would alter the slope of the decrease of L̂_i, and would affect the slope of the final relationship between l_mix and Log(Pe), as well as the intercept.

For variations on the SHM, and for any similar stokes-flow chaotic advection mixer, a relationship of the form found in Equation 6 is expected. Three data points from confocal experiments or CFD modeling may be sufficient to estimate a performance curve, and possibly only two if the mixer is sufficiently similar to the SHM tested here. Equation 5 is independent of mixer type, though it does assume a Stokes-flow mixer with near-uniform residence time distribution. If the mixer is non-chaotic, dispersion is likely to be an issue, but an estimate of performance may still be attempted. Such mixers stretch fluids linearly,³⁴ and L̂_i, and the resulting relationship between l_mix and Pe, should follow a power-law. This analysis may be applied to a range of Stokes-flow mixers—chaotic, non-chaotic, or undetermined—if relative efficiency can be normalized to another measure, such as vortex number²⁷ or a more easily determined quantity.

Conclusions

The analytical model of SHM behavior yields a simple relationship between required mixing length and Pe. Simplifications introduced during the derivation, such as a uniform residence time distribution, the distance to the other side of the layer, and the exponential distribution of L̂_i may reduce the strict accuracy of the analysis. The resulting expression for required mixing length, however, matches the data relatively well, and can be used for an SHM of these dimensions with Re < 15 and Pe < 6.25×10⁵ without reservation. This analysis has the advantages that it is simple to use, and, unlike CFD and confocal experiments, is free of hard Pe limits. Theoretical analysis suggests logarithmic behavior with respect to required mixer length continues to Pe > 6.25×10⁵, but higher resolution modeling or imaging, or a precise kinetic mixing experiment, would be required to test its accuracy. With a similarly dimensioned device, a flow rate of 1 μl/s – 5 μl/s (Re = 2.7 – 14) will produce optimal mixing, reducing CV < 0.1 in 100 ms - 1 s in 5 – 12 cycles of herringbones (16 mm – 40 mm) for most solutes, making the SHM ideal for a wide range of applications.

Abbreviations used

SHM

staggered herringbone mixer ¹

CFD

computational fluid dynamics

CV

coefficient of variation = standard deviation / mean

L

a characteristic length for the definition of dimensionless groups

x

horizontal axis, orthogonal to primary flow

y

horizontal axis along mixer length, primary axis of flow

z

vertical axis, orthogonal to primary flow

u

linear flow rate along channel length (y), m/s

v

linear flow rate, across channel width (x), m/s

ρ

fluid density, 1×10³ kg/m³ for aqueous solutions

μ

dynamic viscosity, 1×10^-3 Pa·s for water

D

solute diffusivity, m²/s

p

pressure, Pa

p(n=m)

probability that a variable, n, is equal to a value, m

P(n<m)

cumulative probability that a variable, n, is less than a value, m

w

channel width (along x axis), μm

h

height of main channel (along z axis, exclusive of grooves), μm

l

mixer length (along y axis), cycles

d

length per mixing cycle, μm/cycle

a

distance in the x-z plane, orthogonal to the fluid interface

Re

Reynolds number, relates inertial forces to viscous forces, $\frac{Lu\rho }{\mu }$, where L = h

Pe

Péclet number, relates convective motion to diffusion $\frac{Lu}{D}$, where $L=\stackrel{w}{}/\underset{2}{}$

erf

the error function

L_d

distance traveled by a solute due to diffusion, ${\widehat{L}}_d=\sqrt{2Dt}$

L_i

minimum distance from a fluid element to the interface

NS

Navier-Stokes

CD

convection-diffusion