Abstract
An accurate determination of the intrinsic hydrophilicity/hydrophobicity of amino acid side-chains in peptides and proteins is fundamental in understanding many areas, including protein folding and stability, peptide and protein function, protein-protein interactions and peptide/protein oligomerization, as well as the design of protocols for purification and characterization of peptides and proteins. Our definition of intrinsic hydrophilicity/hydrophobicity of side-chains is the maximum possible hydrophilicity/hydrophobicity of side-chains in the absence of any nearest-neighbor effects and/or any conformational effects of the polypeptide chain that prevent full expression of side-chain hydrophilicity/hydrophobicity. In this review, we have compared an experimentally-derived intrinsic side-chain hydrophilicity/hydrophobicity scale generated from RP-HPLC retention behavior of de novo designed synthetic model peptides at pH 2 and pH 7 with other RP-HPLC-derived scales, as well as scales generated from classic experimental and calculation-based methods of octanol/water partitioning of Nα-acetyl-amino-acid amides or free energy of transfer of free amino acids. Generally poor correlation was found with previous RP-HPLC-derived scales, likely due to the random nature of the peptide mixtures in terms of varying peptide size, conformation and frequency of particular amino acids. In addition, generally poor correlation with the classical approaches served to underline the importance of the presence of a polypeptide backbone when generating intrinsic values. We have shown that the intrinsic scale determined here is in full agreement with the structural characteristics of amino acid side-chains.
INTRODUCTION
An accurate determination of the intrinsic hydrophilicity/hydrophobicity of amino acid side-chains in peptides and proteins is fundamental to understanding such areas as protein folding and stability, peptide and protein function, protein-protein, ligand-peptide/protein, peptide hormone-receptor or peptide-biomolecular interactions and peptide/protein oligomerization, as well as solubility, purification and characterization of peptides and proteins. It is interesting that, over the past 25 years, over 100 hydrophilicity/hydrophobicity scales for amino acid side-chains have been derived from physical properties of amino acids, peptides or organic molecules and from computational methods 1-3. However, in our judgment, none of these scales represent the intrinsic hydrophilicity/hydrophobicity of amino acid side-chains in peptides/proteins, i.e., the maximum possible hydrophilicity/hydrophobicity of side-chains in the absence of any nearest-neighbor effects and/or any conformational effects of the polypeptide chain that prevent full expression of side-chain hydrophilicity/hydrophobicity 4. Only with a knowledge of such intrinsic hydrophilicity/hydrophobicity values for all side-chains is it possible to understand all the interactions that may modify these values to affect structure and function and the fundamental properties of peptides and proteins described above.
A review by Biswas et al 2 noted how reversed-phase high-performance liquid chromatography (RP-HPLC) showed much promise as a generator of amino acid side-chain hydrophilicity/hydrophobicity scales, with Kovacs et al 4 recently designing de novo a model peptide sequence to determine by a RP-HPLC approach the intrinsic hydrophilicity and hydrophobicity of 23 amino acid side-chains, i.e., the 20 naturally occurring amino acid side-chains found in peptides and proteins plus ornithine, norvaline and norleucine. The sequence chosen was Ac-X-G-A-K-G-A-G-V-G-L-amide, where X was the substitution site and the resulting 23 peptides were subjected to RP-HPLC to determine intrinsic side-chain hydrophilicity/hydrophobicity coefficients at pH 2, pH 5 and pH 7. The coefficients were then expressed as ΔtR, where ΔtR = tR X-substituted peptide minus tR Gly-substituted peptide. The Gly-substituted peptide was used as a reference since Gly only has an hydrogen atom as its side-chain. The details of the model peptide design have been previously described 4 but the critical aspects of the sequence design were as follows: (1) the sequence should have no tendency to form any type of secondary structure (α-helix, β-sheet or β-turn) in any environment (aqueous or hydrophobic) which could restrict the interaction of the substitution site with the hydrophobic reversed-phase matrix during gradient elution; (2) nearest-neighbor effects (i to i ± 1 interactions) between the substituting residue and adjacent residues are eliminated if there is free rotation about the peptide bonds between the substituting residue and its neighbors; (3) selection of the N-terminal residue as the substitution site ensures there is no restriction of the interaction between the stationary phase and the substituted amino acid side-chain; and (4) the N-terminus was acetylated to remove any effects of the positively charged α-amino group on the hydrophilicity/hydrophobicity of the side-chain.
The goal of the present manuscript was to compare the intrinsic scale of Kovacs et al 4 determined at pH 2 and pH 7 to those scales previously determined by RP-HPLC of peptides from a variety of sources (e.g., de novo designed model peptides, random collections of peptides) and types of structure in the peptides (e.g., unstructured, random coil peptides or peptides with α-helical structure). In addition, comparisons are also made with scales determined by classic approaches such as octanol/water partitioning of Nα-acetyl-amino-acid amides, free energy of transfer of free amino acids or calculated values.
MATHEMATICAL VALIDATION OF AMINO ACID COEFFICIENTS OF KOVACS ET AL4 AS CONCENSUS (“INTRINSIC”) VALUES FOR COMPARISON WITH OTHER SCALES
As noted above, the peptides of Kovacs et al 4 were designed to generate intrinsic amino acid coefficients, where the expression of side-chain hydrophilicity/hydrophobicity was not distorted by nearest-neighbor and/or conformational (as well as polypeptide chain length effects. Any meaningful comparisons with other scales must be carried out with such intrinsic coefficients which represent full expression of side-chain hydrophilicity/hydrophobicity. A study by Tripet et al 5 subsequently examined the effect of positional differences, coupled with environmental variations, of amino acid substitutions within a peptide on expressed side-chain hydrophilicity/hydrophobicity. The sequences of the five peptide groups designed for this purpose are shown in Table I. Note that the Group 3 peptides are those of Kovacs et al. 4 In Group 1, the substitution position is at the C-terminus adjacent to a free α-carboxyl group (mainly protonated and, hence, uncharged under the acidic conditions used in the study of Tripet et al 5), while the free α-amino group has a positive charge; in Group 2, the substitution position is also at the C-terminus but adjacent to a blocked carboxyl group (Cα-amide), while the free α-amino group has a positive charge; in Group 3, both termini are blocked, with the substitution position adjacent to the N-terminus; Group 4 has the same sequence as Group 3 except for a free, positively charged free α-amino group, i.e., the positive charge is adjacent to the substitution site in the peptide; Group 5 was designed to assess any effect of amino acid substitutions towards the center, as opposed to the N- or C-terminus, of the peptide. It should be noted that all five peptide groups were designed to ensure unrestricted rotation on either side of the peptide bond between the substitution site and the adjacent residue. In addition, since the substitution site (of Groups 1-4) is the N-terminal or C-terminal residue, there is no restriction of the substituted residue for full exposure with the reversed-phase matrix; thus, any variation in expressed side-chain hydrophilicity/hydrophobicity will be a result of end effects of blocked or unblocked termini adjacent to the substitution position. Tripet et al 5 showed that there was, indeed, a variation in side-chain coefficients derived from the five peptide groups, as shown in Table II. Since there is clearly some variation in relative hydrophilicity/hydrophobicity values dependent on positional and/or end effects, it was decided that it would be useful to obtain a “concensus” opinion of the relative intrinsic hydrophilicity/hydrophobicity of each amino acid. This information could then be used to study the physical cause of any deviation from this intrinsic relative hydrophilicity/hydrophobicity in different environments. In addition, a satisfactory match of such calculated coefficients (now referred to as “latent” coefficients) with what we perceive as intrinsic RP-HPLC-derived coefficients (Group 3 in Table II) would validate our employment of these experimentally observed values for comparison with other scales.
Table I.
Synthetic Peptide Sequences
| Peptide group number | Sequencea |
|---|---|
| 1 | G A G A G V G L G X |
| 2 | G A G A G V G L G X - amide |
| 3 | Ac - X G A K G A G V G L - amide |
| 4 | X G A K G A G V G L - amide |
| 5 | L G L G X G L G L G K |
x (bolded) denotes substitution position; Ac- denotes Nα-acetyl and - amide denotes Cα-amide.
Table II.
Comparison of Calculated Latent Amino Acid Side-Chain Coefficients and RP-HPLC-Derived Amino Acid Coefficients
| Amino Acid |
Latenta Coeffs. |
Group 1b (-GX-OH) |
Group 2 (-GX-amide) |
Group 3 (Ac-XG-) |
Group 4 (NH3+-XG-) |
Group 5 (-GXG-) |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeffs.c | Normd | Norm ’e | Δ f | Coeffs. | Norm | Norm ’ | Δ | Coeffs. | Norm | Norm ’ | Δ | Coeffs. | Norm | Norm ’ | Δ | Coeffs. | Norm | Norm ’ | Δ | ||
| Trp | 100.00 | 40.0 | 100.00 | 94.49 | −5.51 | 36.5 | 100.00 | 100.98 | 0.98 | 33.2 | 100.00 | 100.77 | 0.77 | 27.9 | 100.00 | 114.50 | 14.50 | 22.9 | 100.00 | 101.14 | 1.14 |
| Phe | 90.17 | 37.0 | 92.98 | 87.71 | −2.46 | 32.9 | 90.24 | 91.30 | 1.13 | 29.6 | 89.42 | 90.17 | 0.00 | 22.3 | 80.13 | 92.23 | 2.06 | 20.6 | 91.00 | 91.61 | 1.44 |
| Leu | 73.84 | 32.2 | 81.75 | 76.84 | 3.00 | 26.0 | 71.52 | 72.74 | −1.10 | 23.7 | 72.09 | 72.80 | −1.04 | 15.8 | 57.07 | 66.37 | −7.47 | 16.8 | 76.13 | 75.86 | 2.02 |
| Ile | 69.53 | 30.5 | 77.77 | 73.00 | 3.47 | 25.2 | 69.35 | 70.59 | 1.06 | 21.8 | 66.51 | 67.20 | −2.33 | 14.2 | 51.39 | 60.01 | −9.52 | 15.3 | 70.26 | 69.65 | 0.12 |
| Met | 51.64 | 21.2 | 56.00 | 51.95 | 0.31 | 18.0 | 49.82 | 51.22 | −0.42 | 16.5 | 50.94 | 51.60 | −0.04 | 11.8 | 42.87 | 50.46 | −1.18 | 11.2 | 54.22 | 52.66 | 1.02 |
| Tyr | 47.49 | 18.9 | 50.62 | 46.74 | −0.75 | 16.4 | 45.48 | 46.92 | −0.57 | 15.6 | 48.30 | 48.95 | 1.46 | 12.8 | 46.42 | 54.44 | 6.95 | 8.2 | 42.48 | 40.23 | −7.26 |
| Val | 44.60 | 20.0 | 53.19 | 49.23 | 4.63 | 15.4 | 42.77 | 44.23 | −0.37 | 13.8 | 43.01 | 43.65 | −0.95 | 8.1 | 29.74 | 35.74 | −8.86 | 8.6 | 44.04 | 41.89 | −2.71 |
| Pro | 27.54 | 12.2 | 34.94 | 31.58 | 4.04 | 7.5 | 21.34 | 22.97 | −4.57 | 10.2 | 32.43 | 33.05 | 5.51 | 4.5 | 16.97 | 21.42 | −6.12 | 3.6 | 24.48 | 21.17 | −6.37 |
| Cys | 26.84 | 10.8 | 31.66 | 28.41 | 1.57 | 8.6 | 24.33 | 25.93 | −0.91 | 8.1 | 26.26 | 26.87 | 0.03 | 4.3 | 16.26 | 20.63 | −6.21 | 6.0 | 33.87 | 31.12 | 4.28 |
| Ala | 13.26 | 5.0 | 18.09 | 15.29 | 2.03 | 3.0 | 9.14 | 10.87 | −2.39 | 3.4 | 12.46 | 13.03 | −0.23 | 1.5 | 6.32 | 9.49 | −3.77 | 2.8 | 21.35 | 17.86 | 4.60 |
| Glu | 11.12 | 2.1 | 11.30 | 8.73 | −2.39 | 3.8 | 11.31 | 13.02 | 1.90 | 3.1 | 11.58 | 12.15 | 1.03 | 1.4 | 5.97 | 9.09 | −2.03 | 2.3 | 19.39 | 15.79 | 4.67 |
| Thr | 11.64 | 3.6 | 14.81 | 12.12 | 0.48 | 3.3 | 9.95 | 11.68 | 0.04 | 2.8 | 10.69 | 11.26 | −0.38 | 1.9 | 7.74 | 11.08 | −0.56 | 1.5 | 16.26 | 12.47 | 0.83 |
| Arg | 10.24 | 2.5 | 12.23 | 9.63 | −0.61 | 3.7 | 11.04 | 12.75 | 2.51 | 2.4 | 9.52 | 10.09 | −0.15 | 3.0 | 11.65 | 15.46 | 5.22 | −1.1 | 6.09 | 1.70 | −8.54 |
| Asp | 8.15 | 1.4 | 9.66 | 7.14 | −1.01 | 1.9 | 6.15 | 7.91 | −0.24 | 1.7 | 7.46 | 8.03 | −0.12 | 1.4 | 5.97 | 9.09 | 0.94 | 1.5 | 16.26 | 12.47 | 4.32 |
| Gln | 6.00 | 0.0 | 6.38 | 3.97 | −2.03 | 1.6 | 5.34 | 7.10 | 1.10 | 0.7 | 4.53 | 5.08 | −0.92 | 1.4 | 5.97 | 9.09 | 3.09 | 0.8 | 13.52 | 9.57 | 3.57 |
| Gly | 3.80 | 0.0 | 6.38 | 3.97 | 0.17 | 0.0 | 1.00 | 2.80 | −1.00 | 0.0 | 2.47 | 3.02 | −0.78 | 0.0 | 1.00 | 3.52 | −0.28 | 0.0 | 10.39 | 6.26 | 2.46 |
| His | 4.14 | 0.0 | 6.38 | 3.97 | −0.17 | 1.2 | 4.25 | 6.03 | 1.89 | 0.0 | 2.47 | 3.02 | −1.12 | 1.4 | 5.97 | 9.09 | 4.95 | −2.4 | 1.00 | −3.68 | −7.82 |
| Ser | 3.53 | −0.8 | 4.51 | 2.16 | −1.37 | 0.0 | 1.00 | 2.80 | −0.73 | 0.0 | 2.47 | 3.02 | −0.51 | 0.0 | 1.00 | 3.52 | −0.01 | 0.6 | 12.74 | 8.74 | 5.21 |
| Lys | 2.92 | −1.0 | 4.04 | 1.71 | −1.21 | 0.0 | 1.00 | 2.80 | −0.12 | −0.3 | 1.59 | 2.14 | −0.78 | 1.3 | 5.61 | 8.69 | 5.77 | −2.3 | 1.39 | −3.27 | −6.19 |
| Asn | 1.00 | −2.3 | 1.00 | −1.23 | −2.23 | 0.0 | 1.00 | 2.80 | 1.80 | −0.5 | 1.00 | 1.55 | 0.55 | 0.0 | 1.00 | 3.52 | 2.52 | −0.5 | 8.43 | 4.19 | 3.19 |
| Aveg | Ave. | Ave. | Ave. | Ave. | |||||||||||||||||
| 1.97 | 1.24 | 0.94 | 4.60 | 3.89 | |||||||||||||||||
Calculated coefficients derived from the five peptide groups shown in Table I by latent regression modeling (see Computational Methods for details).
The sequences of peptide Groups 1-5 are shown in Table I.
Peptide mixtures were eluted from a Kromasil C18 column (150 × 2.1 mm I.D., 5 μm particle size, 100 Å pore size) by a linear AB gradient (0.25% B/min) at a flow-rate of 0.3 ml/min and a temperature of 25°C, where eluent A was 20 mM aq. TFA containing 2% (v/v) acetonitrile and eluent B was 20 mM TFA in acetonitrile; coefficients were subsequently expressed as peptide retention time relative to the Gly-substituted peptide for that sequence.
Coefficient normalization was achieved by assigning a value of 100 and 1, respectively, to the highest and lowest RP-HPLC derived coefficients, thus being consistent with the approach to calculation of the latent coefficients.
Norm ’ denotes adjustment of the normalized coefficients of all five peptide groups to achieve a slope of 1.0 and an intercept of zero when plotted against the calculated latent coefficients (Figure 2C).
Δ denotes deviation of RP-HPLC-derived coefficients (Norm ’ values) and calculated latent coefficients.
Average of absolute Δ values.
Thus, it was attempted to parameterize the latent hydrophilicity/hydrophobicity of amino acid side-chains using a latent regression model with a Markov Chain Monte Carlo (MCMC) procedure. Briefly, latent variables, as opposed to observable variables, are variables that are not directly observed but are rather inferred from other variables that are observed and directly measured: in the present case, the variables are the position of an amino acid substitution within a peptide sequence, concomitant with a variation in environment. One advantage of using latent variables is that it reduces the dimensionality of data. A large number of observable variables (such as peptide retention times or amino acid side-chain coefficients derived from peptides of varying sequences) can be aggregated to represent an underlying concept (amino acid side-chain hydrophilicity/hydrophobicity in the current case). Thus, the question to be answered was whether there is a latent hydrophilicity/hydrophobicity of side-chains independent of sequence environment and, hence, application of this computational procedure to the peptide groups shown in Table I was carried out. Details of this procedure are reported at the end of this review and the calculated latent values (or coefficients) are shown in Table II.
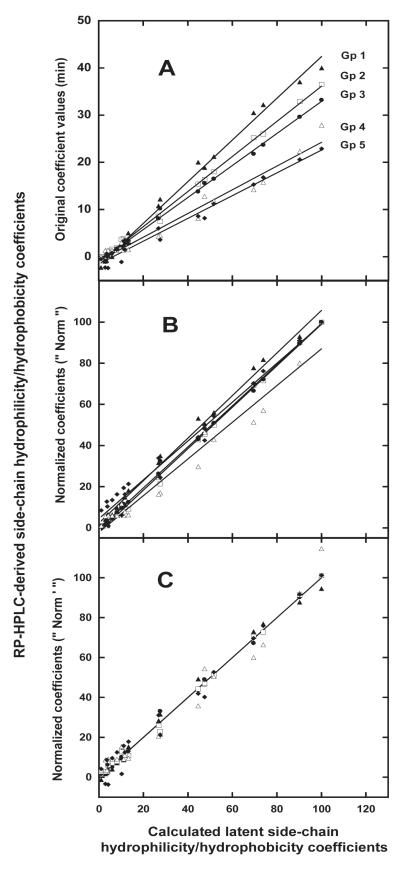
Figure 1A plots calculated latent side-chain coefficients versus the RP-HPLC-derived coefficients of peptide groups 1-5 as reported by Tripet et al 5 (Table II). From Figure 1A, there is a generally satisfactory linear relationship between calculated latent values and observed RP-HPLC-derived values, with correlations of r = 0.9968, 0.9987, 0.9988, 0.9807 and 0.9893 for Groups 1-5, respectively, the Group 3 peptides exhibiting closest correlation with the latent values. However, this approach does not provide an optimum, quantifiable assessment of deviation from latent values resulting from individual amino acid substitutions within each peptide group. Thus, the coefficients of Tripet et al 5 were then normalized in a similar way to the latent coefficients, i.e., values of 100 and 1 were assigned to the most hydrophobic and hydrophilic side-chains, respectively (values referred to as “ Norm ” in Table II). These normalized values were then plotted against the calculated latent values (Figure 1B). A best fit line with a slope of 1.0 and an intercept at zero would, of course, represent an ideal correlation between two sets of parameters. From Figure 1B, the Group 3 values were closest to this situation, with a slope (correlation) of 0.998 and an intercept of −0.545. A direct and measurable comparison of the RP-HPLC-derived values and the calculated latent values then required that the former be renormalized so that the slopes of all five plots were 1.0, with intercepts at zero, as shown in Figure 1C (renormalized values expressed in Table II as “ Norm ’ ”). From Figure 1C, data scatter around the (now) single line of the plot represents readily quantifiable deviations of the RP-HPLC-derived values from the calculated latent values (denoted as Δ in Table II), as illustrated in Figure 2.
FIGURE 1.
A: Relationship between RP-HPLC-derived amino acid hydrophilicity/hydrophobicity coefficients and calculated latent coefficients. B: Relationship between normalized (“ Norm ”) RP-HPLC-derived coefficients and calculated latent coefficients. C: Relationship between normalized (“ Norm ’ “) RP-HPLC-derived coefficients and calculated latent coefficients; the original normalized coefficients (Norm; Figure1B) have been adjusted to produce a best-fit plot whereby the slope is 1.0 and the intercept is zero for all five peptide groups. Data taken from Table II; peptide sequences shown in Table I.
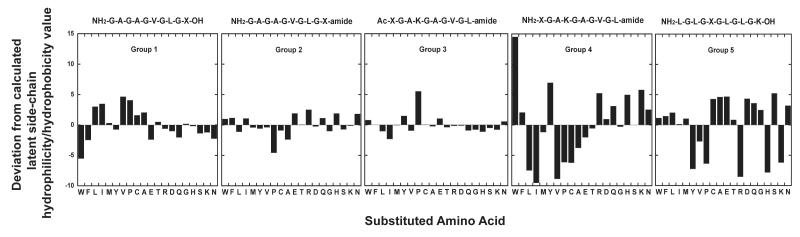
FIGURE 2.
Deviation (Δ values in Table II) normalized amino acid hydrophilicity/hydrophobicity coefficients (Norm ’ in Table II) from calculated latent coefficients (Table II) for five peptide groups.
From Figure 2, least to most deviations from latent values are observed for Group 3 < Group 2 < Group 1 << Group 5 < Group 4, highlighted by average deviations of 0.94, 1.24, 1.97, 3.89 and 4.60, respectively (Table II). The only significant deviation for Group 3 was that of Pro which, indeed, was the only amino acid substitution to show significant deviations from latent values in all five peptide groups. Pro, of course, is the only amino acid with a cyclic side-chain and, hence, may cause structural restrictions of the polypeptide backbone even in peptides designed to be random coils such as the Group 1-5 peptides.4,5 It is interesting to note that the deviation values for Pro are negative for Groups 2, 4 and 5 but positive for Groups 1 and 3. A major observation from Figure 2 is that deviations are minimized when the substitution position, X, is at the C-terminus (mainly uncharged) relative to the positively charged N-terminus (compare Groups 1 and 2 with Group 4). The effect of charge is shown even more dramatically when the substitution position is at the N-terminus with the α-amino group blocked (i.e., acetylated and, hence, uncharged; Group 3) versus unblocked (i.e., positively charged; Group 4). The substantial deviations exhibited by the Group 5 peptides (with the substitution position position internal in the peptide) is, perhaps, surprising given that position X is some distance from the free N-terminus; distant enough, at least, so that the positive charge at the N-terminus would not be expected to influence the apparent hydrophilicity/hydrophobicity of a side-chain at position X.
Overall, it is clear from Table II and Figures 1 and 2 that the Group 3 side-chain hydrophilicity/hydrophobicity coefficients are validated as the most suitable for comparison with other scales, representing accurate RP-HPLC-derived intrinsic amino acid side-chain hydrophilicity/hydrophobicity coefficients.
CRITERIA FOR EXPECTATIONS OF A HYDROPHILICITY/HYDROPHOBICITY SCALE
Prior to any comparisons of normalized hydrophilicity/hydrophobicity scales, it is important to identify expectations of such scales based on our general understanding of the structures of amino acid side-chains. For example, Ile and Val are both β-branched hydrophobic amino acid side-chains, with Ile possessing an additional CH2 group, i.e., one would expect Ile to be more hydrophobic than Val based on structure. Similarly, Ala would be expected to be more hydrophobic than Gly. Leu and Ile are isosteric but the Leu side-chain is more distant from the polypeptide backbone, i.e., more exposed to potential hydrophobic interactions in general and with an hydrophobic stationary phase in RP-HPLC and, thus, making it likely that Leu would be more hydrophobic than Ile. In addition, side-chains with functional groups would always be expected to be more hydrophobic through addition of a CH2 group in the side-chain; thus, Glu would be expected to be more hydrophobic than Asp, and Thr more hydrophobic than Ser.
Such criteria as those outlined above will be used to evaluate all scales reviewed in the present manuscript. In addition, it is our view that, if a value for a particular side-chain significantly deviates from other scales, then this value is most likely incorrect. Furthermore, if overall expectations of the value of a particular hydrophilicity/hydrophobicity scale are not met, based on the above criteria, it is our opinion that a careful evaluation of the samples used to generate the coefficients, as well as the methods used to calculate these coefficients, must be performed.
Although determination of the hydrophilicity/hydrophobicity of amino acid side-chains in random coil peptides is important (indeed, true “intrinsic” values can only be obtained from such a model), determination of such values from peptides with a defined conformation (e.g, α-helix, β-sheet) is also critical considering the ubiquitous presence of such conformations in folded proteins. However, caution must be taken since amino acid substitutions in a folded conformation can also alter this conformation and, thus, prevent the true measurement of the side-chain hydrophilicity/hydrophobicity since the hydrophobicity of the peptide as a whole is being measured with the assumption that the conformation does not change from one substitution to the next.
In the present manuscript, the scales being compared are listed in Table III, which shows the original coefficient values reported by the authors. Considering the plethora of RP-HPLC-derived scales in the literature, we chose a range of scales which we considered an excellent representation of such scales, being based as they are on, as noted above, peptides from a variety of sources and types of structure; in addition, scales derived from conditions of pH 2 (Scales 1-11) and pH 7 (Scales 12-17) are included. More classically-derived scales include coefficients obtained from partitioning of Nα-acetyl-amino-acid amides (experimental, Scale 18; calculated, Scale 19) and free energy transfer of amino acids (experimental from observation of surface tension in 0.1 M NaCl, Scale 20; calculated, Scale 21). Table IV shows sequences of model peptide sequences used to generate some of the scales shown in Table III. Since scales being compared were derived by different methods and under different conditions, normalization of the scales was needed to enable valid comparisons. Thus, the average of the values of each scale was taken as zero with a population standard deviation of 1. These normalized sets of values (Table V) were examined to determine how well they met the general expectations outlined above. Boxed values are representative coefficients derived from RP-HPLC-based approaches we believe are significantly in error compared to intrinsic values and potential explanations for such discrepancies are offered.
Table III.
Comparison of Amino Acid Side-Chain Hydrophilicity/Hydrophobicity Scales
| Random coil peptides (pH 2) | α-Helical peptides (pH2) |
Random coil peptides (pH 7) |
α-Helical peptides (pH7) |
Other approaches | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Amino Acid |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Trp | 32.4 | 32.3 | 18.1 | 15.1 | 8.8 | 16.3 | 2.29 | 5.91 | 7.1 | 1.6 | 4.88 | 33.0 | 33.7 | 14.9 | 9.5 | 7.6 | 5.1 | 2.25 | 1.88 | −2010 | 2.60 |
| Phe | 29.1 | 29.1 | 13.9 | 12.6 | 8.1 | 19.2 | 4.80 | 9.24 | 7.9 | 4.0 | 5.00 | 30.1 | 30.8 | 13.2 | 9.0 | 7.8 | 5.8 | 1.79 | 1.87 | −2330 | 2.30 |
| Leu | 23.3 | 23.4 | 10.0 | 9.6 | 8.1 | 20.0 | 3.50 | 6.57 | 8.5 | 5.0 | 4.76 | 24.6 | 25.1 | 8.8 | 9.0 | 7.6 | 7.8 | 1.70 | 1.81 | −2460 | 1.90 |
| Ile | 21.4 | 21.3 | 11.8 | 7.0 | 7.4 | 6.6 | 3.48 | 4.38 | 8.5 | 5.4 | 4.41 | 22.8 | 23.0 | 13.9 | 8.3 | 7.7 | 7.9 | 1.80 | 1.81 | −2260 | 1.90 |
| Met | 15.7 | 16.1 | 7.1 | 4.0 | 5.5 | 5.6 | 0.21 | −3.12 | 6.3 | 3.0 | 3.23 | 17.3 | 16.8 | 4.8 | 6.0 | 5.8 | 4.3 | 1.23 | 0.81 | −1470 | 2.40 |
| Tyr | 14.7 | 15.4 | 8.2 | 6.7 | 4.5 | 5.9 | 1.89 | 1.39 | 4.2 | −0.9 | 2.00 | 16.0 | 15.1 | 6.1 | 4.6 | 4.9 | −0.8 | 0.96 | 1.20 | −2240 | 1.60 |
| Val | 13.4 | 13.8 | 3.3 | 4.6 | 5.0 | 3.5 | 1.59 | 2.30 | 6.7 | 4.9 | 3.02 | 15.0 | 14.6 | 2.7 | 5.7 | 5.9 | 4.9 | 1.22 | 1.27 | −1560 | 1.50 |
| Pro | 9.0 | 9.4 | 8.0 | 3.1 | 2.0 | 5.1 | 0.71 | −0.12 | −3.9 | −5.0 | −4.92 | 10.4 | 9.9 | 6.1 | 2.2 | −2.2 | −7.2 | 0.72 | 0.95 | −980 | 1.20 |
| Cys | 7.6 | 8.1 | −2.2 | 4.6 | 2.6 | −9.2 | 0.49 | 0.73 | 4.4 | 3.0 | 2.49 | 9.1 | 8.2 | −6.8 | 2.6 | 3.8 | --- | 1.54 | 0.43 | −450 | 0.38 |
| Lys | 2.8 | −7.0 | −3.2 | −3.0 | −2.1 | −3.7 | −1.62 | −2.78 | −3.1 | −9.2 | −5.00 | −2.0 | 3.4 | 0.1 | −0.2 | −1.8 | −6.3 | −0.99 | −1.80 | −350 | −0.57 |
| Glu | 2.8 | 3.6 | −7.5 | 1.1 | 1.1 | −7.1 | −0.10 | −0.45 | 0.7 | −3.9 | −1.49 | −0.4 | −7.1 | −16.9 | −1.3 | −2.4 | −11.7 | −0.64 | −3.84 | −300 | −0.76 |
| Ala | 2.8 | 3.6 | −0.1 | 1.0 | 2.0 | 7.3 | −0.06 | 2.62 | 4.0 | 3.0 | 0.17 | 4.1 | 3.4 | 0.5 | 2.2 | 3.2 | 0 | 0.31 | 0.32 | −200 | 0.67 |
| Thr | 2.3 | 2.8 | 1.5 | −0.6 | 0.6 | 0.8 | 0.65 | 1.81 | 1.1 | 0.5 | −1.08 | 4.1 | 2.5 | 2.7 | 0.3 | 1.0 | −2.5 | 0.26 | −0.30 | −520 | 0.52 |
| Asp | 1.6 | 2.2 | −2.8 | −0.5 | 0.2 | −2.9 | −0.20 | −2.84 | −1.5 | −4.4 | −2.49 | −0.8 | −7.6 | −8.2 | −2.6 | −4.3 | −11.3 | −0.77 | −3.18 | −200 | −1.20 |
| Arg | 0.6 | −5.0 | −4.5 | −2.0 | −0.6 | −3.6 | −0.85 | 1.26 | −2.2 | −8.3 | −2.77 | 4.1 | 6.4 | 0.8 | 0.9 | −1.1 | −6.5 | −1.01 | −3.04 | −120 | −2.10 |
| Gln | 0.6 | 0.5 | −2.5 | −2.0 | 0 | −0.3 | 0.31 | −1.69 | −1.5 | −5.8 | −2.75 | 1.6 | 0 | −4.8 | 0 | −0.8 | −7.3 | −0.22 | −1.15 | 160 | −0.22 |
| His | 0 | −7.0 | 0.8 | −2.2 | −2.1 | −2.1 | −2.24 | −0.74 | −3.6 | −8.6 | −4.63 | 4.7 | 3.4 | −3.5 | 2.2 | 0.6 | −6.3 | 0.13 | 0.01 | −120 | 0.64 |
| Ser | 0 | 0 | −3.7 | −2.9 | −0.2 | −4.1 | −0.62 | −1.39 | −0.6 | −1.2 | −2.84 | 1.2 | −0.5 | 1.2 | −0.5 | −0.4 | −5.6 | −0.04 | −0.62 | −390 | 0.01 |
| Gly | 0 | 0 | −0.5 | 0.2 | −0.2 | −1.2 | 0.21 | −1.15 | 0 | 0 | −3.31 | 0 | 0 | 0 | −0.2 | 0 | −6.6 | 0 | 0 | 0 | 0 |
| Asn | −0.6 | 0 | −1.6 | −3.0 | −0.6 | −5.7 | 0.25 | −1.27 | −3.5 | −5.8 | −3.79 | 1.0 | −0.8 | 0.8 | −0.8 | −2.2 | −8.2 | −0.60 | −0.97 | 80 | −0.60 |
Kovacs et al, 2005. 4 RP-HPLC of model random-coil synthetic peptides (20 amino acid substitutions). Column: Kromasil C18 (150 × 2.1 mm I.D., 5 μm particle size, 100 Å pore size). Conditions: linear AB gradient (0.25% CH3CN/min, starting from 2% CH3CN) at a flow-rate of 0.3 ml/min, where eluent A is 20 mM aq. TFA and eluent B is 20 mM TFA in CH3CN; temperature, 25°C. Values denote change in peptide retention time relative to the Gly-substituted analog. Peptide sequences shown in Table IV.
Kovacs et al, 2005. 4 Details as Scale 1, except for 20 mM H3PO4 in place of TFA.
Meek, 1980. 8 RP-HPLC of random peptide mixture (25 peptides). Column: Bio-Rad ODS (C18). Conditions: linear AB gradient (0.75% CH3CN/min) at a flow-rate of 1.0 ml/min, where eluent A is 0.1% aq. phosphoric acid (pH 2.1) and eluent B is 0.1% phosphoric acid in CH3CN, both eluents also containing 0.1 M NaClO4; room temperature. Values obtained by repetitive regression analysis; refers to cystine in the publication.
Meek and Rossetti, 1981. 17 RP-HPLC of random peptide mixture (100 peptides). Column: Bio-Rad ODS (C18) (250 × 4.0 mm I.D., 10 μm). Conditions: linear AB gradient (0.75% CH3CN/min) at a flow-rate of 1.0 ml/min, where eluent A is 0.1 M aq. NaH2PO4 containing 0.2% H3PO4 and eluent B is 0.1 % H3PO4 in CH3CN. Values obtained by repetitive regression analysis; refers to cystine in the publication.
Guo et al, 1986. 18 RP-HPLC of model random-coil synthetic peptides (20 amino acid substitutions). Column: SynChropak RP-P C18 (250 × 4.1 mm I.D., 6.5 μm, 300 Å). Conditions: linear AB gradient (1% CH3CN/min) at a flow-rate of 1 ml/min, where eluent A is 0.1% aq TFA and eluent B is 0.1% TFA in CH3CN; temperature, 26 °C. Peptide sequences shown in Table IV. Values derived from average of simultaneous equation and “core” peptide approaches, as described in the text.
Browne et al, 1982. 22 RP-HPLC of 25 native peptides. Column: Waters μBondapak C18. Conditions: linear AB gradient (20% CH3CN/h), starting from 1.6% CH3CN) at a flow-rate of 1.5 ml/min, where eluent A is 0.1% aq TFA and eluent B is 0.1% TFA in CH3CN. Values obtained by repetitive regression analysis.
Wilce et al, 1995. 16 RP-HPLC of random peptide mixture (1738) from 2-50 amino acid residues. Column: Bakerbond WP n-octadecylsilica (C18; 250 × 4.6 mm I.D., 5 μm, 300 Å). Conditions: linear AB gradient, where eluent A is 0.1% aq. TFA and eluent B is 0.1% TFA in CH3CN (gradient rate and flow-rate not reported); temperature ca. 20°C. Values obtained by multiple linear regression analysis.
Wilce et al, 1995. 16 Details as Scale 7, except for a column of Bakerbond WP n-octylsilica (C8).
Sereda et al, 1994. 23 RP-HPLC of model amphipathic α-helical synthetic peptides (20 amino acid substitutions) (“Alα-face” helical net shown in Fig. 3). Column: Aquapore RP-300 C8 (220 × 4.6 mm I.D., 7 μm, 300 Å). Conditions: linear AB gradient (1% CH3CN/min) at a flow-rate of 1.0 ml/min, where eluent A is 0.1% aq. TFA and eluent B is 0.1% TFA in CH3CN. Values denote change in peptide retention time relative to the Gly-substituted analog. Peptide sequences shown in Table IV.
Sereda et al, 1994. 23 Details as Scale 9, except for the amino acid substitutions being made in the “Leu-face” (helical net shown in Figure 3) of the amphipathic α-helix. Peptide sequences shown in Table IV.
Liu and Deber, 1998. 25 RP-HPLC of model α-helical synthetic peptides (20 amino acid substitutions) (helical net shown in Figure 3). Column: Primesphere C4 (250 × 4.6 mm I.D. 10 μm, 300 Å). Conditions: linear AB gradient (2% CH3CN/min) at a flow-rate of 1 ml/min, where eluent A is 0.1% aq TFA and eluent B is 0.1% TFA in CH3CN. Scale obtained by assigning a value of +5 and −5 to the most hydrophobic (Phe) and most hydrophilic (Lys) amino acid residues. Peptide sequences shown in Table IV.
Kovacs et al, 2005. 4 RP-HPLC of model random-coil synthetic peptides (20 amino acid substitutions). Column: Zorbax Eclipse XDB C8 (150 × 2.1 mm I.D., 5 μm, 80 Å). Conditions: linear AB gradient (0.25% CH3CN/min) at a flow-rate of 0.3 ml/min, where eluent A is 10 mM aq. NaH2PO4 (pH 7) and eluent B is 10 mM NaH2PO4 in 50% aq. CH3CN, both eluents also containing 50 mM NaCl ; temperature, 25°C. Values denote change in retention time relative to the Gly-substituted analog. Peptide sequences shown in Table IV.
Kovacs et al, 2005. 4 Details as Scale 12, except for 50 mM NaClO4 in both eluents in place of NaCl.
Meek, 1980. 8 Details as Scale 3, except for buffer conditions where eluent A is 5 mM aq. phosphate buffer (pH 7.4) and eluent B is 5 mM phosphate buffer in 60% aq. CH3CN, each eluent also containing 0.1 M NaClO4
Guo et al, 1986. 18 Details as Scale 5, except for the buffer conditions where eluent A is 10mM aq. (NH4)2HPO4 (pH 7) and eluent B is 10mM (NH4)2HPO4 in 60% aq. CH3CN, both eluents also containing 0.1 M NaClO4. Peptide sequences shown in Table IV.
Monera et al, 1995. 24 Details as Scale 9, except for the buffer conditions where eluent A is 100 mM aq. triethylammonium phosphate (TEAP) (pH 7) and eluent B is 100 mM TEAP in 50% aq. CH3CN. Peptide sequences shown in Table IV.
Tripet et al, 2000. 26 RP-HPLC of model amphipathic α-helical synthetic peptides (20 amino acid substitutions) (helical net shown in Figure 3). Column: Zorbax Eclipse XDB-C8 (150 × 4.6 mm I.D., 5 μm, 300 Å). Conditions: linear AB gradient (1% CH3CN/min) at a flow-rate of 1 ml/min, where eluent A is 50 mM aq KH2PO4 (pH 7) and eluent B is 50 mM KH2PO4 in 50% aq. CH3CN, both eluents also containing 100 mM NaClO4; temperature 70 °C. Values denote change in peptide retention time relative to the Ala-substituted analog. Peptide sequences shown in Table IV.
Fauchere and Pliska, 1983. 48 Water/octanol partitioning of Nα-acetyl-amino-acid amides at pH 7.0 - 7.2 and room temperature. The values shown are derived from the equation: side-chain hydrophobicity = log distribution coefficient (D) (acetyl-amino-acid amide) − (acetyl-glycine amide).
Abraham and Leo, 1987. 49 Calculation of amino acid side-chain partition coefficients relative to glycine by the fragment method. Calculations are based on Nα-acetyl-amino-acid amide analogs. The values for His, Asp and Glu are based on the assumption that their side-chains are deprotonated, i.e., His is classed as polar uncharged; Asp and Glu are negatively charged.
Bull and Breese, 1974. 50 Values represent free energies of transfer of amino acids relative to glycine derived from their surface tension in 0.1 M NaCl at 30°C. Amino acid solutions were at or near the isoelectric point of the acid. Due to solubility problems, the value for Tyr is only an estimate. The greater the surface tension lowering by an amino acid, the greater its hydrophobicity and, hence, the more negative its value in this hydrophilicity/hydrophobicity scale.
Eisenberg and McLachlan, 1986. 51 Calculated values of free energy of transfer to water of amino acid residues immersed in protein (relative to glycine). The value for Cys was calculated for half-cystine.
Table IV.
Sequences of Model Synthetic Peptides
| Peptide Sequencea | Coefficient Scaleb |
|---|---|
| Random coil peptides | |
| Ac - X G A K G A G V G L - amide | 1,12,13 |
| Ac - G X X L L L K K - amide | 5,15 |
| α-Helical peptidesc | |
| Ac - E A E K A A K E X E K A A K E A E K - amide | 9,16 |
| Ac - E L E K L L K E X E K L L K E L E K - amide | 10 |
| Ac - C G G E V G A L K A E V G A L K A Q I G A X Q K Q I G A L - Q K E V G A L K K - amide |
17 |
| K K A A A X A A A A A X A A W A A X A A A K K K K - amide | 11 |
Table V.
Comparison of Normalizeda Amino Acid Side-Chain Hydrophilicity/Hydrophobicity Scales

|
Normalization method assigns the average of the coefficient values to zero and the standard deviation of the scale to one.
Descriptions of the derivations of the scales are shown in the footnotes to Table III.
From Table III, the + and − signs were reversed for the original coefficient values determined by this method compared to the other 20 approaches; for ease of comparison, the normalized Scale 20 has been adapted to conform to the other scales.
Boxed values denote significant discrepancies with the intrinsic random coil scales, 1 (pH 2) and 12 (pH 7) used for comparison.
It should be noted that although Tables III and V refer to “pH 2” (Scales 1-11) and “pH 7” (Scales 12-17) RP-HPLC conditions, such pH values are frequently either not specified by the authors of the scales or are not precisely pH 2 or pH 7. However, by experience, acidic conditions (mobile phases containing TFA or phosphoric acid are generally pH 2 +/− 0.1) and certainly assure protonation of Glu, Asp (pKa values ~ 4) and His (pKa value ~ 6) side-chains, whilst pH values around neutrality will deprotonate these side-chains.6
COMPARISON OF AMINO ACID SIDE-CHAIN HYDROPHILICITY/HYDROPHOBICITY SCALES GENERATED FROM RP-HPLC OF PEPTIDE MIXTURES
Random Coil Peptides
From Table V, there are no significant discrepancies from a structural point of view between the coefficients determined by Kovacs et al 4 at pH 2 in the presence of TFA (Scale 1) or phosphoric acid (Scale 2). The most significant differences between the two scales, i.e., the considerably lesser values for the basic residues Lys, His and Arg, are due to the hydrophilic nature of the phosphate counterion (which will interact with the positively charged side-chains of these residues) compared to the considerably more hydrophobic trifluoroacetate counterion.7
The scale of Meek 8 at pH 2 (Scale 3) contains a considerable number of deviations from expected results based on the above criteria and the intrinsic scale of Kovacs et al 4 (Scale 1; Table V). For example, Glu and Gln are determined as being less hydrophobic than Asp and Asn, respectively, despite the presence of an extra CH2 group in the side-chains of Glu and Gln; despite the greater overall exposure of the side-chain of Leu compared to the isosteric Ile (with a β-branched side-chain), the latter is determined as being more hydrophobic than the former, a result not observed in any of the other scales. In addition, Cys (noted as cystine in this scale instead of cysteine) should be more hydrophobic than Ala and Val should be more hydrophobic than Pro. These numerous discrepancies likely arise from the very small (25) pool of peptides from which these coefficients were generated coupled with a wide distribution of peptide size (2-29 residues) and amino acid distribution (ranging from only 2 Cys residues up to a high of 13 Gly and 13 Phe residues of the total number of amino acid residues present). Ideally, the distribution of each amino acid residue of the total residues present should be equal. In addition, any peptide secondary structure (induced by the hydrophobic environment of RP-HPLC 9-13) and/or conformational constraints caused by nearest-neighbor effects 14 may also affect measured coefficients, particularly in such a small sample size. Wilce et al 15, 16 noted that at least 100 retention time entries of different randomly selected peptides are required to sample the contribution of an amino acid side-chain in a suitably large number of peptide sequences. It is, thus, interesting to note that, when the sample size is increased to 100 peptides by Meek’s group 17 (Scale 4), there is a significant improvement in terms of relative side-chain hydrophilicity/hydrophobicity values according to our criteria; indeed, the worst discrepancies noted for Scale 3 are no longer apparent. Thus, in this case, an increase in sample size appears to have successfully overcome the severest problems of Scale 3 despite there still remaining a wide range of peptide size (2-62 residues) and amino acid distribution (5 Cys up to 50 Gly of the total number of amino acid residues present).
Both Scales 3 and 4 were determined by repetitive regression analysis with concomitant risks of lesser or greater weighting of side-chain coefficients depending on amino acid distribution through the samples of random collections of peptides. In contrast, Guo et al 18 (Scale 5; Table V) were the first group to determine coefficients based on substitution of the 20 amino acids into a defined model peptide sequence (Ac-Gly-X-X-(Leu)3-(Lys)2-amide). For this scale, coefficients were obtained in two ways:(1) a “core peptide” approach , where the retention time of the core peptide, Ac-Gly-(Leu)3-(Lys)2-amide), was subtracted from those of the disubstituted (at positions X-X) peptide sequences, this value then being divided by 2 to generate the side-chain coefficient for a single substituted side-chain; and (2) a simultaneous equation approach, where values for Gly, Lys and Leu were solved from retention time values for the Gly-, Lys- and Leu-substituted peptides and then used to calculate coefficients for the remaining amino acid side-chains. The final side-chain coefficients were then taken as the average of the very similar values obtained from these two approaches. Despite the generally satisfactory comparison of relative side-chain hydrophilicity/hydrophobicity obtained via this peptide model, some clear deviations were still apparent, particularly the identical values of Ala (with a moderately hydrophobic side-chain) and Pro (which should be significantly more hydrophobic than Ala). These results likely arise from the unique sequence of the model peptide, where double amino acid substitutions are made adjacent to each other. The Pro side-chain is cyclized to its N-terminal amino group which makes up part of the polypeptide backbone, coupled with the double substitution, likely causes the resulting peptide to have an unique conformation wherein the full hydrophobicity of the alkyl Pro side-chain is not expressed. It should also be noted that, despite the overall proven usefulness of this model peptide approach generally (and Scale 5 in particular) for predictive purposes 19-21, nearest-neighbor effects are undoubtedly present (double adjacent amino acid substitutions coupled with a Leu residue adjacent to the second substitution site. Hence, the recent redesign of this model peptide approach to produce genuine intrinsic coefficients (Scale 1).4
The scale of Browne et al 22 (Scale 6) in a similar manner to that of Meek 8 (Scale 3) exhibits many of the problems associated with regression analysis of the RP-HPLC retention behavior of a random collection of just 25 peptides of widely varying size (9-39 residues) and (although not reported) undoubted differences in amino acid distribution. Thus, for example, Leu was determined to have a much more hydrophobic side-chain than that of the isosteric Ile, rather than the more modest difference seen in most scales; indeed, Ile had the lowest value relative to Leu in Scale 6 compared to any other scale, lower even than Ala. Trp, the most hydrophobic residue in most scales (and certainly in terms of intrinsic hydrophobicity; Scale 1) is determined as less hydrophobic than Leu and Phe. The hydrophobic Val side-chain is unexpectedly determined in Scale 6 to be less hydrophobic than Pro and Ala. Cys, a moderately hydrophobic side-chain, is determined to be the most hydrophilic of all 20 amino acids. Glu, with an extra CH2 group in its side-chain compared to Asp, should not be characterized as less hydrophobic than the latter amino acid as it is in this scale. Also, Pro, Met and Tyr should all exhibit higher hydrophobicity values than the only moderately hydrophobic Ala.
Scales 7 and 8 offer an interesting perspective on the limitations of regression analysis of even a very large collection of random peptides (1,738 peptides ranging from 2-50 residues in size) to eliminate potential coefficient discrepancies arising from such an approach. Thus, while Scale 7 (determined from a C18 column by Wilce et al 16) shows a reasonable general correlation with our expectations for an hydrophilicity/hydrophobicity scale, discrepancies are still noted, particularly for Trp and Met, where the former should be the most hydrophobic of all 20 amino acids (and not less hydrophobic than Phe, Leu and Ile, as determined by these researchers) and the latter should be classified as one of the more hydrophobic amino acids (fifth most intrinsic hydrophobicity as seen in Scale 1) rather than being of a similar hydrophilicity/hydrophobicity to such polar amino acids as Gln, Asn and Gly as seen in the Wilce et al 16 scale. Similar, albeit more profound, problems are seen in Scale 8, generated from the same group of peptides and under the same conditions as Scale 7, but on a C8 column. Thus, similar discrepancies in the values for Trp and Met are again seen. In addition, despite its extra CH2 group compared to Asn, Gln is determined as being less hydrophobic than the former amino acid; Tyr is considerably less hydrophobic than would be expected, even compared to Scale 7 from the same authors; Ala, despite possessing only a CH3 group as its side-chain, is determined as being more hydrophobic than Val, with a CH group and two CH3 groups, as well as being considerably more hydrophobic than Pro. In addition, the value for the positively charged Arg is considerably higher than expected; higher, indeed, than any other scale. Interestingly, the often wide variations in coefficient values for the same amino acid side-chain between Scales 7 and 8 do not agree with our observations that such coefficients are independent of the stationary phase employed 4. An explanation for such discrepancies may lie in the wealth of possible selectivity variations which may occur between two stationary phases when coefficients are determined from a random collection of peptides, however large, e.g., differential induction of secondary structure between the two phases producing differences in relative peptide retention behavior. Such potential effects were eliminated/minimized in the model peptide approach to determining intrinsic hydrophilicity/hydrophobicity values described by Kovacs et al 4.
As demonstrated by Kovacs et al 4 and as shown in Table V, hydrophilicity/hydrophobicity values for neutral side-chains (i.e., 15 out of 20 amino acids) generated from random coil model peptides are essentially independent of pH and mobile phase components such as ion-pairing reagents (e.g., H3PO4, TFA, HFBA) or salts (e.g., NaCl, NaClO4) (compare intrinsic Scale 1, obtained in TFA at pH 2 with intrinsic Scales 12 and 13, obtained at pH 7 in the presence of NaCl and NaClO4, respectively). Thus, it should follow that coefficients obtained at pH 7 with the same peptide samples used at pH 2 should see little, if any, variation in values except for the potentially positively charged side-chains (Lys, His, Arg) and the potentially negatively charged side-chains (above pH ~4) (Asp and Glu) over those obtained at pH 2. Further, any significant discrepancies seen at pH 2 are likely to be repeated at pH 7. This is, indeed, shown to be generally true for both the Meek 7 (Scale 14) and Guo et al 18 (Scale 15) values obtained, as described above, from regression analysis of the RP-HPLC retention behavior of a random collection of 25 peptides (Scale 14) or a mixture of defined model peptides (Scale 15). Thus, for the scale of Meek (Scale 14), the same discrepancies in relative values are seen for Glu vs. Asp, Gln vs. Asn, Ile vs. Leu, Val vs. Pro and for Cys as were discussed above. In a similar manner, the clear discrepancies for Pro and Ala seen in the scale at pH 2 for Guo et al 18 (Scale 5) are also seen at pH 7 (Scale 15).
α-Helical Peptides
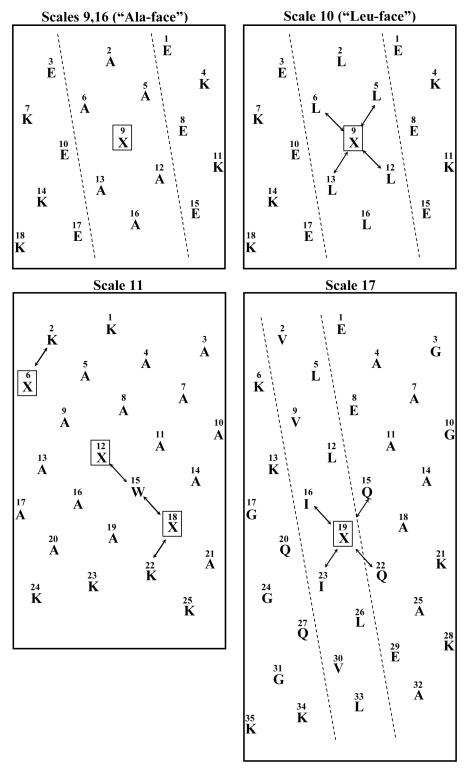
The α-helical peptide models (sequences shown in Table II) designed to determine relative hydrophilicity/hydrophobicity values of side-chains within this secondary structure are shown in Figure 1 for Scales 9 and 16 (Figure 3, top left helical net), Scale 10 (Figure 3, top right), Scale 11 (Figure 3, bottom left) and Scale 17 (Figure 3, bottom right). For Scales 9 23 and 16 24, the substitution site, X, is at the center of a wide, moderately hydrophobic face (made up of Ala residues; hence “Ala-face” model) of an amphipathic α-helix; for Scale 10 23, this substitution site is at the center of a wide, extremely hydrophobic face (made up of Leu residues; hence “Leu-face” model) of an amphipathic α-helix; for Scale 11 25, the three substitution sites are distributed throughout a non-amphipathic α-helix, mainly made up of Ala residues, plus a Trp residue; and for Scale 17 26, the substitution site is within a narrow hydrophobic face adjacent to two Ile residues. From Figure 3, the arrows in the “Leu-face” model 23 (Scale 10) denote potential i → i + 3 and i → i + 4 interactions of bulky Leu side-chains with the substituted residue. The arrows in the Liu and Deber model24 (Scale 11) denote potential i → i + 4 (with Lys 2), i → i + 3 (with Trp 15) and i → i + 4 (with Lys 22) interactions with substituted side-chains. Finally, the arrows in the Tripet et al 26 model (Scale 17) denote potential i → i + 3 and i → i + 4 interactions of bulky Ile side-chains with the substituted residue and similar interactions with polar Gln side-chains. The small size of the Ala side-chain precludes any interaction of substituted residues with surrounding Ala residues in the “Ala-face” model of Scales 9 and 16. Note that the preferred binding of these non-polar, amphipathic α-helical faces (“preferred binding domains”) to the non-polar stationary phase results in a more intimate contact of the substituted side-chains with the stationary phase than is usual when substitutions are made in a random coil peptide model or, indeed, in a non-amphipathic α—helical peptide. 9 In addition, the microenvironment surrounding the substituted side-chains is more hydrophobic, considerably so in the case of the Leu-face model (Scale 10), than would be the case for a random coil peptide model since these side-chains are surrounded by hydrophobic residues concomitant with interacting with an hydrophobic stationary phase. Indeed, such α-helical peptide models were originally designed to assess the effect of the environment characteristic of the interface of ligand-receptor interactions 23 (Scales 9 and 10), or within a protein fold 25 (Scale 11) on the apparent hydrophilicity/hydrophobicity of amino acid side-chains or the effect of different side-chains on protein stability (α-helical coiled-coil 26) (Scale 17) and, as such, will not represent intrinsic values. However, within the parameters of such secondary structure peptide models, conclusions may still be drawn about the relative merits of such models for measurement of apparent hydrophilicity/hydrophobicity within a folded polypeptide motif. For Scales 9, 10 and 16, the coefficients were expressed as ΔtR, where ΔtR = tR X-substituted peptide minus tR Gly-substituted peptide; for Scale 17, the coefficients were expressed as ΔtR, where ΔtR = tR X-substituted peptide minus tR Ala-substituted peptide. Scale 11 converted experimentally measured RP-HPLC retention times to a relative hydropathy index for the substituted residues; note that this scale was based on the “Phe” peptide and “Lys” peptide being the most hydrophobic and most hydrophilic peptides, respectively, with all side-chain coefficient values being based on these extremes.
FIGURE 3.
Helical net representations of model α-helical synthetic peptides used to determine hydrophilicity/hydrophobicity scales. Top left: sequence used in Scales 9 (Sereda et al; 23 “Ala-face”) and 16 (Monera et al 24). Top right: sequence used in Scale 10 (Sereda et al; 23 “Leu-face”). Bottom left: sequence of a non-amphipathic α-helix used in Scale 11 (Liu and Deber 25). Bottom right: sequence used in Scale 17 (Tripet et al 26). Dashed line enclosures represent the hydrophobic faces of amphipathic α-helical model peptides: the faces of the top two helices represent “wide” hydrophobic faces, whilst the helix shown at bottom right exhibits a “narrow” hydrophobic face where the helices form coiled-coils. Sites denoted with an “X” are the substitution sites; arrows denote possible interactions of adjacent residues with the substitution site(s), as discussed in the text.
From Table V, the coefficients for Trp are significantly lower than expected for all α-helical peptide models, both at pH 2 (Scales 9-11) and at pH 7 (Scales 16 and 17). It is likely that the steric bulk of the side-chain of this amino acid could disrupt the interaction of the hydrophobic preferred binding domain of these amphipathic α-helices (Figure 3) with the reversed-phase matrix, giving the perception of lower hydrophobicity.
Interestingly, Pro substitution resulted in very hydrophilic values relative to Ala in all five α-helical peptide scales (i.e., at both pH 2 and pH 7). These results can be readily explained by the known fact that Pro disrupts α-helical structure 24, 27, thus disrupting the interaction of the α-helix with the hydrophobic stationary phase matrix. Hence, what results is not a true measure of the hydrophobicity of Pro within such a peptide model.
The values for Tyr are lower than expected for Scale 10 (pH 2) and Scale 17 (pH 7). In the case of Scale 10, it was demonstrated 23 that the very hydrophobic environment of the Leu-face amphipathic α-helical peptide model (Figure 3, top right) enhanced any hydrophilic characteristics of side-chains such as the hydroxyl group of Tyr, possibly explaining the lower than expected hydrophobicity of this side-chain in this peptide model. The reason for the discrepancy in Scale 17 (pH 7) is not quite as clear, albeit an explanation may lie with the potentially extensive interactions of the Tyr (and indeed, the other aromatic side-chains of Phe and Trp) substitution with adjacent side-chains on the face of the helix, as outlined above, somehow diminishing the apparent, expressed hydrophobicity of Tyr.
Finally, a significant discrepancy of Scale 17 (pH 7) lies in the value of Glu relative to Asp, where the hydrophilicity of the negatively charged side-chain of Glu is greater than that of Asp, despite the extra CH2 group in the side-chain of the former amino acid.
OVERALL CORRELATION AND EVALUATION OF SIDE-CHAIN HYDROPHILICITY/HYDROPHOBICITY SCALES
We have chosen the Kovacs et al 4 scales at pH 2 and pH 7 to be most representative of intrinsic hydrophilicity/hydrophobicity coefficients since, as noted previously, nearest-neighbor effects have been eliminated, the peptide sequence is a random coil and the N-terminal site of substitution allows the amino acid side-chain to partition freely between the mobile phase and the stationary phase without any impediment of the remainder of the polypeptide chain. Thus, the values obtained represent the maximum hydrophilicity/hydrophobicity possible for any side-chain, a standard to which all other scales are now compared as correlation plots. If the scales do not correlate with a correlation coefficient of at least 0.90, we consider that such scales do not represent the true intrinsic hydrophilicity/hydrophobicity values of amino acid side-chains generally.
Random Coil Peptides versus Random Peptide Mixtures
Figure 4 includes an interesting demonstration of how a scale derived from a very small random collection of just 25 peptides 8 (Scale 3; Table V)) may be improved by an increase in the sample to 100 peptides 17 (Scale 4; Table V). Thus, a correlation of just 0.9208 for Scale 3 (25 peptides; not shown) versus the intrinsic values of Kovacs et al 4 (Scale 1) improved to 0.9675 for Scale 4 (100 peptides; Figure 4A). Such a result reflects the earlier observation 15, 16 that at least 100 peptide retention time entries of randomly selected peptides are required to sample the contribution of an amino acid in a suitably large number of sequences. It is interesting to note that, while Scale 3 exhibited a fairly good correlation with Scale 1 (r = 0.9208), several major discrepancies within Scale 3 were observed (Table V) as discussed above.
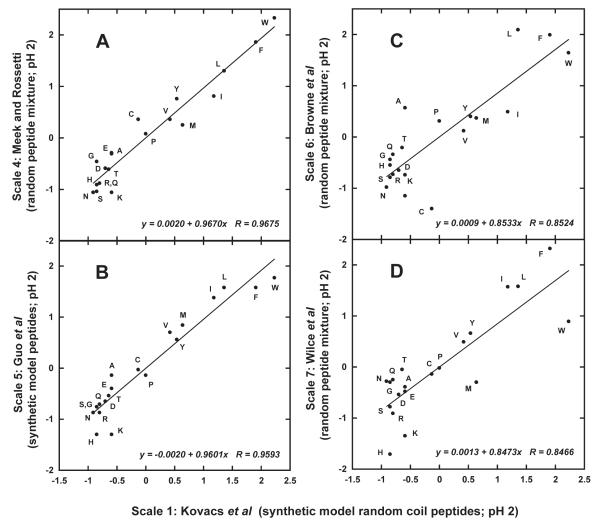
FIGURE 4.
Plot of normalized RP-HPLC-derived amino acid hydrophilicity/hydrophobicity Scales 4 (A; random peptide mixture), 5 (B; synthetic model random coil peptides), 6 (C; random peptide mixture) and 7 (D; random peptide mixture), all at pH 2, versus Scale 1 (synthetic model random coil peptides) at pH 2. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III.
The scale of Guo et al 18 (Scale 5) also produced a satisfactory correlation of 0.9593 (Figure 4B), with discrepancies likely arising from the presence of nearest-neighbor effects in the synthetic peptide model designed for this early attempt at a model peptide approach Table IV). In contrast, the poor correlation of Scale 6 (0.8524; Figure 4C) clearly highlights the large discrepancies (as noted in the discussion above) which may arise from employing a random collection of just 25 peptides 22, with a concomitant wide variation in amino acid distribution and potential secondary structure, to generate a side-chain hydrophilicity/hydrophobicity scale.
The poor correlations of Scales 7 (r = 0.8466; Figure 4D) and 8 (r = 0.7839; not shown) with the intrinsic values of Scale 1 underline the fundamental problem with linear regression calculations of even a very large collection of random peptides (a sample size of 1,738 peptides for Scales 7 and 8), supposedly designed to accommodate into the derivation of the median values of the side-chain coefficients the influence of nearest-neighbor effects on the microenvironment of a particular amino acid residue 16. Interestingly, the correlations for Scales 7 and 8 to Kovacs et al 4 (Scale 1), using 1738 peptides, were significantly below that of Scale 4 (r = 0.9675) which was generated from just 100 peptides, suggesting, perhaps, how serendipity may play a significant role in the potential accuracy of side-chain hydrophilicity/hydrophobicity coefficients derived from approaches based on collections of random peptides.
In a similar manner to where the scales determined at pH 2 were compared to the intrinsic hydrophilicity/hydrophobicity values of Scale 1, scales determined at pH 7 were now compared to an intrinsic scale of Kovacs et al 4 also determined at pH 7 (Scale 12). Figure 5A correlates intrinsic hydrophilicity scales of Kovacs et al 4, where the mobile phase contained either 50 mM NaCl (Scale 12) or 50 mM NaClO4 (Scale 13). Clearly, the correlation between the scales is very good (r = 0.9779) the only serious variations occurring due to the negatively charged Asp and Glu and the positively charged Lys. It was found by Kovacs et al 4 that the presence of NaClO4 in the mobile phase had a much greater effect on relative hydrophilicity/hydrophobicity coefficients of potentially charged side-chains than NaCl, the perchlorate anion being much more effective at ion-pairing than the chloride anion 28. Indeed, the presence of NaCl in the mobile phase served little more than as a guarantee of negligible electrostatic interactions between the peptides and the silica-based stationary phase at neutral pH 28. Thus, with the presence of NaCl (as opposed to NaClO4) having a minimal effect on observed peptide retention behavior compared to its absence 4, the coefficients of Scale 12 were chosen as our representative intrinsic values at pH 7 (note that the values for neutral side-chains are essentially independent of pH; Kovacs et al 4).
FIGURE 5.
Plot of normalized RP-HPLC-derived amino acid hydrophilicity/hydrophobicity Scales 13 (A; synthetic model random coil peptides), 15 (B; synthetic model random coil peptides) and 14 (C; random peptide mixture), all at pH 7, versus Scale 12 (synthetic model random coil peptides) at pH 7. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III.
From Figure 5B, the model peptide approach of Guo et al 18 at pH 7 (Scale 14) again achieved a good correlation (r = 0.9517, compared to a similar value of 0.9593 at pH 2) with little scatter of data points. In contrast, from Figure 5C, the Meek scale at pH 7 (Scale 14), derived from a random collection of just 25 peptides 8 shows a significant decrease in correlation (r = 0.8045) over the scale at pH 2 (Scale 3; r = 0.9208), with a significant degree of scatter about the best fit line.
Scale 2 was used for a pH 2 comparison to pH 7 conditions (Scales 12 and 13) for the synthetic random coil peptides of Kovacs et al 4 in Figure 6 since the counterion at pH 2 was phosphate, more analogous to the phosphate buffer-containing mobile phases used to generate Scales 12 and 13 than the trifluoroacetate of Scale 1. From Figure 6, correlations of Scale 2 (pH 2) with Scale 12 (with NaCl) and Scale 13 (with NaClO4) were essentially unity when potentially charged side-chains (open circles) are not included in the correlation determination, clearly confirming the aforementioned independence of intrinsic hydrophilicity/hydrophobicity values for neutral side-chains to pH variations. The deviation of the His side-chain (pKa ~6) from the plot is due to its deprotonation at neutral pH values, making it more hydrophobic compared to pH 2. This is also confirmed by the identical value for this side-chain in the presence of both NaCl (Scale 12) and the more effective ion-pairing perchlorate ion of NaClO 28 4 (Scale 13) at pH 7 (Table V). Lys and Arg also deviate from the plot, possibly due to some partial deprotonation effects at pH 7 compared to pH 2 4. Their greater hydrophobicity in Scale 12 compared to Scale 13 reflects the aforementioned more effective ion-pairing character of the negatively charged perchlorate ion (Scale 13) compared to the chloride ion (Scale 12). Asp and Glu, of course will be totally deprotonated (negatively charged) at pH 7 compared to pH 2, making them more hydrophilic at pH 7 compared to pH 2. Note the greater apparent hydrophilicity of these two side-chains in the presence of NaClO4 (Scale 13) compared to NaCl (Scale 12). Although not shown here, it is worth noting that there is a correlation of unity between Kovac et al 4 Scales 1 (pH 2, TFA) and 2 (pH 2, H3PO4) when Asp and Glu (neutral at pH 2, negatively charged at pH 7) are excluded from the plot, demonstrating, in an analogous manner to pH variations, that the hydrophilicity/hydrophobicity values of neutral side-chains are also independent of the type of counterion (the hydrophobic trifluoroacetate and hydrophilic phosphate, respectively, counterions in this case).
FIGURE 6.
Plot of normalized RP-HPLC-derived amino acid hydrophilicity/hydrophobicity Scales 12 (A; synthetic model random coil peptides) and 13 (B; synthetic model random coil peptides), both at pH 7, versus Scale 2 (synthetic model random coil peptides) at pH 2. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III.
Random Coil Peptides versus α-Helical Peptides
It would not be expected that the hydrophilicity/hydrophobicity coefficients determined from random coil peptides will equate with those determined on the surface of an α-helix, since values determined on the surface of an α-helix reflect a combined effect of single substitutions on α-helical propensity, hydrophobicity and stability which are important for understanding α-helical structure and surface interactions. Indeed, it has been well documented that a single substitution on the surface of an amphipathic α-helix has dramatic effects on α-helical structure 9, 24, 27, 29-43. An extreme example of this is the helix-disrupting effect of Pro described earlier, although other residues may have similar effects, albeit to a lesser extent based on their α-helical propensity/hydrophobicity. Thus, the coefficients derived from α-helical peptide models cannot represent intrinsic hydrophilicity/hydrophobicity effects alone but, instead, a combination of, as noted above, α-helical propensity and side-chain hydrophobicity. This is highlighted in Figure 7, where the intrinsic coefficients of Kovacs et al 4 at pH 2 (Scale 1), derived from a random coil peptide model, are plotted against the α-helical peptide-derived coefficients of Sereda et al 23 at pH 2 for Scales 9 (“Ala-face”; Figure 3, top left) and 10 (“Leu-face”; Figure 3, top right), shown in Figures 7A and 7B, respectively. Both correlations are poor, that of Scale 10 (r = 0.6543) particularly so even when compared to the poor correlation of Scale 9 (r = 0.8286). In addition to the potential effects of single amino acid substitutions on helix stability, it has been shown that the hydrophobic environment of the Leu-face model (Scale 10) magnifies the polar character of amino acid side-chains, 23 in addition to the potential for interactions (i → i + 3 and i → i + 4) between side-chains at the substitution site and the bulky Leu residues surrounding it (Figure 3). Further, there is also potential in this model for dimerization during partitioning, such dimerization being affected by the substituting amino acid and, hence, affecting its expressed side-chain hydrophilicity/hydrophobicity. 44-47
FIGURE 7.
Plot of normalized amino acid hydrophilicity/hydrophobicity Scales 9 (A; synthetic model α-helical peptides; Sereda et al, “Ala-face” 22), 10 (B; synthetic model α-helical peptides; Sereda et al, “Leu-face” 22) and 11 (C; synthetic model α-helical peptides; Liu and Deber 24), all at pH 2, versus Scale 1 (synthetic model random coil peptides; Kovacs et al 4) at pH 2. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III. Helical net representations shown in Figure 3.
In contrast to the “Leu-face” α-helical peptide model, the “Ala-face” peptides offer a model wherein no interactions of substituted side-chains can occur with the surrounding small Ala side-chains (Figure 3, top left). In addition, substituted side-chains, unlike in the “Leu-face” model, should be fully exposed to the reversed-phase matrix. Finally, it is known that the “Ala-face” peptide model does not dimerize due to the relatively low hydrophobicity of the non-polar face, particularly compared to the extremely high hydrophobicity of the “Leu-face” model non-polar face. 23 Thus, we believe that Scale 9 in Table V best represents data for hydrophilicity/hydrophobicity coefficients at pH 2 on the surface of an α-helix.
Figure 7C now plots the α-helical-peptide derived coefficients of Liu and Deber 25 (Scale 11) generated from a random coil peptide model (Figure 3, bottom left) against the intrinsic coefficients of Kovacs et al 4 (Scale 1) generated from a random coil peptide model. As expected, the correlation with Scale 1 was fairly poor (r = 0.8652) (Figure 7C) but, as is detailed below (Figure 9A), showed a much improved correlation of r = 0.9817 when compared to the α-helical-derived Scale 9 of Sereda et al. 23 It should be noted at this point that the poor correlations of the random coil-derived coefficients of Kovacs et al 4 (Scale 1) with those of the three α-helical model peptide-derived scales (Scales 9-11), coupled with the significant scattering of data points for all three scales, confirm potential discrepancies which may arise from coefficients generated from random collections of peptides which almost certainly contain peptides exhibiting various degrees of secondary structure induced by the non-polar RP-HPLC environment.
FIGURE 9.
Plot of normalized amino acid hydrophilicity/hydrophobicity Scale 11 at pH 2 (A; synthetic model α-helical peptides; Liu and Deber 25) and Scale 16 (synthetic model α-helical peptides; Monera et al, “Ala-face” 24) at pH 7 (B) versus Scale 9 (synthetic model α-helical peptides) at pH 2; Scale 17 (synthetic model α-helical peptides; Tripet et al 26) at pH 7 (C) versus Scale 16 (synthetic model α-helical peptides; Monera et al, “Ala-face” 24) at pH 7. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III. Helical net representations shown in Figure 3.
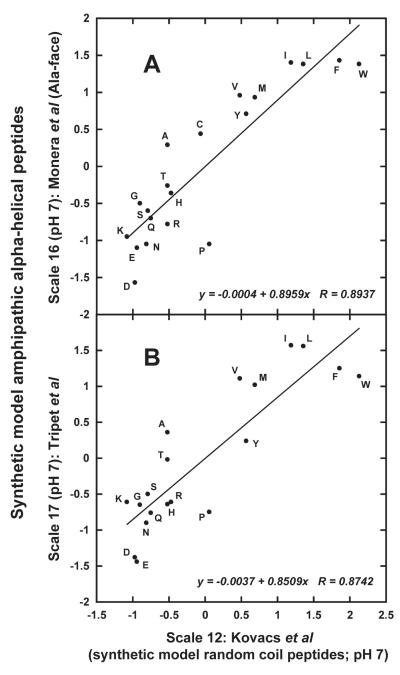
Figure 8 clearly demonstrates, in a similar fashion to that seen at pH 2 (Figure 7), that the pH 7 intrinsic coefficients of Kovacs et al 4 in the presence of NaCl (Scale 12) do not correlate well with α-helical-peptide derived scales, i.e., Scale 16 (Figure 8A; r = 0.8937) and Scale 17 (Figure 8B; r = 0.8742). In addition, at both pH 2 (Figure 7) and pH 7 (Figure 8), there is considerable scatter of data points about the best fit line for all plots.
FIGURE 8.
Plot of normalized amino acid hydrophilicity/hydrophobicity Scales 16 (A; synthetic model α-helical peptides; Monera et al, “Ala-face” 24) and 17 (B; synthetic model α-helical peptides; Tripet et al 26), both at pH 7, versus Scale 12 (synthetic model random coil peptides; Kovacs et al 4) at pH 7. Normalized data taken from Table V. Descriptions of how scales were generated shown in footnotes to Table III.
α-Helical Peptides versus α-Helical Peptides
Figure 9A shows a good correlation (r = 0.9817) between what, as noted above, we believe to be the best data to represent side-chain hydrophilicity/hydrophobicity coefficients at pH 2 on the surface of an α-helix (Scale 9) and the scale of Liu and Deber (Scale 11). Any discrepancies between the two scales likely arise from the substituted amino acid being substituted three times in this model synthetic transmembrane helix of Scale 11 with concomitant potential for i → i ± 3 and i → i ± 4 interactions along the α-helix with Lys and Trp residues (Figure 3). In addition to the effects of the three substituted side-chains on α-helix stability and conformation, such interactions could affect the side-chain hydrophilicity/hydrophobicity values (note that these would be averaged values of the three substitutions).
The scale of Monera et al 24 at pH 7 (Scale 16; Figure 3, top left, and Table IV) is based on the same “Ala-face” peptide model at pH 2 23 (Scale 9), i.e., we believe that Scale 16 could thus be the best representative scale at pH 7 for α-helical peptides. Note that, at pH 7, i → i + 3 and i → i + 4 electrostatic interactions between Lys and Glu residues on the polar face of the helix will stabilize the helix (Figure 3). Figure 9B shows a very good correlation, as expected, between the pH 2 (Scale 9) and pH 7 (Scale 16) scales derived from the “Ala-face” model (Figure 3, top left). Thus, without including His (deprotonated, i.e., neutral, at pH 7 compared to pH 2), Asp and Glu (deprotonated, i.e., negatively charged, at pH 7 compared to pH 2), the correlation coefficient was 0.9913.
When the “Ala-face” pH 7 scale of Monera et al 24 (Scale 16) is compared to the Tripet et al 26 pH 7 scale (Scale 17), the correlation is much improved to (0.9744; Figure 9C) compared to the correlation with coefficients obtained from random coil peptides (Scale 12; Figure 8B, r = 0.8742). For Scale 17, any major discrepancies from that of Monera et al 24 likely arise from i → i ± 3 and i → i ± 4 interactions along the α-helix (Figure 3, bottom right), as well as any effects of the substituting residue on the conformation and dimerizing (as a coiled-coil 26) ability of the α-helix.
Random Coil Peptides versus Non-Peptide Models
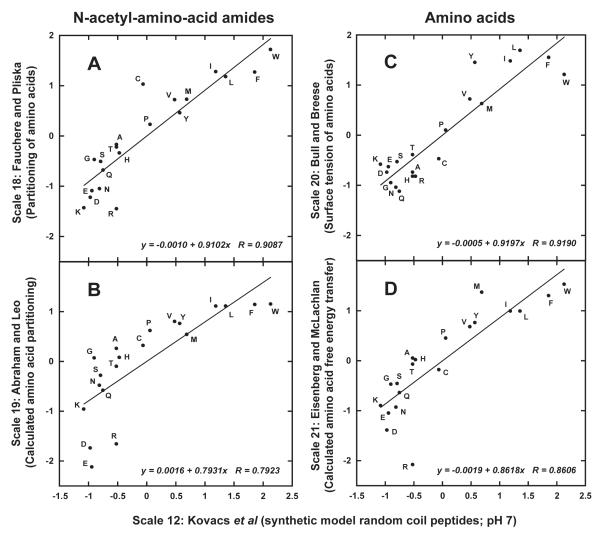
Figure 10 now compares the intrinsic coefficients of Kovacs et al 4 at pH 7 (Scale 12) with experimentally derived (Scales 18 and 20) or calculated (Scales 19 and 21) coefficients based on N-acetyl-amino-acid amides (Scales 18 and 19) or free amino acids (Scales 20 and 21). The coefficients generated from these non-peptide-derived models were explicitly (experimental Scales 18 and 20) or implicitly (calculated scales 19 and 21) obtained under neutral pH conditions; implicitly in the latter scales in the sense that calculations for potentially charged side-chains Lys, Arg, Asp and Glu were based on the assumption that these residues were in their charged forms, while His was deprotonated (i.e., uncharged). Thus, the pH 7 scale of Kovacs et al 4 was deemed the correct scale with which to make comparisons.
FIGURE 10.
Plot of normalized amino acid hydrophilicity/hydrophobicity Scales 18 (A; experimental water/octanol partitioning of Nα-acetyl-amino-acid amides), 19 (B; calculated partitioning of Nα-acetyl-amino-acid amides), 20 (C; experimental free energies of transfer of amino acids) and 21 (D; calculated free energies of transfer of amino acids) versus Scale 12 (synthetic model random coil peptides Kovacs et al 4) at pH 7. Normalized data taken from Table V. Descriptions of how scales were generated shown in Table III.
Scale 18 was based on Fauchere and Pliska’s classic experimental partitioning of Nα-acetyl-amino-acid amides between octanol and water.48 It might be expected that a relatively satisfactory correlation between this scale and that of the intrinsic coefficients (Scale 12) would be achieved since Nα-acetyl-amino-acid amides should theoretically produce an intrinsic hydrophilicity/hydrophobicity value for the completely exposed side-chain. Indeed, major discrepancies of Scale 18 compared to the intrinsic values of Scale 12 were not observed (Table V). However, the correlation of r = 0.9087 for the Fauchere and Pliska scale 48 (Scale 18) (Figure 10A), although reasonable, does suggest some significant variability from the intrinsic, peptide-based scale (Scale 12). Such variability likely arises from factors such as the absence of a polypeptide backbone 16 during the determination of Scale 18. Indeed, if the goal is to determine intrinsic hydrophilicity/hydrophobicity coefficients for extrapolation to peptide/protein systems, one might expect some effect from the polypeptide backbone and an overall non-specific effect of the peptide/protein side-chains on the intrinsic hydrophilicity or hydrophobicity of a side-chain at a particular position in the sequence. Such effects would not be encompassed in the Nα-acetyl-amino-acid amide models of Scale 18. In addition, since octanol and water are slightly miscible, the true values would be expected to be slightly in error compared to the aqueous acetonitrile system used in RP-HPLC, where the acetonitrile and water are completely miscible and the partitioning takes places between the mobile phase and the hydrophobic surface of the matrix.
Abraham and Leo 49 took an interesting approach to calculation of side-chain hydrophilicity/hydrophobicity values (termed “side-chain partition coefficients”), using a fragment method of calculating log P (where P denotes the octanol/water partition coefficient). Thus, by determining a hydrophobicity value for each atom or groups of atoms in an amino acid, the overall hydrophobicity was determined by adding each contribution of hydrophobicity (Scale 19 in Tables III and V). From Table V, in a similar manner to Scale 18, also based on (experimental) octanol/water partitioning, no major discrepancies were noted in the majority of the relative side-chain hydrophilicity/hydrophobicity rankings but the low correlation with the pH 7 intrinsic random coil peptide-based scale of Kovacs et al 4 (Scale 12) (Figure 10B; r = 0.7923) signaled that even a calculation-based partition approach of single amino acids would not produce an intrinsic scale for reasons described above (Scale 18) for an amino acid in the absence of a polypeptide backbone.
Figure 10C compares the intrinsic pH 7 scale (Scale 12) to that of Bull and Breese 50 (Table V; Scale 20), who determined a hydrophobicity scale of amino acid residues based on surface tension of free amino acid solutions, i.e., the greater the surface tension lowering of an amino acid solution, the greater its hydrophobicity. Since the amino acid solutions were at or near their respective isoelectric points, this was considered a pH 7 system for comparison. The correlation (Figure 10C) of this scale versus that of the intrinsic peptide-based pH 7 scale (Scale 12) was similar (r = 0.9190) to that of the other experimentally-derived scale (Scale 18; Figure 10A; r = 0.9087), i.e., the problem of generating an intrinsic amino acid side-chain hydrophilicity/hydrophobicity scale relevant to amino acids within polypeptides from single amino acid-based systems remains.
Finally, the same reasoning concerning the lack of a polypeptide backbone can be applied to the relatively low correlation of the scale of Eisenberg and McLachlan 51 (Scale 21) with that of intrinsic Scale 12 (r = 0.8606; Figure 10D), since this scale was essentially a calculation approach to free energy of transfer of free amino acids, mathematically taking into account the contribution of side-chains that have both apolar and polar characteristics (Trp, Tyr, Glu, Gln, Lys, Arg). On a final note, it is interesting that the two experimentally derived scales (Scale 18, r = 0.9087; Scale 20, r = 0.9190) exhibited significantly improved correlation with intrinsic scale 12 than that of their respective calculated counterparts (Scale 19, r = 0.7923; Scale 21, r = 0.8606).
CONCLUSIONS
In this study, we have compared an intrinsic side-chain hydrophilicity/hydrophobicity scale, developed from RP-HPLC retention behavior of synthetic model peptides at pH 2 and pH 7 in the absence of conformational or nearest-neighbor effects, with other scales previously determined by RP-HPLC of peptides. Poor correlation was generally seen with scales generated from RP-HPLC retention behavior of random collections of peptides, these mixtures containing peptides of varying size, conformation and frequency of particular amino acids. It was also found that side-chain coefficients generated from an α-helical peptide model (specifically, where substitutions were made in the center of the moderately non-polar face of an amphipathic α-helix) gave more accurate correlation with coefficients generated from other such models than an intrinsic hydrophilicity/hydrophobicity scale generated from a random coil peptide model. The intrinsic scale also produced poor correlations with side-chain coefficients generated from experimental and calculation-based methods of octanol/water partitioning of Nα-acetyl-amino-acid amides or free energy of transfer of free amino acids, underlining the importance of the presence of a polypeptide backbone when generating intrinsic values. The significance of an intrinsic scale, specifically the scale described in the current manuscript, lies in its full agreement with the structural characteristics of amino acid side-chains. Only a knowledge of such intrinsic values will enable an understanding of the interactions that may modify these values to affect structure, function and fundamental properties of peptides and proteins. In addition, general acceptance of a single, accurate intrinsic scale will allow a consistent comparison of results between researchers in the peptide and protein field.
COMPUTATIONAL METHODS
Latent Regression Model
The observed retention time Yij ’s of amino acid i were independently normally distributed within each of j peptide groups. The mean value was linearly modeled with respect to latent variable Xi, which represents an unobserved or latent effect of hydrophobicity of amino acid i. We refer to the model as a latent regression model with the goal of estimating the parameters of the model when Xj is unobserved. The hierarchical normal model was:
| (1) |
| (2) |
| (3) |
| (4) |
Here, τc, τα and τβ represent the precisions (the inverse of the variance) of normal distributions. We explicitly modeled the intercept and slope of hydrophobicity effects in a peptide group j with normal distributions of αj and βj, respectively. The latent variable X followed a uniform distribution with fixed boundaries of 1 and 100. αc, βc, τα, τβ, τc were given independent “noninformative” priors. Using the Brugs package in R, we implemented the model in Figure 11. Brugs is a collection of R functions that allow users to analyze graphical models using MCMC techniques.
FIGURE 11.
Computational model used in the Brugs program. The formatting of this model is according to Brugs conventions.
Model Diagnostics
Using the Brugs R package, we tested three diagnostics: trace plot, autocorrelation and Gelman-Rubin statistic. If a model has converged, the trace plot will snake around the mode of the distribution. Otherwise, some trending in the sample space will be observed. To make sure whether the chain was trapped, we used the autocorrelation function, which refers to a pattern of serial correlation in the chain. If the level of autocorrelation is high for a parameter of interest, it will take a long time to explore the entire posterior distribution. One would see a declining level of autocorrelation with an increasing number of lags in the chain. The Gelman-Rubin statistic is based on the following procedure: (1) estimate your model with a variety of different initial values and iterate for an n-iteration burn-in and an n-iteration monitored period; (2) take the n-monitored draws of m parameters and calculate the following statistics:
| (5) |
| (6) |
| (7) |
| (8) |
A 10,000 update burn-in followed by a further 10,000 updates gave the parameter estimates shown in Table VI, with the mean estimates representing latent coefficients. Note that Figure 12, which illustrates autocorrelations of three parameter types, clarifies that our model is converged.
Table VI.
Computational Estimates of Latent Amino Acid Side-Chain Hydrophilicity/Hydrophobicity
| Credible Region | ||||||
|---|---|---|---|---|---|---|
| Meana | sddev | var | 2.50% | median | 97.50% | |
| Intercept | ||||||
|
| ||||||
| alpha[1] | −1.318 | 0.4187 | 1.74E02 | −2.231 | −1.293 | −0.5699 |
| alpha[2] | −1.171 | 0.3878 | 1.61E02 | −1.938 | −1.163 | −0.4337 |
| alpha[3] | −1.171 | 0.3766 | 1.57E02 | −1.924 | −1.164 | −0.4622 |
| alpha[4] | −1.147 | 0.3681 | 1.49E02 | −1.87 | −1.141 | −0.4346 |
| alpha[5] | −1.279 | 0.3745 | 1.57E02 | −2.053 | −1.265 | −0.5887 |
|
| ||||||
| Slope | ||||||
|
| ||||||
| beta[1] | 0.4338 | 0.009797 | 2.10E04 | 0.4148 | 0.4337 | 0.4536 |
| beta[2] | 0.3733 | 0.009241 | 2.02E04 | 0.3551 | 0.3733 | 0.3916 |
| beta[3] | 0.3416 | 0.008948 | 1.98E04 | 0.3242 | 0.3415 | 0.3594 |
| beta[4] | 0.2557 | 0.008646 | 1.94E04 | 0.2386 | 0.2558 | 0.2729 |
| beta[5] | 0.2379 | 0.008586 | 2.10E04 | 0.2214 | 0.2378 | 0.2549 |
|
| ||||||
| Hydrophobicity | ||||||
|
| ||||||
| x[1](Trp) | 100 | 0 | 5.00E13 | 100 | 100 | 100 |
| x[2](Phe) | 90.17 | 2.185 | 3.23E02 | 86.01 | 90.11 | 94.6 |
| x[3](Leu) | 73.84 | 2.046 | 3.01E02 | 69.91 | 73.81 | 77.96 |
| x[4] (Ile) | 69.53 | 1.995 | 3.02E02 | 65.67 | 69.52 | 73.55 |
| x[5](Met) | 51.64 | 1.891 | 3.10E02 | 47.99 | 51.62 | 55.43 |
| x[6] (Tyr) | 47.49 | 1.865 | 3.24E 02 | 43.83 | 47.49 | 51.16 |
| x[7] (Val) | 44.6 | 1.854 | 3.26E02 | 40.97 | 44.6 | 48.25 |
| x[8](Pro) | 27.54 | 1.812 | 3.53E02 | 24.01 | 27.53 | 31.16 |
| x[9](Cys) | 26.84 | 1.806 | 3.68E02 | 23.35 | 26.84 | 30.41 |
| x[10](Ala) | 13.26 | 1.837 | 4.18E02 | 9.671 | 13.26 | 16.84 |
| x[11](Glu) | 11.12 | 1.849 | 4.36E02 | 7.513 | 11.12 | 14.75 |
| x[12](Thr) | 11.64 | 1.845 | 4.39E02 | 7.996 | 11.65 | 15.25 |
| x[13](Arg) | 10.24 | 1.851 | 4.38E02 | 6.65 | 10.23 | 13.87 |
| x[14](Asp) | 8.146 | 1.853 | 4.40E02 | 4.518 | 8.15 | 11.79 |
| x[15](Gln) | 5.996 | 1.834 | 4.40E02 | 2.452 | 5.998 | 9.619 |
| x[16](Gly) | 3.798 | 1.599 | 3.70E02 | 1.233 | 3.662 | 7.277 |
| x[17] (His) | 4.143 | 1.669 | 3.99E02 | 1.331 | 4.048 | 7.704 |
| x[18](Ser) | 3.526 | 1.538 | 3.54E02 | 1.167 | 3.36 | 6.907 |
| x[19](Lys) | 2.917 | 1.343 | 2.80E02 | 1.091 | 2.69 | 6.062 |
| x[20](Asn) | 1 | 0 | 5.00E13 | 1 | 1 | 1 |
Mean estimates taken as latent coefficients
FIGURE 12.
Autocorrelation of parameters in chain one. Autocorrelation of five alpha (intercept, A), five beta (slope B) and X (free amino acid specific mean, C) are shown.
Acknowledgment
This work was supported by a grant from the National Institutes of Health (R01 GM 61855) to R.S.H.
REFERENCES
- 1.Palliser CC, Parry DAD. Proteins: Struc Func Genet. 2001;42:243–255. doi: 10.1002/1097-0134(20010201)42:2<243::aid-prot120>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 2.Biswas KM, DeVido DR, Dorsey JG. J Chromatogr A. 2003;1000:637–655. doi: 10.1016/s0021-9673(03)00182-1. [DOI] [PubMed] [Google Scholar]
- 3.Baczek T, Kaliszan R. Proteomics. 2009;9:835–847. doi: 10.1002/pmic.200800544. [DOI] [PubMed] [Google Scholar]
- 4.Kovacs JM, Mant CT, Hodges RS. Biopolymers (Peptide Sci) 2005;84:283–297. doi: 10.1002/bip.20417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tripet B, Cepeniene D, Kovacs JM, Mant CT, Krokhin OV, Hodges RS. J Chromatogr A. 2007;1141:212–225. doi: 10.1016/j.chroma.2006.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sereda TJ, Mant CT, Quinn AM, Hodges RS. J Chromatogr. 1993;646:17–30. doi: 10.1016/s0021-9673(99)87003-4. [DOI] [PubMed] [Google Scholar]
- 7.Guo D, Mant CT, Hodges RS. J Chromatogr. 1987;386:205–222. doi: 10.1016/s0021-9673(01)94598-4. [DOI] [PubMed] [Google Scholar]
- 8.Meek JL. Proc Natl Acad Sci USA. 1980;77:1632–1636. doi: 10.1073/pnas.77.3.1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhou NE, Mant CT, Hodges RS. Peptide Res. 1990;3:8–20. [PubMed] [Google Scholar]
- 10.Blondelle SE, Ostresh JM, Houghten RA, Pérez-Payá E. Biophys J. 1995;68:351–359. doi: 10.1016/S0006-3495(95)80194-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Purcell AW, Aguilar MI, Wettenhall REW, Hearn MTW. Peptide Res. 1995;8:160–170. [PubMed] [Google Scholar]
- 12.Blondelle SE, Forood B, Pérez-Payá E, Houghten RA. Int J Biochromatogr. 1996;2:133–144. [Google Scholar]
- 13.Steer DL, Thompson PE, Blondelle SE, Houghten RA, Aguilar MI. J Peptide Res. 1998;51:401–412. doi: 10.1111/j.1399-3011.1998.tb00638.x. [DOI] [PubMed] [Google Scholar]
- 14.Kovacs JM, Mant CT, Kwok SC, Osguthorpe DJ, Hodges RS. J Chromatogr A. 2006;1123:212–224. doi: 10.1016/j.chroma.2006.04.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wilce MCJ, Aguilar MI, Hearn MTW. J Chromatogr. 1991;536:165–183. [Google Scholar]
- 16.Wilce MCJ, Aguilar MI, Hearn MTW. Anal Chem. 1995;67:1210–1219. [Google Scholar]
- 17.Meek JL, Rossetti ZL. J Chromatogr. 1981;211:15–28. [Google Scholar]
- 18.Guo D, Mant CT, Taneja AK, Parker JMR, Hodges RS. J Chromatogr. 1986;359:499–517. [Google Scholar]
- 19.Guo D, Mant CT, Taneja AK, Hodges RS. J Chromatogr. 1986;359:519–532. [Google Scholar]
- 20.Mant CT, Burke TWL, Black JA, Hodges RS. J Chromatogr. 1988;458:193–205. doi: 10.1016/s0021-9673(00)90564-8. [DOI] [PubMed] [Google Scholar]
- 21.Mant CT, Burke TWL, Zhou NE, Parker JMR, Hodges RS. J Chromatogr. 1989;485:365–382. doi: 10.1016/s0021-9673(01)89150-0. [DOI] [PubMed] [Google Scholar]
- 22.Browne CA, Bennett HPJ, Solomon S. Anal Biochem. 1982;124:201–208. doi: 10.1016/0003-2697(82)90238-x. [DOI] [PubMed] [Google Scholar]
- 23.Sereda TJ, Mant CT, Sönnichsen FD, Hodges RS. J Chromatogr A. 1994;676:139–153. doi: 10.1016/0021-9673(94)00371-8. [DOI] [PubMed] [Google Scholar]
- 24.Monera OD, Sereda TJ, Zhou NE, Kay CM, Hodges RS. J Pep Sci. 1995;1:319–329. doi: 10.1002/psc.310010507. [DOI] [PubMed] [Google Scholar]
- 25.Liu L-P, Deber CM. Biopolymers (Peptide Sci) 1998;47:41–62. doi: 10.1002/(SICI)1097-0282(1998)47:1<41::AID-BIP6>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 26.Tripet B, Wagschal K, Lavigne P, Mant CT, Hodges RS. J Mol Biol. 2000;300:377–402. doi: 10.1006/jmbi.2000.3866. [DOI] [PubMed] [Google Scholar]
- 27.Zhou NE, Monera OD, Kay CM, Hodges RS. Prot Pep Lett. 1994;1:114–119. [Google Scholar]
- 28.Shibue M, Mant CT, Hodges RS. J Chromatogr A. 2005;1080:49–57. doi: 10.1016/j.chroma.2005.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sueki M, Lee S, Powers SP, Denton JB, Konishi Y, Scheraga HA. Macromolecules. 1984;17:148–155. [Google Scholar]
- 30.Wojcik J, Altmann K-H, Scheraga HA. Biopolymers. 1990;30:121–134. doi: 10.1002/bip.360300112. [DOI] [PubMed] [Google Scholar]
- 31.Padmanabhan S, Marqusee S, Ridgeway T, Lane TM, Baldwin RL. Nature. 1990;340:268–270. doi: 10.1038/344268a0. [DOI] [PubMed] [Google Scholar]
- 32.O’Neil KT, DeGrado WF. Science. 1990;250:646–651. doi: 10.1126/science.2237415. [DOI] [PubMed] [Google Scholar]
- 33.Merutka G, Stellwagen E. Biochemistry. 1990;29:894–898. doi: 10.1021/bi00456a007. [DOI] [PubMed] [Google Scholar]
- 34.Merutka G, Lipton W, Shalongo W, Park SH, Stellwagen E. Biochemistry. 1990;29:7511–7515. doi: 10.1021/bi00484a021. [DOI] [PubMed] [Google Scholar]
- 35.Lyu PC, Liff MI, Marky LA, Kallenbach NR. Science. 1990;250:669–673. doi: 10.1126/science.2237416. [DOI] [PubMed] [Google Scholar]
- 36.Mant CT, Hodges RS. In: The Amphipathic Helix. Epand RM, editor. CRC Press, Inc.; Boca Raton, FL, USA: 1993. pp. 39–64. [Google Scholar]
- 37.Huyghues-Despointes BMP, Scholtz JM, Baldwin RL. Protein Sci. 1993;2:1604–1611. doi: 10.1002/pro.5560021006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhou NE, Kay CM, Sykes BD, Hodges RS. Biochemistry. 1993;32:6190–6197. doi: 10.1021/bi00075a011. [DOI] [PubMed] [Google Scholar]
- 39.Park SH, Shalongo W, Stellwagen E. Biochemistry. 1993;32:7048–7053. doi: 10.1021/bi00078a033. [DOI] [PubMed] [Google Scholar]
- 40.Armstrong KM, Baldwin RL. Proc Natl Acad Sci USA. 1993;90:11337–11340. doi: 10.1073/pnas.90.23.11337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Scholtz JM, Qian H, Robbins VH, Baldwin RL. Biochemistry. 1993;32:9668–9676. doi: 10.1021/bi00088a019. [DOI] [PubMed] [Google Scholar]
- 42.Chakrabartty A, Kortemme T, Baldwin RL. Protein Sci. 1994;3:843–852. doi: 10.1002/pro.5560030514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chen Y, Mant CT, Hodges RS. J Pep Res. 2002;59:18–33. doi: 10.1046/j.1397-002x.2001.10994.x. [DOI] [PubMed] [Google Scholar]
- 44.Mant CT, Chen Y, Hodges RS. J Chromatogr A. 2003;1009:29–43. doi: 10.1016/s0021-9673(03)00621-6. [DOI] [PubMed] [Google Scholar]
- 45.Mant CT, Tripet B, Hodges RS. J Chromatogr A. 2003;1009:45–59. doi: 10.1016/s0021-9673(03)00919-1. [DOI] [PubMed] [Google Scholar]
- 46.Lee DL, Mant CT, Hodges RS. J Biol Chem. 2003;278:22918–22927. doi: 10.1074/jbc.M301777200. [DOI] [PubMed] [Google Scholar]
- 47.Chen Y, Mant CT, Farmer SW, Hancock REW, Vasil ML, Hodges RS. J Biol Chem. 2005;280:12316–12329. doi: 10.1074/jbc.M413406200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fauchère J-L, Pliska V. Eur J Med Chem. 1983;4:369–375. [Google Scholar]
- 49.Abraham DJ, Leo AJ. Proteins: Struc Func Genet. 1987;2:130–152. doi: 10.1002/prot.340020207. [DOI] [PubMed] [Google Scholar]
- 50.Bull B, Breese K. Arch Biochem Biophys. 1974;161:665–670. doi: 10.1016/0003-9861(74)90352-x. [DOI] [PubMed] [Google Scholar]
- 51.Eisenberg D, McLachlan AD. Nature. 1986;319:199–203. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]